Abstract
Stochastic gradient descent is an optimisation method that combines classical gradient descent with random subsampling within the target functional. In this work, we introduce the stochastic gradient process as a continuous-time representation of stochastic gradient descent. The stochastic gradient process is a dynamical system that is coupled with a continuous-time Markov process living on a finite state space. The dynamical system—a gradient flow—represents the gradient descent part, the process on the finite state space represents the random subsampling. Processes of this type are, for instance, used to model clonal populations in fluctuating environments. After introducing it, we study theoretical properties of the stochastic gradient process: We show that it converges weakly to the gradient flow with respect to the full target function, as the learning rate approaches zero. We give conditions under which the stochastic gradient process with constant learning rate is exponentially ergodic in the Wasserstein sense. Then we study the case, where the learning rate goes to zero sufficiently slowly and the single target functions are strongly convex. In this case, the process converges weakly to the point mass concentrated in the global minimum of the full target function; indicating consistency of the method. We conclude after a discussion of discretisation strategies for the stochastic gradient process and numerical experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The training of models with big data sets is a crucial task in modern machine learning and artificial intelligence. The training is usually phrased as an optimisation problem. Solving this problem with classical optimsation algorithms is usually infeasible. Classical algorithms being gradient descent or the (Gauss–)Newton method; see Nocedal and Wright (2006). Those methods require evaluations of the loss function with respect to the full big data set in each iteration. This leads to an immense computational cost.
Stochastic optimisation algorithms that only consider a small fraction of the data set in each step have shown to cope well with this issue in practice; see, e.g., Bottou (2012), Chambolle et al. (2018) and Robbins and Monro (1951). The stochasticity of the algorithms is typically induced by subsampling. In subsampling the aforementioned small fraction of the data set is picked randomly in every iteration. Aside from a higher efficiency, this randomness can have a second effect: The perturbation introduced by subsampling can allow to escape local extrema and saddle points. This is highly relevant for target functions in, e.g., deep learning, since those are often non-convex; see Choromanska et al. (2015) and Vidal et al. (2017).
Due to the randomness in the updates, the sequence of iterates of a stochastic optimisation algorithm forms a stochastic process; rather than a deterministic sequence. Stochastic properties of these processes have been hardly studied in the literature so far; see Benaïm (1999), Dieuleveut et al. (2020) and Hu et al. (2019) for earlier studies. However, understanding these properties seems crucial for the construction of efficient stochastic optimisation methods.
In this work, we study the stochastic processes generated by the stochastic gradient descent (SGD) algorithm. More precisely, the contributions of this work are:
-
1.
We construct the stochastic gradient process (SGP), a continuous-time representation of SGD. We show that SGP is a sensible continuum limit of SGD and discuss SGP from a biological viewpoint: a model of the same type is used to model growth and phenotypes of clonal populations living in randomly fluctuating environments.
-
2.
We study the long-time behaviour of SGP: We give assumptions under which SGP with constant learning rate has a unique stationary measure and converges to this measure in the Wasserstein distance at exponential rate. In this case, SGP is exponentially ergodic. If the learning rate is decreasing to zero and additional assumptions hold, we will prove that SGP converges weakly to the Dirac measure concentrated in the global optimum.
-
3.
We discuss discretisation strategies for SGP. Those will allow us to derive practical optimisation algorithms from SGP. We also discuss existing algorithms that can be retrieved in this way.
-
4.
We illustrate and investigate the stochastic gradient process and its stationary regime alongside with stochastic gradient descent in numerical experiments.
This work is organised as follows: we introduce notation and background in the remainder of Sect. 1. In Sect. 2, we introduce the stochastic gradient process and justify our model choice. We study the long-time behaviour of SGP in Sect. 3. After discussing discretisation strategies for SGP in Sect. 4, we give numerical experiments in Sect. 5 and conclude the work in Sect. 6.
1.1 Stochastic gradient descent
Let \((X, \Vert \cdot \Vert ) := (\mathbb {R}^K, \Vert \cdot \Vert _2)\), let \(\langle \cdot , \cdot \rangle \) be the associated inner product, and let \({\mathcal {B}}X := {\mathcal {B}}(X, \Vert \cdot \Vert )\) be the Borel \(\sigma \)-algebra on X. Functions defined throughout this work will be assumed to be measurable with respect to appropriate \(\sigma \)-algebras. Let \({\bar{\varPhi }}: X \rightarrow \mathbb {R}\) be some function attaining a global minimum in X. We assume that \({\bar{\varPhi }}\) is of the form
Here, \(N \in \mathbb {N} := \{1, 2, \ldots \}\), \(N \ge 2\), and \(\varPhi _i: X \rightarrow \mathbb {R}\) is some continuously differentiable function, for i in the index set \(I := \{1,\ldots ,N\}\). In the following, we aim to solve the unconstrained optimisation problem
Optimisation problems as given in (1) frequently arise in data science and machine learning applications. Here \({\bar{\varPhi }}\) represents the negative log-likelihood or loss function of some training data set y with respect to some model. An index \(i \in I\) typically refers to a particular fraction \(y_i\) of the data set y. Then, \(\varPhi _i(\theta )\) represents the negative log-likelihood of only this fraction \(y_i\) given the model parameter \(\theta \in X\) or the associated loss, respectively.
For optimisation problems of this kind, we employ the stochastic gradient descent algorithm, which was proposed by Robbins and Monro (1951). We sketch this method in Algorithm 1. In practice, it is implemented with an appropriate termination criterion.

The elements of the sequence \((\eta _k)_{k=1}^\infty \) defined in Algorithm 1 line 2 are called step sizes or learning rates. SGD is typically understood as a gradient descent algorithm with inaccurate gradient evaluations: the inaccuracy arises since we randomly substitute \({\bar{\varPhi }}\) by some \(\varPhi _i\). If \(\lim _{k \rightarrow \infty } \eta _k = 0\) sufficiently slowly, one can show convergence for convex target functions \({\bar{\varPhi }}\); see, e.g., Jentzen et al. (2018) and Nemirovski et al. (2009). Moreover, as opposed to descent methods with exact gradients, the inexact gradients can help the algorithm escaping local extrema and saddle points in non-convex problems; see, e.g., Hu et al. (2019).
In this work, we consider gradient descent algorithms as time stepping discretisations of a certain gradient flow. The potential of this gradient flow is the respective target function \({\bar{\varPhi }}\), \(\varPhi _1, \ldots , \varPhi _N\). Thus, we refer to these target functions as potentials. In SGD, the potentials of these gradient flows are randomly switched after every time step.
We now comment on the meaning of the learning rate \(\eta _k\).
Remark 1
In the gradient flow setting, the learning rate \(\eta _k\) has two different interpretations/objectives:
-
(i)
It represents the step size of the explicit Euler method that is used to discretise the underlying gradient flow.
-
(ii)
It represents the length of the time interval in which the flow follows a certain potential \(\varPhi _{i}\) at the given iteration k, i.e. the time between two switches of potentials.
Recently, several authors, e.g. García-Trillos (2018), Kuntz et al. (2019) and Schillings and Stuart (2017), have been studying the behaviour of algorithms and methods at their continuum limit; i.e. the limit as \(\eta _j \downarrow 0\). The advantage of such a study is that numerical aspects, e.g., arising from the time discretisation can be neglected. Also, a new spectrum of tools is available to analyse, understand, and interpret the continuous system. If the continuous system is a good representation of the algorithm, we can sometimes use the results in the continuous setting to improve our understanding of the discrete setting.
Under some assumptions, a diffusion process is a good choice for a continuous-time model of SGD. Diffusion processes, such as Langevin dynamics, are traditionally used in statistical physics to represent the motion of particles; see, e.g., Section 8 in Schwabl (2006).
1.2 Diffusions and piecewise-deterministic Markov processes
Under assumptions discussed in Hu et al. (2019) and Li and Orabona (2019), one can show that the sequence of iterates of the SGD algorithm, with, say, constant \((\eta _k)_{k=1}^\infty \equiv \eta \), can be approximated by a stochastic differential equation of the following form:
Here, \(\varSigma (\theta ): X \rightarrow X\) is symmetric, positive semi-definite for \(\theta \in X\) and \(W:[0, \infty ) \rightarrow X\) is a K-dimensional Brownian motion. ‘Can be approximated’ means that as \(\eta \) goes to zero, the approximation of SGD via such a diffusion process is precise in a weak sense. In the following remark, we give a (rather coarse) intuitive explanation, how this diffusion process could be derived using the Central Limit Theorem and discretisation schemes for stochastic differential equations.
Remark 2
Let \(\eta \approx 0\). Then, for some \(k \in \mathbb {N}\), we have
The term \(\sum _{\ell =1}^{k} \frac{\nabla \varPhi _{{{\varvec{i}}}_\ell }(\theta _{0}) }{k}\) is now the sample mean of a finite sample of independent and identically distributed (i.i.d.) random variables with finite variance. Hence, by the Central Limit Theorem,
where \(\gamma _0 \sim \mathrm {N}(0, \varSigma (\theta _0))\) and the covariance matrix is given by
Then, we have
which is the first step of an Euler–Maruyama discretisation of the diffusion process in (2) with step size \(\eta k\). See, e.g., Lord et al. (2014) for details on discretisation strategies for stochastic differential equations.
The diffusion view (2) of SGD has been discussed by Li et al. (2017, 2019), Li et al. (2019) and Mandt et al. (2016, 2017). Moreover, it forms the basis of the Stochastic Gradient Langevin MCMC algorithm Mandt et al. (2017) and Welling and Teh (2011). A diffusive continuous-time version of stochastic gradient descent also arises when the underlying target functional itself contains a continuous data stream; see Sirignano and Spiliopoulos (2017) and Sirignano and Spiliopoulos (2020) this however is not the focus of the present work.
Unfortunately, the process of slowly switching between a finite number of potentials in the pre-asymptotic phase of SGD is not represented in the diffusion. Indeed, the diffusion represents an infinite amount of switches within any strictly positive time horizon. In SGD this is only the case as \(\eta _k\downarrow 0\); see Brosse et al. (2018). The pre-asymptotic phase, however, is vital for the robustness of the algorithm and its computational efficiency. Moreover, the SGD algorithm is sometimes applied with a constant learning rate; see Chee and Toulis (2018). Here, the regime \(\eta _k\downarrow 0\) is never reached. Finally, one motivation for this article has been the creation of new stochastic optimisation algorithms. Here, the switching between a finite number of potentials/data sets is a crucial element to reduce computational cost and memory complexity. Replacing the subsampling by a full sampling and adding Gaussian noise is not viable in large data applications.
In this work, we aim to propose a continuous-time model of SGD that captures the switching of the finite number of potentials. To this end we separate the two different learning rate objects: the gradient flow discretisation and the waiting time between two switches of potentials; see Remark 1 (i) and (ii) respectively. We proceed as follows:
-
1.
We let the discretisation step width go to zero and thus obtain a gradient flow with respect to some potential \(\varPhi _i\).
-
2.
We randomly replace \(\varPhi _i\) by another potential \(\varPhi _j\) after some strictly positive waiting time.
Hence, we take the continuum limit only in the discretisation of the gradient flows, but not in the switching of potentials. This gives us a continuous-time dynamic in which the randomness is not introduced by a diffusion, but by an evolution according to a potential that is randomly chosen from a finite set. This non-diffusive approach should give a better representation of the pre-asymptotic phase. Moreover, since we do not require the full potential in this dynamical system, we obtain a representation that is immediately relevant for the construction of new computational methods.
We will model the waiting times T between two switches as a random variable following a failure distribution, i.e. T has survival function
where \(t \in \mathbb {R}\), \(t_0 \ge 0\) is the current time, \(\nu : [0, \infty ) \rightarrow (0, \infty )\) is a hazard function that depends on time, and \({\mathbf {1}}[\cdot ]\) represents the indicator function: \({\mathbf {1}}[\text {true}] := 1\) and \({\mathbf {1}}[\text {false}]:=0\). We denote \(\mathbb {P}(T \in \cdot ) =: \pi _\mathrm{wt}(\cdot | t_0)\). Note that when \(\nu \) is constant, T is exponentially distributed.
Then, we obtain a so-called Markov switching process; see, e.g. Bakhtin and Hurth (2012), Benaïm et al. (2012, 2015), Cloez and Hairer (2015) and Yin and Zhu (2010). Markov switching processes are a subclass of piecewise deterministic Markov processes (PDMPs). PDMPs were first introduced by Davis (1984) as ‘a general class of non-diffusion stochastic models’; see also Davis (1993). They play a crucial role in the modelling of biological, economic, technical, and physical systems; e.g., as a model for internet traffic (Graham and Robert (2011)) or in risk analysis (Kritzer et al. (2019)). See also Sect. 2.4, where we discuss a particular biological system that is modelled by a PDMP. Furthermore, PDMPs have recently gained attention in the Markov chain Monte Carlo literature as efficient way of sampling from inaccessible probability distributions; see, e.g., Bierkens et al. (2019), Fearnhead et al. (2018) and Power and Goldman (2019).
2 From discrete to continuous
In the following, we give a detailed description of the two PDMPs that will be discussed throughout this article: One PDMP will represent SGD with constant learning rate, the other PDMP models SGD with decreasing learning rate. Then, we will argue, why we believe that these PDMPs give an accurate continuous-time representation of the associated SGD algorithms. Finally, we give a biological interpretation of the PDMPs discussed in this section.
2.1 Definition and well-definedness
Let \((\varOmega , {\mathcal {A}}, \mathbb {P})\) be a probability space on which all random variables in this work are defined. We now define two continuous-time Markov processes (CTMPs) on I \(:= \{1,\ldots ,N\}\) that will model the switching of the data sets in our PDMPs. For details on continuous-time Markov processes on finite state spaces, we refer to Anderson (1991). We start with the constant learning rate. Let \(\lambda > 0\) be a positive constant and let \({{\varvec{i}}}: \varOmega \times [0, \infty ) \rightarrow I\) be the CTMP on I with transition rate matrix
and with initial distribution \({{\varvec{i}}}(0) \sim \mathrm {Unif}(I). \) Here, \(\mathrm {Id}_I\) is the identity matrix in \(\mathbb {R}^{N \times N}\). Let \(M_t: I \times 2^I \rightarrow [0,1]\) be the Markov kernel representing the semigroup of \(({{\varvec{i}}}(t))_{t \ge 0}\), i.e.
This Markov kernel can be represented analytically by solving the associated Kolmogorov forward equation. We do this in Lemma 5 in Appendix A and show that
where \(i, i_0 \in I, t \ge 0\). Moreover, note that the waiting time between two jumps of the process \(({{\varvec{i}}}(t))_{t\ge 0}\) is given by an exponential distribution with rate \((N-1)\lambda \), i.e. \(\pi _\mathrm{wt}(\cdot | t_0) = \mathrm {Exp}((N-1)\lambda )\). The CTMP \(({{\varvec{i}}}(t))_{t\ge 0}\) will represent the switching among potentials in the SGD algorithm with constant learning rate.
Now, we move on to the case of a decreasing learning rate. Let \(\mu : [0, \infty ) \rightarrow (0,\infty )\) be a non-decreasing, positive, and continuously differentiable function, with \(\mu (t) \rightarrow \infty ,\) as \(t \rightarrow \infty \).
We define \({{\varvec{j}}}: \varOmega \times [0, \infty ) \rightarrow I\) to be the inhomogeneous CTMP with time-dependent transition rate matrix \(B: [0, \infty ) \rightarrow \mathbb {R}^{N \times N}\) given by
Again, we assume that the initial distribution \({{\varvec{j}}}(0) \sim \mathrm {Unif}(I)\). Equivalently to (5), we can compute the associated Markov transition kernel in this setting. First note that since \(({{\varvec{j}}}(t))_{t \ge 0}\) is not homogeneous in time, it is not sufficient to construct the Markov kernel with respect to the state of the Markov process at time \(t_0 = 0\). Indeed, we get a kernel of type
where \(j_0 \in I\) and \( t \ge t_0 \ge 0.\) This kernel is given by
where \(j, j_0 \in I\) and \(t \ge t_0 \ge 0\); see again Lemma 5 in Appendix A. In this case, the waiting time at time \(t_0 \ge 0\) between two jumps is distributed according to the failure distribution \(\pi _\mathrm{wt}\) in (3), with \(\nu \equiv (N-1)\mu \). The CTMP \(({{\varvec{j}}}(t))_{t\ge 0}\) represents the potential switching when SGD has decreasing learning rates.
Based on these Markov jump processes, we can now define the stochastic gradient processes that will act as continuous-time version of SGD as defined in Algorithm 1.
Definition 1
Let \(\theta _0, \xi _0 \in X\). We define
-
(i)
the stochastic gradient process with constant learning rate (SGPC) as a solution of the initial value problem
$$\begin{aligned} \frac{\mathrm {d}\theta (t)}{\mathrm {d}t}&= - \nabla \varPhi _{{{\varvec{i}}}(t)}(\theta (t)), \qquad \theta (0) = \theta _0, \end{aligned}$$(8) -
(ii)
the stochastic gradient process with decreasing learning rate (SGPD) as a solution of the initial value problem
$$\begin{aligned} \frac{\mathrm {d}\xi (t)}{\mathrm {d}t}&= - \nabla \varPhi _{{{\varvec{j}}}(t)}(\xi (t)), \qquad \xi (0) = \xi _0. \end{aligned}$$(9)
Also, we use the denomination stochastic gradient process (SGP) when referring to (i) and (ii) at the same time.
We illustrate the processes \(({{\varvec{i}}}(t))_{t \ge 0}\) and \((\theta (t))_{t \ge 0}\) in Fig. 1. We observe that SGP constructs a piecewise smooth path that is smooth between jumps of the underlying CTMP.
Cartoon of SGPC: the process \(({{\varvec{i}}}(t))_{t \ge 0}\) is a right continuous, piecewise constant process on the set I, whereas the process \((\theta (t))_{t \ge 0}\) on X is continuous and piecewise smooth. The pieces on which the processes are constant resp. smooth are identical, since the dynamic of \((\theta (t))_{t \ge 0}\) is controlled by \(({{\varvec{i}}}(t))_{t \ge 0}\). Note that, \(T_0\) is the initial time and the increments \(T_k -T_{k-1}\) are the random waiting times
In order to show that the dynamics in Definition 1 are well-defined, we require regularity assumptions on the potentials \((\varPhi _i)_{i \in I}\). After stating those, we immediately move on with proving well-definedness in Proposition 1.
Assumption 1
For any \(i \in I\), let \(\varPhi _i: X \rightarrow \mathbb {R}\) be continuously differentiable, i.e. \(\varPhi _i \in C^{1}(X; \mathbb {R})\), and let \(\nabla \varPhi _i\) be locally Lipschitz continuous.
Proposition 1
Let Assumption 1 hold. Then, the initial value problems (8) and (9) have a unique solution for \(\mathbb {P}\)-almost any realisation of the CTMPs \(({{\varvec{i}}}(t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\), and for any initial values \(\theta _0, \xi _0 \in X\). Moreover, the sample paths \(t \mapsto \theta (t)\) and \(t \mapsto \xi (t)\) are \(\mathbb {P}\)-almost surely in \(C^0([0, \infty ); X).\)
Proof
We first discuss the process \((\theta (t))_{t \ge 0}\). Let \(T_0 = 0\) and \(T_1,T_2,\ldots \) be the jump times of \(({{\varvec{i}}}(t))_{t \ge 0}\). Let \(k \in \mathbb {N}\). Note that the increments \(T_k - T_{k-1} \sim \mathrm {Exp}((N-1)\lambda )\). Hence, \(\mathbb {P}(T_k - T_{k-1} > 0) = 1\). By Assumption 1 the \((\varPhi _i)_{i=1}^N\) are locally Lipschitz continuous. Hence, the process \((\theta (t))_{t \ge 0}\) can be defined iteratively on the intervals
where \(f(x-) := \lim _{x' \uparrow x}f(x')\) and \(T_0-:= 0\). Iterative application of the Picard–Lindelöf Theorem for \(k \in \mathbb {N}\) gives unique existence of the trajectory. Picard–Lindelöf can be applied, since \(\nabla \varPhi _i\) is locally Lipschitz continuous for any \(i \in I\) by Assumption 1.
The proof for \((\xi (t))_{t \ge 0}\) is partially analogous. Importantly, we now need to make sure that
Otherwise, \(({{\varvec{j}}}(t))_{t \ge 0}\) would only be well-defined up to a possibly finite explosion time \(T_\infty :=\lim _{k\rightarrow \infty } T_k <\infty \). Under our assumptions, \(({{\varvec{j}}}(t))_{t \ge 0}\) is indeed ‘non-explosive’, we prove this in Lemma 6 in Appendix A. Moreover, let \(k \in \mathbb {N}\). Then, we have
for any \(t_{k-1} \ge 0\). This is implied by the continuous differentiability of \(\mu \). Thus, we also have
Then, as for \((\theta (t))_{t \ge 0}\) we can employ again Picard–Lindelöf iteratively to show the \(\mathbb {P}\)-a.s. well-definedness of \((\xi (t))_{t \ge 0}\).
\(\square \)
2.2 Choice of model
In this section, we reason why the dynamical systems in Definition 1 are sensible continuous-time models for SGD given in Algorithm 1 with constant, resp. decreasing learning rate.
Gradient flow. The update in line 5 of Algorithm 1 is an explicit Euler update of the gradient flow with respect to the potential \(\varPhi _i\), for some \(i \in I\). In this model, we replace this discretised gradient flow with the continuous dynamic. Hence, we replace
Uniform sampling We aim to accurately represent the uniform sampling from the index set I, given in line 4 of the algorithm. Indeed, at each point in time \(t \in [0, \infty )\), we can show that both \({{\varvec{i}}}(t) \sim \mathrm {Unif}(I)\) and \({{\varvec{j}}}(t) \sim \mathrm {Unif}(I)\).
Proposition 2
We have \(\mathbb {P}({{\varvec{i}}}(t) \in \cdot )=\mathbb {P}({{\varvec{j}}}(t) \in \cdot )= \mathrm {Unif}(I)\) for any \(t \ge 0\).
Proof
To prove this proposition, we need to show that \(\mathrm {Unif}(I)\) is stationary with respect to the Markov transition kernels \(M_t\) and \(M'_{t|t_0}\) given in (5) and (7), respectively. In particular, we need to show that
for \(i \in I\) and \(0 \le t_0 \le t.\) We show only the decreasing learning rate case, the proof for the constant learning rate proceeds analogously. A calculation gives:
for any \(i \in I\) and \(0 \le t_0 \le t\). \(\square \)
Hence, the CTMPs \(({{\varvec{i}}}(t))_{t\ge 0}, ({{\varvec{j}}}(t))_{t \ge 0}\) indeed represent the uniform sampling among the data set indices \(i \in I\).
Markov property The trajectory \((\theta _k)_{k=0}^\infty \) generated by Algorithm 1 satisfies the Markov property, i.e. the distribution of the current state given information about previous states is equal to the distribution of the current state given only information about the most recent of the previous states. By the particular structure we chose for the continuous-time processes \((\theta (t), {{\varvec{i}}}(t))_{t > 0}\) and \((\xi (t), {{\varvec{j}}}(t))_{t > 0}\), we indeed retain the Markov property.
Proposition 3
\((\theta (t), {{\varvec{i}}}(t))_{t \ge 0}\) and \((\xi (t), {{\varvec{j}}}(t))_{t \ge 0}\) are Markov processes.
Proof
This follows from the particular choice of waiting time distribution, see e.g. the discussion in Section 3 of Davis (1984). \(\square \)
Choosing random waiting times between switches allows us to analyse SGD as a PDMP. However, this choice comes at some cost. In Algorithm 1, the waiting times are all deterministic; a feature we, thus, do not represent in SGP. We briefly discuss a continuous-time version of SGD with deterministic waiting times in Remark 6 as a potential extension of the SGP framework, but do not consider it otherwise in this work. In the next two steps, we will, thus, explain how we connect the deterministic waiting times in SGD and the random waiting times in SGP.
Constant learning rate We have defined \((\theta (t))_{t \ge 0}\) as a continuous-time representation of the trajectory returned by Algorithm 1 with a constant learning rate \(\eta _k \equiv \eta \). The hazard function of the waiting time distribution of \(({{\varvec{i}}}(t))_{t \ge 0}\) is just constant \(\nu \equiv (N-1)\lambda \). The waiting time T is the time \(({{\varvec{i}}}(t))_{t \ge 0}\) remains in a certain state. Note that the hazard function satisfies
where T is a waiting time; see, e.g., Section 21 in Davis (1993). Hence, the hazard function describes the rate of events happening at time \(u \ge 0\). In SGD with constant learning rate, the waiting time is constant \(\eta \). Hence, the number of data switches in a unit interval is \(1/\eta \). Hence, we mimic this behaviour by choosing \(\lambda \) in the matrix A such that it satisfies \((N-1)\lambda = 1/\eta \). Indeed, we set \(\lambda := 1/( (N-1)\eta )\).
Decreasing learning rate Let now \((\eta _k)_{k=1}^\infty \in (0, \infty )^{\mathbb {N}}\) be a non-increasing sequence of learning rates, with \(\lim _{k \rightarrow \infty } \eta _k = 0\). Moreover, we assume that \(\sum _{k=1}^\infty \eta _k = \infty \). Similarly to the last paragraph, we now try to find a rate function \((\mu (t))_{t \ge 0}\) such that the PDMP \((\xi (t))_{t \ge 0}\) represents the SGD algorithm with the sequence of learning rates \((\eta _k)_{k=1}^\infty \). To go from discrete time to continuous time, we need to define a function H that interpolates the sequence of learning rates \(\eta _k\), i.e. \(H:[0,\infty ) \rightarrow (0, \infty )\) is a non-increasing, continuously differentiable function, such that
where the \(t_k\) are chosen like this, since the \(\eta _k\) themselves represent the time stepsizes in the sequence of learning rates. H could for instance be chosen as a sufficiently smooth interpolant between the \(\eta _k\). Equivalently to the case of the constant learning rate, we now argue via the hazard function of the waiting time distribution \(\nu (t) := (N-1) \mu (t)\) \((t \ge 0)\) that \(\mu (t) := 1/((N-1)H(t))\) \((t \ge 0)\) is a reasonable choice for the waiting time distribution.
Approximation of the exact gradient flow We now consider SGD, i.e. Algorithm 1. If the learning rate \(\eta \downarrow 0\), we discretise the gradient flow precisely. Moreover, the waiting time between two data switches goes to zero. Hence, intuitively we switch the data set infinitely often in any finite time interval. By the Law of Large Numbers, we should then anticipate that the limiting process behaves like the full gradient flow
with initial value \(\zeta (0) = \zeta _0 :=\theta _0\) as chosen in SGPC and \({\bar{\varPhi }}:= \sum _{i=1}^N \varPhi _i/N\) being the full potential. This behaviour can also be seen in the diffusion approximation to SGD (2), where the stochastic part disappears as \(\eta \downarrow 0\).
So we should now show that this is also true for SGPC. Indeed, we will give assumptions under which the SGPC \((\theta (t))_{t \ge 0}\) converges weakly to \((\zeta (t))_{t \ge 0}\), as \(\eta \downarrow 0\). Weak convergence of \((\theta (t))_{t \ge 0}\) to \((\zeta (t))_{t \ge 0}\) means that
for any bounded, continuous function F mapping from \(C^0([0, \infty ); X)\) to \(\mathbb {R}.\) Here, \(C^0([0, \infty ); X)\) is equipped with the supremum norm \(\Vert f\Vert _\infty := \sup _{t \in [0, \infty )}\Vert f(t)\Vert \). We denote weak convergence by \((\theta (t))_{t \ge 0} \Rightarrow (\zeta (t))_{t \ge 0}\).
To show weak convergence, we need some stronger smoothness assumption concerning the potentials \(\varPhi _i\). We denote the Hessian of \(\varPhi _i\) by \(\mathrm {H} \varPhi _i\) for \(i \in I\).
Assumption 2
For any \(i \in I\), let \(\varPhi _i \in C^2(X; \mathbb {R})\) and let \(\nabla \varPhi _i, \mathrm {H}\varPhi _i\) be continuous.
Please note that Assumption 1 is already implied by Assumption 2.
Theorem 1
Let \(\theta _0= \zeta _0\) and let Assumption 2 hold, then the stochastic gradient process \((\theta (t))_{t \ge 0}\) converges weakly to the full gradient flow \((\zeta (t))_{t \ge 0}\), as the learning rate \(\eta \downarrow 0\); i.e. \( (\theta (t))_{t \ge 0} \Rightarrow (\zeta (t))_{t \ge 0}\), as \(\eta \downarrow 0\).
We prove Theorem 1 rigorously in Sect. 2.3. We illustrate the shown result in Fig. 2, where we can see that indeed as \(\eta \) decreases, the processes converge to the full gradient flow.
Exemplary realisations of SGPC for potentials \(\varPhi _1(\theta ) := (\theta -1)^2/2\) and \(\varPhi _2(\theta ) := (\theta +1)^2/2\) and learning rates \(\eta \in \{0.001, 0.01, 0.1, 1 \}\) and a plot of the full gradient flow corresponding to \({\bar{\varPhi }}:= \varPhi _1/2 + \varPhi _2/2\). The latter has 0 as a stationary point. The ODEs are solved with ode45 in Matlab - an explicit high-order Runge-Kutta method with adaptive discretisation step size
Following our reasoning above, we assert that SGPC, resp. SGPD, are suitable continuous-time representations of SGD with constant, resp. decreasing, learning rate.
2.3 Proof of Theorem 1
We prove Theorem 1 using the perturbed test function theory. In particular, we apply a result from Kushner (1984) that we summarise below. We note that a similar technique is used to derive the Infinite Swapping Markov Chain Monte Carlo technique; see Dupuis et al. (2012) for details from the statistical mechanics viewpoint and Latz et al. (2020) for the discrete-time MCMC viewpoint. In the following, we adapt the notation of Kushner (1984).
Let \((\xi ^{\varepsilon }(t))_{t \ge 0}\) be a right-continuous stochastic process on \(Y \subseteq \mathbb {R}^{L}\) that depends on \(\varepsilon > 0\). Moreover, let \(G: X \times Y \rightarrow X\) and \({\bar{G}}: X \rightarrow X\) be vector fields on X. Moreover, let \(x_0, x_0^{\varepsilon } \in X\). Let now \((x^{\varepsilon }(t))_{t \ge 0}\) be the stochastic process generated by
Moreover, let \((x(t))_{t \ge 0}\) solve the following ODE:
We will now give assumptions under which \((x^{\varepsilon }(t))_{t \ge 0} \Rightarrow (x(t))_{t \ge 0}\) as \(\varepsilon \downarrow 0\).
Assumption 3
We consider the following three assumptions:
-
(i)
Let G and \(\nabla _x G\) be continuous and bounded on \(X' \times Y\), where \(X' \subseteq X\) is bounded,
-
(ii)
let \({\bar{G}}: X \rightarrow X\) be continuously differentiable and let for any \(0 \le {\underline{t}}< {\overline{t}} < \infty \) and \( x \in X\):
$$\begin{aligned} \int _{{\underline{t}}}^{{\overline{t}}} \mathbb {E}[G(x, \xi ^{\varepsilon }(s)) - {\bar{G}}(x)| \{\xi ^{\varepsilon }(s') : s' \le {\underline{t}} \}] \mathrm {d}s \rightarrow 0, \end{aligned}$$in probability, as \(\varepsilon \downarrow 0\), and
-
(iii)
let \((\xi ^{\varepsilon }(t))_{t \ge 0}\) be tight with respect to \(\varepsilon \).
The associated result reads then:
Theorem 2
(Kushner 1984) Let Assumption 3 (i)–(iii) hold. Moreover, let \(x_0^{\varepsilon } \Rightarrow x_0\), as \(\varepsilon \downarrow 0\). Then, \((x^{\varepsilon }(t))_{t \ge 0} \Rightarrow (x(t))_{t \ge 0}\), as \(\varepsilon \downarrow 0\).
Proof
The proof uses the perturbed test function method; see (Kushner 1984, Theorem 4.1). \(\square \)
To prove Theorem 1, we now show that Assumption 3 (i)-(iii) hold for SGPC. Then, Theorem 2 will imply weak convergence.
Proof of Theorem 1
We commence by transferring the SGPC set-up into the framework employed in this subsection. Let \({\bar{G}} := \nabla {\bar{\varPhi }}\), \(Y:= [0,1]^N\), and \(G(\theta , w) := \sum _{i=1}^N w_i\nabla \varPhi _i(\theta )\). Moreover, we define \(\varepsilon := 1/\lambda \) and \(\xi ^{\varepsilon }(t) := e_{{{\varvec{i}}}(t)}\), where \(e_i\) is the i-th unit-vector in Y. Then, we have \(\nabla \varPhi _{{{\varvec{i}}}(t)} = G(\cdot , \xi ^{\varepsilon }(t))\). Assumption 3(i) is now immediately implied by Assumption 2; note that any continuous function on \(X =\mathbb {R}^K\) is bounded on a bounded subset of X. The tightness in Assumption 3(iii) follows from \((\xi ^{\varepsilon }(t))_{t \ge 0}\) being a càdlàg process taking values in the finite set \(\{e_i : i \in I \}\); see Theorem 16.8 from Billingsley (1999). To show Assumption 3(ii), we employ the explicit representation of the transition kernel \(M_t\) of \(({{\varvec{i}}}(t))_{t \ge 0}\) given in (5). Since \((\xi ^{\varepsilon }(t))_{t \ge 0}\) is a Markov process and homogeneous in time, we assume without loss of generality that \({\underline{t}} = 0\). Let now \(i_0 \in I\). Then, we have for \(s \in [0, {\overline{t}}]\) the following expression for the conditional expectation:
Now we integrate the resulting function on \([0, {\overline{t}}]\):
as \(\varepsilon \downarrow 0\). Since \(i_0\) was arbitrary, we have
almost surely, as \(\varepsilon \downarrow 0\), which implies Assumption 3(ii). Finally, we note that \(\theta (0) = \zeta (0)\), hence: \(x_0^\varepsilon = x_0\), for \(\varepsilon > 0\). \(\square \)
2.4 Stochastic gradient descent in nature
PDMPs are popular models for random or uncertain processes in biological systems; see Chapter 1 of Rudnicki and Tyran-Kamińska (2017) for an overview. In the following, we briefly discuss a biological system that is modelled by a dynamical system that corresponds to the SGP. This model was proposed by Kussell and Leibler (2005). The modelled biological system contains clonal populations that diversify to survive in randomly fluctuating environments.
Diversified bet-hedging In the following, we consider clonal populations, such as bacteria or fungi, that live in fluctuating environments, i.e., environments that are subject to temporal change. Examples are the fluctuation of temperature and light during the day-night-cycle or a different supply of nutrients; see Ardaševa et al. (2019) and Canino-Koning et al. (2019). We define the set of environments to be \(I := \{1,\ldots ,N\}\). Here, populations typically adapt their phenotypes to retain a high fitness in any environment. If the fluctuations within I are irregular or even random, the organisms in a population cannot adapt to the changes in the environment sufficiently fast; see, e.g., Kussell and Leibler (2005). To prevent extinction and retain high fitness in such fluctuating environments, some populations employ so-called diversified bet-hedging strategies; see, e.g., Haccou and Iwasa (1995), Olofsson et al. (2009), Sasaki and Ellner (1995) and Simovich and Hathaway (1997). That means, rather than relying on homogeneous switching of phenotypes in the population, the population has heterogeneous phenotypes that are developed and switched based on the current environment \(i \in I\) or even completely randomly.
A PDMP model. Next, we briefly explain the way Kussell and Leibler (2005) model the growth of this population and the phenotype distribution among its individuals. Indeed, there is a set of N phenotypes, which will be identical to I. Indeed, the i-th phenotype is the one with the highest fitness in environment i, for \(i \in I\). The fluctuation between environments is modelled by a CTMP \(({{\varvec{i}}}(t))_{t \ge 0}\) on I with a certain transition matrix. Let \(\theta _0 \in X := \mathbb {R}^N\). Here, the i-th component \(\theta ^{(i)}_0\) of \(\theta _0\) describes the number of organisms in the population having phenotype \(i \in I\). Given we are currently in environment \(k \in I\), we assume that organisms with phenotype i grow at a rate \(f^{(k)}_i \ge 0\) and that organisms switch from phenotype i to j at rate \(H_{j,i}^{(k)}\). Knowing this, we define
where \(H_{i,i}^{(k)} = - \sum _{j \in I \backslash \{i\}}^N H_{j,i}\), for \(i \in I\). Given an initial vector \(\theta _0 \in (0, \infty )^N\) of phenotypes, we can now model the amount of organisms with a particular phenotype via the dynamical system
The dynamical system (12) is a Markov switching process closely related to SGP. Indeed, we have a homogeneous ODE the right-hand side of which is switched according to a CTMP.
The different environments in the population model represent the different subsamples of the data set that are trained with SGP. While the population aims to reach a high fitness in the current environment, SGP aims to optimise an underlying model with respect to the partition of the data set that is currently subsampled. Overall, SGP aims at solving a certain optimisation problem. In general there is not ad hoc an equivalent optimisation problem in the population dynamic: Positive growth rates \((f^{(k)})_{k \in I}\) should lead to
as \(t \rightarrow \infty \). Moreover, the flows in (12) are likely no gradient flows with underlying scalar potential. However, diversified bet-hedging strategies also overall aim at long-term high fitness; see Olofsson et al. (2009). Hence, both, SGP and diversified bet-hedging aim to enhance a system by enhancing this system in randomly switching situations. Therefore, we believe that bet-hedging gives a good background for interpreting SGP.
3 Long-time behaviour
PDMPs have been subject of extensive studies throughout the last decades, ever since they were introduced by Davis (1984). Many of the results derived in the past also apply to SGP. Hence, the PDMP view of SGD gives us access to a large set of analytical tools. Those allow us to study mixing properties or the long-time behaviour of the algorithm, such as convergence to stationary distributions and ergodicity.
In the following, we will use tools provided by Bakhtin and Hurth (2012), Benaïm et al. (2012), Benaïm et al. (2015), Cloez and Hairer (2015) and Kushner (1984) to study the long-time behaviour of SGP. Indeed, we will give assumptions under which the processes generated by SGPC and SGPD have a unique stationary measure and are ergodic or exponentially ergodic. For SGPD, we discuss especially the convergence to the minimum of \({\bar{\varPhi }}\). After proving our assertions, we discuss the required assumptions regarding linear least squares estimation problems.
3.1 Preliminaries
We collect some notation and basic facts that will be required in the following. First, we define a distance measure on X for some \(q \in (0,1]\):
Note that \(d'\) is a metric on X and \((X, d')\) forms a Polish space, i.e. it is separable and complete. Let \(\pi , \pi '\) be two probability measures on \((X, {\mathcal {B}}X)\). We define the Wasserstein(-1) distance between those measures by
where \(\mathrm {Coup}(\pi , \pi ')\) is the set of couplings of \(\pi , \pi '\). This is the set of probability measures H on \((X \times X, {\mathcal {B}}X \otimes {\mathcal {B}}X)\), with \(H(\cdot \times X) = \pi \) and \(H(X \times \cdot ) = \pi '\). Note that due to the boundedness of \(d'\), the distance \({\mathrm {W}_q}\) is well-defined for any two \(\pi , \pi '\) probability measures on \((X, {\mathcal {B}}X)\). Indeed, the boundedness of \(d'\) also implies that convergence in \({\mathrm {W}_q}\) is equivalent to weak convergence on \((X, {\mathcal {B}}X)\). Finally, note that \(d'\) being a metric implies that \({\mathrm {W}_q}\) is a metric as well. For details see Chapter 6 in the book by Villani (2009). Additionally, we define the Wasserstein distance \({\mathrm {W}}_{\Vert \cdot \Vert }\) that arises, when the metric \(d'\) is replaced by the norm-induced metric \((x,x') \mapsto \Vert x-x' \Vert \). Moreover, we define the Dirac measure concentrated in \(\theta _0 \in X\) by \(\delta (\cdot - \theta _0) := {\mathbf {1}}[\theta _0 \in \cdot ].\)
Next, we define the flow \(\varphi _i: X \times [0, \infty ) \rightarrow X\) associated to the i-th potential \(\varPhi _i\), for \(i \in I\). In particular, \(\varphi _i\) satisfies
for any \(i \in I\) and \(\theta _0 \in X\). Similarly, we define the Markov kernels associated with the processes \((\theta (t))_{t > 0}\) and \((\xi (t))_{t > 0}\):
where \(t \ge t_0 \ge 0\). We now note two different assumptions on the convexity of the \(\varPhi _i\); a weak and a strong version.
Assumption 4
(Strong convexity) For every \(i \in I\), there is a \(\kappa _i \in \mathbb {R}\), with
with either
-
(i)
\(\kappa _1 + \cdots + \kappa _N > 0\) and for every \(\theta _0 \in X\) there is some bounded \(S \in {\mathcal {B}}X\), \(S \ni \theta _0\), such that
$$\begin{aligned}\varphi _i(S,t) \subseteq S \qquad (i \in I, t \ge 0)\end{aligned}$$(weak) or
-
(ii)
\(\kappa _1 = \cdots =\kappa _N > 0\) (strong).
In the strong version, we assume that all of the potentials \(\{\varPhi _i\}_{i \in I}\) are strongly convex. In the weak version, strong convexity of some potentials is sufficient; however, we need to ensure additionally that none of the flows escapes to infinity. The set S, in which we trap the process, is called positively invariant for \((\varphi _i)_{i \in I}\). The uniform strong convexity in Assumption 4(ii), indeed, implies the existence of such a set for all \(\theta _0 \in X\).
Both, Assumption 4(i) and (ii) are quite strong. As we have mentioned before, optimisation problems in machine learning are often non-convex. However, we focus on convex optimisation problems in this study. Strong convexity implies for instance that the associated flows contract exponentially:
Lemma 1
Inequality (14) for some \(i \in I\) implies that the corresponding flows contract exponentially, i.e.
Proof
This is implied by Lemma 4.1 given in Cloez and Hairer (2015). \(\square \)
Given this background, we now study the ergodicity of SGP. We commence with the case of a constant learning rate.
3.2 Constant learning rate
Under Assumption 4(i), the SGP \((\theta (t), {{\varvec{i}}}(t))_{t > 0}\) has a unique stationary measure \(\pi _{\mathrm {C}}\) on \((Z, {\mathcal {B}}Z) := (X \times I, {\mathcal {B}}X \otimes 2^I)\) and it contracts with respect to this measure in the Wasserstein distance \({\mathrm {W}_q}\). As the Markov process contracts exponentially, we say, the Markov process is exponentially ergodic. We now state this result more particularly:
Theorem 3
Let Assumptions 2 and 4(i) hold. Then, \((\theta (t), {{\varvec{i}}}(t))_{t > 0}\) has a unique stationary measure \(\pi _{\mathrm {C}}\) on \((Z, {\mathcal {B}}Z)\). Moreover, there exist \(\kappa ', c > 0\) and \(q \in (0, 1]\), with
for any \(i_0 \in I\) and \(\theta _0 \in X\).
The proof of this theorem follows similar lines as the proof of Theorem 5. Thus, we prove both in Sect. 3.4. Note that in Theorem 3, q influences the metric \(d'\) that is defined in (13) and that is part of the Wasserstein distance \(\mathrm {W}_q\). This result implies that SGPC converges very quickly to its stationary regime. For estimates of the constants in Theorem 3, we refer to Benaïm et al. (2012). Determining the stationary measure \(\pi _{\mathrm {C}}\) may be rather difficult in practice; see Costa (1990) and Durmus et al. (2018). We give numerical illustrations in Sect. 5.
3.3 Decreasing learning rate
Next, we study the longtime behaviour of SGP with decreasing learning rate. Here, we are less interested in the convergence of SGP to some abstract probability measure. Instead, we study the convergence of SGPD to the minimum \(\theta ^* \in X\) of the full potential \({\bar{\varPhi }}\). Hence, we aim to analyse the behaviour of
as \(t \rightarrow \infty \). Here, we have anticipated that the Dirac measure \(\delta (\cdot - \theta ^*)\) is the stationary measure of SGPD as \(t \rightarrow \infty \). This can be motivated by Theorem 1 where SGPC converges to the full gradient flow, as \(\eta \downarrow 0\).
Two aspects of SGPD imply that the analysis of this distance is significantly more involved than that of SGPC. First, the process is inhomogeneous in time; a case hardly discussed in the literature. We use the following standard idea to solve this issue:
-
(i)
We define a homogeneous Markov chain \((\xi '(t))_{t \ge 0}\) on an extended state space \(X \times \mathbb {R}\) where the transition rate matrix of \(({{\varvec{j}}}(t))_{t \ge 0}\) will not depend on time, but on the current position of \((\xi '(t))_{t \ge 0}\).
Second, as \(t \rightarrow \infty \) the rate matrix B(t) degenerates; the diagonal entries go to \(-\infty \), the off-diagonal entries will go to \(\infty \). This case is not covered by Cloez and Hairer (2015) or related literature on PDMPs—to the best of our knowledge. However, we were discussing a closely related problem in Theorem 1. To apply the perturbed test function theory, we require three fold actions:
-
(ii)
We define an auxiliary Markov jump process with bounded transition rate matrix.
-
(iii)
We show that the PDMP based on this Markov jump process converges to a unique stationary measure at exponential rate.
-
(iv)
We show that this stationary measure approximates \(\delta (\cdot - \theta ^*)\) at any precision. Also, we show that the auxiliary PDMP approximates SGPD.
Finally, we will obtain the following result:
Theorem 4
Let Assumptions 2 and 4(ii) hold. Then,
for any \(j_0 \in I\) and \(\xi _0 \in X\).
Hence, as \(t \rightarrow \infty \), the state \(\xi (t)\) of the SGPD converges weakly to the Dirac measure concentrated in the minimum \(\theta ^*\) of the full target function \({\bar{\varPhi }}\).
To prove this theorem, we now walk through steps (i)-(iv). Using several auxiliary results, we are then able to give a proof of Theorem 4. (i) A homogeneous formulation. We now formulate the SGPD in a time-homogeneous fashion. Indeed, we define \((\xi '(t))_{t \ge 0} := (\xi (t), \tau (t))_{t \ge 0}\), with
and \(({{\varvec{j}}}(t))_{t \ge 0}\) has transition rate matrix
One can see easily that this definition of SGPD is equivalent to our original Definition 1(ii). Note furthermore that the dynamic is defined such that if \(\{ \nabla \varPhi _i \}_{i \in I }\) satisfies Assumption 4(i) (resp. (ii)) \(\{ {{\Psi }}_i \}_{i \in I }\) does as well.
(ii) An auxiliary PDMP. Let \(\varepsilon \in (0,1)\). We define the PDMP \((\xi _\varepsilon (t), {{\varvec{j}}}_\varepsilon (t))_{t \ge 0}\) by
where the Markov jump process \(({{\varvec{j}}}_\varepsilon (t))_{t \ge 0}\) has transition rate matrix \(B_\varepsilon (\cdot ) := B(-\log (\tau _\varepsilon )).\) Note that – as opposed to \(B(\cdot )\) – this transition rate matrix converges to \(B(-\log (\varepsilon ))\), as \(t \rightarrow \infty \). Moreover, we define the Markov transition kernel of \((\xi _\varepsilon (t))_{t \ge 0}\) by \(\mathrm {D}^{\varepsilon }_{t|t_0}\).
(iii) Ergodicity of the auxiliary process. The following theorem shows that the auxiliary process \((\xi _\varepsilon (t), {{\varvec{j}}}_\varepsilon (t))_{t \ge 0}\) converges at exponential rate to its unique stationary measure.
Theorem 5
Let Assumptions 2 and 4(ii) hold and let \(\varepsilon > 0\). Then, \((\xi _\varepsilon (t), {{\varvec{j}}}_\varepsilon (t))_{t \ge 0}\) has a unique stationary measure \(\pi _{\varepsilon }\) on \((Z, {\mathcal {B}}Z)\). For any \(j_0 \in I\) and \(\xi _0 \in X\), there exist \(\kappa ', c, c' > 0\) with
As mentioned before, we give the proof of Theorem 5 in Sect. 3.4. Note that we now require Assumption 4(ii), i.e., the strong version.
(iv) Weak convergence of the auxiliary process. The last preliminary step consists in showing that the auxiliary process \((\xi _\varepsilon (t))_{t \ge 0}\) approximates the SGPD \((\xi (t))_{t \ge 0}\). Moreover, the same needs to hold for the respective stationary measures.
Proposition 4
Let Assumptions 2 and 4(ii) hold. Then,
-
(i)
there is a function \(\alpha ': [0,1) \rightarrow [0, \infty )\), that is continuous at 0 and satisfies \(\alpha '(0) = 0\), such that
$$\begin{aligned}{\mathrm {W}}_1(\mathrm {D}^{\varepsilon }_{t|0}(\cdot |\xi _0,j_0), \mathrm {D}_{t|0}(\cdot |\xi _0,j_0)) \le \alpha '(\varepsilon ),\end{aligned}$$for any \(j_0 \in I, \xi _0 \in X, t \ge t_0 \ge 0\),
-
(ii)
there is a function \(\alpha '': [0,1) \rightarrow [0, \infty )\), that is continuous at 0 and satisfies \(\alpha ''(0) = 0\), such that
$$\begin{aligned}{\mathrm {W}}_1(\delta (\cdot - \theta ^*), \pi _\varepsilon (\cdot \times I)) \le \alpha ''(\varepsilon ) \end{aligned}$$
The proof of Proposition 4 is more involved. We present our proof along with several auxiliary results in Sect. 3.5.
Given the results in (i)-(iv), we can proceed to proving the main result.
Proof of Theorem 4
Note that by the triangle inequality, we have
Now, we employ Theorem 5 and obtain
for some \(\kappa ', c, c' > 0\). Moreover, with Proposition 4, we can bound
and
where \(\alpha ', \alpha ''\) are continuous at 0 and \(\alpha '(0) = \alpha ''(0) = 0\). Then, we have
As this bound holds for any \(\varepsilon > 0\) and as the Wasserstein distance is bounded below by 0, we obtain the result \({\mathrm {W}}_1(\delta (\cdot - \theta ^*), \mathrm {D}_{t|0}(\cdot |\xi _0, j_0)) \rightarrow 0\), as \(t \rightarrow \infty \). \(\square \)
3.4 Proofs of Theorem 3 and Theorem 5
The proof of Theorem 3 proceeds by showing the assumptions of Theorem 1.4 in Cloez and Hairer (2015), which implies exponential ergodicity of the PDMP. Under the same assumptions, Corollary 1.11 of Benaïm et al. (2012) implies uniqueness of the stationary measure. We denote the necessary assumptions below, then we proceed with the proof.
Assumption 5
We consider the following three assumptions:
-
(i)
the process \(({{\varvec{i}}}(t))_{t \ge 0}\) is non-explosive, irreducible and positive recurrent,
-
(ii)
the Markov kernels representing the different gradient flows \(\mathrm{C}^{(i)}_t(\cdot |\theta _0) := \delta (\cdot - \varphi _i(\theta _0,t))\) are on average exponentially contracting in \(\mathrm {W}_{\Vert \cdot \Vert }\), i.e. for any two probability measures \(\pi , \pi '\) on \((X, {\mathcal {B}}X)\) satisfy
$$\begin{aligned} {\mathrm {W}}_{\Vert \cdot \Vert }(\pi \mathrm{C}^{(i)}_t, \pi ' \mathrm{C}^{(i)}_t) \le \exp (-\kappa _it) \mathrm{W}_{\Vert \cdot \Vert }(\pi , \pi ') \quad (i \in I) \end{aligned}$$for any \(t > 0\) and \(\kappa _1 + \cdots +\kappa _N > 0\), and
-
(iii)
the Markov kernel \(\mathrm{C}_t\) has a finite first absolute moment, i.e.
$$\begin{aligned}\frac{1}{N}\sum _{i_0=1}^N\int \Vert \theta \Vert \mathrm{C}_t(\mathrm {d}\theta |\theta _0,i_0) < \infty ,\end{aligned}$$for \(t \ge 0\) and \(\theta _0 \in X\).
Proof of Theorem 3
Assumption 5(i) is satisfied by standard properties of homogeneous continuous-time Markov processes on finite sets. Assumption 5(ii) is implied by Assumption 4(i); see also the proof of Lemma 2.2 in Cloez and Hairer (2015): Let G be a coupling in \(\mathrm {Coup}(\pi , \pi ')\) and choose a coupling \(H \in \mathrm {Coup}(\pi \mathrm{C}^{(i)}_t, \pi ' \mathrm{C}^{(i)}_t)\), such that
By Assumption 4(i) and Lemma 1, we have
Thus, we have indeed the required contractivity in the Wasserstein distance:
As \(\mathrm {W}_q(\pi \mathrm{C}^{(i)}_t, \pi ' \mathrm{C}^{(i)}_t)\) does not depend on H and G, we finally obtain
Concerning Assumption 5(iii), we employ the boundedness of the flows in Assumption 4(i). \(\square \)
Now we move on to the proof of Theorem 5. It is conceptually similar to the proof of Theorem 3: It relies on proving the necessary assumptions of Corollary 1.16 in Benaïm et al. (2012). We state these assumptions below.
Assumption 6
We consider the following four assumptions:
-
(i)
there is a \(\kappa _1 > 0\) such that for every \(i \in I\), we have
$$\begin{aligned} \left\langle \theta _0 - \theta _0', \nabla \varPhi _i(\theta _0) - \nabla \varPhi _i(\theta _0')\right\rangle \ge \kappa _1\Vert \theta _0 - \theta _0' \Vert ^2 \end{aligned}$$and
-
(ii)
the transition rate matrix \(B_{\varepsilon }\) is bounded in the sense that there are \({\overline{b}}> {\underline{b}} > 0\), with
$$\begin{aligned}{\underline{b}} \le B_{\varepsilon }(\tau )_{i,j} \le {\overline{b}} \qquad (i, j \in I, i \ne j, \tau \in (\varepsilon ,1])\end{aligned}$$and there is some \(L > 0\), with
$$\begin{aligned} \sum _{j \in I} \left|B_{\varepsilon }(\tau )_{i,j} - B_{\varepsilon }(\tau ')_{i,j}\right|\le L&|\tau - \tau '| \\&(i \in I, \tau , \tau ' \in (\varepsilon , 1]). \end{aligned}$$
Note that Assumption 6 closely corresponds to Assumption 5.
Proof of Theorem 5
Assumption 6(i) is implied by Assumption 4(ii). We move on to Assumption 6(ii): Boundedness and Lipschitz continuity of this function, follows from the boundedness of \(\tau \in (\varepsilon , 1]\) and the continuous differentiability of \(\mu \). \(\square \)
3.5 Proof of Proposition 4
In this subsection, we prove Proposition 4. First, we show weak convergence of \((\xi _{\varepsilon }(t))_{t \ge 0} \Rightarrow (\xi (t))_{t \ge 0}\) in the sense of (11). Given this result, we will be able to construct the function \(\alpha '\) and thus prove Proposition 4(i). Part (ii) of the proposition will rely on showing that \((\xi _{\varepsilon }(t))_{t \ge 0}\) approximates the underlying gradient flow, as discussed in Theorem 1.
Lemma 2
Let Assumptions 2 and 4(ii) hold. Then,
as \(\varepsilon \downarrow 0\).
Proof
Let \(Z' := X \times \mathbb {R} \times \mathbb {R}\), let \({\mathcal {A}}\) be the (infinitesimal) generator of \((\xi (t), \tau (t), {{\varvec{j}}}(t))_{t \ge 0}\), and let analogously \({\mathcal {A}}_{\varepsilon }\) be the generator of \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0} \), for any \(\varepsilon > 0\). We will now employ Theorem 3.2 of Kushner (1984) which implies our assertion, if
-
(i)
the family \((\xi _{\varepsilon }(t))_{t \ge 0, \varepsilon > 0}\) is tight with respect to \(\varepsilon \),
-
(ii)
for any \(T \in (0, \infty )\) and any test function \(f \in C'\) there is a ‘perturbed’ test function \(f^{\varepsilon }: [0, \infty ) \rightarrow \mathbb {R}\), such that
$$\begin{aligned}&\sup _{\begin{array}{c} t \ge 0 \\ \varepsilon \in (0,1] \end{array}}\mathbb {E}\left[ \left|f^\varepsilon (t)-f(\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))\right|\right] < \infty , \end{aligned}$$(15)$$\begin{aligned}&\lim _{\varepsilon \downarrow 0}\mathbb {E}\left[ \left|f^\varepsilon (t)-f(\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t)) \right|\right] =0 \nonumber \\&\quad (t \ge 0), \end{aligned}$$(16)$$\begin{aligned}&\sup _{\begin{array}{c} t \in (0, T] \\ \varepsilon \in (0,1] \end{array}}\mathbb {E}\left[ \left|{\mathcal {A}}_{\varepsilon }f^\varepsilon (t)-{\mathcal {A}}f(\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))\right|\right] < \infty , \end{aligned}$$(17)$$\begin{aligned}&\lim _{\varepsilon \downarrow 0}\mathbb {E}\left[ \left|{\mathcal {A}}_{\varepsilon }f^\varepsilon (t)-{\mathcal {A}}f(\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t)) \right|\right] =0 \nonumber \\&\qquad (0 \le t \le T). \end{aligned}$$(18)Here, \(C'\) is uniformly dense in the space \(C^0_c(Z')\) of continuous functions with compact support.
First, note that the generators are given by
for any \(f: Z' \rightarrow \mathbb {R}\) that is twice continuously differentiable and vanishes at infinity; see, e.g., Davis (1984) for details. Here, we understand the processes \((\xi (t), \tau (t), {{\varvec{j}}}(t))_{t \ge 0}\) and \((\xi _\varepsilon (t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0}\) as Markov jump diffusions. Tightness in (i) follows from the boundedness of the gradient in Assumption 2: According to Theorem 2.4 in Kushner (1984) (or, e.g., Theorem 7.3 in Billingsley 1999), we need to show that (i1), (i2) are satisfied by \((\xi _{\varepsilon }(t))_{t \ge 0}\):
-
(i1)
For all \(\eta _* > 0\), there is an \(N_* \in (0, \infty )\), with
$$\begin{aligned} \mathbb {P}(\Vert \xi _{\varepsilon }(0)\Vert \ge N_*) \le \eta _* \qquad (\varepsilon >0). \end{aligned}$$ -
(i2)
For all \(\eta _* >0\), \(\varepsilon _*>0, {\overline{t}}>0\) there is \(\delta _* > 0\) and an \(n_0 \in (0, \infty )\), such that
$$\begin{aligned} \mathbb {P}\left( \sup _{|s-t|< \delta _*, 0 \le s \le t \le {\overline{t}}}\Vert \xi _{\varepsilon }(t)-\xi _{\varepsilon }(s)\Vert \ge \varepsilon _*\right) \le \eta _*,\end{aligned}$$for \(\varepsilon \in (0, n_0)\).
(i1) is satisfied as the initial value \(\xi _{\varepsilon }(0)\) is \(\mathbb {P}\)-a.s. constant throughout \(\varepsilon >0\). To prove (i2), note that \((\xi _{\varepsilon }(t))_{t \ge 0}\) has \(\mathbb {P}\)-a.s. continuous paths that are almost everywhere differentiable. Let \(B \subseteq X\) be a closed ball with \(\mathbb {P}(\xi _{\varepsilon }(t) \in B) = 1\) \((t \ge 0)\); see Lemma 1.14 in Benaïm et al. (2012). The derivative of \((\xi _{\varepsilon }(t))_{t \ge 0}\) is bounded by some finite
as the \((\nabla \varPhi _i)_{i \in I}\) are continuous. Importantly, L does not depend on \(\varepsilon \). Hence, we have
\(\mathbb {P}\)-a.s. for \(0 \le s \le t\). This implies
\(\mathbb {P}\)-a.s. for any \(\delta _{*}>0\). Thus, we get for any \(\varepsilon _*>0, {\overline{t}}>0\): \(\delta _* := \varepsilon _*/L\) and
This implies
which means
giving us (i2).
To prove (ii), we choose the test space \(C' := C^2_{{c}}(Z')\), which is the space of twice continuously differentiable functions that have compact support and that have bounded \(C^2\)-sup-norm. Note that the Stone-Weierstrass Theorem for locally compact \(Z'\) implies that \(C^2_{{c}}(Z')\) is uniformly dense in \(C^0_0(Z')\); see, e.g., Corollary 4.3.5 in Pedersen (1989). Thus, \(C^2_{{c}}(Z')\) is also uniformly dense in \(C^0_c \subseteq C^0_0\).
Now, for any test function \(f \in C'\) we choose the perturbed test function \(f^\varepsilon (t) := f(\xi _{\varepsilon }(t))\), \(t \ge 0, \varepsilon \in (0,1]\). Then, we have \(f^\varepsilon -f(\xi _{\varepsilon }) \equiv 0\), for any \(\varepsilon \in (0,1]\). Hence, (15) and (16) are satisfied. Now towards (17) and (18). For \(\varepsilon > 0\) and \(t \in [0, T]\), we compute
By assumption the partial derivatives of f are bounded. Hence, we obtain
where the supremum on the right-hand side is finite, as \(f \in C'\). This proves (17), (18) and concludes the proof. \(\square \)
We can now employ Lemma 2 to find an appropriate bound for the Wasserstein distances in the first part of Proposition 4.
Proof of Proposition 4 (i)
From Lemma 2, we know that \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0} \Rightarrow (\xi (t), \tau (t), {{\varvec{j}}}(t))_{t \ge 0}\), as \(\varepsilon \downarrow 0\). Note that this is equivalent to \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0} - (\xi (t), \tau (t), {{\varvec{j}}}(t))_{t \ge 0} \Rightarrow 0\). We now construct the function \(\alpha '(\cdot )\). Let
where \( (\xi , \tau , {{\varvec{j}}}) \in C^0([0, \infty ); Z')\). F is bounded and continuous on \((C^0([0, \infty ); Z), \Vert \cdot \Vert _\infty )\), since
is continuous for any \((\xi , \tau , {{\varvec{j}}}) \in C^0([0, \infty ); Z')\). The weak convergence of
implies
as \(\varepsilon \downarrow 0\). Now, the definition of the Wasserstein distance and the monotonicity of the integral imply for any \(t \ge 0\):
Hence, we obtain the desired results by setting \(\alpha '(\varepsilon ) := {\mathbf {1}}[\varepsilon > 0] \mathbb {E}\left[ F \left( (\xi _{\varepsilon }(t)-\xi (t), \tau _{\varepsilon }(t)-\tau (t), {{\varvec{j}}}_{\varepsilon }(t)-{{\varvec{j}}}(t))_{t \ge 0} \right) \right] \). \(\square \)
To prove the second part of this proposition, we proceed as follows: we argue that the auxiliary process \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0}\) behaves in its stationary regime like the SGPC setting with \(\lambda := \mu (-\log (\varepsilon ))\) in Lemma 3. Then, however, we can show with Theorem 1, that the process behaves like the full gradient flow, as \(\varepsilon \downarrow 0\). In Lemma 4, we remind ourselves that the full gradient flow has \(\delta (\cdot - \theta ^*)\) as a stationary measure. Finally, to prove Proposition 4(ii) it will suffice to show that in Theorem 1, also the corresponding stationary measures converge weakly.
Lemma 3
Let Assumptions 2 and 4(ii) hold. Moreover, let \(\lambda := \mu (-\log (\varepsilon ))\), let \(\pi _C\) be the stationary distribution of \((\theta (t), {{\varvec{i}}}(t))_{t \ge 0}\), and let \(\pi _{\varepsilon }\) be the stationary distribution of \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0}.\) Then,
for any \(A \in {\mathcal {B}}X\) and \(J \subseteq I\).
Proof
Note that the stationary measure of the process \((\xi _{\varepsilon }(t), \tau _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0}\) does not change, when setting \(\tau _{\varepsilon }(0) := \varepsilon \). Then however, \((\xi _{\varepsilon }(t), {{\varvec{j}}}_{\varepsilon }(t))_{t \ge 0}\) and \((\theta (t), {{\varvec{i}}}(t))_{t \ge 0}\) are identically generated. Hence, they have the same stationary distribution. Also, Theorems 3 and 5 imply that those stationary distributions are unique. \(\square \)
Lemma 4
Let Assumptions 2 and 4(ii) hold. Then, \({\bar{\varPhi }}\) is strongly convex and for the flow \(\bar{\varphi }\) corresponding to \(\nabla {\bar{\varPhi }}\), we have
where \(\theta _0, \theta _0' \in X, t \ge 0\). Hence, \(\delta ( \cdot - \theta ^*)\) is the unique stationary measure of the full gradient flow defined in (10).
Proof
The first part follows from Lemma 1. The second part is implied by the Banach Fixed-Point Theorem and by the stationarity of \(\theta ^*\) with respect to \(\nabla {\bar{\varPhi }}\). \(\square \)
Now, we proceed to prove the second part of the main proposition.
Proof of Proposition 4(ii)
By Lemmas 3 and 4, it will be sufficient to show that in the setting of Theorem 1, the stationary measure of SGPC with \(\lambda := \mu (-\log (\varepsilon ))\) converges to the stationary measure of the gradient flow \((\zeta (t))_{t \ge 0}\). We proceed as in Chapters 6.4 and 6.5 of Kushner (1984), i.e. we need to show
-
(i)
\((\zeta (t))_{t \ge 0}\) has a unique stationary measure \(\bar{\pi }\) and \(\zeta (t) \Rightarrow \bar{\pi }\), as \(t \rightarrow \infty \),
-
(ii)
\(\theta ^*\) is Lyapunov stable for \((\zeta (t))_{t \ge 0}\),
-
(iii)
Let \(t_\varepsilon \rightarrow t_0 \in \mathbb {R}\), as \(\varepsilon \downarrow 0\). Then, \(\mathbb {P}(\theta (t_{\varepsilon }) \in \cdot ) \Rightarrow \mathbb {P}(\zeta (0) \in \cdot )\), as \(\varepsilon \downarrow 0\), implies that \((\theta (t_{\varepsilon } + t))_{t \ge 0} \Rightarrow (\zeta (t))_{t \ge 0}\), as \(\varepsilon \downarrow 0,\)
-
(iv)
There is an \(\varepsilon ' > 0\), such that \((\theta (t))_{t \ge 0, \varepsilon ' \ge \varepsilon > 0}\) is tight with respect to both t and \(\varepsilon \).
Those assumptions will imply that \(\theta (t) \Rightarrow \bar{\pi }\), as \(\varepsilon \downarrow 0\) and \(t \rightarrow \infty \); see Theorem 6.5 in Kushner (1984). As \((\theta (t))_{t \ge 0}\) has a unique stationary measure, we have that \(\pi _{C} \Rightarrow \bar{\pi }\). Now to prove these four assertions. (i), (ii) follow immediately from Lemma 4, with \(\bar{\pi } := \delta (\cdot - \theta ^*)\). (iii) is implied by Theorem 2. Due to the strong convexity that we have assumed in Assumption 4(ii), we know that the process cannot escape a certain compact set; see Lemma 1.14 in Benaïm et al. (2012) for details. This implies tightness as needed in (iv).
Finally, note that \(\pi _C \Rightarrow \bar{\pi }\) already implies that they also converge in \(\mathrm {W}_1\). Hence, we can construct a function \(\alpha ''\) accordingly. \(\square \)
3.6 Linear least squares problems
In this section, we illustrate the theoretical results of Sects. 3.2–3.5 with an abstract example. In particular, we show that Assumptions 2 and 4 hold for linear least squares problems under weak assumptions. Those appear in (regularised) linear or polynomial regression.
Let \(Y:= \mathbb {R}^M\), \(y \in Y\), and \(G: X \rightarrow Y\) be a linear operator. Y is the data space, y is the observed data set, and G is the parameter-to-data map. We consider the problem of estimating
which is called linear least squares problem.
We aim to solve this problem by the stochastic gradient descent algorithm. Indeed, we define
where \(y_i\) is an element of another Euclidean vector space \(Y_i := \mathbb {R}^{M_i}\) and \(G_i: X \rightarrow Y_i\) is a linear operator, for \(i \in I\). We assume that these are given such that the space \(Y = \prod _{i \in I}Y_i\), the vector \((y_i)_{i \in I} = N\cdot y\), and the operator \([G_1^T, \ldots , G_N^T]^T = N \cdot G.\) To define the SGP, we now need to derive the gradient field. This is given by the associated normal equations:
These vector fields are linear, thus, satisfy Assumption 2. Now we discuss Assumption 4. Let \(i \in I\). Note that \(G_i^TG_i\) is symmetric, positive semi-definite. We have
where \(\kappa _i \ge 0\) is the smallest eigenvalue of \(G_i^TG_i\). This implies that Assumption 4(i) holds, if there is some \(i \in I\) with \(G_i^TG_i\) strictly positive definite. Furthermore, Assumption 4(ii) holds, if for all \(i \in I\) the matrix \(G_i^TG_i\) is strictly positive definite.
Strict positive definiteness of \(G_i^TG_i\) is satisfied, if \(\dim Y_i \ge \dim X\) and \(G_i\) has full rank, for \(i \in I\). The inequality \(\dim Y_i \ge \dim X\) is not restrictive, as we apply SGD typically in settings with very large data sets. If the \(G_i\) do not have full rank, one could add a Tikhonov regulariser to the target function in (19).
4 From continuous to discrete
In the previous sections, we have introduced and discussed SGP mainly as an analytical tool and abstract framework to study SGD. However, we can also apply SGP more immediately in practice. To this end, we need to consider the following computational tasks:
-
(i)
discretisation of deterministic flows \((\varphi _i)_{i \in I}\)
-
(ii)
discretisation of continuous-time Markov processes \(({{\varvec{i}}}(t))_{t \ge 0}\), resp. \(({{\varvec{j}}}(t))_{t \ge 0}\)
The discretisation of the \((\varphi _i)_{i \in I}\) consists in the discretisation of several homogeneous ODEs. The discretisation of ODEs has been studied extensively; see, e.g., Iserles (2008). Thus, we focus on (ii) and discuss a sampling strategy for the CTMPs in Sect. 4.1.
A different aspect is the following: note that when specifying strategies for (i) and (ii), we implicitly construct a stochastic optimisation algorithm. Since we have introduced SGP as a continuous-time variant of SGD, one of these algorithms should be the original SGD algorithm. Indeed, in Sect. 4.2 we will explain a rather crude discretisation scheme which allows us to retrieve SGD. Well-known algorithms beyond SGD that can be retrieved from SGP are discussed in Sect. 4.3.
4.1 Applying SGP
We now briefly explain a strategy that allows us to sample the CTMPs \(({{\varvec{i}}}(t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\). Without loss of generality, we focus on the second case, \(({{\varvec{j}}}(t))_{t \ge 0}\).
Indeed, we give a sampling strategy in Algorithm 2. It commences by sampling an initial value \({{\varvec{j}}}(0)\). This value remains constant for the duration of the random waiting time. After this waiting time is over, we sample the next value of the process from a uniform distribution on all states, but the current state. This value is kept constant for another random waiting time and so on. This strategy goes back to Gillespie (1977); see also Rao (2012) for this and other sampling strategies for CTMPs on discrete spaces.

The potentially most challenging step in Algorithm 2 is the sampling from the distribution \(\pi _\mathrm{wt}(\cdot | t_0)\) in line 4. In the case of SGPC, i.e. if \(\eta \) is constant, this sampling just comes down to sampling from an exponential distribution. In SGPD, the sampling could be performed using the quantile function of \(\pi _\mathrm{wt}(\cdot | t_0)\), if accessible. We sketch the method below. If the quantile function is not accessible, strategies such as rejection sampling may be applicable; see Robert and Casella (2004) for details. In the following, we consider first the case where \(1/\eta (\cdot )\) is an affine function and then the case where \(\eta \) scales exponentially in time. Both of these cases lead to a continuously differentiable function \((\mu (t))_{t \ge 0}\), as required in §2. Thus, our theory applies to the SGPD employing either of these learning rate functions.
Example 1
Let \(\eta (t) := (at +b)^{-1}\), for \(t\ge 0\) and some \(a, b > 0\). Then, we have for \(t_0 \ge 0\) and \(t \ge t_0\):
By inverting this formula, we obtain the quantile function
where \(s \in (0,1), t_0 \ge 0\). Using this quantile function, we are able to sample from \(\pi _\mathrm{wt}( \cdot | t_0)\). Note that for \({U} \sim \mathrm {Unif}((0,1))\) we have \(\mathbb {P}(Q({U}|t_0) \in \cdot ) = \pi _\mathrm{wt}(\cdot | t_0)\). We have used this technique to estimate mean and standard deviations of \(\pi _\mathrm{wt}( \cdot | t_0)\) for \(t_0 \in [0, {10}]\) and \(a = b = 1\); see Fig. 3. We observe that the mean behaves as \(\eta (\cdot )\), showing a similarity with the exponential distribution.
Example 2
Let \(\eta (t) := a\exp (-bt)\), for \(t\ge 0\) and some \(a, b > 0\). Then, we have for \(t_0 \ge 0\) and \(t \ge t_0\):
We can again compute the quantile function
where \(s \in (0,1), t_0 \ge 0\). We again use the quantile function to estimate mean and standard deviations of the distribution for \(a = b = 1\) and \(t_0 \in [0,10]\); see Fig. 3.
4.2 Retrieving SGD from SGP
Now, we discuss how the SGP dynamic needs to be discretised to retrieve the SGD algorithm. To this end, we list some features that we need to keep in mind:
The waiting times between switches of the data sets are deterministic in SGD and random in SGP. The processes \(({{\varvec{i}}}(t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\) in SGP indeed jump with probability one after the waiting time is over, i.e. \({{\varvec{i}}}(t) \ne {{\varvec{i}}}(s)\) when one jump occurred in (t, s]. In SGD, however, it is possible to have a data set picked from the sample twice in a row. Finally, we need to discretise the flows \((\varphi _i)_{i \in I}\) using the explicit Euler method.
We approximate the process \(({{\varvec{j}}}(t))_{t \ge 0}\) by
where \({{\varvec{j}}}_0,{{\varvec{j}}}_1,\ldots \sim \mathrm {Unif}(I)\) i.i.d. and the sequence \(({\hat{t}}_k)_{k=0}^\infty \) is given by
Note that with this definition of the sequence \(({\hat{\eta }}_k)_{k=1}^\infty \) , we obtain \({\hat{\eta }}_k = \eta _k\), \(k \in \mathbb {N}\), which was the discrete learning rate defined in Algorithm 1. See our discussion in Sect. 2.2 for the choice of \(({\hat{{{\varvec{j}}}}}(t) )_{t \ge 0}\) as an approximation of \(({{{\varvec{j}}}}(t) )_{t \ge 0}\). If we employ \(({\hat{{{\varvec{j}}}}}(t))_{t \ge 0}\) and an explicit Euler discretisation with step length \(\eta _k\) in step \(k \in \mathbb {N}\) to discretise the respective flows \((\varphi _i)_{i \in I}\), we obtain precisely the process defined in Algorithm 1.
4.3 Beyond SGD
In Sect. 4.2, we have discussed how to discretise the SGP \((\xi (t))_{t \ge 0}\) to obtain the standard SGD algorithm. It is also possible to retrieve other stochastic optimisation algorithms by employing other discretisation strategies for the flows \((\varphi _i)_{i \in I}\). Note, e.g., that when replacing the explicit Euler discretisation of the flows \((\varphi _i)_{i \in I}\) in Sect. 4.2 by an implicit Euler discretisation, we obtain the stochastic proximal point algorithm; see, e.g., Proposition 1 of Bertsekas (2011) for details.
Using higher-order methods instead of explicit/implicit Euler, we obtain higher-order stochastic optimisation methods. Those have been discussed by Song et al. (2018). Adaptive Learning Rates for SGD are conceptually similar to adaptive stepsize algorithms in ODE solvers, but follow different ideas in practice; see Duchi et al. (2011) and Li and Orabona (2019).
Linear-complexity SGD-type methods, like Stochastic Average Gradient (SAG) (Schmidt et al. (2017)), Stochastic Variance Reduced Gradient (SVRG) (Johnson and Zhang (2013)), or SAGA (Defazio et al. (2014)) remind us of multistep integrators for ODEs. Here, the update does not only depend on the current state of the system, but also on past states. On the other hand, variance reduction in the discretisation of stochastic dynamical systems is, e.g., the object of Multilevel Monte Carlo path sampling, as proposed by Giles (2008).
5 Numerical experiments
We now aim to get an intuition behind the stationary measures \(\pi _C\), \(\pi _\varepsilon \) (Theorems 3 and 5), study the convergence of the Markov processes, and compare SGP with SGD.
Estimated stationary measures of SGD and SGPC with different \(\eta \in \{1, 10^{-1}, 10^{-2}, 10^{-3}\}\) and initial value \(\theta _0 = -1.5\). The results are based on kernel density estimations with \(10^4\) samples each of \(\theta (10)\) for SGPC and \(\theta _k\) with \(k = 10/\eta \) for SGD. Note that for SGD with \(\eta = 1\), the samples are concentrated in 3 points, which is why we plot a histogram rather than a density
Below, we define the academic example that we study throughout this section. It fits into the linear least squares framework discussed in Sect. 3.6. Moreover, it satisfies Assumptions 2 and 4(i) and (ii); see Sect. 3.6. Then, we proceed by applying SGD, SGPC, and SGPD.
Example 3
Let \(N := 3\), i.e. \(I:=\{1, 2, 3\}\), and \(X := \mathbb {R}\). We define the potentials
The minimiser of \(\bar{\varPhi } \equiv \varPhi _1/3 + \varPhi _2/3 + \varPhi _3/3\) is \(\theta ^* = 0.5\).
5.1 Constant learning rate
Approaching the optimisation problem in Example 3, we now employ SGPC with initial value \(\theta _0 = -1.5\) and \(\eta \in \{1, 10^{-1}, 10^{-2}, 10^{-3}\}\). We sample from this process using Algorithm 2 for the CTMP \(({{\varvec{i}}}(t))_{t \ge 0}\) and the analytical solution of the gradient flows \((\varphi _i)_{i \in I}\). Throughout this section, we use the Matlab function ksdensity to compute kernel density estimates. All of those are based on Gaussian kernel functions with boundary correction at \(\{-2, 2\}\), if necessary.
We now sample SGPC as discussed above and collect the samples \(\theta (10)\), i.e. the value of the process at time \(t = 10\). In Fig. 4, we show kernel density estimates based on \(10^4\) of these samples. For large \(\eta \), the density has mass all over the invariant set of the \((\varphi _i)_{i \in I}\). If \(\eta \) is reduced, we see that the densities become more and more concentrated around the optimum \(\theta ^*\).
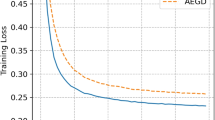
Next, we compare SGPC with SGD. Indeed, we compute kernel density estimates of \(10^4\) samples of the associated SGD outputs. In particular, we run SGD with the same learning rates up to iterate \(10/\eta \). For \(\eta = 1\), the numerical artifacts seem to dominate SGD. For smaller \(\eta \), the densities obtained from both algorithms behave very similarly: we only see a slightly larger variance in SGP. Indeed, when looking at the values of the variances of \(\theta (10)\) for \(\eta \in \{10^{-1}, 10^{-2}, 10^{-3}\}\), they seem to depend linearly on \(\eta \) and only differ among each other by about factor 1.3, see the estimates in Table 1.
We next take a look at the sample paths of said SGPC runs; consider Fig. 5. As anticipated and actually already shown in Fig. 2, the smaller \(\eta \) leads to a faster switching and to a sample path that well approximates the full gradient flow. Large \(\eta \) leads to slow switching. It is difficult to recognise the actual speed of convergence shown in Theorem 3. However, we see that each of the chains indeed reaches a stationary regime. The time at which those regimes are reached highly depends on \(\eta \). Indeed, for \(\eta = 1\) we seem to be almost right away in said regime. For the smallest learning rate \(\eta = 10^{-3}\), it appears to take up to \(t \approx 3.5\). What does this mean from a computational point of view? The approach with a small learning rate is computationally inefficient: the large number of switches makes the discretisation of the sample paths computationally expensive; the slow convergence to the stationary regime implies that we need to run the process for a relatively long time. For large \(\eta \), however, we are not able to identify the optimal point; see Fig. 4. Hence, with large and constant \(\eta \) the method is ineffective.
Sample paths of SGPC as in Fig. 4. Left: four sample paths \((\theta (t))_{t \ge 0}\), right: associated distances between sample paths and optimal point, i.e. \((|\theta (t)-0.5|)_{t \ge 0}\)
5.2 Decreasing learning rate
In SGPD, we can solve the efficiency problem of SGPC noted in the end of Sect. 5.1: we start with a large \(\eta \), which is decreased over time. Hence, we should expect to see fast convergence in the beginning and accurate estimation of \(\theta ^*\) later on. To test this assertion we get back to the problem defined in Example 3.
A sample path of \((\xi (t), {{\varvec{j}}}(t))_{t \ge 0}\), as specified in Sect. 5.2. The top two figures refer to the rational learning rate, the bottom two figures refer to the exponential rate
We study two different time-dependent learning rates: a rational rate that is the reciprocal of an affine function, as in Example 1, as well as an exponential learning rate; as in Example 2. In particular, we choose
and sample from the associated waiting time distribution using the quantile functions (20) and (21), respectively. Note that, as mentioned before, the reciprocal of both learning rate functions satisfies the continuous differentiability condition in Sect. 2. All the other specifications are identical to the ones given in Sect. 5.1: we set, e.g., \(\xi _0 := -1.5\) as an initial value for the process. In Fig. 6, we show single sample paths of the processes \((\xi (t), {{\varvec{j}}}(t))_{t \ge 0}\), with the different learning rate functions. In both cases, we can see that the waiting times between jumps in \(({{\varvec{j}}}(t))_{t \ge 0}\) go down as t increases: the (vertical) jumps become denser over time. For small \(t > 0\), one can also recognise the coupling between \((\xi (t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\). If we compare the paths with the different learning rate functions, we see that the exponential rate allows for much larger steps in the beginning and then decreases quite quickly. The rational rate leads to fast switching early on, which decreases further rather slowly over time. Note that these plots are essentially realistic versions of the cartoon in Fig. 1.
Next, we look at the distribution of \(\xi (t)\) for particular \(t > 0\). In Fig. 7, we plot kernel density estimates for the distributions of \(\xi (1/4),\) \(\xi (1/2),\) \(\xi (1),\) \(\xi (2),\) \(\xi (4),\) \(\xi (8)\) and \(\xi (10)\). Those estimates are each based on \(10^4\) independent Monte Carlo samples. Hence, we show how the distribution of the processes evolves over time. We observe that the process starting at \(\xi (0) = -1.5\) moves away from that state and slowly approaches the optimal point \(\theta ^* = 0.5\). Doing so, it starts with a large variance that is slowly decreased over time. This is consistent with what we have observed in Fig. 4 and Table 1. In case of the exponential learning rate, this behaviour is much more pronounced: we start with a much higher variance but end up at \(t=10\) with a smaller variance.
In Fig. 8, we additionally compare the distribution of the constant learning rate process with \(\eta = 10^{-3}\) with the exponential and rational rate processes at the time at which their learning rate is approximately equal to \(10^{-3}\). We see that the states of the constant and rational rate processes have almost the same distribution, which is what we would hope to see. The exponential learning rate process has a larger variance.
Comparison of the densities of SGPC state \(\theta (10)\) where \(\eta = 10^{-3}\) taken from Fig.4, the rational learning rate SGPD \(\xi (9.99)\), and the exponential learning rate SGPD \(\xi (6.91)\). The densities are estimated with \(10^4\) samples
To study the performance of SGPD quantitatively, we estimate mean and standard deviation of the absolute error \(|\xi (t)-0.5|\) at \(t = 1,2,\ldots ,10\) using \(10^4\) Monte Carlo samples. To see the full context, we also performed \(10^4\) runs of the associated discrete-time SGD algorithms. The learning rate sequences \((\eta _k)_{k=1}^\infty \) are chosen as we have suggested in (23). We show the results in Fig. 9. In the exponential, continuous case, we see an exponential convergence rate. In all the other settings, the rates are sublinear. For the discrete settings, this is exactly what we would expect based on the literature; see Jentzen et al. (2018) and the references therein. Interestingly, the rational, continuous case appears to be less efficient than the rational, discrete case. This could imply that the learning rate function is supposed to be chosen according to the convergence rate of the underlying deterministic dynamical system.
6 Conclusions
We have proposed the stochastic gradient process as a natural continuum limit of the popular stochastic gradient descent algorithm. It arises when replacing the explicit Euler updates by the exact gradient flows and the waiting times between data switches by appropriate random waiting times. This continuous-time model is a piecewise-deterministic Markov process. It represents the uniform subsampling from a finite set of potentials after strictly positive waiting times, the Markovian nature of SGD, the switching of potentials, and the approximation of the full deterministic gradient flow. Moreover, the process has an interpretation in population dynamics.
Within this continuum limit, we are able to study Wasserstein ergodicity in the case of strongly convex target functions. In the case of constant learning rates, we obtain exponential ergodicity. A similar result has been established by Dieuleveut et al. (2020) in discrete time. In the case of decreasing learning rates, we could show weak convergence to the minimiser of the target function. Our results do not allow us to assess the convergence rate in that case. Numerical experiments indicate that it depends on the underlying data switching process and could in certain cases be exponential as well.
In the numerical experiments, we compared samples from SGP with samples from SGD. Here, we, for instance, observed strong similarities between the stationary measure of the two processes. Indeed, we claim that our continuum limit is a good representation of stochastic gradient descent in the long-time limit.
Here, we have been able to sample accurately from SGP, as the flows attain analytical representations. In most practical cases, we would need to construct a discrete stochastic optimisation algorithm from SGP using an ODE integrator. Following this machinery, one can also retrieve known stochastic optimisation algorithms, showing that SGP is also a generalisation of those.
We conclude this work with four remarks. Here, we discuss possible extensions of the stochastic gradient process framework.
Remark 3
(Global, non-convex) Throughout our long-time analysis, we have required strong convexity of the target functions. In practical applications, e.g. the training of deep neural networks, convexity is too strong. If certain Hörmander bracket conditions are satisfied, exponential ergodicity may also be shown without the strong convexity assumption, see, e.g. Bakhtin and Hurth (2012) and Cloez and Hairer (2015). This does not yet imply that the processes will converge to the global optimum, if \(\eta \downarrow 0\). However, we remark that the densities in the numerical illustrations in Sect. 5 very much remind us of a simulated annealing scheme, where \(\eta \) controls the variance of the target measure; see e.g. Section 5.2.3 of Robert and Casella (2004). In some cases, simulated annealing is able to find global extrema of non-convex target functions; see Yang (2000). Hence, this connection may fertilise future research in this direction.
Remark 4
(Constrained) SGD has been successfully applied in constrained optimisation; typically by projecting each update on the space of feasible vectors. This is difficult to represent in the SGP setting; as the projection would need to be part of the piecewise ODEs. However, PDMPs on bounded sets already appear in the original paper by Davis (1984). Here, a jump is introduced as soon as the boundary of the feasible set is reached. In SGP, one could introduce a jump in the continuous-time Markov process \(({{\varvec{i}}}(t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\), as soon as the boundary is hit. Hence, the data set is randomly switched until the process moves away from the boundary or the boundary point is stationary for the process.
Remark 5
(Gradient-free) In this work, we cover only methods that are fundamentally based on discretised gradient flows. Other stochastic optimisation algorithms are based on other underlying dynamics. Such are ensemble-based methods or evolutionary algorithms. Consider, for instance, the ensemble Kalman inversion framework, which was proposed by Schillings and Stuart (2017) as a continuum limit of some ensemble Kalman filter. Using our SGP view, one may be able to analyse subsampling in ensemble Kalman inversion, as proposed by Kovachki and Stuart (2019).
Remark 6
(Non-Markovian) We have modelled SGP as a piecewise-deterministic Markov process. In practice, one might be interested in non-Markovian extensions to this setting. Non-Markovian settings arise, e.g., when adapting the learning rate throughout the algorithm, as in the celebrated AdaGrad algorithm Duchi et al. (2011).
Another non-Markovian extension is the following. In the present work, we have decided to switch the potentials in the SGPs after random waiting times. While this allowed us to study SGP as a (piecewise-deterministic) Markov process, it did not retain SGD’s property of jumping after deterministic waiting times. If we model the waiting times deterministically, the processes \(({{\varvec{i}}}(t))_{t \ge 0}\), \(({{\varvec{j}}}(t))_{t \ge 0}\) become general renewal processes and non-Markovian. Especially since deterministic waiting times are easier to handle in practice, the then resulting ‘renewal stochastic gradient processes’ are highly interesting objects for future studies.
References
Anderson, W.J.: Continuous-Time Markov Chains: An Applications-Oriented Approach. Springer, New York (1991)
Ardaševa, A., Gatenby, R.A., Anderson, A.R.A., Byrne, H.M., Maini, P.K., Lorenzi, T.: Evolutionary dynamics of competing phenotype-structured populations in periodically fluctuating environments. J. Math. Biol. 80(3), 775–807 (2019)
Bakhtin, Y., Hurth, T.: Invariant densities for dynamical systems with random switching. Nonlinearity 25(10), 2937–2952 (2012)
Benaïm, M.: Dynamics of stochastic approximation algorithms. In: Azéma, J., Émery, M., Ledoux, M., Yor, M. (eds.) Séminaire de Probabilités XXXIII, pp. 1–68. Springer, Berlin Heidelberg, Berlin, Heidelberg (1999)
Benaïm, M., Le Borgne, S., Malrieu, F., Zitt, P.A.: Quantitative ergodicity for some switched dynamical systems. Electron. Commun. Probab. 17, 14 (2012)
Benaïm, M., Le Borgne, S., Malrieu, F., Zitt, P.A.: Qualitative properties of certain piecewise deterministic Markov processes. Ann. Inst. H. Poincaré Probab. Stat. 51(3), 1040–1075 (2015)
Bertsekas, D.P.: Incremental proximal methods for large scale convex optimization. Math. Program. 129(2, Ser. B), 163–195 (2011)
Bierkens, J., Fearnhead, P., Roberts, G.: The zig–zag process and super-efficient sampling for Bayesian analysis of big data. Ann. Stat. 47(3), 1288–1320 (2019). https://doi.org/10.1214/18-AOS1715
Billingsley, P.: Convergence of probability measures, second edn. Wiley Series in Probability and Statistics: Probability and Statistics. Wiley, New York (1999). A Wiley-Interscience Publication
Bottou, L.: Online algorithms and stochastic approximations. In: Saad, D. (ed.) Online Learning and Neural Networks. Cambridge University Press, Cambridge (1998)
Brosse, N., Moulines, E., Durmus, A.: The promises and pitfalls of stochastic gradient langevin dynamics. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS’18, pp. 8278–8288. Curran Associates Inc., Red Hook (2018)
Canino-Koning, R., Wiser, M.J., Ofria, C.: Fluctuating environments select for short-term phenotypic variation leading to long-term exploration. PLoS Comput. Biol. 15(4), 1–32 (2019)
Chambolle, A., Ehrhardt, M.J., Richtárik, P., Schönlieb, C.B.: Stochastic primal-dual hybrid gradient algorithm with arbitrary sampling and imaging applications. SIAM J. Optim. 28(4), 2783–2808 (2018)
Chee, J., Toulis, P.: Convergence diagnostics for stochastic gradient descent with constant learning rate. In: A. Storkey, F. Perez-Cruz (eds.) Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, vol. 84, pp. 1476–1485. PMLR, Playa Blanca (2018)
Choromanska, A., Henaff, M., Mathieu, M., Arous, G.B., LeCun, Y.: The loss surfaces of multilayer networks. In: G. Lebanon, S.V.N. Vishwanathan (eds.) Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, vol. 38, pp. 192–204. PMLR, San Diego (2015)
Chow, P.L., Khasminskii, R.Z.: Method of Lyapunov functions for analysis of absorption and explosion in Markov chains. Prob. Inf. Transm. 47(3), 232 (2011). https://doi.org/10.1134/S0032946011030033
Cloez, B., Hairer, M.: Exponential ergodicity for Markov processes with random switching. Bernoulli 21(1), 505–536 (2015)
Costa, O.L.V.: Stationary distributions for piecewise-deterministic Markov processes. J. Appl. Probab. 27(1), 60–73 (1990)
Davis, M.: Markov Models and Optimization. Chapman & Hall/CRC Monographs on Statistics & Applied Probability, Taylor & Francis, London (1993)
Davis, M.H.A.: Piecewise-deterministic Markov processes: a general class of non-diffusion stochastic models. J. R. Stat. Soc. Ser. B (Methodol.) 46(3), 353–388 (1984)
Defazio, A., Bach, F., Lacoste-Julien, S.: SAGA: A fast incremental gradient method with support for non-strongly convex composite objectives. In: Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 1, NIPS’14, pp. 1646–1654. MIT Press, Cambridge (2014)
Dieuleveut, A., Durmus, A., Bach, F.: Bridging the gap between constant step size stochastic gradient descent and Markov chains. Ann. Stat. 48(3), 1348–1382 (2020). https://doi.org/10.1214/19-AOS1850
Duchi, J., Hazan, E., Singer, Y.: Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 12, 2121–2159 (2011)
Dupuis, P., Liu, Y., Plattner, N., Doll, J.D.: On the infinite swapping limit for parallel tempering. Multiscale Model. Simul. 10(3), 986–1022 (2012)
Durmus, A., Guillin, A., Monmarché, P.: Piecewise deterministic Markov processes and their invariant measure. arXiv:1807.05421 (2018)
Fearnhead, P., Bierkens, J., Pollock, M., Roberts, G.O.: Piecewise deterministic Markov processes for continuous-time Monte Carlo. Stat. Sci. 33(3), 386–412 (2018)
García-Trillos, N., Sanz-Alonso, D.: Continuum limits of posteriors in graph Bayesian inverse problems. SIAM J. Math. Anal. 50(4), 4020–4040 (2018)
Giles, M.B.: Multilevel Monte Carlo path simulation. Oper. Res. 56(3), 607–617 (2008)
Gillespie, D.T.: Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81(25), 2340–2361 (1977)
Graham, C., Robert, P.: Self-adaptive congestion control for multiclass intermittent connections in a communication network. Queueing Syst. 69(3–4), 237–257 (2011)
Haccou, P., Iwasa, Y.: Optimal mixed strategies in stochastic environments. Theor. Popul. Biol. 47(2), 212–243 (1995)
Hu, W., Li, C.J., Li, L., Liu, J.G.: On the diffusion approximation of nonconvex stochastic gradient descent. Ann. Math. Sci. Appl. 4(1), 3–32 (2019)
Iserles, A.: A First Course in the Numerical Analysis of Differential Equations. Cambridge Texts in Applied Mathematics, 2nd edn. Cambridge University Press (2008). https://doi.org/10.1017/CBO9780511995569
Jentzen, A., Kuckuck, B., Neufeld, A., von Wurstemberger, P.: Strong error analysis for stochastic gradient descent optimization algorithms. arXiv:1801.09324 (2018)
Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. In: Proceedings of the 26th International Conference on Neural Information Processing Systems—Volume 1, NIPS’13, pp. 315–323. Curran Associates Inc., Red Hook (2013)
Kolmogorov, A.: Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung. Math. Ann. 104(1), 415–458 (1931). https://doi.org/10.1007/BF01457949
Kovachki, N.B., Stuart, A.M.: Ensemble Kalman inversion: a derivative-free technique for machine learning tasks. Inverse Prob. 35(9), 095005 (2019)
Kritzer, P., Leobacher, G., Szölgyenyi, M., Thonhauser, S.: Approximation methods for piecewise deterministic Markov processes and their costs. Scand. Actuar. J. 2019(4), 308–335 (2019)
Kuntz, J., Ottobre, M., Stuart, A.M.: Diffusion limit for the random walk Metropolis algorithm out of stationarity. Ann. Inst. H. Poincaré Probab. Stat. 55(3), 1599–1648 (2019)
Kushner, H.J.: Approximation and Weak Convergence Methods for Random Processes, with Applications to Stochastic Systems Theory, MIT Press Series in Signal Processing, Optimization, and Control, vol. 6. MIT Press, Cambridge (1984)
Kussell, E., Leibler, S.: Phenotypic diversity, population growth, and information in fluctuating environments. Science 309(5743), 2075–2078 (2005)
Latz, J., Madrigal-Cianci, J.P., Nobile, F., Tempone, R.: Generalized Parallel Tempering on Bayesian Inverse Problems. arXiv:2003.03341 (2020)
Li, Q., Tai, C., Weinan, E.: Stochastic modified equations and adaptive stochastic gradient algorithms. In: D. Precup, Y.W. Teh (eds.) Proceedings of the 34th International Conference on Machine Learning, Proceedings of Machine Learning Research, vol. 70, pp. 2101–2110. PMLR, International Convention Centre, Sydney, Australia (2017). http://proceedings.mlr.press/v70/li17f.html
Li, Q., Tai, C., Weinan, E.: Stochastic modified equations and dynamics of stochastic gradient algorithms i: mathematical foundations. J. Mach. Learn. Res. 20(40), 1–47 (2019)
Li, Q., Tai, C., Weinan, E.: Stochastic modified equations and dynamics of stochastic gradient algorithms i: mathematical foundations. J. Mach. Learn. Res. 20, 1–40 (2019)
Li, X., Orabona, F.: On the convergence of stochastic gradient descent with adaptive stepsizes. In: K. Chaudhuri, M. Sugiyama (eds.) The 22nd International Conference on Artificial Intelligence and Statistics, AISTATS 2019, 16-18 April 2019, Naha, Okinawa, Japan, Proceedings of Machine Learning Research, vol. 89, pp. 983–992. PMLR (2019)
Lord, G.J., Powell, C.E., Shardlow, T.: Stochastic Ordinary Differential Equations. Cambridge Texts in Applied Mathematics, pp. 314–371. Cambridge University Press, Cambridge (2014). https://doi.org/10.1017/CBO9781139017329.009
Mandt, S., Hoffman, M.D., Blei, D.M.: A variational analysis of stochastic gradient algorithms. In: Proceedings of the 33rd International Conference on International Conference on Machine Learning—Volume 48, ICML’16, pp. 354–363. JMLR.org (2016)
Mandt, S., Hoffman, M.D., Blei, D.M.: Stochastic gradient descent as approximate Bayesian inference. J. Mach. Learn. Res. 18(1), 4873–4907 (2017)
Nemirovski, A., Juditsky, A., Lan, G., Shapiro, A.: Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 19(4), 1574–1609 (2009)
Nocedal, J., Wright, S.J.: Numerical Optimization, pp. 1–9. Springer, New York (2006)
Olofsson, H., Ripa, J., Jonzén, N.: Bet-hedging as an evolutionary game: the trade-off between egg size and number. Proc. R. Soc. B Biol. Sci. 276(1669), 2963–2969 (2009)
Pedersen, G.: Analysis Now. Springer, Berlin (1989)
Power, S., Goldman, J.V.: Accelerated Sampling on Discrete Spaces with Non-Reversible Markov Processes. arXiv:1912.04681 (2019)
Rao, V.A.P.: Markov chain Monte Carlo for continuous-time discrete-state systems. Ph.D. thesis, University College London (2012)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. 22(3), 400–407 (1951)
Robert, C.P., Casella, G.: Random Variable Generation, pp. 35–77. Springer, New York (2004)
Rudnicki, R., Tyran-Kamińska, M.: Piecewise Deterministic Processes in Biological Models. Springer Briefs in Applied Sciences and Technology and Springer Briefs in Mathematical Methods. Springer, Cham (2017)
Sasaki, A., Ellner, S.: The evolutionarily stable phenotype distribution in a random environment. Evolution 49(2), 337–350 (1995)
Schillings, C., Stuart, A.M.: Analysis of the ensemble Kalman filter for inverse problems. SIAM J. Numer. Anal. 55(3), 1264–1290 (2017)
Schmidt, M., Le Roux, N., Bach, F.: Minimizing finite sums with the stochastic average gradient. Math. Program. 162(1–2), 83–112 (2017)
Schwabl, F.: Statistical Mechanics. Springer, Berlin, Heidelberg (2006)
Simovich, M.A., Hathaway, S.A.: Diversified bet-hedging as a reproductive strategy of some ephemeral pool anostracans (branchiopoda). J. Crustac. Biol. 17(1), 38–44 (1997)
Sirignano, J., Spiliopoulos, K.: Stochastic gradient descent in continuous time. SIAM J. Financ. Math. 8(1), 933–961 (2017). https://doi.org/10.1137/17M1126825
Sirignano, J., Spiliopoulos, K.: Stochastic gradient descent in continuous time: a central limit theorem. Stoch. Syst. 10(2), 124–151 (2020). https://doi.org/10.1287/stsy.2019.0050
Song, Y., Song, J., Ermon, S.: Accelerating natural gradient with higher-order invariance. In: J. Dy, A. Krause (eds.) Proceedings of the 35th International Conference on Machine Learning, Proceedings of Machine Learning Research, vol. 80, pp. 4713–4722. PMLR, Stockholmsmössan, Stockholm Sweden (2018)
Vidal, R., Bruna, J., Giryes, R., Soatto, S.: Mathematics of Deep Learning. arXiv:1712.04741 (2017)
Villani, C.: Optimal transport, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 338. Springer, Berlin (2009)
Welling, M., Teh, Y.W.: Bayesian learning via stochastic gradient langevin dynamics. In: Proceedings of the 28th International Conference on International Conference on Machine Learning, ICML’11, pp. 681–688. Omnipress, Madison (2011)
Yang, R.L.: Convergence of the simulated annealing algorithm for continuous global optimization. J. Optim. Theory Appl. 104(3), 691–716 (2000)
Yin, G.G., Zhu, C.: Hybrid Switching Diffusions: Properties and Applications. Springer, New York (2010)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author acknowledges support from the EPSRC grant EP/S026045/1 “PET++: Improving Localisation, Diagnosis and Quantification in Clinical and Medical PET Imaging with Randomised Optimisation”. The author is very grateful for insightful discussions with Claire Delplancke, Matthias Ehrhardt, and Carola-Bibiane Schönlieb that contributed to this work. Furthermore, the author thanks Christian Etmann and Felipe Uribe for carefully reading and commenting on this manuscript. Finally, the author thanks the anonymous reviewers for their helpful and constructive reports.
A: Auxiliary results concerning CTMPs
A: Auxiliary results concerning CTMPs
In this appendix, we give a brief derivation of the Markov kernel describing the processes \(({{\varvec{i}}}(t))_{t \ge 0}\) and \(({{\varvec{j}}}(t))_{t \ge 0}\). Moreover, we discuss the non-explosiveness of \(({{\varvec{j}}}(t))_{t \ge 0}\), i.e. we show that the sequence of jump times \((T_k)_{k=1}^\infty \) satisfies
We commence with the discussion of the Markov kernels.
Lemma 5
Let \(M_t: I \times 2^I \rightarrow [0,1]\) be given by
for \(i, i_0 \in I, t \ge 0.\) Then,
Moreover, let \(M_{t|t_0}': I \times 2^I \rightarrow [0,1]\) be given by
for \(j, j_0 \in I\) and \( t \ge t_0 \ge 0.\) Then,
Proof
We prove only the assertion concerning \(({{\varvec{j}}}(t))_{t \ge 0}\), the proof for \(({{\varvec{i}}}(t))_{t \ge 0}\) is analogous. Indeed, we show that \((M_{t|t_0}'(\{j\}|j_0))_{j, j_0 \in I}\) satisfies the Kolmogorov forward equation for any \(t_0 \ge 0\):
For details, we refer to the fundamental work by Kolmogorov (Kolmogorov 1931, Equations (47), (52)). The initial condition (27) is obviously satisfied. Moving on to (26). We have
Due to symmetry, it is sufficient to consider the cases \(j=j_0\) and \(j \ne j_0\). Let first \(j=j_0\). Then,
If on the other hand, \(j \ne j_0\), we have
Hence, \(M_{t|t_0}'\) is indeed the Markov kernel describing the transition of the CTMP \(({{\varvec{j}}}(t))_{t \ge 0}\). \(\square \)
We now move on to proving the non-explosiveness of \(({{\varvec{j}}}(t))_{t \ge 0}\).
Lemma 6
Let \((T_k)_{k=1}^\infty \) be the jump times of \(({{\varvec{j}}}(t))_{t \ge 0}\). Then,
Proof
In the following, we construct a CTMP \(({{\varvec{k}}}(t))_{t \ge 0}\) on \(\mathbb {N}\) which has the same jump times \((T_k)_{k=0}^\infty \) as \(({{\varvec{j}}}(t))_{t \ge 0}\). Then, we show that \(({{\varvec{k}}}(t))_{t \ge 0}\) satisfies the assumptions of Proposition 1 in Chow and Khasminskii (2011) on any compact intervall in \([0,\infty )\). This will imply our assertion. Let \(({{\varvec{k}}}(t))_{t \ge 0}\) be the CTMP on \(\mathbb {N}\) with transition rate matrix \( \varLambda (t): \mathbb {R}^{\mathbb {N}} \rightarrow \mathbb {R}^{\mathbb {N}} (t \ge 0), \) with
We now need to check the following assertions for \({\overline{t}}>{\underline{t}}\ge 0.\)
-
(i)
\(\inf _{t \in [{\underline{t}}, {\overline{t}}]} \sum _{i=1}^n\frac{1}{-\varLambda (t)_{i,i}} \rightarrow \infty \), as \(n \rightarrow \infty \),
-
(ii)
there is a constant \(C_{{\overline{t}}}^{(0)}>0\), such that \(-\varLambda (t)_{i,i} > C_{{\overline{t}}}^{(0)}(-\varLambda (t)_{j,j}) \), for \(i >j\), \(t \in [{\underline{t}}, {\overline{t}}]\)
-
(iii)
there is a constant \(C_{{\overline{t}}}^{(1)}>0\), such that
$$\begin{aligned} \sum _{j=i+1}^\infty \frac{\varLambda (t)_{i,j}}{-\varLambda (t)_{i,i}}(j-i) \le C_{{\overline{t}}}^{(1)} \sum _{j=1}^i \frac{1}{-\varLambda (t)_{j,j}}, \end{aligned}$$for \(i \in \mathbb {N}, t \in [{\underline{t}}, {\overline{t}}]\), and
$$\begin{aligned} \left|-\frac{\partial }{\partial t}{\varLambda }(t)_{i,i} \right|\le C_{{\overline{t}}}^{(1)}(-\varLambda (t)_{i,i}). \end{aligned}$$for \(i \in \mathbb {N}, t \in [{\underline{t}}, {\overline{t}}]\).
Since \(-\varLambda (t)_{i,i}\) is constant in \(i \in \mathbb {N}\) and non-decreasing in t, the infimum in (i) is given by \(-n/\varLambda ({\overline{t}})_{1,1}.\) This indeed goes to \(\infty \), as \(n \rightarrow \infty \), proving (i). Again, as \(-\varLambda (t)_{i,i}\) is constant in \(i \in \mathbb {N}\), (ii) holds, with \(C_{{\overline{t}}}^{(0)} = 0.9\). Moreover, we have
Choosing \(C_{{\overline{t}}}^{(1)} \ge -\varLambda ({\overline{t}})_{1,1}\), we can verify the first assertion of (iii), since \(-\varLambda (t)_{1,1}\) is non-decreasing in t. The second assertion of (iii) holds with a constant \(C_{{\overline{t}}}'\), as by assumption \(-\varLambda (t)_{i,i}\) and \(|-\frac{\partial }{\partial t} \varLambda (t)_{i,i}|\) are both continuous functions on the compact interval \( [{\underline{t}}, {\overline{t}}]\) and
(iii) is satisfied with \(C_{{\overline{t}}}^{(1)}:= \max \{-\varLambda ({\overline{t}})_{1,1}, C_{{\overline{t}}}'\}\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Latz, J. Analysis of stochastic gradient descent in continuous time. Stat Comput 31, 39 (2021). https://doi.org/10.1007/s11222-021-10016-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-021-10016-8