Abstract
The Mercury Orbiter Radio Science Experiment (MORE) of the ESA mission BepiColombo will provide an accurate estimation of Mercury’s gravity field and rotational state, improved tests of general relativity, and a novel deep space navigation system. The key experimental setup entails a highly stable, multi-frequency radio link in X and Ka band, enabling two-way range rate measurements of 3 micron/s at nearly all solar elongation angles. In addition, a high chip rate, pseudo-noise ranging system has already been tested at 1-2 cm accuracy. The tracking data will be used together with the measurements of the Italian Spring Accelerometer to provide a pseudo drag free environment for the data analysis. We summarize the existing literature published over the past years and report on the overall configuration of the experiment, its operations in cruise and at Mercury, and the expected scientific results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mercury is one of the most interesting objects in the solar system, and, till the arrival of NASA’s MESSENGER spacecraft, one of the least known. The 3:2 resonance between its rotational and orbital periods, its large density and the unexpected discovery of a substantial magnetic field were and still are some of the most fascinating problems in planetary science. However, Mercury was visited only twice by a spacecraft since the large energy required to reach the planet and the harsh thermal and radiation environment represent formidable obstacles to its exploration. Mariner 10 flybys in 1974–1975 provided a first glimpse on the planet, revealing the main characteristics of the surface morphology. But much was yet to be discovered. The interior structure and the gravity field were essentially unknown. The magnetic field measured by Mariner 10 puzzled the planetary community, as the geophysical models predicted a solid core for the planet.
S. Peale (1976) defined the internal structure of Mercury and the physical state of the core as one of the most important science themes regarding the formation and evolution of the Solar System. Either a new mechanism other than a planetary dynamo was at play or the models for the composition and thermal history of Mercury were inaccurate. The estimation of Mercury’s rotation through Earth-based radar measurements (Margot et al. 2007) provided crucial experimental evidence that Mercury has a partially molten core. The real breakthrough in our understanding of the planet came from the results of the NASA mission MESSENGER, whose planetary phase lasted four years (from April 2011 to April 2015). An in-depth characterization of Mercury’s surface and interior through the analysis of the MESSENGER data revealed a dynamic past, made up probably by an early magma ocean and billions of years of active volcanism (Johnson and Hauck 2016). Gravity (Smith et al. 2012; Genova et al. 2013, 2019; Mazarico et al. 2014) and rotation measurements (Margot et al. 2012; Stark et al. 2015) unveiled the broad structure of Mercury’s interior, whose outer part was at least few Ga ago robustly convective (Breuer et al. 2007; Tosi et al. 2013).
The orbital evolution of Mercury about the Sun has also been an important objective of a long and fascinating scientific investigation to study theories of gravitation. The anomalous precession of its perihelion was difficult to explain in the framework of classical physics. In the attempt to reconcile Newtonian mechanics with observations, Le Verrier suggested the existence of Vulcan, an inner planet closer to the sun than Mercury (Hanson 1962). It was soon recognized that only a belt of many small bodies, the Vulcanoids, could explain the astrometric observations, but neither Vulcan nor the Vulcanoids were ever discovered. Rather, the orbit of Mercury gave General Relativity its first experimental success. Solving the equation of motion in a relativistic formalism, Einstein and de Sitter computed a perihelion drift incredibly close to the observed one. It was a brilliant success for the new theory of gravity. Today GR has passed many experimental tests, such as the measurement of the parameterized post-Newtonian (PPN) parameter \(\gamma \) obtained in 2003 by Doppler tracking of the Cassini spacecraft (Bertotti et al. 2003). But it is very unlikely that GR is the ultimate theory of gravity. The intrinsic incompatibility of GR with quantum mechanics has motivated a long lasting, but still unsuccessful search for violations of Einstein’s paradigm. Recent theoretical developments have suggested that the field equations might be changed to accommodate the contribution from a small scalar field, remnant of the age of inflation. Such a scalar field entails violations of GR in classical tests, and there is no solar system body better than Mercury to carry out these tests. The discovery of a link between theories of gravity and cosmology would have profound consequences in physics.
The Mercury Orbiter Radio-science Experiment (MORE) of the BepiColombo mission will tackle these outstanding and complex scientific problems. The goal is to make major step forward in our knowledge of Mercury. This requires a) substantial extensions and increase in accuracy of the results obtained by MESSENGER and b) a full exploitation of the unique characteristics of Mercury as a laboratory for fundamental physics. The experimental setup considered for BepiColombo exploits dedicated onboard and ground hardware to carry out accurate measurements of the spacecraft range and range-rate. The physical parameters of interest will be derived from these observable quantities, supplemented by a measurement of the non-gravitational accelerations provided by the onboard Italian Spring Accelerometer (ISA). The use of an accelerometer and a Ka-band radio link at 32–34 GHz (a first for a European interplanetary mission) are the crucial and necessary technological steps.
The plan of the paper is the following. In Sect. 2 we outline the main scientific goals of MORE in the context of the mission, focusing on the estimate of the gravity field and tests of relativistic gravity. In Sect. 3 we describe the observable quantities (Doppler and range) used in the estimation of the derived parameters, including the data calibration procedures. Section 4 presents the architecture of the onboard and ground radio system. Section 5 describes the crucial media calibration system needed to attain the required performances. Section 6 provides the error budget for all observable quantities (range, range rate and \(\Delta\)-Differential One-way Ranging (\(\Delta \)DOR)). The non-gravitational and inertial accelerations and their suppression by means of the Italian Spring Accelerometer (ISA) are treated in Sect. 7. Section 8 describes the MORE operations during cruise and in the hermean phase. Section 9 outlines the numerical procedures employed or developed for orbit determination and the estimation of the derived parameters (i.e., gravity coefficients, rotational state, PPN parameters). Finally, Sect. 10 presents the expected results for geodesy and geophysics of the planet Mercury, and the expected improvements in the parameters relevant to fundamental physics.
2 MORE Science Goals
Concisely, the Level 1 scientific goals of MORE are threefold:
-
Gravity: high fidelity determination of the static gravity field and the gravitational tidal response (i.e., Love number \(k_{2}\)) of Mercury;
-
Rotation: estimation of Mercury’s rotational state (i.e., pole orientation, spin rate, and amplitude and phase of physical librations in longitude);
-
Fundamental physics: test different aspects of General Relativity (GR) through a precise determination of several parametrized post-Newtonian (PPN) parameters.
In addition, MORE will test the novel radio system and the availability of a precise measurement of the non-gravitational accelerations provided by ISA (Santoli et al. this issue) for precise spacecraft navigation. This engineering by-product of the technology used by the MORE investigation (Ka-band and multi-frequency radio links, high-rate pseudo-noise ranging system) may pave the way to an upgrade of the ESA ground tracking infrastructure.
The interpretation of the geodesy and geophysics measurements of the BepiColombo mission, to which MORE will contribute, are described in depth in a separate paper (Genova et al. this issue). Here we limit ourselves to an overview of the scientific investigations made possible by MORE.
2.1 Gravity and Rotation
The precise gravity measurements enabled by the radio system onboard the Mercury Planetary Orbiter (MPO) of the BepiColombo mission will enable a thorough insight into the subsurface and deep interior of Mercury, to an enhanced level of accuracy compared to our current knowledge (see Sect. 6). The main science goal of MORE related to geodesy and geophysics is the precise retrieval of the static and time-varying gravity field of Mercury through an extremely high-accurate analysis of the spacecraft orbital motion. The ultimate goal of this study is to improve our knowledge of the structure of the mantle, the crust/mantle interface, and the deep internal structure of Mercury. The main science objectives of our gravity investigation are:
-
Static gravity field to maximum degree and order 45 (or 35 when Kaula regularization is not used) to constrain the properties of the crust and the lithosphere, accounting for Mercury’s internal loading.
-
Subsurface properties of Mercury to infer the internal heat flow at different epochs.
-
Tidal variations of the gravity field through the estimation of the Love number \(k_{2}\), which, in combination with the Love number \(h_{2}\) and the measurements of the rotational state, allows determining the state and dimension of the liquid outer core and the solid inner core.
-
Principal moments of inertia of Mercury by estimating the low degree gravity coefficients \(J_{2}\) and \(C_{22}\), the librations and pole obliquity to better characterize the deep interior.
The rotational state (i.e., pole location, obliquity and physical librations in longitude) will be derived by gravity measurements (see the results on Table 5, Sect. 10.2), also in combination with observations from the BepiColombo Laser Altimeter (BELA) (Thomas et al. 2020, this journal) and High Spatial Imaging Channel (HRIC) of the Spectrometer and Imaging for MPO BepiColombo Integrated Observatory SYStem (SIMBIO-SYS) (Cremonese et al. 2020).
Gravity anomalies are due to the uneven distribution of mass in the planet, as, for example, induced by the topography. The accurate mapping that will be accomplished by the laser altimeter BELA is thus fundamental for recovering the volume of surface features that enables the computation of the gravity from topography (Wieczoreck and Phillips 1998; Neumann et al. 2004). By removing the gravity signals associated with topographic relief (i.e., Bouguer correction), the measured gravity anomalies provide crucial information on the planetary internal structure. In addition to the position and amplitude of the anomalies, their spectral content is of great interest to distinguish between near-surface and deep mass anomalies. Short-wavelength anomalies reveal the structure of the crust and upper mantle, whereas large-wavelength anomalies reflect features in the deeper mantle, such as plumes due to mantle convection or undulations of the core-mantle boundary (CMB). The gravity signal depends on the CMB loads and deformation, yielding constraints on the rigidity of the lithosphere (Karner and Watts 1983). Topographical and internal loads may cause lithospheric deformations through crustal thickness variations or the presence of mantle plumes, which act as a buoyant support. The estimated lithospheric thickness depends on the surface heat flow at the time of loading, essential information for the reconstruction of the thermal history of Mercury (Tosi et al. 2013).
One of the most interesting constraints on Mercury’s internal structure will be obtained from the accurate measurements of the moments of inertia of the planet in the equatorial plane as well as in the rotation axis direction. Combinations of these moments of inertia are provided by the degree 2 coefficients \(J_{2}\) and \(C_{22}\) of the gravity field (Peale et al. 2002). Gravity data from MESSENGER confirmed the original indications by Mariner 10 of a strong non-hydrostatic contribution at harmonic of degree 2 (Smith et al. 2012). These coefficients will be jointly used with precise estimates of the pole obliquity based on independent altimetry and gravity investigations (Genova et al. 2021, this journal) to retrieve the mean scaled moment of inertia factor of Mercury C/MR2 (\(C \) is the polar moment of inertia, \(M\) the mass and \(R\) the mean radius of Mercury) with a precision of at least 0.003 (e.g., Imperi et al. 2018).
Mercury is known to be differentiated into relatively thin outer silicate layers, i.e., the crust and the mantle, and a large core (Hauck et al. 2013). The presence of a weak global magnetic field, as observed originally by Mariner 10 (Ness et al. 1974) and confirmed in much greater detail by MESSENGER (Anderson et al. 2011), suggests that the deep interior includes a solid inner core and an outer molten core made by iron alloyed with a single or a combination of light elements (e.g., sulphur, silicon). Accurate estimates of the amplitude of physical librations in longitude with the analysis of Earth-based radar measurements (Margot et al. 2007) and the degree-2 gravity field coefficients by the MESSENGER radio science investigation (Smith et al. 2012) enabled the determination of the size of the entire core with a radius of \(2020\pm 30\) km (Hauck et al. 2013) with a mean core density of \(6980 \pm 280\) kg m−3. Mercury’s rotational state parameters were also adjusted by processing MESSENGER imaging and altimetric data confirming previous results (Stark et al. 2015). An enhanced measure of Mercury’s pole obliquity with the latest gravity solution of the MESSENGER mission (Genova et al. 2019) suggests a slightly lower radius of the outer core (i.e., \(1985 \pm 39\) km), and the possible presence of a large inner core.
A comprehensive understanding of Mercury’s interior is also based on a thorough knowledge of the gravitational and deformation tides. The main tidal waves have periods related to the orbital and rotational period of Mercury, and integer divisors thereof (Van Hoolst and Jacobs 2003). Classically, the deformation of a planet and the change of its potential are expressed in the Love number formalism: the deformation equations are linearized, and the changes are given by the product of a dimensionless Love number and the tidal potential. For instance, the mass redistribution potential induced by the tides on an object on or above the surface is given by the product of the Love number \(k_{2}\) and the forcing potential. The Love number \(k_{2}\) measured by MESSENGER is still subject to considerable uncertainty. Mazarico et al. (2014) report a central value of 0.451 with a recommended realistic range of acceptable values of 0.43–0.50. Verma and Margot (2016) quote a similar central value and a recommended range of 0.420–0.465. The latest gravity solutions carried out by analyzing the whole MESSENGER radio science dataset, including the low-altitude campaign, show independent adjustments of the Love number \(k_{2} = 0.57\pm 0.03\) (Genova et al. 2019) and \(k_{2} = 0.53\pm 0.03\) (Konopliv et al. 2020). These larger estimates, which were retrieved by accounting for radio tracking data more sensitive to the gravitational tidal response, suggest a warm and weak mantle (Padovan et al. 2014). The uncertainties of these tidal measurements are affected by the MESSENGER orbit geometry (i.e., high-eccentric orbit) and by the strong perturbations of the non-conservative forces on the spacecraft dynamics.
BepiColombo’s MPO will help enhance our knowledge of Mercury’s tidal response by measuring the planetary gravity field from a low-eccentric orbit. The precise orbit determination of the spacecraft will be based on the processing of MORE radio tracking data and ISA observations to accurately measure the accelerations induced by non-gravitational perturbations, including solar, albedo, and thermal radiation pressure. This experiment configuration enables a significant refinement of the Love number \(k_{2}\) and a first estimate of its phase lag (Imperi et al. 2018), which allows constraining the rheological properties of the mantle and outer core. The improved determination from MORE (at the level of \(2\times 10^{-4}\) both for the real and imaginary part) would be highly relevant to a better knowledge of the planet, as the Love number varies significantly for different interior models as a function of parameters such as the percentage of light element within the core (see Van Hoolst and Jacobs 2003). Extremely precise tidal measurements yield powerful insight into the interior of Mercury by providing geophysical constraints that are fundamental for a thorough modeling of Mercury.
Furthermore, the precise orbit determination of the MPO through the analysis of MORE data will greatly help the determination of the Love number \(h_{2}\), which measures the physical displacement of the planetary surface. Thor et al. (2020) indicate that \(h_{2}\) may be determined with a formal uncertainty of 0.012 by using BELA laser altimetric measurements that are opportunely processed with a refined orbit reconstruction. A combined knowledge of the Love numbers \(k_{2}\) and \(h_{2}\) will result in outstanding refinements of the interior modeling (Steinbrügge et al. 2018) and composition (Van Hoolst and Jacobs 2003).
The measurement of the lag angle and its uncertainty yields an upper bound to the value of the quality factor \(Q\) of Mercury’s mantle. By using the values reported by Imperi et al. (2018), the phase lag error can be as small as \(0.016^{\circ}\), corresponding to a largest measurable value \(Q\sim 1730\). Since moments of inertia and Love numbers have a complementary dependence on the core properties, joint analysis of these key geophysical constraints are essential for improving the determination of the composition and size of the inner core, outer core and mantle. To infer the radius, density and rigidity of these interior layers, the observed geophysical quantities will be processed in interior modeling solutions (Rivoldini et al. 2009; Knibbe and van Westrenen 2015; Matsuyama et al. 2016; Knibbe and van Westrenen 2018).
A precise characterization of Mercury’s internal structure strongly relies on the knowledge of the polar moment of inertia of the entire planet, \(C\), and of the outer silicate layers, \(C_{cr+m}\). Peale (1988) demonstrated the relevance of determining Mercury’s rotational state to compute the ratio \({C_{cr+m}} / {C}\) from measurements of the quadrupole gravity coefficients, the obliquity and the amplitude of the physical librations in longitude. As proposed by Colombo and Shapiro (1966), the resonant rotation state can be analyzed in terms of Cassini states, generalizing the ones well known for the 1:1 resonance, e.g., for the Moon. In this theory the rotation axis of Mercury lies in the plane (i.e., the Cassini plane) defined by the orbit normal and the normal to the invariable plane of the Solar System, and, in between the two, with the rotation axis (much closer to the orbit normal). The exact value of the pole obliquity, which is the angle between the spin axis and the normal to the orbit plane, is a function of the normalized polar moment of inertia \(C/\mathit{MR}^{2}\).
Because of the large eccentricity of Mercury’s orbit, a periodic forcing torque acts on the equatorial asymmetric bulge of the planet. This torque has the orbital period of ∼88 days. Thus the main component of the libration, i.e., the variation in longitude with respect to the nominal resonant rotation, has a period equal to the orbital period. Given the magnitude of the forcing torque, which can be derived from the value of the gravity coefficient \(C_{22}\), the amplitude of the libration in longitude is small in case of an entire rigid body, and large with decoupling between the outer layers (crust and mantle) and the core. Accurate measurements of the large libration amplitude (i.e., ∼400 m) with Earth-based radar observations (Margot et al. 2007, 2012) and the combination of MESSENGER imaging and altimetric data (Stark et al. 2015) confirmed that Mercury has a liquid layer in the upper core similarly to the Earth.
In quantitative terms, the ratio of the moment of inertia of the decoupled silicate layers \(C_{cr+m}\) to the moment of inertia \(C\) of the entire planet (along the rotation axis) can be computed as the product of three factors,
Here \(A \) and \(B\) are the equatorial moments of inertia, and \(C\) is the polar moment of inertia of the planet. The first factor is determined by measuring the amplitude of the forced libration in longitude (Peale et al. 2002). The second factor from the \(C_{22}\) harmonic coefficient; the third factor from the Cassini state obliquity of the rotation axis (Peale 1988). The combination of multidisciplinary science investigations (Margot et al. 2012; Mazarico et al. 2014; Stark et al. 2015; Genova et al. 2019) have enabled the computation of this ratio to constrain the properties of Mercury’s interior (Hauck et al. 2013; Knibbe and van Westrenen 2015; Knibbe and van Westrenen 2018; Genova et al. 2019). The gravity data collected by MORE will allow measuring all the geodetic parameters necessary to compute the ratio \(\frac{C_{cr+m}}{C}\) with unprecedented accuracies (Imperi et al. 2018). Furthermore, independent estimates of Mercury’s obliquity with gravity and altimetric data may provide information on the shape of the inner core and the core-mantle boundaries (Peale et al. 2016).
Although it is not expected that Mercury would show a measurable polar motion (0.2 arcsec on the Earth), it is also desirable to constrain the displacement of the pole transversal to the Cassini plane to a comparable level of accuracy.
2.2 Fundamental Physics
Mercury is the innermost and fastest planet of the solar system. Relativistic effects on its motion are therefore larger than for any other solar system body, making it a unique laboratory for probing gravity and its theoretical description. The brilliant explanation of the anomalous periastron advance of Mercury’s orbit, incompatible with Newtonian physics, was the first experimental success of general relativity. MORE can repeat classical tests with much improved accuracy and, thanks to the proposed system configuration, explore new aspects of gravitational theories.
Mercury is such a unique body for gravitational physics that dedicated missions have been proposed in the past (e.g. Bender et al. 1989, 1994). Preliminary simulations indicated that radio tracking of a small spacecraft inserted in a high, circular orbit about Mercury could lead to a large improvement in the determination of many Parametrized Post-Newtonian (PPN) parameters. (The PPN formalism is a way to classify alternative theories of gravity using a set of ten parameters.) Although these proposals were never followed by a space mission, space agencies became aware that any future mission to Mercury could be potentially exploited for fundamental as well as planetary physics. Testing relativistic gravity was indeed recognized as a crucial scientific objective of BepiColombo since the inception of the project. The accelerometer and the radio system proposed for investigating the gravity field and the deep internal structure of the Mercury could be used with minor addition (namely a high precision ranging system) to carry out many classical tests of general relativity with unprecedented accuracy.
MORE scientific goals in fundamental physics are summarized as follows:
-
Test General Relativity and alternative theories of gravity to a level better than \(10^{-5}\) by measuring the time delay and Doppler shift of radio waves, and the precession of Mercury’s perihelion.
-
Test the strong equivalence principle to a level better than \(4 \cdot 10^{-5}\).
-
Test the isotropy of space and preferred frame effects.
-
Determine dynamically the gravitational oblateness of the Sun (\(J_{2}\)) to better than \(10^{-8}\).
-
Set improved upper limits to the time variation of the gravitational “constant” \(G\).
-
Set upper limits to the Compton wavelength of the graviton.
Detailed orbital simulations of the radio science experiment using realistic error models are described later in Sect. 10 of the paper. In general, all PN parameters can be determined with considerable improvement over present accuracies (De Marchi and Cascioli 2020). MORE will also be able to test gravity theories with torsion and set constraints on modified Newtonian gravity theories (MOND).
It is important to look at these goals in the general framework of experimental gravity. First of all, it should be stressed that the experimental investigation of the nature of the gravitational interaction to the best possible accuracy is a priority goal for the foundations of physics, in particular in relation to the question, whether the force between macroscopic neutral bodies can be fully understood in the framework of the Riemannian geometry of spacetime. The Cassini measurement of the deflection parameter \(\gamma \) (Bertotti et al. 2003), about 50 times better than what had been previously achieved, has made a large advance toward this goal; the Doppler technique used in this experiment will be replaced by the classical ranging observable in BepiColombo’s radio science experiment. The measurement of the relativistic parameters \(\gamma\) and \(\beta\) (which take the values 1 in Einstein’s theory) is inextricably connected with the solar quadrupole moment \(J_{2}\), which contributes, just as the relativistic corrections, to the advance of Mercury’s perihelion. The expected accuracy for \(J_{2}\) will provide information about the differential rotation of the solar core and will be quite relevant for a better understanding of the structure of the deep interior of the Sun.
With the steadily increasing accuracy in space experiments (GAIA in particular) we are approaching the regime at which violations of Einstein’s theory are predicted by some theories, rooted in the role of string theory in early cosmology, due, in particular to T. Damour, G. Veneziano, A.M. Polyakov and several others (see, for example, Damour et al. 2002). In this view the Equivalence Principle and General Relativity are generically and jointly violated, due to a small scalar field \(\phi \) which is a present-day remnant of the “dilaton” field of string theory. The crucial point is that \(\phi \), with its own dependence on time and space, is expected to affect in a different way all the different physical interactions. While a real, computable theory seems at this time difficult to achieve, we have at least, based on general considerations, a firm prediction, that \(\gamma < 1\); disproving this constraint would constitute a major advance.
The accurate tracking of BepiColombo will involve at least four bodies: the spacecraft, the Earth, the Sun and Mercury. Their masses result from different combinations of different binding energies – for the three big bodies, mainly the gravitational contribution. It will be interesting to test their separate compliance with the Weak Equivalence Principle, to wit, whether they fall with the same acceleration in the gravitational field. BepiColombo will be able to test the strong equivalence principle in the weak field regime. A comparison with the recent test carried out in a different regime with the data analysis of the triple pulsar system (Archibald et al. 2018; Voisin et al. 2020) provides an upper bound on \(\eta \) at the level of \(10^{-6}\).
2.3 Other Science and Engineering Goals
In order to determine the topography of Mercury, it is essential to combine the data from the radio tracking (and the accelerometer) with the data from the laser altimeter. The elevation model, as a data product, will be a result of the laser altimeter processing. On the other hand, MORE will provide the laser altimeter team with the data products they need, namely the orbit of the MPO with a radial accuracy of ≤10 cm during the tracking sessions (a few tens of cm for the entire mission duration), and the hermesoid (geoid), to be used as reference surface, enabling the transformation of the laser distance measurements into a true topography of the planet.
A geodetic control network could be realized by using the camera instrument (in the horizontal direction, but also in the vertical one if stereo capabilities are included). However, to put the control network in an absolute body-fixed reference frame, the orbit of the MPO needs to be used as reference. MORE will provide precise spacecraft ephemerides to the camera team, with an accuracy more than adequate to the task at hand.
Finally, the orbit determined by MORE could be useful also for operational purposes, although the delivery of quick look orbit data is currently not planned: processing will be in batch, over time scales of several weeks.
3 Observable Quantities
As a consequence of the equivalence principle, every gravity measurement in space requires the measurement of the relative acceleration of two bodies. In planetary geodesy one uses on one end the spacecraft as a mass in free fall in the combined gravity field of the planet and solar system bodies, and a ground antenna, used as a fiducial point, on the other end. Radio signals exchanged between the ground antenna and the spacecraft are then used to obtain radio-metric measurements (range, range rate, and angles), which are then fitted to a dynamical model of the solar system to derive a variety of quantities for solar system dynamics, tests of relativistic gravity, planetary geodesy, probing of atmospheres and ionospheres. Spacecraft tracking with microwave links provides a number of observable quantities used for navigation and orbit determination. The MORE investigation requires only range and range rate. Angular information from \(\Delta \)DOR observations, although not strictly needed, are useful to constrain the inclination of Mercury’s orbit.
3.1 Range Rate
Range rate is obtained by measuring the Doppler shift of a radio carrier between transmission and reception from and to a ground station. In the simplest implementation, a carrier of very stable frequency \(f_{0}\) is transmitted from ground toward the spacecraft. The onboard transponder receives the signal and generates a cleaned, coherent replica by means of a phase-locked loop (PLL). In order to avoid interference between incoming and outgoing signals, the replica is frequency-shifted by an amount \(\alpha \) (the transponding ratio) before amplification and retransmission to ground. The ground station receives the carrier from the spacecraft and beats it against a signal of frequency \(\sim \alpha *f_{0}\). The accumulated phase of the resulting signal is measured and used to reconstruct the sky frequency. This experimental setup (typical of closed loop receivers) is especially suitable for near-real-time measurements, but it is not always the preferred one for precision measurements. MORE primary observables will be phases derived from wideband sampling (at about 1 kHz) of the received signal (after suitable downconversion). The recorded carrier samples will be later processed by means of a fully digital phase-locked loop which allows a very precise reconstruction of the received signal (phase, frequency and amplitude). This open loop implementation has several advantages: a greater flexibility in adapting the PLL to the varying noise level (reduces noise at low integration times); a superior robustness to the effects of plasma noise when tracking occurs near superior solar conjunctions; a better capability of tracing instrumental problems.
3.2 Range
Spacecraft range is obtained by measuring the time delay between transmission and reception of a known modulation of the carrier. In the coherent two-way configuration, the ground station transmits a modulation onto the uplink carrier, which is then retransmitted back by the spacecraft and received by the ground station. The on-board transponder demodulates the uplink ranging signal and re-modulates it on the downlink for better performance (regenerative ranging), or can just remodulate the carrier (transparent ranging) The round-trip light time (RTLT) of this cycle represent the range measurement. The ESA/NASA stations enable both the classical sequential ranging (810-005 203, Rev. B) and the novel PN (pseudo-noise) range (810-005 214, Rev. B). BepiColombo is the first ESA mission to routinely use PN range for spacecraft navigation. The Deep Space Transponder (DST) used for telecommunication and telemetry, hosts a PN range at 3 McpsFootnote 1 while MORE’s Ka-band Transponder (KaT), able to receive an uplink at 34 GHz and retransmit it coherently to the ground at 32.5 GHz, exploits a custom implementation at 24 Mcps (called Wide-Band Ranging System, WBRS), outside CCSDS specifications. The PN range code is a weighted-voting (\(\nu =2\)) balanced Tausworthe code, often indicated as T2B, based on the combination of six predefined component sequences (CCSDS green book). The ranging signal repeats itself after the ranging clock time and hence it is subject to a phase ambiguity. This ambiguity is solved by knowing the a priori position of the spacecraft. The measurement accuracy is inversely proportional to the ranging clock component of the ranging signal, therefore the highest the better.
Recent in-flight tests of BepiColombo have proven an extreme accuracy of less than 1 cm for MORE’s PN regenerative range at 24 Mcps at 0.3 AU (Cappuccio et al. 2020b). Further tests, at a distance in the range 0.7–1.4 AU, will be executed in September and November 2020.
3.3 DeltaDOR
Delta-Differential One-way Ranging (Delta-DOR) is a Very Long Baseline Interferometry (VLBI) technique that is used to determine spacecraft angular position in the plane of sky. This technique is based on the measurements of the range at two different ground stations separated by a baseline, B. The two measurements are combined to compute the angle between the baseline and the spacecraft direction. The accuracy of Delta-DOR measurements is inversely proportional to the baseline and depends on the stations’ clock synchronization accuracy. To synchronize the stations’ clock, the signal from a quasar is used and, hence, a pass for Delta-DOR acquisition includes at least three scans (spacecraft-quasar-spacecraft or quasar-spacecraft-quasar). Regarding BepiColombo, this technique is used mostly for navigation from ESTRACK stations. Measurements from the NASA DSN stations are also possible and tests will be carried out during the cruise phase. BepiColombo is being used as a benchmark for Delta-DOR measurements in Ka-band, never tried before.
4 The BepiColombo Radio System
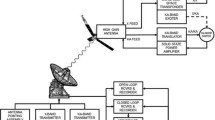
The required accuracy of the BepiColombo radio science experiment entails a suitable radio link configuration, sketched in Fig. 1. All measurements are carried out in a coherent two-way mode, in which the frequency reference is generated at the ground station and all onboard transponders (KaT, or Ka band transponder, and DST, deep space transponder) are commanded in a coherent mode. The key aspect is the implementation of a multi-frequency link, in which two uplink and three downlink carriers are simultaneously used:
-
A X-band downlink (\(\mathbf{X}\), at 8.419 GHz) coherent with an X-band uplink (at 7.166 GHz).
-
A Ka-band downlink (Ka1, at 31.992 GHz) coherent with the same X-band uplink.
-
A Ka-band downlink (Ka2, at 32.075 GHz) coherent with a Ka-band uplink (at 34.357 GHz).
The downlink carriers Ka1 and Ka2 are separated by about 80 MHz. This configuration, successfully used by the Cassini spacecraft, ensures a nearly complete plasma cancellation, as detailed in Sect. 5.2. The Ka2 link will be the primary link for the radio science experiment. The X and Ka1 link will be used for the elimination of the plasma noise (the dominant noise source in Doppler and range measurements near superior solar conjunctions). All carriers may be phase modulated by the standard PN (pseudo noise) ranging to a chip rate of 3 Mcps. In addition, the primary radio science link (Ka2) will also support a higher frequency PN modulation at 24 Mcps (Wide-Band Ranging System, WBRS), used for precision measurements.
The onboard deep space transponder (DST, part of the spacecraft telecommunication system) receives the uplink X-band signal and generates the coherent X and Ka1 downlink carriers, routed to ground after being amplified by two Travelling Wave Tube Amplifier (TWTA), (35 W at X and Ka band). Being critical units, both the DST and the TWTA will be duplicated for redundancy (not shown in Fig. 1). The KaT uses an internal solid state amplifier (SSA) providing an output power of 1.9 W. The onboard radio system is completed by a 1 m fully steerable high gain antenna (HGA), capable of withstanding the extreme temperature variations of the hermean environment.
The SNR controls the telemetry rate and is therefore a crucial parameter in the design of any space radio link. This parameter is however much less critical in Doppler and range measurements, where it affects essentially the receiver thermal noise. For the SNR levels provided by BepiColombo, thermal noise gives a negligible contribution to the overall error budget. It becomes important in Doppler measurements only at frequencies larger than 1 Hz, i.e. outside the measurement bandwidth. For range measurements, thermal noise may be successfully reduced by increasing the integration time.
Doppler and range measurements will be carried out whenever the radio link will be established. The experiment simulations have shown that one pass per day (for a duration ranging from 2 to 8 hours) will be sufficient to achieve the required accuracies. Samples of the down-converted signal received in the three bands at the ground station will be recorded open-loop in a 1 kHz bandwidth (2 kHz sampling rate). Standard navigation products from closed-loop receivers will be used for back-up and diagnostic purposes.
ESA’s 35 m station DSA-3 (Deep Space Antenna 3), located in Malargue, Argentina, will be the primary ground antenna for the MORE experiment. It fully supports multifrequency links and is equipped with a water vapor radiometer for wet tropospheric delay calibrations. Ka band uplink from this antenna was first tested in 2014 to track NASA’s Juno spacecraft. Nearly full functionality was proven by tracking BepiColombo in a full multilink configuration in an experimental campaign in 2019. DSA-3 fully supports the novel PN ranging system used by MORE (WBRS), attaining rms range residuals over a whole pass as small as 7 mm (Cappuccio et al. 2020b).
NASA’s DSS 25 (one of the Deep Space Network antennas at the Goldstone site in California) was for a long time the only antenna with Ka band uplink capabilities. It was extensively used to support the Cassini radio science cruise experiments and is currently used for Juno gravity measurements at Jupiter. The WBRS is also fully supported by this antenna, as proven in the experimental campaign in 2019. While the range measurement at DSA-3 is directly provided by the new TTCP receiver, at DSS 25 the ranging signal is sampled at high frequency and post-processed in software. The attained range accuracies are similar to those of DSA-3.
Although MORE science goals can be achieved using only one station, the benefits of using two antennas are obvious: a) larger flexibility in the scheduling of the antenna time; b) larger immunity to hardware failures; c) less sensitivity to local weather conditions; d) less sensitivity to possible systematic effects; e) easier identification of noise-related effects in the data analysis; f) improved accuracies in the determination of physical parameters of interest.
The ground stations are expected to meet two crucial requirements for the Ka2 link: an Allan deviation of 6 \(10^{-15}\) at 1000 s integration time and a station delay calibration of at least 0.3 ns (9 cm). The requirements in the other two links are less stringent and fully compatible with the current performance of the ESA and DSN ground stations. Indeed, the construction of the non-dispersive sky frequency and range entails a linear combination of the X, Ka1 and Ka2 observables, whose coefficients (and relative weights) are respectively about 1/13, 1/34 and 1. The Allan deviation at integration times between 10 and 1000 s (corresponding to the measurement bandwidth) should not exceed the limit \(\sigma _{y} \left ( \tau \right ) = \sigma _{y} \left ( 1000s \right ) \left ( 1000 {s} / {\tau } \right )^{{1} / {2}}\). The delay calibration shall be carried out a few times during the pass. DSA-3 is equipped with an experimental system (at the time of this writing) for in-line, continuous delay calibration. The high SNR levels and the use of the WBRS allow for short integration times, of the order of a few seconds (Iess and Boscagli 2001; Cappuccio et al. 2020b).
4.1 The Ka-Band Transponder (KaT)
The MORE KaT is a fully digital transponder using state of the art technologies. It has been funded by the Italian Space Agency and built by Thales Alenia Space Italia, according to the specifications of the science team. The unit is based on a combination of advanced signal processing algorithms and novel digital technology implementation. Its mass and dimensions are, respectively 3.5 kg and \(216\times 188\times 140~\mbox{mm}\). Although it has been derived from an older unit developed for the gravity measurements of the Juno spacecraft at Jupiter, it includes substantial architectural improvements, namely:
-
The digital module is conceived around an ASIC developed with 0.18 micron technology. In combination with the LEON2FT Microprocessor, this module represents a true System-on-Chip integrating custom digital signal processing;
-
An on-board calibration module is included, allowing the estimation on the transponder’s group delay during the mission.
The KaT core digital architecture provides broad advantages over an analogue solution (such as the one used for the Cassini unit):
-
Optimization of carrier acquisition and tracking performance.
-
Inclusion of PN ranging processing capabilities (demodulation and remodulation).
-
Data rate flexibility with easy matched filtering implementation.
-
Design flexibility with receiver tuning based on programmable constants.
-
All-digital modulation capabilities based on Direct Digital Frequency Synthesis.
Extensive performance tests carried out in thermal vacuum conditions have shown the KaT has an internal stability (Allan deviation) of \(\sim 4\times 10^{-16}\) at 1000 s integration time. Another crucial feature of the MORE KaT is the WBRS, based on a PN ranging modulation scheme up to 24.3 Mcps (although also a lower chip rate at approximately 3.1 Mcps is supported for compatibility with the ranging system used for spacecraft navigation). The unit is endowed with an internal group delay calibration module, providing an internal delay accuracy better than ±0.4 ns pk-pk and a stability of ±0.2 ns pk-pk. Actual measurements carried out in 2019 showed a significantly better stability (Cappuccio et al. 2020b).
4.2 The Ground System
Since RS observables are generated at the ground stations, only a very small fraction of telemetry, such as equipment housekeeping parameters, spacecraft attitude measurements, maneuvers, and orientation of movable parts are of interest to MORE data analysis. (Mass history, also important, is estimated on ground by the flight dynamics team.) The microwave signals are mixed to lower frequencies, where they are sampled, averaged, and recorded for later analysis. Two- and three-way uplink transmissions are modulated with ranging codes, allowing the determination of round-trip light times after correlation with the modulation on the downlink signal. RS data are acquired via two types of receivers, closed- and open-loop.
In order to track a spacecraft signal carrier, the closed-loop receiver utilizes a phase-locked loop (PLL) that precisely measures and records the carrier’s phase. The Doppler shift is estimated from the phase and converted to relative velocity. Separately, ranging code modulation is extracted and correlated with the uplink code to determine absolute range. The closed-loop tracking receiver provides carrier phase and range at a rate that depends on the code repetition period and user-selected averaging interval. In open-loop reception, an independent broad band receiver is used without the phase-lock loop tracking mechanism described above. The receiver down-converts the spacecraft signal via a local oscillator heterodyne process guided by a prediction of the expected frequency.
The BepiColombo radio science system is distributed, consisting of elements on the spacecraft and on the ground. The ground elements consist of antennas of the NASA/JPL Deep Space Network, DSN, and the ESA ground network (ESTRACK). Figure 3 shows DSN station DSS25 (in a stowed position), which is specifically instrumented to support Ka band radio science investigations. It is a 34-m aperture beam waveguide antenna equipped with X and Ka band transmitters that can be operated simultaneously. The ESA 35 m DSA 3 antenna located in Malargue, Argentina, has similar capabilities, with the addition of an inline delay calibration system at Ka-band,
NASA/JPL Deep Space station 25 (DSS25), a 34-m beam waveguide antenna, shown here in the stowed position. It was specifically instrumented for Cassini radio science with high-stability electronics, Ka-band up-and downlinks, and advanced media calibration systems to correct for tropospheric scintillation (credit; NASA-DSN)
Precision Doppler tracking of BepiColombo is done in the so-called “two-way” mode; that is, signals are transmitted from the ground to the spacecraft where they are phase-coherently retransmitted back to the same ground antenna. The Doppler shift is then extracted by comparing the frequency of the transmitted and received signals. As indicated earlier in this section, the BepiColombo radio science system exploits five links, each one with high Doppler stability, the Ka/Ka link attaining the best Allan deviation due to larger immunity to charged particle noise. A highly stable frequency standard (hydrogen maser) provides the reference for both transmission and reception. As indicated in Fig. 1, there are two uplink signals, one at X-band (∼8.4 GHz) and one at Ka-band (∼34 GHz). The X-band uplink is coherently retransmitted to the Earth on an X-band downlink using the standard TT&C transponder. Additionally, the X-band uplink is coherently retransmitted back to the Earth also at Ka-band. Simultaneously, a Ka-band uplink from the ground antenna is received by the spacecraft and coherently retransmitted to the Earth via the Ka-band Transponder (KaT).
5 Media Calibrations
5.1 Troposphere
DSS25 is endowed with an Advanced Media Calibration (AMC) unit to correct for Doppler noise caused by path delays due to Earth’s troposphere (Fig. 4). A simpler unit has been deployed at DSA-3 for the same goal. It will be used during the second phase of the end-to-end test of the MORE radio system in November 2020.
This high-performance multi-link system and the AMC units are expected to provide Doppler data of excellent quality, similar to those attained by the Cassini and Juno missions in simpler operational conditions. We summarize here the main error sources in range rate measurements and present the expected error budget.
5.2 Ionosphere, Interplanetary Plasma and Solar Corona
The key to the success of both relativistic gravity and geodesy measurements is the ability to remove almost completely the noise due to charged particle effects. This is especially true for tests of the relativistic delay and Doppler shift during superior solar conjunctions. Indeed, the GR signal attains its largest value close to the sun, exactly when phase scintillation noise increases dramatically. The multilink plasma calibration scheme for deep space missions was proposed by Bertotti et al. (1993), who relied on the well-known dispersive properties of plasmas, already exploited by GPS. (The refractive index of plasmas at microwave frequencies differs from unity by an amount inversely proportional to the square of the carrier frequency.) With three observable quantities available (the path delay variation or relative frequency shift in the X/X, X/Ka and Ka/Ka link, indicated respectively with \(\varGamma _{XX}, \varGamma _{XK}, \varGamma _{KK}\)) and three unknown quantities (the non-dispersive path delay variation or relative frequency shift \(\varGamma _{nd}\), and the contributions from the uplink and downlink plasma at a reference frequency, \(\varGamma _{\uparrow }\) and \(\varGamma _{\downarrow } \)), in the geometric optics limit one writes
where
-
\(\alpha _{XX} = \frac{f_{X_{D}}}{f_{X_{U}}} = \frac{880}{749}\) is the X/X link turn-around ratio (via X/X/Ka Deep Space Transponder).
-
\(\alpha _{XK} = \frac{f_{K_{D}}}{f_{X_{U}}} = \frac{3344}{749}\) is the X/Ka link turn-around ratio (via X/X/Ka Deep Space Transponder).
-
\(\alpha _{KK} = \frac{f_{K_{D}}}{f_{K_{U}}} = \frac{3360}{3599}\) is the Ka/Ka link turn-around ratio (via the Ka/Ka link enabled by the KaT).
-
\(\beta = \frac{f_{K_{U}}}{f_{X_{U}}}\), i.e. the ratio between the two uplink frequencies.
In the above equations, the dispersive (plasma) contributions \(\varGamma _{\uparrow } \) and \(\varGamma _{\downarrow } \) are referred to a X-band uplink carrier. This set of equations provides straightforwardly the non-dispersive observable (range or range rate) and, separately, the uplink and downlink plasma contributions:
Using the transponding ratios indicated above, the non dispersive observable can be approximated as
This equation indicates that the accuracy of the Ka/Ka link observable is the most important for a precise determination of the non-dispersive observable.
The computation of the uplink and downlink plasma has been used for space-time localization of plasma features in the solar wind, providing a useful, additional tool to probe the regions near the sun (Richie-Halford et al. 2009). The above equations fail when the radio beam is too close to the sun (impact parameter ≈7-8 solar radii, depending on solar activity). At those distances from the sun the X band signal enters the strong scintillation regime, impairing the signal lock.
The effectiveness of the Cassini plasma calibration scheme can be appreciated in Fig. 5, showing the power spectrum of the Ka band frequency residuals before (red) and after (green) the removal of plasma scintillation.
Power spectrum of relative frequency shift residuals obtained on DOY 155 2001, during the tests of the DSS 25 Ka band system, at a minimum impact parameter of 8 solar radii. The uncalibrated residuals (red) show the expected Kolmogorov spectrum (\(f^{{-2} /{3}}\)). After the plasma calibrations, the spectral power of plasma noise is strongly reduced and becomes white, an indication that the calibrated residuals are dominated by other noise sources
So far, this method has been applied to Doppler measurements only, but the same equations are valid for range data as well. However, absolute range plasma calibrations require the knowledge of the internal delays of the transponder (the KaT delay is internally calibrated), as well as those of the ground antenna.
6 Error Budget
6.1 Range Rate
Table 1 shows the principal noises sources and the associated Allan deviation at 1000 s, derived and updated from Asmar et al. (2005) and Iess et al. (2017).
Inflight tests carried out in 2019 with an inertially pointed spacecraft have shown significantly better stability at 1000 s (Cappuccio et al. 2020b). In the following, we comment briefly on the various noise sources.
Frequency Standard. As the frequency standard is used to generate the uplink carrier and all IF frequencies at the ground antenna, it provides the ultimate limit to the link stability. The ground antennas make use of hydrogen masers (H-masers), the best frequency standards at time scales of typical round-trip light-times. The typical Allan deviation of commercial units under thermally controlled conditions is \(\sigma _{y}\) \((1000~\mbox{s})=10^{-15}\). At shorter integration times the Allan deviation varies approximately as the reciprocal of the integration time (white phase noise).
Propagation Noise. Propagation noise, due to intervening plasmas (interplanetary plasma and ionosphere) and troposphere, constitute a major noise source in Doppler measurements. Cassini measurements have shown that the multi-frequency link is extremely effective in suppressing plasma noise. The residual plasma noise after the multi-link calibration is not expected to exceed \(2\times 10^{-16}\) at most solar elongation angles. However, the plasma environment at Mercury is less benign due to the proximity to the Sun, we conservatively increase the anticipated residual plasma Allan deviation to \(5\times 10^{-16}\) at 1000 s.
Tropospheric noise has two components, usually called “dry” and “wet”. While the dry component can be accurately measured by means of barometric pressure and temperature measurements at the station, the wet delay due to water vapor, although smaller, is much more difficult to estimate. Humidity data and GNSS estimates are not adequate due to the usually poor mixing of water vapour. Its magnitude and time variability are strongly dependent on local weather, with typical path delays from 3 to 20 cm (for zenithal elevations). The use of water vapour radiometer (WVR) has proven effective in Cassini and Juno radio science experiments (see Figs. 6 and 7).
Allan deviation at 1000 s integration time for each pass of Cassini GWE1, Nov. 26, 2001 to Jan. 4, 2002, with and without AWVR calibration. The plot indicates that tropospheric water vapour is the leading noise source in Cassini radio science experiments. To reduce the contributions from elevation-dependent effects, only data acquired at elevations larger than 30 deg (both in downlink and uplink) have been considered
An advanced WVR is in operation at DSS 25 and is expected to support MORE measurements in cruise. ESA has recently developed a microwave radiometer to be used for tropospheric calibrations at DSA-3. Its deployment is expected by the end of 2020.
Spacecraft and Ground Electronics Noise. The noise due to electronic instrumentation at the ground antenna (transmitter, exciter, receiver) has been measured during the test campaign of the units and is very low (see Table 1, reporting actual values). Similarly, pre-launch testing of the KaT showed a very high stability (Table 1).
Receiver Thermal Noise. In the receiving chain the dominant noise source is thermal noise. Thermal noise adds an incoherent phasor to the phasor of the received carrier. The resulting phasor (signal plus noise) jitters both in phase and amplitude. As the SNR is quite high (35 dBHz) in spite of the small transmitting power (1.9 W) at Ka band, with a loop bandwidth of 1 Hz the Allan deviation at 1000 s integration time is negligible (\(\sigma _{y}\) (\(1000~\mbox{s}\)) \(= 1.5\times 10^{-16}\)). However, a more conservative value of \(3\times 10^{-16}\) at 1000 s was assumed in the error budget for all three links.
Antenna Mechanical Noise. This noise source is due to thermal deformation of the structure, and gravitational and wind loading. Thermal deformations are related to slow temperature drifts and uneven, heating of the structure. Using the fractional dilatation of steel (\(\Delta {l} / {l} \approx 1.1\times 10^{-5}\)/K), a typical 30 m antenna undergoes a change in linear dimensions \(\Delta l\approx 0.3\) mm/K. The relative frequency shift is therefore proportional to the time derivative of the temperature variation. At a time scale of 1000 s the corresponding relative frequency shift is about \(2.2 \times 10^{-15}\) per degree C, a small quantity for the expected temperature changes.
Mechanical deformations of the antenna structure due to wind loading, buffeting and gravity loading are a potentially more dangerous error source. Wind gusts excite the antenna structure, with effects that appear however at the typical frequencies of the antenna normal modes, generally outside the frequency band of the experiment. An attempt to quantify the effect of wind in range rate measurements at DSS 25 is reported in Armstrong et al. (2003), Asmar et al. (2005). Antenna mechanical noise has been estimated at a level of about \(5\times 10^{-15}\). It is the major error source in the ground segment contribution.
6.2 Range and Delta-DOR
Table 2 summarizes the range error budget evaluated at 1000 s integration time in nominal conditions (always assuming a multi-frequency link and WVR troposphere calibration). At short time scales, considering a sine-sine shaped signal and a ground station loop bandwidth narrower than the on-board loop bandwidth, the dominant source of error is thermal noise that causes jitters on the signal, other minor contributions derive from the propagation media and location errors. In this case the end-to-end system contribution follows Eq. (5) (see CCSDS 2014, Sect. 2.7.3.2.3)
where \(c\) is the speed of light, \(f_{RC}\) is the clock frequency, \(B_{{l_{G}} / {S}}\) is the one-sided bandwidth of the PLL in the receiver, \(\frac{P_{RC_{KaT}}}{N_{0_{KaT}}}\) and \(\frac{P_{{RC_{G}} / {S}}}{N_{{0_{G}} / {S}}}\) are the ranging clock (RC) component signal to noise spectral density in the KaT and in the ground station (G/S) receiver.
At longer time scales systematic variations of the group delay are a potentially more serious source of errors. The main systematic error at longer time scales is the error due to KaT aging, which was evaluated at 15 cm. The onboard and ground station group delay is affected by temperature, Doppler shift and power level. These effects need to be carefully controlled by a calibration system and ground testing. The KaT hosts a dedicated calibration system, to be operated during each tracking pass. The DST contribution should be kept under control, but it does not host a dedicated calibration loop. Similarly, the ground station error contribution can be strongly reduced by carrying out calibration measurements during the pass using a dedicated loop. Aging of components can produce significant drifts at very long-time scales superimposed to high frequency variations of the path delay.
For the rest of the spacecraft contribution, we considered the Allan deviation requirement of \(8.5\times 10^{-15}\) at 1000 s. To meet this requirement, the delay variation over 1000 s should not exceed 0.25 cm. Assuming that over 1 pass the delay variation should follow the orbital period, the maximum delta-delay should appear in half an orbit i.e. 4500 s, and it is expected of the order of 1.2 cm (having assumed a temperature variation linear in time). Over long-time scales, drifts of the internal delay should be more significant.
Concerning the ground station delays, the error contribution is more difficult to assess, because there is no heritage on Ka/Ka ranging calibration systems. However, an inline station delay calibration has been recently installed at DSA-3. Its accuracy is predicted to be within 1-2 cm, and will be tested during the end-to-end test of the system in November 2020.
In the budget, the plasma free observables have been considered as computed by the procedure outlined in Sect. 5.2. Each plasma free error has been formed from the three links contributions via weighted residual sum of squares for uncorrelated errors and weighted linear sum for correlated ones. The Ka/Ka, X/Ka and X/X link have a weight value of 1, 0.03 and 0.08 respectively.
Delta-DOR is not a primary observable for the MORE experiment, but it is used for navigation in specific mission phases. For the Delta-DOR error budget we rely on the indication of the CCSDS, based on ESA/NASA state-of-the-art capabilities (CCSDS 2019). Among the systematic errors, the main sources are the uncertainty in quasar coordinate and atmospheric calibrations (both troposphere and ionosphere). Random errors are due to thermal noises and the dispersion of the DOR-tone phase. All these terms are summarized in Table 3 and can be treated as uncorrelated noises. The total accuracy for a Delta-DOR measurement (see Sect. 3.3) is estimated to be 0.057 ns.
7 Non-gravitational Accelerations and Spacecraft Rotations
The hermean environment produces significant non gravitational accelerations (NGA) on the spacecraft. The direct solar radiation pressure on a spacecraft that continuously changes its attitude with respect to the Sun, the pressure from the infrared radiation of the planet, the thermal recoil due to the onboard thermal anisotropies have a strong effect on the spacecraft dynamics. To this end the mission is endowed with a precise accelerometer (ISA), whose data will help recreating, in software, a pseudo drag-free system. The use of ISA is however not limited to the measurement of the non-gravitational accelerations, but also to the compensation of the effects of the spacecraft attitude motion.
7.1 A Pseudo Drag-Free System with the ISA Accelerometer
The orbit determination (OD) process requires accurate dynamical and observation models. Crucial to the success of the MORE experiment is a precise representation of the forces acting on the spacecraft. The center of mass (COM) equation of motion (in the inertial frame) is
where \(f_{\mathit{NGA}}\) is the non-gravitational acceleration. Newtonian and relativistic accelerations have been generically expressed as the gradient of a potential.
The OD process is usually carried out using a mathematical model for the NGA. When NGA are large (for example the acceleration due to solar radiation pressure at Mercury), an incorrect modelization can produce significant errors in the estimate. In such a situation (or when the NGA are difficult to model), an on-board accelerometer can be used.
The accelerometer measures all accelerations but gravitational ones (at its location):
where:
-
\(\nabla U \left ( r+ r_{\mathit{ACC}}^{SC} \right )\) is the gravitational acceleration evaluated at the accelerometer position in the inertial frame;
-
\(\ddot{r}_{\mathit{ACC}}\) is the total acceleration (in the inertial frame) of the accelerometer reference point, sum of the COM acceleration in the inertial frame and the inertial accelerations due to rotations;
-
\(r_{\mathit{ACC}}^{SC}\) is the position vector of the accelerometer reference point in the inertial frame with origin at the COM.
The gravitational acceleration at the accelerometer position is the gravitational acceleration of the COM and the acceleration due to gravity gradient, \(a_{GG}\). The accelerometer measurement can therefore be expressed as
The acceleration measured by the accelerometer in the inertial frame depends on the acceleration of the COM and the inertial acceleration due to rotations. It can be written as
where \(\omega \) is the angular velocity. The accelerometer measurement can be written as
The equation of motion of the COM using the accelerometer measurements \(a_{\mathit{ACC}}\) is
This equation shows that the orbit determination of the COM using the accelerometer readings can be carried out only if the position of the accelerometer with respect to the COM is known.
When the accelerometer measurements are introduced, the equation of motion of the accelerometer reference point becomes
which is much simpler. Note that every reference to the COM is no longer required. Indeed, adopting this reference point waives the need to know the COM position with respect to the spacecraft structure, and the gravity field can be estimated without any requirement on the knowledge of the COM position (Schulte 2007; Milani and Gronchi 2009).
7.2 Effect of the Attitude Motion on the Observable Quantities
In order to carry out the orbit determination of the ISA reference point applying the pseudo drag-free system, it is mandatory to transform the range and the range rate observables of the antenna reference point to range and range rate of the ISA reference point. Since the MPO is nadir pointed and the antenna is steered to maintain the radio link with the Earth, the effects on the range and Doppler observables of the non-coincidence of ISA with the antenna phase center (or any reference point on the antenna dish) vary with time. This is possible by knowing the so-called Schulte’s vector, defined as the vector between the antenna phase center (or any antenna reference point) and the ISA reference point (fixed in the spacecraft frame). The range and range rate observables of the ISA reference point can be computed using the Schulte’s vector (whose components in the body frame are continuously changing with time) and the MPO’s attitude (e.g. the attitude quaternions and angular velocity).
8 MORE Operations and Data Acquisition
8.1 Cruise
After launch, BepiColombo underwent a Near Earth Commissioning Phase (NECP) to test the functionality of each subsystem and instrument on-board the spacecraft. The MORE commissioning, carried out on 9 December 2018, indicated that the KaT instrument was operating nominally. The MORE team performed a test in May from ESA ESTRACK DSA-3, located in Malargue, Argentina and in August from NASA DSN DSS-25, located in Goldstone, California, to verify the in-flight performances of the Ka/Ka radio link (Cappuccio et al. 2020b). In 2020, the MORE team executed the End-to-End (E2E) test of the tracking system. The purpose of this test is to demonstrate the operations of the full experiment setup. The data from the ESA DSA-3 are collected during 18 passes: 9 in September 2020 and 9 in November 2020. The capability of the complete radio link will also be tested from the NASA DSS-25 with an additional 4 passes in November-December 2020, in addition to 7 shadow passes (3-way) in parallel with the DSA-3 2-way passes. These tests are performed with the spacecraft in a quiet dynamical state in order to minimize buffeting noise and to provide the dynamical coherence of the orbit. In the orbital phase around Mercury, ISA readings will be used to compensate for non-gravitational acceleration mainly due to solar radiation pressure (Iafolla 2010). During the E2E test the ISA accelerometer data are collected to verify the in-flight performances.
In April 2020 BepiColombo completed the Earth flyby. The MORE team used the X-band data from the DST to assess if a good orbital fit in unusual geometrical conditions and with a standard dynamical model was possible. While anomalies were reported with other spacecraft, such as the Galileo spacecraft in 1990 (Antreasian and Guinn 1998), no unexpected accelerations were found by BepiColombo. During the two Venus flybys, 15 October 2020 and 10 August 2021, MORE plans to operate around the closest approach to collect data useful to improve planetary ephemerides (Di Ruscio et al. 2020).
During several superior solar conjunctions in the cruise phase, MORE will repeat several times the classical test of general relativity based on the time delay and Doppler shift of radio signals. Table 4 summarizes the dates of the BepiColombo superior solar conjunctions. The experiment will start 7 days before and will end 7 days after each conjunction, where a quiet spacecraft dynamics (no maneuvers) is again requested. Figure 8 shows the Solar-Probe-Earth (SPE) angle evolution during the cruise phase of BepiColombo, with the cyan line representing the 14 days across the conjunction. Unfortunately, solar electric thrusters, which hamper the experiment with their dynamical noise, will be off only during the first 6 conjunctions. The relativistic signal is stronger at low values of the impact parameter, i.e. the minimum distance between the Earth-spacecraft line of sight and the Sun, and when the impact parameter varies rapidly. A rule of thumb to assess how useful a conjunction could be is to observe how small the SPE is and how fast it changes (see Fig. 8). Therefore, the best conjunctions are expected to be the third one (July 2022) and the fifth (June 2023) (Imperi and Iess 2017; di Stefano et al. 2020).
Sun-Probe Earth angle during the BepiColombo cruise phase, computed using the notional trajectory (ESA SPICE Service 2018). The cyan line represents the 14 days around the conjunctions. The green dot is the Earth flyby, the purple dots are the Venus flybys and six red dots are the Mercury flybys
8.2 Hermean Phase
The hermean phase of BepiColombo will last one year, with a possible extension by one additional year. The MPO will be injected into a polar, low eccentricity orbit (\(480 \times 1500\) km altitude), with a period of about 2.3 hours and periherm latitude at 16° N. As indicated in previous sections, two ground antennas will support MORE operations: ESA’s DSA 3, located in Malargue (Argentina) and NASA’s DSS 25, located in Goldstone (California). Both stations have Ka band uplink capabilities, an essential feature for precise gravity and rotation measurements. Due to the considerable visibility overlap of the two antennas, the actual tracking schedule has still to be fully defined. Considerations based on pass duration and maximum elevation will be important factors to consider in the definition of the ground coverage.
In general, spacecraft operations require contact to ground for at least 8 hours per day (excluding occultations by the planet). The availability of a steerable HGA may further extend the tracking time, without hampering the operations of other instruments. High quality Doppler data are possible only when the spacecraft is well above the horizon (otherwise tropospheric noise becomes too large). Data acquisition will start when the spacecraft elevation above the local horizon is >15°.
Power limitations onboard the MPO around perihelia (mean anomaly ±30°, or about 10 days) indicate that some instruments need to be switched off in those phases. Based on the predicted degradation of the solar panels, the KaT could be operated only during one perihelion passage. This important restriction can potentially affect some of the MORE science goals and will be revisited once the actual performance of the flight system will be better known.
Off-loading of the momentum wheels are another limitation to the gravity and relativity measurements at Mercury. The analysis carried out by the BepiColombo project indicate that wheel off-loading occur, on average, twice a day, depending on the momentum build-up caused by the external torques. These events, whose magnitude can be in the range of several cm/s, destroy the dynamical continuity of the orbit and need to be planned at times when they create the least damage. MORE requires that one of the two events take place while tracking right after the end of a MORE pass, while the second takes place when the spacecraft is tracked by another station (see Imperi et al. 2018).
9 Orbit Determination
The MORE investigation exploits Doppler and range data to solve the orbit determination problem. The radio observables collected at ground stations are compared with the predictions obtained from an observation model to a reference solution, leading to a vector of residuals. A cost function derived from the vector of the residuals is then minimized by correcting the spacecraft initial state and other solved-for parameters in a weighted least-squares filter with a priori information (Tapley et al. 2004):
where \(x\) is n-dimensional vector of differential corrections to the solved-for parameters, the matrix \(H\), called design matrix, contains the partial derivatives of the observables with respect to the solve-for parameters, \(W\) is the measurements weight matrix, and \(\delta \underline{x}\) and \(\underline{P}\) represent respectively the a priori estimate and covariance matrix of \(x\). Since the problem has been linearized, the estimate is obtained through an iterative process. After k-steps, when convergence is reached, the inverse of the information matrix \(H_{k}^{T} W_{k} H_{k} + \underline{P}_{k}^{-1}\) is the covariance matrix of the vector \(x\). During the orbital phase around Mercury, MORE will use Doppler and range data to (i) determine the motion of MPO around Mercury, enabling the gravity and rotational experiments; (ii) determine the heliocentric motion of Mercury, allowing fundamental physics tests. The orbit of the MPO, characterized by a fast dynamic (orbital period ∼2.3 h), is assessed through the Doppler observables. On the contrary, the slower heliocentric motion of Mercury is essentially inferred from range data.
We plan to adopt a multi-arc strategy (Milani and Gronchi 2009, Chap. 15) to compensate for un-modeled effects by means of an over-parameterization of the problem. The spacecraft trajectory is divided into non-overlapping “arcs”. The parameters are split into a local set \(l_{i}\), pertaining to each single arc \(i\) (e.g. the spacecraft state vector and the maneuvers) and a global set \(g\), common to the all arcs (e.g. gravity coefficients). For each set of observables \(y_{i}\) belonging to the arcs, the design matrix that links the observable residuals to the vector of solved-for parameters correction is expressed by separating the local parameters from the global ones. Considering for simplicity only two arcs, we have the two solved-for-parameters vectors \(Z_{1} = \left [ X_{1} X_{g} \right ]\) and \(Z_{2} = \left [ X_{2} X_{g} \right ]\), where \(X_{1}\) and \(X_{2}\) are locally estimated parameters and \(X_{g}\) is the vector of global parameters. The two vectors can be merged into \(Z= \left [ X_{1} X_{2} X_{g} \right ]\) and the \(H\) matrix can be written as:
where \(y_{1}\) and \(y_{2}\) are data from the two arcs. The \(H\) matrix reflects the fact that partial derivatives from arc 1 are null with respect to local parameters of arc 2 (and vice versa). However, the estimation covariance matrix \(P_{k}\) is a fully populated one, with diagonal terms representing the \(j\)-th parameter estimated variance \(\sigma _{j}^{2}\), with \(j=1,\dots ,n\). The technique is called pure multi-arc strategy when the arcs are handled as completely independent from each other, i.e. the corresponding orbits are effectively treated as they would belong to different spacecraft.
We implement a constrained multi-arc approach, where positions and velocities of two adjacent arcs (end of arc \(i\) and beginning of arc \(i+1\)) cannot exceed a given threshold at their connection time. The multiarc strategy is an effective way to absorb the adverse effect of the desaturation maneuvers. Note that the continuity condition is not exact. The selection of the continuity threshold, which requires some experimenting, is a compromise between underconstraining and overconstraining the solution.
9.1 Dynamical Model
The gravity field outside a planet of mass \(M\) and reference radius \(a_{e}\) can be derived from the spherical harmonic expansion of the gravity potential \(U\) in the body fixed-reference frame:
where \(\left ( \underline{C}_{lm}; \underline{S}_{lm} \right )\) are the normalized coefficients of degree \(l\) and order \(m\), \(G\) is the gravitational constant, \(\underline{P}_{lm}\) are the fully normalized associated Legendre polynomials, while \(\phi \), \(\lambda \), and \(r\) are, respectively, latitude, longitude and radial distance. Terms with \(l=1\) are null when the origin of coordinates coincides with the body’s center of mass. Higher degree terms provide a finer description of gravity features on smaller regional scales, of order \(\pi a_{e}\)/\(l\). The BepiColombo gravity model also includes the point mass accelerations of the Sun, all solar system planets and the main satellites. For the position of all bodies included in the spacecraft gravity model we have used the DE430 planetary ephemerides model.
Due to the proximity of Mercury to the Sun, the spacecraft dynamics is heavily affected by intense non-gravitational perturbations due to planetary albedo, infrared emission, and solar radiation pressure. To mitigate the problem, the MPO is equipped with a sensitive accelerometer, the Italian Spring Accelerometer (ISA, Iafolla et al. 2010; Santoli et al. 2020), which will directly measure the vectorial non-gravitational accelerations. The instrument consists of three linear accelerometer elements, arranged along three orthogonal directions. The ISA readouts will be used to replace non-gravitational accelerations in the dynamical model of MPO, which therefore need not to be modeled (Cappuccio et al. 2020a). Among different issues (see Milani and Gronchi 2009), the main problem in using the ISA inputs is that such readings will be unavoidably affected by some sort of error \(\varepsilon \)(t). Especially important are systematic errors driven by temperature variations of the sensitive elements. To reduce adverse effects on the estimation of the physical quantities of interest, a suitable calibration strategy must be envisaged. In particular, calibration coefficients of ISA low-frequency (planet orbital period) and high-frequency (MPO orbital period) are estimated respectively as local and global parameters.
The presence of a single solar panel and the ensuing asymmetric shape of the spacecraft generate large torques, which are balanced by reaction wheels. Desaturation maneuvers may occur up to twice per day. The estimated maximum magnitude of the uncompensated delta-V is 17 mm/s, 0.2 mm/s and 42 mm/s respectively for the radial (R), transversal (T) and normal (N) components in the orbital reference frame (Iafolla et al. 2011). Even using the ISA readings of the non-gravitational accelerations along with a suitable calibration strategy and including desaturation maneuvers in the set of solve-for parameters, unavoidable residual inaccuracies can still generate significant errors in the state propagation. To cope with this problem, a multi-arc strategy, as described in the previous section, is used.
9.2 Data Analysis Setup
The initial MPO orbit around Mercury is near-polar with pericenter and apocenter altitudes respectively at 480 km and 1500 km. The simulation covers the nominal mission of one terrestrial year and investigates the improvements that can be obtained with a mission extension of another year. In the simulation setup, the Hermean gravity field is expanded in spherical harmonics up to degree and order 50 adopting the coefficients of the solution HgM005, as well as, the tidal effects described by the Love number \(k_{2}\) (Mazarico et al. 2014). Recent results from (Genova et al. 2019) updated the gravity field and the determination of the Love numbers do not affect the validity of the covariance analysis.
The most recent simulation setup (Imperi and Iess 2017; Imperi et al. 2018) considered different cases for ground tracking. Although the operational scenario differs somewhat from the actual configuration, the sensitivity of the gravity and relativity experiments is still faithfully represented. Two ground antennas are assumed available for tracking, namely DSS 25 in Goldstone, with Ka-band uplink capabilities, and DSA 2 in Cebreros, enabling only X-band uplink. The data are included in the analysis when the spacecraft elevation above the ground station local horizon is \(>15\)°. Occultations of the orbiter behind Mercury are considered as well. As both antennas are in the boreal hemisphere, the observation windows change seasonally from about 6 h in the boreal winter up to about 11 h in the boreal summer, when they overlap. ESA DSA 3 antenna in Malargue (Argentina) has currently Ka-band uplink capabilities and it is currently providing operational support to MORE and BepiColombo. Its use for MORE allows a better tracking from ground, as DSS 25 and DSA 3, in spite of the considerable overlap in longitude coverage, are complementary in terms of maximum spacecraft elevation. For simplicity, the analysis is based on multifrequency data from DSS 25 only. Plasma noise cancellation is assumed to be possible till the signal path passes at seven solar radii from the center of the Sun (Tortora et al. 2004), data under this threshold are discarded. The measurement error is considered white and Gaussian. Therefore, the standard deviation of the measurement noise can be straightforwardly rescaled at any integration time: Doppler and range are simulated respectively every 60 and 300 s, with accuracies of \(12.25 \times 10^{-4}\) cm/s and 30 cm. These values are equivalent to an ADEV of 10−14 at 1000 s integration time for Doppler and the acquisition of one range measurement with an accuracy of 20 cm every 10 min. Recent inflight test during cruise demonstrated MORE ranging capabilities at 1-centimeter level and confirmed range-rate accuracy (Cappuccio et al. 2020b). Further improvements can be obtained exploiting a secondary small and stiff antenna to apply a local noise cancellation technique (Armstrong et al. 2008; Notaro et al. 2020).
As DSA 2 only uses X-band uplink, noise is assumed up to ten times larger than at Ka band (e.g. near superior solar conjunctions). One of the two desaturation maneuvers is assumed to happen during the X-band pass, while the second one after the DSS-25 pass. This allows the reconstruction of a continuous trajectory since the first maneuver can be directly estimated, while the second one is determined due to the inter-arc constraint (see Sect. 8).
In order to account for ISA errors, we estimate two unknown accelerations respectively at the low and high frequency components of the error, mainly driven by thermal variations. The time scales of the two components are respectively the orbital period of Mercury (88 d) and the MPO orbital period (2.3 h).
10 Expected Accuracies
10.1 Fundamental Physics and Solar System Dynamics
MORE will probe relativistic gravity both during the almost 7 years’ cruise to Mercury and during the hermean phase (extending up to two years). The interplanetary trajectory of BepiColombo will provide several opportunities to measure the relativistic deflection of light during superior solar conjunctions (SSC). The consequent time delay undergone by the radio signal exchanged by the spacecraft and the Earth station, can be expressed as a function of the post-Newtonian parameter \(\gamma \) as (Moyer 2008, Appendix C):
Where \(\Delta T\) is the relativistic time delay, \(G\) and \(M_{\odot }\) are the gravitational constant and the mass of the sun, while \(r_{1}, r_{2}\) and \(r_{12}\) are respectively the positions of the transmitter and the receiver, and their mutual distance, in a reference system centered in the center of mass of the sun. More accurate equations of the light time can be used (Kopeikin 2009; Ashby and Bertotti 2010), although the corrections are below the sensitivity of the radio system. The relativistic signal is amplified and thus easier to be detected, when the impact parameter \(b\) (the minimum distance between the light path of the radio signal and center of mass of the Sun) is minimum (i.e. close to a SSC). In this case, the expressions of the relativistic time delay and frequency shift can be approximated as (Will 2018):
where \(\frac{\Delta \nu }{\nu } \) is the relativistic fractional frequency shift of the two-way signal.
These observations will indeed provide an estimate of \(\gamma \), with the aim of constraining the value of this parameter to better than \(10^{-5}\) (the accuracy of the Cassini test is about \(2x10^{-5}\)).
During the long approach to Mercury, BepiColombo will undergo eleven SSC, with the first one occurring in March 2021. Differently from the Cassini experiment, BepiColombo can count on a very accurate ranging system, in addition to the Doppler measurements, and on multiple repetitions of the observations. However the large non-gravitational accelerations due to solar radiation pressure may prove difficult to model (di Stefano et al. 2019a). Indeed, the random fluctuations of solar irradiance (ranging between 0.1% and 0.01% of the central value) which cannot be modelled or measured by the ISA accelerometer (di Stefano et al. 2019b), whose bandwidth is limited to about \(10^{-4}\) Hz, become a potential issue for the experiment. The SCE has been simulated in di Stefano et al. (2020) including the effect of unknown solar irradiance variations in the dynamical model. These unmodeled accelerations have been compensated by estimating the solar irradiance pattern as a stochastic process. It has been verified that the possibility to obtain a tight constraint on \(\gamma \) depends on the magnitude of the irradiance oscillations at the time of the experiment. The solar activity during the conjunctions is forecasted to be strongly irregular, varying between periods of strong fluctuations and brief periods of faint activity. A notable exception being the first conjunction, happening before the ascending phase of the 11-years solar cycle, when the irradiance fluctuations are expected to be low. The results presented in di Stefano et al. (2020) are based on a large set of simulations performed with different solar activity realizations in order to indicate a realistic and conservative prediction on the accuracy connected to the estimation of \(\gamma \). Analyzing each single conjunction, SSC #1, #3 and #5 prove to be the most convenient because of the specific configuration. Exploiting the joint dataset of all conjunctions the accuracy attainable on \(\gamma \) lays in the range [6-13] \(\times 10^{-6}\).
In addition to the effect on the propagation of the radio waves, \(\gamma \) intervenes in the equations of motion of Mercury contributing to the advance of the perihelion. The novelty of MORE with respect to previous experiments (Viking, Cassini) aiming to constrain the value of \(\gamma \) (Bertotti et al. 2003) relies on the possibility of measuring both propagation and dynamical effects, thus decorrelating \(\gamma \) from the other parameters responsible for the perihelion advance (Eq. (66) in Will 2014) (i.e. the solar oblateness \(J_{2}\) and the PPN parameter \(\beta \)). Mercury, as seen by the Earth, undergoes three SSC per year, allowing MORE to perform additional SCE during the hermean phase. In this case the fast orbital dynamics tightens the trajectory reconstruction, thus mitigating the adverse effects of solar irradiance fluctuations and considerably improving the estimate of the \(\gamma \) to level of \(1.2\times 10^{-6}\) (Imperi et al. 2018; De Marchi and Cascioli 2020).
The orbital phase of BepiColombo constitutes a unique opportunity for constraining Mercury’s orbit and using it to obtain updated estimates of fundamental physics parameters (Fienga et al. 2015; Genova et al. 2018). During the hermean phase, BepiColombo trajectory will be reconstructed mostly by Doppler tracking, while range measurements effectively constrain the planet’s orbit. Being Mercury the innermost planet of the Solar System, the sensitivity of its motion to the effects of gravity allows the observability of the finest deviations (if present) from Einstein’s General Relativity theory. The orbital phase of BepiColombo will be used to measure not only PPN parameter \(\gamma \) but also \(\beta \), related to the degree of non-linearity in the superposition law for gravity (Will 2018), the Sun oblateness \(J_{2}\) and the preferred frame parameters \(\alpha _{1}, \alpha _{2}\) (null in GR) to test Einstein’s principle of relativity, stating that the laws of physics are independent of the reference frame. Furthermore BepiColombo’s measurement will lead to a better constraint of the validity of the strong equivalence principle. The widely accepted theory for SEP violation is based on relating the gravitational and inertial mass via the self-gravitational potential of the involved bodies, scaled by the Nordtvedt parameter \(\eta \). For metric theories of gravitation, \(\eta \) is related to the PPN parameters through the Nordtvedt equation (Will 2018; Nordtvedt 1970)
providing an additional constraint for decorrelating the estimates of \(\beta \) and \(J_{2}\).
A precise determination of the hermean orbit will enable an accurate measurement of the Sun gravitational constant (\(G M_{\odot } \)), its time variation (\(\zeta = {\hat{GM}_{\odot }} / {G} M_{\odot } \)), and the test of alternative theories of gravitation such as the Yukawa-like decay of the gravitational potential \(U\) for a \(N\)-body system:
where \(r_{ij}\) is the distance between bodies i and j of mass \(m_{i}\) and \(m_{j}\) respectively, and \(\lambda _{g}\) is the so-called “Compton wavelength”.
Several numerical simulations have been performed to assess the attainable accuracies on the estimation of the aforementioned parameters. A major difficulty for an efficient determination of Mercury’s orbit arises from the approximate rank deficiency of the orbit determination problem in a configuration like the BepiColombo one (Milani et al. 2002). If no mitigation strategy is employed the solution is strongly degraded. In Imperi et al. (2018) in-depth numerical simulations (see Table 5) of the full fundamental physics experiment were performed employing the so-called descoping strategy aiming to counteract the approximate rank deficiencies by excluding Earth position and velocity components orthogonal to the ecliptic orbital plane from the solve-for parameters list. In Table 5 we report the results for both the nominal and extended mission scenario. De Marchi and Cascioli (2020) have shown that the descoping, however, coincides with artificially providing information on the barycentric position of the Sun, thus leading to results that are too optimistic. A possible alternative strategy, as proposed in De Marchi and Cascioli (2020), consists in a combined analysis of BepiColombo with other planetary mission data. This strategy allows to overcome approximate rank deficiencies without artificially providing information on the parameters of interest. The simulations of De Marchi and Cascioli (2020), for the extended mission scenario, have been conducted as a proof of concept of this rank deficiency mitigation strategy employing a simplified semi-analytical model under very conservative hypotheses on the expected performances of MORE ranging system, thus leading to pessimistic results. In Table 5 we report the retrieved formal uncertainties on the parameters of interest for the extended mission scenario both by Imperi et al. (2018) and De Marchi and Cascioli (2020). The true expected performances of MORE fundamental physics experiment will lie in between the two. Improvements on the De Marchi and Cascioli model (to make it more realistic) are needed to make a more precise assessment.
10.2 Gravity Field and Rotational State of Mercury
Figure 9 represents the MORE estimate of the global gravity field in terms of RMS power associated with degree \(\ell \), compared with the MESSENGER HgM005 solution (Mazarico et al. 2014), for the nominal and extended mission. Not surprisingly, the accuracies of MORE global solution will lead to a substantial improvement with respect to the actual knowledge of the hermean gravity field. The dotted curves in Fig. 9 represent the case in which the experiment is simulated without any regularization, suggesting that the spherical harmonic expansion of the gravity field is able to reach at least degree and order 30 without being constrained by Kaula rule (Mazarico et al. 2014).
MORE estimate of gravity field in terms of power associated with degree l. The formal error spectrum is reported for both the nominal and the extended mission. Dotted lines give the error spectrum when the Kaula regularization is not used. (From Imperi et al. 2018)
The global map of the predicted gravity anomalies uncertainty is reported in Fig. 10 (top), showing that their values lie below the level of 5 mGal on the whole planetary surface, while the local resolution of the determined hermean gravity is specified in the degree strength map (Konopliv et al. 1999) shown in Fig. 11 (top). The percentage of the hermean surface expected to be mapped at a given resolution (degree strength) is reported in Fig. 12, again for the nominal and the extended mission. Note that the smallest uncertainties are found in the equatorial and southern mid-latitude regions, due to the latitude and altitude of the pericenter. During the nominal one-year mission, the pericenter will undergo a precession toward the South pole, drifting from 15° N to the specular position at 15° S, and at the same time the perturbations due to the odd zonal harmonics (Genova et al. 2013) will cause a decrease of the periherm altitude from the initial value of 480 km to 330 km. Considering the case of an extended mission, the pericenter would be driven further to the south, reaching 43° S after two years, with an altitude of 255 km. This leads to further improvement on the resolution and accuracy of the gravity field determination at the southern hemisphere (bottom panel of Fig. 10, bottom panel of Fig. 11). In the southern hemisphere the gravity anomalies uncertainty would be reduced to about 1 mGal over several regions, while the picture in the northern hemisphere would be basically unchanged.
MORE gravity anomalies uncertainty. Top panel: nominal mission. Bottom panel: extended mission (from Imperi et al. 2018)
The predicted uncertainties connected to the estimate of static quadrupole coefficients, the tidal Love number \(k_{2}\), and the rotational parameters, are reported in Table 6.
Determining both the real and imaginary part of the tidal love number \(k_{2}\) at the levels indicated in Table 6 could give fundamental information and constraints on the interior structure of Mercury. The concentration factor \({C} / {\mathit{MR}^{2}}\) can be estimated with an accuracy of \(2.1\times 1 0^{-3}\), given a predicted uncertainty on the obliquity measurement of \(1\times 1 0^{-3}\) arcmin. However, as stated in Sect. 1, the reliability of this prediction is affected by the influence that a large inner core (Peale et al. 2016), if present, would have on the obliquity. The 88 days libration in longitude can be estimated with an accuracy of 1.5 m at the equator, enabling the detection of a large inner core inside the outer liquid core (Van Hoolst et al. 2012). The value presented in Table 6 would be reduced by a factor of ∼1.5–2 in the case of the extended mission.
11 Conclusions
This paper is intended to provide a reference for the overall setup of the Mercury Orbiter Radioscience Experiment (MORE), including the novel radio system, the in-flight operations during cruise and at Mercury, and summarize the expected results in geodesy, relativity and space navigation. Together with the other onboard instruments, especially the Italian Spring Accelerometer (ISA), the BELA laser altimeter, the MERMAG magnetometer and the HRIC camera, MORE is set to improve our knowledge of the interior structure of the planet Mercury, answering many questions left open by the extraordinary MESSENGER mission. This work is based on the established hardware configuration and the predictions of the many numerical simulations carried out over the past years. We are also aware that parts of its content will be superseded once MORE and BepiColombo will start producing new data and new discoveries.
Notes
The Megachips per second (Mcps) is a measure of the speed with which encoding elements, called chips, are transmitted in the phase-modulated carrier.
References
B.J. Anderson, C.L. Johnson, H. Korth, M.E. Purucke, R.M. Winslow, J.A. Slavin, S.C. Solomon, R.L. McNutt, J.M. Raines, T.H. Zurbuchen, Science (2011). https://doi.org/10.1126/science.1211001
P.G. Antreasian, J.R. Guinn, in AIAA/AAS Astrodynamics Specialist Conf. and Exhibition (98-4287) (1998)
A.M. Archibald, N.V. Gusinskaia, J.W.T. Hessels, A.T. Deller, D.L. Kaplan, D.R. Lorimer, R.S. Lynch, S.M. Ransom, I.H. Stairs, Nature (2018). https://doi.org/10.1038/s41586-018-0265-1
J.W. Armstrong, L. Iess, P. Tortora, B. Bertotti, Astrophys. J. (2003). https://doi.org/10.1086/379505
J.W. Armstrong, F.B. Estabrook, S.W. Asmar, L. Iess, P. Tortora, Radio Sci. (2008). https://doi.org/10.1029/2007RS003766
N. Ashby, B. Bertotti, Accurate light-time correction due to a gravitating mass. Class. Quantum Gravity 27(14), 145013 (2010). https://doi.org/10.1088/0264-9381/27/14/145013
S.W. Asmar, J.W. Armstrong, L. Iess, P. Tortora, Radio Sci. (2005). https://doi.org/10.1029/2004RS003101
P.L. Bender, N. Ashby, M.A. Vincent, J.M. Wahr, Adv. Space Res. (1989). https://doi.org/10.1016/0273-1177(89)90015-X
P.L. Bender, N. Ashby, I. Ciufolini, L. Iess, Mercury relativity orbiter mission, in First ESA Conference on Fundamental Physics and Enabling Technologies (1994)
B. Bertotti, G. Comoretto, L. Iess, Astron. Astrophys. 269, 608 (1993)
B. Bertotti, L. Iess, P. Tortora Nature 425, 374–376 (2003). https://doi.org/10.1038/nature01997
D. Breuer, S.A. Hauck, M. Buske, M. Pauer, T. Spohn Space Sci. Rev. 132, 229–260 (2007). https://doi.org/10.1007/s11214-007-9228-9
P. Cappuccio, A. Di Ruscio, L. Iess, M.J. Mariani (2020a). https://doi.org/10.2514/6.2020-1095
P. Cappuccio, V. Notaro, A. Di Ruscio, L. Iess, A. Genova, D. Durante, I. di Stefano, S.W. Asmar, S. Ciarcia, L. Simone (2020b). https://doi.org/10.1109/TAES.2020.3008577
CCSDS, Pseudonoise (PN) Ranging Systems, Informational report 414.0-G-2, CCSDS (2014). https://public.ccsds.org/Pubs/414x0g2.pdf
CCSDS, Delta-DOR Technical Characteristics and Performance. Informational report 500.1-G-2, CCSDS (2019). https://public.ccsds.org/Pubs/500x1g2.pdf
G. Colombo, I.I. Shapiro, Astrophys. J. 145, 296 (1966)
G. Cremonese, F. Capaccioni, M.T. Capria, A. Doressoundiram, P. Palumbo, M. Vincendon, M. Massironi, S. Debei, M. Zusi, F. Altieri, M. Amoroso, G. Aroldi, M. Baroni, A. Barucci, J. Benkhoff, S. Besse, C. Bettanini, M. Blecka, D. Borelli, J.R. Brucato, C. carli, V. Carlier, P. Cerroni, A. Cicchetti, L. Colangeli, M. Dami, V. Da Deppo, V. Della Corte, M.C. De Sanctis, S. Erard, F. Esposito, D. Fantinel, L. Ferranti, F. Ferri, I. Ficai Veltroni, G. Filacchione, E. Flamini, G. Forlani, S. Fornasier, O. Forni, M. Fulchignoni, V. Galluzzi, K. Gwinner, W. Ip, L. Jorda, Y. Langevin, L. Lara, F. Leblanc, C. Leyrat, Y. Li, S. Marchi, L. Marinangeli, F. Marzari, E. Mazzotta Epifani, M. Mendillo, V. Mennella, R. Mugnuolo, K. Muinonen, G. Naletto, R. Noschese, E. Palomba, R. Paolinetti, D. Perna, G. Piccioni, R. Politi, F. Poulet, R. Ragazzoni, C. Re, M. Rossi, A. Rotundi, G. Salemi, M. Sgavetti, E. Simioni, N. Thomas, L. Tommasi, A. Turella, T. Van Hoolst, L. Wilson, F. Zambon, A. Aboudan, O. Barraud, N. Bott, P. Borin, G. Colombatti, M. El Yazidi, S. Ferrari, J. Flahaut, L. Giacomini, L. Guzzetta, A. Lucchetti, E. Martellato, M. Pajola, A. Slemer, G. Tognon, D. Turrini, SIMBIO-SYS: scientific cameras and spectrometer for the BepiColombo mission. Space Sci. Rev. 216, 75 (2020)
T. Damour, F. Piazza, G. Veneziano Phys. Rev. Lett. 89, 081601 (2002). https://doi.org/10.1103/PhysRevLett.89.081601
F. De Marchi, G. Cascioli, Testing General Relativity in the Solar System: present and future perspectives. Class. Quantum Gravity (2020). https://doi.org/10.1088/1361-6382/ab6ae0
A. Di Ruscio, A. Fienga, D. Durante, L. Iess, J. Laskar, M. Gastineau, Astron. Astrophys. (2020). https://doi.org/10.1051/0004-6361/202037920
I. di Stefano, P. Cappuccio, L. Iess in 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace) (2019a). https://doi.org/10.1109/MetroAeroSpace.2019.8869622.
I. di Stefano, G. Cascioli, L. Iess, P. Cappuccio, Environmental disturbances on mission for precise tests of relativistic gravity and solar system dynamics: the BepiColombo case, in Proceedings of the International Astronautical Congress, IAC (2019b)
I. di Stefano, P. Cappuccio, L. Iess, Class. Quantum Gravity (2020). https://doi.org/10.1088/1361-6382/abd301
ESA SPICE Service, BepiColombo Operational SPICE Kernel Dataset. Operational SPICE Kernel Dataset (2018). https://doi.org/10.5270/esa-dwuc9bs
A. Fienga, J. Laskar, P. Exertier, H. Manche, M. Gastineau, Celest. Mech. Dyn. Astron. 123(3), 325–349 (2015). https://doi.org/10.1007/s10569-015-9639-y
A. Genova, L. Iess, M. Marabucci, Planet. Space Sci. (2013). https://doi.org/10.1016/j.pss.2013.02.006
A. Genova, E. Mazarico, S. Goossens, F.G. Lemoine, G.A. Neumann, D.E. Smith, M.T. Zuber, Nat. Commun. (2018). https://doi.org/10.1038/s41467-017-02558-1
A. Genova, S. Goossens, E. Mazarico, F.G. Lemoine, G.A. Neumann, W. Kuang, T.J. Sabaka, S.A. Hauck, D.E. Smith, S.C. Solomon, M.T. Zuber, Geophys. Res. Lett. (2019). https://doi.org/10.1029/2018GL081135
A. Genova, H. Hussmann, T. Van Hoolst, D. Heyner, L. Iess, F. Santoli, N. Thomas, P. Kolhey, B. Langlais, J.Z.D. Mieth, J.S. Oliveira, A. Stark, N. Tosi, J. Wicht, J. Benkhoff, Geodesy, geophysics and fundamental physics investigations of the BepiColombo mission. (2021, this journal)
N.R. Hanson, Isis 53(3), 359 (1962)
S.A. Hauck, J.-L. Margot, S.C. Solomon, R.J. Phillips, C.L. Johnson, F.G. Lemoine, E. Mazarico, T.J. McCoy, S. Padovan, S.J. Peale, M.E. Perry, J. Geophys. Res., Planets 118(6), 1204–1220 (2013)
V. Iafolla, E. Fiorenza, C. Lefevre, A. Morbidini, S. Nozzoli, R. Peron, M. Persichini, A. Reale, F. Santoli, Italian Spring Accelerometer (ISA): A fundamental support to BepiColombo Radio Science Experiments. Planet. Space Sci. 58(1–2), 300–308 (2010). https://doi.org/10.1016/j.pss.2009.04.005
V. Iafolla, D.-M. Lucchesi, S. Nozzoli, F. Santoli, The BepiColombo mission to Mercury: Reaction wheels desaturation manoeuvres and the ISA accelerometer \(\delta \Rightarrow{V}\) measurements. Planet. Space Sci. 59(1), 51–62 (2011). https://doi.org/10.1016/j.pss.2010.11.001
L. Iess et al., MORE Science Performance Report (SPR) ESA document BC-MRE-RP-20020, Issue 3, 31/10/2017
L. Iess, G. Boscagli, Planet. Space Sci. (2001). https://doi.org/10.1016/S0032-0633(01)00096-4
L. Imperi, L. Iess, Class. Quantum Gravity (2017). https://doi.org/10.1088/1361-6382/aa606d
L. Imperi, L. Iess, M.J. Mariani, Icarus (2018). https://doi.org/10.1016/j.icarus.2017.09.008
C.L. Johnson, S.A. Hauck, J. Geophys. Res., Planets (2016). https://doi.org/10.1002/2016JE005150
G.D. Karner, A.B. Watts, J. Geophys. Res., Solid Earth 88(B12), 10449 (1983)
J.S. Knibbe, W. van Westrenen, J. Geophys. Res., Planets 120(11), 1904 (2015)
J.S. Knibbe, W. van Westrenen, Earth Planet. Sci. Lett. (2018). https://doi.org/10.1016/j.epsl.2017.11.006
A.S. Konopliv, W.B. Banerdt, W.L. Sjogren, Icarus (1999). https://doi.org/10.1006/icar.1999.6086
A.S. Konopliv, R.S. Park, A.I. Ermakov, Icarus (2020). https://doi.org/10.1016/j.icarus.2019.07.020
S.M. Kopeikin, Post-Newtonian limitations on measurement of the PPN parameters caused by motion of gravitating bodies. Mon. Not. R. Astron. Soc. 399(3), 1539–1552 (2009). https://doi.org/10.1111/j.1365-2966.2009.15387.x
J.L. Margot, S.J. Peale, R.F. Jurgens, M.A. Slade, I.V. Holin, Science 316(5825), 710–714 (2007)
J.L. Margot, S.J. Peale, S.C. Solomon, S.A. Hauck, F.D. Ghigo, R.F. Jurgens, M. Yseboodt, J.D. Giorgini, S. Padovan, D.B. Campbell, J. Geophys. Res., Planets 117(E12) (2012)
I. Matsuyama, F. Nimmo, J.T. Keane, N.H. Chan, G.J. Taylor, M.A. Wieczorek, W.S. Kiefer, J.G. Williams, Geophys. Res. Lett. 43(16), 8365–8375 (2016)
E. Mazarico, A. Genova, S. Goossens, F.G. Lemoine, G.A. Neumann, M.T. Zuber, D.E. Smith, S.C. Solomon, J. Geophys. Res., Planets (2014). https://doi.org/10.1002/2014JE004675
E. Mazarico, A. Genova, S. Goossens, F.G. Lemoine, G.A. Neumann, M.T. Zuber, D.E. Smith, S.C. Solomon, J. Geophys. Res. (2014). https://doi.org/10.1002/2014JE004675
A. Milani, G. Gronchi, Theory of Orbit Determination (Cambridge University Press, Cambridge, 2009)
A. Milani, D. Vokrouhlický, D. Villani, C. Bonanno, A. Rossi, Phys. Rev. D (2002). https://doi.org/10.1103/PhysRevD.66.082001
T.D. Moyer, Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation. JPL Deep-Space Communications and Navigation Series (Wiley, New York, 2008)
N.F. Ness, K.W. Behannon, R.P. Lepping, Y.C. Whang, K.H. Schatten, Science 185(4146), 151–160 (1974)
G.A. Neumann, M.T. Zuber, M.A. Wieczorek, P.J. McGovern, F.G. Lemoine, D.E. Smith, J. Geophys. Res., Planets 109(E8) (2004)
K. Nordtvedt, Astrophys. J. 161, 1059 (1970)
V. Notaro, L. Iess, J.W. Armstrong, S.W. Asmar, Acta Astronaut. (2020). https://doi.org/10.1016/j.actaastro.2020.04.009
S. Padovan, J.-L. Margot, S.A. Hauck, W.B. Moore, S.C. Solomon, J. Solomon, J. Geophys. Res., Planets 119(4), 850–866 (2014)
S.J. Peale, Nature (1976). https://doi.org/10.1038/262765a0
S.J. Peale, The Rotational Dynamics of Mercury and the State of Its Core (Univ. Arizona Press, Tucson, 1988), p. 461
S.J. Peale, R.J. Phillips, S.C. Solomon, D.E. Smith, M.T. Zuber, Meteorit. Planet. Sci. 37(9), 1269–1283 (2002)
S.J. Peale, J.-L. Margot, S. Hauck, S. Solomon, Icarus 264, 443–455 (2016)
A.C. Richie-Halford, L. Iess, P. Tortora, J.W. Armstrong, S.W. Asmar, R. Woo, S.R. Habbal, H. Morgan, Space Weather 7, S12003 (2009)
A. Rivoldini, T. Van Hoolst, O. Verhoeven, Icarus 201(1), 12–30 (2009)
F. Santoli, E. Fiorenza, C. Lefevre, D.M. Lucchesi, M. Lucente, C. Magnafico, A. Morbidini, R. Peron, V. Iafolla, ISA, a high sensitivity accelerometer in the interplanetary space. Space Sci. Rev. 216, 145 (2020)
H.R. Schulte, ISA-MORE Measurements Interface. Astrium technical note BC-ASD-TN-00090, 5 (Oct. 2007)
D.E. Smith, M.T. Zuber, R.J. Phillips, S.C. Solomon, S.A. Hauck, F.G. Lemoine, E. Mazarico, G.A. Neumann, S.J. Peale, J.-L. Margot, C.L. Johnson, M.H. Torrence, M.E. Perry, D.D. Rowlands, S. Goossens, J.W. Head, A.H. Taylor, Science (2012). https://doi.org/10.1126/science.1218809
A. Stark, J. Oberst, F. Preusker, S.J. Peale, J.-L. Margot, R.J. Phillips, G.A. Neumann, D.E. Smith, M.T. Zuber, S.C. Solomon, Geophys. Res. Lett. (2015). https://doi.org/10.1002/2015GL065152
G. Steinbrügge, S. Padovan, H. Hussmann, T. Steinke, A. Stark, J. Oberst, J. Geophys. Res., Planets (2018). https://doi.org/10.1029/2018JE005569
B. Tapley, B. Schutz, G. Born, Statistical Orbit Determination (Elsevier, Amsterdam, 2004)
N. Thomas et al. (2020, this journal)
R.N. Thor, R. Kallenbach, U.R. Christensen, A. Stark, G. Steinbrügge, A. Di Ruscio, P. Cappuccio, L. Iess, H. Hussmann, J. Oberst, Astron. Astrophys. (2020). https://doi.org/10.1051/0004-6361/201936517
P. Tortora, L. Iess, J.J. Bordi, J.E. Ekelund, D.C. Roth, Precise cassini navigation during solar conjunctions through multifrequency plasma calibrations. J. Guid. Control Dyn. 27(2), 251–257 (2004). https://doi.org/10.2514/1.997
N. Tosi, M. Grott, A.C. Plesa, D. Breuer, J. Geophys. Res., Planets 118(12), 2474–2487 (2013)
T. Van Hoolst, C. Jacobs, J. Geophys. Res. (2003). https://doi.org/10.1029/2003JE002126
T. Van Hoolst, A. Rivoldini, R. Baland, M. Yseboodt, Earth Planet. Sci. Lett. 333–334, 83–90 (2012)
G. Voisin, I. Cognard, P.C.C. Freire, N. Wex, L. Guillemot, G. Desvignes, M. Kramer, G. Theureau, Astron. Astrophys. (2020). https://doi.org/10.1051/0004-6361/202038104
M.A. Wieczoreck, R.J. Phillips, J. Geophys. Res. 103(El), 1715–1724 (1998)
C.M. Will, Living Rev. Relativ. 17, 14 (2014). https://doi.org/10.12942/lrr-2014-4
C.M. Will, Theory and Experiment in Gravitational Physics, 2nd edn. (Cambridge University Press, Cambridge, 2018)
Acknowledgements
The authors would like to thank the ESA BepiColombo Project for its continuous support. The MORE team acknowledges the crucial and inspiring contribution of the late Andrea Milani, who died prematurely on Nov. 28, 2018. LI, PC, GC, GDA, FDM, IDS, AG, ADR, VN, GM, AP, GS, DS, GT, PT, MZ acknowledge support from the Italian Space Agency (grant 2017-40-H.1-2020). This work was carried out, in part, at the Jet Propulsion Laboratory, California Institute of Technology, under contract for the National Aeronautics and Space Administration.
Funding
Open Access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The BepiColombo mission to Mercury
Edited by Johannes Benkhoff, Go Murakami and Ayako Matsuoka
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iess, L., Asmar, S.W., Cappuccio, P. et al. Gravity, Geodesy and Fundamental Physics with BepiColombo’s MORE Investigation. Space Sci Rev 217, 21 (2021). https://doi.org/10.1007/s11214-021-00800-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-021-00800-3