Abstract
The payload of the UFFO (Ultra-Fast Flash Observatory)-pathfinder now onboard the Lomonosov spacecraft (hereafter UFFO/Lomonosov) is a dedicated instrument for the observation of GRBs. Its primary aim is to capture the rise phase of the optical light curve, one of the least known aspects of GRBs. Fast response measurements of the optical emission of GRB will be made by a Slewing Mirror Telescope (SMT), a key instrument of the payload, which will open a new frontier in transient studies by probing the early optical rise of GRBs with a response time in seconds for the first time. The SMT employs a rapidly slewing mirror to redirect the optical axis of the telescope to a GRB position prior determined by the UFFO Burst Alert Telescope (UBAT), the other onboard instrument, for the observation and imaging of X-rays. UFFO/Lomonosov was launched successfully from Vostochny, Russia on April 28, 2016, and will begin GRB observations after completion of functional checks of the Lomonosov spacecraft. The concept of early GRB photon measurements with UFFO was reported in 2012. In this article, we will report in detail the first mission, UFFO/Lomonosov, for the rapid response to GRB observations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gamma Ray Bursts (GRB) are the most luminous explosions in the universe, emitting the highest energy photons, and detected at the highest redshift of any discrete source in the universe (Salvaterra et al. 2009; Tanvir et al. 2009). These properties provide great leverage in time, wavelength, and information, and thus a unique opportunity to understand not only the nature of the universe but fundamental physics (Lamb and Reichart 2000; Bromm and Loeb 2006; Kistler et al. 2009; Amati et al. 2008; Ghirlanda et al. 2006; Panaitescu and Vestrand 2008; Kocevski 2012; Shahmoradi and Nemiroff 2011; Bernardini et al. 2012; Zhang et al. 2009; Greiner et al. 2011). GRB emission spans some 9 orders of magnitude in photon energy, a prime opportunity for synoptic observations.
GRBs are believed to be sources of ultra-high energy cosmic rays (UHECR) (Waxman 2006; Abu-Zayyad et al. 2012; Tokuno et al. 2012; Abraham et al. 2004; Panasyuk et al. 2012; Takahashi 2009; Halzen and Klein 2010; Gorham et al. 2009) and gravitational waves (GW) whose detection has been reported recently (Cutler and Thorne 2002; Abramovici et al. 1992; Abbott et al. 2016a), and is a prime example of multi-messenger astronomy. The rapid-response in the observation of electromagnetic counterparts to GW (Abbott et al. 2016b) is important to obtain the rich information in physical processes of GRBs giving rise to each messenger and the time delay between them.
In spite of the wide knowledge already acquired about GRBs from space (Klebesadel et al. 1973; Fishman 1994; Boella et al. 1997; Piro et al. 1998a; MacFadyen and Woosley 1999; Ricker et al. 2002; Winkler et al. 2003; Gehrels et al. 2004; Perna et al. 2003; Piran 2004; Nakar 2007) and on the ground there are still many open questions about their progenitors and environment. Deeper understanding of GRBs requires more statistics of GRBs, particularly of high-z GRBs, measurements of polarization, and a wider range of not only spectral coverage extending to sub-keV X-ray and infrared (IR) but also temporal coverage through rapid pointing of telescopes at GRBs. These observational capabilities are to be incorporated in future missions (Paul et al. 2011; Roming et al. 2012; Produit et al. 2005; Park et al. 2013). They are expected to enlarge the detection area and/or volume of X-rays and the aperture of UV/optical/IR telescopes, and improve photometric, temporal and spectral sensitivities as well.
Hundreds of GRB UV/optical light curves have been measured since the discovery of optical afterglows (van Paradijs et al. 1997; Costa et al. 1997) and their distance measurement with the event on May 8, 1997 (Metzger et al. 1997; Piro et al. 1998). The Swift spacecraft is currently in operation in space with the fastest high-sensitivity in the UV/optical (Gehrels et al. 2004). However, after a decade of operation of Swift, the immediate aftermath of the explosion is scarcely observed in the optical or UV because the Swift instrument typically responds in ∼100 s or more. Ground-based telescopes do occasionally respond faster, but only a relatively small number of rapid detections have been produced to date with heterogeneous sensitivities and other characteristics. Only a few short duration GRBs have been detected in the UV/optical/IR within the first minute after the gamma-ray signal.
Swift BAT broadcasts the coordinates of GRBs detected within 5–7 s over the internet via the gamma-ray coordinate network (GCNFootnote 1) which ground telescopes may respond to and follow their coordinates. Large terrestrial telescopes such as Keck have better sensitivity than Swift UVOT, but slower slew times which makes them uncompetitive for the sub-1000 s regime. The response of robotic telescopes on ground (e.g. ROTSE-I-III (Akerlof et al. 2003), RAPTOR (Vestrand et al. 2002), PAIRITEL (Bloom et al. 2006), Super-LOTIS (Williams et al. 2004), BOOTES (Jelinek et al. 2010), MASTER (Lipunov et al. 2010)) is extremely rapid, e.g. 25 s for ROTSE-III, however, the sensitivity is far less than that of the Swift UVOT (Roming et al. 2005). Due to their small size, and to the limitations of ground-based observations including daytime and weather, together these instruments have managed only a handful of rapid detections (Akerlof et al. 1999). An observation of prompt optical from GRB080319B (Racusin et al. 2008) happened to be made by TORTORA (Beskin et al. 2010) on the REM telescope and by ‘Pi of the Sky’ (Burd et al. 2005) when this GRB took place in their field of view.
Therefore, the Swift limit of a 60 s response is the practical minimum for sensitive UV/optical GRB studies for the near to mid-term future. This lack of early observations and the blindness to the rise phase of many GRB optical light curves, along with those of other rapidly variable transient sources, leaves fertile astrophysical territory. Many important physical questions arising at the short time scales remain unexplored (Molinari et al. 2007; Panaitescu and Vestrand 2008; Cline et al. 2011). Rapid data collection is also essential for tests of fundamental physics such as constraints on Lorentz violations (Ellis et al. 2006) and CPT (Kostelecky and Mewes 2008) from the time delay between different energy photons, or between photons and neutrinos. Coincident or successive observations of the explosion event as an electromagnetic counterpart to a neutrino or gravitational wave observatory signal would revolutionize astronomy, and greatly improve our understanding of black holes, neutron stars, and strong field gravity.
The Ultra-Fast Flash Observatory (UFFO) was proposed to measure the UV/optical counterpart on second time scales (Park et al. 2013) after the gamma ray trigger from GRBs by introducing very fast pointing of the narrow-FOV UV/optical telescope using a fast slewing mirror or mirror array (Park et al. 2009). It provides a reliable method to lower the current response limit by one to two orders of magnitude in order to obtain a large statistically meaningful sample of GRB light curves including the rise phase for the first time. The instrument idea and fabrication, and its physics potential were described in previous reports (Park et al. 2013; Jeong et al. 2013; Kim et al. 2013; Nam et al. 2013).
As the first one of its kind, the UFFO/Lomonosov instrument has been developed as one of science payloads onboard the Lomonosov satellite that was successfully launched in April 28, 2016. As its name UFFO-pathfinder (Park et al. 2009) suggests, UFFO/Lomonosov is a pathfinder of the UFFO, which serves as the observational cornerstone of future mission development for rapid responses, though small and limited. An overview of the Lomonosov spacecraft and its payload is presented as a separate paper in the same issue of this journal. Here we describe the details and update of the flight model of UFFO/Lomonosov together with the status of operation in space, while the X-ray telescope of UFFO/Lomonosov (UBAT) is detailed in a separate paper in this issue. The concept of early photon measurements is introduced in Sect. 2. Section 3 summarizes the instrumentation of UFFO/Lomonosov followed by the running efficiency in space. The telescopes for X-rays and UV/optical are described in Sects. 5 and 6. In Sect. 7, the expected brightness of GRBs is estimated for UFFO/Lomonosov. Section 8 demonstrates the operation of the UFFO/Lomonosov in space. The mission summary is given in Sect. 9.
2 The Method of Early Photon Measurements in UFFO/Lomonosov
Swift responds to GRB triggers by rotating the entire spacecraft to point its optical telescopes at the GRB. Swift has a lower limit of around 60 s to the response time for its optical measurements. Ground-based telescopes do occasionally respond faster, but only a handful of rapid detections have been produced to date. Our approach to accelerate the slew capabilities is to redirect the optical path at an astronomical telescope by using a lightweight slewing mirror rather than move the entire payload or telescope (Park et al. 2009). The slewing system of UFFO/Lomonosov is a flat mirror mounted on a gimbal platform. This concept of steering a telescope via steering mirror(s), called Slewing Mirror Telescope (SMT), enables in practice a large field of view (FOV) to be accessible without aberrations inherent in wide-field optical systems. The rotating mirror of SMT in UFFO/Lomonosov moves across the entire field of view wider than 70° × 70°, points, and settles in less than 1 s.
Apart from SMT for UV/optical measurements, UBAT (UFFO Burst Alert Telescope) in UFFO/Lomonosov measures X-rays by using a coded mask similar to Swift BAT (Burrows et al. 2005; Barthelmy et al. 2005), but the effective area of X-ray detection in UFFO/Lomonosov is smaller than Swift by 50 times. Typically bright GRBs have been localized by Swift BAT with the time of about 20 ms for X-ray acquisition, while 1 s would be taken for UFFO/Lomonosov. This means that for simple location of a GRB, rather than a detailed study of the X-ray through gamma-ray spectrum, a small instrument can locate a large fraction of those detected by much larger instruments. It makes possible very advanced missions improving on this UFFO-pathfinder with relatively modest size.
It is noted that the trigger latency of GRB localization with X-rays, the calculation time for alerting a GRB with its position in the sky, takes 5–7 s for Swift, which dominates in prompt alarm process for optical follow-ups. In UFFO/Lomonosov trigger calculations with X-rays, including rate trigger and imaging trigger, are performed in a couple of Field Programmable Gate Arrays (FPGAs), which reduces the latency significantly, e.g. “below 1 s”. Figure 1 shows the measurement concept of how to achieve the fast response of UV/optical observation. Figure 2 shows the domain of frequency and time accessible by space and ground experiments.
3 Instrument Configuration
The payload of UFFO/Lomonosov is composed of two telescopes: a wide-FOV trigger telescope for X-ray measurements, UBAT, and a narrow-FOV fast telescope for UV/optical observations, SMT. Functionally, it is a large-scale version of the tracking mirror telescope for wide FOV coverage of sky with milliseconds-slewing capability on trigger with coarse location (Park 2004; Park et al. 2008; Lee et al. 2012). Apertures of the telescopes are co-aligned providing multi-wavelengths measurement of GRBs in X-ray and UV/optical ranges.
The SMT is a 10-cm diameter aperture modified Ritchey-Chretien telescope equipped with a reflector of 15-cm diameter flat mirror that is rotated towards any light source within the solid angle view of 70° × 70° at the speed of a second after receiving the trigger from the UBAT. The SMT will be described in Sect. 6.
The signal for burst recognition to trigger UV/optical observations is provided by the UBAT. Being conceptually a down-sized version of the Swift BAT, it is a coded mask aperture camera which provides not only localization of a burst but flux and energy measurements. By using advanced FPGA with a lower number of detector channels, however, we reduce the trigger latency significantly, the required time of trigger decision, including computation speed for the trigger processing, less than a second and thus an order of magnitude faster than that of the Swift. The FOV of UBAT is \(90.4\times 90.4~\mbox{deg}^{2}\) for partial coded and \(70.4 \times 70.4~\mbox{deg}^{2}\) for half coded, which overlaps the full coverage of the SMT, \(70 \times 70~\mbox{deg}^{2}\), and the location accuracy, \(10\times 10~\mbox{arcmin}^{2}\), is comparable to the FOV of the SMT, \(17\times 17~\mbox{arcmin}^{2}\). Less accurate pointing gives higher computation speed of the UBAT.
Due to the limitation in mass for the UFFO-pathfinder, its structure including the SMT and UBAT was fabricated to be lightweight, whereas meeting structural and functional requirements in stiffness, strength, dimensional restriction and thermal conduction. The housing was made of carbon fiber. Mirrors and substructure were manufactured through finite element analysis and lightweight engineering. The overall mass, power consumption, and the total volume of the UFFO/Lomonosov including electronics and support structure are 25 kg, 25 Watts, and \(950 \times 400 \times 365~\mbox{mm}^{3}\), respectively. The UBAT has the size of \(400 \times 400 \times 365~\mbox{mm}^{2}\), while the size of SMT is very compact. The SMT has a focal length of 1140 mm for which a small size focal plane detector is used. From the effective FOV and focal length the optimized size of the SMT was built to be \(600\times 320 \times 200~\mbox{mm}^{3}\).
The readout, data acquisition and control electronics with a bus interface to the satellite, UFFO Data Acquisition system (UDAQ), is located at the bottom of the UFFO. The UDAQ is in charge of automatic control of the payload not only with the predefined list of commands but the list uploaded from the ground; interfacing to the satellite; data collection from the two telescopes, storing in several NOR flash memories and transfer to the satellite. It is also responsible for monitoring of all housekeeping parameters; calculation of the orbit and recognition of day and night with in-house photo sensors; power management, etc. All of these functions are implemented in an ACTEL FPGA for the low power consumption and fast real-time processing.
Table 1 lists the observation parameters of UFFO/Lomonosov in comparison to terminated and ongoing space missions. Figure 3 shows schematic views of the UFFO-pathfinder optimizing the space and position of each telescope as well as the manufactured flight model. The UFFO-pathfinder has successfully passed space environments test, including thermal, vacuum, shock, and vibrations, at the National Space Organization of Taiwan (NSPO) in August 2011. The final integration of the flight model to the Lomonosov spacecraft and space environments test was carried out at VNIIEM in Russia between 2013 and 2015, before being moved to Vostochny in 2016 (see Fig. 4).
4 Running Efficiency and Observation Time of UFFO/Lomonosov
The Lomonosov satellite has a Sun-synchronous orbit with an inclination angle of 98 degrees and orbit altitude of 550 km. It turns 15 orbits every day, corresponding to 96 minutes taken per orbit. UFFO/Lomonosov will be powered off at polar regions for protection of the instrument against particle radiations. The fraction facing the Sun will be about 20% when the instrument is powered off. Therefore the power-on fraction per orbit is 55%, which corresponds to the running time of 13.2 hours per day.
The velocity of the Lomonosov satellite is about 7.6 km/s, and thus the angle of transverse is 0.0625 deg/s. The time of a point object passing through a SMT pixel is 0.018 s, while the time passing through the entire SMT is 4.551 s. The UBAT has about 70.4 degrees for half-coded FOV and about 43.6 degrees for full coded FOV, as shown in Fig. 5. So, the practical maximum observation time is about 18.8 min per orbit for a given GRB for the half-coded case.
The UFFO-pathfinder has a limit in the data size for transfer to Earth every day, designed to be 300 Mbytes/day. The event size including SMT, UBAT and other housekeeping information, amounts to 20 Mbytes. Therefore, the maximum number of triggers available every day is 15; however, due to the bottleneck in data transfer from the payloads of Lomonosov to the spacecraft via CAN bus, the speed of data transfer is limited for UFFO to be 4 triggers every day.
5 X-Ray Observation with UBAT of UFFO/Lomonosov
The UBAT is a coded mask aperture shadow camera. GRBs will be localized by the UBAT at the confidence level of 7\(\sigma \) to a region 10 arcmin across, thus contained fully within the FOV of the SMT. From the fact that we make no specific requirements on energy resolution or flux measurements, the coded mask technique would be the best way to obtain large FOV for hard X-rays in the energy range of about 10 to 200 keV with an excellent location accuracy. This is true for the UBAT which has modest detection area, i.e. smaller than Swift BAT by factor 25, so the UBAT needs 25 times longer collection time to recognize the same burst, assuming the same detection efficiency. We found that Swift can trigger (rate trigger) GRBs typically with 50 ms of the collection time of X-rays. That is, 50 ms is the mean value. It implies that we will have 50% of Swift bursts within 1.25 s collection time. The trigger window for the UBAT is set to be between 1–64 s. Our estimate is to see 60% of Swift BAT bursts with about 1.5 s of collection time. Figure 6 shows the calculation of the UBAT sensitivity in comparison to Swift BAT, SVOM, Fermi GBM, and BATSE sensitivities. The sensitivity is specified in the form of a graph of detection threshold, i.e. peak flux sensitivity versus GRB spectral peak energy Epeak (see Band 2003, and \(\alpha=-1\), \(\beta=-2\) are chosen). The nominal value of signal-to-noise ratio (SNR) used in UBAT is 8, while effective detection area of 0.88, solid angle of 1.8, and mask open fraction of 0.45 are used in the calculation of sensitivity. On the other hand, a larger detection area of Swift BAT compared to UBAT greatly improves the localization accuracy, i.e. 1–4 arcmin for Swift as opposed to 10 arcmin for UBAT. We assume the number of BAT/Swift triggers to be about 100/year. Taking into account the duty cycle concerning day and night ration and chances of passing through SAA and polar regions,
Assuming 30% degradation by unknown factors, the UBAT foresees about 35% of Swift (∼90 GRBs/year), that is, 20–30 events every year.
The sensitivity of UBAT (blue solid line) in comparison to Swift/BAT (green dashed), SVOM/ECLAIR (red solid), Fermi/GBM (cyan solid dot) and BATSE (purple dot) in terms of peak flux sensitivity as a function of GRB spectral peak energy Epeak (Band (2003), and \(\alpha=-1\) and \(\beta=-2\) are chosen). The nominal value of SNR used in UBAT is 8, while \(f_{\mathrm{det}}=0.88\), \(\varOmega=1.8\) and \(f_{\mathrm{mask}}=0.45\)
The UBAT hardware consists of three major components: a coded mask, detectors and electronics, and shield and hopper structures. The coded mask made of 1-mm thick Tungsten Alloy has randomized rectangular hole patterns, each area being 5.67 × 5.67 \(\mbox{mm}^{2}\), with a 44.5% open fraction (see red rectangle in Fig. 9). Shielding around the four sides against diffused X-ray backgrounds is made from passive layers of dense material. All electronics for analog readout, digital processing, trigger decision logic, high voltage distribution and interface to UDAQ are located underneath the MAPMT array, forming a compact structure of the UBAT detector, as shown in Fig. 7 (bottom left). Like SMT and UDAQ, all digital processing in UBAT are realized with FPGAs which provides great advantages in fast response, low power consumption and parallel processing and control. Figure 7 (top left) shows the integrated UBAT system, and major parameters including its mass, volume and power consumption are listed in Table 2.
The detection of X-rays is made by a 48 × 48 array of pixelated scintillators of YSO crystal, arranged in a 6 × 6 group of 8 × 8 pixel modules. The area and height of a pixel are 2.68 × 2.68 \(\mbox{mm}^{2}\) and 3.0 mm, respectively. YSO (Y2SiO5) is a Ce-doped (0.04%) crystal with a peak emission around 400 nm under X-ray excitation and an absorption efficiency of close to 100% for X-ray energy below 30 keV. It presents an excellent light yield of ∼25 photons/keV similar to LSO (Lu2SiO5), but does not have inherent radiative noise unlike LSO.
The YSO array is attached on the 6 × 6 array of multi-anode photomultipliers (MAPMT, Hamamatsu R11265-03-M64, bi-alkali photocathode) each of 8 × 8 pixels. Each MAPMT is read out by a 64-channel SPACIROC ASIC. The MAPMT is ultimately sensitive by exhibiting a single photon counting with a gain of 106, while having low thermal noise. The photocathode of MAPMT has a quantum efficiency of 30–35% at its spectral response range of 185–650 nm, so that UBAT is able to detect X-rays at the level of keV in principle.
When an X-ray hits an YSO pixel, some of the UV generated inside the YSO are refracted onto neighboring MAPMT pixels, which cause optical cross talk. The level of cross talk at the nearest neighbors is 30% of the signal, but is negligible at the next nearest neighbors. Therefore, any cross talk mostly appears at the nearest neighbors, and the observed hit patterns are mostly a cross pattern (with the pixel hit by X-ray at the center and with the remaining four pixels at the nearest neighbors), and some variants with the smaller number of pixels. We implemented a simple algorithm in a FPGA that finds the hit center from these distinctive patterns. Therefore the cross talk has no bearing on the instrument background. On the other hand, X-rays produce such distinctive hit patterns that we can use these patterns to identify, for example, X-ray events against cosmic backgrounds.
As shown in Fig. 8, we see that the UBAT is able to reproduce an X-ray peak at 8.6 keV with a spectral resolution of about 2 keV, which implies UBAT to be sensitive at 5 keV and even below. A detailed study of energy sensitivity will be reported later. Alternatively, the coded mask loses opacity for high energy x-rays, and YSO efficiency drops significantly at energies above 200 keV; in practice, the maximum energy detectable from the UBAT is limited to 200 keV.
Within a second time bin, a typical burst could alert UBAT by tripping a “rate trigger” which exhibits an excess in the total number of X-rays over the ambient background. The “image trigger” processing which locates a GRB runs in parallel with the same X-rays in independent logic units of a dedicated FPGA. The algorithm for the localization of a burst, called image trigger or correlation imaging, comes from the fact that UBAT detector pixels will see a subset of the mask pattern that is different depending on where the GRB is located in the UBAT field of view. Figure 9 shows how hit pattern of the detector (blue colored in the figure) best fits the mask pattern (red). To find the GRB location, the detector illumination pattern is placed on top of the mask pattern and moved around until a good fit or best correlation between the detector pattern and the mask hole pattern is found. The offset location (X, Y) of the center point of the detector pattern from the mask center point gives the location of the GRB, although in distance units, not angular units. If the mask height above the detector is H, then the GRB location vector for the SMT instrument is just (X, Y, H) or some normalized (x, y, h) version. The detailed description of the trigger algorithm which takes into account the drift of the satellite and different pixel response, as well as the hardware and the performance, is given in a separate paper in this issue.
Schematic demonstration of how a detector illumination pattern in a 58 × 58 pixel matrix (blue) changes with the GRB offset location from the UBAT z-axis—pointing away from the Earth center—on a 135 × 135 array of possible FOV locations. The actual detector pixel array is 48 × 48, but a spacing of 2 pixels between the 8 × 8 modules is taken into account
After a positive rate trigger, the image trigger processor of UBAT starts to output the position of a burst candidate every second, and its probability in terms of a SNR. This image processing will last up to 64 seconds, depending on the brightness of GRBs. If the SNR becomes greater than a threshold value, currently set to be 7 as the default but changeable in space by uploading the list of run parameters, then the image trigger will be fired to start a subsequent slewing of the SMT to target the position followed by acquisition of both UBAT and SMT data. It is noted that the calculation of position and the decision of image trigger, called trigger latency, takes only less than a second to determine the position of GRB, thanks to FPGA’s fast parallel processors. Short trigger latency in UFFO/Lomonosov would be an advanced feature over the previous space missions like Swift BAT. However, due to the limitation in power consumption which constrained the memory resource of the UBAT FPGA, the latency for the GRB localization turns out to be 1 s.
The performance of the UBAT, i.e., determination of the position and its accuracy for a given source, was tested by using an X-ray tube with energies below 50 keV. This mini-tube was placed 8 m away from the UBAT. The laboratory background rate was measured to be 0.84 cnts/s/cm2, while the count rates resulting from the X-ray source on the detector below the mask were 0.73, 1.19, 2.24, and 4.10 cnts/s/cm2. We found the image trigger with SNR = 7 in ∼12 s, 11 s, 4 s, and 1 s, respectively. That is, the UBAT is capable of localizing sources with flux similar to the background level within a few seconds. Figure 10 shows the result of the image as an SNR map for the signal rate of 4.10 cnts/s/cm2 (left) for which localization is made in a second. The center and right plots show the SNR map for the source rate of 0.73 cnts/s/cm2 and the SNR values as a function of elapsed time, respectively, i.e. 12 seconds are taken before SNR reaches 7. It is noted that a reliable localization can be made even with only half of the detector pixels with a little extension of collection time, which demonstrates the robustness of localization capability against possible aging effects in the detector channels in space.
The UBAT imaging of the sky as a function of SNR values for the signal rate of 4.10 cnts/s/cm2 (left) right after one second of collection time, and 0.73 cnts/s/cm2 (center) for which the right plot shows the SNR reaching 7 at 12 seconds of X-rays collection (right). The background rate was 0.84 cnts/s/cm2, the same for both tests
6 UV/Optical Observation with SMT of UFFO/Lomonosov
As a key component of UFFO missions, a Slewing Mirror Telescope (SMT) was proposed for rapid response to prompt UV/optical photons from GRBs. The SMT of UFFO/Lomonosov consists of a fast slewing mirror mounted on a two-axis gimbal stage, placed in front of a Ritchey-Chrétien telescope (RC telescope), a focal plane detector, and associated readout and mirror control electronics. The parallel lights from GRB are always directed on axis to the RC telescope by the slewing mirror. The maximum tilting angle of the mirror is ±35°, resulting in 70° × 70° of an effective coverage of SMT which covers the half-coded FOV of UBAT.
The slewing mirror is made of Zerodur and has a diameter of 15-cm and a weight of 0.482 kg. It is driven by two geared stepping motors with sealed bearings that provide sub-second response over the entire FOV (±90 deg) and a settling time of less than 350 ms. These electric motors driving the gimbal-mounted mirror are simple, robust, and space qualified. A precise motion control using a micro-stepping technique and a close-loop control using high resolution rotary encoders enable targeting resolution to be better than 2 arcmin.
The Ritchey-Chrétien type telescope was chosen to have a long focal length (f-number of 11.4) for an aperture of 100 mm diameter and FOV of 17 × 17 arcmin2. The optics system with the slewing mirror were fabricated not only for light but highly hardened against shock and vibrations at time of launch, and against degradation in optical performance by thermal stress in orbit. The primary and secondary mirrors were fabricated with a precision of about RMS 0.02 waves in wave front error (WFE) and 84.7% in average reflectivity over 200–650 nm. The entire SMT optics was aligned at an accuracy of RMS 0.05 waves in WFE at 632.8 nm.
The focal plane detector is an Intensified Charge-Coupled Device (ICCD) which consists of 256 × 256 monochromic pixels with a pixel FOV of 4 × 4 arcsec2. So the FOV of the SMT is 17 × 17 arcmin2 which is wide enough to contain a potential source of GRB triggered by UBAT, with a localization accuracy of 10 arcmin at 7 \(\sigma \). We chose a UV-enhanced S20 photocathode which is sensitive to photons of 200–650 nm in wavelength with quantum efficiencies of 40%, 70% and 20% at 200 nm, 400 nm, and 600 nm, respectively. Double multi-channel plates (MCPs) were adopted as an intensifier of ICCD for the amplification of photoelectrons at a gain up to 106 so that the focal detector operates in photon counting mode and thus SMT could observe faint objects up to ∼19 magnitude in B-filter per 100 s, assuming the same performance as Swift. The gain of the intensifier can be adjusted from 103 to 106 by the control program. These photons are read out at a rate of 50 frames per second by a Kodak KAI-0340 interline CCD sensor (640 × 480 pixels, with a charge capacity of 40,000 electrons, and readout noise of 16 electrons) and a CCD signal processor with a 10-bit Analog-to-Digital Converter. Various control clocks for the CCD readout are implemented using a Field Programmable Gate Array (FPGA). The SMT records the arrival time of individual photons and provides positioning of sources with 4.3 arcsec (1\(\sigma \) width) point spread function (PSF). The angular resolution could be improved by a centroiding algorithm.
The SMT electronics controls the slewing mirror, reads out the ICCD, adjusts ICCD high voltage, monitors housekeeping sensors, and communicates with and transfers the ICCD data to the central data acquisition system of UFFO/Lomonosov (UDAQ). As with other space experiments, the UFFO/Lomonosov has substantial limitations both in power consumption and real-time processor speed. Additionally, the SMT requires fast algorithms to slew the mirror in response to the UBAT trigger. These requirements are satisfied by employing a FPGA in place of a CPU. The FPGA includes a variety of functions required for the SMT readout and control as well as the interface to the payload system. Apart from minimization of power consumption and enhancement of processing time, the best performance of the ICCD was realized through the customization of the control of CCD clocks and MCPs high voltages in the FPGA.
The entire system of SMT has been tested and satisfies the conditions of launch and those of operation in space: those associated with shock and vibration and those associated with thermal and vacuum, respectively.
Figure 11 shows the integrated SMT, and its major parameters are presented in Table 3. The details of SMT optics design, manufacture, integration and test including space qualification and laboratory scale end-to-end validation tests were reported in Jeong et al. (2013). The technical details of the focal plane detector and its associated electronics, as well as precision control of the slewing mirror, are found in Kim et al. (2013).
7 Expected GRB Brightness by UFFO/Lomonosov
The optical brightness of GRBs at their early phase, and their mechanisms, are hardly understood, so we assume two simple known cases to estimate GRB magnitudes at the SMT observation, that is, afterglows might dominate by forward shock (\(\alpha \sim1\)) or reverse shock (\(\alpha \sim2\)). The calculation from the data of UVOT shows ∼0.0947 photons from a 17-magnitude GRB. Apparent optical magnitude distribution has a peak at 19.5 magnitude for 1000 s exposure (Akerlof and Swan 2007). GRB afterglows follow a power law decay (\(F = t^{\alpha }\), temporal decay index is ∼1 up to 500 s (Oates et al. 2015). Early optical glows could be contaminated by reverse shock, for which the temporal decay index would be 2. Figure 12 shows the sensitivity of the UFFO/Lomonosov SMT. The SMT has the frame exposure time of 20 ms, which is short enough to detect a burst as bright as 11.5 magnitude. On the other hand, total observation time of SMT is 78 s, which is long enough to observe a burst of up to 19 magnitude. These values, 20 ms and 78 s, are default and changeable in orbit. It is noted that the SMT is able to detect very bright GRBs, i.e. 7 magnitude, by decreasing the gain of ICCD down to 103. As shown in Table 3, this estimate is extracted from the following.
The sensitivity (red colored arrow) in the unit of number of photons (left axis) and magnitude (right axis) and the primary observation time (black colored arrow) of the UFFO/Lomonosov SMT. The number of photons are the ones read into a pixel of the SMT for a 20-ms frame time, assuming Vega spectral type
Nineteenth magnitude was calculated using a 10-cm aperture telescope with the same performance as Swift UVOT. UVOT can detect a \(m_{B}=22.3\) point source in 1000 s (http://heasarc.gsfc.nasa.gov/docs/swift/about_swfit/uvot_desc.html).
A comparable 30-cm ground telescope is limited to 20 magnitude due to sky brightness. The star of 20 magnitude for 1000 s was measured to give 1300 photon counts using a white filter on ground. 1300 photons are expected in space as well. We assume in a conservative way that Swift can see a 22.3 magnitude star with 5 sigma. Then, one estimates the background in space to be 1600 in 1000 s for 30-cm aperture telescope. In our case for UFFO/Lomonosov, we are supposed to see the source of 19 magnitude at 8 sigma, because a 19-magnitude source gives 13 photons in 100 s for 10-cm aperture while the background is 1600, so \(1300\times 2.5/10/10/\sqrt{(1600/10/10)} = 8 \sigma \). We have measured the performance of SMT in the lab by illuminating 4 photons on SMT and by taking into account the readout noise, which verifies that we are able to observe a source dimmer than 19 magnitude.
8 On-orbit Operation of UFFO/Lomonosov
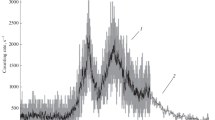
Since the launch, UFFO/Lomonosov has been tested and calibrated till the end of Nov. 2016 for which the UFFO instrument was powered on 20 times, each time orbiting once and running about 25 min. Several sets of parameters designed for X-ray trigger and alignment of the slewing mirror for a given direction were examined. Figure 13 shows the behavior of UFFO power consumption in terms of currents measured from 5 current sensors of UFFO. The UFFO was found to run as designed, i.e., after initialization of the instrument, trigger occurred which enabled data taking of SMT and UBAT, followed by data transfer to the satellite. We tested such a run sequencing several times to find working as designed. In this calibration, we set the trigger threshold low enough on purpose to generate a false trigger from backgrounds.
Figures 14 shows a sky image obtained by SMT on Sep. 8, 2016 for a calibration run of the UFFO. The exposure time was 0.6 s. The SMT has \(17.7'\times 17.7'\) field of view. The image center lies at RA = 22:46:46.56, \(\mathrm{Dec}=-08{:}14{:}31.20\). Comparing the USNO B catalogue, we found the upper limit of SMT to be about 19 magnitude for 100 s, which agrees with the designed.
The sky image of SMT observed on Sep. 8, 2016 during the SMT calibration on orbit. The exposure time was 0.6 s. It has \(17.7'\times 17.7'\) field of view. The image center lies at RA = 22:46:46.56, \(\mathrm{Dec}=-08{:}14{:}31.20\). Comparing the USNO B catalogue, we found the upper limit of SMT to be about 19 magnitude for 100 s as expected
9 Summary
The UFFO/Lomonosov has been successfully launched into Earth orbit and is operational through tests and calibrations for last several months. As a pathfinder, it will be the very first space instrument to use a fast slewing mirror which shortens the trigger latency significantly, less than a second, to pioneer the hitherto unexplored time domain nature and the rise phase of GRBs. It will respond to initial photons within a couple of seconds after GRB detection, which improves on current response times by a couple of orders of magnitude. The number of GRBs with rising light curve is expected to be 10–20 per year, depending on the magnitude of GRBs at their early phase. We foresee not only such outcomes but the proof-of-principle of this new approach for future GRB missions.
Notes
References
B.P. Abbott et al., Localization and broadband follow-up of the gravitational-wave transient GW150914. Astrophys. J. 826L, 13 (2016a)
B.P. Abbott et al., Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016b)
J. Abraham et al., Properties and performance of the prototype instrument for the Pierre Auger Observatory. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 523, 50 (2004)
A. Abramovici et al., LIGO: the laser interferometer gravitational-wave observatory. Science 256, 325 (1992). http://www.ligo.caltech.edu
T. Abu-Zayyad et al., The surface detector array of the Telescope Array experiment. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 689, 87 (2012)
C.W. Akerlof, H.F. Swan, An estimation of the gamma-ray burst afterglow apparent optical brightness distribution function. Astrophys. J. 671, 1868 (2007)
C. Akerlof et al., Observation of contemporaneous optical radiation from a \(\gamma \)-ray burst. Nature 398, 400 (1999)
C.W. Akerlof et al., The ROTSE-III robotic telescope system. Publ. Astron. Soc. Pac. 115, 132 (2003)
L. Amati et al., Measuring the cosmological parameters with the \(E_{\mathrm{p},i}\)–\(E_{\mathrm{iso}}\) correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 391, 577 (2008)
D.L. Band, Comparison of the gamma-ray burst sensitivity of different detectors. Astrophys. J. 588, 945–951 (2003)
S.D. Barthelmy et al., The Burst Alert Telescope (BAT) on the SWIFT MIDEX mission. Space Sci. Rev. 120, 143 (2005)
M.G. Bernardini, R. Margutti, E. Zaninoni, G. Chincarini, A universal scaling for short and long gamma-ray bursts: \(E_{\mathrm{X},\mathrm{iso}}\) - \(E_{ \gamma ,\mathrm{iso}}\) - \(E_{\mathrm{pk}}\). Mon. Not. R. Astron. Soc. 425, 1199 (2012)
G. Beskin et al., From TORTORA to Mega TORTORA—results and prospects of search for fast optical transients. Adv. Astron. 2010, 171569 (2010)
J.S. Bloom et al., Autonomous observing and control systems for PAIRITEL, a 1.3 m infrared imaging telescope. ASP Conf. 351, 751 (2006)
G. Boella et al., BeppoSAX, the wide band mission for X-ray astronomy. Astron. Astrophys. Suppl. Ser. 122, 299 (1997)
V. Bromm, A. Loeb, High-redshift gamma-ray bursts from population III progenitors. Astrophys. J. 642, 382 (2006)
A. Burd et al., Pi of the sky – all-sky, real-time search for fast optical transients. New Astron. 10, 409 (2005)
D.N. Burrows, J. Hill, J. Nousek, J. Kennea, A. Wells et al., The Swift X-ray telescope. Space Sci. Rev. 120, 165 (2005)
D.B. Cline et al., Do very short gamma ray bursts originate from primordial black holes? Review. Int. J. Astron. Astrophys. 1, 164 (2011)
E. Costa et al., Discovery of the X-ray afterglow of the gamma-ray burst of February 28 1997. Nature 387, 783 (1997)
C. Cutler, K.S. Thorne, An overview of gravitational-wave sources (2002). gr-qc/0204090
J. Ellis et al., Robust limits on Lorentz violation from gamma-ray bursts. Astropart. Phys. 25, 402 (2006)
G.J. Fishman, The first BATSE gamma-ray burst catalog. Astrophys. J. Suppl. Ser. 92, 22 (1994)
N. Gehrels et al., The Swift gamma-ray burst mission. Astrophys. J. 611, 1005 (2004)
G. Ghirlanda et al., Gamma-ray bursts as standard candles to constrain the cosmological parameters. New J. Phys. 8, 123 (2006)
P.W. Gorham et al., The Antarctic impulsive transient antenna ultra-high energy neutrino detector: design, performance, and sensitivity for the 2006–2007 balloon flight. Astropart. Phys. 32, 10 (2009)
J. Greiner et al., The nature of “dark” gamma-ray bursts. Astron. Astrophys. 526, 10 (2011)
F. Halzen, S.R. Klein, Invited review article: IceCube: an instrument for neutrino astronomy. Rev. Sci. Instrum. 81, 08110 (2010)
M. Jelinek et al., Four years of real-time GRB follow up by BOOTES-1B (2005–2008). Adv. Astron. 2010, 432172 (2010)
S. Jeong et al., Slewing mirror telescope optics for the early observation of UV/optical photons from gamma-ray bursts. Opt. Express 21(2), 2263 (2013)
J.E. Kim et al., Readout of the UFFO slewing mirror telescope to detect UV/optical photons from gamma-ray bursts. J. Instrum. 8, P07012 (2013)
M.D. Kistler et al., The star formation rate in the reionization era as indicated by gamma-ray bursts. Astrophys. J. 705, L104 (2009)
R.W. Klebesadel, I.B. Strong, R.A. Olson, Observations of gamma-ray bursts of cosmic origin. Astrophys. J. 182, 85 (1973)
D. Kocevski, On the origin of high-energy correlations in gamma-ray bursts. Astrophys. J. 747, 146 (2012)
V.A. Kostelecky, M. Mewes, Astrophysical tests of Lorentz and CPT violation with photons. Astrophys. J. 689, L1 (2008)
D.Q. Lamb, D.E. Reichart, Gamma-ray bursts as a probe of the very high redshift universe. Astrophys. J. 536, 1 (2000)
J. Lee et al., A new type of space telescope for observation of extreme lightning phenomena in the upper atmosphere. IEEE Trans. Geosci. Remote Sens. 50(10), 3941 (2012)
V. Lipunov et al., Master robotic net. Adv. Astron. 2010, 349171 (2010)
A.I. MacFadyen, S.E. Woosley, Collapsars: gamma-ray bursts and explosions in “failed supernovae”. Astrophys. J. 524, 262 (1999)
M.R. Metzger et al., Spectral constraints on the redshift of the optical counterpart to the \(\gamma \)-ray burst of 8 May 1997. Nature 387, 878 (1997)
E. Molinari et al., REM observations of GRB 060418 and GRB 060607A: the onset of the afterglow and the initial fireball Lorentz factor determination. Astron. Astrophys. 469, 13 (2007)
E. Nakar, Short-hard gamma-ray bursts. Phys. Rep. 442, 166 (2007)
J.W. Nam et al., The UFFO slewing mirror telescope for early optical observation from gamma ray bursts. Mod. Phys. Lett. A 28, 1340003 (2013)
S.R. Oates et al., Exploring the canonical behaviour of long gamma-ray bursts using an intrinsic multiwavelength afterglow correlation. Mon. Not. R. Astron. Soc. 453, 4121 (2015)
A. Panaitescu, W. Vestrand, Taxonomy of gamma-ray burst optical light curves: identification of a salient class of early afterglows. Mon. Not. R. Astron. Soc. 387, 497 (2008)
M.I. Panasyuk et al., Detector of extreme energy cosmic rays on board Lomonosov satellite. J. Cosmol. 18, 7964 (2012)
I.H. Park, MEMS based space telescope for extreme energy cosmic rays experiments. Nucl. Phys. B, Proc. Suppl. 134, 196 (2004)
I.H. Park et al., The UFFO (Ultra-Fast Flash Observatory) pathfinder (2009). arXiv:0912.0773
J.H. Park et al., Obscura telescope with a MEMS micro mirror array for space observation of transient luminous phenomena or fast-moving objects. Opt. Express 16, 20249 (2008)
I.H. Park et al., Ultra-fast flash observatory for the observation of early photons from gamma-ray bursts. New J. Phys. 15, 023031 (2013)
J. Paul et al., The Chinese-French SVOM mission for gamma-ray burst studies. C. R. Phys. 12, 298 (2011)
R. Perna et al., Time-dependent photoionization in a dusty medium. II. Evolution of dust distributions and optical opacities. Astrophys. J. 585, 775 (2003)
T. Piran, The physics of gamma-ray bursts. Rev. Mod. Phys. 76, 1143 (2004)
L. Piro et al., The first X-ray localization of a gamma-ray burst by BeppoSAX and its fast spectral evolution. Astron. Astrophys. 329, 906 (1998a)
L. Piro et al., Evidence for a late-time outburst of the X-ray afterglow of GB970508 from BeppoSAX. Astron. Astrophys. 331, L41 (1998)
N. Produit et al., POLAR, a compact detector for gamma-ray bursts photon polarization measurements. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 550, 616 (2005)
J.L. Racusin et al., Broadband observations of the naked-eye \(\gamma \)-ray burst GRB 080319B. Nature 455, 183 (2008)
G. Ricker et al., GRB 010921: localization and observations by the high energy transient explorer satellite. Astrophys. J. 571, L127 (2002)
P.W. Roming et al., The Swift ultra-violet/optical telescope. Space Sci. Rev. 120, 95 (2005)
P.W.A. Roming et al., Joint astrophysics nascent universe satellite: utilizing GRBs as high redshift probes. Mem. Soc. Astron. Ital. 21, 155 (2012)
R. Salvaterra et al., GRB 090423 at a redshift of z ∼ 8.1. Nature 461, 1258 (2009)
A. Shahmoradi, R.J. Nemiroff, The possible impact of gamma-ray burst detector thresholds on cosmological standard candles. Mon. Not. R. Astron. Soc. 411, 1843 (2011)
Y. Takahashi, The JEM-EUSO mission. New J. Phys. 11, 065009 (2009)
N.R. Tanvir et al., A glimpse of the end of the dark ages: the gamma-ray burst of 23 April 2009 at redshift 8.3. Nature 461, 1254 (2009)
H. Tokuno et al., New air fluorescence detectors employed in the Telescope Array experiment. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 676, 54 (2012)
J. van Paradijs et al., Transient optical emission from the error box of the \(\gamma \)-ray burst of 28 February 1997. Nature 386, 686 (1997)
W.T. Vestrand et al., The RAPTOR experiment: a system for monitoring the optical sky in real time. Proc. SPIE 4845, 126 (2002)
E. Waxman, Gamma-ray bursts: potential sources of ultra high energy cosmic-rays. Nucl. Phys. B, Proc. Suppl. 151, 46 (2006)
G.G. Williams et al., The search for optical and near-infrared counterparts of GRBs with the super-LOTIS telescope. AIP Conf. Proc. 727, 723 (2004)
C. Winkler et al., The INTEGRAL mission. Astron. Astrophys. 411, L1 (2003)
B. Zhang et al., Discerning the physical origins of cosmological gamma-ray bursts based on multiple observational criteria: the cases of \(z= 6.7\) GRB 080913, \(z= 8.2\) GRB 090423, and some short/hard GRBs. Astrophys. J. 703, 1696 (2009)
Acknowledgements
The Korean work is supported by the National Research Foundation grants funded by MSIP of Korea (Creative Research Initiatives program for RCMST, No. 2015R1A2A1A01006870, and No. 2015R1A2A1A15055344). The Russian work was partially supported by ROSCOSMOS grants and by RFFI grants No. 13-02-12175 and No.15-35-21038 and acknowledges support from the Development Program of Lomonosov Moscow State University. AJCT acknowledges support from the Spanish MINECO Projects AYA 2009-14000-C03-01/ESP and AYA 2015-71718R (including EU/FEDER funds). The Taiwanese authors thank Taiwan’s National Science Council Vanguard Program (100-2119-M-002-025) and Ministry of Science and Technology (MOST) funding (104-2811-M-002-160). SJ acknowledges the support from the Korea Basic Science Research Program through NRF-2014R1A6A3A03057484 and NRF-2015R1D1A4A01020961. MBK acknowledges the support from NRF-2015-GPF.
Author information
Authors and Affiliations
Corresponding author
Additional information
The Lomonosov Mission
Edited by Yuri Shprits, Hans Bloemen and Jim Burch
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Park, I.H., Panasyuk, M.I., Reglero, V. et al. UFFO/Lomonosov: The Payload for the Observation of Early Photons from Gamma Ray Bursts. Space Sci Rev 214, 14 (2018). https://doi.org/10.1007/s11214-017-0444-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-017-0444-7