1 Introduction

Knowledge of space climate is a necessary first step to understanding past and future space weather (Temmer, Veronig, and Hanslmeier, 2003; Barnard et al., 2011; Lockwood et al., 2017; Riley and Love, 2017; Lockwood et al., 2018; Hayakawa et al., 2020a; Owens et al., 2021; Pevtsov et al., 2023). Historical space climate can be reconstructed from a range of disparate observational sources (e.g. Usoskin, 2023). In order of increasing time span these are:

  • Spacecraft data. High-resolution in-situ measurements of the near-Earth solar wind and heliospheric magnetic field have been made since 1964 (King and Papitashvili, 2005), though with patchy coverage prior to 1995 (Lockwood et al., 2019).

  • Neutron monitors. High-resolution measurements of the atmospheric neutron intensity have been made back to 1951 (Simpson, 2000). This provides information about the energy-integrated flux (above a threshold set by the instrument’s geomagnetic latitude) of galactic cosmic rays (GCRs) at the top of the atmosphere, which is modulated by the solar and geomagnetic magnetic fields (e.g. Potgieter, 2013).

  • Geomagnetic data. Ground-based magnetometer data measure the disturbance to the terrestrial system resulting from near-Earth solar-wind conditions (Feynman and Crooker, 1978). This can be used to reconstruct near-Earth magnetic-field intensity (\(B\)) and solar-wind speed (\(V\)) at annual time scale, back to around 1845 (Lockwood, Stamper, and Wild, 1999; Svalgaard and Cliver, 2010; Lockwood and Owens, 2011; Lockwood et al., 2022).

  • Sunspot observations. Sunspot number (SSN) is a proxy for photospheric magnetic flux intensity. Semi-homogeneous monthly SSN records can be reconstructed back to 1749 (e.g. Clette et al., 2023, and references therein) with a reasonable degree of certainty. Prior to that, data coverage is poorer (Hayakawa et al., 2022) and producing a consistent SSN record is difficult. However, incomplete records exist back to 1610 (e.g. Vokhmyanin, Arlt, and Zolotova, 2020; Arlt and Vaquero, 2020; Usoskin, 2023).

  • Cosmogenic isotopes. In addition to energetic neutrons, GCR interaction with the atmosphere produces radioactive isotopes that are not otherwise naturally occurring, such as 14C, which gets stored in tree rings that can be annually dated, and 10Be, which is deposited in ice sheets (e.g. Beer et al., 2013; Muscheler et al., 2016). Ice sheet dating for more recent times is possible by counting annual striations in ice colour, but for earlier times requires ice sheet modelling, constrained by layers of ash from identified volcanic eruptions. Recently, annual 14C has been used to derive sunspot number on a millennial timescale (Brehm et al., 2021; Usoskin et al., 2021).

In addition to these quasi-continuous time series, there also exist episodic measurements of the corona, in the form of solar eclipse observations. Total solar eclipses enable the solar coronal streamers to be observed with the naked eye, serving as independent spot references for estimates of the large-scale solar magnetic field. Solar coronal streamers typically concentrate near the solar equator around solar minimum and radiate all the directions near solar maximum (Loucif and Koutchmy, 1989; Riley et al., 2015). Dateable graphical records of eclipses are confirmed up to 1706, including during the Dalton Minimum and Maunder Minimum (Vaquero, 2003; Hayakawa et al., 2020b, 2021; Lockwood and Owens, 2021; Hayakawa, Sôma, and Daigo, 2022).

While information about space climate can be extracted from each of these data sources, they reflect very different facets of solar activity. Spacecraft and geomagnetic reconstructions pertain to local, near-Earth solar-wind conditions. Conversely, GCRs traverse the whole heliosphere to reach Earth and thus solar modulation of GCRs is a measure of the global heliosphere (Potgieter, 2013). Similarly, sunspot number provides information about the synoptic magnetic field in the solar photosphere, rather than the near-Earth conditions specifically. Eclipse observations provide mainly qualitative evidence about the state of the coronal magnetic field, although the width of the streamer belt can be estimated (Lockwood et al., 2022). In order to assess and compare these different data sources, it is necessary to find some common ground.

The open solar flux (OSF) is the total magnetic flux that is dragged out from the corona by the solar wind to form the heliospheric magnetic flux (HMF, Lockwood, 2013; Owens and Forsyth, 2013). Thus it is useful to define a theoretical ‘source surface’, typically around 2 to 3 solar radii, where the field is everywhere radial (Arge and Pizzo, 2000). This means the OSF can be simply defined as the integrated unsigned magnetic flux (with both toward and away polarities) threading the source surface. OSF is closely related to the solar modulation of GCRs (Herbst et al., 2010; Usoskin et al., 2002, 2021). It can also be computed from local (e.g. near-Earth) HMF observations (Owens et al., 2008), owing to the observed latitudinal invariance in the radial component of the HMF (Smith and Balogh, 1995; Lockwood et al., 2004). Finally, OSF can be modelled by a continuity equation, using sunspot number as the source of new OSF (Solanki, Schüssler, and Fligge, 2000; Krivova, Balmaceda, and Solanki, 2007; Owens and Lockwood, 2012; Krivova et al., 2021).

While OSF serves as a useful common factor relevant to the different space climate proxies, it is important to relate this variable to other commonly used measures of solar activity. Of particular interest is SSN, as it most readily enables solar-cycle information (e.g. cycle amplitude, cycle length, cycle start/end dates) to be estimated. Furthermore, it is SSN, not OSF, that is used as a general measure of solar activity levels, as well as for input to models of total solar irradiance (Lean, 2000; Krivova, Balmaceda, and Solanki, 2007; Solanki, Krivova, and Haigh, 2013), which in turn is used by climate models to incorporate the effect of solar forcing (e.g. Solanki, Krivova, and Haigh, 2013; Owens et al., 2017a).

Here we demonstrate a new method for reconstructing SSN purely from OSF, without the need to prescribe solar cycle start/end dates, which have been required by previous approaches (Owens and Lockwood, 2012). This can be particularly important during times of very low solar activity, when the simple correlation between OSF and SSN breaks down (Owens, Usoskin, and Lockwood, 2012). In Section 2 we describe the OSF data used in this study, while Section 3 outlines the sunspot data and the method for determining the solar cycle start/end dates. An existing model for reconstructing OSF from a known SSN record and known solar cycle start dates is demonstrated in Section 4. A new approach to the inverse problem – estimating SSN from OSF – is outlined in Section 5. To assess the performance of this new method, we outline benchmark methods, based on regression, in Section 6. The results are evaluated in Section 7. Implications of these results and future use of this methodology are discussed in Section 8.

2 OSF Data

In principle, OSF can be estimated from in-situ observations of the radial component of the HMF, \(B_{\mathrm{R}}\), made at a heliocentric distance, \(r\), by computing \(\mathrm{OSF} = 4 \pi r^{2} |B_{\mathrm{R}}|\). This assumes that local measurements of \(B_{\mathrm{R}}\) are representative of the whole sphere of radius \(r\). Longitudinal structure is accommodated by integrating over a solar rotation (≈ 27 days, for spacecraft in near-Earth space). Integration in latitude is achieved by assuming no variation in \(B_{R}\) with latitude, an assumption found to be valid to considerable accuracy by measurements from the Ulysses spacecraft (Smith and Balogh, 1995; Lockwood et al., 2004). However, calculating OSF in this way is further complicated by the existence of inverted HMF (Kahler, Crooker, and Gosling, 1998; Crooker et al., 2004); flux tubes which thread a sphere at the point of observation, typically \(r = 1\) AU, multiple times, but only thread the coronal source surface once. This produces an ‘excess flux’ in the heliosphere compared to the corona, which may partially explain the difference between in-situ and photospheric OSF estimates (Linker et al., 2017; Wallace et al., 2019). Excess flux is caused by any processes generating inverted HMF (Lockwood, Owens, and Macneil, 2019), including coronal interchange reconnection (Owens, Crooker, and Lockwood, 2013), large-scale solar-wind stream shears (Lockwood, Owens, and Rouillard, 2009), turbulence (Bruno and Carbone, 2005) and kinetic-scale ‘switchbacks’ (e.g. Mozer et al., 2021).

The most accurate OSF estimate is obtained by combining in-situ HMF and suprathermal electron observations of the field-aligned beam, or ‘strahl’ (Pilipp et al., 1987; Gosling et al., 1987), which allows inverted HMF to be directly detected and accounted for. The methodology for calculating OSF in this way is described in Owens et al. (2017b). We here use the 27-day averages of OSF provided as supplementary material to Frost et al. (2022). These span 1995 to 2021 and are here further averaged to annual resolution. This strahl-based OSF time series is shown in red in Figure 1 and referred to as OSFS.

Figure 1
figure 1

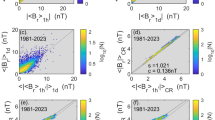
Estimates of annual open solar flux (OSF) from in-situ near-Earth solar-wind measurements. For the time series in panels a and c, red lines show \({\mathrm{OSF_{S}}}\), the strahl-based OSF (Frost et al., 2022), while black lines show \({\mathrm{OSF_{BR}}}\), estimated from OMNI data using averages of \(B_{\mathrm{R}}\) over the optimum intervals of 20 hours. Blue lines show OSF estimate from annual means of magnetic field intensity, \(B\), and solar-wind speed, \(V\). For panel a, this is \({\mathrm{OSF_{PS}}}\), which assumes an ideal Parker spiral. For panel c, this is \({\mathrm{OSF_{PS}*}}\), the corrected OSF reconstruction from \({\mathrm{OSF_{PS}}}\), using the regression shown in panel b. The scatter plot in panel b shows \({\mathrm{OSF_{BR}}}\) as a function of \({\mathrm{OSF_{PS}}}\), while panel d shows \({\mathrm{OSF_{BR}}}\) as a function of \({\mathrm{OSF_{PS}*}}\). Blue lines show the orthongonal least-squares best fits. Blue-shaded regions show 95% confidence intervals estimated from a boot-strapped procedure. Dashed lines in show \(y=x\).

Full size image

To estimate OSF from in-situ observations prior to 1994, when strahl observations are not routinely available, observations of \(B_{\mathrm{R}}\) must be used in isolation. Frost et al. (2022) showed that the removal of inverted HMF can be approximated by taking 20-hour averages of \(B_{\mathrm{R}}\) before integrating over the source surface (i.e. before computing OSF = \(4 \pi r^{2} |B_{\mathrm{R}}|\)). This estimate is referred to as OSFBR. Using in-situ measurements of the near-Earth HMF \(B_{\mathrm{R}}\), as compiled by the OMNI database of near-Earth spacecraft observations (King and Papitashvili, 2005), OSFBR is shown as the black line in Figure 1. At the annual time scale, OSFS and OSFBR agree extremely well, with a linear correlation coefficient of \(r_{L} = 0.99\) and a mean absolute error (MAE) of \(0.175 \times 10 ^{14}\) Wb.

Geomagnetic reconstructions of near-Earth solar-wind conditions, discussed further below, do not directly reconstruct \(|B_{\mathrm{R}}|\). Instead, they provide the near-Earth \(B\) and \(V\) at annual resolution. It is important to test how well OSF can be reconstructed from such parameters. To do so, we follow a similar approach here as in Lockwood et al. (2022). The first step is to estimate annual \(|B_{R}|\) from the annual \(B\) and \(V\) values. If an ideal Parker spiral (Parker, 1958) is assumed, then:

$$ |B_{\mathrm{R}}| = B \cos \gamma , $$
(1)

where \(\gamma \) is the angle of the Parker spiral HMF to the radial direction, given by:

$$ \gamma = \arctan \frac{\Omega r}{V}, $$
(2)

where \(\Omega \) is the mean angular rotation speed of the Sun, taken to be \(2.865 \times 10^{-6}\text{ rad}\mbox{ s}^{-1}\).

The blue line in Figure 1a shows OSFPS, the OSF estimate from annual OMNI \(B\) and \(V\) values, assuming an ideal Parker spiral to compute the equivalent \(|B_{\mathrm{R}}|\). While the relative variations are in good agreement, there is a systematic overestimate compared with both OSFS and OSFBR. This is expected, as inverted HMF means that for a given \(B\), the effective \(B_{\mathrm{R}}\) is lower than that for an ideal Parker spiral. As discussed above, where vector HMF data are available, this can be accounted for by taking 20-hour average of \(B_{\mathrm{R}}\) before computing the modulus, which results in about a 75% reduction from 1-minute \(B_{\mathrm{R}}\) (Frost et al., 2022). To account for this, we compute the total (or orthogonal) least-squares linear regression (Markovsky and Van Huffel, 2007) between OMNI OSFBR and OMNI OSFPS, which is given by:

$$ {\mathrm{OSF_{PS*}}} = 0.665^{+0.703}_{+0.627} ~{\mathrm{OSF_{PS}}} - 1.15 ^{-0.701}_{-1.60} ~ \times 10^{14}~\textrm{Wb}, $$
(3)

where \({\mathrm{OSF_{PS*}}}\) is the best estimate of OSF from Parker spiral analysis of \(B\) and \(V\), and uncertainty ranges are the 95% confidence level determined by a bootstrap resampling process (Press et al., 1989). This is shown by the blue-shaded region in Figure 1b. As this is a simple regression, it is important not to apply it outside the valid parameter range. Fortunately, the deep 2009/2010 solar minimum and the high 1991 solar maximum mean that OSF conditions have been sampled over a wide range of conditions during the OMNI era, meaning valid parameter space is not a major concern for subsequent use with geomagnetic data.

Applying this linear correction to the OMNI \(B\) and \(V\) data produces OMNI \({\mathrm{OSF_{PS}*}}\), shown as the blue line in Figure 1c. Again, the 95% confidence interval is computed from a bootstrap method and is shown as a blue shaded area. Comparing \({\mathrm{OSF_{PS}*}}\) with \({\mathrm{OSF_{BR}}}\) gives \(r_{L} = 0.98\) and MAE = \(0.31 \times 10^{14}\) Wb.

Having established the procedure by processing the OMNI data, we can now apply these methods to the geomagnetic reconstructions of annual \(B\) and \(V\). Geomagnetic (GEO) reconstructions, along with their uncertainties, are provided by Lockwood et al. (2022). Figures 2a and b show the geomagnetic \(B\) and \(V\) reconstructions, respectively. The pink-shaded regions show the prediction intervals at the 95% confidence level computed from both the uncertainty in the regression between geomagnetic indices and solar-wind parameters, and the intrinsic uncertainty in the geomagnetic indices themselves. The latter results in a wider uncertainty range in the 19th century. Geomagnetic \(B\) and \(V\) are converted to \({\mathrm{OSF_{PS}}}\) using the Parker spiral equations 1 and 2, then corrected to \({\mathrm{OSF_{PS}*}}\) using the regression in Equation 3. Note that in Lockwood et al. (2022), geomagnetic OSF estimates were scaled to OMNI estimates of OSF made using a kinematic correction (Lockwood, Owens, and Rouillard, 2009), rather than to \({\mathrm{OSF_{S}}}\) and \({\mathrm{OSF_{BR}}}\). This produces slightly higher values than those shown here. This GEO \({\mathrm{OSF_{PS}*}}\) is shown in red in Figure 2c. There is very good agreement with OMNI \({\mathrm{OSF_{BR}}}\), with a linear correlation coefficient of 0.91. The GEO \({\mathrm{OSF_{PS}*}}\) series is used in the following sections to test the SSN reconstruction procedure.

Figure 2
figure 2

Time series (left) and scatter plots (right) of annual solar-wind properties. In all panels, black indicates OMNI observations, while red indicates GEO reconstructions. (a and b): Heliospheric magnetic-field intensity, \(B\). (c and d): Solar-wind speed, \(V\). (e and f): OSF using 20-hour averages of \(B_{\mathrm{R}}\) from the OMNI dataset (black) and \({\mathrm{OSF_{PS}*}}\) computed from GEO \(B\) and \(V\) with the appropriate correction for non-Parker spiral flux (red).

Full size image

3 Solar Cycle Start/End Dates

To both demonstrate the existing OSF forward model and validate the new SSN reconstruction method, we require accurate SSN and accurate solar cycle start/end dates. SSN is provided by the Sunspot Index and Long-term Solar Observations (SILSO) Version 2.0 (SILSO) sunspot number record, which provides monthly values back to 1749 (Clette et al., 2016). There are alternative sunspot series (e.g. Chatzistergos et al., 2017), which may differ in the cycle amplitude, particularly prior to 1830 (e.g. Hayakawa et al., 2022). However, the cycles themselves are defined robustly throughout.

Precise determination of the solar cycle start/end dates from SSN alone can be ambiguous, as it requires pinpointing the minimum in a long and shallow variation at solar minimum. However, the position of sunspots – specifically their heliographic latitude, \(\theta \) – can provide an additional constraint (Owens et al., 2011). We here update the solar cycle start/end dates using the average latitude of sunspots. Figure 3 shows sunspot area and latitude data from a range of observatories, compiled and inter-calibrated by Mandal et al. (2020). The familiar ‘butterfly diagram’ (Maunder, 1904) of sunspot occurrence with latitude and time is shown in Figure 3a. Integrating the total sunspot area over all latitudes gives the time series shown in Figure 3b, which follows a very similar pattern to the SILSO SSN record, shown in Figure 4b. Figure 3c shows \(\langle |\theta |\rangle \), the mean absolute latitude of all sunspots, weighted by area. At the start of each cycle, there is a sharp rise in \(\langle |\theta |\rangle \), as spots from the new cycle emerge at high latitude. We use the time when \(\langle |\theta |\rangle \) exceeds 20∘ to define the cycle start/end dates. These times are shown as vertical red dashed lines and listed in Table 1. It can be seen that these dates occur during the times of sunspot number minimum, as expected. By using the rise in \(\langle |\theta |\rangle \), rather than the appearance of the first spot group of the new cycle at high latitudes, the cycle start/end times are not as variable because they are not influenced by the formation of just one group.

Figure 3
figure 3

Carrington rotation averages of sunspot data from a number of observatories (Mandal et al., 2020). Top: Sunspot area as a function of sine latitude (\(\theta \)) and time. Middle: Total sunspot area, expressed as percentage of hemisphere. Bottom: Average sunspot absolute latitude, \(\langle|\theta |\rangle\), weighted by sunspot area. Red dashed lines show the solar cycle start/end times estimated from the sharp rise in \(\langle|\theta |\rangle\).

Full size image
Figure 4
figure 4

Annual time series over the period from 1880 to 2020. (a) The geomagnetic estimate of OSF, GEO \({\mathrm{OSF_{PS}*}}\). (b) SILSO sunspot number (black), and the resulting OSF source rate, \(S\) (blue). (c) \(\chi \), the OSF loss rate expressed as a percentage of the current OSF. This property is computed from the observed OSF and sunspot-based OSF source term \(S\). In all panels, red dashed lines show the solar cycle start dates obtained from sunspot latitude data.

Full size image
Table 1 Solar cycle start/end dates used in this study. Where possible, these are estimated from the sharp rise in average sunspot latitude. Prior to the availability of continuous sunspot latitude data in 1874, cycle start years are estimated from the minima in 13-month smoothed sunspot number. **The start of Cycle 26 is taken to be 11 years after Cycle 25. Also listed are reconstructed solar cycle start/end dates using the time of GEO OSF minimum, and from the forward modelling approach.
Full size table

Prior to 1874, inter-calibrated routine observations of sunspot latitude are not available (Mandal et al., 2020) and cycle start/end dates must be estimated from sunspot number alone. For these cycles, we define the solar cycle start/end dates as the time of the lowest 13-month smoothed SILSO SSN value. During extended minima, when this value remains at zero for multiple months (e.g. around 1810, in the middle of the Dalton minimum) we take the mid-point of the zero SSN interval. These dates are also shown in Table 1. The mean absolute error between the two methods is 0.3 years. Solar-cycle phase is then defined as 0 at the start of a cycle, increasing linearly to 1 at the end of a cycle. In order to compute the solar-cycle phase during the current solar cycle (25), we use a Solar Cycle 26 start year of 2031.0. This is 11 years from the Solar Cycle 25 start year, which agrees well with the observed \(\langle |\theta |\rangle \) progression to date.

4 Reconstructing OSF from SSN

Before outlining the new method for reconstructing SSN and solar-cycle phase from OSF, we first demonstrate the inverse problem: reconstructing the OSF using the known SSN record and associated solar-cycle phase as input. We follow the approach first established by Solanki, Schüssler, and Fligge (2000), wherein the rate of change of the OSF with time \(t\) can be modelled as a continuity equation:

$$ \frac{\mathrm{d OSF}}{ \mathrm{d}t} = S - L, $$
(4)

where \(S\) is the OSF source term (i.e. rate of production of new OSF) and \(L\) is the OSF loss rate. \(S\) is expected to be closely related to the sunspot number (Solanki, Schüssler, and Fligge, 2000; Owens and Lockwood, 2012; Goelzer et al., 2013; Krivova et al., 2021). OSF increases when new magnetic flux emerges through the source surface. Thus a significant contribution to \(S\) is expected to be the magnetic flux carried out from the corona by coronal mass ejections over the solar cycle (Owens and Crooker, 2006).

A number of functional forms have been used to relate SSN and \(S\). Here we use the empirically optimised form and coefficients from Owens et al. (2016):

$$ S = \left [0.84 (\mathrm{SSN} + 2.67) ^{0.54} - 0.0055 \right ] ~ \times 10 ^{14}~ \mathrm{Wb~yr}^{-1}. $$
(5)

The exact details of this equation and coefficients do not greatly affect the resulting OSF reconstruction, as \(L\) is subsequently computed to provide the best agreement between OSF and \(S\). Specifically, Owens and Lockwood (2012) used Equation 4 with known OSF and SSN (and hence \(S\)) time series to compute the required \(L\) as a function of time. We here repeat this method with the newly updated data: The GEO \({\mathrm{OSF_{PS}*}}\) series and \(S\) computed using Equation 5 and the SILSO sunspot record. They are shown in Figures 4a and b, respectively. The resulting OSF loss term is shown in Figure 4c, where \(L\), the absolute OSF loss, has been converted to \(\chi \), the percentage loss. I.e. \(L = \chi \) OSF.

While peak SSN varies by around a factor 2.5 between cycles, and peak \(S\) by around a factor 2, \(\chi \) is remarkably consistent between cycles, both in amplitude and waveform. For example, Cycle 12 peaked around 1885 with a maximum SSN of about 100 and hence a peak OSF source rate of around \(1 \times 10 ^{15}\) Wb/yr. Conversely, Cycle 19 peaked around 1960 with SSN around 270, and hence a peak OSF source rate of around \(1.75 \times 10 ^{15}\) Wb/yr. These are approximately a factor two variations. In contrast, \(\chi \) peaks at around 150 %/yr for both Cycles 12 and 19, despite the large difference in the SSN peaks for these two cycles.

Owens and Lockwood (2012) exploited the cyclic nature of \(\chi \) to reconstruct OSF from knowledge of SSN and solar-cycle phase alone (i.e. without needing any further information to estimate \(\chi \)). Using the GEO \({\mathrm{OSF_{PS}*}}\) and SILSO SSN time series, the cycle-averaged profiles of \(\chi \) and SSN are shown in Figure 5. Panels a and b show the SSN variation with solar-cycle phase. There is large variability in SSN amplitude between individual cycles. Panels c and d show the same SSN variation normalised by the maximum 13-month smoothed SSN value in that cycle. This is equivalent to the Solar Activity Index used by Owens et al. (2022) and is tabulated in Table 2. From these panels it can be seen that the quasi-sinusoidal waveform of SSN is fairly consistent between cycles, despite the variation in amplitude (e.g. Pesnell, 2012). However, the rising phase is generally shorter for higher cycles (the so-called Waldmeier rule; Hathaway, 2010), which is not captured by an average variation over all cycles.. Panels e and f show the cycle-averaged profile of \(\chi \), the fractional OSF loss rate. It is also tabulated in Table 2. The waveform is different to that of SSN, being more saw-tooth in nature and closely mimicking the heliospheric current sheet tilt angle (Alanko-Huotari et al., 2007; Owens, Crooker, and Lockwood, 2011; Asvestari and Usoskin, 2016), as expected from OSF disconnection observations (Sheeley, Knudson, and Wang, 2001).

Figure 5
figure 5

Average variations of parameters with solar-cycle phase, defined as 0 at the start of a cycle and 1 at the end of a cycle. Left-hand panels show individual cycles, while right-hand panels showing the median variation in white, with coloured bands containing 99, 90 and 68% of values. (a and b): Sunspot number, SSN. (c and d): SSN normalised to the maximum value in a given cycle. (e and f) OSF fractional loss rate, \(\chi \).

Full size image
Table 2 Table of sunspot number and fractional OSF loss as a function of solar-cycle phase.
Full size table

We now use SSN and solar-cycle phase (computed from the dates in Table 1) as input to the OSF model. \(S\) is determined from SSN using Equation 5 and \(\chi \) is computed from the solar-cycle phase using the cycle-averaged average profile, shown in Figure 5f and Table 2. These time series are used with a numerical method, with a 1-year time step and an initial value for the OSF. We use \(8\times 10^{14}\) Wb, though the choice of this value is lost within a few time steps and so does not greatly affect the resulting time series. At each time step, \(L\) is computed using \(\chi \) and the OSF at the previous time step. We then apply Equation 4 to compute the OSF. See Owens and Lockwood (2012) for more details.

The resulting OSF variation is shown in Figure 6. There is good agreement between the SSN-based model and observed OSF (GEO \({\mathrm{OSF_{PS}*}}\)), with a linear correlation coefficient of 0.84 (\(p < 0.00001\)), and a mean absolute error of \(0.8 \times 10^{14}\) Wb (i.e. around 10%). Note that the largest disagreement is prior to 1880: this could be from an overestimate of the sunspot numbers at this time, but more likely is an underestimate in the early geomagnetic observations. In fact, the reconstructions in Figure 12 of Lockwood et al. (2022) show that using using different combinations of geomagnetic indicies to reconstruct \(B\) and \(V\) can reduce this disagreement.

Figure 6
figure 6

(a) Time series of OSF from the SSN-based model (blue line), over the duration of the SILSO sunspot record, 1750 - present. The blue shaded region shows the 95 % confidence interval. The red line shows the geomagnetic \({\mathrm{OSF_{PS}*}}\) reconstruction. The grey-shaded area shows the SILSO sunspot number, scaled by a factor 0.01 for plotting purposes. (b) The scatter plot of the GEO \({\mathrm{OSF_{PS}*}}\) as a function of the SSN OSF estimate. The blue line shows the best fit, while the blue-shaded region shows the 95 % confidence interval. The black dashed line is \(y=x\).

Full size image

5 Reconstructing SSN from OSF

We now consider the inverse problem: reconstructing SSN using only the observed OSF. This is again achieved by assuming a purely cyclic variation in the fractional OSF loss rate, \(\chi \). The time dependence of Equation 4 and the lack of knowledge of solar-cycle phase – as the cycle start/end dates are not known a priori – means the model cannot be directly inverted. We will later demonstrate that assuming the time of minimum OSF is the cycle start date is only accurate to within around 0.5 years. Furthermore, this error is expected to increase significantly during times of very low OSF (Owens, Usoskin, and Lockwood, 2012). Instead, we take a Monte Carlo approach of producing random realisations of SSN times series and forward modelling the associated OSF for comparison with observed OSF. It is presumed that the best match to the observed OSF results from the SSN time series closest to the true value.

An example is shown in Figure 7, considering a 22-year window spanning 1920 to 1942. Figure 7a shows the result of selecting a random start date for the first solar cycle of 1912.8, and a random length and amplitude for this cycle of 11 years and 203, respectively. This is followed by a cycle of length 11.6 and amplitude 68, again selected randomly. Finally, this is followed by a third cycle of 9.4 years and amplitude 177. This reaches the end of the window of interest. (In some instances, a fourth cycle is required to span the 22-year window.) The solar-cycle length and amplitudes are used with the average SSN waveform (Figure 5d) to produce the synthetic SSN time series shown in red. This SSN time series is then used as input to the OSF model (Equation 4). The resulting OSF is shown in red in Figure 7b. There is little correspondence with the observed OSF (GEO OSF\(_{\rm PS}*\)), shown in black, as reflected by the high mean absolute error (MAE) of \(1.8\times 10^{14}\) Wb. Thus we would assume the synthetic SSN time series is not a good reproduction of the true SSN variation.

Figure 7
figure 7

Examples of the OSF forward modelling used to reconstruction SSN. The left-hand panels show the observed SSN (black) and examples of synthetic SSN time series constructed from the average SSN waveform (show in Figure 5d) with different random values for solar-cycle length, solar-cycle amplitude, and the start date of the first cycle. The right-hand panels show the observed OSF (GEO \({\mathrm{OSF_{PS}*}}\), black), and the OSF obtained from forward modelling of the synthetic SSN time series (red). The most probable synthetic SSN time series is assumed to be the one which results in the best match to the observed OSF, as given by the lowest mean absolute error (MAE). In this illustration, that is the bottom panels.

Full size image

A second attempt at a random SSN time series is shown in Figure 7c. This produces an even worse match to the observed OSF, with \(\text{MAE} = 2.2\times 10^{14}\) Wb. It can be seen that this is largely due to setting the wrong solar cycle start date and hence a synthetic SSN time series out of phase with the true SSN (though the true SSN is obviously not available to the reconstruction process). Finally, the bottom panel shows a synthetic SSN time series which produces good match to the observed OSF, with \(\text{MAE} = 0.6\times 10^{14}\) Wb. Thus out of these three random SSN realisations, we would select the one in the bottom panels. As the SSN is known in this example, we can confirm that it is indeed the closest to the true value.

More specifically, the implementation of the process can be described as follows: We first split the observed OSF time series (in this case GEO OSF\(_{\rm PS}*\)) into overlapping 22-year windows, spaced at 1-year intervals. For each window we then:

  1. a.

    Draw a random solar-cycle phase for the start of the window from a uniform distribution between 0 and 1.

  2. b.

    Select a random solar-cycle length from a Gaussian distribution with mean of 10.5 years and a standard deviation of 2 years.

  3. c.

    Combine the starting solar-cycle phase with the cycle length to determine the start and end years for this cycle.

  4. d.

    Select additional random cycle lengths and append them to the previous cycles until the the whole 22-year window is filled.

  5. e.

    Compute solar-cycle phase over the whole 22-year window from the cycle start/end times.

  6. f.

    For each cycle, select random peak SSN amplitudes from a Gaussian distribution with a mean of 140 and a standard deviation of 70.

  7. g.

    Use the average sunspot-cycle shape (Table 2) with the amplitudes and solar-cycle phase to construct synthetic SSN time series spanning the 22-year window. Three examples are shown in red in the left-hand panels of Figure 7.

  8. h.

    Use the synthetic SSN time series to forward model the OSF using Equation 4 and \(\chi \) determined from Table 2. Three examples are shown in red in the right-hand panel of Figure 7.

  9. i.

    Compute the mean absolute error (MAE) between the model and observed OSF.

  10. j.

    Repeat steps (a) to (i) 10k times to create 10k OSF realisations from 10k random synthetic SSN time series.

  11. k.

    On the basis of the lowest MAE between synthetic and observed OSF, identify the ‘best’ OSF realisation from the 10k available, and store the corresponding synthetic SSN time series for this 22-year window.

Once the entire OSF dataset has been modelled in this way, the over-lapping nature of the windows mean that each individual year will have 22 independent ‘best’ estimates of OSF and SSN. There are also 22 sets of solar cycle start dates. We produce consensus values of OSF and SSN for each year by taking the average values across all 22 windows, weighted according to their MAE (specifically, by \(\exp [{-\mathrm{MAE}}]\)). Consensus solar cycle start dates are produced using a method explained in Section 7.

In Section 7 we apply this method to the GEO \({\mathrm{OSF_{PS}*}}\) series, as well as independently to the upper and lower 95% confidence bounds of the GEO \({\mathrm{OSF_{PS}*}}\) series. This gives the uncertainty in the reconstructed SSN record that is a result of the uncertainty in the input OSF data.

6 Benchmark Reconstruction Methods

In order to assess the performance of the forward-modelling approach outlined in Section 5, it is useful to compare it with existing benchmark models for estimating SSN from OSF. Svalgaard and Cliver (2005) and Wang, Lean, and Sheeley (2005) proposed a linear relation between OSF and the square root of SSN. As we require the inverse relation, we consider the linear regression between SSN and OSF2. An orthogonal least-squares fit using SILSO and GEO OSF\(_{\rm PS}*\) gives:

$$ \mathrm{SSN} = 3.16^{+3.60}_{+2.72} \left ( \mathrm{OSF [\times 10^{14} Wb]} \right )^{2} - 82.2^{-61.5}_{-102.8}, $$
(6)

where uncertainties are the 95% confidence interval from a bootstrapping analysis. The best fit is shown as the blue line in Figure 8a.

Figure 8
figure 8

Top panels, a to c, show the relations between SSN and OSF that are used to construct the benchmark regression-based SSN reconstructions. Bottom panels, d to f, show the performance of different SSN reconstruction methods. (a) Annual SSN as a function of OSF, with the best fit (blue) resulting from the SSN-OSF2 linear regression. (b) 11-year smoothed SSN, \(\langle \mathrm{SSN}\rangle _{11}\), as a function of 11-year smoothed OSF, \(\langle \mathrm{OSF}\rangle _{11}\). The blue line shows the linear best fit. (c) Annual deviation from the 11-year smoothed values, i.e. \(\mathrm{SSN} - \langle \mathrm{SSN}\rangle _{11}\) as a function of \(\mathrm{SSN} - \langle \mathrm{SSN}\rangle _{11}\). The blue line shows the linear best fit. (d) Reconstruction using the fit between annual SSN and \(\mathrm{OSF}^{2}\), shown in panel a. (e) Reconstruction using both the annual and 11-year linear regressions, shown in panels b and c. (f) Reconstruction using the OSF forward-modelling approach. In the bottom three panels, red lines show \(y = x\).

Full size image

Figure 9a shows the SSN time series which results from this OSF2 regression applied to GEO \({\mathrm{OSF_{PS}*}}\). The general trends in cycle-to-cycle amplitude are present, but there are obvious issues, in particular the solar minima often produce unphysical negative SSN values (though most of these are consistent with SSN = 0 to within uncertainty). Figure 8d shows the same data as a scatter plot. The linear correlation coefficient is 0.78, with a mean absolute error of 38.4. More advanced forms of regression, such as Gaussian processes, could be used to further optimise the agreement, but a fundamental issue is the underlying assumption that a single value of OSF maps to a single value of SSN. This assumption means that there is no allowance for time history, which at least partially explains the large range of OSF for low SSN values; zero SSN after a period of previously high SSN does not result in as low OSF as an extended period of zero SSN. And this degeneracy is expected to increase further at even lower solar activity considered here: During grand solar minima, such as the Maunder minimum, it has been proposed that OSF peaks at solar minimum, rather than solar maximum (Owens, Usoskin, and Lockwood, 2012). Hence there are considerable limitations to any simple regression-based method.

Figure 9
figure 9

Time series of solar-cycle reconstructions. (a) SSN observed (SILSO, black) and reconstructed by regression of GEO OSF2 (blue) and from the 1y + 11y regression (red). (b) SSN observed (black) and reconstructed by the forward model (red). The pink-shaded region shows the uncertainty obtained from the 95 % confidence interval in the GEO OSF record. (c) Geomagnetic (black) and forward-model (red) OSF. Pink-shaded regions again show 95 % confidence intervals. (d) Kernel-density estimate of the forward-model solar-cycle starts (red), with observed times from sunspot latitude (black) and estimated from OSF minima (blue dashed). Pink lines show the kernel density obtained from the upper and lower confidence intervals of geomagnetic OSF.

Full size image

A more nuanced approach to the regression between OSF and SSN is to independently account for the short (year-to-year) and long (cycle-to-cycle) timescale variations in OSF (Usoskin and Kovaltsov, 2004). Considering first the cycle-to-cycle variations, Figure 8b shows the scatter plot of 11-year running means of SSN and OSF, denoted \(\langle \mathrm{SSN}\rangle _{11}\) and \(\langle \mathrm{OSF}\rangle _{11}\), respectively. The best linear regression from an orthogonal least-squares fit is given by:

$$ \langle \mathrm{SSN}\rangle _{11} = 24.6^{+25.8}_{+23.3} \langle \mathrm{OSF}\rangle _{11} [\times 10^{14} \mathrm{Wb}] -89.4 ^{-80.2}_{-98.5}, $$
(7)

where uncertainties are again the 95% confidence interval from a bootstrapping analysis.

We then fit the shorter-term variations by considering the anomalies from the 11-year mean values. The scatter plot of \(\mathrm{SSN} - \langle \mathrm{SSN}\rangle _{11}\) versus \(\mathrm{OSF} - \langle \mathrm{OSF}\rangle _{11}\) is shown in Figure 8c. The best fit is given by:

$$ \mathrm{SSN} - \langle \mathrm{SSN}\rangle _{11} = 59.6^{+67.6}_{+51.5} (\mathrm{OSF} - \langle \mathrm{OSF}\rangle _{11}) [\times 10^{14} \mathrm{Wb}] - 0.07^{+7.7}_{-7.8}. $$
(8)

Combining Equations 7 and 8 with the observed GEO \({\mathrm{OSF_{PS}*}}\) results in the SSN reconstruction shown in Figure 8e. This is referred to as the ‘1 + 11y regression’. The linear correlation coefficient is 0.80, with a mean absolute error of 30.3. Using a Meng’s z-test (Meng, Rosenthal, and Rubin, 1992), this correlation is not found to be significantly different from the OSF2 regression in Figure 8d. Figure 9b shows that the OSF2 and 1 + 11y regression time series are similar. The 1 + 11y regression still produces unphysical negative sunspot numbers, though these are again mostly consistent with zero to within regression and OSF uncertainties, as shown by Figure 8e.

To obtain benchmark estimates of the solar cycle start/end dates, we assume that the solar cycle start coincides with minima in annual OSF. These dates are given in Table 1. From these we compute \(\Delta t\), the absolute timing error compared with the observed cycle start/end dates derived from sunspot number latitude. The cumulative distribution function of \(\Delta t\) is shown in Figure 10. The median \(\Delta t\) is 0.5 years, with an inter-quartile range (IQR) spanning 0.2 to 0.60 years.

Figure 10
figure 10

Cumulative distribution functions of \(\Delta t\), the absolute timing error between reconstructed and observed solar cycle start dates. The blue line shows the regression approach, which assumes the OSF minimum is the solar cycle start, while the red line shows the OSF forward modelling approach. The shaded area shows the interquartile range, while the black line shows the median.

Full size image

7 Results

We now apply the forward-modelling methodology to the observed OSF (GEO OSF\(_{\rm PS}*\)) series. The model OSF is shown in Figure 9c and the associated model SSN in Figure 9b. The fact that the model OSF agrees well with the observed OSF is to be expected, as the model specifically selects the random SSN realisations that produce the best match to the observed OSF. Indeed, given enough free parameters in the construction of the underlying SSN series, a perfect match with the observed OSF could likely be produced. Times when the model is unable to reproduce the observed OSF record could result from one or more of three possibilities: 1. the assumption of the cycle-average SSN waveform is insufficient, such as the single year spikes in OSF around cycle maxima; 2. the assumed model loss term does not permit the required rate of change of OSF; or 3. the geomagnetic OSF record is inaccurate because of magnetometer calibration errors.

The test of the reconstruction methodology is the obtained SSN time series, shown in 9b. By eye, the model reconstructs the timing of the SSN maxima and minima very well. As shown in Figure 8f, we find a linear correlation coefficient of 0.95 and a MAE of 15.9, greatly improved over both regression methods. A Meng’s z-test finds the increase in correlation compared with regression to be significant at the 99.99% level.

For the forward modelling SSN, the relative amplitude of the cycle maxima is also well matched, and the minima are far improved over the regression methods. There is a slight tendency for the reconstruction to underestimate the cycle peaks. This is likely due to the average SSN waveform used by the model, which produces a smooth, quasi-sinusoidal SSN variation. The largest differences between the model and observed SSN are the early cycle peaks between 1845 and 1880, and – to a lesser extent – the later peaks in 1970 and 1980. Here the model values are between a factor 1.2 to 1.7 lower than observed. For the early cycles, the uncertainty in the geomagnetic OSF record is expected to be a significant contribution to the disagreement. In other words, our results suggest the GEO OSF is too low at this time, assuming the SSN record to be correct, which may be also not exactly true (see, e.g. discussion in Usoskin, 2023). However, for the 1970 peak, OSF uncertainty cannot completely explain the SSN underestimate. This is discussed further in Section 8. However, in general, the reconstructed and observed SSN agree within observational uncertainties.

As the SSN reconstruction works on a 22-year window which slides forward 1 year at a time, we obtain 22 estimates of each solar cycle start/end date. In order to produce consensus estimates of the solar cycle start dates, a Gaussian kernel density with a width of 0.05 years is applied to the solar-cycle start date in each 22-year window and then summed across all windows. A range of kernel widths were tried and 0.05 years was found to be broad enough to combine information from multiple windows, but narrow enough to resolve individual cycles. The resulting kernel-density time series is shown in red in Figure 9. It can be considered to be the model (unnormalised) probability of a cycle starting on a given date. Note that the units are arbitrary. Taking maxima in the kernel density to be the model cycle start/end dates results in the values listed in Table 1. The cumulative distribution of the solar cycle timing error, \(\Delta t\), is shown as the red line in Figure 10. The \(\Delta t\) median value is 0.29 years, with an IQR of spanning 0.14 to 0.34 years (cf. the regression approach, with a median \(\Delta t\) of 0.5 years, and an IQR spanning 0.2 to 0.60 years). Note that the forward-model approach additionally gives estimates of the Cycle 9 and 25 start dates, even though the input OSF data did not contain these minima. This is because the solar-cycle phase is fitted to the available data, enabling extrapolation beyond the period of observations. In principle, the width of each kernel-density peak also provides information about uncertainty in the reconstructed cycle start date, but that information is not exploited here.

8 Discussion

This study has described a method for reconstructing sunspot number (SSN) from open solar flux (OSF) estimates by the use of a forward model. The method was tested over the period 1850 to present, when the OSF is known from a newly calibrated geomagnetic OSF estimate and the reconstructed SSN can be verified against the observed record. The primary motivation for developing this method is to reconstruct SSN prior to 1610 using cosmogenic isotope estimates of OSF.

Compared with simple regressions between SSN and OSF, the forward modelling approach significantly improves the reconstruction of SSN. The linear correlation coefficient for forward modelling of SSN is 0.95, compared to 0.78 or 0.80 for regression methods. And the mean absolute error in SSN is more than halved (15.9 versus 38.4 or 40.7). The estimates of the solar cycle start/end dates are also substantially improved, with the median timing error being reduced from 0.5 to 0.29 years. As the forward modelling approach has a theoretical underpinning, it is also expected to be more reliable during periods of extremely low SSN and OSF – grand solar minima – when a simple regression is expected to further break down (Owens, Usoskin, and Lockwood, 2012). Though this cannot be directly tested with the available data.

Future work will apply this new method to OSF inferred from cosmogenic isotope records, such as annual 14C and 10Be (McCracken, 2007; Muscheler et al., 2007; McCracken and Beer, 2015; Muscheler et al., 2016; Usoskin et al., 2021; Nguyen et al., 2022). It may also be possible to adapt the forward-modelling approach to directly link SSN to the cosmogenic isotope production rate, without the intermediate step of computing OSF. By inferring the solar-cycle phase as part of the reconstruction process, this would enable known heliospheric current sheet inclination effects (Alanko-Huotari et al., 2007) to be accounted for. Additionally, by working backwards from the present era, the effect of odd/even cycle drift effects can also be incorporated, which is presently difficult to achieve, for example the solar-cycle parity is unknown prior to the Dalton minimum (Usoskin, Mursula, and Kovaltsov, 2001; Owens et al., 2015). These advances in interpretation of cosmogenic isotope abundance data may enable reconstruction of SSN from proxy data that is sufficiently accurate to provide a link between observed SSN records across gaps in observational coverage, such as the early 18th century (Hayakawa et al., 2022).

However, as shown in this study, even in the modern era, when the SSN is known from direct observations, the method can still provide valuable insight. It provides an assessment of when the independent OSF and SSN records agree within the model and observational uncertainties. For example, Solar Cycle 20 – spanning approximately 1965 to 1975 – has a higher SSN than the low-and-flat OSF variation would suggest. While violation of the model assumptions at this time cannot be ruled out, they do appear to hold well for other cycles. The observational uncertainties in geomagnetic solar-wind reconstructions and sunspot-number records are also very low at this time, and thus unlikely to be the entire source of the disagreement. We note that the geomagnetic (and in-situ) estimates of OSF are based purely on local, near-Earth solar wind conditions. Thus while the uncertainty in measuring annual \(B\), \(V\) or \(B_{\mathrm{R}}\) is low, the extrapolation to global OSF may be less certain. Unfortunately, there were no 1 AU out-of-ecliptic observations available at the time to test this hypothesis (Owens et al., 2008). However, careful analysis of the Pioneer 6, 7, and 11 data in the more distant heliosphere may provide some information. There is also a disagreement between model and observed SSN in the very early geomagnetic OSF record. During Cycle 9 – spanning approximately 1844 to 1856 – the observed SSN is higher than the geomagnetic OSF suggests. However, the uncertainty in the geomagnetic \(V\) and \(B\) records, from which OSF is estimated, is much larger than the later record. Thus observational error is the most likely explanation for this discrepancy at this time.

The method used here can also bring the cosmogenic isotope data to bear on debates about calibration differences in the various data series. For example, Figure 9 shows that the forward modelling is giving SSN peaks that are lower than the SILSO values in Solar Cycles 9 – 11, with the largest difference in Cycle 9. This is most likely due to the calibration of the magnetometer data which underpins the geomagnetic OSF data, but could also reflect in the increasing and accumulating uncertainties in the calibration of the SSN record as we go back in time (e.g. Bhattacharya et al., 2023). Version 3 of the SILSO SSN record is currently under construction and may shed some light on this journal. The forward modelling approach using cosmogenic isotope data will also allow us to test for the origin of the early differences.