On the Origin of Ortho-Gardenhose Heliospheric Flux

Abstract

Parker-spiral theory predicts that the heliospheric magnetic field (HMF) will have components of opposite polarity radially toward the Sun and tangentially antiparallel to the solar rotation direction (i.e., in Geocentric Solar Ecliptic (GSE) coordinates, with $B _{X}/B _{Y} < 0$). This theory explains the average orientation of the HMF very well indeed but does not predict the so-called “ortho-gardenhose” (hereafter OGH) flux with $B _{X}/B _{Y} > 0$ which is frequently observed. We here study the occurrence and structure of OGH flux, as seen in near-Earth space (heliocentric distance $r = 1~\mbox{AU}$) by the Wind and Advanced Composition Explorer (ACE) spacecraft (for 1995 – 2017, inclusive) and by the Helios-1 and -2 spacecraft at $0.29~\mbox{AU} < r \leq 1~\mbox{AU}$ (for December 1974 to August 1981), in order to evaluate the contributions to OGH flux generation of the various mechanisms and factors that are not accounted for by Parker-spiral theory. We study the loss of OGH flux with increasing averaging timescale [$\tau$] between 16 seconds and 100 hours and so determine its spectrum of spatial/temporal scale sizes. OGH flux at Earth at sunspot minimum is shown to be more common than at sunspot maximum and caused by smaller-scale structure in the HMF (with a mode temporal scale at a fixed point of $\tau_{\text{mp}} \approx 10$ hours compared to $\tau_{\text{mp}} \approx 40$ hours for sunspot maximum, corresponding to about 5.5^∘ and 22^∘ (respectively) of heliocentric angular width for corotational motion or 21 $\mathrm{R}_{\odot}$ and 84 $\mathrm{R}_{\odot}$ for radial solar-wind flow (where $\mathrm{R}_{\odot}$ is the mean solar radius). OGH field generated by rotating the HMF through the radial direction is also shown to differ in its spectrum of scale sizes from that generated by rotating the HMF through the tangential direction – the former does not contribute to the “excess” open heliospheric flux at a given $r$ but the latter does. We show that roughly half of the HMF deflection from the ideal Parker-spiral needed to give the observed occurrence of OGH flux at Earth occurs at $r$ below 0.3 AU. By comparing the Helios and near-Earth data we highlight some questions that can be addressed by the Parker Solar Probe mission, which will study the HMF down to $r = 0.046~\mbox{AU}$. We suggest that with decreasing heliocentric distance, Probe will detect decreased OGH field due to draping around transient ejecta, such as blobs and coronal mass ejections, but increasing structure in the radial field within traditional HMF sectors that are remnant Alfvénic disturbances in outflow regions from coronal reconnection sites.

1 Introduction

The Archimedean spiral in the heliospheric magnetic field (HMF), known as the Parker-spiral, was first proposed by Parker (1958). The theory is based on consideration of the effect of magnetic flux that is frozen-in in radial solar-wind flow and dragged out of the solar atmosphere (Ness and Wilcox, 1964) whilst being rooted in the rotating solar corona. The theory is very successful at predicting the average orientation of the field that is observed at a wide variety of locations in the heliosphere (Behannon, 1978; Burlaga et al., 1982; Bruno and Bavassano, 1997; Forsyth, Balogh, and Smith, 2002; Jackman, Forsyth, and Dougherty, 2008; Borovsky, 2010; Owens and Forsyth, 2013, James et al., 2017). The theory predicts that the field will make an angle $\theta$ (called the “gardenhose angle”) between the sunward radial, and that $\theta$ will be between 0 and 90^∘ for T-flux (toward the Sun) and between −180^∘ and −90^∘ for A-flux (away from the Sun); the value of $\theta$ depending on the local solar-wind radial velocity [$V$] and the heliocentric distance [$r$]. Note that Section 1.1 shows that for the radial-field limits ($\theta = 0$ for T-field and $\theta = 180^{\circ}$, which is the same orientation as $\theta = -180^{\circ}$, for A-field) the theory requires an infinite $V$ and for the tangential-field limits ($\theta = 90^{\circ}$ and $\theta = -90^{\circ}$) the theory requires $V = 0$: hence these limits are only approached asymptotically in Parker-spiral theory. At Earth ($r = 1~\mbox{AU}$, where AU is an Astronomical Unit), the average value of $\theta$ is predicted to be close to 45^∘ or −135^∘, i.e. near the centres of the two allowed quadrants (see reviews by Gazis, 1996; Borovsky, 2010; Owens and Forsyth, 2013). However, as discussed in Section 1.2, factors outside those considered by the theory cause some heliospheric field to lie outside the two allowed quadrants predicted by the theory and such flux is called “ortho-gardenhose” (OGH – as opposed to the field for which $\theta$ is within one of the two allowed quadrants which is called “gardenhose” or GH field). This article studies the variation and structure of OGH field with $r$ and its spatial and temporal scales, with a view to defining its origins.

1.1 Parker Spiral Theory and the HMF Gardenhose Angle

The gardenhose angle that the heliospheric field makes with the direction radially toward the Sun is

$$ \theta = \tan ^{- 1} (-B_{Y}/B_{X}) $$

(1)

where $B _{X}$ and $B _{Y}$ are the IMF components in the $X$-(sunward) and $Y$-directions of the Geocentric Solar Ecliptic (GSE) reference frame. We define GH flux as having

$$ -\infty \leq B_{Y}/B_{X} \leq 0 $$

(2)

and OGH flux as having

$$ 0 < B_{Y}/B_{X} < \infty $$

(3)

These definitions mean that purely tangential field with no radial component ($B _{X} = 0$), predicted by Parker-spiral theory in the limit of zero radial solar-wind speed [$V$], would be counted as GH (rather than OGH) orientation, as would purely radial T- or A-flux ($B _{Y} = 0$), predicted for infinite $V$. A value of $\theta$ in the first quadrant (Q1: $0 \leq \theta \leq 90^{\circ}$) is T HMF ($B _{X} > 0$) in the GH orientation, $\theta$ in the second quadrant (Q2: $90 < \theta < 180^{\circ}$) is A HMF ($B _{X} < 0$) with the OGH orientation, $\theta$ in the third quadrant (Q3: ${-}180^{\circ}\leq \theta < -90^{\circ}$) is A HMF with the GH orientation, and $\theta$ in the fourth quadrant (Q4: $-90^{\circ}< \theta < 0$) is T HMF with the OGH orientation.

Parker-spiral theory gives a predicted gardenhose angle of

$$ \theta _{\mathrm{p}} = \tan ^{-1}(\omega r/V) + \theta _{0} $$

(4)

where $\omega$ is the angular rotation velocity of the corona (with respect to the fixed stars) and heliosphere and $\theta _{0}$ is zero for T HMF and −180^∘ for A HMF. Deviations from Parker-spiral theory also occur in the form of latitudinal deflections of the field, but we here place no constraints on the out-of-ecliptic ($Z$) component or elevation angle of the field.

To demonstrate how good Parker-spiral theory is in predicting the average HMF orientation in near-Earth space, Figure 1 presents polar histogram plots of the occurrence distribution of near-Earth heliospheric field (HMF) orientation in the Ecliptic plane. The grey bars show the distributions of the observed field gardenhose angle [$\theta$] (from Equation 1) in the GSE $X$–$Y$ frame from one-hour averages ($\tau = 1~\mbox{hour}$) of the HMF for the years 1996 – 2017 (inclusive). Using the criterion for gaining an hourly mean of the IMF orientation that is accurate to within 5%, as derived by Lockwood et al. (2019), this interval yields 161,620 valid samples: an availability of 83.8%. The data are divided into 12 bins of equal sample numbers (13,468 in each) between the percentiles of the distribution of the radial solar-wind speeds [$V$] which are 315, 337, 355, 372, 390, 408, 428, 451, 483, 528 and 593 km s⁻¹ (see Figure 2). The mauve histograms show the distributions of the orientation predicted from Parker-spiral theory [$\theta _{\mathrm{p}}$] for each of these intervals using Equation 4 with the observed hourly mean radial solar-wind speed $V$. The rotation of the means and modes of the distributions of both $\theta$ and $\theta _{\mathrm{p}}$ towards radial with increasing $V$ matches that in the predicted field orientation. The OGH and GH sectors are shaded orange and green, respectively. OGH flux is most common for the lowest $V$ and less common for the highest $V$.

Figure 1

Occurrence distribution of near-Earth heliospheric field (HMF) orientation. The grey polar histograms show the distributions of the observed field gardenhose angle $\theta$ (computed using Equation 1) in the GSE $X\,\mbox{--}\,Y$ frame from 1-hour averages ($\tau = 1~\mbox{hour}$) of the HMF components for the years 1996 – 2017 (inclusive, giving 161,620 valid samples). The data are divided into twelve bins of equal sample numbers (13,468 in each) between the percentiles of the distribution of the radial solar-wind speeds [$V$], which are 315, 337, 355, 372, 390, 408, 428, 451, 483, 528 and 593 km s⁻¹. The mauve histograms show the corresponding distributions of the orientation predicted from Parker-spiral theory ($\theta _{\mathrm{p}}$, computed using Equation 4) for the hourly mean observed radial solar-wind speed $V$. The rotation of the means and modes of the observed gardenhose distribution towards the $X$ axis with increasing $V$ matches well that in the predicted field orientation. The ortho-gardenhose (OGH) and gardenhose (GH) sectors are shaded orange and green, respectively. The toward the Sun (T) OGH field is in the positive $Y$, positive $X$ sector and the away from the Sun (A) OGH field is the negative $Y$, negative $X$ sector and both are seen in all velocity ranges being most common for the lowest $V$ and less common for the highest $V$.

Figure 2

Effect of radial solar-wind speed on averages of the near-Earth HMF. (a) the probability density of the radial solar-wind velocity, $V\ ( = - V _{X})$ for the $N = 16\mbox{,}1620$ hourly means ($\tau = 1~\mbox{hour}$) for 1965 – 2017 (inclusive). The vertical-grey lines show the percentiles that give $N/12$ samples in each bin (as used in Figure 1). (b) The fraction of time $T$ in which the HMF is in an OGH orientation for each bin of $V$ (black points and line, $T$_OGH) and for Class-A and Class-B rotations into that OGH orientation (red and blue points and lines, $T$_OGH,A and $T$_OGH,B, respectively). (c) The fraction $F$_OGH of the total unsigned radial magnetic flux ($=\int |B _{X}|\,\mathrm{d}t$) passing through unit width of the Ecliptic plane at heliocentric distance $r = 1~\mbox{AU}$ that is in an OGH orientation (black line, $F$_OGH) and its two subdivisions of Class-A and Class-B OGH flux (red and blue lines, $F$_OGH,A and $F$_OGH,B, respectively). (d) the average values for the $V$-bins of (mauve) $|B _{X}|$, (green) $|B _{Y}|$, and (black) $B _{XY} = (B _{X} ^{2} + B _{Y} ^{2})^{1/2}$ where $B _{X}$ and $B_{Y}$ are the $X$- and $Y$-components of the HMF in the GSE frame.

Figure 1 shows that the distributions in $\theta$ are continuous across the OGH/GH boundaries. Thus, the processes that cause the spread in $\theta$ away from the predicted Parker-spiral value [$\theta _{\mathrm{p}}$] within GH sectors are either the same as, or are convolved with, those that cause GH flux to become classified as OGH: the combined processes just need to be effective enough to make $|\theta - \theta _{\mathrm{p}}|$ sufficiently large that one of the dividers between the four quadrants is crossed. Given that the Parker-spiral direction at a general $V$ and $r$ does not sit at exactly the centre of the GH quadrants, the proximity of the relevant quadrant boundary depends on which direction the field is deflected in. Figure 3 defines “Class-A” and “Class-B” OGH flux by the sense of rotation from the predicted Parker-spiral (gardenhose angle $\theta _{\mathrm{p}}$) to the local HMF direction (gardenhose angle $\theta$): Class-A flux requires rotation from a GH orientation through the radial direction, Class-B rotation through the tangential direction. As shown in Figure 3, Class-A rotation (pink arrow) is anticlockwise around the $Z$_GSE axis when viewed from the northward side of the Ecliptic; Class-B rotation is in the opposite sense (pale blue arrow). The schematic also shows in the lower panels the corresponding Parker-spiral field line and deflected field line in a wider-scale view of the inner heliosphere looking down from above the North Pole of the Sun.

Figure 3

Schematic of $\theta$, sectors and HMF deviations from Parker-spiral. The top panels show are local views of the near-Earth Ecliptic plane from the North (i.e. looking in the – $Z$ GSE direction): as in Figure 1, the OGH and GH quadrants are shaded orange and green, respectively. The lower panels are views of the inner heliosphere looking down from over the North Pole of the Sun. In both cases, OGH field is shown by solid arrows with open and dashed arrows giving the ideal Parker-spiral field direction. Parts a and b are termed Class-A deflections of the local IMF vector from the Parker-spiral with anticlockwise rotation of the near-Earth field vector when viewed in the – $Z$-direction (pink arrows); parts c and d are termed Class-B deflections from the Parker-spiral with clockwise rotation of the field vector when viewed in the – $Z$-direction (pale blue arrows). Note that in the lower panels the arrows show the displacement of the HMF field lines from the Parker spiral, not the sense of rotation.

Figure 2a gives the probability density function of the observed radial solar-wind speed [$V$] that yields the percentiles adopted in Figure 1, those percentiles being given by the vertical grey lines. The solid points in Figure 2b show the fraction of time that the HMF is in a given OGH orientation ($T$_OGH, in black) for each of the 12 bins between these percentiles. This is also subdivided into Class-A and Class-B OGH flux by assuming the rotation sense gives the smaller rotation angle needed to give the observed orientation (i.e. $|\theta - \theta _{\mathrm{p}}| < 180^{\circ}$). Given that Figure 1 shows that the Parker-spiral orientation is closer to the tangential at low $V$ and closer to the radial at high $V$, it is not surprising that Class-B OGH flux is more common (blue points, $T$_OGH,B) at low $V$ but Class-A OGH flux becomes the more common at high $V$ (red points, $T$_OGH,A). OGH flux in general becomes less common at high $V$, as noted from Figure 1. The fraction of the total radial magnetic flux in the total, Class-A, and Class-B OGH are presented in Figure 2c and will be discussed further in Section 2. Figure 2d shows the magnitude of the average $B _{X}$, $B _{Y}$ and in-Ecliptic HMF $(B _{XY} = B _{X} ^{2} + B _{Y} ^{2})^{1/2}$ components for the 12 averaging bins of $V$. Parker-spiral theory predicts that, as the spiral unwinds with higher $V$, the magnitude of the HMF will fall for a given strength of the source field at the top of the solar corona. Figure 2d shows that this does not occur and that $B _{XY}$ actually rises with increasing $V$. This is not necessarily a failing in Parker-spiral theory and implies that the source field is stronger in regions of the corona that give faster wind. However, higher $V$ also implies greater variability in $V$ and a factor in the rise in $B_{XY}$ with average $V$ will be the compression of the field in corotating interaction regions (CIRs) ahead of fast streams.

1.2 Sources of Ortho-Gardenhose HMF

Figure 4 presents schematics of some of the mechanisms that could generate OGH flux, given that it is not predicted by Parker-spiral theory. Borovsky (2010) discussed the magnetic “braiding” concept, whereby twisting of field lines around each other close to the Sun gives small differences in gardenhose angle, which become amplified with increasing $r$, as the solar wind expands in both latitude and longitude to fill the heliosphere. This concept is shown schematically in Figures 19 and 22 of Borovsky (2010). It is proposed that this yields large, amplitude gardenhose-angle structure on relatively short spatial scales at $r = 1~\mbox{AU}$ and so broadens the distribution of $\theta$ around $\theta _{\mathrm{p}}$. This passive broadening of the spectrum of $\theta$-values is predicted to give half widths up to an asymptotic limit of about 40^∘ which is not sufficient to drive much of the OGH flux shown in Figure 1 (which requires $|\theta - \theta_{\mathrm{p}}|$ to be greater than typically 45^∘ at $r = 1~\mbox{AU}$), indicating that dynamical processes are needed to generate much of the OGH flux. Figure 4 presents possible mechanisms.

Figure 4

Schematics of some of the dynamical causes of OGH HMF orientations in near-Earth interplanetary space. The areas shaded pink and pale blue are snapshots of where Class-A and Class-B OGH flux (see Figure 3) exist at a given time and hence in cases d and $\mathbf{e}$, their radial extent depends on how long the reconnection and new loop emergence (respectively) persist. The dashed lines are an undisturbed Parker-spiral HMF field-line orientation.

Figure 4a is a general schematic noting that waves, shocks, and turbulence can all deflect the field over a range of temporal and spatial scales (Burlaga et al., 1982; Roberts, Goldstein, and Klein, 1990; Smith and Phillips, 1996; Horbury and Balogh, 2001; Ragot, 2006; Bruno and Carbone, 2013; Horbury, Matteini, and Stansby, 2018). Figure 4b would arise if an emerging loop of magnetic flux leaving the solar corona spans a fast solar-wind steam. This could arise from footpoint-exchange reconnections that cause such a configuration over an existing fast steam or from a flow-speed enhancement forming underneath a pre-existing coronal loop. Either causes the field in the stream to be dragged out further than the parts of the loop embedded in slower flow: this sort of effect was invoked as an explanation for near-radial HMF at the tail end of fast-stream intervals by Jones, Balogh, and Forsyth (1998), Gosling and Skoug (2002), and Riley and Gosling (2007). To the leading side of the stream in the schematic, the field tends to radial but as the fast stream is likely to be radial, it will probably remain in the GH quadrant. On the other hand, to the trailing side of the stream, the field could become OGH in nature (in the area shaded blue) and this would be a Class-B rotation. This means that the seeds of the deviation from Parker-spiral orientation are sown close to the Sun in the solar atmosphere or even photosphere, as was also proposed in the magnetic braiding concept proposed by Borovsky (2010).

Another class of cause of deviations from Parker-spiral orientation arises from the effect of draping pre-existing HMF over coronal ejecta released underneath it, as illustrated in Figure 4c (Gosling and McComas, 1987; Burlaga and Ness, 1993; Richardson and Cane, 1996; Smith and Phillips, 1996, 1997). This could range from large CMEs (McComas et al., 1989; Kaymaz and Siscoe, 2006) to smaller CME events, down to small-scale transient blobs (Sheeley et al., 1997; Kilpua et al., 2009; Rouillard et al., 2010a, 2010b; Viall and Vourlidas, 2015; Kepko et al., 2016). In this case, the event is likely to expand as it propagates which means that the draped field to the left side of the event (as viewed in Figure 4) may well be deflected past the radial direction and become Class-A OGH flux (the pink-shaded area). To the right of the event, the draping is likely to give Class-B OGH flux. Figure 4d points out that both classes of OGH are likely to be formed in the outflow regions of reconnection sites. These may be relatively local sites in the heliosphere, as observed by Phan et al. (2006) and Mistry et al. (2017), or they may be back in the solar corona giving disconnected or folded flux, as inferred by Owens et al. (2017, 2018). Similarly, the leading edge of an erupting loop would give both clas of OGH flux as it passed over a given location (Figure 4e) and that loop may have a flux rope form (e.g. Chen et al., 1997) which would allow the OGH flux regions to cover a more extensive region (Figure 4f). The key point that we wish to make here is that this wide variety of processes can give OGH flux over a wide range of temporal and spatial scales.

1.3 The Variation with Heliocentric Distance [$r$]

The launch of the Parker Solar Probe (Fox et al., 2016) gives us an opportunity to study the variation of OGH flux, and the gardenhose-angle distribution in general, closer into the Sun and so understand more about how and where deviations from the Parker-spiral are generated. This mission will study the HMF at exceptionally high temporal resolution and uniquely close to the Sun. The first three orbits have perihelia at $r = 0.16~\mbox{AU}$ and later in the mission this a gradually reduced to $r = 0.046~\mbox{AU}$. In anticipation of these observations, we study here data from the two Helios spacecraft that made measurements down to $r = 0.29~\mbox{AU}$.

1.4 Ortho-Gardenhose Flux, Folded Flux, and Excess Flux

Owens et al. (2008) surveyed radial HMF measurements throughout the heliosphere and found that the modulus of the radial component $[|B _{\mathrm{r}}|]$ was largely independent of heliographic latitude, as expected from consideration of tangential magnetic pressure in the low-$\beta$ solar wind close in to the Sun (Suess and Smith, 1996). However, these authors found a consistent rise in $|B _{\mathrm{r}}|$ with radial distance. Lockwood, Owens, and Rouillard (2009a,b) deployed the term “excess flux” for the difference between the total unsigned open solar flux that leaves the top of the solar atmosphere (the “coronal source surface” by convention usually taken to be at $r = 2.5~\mathrm{R}_{\odot}$), $[4\pi r^{2} \mid B_{\mathrm{r}} \mid ]_{r=2.5\mathrm{R}}$, and the total unsigned flux threading a sphere at a general heliocentric distance $r$ in the heliosphere $[4\pi r^{2} \mid B_{\mathrm{r}} \mid ]_{{r}}$ and noted that the result of Owens et al. (2008) means that this “excess flux” increases with $r$. Smith (2011) argued this was merely an artefact of taking the modulus of the radial field and that excess flux violated Maxwell’s equations by requiring magnetic monopoles between 2.5 $\mathrm{R}_{\odot}$ and $r$. This is not the case because a heliospheric field line of a given polarity can fold back on itself (the so-called “folded flux”) such that it threads the surface at $r$ a total of $n$ times, where $n$ is 3, or indeed any larger odd number, whereas it threads the surface at 2.5 $\mathrm{R}_{\odot}$ only once. Smith attributed the excess flux to an unspecified “noise” that grew with $r$ and so advocated avoiding the use of the modulus by averaging over T- and A-sectors in the field. However, the problem with this method was pointed out by Lockwood and Owens (2013), namely that there is a large uncertainty in deciding what was a true sector boundary (i.e. a T/A-field polarity reversal at a given observation point that is known to map all of the way back to the coronal source surface) and so this could not be done routinely. (In fact, that can be done in the presence of detectable unidirectional strahl-electron flows because, although the field reverses at a true sector boundary, the electron flow direction is always away from the Sun, whereas for folded flux both field and the strahl-electron flow reverse direction – see below.) Lockwood, Owens, and Rouillard (2009a) used the third perihelion pass of the Ulysses spacecraft to show that the excess flux mainly arose in the streamer belt where variability in solar-wind velocity is high, and Lockwood, Owens, and Rouillard (2009b) developed a kinematic correction to allow for this effect, which Lockwood and Owens (2009) showed explained the results of the data survey as a function of $r$ by Owens et al. (2008) very well.

More recently, Owens et al. (2017) have been able to use strahl-electron data to identify folded flux and so subtract its contribution to the open solar flux. The results are consistent with the kinematic correction of Lockwood, Owens, and Rouillard (2009b) to within the computed uncertainties; however, it is also true that the kinematic correction consistently gives slightly larger excess flux values than the strahl/folded flux method.

The point that we wish to make here is that folded flux may often be associated with Class-B OGH flux. Class-A OGH flux makes no contribution to excess flux because by rotating through the radial direction the field line still only threads the spherical sphere of radius $r$ the one time. However, Class-B OGH flux does because it generates field lines that thread the surface multiple times and one in three of those crossings are in an OGH orientation. However, note that not all of the folded flux gives Class-B OGH flux: if the field-line folding is by an angle greater than $180^{\circ}\,\mbox{--}\,\theta_{\mathrm{p}}$, then the flux is folded back on itself and so changes its T/A polarity but remains in a GH orientation; hence this would contribute to excess flux but not to Class-B OGH. Therefore, although Class-B OGH always contributes to excess flux, not all excess flux involves Class-B OGH flux.

2 Analysis

For data on near-Earth space ($r = 1~\mbox{AU}$) we here employ the Omni composite of data at one-minute resolution (made available by the Space Physics Data Facility (SPDF), NASA/Goddard Space Flight Center from omniweb.gsfc.nasa.gov/ow_min.html) (King and Papitashvili, 2005). We use data for 1995 – 2017 when the ACE and Wind spacecraft provide near-continuous observations of the HMF. This yields a total of 11,046,240 valid HMF samples, which is an availability of 97.87% so the data are indeed very nearly continuous. We extend some studies in resolution down to 16 seconds using 39,446,983 16-second samples from the ACE magnetometer (Smith et al., 1998) taken between 1998 and September 2018 (an availability of 99.86%). These data are made available by SPDF via CDAWeb (cdaweb.sci.gsfc.nasa.gov/index.html).

We also study data from the Helios-1 and -2 spacecraft, which executed orbits from $r = 0.29$ to 1 AU with roughly a six-month orbital period. We employ solar-wind flow data from the plasma experiments (Rosenbauer et al., 1977) and HMF observations from the magnetometers (Neubauer et al., 1977) onboard both spacecraft. The datasets have (approximately) 40-second resolution, with some datagaps being caused by loss of telemetry when the spacecraft were behind the Sun. The data were also downloaded from CDAWeb (from the same URL as given above) and were linearly interpolated onto regular times one minute apart. Any one-minute point that was separated from a valid data point by more than 40 seconds was treated as a data gap. This yielded 1,517,731 one-minute HMF samples from Helios 1 (which made 13 orbits between December 1974 and June 1981: an average data availability of 44.1 %) and 895,185 one-minute HMF samples from Helios 2 (which made orbits between January 1976 and May 1979: an average data availability of 51.1%). The Helios data commence shortly before the sunspot minimum between Solar Cycles 20 and 21 and end at the peak of Cycle 21: hence they cover a sunspot minimum and a rising phase of the solar cycle. The daily sunspot number (we here use the new version of the International Sunspot Number downloaded from the World Data Center for the Production, Preservation and Dissemination of the International Sunspot Number, at the Royal Observatory of Belgium: www.sidc.be/silso) vary between zero and 428 in this interval; by way of comparison, the largest value in the record, which starts in 1818, is 528 on 26 August 1870. The mode and mean values of the distribution for the times of all Helios samples (from both spacecraft) are zero and 112.2, respectively. Hence the Helios data are dominated by sunspot minimum conditions, but they do contain some samples at all activity levels up to sunspot maximum.

2.1 Observations of the Parker Spiral and OGH Flux at $r = 1~\mbox{AU}$

In this section we continue the investigation of one-minute Omni samples of the HMF in near-Earth space that was used to introduce the Parker-spiral in Section 1.1 of the present article.

The black lines in Figure 5 show distributions of $\theta$ for the near-continuous IMF data available for 1996 to 2017 (inclusive), these 22 years giving 11,046,240 valid one-minute averages ($\tau = 1$ minute, top panel) and 6428 30-hour averages ($\tau = 30$ hours, bottom panel). In both cases, the number of valid samples in 4^∘-wide bins of gardenhose angle $\theta$ are counted, [$N$], and normalised to the sum for all 90 bins [$\sum N$]. The red lines are for three years around the sunspot maxima (the years 2000, 2001, 2002, 2012, 2013, and 2014, which yield 2,891,693 one-minute samples and 1753 30-hour samples) and the blue lines are for three years around sunspot minimum (the years 1996, 1997, 2007, 2008, 2009, and 2017 which yield 2,424,326 one-minute samples but only 1751 30-hour samples: two 30-hour intervals are lost because these sunspot minimum data come from three intervals, not the two used for sunspot maximum). The four quadrants are marked in the upper panel and clear peaks are seen in the GH quadrants (Q1 and Q3) in both cases. Note that noise is greater in Figure 5b than in Figure 5a because of the smaller number of samples. The averaging timescale [$\tau$] has a very clear effect on the occurrence of OGH flux (quadrants Q1 and Q3) as at $\tau = 30$ hours it is very rare, whereas at $\tau = 1$ minute even its minimum occurrence is about a quarter of the maxima in the GH quadrants. Comparison of the red and blue histograms in Figure 5a shows that OGH flux (in Q2 and Q4) is, surprisingly, more common at sunspot minimum than at sunspot maximum (and so the peaks in Q1 and Q2 are lower because the histograms are normalised).

Figure 5

Occurrence distribution histograms as a function of observed gardenhose angle [$\theta$] for the near-continuous IMF data available for 1996 to 2017 (inclusive): the black lines are for all data, red lines for the six years within one year of one of the two sunspot maxima, and the blue lines are for the six years within one year of a sunspot minimum (which is here taken to include 2017). The number [$N$] of valid samples in 4^∘-wide bins of $\theta$ are counted and normalised to the sum for all 90 bins [$\sum N$]. (a) is for an averaging timescale $\tau = 1$ minute, and (b) is for $\tau = 30$ hours. As in Figures 1 and 2, OGH and GH sectors are shaded orange and green, respectively. The four quadrants are labelled Q1 (T-field in gardenhose orientation), Q2 (A-field in ortho-gardenhose orientation), Q3 (A-field in gardenhose orientation), and Q4 (T-field in ortho-gardenhose orientation), where T and A are “Toward” and “Away” from the Sun, respectively ($B _{X}\ \geq$ 0 and $B _{X} < 0$).

The GH peaks for T-flux (Q1) and A-flux (Q3) are not symmetrical in Figure 5, with the A-peak being larger than the T-peak for sunspot maximum and the overall average. This is despite the data covering a whole Hale cycle (22 years) and hence both polarities of solar polar fields with equal weighting in terms of time. However, the two solar maxima in this interval are not of equal amplitude in terms of solar activity (Solar Cycle 24 being considerably weaker in sunspot number than Cycle 23), and this may have introduced an asymmetry in the case of sunspot maximum. For sunspot minimum, the asymmetry is the other way round with the T-peak (Q1) being larger than the A-peak (Q3) – this may also be due to an asymmetry in solar activity for the two polar-field polarities with the minimum between Cycles 23 and 24 being considerably deeper and longer-lived than that between Cycles 22 and 23. This asymmetry is the same in the one-minute and 30-hour data. In this article we are concerned with the effect of averaging timescale [$\tau$], in particular on OGH flux, and discussion of asymmetries in the GH flux shown in Figure 5 will be left to a later article.

Increasing the averaging timescale [$\tau$] removes OGH flux because within a period of larger $\tau$, intervals of the non-GH polarity $B _{X}$ or $B _{Y}$ (giving positive-polarity HMF $B _{X}/B _{Y}$) that are seen at low $\tau$ are cancelled out. Thus studying the variation of the occurrence of OGH with $\tau$ reveals the spectrum of temporal scales at which the OGH exists at a given point. This could reflect stable longitudinal spatial structure in the heliosphere that is moved over the spacecraft with the Carrington rotation of the heliosphere or transient radial structure that is propagated over the spacecraft by the solar-wind flow. In general, both will contribute, and so we refer to the study of OGH flux as a function of $\tau$ as revealing its spatial and temporal structure. We can study the occurrence frequency of OGH orientations in this way, but often of greater interest is the amount of magnetic flux contained in the OGH sectors, and for studies of folded flux and excess flux, it is the flux in the radial direction that is most important. In Section 2.2 we define how this is quantified.

2.2 Helios Observations of the Parker Spiral at $r < 1~\mbox{AU}$

Figure 6a presents the distributions of $\theta$ seen by the Helios-1 and -2 spacecraft in eight non-overlapping ranges of heliocentric distance [$r$] that are 0.1 AU wide and centred on $r$ of [0.3:0.1:1.0] AU. Histograms of the normalised number of samples in bins of gardenhose angle $\theta$ that are 4^∘ wide [$N/ \sum N$] are colour-coded by the range of $r$ using the key given. The evolution of the Parker-spiral angle with $r$, expected from Equation 4, can clearly be seen, with the distribution closest to the Sun ($r < 0.35~\mbox{AU}$, in black) peaking closest to the radial direction, and the average gardenhose angle increasing with increasing $r$. The width of the distributions also increases a little with $r$. This can be seen most clearly in Figure 6b which plots the distributions of the deviations from the predicted Parker-spiral angle $\delta \theta = \theta - \theta _{\mathrm{p}}$ for the same ranges of $r$ and using the same colour scheme. Given that $\theta _{\mathrm{p}}$ is close to 45^∘ for near-Earth space, the fractions of the distributions with $|\delta \theta | \geq 45^{\circ}$ is of interest because this is roughly sufficient deviation to cause OGH at $r = 1~\mbox{AU}$. This fraction rises linearly from 0.16 at $r = 0.3~\mbox{AU}$ to 0.32 at $r = 1~\mbox{AU}$. On this basis we can say that roughly half of the HMF deflection needed to give the observed occurrence of OGH $r = 1~\mbox{AU}$ occurs at $r < 0.3~\mbox{AU}$ and half occurs between $r = 0.3~\mbox{AU}$ and 1 AU.

Figure 6

Helios-1 and Helios-2 data showing how the gardenhose-angle distribution varies between 0.3 and 1 AU. Data are sorted into eight non-overlapping bins of heliocentric distance [$r$] that are 0.1 AU wide and centred on [0.3:0.1:1.0] AU. (a) Histograms of the normalised number of samples in bins of gardenhose angle $\theta$ that are 4^∘ wide [$N/\sum N$] colour-coded by the range of $r$ using the key given. (b) The distributions of the deviations from the predicted Parker-spiral angle $\delta \theta$ for the same ranges of $r$ and using the same colour scheme. (c) The variations with $r$ of the means and standard deviations of the $\delta \theta$ distributions shown in (b) [respectively $\langle\delta \theta \rangle$ and $\sigma _{\delta \theta }$]. The black lines are the best least-squares linear regression fits.

Figure 6c gives the variations with $r$ of the means and standard deviations of the $\delta \theta$-distributions shown in Figure 6b (respectively, $\langle\delta \theta \rangle$ and $\sigma_{\delta \theta}$), the black lines being the best least-squares linear regression in each case. The standard deviations $\sigma_{\delta \theta }$ confirm the broadening described above. The average values $\langle\delta \theta \rangle$ are less consistent but show a marked tendency to be negative. This means that the Helios spacecraft were detecting a tendency towards “underwound” HMF (with $\theta < \theta_{\mathrm{p}}$). This has been noted by several authors particularly in Ulysses data at $r$ around 5 AU and within corotating rarefaction regions where deviations from the predicted Parker-spiral angle can be as large as 30^∘ (Murphy, Smith, and Schwadron, 2002). Schwadron (2002) modelled the underwound HMF resulting from magnetic-footpoint motion at the Sun. The resulting field strays further from the Parker-spiral angle with radial distance (see their Figure 3). This explains the relatively small deviations observed here by Helios, compared to the large 30^∘ deviations observed by Ulysses. Note that sub-Parker-spiral/underwound HMF can never contribute to OGH flux because it is always deflected towards the radial, and it can never cross out of the GH sector.

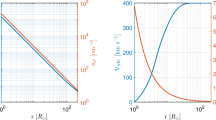
Using the variation of $\langle\delta \theta \rangle$ and $\sigma_{\delta \theta}$ and extrapolating towards the Sun using the linear regressions, shown in Figure 6d, along with the predicted variation of $\theta _{\mathrm{p}}$ with $r$, we can predict what the gardenhose-angle distribution might look like at the smaller $r$ that the Parker Solar Probe will access. The results are shown in Figure 7. In order to predict $\theta _{\mathrm{p}}$ as a function of $r$ using Equation 4, we employ the model radial solar velocity profile [$V(r)$] shown in Figure 7c, which is a fifth-order polynomial fit to the observed average velocities in the Helios data (solid points) and values at $r$ of 6 $\mathrm{R}_{\odot}$ and 26 $\mathrm{R}_{\odot}$ (open circles) derived by applying Fourier motion filters to SOHO/LASCO-C3 movies observed from 1999 to 2010 by Cho et al. (2018). Figure 7a presents colour contours the derived p.d.f. as a function of gardenhose angle [$\theta$] with heliocentric distance [$r$] using Gaussian distributions of the deviations from the Parker-spiral direction of mean $\langle \delta \theta \rangle$ and standard deviation $\sigma_{\delta \theta}$. The total toward and away distributions are assumed to be symmetrical. Figure 7b shows the predicted fraction of time that the field is in an OGH orientation [$T$_OGH]: the black line is for all field, the red line for Class-A OGH field and the blue line for Class-B OGH field (see Figure 3). The areas shaded grey, pink, and pale blue around the black, red, and blue lines are the uncertainties introduced by the uncertainty in $\langle \delta \theta \rangle$. As would be expected, the fraction of Class-B OGH falls and of Class-A OGH rises with decreasing $r$ as $\theta _{ \mathrm{p}}$ tends to zero.

Figure 7

(a) Model of the evolution of the distributions of gardenhose angle $\theta$ with heliocentric distance $r$ using Gaussian distributions of the deviations from the Parker-spiral direction of mean $\langle \delta \theta \rangle$ and standard deviation $\sigma _{\delta \theta }$ given by the regression fits in Figure 6c. The total toward and away distributions are assumed to be symmetrical and the linear variations in $\langle\delta \theta \rangle$ and $\sigma_{\delta \theta}$ seen at $r > 0.3$ are extrapolated to closer to the Sun. The Parker-spiral direction at each $r$ is evaluated using the velocity variation [$V(r)$] shown in Panel c, which is a fifth-order polynomial fit to the observed average velocities in the Helios data (solid circles) and values at $r$ of 6 $\mathrm{R}_{\odot}$ and 26 $\mathrm{R}_{\odot}$ (open circles) derived by applying Fourier motion filters to SOHO/LASCO-C3 movies observed from 1999 to 2010 by Cho et al. (2018). Panel $\mathbf{b}$ shows the predicted fraction of time that the field is in an OGH orientation, $T$_OGH: the black line is for all field, the red line for Class-A OGH field, and the blue line for Class-B OGH field (see Figure 2). The areas shaded grey, pink, and pale blue around the black, red, and blue lines are the uncertainties introduced by the uncertainty in $\langle\delta \theta \rangle$.

We note that the assumption that the variation of $\sigma_{\delta \theta }$ remains linear is a major one that may well not be valid as, for example, turbulent perturbations of the plasma and field have been observed to grow rapidly between around $r$ of 15 $\mathrm{R}_{\odot}$ and 69 $\mathrm{R}_{\odot}$ (0.7 – 0.32 AU) by DeForest et al. (2016) using images from the HI instruments of the STEREO spacecraft. Parker Solar Probe will reach down to $r$ of 0.046 AU, and so it will study this region in situ for the first time. Deviations of the pattern in Figure 7a from that for Probe data (or a lack of them) will help us define the processes giving the spread in $\theta$ that arises for $r < 0.3~\mbox{AU}$. Of particular interest for the present authors will be the reconnection of open flux with coronal loops. Owens et al. (2018) have recently used isotopic abundances to infer that this can occur right down into the low corona and that the subsequent evolution of the field lines gives OGH flux (they propose a more complex variant of Figure 4d). Because we can see no obvious reason why this should not also occur for more distended loops or at greater $r$ in the corona or inner heliosphere, we predict that at the lowest $r$ Probe is likely to find considerable mixtures of near-radial T- and A-field within a classic HMF sector. The outflow-exhaust regions from reconnection sites will be Alfvénic structures, and if reconnection outside the corona and in the heliosphere is a factor as $r$ increases, the probability of outward flow would increase and the probability of inflow (or very slow outflow) will decline. Over larger distances the strength of these Alfvénic structures will decline and the dominant field polarity of the sector should begin to emerge more strongly and this change would be accompanied by a rise in the Class-A OGH flux and of the gardenhose-angle distribution width [$\sigma_{\delta \theta }$].

Lastly, Figure 8 compares the distributions of $\theta$ at $r < 0.39$ (i.e. the innermost 0.1 AU covered by the Helios mission, shown in Panel b) with those for $r = 1~\mbox{AU}$ (the Omni data, shown in Panel a). In both cases the black lines are for one-minute data and the red lines are for 30-hour averages. As for Figures 1, 2, and 5, the orange and green bars at the top of each panel mark the OGH and GH sectors, respectively. In both cases, the OGH flux has almost vanished for $\tau = 30$ hours. For both $\tau$, the distribution is broader for $r = 1~\mbox{AU}$ than for $r < 0.39~\mbox{AU}$. (This figure will be discussed again later in connection with Figure 13.)

Figure 8

Comparison of probability density histograms [$N/\sum N$], where $N$ is counted in 4^∘-wide bins of HMF gardenhose angle [$\theta$] at (a) $r = 1~\mbox{AU}$ (from the Omni dataset for 1996 – 2017, inclusive) and at (b) $r\leq 3.9~\mbox{AU}$ (from the Helios-1 and -2 data for December 1974 to August 1981). In both cases $\theta$ has been determined using Equation 1 from one-minute (in black) and 30-hour (in red) averages of HMF $B _{X}$ and $B _{Y}$ ($\tau = 1$ minute and $\tau = 30~\mbox{hours}$). The Helios data are taken from 40-second averages and linearly interpolated onto times one-minute apart: interpolation points that are separated from a valid 40-second mean by more than 40 seconds are treated as data gaps. For both datasets the one-minute samples were averaged in 30 hour intervals and treated as valid means if the number of available one-minute samples in each exceeded 1350, which is 75% of the maximum number of 1800. The orange and green bars at the top of each panel show ortho-gardenhose and gardenhose orientations, respectively, and the pink and blue shading show the definitions of Class-A and Class-B flux used in the remainder of this article. For $r = 1~\mbox{AU}$ in Panel a, A and B are defined as two sub-classes of OGH flux, separated by the orthogonal to the average spiral direction. For the near-Sun field observed by Helios ($r < 0.29~\mbox{AU}$) the same definitions are not greatly informative as the smaller Parker-spiral angle means that there would be almost no flux in Class-B and a lot in Class-A (as shown by Figure 7b): hence wider bands in $\theta$ are used, as defined in the text.

2.3 Ortho-Gardenhose Flux Fraction

In this section, we describe how we quantify the fraction of the total unsigned near-Earth heliospheric magnetic flux that is in an OGH orientation. We study this ratio of the total unsigned flux values because both the numerator and denominator of this ratio rise and fall over the solar cycle with the total open solar flux. This also means that the decrease in the total unsigned flux with $r$ (predicted by Parker-spiral theory to be a $r ^{-2}$ decrease but not, in general, valid because of Class-B OGH departures from Parker-spiral orientations and because of “folded” GH flux both give “excess flux” (Lockwood, Owens, and Rouillard, 2009a, 2009b; Owens et al., 2018) is automatically accounted for.

Consider a band of unit length in the GSE $Z$-direction that is around the Sun at heliocentric distance $r = r _{1}= 1~\mbox{AU}$, which therefore has a surface area $2\pi r _{1}$. The total flux sum of inward and outward magnetic flux (i.e. the unsigned flux) threading the surface of this band for data averaged over a timescale $\tau$ is

$$ \int _{\text{n yr}} \bigl|\langle B _{X}\rangle_{\tau }\bigr| \,\mathrm{d}t = \int _{\text{n yr}} \bigl| \bigl\langle [B _{X}]_{\text{GH}}\bigr\rangle _{\tau }\bigr| \,\mathrm{d}t + \int _{\text{n yr}} \bigl|\bigl\langle [B _{X}]_{\text{OGH}}\bigr\rangle _{\tau }\bigr| \,\mathrm{d}t $$

(5)

where the integral is over a whole number [$n$] of years such that Earth and its L₁ spacecraft have moved around the band an integer number of times. We use the years 1996 – 2017 (inclusive, i.e. $n = 22$), which equals 299.75 rotation periods (which is 300 to within an accuracy of 0.08%). Thus, our choice of $n$ covers approximately one whole Hale solar cycle, 22 whole solar orbits of the L₁ spacecraft and very close to 300 whole Carrington solar rotations. [$B _{X}$]_GH is the (sunward) $B _{X}$ field component for field for which $\theta$ is in one of the two GH quadrants and [$B _{X}$]_OGH is the $B _{X}$ field component field for which $\theta$ is in one of the two OGH quadrants. The use of the modulus means that both inward and outward flux are included but because $B _{X}$ can have either polarity (T- and A-flux) all terms depend on the averaging timescale [$\tau$]. The fraction of the total radial flux that is in the OGH orientation is

$$ F_{\text{OGH}}(\tau ) = \int_{\text{n yr}} \bigl|\bigr\langle [B _{X}]_{\text{OGH}}\bigr\rangle _{\tau }\bigr| \,\mathrm{d}t \Big/ \int_{\text{n yr}} \bigl|\langle B _{X}\rangle_{\tau }\bigr|\, \mathrm{d}t = \bigl\langle \bigl| \bigl\langle [B _{X}]_{\text{OGH}}\bigr\rangle _{\tau }\bigr|\bigr\rangle \big/ \bigl\langle \bigl|\langle B _{X}\rangle_{\tau }\bigr| \bigr\rangle . $$

(6)

We use the one-minute Omni data of the component $B _{X}$ and determine $[B _{X}]_{\text{OGH}}$ (which equals $B _{X}$ if $\theta$ is in the OGH quadrants Q2 and Q4 but zero if $\theta$ is in the GH quadrants Q1 and Q3). These are then averaged into intervals of duration $\tau$ to give $\langle [B _{X}]\rangle _{\tau }$ and $\langle[B _{X}]_{\text{OGH}}\rangle _{\tau }$. The modulus is then taken, and the average of those modulus values for all the intervals of duration $\tau$ taken. The ratio then yields $F_{\text{OGH}}$, which will depend on $\tau$, which is varied between two minutes and 100 hours in 1000 steps that are multiples of one minute and are spaced quasi-logarithmically. This analysis was also extended back to sub-minute timescale using the 16-second ACE data, which are averaged over intervals of $\tau = 32$ and 48 seconds.

Figure 9 shows the effect of averaging on gardenhose flux and on $F$_OGH. The black line in the top panel shows the unsigned radial flux fraction for OGH flux [$F$_OGH] as a function of $\tau$. The red and blue lines show the variations of the corresponding values for data taken in three-year intervals around sunspot maximum and sunspot minimum, respectively. As expected, the cancellation of opposite-polarity $B _{X}$ and $B _{Y}$ within averaging intervals causes a reduction in the width of the $\theta$-distribution peaks and a fall in the OGH flux with increasing $\tau$ (plotted in Figure 9a as $\log_{10}(\tau )$ to reveal the changes a low $\tau$). This fall is not the same at sunspot maximum as at sunspot minimum, and as noted above there is more OGH flux at sunspot maximum at low $\tau$. (Note that Figure 9a shows that at $\tau$ above about eight hours there is actually more OGH flux at sunspot maximum; this is explained below.) Figure 9b shows $N/\sum N$ colour-contoured as a function of $\theta$ and $\log_{10}(\tau )$, where $N$ is the number of samples in 90 bins of $\theta$ that are $\mathrm{d}\theta = 4^{\circ}$ wide, and $\sum N$ is the sum of $N$ over all bins. This plot demonstrates how increased $\tau$ sharpens and raises the peaks in the distribution of GH flux as the OGH flux is averaged out.

Figure 9

The effect of averaging on the distribution of gardenhose angle $\theta$ for $r = 1~\mbox{AU}$. For timescales $\tau \geq 1~\mbox{minute}$ ($\log_{10}(\tau~\mbox{in hours}) \geq 1.77$) the data used are one-minute averages from the Omni dataset for 1996 – 2017. Plots are extended to $\tau$ below one minute using 15-second averages of data from the ACE and Wind spacecraft for the same interval. Panel b shows $N/\sum N$ (where $N$ is counted in 4^∘-wide bins of HMF gardenhose angle [$\theta$]) colour-coded as a function of $\log_{10}(\tau~\mbox{in hours})$ and $\theta$. Panel a shows the fraction $[F]$ of the integrated total of the radial magnetic flux (toward or away) that is in a non-Parker-spiral Class-A or Class-B orientation (as defined by Figure 7a), as a function of $\log_{10}(\tau~\mbox{in hours})$: the black line is for all years, the red line for three-year intervals around sunspot maxima, and the blue line for three-year intervals around sunspot minima.

2.4 Spectra of OGH Flux Scale Sizes

Figure 9a demonstrates that increasing the averaging timescale from $\tau _{1}$ to $\tau _{2}$ causes a decrease in the OGH unsigned radial flux fraction as OGH flux is cancelled. However, the change in gradient in the plots tells us that some changes from $\tau _{1}$ to $\tau _{2}$ cause more flux loss than others, which in turn tells us about the amount of structure in the HMF giving OGH flux that is of scale between $\tau _{1}$ to $\tau _{2}$. This structure is cancelled by averaging in the time domain but as the time series is at a fixed point the temporal variation tells us about larger-scale temporal variations in the heliosphere around the point, or radial spatial structure that is moved over the location by the solar-wind flow, or tangential spatial structure rotated over the point by rotation of the heliosphere. For the radial structure, the spatial scale is related to the temporal scale $\tau$ by $V \tau$ (where $V$ is the solar-wind speed) and for the tangential structure it is related by $\omega r \tau$ (where $\omega$ is the angular velocity of heliospheric rotation relative to the observing platform).

Figure 10 analyses the spectrum of scales of all OGH flux (Class-A and Class-B flux combined) at $r = 1~\mbox{AU}$. The plots on the left-hand side use an $x$-axis that is linear in averaging timescale [$\tau$] the right-hand plots are the same, except that the $x$-axis is logarithmic. Figures 10a and 10b show $\Delta F$: the fraction of the total radial magnetic flux that is present at 16-second resolution that is lost by cancellation by averaging over an interval $\tau$ (by definition zero for the fundamental resolution of the data which is $\tau = 16$ seconds). The grey line is the observed value and the mauve line a sixth-order polynomial fit to smooth out the small numerical noise associated with the start times of the averaging intervals relative to features in the data. This noise gets greater at large $\tau$ because the number of available samples falls. The polynomial fit is actually generated using the $\log_{10}(\tau )$ variation shown in Figure 10b and then plotted on a linear scale in 10a as this captures the variation at small $\tau$ more satisfactorily. Figures 10c and 10d show the flux lost in increasing the averaging time between $\tau _{1}$ and $\tau _{2}$ [$\delta F$]; in Figure 10c the area shaded grey is made up of vertical bars of height $\delta F$ between $\tau _{1}$ and $\tau _{2}$ and in Figure 10d the bars are again of height $\delta F$ but between $\log_{10}(\tau _{1})$ and $\log_{10}(\tau _{2})$. In this way, the total area shaded grey in both plots equals the total fraction of radial unsigned OGH flux data that is lost by averaging over intervals of duration $\tau = 100$ hours and the shapes of the grey areas allow us to identify what timescales [$\tau$] contribute most to this loss, and hence gives the spectrum of scale sizes of the OGH flux. The linear plot (Figure 10c) allows us to see the structure at high $\tau$ most clearly, while the logarithmic plot (Figure 10d) reveals structure at low $\tau$. In each panel vertical blue lines are drawn for $\tau = 1$ hour and $\tau = 50$ hours for reference. To interpret the spectra we note that $\tau = 1$ hour corresponds to a tangential structure scale length of $1.55\times 10^{6}~\mbox{km}$ (i.e. 0.01 AU, 2.2 $\mathrm{R}_{\odot}$, or 243 $R _{\mathrm{E}}$, where $\mathrm{R}_{\odot}$ is a solar radius and $R _{\mathrm{E}}$ is a mean Earth radius or an angular width of 0.6^∘ subtended at the Sun); $\tau = 50$ hours corresponds to a tangential structure scale length of $7.74\times 10^{7}~\mbox{km}$ (i.e. 0.5 AU, 111 $\mathrm{R}_{\odot}$, 12145 $R _{\mathrm{E}}$, or an angular width of 30^∘). These distances also apply to radial structure for a radial solar-wind velocity of 430 km s⁻¹ (which makes $\theta _{\mathrm{p}} = 45^{\circ}$ for T-flux and −135^∘ for A-flux).

Figure 10

Analysis of the structure scale of all non-Parker-spiral (Class-A and Class-B flux combined) at $r = 1~\mbox{AU}$. The plots on the left-hand side use an $x$-axis that is linear in averaging timescale [$\tau$], the right-hand plots are the same, other than the $x$-axis is logarithmic. Panels a and b show $\Delta F$, the fraction of the total radial magnetic flux that is lost by cancellation by averaging over an interval $\tau$ (by definition zero for the fundamental resolution of the data which is $\tau = 1$ minute). The grey line is the observed value and the mauve line a sixth-order polynomial fit to smooth out the small numerical noise associated with the start times of the averaging intervals relative to features in the data. (Note that the fit is generated using the $\log_{10}(\tau)$ variation shown in Panel b). Panels c and d show the flux lost in increasing the averaging time between $\tau _{1}$ and $\tau _{2}$ [$\delta F$]: in c the area shaded grey is made up of vertical bars of height $\delta F$ between $\tau _{1}$ and $\tau _{2}$ and in d the bars are again of height $\delta F$ but between $\log_{10}(\tau _{1})$ and $\log_{10}(\tau _{2})$. In this way, the total area shaded grey in both plots equals the total fraction of radial OGH flux in one-minute data that is lost by averaging over intervals of duration $\tau = 100$ hours, and the shapes of the grey areas allow us to identify what timescales $[\tau]$ contribute most to this loss, and hence gives the spectrum of scale sizes of the OGH flux. The linear Panel c allows us to see structure at high $\tau$; the logarithmic Panel d reveals structure at low $\tau$. In each panel vertical blue lines are drawn for $\tau = 1$ hour and $\tau = 50$ hours for reference.

Figures 10c and 10d show a clear peak at around $\tau = 8$ hours, which corresponds to a distance of about 0.08 AU or an angular width of about 5^∘. Figure 11 is the equivalent of Figures 10c and 10d, again for $r \approx 1~\mbox{AU}$, and for (top panels) data taken within one year of sunspot minimum; and (bottom panels) data taken within one year of sunspot maximum. The spectra are considerably different. Figures 11a and 11b show that the peak at $\tau = 8~\mbox{hours}$ is a sunspot-minimum phenomenon that is not seen a sunspot maximum for which, instead, there is an almost flat plateau rising up to a mode value of about $\tau = 40~\mbox{hours}$. We conclude that there are significantly more large structures contributing to OGH flux at sunspot maximum and because they last up to almost two days these appear to be the effect of large CMEs.

Figure 11

The same as Figures 10c and 10d for (top) data at $r = 1~\mbox{AU}$ within one year of sunspot minimum and (bottom) one year of sunspot maximum. In each panel, the area shaded grey gives the flux lost in increasing the averaging time between $\tau _{1}$ and $\tau _{2}$ [$\delta F$]: a and c show vertical bars of height $\delta F$ between $\tau _{1}$ and $\tau _{2}$ and in b and d the bars are again of height $\delta F$ but between $\log_{10}(\tau _{1})$ and $\log_{10}(\tau _{2})$. Panels a and b are for observations in a three-year interval around sunspot minimum (the years 1996, 1997, 2007, 2008, 2009, and 2017); c and d are for observations in a three-year interval around the sunspot maxima (the years 2000, 2001, 2002, 2012, 2013, and 2014). In each panel vertical blue lines are drawn for $\tau = 1~\mbox{hour}$ and $\tau = 50~\mbox{hours}$ for reference.

Figure 12 shows a similar difference in the data $r \approx 1~\mbox{AU}$ when the Class-A and Class-B OGH flux are compared. An obvious difference between the two is that there is less Class-B OGH flux to lose, but this is not surprising because for Class-B the field is deflected towards and past the tangential direction, for which the $B _{X}$ component is zero, whereas Class-A is deflected towards and past the radial direction for which $|B _{X}|$ is large. Comparing the shapes of the spectra the peak around $\tau = 8$ hours is again present but only for the Class-A flux and Class-B exhibits a plateau between 8 hours and 50 hours, suggesting a wide range of ejecta, from blobs to large CMEs are involved.

Figure 12

The same as Figures 10c and 10d for (top) Class-A flux and (bottom) Class-B flux at $r = 1~\mbox{AU}$, as defined by the pink and pale blue areas, respectively, in Figure 8a. In each panel, the area shaded grey gives the flux lost in increasing the averaging time between $\tau _{1}$ and $\tau _{2}$ [$\delta F$]: a and c show vertical bars of height $\delta F$ between $\tau _{1}$ and $\tau _{2}$ and in b and d the bars are again of height $\delta F$ but between $\log_{10}(\tau _{1})$ and $\log_{10}(\tau _{2})$. Panels a and b are for Class-A OGH flux; c and d are for Class-B OGH flux. In each panel vertical blue lines are drawn for $\tau = 1~\mbox{hour}$ and $\tau = 50~\mbox{hours}$ for reference.

2.5 Spectra of OGH Flux Scale Sizes at $r < 0.39~\mbox{AU}$

Figure 13 repeats Figure 12 for the Helios data taken near perihelion. In order to keep sample sizes high enough at large $\tau$, the Class-A and Class-B bin widths have been increased, as shown in Figure 8b. This increases the number of samples but does not have a strong influence on the spectral shape. The pink and pale blue areas in Figure 8a define the Class-A and Class-B OGH flux. The divider between them is at the orthogonal to the average Parker-spiral direction. The ranges of $\theta$ covered by the pink and pale-blue areas in Figure 8b have been expanded in width to cover some of the GH sectors as well as the OGH sectors to allow for the fact that the distributions in the GH sectors are narrower: again the divider between them is the orthogonal to the average spiral direction but the width of the A- and B-bins has been increased until the total fraction of $\tau = 30~\mbox{hour}$ samples in such bins is the same as for the A- and B-ranges in the $r = 1~\mbox{AU}$ data shown in Figure 8a. This somewhat arbitrary choice is only relevant to Figure 13, and the change to the bin width is made to ensure that the number of samples available for analysis at large $\tau$ (30 – 100 hours) is comparable in the two cases. The required Class-A and Class-B sector width is 72^∘ in Figure 8b, as opposed to the bins of near 45^∘ width in Figure 8a.

Figure 13

The same as Figures 10c and 10d for (top) Class-A flux and (bottom) Class-B flux observed by the Helios spacecraft at $r < 0.39~\mbox{AU}$, as defined by the pink and pale blue areas, respectively, in Figure 8b. In each panel, the area shaded grey gives the flux lost in increasing the averaging time between $\tau _{1}$ and $\tau _{2}$ [$\delta F$]: a and c show vertical bars of height $\delta F$ between $\tau _{1}$ and $\tau _{2}$ and in b and d the bars are again of height $\delta F$ but between $\log_{10}(\tau _{1})$ and $\log_{10}(\tau _{2})$. Panels a and b are for Class-A OGH flux; c and d are for Class-B OGH flux. In each panel vertical blue lines are drawn for $\tau = 1$ hour and $\tau = 50$ hours for reference.

Because the spacecraft is at smaller $r$, (where the solar-wind speed is lower), all of the spatial distances for a given $\tau$ are decreased pro-rata, except the angular tangential widths for the same $\tau$. The peak of the spectrum for Class-A for these near-Sun observations is around three hours (corresponding to an angular width of just under 2^∘). This implies that the structures giving Class-A OGH expand from about 2^∘ to about 5^∘ in propagating from about 0.3 AU to about 1 AU. Kilpua et al. (2009) report measurements of structures that they argue are consistent with being the in-situ manifestation of the blobs observed remotely (at approximately 3 – 30 $\mathrm{R}_{\odot}$) by Sheeley et al. (1997) and have sizes that are reasonably consistent with the dominant scale sizes found here. Kepko et al. (2016) report blobs, which last of order 1.5 hours, which is a bit smaller than the scale of OGH flux that we find. This may, however, not be inconsistent as the OGH scale is the scale of field-line draping over the blob and not of the blob itself.

On the other hand, Panels c and d of Figure 13 are not greatly dissimilar from the corresponding plots in Figure 12, although rather than the plateau there is a suggestion of two peaks at $\tau$ near 1 hour and 35 hours.

3 Discussion and Conclusions

The survey presented here shows there is an approximately linear growth in the non-Parker-spiral component of the HMF with radial distance. The available data suggest significant non-Parker-spiral fields, if not actually present at the source surface, are established in the very early evolution of the solar wind. By $r \approx 0.3~\mbox{AU}$ roughly half of the deflection needed to give the OGH at Earth is present. In this article, we have projected the trends to $r < 0.3~\mbox{AU}$, using simple empirical extrapolation. However, remote sensing observations (DeForest et al., 2016) suggest that the deflection by waves and turbulence on small spatial scales grows rapidly between 0.07 and 0.3 AU, and so this extrapolation may well not be valid. Parker Solar Probe will help define the role of waves and turbulence by observing the radial evolution of the fraction of flux that is OGH-orientated.

Perhaps surprisingly, OGH flux at sunspot maximum is found to be rarer than at sunspot minimum. This may well be because OGH flux generation by draping is more effective when events are isolated. We have also shown that the spectra of OGH scale sizes are significantly different at sunspot minimum and maximum. The peak at sunspot minimum is at a scale of about ten hours which, if it were due to the draping over transients, is broadly consistent with the effect of draping over, and/or release of, transient blobs (Kilpua et al., 2009; Kepko et al., 2016). From the remote-sensing data, the occurrence of blobs appears to be rather even across the solar cycle in the Ecliptic plane (e.g. Luhmann, Petrie, and Riley, 2013) which makes it surprising that the small-scale (of order ten hours) OGH structure at sunspot minimum is so very much greater than at sunspot minimum if transient blobs are the only cause.

At sunspot maximum, structure at a scale of ten hours is again observed, but with much lower amplitude than at sunspot minimum. The overall spectrum has a quite different shape in this case, with amplitude increasing weakly with increasing timescale up to a mode value of about 40 hours. This is greater than the mode of the distribution of durations of coronal mass ejection (CME) events which is of order 20 hours (Mitsakou and Moussas, 2014), but, as for the blobs, this is likely to represent the difference between the characteristic scale of the draping region and the scale of the structure that the field is draped around.

We have also found a similar difference between OGH flux that is Class-A (rotated through the radial) and Class-B (rotated through the tangential). Figures 4b and 4c suggest that CMEs, blobs, and fast streams will predominantly generate Class-B OGH flux and this is consistent with the idea that these are the predominant drivers of sunspot-maximum OGH flux.

The Class-A OGH flux at small scales (ten hours or less) is particularly common at sunspot minimum, and at both $r = 1~\mbox{AU}$ and at $r = 0.3~\mbox{AU}$. As illustrated by Figure 4c, Class-A OGH can be generated by CMEs because they expand as they propagate. However, because this effect would increase in magnitude and scale with increased $r$, this does not appear to be a candidate driver for this Class-A OGH flux. A much more likely candidate is suggested by our studies of sunward strahl-electron flows, namely that this Class-A OGH is caused by magnetic reconnection in the corona, as shown schematically in Figure 4d. This makes some specific suggestions that can be tested by Parker Solar Probe. The Class-A OGH flux in reconnection outflow regions will be Alfvénic disturbances emanating from the reconnection site and standing in the inflow regions. Owens et al. (2018) have recently used isotopic abundances to infer that this reconnection can occur right down in the low corona with open flux reconnecting with hot, dense coronal loops. Hence the outflows detected by Owens et al. (2018) are likely to be from the “interchange” reconnections that allow corotation of the corona. At greater $r$, at the coronal source surface and beyond, reconnections associated with the main (tilted) heliospheric current sheet (HCS) will be present and these give loss of open flux by disconnection at a rate that varies over the solar cycle with the tilt of the HCS (Owens, Crooker, and Lockwood, 2011). Lockwood et al. (2017) point out that the HCS is highly unlikely to have a sharp inner edge at the source surface and propose that with decreasing $r$ within the corona, the main HCS increasingly breaks up into a network of smaller-scale sheets, an idea that can be merged with the “S-Web” concept of slow solar-wind origin (Antiochos et al., 2011). This would be a mixture of both disconnection and interchange reconnections and would cause a spreading of the source locations of the reconnection outflows away from the sector boundaries and to within the HMF sectors. Hence, we predict that at perihelion Parker Solar Probe is likely to find considerable mixtures of near-radial T- and A-field within the classic HMF sectors. These will usually be Alfvénic structures being the outflow regions of coronal reconnection sites and may often be associated with sunward strahl, OGH field orientations, and, for the lowest $r$ interchange reconnections, hot and dense plasma. The reconnections, and their outflow regions, will often be transient in nature but could be persistent, corotating structures such as on coronal-hole boundaries. In general, these Alfvénic structures will be smoothead out with increasing $r$ by the curvature force of the reconnected field lines; however, as pointed out by Owens et al. (2018), in the case of the lowest-$r$ reconnections, the field rotation may be embedded in slow solar wind that is outrun by the fast flow on either side of it and the structure persists right out to, and past, 1 AU. If for the majority of cases, the curvature force does smooth-out the field structure, the dominant field polarity of the sector emerges more clearly as $r$ increases. If these interchange reconnections in the corona are indeed the origin of the Class-A OGH detected here at both 1 AU and by the Helios spacecraft, Parker Solar Probe would see the variations with $r$ predicted here by the simple model presented.