Systems Approach to Polarization Calibration for the Daniel K. Inouye Solar Telescope (DKIST)

Abstract

The Daniel K. Inouye Solar Telescope (DKIST) advances studies of solar magnetism through high-precision and accuracy in polarimetry at frontier spatial and temporal scales. A system model for polarization response in azimuth and altitude has been developed to calibrate DKIST instruments. The DKIST team has developed several new modeling and performance-estimation techniques coupled with thorough metrology. These efforts ensure that quality polarimetry is delivered to meet stringent accuracy requirements. A custom spectropolarimetric calibration system was designed, installed, and used to perform end-to-end calibration of the telescope using the beam within the Cryo-NIRSP instrument. Extensive optical and polarization characterization efforts allow for the reduction of systematic errors within a detailed system model that includes elliptical calibration retarders. Coating witness samples for every relevant optic in the system have been measured. Aperture-dependent variations in polarizer, retarder, and optic-coating performance have been measured and used to simulate both the polarization dependence on field angle and errors within the optical-system model. Multiple observations on-Sun and with a calibration lamp agree well with each other and with the system model. Upcoming multi-instrument observations are expected to be well calibrated with detailed understanding of major error limitations.

1 Introduction: DKIST and Polarization Models for Calibration

The National Science Foundation’s (NSF’s) Daniel K. Inouye Solar Telescope (DKIST) on Haleakalā, Maui, Hawai´i, USA, is presently beginning early operations. An observatory-level summary is given by Rimmele et al. (2020). The wide array of science topics that DKIST will address in the upcoming years is described in the Critical Science Plan (Rast et al., 2021). This article summarizes the current polarization-calibration model for DKIST instruments released as part of the commissioning phase. We present new on-Sun system-polarization calibrations, create an improved system model, and compare them with our prior calibration efforts. We collect all of the required mathematics and nominal procedures to summarize the current state of the DKIST system calibrations along with ongoing metrology and system-modeling improvements. In addition, we present two new, upgraded calibration optics, and we outline improvements anticipated for the upcoming commissioning phases. The successful suppression of interference fringes in the polarized data for two of the DKIST instruments is highlighted using the preliminary science-verification data.

Each optical component in a telescope will modify the polarization properties of the incoming light source. The combined effect of all optical elements on the incoming flux must be quantified. Telescopes that are articulated along certain axes such as azimuth and elevation can be calibrated using a pointing-dependent system model. The goal of a system-polarization calibration is then to transform the polarization components measured at a sensor back to the original components from the astronomical source. Often this calibration includes additional functional dependencies such as field-scanning position, modulator-rotational position, filter position, slit width and position, optical offset from adaptive-optics (AO) lock point, instrument-alignment offset from optical bore-sight, etc.

DKIST uses six mirrors to relay solar light into a rotating coudé platform and environmentally controlled laboratory, providing flexible instrumentation capabilities (Rimmele et al., 2020). Additional details are given by Rimmele et al. (2004), Keil et al. (2011), Elmore, Sueoka, and Casini (2014), Elmore et al. (2014), Marino, Carlisle, and Schmidt (2016), McMullin et al. (2016), Johnson et al. (2016), Sekulic et al. (2016a), Hubbard, Craig, and Kneale (2016). The first two system mirrors (M1 and M2) comprise the off-axis Gregorian telescope. Figure 1 of Rimmele et al. (2020) shows the full telescope structure while Figure 3 shows the optical beam from M1 through M10. DKIST has a Gregorian Optical System (GOS) with calibration optics, apertures, and targets built around the Gregorian Focus (GF). The GOS also contains retarders, polarizers, and an artificial light source at other levels above the GF (Elmore et al., 2010; Elmore, 2010; Ferayorni et al., 2014; Sueoka, Chipman, and Elmore, 2014; Elmore, Sueoka, and Casini, 2014; Sueoka, 2016; Kootz, 2018). The GOS is seen in Rimmele et al. (2020, Figures 7 and 8). Mirrors M3 through M6 include the altitude and azimuth rotation axes. Three more static mirrors (M7 through M9) level and collimate the beam in the coudé laboratory. See Rimmele et al. (2020, Figures 9 through 12) for details.

The DKIST active-optics system (aO) and adaptive-optics systems (AO) coordinate alignment and wavefront correction of the beam delivered to the instruments (Richards et al., 2010; Johnson et al., 2012, 2014, 2016; Marino, 2012; Marino, Carlisle, and Schmidt, 2016; Schmidt et al., 2016a). The quality of the time-dependent active alignment is important for maintaining a stable optical beam and preserving polarization performance. M3, M5, and M6 are all part of the aO system and are controlled in tip and tilt for beam alignment. The aO system also influences the shape of M1 and uses six axes of control for M2. From a calibration standpoint, the DKIST optics and their active alignment can be split into a few functional sub-groups that logically divide up the articulated-system model.

Three polarimetric instruments are installed in the coudé laboratory currently spanning the 380 nm to 5000 nm wavelengths. The Visible Spectro-Polarimeter (ViSP) is a three-arm, slit-based spectropolarimeter currently available for science observation, and summarized by de Wijn et al. (2022). The Diffraction-Limited Near Infrared Spectro-Polarimeter (DL-NIRSP) is a fiber-optic-based integral-field spectropolarimeter (Jaeggli et al., 2022). The Cryogenic Near Infrared Spectro-Polarimeter (Cryo-NIRSP) is a slit-based system optimized for the infrared (Fehlmann et al., 2023). A fourth instrument called the Visible Tunable Filter (VTF), planned for installation, is a tunable Fabry–Perot type imaging spectropolarimeter (Schmidt et al., 2014, 2016b). DKIST also has two high-speed (30 Hz) 4k full-frame cameras within the Visible Broadband Imager Red and Blue instruments (VBI-red and VBI-blue), described by Wöger et al. (2021) and other references (Ferayorni, 2012; Wöger and Ferayorni, 2012; McBride et al., 2012; Wöger, 2014; Ferayorni et al., 2016; Beard, Cowan, and Ferayorni, 2014; Sekulic et al., 2016b). We use the VBI camera system for certain polarization alignments.

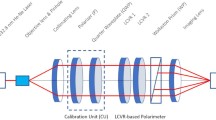
Cryo-NIRSP can receive all wavelengths to 5000 nm and beyond by using a pick-off mirror called M9a, insertable at a station downstream of M9. This current M9a optic excludes Cryo-NIRSP from simultaneous use of the AO system. An upgrade to allow simultaneous use of Cryo-NIRSP with other instruments using a new type of dichroic beam splitter is in progress. If M9a is not inserted in the beam, the next mirror, M10, is the deformable mirror (DM) for the AO system. Following the DM, a sequence of dichroic beam splitters, windows, and/or mirrors, called the Facility Instrument Distribution Optics (FIDO), allows changing of instrument configurations on a timescale of less than half an hour. The FIDO optics allow simultaneous operation of VBI and the three polarimetric instruments (ViSP, DL-NIRSP, VTF) optimized for 380 nm to 1800 nm, while using the facility AO system for correction to provide diffraction-limited performance (Socas-Navarro et al., 2005; Richards et al., 2010; Elmore, Sueoka, and Casini, 2014; Elmore et al., 2014; Schmidt et al., 2014). We show a cartoon optical layout for the coudé-laboratory optics and instruments in Figure 1.

Figure 1

An optical layout cartoon showing the coudé-laboratory optics. The beam enters the laboratory and is leveled by M7. The optic M8 roughly collimates the beam (F/4500). The Cryo-NIRSP (CN) pickoff station is shown in green with optic choices M9a mirror and M9b dichroic (upcoming upgrade). Cryo-NIRSP itself has a spectropolarimeter (SP) channel and context imager (CI) channel. The National Solar Observatory Coudé lab Spectro-Polarimeter (NCSP) picking off the Cryo-NIRSP beam is shown in red. The Deformable Mirror (DM) is the tenth mirror in the system (M10). The wavefront correction system (WFC) is shown in light blue. WFC has both High-Order (HO) and Low-Order (LO) wavefront sensors (WFS) in addition to a context-viewer camera. The FIDO optical stations are denoted numerically as Coudé Lab (CLn), where $n$ is an alpha-numeric identifier (2, 2a, 3, 3a, 4). The FIDO beam splitters, mirrors, and windows distribute light to the instruments: VBI-Red, VBI-Blue, ViSP, VTF, and DL-NIRSP. Each of the instruments ViSP, VTF, and DL-NIRSP have three separate cameras within performing different spectropolarimetric measurement techniques.

Accurate polarimetry is a key design driver for DKIST. Polarimetric accuracy is particularly important in cases where the linearly and circularly polarized signals produced by the Sun do not have similar intensities and are susceptible to even small levels of crosstalk from instrumental polarization. The circularly polarized signals from coronal emission lines are smaller than the linearly polarized signals by about a factor of ten in active regions, and provide critical information on the magnetic-field strength along the line of sight. Mitigation and correction of polarization will allow for studies of the coronal magnetic field without having to resort to ad-hoc techniques that enforce particular assumptions about the line- and continuum-formation physics (Lin, Kuhn, and Coulter, 2004; Schad, Jaeggli, and Dima, 2022).

The component of the photospheric magnetic field perpendicular to the line of sight produces weak linear polarization signals in close proximity to stronger circular-polarization signals from fields along the line of sight (e.g. Lites et al., 2008). Accurate polarimetry is also required to properly characterize small changes in strong polarization signals. Small deviations from non-local-thermodynamic equilibrium in the Sun’s lower atmosphere cause subtle changes in the polarization of spectral lines, but are important for the interpretation of spectropolarimetric measurements using advanced radiative-transfer-based modeling (Ariste, 2002). The accurate polarimetry that DKIST provides will enable much deeper physics-based interpretation of the polarized signals produced by the Sun.

Several types of polarization modulation and calibration strategies are required for multi-instrument systems (Elmore et al., 2010; de Wijn et al., 2012; Elmore, Sueoka, and Casini, 2014; Elmore et al., 2014; Sueoka, Chipman, and Elmore, 2014; Schubert, Petrak, and Baur, 2015). The four-meter, on-axis European Solar Telescope (EST) project will also require similar calibration considerations (Sánchez-Capuchino et al., 2010; Bettonvil et al., 2010; Collados et al., 2010). Many solar and night-time telescopes have performed detail-oriented polarization calibration of complex many-mirror pathways using various techniques to achieve precision solar-continuum polarimetry, stellar photopolarimetry, planet finding, etc. (Sánchez Almeida, Martínez Pillet, and Wittmann, 1991; Sánchez Almeida and Martínez Pillet, 1992; Sánchez Almeida, 1994; Stenflo et al., 1997; Keller, 2003; Schmidt et al., 2003; Strassmeier et al., 2003; Spano et al., 2004; Beck et al., 2005a,b; Socas-Navarro, 2005a,b; Hough et al., 2006; Snik, 2006; Bailey et al., 2008; Snik et al., 2008; Joos et al., 2008; Strassmeier et al., 2008; Bianda, Ramelli, and Gisler, 2009; Keller and Snik, 2009; Keller et al., 2010; Roelfsema et al., 2010; Bianda et al., 2011; Socas-Navarro et al., 2011; Bazzon et al., 2012; Rodenhuis et al., 2012; Schmid et al., 2012; Snik et al., 2012; Wiktorowicz et al., 2012; Roelfsema et al., 2013; Stenflo, 2013; de Juan Ovelar et al., 2014; Wiktorowicz et al., 2014; Harrington et al., 2015; Perrin et al., 2015; Gisler, Berkefeld, and Berdyugina, 2016; Millar-Blanchaer et al., 2016; Roelfsema et al., 2016; Schmid et al., 2018; Bailey et al., 2020; de Boer et al., 2020; Kleint et al., 2020; Piirola et al., 2020; van Holstein et al., 2020; Ballester, Belluzzi, and Bueno, 2021; Zeuner et al., 2022). Polarization-calibration optics are commonly mounted as far up the optical path as feasible to inject signals of known properties through the system. In the case of DKIST, calibration optics are mounted upstream of the Gregorian focus, after the secondary mirror but before the tertiary mirror. Modulators of different types are included within the instruments.

Characterizing and/or modeling the polarimetric response of an articulated system is limited in accuracy by systematic behavior of the system optics and calibration optics. As described above, the DKIST system contains many diverse optical systems. For an accurate calibration, the calibration optics (i.e. the retarder and polarizer) must be stable and known very accurately to minimize systematic errors in any system calibration. DKIST has invested heavily in the development of large-aperture optics with stringent performance specifications. This includes ongoing retarder and polarizer improvements. Misalignment of retarder components produces spectral oscillations in retardance. This in turn introduces coupling between temperature changes and the spectral drift of these elliptical-retardance oscillations (Harrington et al., 2020, 2021a).

We developed new metrology tools to measure spatial variation of the Mueller-matrix elements across optics with apertures over 150 mm. This equipment measures spatial variations of transmission to better than 0.01%, polarizer contrast ratios in excess of 100,000, and orientation changes in the polarizer extinction axis at levels below $0.002^{\circ}$. These parameters have been included in an optical model of DKIST. We combined these polarizer imperfections (transmission, contrast, extinction angle) with spatial variations of the calibration retarders (transmission and elliptical retardance).

We showed in Harrington et al. (2021a) successful on-Sun use of an optically contacted calibration retarder using a new time-efficient, ten-state calibration sequence. We extend our development work here by showing improved optical-contacting techniques using MgF₂ crystals to minimize thermal impacts. We present here a new design and fabrication progress for a new elliptical calibration retarder to cover the 380 nm to 5000 nm bandpass using two optically contacted MgF₂ crystal pairs. We also describe here the development and installation of a new spatially uniform calibration polarizer recently deployed at the telescope.

The optical metrology, efficient calibration sequence, and elliptical retarders can be synthesized in a system-performance model. The model shows how large of a field any particular instrument can observe at any particular wavelength before the polarization error-matrix terms grow larger than a user-specified error threshold. We highlight estimates for the calibration-accuracy impact using our newly measured calibration-polarizer optical properties including spatial variations across individual beam footprints as well as mis-alignments in a Mueller-matrix propagation model (see Harrington et al., 2021b).

Further error terms in a polarimetric system model can include the role of strong aperture- and/or spectral-dependent gradients in polarimetric response. We have measured polarization response for every single coated optic contributing significantly to the system model, as a function of incidence angle over a broad wavelength range. These measurements are detailed in our prior works (Harrington, Kuhn, and López Ariste, 2017; Harrington and Sueoka, 2017; Harrington, Sueoka, and White, 2019; Harrington et al., 2021a,b) and are outlined in the Appendix. We include special consideration for dichroic beam splitters within the FIDO system due to narrow spectral features and very strong spectral changes in polarization due to thick coatings in Harrington et al. (2021c).

In Section 2, we describe the mathematics and assumptions of the DKIST articulated system model. In Section 3, we present a new system calibration using on-Sun observations. We use the solar beam and a dedicated custom metrology tool called the National Solar Observatory Coudé lab Spectro-Polarimeter (NCSP), described by Harrington et al. (2021a). The NCSP metrology system has determined the optical parameters constraining the system polarization model using both the Gregorian focus calibration lamp and the solar beam itself. We show the first-ever fits to the DKIST primary- and secondary-mirror polarization over the first-light bandpass. We compare this new on-Sun calibration to our prior work calibrating DKIST and show very close agreement between system models derived both on-Sun and with the system calibration lamp.

Spectral-interference fringes also adversely impact polarization accuracy for astronomical instruments requiring optical-fringe modeling and/or removal methods through design and data processing (Heavens, 1965; Harries and Howarth, 1996; Aitken and Hough, 2001; Semel, 2003; Schmidt et al., 2003; Clarke, 2004a,c,b; Beck et al., 2005b; Clarke, 2005, 2009; Rojo and Harrington, 2006; Casini, Judge, and Schad, 2012; Snik et al., 2012; Harrington et al., 2015; Snik et al., 2015; Derks, Beck, and Martínez Pillet, 2018; Casini and Li, 2019). We designed and built several newly upgraded polarization optics based on fringe-suppression techniques described in our prior works (Harrington and Sueoka, 2018a; Harrington et al., 2020). We show in Section 4 the suppression of fringes within the ViSP instrument below currently detectable levels, using the first on-Sun observations. We also show here the first fringe-suppression results from DL-NIRSP observations. Fringe-suppression dependence on coatings and beam focal ratio are outlined. In Section 5, we show fringe suppression in calibration retarders using an optically contacted quartz retarder and relate these fringe magnitudes to the successful suppression of fringes in the preliminary ViSP on-Sun calibration and commissioning data. We outline a new, upgraded elliptical MgF₂ calibrator design and performance that was installed in late 2022.

We end with a detailed Appendix showing the system-performance model and metrology campaign results along with metrology of our new, upgraded calibration polarizer. Correlated errors coupling between the system-model variables and the initial fits to the DKIST system model with an imperfect alignment of a calibration polarizer are shown. The appendices detail changes in the system error-matrix and instrument-modulation matrix errors. We also include the first primary- and secondary-mirror polarization fits.

2 A System Model

In this section we show how we transfer solar Stokes vectors through the articulated optical system, modulate the flux in an instrument, and calibrate the measured intensities. We provide the baseline DKIST calibration procedure and show some options that we explored for optimizing this procedure. We finish this section with a definition of the error matrix, which is used to assess the accuracy of the calibrated Stokes vectors. We note that we must provide a system polarization model for every wavelength used by DKIST, currently observing from 380 nm to 5000 nm, with upgrades extending this bandpass anticipated.

2.1 Transfer Matrices: Mueller and Berreman

$$ \mathbf{M} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} II & QI & UI & VI \\ IQ & QQ & UQ & VQ \\ IU & QU & UU & VU \\ IV & QV & UV & VV \end{array}\displaystyle \right ) $$

(1)

There are two main transfer formalisms that we use to propagate polarized light through the DKIST system model: Mueller and Berreman. The Mueller matrix is the $4\times4$ matrix shown in Equation 1 that transfers Stokes vectors $[I,Q,U,V]^{T}$ between input and output (Collett, 1992; Chipman, 2010a,b; Chipman, Lam, and Young, 2018). With this formalism, the Stokes vector originating from some patch of the solar atmosphere would be transferred by the Mueller matrix of each optic between the Sun and the sensor to the final Stokes vector incident on the sensor. See the textbook Polarized Light and Optical Systems by Chipman, Lam, and Young (2018).

The textbook Birefringent Thin Films and Polarizing Elements by McCall, Hodgkinson, and Wu (2014) summarizes the Berreman calculus (Berreman, 1972; McCall, Hodgkinson, and Wu, 2014), which uses a $4\times4$ transfer matrix of electric- and magnetic-field components to compute transmission and reflection, including interference effects from both forward- and backward-propagating waves. This Berreman calculus is limited to infinite plane-wave solutions, but it is very useful for assessing fringes, coatings, and propagation in birefringent media. We use it extensively in our crystal-tolerance analysis and in fitting optical-coating properties. The Berreman calculus is used to calculate a Mueller matrix for an optic at some individual wavelength and incidence angle, which accounts for the interference effects within internal components such as coatings, bonding layers, or multiple stacked crystal retarders. The optic Mueller matrix can then be used in optical-propagation simulations.

2.2 Optical Elements of a System Model

Each major grouping of optics requires specification of a Mueller matrix to transfer the Stokes vectors through the optics. We show here the equations for a group of mirrors, a linear polarizer, and an elliptical retarder.

2.2.1 Mirror Grouping and Intensity Normalized Mueller Matrix Equations

We create a physical model for the Mueller matrix of the mirrors as installed between the various mechanical rotation axes. For mirrors that share a plane of incidence, the individual mirror Mueller matrices are combined by grouping into a single common Mueller matrix. We call this process the group model. A fundamental assumption of the group model is that the mirrors can have their Mueller matrices combined and fit with a greatly reduced number of variables.

Many solar telescopes use a Mueller matrix for a grouping of mirrors using ($X,\tau$) variable style. The $X$-term relates to the diattenuation for a mirror-group, and $\tau$ is the retardance for the mirror-group (Capitani et al., 1989; Makita, Funakoshi, and Polarimetry, 1991; Skumanich et al., 1997; Kiyohara et al., 2004; Beck et al., 2005a,b; Hanaoka, 2009). For mirrors that share a plane of incidence, the individual retardance and diattenuation terms simply add together. We also show how this solar-telescope-style formalism relates to a reflectivity and phase formalism common in physical optics. Switching between conventions allows us to compare reflectivity, diattenuation, and retardance for mirror Mueller matrices (Chipman, 2010a,b; Chipman, Lam, and Young, 2018). We adopt a standard notation where the P- and S- polarization states represent incoming linear-polarization states parallel and perpendicular to the plane of incidence, respectively. Their reflectivity is denoted as $R_{\mathrm{p}}$ and $R_{\mathrm{s}}$ respectively, and their average is denoted as $R_{\mathrm{avg}}$. Retardance is denoted as $\delta$, which has the same meaning as $\tau$ in the solar telescope ($X,\tau$) convention.

$$ {\mathbf{M}}_{\mathrm{ij}} = R_{\mathrm{avg}} \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & \Delta & 0 & 0 \\ \Delta & 1 & 0 & 0 \\ 0 & 0 & \frac{\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}}}{R_{\mathrm{avg}}}C_{ \delta }& \frac{\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}}}{R_{\mathrm{avg}}}S_{ \delta } \\ 0 & 0 & - \frac{\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}}}{R_{\mathrm{avg}}}S_{ \delta }& \frac{\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}}}{R_{\mathrm{avg}}}C_{ \delta } \end{array}\displaystyle \right ) $$

(2)

$$ {\mathbf{M}}_{ij} = \frac{R_{\mathrm{s}} (1+X^{2})}{2}\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & \frac{1-X^{2}}{1 + X^{2}} & 0 & 0 \\ [7pt] \frac{1 - X^{2}}{1 + X^{2}} & 1 & 0 & 0 \\ [7pt] 0 & 0 & \frac{2X}{1 + X^{2}}C_{\tau }& \frac{2X}{1 + X^{2}} S_{\tau } \\ [7pt] 0 & 0 & \frac{-2X}{1 + X^{2}} S_{\tau }& \frac{2X}{1 + X^{2}} C_{ \tau } \end{array}\displaystyle \right ) $$

(3)

In Equation 2 we show the Mueller matrix for a mirror (or group of mirrors) folded along the +$Q$ plane. The $II$-element is the average of S and P linear-polarization-state reflectivities. We use an intensity-normalized convention for the Mueller matrix where the total transmission term is outside the matrix and $II=1$.

The retardance [$\delta = \tau$] is a term in the sine and cosine functions in the $UV$-rotation matrix of the lower-right quadrant. We have abbreviated these terms as ${C}_{\delta}$ and ${S}_{\delta}$ or ${C}_{\tau}$ and ${S}_{\tau}$. In the normalized Mueller matrix the $\frac{IQ}{II}$ and $\frac{QI}{II}$ terms are denoted as $\Delta$ representing a normalized reflectivity difference ratio (${R}_{\mathrm{s}} - {R}_{\mathrm{p}}$)/(${R}_{\mathrm{s}} + {R}_{\mathrm{p}}$). The lower-right $UV$ rotation-matrix terms are modified by the scale factor $\frac{\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}}}{R_{\mathrm{avg}}}$. Equation 3 shows the same Mueller matrix in a solar-telescope-type convention. A reflectivity ratio denoted $X$ is defined as $X = \sqrt{\frac{R_{\mathrm{p}}}{R_{\mathrm{s}}}}$. This can be computed from the $IQ$- or $QI$-elements of the intensity-normalized Mueller matrix ($IQ/II$ or $QI/II$). We divide out one of the polarized reflectivities and denote the upper $2\times2$ sub-matrix in terms of this intensity reflection coefficient $X$. Retardance is denoted by $\tau$.

Non-collimated (powered) beams introduce depolarization through an average over the range of incidence angles contained within the beam over the aperture. These terms are small and often ignored. For instance, we show in Harrington and Sueoka (2017) that the F/2 beam from the primary and the conversion to F/13 by the secondary introduce diagonal depolarization at levels below 0.2% when using realistic coating variables (Harrington and Sueoka, 2017). We ignore the nine depolarization variables in the Mueller matrix for now (Chipman and Lu, 1997; Chipman, 1999, 2003, 2005a,b, 2006, 2007; Deboo, Sasian, and Chipman, 2004; Noble, 2011; Noble, McClain, and Chipman, 2012). Mirror-tilt misalignments can introduce additional retardance and diattenuation variables, although we ignore these four variables.

2.2.2 Polarizer Mueller Matrices: Extinction Ratio and Intensity Normalization

$$ {\mathbf{M}}_{ij} = \frac{t_{\mathrm{pol}}(1+p_{y}^{2} )}{2} \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & \frac{1-p_{y}^{2}}{1+p_{y}^{2} } & 0 & 0 \\ \frac{1-p_{y}^{2}}{1+p_{y}^{2} } & 1 & 0 & 0 \\ 0 & 0 & \frac{2p_{y}}{1+p_{y}^{2} } & 0 \\ 0 & 0 & 0 & \frac{2p_{y}}{1+p_{y}^{2} } \end{array}\displaystyle \right ) $$

(4)

The normalized form of the Mueller matrix used to describe the DKIST calibration polarizer is given in Equation 4. A matrix form common in solar-telescope calibration is to describe the transmission of the more transmissive linear-polarization state as the transmission of the polarizer [$t_{\mathrm{pol}}$]. There is another variable as the ratio of horizontal and vertical polarization state transmission as $p_{y}^{2}$ relating to the imperfect extinction (contrast) of a polarizer. If the input Stokes vector is purely unpolarized as $[1,0,0,0]^{T}$ then we recover an output Stokes vector with a transmission $t_{\mathrm{pol}}(1+p_{y}^{2})/2$ and a vector $[1, 1-p_{y}^{2},0,0]^{T}$. We note that around 630 nm wavelength for the DKIST nominal values, we use $p_{y}^{2}$ of roughly $5\times 10^{-5}$ as shown in the contrast measurements of Harrington et al. (2021b, Section 2). Under these circumstances, the normalization puts the fit transmission modification at 0.005% due to the imperfect polarizer contrast. See Harrington et al. (2021a, Appendix D) for more details. We do include the ($1+p_{y}^{2}$) term with the polarizer-transmission function in the DKIST system model per Equation 4.

2.2.3 Retarder Mueller Matrices: Axis-Angle Rotation Matrix as Elliptical Retarder

Here we describe the elliptical-retarder models and rotation-matrix formalism that we use for describing retarders. A retarder represents a rotation in $QUV$-coordinates. As such, many rotation-matrix formalisms, such as Euler angles or Euler axis-angle representations of a rotation, all produce identical Mueller matrices. We choose the axis-angle formalism for convenience. In this formalism, a unit vector $\hat{\boldsymbol{e}}$ indicates the direction of an axis for the rotation, and the angle $\theta$ specifies the magnitude of the rotation about this axis. Only two numbers are needed to define the direction of a unit vector because the magnitude of $\hat{\boldsymbol{e}}$ is an implicit constraint. The equation for the rotation in matrix notation is thus a magnitude times the basis vector $\boldsymbol{r} = \theta \hat{\boldsymbol{e}}$. Alternatively, the three components of the vector can be specified and the magnitude computed from the vector components.

$$ {\mathbf{M}}_{ij} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 \\ 0 & \frac{r_{x}^{2}}{\theta ^{2}} + \frac{r_{y}^{2} + r_{z}^{2}}{\theta ^{2}} C_{\theta }& \frac{r_{x} r_{y}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) + \frac{r_{z}}{\theta} S_{\theta }& \frac{r_{x} r_{z}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) - \frac{r_{y}}{\theta} S_{\theta } \\ 0 & \frac{r_{x} r_{y}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) - \frac{r_{z}}{\theta} S_{\theta }& \frac{r_{y}^{2}}{\theta ^{2}} + \frac{r_{x}^{2} + r_{z}^{2}}{\theta ^{2}} C_{\theta }& \frac{r_{y} r_{z}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) + \frac{r_{x}}{\theta} S_{\theta } \\ 0 & \frac{r_{x} r_{z}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) + \frac{r_{y}}{\theta} S_{\theta }& \frac{r_{y} r_{z}}{\theta ^{2}} \left ( 1-C_{\theta }\right ) - \frac{r_{x}}{\theta} S_{\theta }& \frac{r_{z}^{2}}{\theta ^{2}} + \frac{r_{x}^{2} + r_{y}^{2}}{\theta ^{2}} C_{\theta } \end{array}\displaystyle \right ) $$

(5)

We follow Chipman, Lam, and Young (2018, Chapter 6.6) closely. We use a notation where $\cos \theta$ is denoted $C_{\theta}$ and $\sin \theta$ is denoted $S_{\theta}$. We substitute the ($H,45,R$) notation of Chipman, Lam, and Young (2018) for a more direct ($x,y,z$) notation: $r_{H} = r_{x}$, $r_{45} = r_{y}$, and $r_{z} = r_{r}$. We explicitly denote an $xyz$-coordinate frame equivalent to $quv$-coordinates for the lower-right-hand $3\times3$ sub-matrix rotation [${\mathbf{R}}$]. The $(H,45,R)$ notation corresponds to naming conventions of horizontal as the $x$-axis or Stokes-$Q$, the 45 as $y$ or Stokes-$U$, and -$R$ as $z$ or Stokes-$V$. In this notation, the total-retardance magnitude is the rotation angle $\theta$, computed as the root-sum-square (RSS) of the individual components $r_{x},r_{y},r_{z}$.

2.3 Articulation in Azimuth, Elevation, Table Angle

We model the telescope as a time-dependent system in azimuth–elevation–coudé coordinates (Az–El–TA, where TA is the coudé rotating table angle) to account for the relative motion of mirrors changing as astronomical targets are tracked. This articulation in Az–El–TA allows the model to be optimized by a limited number of measurements at discrete times and pointings and then accurately applied to an arbitrary time and pointing.

We adopt a notation where a rotation is denoted as ${\mathbf{R}}$. There are three main coordinate rotations in the DKIST system model. The elevation axis is between M4 and M5 [${\mathbf{R}}_{45}$]. The azimuth axis [Az] is between M6 and M7. The DKIST coudé platform rotation introduces an additional degree of freedom, called the coudé table angle [TA]. These rotation matrices combine to create the effective angle [Az–TA] in the rotation matrix [${\mathbf{R}}_{67}$] between M6 mounted on the telescope and the first coudé-laboratory mirror (M7). We include a static rotation between the M1:M2 mirror-group tilt axes and the M3:M4 mirror-group tilt axes as (${\mathbf{R}}_{23}$), as these two mirror groups do not share a plane of incidence. We note that ${\mathbf{R}}_{23}$ is a constant $90^{\circ}$ rotation along with a $3.5^{\circ}$ offset included in the optical design. We also account for another static $4.4^{\circ}$ incidence-plane offset along the elevation axis between mirrors 4 and 5. We show a block diagram of the optical model in Figure 2 where each major mirror grouping and the mount articulations are shown. The coudé-laboratory mirrors are all grouped and combined as they share a common articulated laboratory platform.

$$\begin{aligned} {\boldsymbol {S}}_{\mathrm{coude}} &= {\mathbf{R}}_{67} {\mathbf{M}}_{6} {\mathbf{M}}_{5} {\mathbf{R}}_{45} {\mathbf{M}}_{4} {\mathbf{M}}_{3} {\mathbf{R}}_{23} {\mathbf{M}}_{2} {\mathbf{M}}_{1} {\boldsymbol {S}}_{ \mathrm{input}} \end{aligned}$$

(6)

$$\begin{aligned} {\boldsymbol {S}}_{\mathrm{coude}} &= {\mathbf{R}}_{\mathrm{Az-TA}} {\mathbf{M}}_{5:6} { \mathbf{R}}_{\mathrm{-El+4.4^{\circ}}} {\mathbf{M}}_{3:4} {\mathbf{R}}_{-93.5^{\circ}} {\mathbf{M}}_{1:2} {\boldsymbol {S}}_{\mathrm{input}} \end{aligned}$$

(7)

Figure 2

The basic elements of the articulated-system model. The solar incoming Stokes vector is at the far left. The rotation matrices of the articulated optical system are shown with the bold R-elements, including static offset angles from the design. The M1:M2 mirror grouping is encountered first, with a $-93.5^{\circ}$ rotation to the next mirror grouping M3:M4. The elevation axis along with a $4.4^{\circ}$ clocking is included between mirrors 4 and 5. The M5:M6 grouping is ahead of the azimuth axis, which also combines with the coudé-laboratory table angle [TA]. All coudé-laboratory mirrors are grouped into the appropriate instrument calibration.

We transfer the Stokes vectors from upstream of the DKIST primary mirror to the Stokes vectors incident on M7 in the coudé-laboratory floor. Equation 6 shows the input Stokes vector ${\boldsymbol {S}}_{\mathrm{input}}$ being transferred from ahead of the primary mirror to the coudé laboratory [${\boldsymbol {S}}_{\mathrm{coude}}$] just before arriving at M7. Nominal DKIST calibrations point at solar disk center where the continuum polarization is nearly zero and thus ${\boldsymbol {S}}_{\mathrm{input}} = [1,0,0,0]^{T}$ to well within common instrument systematic errors. We show the group model in Equation 7, where pairs of mirrors are represented by a single Mueller matrix. The sign convention and static angular offsets for each rotation matrix are given as subscripts in Equation 7.

The system transfer matrix above is implicitly wavelength-dependent, and we must calibrate DKIST at all wavelengths separately. This transfer matrix can also have other dependencies that are currently not included for system calibration, in particular the field angle of the target away from the optical boresight. We have estimated the field-dependence magnitude in Harrington and Sueoka (2017) and summarize the behavior in the Appendix. The current field-dependent errors are below error-budget thresholds to a limiting field angle that depends on wavelength, instrument, and calibration details. We can make the models more complex to included field dependence using our coating models at a later date.

2.4 Elements of a System Model: Modulation Matrix

The modulation matrix [${\mathbf{O}}_{m}$] is commonly defined as the $m \times 4$ matrix that linearly transforms the four vector components [$I,Q,U,V$] of an input Stokes vector, here ${\boldsymbol {S}}_{\mathrm{coude}}$, into $m$ temporally or spatially independent measurements of the total modulated intensity [$i_{m}$] as in Equation 8 (Skumanich et al., 1997; del Toro Iniesta and Collados, 2000; del Toro Iniesta, 2003; Socas-Navarro, 2005b,a; Snik, Karalidi, and Keller, 2009; Tomczyk et al., 2010; de Wijn et al., 2011; Socas-Navarro et al., 2011; del Toro Iniesta and Martínez Pillet, 2012; Snik et al., 2012; Chipman, Lam, and Young, 2018).

$$ \left ( \textstyle\begin{array}{c} i_{1} \\ i_{2} \\ ... \\ i_{m} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} O_{I1} & O_{Q1} & O_{U1} & O_{V1} \\ O_{I2} & O_{Q2} & O_{U2} & O_{V2} \\ ... & \ldots & \ldots & ... \\ O_{Im} & O_{Qm} & O_{Um} & O_{Vm} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} I \\ Q \\ U \\ V \end{array}\displaystyle \right ) $$

(8)

We use subscripts [$I,Q,U,V$] in the first index of the modulation matrix to denote which Stokes-vector component is being modulated. The numerical second index denotes the modulation state 1 through $m$ ($1,2,\ldots,m$), corresponding to the modulating retarder setting (orientation, voltage, etc.) of a given polarimetric instrument.

There are two approaches to modeling the instrument suite. In the first approach, we can group mirrors to combine all the optics contributing to a modulation matrix from M7 through the instrument sensor. The modulator is only given the free parameters corresponding to a rotating elliptical retarder (no depolarization, no diattenuation). In the second approach, only the modulation matrix is derived: there are no assumptions about the form of the Mueller matrix for particular optics or their grouping. The modulation matrix represents the combined influence of all optics from M7 to the sensor often accounting for some optical errors. Often the modulation matrix for a beam with minimal systematic errors is close to a physical propagation model using Mueller matrices. We refer the reader to a detailed example by Harrington et al. (2021a), where the NCSP system optics were modeled under both approaches. For DKIST instruments, we only use the first approach to assess the quality of our system model. DKIST instruments are calibrated by deriving the modulation matrix directly for optics from M7 through the instrument sensor.

2.5 Mueller Matrix Model on the Optical Axis

We show a model of the Mueller matrix for the optics from M1 to the ViSP slit as an example of the Stokes-vector transformations caused by DKIST and ViSP feed optics. The beam propagating along the optical axis is modeled using the mirror-coating properties similar to Harrington and Sueoka (2017), Harrington, Sueoka, and White (2019), and Harrington et al. (2021a). This Mueller matrix shows the level of changes between incoming and measured Stokes vectors. We calculate the sequence of individual-optic Mueller matrices and then apply the mirror groupings using Equation 7 articulating the telescope in azimuth and elevation angles. As shown with our Zemax analysis in Harrington and Sueoka (2017, Figure 19), the field-angle dependence of the system Mueller-matrix elements is at or below 0.02 for wavelengths where the mirror coatings have maximal retardance over the full five arcminute field of view. The error-matrix assessments of Harrington et al. (2021b) shows the impact of many other field-dependent errors caused by GOS calibration optics that compete with the mirror-coating-induced field dependence to be the limiting error. The modeling by Harrington et al. (2021b) suggested that the calibration procedure is sufficient to calibrate a field of many arcseconds to tens of arcseconds depending on the wavelength. The mirror coating incidence-angle dependence is quite small over such a small field angle. The error-matrix levels do not go above error-budget limits for a field typically at or greater than the adaptive-optics corrected field.

Symmetric behavior of a system of articulated mirrors is seen as pairs of mirrors share planes of incidence. When mirror-incidence planes are crossed, polarization response subtracts while parallel mirrors have responses add. Articulated mirror systems have additional coordinate rotations for linear polarization included in the Mueller matrices. Figure 3 shows the Mueller matrix of the system articulating the telescope through elevation angles of $0^{\circ}$ to $180^{\circ}$ and azimuth angles of $0^{\circ}$ to $360^{\circ}$ at a single wavelength of 393 nm and a single coudé-table angle of $0^{\circ}$. This articulation range covers the entire sky in double redundancy. Often, telescope mounts can articulate through more than $90^{\circ}$ elevation and more than $360^{ \circ}$ azimuth. For instance, DKIST typically parks the mount near an elevation angle of $104^{\circ}$, which is $14^{\circ}$ past the zenith. Our calibrations recorded at this pointing would not represent the same mirror geometry if using the alternate pointing of $90^{\circ}\,\text{--}\,14^{\circ}$ and an azimuth exchange of $180^{\circ}$ although the mirror-polarization response is symmetric for the on-axis beam. The symmetry and functional dependence of the system Mueller-matrix calibration is best seen under this full range of simulated mirror orientations. An elevation angle of $180^{\circ}$ would represent the same mirror configuration on-axis for an elevation angle of $0^{\circ}$ but with $180^{\circ}$ added to the azimuth angle. We note that the azimuth axis is articulated after the elevation axis for DKIST, giving rise to additional geometric rotation in the inner $2\times2$ sub-matrix corresponding to $QQ$-, $QU$-, $UQ$-, and $UU$-terms.

Figure 3

The Mueller matrix of the system from M1 through to the ViSP slit using a nominal coating model on each mirror at 393 nm wavelength and coudé-table angle of $0^{\circ}$. We have followed a normalization convention where each individual matrix element has been normalized by the throughput, represented as the $II$-element, except the $II$-element itself. We show the original $II$-element without normalization in the upper-left panel. Each Mueller matrix has only $Q$-diattenuation and $U$- to $V$-retardance in the local mirror coordinates. We note the gray-scale range of each Mueller-matrix element is shown as the numbers on the right-side of each panel. For instance, the $VV$-element in the lower right-hand corner is scaled from 0.275 as black to 0.999 as white.

The mirror articulation along azimuth and elevation angles gives rise to simple periodic dependence in the Mueller-matrix system model. Each sub-panel of Figure 3 shows the Mueller-matrix numerical range as the color scale bar on the right-hand side. For instance, the $QQ$ matrix element is scaled from black at 0.681 to white at 1, while the $VV$ element is scaled from black at 0.275 to white at 0.999. We note that at the particular 393 nm wavelength modeled, the two articulated mirror-group retardances are near $20^{\circ}$ and $30^{\circ}$, respectively. Thus an incoming $V$ signal might only be preserved as $V$ incident on the ViSP slit at 0.275 magnitude as the minimum magnitude for the $VV$-element. At this particular telescope pointing, most of the solar signal at the ViSP slit would be rotated into some combination of $Q$ and $U$. The $V$- to $Q$-term of the Mueller-matrix ranges over $\pm0.674$. The first column shows the $I$- to $QUV$-terms can be up to 3.6% creating a continuum polarization seen at the ViSP slit. By having an articulated system model such as Figure 3, these telescope-caused rotations and offsets are compensated during the calibration process.

This system Mueller-matrix behavior is similar to existing system models for other altitude–azimuth telescopes. For instance, the Advanced Electro-Optical System telescope (AEOS) and the High-resolution Visible and Infrared Spectrograph (HiVIS) reported by Harrington, Kuhn, and López Ariste (2017) have symmetric behavior of the Mueller matrix, as confirmed by daytime-sky polarization calibrations using thousands of calibration observations reported by Harrington, Kuhn, and López Ariste (2017, Figure 14). This can be compared to the DKIST optical-model predictions using the Zemax (OpticStudio) predictions of Harrington and Sueoka (2017, Figure 17). The Zemax model for this system shown by Harrington, Kuhn, and López Ariste (2017, Figure 16) has the same azimuth and elevation symmetry as DKIST, as expected for all articulated Az–El telescopes.

2.6 Calibration Sequence: 10 States Created with a Polarizer and Retarder

During calibration, the polarizer and retarder are independently, and/or in combination, inserted and discretely rotated ahead of the Gregorian focus as part of the Gregorian Optical System (GOS). A series of exposures using these polarization-calibration optics is used to create a diversity of Stokes-vector inputs. This series is commonly called a Calibration Sequence (CS), and it can include polarizer-only, retarder-only, and both polarizer and retarder configurations. The collection of modulated-flux measurements by an instrument for each state in a CS is commonly called a Polarization Calibration (PolCal). A single PolCal, combined with a database of mirror-polarization responses for M1 through M6, can be used to derive an instrument modulation matrix.

Calibrating the polarization response of the entire system Mueller matrix through the instrument, as well as the instrument-modulation matrix, requires a series of many PolCals. These many PolCals must be collected with enough diversity to separate the articulated-mirror polarization from instrument modulation and fit many tens of variables simultaneously. We describe this process of fitting the model for the many parameters for each grouping of mirrors in more detail in Section 3.

The rotation of optics within the system requires its Mueller matrix to include rotation matrices on both sides to preserve local coordinate systems: ${\mathbf{R}}(-\theta )$ ${\mathbf{M}}$ ${\mathbf{R}}(\theta )$. The single-sided rotations of Equations 6 and 7 rotate the coordinate frame sequentially. We use Equation 9 to define the Mueller matrix for the calibration optics as it is in the coordinates of the beam after M2 and ahead of M3.

$$ {\mathbf{M}}_{\mathrm{GOS}} = {\mathbf{R}}_{\mathrm{-ret}} {\mathbf{M}}_{ \mathrm{ret}} {\mathbf{R}}_{\mathrm{ret}} {\mathbf{R}}_{\mathrm{-pol}} {\mathbf{M}}_{ \mathrm{pol}} {\mathbf{R}}_{\mathrm{pol}} $$

(9)

The polarizer is rotated into local coordinates by the angle denoted as pol. The elliptical retarder rotated into local coordinates by the angle denoted as ret. The GOS calibration optics combine with the telescope when inserted as per Equation 10.

$$ {\boldsymbol {S}}_{\mathrm{coude}} = {\mathbf{R}}_{67} {\mathbf{M}}_{5:6} {\mathbf{R}}_{45} { \mathbf{M}}_{3:4} {\mathbf{R}}_{23} {\mathbf{M}}_{\mathrm{GOS}} {\mathbf{M}}_{1:2} {\boldsymbol {S}}_{ \mathrm{input}} $$

(10)

Optimizing operational efficiency requires DKIST to calibrate as many instruments as possible quickly and simultaneously. Furthermore, thermal loads up to 300 watts on the calibration optics drive minimizing the measurement duration to ensure stable calibrations. The thermal performance of the retarder also motivated leaving the polarizer always in the beam ahead of the retarder (Harrington and Sueoka, 2018a; Harrington et al., 2020). We define a CS that maximizes the calibration efficiency as computed analogously to modulation efficiency (del Toro Iniesta and Collados, 2000; Tomczyk et al., 2010; de Wijn et al., 2010; Snik et al., 2012).

By calibration efficiency, we refer to the proper selection and conditioning of the input Stokes vector that maximizes the use of the available photons while reducing the sensitivity of the calibration to errors in the inputs. Selbing (2005, Section 2.5.2) describes some simple optimization strategies wherein the orthogonality of the Stokes vectors created by the calibration unit is assessed in matrix form with one row per input state. A condition number and the relative calibration efficiency can be derived from the collection of $n$ input calibration states $[I,Q,U,V]_{n}^{T}$ stacked as rows in a matrix as

$$ {\boldsymbol {S}}_{\mathrm{CS}} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} I_{1} & Q_{1} & U_{1} & V_{1} \\ I_{2} & Q_{2} & U_{2} & V_{2} \\ \vdots & \vdots & \vdots & \vdots \\ I_{n} & Q_{n} & U_{n} & V_{n} \end{array}\displaystyle \right ). $$

(11)

The pseudo-inverse of ${\boldsymbol {S}}_{\mathrm{CS}}$ is created as Equation 12.

$$ {\boldsymbol {E}} = ( {\boldsymbol {S}}^{T}_{\mathrm{CS}}{\boldsymbol {S}}_{\mathrm{CS}})^{-1}{ \boldsymbol {S}}^{T}_{\mathrm{CS}} $$

(12)

The Stokes-vector efficiencies are computed from the pseudo-inverse as usual using the sum of squared elements, i.e. $\xi _{i} = \left ( n \sum _{j=1}^{n} E_{ij}^{2}\right )^{-1/2}$.

This pseudo-inverse [${\mathbf{E}}$] can also be assessed by its condition number. This is the same approach as for finding optimum demodulation matrices (del Toro Iniesta and Collados, 2000; Tomczyk et al., 2010; de Wijn et al., 2010; Snik et al., 2012)

In the National Solar Observatory Lab Spectro-Polarimeter (NLSP), used for metrology, an ansatz sequence was implemented to measure polarization with high efficiency across the 380 nm to 1650 nm wavelength range. NLSP used a rotating polarizer and retarder for creating a diversity of input Stokes vectors. The calibration sequence rotated these optics in $60^{\circ}$ steps with a $30^{\circ}$ offset between the polarizer extinction axis and the retarder fast axis at 630 nm wavelength. The sequence worked well for reconstructing sample Mueller matrices with simultaneous fits to all polarization optic parameters. We optimized a similar sequence for DKIST polarization calibration by adding an additional state and optimizing the calibration efficiency. We show the ten input states as the baseline for DKIST in Table 1 along with the modulated flux without calibration optics in the beam before and after, commonly called the clear states. These clears can be used for intensity temporal drift correction. The clears also provide some improved sensitivity to fitting the incoming beam partial polarization. The optimization and efficiencies are outlined in Harrington et al. (2020, Section 3.1). We note the second-to-last row of Table 1 is highlighted in bold to denote that state being the one state we freely optimized for orientation of both optics to maximize calibration efficiency. Often, instruments record background-level calibrations, commonly called darks, before and/or after a Calibration Sequence to ensure a good correction.

Table 1 The Calibration Sequence (CS) for GOS polarizer and retarder settings

When the GOS calibration lamp is used, the input Stokes vector is partially polarized and elliptical as the beam contains all $QUV$-states at significant levels. This requires a fit for all three partial polarizations [$Q,U,V$] created by the lamp as in Equation 13

$$ {\boldsymbol {S}}_{\mathrm{coude}} = {\mathbf{R}}_{67}\,{\mathbf{M}}_{5:6} \,{\mathbf{R}}_{45} \,{\mathbf{M}}_{3:4}\,{\mathbf{R}}_{23} \,{\mathbf{M}}_{\mathrm{GOS}}\,{\boldsymbol {S}}_{ \mathrm{lamp}} $$

(13)

2.7 Fitting Instrument Modulation Matrices Using a Calibration Sequence

The DKIST first-light instruments have options for continuously rotating or discretely stepped modulation when using the various retarders and cameras mounted within each instrument. Individual polarization-calibration measurements for each camera arm within each of the DKIST instruments at each wavelength derive a unique modulation matrix [$\mathbf{O}$] by using a combination of database values for the system optic variables, and fits to particular instrument modulation variables. Nominal defaults for ViSP, DL-NIRSP, and Cryo-NIRSP are between six and ten states for 24 to 40 modulation-matrix element variables. In the case of the VTF, the liquid-crystal-based modulator is electrically controlled. The minimum number of modulation state variables is 16 to solve for the four Stokes input vector components with four photometric measurements.

A sequence of PolCal data sets can be used to fit for the database parameters of the optical system for each wavelength. We show in Figure 4 a block-diagram layout of the nominal model variables and general structure of the geometry and detail the variables below. Independent calibrations for the modulation-matrix elements are anticipated for separate instrument configurations (e.g. wavelength, filter selection, field angles, camera arm, etc.). The modulation-matrix calibration procedure uses the best-fit mirror-group model parameters for mirrors 1 through 6 stored in the telescope-system-model database to transfer the source calibration Stokes states from M1 to the instrument via Equations 6 – 13. The modulation matrix formally includes the polarization response of all optics starting with DKIST M7. Derivation of an instrument modulation matrix is typically done daily. Currently, each modulation-matrix calculation involves multi-variable fits to at least one calibration-sequence data set. As DKIST can run all cameras within all instruments strictly simultaneously, and expects to include CN with all others using the M9b optic upgrade, we have implemented calibration sequences that are efficient for all instruments at all wavelengths, calibrated all at the same time. Depending on the fitting options selected (see Table 2, simultaneous fits to several calibration-optic parameters are also included. The baseline DKIST calibration approach is given in the third column of the table. The same modulation matrix should be derived within the error limits regardless of which calibration optics or calibration sequence is used. Stability analysis in the coming years may suggest some instruments or configuration modes may require more, or less, frequent calibration.

Figure 4

The major elements of the articulated system model at each wavelength. The solar input for disk-center flux is assumed to be unpolarized. The system throughput is fit as $I_{\mathrm{sys}}$. The M1:M2 mirror-grouping variable $X_{12}$, corresponding to diattenuation, can be fit. The retardance variable $\tau _{12}$ cannot be fit for unpolarized input. The GOS-elements are shown in the gray box with the ability to insert and remove shown as red double-sided arrows. If the GOS lamp is inserted, the system intensity [$I_{\mathrm{sys}}$] along with the elliptical partial polarization [$Q_{\mathrm{in}},U_{\mathrm{in}},V_{\mathrm{in}}$] variables can be fit. The calibration polarizer (CalPol) and calibration retarder (CalRet) variables are represented in the box for each optic. The angles of the calibration sequence are denoted $\theta _{\mathrm{pol}}$ and $\theta_{\mathrm{ret}}$. The rotation matrices of the articulated system are shown with the bold R-elements, including the static offset angles included in the design. The variables for the two major mirror groups M3:M4 and M5:M6 are shown in the appropriate box.

Table 2 Instrument PolCal fit settings.

Instrument modulation matrix [O] fits involve interaction with the DKIST system-model database. A daily calibration must look up the current value for the M3:M4 and M5:M6 mirror-group polarization properties from the Database (DB), shown as the first four rows of Table 2. Retardance of each mirror group is denoted with the variable $\tau$. The diattenuation of each mirror group is denoted as $\Delta$. The subscripts correspond to mirror groupings 3:4 and 5:6, respectively. We also include the measured extinction ratio for the calibration polarizer in the calibration. We use the variable $p_{y}$ following Equation 20 and Figure 44 of Harrington et al. (2021a), where the Mueller matrix of a pair of crossed polarizers is diagonal with elements $p_{y}^{2}$, and the contrast ratio of a pair of polarizers is approximated by 1/2 $p_{y}^{2}$. We note that spatial and spectral mapping of polarizer transmission and contrast was detailed by Harrington et al. (2021b). This is shown in the fifth row of Table 2. This database value accounts for the imperfect contrast of the calibration polarizer.

The Stokes vector entering the calibration optics, either from the M1:M2 group or the lamp, needs to be fit and handled using separate procedures. We can optionally fit for each of the $QUV_{\mathrm{in}}$ partial-polarization states created by optics upstream of the GOS calibration unit. The temporal stability of the DKIST primary and secondary mirror coating diattenuation, or GOS lamp optics, impacts the decision to use database values. We denote this fitting option as DB or one to three variables. We have run testing with all options on both lamp- and Sun-based data sets. Our initial testing, detailed below, shows that using the metrology for DKIST M1:M2 gives better modulation-matrix stability. The model-fitting outputs are perturbed by the presence of systematic errors. We nominally use the database for the $Q$-input created by the primary and secondary with more testing planned. We show assessments of both fit types in a later section. The lamp suffers much less temporal variation due to the solar temporal evolution and/or atmospheric changes. The lamp can provide a greater diversity of telescope pointings as we are not constrained to point at the Sun. This improves the fidelity of the telescope-model fitting through the increased azimuth and elevation ranges (diversity) when fitting a system model. In addition, stellar and daytime sky calibration sources are present over the full range of telescope pointings anticipated for upcoming calibration verification. We use both options of the database and all three $QUV$ input fitting variables.

Similarly, we can fit variables or use database values for the transmission of the calibration polarizer [${t}_{\mathrm{pol}}$] and calibration retarder [${t}_{\mathrm{ret}}$]. The Calibration Retarder (CalRet) elliptical retardance values, if stable, can also become database lookup tables. The nominal procedure is to fit for the transmission of the two GOS optics, three elliptical parameters for the calibration retarder and a full modulation matrix. We note, however, that these transmission and retardance values can also be database lookup-table values. Given the many transmission and intensity variables, we always fit for a global system throughput variable ${I}_{ \mathrm{sys}}$ to set the measured unpolarized flux levels.

In the third column of Table 2 we show the nominal default settings for deriving an instrument modulation matrix using on-Sun calibrations. We use databases for the articulated telescope mirrors M3:M4 and M5:M6. We use one database value for the diattenuation of the M1:M2 group [$Q_{\mathrm{in}}$] and one database value for the calibration polarizer contrast [${p}_{y}$]. The $U$- and $V$-inputs are set to zero. We show example outputs for various fitting options later in this work.

The modulation matrix can be reduced to a five-variable model if we force the system model to be a two-variable mirror-group Mueller matrix followed by a rotating-elliptical-retarder Mueller matrix (three variables). We note that we assessed several separate algorithms that fit or ignore several variables detailed by Harrington et al. (2021b), including a common relative normalization scheme by Harrington et al. (2021b, Appendix B, Section 9.1).

2.8 Assessing Calibration Inaccuracies: The Error Matrix

$$\begin{aligned} {\boldsymbol {\Delta}\boldsymbol {S}} &= {\boldsymbol {S}}_{\mathrm{meas}} - {\boldsymbol {S}}_{\mathrm{true}} \end{aligned}$$

(14)

$$\begin{aligned} {\boldsymbol {\Delta}\boldsymbol {S}}& = \mathbf{D}_{\mathrm{fit}} {\boldsymbol {I}}_{\mathrm{meas}} - { \boldsymbol {S}}_{\mathrm{true}} \end{aligned}$$

(15)

$$\begin{aligned} {\boldsymbol {\Delta}\boldsymbol {S}}& = \mathbf{D}_{\mathrm{fit}} \mathbf{O}_{\mathrm{true}} { \boldsymbol {S}}_{\mathrm{true}} - {\boldsymbol {S}}_{\mathrm{true}} \end{aligned}$$

(16)

$$\begin{aligned} {\boldsymbol {\Delta}\boldsymbol {S}} &= (\mathbf{D}_{\mathrm{fit}} \mathbf{O}_{\mathrm{true}} - { \bf 1}_{ij} ) {\boldsymbol {S}}_{\mathrm{true}} \end{aligned}$$

(17)

$$\begin{aligned} {\boldsymbol {\Delta}\boldsymbol {S}}& = \boldsymbol{\epsilon}_{ij} {\boldsymbol {S}}_{\mathrm{true}} \end{aligned}$$

(18)

We estimate the errors introduced in a measured Stokes vector using an error-matrix formalism. We show a $4\times4$ transfer matrix of errors demonstrating the role of spatial inhomogeneities and beam mis-alignments in the calibration optics on the calibration scheme. In absolute terms, the errors are quantified as the difference between the calibrated Stokes-vector measurement [$\boldsymbol{S}_{\mathrm{meas}}$] and the true incoming Stokes vector [$\boldsymbol{S}_{\mathrm{true}}$] shown in Equation 14. For our case of a system characterized by and calibrated using the optimal modulation-matrix formalism (del Toro Iniesta and Collados, 2000), the measured Stokes vector is the calibrated demodulation matrix [$\textbf{D}_{ \mathrm{fit}}$] multiplied by the measured intensities [$\boldsymbol{I}_{ \mathrm{meas}}$], as shown in Equation 15. To create an estimate of error, we substitute in the true incoming Stokes vector [$\boldsymbol{S}_{\mathrm{true}}$] multiplied by the true modulation matrix [$\textbf{O}_{ \mathrm{true}}$] in place of the measured intensities, as shown in Equation 16. This simplifies to a single expression multiplying the true incoming Stokes vector in Equation 17, where $\textbf{1}_{ij}$ is the identity matrix. We set this expression as the $4\times4$ error-matrix $\boldsymbol{\epsilon}_{ij}$ in Equation 18. In many cases, the true modulation matrix is unknown, but can be estimated from larger, more constrained fits, modeled in simulation or perturbed to assess error levels.

This concept of an error matrix was previously introduced by Elmore (1990) on the Advanced Stokes Polarimeter (ASP) and Ichimoto et al. (2008) on the calibration of the Solar Optical Telescope onboard the Hinode spacecraft. However, in those cases, the modulation matrix applied to the data was not an optimal one from a statistical-noise perspective del Toro Iniesta and Collados (2000). This led to the use of a polarization response matrix [$\textbf{X}_{ij}$] that described how a measured Stokes vector related to the true incident Stokes vector with terms far away from the identity matrix. The error matrix in this case was not given by [$\textbf{D}_{ \mathrm{fit}}$ $\textbf{O}_{\mathrm{true}}$ - $\textbf{1}_{ij}$], but instead is given by the difference from identity for the product of the calibrated best-fit response matrix and the true response matrix [$\textbf{X}_{ \mathrm{fit}}^{-1}$ $\textbf{X}_{\mathrm{true}}$ - $\textbf{1}_{ij}$].

$$ \boldsymbol{\epsilon}_{ij} =10^{-2} \left ( \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 1 & 1 & 1 & 1 \\ 0.05 & 1 & 0.5 & 0.5 \\ 0.05 & 0.5& 1 & 0.5 \\ 0.05 & 0.5& 0.5& 1 \end{array}\displaystyle \right ) $$

(19)

For DKIST, a nominal generic specification for these error limits is shown in Equation 19. We followed a similar approach to that used for Hinode by Ichimoto et al. (2008) and choose incoming linear and circular polarization signals of 10% magnitudes. We further assume limits on depolarization at 1% for $QUV$ to $I$ terms, and on polarizance of 0.05% for $I$ to $QUV$ terms (see first row, the diagonal, and first column of Equation 19). The off-diagonal rotation sub-matrix terms are 0.5%. Actual error-matrix limits will depend on the particular science use case, observing strategy, weather, wavelengths, and a very long list of instrument performance parameters. In general, concerns about the continuum-polarization stability, depolarization, and retardance can be specified, considering constraints on the length, zero point, and orientation of the reconstructed Stokes vectors.

3 System Calibration Using the NSO Coudé Spectropolarimeter

The National Solar Observatory Coudé Laboratory Spectro-Polarimeter (NCSP) was designed to perform polarization calibrations of DKIST. It can use real solar observations as well as the Gregorian Optical System (GOS) calibration-lamp beam. We use the formalism introduced above in Section 2 to fit an articulated-telescope-system model, show instrument modulation matrices, and derive error-matrix elements to show accuracy estimates. A more detailed description of the NCSP can be found in Harrington et al. (2021a).

The NCSP uses two separate fiber-fed spectrographs covering visible (VIS) and near-infrared (NIR) wavelengths, respectively, to collect DKIST solar or lamp flux. Processing of raw NCSP spectra is independent of any complex data-processing software typically required to reduce data from the DKIST instrument suite. By using commercial-off-the-shelf (COTS) spectrographs, we can demonstrate DKIST calibrations continuously covering wavelengths from 383 nm to 1638 nm with minimal data-processing or software development. We show here that we can calibrate DKIST articulated telescope mirrors and verify the major components of the system-polarization model.

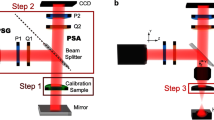
The NCSP was installed in the DKIST coudé laboratory in 2019. NCSP is aligned to the optical bore-sight of the telescope. A custom opto-mechanical interface situates NCSP among the DKIST instrument suite. A series of fold mirrors pick off the beam converging at F/18 within the Cryo-NIRSP (CN) instrument mirror path. The NCSP uses the same Cryo-NIRSP F/18 focus apart from a few fold mirrors. Figure 5 shows the NCSP and relevant optics installed on the summit. We refer the reader to Rimmele et al. (2020, Figure 10), showing NCSP in the entire coudé laboratory. We also show a closer view of the NCSP optical bench in front of the Cryo-NIRSP instrument in Figure 6. See Harrington et al. (2021a, Figures 2 and 3) for a CAD model of the NCSP and opto-mechanical layout. Given this optical configuration, the NCSP spectrograph optical fiber collects roughly a three-arcsecond round field of the solar image formed on this diverted CN focal plane. NCSP is non-imaging and averages the flux spatially over this few arcsecond round patch near the system bore sight.

Figure 5

The NCSP installed in the DKIST coudé laboratory. We highlight the DKIST relay optical path used by NCSP. M7, M9 and M9a are seen in the image. M9 is 600 mm diameter and is seen in the image to the far left. Half of M8 with a 900 mm diameter is visible on the far-right-edge of the image. The Cryo-NIRSP steering mirror (CSM) and the focusing F/18 mirror (CN F/18) are used in the NCSP optical path. The 1.5 m tall optical systems engineer is standing next to NCSP, adjacent to CN for scale. The black anodized metal structure immediately under the blue text “Cryo-NIRSP” is the CN spectrograph dewar, roughly 2 m high. The optical bench and enclosure under the text “DL-NIRSP” is the DL spectrograph optical bench, with the enclosure rails about 2 m high for scale. The DL-NIRSP instrument seen in far back of the image is approximately 2 m high. Components of the VBI and adaptive optics system are seen to the far right.

Figure 6

The NCSP showing several of the optics along with the co-author Sueoka at 1.5 m height for scale. The Cryo-NIRSP steering mirror (CSM) is at the far right. The four NCSP fold mirrors are annotated as FM1, 2, 3, 4. DKIST M9 has a 600 mm diameter and is partially seen in the background top right. The NCSP FM3 is at 75 mm diameter and FM4 is at 50 mm diameter for scale.

The VIS channel spectrograph has spectral sampling of 0.8 nm per pixel at 370 nm wavelength, reducing to 0.7 nm per pixel at 1100 nm. The NIR channel spectrograph has an average sampling of 1.65 nm per pixel. Given the delivered solar and lamp flux, we trim the VIS system to cover a wavelength range of 383 nm to 1098 nm and the NIR system to the range 918 nm to 1638 nm. Figure 7 shows the NCSP system in the left-hand panel illuminated by roughly 70 watts of optical power from the DKIST solar beam. The bright illuminated mirrors are NCSP fold mirrors 3 and 4 through multiple baffles, converging towards the F/18 focus. Two drilled metal plates with a rough surface and black anodization are used as additional heat dissipating stops ahead of the F/18 focus. These stops assist on-Sun observing where more than 70 watts of optical power would otherwise be concentrated in the 2.8 arcminute field beam at this F/18 focus. The right-hand panel of Figure 7 shows some of the internal components of NCSP.

Figure 7

The left-hand panel shows NCSP during on-Sun observations in August 2020. The NCSP fold mirrors 3 and 4 are saturated in the image and fully illuminated by the 70 watts of optical power covering the 2.8 arcminute DKIST field of view. The right-hand panel shows the internal components of NCSP as installed on the summit. For scale, FM3 is a 75 mm diameter optic, FM4 is a 50 mm diameter optic, and the breadboard hole pattern has 25 mm spacing. A laser-cut circular mask serves as a field stop. This passes a $\approx2.9$ arcsecond field-angle beam to the collimating lens. This few-millimeter diameter beam is modulated by the rotating polycarbonate retarder. A 50 mm square wire-grid polarizer is used as an analyzer at $45^{\circ}$ incidence, splitting the two orthogonal linear states into separate beams. The transmitted beam goes to the VIS channel. The reflected beam goes to the NIR channel where an additional wire-grid polarizer, oriented parallel to the analyzed state, removes the unwanted Fresnel reflection from the analyzer to preserve high contrast. Each channel has its own achromatic doublet lens focusing the beam onto an optical fiber. The fiber is connected to the entrance slit of the spectrographs.

3.1 System Model Fitting Complexity: Physical Motivation for Including Variables

We used NCSP data sets as modulated spectral intensities over a range of telescope azimuth, elevation, and coudé-table angles to fit for the DKIST system-model variables. NCSP allows us to test for the success in reducing photometric fitting errors, deriving temporally stable instrument-modulation matrices, and assessing the improvement or lack thereof when including new system-model variables. See Section 4 of Harrington et al. (2021a) for a detailed examination of fitting an NCSP data set to a system model. The number of variables used in a system model needs to be limited to those that are significant, well conditioned to fit, and useful for substantially reducing errors in the system. We used several versions of our system-polarization model for DKIST to assess the accuracy and quality of our fitting procedures. We ultimately find that limiting the system model to a minimum number of variables, combined with using high-quality metrology, is a more successful approach.

On 6 March 2020, several hours of NCSP data were recorded using the GOS lamp at a range of telescope altitudes, azimuths, and coudé-table angles to fit multiple versions of the system-polarization model. Details of this data set and associated fits are given by Harrington et al. (2021a). We recorded 1872 spectra with NCSP, using 26 individual PolCals, each with the ten-input-state sequence as well as modulated flux without the calibration polarizer or retarder, both pre- and post-sequence.

We assessed the photometric accuracy and improvement of model fitting using a range of variables. The system was modeled with as few as 9 variables and as many as 137. We explored the physical motivation for including or ignoring the many variables in a telescope and instrument system model. Most variables are assumed to have negligible influence on the optical path. For instance, there are 16 degrees of freedom (variables) in each Mueller matrix for each of the 10 to 40 optics between the atmosphere and a DKIST instrument sensor, representing up to 640 degrees of freedom ($16\times40$). However, we model a group of mirrors sharing incidence planes with tight alignment tolerances as just two variables. The retardance in the local Stokes-$UV$-plane and the diattenuation in the local Stokes-$Q$-plane are sufficient. The reflectivity of each mirror group is degenerate and included in the total system throughput variable.

Retarders can have time-dependent properties through thermal changes (see Harrington and Sueoka, 2018a; Harrington et al., 2020). A detailed assessment is required to show if including this variation improves the model. Thermal measurements under solar illumination are shown by Harrington et al. (2021a, Appendix B, Figures 28 – 32). Within the model we can include a linear temporal trend for the retardance under thermal load, but given the stability of retarder results so far in Harrington et al. (2021a) we do not find the many tens of additional variables to be a useful addition to the fit.

We show here progressively more complex fits to the DKIST system model. We include a range of potential phenomena allowing us to compare fit results with metrology of various DKIST optical components. We list the various model variables in Table 3. The first column describes the variables. The second column shows specific number of variables used when fitting a system model to our 26 PolCal lamp data set. We have the option to ignore the polarization caused by optics upstream of the GOS. We can include constrained fits for just the input Stokes-$Q$ in the plane of the M1:M2 mirror tilt axis [$Q_{\mathrm{in}}$]. We also can include fully elliptical fits [$Q_{\mathrm{in}}$, $U_{\mathrm{in}}$, $V_{\mathrm{in}}$]. This is listed in the first row of Table 3 as 0, 1, or 3 possible variables. In all our models, we fit the transmission of the calibration polarizer (CalPol) and the transmission of the calibration retarder (CalRet). However, we have the option to fit the calibrator-transmission functions for each of the 26 PolCal’s separately to assess if there are any time- or temperature-dependent changes in transmission. This is listed in the second and third rows of Table 3 as 1 or 26 possible variables. We always fit the diattenuation and retardance for two groups of DKIST mirrors, as we assessed that the mirror retardance is one of the most dominant terms. The three elliptical calibration retarder (CalRet) parameters can be fit independently for each of the 26 PolCals for 78 total variables. They can also be restricted and fit globally, assuming constancy throughout the day for three total variables. We note that some prior telescope calibration efforts have recorded very long calibration sequences with many tens of input states with an allowance for linear temporal variation of retardance within each single calibration sequence. We also have implemented this option, but for this article ignore yet another 78 variables for the calibration retarder.

Table 3 Variables in fitting 26 PolCal.

The modulation matrix can be constrained in a variety of ways. The seventh row of Table 3 lists the 24 free variables for an unconstrained modulation matrix derived from 4 Stokes parameters multiplied by 6 modulation states. The constrained option that we demonstrate here is to group the ten NCSP mirrors and only fit a $Q$-diattenuation and a $UV$-retardance along with the three elliptical retardance parameters for the NCSP modulator. The transmissions of all these mirrors are degenerate with the system-throughput variables, are normalized and combined. We also note the modulation matrix has several techniques for enforcing normalization, with some examples in Appendix D of Harrington et al. (2021a). Thus, we list the physically constrained models for two mirror-polarization terms and three elliptical retardance terms in the eighth and ninth rows of Table 3.

We assume temporal stability of the unpolarized input beam (lamp or Sun) for this fitting process. The 26 PolCal data sets are initially normalized by the average of the modulated clear exposures. These data sets range from intensity values of 0 to slightly over 1. The individual PolCal fits can either be given a separate free ${I}_{\mathrm{sys}}$ variable (26 total), be given a single global ${I}_{\mathrm{sys}}$ variable, or we can ignore these terms (shown by Harrington et al., 2021a) to be small) to reduce the model complexity significantly. This is shown in the last row of Table 3.

The progressively more complex variable scenarios assessed here, using 17, 36, 62, and 137 variables, are outlined by number and type in Table 4. Columns 2, 3, and 4 showing the number of calibrator elliptical retardance (ER) variables, system-intensity variables, and modulation-matrix variables (Mod) changed to increase complexity. Other variables such as Stokes inputs and mirror-group variables remain stable in number.

Table 4 Fit scenarios.

The first scenario includes 17 total variables that reduces the 24 independent modulation-matrix elements (24 variables) to a grouping of mirrors sharing incidence planes, followed by a rotating elliptical retarder (three variables). In the second 36-variable scenario, we relax the 5 physically constrained variables and fit all 24 elements of the modulation matrix freely. Both 17- and 36-variable scenarios ignore the difference between the mean of the modulated clear exposures and the actual unpolarized input flux. In the 62-variable scenario, we add 26 independent ${I}_{\mathrm{sys}}$ variables. This allows the incoming Stokes-vector intensity to vary from the mean modulated clear value, which normalizes the data to $\approx1$. The ${I}_{ \mathrm{sys}}$ variables are noted in the third column of Table 4. The 137-variable scenario includes the fit to independent calibration retarder models for every calibration sequence (PolCal), anticipating thermal perturbations through the day. This gives rise to 26 different elliptical calibration retarder fits for each PolCal giving 78 independent variables, adding 75 variables to the fit, as noted in the second column (ER) of Table 4.

3.2 Fit Residuals: Choosing Fewer Global Variables for DKIST Calibration

In this section we show how the photometric-residual fitting errors are reduced as the system-model complexity is increased from 17 to 36 to 62 variables. We find that using fewer variables with better constraints leads to more stable and generally lower error-matrix values, and better DKIST calibration stability. The 137-variable scenario does not fit the photometry substantially better than the 62-variable scenario. The best-fit model should reproduce the measured flux with statistically similar errors for all individual data sets, without any substantial outliers or systematic errors. We assess the error-matrix levels by comparing the many individual modulation matrices derived from each PolCal to the globally fit modulation matrix derived during the system-model fits. While we do not know the actual, true modulation matrix, we assume the single globally fit modulation matrix to 26 PolCals should be a stable representation of the 26 individual modulation matrices fit with the 26 individual PolCals.

We ensure that all PolCal sequences, GOS states, and wavelengths have similar error behavior and are being fit within error limits. Our shot- and read-noise limits are far below several other error sources, thus we are limited by systematic errors. For each wavelength, we compute the standard deviation of all 1872 photometric-residual errors for each model. We compute these errors in units of system intensity at each wavelength [${I}_{\mathrm{sys}}$]. With this normalization, the residual errors are expressed as a ratio (percentage) of the incoming flux. The standard deviation of data minus model in percent is a useful measure of the systematic errors. We see a significant increase in photometric-residual errors by a fraction of a percent over background in the atmospheric-absorption band near 1300 nm to 1450 nm wavelength. The photometric-residual errors reasonably obey Gaussian statistics although they are a combined system response to lamp temporal variation, optical-alignment errors, and other optical instabilities. We derived cumulative distribution functions (CDFs) of the photometric errors to assess that they are smooth, continuous functions. After accounting for the spectrally variable noise scale [$\sigma$], the photometric errors do follow a Gaussian distribution with very few small outliers at $3\sigma$ limits at 0.3% of the distribution (1 – 99.7%). This Gaussian behavior was seen in all model fits.

In Figure 8 we show the $1\sigma$ photometric error spectra for all four scenarios run in Table 4. The 17-variable model with the blue line has $\sigma$ above 1% with a significant wavelength-dependent trend. The bandpass average is near 1.3%. Coupling of the spectral-retardance oscillations (retarder crystal clocking errors) and the 1400 nm atmospheric-absorption-band errors are significant. We note the $\approx59~\text{m}$ of optical path through air contains significant absorption and temporal variability in this bandpass. When adding 17 modulation variables to create the 36-variable fit, the normalized photometric errors reduce strongly to 0.8% and the wavelength dependence also substantially reduces. The additional 26 variables from fitting the unpolarized input further reduce the error to 0.60% and further reduce the wavelength dependence. The red curve shows the nominal 137-variable system-model photometric errors very close to the 62-variable model errors. These additional 75 variables, corresponding to retarder temporal variation, do not substantially reduce the photometric error.

Figure 8

The $1\sigma$ normalized photometric fitting residuals of the 1872 residual error spectra at each wavelength for the different scenario model fits in units of percent normalized flux. The standard deviation ($1\sigma$) of data − model is computed in intensity units, where the system flux [${I}_{\mathrm{sys}}$] is 1. The photometric fitting error is in units of percentage of the system flux at each particular wavelength. The $y$-scale runs from 0.4% to 2.6% showing we fit the measured intensities to better than 1% in most cases. The blue, green, and black curves show the 17-, 36-, and 62-variable models respectively. The nominal 137-variable model error spectra is shown in red. We also note as red dashed lines the photometric fitting error using the same 137 variables but with the calibration polarizer orientation perturbed by $\pm0.5^{\circ}$.

We also performed a simple perturbation analysis using the official DKIST software modules and the 137-variable scenario. The best-fit polarizer orientation of $87.22^{\circ}$ was perturbed by $+0.5^{\circ}$ and $+1^{\circ}$ to assess the change in wavelength-dependent photometric errors as well as the coupled perturbation of all system-model variables. We detail more of this perturbation analysis in Harrington et al. (2021a, Appendix A) as well as Figures 12 and 27. This perturbation shows that the photometric errors are stable without significant change when the calibration polarizer is rotated by up to $1^{\circ}$. This shows that photometric errors are not extremely sensitive to the assumed polarizer orientation. We note that we could fit for this polarizer orientation, but the system accuracy is clearly impacted and limited. In Appendix A, we demonstrate further what issues arise due to imperfect knowledge of the polarizer orientation and why accurate alignment is required.

3.3 On-Sun System Model – 19 NCSP PolCals and Mirror Polarization Fits

We present here the first on-Sun system polarization calibration for DKIST. We compare the above DKIST system-model results making use of NCSP and the GOS lamp with new calibration observations of the solar disk center also recorded with NCSP. This allows us to fit a system-model with actual solar observations and perform an independent assessment of the articulated mirror polarization model. This new data set allows us to assess the polarization caused by the DKIST primary and secondary mirror, which is a new addition from our prior lamp-based calibrations. We also use this data set to assess the 19 independent instrument modulation matrices derived with each individual PolCal.

On 01 May 2021, approximately three hours of NCSP data were acquired while tracking the center of the solar disk. A series of 15 PolCals was collected between 9:30 and 11:30 local time and an other 4 PolCals were collected from 13:30 to 14:30 local time. The coudé table angle [TA], which sets the field rotation, was commanded to track azimuth $minus$ elevation [$\mathrm{TA} = \mathrm{Az} - \mathrm{El}$] in order to fix the NCSP analyzer orientation against the GOS calibration optics during individual PolCals. We expanded the range of coudé-laboratory table angle offsets to include seven positions in steps of $45^{\circ}$. This increases the table-angle diversity (greater range of angles sampled) to improve the fitting of a new system-polarization model. No table angle was exactly repeated given this tracking mode. With six modulator orientations, we record 1368 spectra, 72 spectra for each of the 19 PolCals.

These data were acquired following the installation and alignment of the calibration polarizer, which used VBI measurements to coalign it with a “master” polarizer that can be installed accurately and externally to the GOS enclosure (see Harrington et al., 2021a, Section 3). We now use that absolute polarizer reference frame as aligned with the M1 and M2 tilt plane, which is also aligned with the azimuth and elevation axes. We set the fused-silica calibration polarizer at the nominal orientation and force the Mueller matrix for the polarizer to be fixed in the DKIST telescope coordinate system. These aligned on-Sun observations allow us to assess the +$Q$ orientation, theoretically removing the need to fit for Stokes input $U$-terms.

In contrast to the above lamp measurement, the azimuth and elevation diversity (range of angles used in the fit) are necessarily reduced when tracking the Sun and dependent on the observation duration as well as time of year. We have roughly $50^{\circ}$ of azimuth diversity in the data set after accounting for the degeneracy of polarization parameters upon $180^{\circ}$ rotation. The elevation diversity is only $34^{\circ}$ from roughly $48^{\circ}$ to $82^{\circ}$.

We compare fits of similar complexity where we give the calibration optics many individual variables or single globally constrained variables. We further assess the use of the DKIST primary and secondary metrology as well as the direct fits to the polarization induced by these mirrors. We list the various model variables in Table 5. We name the scenarios according to the number of variables in the model. The model Max has the maximum number of variables (143). The model Max-1 has one less variable than the Max scenario. The model Min has the minimum number of variables of 52. The first column describes the variables. The second column shows the maximum number of variables used when fitting a system model to our 19 PolCal on-Sun data set. We compare here constrained fits for just the input Stokes-$Q$ in the plane of the M1:M2 mirror tilt axis [$Q_{\mathrm{in}}$] against the metrology on recent coating witness samples. This is listed in the Mx-1 second column of Table 5 as 0 for the $Q_{\mathrm{in}}$ variable.

Table 5 Assessed variables in 19 PolCal fitting.

We test the globally constrained models as the fourth and fifth columns of Table 5. In all of our models we fit the transmission of the calibration polarizer (CalPol) and the transmission of the calibration retarder (CalRet). However, we have the option to fit this transmission function for each of the 19 PolCals separately. This is listed in the second and third row of Table 5 as 1 or 19 possible variables. We always fit the diattenuation and retardance for two groups of DKIST mirrors, as we assessed the mirror retardance is one of the most dominant terms. These variables are listed in the fourth and fifth rows of Table 5. The three elliptical-calibration-retarder (CalRet) parameters can be fit independently for each of the 19 PolCals for 57 total variables. They can also be restricted and fit globally to enforce constancy throughout the day for three total variables. This is sixth row of Table 5.

The fitting residuals in normalized photometric units for this on-Sun NCSP data are at similar levels to the lamp-based models near 0.3% to 1% residual $1\sigma$ amplitudes. We have substantially different observing conditions than the lamp-based system model, confirming the system model is not missing impactful variables. In the left-hand panel of Figure 9, we show the photometric residuals for all 1368 spectra in the NCSP data set when using the global fitting 52-variable model. Residuals are computed as data minus model divided by the model flux. Fitting residuals for visible wavelengths are spectrally flat aside from the NCSP VIS channel sensor array edges. The atmospheric-absorption bands in the infrared create large fitting errors as the photometry is impacted by temporally variable atmospheric transmission. The NIR spectrograph does have lower statistical (shot) noise, but with the atmospheric-transmission variability corrupting the photometric stability in the 1200 nm to 1500 nm band. The right-hand panel of Figure 9 shows the $1\sigma$ photometric fitting residuals for each of the 19 PolCals separately. No PolCal data set is a significant outlier.

Figure 9

The normalized photometric residuals for the 1368 spectra comprising the 19 PolCals recorded in May 2021 with NCSP using the 52-variable scenario. Left shows the normalized photometric fitting residuals computed as data − model after normalizing the flux. Right shows the RMS $1\sigma$ photometric residuals for each of the 19 individual PolCals separately. No individual PolCal stands out as a substantial outlier, showing consistency in the data set. The atmospheric-absorption band from roughly 1100 nm to 1500 nm wavelength has significantly larger errors.

Similar photometric-residual levels are found for all the various scenarios of Table 5. As with the lamp-based system models, including extra variables does not substantially improve the photometric residuals. The error-matrix elements described in later sections and Appendix A however show the fewer-variable scenarios to provide more stable results over the day.

3.4 Articulated Mirror Polarization Consistency: Four Variables Both On-Sun and Lamp

The two main variables populating the telescope database for use in the daily derivation of the instrument modulation matrices are the diattenuation related $X$-variable and phase retardance $\tau$-variable for the mirror groups. We show the polarization properties fit for the two DKIST mirror groups articulated in elevation and azimuth in Figure 10. The right-hand panel shows the retardance of the two mirror groups in degrees of phase. The mirror-group $X$-variable derived from diattenuation in shown in the left-hand panel of Figure 10. We show the metrology in black, the March 2020 lamp-based fits in green, and the May 2021 on-Sun based fits in blue. We use the on-Sun as the nominal database values for now. We note that we have no indication that coating performance changes above measurement-error levels in our years of metrology. We view the differences in curves as a consequence of systematic errors and correlation between the many fitted variables in response to those errors.

Figure 10

The various scenario $X$-variables at left and $\tau$-variables at right. The metrology estimates are shown in black. The Lamp March 2020 NCSP GroupCal fits are shown in green. The on-Sun May 2021 NCSP GroupCal fits are shown in blue. We note that we have reversed the sign of lamp and Sun $\tau _{56}$ for clarity to match typical metrology signs. We have interpolated over the atmospheric-absorption band from 1100 nm to 1500 nm given the large systematic errors.

3.5 Summary: NCSP System Model Fitting from 17 to 137 Variables Sun and Lamp

The system-model fits shown here to the March 2020 GOS lamp data set of Figure 8 show that we can reproduce 1872 NCSP measured fluxes to 0.5% photometric error levels using system models with 62 and 137 variables. A second on-Sun observing campaign also reproduced 1368 measured fluxes from 19 PolCals to similar 0.5% levels as in Figure 9. The metrology for mirror coatings and retarders gives a very close approximation of the system, with both sets of fitted values close to metrology expectations. We began with 17-variable model fits to the lamp-data set to show that the 24-variable modulation matrix matches the mirror and modulator metrology when restricting the modulation matrix to be a grouping of mirrors folded in the $Q$-plane along with the rotating polycarbonate retarder installed in NCSP. The modulation matrix when fit with 24 free parameters matches the metrology-based predictions closely. This 17-variable model for the lamp data set had normalized photometric errors already at 1.3% for all 1872 exposures. The additional modulation degrees of freedom improved this fit to 0.8% normalized photometric error. We then introduced 26 free parameters representing fits for the unpolarized incident flux as different from the estimates created as the average of all modulated exposures without GOS polarizing optics in the beam. These extra 26 variables only improved the photometric errors by 0.16% and did not perturb the other 36 variables substantially. We showed a detailed assessment of all the model variable changes between scenarios in Harrington et al. (2021a), including a sensitivity analysis in Appendix A of Harrington et al. (2021a). The addition of 78 additional retardance variables to account for thermal perturbation of the retarder only negligibly improved the photometric errors from $\sigma$ of 0.61% to 0.58%, a relative change of only 5% while increasing the number of variables by more than $2.2\times$. The preliminary indications here show that fitting free parameters for the thermal behavior of the retarders does not improve the accuracy, while complicating the analysis. As we show below in Section 5, we have a MgF₂-based calibrator upgrade in progress that should substantially improve the thermal behavior.

The four DKIST articulated-mirror-group parameters are the main output of this system-model fitting process. Both retardances and diattenuations are quite stable with the variable exchanges. There is good agreement between on-Sun and lamp-based calibrations. These system-model outputs also agree well with multiple metrology tool outputs. With this fit to the DKIST M3:M4 and M5:M6 polarization, and the associated geometry, we can project measured Stokes vectors from an instrument back onto the M1:M2 coordinate systems. Then with the parallactic angle we can convert Az–El coordinate measurements back onto the Sun. The DKIST polarization databases used to calibrate the science observations beginning in the commissioning phase are populated with the on-Sun derived values presented here with refinements to come as more data are acquired. In the next section we look at errors in these calibrations through both modulation-matrix differences and error-matrix elements.

3.6 On-Sun Daily Calibrations: Statistics on 19 Individual Modulation Matrices

A stable and well calibrated instrument should have the same modulation matrix throughout the day. We assess the NCSP modulation matrices for their temporal consistency. For the nominal DKIST system calibrations, we choose to globally fit the transmission of the calibration polarizer and retarder. We also globally fit the three elliptical retardance values as the nominal procedure for the calibrator. We have compared multiple independent fits where the Stokes-$Q$ input is either fixed at our metrology model or a separate free variable, and generally find better fits when using the metrology-database values.

The 19 individual NCSP modulation matrices are very similar to the values from the globally fit system model. The left-hand panel of Figure 11 shows the modulation-matrix element difference between the global fit during the 52-variable system calibration and the 19 individual modulation-matrix fits during the separate PolCal fits. This highlights differences in time. Each modulated Stokes component is shown as a separate color. The errors are an order of magnitude larger at infrared wavelengths, where atmospheric transparency impacts the low spectral resolution NCSP photometry. The right-hand panel shows the $1\sigma$ modulation-matrix element variation levels on a logarithmic $y$-scale. The $QUV$-errors show some mild wavelength trends at visible wavelengths, being lower where the DKIST mirror-group coatings have smaller retardance. The intensity-based errors in black are near 0.2% magnitude.

Figure 11

The modulation-matrix residual differences computed by subtracting the single global modulation-matrix fit during the system modeling process from each of the individual 19 modulation-matrix fits during the PolCal process. The left-hand panel shows the differences from the group-model modulation matrix on a $\pm3.5\%$ scale. Errors are generally statistical with no very large outliers. The infrared bandpass differences are off-scale and much larger than visible wavelengths. Errors are mildly larger where mirror retardance or diattenuation terms are larger (e.g. 393 nm, 630 nm). The right-hand panel shows the $1\sigma$ magnitudes for these modulation-matrix differences. The full NCSP bandpass is shown on a log $y$-scale to show changes in the infrared atmospheric-absorption bandpass. As NCSP uses a six-state modulation sequence, there are six curves for each Stokes vector. Each color corresponds to a single Stokes component. The $1\sigma$ amplitudes are below 0.7% for wavelengths near 470 nm and 850 nm, where the DKIST articulated mirrors have minimal retardance. The $1\sigma$ amplitudes can be up to 1.5% at 630 nm.

3.7 Error Matrix Elements Using On-Sun Data and 52-variable PolCal Scenario

The error-matrix elements can help assess the level of variation in calibrated Stokes vectors that would have resulted from using any of these 19 individual calibrations to demodulate the DKIST science data. Figure 12 shows the standard deviation ($1\sigma$) magnitudes for the 16 error-matrix elements. These error matrices are computed between the globally fit Group Model modulation matrix and the inverse of the individual modulation matrices derived in each of the individual 19 PolCals (demodulation matrices). We show the 52-variable fitting scenario where the Stokes-$Q$ input is fixed to that created by the M1:M2 group diattenuation from ellipsometric metrology values. The atmospheric-absorption band in our low spectral resolving power system drives the errors to at least an order of magnitude larger than at visible wavelengths. For the high spectral-resolving-power instruments, the atmospheric bands can be resolved and these errors suppressed. We note that the 53-variable scenario, where Stokes-$Q$ input is a free parameter for each of the 19 individual PolCals, produces nearly identical results with only slightly worse error-matrix amplitudes. The four intensity-to-polarization curves are near 0.001 error magnitudes and are shown in black. The colored curves show the $QUV$-to-$QUV$ terms with magnitudes ranging from 0.001 to 0.015. There is a substantial reduction in the cross-talk terms at the two wavelengths where the mirror groups have minimum retardance (450 nm and 850 nm), showing some residual correlated errors between fitting variables.

Figure 12

The standard deviation ($1\sigma$) of error-matrix elements computed from the 19 individual PolCals taken with the 52-variable scenario fits. The modulation matrix derived from the global-group-model fit was used as the reference for true although this introduces its own systematic errors. Black curves show the $I$- to $IQUV$-elements. Blue shows $Q$ to $IQUV$-elements. Green shows $U$- to $IQUV$-elements. Red shows $V$ to $IQUV$-elements.

4 Modulator Fringe Suppression and Design Challenges

The fidelity of the system polarimetric calibration relies not only on the system-model development described above, but upon the control of undesirable and systematic behaviors. In comparison to NCSP, DKIST facility instruments provide much higher spectral resolving powers (generally above 100,000), while typically modulating continuously and acquiring images with fast detectors, some of which utilize rolling shutters. The presence of interference fringes and/or beam wobble (i.e. rotation-induced translation or deflection) can significantly impact polarimetric accuracy and precision, and consequently, DKIST has developed and applied several techniques to mitigate interference fringes in DKIST instrument modulators. We increased the number of spatial fringes (fringes of equal inclination or Hadingers Fringes) by using relatively thick cover windows. We combine this with refractive index matching interfaces to produce an optic in a converging beam suppressing spectral interference fringes. A rotating modulator can introduce polarization errors proportional to intensity gradients (spatial and/or spectral) as wedged optics cause the beam to wobble as the optic is rotated. We worked with Meadowlark Optics to develop new low beam-deflection fabrication techniques to minimize beam wobble in polycarbonate optics. We show here some examples of fringe suppression with ViSP and DL-NIRSP using polycarbonate retarders as modulators.

4.1 ViSP Polycarbonate Modulator: No Detectable Fringes

Recently, we upgraded the ViSP modulator from a stack of crystal-quartz retarders, called the ViSP PCM (Harrington and Sueoka, 2018a), to now use a custom polycarbonate three layer design (Harrington et al., 2020). We used 28 mm thickness of BK7 in two anti-reflection-coated glass windows as well as an index-matching adhesive to keep the refractive index of all components close to the nominal $n=1.6$. The ViSP modulator optic is mounted behind the spectrograph entrance slit, which is an effective heat stop. Ultraviolet flux is substantially reduced from all the enhanced protected silver mirrors. We detailed this polycarbonate modulator in Harrington et al. (2020).

Figure 13 shows a preliminary solar observation taken during ViSP site acceptance testing in 2021. As ViSP is a long-slit spectropolarimeter, each panel of Figure 13 shows a Stokes vector [$I, Q, U, V$] in one spatial dimension (horizontal) and one spectral dimension (vertical). The $QUV$-images show large obvious solar spectral signatures. The Stokes-$I$ image shows the solar atmosphere darkens as the two arcminute long slit crosses a region of solar magnetic activity. The spectral dimension covers roughly 1.1 nm of bandpass centered about the Fe i lines at 630.2 nm. The data have been dark subtracted and flat fielded separately for each modulation state. The flat field also had no detectable fringes. The flattened modulation-state fluxes were processed through the DKIST polarization modules. A PolCal recorded before the observations was used to create a modulation matrix. The ViSP data were then de-modulated. No fringe removal or post-processing techniques were applied. Fringes are not present above the detection threshold.

Figure 13

An example of a ViSP Stokes vectors derived from on-Sun testing during site acceptance in October 2021 at a wavelength of 630 nm. The data have been dark subtracted and flat fielded, but no fringe removal or other post-processing steps were taken. The spectral direction is horizontal covering a bit more than 1 nm of bandpass while the spatial direction is vertical covering more than one arcminute of effective solar field angle. The darker patch in the Stokes-$I$ seen in the left-hand image shows a solar magnetic feature, also corresponding to strong spectral-line signatures seen in the $Q$-, $U$-, and $V$-images. The right-hand image corresponds to $V$. Fringes from the modulator are not present at measurable levels in the ViSP data in any presently collected data sets.

4.1.1 ViSP Modulator Fringes Mitigated with Many-Layer Coatings and Beam F/Number

Here we highlight the combined benefits of this new polycarbonate retarder. We show the impact of the broad-band anti-reflection coatings and thick cover windows used to suppress fringes on the polycarbonate retarder. The original six-quartz-crystal retarder, nominally built for this instrument, was previously described with fringe-magnitude predictions well above the new polycarbonate retarder (Harrington and Sueoka, 2018b,a; Harrington et al., 2017).

Fringe amplitudes are approximated as 4$R$, where $R$ is the single-surface reflectivity for a highly transparent plane-parallel window combined with fringe reduction due to the incident F-number per Harrington and Sueoka (2018a). As measured in the laboratory, fringe magnitudes in transmission windows are well approximated by $4\sqrt{R_{1}}\sqrt{R_{2}}$ for the reflectivity of both surfaces $R_{1}$ and $R_{2}$.

Figure 14 shows the predicted fringe magnitude for a collimated beam compared to an F/32 beam for a range of interfaces. The collimated uncoated BK7 window fringes as the green line would be close to 18% magnitude. The anti-reflection coatings reduce the collimated-beam fringes to the 2% to 5% range seen as the blue line. The fringes are further reduced in magnitude when scaled by the $r^{-2}$ spatial-fringe average we approximate (Harrington and Sueoka, 2018a). The black line shows the additional impact of an F/32 beam and the 28 mm thick windows reducing this fringe magnitude by factors of $20\times$ to over $150\times$ at the shorter wavelengths. We note that the internal refractive-index mismatch between the BK7 and the polycarbonate gives internal fringe magnitudes at levels of 0.1% to 0.5%. The red line shows the internal interface between polycarbonate and BK7. As the individual adhesive layers are estimated at 13 μm thickness, and each polycarbonate layer is only 75 μm thick, there is no change in the F/32 beam compared to collimated for these internal layers.

Figure 14

Fringe magnitudes predicted from coating-reflectivity measurements. Green shows an uncoated BK7 window fringe magnitude. Blue shows a both-sides coated optic in a collimated beam. Fringe magnitudes at F/32 were scaled using the marginal ray path estimates of Harrington and Sueoka (2018a) and are shown in black. The red curve shows the fringe magnitude from the internal interface between BK7 and the imperfectly matched adhesive. Vertical black lines indicate common observing wavelengths of 396 nm, 630 nm, and 854 nm.

4.1.2 ViSP Berreman Fringe Modeling: Coatings and Degraded Resolving Power

The limited spectral resolving power of ViSP will further reduce the measured fringe magnitudes for this new polycarbonate upgrade mounted within the ViSP instrument. This polycarbonate modulator was designed with thick cover windows to make the fringes have very small spectral periods, reducing the detected fringe magnitude. We performed a spectral analysis where we convolved a Gaussian instrument profile with the Berreman models to simulate the reduced fringe magnitudes. Figure 4 and Section 2.3 of Harrington et al. (2020) show the additional impact of spectral smoothing reducing the detected fringe magnitudes. This is similar to the simulations published by Harrington and Sueoka (2018a) from Appendix D on the Keck Telescope LRISp six-crystal modulator fringes.

4.1.3 ViSP Berreman Fringe Modeling: Polycarbonate Layer Flatness

The internal reflections of the polycarbonate to adhesive layers are seen in visual inspection. The magnitude of the reflection is quite small and importantly shows that the polycarbonate layers are not at all flat. The adhesive and polycarbonate have clear shape deviations on spatial scales of several millimeters, comparable to the 8.2 mm beam footprints. The BK7 windows are both themselves flat and are both aligned parallel to reduce the beam deflection (from residual wedge). This optic had beam deflection measured at 2.3 arcseconds. Modeling the internal fringe components for such perturbed internal surfaces would be challenging. The current dominant fringe seen in our laboratory BK7 testing showed that polarized fringes are present at periods corresponding to the cover windows and the interference between both air-facing window surfaces. See Harrington et al. (2020, Section 5, Figure 28) for an example. The internal adhesive and polycarbonate will further complicate a fringe analysis, but with the expectation that fringe magnitudes will be suppressed, leaving only fringes from the flat windows in the modulator.

4.2 DL-NIRSP Polycarbonate Modulator and Fringe Suppression

The DL-NIRSP benefits from fringe suppression by using polycarbonate modulators, similar to ViSP. As a short-term fringe-suppression solution for DL-NIRSP, we adapted one of our spare NCSP polycarbonate retarders as an upgrade for the DL-NIRSP instrument modulator. The original six-crystal DL-NIRSP modulator was designed to be efficient from 900 nm to 2500 nm wavelength (Elmore, Sueoka, and Casini, 2014; Elmore et al., 2014; Sueoka, Chipman, and Elmore, 2014; Sueoka, 2016). However, the farthest infrared arm of DL-NIRSP was de-scoped and several new filters were chosen including wavelengths as short as 530.3 nm. Our laboratory polycarbonate retarders were reasonably efficient modulators with anti-reflection coatings covering a wide bandpass from 380 nm to 1700 nm. The short-wavelength requirements reduce performance at all wavelengths, but this optic should suppress fringes significantly. See Harrington et al. (2020, Appendix D) for details on the optical characterization of this polycarbonate modulator. We created a cell with two tilt axes to adapt the NCSP spare polycarbonate retarder to the DL-NIRSP rotation stage.

The DL-NIRSP feed optics create two separate focal ratios for the beam on the modulator at F/24 vs. F/62. The beam footprints vary between these two configurations. We have detailed the polycarbonate-retarder fringe models in Appendix E of Harrington et al. (2020). We show in Figure 15 the predicted fringe-component magnitudes for this optic. We combine the impacts of anti-reflection coatings reducing fringes as 4R for a highly transparent plane-parallel window along with the impact of F/numbers 24 and 62 per Harrington and Sueoka (2018a). The uncoated BK7 and internal polycarbonate-to-BK7 interfaces are the same as for ViSP. The broad-band anti-reflection coating reduces fringes in the collimated beam. The F/62 beam in DL-NIRSP is predicted to have fringes very similar to the collimated-beam case over the DL-NIRSP wavelength range. The F/24 beam suppresses the collimated-beam fringe magnitudes by roughly $20\times$ at 630 nm wavelength. The F/24 beam reduces the fringe magnitudes by only a factor of three at 1565 nm wavelength.

Figure 15

Fringe magnitudes for the DL-NIRSP modulator predicted from coating-reflectivity measurements combined with the marginal-ray path estimates per Harrington and Sueoka (2018a). Green shows an uncoated BK7 window in a collimated beam. Solid blue shows the impact of the anti-reflection coatings in a collimated beam. The dashed-blue line shows how the DL-NIRSP F/62 beam is almost effectively collimated with only a mild difference between dashed and solid-blue curves apparent at shorter wavelengths. The black line shows the F/24 beam having further reduced fringe magnitudes due to the spatial average over the spatial fringes in the converging beam. Red shows the fringe magnitude from the refractive-index mismatch between BK7 and polycarbonate. Vertical black lines indicate observing wavelengths of 630 nm, 1083 nm, and 1565 nm.

Fringes have been suppressed in DL-NIRSP data to magnitudes below our predictions. Figure 16 shows an example of the recovered Stokes-$IQUV$ profiles. We show this only to highlight the lack of fringes detectable in the recovered image. The spectral-fringe periods are also quite under-sampled by DL-NIRSP, leading to a reduction of fringe magnitudes and a separation of fringes from typical solar signals. At 630 nm wavelength, a single five mm BK7 window gives a fringe period [$\lambda ^{2}/2dn$] of 26 picometers, or one part in 24,000. At 1565 nm wavelength, the fringe period is 161 pm, only one part in 10,000.

Figure 16

An example of DL-NIRSP Stokes-$IQUV$ observation at F/24. The top row shows the 630 nm channel. Middle shows 1083 nm. Bottom shows 1565 nm. Each row shows $I, Q, U$, then $V$ from left to right. The bandpass of each image is of order 1 nm. A clear darkening of a solar atmosphere region is seen in each frame along with an associated increase in the polarized spectral signals, particularly seen as the split $\pm V$ signature for 1565 nm (lower-right-hand panel). Some mild spectral fringes are seen intermittently over the image in the 1565 nm channel. The upcoming custom fringe-suppressing modulator should mitigate any residual fringes.

There are several improvements that will be made in the future DL-NIRSP modulator upgrade. We used a five-layer linear-retarder design in our initial laboratory equipment builds. We plan to deploy in late 2022 a three-layer elliptical-retarder design optimized specific to DL-NIRSP. We have tested a new anti-reflection coating for the DL bandpass (530 nm to 1565 nm) with particular long-wavelength targets to improve fringe suppression. The DL-NIRSP image-slicing system sensitivity to image jitter remains an outstanding question to be addressed in upcoming testing. Laboratory testing suggests the two-axis tilt mechanism on the retarder cell can be used to substantially suppress the image jitter. The current DL modulator uses two cover windows that are only 4.8 mm thick each. Windows a factor of three thicker have been selected to further suppress fringes through both the spatial-fringe averaging, as well as increasing the spectral-fringe period a factor of three faster, beyond detection limits at the shorter wavelengths sampled by DL-NIRSP.

5 Calibrator Fringe Suppression and Design Challenges

The DKIST Gregorian Optical Station (GOS) presently contains three calibration retarders. As described in Section 3, these are used for end-to-end polarization calibration of the entire system, including both the articulated telescope mirrors as well as the instruments (Harrington, Sueoka, and White, 2019). These optics must function in the F/ 13 beam to high accuracy with high spatial uniformity over a 105 mm aperture under 300 watt load, withstanding substantial UV irradiation, in a variable-gravity environment, and while operating at variable mountain-outdoor temperatures. The nominal suite of calibration retarders detailed by Harrington and Sueoka (2018b) were all super-achromatic retarders (SARs) made of three compound retarders in A-B-A style, each with six crystals total. We added to this list an optically contacted compound retarder (OCcal) in Harrington et al. (2020). This optic is not achromatic and is net zero order after two crystals are used for subtraction.

5.1 Optical Contact Development on Large Crystals: SiO₂

We worked with Meadowlark Optics (MLO) starting in 2017 to pursue optical contact as a bonding technique given several performance advantages. A contact bond removes any refractive index mismatch issues with oils or bonding agents. Fringes are created at very low levels from the mis-match between ordinary and extraordinary indices at the internal interface. Contact bonding also removes any infrared absorption bands from oils and removes the possibility for any degradation, seal leaks, or bubble developments. The optical contact bond should be compliant with long-lifetime requirements in the presence of 300 watts of optical power with substantial ultraviolet flux. Harrington et al. (2020) showed that we can achieve very tight clocking requirements ($<0.3^{\circ}$) simultaneously with low deflection and spatial-uniformity requirements. Details are in Appendix B. We summarize here the focal-ratio dependent fringe predictions and compare the super achromats (SARs) to the optical-contact retarder (OCcal).

The OCcal design calls for a net 0.23 waves retardance at 630 nm wavelength in the compound zero-order configuration. One crystal (the subtraction plate) is polished 15.97 μm thicker than the other (bias plate) to achieve this net retardance in subtraction with the fast axes for each crystal optically contacted at $90^{\circ}$ rotational orientation. The optically contacted quartz calibration retarder configuration is shown by Harrington et al. (2020, Table 6). The MLO measurements for each of the two crystals gave thicknesses of 4.234 mm and 4.247 mm, respectively. These thicknesses are used in the fringe modeling. The broad-band anti-reflection coating is about 700 nm thick and is 17 layers.

A further manufacturing challenge was maintaining a defect-free, clear aperture at 105 mm diameter while also minimizing the spectral-clocking oscillations. Harrington et al. (2021b) simulated the impact of transmission defects along with several other artifacts. Transmission uniformity of each particular Calibration Polarizer (CP) used in the Calibration Sequence (CS) was identified as a large issue. Defects in the optical-contact bond were similar to Harrington et al. (2021b, Figure 6).

5.2 DKIST Calibration Retarders

In Harrington et al. (2020, Table 4) we outlined some of the optical details of each crystal-retarder design. Table 6 lists the name of the current calibration-retarder optics in the first column. The SAR names originally corresponded to the wavelength range covered by a particular instrument. Both the instruments and the calibration techniques have changed bandpasses in subsequent years. The nominal DKIST requirement for these optics some years ago was for each calibrator to be a $90^{\circ}\pm30^{\circ}$ magnitude linear retarder also with an achromatic fast-axis orientation within some wavelength bandpass. However, we can easily calibrate all wavelengths with an elliptical retarder of any axis orientation. This allows us to use these optics over a much wider wavelength range for calibration. We also note that a wavelength-dependent fast axis as well as circular retardance are already present in these optics and successfully fit by the DKIST calibration software. A chromatic elliptical calibrator is sufficient to calibrate, just as it is sufficient to modulate. Fabrication of an elliptical calibrator (EliCal) using MgF₂ crystals is complete. The optic is installed on the summit as of late 2022 with on-Sun testing anticipated during 2023. We list this optic in Table 6 and detail the performance below.

Table 6 DKIST calibration retarder names and designs.

In the second column we list the crystal material. The third column shows the individual crystal thickness (Thk. Indiv.). The fourth column shows the total thickness of the retarder stack (Thk. Total). We note there is a detailed description of the individual crystal metrology of these optics published by Harrington and Sueoka (2018b) and Harrington et al. (2020). The fourth column of Table 6 shows the nominal wavelength range where the optic passes the original DKIST specification as a calibrator. Calibration at less efficient wavelengths has already been done for both OCcal and the VISP SAR, without substantial change in calibration output.

5.3 Quartz Retarder Fringes Mitigated at F/13: ViSP SAR vs. SiO₂ Optical Contact

We have used both the ViSP SAR and the new crystal-quartz optically contacted retarder (OCcal) to calibrate DKIST. We compare fringes in these two crystal-quartz calibration retarders here to show the application of fringe mitigation techniques. The left-hand panel of Figure 17 shows the six-crystal ViSP SAR with fringes from 2.1 mm and 12.8 mm thicknesses of quartz. We show the inner 2.1 mm crystals interfacing with both air and oil. The right-hand panel of Figure 17 shows the optically contacted quartz retarder. Solid lines show a collimated beam, while dashed lines show the impact of the F/13 spatial fringe scale factor. Blue shows the air interfaces, while red shows the internal extraordinary to ordinary interface mismatch interfering with the opposite air interface. Note that the dashed red curve is below $4\times 10^{-5}$ for short wavelengths and is off scale.

Figure 17

Fringes for each optical interface. Left shows the ViSP SAR. Right shows the Optical Contact Calibration retarder (OCcal). Fringe magnitudes in both optics are shown as solid lines in a collimated beam. Dashed lines include marginal-ray path $r^{-2}$ scaling in the F/13 beam. At left, the ViSP SAR has three main interfaces: From air through coated crystals to air, from air through coated crystal to oil, and from oil through coated crystal to oil. The right panel shows the air through coated crystal to air fringe for the optical-contact retarder. The dashed line shows the internal fringe created from the index mis-match between ordinary and extraordinary beams. At 1565 nm wavelength, the ViSP SAR would be expected to fringe at 1% amplitudes and a period corresponding to 2 mm of quartz in an F/13 beam. The OCcal has fringes near 0.2% at a spectral period corresponding to 8.4 mm of quartz.

The maximum fringe in the F/13 beam for the ViSP SAR is anticipated to occur from the air-to-oil interfaced first and last crystal. This corresponds to the dashed-blue curve in the left-hand panel of Figure 17. The spatial-fringe average reduces spectral fringes from the 2.1 mm crystals by a factor of $30\times$ at 396 nm wavelength, but only by $3.2\times$ at 1565 nm wavelength. The wavelength dependence of the coatings and also mis-match with the oil gives a fringe-magnitude prediction of 0.11% at 396 nm wavelength up to 1.77% at 1565 nm wavelength after accounting for the $r^{-2}$ reduction factor. These fringe magnitudes are an order of magnitude larger than those of the optical-contact retarder over the same bandpass.

In Table 8 of Harrington et al. (2020) we outlined the individual layers in the Berreman fringe model for this retarder. The anti-reflection coating is a single isotropic MgF₂ layer at 97 nm physical thickness corresponding to a quarter wave at 525 nm central wavelength (CWL). The refractive-index mismatch is modeled to be 0.265 dropping to 0.24, which gives rise to internal reflections of roughly 0.8%. Had a suitable $n=1.5$ oil been identified with an index mismatch below 0.05, this internal reflection could have been reduced by factors of at least $30\times$, reducing the internal fringes by factors of five or more. The fringes in this achromat could have been near levels achieved by the optical-contact retarder if proper oils could be found and had been sealed effectively. We also note that this upgrade included testing of many-layer broad-band anti-reflection coatings on very high aspect-ratio crystal quartz retarders. Significant issues with depth dependence of temperature, wedge angle, and environmental response also complicate the design trade studies.

5.4 MgF₂ Elliptical Calibrator for 0.39-μm to 5-μm: Optical Contact Development

Optimizing an elliptical calibrator for calibration efficiency is the same procedure as optimizing an elliptical modulator for modulation efficiency. We created an elliptical-calibrator design using two MgF₂-based compound retarders to calibrate the 380 nm to 5000 nm bandpass strictly simultaneously. A two-pair design can calibrate this bandpass with relative efficiencies balanced within a factor of two. The efficiency balance is somewhat improved over this bandpass using three-pair-super-achromatic designs. However, there are several fabrication issues, costs, yield limits, AOI dependence, and potential systematic errors. We consider a 2:1 relative spectral difference in statistical noise between Stokes components to be relatively unimportant. Often the major calibration limitation is the many other systematic errors at levels far above statistical limits. Fabrication of this optic is mostly complete, with expected deployment possibly in 2022.

We continued development of calibration retarders by funding and collaborating with Meadowlark Optics on improved fabrication techniques using new large-aperture MgF₂ crystals. We pursue several improvements simultaneously to reduce the sources of systematic errors in DKIST calibration. Meadowlark first had to develop the polishing and fabrication techniques for successful optical-contact bonding of MgF₂ over a 120 mm aperture. We now have a few contacted pairs with no substantial defects in the clear aperture. Clocking mis-alignments have been in the range $0.05^{\circ}$ to $0.2^{ \circ}$ – a substantial improvement. This MgF₂ material offers greatly reduced absorption through the much higher infrared transparency in the 2500 nm to 6000 nm bandpass. For instance, our thermal predictions of Harrington and Sueoka (2018a, Appendix B) show our quartz calibration retarders should expect heating of a few watts. MgF₂ retarders seeing orders of magnitude less heat absorbed as the upstream glass-polarizer substrate blocks any absorbable infrared radiation. Heat limitations for MgF₂ crystals becomes ambient mountain environment changes along with power dissipation within the rotary stages.

Modeling of the calibration efficiency is straightforward using the efficiency equations. Similar to the Harrington and Sueoka (2018b) and Harrington et al. (2020) models, there are significant changes in the calibration efficiency and duration depending on the calibration sequence. The number of input states influences the efficiency but more states extend the calibration duration. Efficiency is also impacted as the optic starting orientation is varied. This four-crystal elliptical retarder has efficiency ranges very similar to the other DKIST retarders. We show examples of the $IQUV$-calibration efficiency in Figure 18 accounting for the 50% calibration polarizer selecting only one linear state. We model a standard 16-state calibration sequence as the optic orientation is varied in $45^{ \circ}$ steps. The thicker lines show the optic starting orientation for having the highest minimum efficiency for any Stokes parameter across the 380 nm to 5000 nm bandpass. The $I$-efficiency is a constant 50% for this long sequence. We note that a new sequence with a few additional states and further state-orientation optimization will be done for this optic once the as-built retardance values are measured and we can balance the thermally induced systematic errors in the optimization. We already have optimized a ten-state sequence having similar efficiencies to Figure 18.

Figure 18

The $I, Q, U$, and $V$ calibration efficiency for the four-crystal MgF2₂ elliptical calibrator as the optic starting orientation is varied. Stokes-$I$ efficiency is shown in black. Stokes-$QU$ efficiency is shown in blue. Stokes-$V$ efficiency is shown in red. We include the 50% efficiency loss for single-beam polarimetry, as the calibration polarizer picks out only a single linear state. We use a 16-state ASP-style sequence as by Harrington et al. (2020). The thick line shows an optic starting orientation chosen to have the highest minimum calibration efficiency in any Stokes parameter across the 380 nm to 5000 nm bandpass. The thinner lines show the optic starting orientation varying in $10^{\circ}$ steps through $180^{\circ}$.

6 Summary

We have demonstrated the first on-Sun polarization calibration of the DKIST telescope using a new custom metrology instrument called NCSP. This calibration will be applied to all upcoming DKIST science observations, beginning with those taken during the observing commissioning phase (OCP). In Section 2 we laid out the major elements of the system-polarization model, including articulated groupings of mirrors and the formalisms used to created the Mueller matrix as a function of azimuth, elevation, and coudé-table angle. We showed the application of calibration-efficiency equations and described the DKIST calibration sequence consisting of modulated flux recorded for ten input states. The calculation of polarization errors via the $4\times4$ error matrix was shown in Section 2.8 as a way to quantify the inaccuracies in calibrating an incident Stokes vector.

In Section 3 we show the NCSP installed within the telescope coudé laboratory. We compare two procedures for creating a polarization model of the system, often called a group model or GroupCal. We showed our prior system model using the DKIST calibration lamp compares very well with these new direct solar observations. Both procedures give very consistent results for the DKIST mirror-group properties, even though both data sets were separated by 14 months, used different calibration retarders, and have completely different light sources.

In Section 3.6, we use NCSP to show examples of error matrices and fitting outputs during the daily calibration procedure commonly called a PolCal. This PolCal process uses the DKIST system-model database values and telescope-pointing information to derive the instrument’s modulation matrix, used to calibrate observations. This process will be used by all DKIST instruments to calibrate polarimetric science data in the commissioning phase. We showed how 19 individual on-Sun modulation matrices were consistent over five hours of NCSP data acquisition. The so-called cross-talk components of the error matrix had $1\sigma$ magnitudes below 1% in all visible wavelengths not impacted by infrared atmospheric-absorption variation. The intensity-to-polarization terms had $1\sigma$ levels near 0.2% levels for the same wavelengths. We showed how we reproduce the expected retardance values in these fits for both the super achromatic six-crystal retarder as well as a single optically contacted compound retarder. We also recover the input M1:M2 diattenuation values near metrology predictions at levels below 0.8% with some variation at wavelengths where the DKIST mirror coatings have relatively higher retardance. We note that the success of this single fit, based on three hours of calibration data recorded on one single day will improve as more data are acquired.

We show the first-ever ViSP measurements with suppression of interference fringes below detectable levels for ViSP in Section 4.1. We outline a new polycarbonate modulator deployed on the instrument along with on-Sun calibration data showing that neither the modulator nor calibrator create substantial fringes. We show some information about the field-angle dependent demodulation and few percent efficiency losses from using relatively non-uniform modulators in the Appendix. This minor complication is easily outweighed by the complete lack of fringes. We show in Section 4.2 some of the same fringe-reduction optical techniques applied to DL-NIRSP through adapting a replica of our NCSP modulator to DL-NIRSP. Fringes are well suppressed. A DL-NIRSP optimized modulator was fabricated and installed in late 2022, now that other optical performance issues are known well enough to apply fringe suppression techniques for a custom modulator.

In Section 5 we outline the optical-contact technique that assisted in suppressing fringes from the calibration retarder. We introduced here a new elliptical MgF₂ calibration-retarder design also using optical contact. This elliptical calibrator is designed to cover the entire 380 nm to 5000 nm with efficient calibration, using strictly simultaneous observations for the same ten-state calibration sequence. Fabrication is complete, and we anticipate on-Sun demonstration in 2023. Substantial optical improvements include the relative alignment of crystals to levels of $0.1^{\circ}$ and deterministic fluid jet polishing to achieve uniform retardance. Given the greatly improved infrared transparency of MgF₂, the anticipated thermal stability should be more than an order of magnitude better.

We show in the Appendices the polarization response of every coated optic contributing to the polarization of DKIST measured on coating witness samples. We address coating incidence-angle variation, wavelength dependence, depolarization through optic curvature (power), and coating uniformity. We also detail known limitations from dichroic-coating spatial variation and narrow spectral features. We show metrology of a newly designed and fabricated more uniform calibration polarizer recently deployed on the telescope. We include the contrast and orientation of maximum extinction variation across the aperture and with wavelength as we anticipate this new polarizer to be used in the near future. Recent polarizer-alignment activities and a perturbation analysis of the system-model fitting techniques in Appendix A show that we have stable fit outputs and that we understand the sensitivities to errors in our model assumptions. The Mueller matrices of the calibration optics have been shown across individual de-centered, spatially variable beam footprints. We thus can derive the DKIST instrument field of view where system calibration errors fall below particular error-budget limits, letting users determine the size of the field calibrated to within user-specified error limits.

DKIST initiated one of the most thorough polarimetric system-characterization efforts to date. Mueller-matrix terms for all contributing optics have been measured in the laboratory, often with custom-built tools. The preliminary Mueller-matrix model fits to the system agree with metrology and also agree between NCSP fits using multiple, independent light sources (lamp vs. Sun). There is a very long list of future calibration upgrades and accuracy verification campaigns planned with multiple DKIST instruments. As more data are acquired with new, improved optics, calibrations will improve. For the ongoing science-commissioning campaigns, we expect the new on-Sun calibrations presented here to be used to deliver a well-calibrated field around the bore-sight delivered to the first-light instrument suite.

Upcoming work will certainly include the first on-Sun use and calibration of the system using the upgrade polarizer and upgrade elliptical MgF₂ calibration retarder. As DKIST instruments go through the operations commissioning phase (OCP), particular calibration strategies and fitting techniques likely will be updated. Each DKIST instrument will have its own challenges possibly requiring changes to the fitting process, database values, or observing techniques. We anticipate at least yearly assessment and update to the mirror-coating polarization models and testing of any temporal evolution of the coatings. Both lamp-based and on-Sun NCSP system models should address any residual errors in the system polarization model. The Cryo-NIRSP should soon begin observing at infrared wavelengths of 3.9 μm and 4.6 μm, where the system-polarization model will need to be extended beyond the 1.7 μm NCSP wavelength limit, initially using the ellipsometry-based model. We presented estimates of the polarization model dependence with effective field of view. Our system model could be extended to include some field-dependent effects if necessary. Depolarization is only modeled in the imperfect contrast of the calibration polarizer. Additional depolarization degrees of freedom can also be included in the system model, or the model for particular optics (e.g. calibration retarder) should these errors arise. We also plan to begin using the ViSP for several additional kinds of polarization-accuracy verification tasks after progress has been made in the science-commissioning phases.

Appendices

Appendix A: Polarization Reference Frames and System Models

1.1 A.1 Master Polarizer and Absolute Coordinates

The absolute polarization-orientation reference for DKIST is set by an optic called the Master Polarizer. All DKIST calibration polarizers are aligned to the altitude–azimuth coordinate frame using the Master Polarizer and measurements of crossed polarizer extinction orientations. An external polarization reference frame tied to solar coordinates is required to provide accurate orientations for the Stokes vectors derived with DKIST instruments. We have multiple DKIST calibration polarizers with the possibility for cleaning, polarizer replacement, and possible future upgrades. We designed this Master Polarizer optic to provide a stable long-term polarization reference frame. For alignment details on the initial fused-silica calibration polarizer see Harrington et al. (2021a, Sections 3.3 and 3.4, Figures 5 through 7). For details on the sapphire-substrate polarizer, see Harrington et al. (2021b, Appendix E, Figures 49 and 50).

This Master Polarizer is a Moxtek UVT240A fused-silica substrate wire-grid polarizer with a conformal protective coating over the wires. This optic was bonded with the polarizer wires down into a special cell that includes three Spherically Mounted Retroreflectors (SMRs) for reference with the DKIST laser tracker metrology tools and telescope coordinate system. Harrington et al. (2021a, Section 3) detailed a laboratory procedure where we oriented the transmission axis of the polarizer (+$Q$ Stokes axis) to these SMRs and the associated SMR nests, bonded directly onto the polarizer cell, using a laser tracker and a coordinate-measuring machine (CMM) arm. This Master Polarizer transmission axis was then aligned on summit to the telescope coordinate system using a laser tracker in January 2020. This provides a well oriented polarizer transmission located in the telescope coordinate reference frame with an estimated error of $\pm0.06^{ \circ}$.

This Master Polarizer was placed in a rotary stage on the top-most Gregorian Optical System (GOS) level furthest away from the Gregorian focus. This level is upstream of the suite of calibration polarizers. We can put both the Master Polarizer and any DKIST calibration polarizer in the beam at the same time. We use Malus’ Law to fit for an intensity null between crossed polarizers. This defines the motor position for each of the calibration polarizers corresponding to the intensity null. Given this null, we have the polarizer in the absolute telescope coordinates, with the +$Q$ transmission axis aligned with the M1:M2 tilt plane. These absolute coordinates are used to transfer the DKIST coordinate system into solar coordinates establishing a tolerance on the DKIST measured polarization frame relative to solar coordinates.

We used this Master Polarizer with both the VBI instrument along with our NCSP metrology system to align the various DKIST calibration polarizers in August 2020. We thus align the calibration-polarizer transmission axis to the shared tilt axis of the DKIST primary and secondary mirrors (M1:M2).

Unfortunately, the software team discovered a bug in the rotary-stage code causing incorrect behavior upon homing our custom rotary stages. We repeated the Master Polarizer alignment with the laser tracker and found an identical orientation for the Master Polarizer with similar errors below $\pm0.1^{\circ}$. We also repeated the VBI observations to align the calibration polarizers using the Master Polarizer in December 2021. We identified and applied a $\approx2^{\circ}$ rotational offset to the current fused silica polarizer. This fit has also been applied to the on-Sun NCSP measurements presented here, and it does improve the error-matrix values substantially.

1.2 A.2 System Model Variable Sensitivity to Assumed Calibration Polarizer Orientation

The many variables included in a system model correlate very strongly. Photometric error is relatively low for a wide combination of calibration retardance, mirror retardance, and modulation-matrix terms. The calibration polarizer reference orientation is not a variable easily fit while preserving accuracy of a system model. Harrington et al. (2021a, Appendix A, Figure 27) showed how the lamp-based NCSP system-model fits were skewed by a change of $\pm0.5^{\circ}$ in the calibration-polarizer assumed orientation. Harrington et al. (2021a, Figure 12) showed how perturbing the calibration polarizer orientation barely changed the photometric errors. The photometric error is easily minimized by an overly complex combination of tens of variables. Having too many inaccurate variable fits with quite unphysical or inaccurate optical parameters leads to inaccurate calibrated Stokes vectors when calibrations are applied under different optical circumstances.

We perturb the assumed calibration-polarizer orientation here for the NCSP on-Sun data set from May 2021 and re-fit the system model (GroupCal). Figure 19 shows the key impacted model variables. We re-fit the system model as the calibration polarizer varies by $\pm4^{\circ}$ about this December 2021 updated orientation. The mirror-group retardance [$\tau$] and diattenuation [$\Delta$] along with calibrator transmission [$T$] are shown in the first two rows. The third row shows the elliptical retardance of the calibrator, where the first linear component (Lin1, $r_{x}$) and second linear component (Lin2, $r_{y}$) mostly see a rotation along with the polarizer rotation. The circular retardance (Circ, $r_{z}$) has a more complex spectral dependence where errors correlate with the magnitude of the mirror retardance. The fourth row shows $QUV$ modulation-matrix elements. The fifth row shows $I$-modulation, the system throughput in parts per thousand [${I}_{\mathrm{sys}}$], and the M1:M2 mirror-group diattenuation creating Stokes-$Q$ incident on the calibration optics ($Q_{\mathrm{in}}$ from $\Delta _{12}$). We fit the system model both with and without the $Q_{\mathrm{in}}$-variable corresponding to the input Stokes-$Q$ created by M1:M2 group diattenuation. The correlated variation in all parameters is similar to the lamp-based sensitivity analysis of Harrington et al. (2021a). We can now show that the on-Sun behavior is similar, and fitting for the input diattenuation from M1:M2 is easily possible although correlated with other variable errors to levels well above our metrology inaccuracies. For the initial DKIST science observations, we consider the metrology to be a more accurate reference than the fit until we accumulate more than a few hours of NCSP data on one single observing day.

Figure 19

The response of particular system-model variables to a perturbation of $\pm4^{\circ}$ in the calibration polarizer orientation. See text for details. See Harrington et al. (2021a) for an in-depth system-model assessment.

1.3 A.3 Photometric Error Sensitivity to Assumed Calibration Polarizer Orientation

The photometric error represents the nominal success criteria of our calibration fitting. The model variables are adjusted until the predicted intensity is as close to the measured intensity as possible, driven by minimizing the sum of the squared errors with weights as described by Harrington et al. (2021a). When fitting a model that includes strong correlations between many variables, the fit can be quite insensitive to particular parameters. For the orientation of the reference polarizer, photometric errors are not sufficient to constrain the orientation anywhere nearly as accurately as modern metrology tools. Furthermore, an error in the calibration-polarizer reference represents an unmitigated systematic error in all Stokes vectors recovered in this inaccurate coordinate system. We have a nominal specification of $\pm0.1^{\circ}$, which was easily achieved with our laser tracker, laboratory procedures, and on-Sun alignment procedures, as shown by Harrington et al. (2021a,b).

A recent discovery of a rotary-stage software bug prompted a re-analysis of the NCSP on-Sun data, as well as repeating of our alignment procedures. We found that the Master Polarizer reference orientation was unchanged with errors below $0.05^{\circ}$. However, we did discover that the calibration-polarizer was improperly oriented by roughly $2^{\circ}$. In response, we re-calibrated this optic and also show a tolerance analysis here. As an example of the impact on photometric fitting errors, we re-fit nine entirely unique system models where we assume the DKIST calibration-polarizer orientation is in the range of $84^{\circ}$ to $92^{\circ}$ in steps of $1^{\circ}$. The photometric-fit residuals do respond, but only significantly at wavelengths where the DKIST mirror coatings in the articulated mirror groups has significant retardance. The left-hand panel of Figure 20 shows the $1\sigma$ photometric-fit residual error spectra for each of the nine independently fit system models. We compute the standard deviation over all 1368 spectra. The blue curves representing $84^{\circ}$ and $92^{\circ}$ are the farthest away from the nominal expectation. The black curve at $88^{\circ}$ is closest to achieving minimum photometric fit residual error.

Figure 20

The photometric fitting error in the system model. The difference between the predicted flux and the measured flux is used to compute $1\sigma$ error levels in percent of normalized counts (maximum detected brightness = 100%). The left-hand panel shows the $1\sigma$ error levels as the calibration polarizer assumed orientation is changed $\pm4^{ \circ}$ about the nominal guess $88^{\circ}$ orientation. The right-hand panel shows the change in these $1\sigma$ levels from the minimum in units of percent for a few select wavelengths. Response is strongest at wavelengths where the articulated DKIST mirrors have the largest retardance. Response is smallest at two wavelengths (470 nm and 850 nm) where the articulated mirrors have nearly zero retardance.

The right-hand panel of Figure 20 shows these photometric-fitting residual errors as a function of assumed calibration-polarizer orientation. Wavelengths where the DKIST mirror coatings have minimum retardance show very small response (470 nm and 850 nm). Wavelengths with larger mirror-retardance values show stronger coupling of photometric fitting errors to the assumed calibration polarizer orientation.

1.4 A.4 Modulation-Matrix Sensitivity to Assumed Calibration Polarizer Orientation

The modulation-matrix elements were also derived in nine completely independent calibrations using the nine separate system-model fits. We treat all 19 individual data sets as separate to compare the differences over the day in response to changes in the assumed calibration-polarizer orientation. These modulation-matrix elements also have very different responses with some terms changing quite substantially, and other terms changing very mildly. Figure 21 shows the modulation-matrix element differences between all 19 individual PolCal derived modulation matrices and the globally fit system model derived modulation matrix as the calibration-polarizer orientation is perturbed $\pm4^{ \circ}$ about the nominal guess $88^{\circ}$ orientation. As with the photometric fitting residuals, small changes are seen at wavelengths of 470 nm and 850 nm, where the DKIST mirror retardance is smallest.

Figure 21

The modulation-matrix response to CalPol orientation perturbation $\pm4^{\circ}$. Left shows $84^{\circ}$ assumed polarizer orientation, middle shows the nominal $88^{\circ}$, right shows $92^{\circ}$. Each color shows the six modulation states corresponding to a particular Stokes parameter.

1.5 A.5 Error Matrix Sensitivity to Assumed Calibration Polarizer Orientation

The calibration accuracy is impacted substantially through the assumed orientation of the calibration polarizer. The different error-matrix elements are individually impacted with some terms more than an order of magnitude more sensitive than others. We can assess the consistency of the derived modulation matrix and error-matrix elements after re-fitting the nine independent system models. The 19 individual PolCals are treated as separate independent calibrations. The error matrix in each case is derived using the appropriate globally fit modulation matrix derived during the system-model fit at each particular assumed calibration polarizer orientation. Figure 22 shows the $1\sigma$ error-matrix magnitudes across all 19 individual PolCals as the assumed calibration-polarizer orientation is varied $\pm4^{\circ}$ about the nominal guess $88^{\circ}$ orientation.

Figure 22

The error-matrix $1\sigma$ magnitude response to CalPol orientation perturbation $\pm4^{\circ}$. Left shows $84^{\circ}$ assumed polarizer orientation, middle shows the nominal $88^{\circ}$, right shows $92^{\circ}$. All panels use a Log-$y$ scale. Particular linear polarization modulation terms stand out as responding by a factor of several higher than others.

The parabolic behavior showing strong response to the assumed calibration-polarizer orientation in error-matrix elements is only present for certain elements. Figure 23 shows error-matrix $1\sigma$ magnitudes as the assumed calibration-polarizer orientation varies at three select wavelengths. As expected, at wavelengths where the articulated DKIST mirrors have higher retardance, the error-matrix elements respond stronger to the polarizer orientation change. However, not all error-matrix elements show minimum error at exactly the same assumed polarizer orientation.

Figure 23

The error-matrix response to changes in the assumed calibration polarizer orientation at wavelengths 393 nm at left, 630 nm in the middle, and 850 nm at right. Each color shows a different error-matrix element. Only certain error-matrix elements show an obvious dependence on the assumed calibration polarizer orientation. At 854 nm, there is relatively low sensitivity to orientation changes. For all wavelengths, different calibration polarizer orientations are found for different error-matrix element minima. This shows the need for exterior knowledge of the calibration polarizer orientation, as minimizing these error-matrix elements gives low accuracy results.

1.6 A.6 System Model Complexity

Testing with DKIST fits so far suggests that adding additional system-model variables degrades the calibration accuracy, while negligibly improving the photometric error. We find that minimizing the number of variables with detailed system metrology and optic characterization leads to more robust and accurate fits. Given the strong correlations between the many possible variables, a mild photometric error can perturb an important polarization variable, which will irrecoverably corrupt future calibrations. We show some examples here of fits to some of the many possible optical variables considered.

1.6.1 A.6.1 On-Sun Fitting: Calibrator Retardance Temporal Drifts

The stability of the calibration retarder is a major limitation to overall accuracy. Thermal forcing can drive both bulk-retardance temporal changes as well as spectral drifts of the clocking oscillations (see Harrington and Sueoka, 2018a; Harrington et al., 2020). The left-hand panel of Figure 24 shows the OCcal retardance parameters fit globally to all PolCals during the 53-variable system model. The retardance values were rotated by $191^{\circ}$ to make the first linear component near maximum and with positive sign. The second linear component and the circular component contain the vast majority of the spectral clocking oscillations at this orientation. These two curves have been multiplied by $20\times$ to clearly show the oscillations. We also note the divergence of these two components from zero in the infrared atmospheric-transmission band, showing the level of systematic-error impact.

Figure 24

The left-hand panel shows the retardance parameters for the OCcal fit during the 53-parameter system model. The parameters were rotated by $191^{\circ}$. The green and red curves show the bulk of the spectral-clocking oscillations in this orientation and have been multiplied by $20\times$ for clarity. The right-hand panel shows the clocking oscillations in both the second linear and circular components in a 40 nm bandpass around 515 nm wavelength. The linear component was offset by $+1.6^{\circ}$ for clarity. The spectral-clocking oscillations are obvious, but temporally stable.

In the right-hand panel of Figure 24 we show the 19 individual retarder parameter fits to the individual PolCals during the multiple independent fits representing the independent instrument calibrations. Only the circular component and second linear component are shown at this $191^{\circ}$ orientation to highlight the clocking oscillations. The spectral-clocking oscillations are reasonably stable in phase for all 19 individual fits. The bulk-retardance levels do seem to change by $\pm0.5^{\circ}$ over the 19 individual fits. This level of magnitude error could be entirely systematic errors. The bulk-retardance changes simulated by Harrington et al. (2020, Figure 20) show that simple thermal changes of the retarder crystal is an order of magnitude below the changes seen in Figure 24. It is easily assumed that this $\pm0.5^{\circ}$ drift represents the systematic error limits of these individual fits.

1.6.2 A.6.2 On-Sun Input Parameter Fits: Transmission and Input Stokes-$Q$

Fitting for the Stokes-vector partial polarization incident on the GOS calibration optics is certainly possible. This allows us to fit for the diattenuation of the DKIST primary and secondary mirror group (M1:M2) and compare it to coating-sample metrology. It remains an open question as to whether fitting for these variables, or using some other metrology-based fixed values with their own systematic errors, leads to more accurate modulation matrices and ultimately DKIST science. We show in this section how we can fit for the input Stokes-$Q$ as well as for the transmission of the polarization-calibration optics. In both cases, photometric errors drive the fits systematically away from laboratory metrology values. In particular, the fitting for Stokes-$Q$ during an individual PolCal seems far less robust and farther away from metrology than the agreement we do get during the group model fitting process.

The right-hand panel of Figure 25 shows the diattenuation fit to the Stokes vector incident on the calibration polarizer at GOS. The 19 individual green curves are comparable with the group-model fit, shown as the solid-blue curve. We also compare with the M1:M2 mirror-group diattenuation metrology model shown as the black curve. Clearly the systematic errors drive the input $Q$ fits over a range of $\pm1\%$ from the nominal value. The atmospheric-absorption band has erratic fitting outputs that are a large factor worse, with values ranging more than ±3%, off the scale of the figure.

Figure 25

The left-hand panel shows 19 individual transmission fits to each individual PolCal as separate curves in blue for the CalRet and in black for the CalPol. The thicker green and red curves show the global fits to the respective transmission functions derived combining all 19 PolCals during the 55-variable Group Model fit using all 19 measurements simultaneously. The polarizer-transmission function in particular shows stronger coupling to the retardance spectral-clocking oscillations as well as some VIS spectrograph-sensor fringing. The right-hand panel shows input Stokes-$Q$ incident on the polarization calibration optics fit, attributable to the M1:M2 mirror group. The left-hand panel shows the $Q$-diattenuation fit during the 52-parameter group model as the blue curve. The black curve shows the Woollam ellipsometry on the M1 (2020 recoat) and M2 coating witness samples at an incidence angle of $15^{\circ}$ with an adjustment to the M2-values. Note that in the 52-variable scenario, the $Q_{\mathrm{in}}$ variable is forced to be this black curve. The right-hand panel shows the same two blue and black curves for reference. Each of the 19 green curves shows one of the 19 individual fits done during the PolCal when the $Q_{\mathrm{in}}$ variable is left as a free variable.

The left-hand panel of Figure 25 shows the transmission fits to the CalPol and CalRet optics in the 53-variable group model fitting scenario, as well as the 19 individual fits during the simulation of the daily calibration PolCal process. Multiple individual thinner lines show the 19 individual PolCal transmission fits. Thick solid lines show the global group model fits. The general spectral shape of both curves is reproduced, but there are variations of roughly $\pm2\%$ at short wavelengths and the derived retarder transmission does go over 100% in some instances. More detailed assessments of the daily-calibration stability and accuracy will certainly be coming in DKIST early operations to test these various fitting options under a range of conditions.

Appendix B: Metrology for System Polarization Modeling

We did extensive metrology, including developing several of our own custom tools, which were then used on many different kinds of optics. We have measured mirror, dichroic, and anti-reflection coatings spatially and spectrally, including Mueller-matrix mapping measurements at high spectral resolving power to characterize narrow features. We have measured polarization for every single coated optic contributing significant polarization to the system. The impact of powered optics, non-uniform coatings, and incidence-angle dependence have all been estimated with ongoing work to improve the system models. We have made Mueller-matrix maps and spectra of all calibration retarders and modulators. We have spatial maps of calibration and analyzing polarizer contrast ratios, maximum extinction orientations, and polarized transmission. These have all been combined into spatially resolved, non-uniform footprint Mueller-matrix propagation models to show depolarization and field dependence. DKIST as a system has been very thoroughly characterized. Many of the current system limitations are understood with ongoing upgrade projects to continue improving system performance. We highlight here some of these metrology efforts with references to the several studies published on DKIST polarization calibration to date.

2.1 B.1 Mirror Coatings and the DKIST Polarization Model

We address the mirror-coating performance and the associated terms of the system model. We have measured samples from all coated optics contributing significantly to the polarization response of the system as well as individual instruments. We have estimates of the performance impact of coatings for powered optics, variable incidence angle impacting wide field angles, and coating non-uniformities impacting system depolarization. Our current understanding is that the current accuracy limitations lie not with coated powered optics, but with systematic errors caused by the calibration optics, their imperfections, and their temporal response to a 300 watt optical beam. We detail here some of the highlights derived from DKIST mirror-coating models and metrology.

2.1.1 B.1.1 Every Mirror Measured with Wavelength and Incidence, Coating Modeled

Metrology on coating witness samples provides a very good initial system metrology model, provided the actual coating samples from the same run as the telescope optics are directly measured. Run-to-run variation is expected, is significant, and is tracked in the DKIST coating database. Many flavors of enhanced protected-silver coatings have similar reflectivity, but the diattenuation and retardance terms vary substantially even for the same coating formula from the same vendor. We show some ellipsometric measurements covering 0.2 μm to $>35~\upmu \text{m}$ wavelengths in Figure 26. Many individual coating-sample measurements have already been presented over a range of incidence angles by Harrington, Sueoka, and White (2019), Harrington et al. (2021a,c).

Figure 26

The retardance at left and diattenuation at right measured on coating witness samples at an incidence angle of $45^{\circ}$. We show in black the many layer protected silver coating used on DKIST mirrors M3, M4, M5, M6. We also include mirrors combined together in the modulation matrices: M7, M8, M9a, the IOI formulation used on M9, some ViSP mirrors from Rocky Mountain Instrument (RMI), and NCSP mirrors from Edmund Optics (Edm). Vertical dashed-black lines show wavelengths for the current infrared Cryo-NIRSP instrument filter set.

In Figure 27 we show ellipsometric measurements from J.A. Woollam at incidence angles from $15^{\circ}$ to $65^{\circ}$ in steps of $10^{\circ}$. We have measurements similar to this for every mirror and dichroic used in the current DKIST telescope and instrument suite. We see similar results when we use our internal Mueller-matrix metrology system NLSP described by Harrington, Sueoka, and White (2019) at $45^{\circ}$ incidence. In particular, Harrington, Sueoka, and White (2019, Figure 29) shows that we can fit this coating polarization spectrum as a silver layer protected with a range of 5 to 12 nm of ZnS coated on top of Al₂O₃ with a thickness range of 95 nm to 120 nm. Our K-cell based measurements for both higher and lower incidence, reported by Harrington, Sueoka, and White (2019) and shown in Figure 48, agree reasonably at similar incidence angles. With these coating measurements and reasonably matched coating material models, we can predict the system polarization due to mirror coatings as a function of incidence angle, wavelength, uniformity, optic curvature, field of view, etc.

Figure 27

Ellipsometric measurements on four coating witness samples included through the chamber with the DKIST deformable mirror M10. The left-hand panel shows retardance in degrees. The right-hand panel shows diattenuation in percent. Incidence angle varies from $15^{\circ}$ to $65^{\circ}$ in steps of $10^{\circ}$ The lowest magnitude curve for both retardance and diattenuation correspond to $15^{ \circ}$ incidence. The highest magnitude curves are at $65^{\circ}$ incidence. The samples are at positions, 4, 9, 12, and an unknown position labeled U. There are four colored curves in each panel, but their overlap is so close that the curves are nearly indistinguishable. The DKIST mirrors with this coating work at incidence angles of $15^{\circ}$, $30^{\circ}$, and $45^{\circ}$.

DKIST has an operational requirement to deliver an optical beam covering wavelengths at least as long as 28 μm. For the first-light instrument suite, the Cryo-NIRSP (CN) has filters at wavelengths significantly longer than the 1.6 μm cut off in our NCSP metrology tool. Existing CN filters include spectral lines of Mg viii at 3.03 μm, Si ix at 3.94 μm, and CO at 4.65 μm. We have confidence that the metrology model presented here can be easily extended to longer wavelengths. We also do not anticipate any greatly different system behavior given the magnitude of polarization spectral features measured in these samples. Given the success of fitting the system model parameters, we conclude that it will be straightforward to extend a few mirror polarization terms to the infrared.

2.1.2 B.1.2 Primary and Secondary Mirror Polarization Properties (M1, M2) from Ellipsometry

We had adjusted our prediction from Harrington and Sueoka (2017) to Harrington, Sueoka, and White (2019) after measuring actual coating samples and fitting a more physical coating model for the oxidized aluminum of M1. The retardance prediction has dropped by roughly $0.6^{\circ}$ to $1.7^{\circ}$ over this wavelength range, also putting the prediction of $\tau _{12}$ around zero for the 650 nm to 750 nm bandpass.

Figure 28 shows the metrology model for the M1:M2 grouping using recent ellipsometry on the 2020 re-coating of M1. The minimal incidence angle for the Woollam RC2 ellipsometer is $15^{\circ}$, although M1 folds at $14.04^{\circ}$ and M2 folds near a chief-ray incidence angle of $11.8^{\circ}$. We scale the M2 values down by 2/3 to account for the difference between the $15^{\circ}$ incidence ellipsometry and the $11.8^{\circ}$ chief-ray incidence angle. The M1 chief-ray incidence angle is $14.04^{\circ}$ so we have left the $15^{\circ}$ incidence metrology for M1 unchanged.

Figure 28

The recent ellipsometry on the 2020 re-coat of M1 as well as the multiple M2 samples at $15^{\circ}$ incidence. Left shows the retardance model [$\tau$]. Green shows the M1 2020 re-coat sample. Red shows the M2 sample recorded at $15^{\circ}$ but scaled down by 2/3 to approximate the $11^{\circ}$ incidence angle. Thick blue shows the current prediction included in the December 2021 Telescope Database model. Right shows the diattenuation values (which get converted to the X-variable). Given the small magnitude of the M1:M2 group diattenuation, we apply a spectral smoothing to reduce the impact of statistical noise.

2.1.3 B.1.3 Mirror Coatings on Powered Optics

Harrington and Sueoka (2017) showed that the main impact of curvature on the powered M1 and M2 optics is to produce diagonal depolarization at magnitudes of a small fraction of a percent. This level is well below the depolarization caused by the DKIST calibration retarders (Sueoka, 2016). The DKIST primary mirror (M1) creates an F/2 beam with incidence angles ranging from $7.1^{\circ}$ to $20.6^{\circ}$ about the on-axis $14.04^{\circ}$ beam. The secondary (M2) converts this F/2 beam to F/13 with incidence angles ranging from $6.0^{\circ}$ to $17.3^{\circ}$ about the on-axis $11.84^{ \circ}$ beam. We note that the total diattenuation measured for the M1:M2 group presented above in Figure 28 is near 0.9% for the shortest wavelengths near 393 nm dropping to below 0.2% at wavelengths beyond 1000 nm. Similarly the retardance is at most $5^{\circ}$ with some wavelengths being near zero. The relative depolarization caused by non-uniformity in these small values is itself second-order small.

2.1.4 B.1.4 Mirror Coatings and Muller Matrix Variation with Field Angle

We estimated the magnitude of the mirror-induced system polarization response as a function of field angle by using coating formulas applied to mirrors by Harrington and Sueoka (2017) using the optical ray-tracing program Zemax (now Optic Studio). The coating model applied was a reasonable fit of common materials to the measured coating polarization (see Harrington and Sueoka, 2017, Figure 6). That work had found a nominal coating of 37.5 nm of ZnS using the Zemax default refractive indices coated over 100 nm of Al₂O₃. The modeled coating behavior is very similar to the revised fits of Harrington, Sueoka, and White (2019) using updated refractive-index equations. They find the top ZnS layer thickness was in the 5 nm to 12 nm range, and the bottom Al₂O₃ layer thickness was in the range of 95 nm to 120 nm. The M3 chief rays range from $42.8^{\circ}$ to $47.2^{\circ}$ about a nominal $45^{\circ}$ incidence angle (Harrington and Sueoka, 2017, Table 1). The M4 chief rays see $\pm0.19^{\circ}$. The chief rays for M5 through the coudé laboratory mirrors see $\pm0.45^{\circ}$ field variation as the pupil is 20 times demagnified onto the deformable mirror (M10).

Different instruments sample the DKIST beam at a range of different field angles. Instruments all have opto-mechanical methods to select a particular field offset from the telescope bore sight either by using slit stepping or scanning mirrors mounted near pupil planes. The resultant field-angle dependence of the system Mueller-matrix elements was below $\pm0.02$ over a full five arcminute field of the entire DKIST system, as seen by Harrington and Sueoka (2017, Figure 19).

Most DKIST instruments observe well below this range of field angles. The systematic errors caused by spatial non-uniformities of the DKIST calibration optics are far larger, limiting the field of view to often some tens of arcseconds or less at visible wavelengths; see Harrington et al. (2021b, Section 5.3) and the Appendix below. We perform a field-angle dependent modulation-matrix calibration, but the field dependence caused by the articulated DKIST telescope mirrors remains an underlying uncalibrated systematic error at levels as predicted by Harrington and Sueoka (2017). For this preliminary commissioning model, we ignore the field-of-view dependence for the DKIST M3:M4 and M5:M6 mirror groups.

2.1.5 B.1.5 Mirror Coating Spatial Non-uniformity and Depolarization

The several varieties of enhanced protected-silver coating used in DKIST follow a common specification for coating layer thickness to be better than a few percent uniform across large apertures. Harrington et al. (2021c) showed examples of data from several coating runs from multiple vendors where we have multiple witness samples distributed throughout the coating chamber. In several instances, we did uniformity testing of particular coatings with arrays of witness samples distributed across the particular coating chamber used for our optics. For instance, coating-uniformity measurements in the DKIST M2, M4, and M10 coating runs show that retardance is stable across the aperture to better than $3^{ \circ}$ retardance across 390 nm to 1600 nm wavelengths. We showed four coatings samples from DKIST M10 in Figure 27. Diattenuation variation is below 0.2% noise limits for all except wavelengths below 400 nm. A test at another vendor (Zygo, Harrington et al., 2021c, Appendix B) for coatings on DKIST M9a and DL-NIRSP fold mirror 1 (DL-FM1) shows a factor of at least three better retardance uniformity over a 405 mm aperture. Spatial non-uniformity of a protected-aluminum coating over a 900 mm aperture for the University of Hawai´i PanStarrs telescope shows similar performance from another vendor: EMF. We used EMF to coat DKIST M8 over an 860 mm aperture with an enhanced protected silver and expect similar spatial variation.

We show good repeatability of polarization, reflectivity, and coating-thickness uniformity covering the four-meter aperture of two bare-aluminum coatings done on the DKIST primary mirror (M1) by Harrington et al. (2021c, Appendix B). A recent study on polarization aberrations for the Habex system by Breckinridge et al. (2018) shows spatial variation in the retardance in reflection for a 3.75-meter diameter mirror coated at the University of Arizona in Figure 19 of (Breckinridge et al., 2018). This measurement gives retardance variation at magnitudes of 0.002 radians, attributed to form birefringence, requiring a special setup developed, built, and measured by B. Daugherty (Breckinridge et al., 2018). Breckinridge et al. (2018) show that spatial variation of coating polarization is present at low but measurable levels across large-area mirrors. Given the factor-of-two thickness variation in the DKIST aluminum coating, we certainly anticipate spatial variations in the mirror at some undetermined magnitude due to the varying properties of the aluminum across the mirror. Given the large incidence-angle range for DKIST shown by Harrington and Sueoka (2017), we also anticipate a fraction of a percent depolarization and some very mild elliptical retardance as second-order impacts from the F/2 DKIST M1. See Harrington and Sueoka (2017) for examples of the depolarization calculations from a spatially variable AOI for DKIST coatings.

2.2 B.2 Calibration Polarizer Mueller Matrix

The DKIST calibration polarizer is the absolute reference for the polarization coordinate system. It also is the generator of very well known input Stokes vectors when the retarder is not inserted in the beam. This calibration optic must be known very accurately. We did extensive calibrations in uniformity for several polarization parameters reported by Harrington et al. (2021b). We ran a simulation by Harrington et al. (2021b) accounting for the known spatial variation of transmission, the extinction-axis orientation, and the contrast variation. We assessed the transmission uniformity to be the dominant factor. This drove DKIST to develop and deploy a new, more uniform calibration polarizer from Moxtek based on Nano-Imprint Lithography (NIL) processing. We detail below some properties of this new polarizer, installed on summit in November 2021 and aligned on-Sun December 2021. See Harrington et al. (2021b) for examples of the existing calibration polarizer non-uniform modulated intensity across beam footprints, field angle, and the impact of transmission uniformity. We anticipate switching to this upgraded polarizer for calibrations in 2023.

2.2.1 B.2.1 Uniformity of Polarizer Transmission, Contrast and Extinction Orientation

The uniformity of any calibration polarizer varies spatially and spectrally. Wafer substrates for wire-grid polarizers fringe. Figure 29 shows the spectral variation of transmission, contrast, and angle of maximum extinction for the NIL polarizer cut from Wafer 4 as installed on the summit. We note that the orientation for maximum extinction is very small, less than $0.05^{\circ}$ with some obvious systematic errors attributable to rotating the analyzing polarizer in a system with substantial retardance and diattenuation from post-analyzer optics. We note that the analyzer in the system is also a Moxtek wire-grid polarizer that does not translate in the beam.

Figure 29

The spectra of polarizer properties derived by NDSP in May 2021 on NILpol Wafer 4 before installation on the summit. The left-hand panel shows transmission spectra. Note that the width of the lines at visible wavelengths is dominated by fringes, not noise. The middle panel shows the contrast-ratio spectra of the calibration polarizer against the NDSP analyzer. Right shows angle of maximum extinction spectra derived from a Malus-Law fit to a range of analyzer orientation spatial maps $\pm6^{\circ}$ about the crossed orientation.

The improvements in the NIL polarizer uniformity are substantial in all three critical performance parameters: transmission, contrast, and extinction orientation. We compare the current DKIST calibration retarder against this new upgrade. Currently the CalPol1 Spare, also called the Polarizer-As-Modulator (PAM), is mounted in the telescope. The NIL polarizer diced from Wafer 4, is now installed on the telescope and is in the process of being aligned.

Figure 30 compares the uniformity of these two DKIST calibration polarizers at particular similar wavelengths, chosen to highlight the differences. The top row shows the current polarizer. The bottom row shows the upgraded NIL polarizer. The left two panels show the transmission at similar wavelengths (868.0 nm vs. 856.5 nm). The current polarizer shows variation from 89.3% to 92.2% for 2.9% PV variation across the aperture. The upgrade NIL4 polarizer is scaled from 89.65% to 90.50% for 0.85% PV variation or an improvement of 3.4 times. Larger spatial scale patches of transmission variation are seen in the current polarizer, which caused the largest errors in the Harrington et al. (2021b) simulations. The middle two panels show the contrast of the polarizer pair (sample + analyzer). As the beam footprint does not change substantially on the NDSP3a analyzer when rotated $\pm6^{\circ}$, all spatial variation is attributable to the large aperture test polarizer being translated. The current polarizer has small spatial scale circular features ($<10~\text{mm}$) along with a large gradient across the aperture from 2500 up to 12,000.

Figure 30

A side-by-side comparison of spatial uniformity for the current DKIST calibration polarizer (CalPol1 Spare/PAM) and the new upgrade. This upgrade is the Nano-Imprint-Lithography process (NILpol), and we selected the best of several manufactured, choosing wafer run number for denoting Wafer4, or W4. The left panels show transmission variation across the aperture. The middle panels show contrast. The right panels show the orientation for maximum extinction. The angle is the best-fit minimum intensity for crossed polarizers at all wavelengths using 29 analyzer orientations on a color scale of $\pm0.01^{\circ}$. The top right-hand panel shows the current DKIST calibration polarizer at a wavelength of 868.7 nm on a color scale of $\pm0.035^{\circ}$ with a clear gradient across the aperture at magnitudes an order of magnitude larger than the new NIL polarizers in the lower-right-hand panel.

The NIL polarizer on the bottom row of Figure 30 shows no large spatial gradients in contrast ratio. The color scale covers the range of 2350 to 3650. The right two panels show the orientation of maximum extinction derived by rotating the NDSP3a analyzer against the fixed large-aperture calibration polarizer. The current calibration polarizer is shown on a scale of $\pm0.035^{\circ}$ about the nominal orientation with a clear gradient in orientation across the aperture. The NIL polarizer maximum extinction orientation is shown on a scale of $\pm0.01^{\circ}$ about nominal with a slight cross feature and some other small-spatial-scale features in a clover-leaf pattern at $\approx12~\text{mm}$ size. We note these small features are seen on all our NIL polarizers and are less than $\pm0.03^{\circ}$ magnitude.

Figure 31 shows the spatial variation of the substrate thickness derived from the spectral interference fringe relative intensity. We used an upgraded version of our laboratory Mueller-matrix system based in Maui called the National Solar Observatory DKIST Science Support Center Spectro-Polarimeter (NDSP). This system uses multiple Avantes spectrographs simultaneously. We show in Figure 31 spatial mapping measurements at 855.2 nm wavelength using a system with spectral resolution 0.25 nm optical profile FWHM. The interference map is computed as the difference in transmission at a single wavelength subtracted from a spectral average over many individual fringe periods ($\pm20$ pixels). Harrington et al. (2021b, Section 6, Figures 17, 18, and 20) show the fringe spatial and spectral properties of the other DKIST polarizers along with details on the NDSP metrology system for fringe detection.

Figure 31

The spatial fringe detected across the aperture for NILpol4 at a wavelength of 855.2 nm. The fringe pattern is derived as the polarized transmission difference between an individual wavelength and the spectral average over several fringe periods. See Harrington et al. (2021b, Section 6) for details.

2.3 B.3 Calibration Retarder Mueller Matrix

Calibration algorithms commonly fit for retardance of the calibration retarder during the system-calibration process as well as during the individual-instrument modulation-matrix derivation process. There are several optical properties that can critically impact calibration errors. The calibration retarder must be spatially uniform, rotationally constant in performance, insensitive to translational and angular misalignments, and temporally stable in the presence of strong thermal forcing.

2.3.1 B.3.1 Retardance Spatial Uniformity Through Mueller Matrix Mapping

We measured the Optically Contacted Calibrator (OCcal) in our Boulder-based laboratory metrology system: NLSP. We used an Avantes EVO spectrograph system covering 541.7 nm of bandpass with 4032 spectral pixels from 390.3 nm to 931.9 nm wavelengths. The system delivers an optical full width half maximum of 0.3 nm. We ran a spatial map of Mueller-matrix spectra covering a 90 mm aperture in a rosette spatial pattern with 3 mm sample steps and a $60^{\circ}$ first ring radius collecting 721 Mueller-matrix spectra.

We show the elliptical-retardance magnitude, circular-retardance component, and fast axis of linear retardance in Figure 32. The magnitude shown in the left-hand panel is nearly identical at all wavelengths, but with a range that decreases as $\lambda ^{-1}$. The measured circular-retardance spatial variation in the middle panel has a range of $\pm0.1^{\circ}$ magnitude with an aperture mean of $0.02^{\circ}$ at this wavelength. The circular retardance does show some significant spatial variation corresponding to polishing non-uniformities, which oscillates between positive and negative sign, following the spectral-clocking oscillations. The fast-axis variation was close to noise limited, with some small but detectable variation at roughly $\pm0.02^{\circ}$ levels shown in the right-hand panel of Figure 32.

Figure 32

Spatial variation of retardance properties across the optically contacted quartz compound retarder at 456.9 nm wavelength measured by NLSP in Boulder in 2019. Left shows spatial variation of elliptical-retardance magnitude. Middle shows the spatial variation of circular retardance on a $10\times$ magnified color scale. Right shows the fast-axis orientation of linear retardance. Spatial sampling covered a 90 mm aperture with 3 mm spacing. Note that our NLSP spatial mapping agrees with these MLO results, although we use very different measurement techniques. Our spatial maps at all wavelengths look similar to these MLO maps at one wavelength.

We show the spectral-clocking oscillations for the central NLSP map spatial location in Figure 33. With 0.3 nm spectral resolution, we measure these oscillations clearly. We highlight the 404 nm to 418 nm bandpass to show a few cycles of oscillation cleanly resolved. We show several spectra over a range of aperture locations to show that statistical noise is small compared to the signal in this bandpass.

Figure 33

The spectral clocking oscillations at selected mapping locations about the NLSP map center point. Each line shows a different aperture location. Circular retardance oscillations, shown as dashed red lines, are over $1.2^{\circ}$ peak-to-peak magnitude. The fast-axis oscillations, shown in black, are at roughly $0.4^{\circ}$ with some systematic errors visible in the wavelength dependence.

We note that statistics computed over the spatial aperture of Mueller-matrix spectra using NLSP is outlined by Harrington et al. (2020, Figure 38). The spatial pattern of retardance magnitude is effectively constant following the left panel of Figure 32, but with a magnitude that decreases as $\lambda ^{-1}$. This is expected for a simple compound retarder with spatial thickness variations and crystal axes aligned to the surface normal better than $\pm0.5^{\circ}$.

2.3.2 B.3.2 Quartz Optical Contact: Modeling Clocking Errors and Thermal Performance

The thermally induced drifts of the spectral-clocking oscillations represent the major temporal-stability limit of these larger compound retarders within DKIST. We note that many commercial products only guarantee clocking alignment to limits of $\pm1^{\circ}$ to $\pm3^{\circ}$. We have had to develop much more stringent clocking alignment to get our first optically contacted quartz crystal to $0.3^{\circ}$ and now two of our MgF₂ crystal pairs to $0.1^{\circ}$.

We model rotational mis-alignment of our two Optical Contacted Calibrator (OCcal) crystals at a nominal measured value of $0.3^{\circ}$ relative clocking with a thermal-perturbation analysis. This informs the temperature limits derived from our measured clocking oscillations.

In Harrington et al. (2020, Table 7), we show the materials properties assumed for the crystal-quartz thermal analysis for the Extraordinary axis (E) and the Ordinary axis (O). The coefficient of thermal expansion (CTE) is the fractional change in physical thickness with temperature [$\mathrm{d}L/\mathrm{d}T$]. The thermo-optic coefficient (TOC) is the change of refractive index with temperature [$\mathrm{d}n/\mathrm{d}T$].

We use temperature offsets of $\pm0.05~^{\circ}\text{C}$ and $\pm0.025~^{\circ}\text{C}$ between each crystal as our estimate of temperature gradients with depth in this optic per our finite-element models (FEMs). We also model environmental temperature changes by letting the bulk temperature of the crystals change by $\pm20~^{\circ}\text{C}$ from ambient of $20~^{\circ}\text{C}$. Figure 34 shows the thermal perturbations causing the spectral-clocking oscillations for a $1^{\circ}$ rotational misalignment. The clocking oscillations are roughly $50\times$ larger in magnitude than a crystal pair with perfectly aligned but thermally perturbed crystals. This oscillation is the dominant temporal stability limit. We showed in Harrington et al. (2020, Appendix C) some detailed mechanical and thermal modeling of this optic under illumination. Note that the OCcal was always used with the calibration polarizer in the beam ahead of the retarder, reducing the thermal loads by more than a factor of three. We also showed thermal testing of a six quartz-crystal test retarder in DKIST using the 300 watt beam in Harrington et al. (2020, Appendix A).

Figure 34

The three elliptical-retardance components when the crystals are bonded with a $0.3^{\circ}$ clocking offset. We use a $20~^{\circ}\text{C}$ ambient temperature with no difference between crystal temperatures. We see a $50\times$ larger perturbation in this panel than a model with perfect rotational alignment between crystals.

2.3.3 B.3.3 Stress Birefringence and Intrinsic Uniformity Limits

Another factor limiting ultimate calibration accuracy is the retardance variation caused by the retarder- and polarizer-substrate materials. The retarder substrates in particular have intrinsic, spatially non-uniform retardance properties. The optical-contact bond causes stress and deformation in addition to any other mounting forces. The stress-induced birefringence can introduce temporally variable retardance through rotation of an imperfectly aligned optic as well as thermal changes. We showed thermal-deformation predictions in Harrington et al. (2020, Appendix C, Figure 39). Subsequently, we have measured the surface figure deforming along the predicted saddle shape (astigmatism) as a function of temperature. With these confirmed deformation predictions, we can put bounds on the stress-induced birefringence.

2.3.4 B.3.4 Transmission Uniformity Limits

Transmission spatial variation is a major limitation as it directly impacts the measured brightness of the signal and is inseparable from real polarization variations. We showed in Harrington et al. (2021b, Figure 7, Section 3.2) some OCcal retarder-transmission measurements using our laboratory metrology equipment with improvements to achieve $\pm0.0025\%$ stability. These crystals are anti-reflection coated and some very small spatial variation of this coating is expected. For our upcoming MgF₂ elliptical calibrator, there will not be any anti-reflection coatings. The accumulated dust and surface defects will likely represent the transmission uniformity limit.

2.3.5 B.3.5 Retarder Optic Axis and Incidence Angle: Depolarization, Field Dependence

In typical compound-retarder stacks, the impacts of incidence angle and crystal-material orientation (optic axis mis-alignments) can cause substantial deviations from the nominal on-axis performance. For compound retarders with thicknesses of millimeters or more, less than one degree of incidence-angle change is required to create a significantly elliptical deviation from the nominal design. In DKIST calibration-retarder designs, the F/13 beam propagates through 8 to 12 mm of crystal at incidence angles over $\pm2.5^{\circ}$. The retardance depends on both the incidence angle as well as the clocking angle (rotational position) of the crystal axes relative to the incoming beam.

We use the Berreman calculus to model these impacts. Our Berreman models compare well with substantial modeling efforts using POLARIS-M ray tracing by Sueoka (2016). Sueoka (2016, Section 4) shows the ellipticity as a function of incidence angle through the ViSP SAR in Figure 4.18. In Sueoka (2016, Section 4.4), the incidence-angle dependence was averaged over simulated beam footprints to show how the optic design linear retardance turned elliptical as a function of DKIST field angle. In Sueoka (2016, Section 5), the footprint averaged Mueller matrices were assessed for errors in fitting only linear retardance and also fully elliptical retardance. Decompositions were done using Lu–Chipman and Symmetric methods. Depolarization terms can be of order 1% at visible wavelengths, and these degrees of freedom can be included in the future DKIST calibration algorithms if necessary. We can also show the importance of this kind of modeling by including clocking mis-alignments and optical-axis mis-alignments on all crystals in our Berreman models. Our crystals have the optical axis within $\pm1^{\circ}$ of the surface normal. These mis-alignments are not a major limitation. Presently, several issues with instrument performance are the major sources of various types of cross-talk in the data calibration. Several improvements to instruments are planned on optical performance topics such as stray-light suppression, faster software execution and response times, and optimization of data-reduction algorithms.

2.3.6 B.3.6 Thermal Perturbation With Clocking Errors

As we have noted, the thermal forcing of spectral-clocking oscillations represent a far larger retardance change than the thermal forcing and non-uniform temperature distributions in perfectly aligned retarder substrates. Minimizing the clocking oscillations minimizes thermal sensitivity, stabilizing the retarder over time under load. We measured temperatures for the three currently installed DKIST retarders, as well as the polarizers directly using thermocouples and remotely using IR diode sensors while observing the Sun. See Harrington et al. (2021a, Appendix B), in particular Figures 28 through 32. We measured a $1.5~^{\circ}\text{C}$ temperature rise for the six MgF₂ crystal Cryo SAR retarder over 30 minutes of 300 watt solar illumination (Harrington et al., 2021a, Figure 31). In this configuration, the retarder was not protected by the calibration polarizer upstream, so infrared flux was present and absorbed in the retarder by both the refractive-index-matching oil and the MgF₂-crystal itself. All current DKIST calibration sequences never allow the retarder to be in the beam without the polarizer upstream. The polarizer reduces the flux by more than 65% and also blocks all infrared wavelengths absorbable by the MgF₂ beyond 6000 nm. We anticipate nearly negligible thermal forcing of the upcoming four MgF₂-crystal optically contacted calibration retarder during the $<15~\text{minutes}$ of a typical calibration sequence. The Cryo SAR MgF₂ retarder has some residual heating from absorption from the oil for wavelengths beyond 3.5-μm, which is not completely blocked by the polarizer.

2.4 B.4 Polarizer and Retarder Spatial Variation Sampled by Beam Footprint

The beam footprints and associated optic apertures vary for the three levels in the DKIST Gregorian Optical System (GOS). In Figure 22 of Harrington et al. (2021b), we show the beam footprints for field angles of 2.0, 2.8, and 5.0 arcminutes as an example.

The optics spin during calibration but the aperture area covered can be optimized when balancing the calibration-sequence efficiency. The area of the optic sampled changes as a function of field angle coupled with mis-alignments de-centering the beam. Each footprint samples a different patch of each optic. The simulations use the metrology from the appropriate optic in a footprint of the appropriate de-center and diameter at the appropriate clocking angle.

We note that the ten-state sequence has non-uniform weighting across the aperture of each calibration optic. The polarizer swings through a $120^{\circ}$ arc but there are four inputs at $0^{\circ}$ and four inputs at $45^{\circ}$ putting 80% of the inputs within a fairly small patch of the polarizer optic aperture. A globally constrained transmission fit adds heavy weighting and constraint to these states, reducing the influence of other issues related to the non-uniform retarder rotating underneath.

We show examples of polarizer transmission and orientation of maximum extinction for two sets of footprints in the top two panels Figure 35. There is $180^{\circ}$ symmetry in the footprints as we graph both positive and negative 114 arcsecond field angles. The bottom two panels of Figure 35 show the calibration-retarder total linear magnitude and circular retardance. These two footprint diagrams are drawn from more detailed examples of the properties of calibration optics by Harrington et al. (2021b, Figures 9 and 10).

Figure 35

The properties within individual footprints for the beam on the calibration polarizer while spinning through the ten-state calibration sequence at a wavelength of 656 nm and field angle of $\pm114$ arcseconds.

Using the spatially variable polarization properties of the calibration optics, the incident flux can be propagated through these non-uniform optics and an analyzer to show the detected intensity through the system. We show examples of modulated intensities varying across a footprint in Harrington et al. (2021b, Figure 11). As examples, we highlight two such non-uniform beam footprints in Figure 36. We select two particular input states and modulation states to show typical variation of the modulated intensities at magnitudes of a few percent about the nominal system transmission through the modulator. We selected modulation states of 0 at left and 2 at right to demonstrate dissimilar spatial behavior. We note that any specks of dust, scratches, or other aperture defects that caused measurable transmission losses in our laboratory metrology are included here giving rise to the small-scale features in addition to the low-order smooth aperture variation.

Figure 36

The intensity variation within individual footprints for the beam when calibrating a $+1.9$ arcminute field angle at a wavelength of 630 nm. The left-hand panel shows an input state with only the polarizer in the beam. Intensity varies with the color scale from 57.7% to 58.95%. The right-hand panel shows another calibration input state with both retarder and polarizer in the beam. Color shows intensity varying from 47.6% to 49.0%. Small structures are seen contributing from the high spatial resolution polarizer metrology, but also some substantial retardance spatial variation influences the intensity at larger spatial scales.

2.4.1 B.4.1 Spatially Varying Calibration Optics: Error Matrix with Field Angle

We can define an effective field angle within which the polarization-calibration inaccuracies stay below a specified error threshold. We showed in Harrington and Sueoka (2017) how the mirror-coating behavior with incidence-angle-created field-dependent polarization errors. We can now add to this the field-angle and wavelength dependence of the inaccuracies caused by the calibration process. The error-matrix elements show how errors in the demodulated Stokes vectors grow as a function of field angle and wavelength. Figure 37 shows the error-matrix variation with field angle at 420 nm for a particular simulation. As we have included the $\approx2.5~\text{mm}$ decenter of the calibration optics, these error terms do not go to zero even for the beam along optical boresight at zero field angle. With the DKIST beam without active optics stabilized to roughly $\pm9.7$ arcseconds field angle on the coudé laboratory, we expect some mild field-dependent errors. See Harrington et al. (2021b) including Appendix A for some error-matrix details at small field angles.

Figure 37

The error-matrix elements across the field of view multiplied by 100 at a wavelength of 420 nm. Each color shows a different Stokes parameter with four matrix elements per Stokes parameter.

As examples of DKIST calibration errors, we show the error matrix at 420 nm wavelength in Equation 20 for the on-boresight beam at zero field angle and in Equation 21 for a field angle of one arcminute.

$$ {\mathbf{E}}_{420~\text{nm}, 1'} = 10^{-3} \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0.2 & 0.9 & 1.4 & -0.3 \\ -1.4 &-0.5 & -1.4 & -0.4 \\ 1.2 & -1.7 & -7.8 & 16.6 \\ 0.6 & 0 & -0.9 & 0.6 \end{array}\displaystyle \right ) $$

(21)

The arrays shown are in parts per thousand and rounded to one decimal place. Errors are typically above a few $10^{-4}$ and above $10^{-3}$ for some terms. We choose these values for comparison with our prior work (Harrington and Sueoka, 2018b, Equation 4), where we only included the terms from the retardance spatial variation in the simulation. The error-matrix values here are more than an order of magnitude larger than from the retardance spatial variation alone. The on-axis beam now shows errors above a few $10^{-4}$ caused by the de-centered footprints seen with spatially mis-aligned calibration optics.

$$ \frac{{\mathbf{E}}_{420~\text{nm}, 0'}}{{\mathbf{E}}_{\mathrm{budget}} } = \left ( \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 0 & 0 \\ 0 & 0.03 & 0.01 & 0 \\ 0 & 0.01 & 0.03 & 0 \\ 0 & 0 & 0 & 0.06 \end{array}\displaystyle \right ) $$

(22)

$$ \frac{{\mathbf{E}}_{420~\text{nm}, 0.2'}}{{\mathbf{E}}_{\mathrm{budget}} } = \left ( \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 0 & 0 \\ 0.8 & 0 & 0.1 & 0 \\ 0.5 & 0.1 & 0.2 & 0.8 \\ 0.2 & 0 & 0 & 0 \end{array}\displaystyle \right ) $$

(23)

If we divide the error-matrix terms of Equation 20 for a field position on axis (0 arcminutes) at 420 nm wavelength by a nominal error-matrix goal of Equation 19, we get the error ratio of Equation 22. This shows that the beam on the telescope boresight is in error by at most 6% of the nominal error budget of Equation 19. In Equation 23 we show the same calculation for a field angle of 0.2 arcminutes field angle (12 arcseconds) where two terms are within 80% of the error-budget limit. The other 14 error terms are low. Similarly, we divide the error-matrix terms for a field angle of 0.2 arcminute at 420 nm wavelength by a nominal error-matrix goal of Equation 19 to get the error ratio of Equation 23. This highlights a few terms that are at 80% of our nominal error limit from Equation 19. The well calibrated field angle is thus $\pm0.2$ arcminutes for this error budget at this wavelength with this calibration sequence using these two calibration optics.

The exact error limits required depend on the science use case, observing conditions, cadence, instrumentation, and a very long list of telescope and instrumental factors. However, the process outlined here shows that we have combined several polarizer inhomogeneities (transmission, contrast, extinction orientation) with several retarder inhomogeneities (transmission, elliptical retardance) including misalignments to the calibration optics to show the combined system error compared to nominal error limits.

These simulations show that the retardance spatial uniformity from Harrington and Sueoka (2018b) and Harrington et al. (2020) is currently not the major limitation of the calibration process. Producing a more detailed error budget extracting the relative contribution of each error term is possible with these kind of simulations. We note that calibrations taken around the telescope optical boresight will have errors much smaller than at the one arcminute field angle. Observations requiring high calibration accuracy can easily be planned with frequent re-pointing of the telescope as opposed to using very wide instrument field scanning techniques. We also note that there are several algorithmic techniques that introduce more fitting variables that can also mitigate these issues for the optics DKIST currently has installed. We show examples of these algorithms in Harrington et al. (2021b, Appendix B).

2.5 B.5 Dichroic Coatings: Narrow Spectral Features, Spatial Variation and Depolarization

Astronomical instruments greatly improve wavelength-multiplexing capabilities by using beam splitters. In the case of the four-meter DKIST solar telescope, over 70 watts of optical power is distributed simultaneously to four instruments, each of which has multiple cameras. Many DKIST observing cases require simultaneous observation of many narrow bandpasses combined with an adaptive-optics system. The DKIST dichroic beam splitters required substantial development to achieve very tight specifications over very large apertures of 290 mm diameter. Meeting each substrate’s optical specification in terms of 5 nm RMS reflected and transmitted wavefront is challenging alone. Significant additional consideration was given to the thick dichroic coatings with tens to nearly one hundred layers and over 8 μm physical thickness.

Coating spectral variation occurs over less than 1 nm wavelength change, comparable with DKIST instrument bandpasses. We measured retardance spectral variation of up to a full wave and diattenuation varying over $\pm 10\%\,\text{per}\,\text{nm}$. Spatial variation of Mueller-matrix elements for coatings in both transmission and reflection requires a detailed metrology campaign. We show mild impacts of depolarization and spectral variation of polarization on modulation efficiency caused by the dichroic coatings. Harrington et al. (2021c) contains detailed performance for all of the DKIST dichroic optics for community use in planning future observations. Here we highlight some of the key features.

2.5.1 B.5.1 DKIST FIDO Dichroic Spectral Performance

Given the dichroic spectral features were 1 nm in width, we performed polarimetric metrology with our systems with resolution of a few times more narrow to capture the polarization performance of the coatings. The spatial uniformity of these thick coatings is a strong function of wavelength, being an order of magnitude or two worse around the narrow spectra features than at other wavelengths. However, coatings can be designed with diattenuation constraints to minimize the coating sensitivity to layer thickness variation.

The first round of dichroic beam splitters were designed to be wavelength-exclusive where transmission or reflection were above 90% with no possibility for simultaneous instrument use at the same wavelength (gray beam spitters). We anticipate a new round of FIDO dichroic beam splitters that do allow for 50/50, 70/30, or 30/70 splits at wavelengths in the 380 nm to 1000 nm bandpass, while preserving transmission above 90% in the 1050 nm to 1800 nm bandpass.

Figure 38 shows the as-built reflection in the left-hand panel and transmission through the front-side coating, substrate, and back-side anti-reflection coating in the right-hand panel. The coatings were only controlled for reflection or transmission in the 380 nm to 1800 nm bandpass with spectral oscillations expected in the UV and IR wavelength regions. The fused-silica substrate also absorbs strongly for wavelengths beyond 2500 nm. In most dichroics, some relatively narrow spectral absorption features can be seen in the reflection spectra.

Figure 38

The left-hand panel shows the FIDO dichroic reflectivity off the front surface. The right-hand panel shows transmission through the front-surface coating, the substrate absorption, and the back-surface anti-reflection coating.

2.5.2 B.5.2 Retardance and Diattenuation in Reflection Example: BS-555 in a K-cell

We show here an example of the narrow spectral features for the BS-555 dichroic coating reflecting in the 380 nm to 545 nm bandpass. This coating has three narrow spectral features. Figure 39 shows the polarization and intensity measured with our NLSP setup in the Boulder laboratories in early 2021 with a spectral resolution of 0.3 nm and sampling roughly at 0.1 nm per pixel. Two bare aluminum-coated mirrors were used at roughly $50^{\circ}$ incidence while the BS-555 witness sample was mounted at $15^{\circ}$ in a K-mirror type setup. The reflectivity is shown in the left-hand panel, diattenuation in the middle, and retardance in the right-hand panel. There are a few features representing roughly 5% throughput losses. The cluster of diattenuation features at $\pm6\%$ magnitude also correlate with retardance features at $\pm300^{\circ}$ magnitudes.

Figure 39

The intensity at left, diattenuation in the middle, and retardance at right in reflection for the final delivered BS-555 coating. Our NLSP system measured coating witness sample at $15^{\circ}$ incidence angle from run 10-0362 in a K-cell type test setup.

We note that the thin-film coating modeling of these narrow spectral features did not accurately correspond with the actual measured wavelengths, or magnitude of the polarization (both retardance and diattenuation). See Harrington et al. (2021c, Figure 61 and 67) as examples. The narrow spectral features in diattenuation and retardance vary substantially with coating shot. A design tolerance analysis does generally indicate the sensitivity to narrow spectral features. The exact wavelength and magnitude of these features depends substantially on the coating-model details.

2.5.3 B.5.3 Narrow Spectral Features in All FIDO Dichroics

All the FIDO dichroics except BS-465 have some kind of narrow spectral feature in the reflection spectrum. We summarize these features for all dichroics in Figure 40. We only show the relevant wavelengths where the dichroic coatings are intended for use. The longer the transition wavelength, the thicker the coating in general and the more narrow spectral features there are in the reflectance. We use the metrology as part of the planning to ensure that no DKIST observations lie within a particular narrow spectral feature. Alternately, calibrations are done at sufficient spectral resolving power to ensure the wavelength dependence of the FIDO dichroics is appropriately captured.

Figure 40

The left-hand panel shows the FIDO dichroic reflection retardance at the appropriate $15^{\circ}$ incidence angle. The right-hand panel shows diattenuation. Curves have been offset vertically for clarity. Each dichroic beam splitter is named for the transition wavelength, and we only show the nominal reflection band as appropriate. The narrow spectral features have roughly 1 nm FWHM and will be included in DKIST performance predictions.

2.5.4 B.5.4 Spatial Variation of Reflected Retardance Example: BS-555 Ellipseometric Map

We had our 100 mm diameter coating stress-testing samples spatially mapped for Mueller-matrix spectra at a range of incidence angles over a 100 mm aperture. We show spatial-coating variation in much more detail in Harrington et al. (2021c). We show in Figure 41 the reflected retardance derived from full Mueller-matrix ellipsometry of a BS-55 test sample serial number 9 (SN9). We note that the retardance spatial variation at 468 nm varies by over $\pm45^{\circ}$ retardance at the nominal $15^{\circ}$ incidence where this coating is intended for use within DKIST. However, at just 2 nm longer wavelength at 470 nm, the spatial variation is less than $\pm4.5^{\circ}$. At another 7 nm longer wavelength at 477 nm, the spatial variation is less than $\pm0.4^{\circ}$. This represents a more than 100-fold change in retardance spatial variation over 9 nm in wavelength.

Figure 41

The reflected retardance maps recorded by J.A. Woollam over a 100 mm aperture for a BS-555 dichroic-coating stress-test sample. The coating performance changes substantially near the edges of the samples. These maps have been trimmed to 90% of the aperture.

2.5.5 B.5.5 Depolarization from Spatial Variation: Footprint Averaged Mueller Matrices

There are at least two separate impacts to consider when using an optic having spatially variable Mueller-matrix elements. The average over the individual beam footprints at any particular field angle will create depolarization. This depolarization is easily calibrated provided the beam is stable and the calibrator is well fit for all relevant errors. In practical terms, the DKIST beam wander and calibration-optic uncertainties are far larger than any depolarization caused by the FIDO dichroics. The second major impact is in having a system Mueller matrix that depends on the field angle. This field dependence also is easily calibrated with a field-dependent demodulation matrix for the system. For DKIST, the individual field-angle footprints are shown by Harrington et al. (2021c, Section 2.3 Figures 3 and 4). The footprints do not separate by more than 30% of their diameters at the FIDO optical station furthest from the pupil plane (DM, M10). DKIST processing modules already implement a field-dependent demodulation matrix, and some mild changes in these Mueller-matrix elements is anticipated from the FIDO dichroic coatings.

As a simple demonstration, we follow Chipman, Lam, and Young (2018, Section 6.11) depolarization, and implement their Equation 6.80, also listed here in Equation 24. We compute the average degree of polarization (AvgDoP) for all possible fully polarized input Stokes vectors (a Poincaré sphere map) shown in Figure 42. In Equation 24, the variable $\theta$ corresponds to the angle of linear polarization and the Stokes-$Q$ and -$U$ components. The variable $\eta$ corresponds to the degree of circular polarization.

$$ \mathrm{AvgDoP} = \frac{1}{2\pi} \int _{0}^{\pi} \int _{-\pi /2}^{\pi /2} \mathrm{DoP}[ \mathrm{M} {\mathbf {S}}({\theta},{\eta} ) ] \ \cos (\eta ) \ \mathrm{d}\eta \mathrm{d} \theta $$

(24)

Figure 42

The depolarization map for a worst-case FIDO coating spatial variation scenario. The color scale is computed as 1-degree of polarization for the full range of fully polarized input Stokes vectors. The horizontal axis represents linear inputs [$QU$], while the vertical axis represents circular input [$V$]. Depolarization of a few parts per thousand is seen varying with input Stokes vector. As this optic has $U$- to $V$-retardance, inputs at $45^{\circ}$ and $135^{ \circ}$ orientation [$U$-terms] see the highest depolarization. A pure $\pm Q$ input is preserved best with the lowest 1-DoP values.

We note that any Stokes vector propagating through the Mueller matrix at any single spatial point in our model would have the degree of polarization preserved at 100%. However, when we average the Stokes vectors across the beam footprint and then compute the AvgDoP, we see depolarization.

We use the FIDO BS-950 coating metrology on a 100 mm diameter stress sample at a wavelength of 1057 nm. See Harrington et al. (2021c, Section 2.3) for more details on this depolarization model. We propagate all possible input Stokes vectors through all locations across the optic aperture and then compute the depolarization as the aperture average. We find 1-DoP to be in a typical range of 1 to 10 parts per million. For particular wavelengths associated with narrow spectral features, the much more non-uniform coatings can cause 1-DoP to be at levels of parts per thousand. As expected for our simple model, there is only $UV$-retardance in the simulation given that the FIDO optics are tilted horizontally in the $Q$-plane. An input $Q$-vector is preserved (the clean vector), while Stokes vectors with $UV$-terms are depolarized by the spatially variable retardance. In the 1-DoP map of Figure 42, the symmetry is broken and the elliptical retardance tilts the regions of higher depolarization between hemispheres.

We note that the depolarization caused by FIDO is very small compared to other sources even within DKIST. In Sueoka (2016), the F/13 beam through the calibration retarders depolarized the beam by roughly 0.5%. In Harrington and Sueoka (2018b), we showed how a continuously rotating modulator introduced depolarization to the modulation matrix, creating a few percent efficiency losses, but otherwise no impact to the system calibration accuracy. In Harrington et al. (2020), we extended the modulation calculations and showed how spatially variable retardance in the modulator-created depolarization caused efficiency losses as well as field dependence calibrated by standard procedures. The ViSP polycarbonate modulator upgrade by Harrington et al. (2020, Section 2.6), for instance, has over $30^{\circ}$ retardance spatial variation, but only a few percent efficiency loss when demodulated. In Harrington and Sueoka (2017) we showed how the aperture average over the aluminum-coated F/2 primary mirror and F/2 to F/13 conversion of the enhanced, protected silver-coated secondary mirror created diagonal depolarization at levels of 0.1% to 0.2%. In Harrington et al. (2021b) we show how spatial variation of retardance across the calibration retarder and calibration polarizer both within a single beam footprint and across a mis-aligned, asymmetric sequence of orientations causes calibration errors. The FIDO dichroics are static through an observation and are easily calibrated, with some mild efficiency loss during demodulation at some particular wavelengths.

Appendix C: Modulation Matrix Fitting with Field Angle

We do fit for the field-angle dependence of instrument-modulation matrices. Adding spatial and spectral degrees of freedom to fitting to instrument demodulation is straightforward and substantially improves the system calibration. We show here examples of a field-angle dependent calibration for the quite non-uniform polycarbonate ViSP modulator. Meadowlark Optics performed spatial maps of the elliptical retardance. We also compared their spatial retardance maps with our own spatial and spectral Mueller-matrix data collection from NLSP described by Harrington and Sueoka (2018b) and Harrington, Sueoka, and White (2019).

The spatial variation of elliptical-retarder fit parameters measured in the laboratory were shown by Harrington et al. (2020, Figures 7, 8, and 9). The typical spatial scale for aperture variation is only a few millimeters, comparable to the ViSP beam footprint. Although the polycarbonate modulator is factors of several more spatially variable in retardance than the six polished crystal retarder, modulation remains efficient over wide fields with de-centered beams. Modulators do not need to be fabricated as spatially uniform as calibrators when a field-dependent calibration and demodulation is performed. We perform the same analysis of a field-dependent modulation matrix for a discrete eight-state sequence as by Harrington and Sueoka (2018b, Section 7).

In Figure 43 we show elliptical retardance magnitude for the beam footprints for an eight-state uniformly spaced (clocked) discrete modulation sequence. Uniform steps of $22.5^{\circ}$ orientation are taken. The ViSP modulator station is located after the spectrograph entrance slit in the diverging F/32 beam. The beam footprint in the first-light optical configuration covers roughly 80 mm of aperture with a mostly rectangular shape. The selected slit width and height set the illuminated region with an 8.1 mm diameter footprint at each unique field angle (for each slit-height position). A continuous modulation will sweep the beam through an arc between the footprint circles. We also have included this time-variable swept footprint in our models by sampling this optic in time over the $22.5^{\circ}$ sweep. We propagate intensity through an analyzer and record that detected intensity. The recorded intensities accounting for this time-dependent sweep are then demodulated.

Figure 43

The retardance extracted for each beam footprint on the ViSP polycarbonate retarder. Each individual field angle propagated through the system maps to an 8.1 mm diameter footprint on this modulator optic. As the modulator spins, the illuminated portion of the optic samples variable portions of the aperture. We choose 429.9 nm wavelength with a mean elliptical retardance of $223.1^{\circ}$. We show footprints for field angles of 0.5, 1.0, 1.5, and 2.0 arcminutes field diameter. We use a discrete modulation scheme with angular steps of $22.5^{\circ}$ starting at $0^{\circ}$. See Harrington et al. (2020, Figure 10) for examples at other wavelengths.

With these retardance spectra at each spatial location, we can build up the field variation of retardance components in each annulus. This shows how symmetric the first and second half-rotation will be for modulation as well as set expectations for depolarization via aperture and temporal averaging.

We detailed the peak-to-peak variation of retardance parameters in Harrington et al. (2020, Figure 11). The linear and elliptical magnitudes are shown along with the linear fast-axis and circular components. We note that a ViSP 1 arcminute slit height corresponds to a maximum de-center of $\pm19.1~\text{mm}$. A 2 arcminute slit would correspond to a de-center of $\pm38.3~\text{mm}$ on this optic. The retardance components can vary by up to $30^{\circ}$ peak to peak given the proportionally larger non-uniformity of polycarbonate. We show that these non-uniformities pose only a small reduction of modulation efficiency, and they are easily calibrated.

We computed the area averaged retardance within each footprint at select field angles as the optic spins through a full revolution. See Harrington et al. (2020, Figure 12). At a wavelength of 409 nm, the elliptical retardance had peak-to-peak variation over $14^{\circ}$. At a longer 704 nm wavelength, this had reduced to roughly $5^{\circ}$ variation for the outer annulus traced at 60 arcsecond field angle.

We model the modulation efficiency with the standard least-squares solution for minimum errors (del Toro Iniesta and Collados, 2000). For continuous and discrete modulation, we use the ViSP beam footprints and the elliptical retardance spatially averaged through the optic rotation over time. For the continuous-rotation case we propagate flux through an ideal analyzer in 50 discrete steps for each $22.5^{ \circ}$ modulation state to approximate the non-uniform optic as it rotates in the beam for each modulation state. The flux in the discrete steps sampling at $0.5^{\circ}$ is then averaged. Figure 13 of Harrington et al. (2020) shows the modulation efficiency for the discrete modulation case as well as the modulation-matrix elements for all field angles at a worst-case example wavelength of 390 nm. The depolarized efficiencies are computed as the time average of the flux through the modulator.

In Figure 44 we show the modulation efficiency losses when continuously rotating the optic during an exposure compared to the discrete modulation case above. The losses include both the nominal fast axis of linear retardance rotation during an integration as well as the spatial variation caused by a position-dependent beam footprints during rotation. The efficiency losses are still dominated by the fast-axis rotation of $22.5^{\circ}$ within an exposure. The 5% $QU$-efficiency loss is fairly constant with wavelength compared to the field dependence of retardance parameters, which drops by a factor of $5\times$ towards long wavelengths over this bandpass. The spatial variation predicted for this polycarbonate modulator only changes the efficiencies by a few percent. This compares to continuous rotation during an exposure, which drops the $I$- and $V$-efficiencies by 1% to 2% and the $QU$-efficiencies by 5% to 7% percent.

Figure 44

The modulation-efficiency change seen at different field angles from both spatial variation of retardance across the aperture and the depolarization caused by continuous rotation. This includes both the fast-axis orientation change and the spatial non-uniformity with field angle. Solid lines show the first half-rotation, while dashed lines show the second half-rotation. See Harrington et al. (2020, Figure 14) and associated text for details.

Temperature sensitivity is a major concern for stability of a retarder. We showed in Harrington et al. (2020, Figure 5, Section 2.4) an assessment of the relatively benign thermal behavior for the polycarbonate in this ViSP modulator upgrade. There are complications with high spectral resolving power instruments in that a few kinds of spectrally variable artifacts are much more temperature sensitive than a simple bulk-material analysis would show. Polycarbonate retarders are thermally sensitive, but spectral oscillations are slow given that the layers are less than 0.1 mm thick.