1 Introduction

Solar radio bursts and their fine structures are used to diagnose solar flare plasmas. Among them, zebra patterns (zebras) belong to the most frequently investigated bursts. An example of the zebra observed in 14 February 1999 is shown in Figure 1. In the radio spectrum, they appear in the form of regularly spaced emission stripes (zebra stripes). Many papers and monographs were devoted to them, e.g., Slottje (Apr 1982), Chernov (2006, 2011), Tan et al. (2012, 2014), Chernov, Formichev, and Fainshtein (2020).

Figure 1
figure 1

An example of the zebra observed on 14 February 1999 by the Ondřejov radiospectrograph (Jiřička and Karlický, 2008).

Full size image

For the interpretation of the zebra stripes, several models have been proposed (Rosenberg, 1972; Kuijpers, 1975; Zheleznyakov and Zlotnik, 1975; Chernov, 1976, 1990; LaBelle et al., 2003; Kuznetsov and Tsap, 2007; Bárta and Karlický, 2006; Ledenev, Yan, and Fu, 2006; Laptukhov and Chernov, 2009; Tan, 2010; Karlický, 2013). In the published literature, the most often used model of zebras is the one based on the double plasma resonance (DPR) condition (Kuijpers, 1975; Zheleznyakov and Zlotnik, 1975; Kuijpers, 1980; Mollwo, 1983, 1988; Winglee and Dulk, 1986; Zlotnik, 2013)

$$ \omega- \frac{s \omega_{\mathrm{ce}}}{\gamma} - \frac{k_{\parallel}u_{\parallel}}{\gamma} = 0, $$
(1)

where \(\omega\) and \(\boldsymbol {k} = (k_{\parallel}, k_{\perp})\) are the frequency and wave vector of the resonant wave, \(\omega_{\mathrm{ce}}\) is the electron cyclotron frequency, \(s\) is the gyro-harmonic number, \(\gamma= \sqrt{1 + (u_{\parallel}^{2} + u_{\perp}^{2})/c^{2}}\) is the relativistic Lorentz factor, \(u_{\parallel}= p_{\parallel}/m_{\mathrm{e}}\), \(u_{\perp}= p_{\perp}/m_{\mathrm{e}}\), in the electron momentum \(\boldsymbol {p} = (p_{\parallel},p_{\perp})\), and \(m_{\mathrm{e}}\) is the electron mass. This condition may be simplified by assuming that the generated waves are upper-hybrid (UH) waves in a non-relativistic plasma and that the DPR resonance is at integer gyro-harmonics of the electron–cyclotron frequency

$$ f_{\mathrm{UH}} = (f_{\mathrm{pe}}^{2} + f_{\mathrm{ce}}^{2})^{1/2} \approx s f_{ \mathrm{ce}}, $$
(2)

where \(f_{\mathrm{UH}}\) and \(f_{\mathrm{pe}}\) are the UH and electron–plasma frequencies, \(f_{\mathrm{ce}}\) is the electron–cyclotron frequency. In the DPR model, superthermal electrons are considered as the driver of the zebra emission. Those electrons are considered to be trapped in a flare loop and to have a loss-cone distribution. At the flare loop locations where such a distribution is present and the DPR condition is fulfilled, the DPR instability generates the UH waves. These UH waves are then converted to the observed electromagnetic waves by merging with low-frequency waves or by scattering on plasma particles. This model is supported by positional observations made by the Owens Valley Solar Array (Chen et al., 2011).

When applying the DPR model to observed zebras and to estimate plasma parameters at the zebra source, the most important is to determine the gyro-harmonic numbers of the zebra stripes \(s\). From the zebra stripe frequencies and their gyro-harmonic numbers, the electron cyclotron frequency and magnetic fields are consequently estimated. Several methods for their determination were developed, as shown, e.g. in Karlický and Yasnov (2015), Yasnov and Karlický (2020), Yasnov (2021).

These methods are based on fitting a set of the observed zebra-stripe frequencies \(f(n)\) by the set of theoretically derived zebra-stripe frequencies \(f_{\mathrm{th}}(n)\) in the form (Yasnov, 2021)

$$ f_{\mathrm{th}}(n)=\frac{(s_{1}-(n-1)) f(s_{1})}{s_{1}} \left( \frac{(s_{1}-(n-1))^{2}-1}{s_{1}^{2}-1}\right)^{\frac{1}{R-2}}, $$
(3)

where \(n\) is the ordinal number of the zebra stripes counted from the lowest to the higher frequencies, \(f(s_{1})\) is the frequency of the stripe with the lowest frequency, \(s_{1}\) is the corresponding gyro-harmonic number, \(R=L_{\mathrm{bh}}\)/\(L_{\mathrm{nh}}\) is the ratio of the spatial scales, which exponentially depend on the magnetic field and density, in the region where zebra-stripes are generated, and \(R = R_{1} + R_{2} (n - 1)\) is taken as a linear function of \(n\), where \(R_{1}\) and \(R_{2}\) are constants.

The fitting procedure is mathematically expressed as a search for the minimum value in the relation

$$\begin{aligned} \frac{1}{N} \sum_{n=1}^{N} (f_{\mathrm{th}}(n) - f(n))^{2}, \end{aligned}$$
(4)

where \(N\) is the total number of the analyzed zebra stripes. The parameters \(s_{1}, R_{1}, R_{2}\), and \(f(s_{1})\) are the result of this fitting procedure. For more details about this method, see Yasnov and Karlický (2020) and Yasnov (2021).

Using this method, seven detected zebras were analyzed at selected times, and gyro-harmonic numbers \(s_{1}\) were determined for the zebra-stripe with the lowest analyzed frequency \(f(s_{1})\), see Table 1. As can be seen there, the gyro-harmonic number \(s_{1}\) is greater than 50 on all these zebras. It is surprising that the physical process that generates zebra stripes operates on such high harmonics instead of the usually preferred low harmonics where the resonance frequency might be achieved easily. These gyro-harmonic numbers are also significantly higher than the \(s\) considered in previous theoretical studies of the DPR instability. Moreover, the theoretical estimations made until now show that both the growth rates and the saturation energies of the UH waves caused by the DPR instability decrease with increasing gyro-harmonic number (Kuznetsov and Tsap, 2007; Benáček and Karlický, 2018). However, the growth rates and saturation energies of the DPR instability have been so far mainly computed for gyro-harmonic numbers \(s \lesssim20\) (Winglee and Dulk, 1986; Benáček, Karlický, and Yasnov, 2017; Lee et al., 2018; Ni et al., 2020; Li et al., 2021). Only Kuznetsov and Tsap (2007) calculated the growth rates for \(s \lesssim50\) for a power-law velocity distribution with a loss-cone angle \(30^{\circ}\), showing that the growth rate maxima are well distinct for selected parameters.

Table 1 Parameters of analyzed zebras according to Karlický and Yasnov (2021).
Full size table

In the present paper, we propose a solution to the problem of the generation of the zebra stripes with high gyro-harmonic numbers by considering a loss-cone distribution with large loss-cone angles. We compute the growth rates of the DPR instability in a broad interval of UH to cyclotron frequency ratios corresponding to the observed gyro-harmonic numbers up to \(s\sim\)100. We solve this problem numerically by integrating the analytical expressions for these growth rates. We consider the loss-cone \(\kappa\)-distribution and vary the loss-cone angle, the electron energies, the background plasma temperature, and the \(\kappa\) parameter. Besides the general results covering a broad range of gyro-harmonic numbers, we also present some results for the zebra observed on 14 February 1999.

The paper is organized as follows: In Section 2 we describe the method of the growth rate calculation. Section 3 presents the results of these calculations for a broad range of gyro-harmonic numbers. Finally, we summarize our results and discuss how zebra stripes with high values of \(s\) can be generated in Section 4.

2 Method for the Growth Rate Calculation

We assume a collisionless plasma consisting of a cold background plasma and hot electron species that are uniformly distributed in space and embedded in a uniform magnetic field. The background plasma consists of cold electrons with number density \(n_{\mathrm{b}}\) and cold protons with density \(n_{\mathrm{i}}\). Hot electrons of density \(n_{\mathrm{h}}\) are also considered. The plasma satisfies the charge neutrality condition, \(n_{\mathrm{i}} = n_{\mathrm{b}} + n_{\mathrm{h}}\). Both cold particle species have Maxwell velocity distributions with thermal velocities \(v_{\mathrm{b,i}} = \sqrt{k_{\mathrm{B}} T_{\mathrm{b,i}} / m_{ \mathrm{b,i}}}\), where \(k_{\mathrm{B}}\) is the Boltzmann constant, \(T_{\mathrm{b,i}}\) are the thermodynamic temperatures, and \(m_{\mathrm{b,i}}\) are the masses of the cold electrons and protons, respectively.

The hot electrons have a loss-cone \(\kappa\)-distribution that can be expressed in cylindrical coordinates as

$$ f(\boldsymbol {u}, \theta_{\mathrm{c}}, \Delta\theta_{\mathrm{c}}, \kappa) = f_{\kappa}(\boldsymbol {u}, \kappa) \, \varphi(\theta_{\mathrm{c}}, \Delta\theta_{\mathrm{c}}), $$
(5)

where \(\varphi\) characterizes the linear transition at loss cone angles

$$ \varphi(\theta_{\mathrm{c}}, \Delta\theta_{\mathrm{c}}) = \left \{ \textstyle\begin{array}{l@{\quad}l} 0, & ~~~~~~ \theta_{\mathrm{c}} - \Delta\theta_{\mathrm{c}} \geq \theta, \\ \frac{\theta- (\theta_{\mathrm{c}} - \Delta\theta_{\mathrm{c}}) }{2 \Delta\theta_{\mathrm{c}}}, & ~~~~~~ \theta_{\mathrm{c}} + \Delta\theta_{\mathrm{c}} > \theta> \theta_{\mathrm{c}} - \Delta\theta_{\mathrm{c}}, \\ 1, & \pi- \theta_{\mathrm{c}} - \Delta\theta_{\mathrm{c}} \geq \theta\geq\theta_{\mathrm{c}} + \Delta\theta_{\mathrm{c}}, \\ \frac{(\pi- \theta_{\mathrm{c}} + \Delta\theta_{\mathrm{c}}) - \theta}{2 \Delta\theta_{\mathrm{c}}}, & \pi- \theta_{\mathrm{c}} + \Delta\theta_{\mathrm{c}} > \theta> \pi- \theta_{\mathrm{c}} - \Delta\theta_{\mathrm{c}}, \\ 0, & ~~~~~~~~~~~~~~~~~~~~~~~~~\theta\geq\pi- \theta_{\mathrm{c}} + \Delta\theta_{\mathrm{c}}, \\ \end{array}\displaystyle \right. $$
(6)

where \(\theta_{\mathrm{c}}\) is the loss-cone angle, \(\Delta\theta_{\mathrm{c}}\) is the angular half-width of the linear loss-cone transition, \(\theta= \arctan(u_{\perp}/u_{\parallel})\) is the particle pitch angle, \(f_{\kappa}(\boldsymbol {u}, \kappa)\) is the \(\kappa\)-distribution (Livadiotis and McComas, 2013)

$$ f_{\kappa}(\boldsymbol {u}, \kappa) = \frac{n_{\mathrm{h}}}{n_{\mathrm{e}}} \frac{1}{(\pi\kappa v_{\mathrm{\kappa}}^{2} )^{\frac{3}{2}} \cos (\theta_{\mathrm{c}})} \frac{\Gamma(\kappa+ 1)}{\Gamma( \kappa- \frac{1}{2})} \left( 1 + \frac{u_{\perp}^{2} + u_{\parallel}^{2}}{\kappa v_{\mathrm{\kappa}}^{2}} \right)^{- \kappa-1}, $$
(7)

characterized by the index \(\kappa= \left(\frac{3}{2}, \infty\right)\), \(v_{\mathrm{\kappa}}\) is the \(\kappa\)-distribution velocity, and \(\Gamma\) is the Gamma function. The distribution function is normalized to the loss-cone angle as \(1/\cos(\theta_{\mathrm{c}})\), assuming that \(\Delta\theta_{\mathrm{c}} \ll1\). Unless otherwise mentioned, we use \(\kappa= 2\) and \(n_{\mathrm{e}} / n_{\mathrm{h}} = 32\). The \(\kappa\) index is in the interval of the observed values during solar flares, see e.g. Lörinčík et al. (2020). The loss-cone angular half-width is taken as \(\Delta\theta_{\mathrm{c}} = 2.5^{\circ}\).

The growth rate of the DPR instability is computed as (Melrose, 1986)

$$ \gamma(\omega, k_{\perp}) = - \frac{ \mathrm{Im} \, \epsilon_{\parallel}^{(1)}}{\left[\frac{\partial\mathrm{Re} \, \epsilon_{\parallel}^{(0)}}{\partial\omega}\right]_{\epsilon_{\parallel}^{(0)} = 0}}, $$
(8)

where \(\mathrm{Re} \, \epsilon_{\parallel}^{(0)}\) and \(\mathrm{Im} \, \epsilon_{\parallel}^{(1)}\) are the real and imaginary parts of the plasma dispersion tensor component along the magnetic field, that are obtained by a perturbation approach from the total dispersion tensor component

$$ \epsilon_{\parallel}= \epsilon_{\parallel}^{(0)} + \epsilon_{ \parallel}^{(1)} + \mathcal{O}(\epsilon_{\parallel}^{(2)}). $$
(9)

The imaginary part of the tensor component in Equation 8 for the growth rate was derived by Kuznetsov (2005)

$$\begin{aligned} \mathrm{Im}(\epsilon_{\parallel}^{(1)}) =& - 2\pi^{2} m_{ \mathrm{e}}^{3} \frac{\omega_{\mathrm{pe}}^{2}}{k^{2}} \sum_{l=s+1}^{ \infty} a^{3} \times \\ & \times\int_{0}^{\pi} J_{l} \left( \frac{\gamma_{\mathrm{rel}} k_{\perp}v_{\perp}}{\omega_{\mathrm{ce}}} \right) \frac{\gamma_{\mathrm{rel}}^{2} \sin\phi}{\frac{\partial\psi }{\partial\rho}} \frac{1}{ v_{\perp}}\frac{\partial f}{\partial u_{\perp}} \, \mathrm{d}\phi, \end{aligned}$$
(10)
$$ \frac{\partial\psi}{\partial\rho} = \frac{1}{c^{2}} \left( v_{ \parallel}^{2} + v_{\perp}^{2} \right). $$
(11)
$$ v_{\parallel}= - a \cos(\phi), \quad v_{\perp}= a \sin(\phi), \quad a^{2} = \frac{ c^{2} (l^{2} \omega_{\mathrm{ce}}^{2} - \omega^{2})}{l^{2} \omega_{\mathrm{ce}}^{2}} $$
(12)
$$ \omega_{\mathrm{pe}}^{2} = \omega_{\mathrm{pb}}^{2} + \omega_{ \mathrm{ph}}^{2} = \frac{ (n_{\mathrm{b}} + n_{\mathrm{h}}) e^{2}}{m_{\mathrm{e}} \epsilon_{\mathrm{0}}}, \qquad\lambda= \frac{k_{\perp}^{2} v_{\mathrm{tb}}^{2}}{\omega_{\mathrm{ce}}^{2}}, $$
(13)

where \(\omega_{\mathrm{pe}}\) is the plasma frequency of both electron species, \(\omega_{\mathrm{ce}} = e B / m_{\mathrm{e}}\) is the electron cyclotron frequency, \(\mathbf{k} = (k_{\perp}, k_{\parallel})\) is the wave vector of the electrostatic waves and we assume \(k_{\parallel}= 0\), \(\omega\) is the wave frequency, \(I_{l}(\lambda)\) is the modified Bessel function of the first kind of the \(l\)-th order, \(\lambda\) is the dimensionless parameter of the Bessel function, \(e\) is the electron charge, \(\epsilon_{0}\) is the permittivity of the vacuum, and \(s\) is the gyro-harmonic number. The integration is done via the resonance ellipse of Equation 1.

The denominator in Equation 8 can be expressed as

$$ \frac{\partial\epsilon_{\parallel}^{(0)}}{\partial\omega} = 4 \omega\omega_{\mathrm{pb}}^{2} \frac{e^{-\lambda}}{\lambda} \sum_{l=1}^{ \infty} \frac{l^{2} I_{l}(\lambda)}{(\omega^{2} - l^{2} \omega_{\mathrm {ce}}^{2})^{2}}. $$
(14)

Equation 8 can be mathematically evaluated in the \(\omega-k_{\perp}\) domain; however, only the waves that are solutions of the plasma dispersion relation are actually present in the plasma and can grow. To simplify the calculation of the growth rates, we choose the dispersion relation of the UH waves as

$$ \omega^{2} = \omega_{\mathrm{pb}}^{2} + \omega_{\mathrm{ce}}^{2} + 3 v_{\mathrm{tb}}^{2} k_{\perp}^{2}, $$
(15)

where we assume that the dispersion relation is given only by the background plasma component, \(\epsilon_{\parallel}^{(0)}\).

The numerical procedure for the computation of a growth rate value for a given set of plasma parameters (\(\omega_{\mathrm{pe}}/\omega_{ \mathrm{ce}}\), \(v_{\mathrm{tb}}\), \(v_{\mathrm{\kappa}}\), \(\kappa\), \(\Delta\theta_{\mathrm{c}}\), and \(\theta_{\mathrm{c}}\)) is the following. We equidistantly divide the wavenumber space of the UH branch into \(N=1500\) grid points in the \(k_{\perp}c /\omega_{\mathrm{pe}} \in[1,40]\) interval. According to our tests, this interval is wide enough for the whole range of studied background temperatures. Approximately, the typical wavenumber \(k_{\perp}\) increases with decreasing background thermal velocity \([v_{\mathrm{tb}}]\) as follows from Equation 13 when the parameter \(\lambda\) is constant. The unstable waves are typically located in an interval \(k_{\perp}c / \omega_{\mathrm{pe}} \approx[4,15]\) for a temperature of 3 MK and in an interval \(k_{\perp}c / \omega_{\mathrm{pe}} \approx[10,37]\) for a temperature of 0.5 MK. Moreover, these intervals slightly vary with other parameters. The grid cell size is \(\Delta k_{\perp}c /\omega_{\mathrm{pe}} = 0.026\). For each grid cell \(k_{\perp i}\), where \(i=1, \ldots, 1500\) is the grid cell index, we compute the frequency of the UH wave \(\omega_{i}\) from Equation 15. For the frequency [\(\omega_{i}\)], we evaluate the growth rate \(\gamma_{i}\) in each grid cell [\(k_{\perp i}\)]. Then, we compute the mean value of the growth rate over all positive \(\gamma_{i}\) as

$$ \Gamma= \frac{1}{\Gamma_{0}} \sum_{i} \gamma_{i}(\omega_{i}, k_{ \perp i}) \sigma_{i}(\omega_{i}, k_{\perp i}) \Delta k_{\perp}, $$
(16)

where \(\sigma_{i}\) is the characteristic width of the dispersion branch for each \(i\)-th element (Benáček and Karlický, 2019; Manthei et al., 2021). The characteristic width \(\sigma_{i}\) is estimated as

$$ \sigma_{i} = \left. \left( \frac{\partial\epsilon_{\parallel}^{(0)}}{\partial\omega} \right)^{-1} \right|_{\omega_{i},k_{\perp i}}, $$
(17)

\(\Gamma_{0}\) is the normalization parameter

$$ \Gamma_{0} = \sum_{i} \sigma_{i}(\omega, k_{\perp}) \Delta k_{ \perp}, $$
(18)

We denote the mean growth rate value \(\Gamma\) as integrated growth rate.

3 Results

In the following, our results on the growth rate of the electrostatic waves are shown as a function of the gyro-harmonic number \(s = \sqrt{\omega_{\mathrm{pe}}^{2} / \omega_{\mathrm{ce}}^{2} + 1}\), as follows from the radio emission process. Because the frequency ratio changes with height in the corona, zebra stripes are produced only when the profile of the integrated growth rate forms peaks at specific frequency ratios. The peaks are not always located at integers of \(s\) (harmonics of the cyclotron frequency) because there are other effects that can shift them, such as the effect due to the Lorentz factor in Equation 1, as shown by Benáček, Karlický, and Yasnov (2017).

Figure 2 shows the growth rates in the \(\omega-k_{\perp}\) space for four selected loss-cone angles \(\theta_{\mathrm{c}} = 30^{ \circ}\), 50∘, 65∘, and 80∘, the background temperature 3 MK (≈130 eV), and the velocity of \(\kappa\)-distribution \(v_{\kappa} = 0.3\) c (≈23 keV). The gyro-harmonic number is fixed at \(s = 50\). The growth rates are smallest for the small loss-cone angle \(30^{\circ}\). By increasing the loss-cone angle to \(50^{\circ}\) and \(65^{\circ}\), the growth rate values increase and the positive growth rate regions shift to smaller wavenumbers. At the loss-cone angle \(80^{\circ}\), the growth rates values and areas of positive growth rate regions decrease.

Figure 2
figure 2

Growth rates as a function of the frequency and wavenumber for four loss-cone angles \(\theta_{\mathrm{c}}\), the gyro-harmonic number is \(s = 50\), the temperature of the background plasma is 3 MK, and the velocity of \(\kappa\)-distribution \(v_{\mathrm{\kappa}} = 0.3\,c\). Note that the color scale in (a) differs from those in (b–d). Green curves: the dispersion branch of the UH waves. All these UH branches are the same in all panels because they are independent of the loss-cone distribution.

Full size image

The growth rates are overlaid by the dispersion branch of the UH waves (Equation 15). If the branch crosses a positive growth rate region, the waves located in the intersection can grow. During the growth phase, the kinetic energy of resonant hot electrons, whose velocities fulfill Equation 1, is converted into electrostatic wave energy and the particle distribution changes. Finally, the growing waves saturate when the electron velocity distribution becomes stable.

Each region in the \(\omega-k_{\perp}\) space with a positive growth rate is associated with a specific gyro-harmonic number \(s\). These regions have a distance in the frequency dimension approximately equal to the electron cyclotron frequency. When the frequency ratio varies, the positive regions shift in frequency so that the crossings of the positive growth rate regions with the UH branch change. This way, we expect the formation of growth rate peaks (which may be responsible for the formation of the zebra stripes). However, the peaks are not so significant if the UH branch crosses several positive regions simultaneously (e.g. Figure 2(b)).

In Figure 3, the integrated growth rates are presented as a function of the gyro-harmonic number for four loss-cone angles, background temperature 3 MK, and the velocity of the \(\kappa\)-distribution \(v_{\kappa}= 0.3\,c\). The integrated growth rates are computed following Equation 16. We have selected four intervals of gyro-harmonic numbers, from small values \(s = 7\), for which the radio zebras are not observed, to the most extreme case of the gyro-harmonic number exceeding 100. In all cases the growth rates are positive. For low gyro-harmonic numbers \(s = 7\,{-}\,10\), the growth rates form distinguishable peaks for all loss-cone angles. With increasing \(s\) the growth rate profiles smooth out; however, the smoothing varies between the different loss-cone angles. For the angle 30∘, the growth rate profile smooths out already for \(s \gtrsim20\), and their values decrease for higher gyro-harmonic numbers. For the angles 50∘ and 65∘, the growth rate profiles smooth out in the gyro-harmonic number interval \(s = 50\,{-}\,53\). Their average values slightly increase and decrease for \(\theta_{\mathrm{c}} = 50^{\circ}\) and for \(\theta_{\mathrm{c}} = 65^{\circ}\), respectively. For the loss-cone angle 80∘, the growth rates monotonically increase within the whole studied interval of gyro-harmonic numbers. For large gyro-harmonic numbers \(s = 100\,{-}\,103\), the growth rate peaks are still formed.

Figure 3
figure 3

Integrated growth rates in four selected intervals of the gyro-harmonic numbers and for four loss-cone angles. The temperature of the background plasma is 3 MK, and the velocity of the \(\kappa\)-distribution \(v_{\mathrm{\kappa}} = 0.3\,c\).

Full size image

Because the highest growth rates for the large gyro-harmonic numbers (derived from zebra observations) occur for the angle \(80^{\circ}\), we studied the dependence of the integrated growth rate profiles on two plasma temperatures (0.5 and 3 MK) and selected values for the velocities of the \(\kappa\)-distribution in the interval \(v_{\kappa}\in[0.15,0.3]c\), see Figures 4 and 5. Though the temperature 0.5 MK may be smaller than those estimated during flares, the accelerated electrons may reach and emit in the colder part of the corona. Moreover, we selected this background temperature range to clearly identify the temperature impact, as the background temperature is known to have a small impact on instability (Benáček, Karlický, and Yasnov, 2017). The integrated growth rates are computed in the same gyro-harmonic number intervals as in Figure 3.

Figure 4
figure 4

Integrated growth rates as a function of the \(\kappa\)-distribution velocity, for four selected intervals of the gyro-harmonic number, the loss-cone angle 80∘ and the temperature of the background plasma 3 MK. Note that the scaling of the growth rates varies between panels.

Full size image
Figure 5
figure 5

Same as Figure 4, but for the temperature of the background plasma 0.5 MK.

Full size image

For plasma temperature 3 MK (Figures 4), the average values (over few \(s\)) of the integrated growth rates increase with the gyro-harmonic number independently of the velocity of the \(\kappa\)-distribution. All growth rate profiles smooth out for \(s\sim50\). The situation is reversed for large gyro-harmonic numbers where the most distinct peaks are formed for the smallest velocity of the \(\kappa\)-distribution \(v_{\mathrm{\kappa}} = 0.15\). In addition, the integrated growth rates for this background velocity and gyro-harmonic numbers form a double peak profile.

The behavior of the integrated growth rates as a function of the gyro-harmonic number is different for the background temperature 0.5 MK in a few aspects, see Figure 5. For velocities of the \(\kappa\)-distribution \(v_{\mathrm{\kappa}} \geq0.2\,c\), the growth rate peaks are well distinct for the whole range of the gyro-harmonic numbers. The distinction occurs because the distribution functions of the hot and cold components are more separated in velocity space than for the temperature 3 MK. Because of this separation, the velocity gradient of the loss-cone distribution increases, and the growth rate reaches higher values. For all velocities of the \(\kappa\)-distribution, the growth rate values increase from \(s = 7\,{-}\,10\) to \(s = 20\,{-}\,23\). Increasing the gyro-harmonic numbers further, the growth rate increases most at the smallest velocities of the \(\kappa\)-distribution. For the case of \(v_{\mathrm{\kappa}} = 0.3\,c\), the growth rates remain almost the same as for \(s \gtrsim20\).

Figure 6 shows a change in the integrated growth rates with the \(\kappa\) index. We compare the integrated growth rates for \(\kappa= 2\) and \(\kappa= 100\) (closer to the Maxwellian velocity distribution). The integrated growth rate profiles for \(\kappa= 100\) are higher and with more distinct peaks than those for \(\kappa=2\).

Figure 6
figure 6

Comparison of the integrated growth rates for \(\kappa\)-indices 2 and 100, temperature is 3 MK, and the velocity of the \(\kappa\)-distribution is \(0.3\,c\).

Full size image

3.1 The 14 February 1999 Zebra Case

Besides the above presented general results covering a broad range of the gyro-harmonic number, let us summarize the results for the specific zebra observed on the 14th February 1999, shown in Figure 1, as an example. In this case, the gyro-harmonic number was estimated as \(s_{1} = 64\) (Table 1). For this zebra, we calculated the integrated growth rates in the range \(s = 64\,{-}\,67\), the loss-cone angles \(55\,{-}\,80\,^{\circ}\), the temperatures 0.5 MK and 3 MK, and \(v_{\kappa}\in[0.1,0.5]c\). From the analysis, it follows that the emission is most likely produced by a loss-cone angle \(\sim(70\pm5)^{\circ}\). The growth rate peaks are formed for a wider range of plasma temperatures and velocities of the \(\kappa\)-distribution. For the plasma temperature of 3 MK, the velocity of the \(\kappa\)-distribution must be ≥ 0.15 \(c\). For the plasma temperature of 0.5 MK, the velocity of the \(\kappa\)-distribution can be in the whole analyzed range of \(v_{\kappa}\in[0.1,0.5]c\). Our conclusion for this zebra is that though the plasma temperature and the velocity of the \(\kappa\)-distribution can be in a broad range of values to produce the emission, the loss-cone angle should be restricted into a narrow range of about \(\sim(70\pm5)^{\circ}\).

4 Discussion and Conclusions

The solar radio zebras are used for diagnostics of plasma parameters during solar flares. One of the crucial parameters is the gyro-harmonic number in the emission region, which allows to estimate the upper-hybrid to cyclotron frequency ratio. Though the gyro-harmonic numbers determined from zebra observations are greater than about 50 and may exceed one hundred, most studies so far have focused on significantly smaller gyro-harmonic numbers, rarely higher than 20. We have addressed the question of how the solar radio zebras can be produced with such high gyro-harmonic numbers by analyzing the DPR instability in a broad range of gyro-harmonic numbers \(s = 7\,{-}\,103\).

We have calculated linear growth rates and studied the effects of the loss-cone angle, the velocity of the \(\kappa\)-distribution, the background plasma temperature, and the \(\kappa\) index on the instability. We found that the zebras with high gyro-harmonic numbers are produced by loss-cone distributions with large loss-cone angles. Moreover, the higher the gyro-harmonic number, the larger the loss-cone angle must be to produce the instability. For the gyro-harmonic number \(\sim100\), a loss-cone angle \(\sim80^{\circ}\) is sufficient. However, for even larger gyro-harmonic numbers, we expect that the necessary high angles of the loss-cone are difficult to produce and therefore unlikely to be observed.

4.1 Growth Rate Properties

Our calculations show that for increasing gyro-harmonic number the integrated growth rates of the DPR instability increase for large values of the loss-cone angle (\(\sim80^{\circ}\)). Moreover, the growth rate peaks are distinct for gyro-harmonic numbers \(s\sim100\) and smooth for smaller loss-cone angles \(<80^{\circ}\). The integrated growth rates are large enough for all loss-cone angles \(\gtrsim50^{\circ}\) to produce zebra type of radio emission.

In some cases, the growth rates show only small variations depending on \(s\). However, we note that these variations may produce a significant difference in the saturation energy levels, as was shown using particle-in-cell simulations by Benáček and Karlický (2018).

The growth rate average values (over a broader range of gyro-harmonic numbers) monotonously decrease only for a loss-cone angle of 30∘. In contrast, for the loss-cone angle of 80∘, the average values monotonously increase.

Moreover, how distinct the integrated growth rate maxima are for high gyro-harmonic numbers \(s \sim50-100\) and at large loss-cone angles depends on the temperature of the background plasma and the velocity of the \(\kappa\)-distribution. Assuming that the instability occurs in a heated plasma during a flare with a temperature of 3 MK, the growth rate profiles are smoothed out around \(s \sim50\) but form emission peaks for \(s \sim100\). Moreover, for the gyro-harmonic number \(s \sim100\), they produce double-peaked profiles for small velocities of the \(\kappa\)-distribution \(v_{\kappa}= 0.15c\). If the emission is formed in a region with a colder plasma of temperature 0.5 MK, e.g. further from the flare region, the growth rates are distinct for the whole range of gyro-harmonic numbers. Nonetheless, for both temperatures and large gyro-harmonic numbers, higher growth rates are favored for smaller \(\kappa\)-distribution velocities in the range \(v_{\kappa}\in[0.15,0.20]c\) than for larger values in the range \(v_{\kappa}\in[0.25,0.3]c\).

4.2 Proposed Zebra Emission Regions

The fact that high gyro-harmonic numbers are detected in zebras means that the zebra-stripe sources are in regions where the ratio of \(\omega_{\mathrm{pe}}/ \omega_{\mathrm{ce}}\) is high. In combination with the result that higher growth rates are favored for large loss-cone angles, two possible explanations can be proposed:

  1. i)

    We may assume that the loop cross-section is only slightly wider at their midpoints than at their footpoints, in agreement with Klimchuk (2000). In such a loop, the change of the magnetic field along the loop is small, and only superthermal electrons with high pitch angles can be trapped (Krucker, Masuda, and White, 2020). This way, a loss-cone distribution with a high loss-cone angle is formed. Thus the instability can generate the UH waves and the corresponding zebra stripes with high gyro-harmonic numbers. Moreover, for the zebra stripes with high \(s\), the magnetic field in this loop must be relatively small (\(\omega_{ \mathrm{pe}}/ \omega_{\mathrm{ce}}\gg 1\)). We also note that the small change of the magnetic-field strength along the loop agrees with the small difference in magnetic-field strength derived from the neighboring zebra-stripe frequencies for high values of the gyro-harmonic numbers. The typical intensity of the magnetic field in these regions can be derived as \(B = f_{s}\)/(2.8\(\cdot s\)), where \(B\) is the magnetic field strength in a unit of gauss, and fs is the zebra-stripe frequency in a unit of MHz with the gyro-harmonic number \(s\) (Karlický and Yasnov, 2018). For low values of \(s\), these differences are much higher. Therefore, in a loop with a small magnetic field gradient, spatial distances of zebra-stripe sources with low values of \(s\) will be much longer than those for high values of \(s\).

  2. ii)

    Considering the standard flare model (Aschwanden, 2004), a region with high values of \(\omega_{\mathrm{pe}}/ \omega_{\mathrm{ce}}\) can be found below the X-point of the flare. The plasma density here is relatively high (comparable to the current sheet density), and the magnetic field in the reconnection outflow is relatively low. The electrons from reconnection move downwards and penetrate into newly formed magnetic loops where they may be trapped (Švestka et al., 1987). If the electrons initially have a perpendicular velocities to the magnetic field larger than their parallel ones, they can form loss-cone distributions with large loss-cone angles. The electrons are accelerated not only at the X-point of the magnetic reconnection, but also during the shrinking of magnetic loops in the reconnection outflow Karlický and Kosugi (2004).

4.3 Double-Peaked Pattern of Growth Rates

We searched for the double-peaked pattern from Figure 4(d), whether it also occurs for smaller gyro-harmonic numbers, various temperatures, and \(\kappa\)-distribution velocities. However, it did not appear anywhere in our calculations. We also performed tests to discard the numerical uncertainty at the origin of the double-peaked profiles. We varied the ranges of the calculations and the precision of the numerical integrals and tested individual parts of the calculations for these parameters, but we found no discrepancies or errors. Nonetheless, due to the complexity of the calculations, we could not say whether there were hidden numerical artifacts produced by an approximation in the analytical growth rate derivation.

The double-peaked growth rate profile is generally formed when the growth rate region in the \(\omega-k_{\perp}\) space is not as the one shown in Figure 2, i.e. when it forms not only one tadpole region for each gyro-harmonic number, but two (or more) separate regions. Therefore, the UH branch could cross two regions and create two growth rate maxima. However, this would require a specific kind of velocity distribution function, probably with two distinct regions in the \(\omega-k\) space of positive velocity gradients.

The question arises how we can observationally recognize that the adjacent zebra stripes are formed by double-peaked growth rates. Assuming that there are two distinct regions in the \(\omega-k\) space, they probably do not have the same shape. Therefore, both generated zebra stripes could be created at different emission intensities, with different frequency ratios between odd and even stripes, and odd and even stripes might have different emission profiles (e.g. odd stripes are narrower and even stripes are broader). Nonetheless, if the regions are similar and regularly distributed in the \(\omega-k\) space, also the emission profiles can be similar. Moreover, we may speculate that a change or evolution of the velocity distribution during the emission might allow the transition from a double-peaked to a single-peaked profile, or vice versa, as in the observed zebras with merging zebra stripes (Chernov et al., 2005).

4.4 Comparison with other Procedures of the Growth Rates Calculation

Kuznetsov and Tsap (2007) (KT07) found that growth rates decrease with increasing gyro-harmonic number. They performed calculations for a power-law distribution (power-law index \(\delta= 10\)) for the loss-cone angle \(30^{\circ}\). Their approach was to estimate the growth rates only for a specific part of the resonance ellipse (Equation 1). In contrast, in our approach we integrate over the whole ellipse in Equation 10 for each specific point in the \(\omega-k_{\perp}\) space (Kuznetsov, 2005) (K05). To obtain the integrated growth rate, we integrate over the UH dispersion branch, which produces more reliable results according to the tests by electromagnetic, relativistic particle-in-cell simulations (Benáček and Karlický, 2019; Manthei et al., 2021) (BK19). Though KT07 used a different kind of loss-cone distribution, the decrease of the growth rates with increasing gyro-harmonic number for the loss-cone angle \(30^{\circ}\) is in agreement with our results. Nonetheless, the exact growth rate values differ.

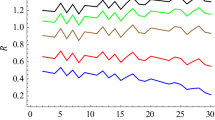
We compare these three approaches to growth rate calculations in Figure 7 for the gyro-harmonic number \(s \sim50\) as a function of the loss-cone angle. In all three cases, the growth rates are selected on the UH dispersion branch for 0.5 MK and \(v_{\mathrm{\kappa}} = 0.3\,c\). The maximal growth rates of the K05 method are smaller than those of the KS07 method for loss-cone angles \({\leq}65^{\circ}\). However, the growth rates for the angle \(80^{ \circ}\), which are smaller for the KT07 method, are largest for the K05 method. Moreover, all growth rate profiles are relatively smoother for the KT07 method than for the K05 method. The integrated growth rates of the BK19 method are systematically lower than the maximal growth rates (from the definition of the average along the dispersion branch in Equation 16). In agreement with BK19, who studied the integrated growth rates only for small gyro-harmonic numbers \(\omega_{\mathrm{pe}}/ \omega_{\mathrm{ce}} \approx 4\,{-}\,5.2\), the peaks of the integrated growth rate are more distinct than (normal) growth rates also for high gyro-harmonic numbers.

Figure 7
figure 7

Comparison of the growth rate calculations: (a) using the maximal method of Kuznetsov and Tsap (2007) with (b) the maximal and (c) the averaged method, which is used in this paper and based on an integration over the whole resonance ellipse (Kuznetsov, 2005). The background temperature is 0.5 MK, and the \(\kappa\)-distribution velocity is \(v_{\mathrm{\kappa}} = 0.3\,c\). Compare the growth rates in panel (c) with the integrated growth rates for higher background temperature in Figure 3c.

Full size image

Yasnov, Benáček, and Karlický (2019) among others computed growth rates for the loss-cone angle 80∘ using the same method as KS07. They found negative growth rates for large loss-cone angles. However, they applied a loss-cone \(\kappa\)-distribution with an additional cut-off at \(v_{\mathrm{m}}=0.3\,c\), where \(v_{\mathrm{m}}\) is the cut-off velocity. For distributions without the cut-off, they found that the growth rates are very broad for \(\theta_{\mathrm{c}} \sim50^{\circ}\). As we show in Figure 7, the integrated growth rate peaks may still be distinct.

Increasing the \(\kappa\) index of the \(\kappa\)-distribution from two to one hundred, the integrated growth rates increase, and their maxima become more distinct. Increasing \(\kappa\) index, there are more particles with smaller \(\kappa\)-distribution velocities. Therefore, these particles increase the distribution gradients and contribute more to the integral of Equation 10 over the resonance ellipse.

We conclude that the DPR instability model may produce solar radio zebras with high gyro-harmonic numbers at large loss-cone angles \(\sim80^{\circ}\). The growth rate maxima are distinct, and they are high enough to generate zebra patterns.