Abstract
Spectropolarimetric reconstructions of the photospheric vector magnetic field are intrinsically limited by the \(180^{\circ}\) ambiguity in the orientation of the transverse component. The successful launch and operation of Solar Orbiter have made the removal of the 180∘ ambiguity possible using solely observations obtained from two different vantage points. While the exploitation of such a possibility is straightforward in principle, it is less so in practice, and it is therefore important to assess the accuracy and limitations as a function of both the spacecrafts’ orbits and measurement principles. In this work, we present a stereoscopic disambiguation method (SDM) and discuss thorough testing of its accuracy in applications to modeled active regions and quiet-Sun observations. In the first series of tests, we employ magnetograms extracted from three different numerical simulations as test fields and model observations of the magnetograms from different angles and distances. In these more idealized tests, SDM is proven to reach a 100% disambiguation accuracy when applied to moderately-to-well resolved fields. In such favorable conditions, the accuracy is almost independent of the relative position of the spacecraft with the obvious exceptions of configurations where the spacecraft are within a few degrees of co-alignment or quadrature. Even in the case of disambiguation of quiet-Sun magnetograms with significant under-resolved spatial scales, SDM provides an accuracy between 82% and 98%, depending on the field strength. The accuracy of SDM is found to be mostly sensitive to the variable spatial resolution of Solar Orbiter in its highly elliptic orbit, as well as to the intrinsic spatial scale of the observed field. Additionally, we provide an example of the expected accuracy as a function of time that can be used to optimally place remote-sensing observing windows during Solar Orbiter observation planning. Finally, as a more realistic test, we consider magnetograms that are obtained using a radiative-transfer inversion code and the SO/PHI Software siMulator (SOPHISM) applied to a 3D-simulation of a pore, and we present a preliminary discussion of the effect of the viewing angle on the observed field. In this more realistic test of the application of SDM, the method is able to successfully remove the ambiguity in strong-field areas.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The magnetic field on the Sun is measured by remote sensing based on the interpretation of spectropolarimetric observations of the emitted light (see, e.g. Lites, 2000). In a traditional inversion technique applied to such measurements, the observed Stokes spectra are parametrically matched by synthetic spectra determined by an emission model (e.g., the Zeeman effect), a propagation model (which requires a model of the solar atmosphere), and the detector system; see, e.g., del Toro Iniesta (2007).
However, even leaving aside any measurement errors affecting the measured spectra and any systematic modeling errors affecting the spectropolarimetric inversions, the vector field at a given location still cannot be fully known. While the line-of-sight (LoS, hereafter) component (to the observer) can be fully reconstructed, the transverse component can be inferred in magnitude and direction only, but not in orientation. This results in an intrinsic 180∘ ambiguity in the orientation of the transverse component. To fully determine the vector magnetic field, this ambiguity must be removed (Harvey, 1969).
In the semi-classical picture, the ambiguity is due to the invariance of the Stokes vector to a 180∘ rotation of the reference system about the LoS-axis. Therefore, the 180∘ ambiguity is an intrinsic limitation of remote sensing that cannot be eliminated by improving spectropolarimetric measurements.
In actual observations, the magnetic field [\({\boldsymbol{B}} \)] in the detector image plane can be decomposed into the sum of a LoS-component [\(\boldsymbol{B}_{\mathrm{los}}\)] and a transverse component [\(\boldsymbol{B}_{\mathrm{tr}}\)] perpendicular to the LoS as
where the LoS is pointing from the Sun toward the observer, and \(\hat{\boldsymbol{t}}\) is the unit vector along the transverse component in the image plane. The removal of the ambiguity corresponds to determining the sign [\(\zeta\)] in each pixel. In this sense, the ambiguity is a parity problem (Semel and Skumanich, 1998) of the transverse component in each pixel of the image plane of the detector.
Several empirical methods are available, proposing solutions to remove the ambiguity. A review is given by Metcalf et al. (2006) with more recent testing by Leka et al. (2009). In particular, Table 1 of Leka et al. (2009) shows that all methods are based on choosing the sign [\(\zeta\)] in each pixel such that a specific quantity is minimized. The quantity to minimize can be, for instance, the angle between the observed transverse field and a reference field (acute-angle method, with the reference field chosen to be, e.g., the potential field; see discussion by Metcalf et al. (2006)), or a weighted combination of current density and the divergence of the field (minimum-energy method; see again Metcalf et al. (2006)), with the vertical derivatives of the field components approximated using extrapolation in height. Such minimization methods require assumptions, and, while such methods have been tested and used extensively, they all propose hypothetical solutions: none can guarantee to correctly remove the ambiguity because it depends on models and assumptions rather than solely on direct observations.
Remote observations of the same area on the Sun from different vantage points open a novel possibility for removing the ambiguity of the transverse component of the magnetic field. From a purely geometrical point of view, if two observations of the same area on the Sun are available, then the 180∘ ambiguity can, in principle, be removed (see, e.g., Solanki et al., 2015; Rouillard et al., 2020). The basic idea is that the unambiguous LoS-component measured by one vantage point will generally have a non-zero projection on the ambiguous transverse component measured by the second instrument. In this way, the “true” orientation of the measured transverse component can be fixed as the sign of \(\zeta\) that reproduces the alignment with the LoS of the other instrument. The stereoscopic disambiguation of the transverse-field orientation can be then derived directly from observations without any additional hypotheses or modeling.
Unlike traditional single-view disambiguation methods, the equations for the stereoscopic disambiguation are exact for continuous magnetic fields. However, several factors can limit the accuracy of the disambiguation in real applications. For the sake of concreteness, we will consider stereoscopic disambiguation applied to vector magnetograms from the Helioseismic and Magnetic Imager (HMI) instrument onboard the Solar Dynamic Observatory (Scherrer et al., 2012, hereafter SDO), and from the High Resolution Telescope (HRT), and Full Disk Telescope (FDT) integrated on the Polarimetric and Helioseismic Imager (PHI) onboard Solar Orbiter (Solanki et al., 2020, hereafter SO). We point out, however, that the method and results illustrated in this article can be applied using magnetograms from other observatories, such as the forthcoming space-weather Lagrange mission (see, e.g., Hapgood, 2017).
First, the stereoscopic removal of the ambiguity requires the direct comparison of vector magnetograms taken from different viewpoints. This implies that the magnetic field observations of one instrument need to be interpolated onto (the image plane and resolution of) the other. Naturally, the finite instrumental resolution will limit the accuracy of the disambiguation method. For the sake of convenience, we assume critical sampling, which is almost perfectly correct for both SO/PHI-HRT and SO/PHI-FDT onboard Solar Orbiter and nearly correct for SDO/HMI. Additionally, for the case of Solar Orbiter, the two available telescopes SO/PHI-HRT and SO/PHI-FDT have markedly different plate scales (Solanki et al., 2020).
Second, Solar Orbiter significantly changes the distance from the Sun along its orbit, which implies that the effective resolution on the Sun of SO/PHI magnetograms, and with them, the accuracy of their stereoscopic disambiguation, will change along the orbit.
Third, measurement errors of different nature are indeed present. These can vary from systematic instrumental errors, such as the accuracy of pointing and the intrinsic sensitivity or spectral resolution of the instrument, to local inaccuracy in the calibration and inversion of spectropolarimetric measurements due to approximations in the employed model atmosphere (see, e.g., Landi Degl’Innocenti, 2013; Borrero et al., 2014). Such errors and properties are generally different for the magnetic-field maps built from different observatories (Borrero et al., 2011; Schou et al., 2012; Albert et al., 2020).
Finally, aside from these geometrical considerations, a more fundamental issue must be raised, namely that two instruments pointing at exactly the same geometrical location on the Sun from different viewpoints do not measure exactly the same field. The reason is that, due to the difference in the optical path, the emission recorded by the two instruments originates from different depths in the photosphere. Hence, even if pointing at the same location on the solar surface, the measured emission would not come from the same parcel of plasma.
Realistic modeling of all of the sources of inaccuracies mentioned above is extremely challenging. As the first one in a planned series of studies, the main goal of this article is to introduce the stereoscopic-disambiguation method (SDM hereafter), described in Section 2, and to verify the practical feasibility of removing the 180∘ ambiguity that is intrinsic to spectropolarimetric inversions from remote-sensing reconstructions of the photospheric magnetic field from two observatories. For this, we consider two types of tests. The first one is a purely geometrical test, where a magnetogram is seen from different viewing angles and distances by the two detectors (see Section 3). For this test, we use a set of three different numerical simulations described in Section 3.1. The accuracy of SDM depending on the geometry of the observations is analyzed in Section 4. In the second type of test, we consider the synthetic emission from a three-dimensional numerical simulation of the photosphere (see Section 5) to treat the additional complication that, when observed from two different viewing angles, the geometrical height of the same optical depth [\(\tau\)] surface is different. In this way, the accuracy of SDM is tested against the influence of radiation detected by the two observatories, which is not actually coming from the same parcel of plasma (Section 6) – an assumption that is implicitly made in the geometrical tests in Section 3. The discussion and conclusions are finally given in Section 7.
2 Stereoscopic Disambiguation Method (SDM)
Let us consider the plane \(\Sigma\) defined by the position of the two detectors, A and B, and the (center of the) Sun, and let \(\hat{\boldsymbol{n}}\) be the unit vector normal to \(\Sigma\), as in Figure 1. For each detector A and B, let us define a base for the reference system defined by the unit vector \(\hat{\boldsymbol{n}}_{X}=\hat {\boldsymbol{n}}\) normal to \(\Sigma\) (positive toward solar North, with X in \([A,B]\)), the unit vector \(\hat{\boldsymbol{l}}_{X}\) of the LoS-direction (positive in the detector direction), and the (solar-West oriented) unit vector \(\hat{\boldsymbol{w}}_{X}=\hat{\boldsymbol{n}}_{X} \times\hat {\boldsymbol{l}}_{X}\), as \(S_{\mathrm{A}}=(\hat{{\boldsymbol {l}}}_{\mathrm{A}},\hat{{\boldsymbol {w}} }_{\mathrm{A}},\hat{ {\boldsymbol {n}}}_{\mathrm{A}})\) and \(S_{\mathrm{B}}=(\hat{{\boldsymbol {l}}}_{\mathrm{B}},\hat{{\boldsymbol {w}} }_{\mathrm{B}},\hat{ {\boldsymbol {n}}}_{\mathrm{B}})\). By construction, \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}=\hat{{\boldsymbol {n}}}_{\mathrm{B}}=\hat {\boldsymbol{n}}\), and the image plane of detector A (respectively, B) is parallel to the plane \((\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat{{\boldsymbol {n}}}_{\mathrm{A}})\) (respectively, \((\hat{{\boldsymbol {w}}}_{\mathrm{B}},\hat{{\boldsymbol {n}}}_{\mathrm{B}})\)). The origin of each coordinate system is placed at the central pixel of the corresponding detector’s image plane. With this choice, the plane identified by \((\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat{{\boldsymbol {n}}}_{\mathrm{A}})\) is basically a rotation of the detector plane of the telescope A (and similarly for B).
Schematic representation of the reference systems for the application of SDM. The plane \(\Sigma\) of normal \(\hat{\boldsymbol{n}}\) passes through the positions of the detectors A and B and the center of the Sun. For the detector A (respectively, B) the Cartesian reference system \(S_{\mathrm{A}}=(\hat{{\boldsymbol {l}}}_{\mathrm{A}},\hat{{\boldsymbol {w}} }_{\mathrm{A}},\hat{ {\boldsymbol {n}}}_{\mathrm{A}})\) (respectively, \(S_{\mathrm{B}}=(\hat{{\boldsymbol {l}}}_{\mathrm{B}},\hat{{\boldsymbol {w}} }_{\mathrm{B}},\hat{ {\boldsymbol {n}}}_{\mathrm{B}})\)) is such that \(\hat{{\boldsymbol {l}}}_{\mathrm{A}}\) (respectively, \(\hat{{\boldsymbol {l}}}_{\mathrm{B}}\)) is oriented along its LoS and \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}\) (respectively, \(\hat{{\boldsymbol {n}} }_{\mathrm{B}}\)) is parallel to \(\hat{\boldsymbol{n}}\). On the plane \(\Sigma\), \(\gamma\) is the separation angle between detectors A and B, defined as the angle between the LoS-directions, \(\hat{{\boldsymbol {l}}}_{\mathrm{A}}\) and \(\hat{{\boldsymbol {l}}}_{\mathrm{B}}\).
Let us now consider the polar decomposition of the transverse component in Equation 1 as
where \(\alpha^{\mathrm{A}}\) is the counter-clockwise polar angle from \(\hat{{\boldsymbol {w}}}_{\mathrm{A}}\) in the \((\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat{{\boldsymbol {n}}}_{\mathrm{A}})\) plane, and \(B_{\mathrm{tr}}^{\mathrm{A}}\ge0\) is the amplitude of the transverse component. Equation 1 then becomes
where, due to the ambiguity in the observations, the values of \(\alpha^{\mathrm{A}}\) are restricted to \(\alpha^{\mathrm{A}}\in[0, \pi]\). For any \(\alpha^{\mathrm{A}}\), the two possible transverse vectors correspond to \(\zeta^{\mathrm{A}}=\pm1\). An analogous vector decomposition is done for \({\boldsymbol{B}} \) in \(S_{\mathrm{B}}\).
Let \(\gamma\) be the separation angle between the lines of sight \(\hat{{\boldsymbol {l}}}_{\mathrm{A}}\) and \(\hat{{\boldsymbol {l}}}_{\mathrm{B}}\) of the two detectors on \(\Sigma\), measured as the counter-clockwise rotation angle around \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}=\hat{{\boldsymbol {n}}}_{\mathrm{B}}\) with \(\gamma\in[-\pi/2,\pi/2]\) and \(\gamma=0\) for \(\hat{{\boldsymbol {l}}}_{\mathrm{A}}=\hat{{\boldsymbol {l}}}_{\mathrm{B}}\), as in Figure 1. By construction, the vector \({\boldsymbol{B}} \) in \(S_{\mathrm{A}}\) can be transformed into \(S_{\mathrm{B}}\) components by the simple rotation \({\boldsymbol{B}} ^{\mathrm{B}}=R(\gamma) {\boldsymbol{B}} ^{\mathrm{A}}\) of \(\gamma\) around \(\hat{\boldsymbol{n}}\), with
where the row and column order follows \((\hat{{\boldsymbol {l}}}_{\mathrm{A}},\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat {{\boldsymbol {n}}}_{ \mathrm{A}})\). This corresponds to a rotation of \(\gamma\) around \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}=\hat{{\boldsymbol {n}}}_{\mathrm{B}}\) of the image plane, from (\(\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat{{\boldsymbol {n}}}_{\mathrm{A}}\)) to (\(\hat{ {\boldsymbol {w}}}_{\mathrm{B}},\hat{{\boldsymbol {n}}}_{\mathrm{B}}\)). Hence, the rotation \(\gamma\) implies a foreshortening in the direction \(\hat{{\boldsymbol {w}}}_{\mathrm{B}}\) only. In components, we have
Equation 7 can be rewritten as
Because of the restrictions on the polar angles \(\alpha^{\mathrm{A}}\) and \(\alpha^{\mathrm{B}}\), both sine functions are always positive, likewise \(B_{\mathrm{tr}}^{\mathrm{A}}\) and \(B_{\mathrm{tr}}^{\mathrm{B}}\) are by definition. Hence, the right-hand side of Equation 8 is always positive and, since both \(\zeta^{\mathrm{A}}\) and \(\zeta^{\mathrm{B}}\) can only take the values \(\pm1\), it follows that
as a direct consequence of having chosen \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}=\hat{{\boldsymbol {n}}}_{\mathrm{B}}\) for the reference systems \(S_{\mathrm{A}}\) and \(S_{\mathrm{B}}\). In view of Equation 9, we can then rewrite Equations 5 and 6 as
or, equivalently,
where we used the notation \(B_{\mathrm{w}}^{\mathrm{A}}=B_{\mathrm{tr}}^{\mathrm{A}}\cos \alpha^{\mathrm{A}}\) (respectively, \(B_{\mathrm{w}}^{\mathrm{B}}=B_{\mathrm{tr}}^{\mathrm{B}}\cos \alpha^{\mathrm{B}}\)). In this notation, all vector-field components appearing in Equations 12 and 13 are signed quantities, and \(\gamma\in[-\pi/2,\pi/2]\). Since \(\zeta\) is defined as taking only the values \(\pm1\), in the numerical implementation of Equations 12 and 13 the sign of the right-hand side may be taken in order to avoid possible numerical oscillations.
Because of Equation 9, either Equation 12 or 13 formally solves the ambiguity for the transverse components on both detectors simultaneously, assuming that they both provide vector information. However, Equation 12, as opposed to Equation 13, only involves \(B_{\mathrm{w}}^{\mathrm{A}}\), i.e. the transverse component of detector A; hence Equation 12 can be used to solve the ambiguity in the transverse component of detector A also when detector B provides only LoS-information. This widens the applicability of Equation 12 to several space- and ground-based observatories, and it is particularly relevant for future space-weather monitoring spacecraft that may not have full spectropolarimetric diagnostics.
Equations 12 and 13 are geometrically equivalent. However, while Equation 13 involves the transverse components on both detectors, Equation 12 involves only \(B_{\mathrm{w}}^{\mathrm{A}}\), i.e. the transverse component on detector A. Since the transverse component is intrinsically noisier than the LoS one in observations (see discussion in Section 5.2), then Equation 12 is expected to be, broadly speaking, more accurate than Equation 13.
The obvious critical value where Equations 12 and 13 fail is \(\gamma=0\), where the two systems are co-aligned, and no stereoscopic view is available. Similarly, close to quadrature (\(\gamma=\pm\pi/2\)), the extreme foreshortening of the field of view is expected to yield large errors, even though Equations 12 and 13 remain formally valid. Other undefined situations may occur in individual pixels. In particular, Equation 12 cannot be used in pixels where \(B_{\mathrm{w}}^{\mathrm{A}}=0\). Similarly, \(\zeta\) cannot be determined by Equation 13 if \(B_{\mathrm{los}}^{\mathrm{A}}=0\) (or, less obviously, if \(\alpha^{\mathrm{A}}=0^{\circ},180^{\circ}\)). However, such conditions will not occur together, which opens the possibility of applying either Equation 13 or Equation 12, depending on which one is expected to yield the most accurate result for any given pixel (see Section 3.3.2 and Section 4.3.2).
In practical applications, the field of view will be different for the two detectors, requiring restriction of the disambiguation area to the overlap area. Also, in a real situation, the observed field in the image plane of each detector needs to be rotated into the frame defined by Equation 2. Such a transformation can be obtained based on the positions of the spacecraft and the characteristics of the detectors employed, and it is not further discussed here.
For the tests presented in this article, the simulations employed are Cartesian, and the magnetogram extracted from the simulation represents the solar magnetic field on the plane of the sky (i.e. as viewed on the image plane), with uniform and homogeneous resolution. In other words, in the following tests in practice, we consider the above-required transformations to be already performed. In particular, we consider the test field to be already rotated such that \((\hat{{\boldsymbol {w}}}_{\mathrm{A}},\hat{{\boldsymbol {n}}}_{\mathrm{A}})\) are the Cartesian axes of the magnetogram, and the detector A is placed vertically above the center of the test magnetogram at a fixed distance (i.e. at constant resolution). The detector B is placed at an angle \(\gamma\) around \(\hat{{\boldsymbol {n}}}_{\mathrm{A}}\) and variable distance (i.e. variable resolution). For simplicity, the fields of view of both detectors are assumed to cover the same area on the Sun, meaning that, at any angle \(\gamma\), the field of view of the two detectors is identical and always covering the entire area of the magnetogram. Similarly, in each pixel, we consider the corresponding magnetic-field value to represent the pixel-average of the magnetic field.
3 Geometrical Tests
We use three different numerical models of solar-like magnetic fields, including solutions of the nonlinear force-free equations and numerical MHD simulations. From our point of view, these simulations model increasingly challenging test fields from smooth and well-resolved ones, proving the feasibility of the method, to more fine-scaled and unresolved fields for the estimation of the performance in slightly more realistic scenarios.
However, we refer to the articles cited below for discussions on model limitations and their physical representation of the solar magnetic field.
3.1 Numerical Models Used to Construct the Test Magnetograms
In Figures 2 – 4, the synthetic magnetic-field data used in this test are obtained from a semi-analytical magnetic-field configuration of a coronal flux rope (Section 3.1.1), showing a smooth distribution of the field, and from two synthetic models presenting more complex field distributions that represent active-region (Section 3.1.2) and predominantly quiet-Sun (Section 3.1.3) configurations.
TD test model: Field distribution for the three components \(B_{\mathrm{los}}\) (left column), \(B_{\mathrm{w}}\) (middle column), and \(B_{\mathrm{n}}\) (right column) in the image plane of SDO/HMI (top row) and SO/PHI-HRT (bottom row), for the reference case (i.e. separated by an angle \(\gamma= 40^{\circ}\), cf. Table 1); the continuous isocontour represents the \(\pm500\) G value. The axes represent the number of pixels in the respective image planes that are used to cover the field of view by each detector in the reference observing configuration; see Section 4 for additional details.
3.1.1 TD: Smooth Test Case
The first numerical test is constructed using the semi-analytical solution of the 3D force-free equation by Titov and Démoulin (1999, hereafter TD), consisting of a flux rope embedded in a potential field. The parameters of the TD model used here are the same as those in the \(N{=}1\) case of Valori et al. (2016). The original number of pixels (428×684) is quadrupled by interpolation with respect to Valori et al. (2016) in order to provide a very smooth and extremely well-resolved field at all viewing angles, which can be used as a proof of principle for SDM; see Figure 2.
3.1.2 PENCIL-AR: Active-Region Test Case
The second test model employs the numerical coronal evolution obtained by driving the PENCIL code as of Chen et al. (2014) with a photospheric driver from the MURaM simulation described by Cheung et al. (2010). The simulation was interpolated to twice the original pixel size and then slightly cropped to reduce the influence of the boundaries. The extracted magnetogram, taken a few pixels above the PENCIL photospheric boundary, has an extent of 463×239 pixels with a uniform pixel size of 192 km. The magnetogram shows some fine scales but is still smooth and well resolved (see Figure 3). This test, hereafter PENCIL-AR, is supposed to represent a mixture of the field on small and large scales typical of an active region.
PENCIL-AR test model: Field distribution for the three components \(B_{\mathrm{los}}\) (left column), \(B_{\mathrm{w}}\) (middle column), and \(B_{\mathrm{n}}\) (right column) in the image plane of SDO/HMI (top row) and SO/PHI-HRT (bottom row), for the reference case (i.e. separated by an angle \(\gamma= 40^{\circ}\), cf. Table 1); the continuous isocontour represents the \(\pm500\) G value. The axes represent the number of pixels in the respective image planes that are used to cover the field of view by each detector in the reference observing configuration; see Section 4 for additional details.
3.1.3 MURaM-QS: Pore and Quiet-Sun Test Case
Magneto-hydrodynamic (MHD) simulations of a typical small-scale photospheric structure observed with the Sunrise balloon-borne observatory were carried out by Riethmüller et al. (2017) with the MURaM numerical-simulation code (Vögler et al., 2005). The pixel sizes in the simulation are (41.67, 41.67, 15.89) km in \(x\), \(y\), and \(z\), respectively. These test data are considered as close as possible to the real observational data provided by SDO/HMI and SO/PHI. They contain a small unipolar flux concentration (pore) surrounded by small-scale magnetic structures and a large quiet-Sun field with strengths from zero up to the kilo-Gauss regime. The slice of the MURaM-QS numerical simulation used as a test model in Section 4 is a plane of 812×812 pixels taken at a depth of 700 km, which was calculated to approximately represent the \(\tau=1\) surface for the continuum at 500 nm, for \(\gamma=0\).
As a test for SDM, the MURaM-QS case is extremely challenging as it contains length-scales of field variations down to the pixel scale; see Figure 4. As discussed in more detail below, in the disambiguation of SDO/HMI magnetograms, it is often the case that in quiet-Sun areas, a random choice of the orientation is adopted due to the difficulties that the annealing encounters in areas of low linear-polarization signal (see, e.g., Hoeksema et al., 2014; Liu et al., 2017).
MURaM-QS test model: Field distribution for the three components \(B_{\mathrm{los}}\) (left column), \(B_{\mathrm{w}}\) (middle column), and \(B_{\mathrm{n}}\) (right column) in the image plane of SDO/HMI (top row) and SO/PHI-HRT (bottom row), for the reference case (i.e. separated by an angle \(\gamma= 40^{\circ}\), cf. Table 1); the continuous isocontour represents the \(\pm500\) G value. The axes represent the number of pixels in the respective image planes that are used to cover the field of view by each detector in the reference observing configuration; see Section 4 for additional details.
3.2 Construction of the Test Magnetograms
For each model in Section 3.1, we extract the vector-field distribution at one (flat) layer at a given height, which we treat as the “photosphere” of the model to be used as a test (called a test model, for brevity). In order to build a homogeneous set of test models out of the test cases in Section 3.1, the pixel size and the maximum field strength are set to be the same for all models, as follows:
First, the vector field of each test model is rescaled such that the maximum value of the norm of the magnetic field is equal to 2000 G.
Second, the spatial sampling of the two detectors A and B of Figure 1 in Section 2 and the pixel size of the test magnetograms must be specified. From now on, we refer to a concrete case where detector A is SDO/HMI, and detector B is SO/PHI. Therefore, we speak of “SDO/HMI spatial sampling” \(\Delta_{\mathrm{SDO{}/HMI{}}}\) (respectively, “SO/PHI spatial sampling” \(\Delta_{\mathrm{{SO/PHI}{}}}\)) as the helioprojective (linear) size in arcsec of the area on the Sun covered by one pixel of SDO/HMI (respectively, SO/PHI) at the center of the solar disk. Due to the choice of the reference system in Section 2, SDO/HMI is by definition at \(\gamma=0\) and at a fixed distance from the test magnetogram (i.e. at 1 AU distance from the Sun). Therefore, SDO/HMI can be assigned a fixed spatial sampling of \(\Delta_{\mathrm{SDO{}/HMI{}}}=0.5\) arcsec, and it is never affected by foreshortening (see Section 2), whereas SO/PHI spatial sampling \(\Delta_{\mathrm{{SO/PHI}{}}}\) varies along its orbit (the plate scale on the SO/PHI-HRT detector is 0.5 arcsec, that of SO/PHI-FDT is 3.75 arcsec). In particular, for a varying distance of Solar Orbiter, the ratio
is equal to the ratio of the SO/PHI spatial sampling \(\Delta_{\mathrm{{SO/PHI}{}}}\) to the SDO/HMI spatial sampling \(\Delta_{\mathrm{SDO{}/HMI{}}}\). By changing \(r_{\Delta}\), we can explore the spatial sampling dependence of both detectors SO/PHI-HRT and SO/PHI-FDT onboard Solar Orbiter.
Similarly, for a given distance, i.e. for a given \(r_{\Delta}\), the variation of the separation angle \(\gamma\) defines the foreshortened resolution (in the \(\hat{{\boldsymbol {w}}}_{\mathrm{B}}\) direction, see again Section 2) that is used by SO/PHI to image the field of view as \(\Delta_{\mathrm{{SO/PHI}{}}}/\cos(\gamma)\). For testing purposes, we vary \(r_{\Delta}\) and \(\gamma\) independently, even though the two quantities are related by the real Solar Orbiter orbit (see discussion in Section 7 and Figure 18 in particular).
Finally, there is a third resolution to be considered, that is the resolution of the test model itself, the native resolution [\(\Delta_{\mathrm{native}}\)]. While for the TD simulation the pixel size is not strictly given, the PENCIL-AR and MURaM-QS simulations have horizontal pixel size approximately equal to 0.27 and 0.06 arcsec, respectively. In order to have comparable test cases and widen the parameter space available for our testing, we chose to assign to all test cases the same pixel size (\(\Delta _{\mathrm{native}}=0.2\) arcsec).
Therefore, there are three basic quantities that define the parameters of each synthetic observation configuration: the natural resolution of the test model [\(\Delta_{\mathrm{native}}\)], the spatial sampling ratio [\(r_{\Delta}\)] parametrizing the distance of Solar Orbiter, and the separation angle between spacecraft [\(\gamma\)]. In summary, as visualized in Figure 5, we simulate an observation from a given detector with three steps:
-
i)
fix the observatory view by specifying \(\gamma\) (finite for SO/PHI, zero for SDO/HMI) and spatial sampling (variable for SO/PHI, fixed to 0.5 arcsec for SDO/HMI);
-
ii)
create the image-plane view of the test model by interpolating the model magnetogram to the effective spatial sampling of the considered detector, as seen from the given angle and distance. For SDO/HMI, since it is always placed on the vertical of the test model, this entails only an interpolation of the test model to the effective SDO/HMI spatial sampling. We use the term “remapping” for this procedure. On the other hand, for SO/PHI the test model is first remapped to the \(\gamma\)-foreshortened field of view at the given SO/PHI spatial sampling, and then the field components of the test model are re-projected on the SO/PHI reference system (i.e. the field components are rewritten in the \(S_{\mathrm{B}}\) reference system of Section 2). At this stage, the image-plane view of the test model field (the “reprojected model field”) still has the correct orientation of the transverse component and is therefore considered the magnetogram to be compared with;
-
iii)
restrict the orientation of the transverse components, i.e. \(\alpha^{\mathrm{A}}\) and \(\alpha^{\mathrm{B}}\), to be within \([0,\pi]\), producing in this way the ambiguity to be removed in the reprojected model field of each instrument.
The last step produces our basic “observation-like” SDO/HMI and SO/PHI magnetograms that reproduce effective spatial sampling and viewing angles and have ambiguous transverse components, complying with the definition in Equation 2.
Flow-diagram of the construction of the test magnetograms for the geometrical tests; see Section 3.2. The procedure is applied on the image plane of each telescope for the given observing configuration specified by \(\gamma\) and \(r_{\Delta}\). Input/output are visualized with green parallelograms, operations with orange rectangles.
3.3 Application of the Disambiguation Equation
Next, Equations 12 and 13 are applied to the SDO/HMI and SO/PHI magnetograms as constructed in Section 3.2. As discussed in Section 2, in principle, either Equation 12 or Equation 13 removes the ambiguity of the transverse component of both SDO/HMI and SO/PHI at the same time. However, one needs to decide which detector grid is used for its application (see Section 3.3.1). In addition, one can choose to use Equation 12, Equation 13, or a combination of both (cf. Section 3.3.2).
3.3.1 Direct and Reverse Procedures
First, one can use the SO/PHI magnetogram to remove the ambiguity on the SDO/HMI transverse component by spatially remapping (but not re-projecting) the SO/PHI grid onto the SDO/HMI one. This requires interpolating the field components of the SO/PHI magnetogram onto the SDO/HMI grid and applying Equations 12 and 13. In this way, \(\zeta\) is determined in each pixel of the SDO/HMI grid, thereby removing the ambiguity. The SDO/HMI disambiguated magnetograms can then be compared directly with the correct reprojected model field obtained in step 2 of Section 3.2 on the same (SDO/HMI) grid to assess the correctness of the disambiguation. The numerical implementation of Equations 12 and 13 that is used in the tests below employs this procedure. In the following plots, we indicate the above procedure as the direct case, plotted as an orange-solid line in, e.g., Figure 10. Figure 6 shows a diagram of the direct application of SDM.
Flow-diagram of the direct application of SDM; see Section 3.3. The reverse application is obtained by formally exchanging A and B. Input/output are visualized with green parallelograms, operations with orange rectangles.
At this point, one could remap the obtained value of \(\zeta\) or the disambiguated \(B_{\mathrm{tr}}\) back onto the SO/PHI magnetogram and remove the ambiguity there too. However, since this operation would imply an additional interpolation, we refrain from this.
On the other hand, one can simply formally exchange the positions of the two detectors and set the separation angle to \(-\gamma\) in the disambiguation routine. In this way, the disambiguation routine employs the field components of the SDO/HMI magnetogram to remove the ambiguity of the SO/PHI transverse component, with the SDO/HMI grid interpolated onto the SO/PHI one. Again, the SO/PHI disambiguated magnetogram is then compared with the correct reprojected model field obtained in step 2 of Section 3.2 on the same (SO/PHI) grid. We indicate this procedure as the reverse case, plotted as a blue-dashed line in, e.g., Figure 10. We present the results of the application of both directions of removal (i.e. direct and reverse cases) in the next sections.
3.3.2 Combined Application of SDM Equations: \(\epsilon_{W}\) Parameter
As explained in Section 2, Equation 12 and Equation 13 are two geometrically equivalent ways of removing the ambiguity. In other words, SDM can be applied using only Equation 12, only Equation 13, or a combination of both. One can use such equivalence to choose which equation to apply to each pixel depending on which one is expected to be more reliable for the given field values. In particular, for generic values of \(\gamma\), Equation 12 is not defined at locations where \(B_{\mathrm{w}}^{\mathrm{A}}\approx0\) (see also Section 2 for the component notation). In such locations, one can use Equation 13 instead. Similarly, Equation 13 yields an undetermined \(\zeta\) where \(B_{\mathrm{los}}^{\mathrm{A}}\approx0\), i.e. at the polarity inversion line as seen from detector A, and the employment of Equation 12 is to be favored instead of Equation 13 to remove the ambiguity at such locations. There are, of course, other locations where, depending on the value of \(\gamma\), either the numerator or the denominator of Equations 12 and 13 vanishes, but these are expected to be isolated points. Therefore, we consider a combined application where Equation 12 is applied everywhere except in pixels where the amplitude of the transverse component \(B_{\mathrm{w}}^{\mathrm{A}}\) is below a given value specified by the parameter \(\epsilon_{W}\) and the relation
The same above prescription for the combined application of SDM holds for both the direct and reverse applications. As our analysis will demonstrate in Section 4.3.2, this combined use of Equations 12 and 13 generally yields the best results.
4 Results of the Geometrical Tests
In this section, we report the results of testing SDM as described in Section 3.3 with the magnetograms obtained following Section 3.2. Varying the test model, the spatial sampling, and separation angles of orbital parameters, and different parameters of the SDM testing procedure, we aim to thoroughly assess the feasibility of stereoscopic disambiguation.
4.1 Evaluation Criteria
To evaluate the success of SDM, we adopt a selection of the metrics introduced by Metcalf et al. (2006) and Leka et al. (2009). In particular, we consider the metrics:
-
Area: For each individual tested configuration (i.e. each data point in, e.g., Figure 10), we quantify the rate of success of the disambiguation as the fraction
$$ \mathcal{M}_{\mathrm{area}}= \frac{\mathrm{Number\ of\ correctly\ disambiguated\ pixels}}{\mathrm {Total\ number\ of\ considered\ pixels}} $$(16)in each magnetogram. Unless stated otherwise (as in, e.g., Section 4.5), the number of pixels in the denominator of Equation 16 is the total number of pixels in the relevant image plane (i.e. in the magnetogram). In Equation 16, the numerator is the number of pixels where the direction of the disambiguated transverse component (obtained applying SDM as described in Section 3.3 to the observation-like magnetogram obtained in Point iii of Section 3.2) matches the true direction as given by the reprojected test-model field (obtained in Point ii of Section 3.2), on the relevant image plane; see also Figure 6. Hence, the case of perfect disambiguation in every pixel corresponds to \(\mathcal{M}_{\mathrm {area}}=1\), whereas systematically incorrect disambiguation in all pixels corresponds to \(\mathcal{M}_{\mathrm{area}}=0\). Random disambiguation would theoretically correspond to \(\mathcal{M}_{\mathrm{area}}=0.5\); hence suitable disambiguation should obtain a score much higher than this.
-
Normalized vertical current density: Difference in the vertical (to the test-model field) current density \(J_{\mathrm{z}}\), computed as
$$\mathcal{M}_{J_{z}}= 1- \frac{\sum|J_{\mathrm{z}}(\mathrm{Reprojected})-J_{\mathrm {z}}(\mathrm {Disambiguated})|}{2\sum|J_{\mathrm{z}}(\mathrm{Reprojected})|} $$(17)where \(J_{\mathrm{z}}\) is computed for the SDM-disambiguated field and for the re-projected model field (obtained in Point ii of Section 3.2), on the relevant image plane, i.e. on the SDO/HMI (respectively SO/PHI) image plane in the direct (respectively reverse) application of SDM.
-
Transverse Field: The fraction of transverse field above a specified threshold \(\mathcal{T}\) that was disambiguated correctly,
$$ \mathcal{M}_{B_{\perp}> \mathcal{T}}= \frac{\sum B_{\mathrm{{tr}>\mathcal{T}}}(\mathrm {Correctly\ resolved\ pixels})}{ B_{\mathrm{tr}>\mathcal {T}}(\mathrm {All\ pixels})} $$(18)on the relevant image plane.
The metrics \(\mathcal{M}_{\mathrm{area}}\) and \(\mathcal{M}_{J_{z}}\) were judged by Leka et al. (2009) to provide enough information for noise-free cases such as those considered in this article. However, in view of the different properties of the tests fields employed here, and of the MURaM-QS case in particular, we find it useful to add the \(\mathcal{M}_{B_{\perp}> \mathcal{T}}\) metric introduced by Leka et al. (2009) for studying noise and unresolved scale effects. Following Leka et al. (2009), the \(\mathcal{M}_{B_{\perp}> \mathcal{T}}\) metric is computed for the threshold values \(\mathcal{T}=100\) and 500 G.
4.2 Reference Case
We consider a reference case summarized in Table 1, where
-
the model test resolution is \(\Delta_{\mathrm{native}}=0.2\) arcsec; this formally results in a field of view of 85.6×136.8, 92.6×47.8, 162×162 arcsec for the TD, PENCIL-AR, and MURaM-QS test cases, respectively;
-
the center-of-disk spatial sampling of SDO/HMI is \(\Delta_{\mathrm{SDO{}/HMI{}}}=0.5\) arcsec with SDO at 1 AU distance from the Sun;
-
the SO/PHI-HRT telescope of Solar Orbiter has a center-of-disk spatial sampling equal to \(\Delta_{\mathrm{{SO/PHI}{}}}=0.3\) arcsec, i.e. \(r_{\Delta}=0.6\); this corresponds to a distance of Solar Orbiter from the Sun of 0.6 AU;
-
the separation angle between SDO and Solar Orbiter is \(\gamma=40^{\circ}\);
-
for the given \(\Delta_{\mathrm{{SO/PHI}{}}}\) and \(\gamma\), the effective spatial sampling, i.e. the \(\hat{{\boldsymbol {w}}}_{\mathrm {B}}\)-foreshortened linear pixel size on the Sun, of SO/PHI-HRT is \(\Delta_{\mathrm{{SO/PHI}{}}}/\cos(\gamma)=0.39\) arcsec;
-
SDM is applied using both Equation 12 and Equation 13, where the parameter for choosing the latter over the former is \(\epsilon_{W}=0.01\); see Section 3.3 for details;
Each of the plots in this section adopts the above values, except for one parameter at a time, which is varied to study the dependence of SDM on this parameter, as indicated in the column “Section” of Table 1.
The geometrical parameters of the reference case are chosen to be representative of a generic situation. In particular, specific combinations are avoided where the grids of the two instruments happen to overlap exactly (e.g. for \(\gamma=60^{\circ}\) and spatial sampling of SO/PHI-HRT equal to exactly half the spatial sampling of SDO/HMI). The corresponding field components in the image plane of SDO/HMI and SO/PHI-HRT for the parameters of the standard case are given in Figures 2 – 4. We note how the same field of view is rendered by a different number of pixels in the image plane of each detector, and that the model test field is interpolated in both cases to produce the detector image (because \(\Delta_{\mathrm{native}}\) is smaller than both \(\Delta_{\mathrm{SDO{}/HMI{}}}\) and \(\Delta_{\mathrm{{SO/PHI}{}}}\)).
4.3 Test of SDM
This section presents the basic tests of the accuracy of SDM using the geometrical configuration of the reference case of Section 4.2. Successful disambiguation is one that scores significantly better than a random choice of orientation in each pixel (see Section 4.3.2 and Table 2 in particular).
4.3.1 Application of SDM to the Reference Case
Table 2 presents the metrics defined in Section 4.1 for the application of SDM to the reference case in Section 4.2. The two values in each entry are obtained from the direct and reverse application of SDM, respectively, as explained in Section 3.3.
The entries for the TD model are all unity for all metrics. This shows that, in the case of a fully resolved and smooth case, SDM can remove the ambiguity in the transverse component of the reference case with 100% accuracy in both the direct and reverse cases. This proves the correctness of the SDM equations and their implementation. Similarly, for the PENCIL-AR model, the SDM rate of success is basically 100% for all metrics, despite the smaller fine scales that are present in the field with respect to the TD model.
In both the TD and PENCIL-AR cases, the rate of success is similar for the direct and reverse cases. In the MURaM-QS case, on the other hand, \(\mathcal{M}_{\mathrm{area}}\) is 87% in the direct case, where the higher-resolution SO/PHI-HRT magnetogram is used to remove the ambiguity on the lower-resolution SDO/HMI. Conversely, in the less favorable reverse case, \(\mathcal{M}_{\mathrm{area}}\) is 82%. The normalized vertical current density metric [\(\mathcal{M}_{J_{z}}\)] is similar for the direct and reverse cases (approximately 80%), indicating that the errors in disambiguation quantified by \(\mathcal{M}_{\mathrm{area}}\) induce only a moderate variation of \(\mathcal{M}_{J_{z}}\). As a comparison, for the multipole test cases in Table 2 of Metcalf et al. (2006), which is a much smoother case than the MURaM-QS discussed here, \(\mathcal{M}_{J_{z}}\) varied from 1 to -0.42, depending on the disambiguation method. Finally, the transverse-field metric, \(\mathcal{M}_{B_{\perp}> \mathcal{T}}\) for \(\mathcal{T}=100\) and \(\mathcal{T}=500\) G, shows that the SDM errors are related to small-field values: with a threshold of 100 G, 92% of the transverse field is correctly disambiguated in the direct case, increasing to 97% for a threshold of 500 G. In the reverse case, the fraction of the transverse field correctly represented is even larger, 96% and 99% for \(\mathcal{T}=100\) and 500 G, respectively. Figure 8b confirms that erroneously disambiguated pixels are all located in small-field areas in the MURaM-QS case. However, we refer to Section 4.3.2 for a more detailed discussion of the origin of SDM errors.
As we have discussed, the MURaM-QS case is extremely challenging, being a realistic simulation of a pore that is surrounded by much less active or even quiet regions. Moreover, in the reference case, the native resolution is smaller than both \(\Delta_{\mathrm{SDO{}/HMI{}}}\) and the (foreshortened) \(\Delta_{\mathrm{{SO/PHI}{}}}\), implying that small scales are also under-resolved. This is the first indication that the correct disambiguation of the transverse field is affected by the interpolation on areas where small scales are present. However, given the challenges posed by the MURaM-QS test case, we regard a rate of success above 80% over the whole magnetogram as a significant improvement with respect to the random choice (\(\mathcal{M}_{\mathrm{area}}=0.5\)) that is usually employed in such cases; see also Section 4.3.2 and Section 4.3.3.
4.3.2 Dependence on the SDM Equations
We noted in Section 2 that Equation 12 and Equation 13 are geometrically equivalent, and in Section 3.3 that a combination of both might be beneficial to the overall SDM accuracy. Here we test such speculations.
Table 3 reports \(\mathcal{M}_{\mathrm{area}}\) in the reference case summarized in Table 1 for the three test models TD, PENCIL-AR, and MURaM-QS. The different SDM rows in Table 3 refer to SDM applied using only Equation 12, only Equation 13, or a combination of both; see discussion in Section 3.3. In each entry, the two values are obtained from the direct and reverse application of SDM, respectively, as explained in Section 3.3. In addition, the row “Random” corresponds to a random choice in each pixel of the orientation of the transverse component. We consider first the top half of Table 3. The bottom part of Table 3 repeats the same tests as in the top half but with measurement errors added and is discussed in Section 4.3.3.
The “Random” entry in the fourth line of Table 3 shows that a random choice of the orientation of the transverse component yields an area metric \(\mathcal{M}_{\mathrm{area}}\approx0.5\), in all cases, reflecting the parity nature of the disambiguation problem.
The dependence of \(\mathcal{M}_{\mathrm{area}}\) on each of Equations 12 or 13 is used to apply SDM and can be assessed comparing the first three lines of Table 3. Employing Equation 12 almost always results in higher values of \(\mathcal{M}_{\mathrm {area}}\) than using Equation 13, and the best results are obtained from a combination of the two (i.e. the reference case, the first line in Table 3).
In this respect, it is interesting to study the locations where errors are found. For this, we use plots of the simpler TD model, but our conclusion holds for all models. The top two panels of Figure 7 show the locations of the wrongly disambiguated pixels (orange squares) obtained in the application of Equation 12 (left column) and Equation 13 (right column). As expected from the discussion of Equations 12 and 13 in Section 2 and 3.3.2, the disambiguation formula is expected to fail in areas where \(\zeta\) is ill-defined, i.e. where \(B_{\mathrm{w}}^{\mathrm{A}}\approx0\) in the denominator of Equation 12 and where \(B_{\mathrm{los}}^{\mathrm{A}}\approx0\) in the numerator of Equation 13 (\(B_{\mathrm{los}}^{\mathrm{A}}\) and \(B_{\mathrm{w}}^{\mathrm{A}}\) are the LoS-component and the transverse component along \(\hat{{\boldsymbol {w}}}\), respectively, defined in Section 2 and Figure 1). This is confirmed by the panels in the top row of Figure 7, where errors in the disambiguation are found for small values of \(B_{\mathrm{w}}\) for Equation 12 (Figure 7a) and of \(B_{\mathrm{los}}\) for Equation 13 (Figure 7b), e.g. around polarity inversion lines. Therefore, we define the error-prone areas for Equation 12 in the direct case on the SDO/HMI image plane, as the area where \(B_{\mathrm{tr}}^{\mathrm{A}}\le5\times10^{-3}\max{|B_{\mathrm {los}}^{\mathrm{A}}|}\) or \((\pi/2 -0.02 \le\alpha^{\mathrm{A}}\le\pi/2 + 0.02)\); see Equations 12 and 13 for notation again. An analogous definition of the error-prone areas employing the same heuristic values is done in the reverse case and on the SO/PHI image plane (not shown). This heuristic definition of the error-prone areas captures all wrongly disambiguated pixels, as Figure 7a, b shows.
Error map of wrongly disambiguated pixels (orange squares) obtained in the application of Equation 12 (left column) and Equation 13 (right column). The background fields represent the component that is determining the error location in the two cases, i.e. of \(B_{\mathrm{w}}\) for Equation 12 (left column) and of \(B_{\mathrm{los}}\) for Equation 13 (right column), shown as \(\pm500\) G isolines, in the direct application on the SDO/HMI image plane, with the corresponding polarity inversion line shown by black-dashed lines. The green areas represent error-prone areas; see Section 4.3.2 for details. The top (respectively, bottom) row corresponds to magnetogram without (respectively, with) measurement errors added; see also Section 4.3.3. The axes represent the number of pixels on the SDO/HMI image plane.
Since such areas can be identified before the disambiguation, this bears two important consequences: First, the two disambiguation equations have, in general, different error-prone areas that are not overlapping, in this way confirming that Equation 12 and Equation 13 can be used alternatively on every given pixel depending on which is the most accurate. The result of this combined application of Equations 12 and 13 as per Section 3.3 is shown in the first line of Table 3 for \(\epsilon_{W}=0.01\). In all test cases, the area metric of the combined SDM equations is higher than when only one of the two equations is applied. In particular, the success rate is exactly \(\mathcal{M}_{\mathrm{area}}=1.0\), i.e. no errors, for the TD model in both direct and reverse cases and for the PENCIL-AR direct case. Only a few pixels are erroneously disambiguated in the PENCIL-AR reverse case (\(\mathcal{M}_{\mathrm{area}}=0.999\)). In the MURaM-QS case, the combined application of Equation 12 and Equation 13 also improves \(\mathcal{M}_{\mathrm{area}}\) but to a lesser extent. The spatial distribution of errors in the PENCIL-AR and MURaM-QS direct cases is shown in Figure 8, confirming the analysis of the error location detailed above for the TD model.
Error map of wrongly disambiguated pixels (orange squares in (a), orange-small squares in (b)) for the reference case (i.e. the combined application of Equation 12 and Equation 13 with \(\epsilon_{W}=0.01\); see Table 1), for the (a) PENCIL-AR and (b) MURaM-QS cases. The background fields represent the \(B_{\mathrm{los}}\)-component shown as \(\pm500\) G isolines in the direct application on the SDO/HMI image plane; see Figure 3d and Figure 4d). The TD case is not shown since no errors are present in this case; see the first row in Table 2. Notice that wrongly disambiguated pixels in Panel b are only 13% of the total; see Table 2. The axes represent the number of pixels on the SDO/HMI image plane.
Then, the possibility of identifying error-prone areas allows the association of a confidence level to the SDM result in each pixel. Thus, \(\epsilon_{W}\) can be used as a parameter to be tuned considering measurements errors in order to produce the most reliable disambiguation based on specific uncertainties and noise levels.
Finally, to complete the test on the combined use of Equations 12 and 13, we consider the dependence of \(\mathcal{M}_{\mathrm{area}}\) on the parameter \(\epsilon_{W}\). Figure 9a – c is obtained for the reference case of Table 1 by varying only \(\epsilon_{W}\) with solid orange and dashed-blue lines representing the direct and reverse direction of applications of Equations 12 and 13, respectively. The top row of Figure 9 shows that the dependence of the success rate \(\mathcal{M}_{\mathrm{area}}\) on \(\epsilon_{W}\) is negligible in the TD and PENCIL-AR cases and very weak (up to 1 – 2%) in the MURaM-QS case. The insensitivity of \(\mathcal{M}_{\mathrm{area}}\) on \(\epsilon_{W}\) can be expected on the grounds of the limited extension of the error-prone areas shown in the top row of Figure 7 for both direct and reverse methods.
Dependence of the success rate [\(\mathcal{M}_{\mathrm {area}}\)] on the parameter \(\epsilon_{W}\) for the three test cases TD (left column), PENCIL-AR (middle column), and MURaM-QS (right column), without (top row) and with (bottom row) measurement errors added. The solid-orange (respectively, blue-dashed) line corresponds to the area metric for the SDO/HMI (respectively, SO/PHI) case where Equation 12 employs the LoS-component of SO/PHI to remove the ambiguity on SDO/HMI (respectively, employs the LoS-component of SDO/HMI to remove the ambiguity on SO/PHI), i.e. to the direct (respectively, reverse) direction of application of Equations 12 and 13. Note the difference in vertical scale between the TD/PENCIL-AR cases (Panels a, b, d, e) and the MURaM-QS cases (Panels c, f).
4.3.3 Effect of Measurement Errors on SDM
In this work, we do not explicitly address the effect of noise or unresolved scales on the accuracy of SDM. Noise impacts will be the subject of a forthcoming, dedicated article. However, given the unique possibility of SDM to predict areas that are prone to errors, we discuss in this section how \(\mathcal{M}_{\mathrm{area}}\) in the reference case of Section 4.3 is changed by the presence of measurement errors. We stress that we do not attempt to provide a physically motivated model of the origin, nature, and spatial distribution of such errors. Instead, we consider an extremely simplified model for the measurement error in each pixel of the image plane given by a random component of amplitude up to 70 G, plus an additional 30% random relative error on the transverse component. The error is added to each pixel of the (ambiguous) SDO/HMI and SO/PHI magnetograms before the application of SDM. The success metrics are again computed as explained in Section 4.1, namely comparing the disambiguated magnetogram with the corresponding (error-free) reprojected model field obtained as in Point ii of Section 3.2.
The bottom half of Table 3 reports the results of the same tests as in the top part but with measurement errors added. Measurement errors do not have any appreciable influence on the value of \(\mathcal{M}_{\mathrm{area}}\) obtained if a random orientation is chosen (“Random” entry in row eight), which is to be expected given the random nature of the error model we adopted. On the other hand, in all cases of separate application of Equation 12 and Equation 13 (sixth and seventh rows, respectively), measurement errors cause a noticeable decrease in the success rate with respect to the corresponding clean cases in the top half of Table 3; see also Section 4.3.2. This decrease in accuracy can be as small as 1%, as, e.g., for the application of Equation 12 in the TD case, but also as large as 9%, as for, e.g., Equation 12 applied to the MURaM-QS case. Consistent losses in accuracy due to measurement errors are also possible even for the smooth and resolved TD test magnetogram (6% for Equation 13). The distribution of wrongly disambiguated pixels is clearly very well captured by the error-prone areas, as Figure 7c, d shows. However, and most importantly, the combined application of Equations 12 and 13, again with \(\epsilon_{W}=0.01\), is able to recover an accuracy of practically 100% in both the TD and PENCIL-AR tests (cf. the fifth and first rows in Table 3 and Section 4.3.1). The corresponding improvement in the MURaM-QS case is more limited, of about 1 – 2%.
Next, let us consider how the dependence of \(\mathcal{M}_{\mathrm{area}}\) on the \(\epsilon_{W}\)-parameter is changed by the presence of measurement errors (see again Section 4.3.2). Figure 9d – f, compared with the clean corresponding cases in Figure 9a – c, shows that for all test fields such dependence is stronger when measurement errors are added than in the clean case. The effect of measurement errors on such dependence is comparatively larger for the TD case than for the PENCIL-AR and MURaM-QS cases (note the difference in the vertical scales between Panels a, b, d, e, and Panels e, f in Figure 9), bringing the range of variation of \(\mathcal{M}_{\mathrm{area}}\) as a function of \(\epsilon_{W}\) to about 2 – 3% for all cases. The value \(\epsilon_{W}=\) 0.01 in the reference case in Table 1 was chosen as a compromise between the maxima of all twelve curves in Figure 9.
In summary, the combined use of Equations 12 and 13 can recover the true field orientation even in the presence of significant measurement errors, at least for field with moderately well-resolved scales such as in the TD and PENCIL-AR test models.
4.4 Orbit Effects: Spatial Sampling and Separation Angle
In this section, we study how the disambiguation of the reference case in Table 1 is affected by the changing separation angle and distance that is caused by spacecraft orbital motion. In particular, Figure 10 summarizes the area metric [\(\mathcal{M}_{ \mathrm{area}}\)] of SDM as a function of the separation angle [\(\gamma\)] (left column) and the spatial sampling ratio [\(r_{\Delta}\)] (right column) in Equation 14. The left and right columns of Figure 10 and the following similar ones are constructed using 36 sample points equally spaced in \(\gamma\) and 11 equally spaced points in \(\log(r_{\Delta})\).
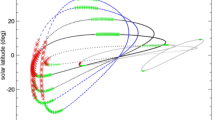
Rate of successful disambiguation [\(\mathcal{M}_{\mathrm {area}}\)] as a function of the separation angle [\(\gamma\)] (left column) and of the SO/PHI-HRT spatial sampling ratio [\(r_{\Delta}\)] (right column) for the TD (Panels a, b), PENCIL-AR (Panels c, d) and MURaM-QS (Panels e, f) test magnetograms for the direct (orange-solid line) and the reverse (blue-dashed line) cases, respectively. The light-green areas in the right column identify the range of spatial sampling of the two telescopes (SO/PHI-HRT and SO/PHI-FDT) along the planned Solar Orbiter orbit. The black vertical-dotted lines mark the native resolution [\(\Delta_{\mathrm{native}}\)] of the test model and the red vertical-dotted lines identify the point of equal spatial sampling of SDO/HMI and SO/PHI-HRT, \(\Delta_{\mathrm{SDO{}/HMI{}}}=\Delta_{\mathrm{{SO/PHI}{}}}\) nominally equal to 0.5 arcsec. Note the difference in vertical scale between the TD case (Panels a and b) and the PENCIL-AR / MURaM-QS cases (Panels c – f).
In the TD case, the area metric of SDM is 100% at all separation angles, see Figure 10a, in both directions of application of Equations 12 and 13 (corresponding to the direct and reverse cases, solid-orange and dashed-blue lines, respectively); see Section 3.3. This plot, like the other two in the left column of Figure 10, is obtained using all the parameters from the standard case, e.g. at spatial sampling ratio \(r_{\Delta}=0.6\), except for \(\gamma\), which is varied. In other words, in the idealized situation where the field is well resolved on both detectors, the application of SDM is able to remove the ambiguity at all values of the viewing angle [\(\gamma\)] without any significant inaccuracy. The only minimal variations in certainty correspond to the already identified situations of \(\gamma=0\) and \(\gamma=\pm90^{\circ}\), in individual pixels, as expected from Section 2.
Similarly, \(\mathcal{M}_{\mathrm{area}}\) as a function of the spatial sampling ratio [\(r_{\Delta}\)] is above 99% for all resolutions considered; see Figure 10b. In the panels on the right column of Figure 10, the two green areas show the spatial sampling intervals spanned by the higher-resolution telescope SO/PHI-HRT (left green area) and the lower-resolution telescope SO/PHI-FDT (right green area) during the orbit of Solar Orbiter. The reference case, used here for all parameters except for \(r_{\Delta}\), sets \(\gamma=40^{\circ}\) in particular for all the plots in the right column of Figure 10. The accuracy of SDM is basically always 100% when SDO/HMI is used to remove the ambiguity of either of the SO/PHI instruments’ transverse component (i.e. in the reverse case, blue-dashed line). In the direct case, where the SO/PHI LoS component is interpolated onto the SDO/HMI image plane (orange-solid line), \(\mathcal{M}_{\mathrm{area}}\) starts deviating from 100% only in the SO/PHI-FDT range of resolutions, down to about 99% for \(r_{\Delta}=10\). This departure is an additional indication that the interplay between the instrument spatial sampling and the native resolution (i.e. the intrinsic scales of the observed field) of the test magnetogram plays a role in the accuracy of SDM.
As a reference, the vertical black-dashed line in the right panels of Figure 10 corresponds to the ratio of the resolution of the test magnetogram to the SDO/HMI spatial sampling [\(\Delta_{\mathrm{native}}/\Delta_{\mathrm {SDO{}/HMI{}}}\)]. Its value is slightly inside the SO/PHI-HRT green area, meaning that, for the highest values of the SO/PHI-HRT spatial sampling, the test field is extrapolated rather than interpolated onto the SO/PHI-HRT grid. This is not optimal, but since it affects the accuracy on the high-resolution side, it has no real effect on the results. On the other hand, a larger value of \(\Delta_{\mathrm{native}}\) allows for a wider extension of the right-hand side of the plot by still having enough grid points on the image plane of SO/PHI-FDT at the lowest resolutions, which is of more relevance to the tests we present here.
For the PENCIL-AR test magnetogram, the variation of \(\mathcal{M}_{\mathrm{area}}\) with the separation angle \(\gamma\) (Figure 10c) can be as large as 10%. However, such large errors are found only close to critical angles (\(\gamma=0, \pm90^{\circ}\)): at a wide range of separation angles, say for \(|\gamma| \in[15^{\circ},70^{\circ}]\), both the direct and the reverse case have accuracy in excess of 99%.
The dependence on spatial sampling in the PENCIL-AR case (Figure 10d) is much stronger but affects the SO/PHI-FDT range of resolutions only. With respect to the TD case (Figure 10b), the PENCIL-AR magnetogram presents a mixture of large and small scales, with the interpolation effect having a larger impact on accuracy. While \(\mathcal{M}_{\mathrm{area}}\) is above 99% in the whole SO/PHI-HRT range of spatial sampling for both direct and reverse cases, its value for the direct case drops rapidly for \(r_{\Delta}>1\), reaching \(\mathcal{M}_{\mathrm{area}}=0.80\) for \(r_{\Delta}=10\). The area metric in the direct case is 99%, unaffected by spatial sampling. Opposite to the reverse case, in the direct case, the progressively less-resolved SO/PHI data are used to remove the ambiguity on (the image plane of) SDO/HMI, hence requiring increasing under-sampling as \(r_{\Delta}\) grows. It is worth noticing, however, that in both directions, \(\mathcal{M}_{\mathrm{area}}\approx1\) within the SO/PHI-HRT resolution span.
In the MURaM-QS case (Figure 10e, f), the small scales in the test magnetogram impact the accuracy \(\mathcal{M}_{\mathrm {area}}\) in the strongest way. In this case, the differences between the direct and the reverse cases are more clearly visible.
In the direct case (Figure 10e), \(\mathcal{M}_{\mathrm{area}}\) monotonically grows between 54% and 88% as \(|\gamma|\) goes from 0 to \(90^{\circ}\). In the reverse case, local maxima are present close to \(\pm50^{\circ}\) with an overall accuracy span between 60% and 87%.
Similarly, Figure 10f shows how \(\mathcal{M}_{\mathrm{area}}\) as a function of the SO/PHI spatial sampling ratio [\(r_{\Delta}\)] in the direct case rapidly changes from 99% at the highest spatial sampling (\(r_{\Delta}=0.1\)) to almost 50% at \(r_{\Delta}=10\). In the reverse case, the area metric is again independent of spatial sampling, and equal to 82%. The slightly increased accuracy at \(r_{\Delta}=1\) and \(r_{\Delta}=10\) is likely only due to an occasional overlap of pixels on the two grids that reduced the interpolation error, thereby increasing the accuracy. Even in the SO/PHI-HRT resolution interval, there is a significant change in \(\mathcal{M}_{\mathrm {area}}\) from 95% to 77%.
In summary, in the MURaM-QS case, the interpolation of the small scales in the test magnetogram lowers the attainable accuracy of the disambiguation with respect to the TD and PENCIL-AR cases. However, we notice that when particular parameters are chosen such that interpolation is not required (e.g. in the already mentioned example of \(\Delta_{\mathrm{{SO/PHI}{}}}=0.25\) arcsec and \(\gamma=60^{\circ }\)), the accuracy of the method in the MURaM-QS case is also 100%. As discussed in Section 3.1.3, the MURaM-QS test is to be considered as a very challenging example with a large fraction of the field below the spatial sampling of both detectors.
In reality, \(\gamma\) and the distance of Solar Orbiter from the Sun (i.e. the spatial sampling ratio [\(r_{\Delta}\)]) are not independent as we have treated them in this section but are linked by the actual orbit. We consider this practical application in Section 7.
4.5 Effect of Threshold on Significant Pixels
The success rate [\(\mathcal{M}_{\mathrm{area}}\)], Equation 16, is computed including all pixels in the image plane regardless of the actual value of the field. However, since accuracy depends on interpolation, in this section, we study how \(\mathcal{M}_{\mathrm{area}}\) changes if only pixels (on the image plane of the detector where the ambiguity is resolved) above a given threshold are included in the calculation of Equation 16.
In real applications, errors in the application of disambiguation methods have been related to high noise levels in the transverse-field component or the presence of under-resolved scales (see, e.g., Leka et al. (2009), Hoeksema et al. (2014)). As an order of magnitude estimation of the noise level in HMI magnetograms, Liu et al. (2017) indicate the value of about 150 Mx cm−2 as an approximate threshold for the pixel-averaged signal below which the transverse field outside active regions is assigned a random value of \(\zeta\).
Figure 11 shows the result for the reference case of Table 1 where such a threshold [\(\mathcal{T}\)] is applied, for value of the threshold varying from 0 to 500 G in 23 steps of increasing amplitude from 1 G to 50 G (we recall that all test cases are normalized such as to have the maximum component at 2000 G). The accuracy in the TD and PENCIL-AR cases is already very high even if all pixels are included in Equation 16, and there is little room for improvement by masking; see Figure 11a, b respectively. In the MURaM-QS case (Figure 11c), however, a strong dependence on the masking values is found. In particular, \(\mathcal{M}_{\mathrm{area}}\) is increased by about 10% in the reverse case by masking all pixels with transverse component below 150 G and reaches \(\mathcal{M}_{\mathrm{area}}\approx 98\)% if only pixels with the transverse component larger than 500 G are considered.
Dependence of the success rate [\(\mathcal{M}_{\mathrm{area}}\)] as a function of the threshold \(\mathcal{T}\) on the amplitude of the transverse component [G] for the (a) TD, (b) PENCIL-AR, and (c) MURaM-QS test magnetograms. See the caption to Figure 10 for additional notation. Please, note the difference in vertical scale between the TD and PENCIL-AR cases (Panels a and b) and MURaM-QS cases (Panel c).
Because of the variation of spatial sampling experienced by SO/PHI along its orbit, we also study how the transverse field is rendered for different re-binning factor [\(r_{\Delta}\)] as quantified by the transverse field metric [\(\mathcal{M}_{B_{\perp}> 100~\text{G}}\)]. Figure 12 shows \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) as a function of \(r_{\Delta}\) with all other geometrical parameters kept at the values of the reference case of Table 1.
First, comparing Panels a, b, and c in Figure 12 with the corresponding panels in Figure 10 (Panels b, d, and f for the TD, PENCIL-AR, and MURaM-QS cases, respectively), we notice that the \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) metric behaves very similarly to the \(\mathcal{M}_{\mathrm{area}}\) metric for all cases and \(r_{\Delta}\)-values. In particular, for the TD and PENCIL-AR cases \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) is unity for the entire range of \(r_{\Delta}\) in the reverse applications, and it departs from unity only for the higher \(r_{\Delta}\)-values in the SO/PHI-FDT range of resolutions. In the MURaM-QS case, the fraction of transverse field correctly represented by the disambiguated magnetogram drops significantly as a function of \(r_{\Delta}\) in the direct case while remaining at the almost-constant value of 0.95 in the reverse case. In other words, in the MURaM-QS case, as the success of the disambiguation quantified as \(\mathcal{M}_{\mathrm{area}}\) decreases with \(r_{\Delta}\), so does the fraction of correctly represented transverse field \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) and at the same rate.
The plots for the transverse field metric for \(\mathcal{T}=500\) G (\(\mathcal{M}_{B_{\perp}> 500~\text{G}}\), not shown here) is practically indistinguishable from Figure 12, except for the constant value of the reverse application to the MURaM-QS case attaining the slighter higher value 0.98, instead of 0.95 as for \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) (see Figure 12c). Considering the MURaM-QS case in the above test and Figure 11c in particular, this implies that a higher threshold [\(\mathcal{T}\)] of the transverse field does increase the relative accuracy of SDM. However, such increased accuracy does not further improve how the transverse field is represented at different \(r_{\Delta}\) in the MURaM-QS case, as quantified by \(\mathcal{M}_{B_{\perp}> \mathcal{T}}\).
Such a strong dependence of \(\mathcal{M}_{\mathrm{area}}\) on the masking of weak fields is an indirect confirmation that the small scales are the most important source of inaccuracies for SDM. On the other hand, even for the quiet-Sun case in MURaM-QS, the area metric is above 80%, which is significantly better than the random orientation. In this respect, SDM is expected to significantly improve disambiguation with respect to state-of-the-art using only one viewpoint.
5 Reconstructed Magnetogram Test
In this section, we describe the test of SDM with simulated observations from different viewpoints, rather than with a 2D-map from a numerical simulation that is simply reprojected at different angles as in Section 3. Such a test has a relevance that goes beyond testing the validity of SDM as such, as it addresses the question of how a field is rendered by the observation and inversion procedure from different viewpoints. Without pretence to exhaust this topic, we include it here as an example to illustrate the complex challenges faced by any stereoscopic method.
5.1 Test Construction
The numerical model used in this test is the full 3D-MURaM-QS simulation of a pore described in Section 3.1.3. We apply multiple steps of processing to this data set to produce a SO/PHI-HRT-like observation and a direct reconstruction from the contributing layers in the 3D-simulation for \(\gamma\in[0, 10, 20, 30, 40, 50, 60, 70]\) degrees. The original resolution of the MURaM-QS simulation is reduced by about 60% resulting in a dimension of \(324\times324\) pixels at \(\gamma=0^{\circ}\). Additionally, all three relevant resolutions (native of the model test [\(\Delta_{ \mathrm{native}}\)], the SDO/HMI spatial sampling [\(\Delta_{\mathrm{SDO {}/HMI{}}}\)], and the SO/PHI-HRT spatial sampling [\(\Delta_{\mathrm{SDO{}/HMI-HRT{}}}\)]) are taken to be all equal to 0.5 arcsec, hence \(r_{\Delta}=1\). This implies that the test simulates the use of the HRT telescope when Solar Orbiter is at 1 AU distance from the Sun. These choices, which are not optimal for the application of SDM and not really representative of the typical case of application, were nevertheless necessary in order to limit the numerical efforts required by the reconstruction method described below. Because of the above limitations, the results in this section are not entirely comparable with those in Section 4, as we were forced to choose different parameters from those in Table 1. Hence, in order to limit the modifications to the model test case, no normalization of the field amplitude is adopted here.
As a matter of fact, different types of magnetograms can be constructed from the MURaM-QS simulations. We discuss these options in the following and refer the reader to Table 4 for a quick view of their essential properties and reference to relevant sections in the article.
5.1.1 Synthetic Magnetograms
In the standard procedure for creating a synthetic SO/PHI-HRT magnetogram, the MURaM-QS simulation data are used as input to the forward-calculation mode of the SPINOR radiative-transfer inversion code (see Solanki, 1987; Frutiger, 2000; Frutiger et al., 2000) to compute synthetic Stokes spectra around the Fe i 617.3 nm line as observed by SO/PHI-HRT, see the shaded box in Figure 14. The resulting spectra are then used as input to the SO/PHI Software siMulator (SOPHISM: see Blanco Rodríguez et al., 2018) to produce SO/PHI-HRT-like observations, including an inversion of the degraded spectra adopting the Milne–Eddington approximation as performed onboard SO/PHI. This operation results in a synthetic (ambiguous) magnetogram of the simulated region that contains fields on all scales down to the resolution limit and with strength up to 3500 G. The LoS of these magnetograms at different viewing angles are shown in the left column of Figure 13.
Isolines of the LoS-field component in the synthetic magnetogram (left column), and the reconstructed magnetogram (central column) saturated at \(\pm3000\) G, and the absolute value of their difference (right column) saturated at 500 G, for viewing angle, from top to bottom, \(\gamma=[0,10,20,30,40,50,60,70]\) degrees. In all plots, the blue contours are the ±500 G-isoline, and axis units are in pixels.
SDM can then be applied to the synthetic SO/PHI-HRT magnetograms obtained in this way. However, since the synthetic magnetograms are themselves ambiguous, such an application is not quite a test of SDM; since the real orientation of the transverse field is not known, the answer provided by SDM cannot be validated. Instead, in order to assess the success of SDM in resolving the ambiguity, one needs to construct a dataset best representing the expected correct result (Leka et al., 2009). In order to obtain that, one needs to know how the transverse field that modulated the synthetic emission is truly oriented in each pixel of the image plane for any angle [\(\gamma\)]. To obtain such information requires more than simply simulating the SO/PHI-HRT observation of a 3D-simulation of the solar photosphere as done for the production of synthetic magnetograms, as it implies tracing back the origin of the optical signal in the simulation, for any given \(\gamma\), and reconstructing the orientation of the transverse field.
5.1.2 Reconstructed Magnetograms
Therefore, in addition to the synthetic SO/PHI observations, non-ambiguous, vector magnetograms describing the solar scene by the MURaM-QS simulations as seen from different viewing angles [\(\gamma\)] were produced, see Figure 14 for a flow diagram of the procedure described below.
Flow-diagram of the construction of synthetic magnetograms (shaded box only; see Section 5.1.1) and of the reconstructed magnetograms; see Section 5.1.2. The procedure is applied on the image plane of each telescope for the given observing configuration specified by \(\gamma\) and \(r_{\Delta}\). Input/output is visualized with green parallelograms, operations are in orange rectangles.
These data contain the reconstructed contribution of each cell along each ray through the MURaM-QS cube. We compute these contributions from magnetic-response functions (Landi Degl’Innocenti and Landi Degl’Innocenti, 1977; Ruiz Cobo and del Toro Iniesta, 1994) as a function of the optical depth, which we use as a weighting function to extract and integrate over the relevant cells from the MURaM-QS data. These magnetic-response functions are computed from the atmospheric model that SPINOR creates for an inversion of the SO/PHI-HRT-like observations as described in Section 5.1.1. Before they can be used to access the magnetic-field data in the MURaM-QS cube, they must be transformed such that they depend on the geometrical height rather than on the optical depth. This was achieved with the MapTau subroutine of SPINOR, which emulates the radiative transport through the MURaM-QS simulation for each viewing angle [\(\gamma\)]. From the temperature stratifications in the MURaM-QS atmospheres, all other thermodynamic quantities such as the gas pressure, the electron pressure, or the density are derived, assuming hydrostatic and local thermodynamic equilibrium. The optical depth is then computed using the frequency-dependent absorption coefficient for the continuum (see, e.g., del Toro Iniesta, 2007). The output is a height coordinate along the given, inclined LoS, which is directly compatible with the optical-depth scale of the magnetic-response functions. We rebin this dataset to match the resolution of the observation-based response functions. In order to include the instrument degradation as simulated by SOPHISM, we convolve the rebinned dataset with the optical-transfer function for a 14 cm telescope aperture (this operation is marked as PHI OTF in Figure 14). The subsequent weighted integration along the LoS for each pixel results in what we call a reconstructed magnetogram, i.e. a best-effort approximation to the “true” solar scene represented by the MHD simulation; see Figure 15b. The reconstructed magnetograms at different values of \(\gamma\) are used to test SDM in Section 6, and they are shown (without any instrument degradation) in the central column of Figure 13 for different values of \(\gamma\). A case that also includes the effect of instrument degradation is shown in Figure 15b and discussed in the next section. Since the reconstructed magnetograms retain the information about the orientation of the transverse-field component, they can be used as a test for SDM that includes the spectropolarimetric influence of the viewing angle; see Section 6.
\(B_{\mathrm{w}}\)-component on the SO/PHI-HRT image plane of (a) the reproj-reconstructed and (b) the reconstructed magnetogram, showing the effect of instrument degradation; (c) difference between the reproj-reconstructed and the reconstructed \(B_{\mathrm{w}}\)-components as quantified by \(\epsilon(B_{\mathrm{w}})\) defined in Equation 19, at \(\gamma=40^{\circ}\) for \(r_{\Delta}=1\) and \(\Delta_{\mathrm{native}}=\Delta_{\mathrm{SDO{}/HMI{}}}=0.5\) arcsec. In all panels, the black contour represents the 500 G isoline of \(|B_{\mathrm{w}}|\), and axis units are in pixels.
5.1.3 Difference Between the Synthetic and the Reconstructed Magnetograms
We notice that, in the reconstruction procedure described above, the weighted integration is done with respect to an average \(\tau=1\) surface for the solar scene at the given \(\gamma\). As a result, the formation of the reconstructed magnetograms are slightly shifted towards larger heights for larger \(\gamma\), and they also do not necessarily coincide with the formation heights of the synthetic observations, even for the same viewing angle. The effect of this shift is shown in the right column of Figure 13: the difference between the synthetic magnetogram (left column) and the reconstructed magnetogram (central column) for a same value of \(\gamma\) can be locally very large, and it is on average of the order of 20 – 35 G for the LoS-component and 70 – 140 G for the transverse one, depending on \(\gamma\).
The natural discrepancy of reconstructed vs. synthetic magnetograms and the increase of the formation height with \(\gamma\), which is identical to the center-to-limb variation, affect both the magnitude and orientation of the resulting field vector. Therefore, the reconstructed magnetogram never perfectly matches the synthetic magnetogram obtained from the direct application of the SPINOR inversion code. This is the price that we need to pay in order to retain the information about the orientation of the transverse component that is needed for testing SDM.
5.2 Difference Between the Reprojected-Reconstructed and the Reconstructed Magnetograms
In the previous section, we introduced the reconstructed magnetograms to be used as tests of SDM and discussed how such magnetograms differ from the synthetic magnetograms (Figure 13) for a given value of the viewing angle \(\gamma\). In this section, we further discuss the geometrical effect of the viewing angle on the reconstructed magnetograms. This is an attempt to quantify the fact that the observed emission from a feature at different \(\gamma\) will never originate from the exact same parcel of plasma. This particularly affects weak-magnetic-field structures, especially where such structures are found to be predominantly horizontal (see, e.g., Danilovic, van Noort, and Rempel, 2016, and references therein). In such a case, first, only a small change of the formation height can change the LoS-component from positive to negative if the field lines are even only slightly changing their orientation with height. Second, as the transverse Zeeman effect is a second-order effect, i.e. the amplitudes of the corresponding Stokes parameters are proportional to \(B^{2}\), the measurements of the transverse field strength are significantly more sensitive to noise effects in the observations than those of the LoS-components.
In order to test for the change in the depth of the \(\tau\)-surface due to the different viewing angles, we compare the reconstructed magnetograms at any given \(\gamma\) with the magnetogram obtained by applying the geometrical re-projection described in Section 3 and Figure 5 to the \(\gamma=0\) reconstructed magnetogram. We identify the latter as the (geometrically) reprojected-reconstructed magnetogram (“Reproj-reconstructed” in Table 4). This comparison between reconstructed and reprojected magnetograms specifically addresses the question of what is the effect of different viewing angles on the reconstructed field, to the best of our abilities, at simulating real observations that retain the information about the orientation of the transverse field. Again, this is not a test for SDM but, instead, it is a direct comparison where we do not apply any disambiguation and indeed employs unambiguous reconstructed model fields. In fact, both magnetograms have the correct (reprojected or reconstructed) orientation of the transverse field, and we retain this information here since the above question is unrelated to the disambiguation problem.
Panels a and b in Figure 15 show the \(B_{\mathrm {w}}\)-component of the reproj-reconstructed Panel a and reconstructed Panel b magnetograms in the image plane of SO/PHI-HRT for \(\gamma=40^{\circ}\). At first glance, the two distributions look similar enough with the reconstructed field appearing smoother than the reprojected field. This is confirmed by differences in the blue isolines, corresponding to \(|B_{\mathrm{w}}|{=}500\) G.
A more quantitative and local measure of the difference between the two magnetograms can be computed in each pixel as
i.e. by the absolute value of the average divided by the average of the absolute values. In each pixel, \(\delta B_{\mathrm{w}}=0\) means that \(B_{\mathrm{w}}\) is identical in the reproj-reconstructed and reconstructed magnetograms, whereas \(\delta B_{\mathrm{w}}=1\) corresponds to the case where the field has the same amplitude in both magnetograms but is opposite in sign. Figure 15c shows that the differences between the two magnetograms are actually quite significant in low-field regions. The value of \(\delta B_{\mathrm{w}}\) is smaller than 0.5 in 31% of the pixels in Figure 15c. Values close to zero are quite obviously found in high-field areas. On the other hand, in small-field areas, the distribution of \(\delta B_{\mathrm {w}}\) is rather granular, and it is difficult to identify a pattern for the location where \(\delta B_{\mathrm{w}}\) is close to one. Similar plots and conclusions are also obtained for the other field components (not shown).
Therefore, according to our computational model of the observation (Section 5.1), the differences in the observed field as a function of the observing angle are significant. More generally, the discussion in this section and Section 5.1.1 shows the complexity and intrinsic limitations of creating observation-like test magnetograms. Such a difficulty adds to the complexity of the MURaM-QS numerical solution used as a basis for the test production, which were extensively discussed in Section 4. Hence, the application of SDM to reconstructed magnetograms described in Section 6 offers an exceptionally challenging test that we regard as a first application.
6 Test of SDM on Reconstructed Magnetograms
In this section, we apply SDM to the ambiguous reconstructed magnetograms obtained as described in Section 5.1.2 for \(\gamma=[10,20,30,40,50,60,70]\) degrees, i.e. using only the magnetograms shown in the central column in Figure 13. This test is similar to the geometrical test of Section 3, except that we used the reconstructed magnetograms obtained in Section 5.1.2 for its application. In particular, we first apply Point iii of Section 3.2 to the reconstructed magnetograms at \(\gamma=0\) and at finite values of \(\gamma\) to introduce the ambiguity; second, we apply SDM as described in Section 3.3 to the (now) ambiguous reconstructed magnetograms, for \(r_{\Delta}=1\) and different separation angles [\(\gamma\)]; third, we then use the knowledge of the real orientation of the transverse component in the reconstructed magnetograms to assess the correctness of the disambiguation using the success metrics \(\mathcal{M}_{\mathrm{area}}\), \(\mathcal{M}_{J_{z}}\), and \(\mathcal{M}_{B_{\perp}> \mathcal{T}}\) for \(\mathcal{T}=100\) G and \(\mathcal{T}=500\) G defined in Section 4.1 as a function of \(\gamma\) (see Figure 16).
The metrics (a) \(\mathcal{M}_{\mathrm{area}}\); (b) \(\mathcal{M}_{J_{z}}\); (c) \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\); (d) \(\mathcal{M}_{B_{\perp}> 500~\text{G}}\) as a function of the separation angle [\(\gamma\)] for the reconstructed magnetogram. Direct and reverse applications are coded in orange and blue colors, respectively.
Figure 16a shows that the accuracy of the disambiguation as quantified by \(\mathcal{M}_{\mathrm{area}}\) is almost monotonically decreasing from 79% to 65% in the direct case, while it is flatter between 78% and 83% in the reverse case, with a peak at \(\gamma=20^{\circ}\). The other three metrics (\(\mathcal{M}_{J_{z}}\), \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\), and \(\mathcal{M}_{B_{\perp}> 500~\text{G}}\), shown in Figure 16b, c, and d, respectively) have basically opposite trends for the direct and reverse cases, as a function of \(\gamma\). For instance, the total vertical current metric [\(\mathcal{M}_{J_{z}}\), Panel b] increases in the reverse application from 57% to 71% for increasing \(\gamma\), whereas it decreases to about 50% in the direct application. A similar anti-symmetric dependence on \(\gamma\) is true for the transverse-field metrics \(\mathcal{M}_{B_{\perp}> 100~\text{G}}\) and \(\mathcal{M}_{B_{\perp}> 500~\text{G}}\). In this case, it is worth noticing that for separation angles larger than about 30∘, the fraction of the transverse field above 100 G that is correctly disambiguated is above 90% in the direct case, and this fraction becomes almost 100% if the threshold [\(\mathcal{T}\)] is raised to 500 G. We recall that, in the case examined in this section, the spatial sampling ratio is unity [\(r_{\Delta}=1\)], hence, from the geometrical point of view, there is a pure foreshortening effect, but the spatial sampling of the two detectors is the same. Therefore, the decrease in the success metrics with increasing \(\gamma\) in the direct case is likely the consequence of probing increasingly different layers in the modeled atmosphere. Since, as noted already above, the MURaM-QS field is mostly vertical, such an effect is less pronounced when using the top-view from SDO/HMI to resolve the ambiguity of SO/PHI-HRT, i.e. in the reverse case.
When considered together, the most notable qualitative change between the geometrical case in Figure 10e and SDM application to reconstructed magnetograms of Figure 16a, b is the absence of a clear maximum at intermediate values of \(\gamma\). Moreover, the introduction of a threshold in the computation of \(\mathcal{M}_{\mathrm{area}}\), while sensibly improving the rate of successful disambiguation in the reverse case, it is counter-productive in the direct case.
To complete the above picture, Figure 17 shows the variation of \(\mathcal{M}_{\mathrm{area}}\) as a function of the threshold on included pixels, for the fixed value \(\gamma=40^{\circ}\), computed as described in Section 4.5. Again, we find a more complex qualitative dependence than in the geometrical case in Figure 11c; as the computation of \(\mathcal{M}_{\mathrm{area}}\) is restricted to pixels with increasingly larger values of the transverse component, the area metric for the reverse case is increasing, up to a very high value of \(\mathcal{M}_{\mathrm{area}}=97\%\) for a threshold of 500 G. On the other hand, the same threshold has the opposite effect largely in the direct case, where a value of almost 400 G is required in order to increase on the \(\mathcal{M}_{\mathrm{area}}\) obtained without any threshold. The lower success rate in the direct case is identified as a consequence of the intrinsic properties of stereoscopic measurements, which do not allow identically probing small-scale and low magnetic solar regions when seen from different vantage points.
Dependence of the metric \(\mathcal{M}_{\mathrm {area}}\) as a function of the threshold [\(\mathcal{T}\)] on the amplitude of the transverse component (see also Section 4.5) for the reconstructed magnetogram, at \(\gamma=40^{\circ}\). Direct and reverse applications are coded in orange and blue colors, respectively.
In conclusion, the spectropolarimetric effect of different viewing angles has significant consequences applying (possibly any) disambiguation method. In consideration of the analysis in Sections 5.1 – 5.2, this is hardly surprising, given that SDM assumes that the same field is observed from different viewpoints. Since observing from different directions produces significantly different fields (see Section 5.2), any geometrically based method of disambiguation such as SDM translates such differences into inaccuracies. On the other hand, the application in the reverse case (i.e. basically using SDO/HMI to remove the ambiguity of SO/PHI-HRT) has, even in such a complex case, an accuracy in excess of 80%, which can rise to above 90% if a 200 G-threshold on the transverse component is introduced. Considering the unfavorable (and unrealistic) parameters that we were forced to adopt for the SDM test presented in this section, namely the simulated observation of a small pore surrounded by the large area of quiet-Sun with the limited resolution provided by Solar Orbiter at 1 AU (\(r_{\Delta}=1\)), we find the above results very encouraging for the application of SDM even when the effect of optical path is included. A more extended exploration of parameter space, as well as application to higher-resolution simulation of active-region field, is needed, and it is planned for future publications.
7 Conclusions
We present in this article the analytical formulae, Equations 12 and 13, that enable observational resolution of the ambiguity of the transverse component in the image planes of two telescopes observing the same region on the Sun from two different vantage points. These formulae are implemented in the stereoscopic disambiguation method (SDM) for application to two observatories. SDM is designed to be applied to any chance of stereoscopic observations, as currently given by SDO/HMI and SO/PHI, but also to other existing observatories as well as forthcoming missions (e.g. Lagrange) or ground-based observations. In particular, we notice that SDM can in principle be applied even if one of the two detectors only measures the LoS-component of the magnetic field (i.e. using the latter as detector B in Equation 12 and discarding Equation 13).
SDM is then thoroughly benchmarked using geometrical tests and tests employing reconstructed magnetograms. In the first type of test, an identical 2D vector magnetogram is viewed from different angles and distances, i.e. spatial sampling. We consider three types of test magnetograms going from the very smooth field (TD) to the one with both large and small scales (PENCIL-AR), to a simulation of a pore surrounded by a large quiet-Sun area (MURaM-QS).
The result of the geometrical tests can be summarized as follows:
-
in an idealized situation such as the TD where the field is smooth and well resolved on both detectors, the application of SDM is able to remove the ambiguity with 100% accuracy, at all separation angles and considered spatial sampling;
-
for an active-region field (PENCIL-AR), the disambiguation accuracy is also 100%, with small decreases at expected locations (e.g. when the spacecraft are co-aligned or close to quadrature), or for the lower resolution of the SO/PHI-FDT telescope;
-
the accuracy is modulated by both the separation angle between detectors as well as by the SO/PHI-HRT effective resolution, i.e. by the distance of the Solar Orbiter spacecraft from the Sun;
-
the disambiguation accuracy is found to be mostly sensitive to the small scales present in the test magnetogram, going from perfect disambiguation (e.g. for the smooth TD-test magnetogram) to almost 50% accuracy, equivalent to a random resolution of the ambiguity, in the least favorable case of observing fields with very small scales (such as the MURaM-QS) with the lower-resolution SO/PHI-FDT telescope when Solar Orbiter is at 1 AU;
-
furthermore, the success rate is found to increase sensibly even in the most challenging MURaM-QS case if pixels with small values of the transverse component are not included in the disambiguation procedure;
In addition to testing the method, our parametric study allows the meaningful application to the Solar Orbiter observations. The practical case of the expected accuracy of SDM during the years 2022 – 2024 can be obtained by using orbit information. Figure 18 shows the expected accuracy for the PENCIL-AR case as a function of time from 2021 to 2024. This type of study can be used to place remote-sensing windows at times that are favorable to stereoscopic disambiguation. The systematic exploration of the best placement of observing remote-sensing windows that includes such effects is straightforward but extensive, and we reserve this study for dedicated work. Here we limit ourselves to notice the anti-correlation (clearly visible for the SO/PHI-FDT telescope) between distance, i.e. spatial sampling, and accuracy, and that this effect is stronger than the separation-angle effect.
Expected \(\mathcal{M}_{\mathrm{area}}\) during the years 2021 – 2024 as Solar Orbiter travels on its orbit. The top panel shows the orbit of the spacecraft in terms of the separation angle with SDO/HMI [\(\gamma\)] and the distance from the Sun (\(R_{\mathrm{SO}}\), related to \(r_{\Delta}\) by Equation 14); the middle panel shows the expected \(\mathcal{M}_{\mathrm {area}}\) from the application of SDM using the SO/PHI-HRT telescope, while the bottom one is for the SO/PHI-FDT telescope (notice the different vertical axis range for \(\mathcal{M}_{\mathrm {area}}\) in the middle and bottom panels). Orange crosses (respectively, blue squares) show the results of the direct (respectively, reverse) application of SDM. The green areas correspond to times where SDO and Solar Orbiter are on the same side of the Sun, i.e. when stereoscopic disambiguation is possible. The model field used for this test is the PENCIL-AR case; see Section 3.1.2.
The second type of test that we perform employs reconstructed magnetogram, i.e. synthetic spectropolarimetric observations at different angles obtained using a 3D-MURaM-QS simulation of the upper photospheric layers; see Section 5.1.2. By testing SDM with reconstructed magnetograms we can draw the following conclusions:
-
viewing the same area from different angles has a significant influence on the observed values. Since stereoscopic methods are based on combining two different viewpoints, this implies that any stereoscopic disambiguation method faces serious challenges, in particular in low-field areas, regardless of the method details;
-
as a consequence, the application of SDM to reconstructed magnetograms translates the differences in the reconstructed magnetograms as seen from different angles into inaccuracies of the disambiguation. Such inaccuracies are expected to be small in the case of strong-field areas such as active regions, but proper testing of such supposition requires suitable numerical simulations. However, even in the challenging case of reconstructed observations of a pore surrounded by quiet Sun, the SDM accuracy can attain significant improvements (above 80%) with respect to a random choice of orientation when applied in the reverse mode, i.e. when SDO/HMI is used to remove the ambiguity of SO/PHI-HRT.
We regard these results as preliminary. On the grounds of the geometrical tests summarized above, there is basically a 10% difference between geometrical and reconstructed tests in the disambiguation accuracy of the MURaM-QS magnetogram. As in the geometrical test case, the success rate in strong magnetic-field regions of these simulations is easily 10 – 15% better than in the quiet Sun, we would expect a success rate in excess of 90% if applied to magnetograms thresholded for only sunspot areas (see, e.g., Figure 11c). We have chosen this type of MURaM-QS simulation to test SDM under conditions as close as possible to a realistic case. It has to be emphasized that during periods of high solar activity, typical magnetograms obtained by SDO/HMI contain only a very small area of regions with pixel-averaged signal above 150 Mx cm−2 (cf. Liu et al., 2017). In the weak-field regions, the success rate of SDM is highly dependent on the ratio of spatial resolutions of the input data since reliable disambiguation needs to take into account the magnetic fine scale of the solar photosphere. Despite the intrinsic limitations of observing the exact fine structure of weak transverse field regions from different viewpoints particularly (see discussion in Section 5), a success rate of above 80% (Figure 16a) can be achieved with SO/PHI-HRT observations with a spatial sampling comparable or better than that of SDO/HMI.
In conclusion, the stereoscopic disambiguation method [SDM] is in principle an exact method of removing the ambiguity, which is proven to yield 100% accuracy when applied to idealized conditions. The accuracy of SDM is found to depend mostly on the amount of unresolved structure at a given spatial sampling (i.e. distance from the Sun), but it can otherwise remove the ambiguity with excellent accuracy. Even for the quiet-Sun case (MURaM-QS), the rate of success of SDM is found to be above 80%, which is significantly better than the random orientation currently adopted in many situations. In this respect, SDM is expected to improve disambiguation significantly with respect to the current state-of-the-art using one viewpoint only, and it can be used as a reliable benchmark for other single-viewpoint methods not only in strong-field areas but also on quiet-Sun areas.
The study presented here is preliminary in many ways. First, a systematic study of the influence of noise and unresolved scales on the accuracy of SDM along the lines of Leka et al. (2009) is required to assess such effects in a realistic way. On the other hand, a direct extension of the present work will be to test SDM employing reconstructed magnetograms of an extended sunspot, such as modeled by Siu-Tapia et al. (2018).
Second, and more specific to the stereoscopic nature of SDM, a difference in the calibration of the two employed telescopes may potentially be an issue in real applications. Our preliminary investigations indicate that a difference in the field strength measured by the two telescopes up to 10% results in a decrease in accuracy in SDM disambiguation of about 2% at most. In other words, a moderate difference in the calibration functions of the observing instruments is not expected to greatly affect the accuracy of SDM. However, a proper estimation of the effect of calibration differences on SDM is best done once the actual calibration functions of SDO/HMI and SO/PHI become available.
Third, the application to real Solar Orbiter observations will require the implementation of SDM in the Solar Orbiter pipeline and the inclusion of maps of estimated errors based on the parameter optimization presented here. In this respect, one notable missing test is the dependence of SDM on pointing errors. Since the pointing information is essentially labeling of pixels with coordinates that is an integral part of the data processing of each telescope, we postpone this test to the implementation of SDM in the Solar Orbiter data pipeline.
Finally, a comparison with traditional, single-view disambiguation methods would be desirable in order to quantitatively assess how SDM can be used to benchmark more traditional, single-viewpoint disambiguation methods.
Data Availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Albert, K., Hirzberger, J., Kolleck, M., Jorge, N.A., Busse, D., Blanco Rodríguez, J., Carrascosa, J.P.C., Fiethe, B., Gandorfer, A., Germerott, D., Guan, Y., Guerrero, L., Gutierrez-Marques, P., Expósito, D.H., Lange, T., Michalik, H., Suárez, D.O., Schou, J., Solanki, S.K., del Toro Iniesta, J.C., Woch, J.: 2020, Autonomous on-board data processing and instrument calibration software for the polarimetric and helioseismic imager on-board the solar orbiter mission. J. Astron. Telesc. Instrum. Syst. 6, 048004. DOI. ADS.
Blanco Rodríguez, J., del Toro Iniesta, J.C., Suárez, D.O., Pillet, V.M., Bonet, J.A., Feller, A., Hirzberger, J., Lagg, A., Piqueras, J., Blesa, J.L.G.: 2018, SOPHISM: An end-to-end software instrument simulator. Astrophys. J. Suppl. 237, 35. DOI. ADS.
Borrero, J.M., Tomczyk, S., Kubo, M., Socas-Navarro, H., Schou, J., Couvidat, S., Bogart, R.: 2011, VFISV: Very fast inversion of the Stokes vector for the helioseismic and magnetic imager. Solar Phys. 273, 267. DOI. ADS.
Borrero, J.M., Lites, B.W., Lagg, A., Rezaei, R., Rempel, M.: 2014, Comparison of inversion codes for polarized line formation in MHD simulations. I. Milne-Eddington codes. Astron. Astrophys. 572, A54. DOI. ADS.
Chen, F., Peter, H., Bingert, S., Cheung, M.C.M.: 2014, A model for the formation of the active region corona driven by magnetic flux emergence. Astron. Astrophys. 564, A12. DOI. ADS.
Cheung, M.C.M., Rempel, M., Title, A.M., Schüssler, M.: 2010, Simulation of the formation of a solar active region. Astrophys. J. 720, 233. DOI. ADS.
Danilovic, S., van Noort, M., Rempel, M.: 2016, Internetwork magnetic field as revealed by two-dimensional inversions. Astron. Astrophys. 593, A93. DOI. ADS.
del Toro Iniesta, J.C.: 2007, Introduction to Spectropolarimetry, Cambridge University Press, Cambridge. ADS.
Frutiger, C.: 2000, Inversions of Zeeman split Stokes profiles application to solar and stellar surface structures. Phd thesis no. 13896, ETH Zürich.
Frutiger, C., Solanki, S.K., Fligge, M., Bruls, J.H.M.J.: 2000, Properties of the solar granulation obtained from the inversion of low spatial resolution spectra. Astron. Astrophys. 358, 1109. ADS.
Hapgood, M.: 2017, L1L5Together: Report of workshop on future missions to monitor space weather on the Sun and in the solar wind using both the L1 and L5 Lagrange points as valuable viewpoints. Space Weather 15, 654. DOI. ADS.
Harvey, J.W.: 1969, Magnetic fields associated with solar active-region prominences. PhD thesis, University of Colorado, Boulder. ADS.
Hoeksema, J.T., Liu, Y., Hayashi, K., Sun, X., Schou, J., Couvidat, S., Norton, A., Bobra, M., Centeno, R., Leka, K.D., Barnes, G., Turmon, M.: 2014, The Helioseismic and Magnetic Imager (HMI) vector magnetic field pipeline: Overview and performance. Solar Phys. 289, 3483. DOI. ADS.
Landi Degl’Innocenti, E.: 2013, Spectropolarimetry with new generation solar telescopes. Mem. Soc. Astron. Ital. 84, 391. ADS.
Landi Degl’Innocenti, E., Landi Degl’Innocenti, M.: 1977, Response function for magnetic lines. Astron. Astrophys. 56, 111. ADS.
Leka, K.D., Barnes, G., Crouch, A.D., Metcalf, T.R., Gary, G.A., Jing, J., Liu, Y.: 2009, Resolving the \(180{\deg}\) ambiguity in solar vector magnetic field data: Evaluating the effects of noise, spatial resolution, and method assumptions. Solar Phys. 260, 83. DOI. ADS.
Lites, B.W.: 2000, Remote sensing of solar magnetic fields. Rev. Geophys. 38, 1. DOI. ADS.
Liu, Y., Hoeksema, J.T., Sun, X., Hayashi, K.: 2017, Vector magnetic field synoptic charts from the helioseismic and magnetic imager (HMI). Solar Phys. 292, 29. DOI. ADS.
Metcalf, T.R., Leka, K.D., Barnes, G., Lites, B.W., Georgoulis, M.K., Pevtsov, A.A., Balasubramaniam, K.S., Gary, G.A., Jing, J., Li, J., Liu, Y., Wang, H.N., Abramenko, V., Yurchyshyn, V., Moon, Y.-J.: 2006, An overview of existing algorithms for resolving the \(180^{0}\) ambiguity in vector magnetic fields: Quantitative tests with synthetic data. Solar Phys. 237, 267. DOI. ADS.
Riethmüller, T.L., Solanki, S.K., Barthol, P., Gand orfer, A., Gizon, L., Hirzberger, J., van Noort, M., Blanco Rodríguez, J., Del Toro Iniesta, J.C., Orozco Suárez, D., Schmidt, W., Martínez Pillet, V., Knölker, M.: 2017, A new MHD-assisted Stokes inversion technique. Astrophys. J. Suppl. 229, 16. DOI. ADS.
Rouillard, A.P., Pinto, R.F., Vourlidas, A., De Groof, A., Thompson, W.T., Bemporad, A., Dolei, S., Indurain, M., Buchlin, E., Sasso, C., Spadaro, D., Dalmasse, K., Hirzberger, J., Zouganelis, I., Strugarek, A., Brun, A.S., Alexandre, M., Berghmans, D., Raouafi, N.E., Wiegelmann, T., Pagano, P., Arge, C.N., Nieves-Chinchilla, T., Lavarra, M., Poirier, N., Amari, T., Aran, A., Andretta, V., Antonucci, E., Anastasiadis, A., Auchère, F., Bellot Rubio, L., Nicula, B., Bonnin, X., Bouchemit, M., Budnik, E., Caminade, S., Cecconi, B., Carlyle, J., Cernuda, I., Davila, J.M., Etesi, L., Espinosa Lara, F., Fedorov, A., Fineschi, S., Fludra, A., Génot, V., Georgoulis, M.K., Gilbert, H.R., Giunta, A., Gomez-Herrero, R., Guest, S., Haberreiter, M., Hassler, D., Henney, C.J., Howard, R.A., Horbury, T.S., Janvier, M., Jones, S.I., Kozarev, K., Kraaikamp, E., Kouloumvakos, A., Krucker, S., Lagg, A., Linker, J., Lavraud, B., Louarn, P., Maksimovic, M., Maloney, S., Mann, G., Masson, A., Müller, D., Önel, H., Osuna, P., Orozco Suarez, D., Owen, C.J., Papaioannou, A., Pérez-Suárez, D., Rodriguez-Pacheco, J., Parenti, S., Pariat, E., Peter, H., Plunkett, S., Pomoell, J., Raines, J.M., Riethmüller, T.L., Rich, N., Rodriguez, L., Romoli, M., Sanchez, L., Solanki, S.K., St Cyr, O.C., Straus, T., Susino, R., Teriaca, L., del Toro Iniesta, J.C., Ventura, R., Verbeeck, C., Vilmer, N., Warmuth, A., Walsh, A.P., Watson, C., Williams, D., Wu, Y., Zhukov, A.N.: 2020, Models and data analysis tools for the solar orbiter mission. Astron. Astrophys. 642, A2. DOI. ADS.
Ruiz Cobo, B., del Toro Iniesta, J.C.: 1994, On the sensitivity of Stokes profiles to physical quantities. Astron. Astrophys. 283, 129. ADS.
Scherrer, P.H., Schou, J., Bush, R.I., Kosovichev, A.G., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall, T.L., Zhao, J., Title, A.M., Schrijver, C.J., Tarbell, T.D., Tomczyk, S.: 2012, The helioseismic and magnetic imager (HMI) investigation for the solar dynamics observatory (SDO). Solar Phys. 275, 207. DOI. ADS.
Schou, J., Scherrer, P.H., Bush, R.I., Wachter, R., Couvidat, S., Rabello-Soares, M.C., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall, T.L., Akin, D.J., Allard, B.A., Miles, J.W., Rairden, R., Shine, R.A., Tarbell, T.D., Title, A.M., Wolfson, C.J., Elmore, D.F., Norton, A.A., Tomczyk, S.: 2012, Design and ground calibration of the helioseismic and magnetic imager (HMI) instrument on the solar dynamics observatory (SDO). Solar Phys. 275, 229. DOI. ADS.
Semel, M., Skumanich, A.: 1998, An ambiguity-free determination of \(J_{Z}\) in solar active regions. Astron. Astrophys. 331, 383. ADS.
Siu-Tapia, A.L., Rempel, M., Lagg, A., Solanki, S.K.: 2018, Evershed and counter-evershed flows in sunspot MHD simulations. Astrophys. J. 852, 66. DOI. ADS.
Solanki, S.K.: 1987, Phd thesis no. 8309. PhD thesis, ETH Zürich. ADS.
Solanki, S.K., del Toro Iniesta, J.C., Woch, J., Gandorfer, A., Hirzberger, J., Schmidt, W., Appourchaux, T., Alvarez-Herrero, A.: 2015, The polarimetric and helioseismic imager for solar orbiter: So/phi. In: Nagendra, K.N., Bagnulo, S., Centeno, R., Martínez González, M.J. (eds.) Polarimetry: From the Sun to Stars and Stellar Environments, IAU Symposium 305, 108. Cambridge University Press, Cambridge, UK. DOI. ADS.
Solanki, S.K., del Toro Iniesta, J.C., Woch, J., Gandorfer, A., Hirzberger, J., Alvarez-Herrero, A., Appourchaux, T., Martínez Pillet, V., Pérez-Grande, I., Sanchis Kilders, E., Schmidt, W., Gómez Cama, J.M., Michalik, H., Deutsch, W., Fernandez-Rico, G., Grauf, B., Gizon, L., Heerlein, K., Kolleck, M., Lagg, A., Meller, R., Müller, R., Schühle, U., Staub, J., Albert, K., Alvarez Copano, M., Beckmann, U., Bischoff, J., Busse, D., Enge, R., Frahm, S., Germerott, D., Guerrero, L., Löptien, B., Meierdierks, T., Oberdorfer, D., Papagiannaki, I., Ramanath, S., Schou, J., Werner, S., Yang, D., Zerr, A., Bergmann, M., Bochmann, J., Heinrichs, J., Meyer, S., Monecke, M., Müller, M.F., Sperling, M., Álvarez García, D., Aparicio, B., Balaguer Jiménez, M., Bellot Rubio, L.R., Cobos Carracosa, J.P., Girela, F., Hernández Expósito, D., Herranz, M., Labrousse, P., López Jiménez, A., Orozco Suárez, D., Ramos, J.L., Barandiarán, J., Bastide, L., Campuzano, C., Cebollero, M., Dávila, B., Fernández-Medina, A., García Parejo, P., Garranzo-García, D., Laguna, H., Martín, J.A., Navarro, R., Núñez Peral, A., Royo, M., Sánchez, A., Silva-López, M., Vera, I., Villanueva, J., Fourmond, J.J., de Galarreta, C.R., Bouzit, M., Hervier, V., Le Clec’h, J.C., Szwec, N., Chaigneau, M., Buttice, V., Dominguez-Tagle, C., Philippon, A., Boumier, P., Le Cocguen, R., Baranjuk, G., Bell, A., Berkefeld, T., Baumgartner, J., Heidecke, F., Maue, T., Nakai, E., Scheiffelen, T., Sigwarth, M., Soltau, D., Volkmer, R., Blanco Rodríguez, J., Domingo, V., Ferreres Sabater, A., Gasent Blesa, J.L., Rodríguez Martínez, P., Osorno Caudel, D., Bosch, J., Casas, A., Carmona, M., Herms, A., Roma, D., Alonso, G., Gómez-Sanjuan, A., Piqueras, J., Torralbo, I., Fiethe, B., Guan, Y., Lange, T., Michel, H., Bonet, J.A., Fahmy, S., Müller, D., Zouganelis, I.: 2020, The polarimetric and helioseismic imager on solar orbiter. Astron. Astrophys. 642, A11. DOI. ADS.
Titov, V.S., Démoulin, P.: 1999, Basic topology of twisted magnetic configurations in solar flares. Astron. Astrophys. 351, 707. ADS.
Valori, G., Pariat, E., Anfinogentov, S., Chen, F., Georgoulis, M.K., Guo, Y., Liu, Y., Moraitis, K., Thalmann, J.K., Yang, S.: 2016, Magnetic helicity estimations in models and observations of the solar magnetic field. Part I: Finite volume methods. Space Sci. Rev. 201, 147. DOI. ADS.
Vögler, A., Shelyag, S., Schüssler, M., Cattaneo, F., Emonet, T., Linde, T.: 2005, Simulations of magneto-convection in the solar photosphere. Equations, methods, and results of the MURaM code. Astron. Astrophys. 429, 335. DOI. ADS.
Acknowledgments
We wish to thank the anonymous reviewer whose constructive comments helped to improve the clarity and focus of the article. This work was developed within the community-led effort by European Space Agency’s Modelling and Data Analysis Working Group (MADAWG). G. Valori acknowledges the support from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 824135 and of the STFC grant number ST/T000317/1. D. Stansby is supported by STFC grant ST/S000240/1. E. Pariat acknowledges financial support from the Programme National Soleil Terre (PNST) of the CNRS/INSU and from the French National Space Agency CNES. G. Valori, P. Löschl, and J. Hirzberger acknowledge funding by the Bundesministerium für Wirtschaft und Technologie through Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR) Grants No. 50 OT 1001/1201/1901 as well as 50 OT 0801/1003/1203/1703, and by the President of the Max Planck Society (MPG). P. Löschl also acknowledges support from the International Max Planck Research School for Solar System Science at the University of Göttingen. The PENCIL-AR simulation was supported by the computational resources from Yellowstone (ark:/85065/d7wd3xhc) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Valori, G., Löschl, P., Stansby, D. et al. Disambiguation of Vector Magnetograms by Stereoscopic Observations from the Solar Orbiter (SO)/Polarimetric and Helioseismic Imager (PHI) and the Solar Dynamic Observatory (SDO)/Helioseismic and Magnetic Imager (HMI). Sol Phys 297, 12 (2022). https://doi.org/10.1007/s11207-021-01942-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-021-01942-x