Decayless Kink Oscillations Excited by Random Driving: Motion in Transitional Layer

Abstract

In this article we study the plasma motion in the transitional layer of a coronal loop randomly driven at one of its footpoints in the thin-tube and thin-boundary-layer (TTTB) approximation. We introduce the average of the square of a random function with respect to time. This average can be considered as the square of the oscillation amplitude of this quantity. Then we calculate the oscillation amplitudes of the radial and azimuthal plasma displacement as well as the perturbation of the magnetic pressure. We find that the amplitudes of the plasma radial displacement and the magnetic-pressure perturbation do not change across the transitional layer. The amplitude of the plasma radial displacement is of the same order as the driver amplitude. The amplitude of the magnetic-pressure perturbation is of the order of the driver amplitude times the ratio of the loop radius to the loop length squared. The amplitude of the plasma azimuthal displacement is of the order of the driver amplitude times $\text{Re}^{1/6}$, where Re is the Reynolds number. It has a peak at the position in the transitional layer where the local Alfvén frequency coincides with the fundamental frequency of the loop kink oscillation. The ratio of the amplitude near this position and far from it is of the order of $\ell$, where $\ell$ is the ratio of thickness of the transitional layer to the loop radius. We calculate the dependence of the plasma azimuthal displacement on the radial distance in the transitional layer in a particular case where the density profile in this layer is linear.

1 Introduction

Kink oscillations of coronal magnetic loops were first observed by the Transition Region and Coronal Explorer (TRACE) mission in 1998 and reported by Aschwanden et al. (1999) and Nakariakov et al. (1999). After that, these oscillations were routinely observed by space missions (e.g. Erdélyi and Taroyan, 2008, Duckenfield et al., 2018; Su et al., 2018; Abedini, 2018, and the references therein). Kink oscillations were also observed in prominence threads (e.g. Arregui, Oliver, and Ballester, 2018). These oscillations have large amplitudes and damp quickly.

Later-low-amplitude undamped or decayless kink oscillations of coronal loops were observed (Wang et al., 2012; Tian et al., 2012; Nisticò, Nakariakov, and Verwichte, 2013; Nisticò, Anfinogentov, and Nakariakov, 2014; Anfinogentov, Nakariakov, and Nisticò, 2015). Recently Duckenfield et al. (2018) reported the observation of multiple harmonics in decayless observations.

At present there are two models of excitation of decayless kink oscillations. Nisticò, Nakariakov, and Verwichte (2013) and Nisticò, Anfinogentov, and Nakariakov (2014) suggested that these oscillations are excited by driving of the loop footpoints by subphotospheric convective motion. Nakariakov et al. (2016) developed the model of decayless kink oscillations where these oscillations are considered as a nonlinear self-oscillatory process.

In this article we consider the first model. The excitation of decayless kink oscillations by driving the loop footpoints was studied in a few articles. Afanasyev, Karampelas, and Van Doorsselaere (2019) and Karampelas et al. (2019) used three-dimensional numerical modelling to study the excitation of kink oscillations in a stratified coronal loop by a continuous monochromatic driving. They considered a few driving frequencies and found that for the same driving amplitude the excitation of kink waves is much more efficient when the driving frequency is equal or close to one of eigenfrequencies of coronal-loop oscillations, which is an expected result. They also observed the development of the Kelvin–Helmholtz (KH) instability that causes the development of turbulence in the transitional layer between the tube core region and surrounding plasma. Thus they confirmed the result previously obtained by other authors (e.g. Terradas et al., 2008; Antolin, Yokoyama, and Van Doorsselaere, 2014; Antolin et al., 2016; Terradas, Magyar, and Van Doorsselaere, 2018). However, it looks doubtful that the decayless kink oscillations are excited by a harmonic driver. It seems much more probable that they are excited by the random driving.

De Groof, Tirry, and Goossens (1998) and De Groof and Goossens (2000, 2002) studied random driving in relation to coronal-loop heating. They modelled a coronal magnetic loop as a magnetic slab. The properties of kink oscillations of magnetic slabs and cylinders are quite different. Hence, their analysis cannot be directly applied to the problem of excitation of decayless kink oscillations of coronal loops.

Recently Afanasyev, Van Doorsselaere, and Nakariakov (2020) studied the excitation of decayless kink oscillations of coronal loops by motions of coronal footpoints using an inhomogeneous wave equation with damping and random driving. They managed to reproduce many observed properties of decayless kink oscillations such as peaks in the Fourier spectrum of oscillations corresponding to eigenmodes of the loop kink oscillation. Motivated by this article, Ruderman and Petrukhin (2021) (Article I below) studied the same problem using the model of a coronal loop in the form of a magnetic-flux tube with a transitional layer at its boundary.

It was assumed in Article I that the footpoint driving is described by a stationary random function. In this case the loop displacement is also a stationary random function of time. The relation between the spectra of the two random functions was obtained. In particular, it was shown that the spectrum of the random function describing the loop displacement has peaks at the loop eigenfrequencies. These peaks are very pronounced at the fundamental frequency and the first overtone, while the peak at the second overtone is much less visible.

In Article I the solution in the transitional layer between the tube core region and the external plasma was obtained. The plasma motion in the transitional layer was thoroughly studied both in the case of harmonic driving as well as in the case of damped oscillations cased by initial perturbations (see Goossens, Erdélyi, and Ruderman, 2011, and the references therein). It was shown that the oscillation amplitude and the gradients of perturbations are very large in a thin dissipative layer embracing the resonant surface. In the case of decaying oscillations excited by an initial perturbation, the resonant surface is defined by the condition that the local Alfvén frequency matches either the fundamental frequency or the frequency of one of overtones. The motion in the dissipative layer is described by the so-called $F_{\Lambda}$- and $G_{\Lambda}$-functions. The function $F_{\Lambda}$ describes the behaviour of the azimuthal plasma displacement in the dissipative layer, and the function $G_{\Lambda}$ describes the behaviour of the radial plasma displacement. The parameter $\Lambda$ measures the relative strength of dissipation and damping in the dissipative layer: $\Lambda$ is small when dissipation dominates, and large when damping dominates. We recall that the damping rate is independent of dissipative coefficients in a weakly dissipative plasma. In the case of driven oscillations, the position of the resonant surface is defined by the condition that the local Alfvén frequency matches the driving frequency. The motion in the dissipative layer is described by the $F$- and $G$-functions that are the limits of $F_{\Lambda}$- and $G_{\Lambda}$-functions for $\Lambda\to0$.

In the case of random driving, the solution obtained in Article I was used to calculate the variation of the radial plasma displacement and the magnetic-pressure perturbation across the transitional layer. However, the details of plasma motion in the transitional layer were not investigated. These details are important, for example, for the stability of plasma motion. The motion in the transitional layer is characterised by strong shear. This can result in the development of the KH instability. If this is the case then the linear description of motion in the transitional layer is not valid. Instead we should assume that there is developed turbulence there.

In this article we study the motion in the transitional layer in the case when a magnetic tube is randomly driven at its footpoint. The article is organised as follows: In the next section we formulate the problem. In Section 3 we present the previously obtained solution to the dissipative MHD equations describing the plasma motion in the transitional layer. In Section 4 we calculate the spectra of radial and azimuthal plasma displacements as well as the magnetic-pressure perturbation and use them to calculate the average squares of these quantities, which can be considered as the squares of their amplitudes. In Section 5 we study the properties of plasma motion in the transitional layer. In Section 6 we consider a particular case where the density profile in the transitional layer is linear. Section 7 contains the summary of results and our conclusions.

2 Problem Formulation

We consider the plasma motion using the zero-$\beta$ approximation. The background magnetic field is straight. In cylindrical coordinates $r,\phi,z$ it is defined by $\boldsymbol{B} = B\hat{\boldsymbol{e}}_{z}$, where $\hat{\boldsymbol{e}}_{z}$ is the unit vector in the $z$-direction and $B$ is a constant. The equilibrium density is given by

$$ \rho(r) = \left\{ \textstyle\begin{array}{l@{\quad}l} \rho_{\mathrm{i}}, & r \leq R(1 - \ell/2), \\ \rho_{\mathrm{t}}(r), &R(1 - \ell/2) \leq r \leq R(1 + \ell/2), \\ \rho_{\mathrm{e}}, & r \geq R(1 + \ell/2), \end{array}\displaystyle \right. $$

(1)

where $R$ is the tube radius, $\rho_{\mathrm{i}}$ and $\rho_{\mathrm {e}}$ are constants, $\rho_{\mathrm{e}} < \rho_{\mathrm{i}}$, $\rho_{\mathrm{t}}(r)$ is a monotonically decreasing function, $\rho(r)$ is continuous at $r = R(1 \pm\ell/2)$, and $R\ell$ is the thickness of the transitional layer. The domain defined by $r \leq R(1 - \ell/2)$ is the core part of the magnetic tube, while $R(1 - \ell/2) \leq r \leq R(1 + \ell/2)$ is the transitional region.

The tube length is $L$. We assume that the tube is thin: $R \ll L$. In addition, we assume that the transitional (also called boundary) layer is also thin: $\ell\ll1$. Hence, we use the thin-tube and thin-boundary-layer (TTTB) approximation. In this approximation the plasma displacement $[\eta]$ in the core region is independent of $r$ (e.g. Goossens et al., 2009; Ruderman, Shukhobodskiy, and Erdélyi, 2017). For simplicity we assume that the tube is driven only at one end, while the second end is frozen in a dense immovable plasma. In accordance with this, we impose the boundary conditions

$$ \xi_{r} = f(t) \quad\text{at} \quad z = 0, \qquad\xi_{r} = 0 \quad \text{at} \quad z = L , $$

(2)

where $f(t)$ is a stationary random function and $\xi_{r}$ is the plasma displacement in the radial direction. It is shown in Article I that adding random driving at the second footpoint does not add any new physics to the problem.

3 Solution in the Transitional Layer

Each magnetic surface in the transitional layer can oscillate in the azimuthal direction with the fundamental frequency $\omega_{\mathrm{A}} = \pi V_{\mathrm{A}}/L$, and also with the frequency of any overtone equal to $n\omega_{\mathrm{A}}$, $n = 2,3\dots$, where $V_{\mathrm{A}} = B(\mu_{0}\rho)^{-1/2}$ is the local Alfvén speed. The union of all intervals $[n\omega_{\mathrm{Ai}},n\omega_{\mathrm {Ae}}]$, and also symmetric intervals constitute the Alfvén continuum. Here the subscripts “i” and “e” indicate that a quantity is calculated at $r \leq R(1 - \ell/2)$ and at $r \geq R(1 + \ell/2)$, respectively. Hence, the Alfvén continuum is defined by

$$ \bigcup_{n=1}^{\infty}\big([-n\omega_{\mathrm{Ae}},-n\omega _{\mathrm{Ai}}] \cup[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]\big). $$

(3)

When a magnetic tube is harmonically driven and the driving frequency is in the Alfvén continuum, there is only one, or a few, resonant surfaces where the driving frequency matches either the local fundamental frequency or the frequency of one of the overtones. There are large gradients in the quantities describing the plasma motion only in the vicinities of resonant surfaces. As a result, dissipation must be taken into account only in these vicinities, while the plasma motion can be described by the ideal magnetohydrodynamic (MHD) equations far from the resonant surfaces.

In the case of random driving, the situation is different. If the driver spectrum contains at least one of the intervals $[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]$, then all surfaces in the transitional layer are resonant. Each surface is in resonance with at least one frequency from the driver spectrum. This implies that dissipation is important everywhere in the transition layer, and the plasma motion must be described by the dissipative MHD equations.

In Article I, the solution to the linear dissipative MHD equations describing the plasma motion in the transitional layer was obtained under a viable assumption that dissipation is weak, that is $\text{Re} \gg1$, where $\text{Re} = RV_{\mathrm{Ai}}/\nu$ is the Reynolds number and $\nu$ is the kinematic viscosity. This solution was also obtained in the leading-order approximation with respect to $\ell$. Below we briefly describe this solution. In Article I the scaled variables $Q = \epsilon^{-2}P$, $T = \epsilon t$, and $Z = \epsilon z$ were used, where $P$ is the perturbation of the magnetic pressure and $\epsilon= R/L \ll1$. We rewrite the equations obtained in Article I in terms of the original variables $P$, $t$, and $z$. Since we consider kink oscillations, we take perturbations of all variables proportional to $\mathrm{e}^{\mathrm{i}\phi}$. This implies that we take $m = 1$, where $m$ is the azimuthal wave number. We do not need to consider $m = -1$ because the tube is not twisted. In this case there is no difference between modes with $m = 1$ and $m = -1$ (see, e.g., Roberts, 2019).

The solution in Article I is given in the form of Fourier expansions,

$$\begin{aligned} \xi_{r} &= f(t)\frac{L - z}{L} + \sum_{n=1}^{\infty}u_{n}(r,t)\sin \frac{\pi n z}{L} , \end{aligned}$$

(4)

$$\begin{aligned} \xi_{\phi}&= \mathrm{i}f(t)\frac{L - z}{L} + \sum_{n=1}^{\infty}v_{n}(r,t) \sin\frac{\pi n z}{L} , \end{aligned}$$

(5)

$$\begin{aligned} P &= \sum_{n=1}^{\infty}P_{n}(r,t)\sin\frac{\pi n z}{L} , \end{aligned}$$

(6)

$$\begin{aligned} \eta&= f(t)\frac{L - z}{L} + \sum_{n=1}^{\infty}\eta_{n}(t)\sin \frac{\pi n z}{L} , \end{aligned}$$

(7)

where $\xi_{\phi}$ is the azimuthal component of the plasma displacement and $\eta= \xi_{r\mathrm{i}}$. The coefficient functions $v_{n}(r,t)$ are defined by

$$ v_{n} = -\mathrm{i}\int_{-\infty}^{t} \mathcal{G}_{n}(t - \theta)g_{n}( \theta)\,\mathrm{d}\theta. $$

(8)

The functions $g_{n}(\theta)$ and $\mathcal{G}_{n}(t)$ are given by

$$\begin{aligned} g_{n}(t) &= \frac{2(\rho- \rho_{\mathrm{i}})}{\pi n\rho} \frac{\mathrm{d}^{2} f}{\mathrm{d}t^{2}} - \frac{\rho_{\mathrm {i}}}{\rho}\left( \frac{\mathrm{d}^{2}\eta_{n}}{\mathrm{d}t^{2}} + n^{2}\omega _{\mathrm{Ai}}^{2} \eta_{n}\right) , \end{aligned}$$

(9)

$$\begin{aligned} \mathcal{G}_{n}(t)& = \exp(-\Lambda n^{2} t^{3}/\text{Re}) \frac{\sin(n\omega_{A} t)}{n\omega_{A}} , \end{aligned}$$

(10)

where

$$ \Lambda= \frac{RV_{\mathrm{Ai}}}{6}\left( \frac{\mathrm{d}\omega_{A}}{\mathrm{d}r}\right)^{2} . $$

(11)

The Fourier coefficients in Equation 4 are defined by the equation and the boundary condition

$$ \frac{\partial(ru_{n})}{\partial r} + \mathrm{i}v_{n} = 0, \quad u_{n} = \eta_{n}\ \ \text{at}\ \ r = R(1 - \ell/2). $$

(12)

Finally, the Fourier coefficients in Equation 6 are defined by the equation

$$ \frac{1}{\rho}\frac{\partial P_{n}}{\partial r} = -\frac{2}{\pi n} \frac{\mathrm{d}^{2} f}{\mathrm{d}t^{2}} - \frac{\mathrm{d}^{2}\eta_{n}}{\mathrm{d}t^{2}} - n^{2}\omega _{A}^{2}\eta_{n} , $$

(13)

and the boundary condition

$$ P_{n} = -\rho_{\mathrm{i}} R\left(\frac{2}{\pi n} \frac{\mathrm{d}^{2} f}{\mathrm{d}t^{2}} + \frac{\mathrm{d}^{2}\eta_{n}}{\mathrm{d}t^{2}} + n^{2}\omega _{\mathrm{Ai}}^{2} \eta_{n} \right)\ \ \text{at}\ \ r = R(1 - \ell/2). $$

(14)

Now, following Article I, we introduce the Fourier transform defined by

$$ \hat{h}(\omega) = \int_{-\infty}^{\infty}h(t) \mathrm {e}^{-\mathrm{i} \omega t}{\mathrm{d}}t, \quad h(t) = \frac{1}{2\pi}\int_{-\infty }^{\infty }\hat{h}(\omega) \mathrm{e}^{\mathrm{i}\omega t}{\mathrm{d}}\omega. $$

(15)

We recall that the driving function [$f(t)$] is assumed to be a stationary random function, that is a function whose unconditional joint probability distribution does not change when shifted in time. In particular, parameters such as mean and variance do not change over time. Consequently $f(t)$ does not possess a Fourier transform. However, we can define its power spectrum [$\Pi_{f}(\omega)$] as (Champeney, 1973)

$$ \Pi_{f}(\omega) = \lim_{T \to\infty}\frac{1}{T}|\hat {f}_{T}(\omega)|^{2} , $$

(16)

where $\hat{f}_{T}(\omega)$ is the Fourier transform of the truncated function

$$ f_{T}(t) = \left\{ \textstyle\begin{array}{c@{\quad}c} f(t), & T_{1} < t < T + T_{1}, \\ 0, & \text{otherwise} . \end{array}\displaystyle \right. $$

(17)

For a stationary random function the limit in Equation 16 is independent of $T_{1}$. It is shown in Article I that the Fourier transforms of $f_{T}$ and $\eta_{Tn}$ are related by

$$ \hat{\eta}_{Tn}\big[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega) \big] = \frac{2\omega^{2}}{\pi n}\hat{f}_{T} , $$

(18)

where for $\omega> 0$ the function $K(\omega)$ is defined by

$$ K(\omega) = \frac{n^{6}\omega_{k}^{2}(\rho_{\mathrm{i}} - \rho_{\mathrm {e}})^{2}}{2R(\rho_{\mathrm{i}} + \rho_{\mathrm{e}})^{2}} \bigg( \frac{\pi{\mathrm{i}}\omega}{4n^{2}\Delta_{n}} + \mathcal{P}\int_{R(1- \ell/2)}^{R(1+\ell/2)} \frac{\omega_{\mathrm{A}}^{2}\,\mathrm{d}r}{\omega^{2} - n^{2}\omega^{2}_{\mathrm{A}}} \bigg) $$

(19)

for $\omega\in[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]$, and

$$ K(\omega) = \frac{n^{6}\omega_{k}^{2}(\rho_{\mathrm{i}} - \rho_{\mathrm {e}})^{2}}{2R(\rho_{\mathrm{i}} + \rho_{\mathrm{e}})^{2}}\int _{R(1-\ell/2)}^{R(1+ \ell/2)} \frac{\omega_{\mathrm{A}}^{2}\,\mathrm{d}r}{\omega^{2} - n^{2}\omega^{2}_{\mathrm{A}}} $$

(20)

for $\omega\notin[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]$, where $\mathcal{P}$ indicates the Cauchy principal part of the integral, and

$$ \omega_{k} = \frac{\pi C_{k}}{L}, \quad C_{k}^{2} = \frac{2B^{2}}{\mu_{0}(\rho_{\mathrm{i}} + \rho_{\mathrm{e}})}. $$

(21)

$$ \Delta_{n} = -n\frac{\mathrm{d}\omega_{A}}{\mathrm{d}r}\bigg|_{r = r_{n}( \omega)}, \quad n\omega_{A}(r_{n}) = \omega. $$

(22)

To define $K(\omega)$ for $\omega< 0$ we use $K(\omega) = K^{*}(-\omega)$, where the asterisk indicates the complex conjugate. We recall that $n = 1$ corresponds to the fundamental mode and $n > 1$ to the overtones. It is shown in Article I that Equations 19 and 20 are only valid when $\omega$ is not very close to $n\omega_{\mathrm{Ai}}$ or $n\omega_{\mathrm{Ae}}$, that is when $|\omega- n\omega_{\mathrm{Ai}}| \gg\omega_{k}(\epsilon\ell^{2} \text{Re})^{-1/3}$ and $|\omega- n\omega_{\mathrm{Ae}}| \gg\omega_{k}(\epsilon\ell^{2} \text{Re})^{-1/3}$. The power spectra of $\eta_{n}$ and $f$ are related by

$$ \Pi_{\eta_{n}}(\omega) = \lim_{T \to\infty}\frac{1}{T}|\hat {\eta}_{Tn}( \omega)|^{2} = |\Upsilon_{n}(\omega)|^{2} \Pi_{f}(\omega), $$

(23)

where

$$ \Upsilon_{n}(\omega) = \frac{2\omega^{2}}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]}. $$

(24)

Using Equations 8, 12, 14, and 23 we will calculate in the next section the power spectra of $u_{n}$, $v_{n}$, and $P_{n}$. Then we will calculate the power spectra of $\xi_{r}$, $\xi_{\phi}$, and $P$.

4 Calculation of Power Spectra

The truncated functions $v_{Tn}$ and $g_{Tn}$ are related by the same Equation 8, where $g_{Tn}(t)$ is given by Equation 9 with $f_{T}(t)$ and $\eta_{Tn}(t)$ substituted for $f(t)$ and $\eta_{n}(t)$, respectively. Applying the Fourier transform to this equation and recalling that $\mathcal{G}_{n}(t) = 0$ for $t < 0$ we obtain

$$ \hat{v}_{Tn}(\omega) = -\mathrm{i}\hat{\mathcal{G}}_{n}(\omega )\hat{g}_{Tn}( \omega), $$

(25)

where

$$\begin{aligned} -\mathrm{i}\hat{\mathcal{G}}_{n}(\omega) =& \frac{1}{2n\omega _{\mathrm{A}}} \left(\frac{\text{Re}}{3n^{2}\Lambda}\right)^{1/3}\bigg[F\bigg(- \left(\frac{\text{Re}}{3n^{2}\Lambda}\right)^{1/3}(\omega+ n \omega_{\mathrm{A}})\bigg) \\ -& F\bigg(-\left(\frac{\text{Re}}{3n^{2}\Lambda}\right)^{1/3} ( \omega- n\omega_{\mathrm{A}})\bigg)\bigg]. \end{aligned}$$

(26)

Here $F$ is the $F$-function first introduced by Goossens, Ruderman, and Hollweg (1995). It is defined by

$$ F(x) = \int_{0}^{\infty}\exp(\mathrm{i}\,x\theta- \theta^{3}/3)\,{ \mathrm{d}}\theta. $$

(27)

Using integration by parts we obtain

$$ F(x) = \frac{\mathrm{i}}{x} + \mathcal{O}\big(x^{-4}\big) \quad \text{for}\ |x| \gg1. $$

(28)

In Appendix A the expression for $\hat{g}_{Tn}(\omega)$ in terms of $f_{T}(\omega)$ and $\eta_{Tn}(\omega)$ is obtained. Using Equations 18 and 72 we obtain

$$ \hat{g}_{Tn}(\omega) = \frac{2\omega^{2}}{\pi n\rho}\left(\rho- \rho_{\mathrm{i}} + \frac{\rho_{\mathrm{i}}(\omega^{2} - n^{2}\omega_{\mathrm {Ai}}^{2})}{n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)}\right )\hat{f}_{T}( \omega) . $$

(29)

Substituting this expression in Equation 25 yields

$$ \hat{v}_{Tn}(r,\omega) = U_{n}(r,\omega)\hat{f}_{T}(\omega), $$

(30)

where

$$ U_{n}(r,\omega) = - \frac{2{\mathrm{i}}\omega^{2}\hat{\mathcal{G}}_{n}(\omega)}{\pi n\rho}\left(\rho- \rho_{\mathrm{i}} + \frac{\rho_{\mathrm{i}}(\omega^{2} - n^{2}\omega_{\mathrm {Ai}}^{2})}{n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)}\right) . $$

(31)

Now the power spectrum of $v_{n}(t)$ is

$$ \Pi_{v_{n}}(r,\omega) = \lim_{T \to\infty}\frac{1}{T}|\hat{v}_{n}(r, \omega)|^{2} = |U_{n}(r,\omega)|^{2} \Pi_{f}(\omega) . $$

(32)

It follows from Equation 12 with $u_{Tn}$, $v_{Tn}$, and $\eta_{Tn}$ substituted for $u_{n}$, $v_{n}$, and $\eta_{n}$, respectively, that

$$ u_{Tn} = \eta_{Tn} - \frac{\mathrm{i}}{R}\int_{R(1-\ell/2)}^{r} v_{Tn}(x) \,\mathrm{d}x , $$

(33)

where we took $r \approx R$ in the transitional layer. Applying the Fourier transform to this equation and using Equation 12, we obtain

$$ \hat{u}_{Tn}(r,\omega) = W_{n}(r,\omega)\hat{f}_{T}(\omega), $$

(34)

where

$$ W_{n}(r,\omega) = \frac{2\omega^{2}}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]} - \frac{\mathrm{i}}{R}\int_{R(1-\ell/2)}^{r} U_{n}(x,\omega)\, \mathrm{d}x . $$

(35)

Then the power spectrum of $u_{n}(t)$ is given by

$$ \Pi_{u_{n}}(r,\omega) = \lim_{T \to\infty}\frac{1}{T}|\hat{u}_{n}(r, \omega)|^{2} = |W_{n}(r,\omega)|^{2} \Pi_{f}(\omega) . $$

(36)

Applying the Fourier transform to Equations 13 and 14 with $f_{T}$ and $\eta_{Tn}$ substituted for $f$ and $\eta_{n}$, respectively, and using Equation 18 yields

$$\begin{aligned} \frac{\partial\hat{P}_{Tn}}{\partial r}& = \frac{2\rho\omega^{2}[n^{2}(\omega_{k}^{2} - \omega_{\mathrm {A}}^{2}) + K(\omega)]}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]} \hat{f}_{T}(\omega) , \end{aligned}$$

(37)

$$\begin{aligned} \hat{P}_{Tn} &= \frac{2\rho_{\mathrm{i}}\omega^{2} R[n^{2}(\omega_{k}^{2} - \omega _{\mathrm{Ai}}^{2}) + K(\omega)]}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]} \hat{f}_{T}(\omega)\quad\text{at}\quad r = R(1 - \ell/2). \end{aligned}$$

(38)

It follows from these equations that

$$ \Pi_{P_{n}}(\omega) = \lim_{T \to\infty}\frac{1}{T}|\hat{P}_{Tn}( \omega)|^{2} = |S_{n}(\omega)|^{2} \Pi_{f}(\omega) , $$

(39)

where

$$ S_{n}(\omega) = \frac{2\rho_{\mathrm{i}}R\omega^{2}[n^{2}(\omega_{k}^{2} - \omega _{\mathrm{Ai}}^{2}) + K(\omega)]}{\pi n[n^{2}\omega_{k}^{2} - \omega ^{2} + K(\omega)]} . $$

(40)

When deriving the expression for $S_{n}(\omega)$ we neglected the terms of the order of $\ell$ in the numerator. We note that $S_{n}(\omega)$ is independent of $r$, which implies that $\Pi_{P_{n}}(\omega)$ is also independent of $r$.

Below we also consider the average values of $|\xi_{r}|^{2}$, $|\xi_{\phi}|^{2}$, and $|P|^{2}$ defined by

$$\begin{aligned} \overline{|\xi_{r}|^{2}}& = \frac{1}{L}\int_{0}^{L} |\xi_{r}|^{2}\,{ \mathrm{d}}z = \frac{1}{2}\sum_{n=1}^{\infty}|u_{n}(t)|^{2} + \frac {1}{3}|f(t)|^{2} + \sum_{n=1}^{\infty}\frac{2}{\pi n}\Re[f^{*}(t)u_{n}(t)] , \end{aligned}$$

(41)

$$\begin{aligned} \overline{|\xi_{\phi}|^{2}} &= \frac{1}{L}\int_{0}^{L} |\xi_{\phi }|^{2}\,{ \mathrm{d}}z = \frac{1}{2}\sum_{n=1}^{\infty}|v_{n}(t)|^{2} + \frac {1}{3}|f(t)|^{2} + \sum_{n=1}^{\infty}\frac{2}{\pi n}\Im[f^{*}(t)v_{n}(t)], \end{aligned}$$

(42)

$$\begin{aligned} \overline{|P|^{2}} &= \frac{1}{L}\int_{0}^{L} |P|^{2}\,\mathrm{d}z = \frac{1}{2} \sum_{n=1}^{\infty}|P_{n}(t)|^{2} , \end{aligned}$$

(43)

where $\Re$ and $\Im$ indicate the real and imaginary parts of a quantity, respectively. Now we introduce the mean value of product of two stationary random functions $f(t)$ and $g(t)$ as

$$ \langle f(t)g(t) \rangle= \lim_{T \to\infty}\frac{1}{T} \int _{-\infty}^{\infty}f_{T}(t)g_{T}(t)\,\mathrm{d}t . $$

(44)

Then we use the relation (Champeney, 1973)

$$ \langle f^{*}(t)g(t) \rangle= \frac{1}{2\pi}\lim_{T \to\infty} \frac{1}{T}\int_{-\infty}^{\infty}\hat{f}_{T}^{*}(\omega)\hat{g}_{T}( \omega)\,\mathrm{d}\omega. $$

(45)

It follows from this relation and Equation 16 that

$$ \langle|f(t)|^{2} \rangle= \frac{1}{2\pi}\int_{-\infty}^{\infty }\Pi_{f}( \omega)\,\mathrm{d}\omega. $$

(46)

It follows from Equations 16, 32, 36, and 39, that

$$\begin{aligned} \langle\overline{|\xi_{r}|^{2}} \rangle&= \frac{1}{2\pi}\int_{- \infty}^{\infty}\bigg(\frac{1}{2} \sum_{n=1}^{\infty}\Pi _{u_{n}}(\omega) + \frac{1}{3}\Pi_{f}(\omega) + \sum_{n=1}^{\infty}\frac{2}{\pi n}\Re[\Pi_{f^{*} u_{n}}(\omega)]\bigg)\mathrm{d}\omega, \end{aligned}$$

(47)

$$\begin{aligned} \langle\overline{|\xi_{\phi}|^{2}} \rangle&= \frac{1}{2\pi}\int_{- \infty}^{\infty}\bigg(\frac{1}{2} \sum_{n=1}^{\infty}\Pi _{v_{n}}(\omega) + \frac{1}{3}\Pi_{f}(\omega) + \sum_{n=1}^{\infty}\frac{2}{\pi n}\Re[\Pi_{f^{*} v_{n}}(\omega)]\bigg)\mathrm{d}\omega, \end{aligned}$$

(48)

$$\begin{aligned} \langle\overline{|P|^{2}} \rangle&= \frac{1}{4\pi}\int_{-\infty }^{\infty}\sum_{n=1}^{\infty}\Pi_{P_{n}}(\omega)\,\mathrm {d}\omega, \end{aligned}$$

(49)

where

$$ \Pi_{f^{*} g} = \lim_{T \to\infty}\frac{1}{T} \big[\hat{f}^{*}_{T}( \omega)\hat{g}_{T}(\omega)\big]. $$

(50)

The quantity $\sqrt{\langle|f(t)|^{2} \rangle}$ can be considered as a measure of amplitude of the random function $f(t)$.

5 Properties of Plasma Motion in Transitional Layer

In this section we use the results obtained in the previous section to investigate the properties of plasma motion in the transitional layer. In accordance with the results obtained in Appendix B (see Equation 100) $\int_{-\infty}^{\infty}\Pi_{v_{n}}(\omega)\,\mathrm{d}\omega$ is of the order of $\text{Re}^{1/3}$. On the other hand, $\Pi_{f}(\omega)$ is independent of Re, which implies that $\int_{-\infty}^{\infty}\Pi_{f}(\omega)\,\mathrm{d}\omega$ is of the order of unity. Since

$$ |f^{*} v_{n}| = \sqrt{|f|^{2}|v_{n}|^{2}}, $$

(51)

it follows from Equation 50 that

$$ |\Pi_{fv^{*}_{n}}(\omega)| = \sqrt{\Pi_{f}(\omega)\Pi_{v_{n}}( \omega)}, $$

(52)

where we assumed that $\Pi_{f}(\omega)$ is an even function. It follows from this equation that $\Pi_{fv^{*}_{n}}(\omega)$ is of the order of $\text{Re}^{1/6}$. Then we conclude that the contributions of the second and third terms in the integrand in Equation 48 are negligible in comparison with the contribution of the first term. Then we have the approximate expression

$$ \langle\overline{|\xi_{\phi}|^{2}} \rangle= \frac{1}{4\pi}\sum _{n=1}^{\infty}\int_{-\infty}^{\infty}\Pi_{v_{n}}(\omega)\, \mathrm{d}\omega. $$

(53)

It follows from Equations 19 and 20 that $K(-\omega) = K^{*}(\omega)$. Then, assuming that $\Pi_{f}(\omega)$ is an even function, we obtain from Equation 78 that $M_{n}(r,-\omega) = M_{n}^{*}(r,\omega)$. Using this result and Equations 76, 78, and 100 from Appendix B, we obtain from Equation 53 in the leading-order approximation with respect to Re

$$ \langle\overline{|\xi_{\phi}|^{2}} \rangle= 3.21 \frac{\omega_{\mathrm{A}}^{2}}{\pi^{3}\rho^{2}}\left(\frac{\text{Re}}{3\Lambda}\right)^{1/3} \sum_{n=1}^{\infty}\frac{\Pi_{f}(n\omega_{\mathrm {A}})}{n^{2/3}}\left| \rho- \rho_{\mathrm{i}} + \frac{\rho_{\mathrm{i}}n^{2}(\omega_{\mathrm{A}}^{2} - \omega _{\mathrm{Ai}}^{2})}{n^{2}(\omega_{k}^{2} - \omega_{\mathrm {A}}^{2}) + K(n\omega_{\mathrm{A}})} \right|^{2} \!\!. $$

(54)

When the density gradient remains of the same order in the whole transitional region, the same is true for $\Lambda$ (see Equation 11). This is the case when, for example, the density profile in the transitional layer is linear. However, when the density gradient is zero at the boundaries of the transitional layer as, for example, in the case of sinusoidal density profile, then $\Lambda\to0$ as $r \to R(1 \pm{\mathrm{l}}/2)$ and Equation 54 is not valid. The easiest way to alleviate this problem is just to slightly reduce the thickness of the transitional layer and include a small part of this layer near its inner boundary in the core region, and that near its outer boundary in the external region. It is possible because in the case when the density gradient is zero near the boundaries of the transitional layer, the density near this boundary is practically constant.

It seems that Equation 54 implies that $\langle\overline{|\xi_{\phi}|^{2}} \rangle= 0$ at $r = R(1-\ell/2)$. However, this is not the case. Since Equation 54 only gives the expression for $\langle\overline{|\xi_{\phi}|^{2}} \rangle$ in the leading-order approximation with respect to Re, the correct statement is that $\langle\overline{|\xi_{\phi}|^{2}} \rangle\text{Re}^{-1/3} \to 0$ as $\text{Re} \to\infty$.

It is shown in Appendix C that $\int_{R(1-\ell /2)}^{r} U_{n}(x,\omega)\,\mathrm{d}x = \mathcal{O}( \ell)$. This implies that $W_{n}(r,\omega)$ is given by the first term on the right-hand side of Equation 35 in the leading-order approximation with respect to $\ell$. Then using Equation 34 and 35 we obtain

$$ \hat{u}_{Tn}(\omega) = \frac{2\omega^{2}\hat{f}_{T}(\omega)}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]}. $$

(55)

Now, it follows from Equation 50 that

$$ \Pi_{f^{*} u_{n}}(\omega) = \frac{2\omega^{2}\Pi_{f}(\omega)}{\pi n[n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)]}. $$

(56)

It follows from Equations 19 and 20 that $K(\omega) = \mathcal{O}(\ell)$. Then, using Equations 56, we obtain the approximate expression

$$ \Re[\Pi_{f^{*} u_{n}}(\omega)] = \frac{2\omega^{2}(n^{2}\omega_{k}^{2} - \omega^{2}) \Pi_{f}(\omega)}{\pi n|n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)|^{2}}. $$

(57)

Substituting Equation 57 and Equation 36 with $W_{n}(r,\omega)$ given by Equation 35 with the second term on the right-hand side neglected in Equation 47 yields

$$ \langle\overline{|\xi_{r}|^{2}} \rangle= \frac{1}{2\pi}\int_{- \infty}^{\infty}\bigg( \frac{2\omega^{2}}{\pi^{2}}\sum _{n=1}^{\infty }\frac{2n^{2}\omega_{k}^{2} - \omega^{2}}{n^{2}|n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)|^{2}} + \frac{1}{3}\bigg) \Pi_{f}(\omega)\,\mathrm{d}\omega. $$

(58)

Equation 58 gives the square of the amplitude of radial plasma displacement. We see that this amplitude is independent of $r$ in the leading-order approximation with respect to $\ell$. This result agrees very well with the fact that the variation of the plasma radial displacement across the transitional layer is of the order of $\ell$.

Finally we proceed to calculating $\langle\overline{|P|^{2}} \rangle$. Using Equations 39, 40, and 49 we obtain

$$ \langle\overline{|P|^{2}} \rangle= \frac{\rho_{\mathrm{i}}^{2} R^{2}}{\pi^{3}}\sum_{n=1}^{\infty }\frac{1}{n^{2}}\int_{-\infty}^{\infty }\frac{\omega^{4}|n^{2}(\omega_{k}^{2} - \omega_{\mathrm{Ai}}^{2}) + K(\omega)|^{2}}{|n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)|^{2}} \Pi_{f}(\omega)\, \mathrm{d}\omega. $$

(59)

Let us compare the behaviour of the plasma displacement and magnetic-pressure perturbation in the transitional layer described in this article with the behaviour of these quantities in the case of harmonic driving. First we consider the plasma radial displacement and the magnetic-pressure perturbation. We see that in the case of stochastic driving the amplitudes of both quantities are of the order of unity with respect to the large parameter Re (however, recall that the amplitude of the magnetic-pressure perturbation is also of the order of $\epsilon^{2}$). The behaviour of the magnetic-pressure amplitude is the same in the case of harmonic driving. The behaviour of the amplitude of the radial plasma displacement in the case of harmonic driving is slightly different. It is of the order of $\ln\text{Re}$ in the vicinity of the resonant surface where the driver frequency coincides with the local Alfvén frequency. We see that, since in the case of stochastic driving each magnetic surface is in resonance with the corresponding component of the driver spectrum, this increased amplitude is smeared out over the whole transitional layer. As a result, it becomes of the order of unity everywhere.

The most interesting is the behaviour of the azimuthal plasma displacement. In the case of harmonic driving, the amplitude of the azimuthal plasma displacement is strongly enhanced in the dissipative layer with the thickness of the order of $\text{Re}^{-1/3}$ that embraces the resonant surface. It is of the order of $\text{Re}^{1/3}$ in this layer. Far from the resonant layer it is of order of unity. Again, in the case of stochastic driving it is smeared out over the whole transitional layer and becomes of order $\text{Re}^{1/6}$ everywhere. This behaviour is similar to that found by Ruderman (1999) who studied driven standing torsional waves in an inhomogeneous magnetic tube. However, there is also some difference. In the case of torsional waves the dependence of the oscillation amplitude on $r$ is defined by the radial dependence of the density and, possibly, the driver amplitude. The characteristic scale of the amplitude variation is the same as that of the density variation. In the case of stochastically driven kink oscillations there is one special magnetic surface $r = r_{k}$ where the local Alfvén frequency coincides with the kink frequency $\omega_{k}$. We consider the vicinity of this surface defined by the inequality $|r - r_{k}| \lesssim\ell^{2} R$. Below we call this vicinity the resonant layer. In this layer we have $|\omega_{k}^{2} - \omega_{\mathrm{A}}(r)| \lesssim\ell\omega_{k}^{2}$. Since in accordance with Equations 19, 20, and 22$K(\omega) \sim\ell\omega_{k}^{2}$ it follows that the term is the square brackets in Equation 54 is of the order of $\ell^{-2}$. This implies that the amplitude of the azimuthal plasma displacement is of the order of $\ell^{-1}\text{Re}^{1/6}$ in the resonant layer, while it is of the order of $\text{Re}^{1/6}$ outside of this layer.

6 Linear Density Profile

In this section we consider a particular case where the density profile in the transitional layer is linear. Hence, the density in the transitional layer is given by

$$ \rho_{\mathrm{t}}(r) = \frac{\rho_{\mathrm{i}}}{2\ell\zeta R}[\ell R(\zeta+ 1) - 2(r - R)(\zeta- 1)] , $$

(60)

where $\zeta= \rho_{\mathrm{i}}/\rho_{\mathrm{e}}$. Similar to Afanasyev, Van Doorsselaere, and Nakariakov (2020) and Article I we assume that $\Pi_{f}(\omega)$ is proportional to $|\omega|^{-5/3}$ for not very small $|\omega|$. We also make a viable assumption that $\Pi_{f}(\omega)$ monotonically decreases to zero as $|\omega|$ decreases from $\kappa\omega_{0}$ to zero, where $\omega_{0}/\omega_{k}$ is of order unity and $\kappa< 1$. Hence, we put

$$ \Pi_{f}(\omega) = d^{2}\left\{ \textstyle\begin{array}{c@{\quad}c} \kappa^{-8/3} |\omega|/\omega_{0}, & |\omega| \leq\kappa\omega_{0}, \\ (\omega_{0}/|\omega|)^{5/3}, & |\omega| \geq\kappa\omega_{0}, \end{array}\displaystyle \right. $$

(61)

where $d^{2}$ is a quantity with the dimension of time times length squared. Then we obtain

$$ \langle|f(t)|^{2} \rangle= \frac{1}{\pi}\int_{0}^{\infty}\Pi_{f}( \omega)\,\mathrm{d}\omega= \frac{2}{\pi}\, d^{2}\omega_{0}\kappa ^{-2/3} . $$

(62)

Introducing the amplitude of the driver $A = \sqrt{\langle|f(t)|^{2} \rangle}$ we obtain

$$ d = A\kappa^{1/3}\sqrt{\frac{\pi}{2\omega_{0}}}. $$

(63)

Using Equations 11, 21, and 60 yields

$$ \omega_{\mathrm{A}}^{2} = \frac{\ell R\omega_{k}^{2}(\zeta+ 1)}{\ell R(\zeta+ 1) - 2(r - R)(\zeta- 1)} $$

(64)

and

$$ \Lambda= \frac{\ell R^{2}\omega_{k}^{3}(\zeta+ 1)^{3/2}(\zeta- 1)^{2}}{6\pi \sqrt{2\zeta}[\ell R(\zeta+ 1) - 2(r - R)(\zeta- 1)]^{3}} . $$

(65)

Using Equations 22 and 64 we obtain for $\omega> 0$ and $\omega\in[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]$

$$ r_{n} = R + \frac{\ell R(\zeta+ 1)(\omega^{2} - n^{2}\omega_{k}^{2})}{2\omega ^{2}(\zeta- 1)}, \quad\Delta_{n} = - \frac{\omega^{3}(\zeta- 1)}{\ell R(\zeta+ 1)n^{2}\omega_{k}^{2}}. $$

(66)

Then using these results yields

$$ K(\omega) = \frac{n^{6}\omega_{k}^{4}(\zeta- 1)}{4\omega^{2}(\zeta+ 1)} \left\{ \textstyle\begin{array}{c@{\quad}c} \ell^{2} + \mathcal{O}(\ell^{3}), & \omega\notin[n\omega_{\mathrm{Ai}},n \omega_{\mathrm{Ae}}], \\ \displaystyle-\frac{\pi i\ell}{2} + \ell^{2} + \mathcal{O}(\ell^{3}), & \omega\in[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}] . \end{array}\displaystyle \right. $$

(67)

We note that this expression is only valid when $|\omega- n\omega_{\mathrm{Ai}}| \gtrsim\ell$ and $|\omega- n\omega_{\mathrm{Ae}}| \gtrsim\ell$. The term $K(\omega)$ in the expression for $\langle\overline{|\xi_{\phi}|^{2}} \rangle$ given by Equation 54 is only important for $|n^{2}\omega_{k}^{2} - \omega^{2}| \lesssim\ell\omega_{k}^{2}$. This implies that in the leading-order approximation with respect to $\ell$ we can use the expression for $K(\omega)$ valid for $\omega\in[n\omega_{\mathrm{Ai}},n\omega_{\mathrm{Ae}}]$ even when $\omega$ is out of this interval. Below we take $\kappa\ll1$. Since the integrand in Equation 58 is very small for $\omega\ll\omega_{k}$ we can use the expression for $\Pi_{f}(\omega)$ valid for $\omega\geq\kappa\omega_{0}$ in the whole interval $\omega\in[0,\infty]$ when calculating the integral in the expression for $\langle\overline{|\xi_{r}|^{2}} \rangle$. We will see that $\langle\overline{|\xi_{r}|^{2}} \rangle$ is proportional to $\ell^{-1}$. Then we can neglect the term 1/3 in the curly bracket in Equation 58 and obtain the approximate expression

$$\begin{aligned} \langle\overline{|\xi_{r}|^{2}} \rangle \approx& \frac{128 d^{2}\omega_{0}^{5/3}(\zeta+1)^{2}}{\pi^{3}} \\ \times& \sum_{n=1}^{\infty}\frac{1}{n^{2}}\int_{0}^{\infty }\frac{\omega^{13/3} (2n^{2}\omega_{k}^{2} - \omega^{2})\,\mathrm{d}\omega}{64\omega ^{4}(\zeta+1)^{2} (n^{2}\omega_{k}^{2} - \omega^{2})^{2} + \pi^{2}\ell^{2} n^{12}\omega_{k}^{8}(\zeta-1)^{2}}. \hphantom{xx} \end{aligned}$$

(68)

The integral on the right-hand side of this equation is evaluated in Appendix D. Using Equations 63 and 129 we reduce Equation 68 to

$$\begin{aligned} \langle\overline{|\xi_{r}|^{2}} \rangle =& \frac{8A^{2}\kappa^{2/3}(\zeta+1)[1 + \mathcal{O}(\ell^{1/2})]}{\pi^{2}\ell(\zeta-1)}\left( \frac{\omega_{0}}{\omega_{k}}\right)^{2/3} \sum_{n=1}^{\infty }\frac{1}{n^{14/3}} \\ \approx& 0.85\frac{A^{2}\kappa^{2/3}(\zeta+1)}{\ell(\zeta-1)} \left(\frac{\omega_{0}}{\omega_{k}}\right)^{2/3} . \end{aligned}$$

(69)

The typical amplitude of the decayless oscillations of coronal loops is 0.2 Mm. We emphasise that this is the amplitude of a coronal-loop oscillation as a whole. The amplitude of radial motion in the transitional layer is approximately the same. However, the amplitude of the azimuthal motion in the transitional layer is $\text{Re}^{1/6}$ larger. This large-amplitude azimuthal motion cannot be observed directly because magnetic surfaces oscillate with random phases and, as a result, signals from various magnetic surfaces cancel each other. Since $\langle\overline{|\xi_{r}|^{2}} \rangle$ is independent of $r$ this amplitude is equal to $\langle\overline{|\xi_{r}|^{2}} \rangle^{1/2}$. We take $\zeta= 3$ as the typical density ratio and $\omega_{0} = \omega_{k}$. We also choose such a value of $\kappa$ that $\kappa\omega_{0} = \frac{1}{2}\omega_{\mathrm {Ai}}$, which gives $\kappa= 1/\sqrt{6}$. Then we obtain $\langle\overline{|\xi_{r}|^{2}} \rangle^{1/2} \approx0.7A\ell^{-1/2}$. If, in addition, we take $\ell= 0.25$ as a typical value, then we obtain $A = 0.13$ Mm.

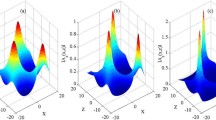
We used Equations 54, 60, and 61 to calculate numerically the dependence of the amplitude of azimuthal plasma displacement on the dimensionless radial variable

$$ x = \frac{2(r - R)}{\ell R}. $$

(70)

Figure 1 displays the dependence of the quantity

$$ D_{\phi}= \sqrt{ \frac{\langle\overline{|\xi_{\phi}|^{2}} \rangle}{\langle \overline{|\xi_{\phi}|^{2}} \rangle_{\mathrm{e}}}} $$

(71)

for $\zeta= 3$ and $\ell= 0.1,\,0.2$, and 0.3. Here the subscript “e” indicates that a quantity is calculate at the external boundary of the transitional layer. It is worth noting that $D_{\phi}$ is independent of $\kappa$ and $\omega_{0}$. The only condition that we imposed when calculating $D_{\phi}$ is that $\kappa\omega_{0} < \omega_{\mathrm{Ai}}$. We can see in Figure 1 that the graph of $D_{\phi}(x)$ has a peak at $x = 0$ corresponding to the spatial position where $\omega_{\mathrm{A}}(x) = \omega_{k}$. The height of this peak increases when $\ell$ decreases. This behaviour is in complete agreement with the qualitative analysis presented in the previous section.

Figure 1

Dependence of $D_{\phi}$ on $x$ for $\zeta= 3$. The solid, dashed, and dash–dotted curves correspond to $\ell= 0.1,\,0.2$, and 0.3, respectively.

7 Summary and Conclusion

In this article we studied the plasma motion in a transitional layer of a magnetic loop stochastically driven in the transverse direction at the footpoint. We used the zero-$\beta$ approximation and the TTTB approximation. We assumed that the driving at the footpoint is described by a stationary random function. We used the results previously obtained by Ruderman and Petrukhin (2021). The plasma displacement and the magnetic-pressure perturbation are also described by stationary random functions. We calculated the mean values of squares of stationary random functions describing the radial and azimuthal plasma displacements as well as the magnetic-pressure perturbation. These mean values can be considered as the squares of amplitudes of the corresponding quantities. The main results obtained in the article can be summarised as follows:

• i) The amplitude of the magnetic-pressure perturbation does not change across the transitional layer. It is of the order of the driver amplitude times the ratio of the loop radius and the loop length squared.

• ii) The amplitude of the plasma radial displacement also does not vary across the transitional layer. It is of the same order as the driver amplitude.

• iii) The amplitude of the plasma azimuthal displacement does vary across the transitional layer. It is of the order of the driver amplitude times $\text{Re}^{1/6}$, where Re is the Reynolds number. It also has a peak at the point $r_{k}$ defined by the equation $\omega_{\mathrm{A}}(r_{k}) = \omega_{k}$, where $\omega_{k}$ is the kink frequency. The ratio of the amplitude at $r = r_{k}$ to its value far from $r_{k}$ is of the order of $\ell^{-1}$, where $\ell$ is the ratio of the thickness of the transitional layer to the loop radius.

Since the ratio of the amplitude of the plasma azimuthal displacement to the driver amplitude is of the order of $\text{Re}^{1/6}$, and the typical value of Re in coronal loops is $10^{12}$, we can expect very high plasma azimuthal displacement, of the order of 10 Mm. This can result in the development of the Kelvin–Helmholtz instability in the transitional layer. We emphasise that this is the displacement in the azimuthal direction. The amplitude of the plasma displacement varies along the loop. It is zero at one footpoint and equal to the driver amplitude at the other footpoint, which is quite small. It takes its maximum value somewhere in the middle of the loop. If we take the loop cross-section radius equal to 2 Mm then the azimuthal displacement equal to 10 Mm corresponds to about one full turn of the cross-section along the loop. The ratio of the velocity to the displacement is about the ratio of the loop radius to the loop length. If we take this ratio equal to $10^{-2}$ then we obtain that the velocity amplitude is 100 km s⁻¹, which is much smaller than the typical Alfvén speed of 1000 km s⁻¹.

It is worth briefly discussing the main assumptions made in our analysis. We assumed that the driver is described by a stationary random function. Obviously this is an idealisation. In reality the mean driver amplitude and energy spectrum vary with time. However, the decayless kink oscillations of coronal loops are only observed for a few tens of periods at best. If the driver parameters do not change during this time interval then the driver is approximately described by a stationary random function. In Section 6 it is described by the power law with the index equal to 5/3. Kolotkov, Anfinogentov, and Nakariakov (2016) used the empirical mode decomposition technique to analyse the spectral distributions of solar signals of various types. They found that, in general, the spectral distribution is not described by a single power law. Rather it is a composite of two or more power laws. Hence, the assumption made in Section 6 is also an idealisation. However, qualitatively, the analysis will remain the same even if we consider a more complex spectral distribution.

Appendices

Appendix A: Calculation of $\hat{g}_{Tn}(\omega)$

In this appendix we calculate $\hat{g}_{Tn}(\omega)$, where $g_{T}(t)$ is given by Equation 9 with $f_{T}(t)$ and $\eta_{Tn}(t)$ substituted for $f(t)$ and $\eta_{n}(t)$, respectively. Differentiating $f_{T}(t)$ we obtain

$$ \frac{\mathrm{d}f_{T}}{\mathrm{d}t} = f(T_{1})\delta(t - T_{1}) - f(T + T_{1}) \delta(t - T - T_{1}) + \left(\frac{\mathrm{d}f}{\mathrm {d}t}\right)_{T} , $$

(72)

where $\displaystyle\left(\frac{\mathrm{d}f}{\mathrm{d}t}\right )_{T}$ is defined by Equation 17 with $\displaystyle\frac{\mathrm{d}f}{\mathrm{d}t}$ substituted for $f(t)$ and $\delta(t)$ is the $\delta$-function. Using this result and integration by parts yields

$$\begin{aligned} \int_{-\infty}^{\infty}\frac{\mathrm{d}f_{T}}{\mathrm {d}t}{\mathrm{e}}^{-{ \mathrm{i}}\omega t}{\mathrm{d}}t &= f(T_{1})\mathrm{e}^{-\mathrm{i}\omega T_{1}} - f(T + T_{1})\mathrm{e}^{-\mathrm{i}\omega(T + T_{1})} \\ & \hphantom{x} +\, \int_{-\infty}^{\infty}\left(\frac{\mathrm{d}f}{\mathrm {d}t}\right)_{T} {\mathrm{e}}^{-\mathrm{i}\omega t}{\mathrm{d}}t = f(T_{1})\mathrm {e}^{-\mathrm{i}\omega T_{1}} - f(T + T_{1})\mathrm{e}^{-\mathrm{i}\omega(T + T_{1})} \\ & \hphantom{x} -\, f(T_{1})\mathrm{e}^{-\mathrm{i}\omega T_{1}} + f(T + T_{1}) \mathrm{e}^{-{ \mathrm{i}}\omega(T + T_{1})} + \mathrm{i}\omega\hat{f}_{T}(\omega ) = \mathrm{i} \omega\hat{f}_{T}(\omega) . \end{aligned}$$

(73)

Using this relation twice, we further obtain

$$ \int_{-\infty}^{\infty}\frac{\mathrm{d}^{2} f_{T}}{\mathrm {d}t^{2}}{\mathrm{e}}^{-{ \mathrm{i}}\omega t}{\mathrm{d}}t = -\omega^{2}\hat{f}_{T}(\omega). $$

(74)

With the aid of this result we arrive at

$$ \hat{g}_{Tn}(\omega) = \frac{2\omega^{2}(\rho- \rho_{\mathrm{i}})}{\pi n\rho}\hat{f}_{T}( \omega) + \frac{\rho_{\mathrm{i}}}{\rho}(\omega^{2} - n^{2}\omega _{\mathrm{Ai}}^{2}) \hat{\eta}_{Tn} . $$

(75)

Appendix B: Calculation of $\int_{-\infty}^{\infty}\Pi _{v_{n}}(\omega)\,\mathrm{d}\omega$

In this appendix we calculate the asymptotic expression for $\int_{-\infty}^{\infty}\Pi_{v_{n}}(\omega)\,\mathrm{d}\omega$ valid for $\text{Re} \gg1$. We introduce the small parameter

$$ \varepsilon= \frac{1}{\omega_{k}}\left( \frac{3n^{2}\Lambda}{\text{Re}}\right)^{1/3}. $$

(76)

Note that $\varepsilon$ depends on $r$ through the variation of $\Lambda$. Using Equations 26 and 31 we rewrite Equation 32 as

$$ \Pi_{v_{n}}(r,\omega) = \varepsilon^{-2}\Big|F\Big(- \frac{\omega+ n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big) - F\Big(- \frac{\omega- n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big)\Big|^{2} M_{n}(r,\omega) , $$

(77)

where

$$ M_{n}(r,\omega) = \frac{\omega^{4}}{\pi^{2} n^{4}\rho^{2}\omega_{\mathrm {A}}^{2}\omega_{k}^{2}} \left|\rho- \rho_{\mathrm{i}} + \frac{\rho_{i}(\omega^{2} - n^{2}\omega_{\mathrm {Ai}}^{2})}{n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)}\right |^{2} \Pi_{f}( \omega) . $$

(78)

Then we obtain

$$ \int_{-\infty}^{\infty}\Pi_{v_{n}}(r,\omega)\,\mathrm{d}\omega= I_{1}(r) - 2I_{2}(r) + I_{3}(r), $$

(79)

where

$$\begin{aligned} I_{1}(r) &= \varepsilon^{-2}\int_{-\infty}^{\infty}\Big|F\Big(- \frac{\omega+ n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big)\Big|^{2} M_{n}(r,\omega)\,\mathrm{d} \omega, \end{aligned}$$

(80)

$$\begin{aligned} I_{2}(r) &= \varepsilon^{-2}\Re\int_{-\infty}^{\infty}F\Big(- \frac{\omega+ n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big) F\Big( \frac{\omega- n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big) M_{n}(r,\omega)\,\mathrm{d}\omega, \end{aligned}$$

(81)

$$\begin{aligned} I_{3}(r)& = \varepsilon^{-2}\int_{-\infty}^{\infty}\Big|F\Big(- \frac{\omega- n\omega_{\mathrm{A}}}{\varepsilon\omega_{k}}\Big)\Big|^{2} M_{n}(r,\omega)\,\mathrm{d} \omega. \end{aligned}$$

(82)

Here we make a comment about the convergence of the integrals in Equations 80 – 82. It follows from Equation 28 that the first multiplier in Equation 77 decays at least as $\omega^{-4}$ as $\omega\to\infty$. It follows from this estimate and Equation 78 that $\Pi_{v_{n}}(r,\omega)$ decays as fast as $\Pi_{f}(\omega)$ as $\omega\to\infty$. Usually it is assumed that $\Pi_{f}(\omega)$ decays at least as $\omega^{-\alpha}$ with $\alpha> 1$ as $\omega\to\infty$. For example, $\alpha= 5/3$ was taken in Article I. This implies that the integral in Equation 79 is convergent. Consequently we can approximate this integral taking $\Pi_{f}(\omega) = 0$ for sufficiently large $|\omega|$. Then we do not have to care about the convergence of integrals in Equations 80 – 82.

Making the variable substitution $\omega= -\varepsilon x\omega_{k} - n\omega_{\mathrm{A}}$ we transform Equation 80 to

$$ I_{1}(r) = \varepsilon^{-1}\omega_{k}[I_{11}(r) + I_{12}(r)] , $$

(83)

where

$$\begin{aligned} I_{11}(r) &= \int_{-\varepsilon^{-1/2}}^{\varepsilon^{-1/2}} |F(x)|^{2} M_{n}(r,-n\omega_{\mathrm{A}} - \varepsilon x\omega_{k})\,\mathrm{d}x, \end{aligned}$$

(84)

$$\begin{aligned} I_{12}(r) &= \bigg(\int_{-\infty}^{-\varepsilon^{-1/2}} + \int_{ \varepsilon^{-1/2}}^{\infty}\bigg) |F(x)|^{2} M_{n}(r,-n\omega _{\mathrm{A}} - \varepsilon x\omega_{k})\,\mathrm{d}x . \end{aligned}$$

(85)

Using Equation 28 we transform Equation 85 to

$$\begin{aligned} I_{12}(r) =& \bigg(\int_{-\infty}^{-\varepsilon^{-1/2}} + \int_{ \varepsilon^{-1/2}}^{\infty}\bigg)\Big|\frac{\mathrm{i}}{x} + \mathcal{O} \big(x^{-4}\big)\Big|^{2} \\ \times& M_{n}(r,-n\omega_{\mathrm{A}} - \varepsilon x\omega_{k})\,{ \mathrm{d}}x = \mathcal{O}(\varepsilon). \end{aligned}$$

(86)

To evaluate $I_{11}(r)$, we use the relation

$$ M_{n}(r,-n\omega_{\mathrm{A}} - \varepsilon x\omega_{k}) = M_{n}(r,-n \omega_{\mathrm{A}}) - \varepsilon x\omega_{k} \frac{\partial M_{n}}{\partial\omega}\bigg|_{\omega= -n\omega_{ \mathrm{A}}}. $$

(87)

Now we assume that the characteristic scale of variation of $\Pi_{f}(\omega)$ is $\omega_{k}$. Then it follows that the ratio of the second term on the right-hand side of Equation 87 to the first term is of the order of $\varepsilon^{1/2}$ for $x \in(-\varepsilon^{-1/2},\varepsilon^{-1/2})$, and we obtain

$$ I_{11}(r) = M_{n}(r,-n\omega_{\mathrm{A}})\int_{-\varepsilon^{-1/2}}^{ \varepsilon^{-1/2}} |F(x)|^{2}\,\mathrm{d}x + \mathcal{O}\big( \varepsilon^{1/2}\big). $$

(88)

Next we use the relation

$$\begin{aligned} \int_{-\varepsilon^{-1/2}}^{\varepsilon^{-1/2}} |F(x)|^{2}\,\mathrm{d}x &= \int_{-\infty}^{\infty}|F(x)|^{2}\,\mathrm{d}x - \bigg(\int_{- \infty}^{-\varepsilon^{-1/2}} +\, \int_{\varepsilon^{-1/2}}^{\infty}\bigg)\Big|\frac{\mathrm {i}}{x} + \mathcal{O}\big(x^{-2}\big)\Big|^{2} {\mathrm{d}}x \\ &= \int _{-\infty}^{\infty}|F(x)|^{2}\,\mathrm{d}x + \mathcal {O}(\varepsilon). \end{aligned}$$

(89)

Now we calculate the integral on the right-hand side of this equation:

$$\begin{aligned} \int_{-\infty}^{\infty}|F(x)|^{2}\,\mathrm{d}x &= \int_{-\infty }^{\infty}{ \mathrm{d}}x \int_{0}^{\infty}\exp(\mathrm{i}x\theta- \theta ^{3}/3)\,\mathrm{d} \theta\int_{0}^{\infty}\exp(-\mathrm{i}x\vartheta- \vartheta^{3}/3) \,\mathrm{d}\vartheta \\ & = \int_{0}^{\infty}{\mathrm{e}}^{-\theta^{3}/3}\,\mathrm {d}\theta\int_{0}^{\infty}{\mathrm{e}}^{-\vartheta^{3}/3}\,\mathrm {d}\vartheta\int_{-\infty}^{\infty}{\mathrm{e}}^{\mathrm {i}x(\theta- \vartheta)}{\mathrm{d}}x \\ & = 2\pi\int_{0}^{\infty}{\mathrm{e}}^{-\theta^{3}/3}\,\mathrm {d}\theta \int_{0}^{\infty}{\mathrm{e}}^{-\vartheta^{3}/3}\delta(\theta- \vartheta)\,\mathrm{d}\vartheta= 2\pi\int_{0}^{\infty}{\mathrm{e}}^{-2 \theta^{3}/3}\,\mathrm{d}\theta \\ & = \pi\left(\frac{2}{3}\right)^{2/3}\int_{0}^{\infty}\theta^{-2/3}{ \mathrm{e}}^{-\theta}\,\mathrm{d}\theta= \pi\left(\frac {2}{3}\right)^{2/3} \Gamma\bigg(\frac{1}{3}\bigg) \approx6.42. \end{aligned}$$

(90)

Using Equations 83, 86, and 88 – 90 we obtain that

$$ I_{1}(r) = 6.42\,\varepsilon^{-1}\omega_{k} M_{n}(r,-n\omega _{\mathrm{A}}) + \mathcal{O}\big(\varepsilon^{-1/2}\big). $$

(91)

In a similar way, we obtain

$$ I_{3}(r) = 6.42\,\varepsilon^{-1}\omega_{k} M_{n}(r,n\omega_{\mathrm{A}}) + \mathcal{O}\big(\varepsilon^{-1/2}\big). $$

(92)

Finally we estimate $I_{2}(r)$. We write

$$ \int_{-\infty}^{\infty}F\Big(- \frac{\omega+ n\omega_{A}}{\varepsilon\omega_{k}}\Big) F\Big( \frac{\omega- n\omega_{A}}{\varepsilon\omega_{k}}\Big) M_{n}(r,\omega)\,\mathrm{d}\omega= J_{1} + J_{2} + J_{3} + J_{4} + J_{5}, $$

(93)

where $J_{1}$, $J_{2}$, $J_{3}$, $J_{4}$, and $J_{5}$ are the integrals over the intervals

$$ \textstyle\begin{array}{l} (-\infty,-n\omega_{\mathrm{A}} - \varepsilon^{1/2}\omega_{k}), \\ (-n\omega_{\mathrm{A}} - \varepsilon^{1/2}\omega_{k},-n\omega _{\mathrm{A}} + \varepsilon^{1/2}\omega_{k}), \\ (-n\omega_{\mathrm{A}} + \varepsilon^{1/2}\omega_{k}, n\omega _{\mathrm{A}} - \varepsilon^{1/2}\omega_{k}) , \\ (n\omega_{\mathrm{A}} - \varepsilon^{1/2}\omega_{k}, n\omega _{\mathrm{A}} + \varepsilon^{1/2}\omega_{k}) , \\ (n\omega_{\mathrm{A}} + \varepsilon^{1/2}\omega_{k},\infty) , \end{array} $$

(94)

respectively. Making the variable substitutions $\omega= -\varepsilon x\omega_{k} - n\omega_{\mathrm{A}}$ in $J_{1}$, $J_{2}$, and $J_{3}$, and $\omega= -\varepsilon x\omega_{k} + n\omega_{\mathrm{A}}$ in $J_{4}$ and $J_{5}$ we obtain

$$\begin{aligned} J_{1} &= \varepsilon\omega_{k}\int_{\varepsilon^{-1/2}}^{\infty}F(x) F(-x - x_{0}\varepsilon^{-1}) M_{n}(r,\omega(x))\,\mathrm{d}x \\ &= \varepsilon\omega_{k}\int_{\varepsilon^{-1/2}}^{\infty}\bigg( \frac{1}{x(x + x_{0}\varepsilon^{-1})} + \mathcal{O}\big(\varepsilon^{4} \big)\bigg) M_{n}(r,\omega(x))\,\mathrm{d}x = \mathcal{O}\big( \varepsilon^{5/2}\big), \hphantom{xx} \end{aligned}$$

(95)

$$\begin{aligned} J_{2} &= \varepsilon\omega_{k}\int_{-\varepsilon^{-1/2}}^{ \varepsilon^{-1/2}} F(x) F(-x - x_{0}\varepsilon^{-1}) M_{n}(r, \omega(x))\,\mathrm{d}x \\ &= \varepsilon\omega_{k}\int_{-\varepsilon^{-1/2}}^{\varepsilon^{-1/2}} F(x) \bigg(\frac{-\mathrm{i}}{x + x_{0}\varepsilon^{-1}} + \mathcal{O} \big(\varepsilon^{2}\big) \bigg) M_{n}(r,\omega(x))\,\mathrm{d}x = \mathcal{O}\big(\varepsilon^{4}\big), \hphantom{xx} \end{aligned}$$

(96)

$$\begin{aligned} J_{3} &= \varepsilon\omega_{k}\int_{\varepsilon^{-1/2} - x_{0} \varepsilon^{-1}}^{-\varepsilon^{-1/2}} F(x) F(-x - x_{0} \varepsilon^{-1}) M_{n}(r,\omega(x))\,\mathrm{d}x \\ & = \varepsilon\omega_{k}\int_{\varepsilon^{-1/2} - x_{0} \varepsilon^{-1}}^{-\varepsilon^{-1/2}} \bigg( \frac{1}{x(x + x_{0}\varepsilon^{-1})} + \mathcal{O}\big(x^{4}\big)\bigg) M_{n}(r, \omega(x))\,\mathrm{d}x = \mathcal{O}\big(\varepsilon^{2}\big), \hphantom{xx} \end{aligned}$$

(97)

$$\begin{aligned} J_{4} &= \varepsilon\omega_{k}\int_{-\varepsilon^{-1/2}}^{ \varepsilon^{-1/2}} F(-x) F(x - x_{0}\varepsilon^{-1}) M_{n}(r, \omega(x))\,\mathrm{d}x \\ &= \varepsilon\omega_{k}\int_{-\varepsilon^{-1/2}}^{\varepsilon^{-1/2}} F(-x) \bigg(\frac{\mathrm{i}}{x - x_{0}\varepsilon^{-1}} + \mathcal{O} \big(\varepsilon^{4}\big) \bigg) M_{n}(r,\omega(x))\,\mathrm{d}x = \mathcal{O}\big(\varepsilon^{2}\big), \hphantom{xxx} \end{aligned}$$

(98)

$$\begin{aligned} J_{5} &= \varepsilon\omega_{k}\int_{-\infty}^{-\varepsilon^{-1/2}} F(-x) F(x - x_{0}\varepsilon^{-1}) M_{n}(r,\omega(x))\,\mathrm{d}x \\ &= \varepsilon\omega_{k}\int_{-\infty}^{-\varepsilon^{-1/2}} \bigg( \frac{1}{x(x - x_{0}\varepsilon^{-1})} + \mathcal{O}\big(x^{-4} \big)\bigg) M_{n}(r,\omega(x))\,\mathrm{d}x = \mathcal{O}\big( \varepsilon^{5/2}\big), \hphantom{xx} \end{aligned}$$

(99)

where $x_{0} = 2n\omega_{\mathrm{A}}\omega_{k}^{-1}$. It follows from Equations 81, 93, and 95 – 99 that $I_{2}(r) = \mathcal{O}(1)$. Using this estimate and Equations 79, 91, and 92 we obtain that in the leading-order approximation with respect to $\varepsilon$

$$ \int_{-\infty}^{\infty}\Pi_{v_{n}}(r,\omega)\,d\omega= 6.42\, \varepsilon^{-1} \omega_{k} [M_{n}(r,n\omega_{\mathrm{A}}) + M_{n}(r,-n \omega_{\mathrm{A}})]. $$

(100)

Appendix C: Evaluation of $\int_{R(1-\ell/2)}^{r} U_{n}(x,\omega)\, \mathrm{d}x$

In the previous appendix, $r$ was a parameter and the dependence of $\varepsilon$ on $r$ did not cause any problem. Since the expression for $W_{n}(r,\omega)$ involves the integral with respect to $r$, it is more convenient in this section to have a small parameter independent of $r$. In accordance with this we re-define the expression for $\varepsilon$ as

$$ \varepsilon= \left(\frac{3n^{2}}{\text{Re}}\right)^{1/3}. $$

(101)

$$ \int_{R(1-\ell/2)}^{r} U_{n}(x,\omega)\,\mathrm{d}x = \frac{\omega^{2}}{\pi n^{2}} \big[I_{+}(\omega) - I_{-}(\omega) \big], $$

(102)

where

$$\begin{aligned} I_{\pm}(\omega) &= \varepsilon^{-1}\int_{R(1-\ell/2)}^{r} \Lambda^{-1/3}(x) N_{n}(x,\omega)F\big(-\varepsilon^{-1}\chi_{n\pm}(x,\omega)\big) \,\mathrm{d}x, \end{aligned}$$

(103)

$$\begin{aligned} N_{n}(x,\omega) &= \frac{1}{\rho(x)\omega_{\mathrm{A}}(x)} \left (\rho(x) - \rho_{\mathrm{i}} + \frac{\rho_{\mathrm{i}}(\omega^{2} - n^{2}\omega_{\mathrm {Ai}}^{2})}{n^{2}\omega_{k}^{2} - \omega^{2} + K(\omega)}\right), \end{aligned}$$

(104)

$$\begin{aligned} \chi_{n\pm}(x,\omega) &= \Lambda^{-1/3}(x)[\omega\pm n\omega_{ \mathrm{A}}(x)]. \end{aligned}$$

(105)

We consider $I_{+}(\omega)$. First we assume that $\omega\notin[-n\omega_{\mathrm{Ae}},-n\omega_{\mathrm{Ai}}]$. Then using Equation 28 we obtain

$$ I_{+}(\omega) = -\int_{R(1-\ell/2)}^{r} \frac{\mathrm{i}N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)}\,\mathrm{d}x + \mathcal{O}(\varepsilon^{3}). $$

(106)

Next we assume that $\omega\in[-n\omega_{\mathrm{Ae}},-n\omega_{\mathrm{Ai}}]$. We introduce $x_{c}$ defined by the equation $n\omega_{\mathrm{A}}(x_{c})= -\omega$. Then we write

$$ I_{+}(\omega) = I_{1+}(\omega) + I_{2+}(\omega) , $$

(107)

where

$$\begin{aligned} I_{1+}(\omega) &= \varepsilon^{-1}\left(\int_{R(1-\ell/2)}^{x_{c}-s} + \int_{x_{c}+s}^{r}\right) \Lambda^{-1/3}(x) N_{n}(x,\omega) F \big(-\varepsilon^{-1}\chi_{n+}(x,\omega)\big)\,\mathrm{d}x , \end{aligned}$$

(108)

$$\begin{aligned} I_{2+}(\omega)& = \varepsilon^{-1}\int_{x_{c}-s}^{x_{c}+s}\Lambda^{-1/3}(x) N_{n}(x,\omega)F\big(-\varepsilon^{-1}\chi_{n+}(x,\omega)\big)\,{ \mathrm{d}}x , \end{aligned}$$

(109)

and $s = \ell R\varepsilon^{1/2}$. Using Equation 28 we obtain

$$ I_{1+}(\omega) = -\mathrm{i}\left(\int_{R(1-\ell/2)}^{x_{c}-s} + \int_{x_{c}+s}^{r}\right) \frac{N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)}{\mathrm {d}}x + \mathcal{O}(\varepsilon^{3}). $$

(110)

Then we obtain

$$\begin{aligned} \left(\int_{R(1-\ell/2)}^{x_{c}-s}\right. +& \left.\int_{x_{c}+s}^{r} \right) \frac{N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)}\, \mathrm{d}x = \mathcal{P} \int_{R(1-\ell/2)}^{r} \frac{N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)}\,\mathrm{d}x \\ -& \int_{x_{c}-s}^{x_{c}+s}\bigg( \frac{N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)} - \frac{N_{n}(x_{c},\omega)}{n\omega'_{\mathrm{A}}(x_{c})(x - x_{c})}\bigg)\mathrm{d}x \\ =& \mathcal{P}\int_{R(1-\ell/2)}^{r} \frac{N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm{A}}(x)}\,\mathrm {d}x + \mathcal{O}(\varepsilon^{5/2}) , \end{aligned}$$

(111)

where the prime indicates the derivative. When obtaining this result, we took into account that the integrand in the integral in the second line is a regular function, which implies that the integral in the second line is of the order of $s = \mathcal{O}(\varepsilon^{1/2})$. We also note that the integral of the second term in the second line is zero. It follows from Equations 110 and 111 that

$$ I_{1+}(\omega) = -\mathcal{P}\int_{R(1-\ell/2)}^{r} \frac{\mathrm{i}N_{n}(x,\omega)}{\omega+ n\omega_{\mathrm {A}}(x)}\,\mathrm{d}x + \mathcal{O}(\varepsilon^{5/2}). $$

(112)

Now we consider $I_{2+}(\omega)$. Using Equation 27 and changing the order of integration we transform Equation 109 to

$$ I_{2+}(\omega) = \varepsilon^{-1}\! \int_{0}^{\infty}\!\! e^{- \theta^{3}/3}{\mathrm{d}}\theta\int_{x_{c}-s}^{x_{c}+s}\!\! \Lambda ^{-1/3}(x) N_{n}(x,\omega) \exp\big(-\mathrm{i}\varepsilon^{-1}\theta\chi_{n+}(x, \omega)\big)\,\mathrm{d}x . $$

(113)

We introduce the function

$$ \psi(x) = \frac{\partial\chi_{n+}}{\partial x} = \frac{n\omega'_{\mathrm{A}}(x)}{\Lambda^{1/3}(x)} - \frac{\Lambda'(x)[\omega+ n\omega_{\mathrm{A}}(x)]}{3\Lambda^{4/3}(x)}. $$

(114)

Since $\omega+ n\omega_{\mathrm{A}}(x_{c}) = 0$, it follows that the ratio of the second term on the right-hand side of this expression to the first term is of the order of $\varepsilon^{1/2}$ in the interval $[x_{c} - s,x_{c} + s]$. Then for $x \in[x_{c} - s,x_{c} + s]$ we have

$$ \psi(x) = \frac{n\omega'_{\mathrm{A}}(x)}{\Lambda^{1/3}(x)} + \mathcal{O}(\varepsilon^{1/2}). $$

(115)

Now, using integration by parts we transform Equation 113 to

$$\begin{aligned} I_{2+}(\omega) =& \frac{\mathrm{i}N_{n}(x_{c} + s,\omega)G(-\varepsilon^{-1} \chi_{n+}(x_{c} + s,\omega))}{\psi(x_{c} + s,\omega)\Lambda ^{1/3}(x_{c} + s)} \\ -& \frac{\mathrm{i}N_{n}(x_{c} - s,\omega)G(-\varepsilon^{-1}\chi _{n+}(x_{c} - s,\omega))}{\psi(x_{c} - s,\omega)\Lambda^{1/3}(x_{c} - s)} \\ -& \mathrm{i}\int_{x_{c}-s}^{x_{c}+s}G\big(-\varepsilon^{-1}\chi_{n+}(x, \omega)\big) \frac{\partial}{\partial x}\left( \frac{N_{n}(x,\omega)}{\psi(x,\omega)\Lambda^{1/3}(x)}\right )\mathrm{d}x , \hphantom{xx} \end{aligned}$$

(116)

where the function $G(x)$ is defined by (Goossens, Ruderman, and Hollweg, 1995; Goossens, Erdélyi, and Ruderman, 2011)

$$ G(x) = \int_{0}^{\infty}\frac{\mathrm{e}^{\mathrm{i}x\theta} - 1}{\theta}{ \mathrm{e}}^{-\theta^{3}/3}{\mathrm{d}}\theta. $$

(117)

Next we use the asymptotic expansion of $G(x)$ valid for $|x| \gg1$ (Goossens et al. 1995)

$$ G(x) = -\ln|x| - \frac{2}{3}\mathrm{C} - \frac{1}{3}\ln3 + \frac{\pi{\mathrm{i}}}{2}\text{sgn}(x) + o(1), $$

(118)

where $o(1)$ is a function tending to zero as $|x| \to\infty$ and $\mathrm{C} \approx0.577$ is the Euler–Mascheroni constant. Using this asymptotic formula we obtain from Equation 118

$$ I_{2+}(\omega) = \frac{\pi N_{n}(x_{c},\omega)}{\psi(x_{c})\Lambda^{1/3}(x_{c})} + o(1), $$

(119)

where we took into account that $\psi$ is independent of $\omega$ at $x = x_{c}$. Then it follows from Equations 112 and 118 that in the leading-order approximation with respect to $\varepsilon$

$$ I_{+}(\omega) = \frac{\pi N_{n}(x_{c},\omega)}{\psi(x_{c})\Lambda^{1/3}(x_{c})} - \mathcal{P}\int_{R(1-\ell/2)}^{r} \frac{\mathrm{i}N_{n}(x,\omega)}{\omega+ n\omega_{A}(x)}\,\mathrm {d}x , $$

(120)

when $\omega\in[-n\omega_{\mathrm{Ae}},-n\omega_{\mathrm{Ai}}]$. Using the relation $N_{n}(x,\omega) = N_{n}^{*}(x,-\omega)$ we obtain $I_{-}(\omega) = I_{+}^{*}(-\omega)$. Then it follows from Equations 102, 106, and 120 that in the leading-order approximation with respect to $\varepsilon$ we obtain for $\omega< 0$

$$ \int_{R(1-\ell/2)}^{r}\!\! U_{n}(x,\omega)\,\mathrm{d}x = \frac{\omega^{2}}{\pi n^{2}} \left\{ \textstyle\begin{array}{l} \displaystyle2\int_{R(1-\ell/2)}^{r}\! \frac{\omega\Im(N_{n}) + \mathrm{i}n\omega_{\mathrm{A}}\Re(N_{n})}{n^{2}\omega_{\mathrm {A}}^{2} - \omega^{2}} \,\mathrm{d}x, \\ \hspace{30mm} \omega\notin[-n\omega_{\mathrm{Ai}},-n\omega_{\mathrm{Ae}}], \\ \displaystyle2\mathcal{P}\int_{R(1-\ell/2)}^{r}\! \frac{\omega\Re(N_{n}) + \mathrm{i}n\omega_{\mathrm{A}}\Im(N_{n})}{n^{2}\omega_{\mathrm {A}}^{2} - \omega^{2}} \,\mathrm{d}x, \\ \hspace{1mm} \displaystyle+\; \frac{\pi N_{n}(x_{c},\omega)}{\psi(x_{c}) \Lambda^{1/3}(x_{c})}, \quad \omega\in[-n\omega_{\mathrm {Ai}},-n\omega_{ \mathrm{Ae}}] . \end{array}\displaystyle \right. $$

(121)

For $\omega> 0$ this integral is defined by

$$ \int_{R(1-\ell/2)}^{r} U_{n}(x,\omega)\,\mathrm{d}x = -\int_{R(1- \ell/2)}^{r} U_{n}^{*}(x,-\omega)\,\mathrm{d}x . $$

(122)

Since the characteristic scale of variation of $\omega_{\mathrm {A}}(x)$ is $\ell R$ it follows that $\psi(x) = \mathcal{O}(\ell^{-1})$. Then it follows from Equation 121 that

$$ \int_{R(1-\ell/2)}^{r} U_{n}(x,\omega)\,\mathrm{d}x = \mathcal{O}( \ell). $$

(123)

Appendix D: Evaluation of Integral in Equation 68

We write the integral in Equation 68 as

$$ \int_{0}^{\infty }\frac{\omega^{13/3}(2n^{2}\omega_{k}^{2} - \omega^{2})\,\mathrm {d}\omega}{64\omega^{4}(\zeta+1)^{2} (n^{2}\omega_{k}^{2} - \omega ^{2})^{2} + \pi^{2}\ell^{2} n^{12}\omega_{k}^{8}(\zeta-1)^{2}} = I_{1} + I_{2}, $$

(124)

where

$$\begin{aligned} I_{1} &= \frac{1}{2n^{2/3}\omega_{k}^{2/3}}\bigg(\int_{0}^{1 - \ell^{1/2}} + \int_{1 + \ell^{1/2}}^{\infty}\bigg) \frac{x^{5/3}(2 - x)\,\mathrm{d}x}{64x^{2}(\zeta+1)^{2}(1 - x)^{2} + \pi^{2}\ell^{2} n^{4}(\zeta-1)^{2}}, \end{aligned}$$

(125)

$$\begin{aligned} I_{2} &= \frac{1}{2n^{2/3}\omega_{k}^{2/3}}\int_{1 - \ell^{1/2}}^{1 + \ell^{1/2}} \frac{x^{5/3}(2 - x)\,\mathrm{d}x}{64x^{2}(\zeta+1)^{2}(1 - x)^{2} + \pi^{2}\ell^{2} n^{4} (\zeta-1)^{2}}. \end{aligned}$$

(126)

When deriving the expressions for $I_{1}$ and $I_{2}$ we made the variable substitution $\omega^{2} = xn^{2}\omega_{k}^{2}$. Using the variable substitution $x = y^{3}$ and integration by parts we obtain

$$\begin{aligned} I_{1} =& \frac{3[1 + \mathcal{O}(\ell^{1/2})]}{128n^{2/3}\omega _{k}^{2/3}(\zeta+1)^{2}} \bigg(\int_{0}^{1 - \ell^{1/2}} + \int_{1 + \ell^{1/2}}^{\infty }\bigg) \frac{y(2 - y^{3})\,\mathrm{d}y}{(1 - y^{3})^{2}} \\ =& \frac{1 + \mathcal{O}(\ell^{1/2})}{128n^{2/3}\omega_{k}^{2/3}(\zeta+1)^{2}} \bigg[\frac{y^{2}}{1-y^{3}}\bigg|_{0}^{1 - \ell^{1/2}} + \frac{y^{2}}{1-y^{3}}\bigg|_{1 + \ell^{1/2}}^{\infty } \\ +& \bigg(\int_{0}^{1 - \ell^{1/2}} + \int_{1 + \ell ^{1/2}}^{\infty}\bigg) \frac{4y\,\mathrm{d}y}{1 - y^{3}}\bigg] = \frac{1}{128n^{2/3}\omega_{k}^{2/3}(\zeta+1)^{2}} \bigg[\frac {2}{3}\ell^{-1/2} \\ -& \frac{4}{3}\bigg(\int_{0}^{1 - \ell^{1/2}} + \int_{1 + \ell ^{1/2}}^{\infty}\bigg)\bigg( \frac{1}{y-1} - \frac{y-1}{y^{2} + y + 1}\bigg){ \mathrm{d}}x + \mathcal{O}(1)\bigg] \\ =& \frac{1}{64n^{2/3}\omega_{k}^{2/3}(\zeta+1)^{2}}\bigg[\frac{1}{3} \ell^{-1/2} - \bigg(\frac{1}{3}\ln\frac{(y-1)^{2}}{y^{2} + y + 1} \\ +& \sqrt{3}\arctan\frac{2y+1}{4\sqrt{3}}\bigg)\bigg(\bigg|_{0}^{1 - \ell^{1/2}} + \bigg|_{1 + \ell^{1/2}}^{\infty}\bigg) + \mathcal{O}(1) \bigg] \\ =& \frac{\ell^{-1/2} + \mathcal{O}(1)}{192n^{2/3}\omega _{k}^{2/3}(\zeta+1)^{2}}. \end{aligned}$$

(127)

Next we proceed to evaluating $I_{2}$. We obtain

$$\begin{aligned} I_{2} =& \frac{1}{2n^{2/3}\omega_{k}^{2/3}}\int_{1 - \ell ^{1/2}}^{1 + \ell^{1/2}} \frac{[1 + \mathcal{O}(\ell^{1/2})]\,\mathrm{d}x}{64(\zeta +1)^{2}(1 - x)^{2} + \pi^{2}\ell^{2} n^{4} (\zeta-1)^{2}} \\ =& \frac{1 + \mathcal{O}(\ell^{1/2})}{16\pi\ell n^{8/3}\omega _{k}^{2/3}(\zeta^{2}-1)} \arctan\frac{8(\zeta+1)(x-1)}{\pi\ell n^{2}(\zeta-1)}\bigg|_{1 - \ell^{1/2}}^{1 + \ell^{1/2}} \\ =& \frac{1 + \mathcal{O}(\ell^{1/2})}{16\ell n^{8/3}\omega _{k}^{2/3}(\zeta^{2}-1)} . \end{aligned}$$

(128)

It follows from Equations 124, 127, and 128 that

$$ \int_{0}^{\infty }\frac{\omega^{19/3}\,\mathrm{d}\omega}{64\omega^{4}(\zeta+1)^{2} (n^{2}\omega_{k}^{2} - \omega^{2})^{2} + \pi^{2}\ell^{2} n^{12}\omega_{k}^{8}(\zeta-1)^{2}} = \frac{1 + \mathcal{O}(\ell^{1/2})}{16\ell n^{8/3}\omega _{k}^{2/3}(\zeta^{2}-1)} . $$

(129)