Abstract
During Solar Cycle 23 16 ground-level enhancement events were registered by the global neutron monitor network. In this work we focus on the period with increased solar activity during late October – early November 2003 producing a sequence of three events, specifically on ground-level enhancement GLE 67 on 2 November 2003. On the basis of an analysis of neutron monitor and space-borne data we derived the spectra and pitch-angle distribution of high-energy solar particles with their dynamical evolution throughout the event. According to our analysis, the best fit of the spectral and angular properties of solar particles was obtained by a modified power-law rigidity spectrum and a double Gaussian, respectively. The derived angular distribution is consistent with the observations where an early count rate increase at Oulu neutron monitor with asymptotic viewing direction in the anti-Sun direction was registered. The quality of the fit and model constraints were assessed by a forward modeling. The event integrated particle fluence was derived using two different methods. The derived results are briefly discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Occasionally, following significant solar eruption(s), which comprises a solar flare and/or a coronal mass ejection (CME), solar energetic particles (SEPs) can be accelerated to energies allowing their registration by ground-based detectors e.g. neutron monitors (NMs) (for details see Hatton, 1971; Stoker, Dorman, and Clem, 2000; Dorman, 2006, and the references therein). In this case the energy of SEPs is of the order of about 1 GeV/nucleon or even greater (e.g. Aschwanden, 2012; Reames, 2013; Desai and Giacalone, 2016, and the references therein), which is high enough to produce particle shower in the atmosphere leading to an increase of count rate of ground-based NMs. Accordingly, this specific class of SEPs is known as ground-level enhancements (GLEs) (e.g. Stoker, Dorman, and Clem, 2000; Poluianov et al., 2017).
GLE events can be considered as extreme class of SEP events (e.g. Gopalswamy et al., 2016), with the occurrence rate being roughly ten per solar cycle (Shea and Smart, 1990). We note that, at periods related to maximum and decline phase of the solar activity cycle, a slightly greater occurrence probability was reported (Shea and Smart, 1990; Stoker, 1995; Bazilevskaya, 2005).
GLEs have been continuously studied over the years with various instruments, in order to reveal particle transport in the interplanetary medium, as well as their acceleration (e.g. Debrunner et al., 1988; Ryan, Lockwood, and Debruner, 2000; Aschwanden, 2012; Shea and Smart, 2012; Miroshnichenko, Vashenyuk, and Perez-Peraza, 2013; Klein and Dalla, 2017, and the references therein).
The first registration of a GLE was carried out by ionization chambers (Forbush, 1946). Lately in the mid 1950 – 1960 the network of NMs, based on improved detectors, was considerably expanded. Nowadays the worldwide NM network is a convenient multi-instrument tool to study GLEs (Simpson, Fonger, and Treiman, 1953; Simpson, 1957; Forbush, 1958; Hatton and Carmichael, 1964; Simpson, 2000). At present, the worldwide NM networks allows one to perform continuous monitoring of the intensity of cosmic-ray particles and it is used also for registration and study of GLEs and the related space weather phenomena (e.g. Mavromichalaki et al., 2011; Miroshnichenko, 2018).
The intensity of high-energy particles of solar origin is not uniform in the vicinity of Earth, specifically during strong or anisotropic SEP events (Bieber and Evenson, 1995; Bütikofer et al., 2009; Mishev, Kocharov, and Usoskin, 2014). Therefore, it is necessary to deploy NMs at different geographic locations in order to derive their characteristics, because NMs are sensitive to SEPs impinging geomagnetosphere and atmosphere from different asymptotic cones. This fact is specifically important during the event’s initial phase when GLE particles reveal an essential anisotropic flux (Debrunner et al., 1988; Shea and Smart, 1990; Vashenyuk et al., 2006; Bütikofer et al., 2009). NM records for all available GLE events are collected in the international GLE database (IGLED) (gle.oulu.fi) (Usoskin et al., 2015) and/or NM data base NMDB (nmdb.eu) (e.g. Mavromichalaki et al., 2011). Here, we employed detrended records of NM count rate increases (Usoskin et al., 2020) retrieved from the IGLED. Detrended data accounts for short-term galactic cosmic-ray variability, such as diurnal variations or recovery phase of Forbush decreases and allows more accurate evaluation of the SEP signal in NM records. Employment of the detrended data is especially significant for obtaining reliable scientific results for weak GLE events during disturbed space weather conditions, in particular for GLE \(\#\) 67, which occurred during the recovery phase of a Forbush decrease after the previous GLE \(\#\) 66.
The main characteristics of GLEs differ from each other. The spectra, anisotropy, duration, apparent source location as well as geomagnetic and interplanetary transport conditions and their time evolution vary from event to event (Gopalswamy et al., 2012; Moraal and McCracken, 2012; Raukunen et al., 2018). This usually leads to a study on a case-by-case basis. For the present study, we focus on the third of the sequence of the three so-called Halloween events, namely the relatively poorly studied 2 November 2003 event (GLE \(\#\) 67).
2 Experimental Data of NMs During GLE \(\#\) 67
During the Solar Cycle 23 16 GLE events were observed (Andriopoulou et al., 2011a,b; Gopalswamy et al., 2012). Here we focused on the period with increased solar activity during late October through early November 2003 producing a sequence of three GLEs \(\#\) 65 – 67, known as Halloween events. In terms of spectral and angular characteristics of SEPs, the Halloween events have been extensively studied, except for GLE \(\#\) 67 (Miroshnichenko et al., 2005; Pérez-Peraza et al., 2009).
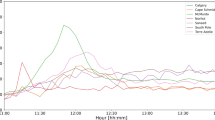
The GLE \(\#\) 67 event on 2 November 2003 was related to an X8.3/2B solar flare, which was close to the west limb of the Sun, namely at S14 W56 in the solar active region AR10486. The 2 November 2003 event was associated with a fast CME with speed of ≈ 2660 km s−1 (for details see Gopalswamy et al., 2012, and the references therein). On ground level, the event onset was observed between 17:30 and 17:35 UT at several NM stations (Figure 1). The strongest count rate increases were observed at SOPO (36.0%), MCMD (15.2), % TERA (14.2%) and FSMT (12.0%) NMs, compared to the pre-increase levels. In general, the event was very anisotropic in its initial phase, since no significant count rate increase at SNAE NM was observed. However, the angular distribution of the GLE particles could not be very narrow i.e., beam like, because an early NM count rate increase was observed at several stations whose asymptotic viewing direction were in the anti-Sun direction e.g. APTY, OULU, TXBY (see Figure 3).
Time variation of CALG, FSMT, TERA, TXBY, SOPO and OULU NMs records during GLE \(\#\) 67 on 2 November 2003. The curves are cubic spline smoothed over the experimental 5-min intervals of NM count rate increases. The station acronyms are given in Table 1.
A non-negligible trend of the NM data was revealed from the experimental records, therefore detrended experimental data of NM count rates during GLE \(\#\) 67 were retrieved from IGLED (gle.oulu.fi) (Usoskin et al., 2015, 2020). This study was based on data of about 30 NM stations, the full list with the corresponding acronyms, cut-off rigidities and altitudes above sea level is given in Table 1, accordingly the map of the used NM stations is shown in Figure 2.
Map of the neutron monitors used for the analysis of GLE \(\#\) 67 (see Table 1).
3 Mathematical Modeling of the Neutron Monitor Response
Using NM records of GLEs allows one to derive the spectral and angular characteristics of quasi-relativistic and relativistic solar protons by modeling the global NM response (e.g. Shea and Smart, 1982). Routinely it is performed employing Equation 1, that is the relationship between the NM count rates and the primary cosmic-ray flux, and appropriate optimization of a set of \(n\) model parameters over \(m\) experimental data points. The modeling of the NM network is usually carried out in the energy range of ∼ 0.3 – 20 GeV/nucleon.
In this study, we employed a method initially developed by Shea and Smart (1982), Cramp et al. (1997), Bombardieri et al. (2006), Vashenyuk et al. (2006), whose detailed description and applications are given elsewhere (Mishev, Kocharov, and Usoskin, 2014; Mishev and Usoskin, 2016a; Mishev, Poluianov, and Usoskin, 2017; Mishev et al., 2018, 2021). For the initial guess of the unfolding procedure, we assumed the apparent source position along the interplanetary magnetic field (IMF) line derived from space-borne measurements and/or employing procedure described by Cramp, Humble, and Duldig (1995), explicitly considering the time shift of IMF direction similarly to Mishev and Usoskin (2016b), Kocharov et al. (2017), Mishev et al. (2018).
The count rate of a given NM can be modeled using the expression
where \(J(P,t)\) is the rigidity spectrum of the primary cosmic ray (CR) of galactic or solar origin at given moment \(t\), \(S(P)\) is the specific NM yield function (for details see Clem and Dorman, 2000; Dorman, 2006, and the references therein), \(G(\alpha (P,t))\) accounts for the angular distribution of cosmic-ray particles i.e. the pitch-angle distribution (PAD) of SEPs, we noted that for galactic cosmic ray (GCRs) it is assumed to be isotropic. The A(P) is a discrete function, which accounts the magnetospheric transmissivity (\(A(P)=1\) for allowed trajectories, accordingly \(A(P)=0\) for forbidden trajectories). \(A\) is standardly derived during NM asymptotic cone computations. In Equation 1\(P_{\mathrm{cut}}\) is the lower cut-off rigidity of the station. For SEPs, we considered \(P_{\mathrm{max}}= 20\) GV, whilst for GCRs \(P_{\mathrm{max}}= \infty \). The contribution of GCRs was computed employing the force-field model (for details see Gleeson and Axford, 1968; Burger, Potgieter, and Heber, 2000; Usoskin et al., 2005; Vos and Potgieter, 2015), where the modulation is considered according to Usoskin, Bazilevskaya, and Kovaltsov (2011). Thus, the modeled relative increase of a NM station count rate is given by the ratio between the SEPs and GCR contributions, the latter typically averaged over two full hours before the event’s onset (e.g. Usoskin et al., 2015).
Herein, for the modeling of NM response, we employed newly computed and experimentally verified specific yield function (Mishev, Usoskin, and Kovaltsov, 2013; Mishev et al., 2020), which is in a conformity with latitude surveys and direct space-borne measurements of GCRs by PAMELA (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics) (Adriani et al., 2016) and AMS 02 (Alpha Magnetic Spectrometer) (Aguilar et al., 2010) (for details see Mishev, Usoskin, and Kovaltsov, 2013; Gil et al., 2015; Mangeard et al., 2016; Nuntiyakul et al., 2018; Koldobskiy et al., 2019a). This new NM yield function is the most suitable for GLE analysis (e.g. Nuntiyakul et al., 2018; Koldobskiy et al., 2019a; Mishev et al., 2021). Moreover, we modeled the response of the corresponding NMs using a specific yield function relevant to the exact station altitude above sea level (for details see Mishev et al., 2018, 2020, 2021), which allowed us to reduce uncertainties connected to the employment of the double-attenuation-lengths method, that is, rescaling of high-altitude NM count rates to sea level (e.g. McCracken, Rao, and Shea, 1962), eventually leading to an improvement of the optimization procedure.
Here, for the modeling we assumed various functional expressions of SEP spectra, that is a modified power-law rigidity spectrum similarly to Cramp et al. (1997), Vashenyuk et al. (2006):
where \(J(P)\) is the particle flux with as a function of rigidity \(P\) in [GV], \(\gamma \) is the power-law spectral exponent at rigidity \(P = 1\) GV, accordingly \(\delta \gamma \) is the rate of the spectrum steepening; or an exponential spectrum:
where \(J(P)\) is defined in the same way as in Equation 2, accordingly \(P_{0}\) is a characteristic proton rigidity.
Here, in all cases the PAD was modeled with a complicated distribution, that is, double (Sun–anti Sun) Gaussian:
where \(\alpha \) is the pitch angle, \(\sigma _{1}\) and \(\sigma _{2}\) are parameters governing the width of the distribution, \(B\) accounts for the contribution of the particles arriving from the anti-Sun direction. One can see that when \(B=0\), Equation 4 is simplified to a Gaussian distribution along IMF. Therefore, we can model both: simple PAD of GLE particles (\(B=0\)), as well as complicated angular distributions, including particle flux from the anti-Sun direction.
In all cases, it is assumed that GLE particles arrive from the Sun along the axis of symmetry whose direction is defined by angles \(\Psi \) and \(\Lambda \) (latitude and longitude). Here, the optimization was performed over the set of parameters given in Equations 2–4 over the experimental NM records, that is by minimizing the difference between the modeled and measured NM responses. The unfolding was based on Levenberg–Marquardt method (Levenberg, 1944; Marquardt, 1963) using specific and improved regularization (for details see Aleksandrov, 1971; Golub and Van Loan, 1980; Golub, Hansen, and O’Leary, 1999). The main advantage of our method is the possibility to solve ill-posed problem(s), occasionally arising from marginal experimental NM responses and/or complicated spectral and angular distribution(s), e.g. bi-directional flux of SEPs, (see the discussions in Tikhonov et al., 1995; Mavrodiev, Mishev, and Stamenov, 2004; Aster, Borchers and Thurber, 2005; Mishev, Poluianov, and Usoskin, 2017; Mishev et al., 2018). The method was recently verified with PAMELA space probe direct observations and good agreement was reported (for details see Koldobskiy et al., 2019b; Mishev et al., 2021, and the discussion therein).
3.1 Results of the Magnetospheric Modeling
As the first step we computed cut-off rigidities and asymptotic directions for all NMs considered in the analysis (Table 1). The magnetospheric transmissivity for the GLE particles was modeled with the MAGNETOCOSMICS code (Desorgher et al., 2005). Here, we used the International Geomagnetic Reference Field (IGRF) geomagnetic model (epoch 2000) as the internal field model (Langel, 1987; Macmillan et al., 2003) and the Tsyganenko 89 model as the external field (Tsyganenko, 1989), which allowed us to obtain the needed rigidity cut-offs and asymptotic directions with a reasonable precision (Kudela and Usoskin, 2004; Kudela, Bučik, and Bobik, 2008; Nevalainen, Usoskin, and Mishev, 2013). Selected NM asymptotic directions used for our analysis are shown in Figure 3. We note that here we presented the asymptotic directions in the rigidity range 1 – 5 GV (range of maximal NM response), whilst in the analysis we used the 1 – 20 GV rigidity range, as described in Section 3.
Asymptotic directions of selected NMs during GLE \(\#\) 67 on 2 November 2003 at event onset (17:30 UT). The acronyms of NMs are given in Table 1. The color lines and acronyms and numbers depict the asymptotic directions and rigidities, which are plotted in the rigidity range 1 – 5 GV. The lines of equal pitch angles relative to the anisotropy axis are plotted for 20∘, 40∘, 60∘ and 80∘ for sunward directions (solid lines), 100∘, 120∘, 140∘ and 160∘, for anti-Sun direction (dashed lines), respectively. The cross depicts the measured by ACE space probe IMF direction.
3.2 Unfolding Procedure Criteria
For the goodness of the fit we employed several criteria: \(i\)) The main criterion is related to minimization of the normalized square root of the sum of squared relative differences between the observed and modeled increases for each NM station (residual) (e.g. Himmelblau, 1972; Dennis and Schnabel, 1996):
A good convergence of the optimization and a robust solution are achieved in the case when \(\mathcal{D} \le 5\) – 10% for strong and moderately strong events, respectively (Vashenyuk et al., 2006; Mishev and Usoskin, 2016a, 2018). In case when the count rate increase of NMs is smaller (weak events or late phase of an event) \(\mathcal{D}\) could be as large as about 15 – 20% (e.g. Mishev, Poluianov, and Usoskin, 2017; Mishev et al., 2018, 2021), but still leading to reliable results.
As additional criteria we employed: \(ii\)) the relative difference between the observed and modeled NM increases must be of the order of about 10 – 15% or smaller; \(iii\)) uniform distribution of the residuals is required; \(iv\)) the value of the reduced \(\chi _{r}^{2}\) should be close to unity, where \(\chi _{r}^{2}= \chi ^{2}\)/DoF, DoF corresponds to degrees of freedom. The combination of these criteria allowed us to select the most relevant solution (e.g. see Dennis and Schnabel, 1996; Tikhonov et al., 1995; Mishev et al., 2018; Mishev and Usoskin, 2018). The corresponding forward modeling allowed us to assess the quality of the derived spectra and angular distribution similarly to Mishev et al. (2021).
4 Results of the Analysis
Using Advanced Composition Explorer (ACE) measurements as initial guess for the optimization procedure (step 2) and (step 3) we derived the spectral and angular characteristics of GLE particles. For the analysis we considered 5-min detrended NM data retrieved from IGLED (Usoskin et al., 2020). The analysis was performed assuming different spectral and PAD shapes of GLE particles in order to encompass all the possibilities in the model (Equations 2–4). Additional modeling of the interplanetary transport of SEPs (the details are given in Kocharov et al., 2005, 2017), allowed us to adjust the derived best fit by selection of appropriate angular distribution of SEPs. Hence, the derived PADs from the interplanetary transport of SEPs were used as initial guess for the optimization as well as a cross check for the derived from NM data analysis PADs. Thus, using the results from interplanetary transport modeling and the global NM response modeling, we derived a set of spectral and angular characteristics of SEPs, which are self consistent.
According to our analysis the most appropriate set of parameters corresponds to modified power-law rigidity spectrum (Equation 2) and double Gaussian PAD (Equation 4) i.e. particles arriving from both sunward and anti-Sun directions. This result is consistent with the NM data where an early count rate increase at Oulu station with asymptotic viewing direction in the anti-Sun direction was observed (see Figure 3). The derived rigidity spectra with the anisotropy characteristics of the high-energy SEPs are presented in Figure 4. The left-hand panels of Figure 4 present the derived rigidity spectra during various stages of the event, namely initial phase (Figure 4a), main phase (Figure 4c) and late phase (Figure 4e). The corresponding pitch-angle distributions are presented in the right-hand panel of Figure 4, accordingly.
Derived SEP rigidity spectra (left panels) and PADs (right panels) during GLE \(\#\) 67 on 2 November 2003, details are given in Table 2. The black solid line denotes the GCR flux, which corresponds to the time period of the event occurrence. Time (UT) refers to the start of the corresponding five minute interval over which the data are integrated.
The rigidity spectrum was gradually softening throughout the event, being moderately hard at the event onset and soft at the late phase of the event. The steepening of the spectrum \(\delta \gamma \) varied throughout the event, resulting in a moderate steepening of the spectrum during the early phase. After 18:10 UT, the derived rigidity spectra can be described by a pure power-law. The particle flux rapidly increased during the initial phase of the event, reached the maximum at about 17:55 UT, and thereafter gradually decreased. The anisotropy was relatively high during the event’s onset, yet not very narrow, that is, not a beam like GLE particles flux was revealed. Lately, the derived PAD broadened out. The derived spectral and anisotropy characteristics are summarized in Table 2, where the fit quality criteria \(\mathcal{D}\) and \(\chi _{r}^{2}\) are also presented.
An additional analysis of the event was performed assuming an exponential shape of the rigidity spectrum (Equation 3). We derived similar anisotropy characteristics (the details are given in Table 3). The derived rigidity spectra were slightly harder compared to a power-law model. The quality of the fit of NM response was similar for both used models. Therefore during the initial phase of the event the NM response can be modeled with either a modified power-law or exponential rigidity spectrum with similar precision. However, after 17:55 UT the modeling with a modified power-law rigidity spectrum was more accurate, but the exponential spectrum still provided a reasonable description. After 18:10 UT, the derived rigidity spectra were described by a pure power-law, while the exponential spectrum modeling leaded to significantly greater difference between modeled and observed NM increases.
We would like to point out that the proposed approach of initial (strong anisotropy and modified power-law or exponential spectrum), main (moderate anisotropy, maximal particle flux and modified power-law spectrum) and late (isotropic flux and pure power-law spectrum) phases of the event differs from that of widely discussed prompt and delayed component proposed by Vashenyuk et al. (2006), Vashenyuk, Balabin, and Gvozdevsky (2011), Miroshnichenko, Vashenyuk, and Perez-Peraza (2013). Yet, the initial and early main phases of the event correspond roughly to the prompt component, whilst the late phase corresponds to the delayed component. Both approaches can be interpreted in relation to different episodes of SEP acceleration (for details see the discussion in Pérez-Peraza et al., 2009; Vashenyuk, Balabin, and Gvozdevsky, 2011; Kocharov et al., 2017, 2018).
4.1 Quality of the Fit
In order to verify the quality of the fit we performed a forward modeling using the derived spectra and PAD. A comparison between modeled and experimental count rate increases during GLE \(\#\) 67 for selected NMs is presented in Figure 5. The quality of the fit is similar for the other NM stations. For the comparison we used the best fit, i.e., modified power-law rigidity spectra and double Gaussian PAD (Table 2), while in the other cases the difference between modeled and experimental NM responses is considerably greater.
Accordingly, the contour plot of the sum of variances (Equation 5) for the best fit solutions vs. geographic latitude \(\Psi \) and longitude \(\Lambda \) is presented in Figure 6. The location of the minimal contour of sum of variances slightly differs from the derived apparent source position (details are given in Table 2). This is due to the application of combination of criteria for the best fit instead of using only one criterion as the minimal residual \(\mathcal{D}\). The results of the forward modeling demonstrate that the derived solutions have good precision and quality and the model describes reasonably the experimental data (Figures 5–6.)
Contour plot of \(\mathcal{D}\) (Equation 5) for the best fit solutions vs. geographic latitude and longitude during GLE \(\#\) 67 event on 2 November 2003 at 18:00 UT, normalized to the minimal \(\mathcal{D}\). The small white oval corresponds to the assumed apparent source position, while the white cross corresponds to the IMF direction.
The existence, uniqueness and stability of the derived solution(s) were also studied. The stability of the solutions is often violated, because the inverse problems are typically ill-conditioned and/or ill-posed (e.g. Tikhonov et al., 1995, and the references therein). However, the large number of NM stations with different response (more than \(2(n-1)\)) and the obtained contour plots of \(\mathcal{D}\) for the best fit solutions, allowed us to assess the uniqueness and stability of the derived solutions. In case when the initial guess is far from the local minimum, the derived solution possessed significantly greater residual compared to that in Table 2 or it was not physical. Note that ill-posed inverse problems typically converge to the global minimum only if the initial guess is close to the final solution (Dennis and Schnabel, 1996; Tikhonov et al., 1995). Thus, the subsequent forward modeling using also the information from the derived angular distributions from interplanetary transport modeling, allowed us to derive a reliable consistent solution, in which small variations of the input (initial guess) do not altered the derived set of model parameters. An estimation of model accuracy, namely confidence limits at a level of 95% of \(J_{0}\) and \(\gamma \) is given in Figure 7.
The determination of the spectral and angular characteristics during the late phase of the event was with smaller precision compared to the initial and main phase. This is most-likely due to isotropization of the SEP flux resulting in more uniform distribution of NM responses, eventually leading to a less accurate assessment of apparent source position.
4.2 Particle Fluence
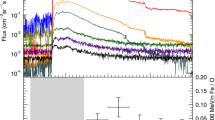
The time, energy and angle integrated particle fluence is presented on Figure 8. Note that for the integration an exponential spectrum was used during the initial stage of the event, whilst modified and pure power-law assumptions were used during the main and late phase of the event, respectively. The fluence during GLE \(\#\) 67 was compared with recent estimation based on simplified “effective rigidity” approach (Koldobskiy et al., 2019a,b), the details are given in Usoskin et al. (2020). The main simplification of this approach is the assumption that SEP fluxes are isotropic. A very good agreement was achieved, specifically in the region of maximal NM response. Yet, a comparison with earlier reconstruction (e.g. Tylka and Dietrich, 2009; Raukunen et al., 2018) agreed within a factor 2 – 3. The observed discrepancy is most likely due to different reconstruction methods and model assumptions, since Tylka and Dietrich (2009) and Raukunen et al. (2018) employed simplified analysis of NM data, different spectral shapes and outdated NM yield function (e.g. Clem and Dorman, 2000). The NM yield function used here (Mishev et al., 2020), is more suitable for GLE analysis (for details see Nuntiyakul et al., 2018; Koldobskiy et al., 2019a), because provides a more realistic assessment of high-altitude NMs responses, that is for AATY, BKSN, CALG, LMKS, MXCO, SNAE, SOPO and TSMB, and was recently verified (Koldobskiy et al., 2019b; Mishev et al., 2021). Modeling of NM response with different specific NM yield functions usually leads to a considerable spread of derived SEP characteristics (Bütikofer and Flückiger, 2015). Therefore, we do not expect exact coincidence, because the simplified modeling in Tylka and Dietrich (2009) and Raukunen et al. (2018), where the anisotropy is neglected and a different yield function was used.
Fluence of high-energy SEPs during GLE \(\#\) 67 compared with the estimations of (Usoskin et al., 2020). Panel A depicts the particle fluence, whilst panel B depicts the corresponding confidence intervals at a level of 95%.
5 Discussion and Conclusions
In the work presented here, we performed a detailed modeling and reconstructed the spectral and angular characteristics of high-energy SEPs in the vicinity of Earth during the GLE \(\#\) 67 on 2 November 2003. In this study we used ground-based NM and space-borne data and employed the corresponding data analysis. We examined several possible shapes of GLE particles spectra and angular distribution, namely exponential or modified power-law rigidity spectrum and single or double Gaussian PAD. The best fit of the global NM network revealed a complicated PAD and moderately hard SEP spectra. However, an exponential rigidity spectrum, specifically during the event onset and initial phase, depicted a similar quality of the fit. The event was characterized by a bi-directional particle flux and relatively strong anisotropy during the initial phase. The anisotropy gradually decreased in the course of the event, but remained significant throughout the whole event. According to our analysis we found evidence of particles arriving from both sunward and anti-sunward directions. The dynamical evolution of the spectral and angular properties of GLE particles was obtained in the course of the event.
During the event’s onset and initial phase, the rigidity spectrum was moderately hard (\(\gamma \approx 5.5\)), with moderate steepness \(\delta \gamma \approx 0.1\) – 0.2. During this stage of the event the derived PAD was relatively narrow for particles arriving from the Sun direction (\(\sigma _{1}^{2} \approx 1.5\) – 2.0 rad2), while particles arriving from anti-Sun direction revealed considerably wider PAD (\(\sigma _{2}^{2} \approx 8\) rad2), which is close to \(\pi \). During the main stage of the event, when the peak of the SEP flux was observed, the rigidity spectrum was softer (\(\gamma \approx 6.5\)), the steepness of the spectrum vanished \(\delta \gamma = 0\), i.e., a pure power-law spectrum was derived, and the PAD of SEP arriving from both directions broadened. During the late phase of the event, the PAD was almost isotropic and a constant softening of the rigidity spectrum was derived.
Here, we explicitly assessed the uncertainty and confidence limits of the derived fit of the GLE particles characteristics in a truly way, that is by forward modeling of the global NM response using the derived spectra and PADs. The estimation of the errors in the apparent source position (\(\Psi \) and \(\Lambda \)) determination is about 10 degrees. The confidence boundaries of the derived spectra are given in great detail in Figure 7. One can see that the derived error estimates and confidence limits are within the systematic errors of the employed NM yield function, that is within atmospheric cascade development (e.g. Engel, Heck, and Pierog, 2011; Mishev et al., 2020, and the references therein).
The derived characteristics during the GLEs could serve as a good basis to study their origin (e.g. Kocharov et al., 2017) and/or for space weather applications similarly to Mishev and Usoskin (2018), Mishev et al. (2021).
References
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A., Bellotti, R., Boezio, M., Bogomolov, E.A., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carlson, P., Casolino, M., Castellini, G., De Donato, C., De Santis, C., De Simone, N., Di Felice, V., Formato, V., Galper, A.M., Karelin, A.V., Koldashov, S.V., Koldobskiy, S., Krutkov, S.Y., Kvashnin, A.N., Leonov, A., Malakhov, V., Marcelli, L., Martucci, M., Mayorov, A.G., Menn, W., Mergè, M., Mikhailov, V.V., Mocchiutti, E., Monaco, A., Mori, N., Munini, R., Osteria, G., Palma, F., Panico, B., Papini, P., Pearce, M., Picozza, P., Ricci, M., Ricciarini, S.B., Sarkar, R., Scotti, V., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y.I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S.A., Yurkin, Y.T., Zampa, G., Zampa, N.: 2016, Measurements of cosmic-ray hydrogen and helium isotopes with the PAMELA experiment. Astrophys. J. 818(1), 68.
Aguilar, M., Alcaraz, J., Allaby, J., Alpat, B., Ambrosi, G., Anderhub, H., Ao, L., Arefiev, A., Arruda, L., Azzarello, P., Basile, M., Barao, F., Barreira, G., Bartoloni, A., Battiston, R., Becker, R., Becker, U., Bellagamba, L., Béné, P., Berdugo, J., Berges, P., Bertucci, B., Biland, A., Bindi, V., Boella, G., Boschini, M., Bourquin, M., Bruni, G., Buénerd, M., Burger, J.D., Burger, W.J., Cai, X.D., Cannarsa, P., Capell, M., Casadei, D., Casaus, J., Castellini, G., Cernuda, I., Chang, Y.H., Chen, H.F., Chen, H.S., Chen, Z.G., Chernoplekov, N.A., Chiueh, T.H., Choi, Y.Y., Cindolo, F., Commichau, V., Contin, A., Cortina-Gil, E., Crespo, D., Cristinziani, M., Dai, T.S., Dela Guia, C., Delgado, C., Di Falco, S., Djambazov, L., D’Antone, I., Dong, Z.R., Duranti, M., Engelberg, J., Eppling, F.J., Eronen, T., Extermann, P., Favier, J., Fiandrini, E., Fisher, P.H., Flügge, G., Fouque, N., Galaktionov, Y., Gervasi, M., Giovacchini, F., Giusti, P., Grandi, D., Grimm, O., Gu, W.Q., Haino, S., Hangarter, K., Hasan, A., Hermel, V., Hofer, H., Hungerford, W., Ionica, M., Jongmanns, M., Karlamaa, K., Karpinski, W., Kenney, G., Kim, D.H., Kim, G.N., Kim, K.S., Kirn, T., Klimentov, A., Kossakowski, R., Kounine, A., Koutsenko, V., Kraeber, M., Laborie, G., Laitinen, T., Lamanna, G., Laurenti, G., Lebedev, A., Lechanoine-Leluc, C., Lee, M.W., Lee, S.C., Levi, G., Lin, C.H., Liu, H.T., Lu, G., Lu, Y.S., Lübelsmeyer, K., Luckey, D., Lustermann, W., Maña, C., Margotti, A., Mayet, F., McNeil, R.R., Menichelli, M., Mihul, A., Mujunen, A., Oliva, A., Palmonari, F., Park, H.B., Park, W.H., Pauluzzi, M., Pauss, F., Pereira, R., Perrin, E., Pevsner, A., Pilo, F., Pimenta, M., Plyaskin, V., Pojidaev, V., Pohl, M., Produit, N., Quadrani, L., Rancoita, P.G., Rapin, D., Ren, D., Ren, Z., Ribordy, M., Richeux, J.P., Riihonen, E., Ritakari, J., Ro, S., Roeser, U., Sagdeev, R., Santos, D., Sartorelli, G., Sbarra, C., Schael, S., Von Dratzig, A.S., Schwering, G., Seo, E.S., Shin, J.W., Shoumilov, E., Shoutko, V., Siedenburg, T., Siedling, R., Son, D., Song, T., Spada, F.R., Spinella, F., Steuer, M., Sun, G.S., Suter, H., Tang, X.W., Ting, S.C.C., Ting, S.M., Tomassetti, N., Tornikoski, M., Torsti, J., Trümper, J., Ulbricht, J., Urpo, S., Valtonen, E., Vandenhirtz, J., Velikhov, E., Verlaat, B., Vetlitsky, I., Vezzu, F., Vialle, J.P., Viertel, G., Vité, D., Von Gunten, H., Wicki, S.W., Wallraff, W., Wang, J.Z., Wiik, K., Williams, C., Wu, S.X., Xia, P.C., Xu, S., Xu, Z.Z., Yan, J.L., Yan, L.G., Yang, C.G., Yang, J., Yang, M., Ye, S.W., Zhang, H.Y., Zhang, Z.P., Zhao, D.X., Zhou, F., Zhou, Y., Zhu, G.Y., Zhu, W.Z., Zhuang, H.L., Zichichi, A., Zimmermann, B., Zuccon, P.: 2010, Relative composition and energy spectra of light nuclei in cosmic rays: results from AMS-01. Astrophys. J. 724(1), 329.
Aleksandrov, L.: 1971, The Newton–Kantorovich regularized computing processes. U.S.S.R. Comput. Math. Math. Phys. 11(1), 46. DOI.
Andriopoulou, M., Mavromichalaki, H., Plainaki, C., Belov, A., Eroshenko, E.: 2011a, Intense ground-level enhancements of solar cosmic rays during the last solar cycles. Solar Phys. 269(1), 155.
Andriopoulou, M., Mavromichalaki, H., Preka-Papadema, P., Plainaki, C., Belov, A., Eroshenko, E.: 2011b, Solar activity and the associated ground level enhancements of solar cosmic rays during solar cycle 23. Astrophys. Space Sci. Trans. 7(4), 439.
Aschwanden, M.: 2012, GeV particle acceleration in solar flares and ground level enhancement (GLE) events. Space Sci. Rev. 171(1-4), 3.
Aster, R.C., Borchers, B., Thurber, C.H.: 2005, Parameter Estimation and Inverse Problems, Elsevier, New York. ISBN 0-12-065604-3.
Bazilevskaya, G.A.: 2005, Solar cosmic rays in the near Earth space and the atmosphere. Adv. Space Res. 35(3), 458.
Bieber, J.W., Evenson, P.A.: 1995, Spaceship Earth - an optimized network of neutron monitors. In: Proc. of 24th ICRC Rome, Italy, 28 August - 8 September 1995 4, 1316.
Bombardieri, D.J., Duldig, M.L., Michael, K.J., Humble, J.E.: 2006, Relativistic proton production during the 2000 July 14 solar event: the case for multiple source mechanisms. Astrophys. J. 644(1), 565.
Burger, R.A., Potgieter, M.S., Heber, B.: 2000, Rigidity dependence of cosmic ray proton latitudinal gradients measured by the Ulysses spacecraft: implication for the diffusion tensor. J. Geophys. Res. 105, 27447.
Bütikofer, R., Flückiger, E.O.: 2015, What are the causes for the spread of GLE parameters deduced from NM data? J. Phys. Conf. Ser. 632(1), 012053. DOI.
Bütikofer, R., Flückiger, E.O., Desorgher, L., Moser, M.R., Pirard, B.: 2009, The solar cosmic ray ground-level enhancements on 20 January 2005 and 13 December 2006. Adv. Space Res. 43(4), 499.
Clem, J., Dorman, L.: 2000, Neutron monitor response functions. Space Sci. Rev. 93, 335.
Cramp, J.L., Humble, J.E., Duldig, M.L.: 1995, The cosmic ray ground-level enhancement of 24 October 1989. In: Proceedings Astronomical Society of Australia 11, 28.
Cramp, J.L., Duldig, M.L., Flückiger, E.O., Humble, J.E., Shea, M.A., Smart, D.F.: 1997, The October 22, 1989, solar cosmic ray enhancement: an analysis of the anisotropy and spectral characteristics. J. Geophys. Res. 102(A11), 24 237.
Debrunner, H., Flückiger, E.O., Gradel, H., Lockwood, J.A., McGuire, R.E.: 1988, Observations related to the acceleration, injection, and interplanetary propagation of energetic protons during the solar cosmic ray event on February 16, 1984. J. Geophys. Res. 93(A7), 7206.
Dennis, J.E., Schnabel, R.B.: 1996, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice-Hall, Englewood Cliffs. ISBN 13-978-0-898713-64-0.
Desai, M., Giacalone, J.: 2016, Large gradual solar energetic particle events. Living Rev. Solar Phys. 13(1), 3. DOI.
Desorgher, L., Flückiger, E.O., Gurtner, M., Moser, M.R., Bütikofer, R.: 2005, A GEANT 4 code for computing the interaction of cosmic rays with the Earth’s atmosphere. Int. J. Mod. Phys. A 20(A11), 6802.
Dorman, L.: 2006, Cosmic Ray Interactions, Propagation, and Acceleration in Space Plasmas, Astrophysics and Space Science Library 339, Springer, Dordrecht. ISBN 13-978-1-4020-5100-5.
Engel, R., Heck, D., Pierog, T.: 2011, Extensive air showers and hadronic interactions at high energies. Annu. Rev. Nucl. Part. Sci. 61, 467.
Forbush, S.E.: 1946, Three unusual cosmic-ray increases possibly due to charged particles from the Sun. Phys. Rev. 70(9-10), 771. DOI.
Forbush, S.E.: 1958, Cosmic-ray intensity variations during two solar cycles. J. Geophys. Res. 63(4), 651.
Gil, A., Usoskin, I.G., Kovaltsov, G.A., Mishev, A.L., Corti, C., Bindi, V.: 2015, Can we properly model the neutron monitor count rate? J. Geophys. Res. 120, 7172.
Gleeson, L.J., Axford, W.I.: 1968, Solar modulation of galactic cosmic rays. Astrophys. J. 154, 1011.
Golub, G.H., Hansen, P.C., O’Leary, D.P.: 1999, Tikhonov regularization and total least squares. SIAM J. Matrix Anal. Appl. 21, 185.
Golub, G.H., Van Loan, C.F.: 1980, An analysis of the total least squares problem. SIAM J. Numer. Anal. 17(6), 883.
Gopalswamy, N., Xie, H., Yashiro, S., Akiyama, S., Mäkelä, P., Usoskin, I.G.: 2012, Properties of ground level enhancement events and the associated solar eruptions during solar cycle 23. Space Sci. Rev. 171(1-4), 23.
Gopalswamy, N., Yashiro, S., Thakur, N., Mäkelä, P., Xie, H., Akiyama, S.: 2016, The 2012 July 23 backside eruption: an extreme energetic particle event? Astrophys. J. 833(2), 216. DOI.
Hatton, C.: 1971, The neutron monitor. In: Progress in Elementary Particle and Cosmic-Ray Physics, North-Holland, Amsterdam. Chapter 1.
Hatton, C., Carmichael, H.: 1964, Experimental investigation of the nm-64 neutron monitor. Can. J. Phys. 42, 2443.
Himmelblau, D.M.: 1972, Applied Nonlinear Programming, McGraw-Hill, New York. ISBN 978-0070289215.
Klein, K.-L., Dalla, S.: 2017, Acceleration and propagation of solar energetic particles. Space Sci. Rev. 212(3-4), 1107. DOI.
Kocharov, L., Kovaltsov, G., Torsti, J., Huttunen-Heikinmaa, K.: 2005, Modeling the solar energetic particle events in closed structures of interplanetary magnetic field. J. Geophys. Res. 110(A12), A12S03.
Kocharov, L., Pohjolainen, S., Mishev, A., Reiner, M.J., Lee, J., Laitinen, T., Didkovsky, L.V., Pizzo, V.J., Kim, R., Klassen, A., Karlicky, M., Cho, K.-S., Gary, D.E., Usoskin, I., Valtonen, E., Vainio, R.: 2017, Investigating the origins of two extreme solar particle events: proton source profile and associated electromagnetic emissions. Astrophys. J. 839(2), 79.
Kocharov, L., Pohjolainen, S., Reiner, M.J., Mishev, A., Wang, H., Usoskin, I., Vainio, R.: 2018, Spatial organization of seven extreme solar energetic particle events. Astrophys. J. Lett. 862(2), L20. DOI.
Koldobskiy, S.A., Bindi, V., Corti, C., Kovaltsov, G.A., Usoskin, I.G.: 2019a, Validation of the neutron monitor yield function using data from AMS-02 experiment 2011 – 2017. J. Geophys. Res. Space Phys. 124, 2367. DOI.
Koldobskiy, S., Kovaltsov, G.A., Mishev, A., Usoskin, I.G.: 2019b, New method of assessment of the integral fluence of solar energetic (>1 GV rigidity) particles from neutron monitor data. Solar Phys. 294, 94. DOI.
Kudela, K., Bučik, R., Bobik, P.: 2008, On transmissivity of low energy cosmic rays in disturbed magnetosphere. Adv. Space Res. 42(7), 1300.
Kudela, K., Usoskin, I.: 2004, On magnetospheric transmissivity of cosmic rays. Czechoslov. J. Phys. 54(2), 239.
Langel, R.A.: 1987, Main field in geomagnetism. In: Jacobs, J.A. (ed.) Geomagnetism, Academic Press, London, 249. Chapter 1.
Levenberg, K.: 1944, A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 2, 164.
Macmillan, S., Maus, S., Bondar, T., Chambodut, A., Golovkov, V., Holme, R., Langlais, B., Lesur, V., Lowes, F., Lühr, H., Mai, W., Mandea, M., Olsen, N., Rother, M., Sabaka, T., Thomson, A., Wardinski, I.: 2003, The 9th-generation international geomagnetic reference field. Geophys. J. Int. 155(3), 1051. DOI.
Mangeard, P.-S., Ruffolo, D., Sáiz, A., Nuntiyakul, W., Bieber, J.W., Clem, J., Evenson, P., Pyle, R., Duldig, M.L., Humble, J.E.: 2016, Dependence of the neutron monitor count rate and time delay distribution on the rigidity spectrum of primary cosmic rays. J. Geophys. Res. Space Phys. 121(12), 11,620. DOI.
Marquardt, D.: 1963, An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11(2), 431.
Mavrodiev, S.C., Mishev, A.L., Stamenov, J.N.: 2004, A method for energy estimation and mass composition determination of primary cosmic rays at the Chacaltaya observation level based on the atmospheric Cherenkov light technique. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 530(3), 359. DOI.
Mavromichalaki, H., Papaioannou, A., Plainaki, C., Sarlanis, C., Souvatzoglou, G., Gerontidou, M., Papailiou, M., Eroshenko, E., Belov, A., Yanke, V., Flückiger, E.O., Bütikofer, R., Parisi, M., Storini, M., Klein, K.-L., Fuller, N., Steigies, C.T., Rother, O.M., Heber, B., Wimmer-Schweingruber, R.F., Kudela, K., Strharsky, I., Langer, R., Usoskin, I., Ibragimov, A., Chilingaryan, A., Hovsepyan, G., Reymers, A., Yeghikyan, A., Kryakunova, O., Dryn, E., Nikolayevskiy, N., Dorman, L., Pustil’Nik, L.: 2011, Applications and usage of the real-time neutron monitor database. Adv. Space Res. 47, 2210.
McCracken, K.G., Rao, V.R., Shea, M.A.: 1962, The trajectories of cosmic rays in a high degree simulation of the geomagnetic field. Technical Report 77, Massachusetts Institute of Technology, Cambridge, MA, USA.
Miroshnichenko, L.I., 2018, Retrospective analysis of GLEs and estimates of radiation risks. J. Space Weather Space Clim. 8(A52), A09S08. DOI.
Miroshnichenko, L.I., Vashenyuk, E.V., Perez-Peraza, J.A.: 2013, Solar cosmic rays: 70 years of ground-based observations. Geomagn. Aeron. 53(5), 541. DOI.
Miroshnichenko, L.I., Klein, K.-L., Trottet, G., Lantos, P., Vashenyuk, E.V., Balabin, Y.V., Gvozdevsky, B.B.: 2005, Relativistic nucleon and electron production in the 2003 October 28 solar event. J. Geophys. Res. Space Phys. 110(A9), A09S08. DOI.
Mishev, A.L., Kocharov, L.G., Usoskin, I.G.: 2014, Analysis of the ground level enhancement on 17 may 2012 using data from the global neutron monitor network. J. Geophys. Res. 119, 670.
Mishev, A., Poluianov, S., Usoskin, S.: 2017, Assessment of spectral and angular characteristics of sub-GLE events using the global neutron monitor network. J. Space Weather Space Clim. 7, A28. DOI.
Mishev, A., Usoskin, I.: 2016a, Analysis of the ground level enhancements on 14 July 2000 and on 13 December 2006 using neutron monitor data. Solar Phys. 291(4), 1225.
Mishev, A., Usoskin, I.: 2016b, Erratum to:analysis of the ground level enhancements on 14 July 2000 and on 13 December 2006 using neutron monitor data. Solar Phys. 291(4), 1579.
Mishev, A.L., Usoskin, I.G.: 2018, Assessment of the radiation environment at commercial jet-flight altitudes during GLE 72 on 10 September 2017 using neutron monitor data. Space Weather 16(12), 1921. DOI.
Mishev, A., Usoskin, I., Kovaltsov, G.: 2013, Neutron monitor yield function: new improved computations. J. Geophys. Res. 118, 2783.
Mishev, A., Usoskin, I., Raukunen, O., Paassilta, M., Valtonen, E., Kocharov, L., Vainio, R.: 2018, First analysis of GLE 72 event on 10 September 2017: spectral and anisotropy characteristics. Solar Phys. 293, 136.
Mishev, A.L., Koldobskiy, S.A., Kovaltsov, G.A., Gil, A., Usoskin, I.G.: 2020, Updated neutron-monitor yield function: bridging between in situ and ground-based cosmic ray measurements. J. Geophys. Res. Space Phys. 125(2), e2019JA027433. DOI.
Mishev, A.L., Koldobskiy, S.A., Usoskin, I.G., Kocharov, L.G., Kovaltsov, G.A.: 2021, Application of the verified neutron monitor yield function for an extended analysis of the ground level enhancement GLE # 71 on May 17, 2012. Space Weather 19, e2020SW002626. DOI.
Moraal, H., McCracken, K.G.: 2012, The time structure of ground level enhancements in solar cycle 23. Space Sci. Rev. 171(1-4), 85.
Nevalainen, J., Usoskin, I., Mishev, A.: 2013, Eccentric dipole approximation of the geomagnetic field: application to cosmic ray computations. Adv. Space Res. 52(1), 22.
Nuntiyakul, W., Sáiz, A., Ruffolo, D., Mangeard, P.-S., Evenson, P., Bieber, J.W., Clem, J., Pyle, R., Duldig, M.L., Humble, J.E.: 2018, Bare neutron counter and neutron monitor response to cosmic rays during a 1995 latitude survey. J. Geophys. Res. Space Phys. 123(9), 7181. DOI.
Pérez-Peraza, J., Vashenyuk, E.V., Miroshnichenko, L.I., Balabin, Y.V., Gallegos-Cruz, A.: 2009, Impulsive, stochastic, and shock wave acceleration of relativistic protons in large solar events of 1989 September 29, 2000 July 14, 2003 October 28, and 2005 January 20. Astrophys. J. 695(2), 865. DOI.
Poluianov, S.V., Usoskin, I.G., Mishev, A.L., Shea, M.A., Smart, D.F.: 2017, GLE and sub-GLE redefinition in the light of high-altitude polar neutron monitors. Solar Phys. 292(11), 176. DOI.
Raukunen, O., Vainio, R., Tylka, A.J., Dietrich, W.F., Jiggens, P., Heynderickx, D., Dierckxsens, M., Crosby, N., Ganse, U., Siipola, R.: 2018, Two solar proton fluence models based on ground level enhancement observations. J. Space Weather Space Clim. 8, A04. DOI.
Reames, D.V.: 2013, The two sources of solar energetic particles. Space Sci. Rev. 175(1-4), 53. DOI.
Ryan, J., Lockwood, J., Debruner, H.: 2000, Solar energetic particles. Space Sci. Rev. 93, 35.
Shea, M.A., Smart, D.F.: 1982, Possible evidence for a rigidity-dependent release of relativistic protons from the solar corona. Space Sci. Rev. 32, 251.
Shea, M.A., Smart, D.F.: 1990, A summary of major solar proton events. Solar Phys. 127, 297.
Shea, M.A., Smart, D.F.: 2012, Space weather and the ground-level solar proton events of the 23rd solar cycle. Space Sci. Rev. 171, 161.
Simpson, J.: 1957, Cosmic-radiation neutron intensity monitor. Ann. Int. Geophys. Year 4, 351.
Simpson, J.: 2000, The cosmic ray nucleonic component: the invention and scientific uses of the neutron monitor. Space Sci. Rev. 93, 11. DOI.
Simpson, J., Fonger, W., Treiman, S.: 1953, Cosmic radiation intensity-time variation and their origin. I. Neutron intensity variation method and meteorological factors. Phys. Rev. 90, 934.
Stoker, P.H.: 1995, Relativistic solar proton events. Space Sci. Rev. 73(3-4), 327. DOI.
Stoker, P.H., Dorman, L.I., Clem, J.M.: 2000, Neutron monitor design improvements. Space Sci. Rev. 93(1-2), 361.
Tikhonov, A.N., Goncharsky, A.V., Stepanov, V.V., Yagola, A.G.: 1995, Numerical Methods for Solving Ill-Posed Problems, Kluwer Academic, Dordrecht. ISBN 978-90-481-4583-6.
Tsyganenko, N.A.: 1989, A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 37(1), 5.
Tylka, A., Dietrich, W.: 2009, A new and comprehensive analysis of proton spectra in ground-level enhanced (GLE) solar particle events. In: Proc. of 31th ICRC, Lodz, Poland, 7-15 July 2009, 0273.
Usoskin, I.G., Bazilevskaya, G.A., Kovaltsov, G.A.: 2011, Solar modulation parameter for cosmic rays since 1936 reconstructed from ground-based neutron monitors and ionization chambers. J. Geophys. Res. 116, A02104.
Usoskin, I., Alanko-Huotari, K., Kovaltsov, G., Mursula, K.: 2005, Heliospheric modulation of cosmic rays: monthly reconstruction for 1951-2004. J. Geophys. Res. 110 A12108.
Usoskin, I.G., Ibragimov, A., Shea, M.A., Smart, D.F.: 2015, Database of ground level enhancements (GLE) of high energy solar proton events. PoS, 30, 054. Proc. of 34th ICRC Hague, Netherlands, 30 July - 6 August 2015.
Usoskin, I., Koldobskiy, S., Kovaltsov, G.A., Gil, A., Usoskina, I., Willamo, T., Ibragimov, A.: 2020, Revised GLE database: fluences of solar energetic particles as measured by the neutron-monitor network since 1956. Astron. Astrophys. 640, 2038272. DOI.
Vashenyuk, E.V., Balabin, Y.V., Gvozdevsky, B.B.: 2011, Features of relativistic solar proton spectra derived from ground level enhancement events (GLE) modeling. Astrophys. Space Sci. Trans. 7(4), 459. DOI.
Vashenyuk, E.V., Balabin, Y.V., Pérez-Peraza, J., Gallegos-Cruz, A., Miroshnichenko, L.I.: 2006, Some features of the sources of relativistic particles at the sun in the solar cycles 21-23. Adv. Space Res. 38(3), 411.
Vos, E.E., Potgieter, M.S.: 2015, New modeling of galactic proton modulation during the minimum of solar cycle 23/24. Astrophys. J. 815, 119. DOI.
Acknowledgements
This work was supported by the Academy of Finland (projects 330064 QUASARE, 321882 ESPERA). The work on comparative analysis of particle fluences was supported by the Russian Science Foundation project no. 20-72-10170. The work benefited from discussions in the framework of the International Space Science Institute International Team 441: High EneRgy sOlar partICle Events Analysis (HEROIC). We acknowledge all the PIs and colleagues from the neutron monitor stations, who kindly provided the data used in this analysis, namely: Alma Ata, Apatity, Athens, Baksan, Barentsburg, Calgary, Cape Schmidt, Forth Smith, Hermanus, Inuvik, Irkutsk, Kerguelen, Kiel, Larc, Lomnicky Štit, Magadan, McMurdo, Mexico City, Moscow, Nain, Newark, Norilsk, Novosibirsk, Oulu, Peawanuck, Rome, Sanae, South Pole, Terre Adelie, Thule, Tixie, Tsumeb and Yakutsk.
Funding
Open access funding provided by University of Oulu including Oulu University Hospital.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure of Potential Conflicts of Interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mishev, A.L., Koldobskiy, S.A., Kocharov, L.G. et al. GLE # 67 Event on 2 November 2003: An Analysis of the Spectral and Anisotropy Characteristics Using Verified Yield Function and Detrended Neutron Monitor Data. Sol Phys 296, 79 (2021). https://doi.org/10.1007/s11207-021-01832-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-021-01832-2