Abstract
We present an analysis of coronal mass ejections (CMEs) observed by the Heliospheric Imagers (HIs) onboard NASA’s Solar Terrestrial Relations Observatory (STEREO) spacecraft. Between August 2008 and April 2014 we identify 273 CMEs that are observed simultaneously, by the HIs on both spacecraft. For each CME, we track the observed leading edge, as a function of time, from both vantage points, and apply the Stereoscopic Self-Similar Expansion (SSSE) technique to infer their propagation throughout the inner heliosphere. The technique is unable to accurately locate CMEs when their observed leading edge passes between the spacecraft; however, we are able to successfully apply the technique to 151, most of which occur once the spacecraft-separation angle exceeds \(180^{\circ }\), during solar maximum. We find that using a small half-width to fit the CME can result in inferred acceleration to unphysically high velocities and that using a larger half-width can fail to accurately locate the CMEs close to the Sun because the method does not account for CME over-expansion in this region. Observed velocities from SSSE are found to agree well with single-spacecraft (SSEF) analysis techniques applied to the same events. CME propagation directions derived from SSSE and SSEF analysis agree poorly because of known limitations present in the latter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In addition to the continuous outflow of the solar wind, coronal mass ejections (CMEs: e.g. Webb and Howard, 2012) are a phenomenon by which the Sun releases large quantities of energy in the form of magnetised plasma. They are known to drive magnetic disturbances at Earth, and they are in fact the purveyors of the most extreme space-weather effects (e.g. Gosling et al., 1991; Kilpua et al., 2005; Richardson and Cane, 2012; Kilpua et al., 2017). CMEs, and their evolution within the solar-wind environment, have been the subject of space-based observations since they were first discovered in images taken by the Orbiting Solar Observatory 7 (OSO 7, 1971 – 74: Tousey, Howard, and Koomen, 1974). Over the following decades, near-continuous coronagraph coverage has been provided by both ground-based instruments, such as the Mauna Loa MK3 Coronameter (Fisher et al., 1981), and their space-based counterparts, most notably the Large Angle and Spectrometric Coronagraph (LASCO: Brueckner et al., 1995) instruments onboard the Solar and Heliospheric Observatory (SOHO). SOHO was launched in 1995 and, despite a brief loss of communication, the LASCO-C2 and -C3 coronagraphs have operated near-continuously ever since; however, the inner C1 camera was lost in 1998. The launch of the Solar Mass Ejection Imager (SMEI, 2003 – 11: Eyles et al., 2003), onboard the Coriolis spacecraft, extended the coverage of CME observations to far greater solar elongation angles into the heliosphere, by means of wide-angle imaging. Since 2006, the STEREO Heliospheric Imagers (HIs: Eyles et al., 2009) have continued to provide wide-angle imaging of CMEs. Each STEREO spacecraft possesses two HIs: the HI-1 cameras have an angular range in elongation from 4 – 24∘ and the HI-2 cameras cover 18.7 – 88.7∘, aligned to the Ecliptic. Since the launch of STEREO, HI observations, complemented by the STEREO coronagraphs (COR-1 and -2: Howard et al., 2008), have provided a considerable amount of information about CME evolution and propagation through the heliosphere (e.g. Byrne et al., 2010; Davis, Kennedy, and Davies, 2010; Möstl et al., 2010; Savani et al., 2012; Harrison et al., 2012; Rollett et al., 2014; Temmer et al., 2014). Coronagraphs provide coverage close to the Sun, for example a plane-of-sky (POS) range of 1.1 – 32 R⊙ in the LASCO field of view (FOV). The POS is defined as the plane that is perpendicular to the Sun–observer line. Conversely, the inner limit of the FOV of the HIs is \(4^{\circ }\) solar elongation (approximately 15 R⊙ in the POS).
Based on observations from LASCO, prior to the loss of C1, and SOHO’s Extreme Ultraviolet Imaging Telescope (EIT) Zhang et al. (2001, 2004) characterise the acceleration of CMEs into three phases: initiation, impulsive acceleration, and propagation. The initiation phase represents the initial acceleration up to approximately 1.3 to 1.5 R⊙. Although the subsequent impulsive acceleration phase of a CME can vary significantly in magnitude and duration, it is typically limited to the inner corona (defined by Zhang et al. (2001) as ≈1 – 3 R⊙). However, the impulsive acceleration phase can extend throughout the entire LASCO FOV (St. Cyr et al., 2000; Zhang et al., 2004). Typically, beyond a few solar radii, the CME enters its so-called propagation phase. This is characterised by a relatively constant speed, although the very fastest events are seen to exhibit a deceleration, well into the LASCO FOV, and the very slowest events an acceleration (Yashiro et al., 2004; Gopalswamy et al., 2009). This is evidence of drag forces acting on CMEs and causing their speeds to tend toward the ambient solar-wind speed, which is typically 300 – 500 km s−1. Sachdeva et al. (2017) quantify the contributions from the Lorentz and drag forces for 38 CMEs observed by SOHO and find that the former are most significant between 1.65 – 2.45 R⊙, whereas the latter can begin to dominate beyond 4 R⊙, or up to 50 R⊙ for slow CMEs.
CMEs can deviate from radial trajectories due to magnetic forces and interaction with background solar-wind plasma (e.g. Kilpua et al., 2009; Byrne et al., 2010; Lugaz et al., 2011; Möstl et al., 2015; Manchester et al., 2017). Cremades and Bothmer (2004) study 276 CMEs observed by LASCO between 1996 and 2002. They find an average latitudinal deflection of \(18.6^{\circ }\) towards the Equator during solar minimum (up to 1998) and a poleward deflection of \(-7.1^{\circ }\) during solar maximum (2000), with a period of intermediate behaviour in 1999. Isavnin, Vourlidas, and Kilpua (2014) studied 14 flux ropes associated with CMEs using multi-viewpoint coronagraph observations combined with MHD modelling to propagate the structures to 1 AU. Whilst deflection most commonly occurs inside 30 R⊙, they find that significant deflection, particularly in longitude, can occur out to 1 AU. Such longitudinal deflections are due to interactions with the background Parker Spiral solar-wind structure. Wang et al. (2004) show that this causes faster CMEs to deflect from West to East and slower CMEs to deflect from East to West. Isavnin, Vourlidas, and Kilpua (2014) showed a maximum longitudinal deflection of 29∘ from the Sun to Earth for an average speed CME, and Wang et al. (2014) study an individual interplanetary CME that exhibits a longitudinal deflection of \(20^{\circ }\).
Due to the wide-angle nature of heliospheric imaging, it is possible to estimate the three-dimensional direction of propagation of a CME using HI data from a single vantage point by assuming that these features are moving at a constant velocity. This is clearly demonstrated in so-called time–elongation maps, or J-maps (Sheeley et al., 1999, 2008), constructed from HI data, in which this constant linear speed is manifested as an apparent angular acceleration that depends on the propagation direction of the feature with respect to the observing spacecraft. Davies et al. (2009) show that the path of a CME through time–elongation maps may be fitted to retrieve its speed, direction, and launch time. Three geometries commonly used to fit CME parameters using a single vantage point are fixed-\(\phi \) (FP: Kahler and Webb, 2007; Rouillard et al., 2008; Sheeley et al., 2008), self-similar expansion (SSE: Davies et al., 2012; Möstl and Davies, 2013), and harmonic mean (HM: Lugaz, Vourlidas, and Roussev, 2009; Lugaz, 2010). Each of these models is based on the assumptions that the CME possesses a circular cross-sectional front that expands self-similarly with a constant half-width [\(\lambda \)] as the CME propagates. The FP and HM models use respective half-widths of \(0^{\circ }\) and \(90^{\circ }\). The SSE geometry is generalised to any half-width and, as such, the FP and HM geometries can be considered as special cases of SSE, where FP is a point source and HM a circle anchored to the Sun. When these geometries are applied to fit CME kinematic properties from time–elongation data, the fitting methods are referred to as FPF, SSEF, and HMF. Many studies have shown that CME expansion is indeed close to self-similar at interplanetary distances (e.g. Bothmer and Schwenn, 1997; Liu, Richardson, and Belcher, 2005; Savani et al., 2009), however cases of flux ropes that deviate from self-similar expansion are presented by Kilpua et al. (2012), Savani et al. (2011, 2012).
In Article 1 (Harrison et al., 2018) we present the HICAT (www.helcats-fp7.eu/catalogues/wp2_cat.html) catalogue, which contains a list of all CMEs that were observed using HI (965 by STEREO-A and 936 by STEREO-B) during the science phase of the STEREO mission (April 2007 to September 2014). In Article 2 (Barnes et al., 2019), we present the kinematic properties of these CMEs from the FPF, SSEF, and HMF methods, based on single-spacecraft observations from STEREO-A and STEREO-B, which resulted in the generation of the HIGeoCAT (www.helcats-fp7.eu/catalogues/wp3_cat.html) CME catalogue containing 801 and 654 CMEs for STEREO-A and -B, respectively. Here, we take a further subset of these events, which we determine to be CMEs observed in HI images from both spacecraft simultaneously. We apply stereoscopic self-similar expansion (SSSE) geometrical analysis, presented by Davies et al. (2013), to determine the kinematic properties of these CMEs using observations from both STEREO spacecraft. The SSSE method is based on the SSE geometry. SSSE with \(\lambda =0^{\circ }\) (i.e. a point source) corresponds to the so-called geometric triangulation (GT) technique, first performed by Liu et al. (2010). SSSE with \(\lambda =90^{\circ }\) (i.e. a circle anchored to the Sun) corresponds to the tangent to a sphere (TAS) technique, introduced by Lugaz et al. (2010). The extra information afforded by using a second vantage point allows one to drop the assumption that a CME is travelling in a constant direction and at a constant speed. However, the CME is still assumed to be self-similarly expanding at a constant half-width. These stereoscopic methods may only be applied to features that propagate in the plane containing both observing spacecraft and the Sun, which, in the case of STEREO, is the Ecliptic.
Lugaz (2010) analysed 12 CMEs that occurred between 2008 and 2009 and were seen in HI on both STEREO spacecraft using single-spacecraft and stereoscopic methods based on the FP (\(\lambda =0^{\circ }\)) and HM (\(\lambda =90^{\circ }\)) geometries. For both methods, they found discrepancies between the propagation direction derived from observations using STEREO-A and STEREO-B, particularly for CMEs propagating outside of \(60^{\circ }\pm 20^{\circ }\) from the Sun–spacecraft line. However, this discrepancy was larger when using the FPF method than when using the HMF method in all but one case. Within \(60^{\circ }\pm 20^{\circ }\), the two methods result in directions within \(\pm 15^{\circ }\) of each other. They identified three main sources of error: the assumption of constant propagation direction when using observations from a single-spacecraft, the assumption of negligible width when using \(\lambda =0^{\circ }\), and the assumption of constant CME velocity. The authors show that the first and third of these may be addressed by using stereoscopic observations, whilst the second may by addressed by modelling the CMEs with non-zero half-width. The single-spacecraft methods, and their ability to predict arrival times, are assessed by Möstl et al. (2011), who find arrival times within ±5 hours can be achieved if CMEs are tracked to at least 30∘ elongation. Möstl et al. (2017) study the HiGeoCAT CMEs, whose kinematic properties are derived by the SSEF method (using \(\lambda =30^{\circ }\)), and their ability to predict arrival times at different spacecraft. They find a range of 23 – 35% of predicted arrivals are actually observed in situ at the various spacecraft. The predicted arrival times are early by an average of 2.6 ± 16.6 hours, excluding predicted and in-situ signatures that lie outside a one-day time window. More sophisticated geometries for modelling CME morphology include the Graduated Cylindrical Shell (GCS) model (Thernisien, Howard, and Vourlidas, 2006), ElEvoHI (Rollett et al., 2016), which employs an elliptical CME front and includes the effects of drag, and 3DCORE (Möstl et al., 2018), which is used to measure CME rotation and deflection and also to give information about magnetic field orientation based on data from the Solar Dynamics Observatory. Both Volpes and Bothmer (2015) and Palmerio et al. (2019) apply SSSE analysis to HI data, where the half-width of the CME is first determined using coronagraph observations. This is rather labour-intensive and so is more challenging to apply to large statistical studies, such as that which we present here.
These single-spacecraft (SSEF, including FPF and HMF) and stereoscopic (SSSE, including GT and TAS) analysis techniques are based on assumptions that often fail to include the more complex physical processes that occur during CME propagation, such as rotations (e.g. Möstl et al., 2008; Vourlidas et al., 2011; Möstl et al., 2018), deformations (Savani et al., 2010), and, for single-spacecraft techniques in particular, deflections (e.g. Byrne et al., 2010; Wang et al., 2014). These effects result from CMEs interacting with other structure in the heliosphere including high-speed streams and other CMEs (Lugaz, Vourlidas, and Roussev, 2009; Lugaz et al., 2012; Liu et al., 2014; Lugaz et al., 2017). Whilst CME–CME interactions may be quite rare during solar minimum, a CME rate of 5 –10 day−1 is not unusual at solar maximum (e.g. Yashiro et al., 2004; Robbrecht, Berghmans, and der Linden, 2009; Gopalswamy, 2010; Vourlidas et al., 2017; Harrison et al., 2018). Indeed, Zhang et al. (2007) show that of the 88 major geomagnetic storms (defined by minimum disturbance storm time index, Dst ≤ 100 nT) that occurred during Solar Cycle 23, 60% were associated with individual CMEs; however 27% were the result of CME interactions with background structure or other CMEs.
Whilst the STEREO mission comprises two spacecraft, contact with STEREO-B was lost in October 2014. The recently launched Parker Solar Probe and Solar Orbiter missions both possess wide-angle imagers (Wide-Field Imager for Parker Solar Probe (WISPR): Vourlidas et al., 2016 and SoloHI: Howard et al., 2013, respectively), as will the upcoming Polarimeter to Unify the Corona and Heliosphere (PUNCH) mission in low-Earth orbit and the potential future mission to the Sun–Earth L5 point (Kraft, Puschmann, and Luntama, 2017). These newly launched spacecraft are already returning CME images (Hess et al., 2020, using WISPR) and it is therefore important to realise the benefits and the limitations of the methods that we use to analyse the data, particularly the assumptions involved when observing from just a single vantage point.
Section 2 includes a description of the SSSE method and an explanation of how we apply it to time–elongation profiles from HI. Section 3 presents the results of the statistical analysis of the SSSE fitting results, including CME acceleration. Finally, we present a comparison between the kinematic properties derived using stereoscopic analysis methods and those that were determined using observations from just a single spacecraft. For a thorough description of the compilation of HICAT the reader is urged to refer to Article 1 (Harrison et al., 2018); furthermore the compilation of HiGeoCAT is the subject of Article 2 (Barnes et al., 2019).
2 Method
Due to the overlap of the FOVs of the HI cameras on the two STEREO spacecraft, a number of CMEs occur that are imaged from both STEREO-A and -B vantage points. Prior to 2014, the HI-A and HI-B cameras were off-pointed towards the eastern and western limbs of the Sun, respectively. The amount by which the FOVs of each spacecraft overlap therefore increased from the start of the mission until late 2010, when the spacecraft separation was close to 180∘, after which time it progressively decreased. This means that it is typically easier to identify CMEs that are observed by HI on both spacecraft near the end of 2010. Additionally, the CME rate was very low at the start of the mission because it coincided with solar minimum (Articles 1 and 2). As a result of these two factors, the first event that we identify to be observed in HI on both spacecraft is in August 2008, nearly two years after the launch of STEREO.
We identify joint events by manual inspection of those events contained in HICAT, based upon their time of entry into the respective HI-1 FOVs. If a HICAT CME enters the HI-1A FOV, we identify if any CMEs have entered the HI-1B FOV within a ±two-day window. This time window is chosen to be large enough that no CME that is observed by both spacecraft is likely to lie outside it. We then determine if the two events are the same CME by examination of sequences of simultaneous images from HI-1A and HI-1B, which have a nominal cadence of 40 minutes. This is achieved by identifying similarities in CME size, morphology, and internal structure. The events that satisfy these conditions are listed in a new, separate catalogue that is available on the HELCATS website (HIJoinCAT: www.helcats-fp7.eu/catalogues/wp2_joincat.html). HIJoinCAT contains just two columns, which list the unique identifier of the CME observed in HI-1 data from STEREO-A and STEREO-B, respectively, as they appear in the single-spacecraft HICAT list (and therefore HIGeoCAT, of which the former is a super-set). HiJoinCAT contains a total of 273 CMEs, observed between 31 August 2008 and 02 April 2014. Unlike both HICAT and HIGeoCAT, the HIJoinCAT list is no longer being updated due to the fact that it requires data from both spacecraft, a condition that is no longer satisfied since the loss of STEREO-B in 2014.
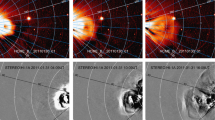
Two HIJoinCAT CMEs are shown in Figure 1; the HICAT unique identifier for each event is printed at the bottom of each panel. The top two panels show simultaneous images from HI-1A (left) and HI-1B (right) at 16:09UT on 02 June 2011 when STEREO-A and STEREO-B were 192∘ apart. We are able to determine quite easily that these images are of the same CME because they exhibit very similar structure. The bottom two panels in Figure 1 show simultaneous images from HI-1A (left) and HI-1B (right), at 20:09 UT on 26 October 2013, when the STEREO spacecraft were 290∘ apart. Although it is less obvious than in the previous example, similar structures can still be identified in each image, which leads us to conclude that this is indeed the same CME observed by both spacecraft.
Background-subtracted images of two example HIJoinCAT CMEs, which were observed by HI-1 on both STEREO-A and -B. Panels a and b show a CME that occurred in June 2011 (HCME_A__20110602_01 or HCME_B__20110602_01) when the STEREO spacecraft were separated by approximately 192∘. Panels c and d show a CME that occurred in October 2013 (HCME_A__20131026_01 or HCME_B__20131026_01) when the spacecraft were on the far-side of the Sun, each close to 145∘ from Earth. 5∘ contours of elongation and position angle are over-plotted in helioprojective coordinates. In each case the upper and lower PA extent of the CME is also over-plotted, as is the approximate elongation of the leading edge.
To the CMEs that are contained in the new catalogue, we apply the SSSE analysis method of Davies et al. (2013) to the time–elongation data that were already determined for each CME front for HIGeoCAT as described in Article 2. It should be noted that the time–elongation data of each CME front were determined at a position angle (PA) close to the apex, which is occasionally far from the Ecliptic. The SSSE fitting method must be applied to a CME front in the plane that contains both spacecraft and the Sun; in the case of STEREO this is the ecliptic plane. As such, we must assume that those time–elongation profiles recorded away from the Ecliptic are a reasonable approximation to the time–elongation profile of the CME front in the ecliptic plane. Examples of CME time–elongation maps are shown in Figure 2, where panels a and b correspond to the CME in the top panels of Figure 1. Likewise, panels c and d of Figure 2 correspond to the CME shown in the bottom of Figure 1. The SSSE method makes the same assumptions about CME morphology as does the SSEF method (Davies et al., 2012): that the CME is a self-similarly expanding structure, with a specified half width and a circular cross-sectional front. However, unlike with the single-spacecraft methods, the extra information afforded by using two spacecraft to track the CME means that we no longer require the assumptions of constant speed and constant propagation direction that were necessary with the single-spacecraft fitting technique. By applying the SSSE method to a CME, using an angular half-width [\(\lambda \)] its position is defined by the points where the line of sight from each spacecraft intercepts its leading edge. Assuming a circle of fixed half-width, we determine the heliocentric distance of the CME apex [\(R\)] using the following equation from Davies et al. (2013):
where \(d\) is the heliocentric distance of the spacecraft, \(\epsilon \) is the solar elongation angle of the CME leading edge, and \(\phi \) is the spacecraft–Sun–CME apex angle. The subscripts A and B refer to the observing spacecraft. From Equation 1, the time–elongation profiles that were used to compile HIGeoCAT are used to solve for \(R\) and \(\phi \), as a function of time. For a full mathematical derivation, the reader is referred to Davies et al. (2013), but Figure 3 illustrates the concept for our two example CMEs.
Time–elongation maps created by stacking slices of HI-1 and HI-2 difference images, taken from a fixed position-angle, in time. The red data over-plotted in each panel correspond to the observed leading edge of the CME. Panels a and b show HCME_A__20110602_01 and Panels c and d show HCME_A__20131026_01, which correspond to the CMEs shown in Figure 1.
Schematic showing example solutions to Equation 1 for two \(\lambda =40^{\circ }\) CMEs in the ecliptic plane using the Heliocentric Earth Ecliptic (HEE) coordinate system. Panels a and b show HCME_A__20110602_01/HCME_B__20110602_01 and Panels c and d show HCME_A__20131026_01/HCME_B__20131026_01, the same CMEs shown in Figures 1 and 2. STEREO-A is labelled \(A\) and STEREO-B is labelled \(B\). The dashed-black lines radiating from each spacecraft are the measured elongation of the CME front and the dotted-grey lines delimit the HI-1 and HI-2 FOVs. Panels a and b show solutions separated by six hours, as do Panels c and d. In all panels the red circle represents the “correct” solution; conversely the blue circle is the solution that we discard.
Figure 3 shows a schematic representation of the solutions for two CMEs with \(\lambda =40^{\circ }\) that were derived for two time-steps in the time–elongation profiles for the CMEs shown in Figures 1 and 2. The method for solving Equation 1 for \(R\) and \(\phi _{A}\) or \(\phi _{B}\) (Davies et al., 2013) depends on a square root and therefore has two solutions. Typically, however, one of these solutions is unphysical and may be easily discarded. Mathematically, the blue circle in panels a and b of Figure 3 describes a CME propagating away from the Sun with a negative \(R\), of which the trailing edge corresponds to the observed elongation. This is why the blue line does not connect from the Sun to the CME centre. In such cases, we can easily discard this solution as incorrect. Conversely, the red circle represents the leading edge of a CME travelling approximately between the two spacecraft, which is consistent with the observations in Figure 1. In some cases there exist two ambiguous, realistic solutions and the appropriate result must be selected manually, for example the second row in Figure 3. In these cases, we assume the CME to be directed approximately towards the Earth because this is the region where the HI-1 FOVs overlap. There exists a further limitation of stereoscopic methods when the observed lines of sight are close to parallel, that is when the CME leading edge passes directly between the two spacecraft. When this happens, \(R\) and \(\phi \) become strongly influenced by small errors in \(\epsilon \) and the resulting solutions give CMEs that vary significantly in apex position between successive observations. For this reason we discard these solutions from the analysis presented in this article; however, these CMEs are still included in HIJoinCAT, which does not contain CME kinematics. This configuration is most common when the spacecraft are separated by approximately 180∘, which is close to solar maximum and when the overlap between the HI FOVs is also maximised, and therefore the time at which the majority of the joint CMEs are detected.
The image cadences of the HI-1 and HI-2 cameras are 40 minutes and 2 hours, respectively, and so we may use successive sets of observations to track the time–elongation profile of the CME’s leading edge, using J-maps, as it propagates through the heliosphere, as shown in Figure 2. The SSSE technique requires that the elongation of the CME front as observed from STEREO-A and -B be simultaneous, so the time–elongation profile from each spacecraft is mapped onto a set of common times using a linear, step-wise interpolation, separated by 30 minutes, limited by the time interval for which data from both vantage points are available. For a given time-step, a value of \(R\) and \(\phi \) is calculated using Equation 1 for ten different half-widths increasing from 0∘ to 90∘ in increments of 10∘. Such analysis is performed for each time-step to produce time profiles of \(R\) and \(\phi \) for the CME. To derive the profiles of the CME velocity [\(V(t)\)] and acceleration [\(A\)] we fit a function to the CME apex radial distance [\(R\)] profile. As is the case with many existing CME catalogues (e.g. Yashiro et al., 2004; Vourlidas et al., 2017), we choose to fit a second-order polynomial.
An example of the analysis of HCME_A__20131026_01 and HCME_B__20131026_01 is shown in Figure 4, where the CME is tracked for just over 24 hours (50 half-hour time-steps). The CME apex longitude, in Heliocentric Earth Ecliptic (HEE) coordinates, as a function of time (Figure 4a) can be seen to shift from approximately +20∘ to −15∘, in the most extreme case of \(\lambda =90^{\circ }\), over this period, where positive is westward. A deflection of this magnitude is feasible (Wang et al., 2014; Isavnin, Vourlidas, and Kilpua, 2014), and the west-to-east direction is consistent with the findings of Wang et al. (2004) for fast CMEs. However, we expect that some contribution is likely to result from errors in the fitting method. Liu et al. (2013) find the HM geometry to be an inaccurate approximation for CMEs near the Sun due to the fact that CMEs expand at a rate greater than self-similarity in their early propagation phase. Indeed, the deflection shown in Figure 4 is most pronounced for \(\lambda =90^{\circ }\) and least so for \(\lambda =0^{\circ }\). Figure 4b shows the CME apex heliocentric distance, in AU, as a function of time. The first time-step corresponds to a CME apex distance close to 0.2 AU, relatively independent of \(\lambda \), and, depending on the chosen half-width, the CME is tracked to just beyond 0.6 AU (red line; \(\lambda =90^{\circ }\)) or well beyond 1.5 AU (black line; \(\lambda =0^{\circ }\)). For each half-width, the second-order polynomial fitted to the \(R\)-profile is over-plotted as a solid line. The velocity profile, in km s−1, derived from this second-order fit is shown in Figure 4c, as is the acceleration, in Figure 4d. The fit to the 0∘ half-width CME suggests an acceleration rate of over 40 m s−2, resulting in a speed that increases from 800 km s−1 to well over 2000 km s−1 in less than eight hours. Such a speed increase is inconsistent with typical CME behaviour, particularly at these radial distances, which suggests that using this half-width to model the CME is a poor approximation. Indeed, for the 90∘ half-width model we find a CME accelerating at approximately 1 m s−2, maintaining a speed between 800 – 900 km s−1, which, although fast, is certainly more realistic behaviour. This example illustrates an important result that is common to many of the CMEs analysed in this article: using a small half-width often results in unphysical CME acceleration to very high velocities. This is unrealistic given that the average speed of ICMEs determined from in-situ measurements is found to be approximately 450 km s−1, regardless of heliocentric distance (Richardson, Liu, and Belcher, 2005).
SSSE-derived kinematic properties for the CME observed on 26 October 2013. The procedure is applied using ten different half-widths in Equation 1, increasing from \(0^{\circ }\) (black profiles) to 90∘ (red profiles) in steps of 10∘. a shows the CME apex longitude in the ecliptic plane relative to the Earth. b shows the CME apex distance from the Sun as a function of time. Panels c and d show CME velocity and acceleration, respectively. The latter are calculated by taking the first and second derivatives of a second-order polynomial fit to \(R\), with respect to time. These fits are over-plotted in panel b for each \(10^{\circ }\) value of \(\lambda \), from \(\lambda =0^{\circ }\) (black) to \(\lambda =90^{\circ }\) (red).
3 CME Statistical Properties
3.1 CME Frequency
Initially we identify CMEs in HICAT that are observed using both STEREO-A and -B. For each CME observed in HI-1A images we identify any CMEs that enter the HI-1B FOV within ±two-days of the time that the CME enters the HI-1A FOV. For all HICAT CMEs (965 from STEREO-A and 936 from -B) observed prior to the loss of communication with STEREO-B, we produced a preliminary list of 475 potentially common CMEs using this method. We refine this list through examination of HI-1 images. This results in a subset of 273 CMEs imaged by both HI-1A and HI-1B for inclusion in our so-called HIJoinCAT catalogue. It is likely that we erroneously exclude some events that were actually observed by both spacecraft due to non-optimal viewing geometry. To these 273 CMEs, we apply the aforementioned stereoscopic fitting analysis to the STEREO-A and STEREO-B time–elongation profiles from the HIGeoCAT catalogue. Figure 5 shows the temporal distribution of the CME count with a bin size of one month. The white bins show the greatest number of CMEs observed by in HI on either STEREO-A, or -B, from HICAT. The shaded regions show the total number of HIJoinCAT CMEs, which is greatest during 2010 and 2011, corresponding to the time when the spacecraft were close to \(180^{\circ }\) separation; Solar Cycle 24 peaked soon after: in 2012. The lighter-grey region of the histogram shows the number of CMEs that were confirmed to be imaged by both HI-1A and HI-1B but that were excluded from the final analysis for one of two reasons: Firstly, we exclude some CMEs for which time–elongation profiles from both STEREO-A and STEREO-B view points are not available in the HIGeoCAT catalogue. This is due to data gaps or CMEs that were too difficult to track. Secondly, and more significantly, the SSSE method breaks down when the LOSs of the observed leading edge of the CME from both spacecraft are approximately parallel. This occurs commonly when the boresights of the HI-1 cameras are directly opposite, because the majority of CMEs were found not to be tracked far into the HI-2 FOV in Article 2 (Barnes et al., 2019). As the HI-1 FOVs are centred at \(14^{\circ }\) elongation in the Ecliptic, this alignment occurs around August 2010, when the spacecraft are separated by \(152^{\circ }\). Figure 5 shows the result of this problem, where all 35 dual-spacecraft CMEs observed in the months July – November 2010 are excluded from the final analysis. The number of CMEs that were analysed using SSSE is greatest during 2011 and 2012, which is when the spacecraft separation approaches \(270^{\circ }\) and coincides with solar maximum. In total, the stereoscopic analysis was successfully applied to 151 CMEs.
Monthly CME count during the period April 2007 to September 2014. The total bin height (white) shows the highest number of CMEs detected by either STEREO-A or -B for a given month from HICAT. The total height of all shaded regions represents CMEs that were identified to be present in both HI-1A and HI-1B images (i.e. the CMEs in HIJoinCAT), whilst the darkest region is the number of CMEs to which the stereoscopic fitting has been applied. The light-grey region shows CMEs that were omitted from the stereoscopic fitting. The vertical-dashed lines represent the evolution of the spacecraft-separation angle during this interval, where 152∘ is when the boresights of the two HI-1 cameras are directly aligned.
3.2 CME Acceleration and Deflection
Figure 6 shows the distributions of both CME acceleration (panels a, c and e), which is assumed to be constant, and CME longitudinal deflection (panels b, d, and f), determined using SSSE with half-widths of 0∘ (top row), 30∘ (middle row), and 90∘ (bottom row). The acceleration distributions are peaked near zero, showing that, typically, CMEs do not experience much acceleration in the HI FOV. For \(\lambda =0^{\circ }\), 46% of events have −1\(< A<+\)1 m s−2, for \(\lambda =30^{\circ }\) the corresponding value is 48% and for \(\lambda =90^{\circ }\) it is 51%. Although accelerations tend to be small, their distribution depends quite strongly on the chosen half-width. For \(0^{\circ }\) half-width, 115 (77%) of CMEs are accelerating and 34 (23%) are decelerating, for \(30^{\circ }\) half-width 98 (66%) of CMEs are accelerating and 51 (34%) are decelerating, and for \(90^{\circ }\) half-width 79 (53%) of CMEs are accelerating and 70 (47%) are decelerating. That most CMEs are accelerating in the HI FOV is inconsistent with results established previously: whilst St. Cyr et al. (1999) show the majority of CMEs to be accelerating within 2.44 R⊙, Gopalswamy et al. (2009) show that almost all have stopped accelerating by 32 R⊙. The mean acceleration for CMEs analysed using \(\lambda =0^{\circ }\) is 6 m s−2, which is skewed well away from zero by CMEs that have unphysically large accelerations that result from fitting with small half-widths, as was discussed in the previous section. In Figure 3c, for example, the location of the CME shown in red is derived using a half-width of \(40^{\circ }\). A CME fitted with a half-width of \(0^{\circ }\) will be further from the Sun than the apex of that 40∘ half-width CME, at the points where the dashed lines intersect, whereas the apex of a CME with a half-width greater than \(40^{\circ }\) will be closer to the Sun. The SSSE method using \(\lambda =0^{\circ }\) can result in increasingly large speeds and large accelerations, as is seen in panels c and d of Figure 4. This effect tends to be less apparent for larger half-widths; in the cases of \(\lambda =30^{\circ }\), and \(\lambda =90^{\circ }\), the mean accelerations are 1 and 0 m s−2, respectively. Regardless of the half-width chosen, we still find, as noted above, that the number of accelerating CMEs is always greater than the number of those decelerating. Even for an intermediate half-width of \(30^{\circ }\), almost two thirds of the events appear to experience acceleration. The results do suggest that, in general, CMEs continue to experience acceleration within the HI FOVs; however, this is usually not significant in magnitude.
The distributions of CME accelerations (panels a, c, and e) calculated with a bin-width of 1 m s−2 and angular deflections (panels b, d, and f) calculated with a bin-width of \(10^{\circ }\). Panels a and b use \(\lambda =0^{\circ }\), panels c and d use \(\lambda =30^{\circ }\), and panels e and f use \(\lambda =90^{\circ }\). The acceleration values are determined by fitting a second-order polynomial to the CME apex-distance profile. CME deflection represents the total change in angular position of the CME apex, between the first and last interpolated time-step. In panels a, c, and e 23, 5, and 3 CMEs, respectively, exceed the upper 10 m s−2 extent of the plot.
Figure 6b, d, and f shows the distributions of CME deflections in ecliptic longitude, determined using SSSE analysis with respective half-widths of 0∘, 30∘, and 90∘. The deflection refers to the difference between the final and initial longitudinal position of the CME apex. For all three half-widths, significant deflections are often seen. For \(\lambda =0^{\circ }\), 33% of CMEs deflect by more than \(\pm 10^{\circ }\); corresponding values for \(\lambda =30^{\circ }\) and \(90^{\circ }\) are 45% and 54%, respectively. In some cases we appear to observe deflections of up to \(90^{\circ }\), far in excess of the maximum deflection of \(29^{\circ }\) observed by Isavnin, Vourlidas, and Kilpua (2014) and indeed of the \(20^{\circ }\) deflection by Wang et al. (2014). This is in contradiction to any known physical process and is instead the result of inadequacies with the assumptions of the analysis method. As was discussed in the previous section, and is seen in Figure 4, the SSSE method is sometimes poor at determining the orientation of wider CMEs when they are close to the Sun, due to the fact that they expand at a rate greater than self-similarity (Liu et al., 2013). Indeed, because of this issue, it is difficult to ascertain how much of the longitudinal deflections determined using SSSE analysis is due to inaccuracies in the method, because we are unable to accurately measure their initial longitude. However, the propagation-direction measurements become more constant as the CME propagates further into the heliosphere and so determining this value further out into the HI FOV is likely to provide a more reliable estimate of the ultimate CME propagation direction.
Figure 7a, d, and e shows a comparison between the initial CME velocities and the CME acceleration using SSSE with respective half-widths of \(\lambda =0^{\circ }\), 30∘, and \(90^{\circ }\). Figure 7 shows no clear correlation between the initial velocity and the measured acceleration when using \(\lambda =0^{\circ }\) to model the CME and the regression line is strongly skewed by CMEs with high acceleration values exceeding the plot range. Likewise, there is little correlation between initial velocity and acceleration for \(\lambda =30^{\circ }\) in Figure 7c. For \(\lambda =90^{\circ }\), in Figure 7e, there appears to be a slight tendency for the slowest CMEs to experience a positive acceleration and, conversely, for the faster CMEs to experience a deceleration, as expected (Yashiro et al., 2004; Gopalswamy et al., 2009). As noted previously, smaller half-widths, particularly \(\lambda =0^{\circ }\), can lead to unphysically large accelerations. Figure 7e is consistent with the idea that CMEs experience drag from the ambient solar wind that causes their speed to tend towards the typical solar-wind speed, which is not the case for Figures 7a and c. This may suggest that a half-width between \(30^{\circ }\) and \(90^{\circ }\) is a better representation of the observed CMEs. Indeed, Yashiro et al. (2004) show that the mean width of CMEs observed using LASCO increases from 46∘ in 1996 (solar minimum) to 57∘ in 2000 (solar maximum); however, this width is measured in PA and not longitude. The regression line in Figure 7e suggests that the juncture between CMEs that accelerate and those that decelerate corresponds to an initial speed of \(660\pm 346\) km s−1, which, although rather imprecise, does correspond to the typical slow solar-wind velocity at 1 AU of around 400 – 500 km s−1.
Panels a, c, and e show the relationship between CME initial velocity and CME acceleration, determined for respective SSSE half-widths of \(\lambda =0^{\circ }\), \(30^{\circ }\), and \(90^{\circ }\). Panels b, d, and f show the relationship between initial and final velocity, again for \(\lambda =0^{\circ }\), \(30^{\circ }\), and \(90^{\circ }\), where the dashed-black line is the identity line. Over-plotted in red, with error bounds as red-dotted lines, in each case is the regression line and printed are the correlation coefficients. On all plots the histograms on the top and right indicate the distributions of \(x\)- and \(y\)-parameter values.
Figures 7d, d, and f show a comparison between the initial CME speed and the final CME speed derived using half-widths of \(0^{\circ }\), \(30^{\circ }\), and \(90^{\circ }\), respectively. In the case of \(\lambda =0^{\circ }\) (Figure 7b) there is little correlation between initial and final velocities, which is due to the fact that many CMEs are found to have unphysically high final speeds when using this half-width, regardless of their initial speed. The regression line is strongly skewed by CMEs with final velocities exceeding 2000 km s−1. In fact, 22 CMEs (15%) analysed assuming \(\lambda =0^{\circ }\) have final velocities that exceed the 2000 km s−1 upper limit of the plot, whereas only three CMEs do so for \(\lambda =30^{\circ }\) and only one for \(\lambda =90^{\circ }\). For \(\lambda =30^{\circ }\) (Figure 7d) and \(90^{\circ }\) (Figure 7f), there is a strong correlation between initial and final velocity, with respective correlation coefficients of 0.75 and 0.74. The CME final velocity is less spread than that of initial velocity in each case, which can be seen in the histograms at the top and right of each panel. This can be explained by the idea that CMEs tend towards the ambient solar, wind speed. For the CMEs analysed using \(\lambda =90^{\circ }\), 60% of slower events, those that have an initial velocity below 500 km s−1, are accelerating and 57% of those with an initial velocity above this value are decelerating. In the case of \(\lambda =30^{\circ }\), the majority of both slower and faster events are accelerating, which is inconsistent with established CME behaviour (e.g. Yashiro et al., 2004; Gopalswamy et al., 2009) and suggests that this may demonstrate inadequacies in the use of this geometry to describe the CMEs.
3.3 A Comparison of Single-Spacecraft and Stereoscopic Techniques
Figure 8 shows a comparison between the velocities determined for each CME from single-spacecraft SSE, and stereoscopic SSSE, analyses, resulting from three assumed geometries corresponding to \(\lambda =0^{\circ }\), \(30^{\circ }\), and \(90^{\circ }\) (equivalent to the single-spacecraft FPF, SSEF30, and HMF techniques); \(v_{\mathrm{A}}\) and \(v_{\mathrm{B}}\) are the velocities resulting from the single-spacecraft fitting methods applied to STEREO-A and STEREO-B time–elongation profiles, respectively, and \(v_{\mathrm{A+B}}\) is the initial speed from the stereoscopic method. Figures 8a, b, and c (top row) correspond to results using a half-width of 0∘, Figures 8d, e, and f (middle row) use 30∘ and Figures 8g, h, and i (bottom row) use 90∘. Each column presents panels corresponding to the three combinations of pairs of \(v_{\mathrm{A}}\), \(v_{\mathrm{B}}\), and \(v_{\mathrm{A+B}}\). The histograms at the top and left of each panel show the speed distribution corresponding to the \(x\)- and \(y\)-parameters plotted in that panel. The correlation coefficient [\(R\)] between each pair of velocity measurement ranges between 0.64 (Figure 8h) and 0.77 (Figure 8c), showing that there is reasonable agreement between speeds derived from all three methods, for each half-width. The best agreement is found for \(\lambda =0^{\circ }\) and the worst agreement for \(\lambda =90^{\circ }\). The CME final speeds derived using the stereoscopic analysis method, over-plotted in light grey (panels in the second and third columns), are found to show a much poorer correlation with the single-spacecraft speeds (with \(R\) ranging from 0.26 in panel b to 0.50 in Figures 8f and i). This correlation is worst for \(\lambda =0^{\circ }\) (Figures 8b and c) and improves with increasing half-width; the best correlation is seen in Figures 8h and i, using \(\lambda =90^{\circ }\). As shown in Figure 4, for example, the final speeds derived using the stereoscopic method with \(\lambda =0^{\circ }\) are often unphysically high. However, even for \(\lambda =90^{\circ }\), the correlation between the final velocity derived from stereoscopic analysis and from single-spacecraft fitting is still far worse than that of the initial velocities. In fact the correlation coefficient has a value of only 0.26 between \(v_{\mathrm{A+B}}\) (final) and \(v_{\mathrm{A}}\) and a value of 0.38 between \(v_{\mathrm{A+B}}\) (final) and \(v_{\mathrm{B}}\). This is consistent with the results of Liu et al. (2013), who find an “apparent late acceleration” for CMEs fitted using FPF (equivalent to SSEF with \(\lambda =0^{\circ }\)). They show that the HMF (\(\lambda =90^{\circ }\)) method can reduce this effect, however, that it can still produce an overestimate of CME speed further out into the heliosphere. Single-spacecraft derived speeds of those CMEs included in the HIGeoCAT catalogue that impact spacecraft throughout the inner heliosphere were compared to in-situ signatures by Möstl et al. (2017). For those predicted impacts of HIGeoCAT CMEs that matched with in-situ impacts, the predicted arrival times (derived using SSE with \(\lambda =30^{\circ }\)) were found to be 2.4±17.1 hours early for HI-A and 2.7±16.0 hours early for HI-B, for events within a time window of ±1 day. The HiGeoCAT speeds were on average 191±341 km s−1 greater than those measured in-situ for HI-A CMEs and 245±446 km s−1 greater for HI-B CMEs. However, a similar study has not been performed using the CMEs in the HIJoinCAT, which are analysed using the SSSE method, and which would provide a measure of ground truth with which to compare all three fitting methods. Without such a ground truth with which to determine whether SSSE or SSEF analysis, and using half-width, is most accurate at determining the true CME speed, we are instead able to draw some conclusions from the results by identifying the weaknesses of these models. The good agreement between SSEF speed and SSSE initial speed suggests that both methods are in fact a reliable means with which to measure CME speed. The extra information afforded by using two spacecraft to track the CME would suggest that this is a better method to use, if data are available from two vantage points; however, the apparent late acceleration identified by Liu et al. (2013) means that the results become less accurate when the CME is observed further into the heliosphere, particularly when using small half-widths.
A comparison between velocities determined from three methods for each of the 151 CMEs to which the stereoscopic analysis was applied. (a), (b), and (c) use \(\lambda =0^{\circ }\), (d), (e), and (f) use \(\lambda =30^{\circ }\) and (g), (h), and (i) use \(\lambda =90^{\circ }\). Panels in the left-hand, centre, and right-hand columns show \(V_{\mathrm{A}}\) versus \(V_{\mathrm{B}}\), \(V_{\mathrm{A+B}}\) versus \(V_{\mathrm{A}}\) and \(V_{\mathrm{A+B}}\) versus \(V_{\mathrm{B}}\), respectively. \(V_{\mathrm{A}}\) and \(V_{\mathrm{B}}\) are the speeds from single-spacecraft fits to HI-A and HI-B time–elongation profiles and \(V_{\mathrm{A+B}}\) is the velocity derived from stereoscopic analysis applied to the same events. In Panels b, c, e, f, h, and i, the initial-velocity values from SSSE are represented by black diamonds, fitted with a red regression line, and the final-velocity values from SSSE are represented by grey diamonds, fitted with a grey regression line. In Panels a, d, and g, the constant velocity values from SSEF analysis are represented by black diamonds, fitted with a red regression line. The equation and correlation coefficient plotted in all nine panels corresponds to the red regression line and the histograms plotted on the top and right of each panel show the distribution of black parameter values on each axis.
Figure 9 shows a comparison between the longitudinal propagation angles determined for each CME, from each of the three methods. Here, lonA and lonB are the derived longitude of the CME apex in Heliocentric Earth Equatorial (HEEQ) coordinates from single-spacecraft analysis and lon\(_{\mathrm{A+B}}\) is the final CME apex longitude derived from stereoscopic analysis in the same coordinate system. The top, middle, and bottom row of panels correspond to a half-width of 0∘, \(30^{\circ }\), and \(90^{\circ }\), respectively. Each plot shows the difference in longitude between two of the three fitting methods, as a function of spacecraft-separation angle. The histogram at the top of each plot shows the distribution of CMEs as a function of spacecraft-separation angle, which increases as a function of time, and therefore they correspond approximately to the dark-grey distribution in Figure 5. The total range of separation angles over which the CMEs are observed is 73∘ to 291∘ and the majority of CMEs (78%) occur once the spacecraft separation is greater than 180∘ because this equates to solar maximum. The longitudes derived from single-spacecraft analysis are in fairly poor agreement with each other; moreover, neither agrees well with the results from stereoscopic analysis. In addition, the discrepancy between each set of results appears to show a systematic variation with spacecraft separation. For each row (i.e. different half-width) the difference between the SSEA and SSEB longitudes (left-hand column) suggests that the methods produce a bias towards a certain range of CME propagation directions relative to the spacecraft. As the spacecraft move apart in longitude, in opposite directions, this bias results in the observed correlation between separation angle and longitude difference. In Sections 3.2 and 3.3 of Article 2 (Barnes et al., 2019), we studied the distribution of CME propagation angle [\(\phi \)] relative to the spacecraft, for all 1455 CMEs in version 5 of the single-spacecraft fitting catalogue HiGeoCAT. We showed that the maximum of each distribution was peaked at around 78∘ (\(\lambda =0^{\circ }\)), 72∘ (\(\lambda =30^{\circ }\)), and 84∘ (\(\lambda =90^{\circ }\)) for STEREO-A CMEs and 72∘ (\(\lambda =0^{\circ }\)), 69∘ (\(\lambda =30^{\circ }\)), and 77∘ (\(\lambda =90^{\circ }\)) for STEREO-B CMEs. This is believed to be due to two effects: The first is an observational effect, whereby it is somewhat easier to observe CMEs travelling close to the Thomson surface (Tappin and Howard, 2009). The second is an inherent bias in the single-spacecraft fitting models, found by Lugaz (2010) who shows that assuming \(\lambda =0^{\circ }\) for a wide CME (with \(90^{\circ }\)) causes a bias towards propagation directions close to \(60^{\circ }\) from the Sun–spacecraft line, for CMEs that propagate at more than \(\pm 20^{\circ }\) from this direction. Systematic effects are also seen in the second (Figures 9b, e, and h) and third (Figures 9c, f, and i) columns, where we compare the stereoscopic results to each of the single-spacecraft results. However, they are less significant because the stereoscopic method only suffers from the Thomson-surface effect and not the bias from the single-spacecraft model assumptions. The regression line in Figure 9a crosses zero on the \(y\)-axis when the spacecraft separation is close to \(150^{\circ }\), which is the sum of the median propagation directions found from SSEF with \(\lambda =0^{\circ }\) (FPF) for each spacecraft in Article 2 (Barnes et al., 2019). That is, these biases cause the FPF longitudes to coincide when the spacecraft separation is \(150^{\circ }\). As we have no ground truth to determine the best method, and half-width, with which to accurately determine CME propagation, we do so based on the observed biases in the results. Clearly, the inherent biases identified by Lugaz (2010) are apparent in the results presented here and we must agree with their findings: using a small half-width with SSEF analysis is a poor method to determine CME propagation direction, and the extra information afforded by SSSE analysis, applied using a large half-width, is the best method to avoid these biases. However, CME over-expansion means that using SSSE analysis to locate CMEs at low elongation angles is less reliable than when it is applied to observations further out in the heliosphere.
Scatter-plots showing the difference in CME apex longitude in HEEQ coordinates between each combination of the three methods versus the spacecraft-separation angle. Panels a, b, and c use \(\lambda =0^{\circ }\), d, e, and f use \(\lambda =30^{\circ }\), and g, h, and i use \(\lambda =90^{\circ }\). lonA and lonB are the CME apex longitude from the methods using SSEF with STEREO-A and STEREO-B and lon\(_{\mathrm{A+B}}\) is the apex longitude from SSSE analysis with both STEREO spacecraft. In each plot the red regression line is over-plotted and the histograms represent the distribution of data points on each axis.
4 Summary
From all CMEs observed by HI on STEREO-A and STEREO-B, whilst contact still existed with the latter, we identify 273 CMEs, occurring between 31 August 2008 and 02 April 2014 that are observed by both. We apply SSSE analysis techniques to these CMEs in order to determine their kinematic behaviour. During this time the spacecraft-longitude separation increased from 73∘ to 291∘. This period spans approximately half a solar cycle, beginning at solar minimum and ending at the peak of Solar Cycle 24.
The main conclusions are summarised as follows:
-
i)
The SSSE method fails when the CME passes between the observing spacecraft and the lines-of-sight of the CME leading edge are close to parallel because small errors in elongation translate to large errors in determining CME position. We therefore apply the technique to just 151 CMEs, 78% of which occur close to solar maximum, after the spacecraft separation exceeds 180∘. These data are too few to perform a thorough investigation of the optimal spacecraft configuration with which to analyse CMEs using the SSSE method. However, the results show that two spacecraft situated at L4 and L5, with a separation of \(120^{\circ }\), would be a feasible configuration to track an Earth-directed CME, until its front reaches \(60^{\circ }\) elongation, where the LOSs would become parallel.
-
ii)
Accelerations derived using the SSSE technique are much higher when a smaller half-width is chosen. For \(\lambda =0^{\circ }\), 76% of CMEs were found to have positive acceleration and 15% showed a final velocity exceeding 2000 km s−1. For \(\lambda =30^{\circ }\), 66% of all CMEs were found to be accelerating, regardless of their initial velocity. Conversely, using \(90^{\circ }\) results in approximately half of CMEs accelerating and half decelerating (52% versus 48%, respectively), suggesting that this model agrees best with the average CME width of 47 – 60∘ (Yashiro et al., 2004). For slower CMEs, with initial speeds below 500 km s−1, 60% are seen to accelerate and 57% of CMEs faster than 500 km s−1 are seen to decelerate when using \(\lambda =90^{\circ }\). This is consistent with the well-established understanding that drag between CMEs and the background solar wind causes the CME speed to tend towards the ambient solar-wind speed. This is an important result, which indicates that CMEs are capable of experiencing acceleration well into the HI FOV. This is contrary to the main assumption used in SSEF analysis, a method that is commonly used to analyse interplanetary CME propagation.
-
iii)
The inferred longitude of CMEs is found to vary greatly when they are close to the Sun, due to the fact that our SSSE analysis does not account for CME over-expansion. As the CME is tracked to larger elongation angles, the propagation direction is found to approach a constant value. It is therefore difficult to draw meaningful information about CME deflections, because we cannot accurately know their initial longitude. However, the final longitude for \(\lambda =90^{\circ }\) is expected to provide a good estimate of the ultimate CME propagation direction.
-
iv)
The velocity for each of the 151 CMEs is determined using three different means: SSEF using STEREO-A data, SSEF using STEREO-B data, and SSSE analysis using data from both spacecraft. Each technique is applied using three different half-widths to fit the CMEs: 0∘, 30∘, and 90∘. Agreement between initial CME speed is good between all methods; however, the final CME speed derived from SSSE analysis does not agree with that from SSEF. This is in part due to the over-estimation of CME acceleration when using a small half-width in the SSSE analysis and in agreement with the apparent late acceleration found by Liu et al. (2013). We therefore conclude that it is best to use the SSSE method with \(\lambda =90^{\circ }\) to determine CME speeds; however, the results become less reliable when the CME is tracked further into the heliosphere.
-
v)
Similarly, we compare the difference in HEEQ longitude of the CME apex between each pair of fitting methods, again using \(\lambda =0^{\circ }\), \(30^{\circ }\), and \(90^{\circ }\). The agreement between the SSEF methods from each spacecraft is poor, with differences close to 180∘ in the worst cases. The effect is systematic and is a function of spacecraft-separation angle, which is due to three causes: Firstly, projection effects caused by Thomson scattering; secondly, biases in the CME direction determined when using a small half-width, as identified by Lugaz (2010); and, thirdly, the incorrect assumptions employed by the single-spacecraft fitting methods. We therefore find that the SSSE method using \(\lambda =90^{\circ }\) is also the best method to determine CME propagation directions, however, it is less accurate at low elongation angles due to the fact that it fails to account for CME over-expansion nearer the Sun.
White-light heliospheric imaging offers a unique way to track CMEs through the inner heliosphere. In Article 1 (Harrison et al., 2018) we presented a catalogue of interplanetary CMEs that, at the time of writing, contains over 2000 events and spans an entire solar cycle. Many of these CMEs have been studied using single-spacecraft analysis techniques in Article 2 (Barnes et al., 2019), and 151 of these events, presented here, have been analysed using stereoscopic observations. If we wish to track CMEs in the heliosphere, for the purposes of both science and space weather, there are, however, many limitations that result from doing so with observations from just one spacecraft, and many still with observations from two. Many of the limitations identified in this article are possible to address by modifying the way that the SSSE analysis is applied to the data. For example, modelling a CME with super self-similar expansion would account for CME over-expansion in the early propagation phase. Alternatively, it may be preferable to analyse the CME in coronagraphs separately using models, such as GCS, that can measure CME expansion, before moving to SSSE analysis at greater distances from the Sun. With the upcoming launches of the PUNCH mission in Earth orbit, ESA’s Lagrange mission to L5, as well as the continued coverage from STEREO-A and the recent launches of the Parker Solar Probe and Solar Orbiter, we are entering an era of unprecedented coverage from wide-angle imagers. It will therefore soon be possible to scrutinise these methods further: for example, the extra information available from three or more vantage points will allow the measurement of non-circular CME fronts and will greatly limit the cases where the SSSE method fails due to parallel LOS observations or when observing CMEs at small elongation angles close to the Sun. Further to this, Solar Orbiter will observe from higher latitudes giving a truly three-dimensional view of CMEs when combined with observations from the Ecliptic. The PUNCH mission possesses the unprecedented advantage of measuring polarisation of Thomson-scattered light in heliospheric observations, which provides a further means to constrain the location of observed features along the LOS (e.g. DeForest et al., 2016).
References
Barnes, D., Davies, J.A., Harrison, R.A., Byrne, J.P., Perry, C.H., Bothmer, V., Eastwood, J.P., Gallagher, P.T., Kilpua, E.K.J., Möstl, C., Rodriguez, L., Rouillard, A.P., Odstrčil, D.: 2019, CMEs in the heliosphere: II. A statistical analysis of the kinematic properties derived from single-spacecraft geometrical modelling techniques applied to CMEs detected in the heliosphere from 2007 to 2017 by STEREO/HI-1. Solar Phys. 294, 57. DOI.
Bothmer, V., Schwenn, R.: 1997, The structure and origin of magnetic clouds in the solar wind. Ann. Geophys. 16, 1. DOI (Article 2).
Brueckner, G.E., Howard, R.A., Koomen, M.J., Korendyke, C.M., Michels, D.J., Moses, J.D., Socker, D.G., Dere, K.P., Lamy, P.L., Llebaria, A., Bout, M.V., Schwenn, R., Simnett, G.M., Bedford, D.K., Eyles, C.J.: 1995, The Large Angle Spectroscopic Coronagraph (LASCO). Solar Phys. 162, 357. DOI. ADS.
Byrne, J.P., Maloney, S.A., McAteer, R.T.J., Refojo, J.M., Gallagher, P.T.: 2010, Propagation of an Earth-directed coronal mass ejection in three dimensions. Nat. Commun. 1, 74. DOI. ADS.
Cremades, H., Bothmer, V.: 2004, On the three-dimensional configuration of coronal mass ejections. Astron. Astrophys. 422, 307. DOI.
Davies, J.A., Harrison, R.A., Rouillard, A.P., Sheeley, N.R., Perry, C.H., Bewsher, D., Davis, C.J., Eyles, C.J., Crothers, S.R., Brown, D.S.: 2009, A synoptic view of solar transient evolution in the inner heliosphere using the Heliospheric Imagers on STEREO. Geophys. Res. Lett. 36, L02102. DOI. ADS.
Davies, J.A., Harrison, R.A., Perry, C.H., Möstl, C., Lugaz, N., Rollett, T., Davis, C.J., Crothers, S.R., Temmer, M., Eyles, C.J., Savani, N.P.: 2012, A self-similar expansion model for use in solar wind transient propagation studies. Astrophys. J. 750, 23. DOI. ADS.
Davies, J.A., Perry, C.H., Trines, R.M.G.M., Harrison, R.A., Lugaz, N., Möstl, C., Liu, Y.D., Steed, K.: 2013, Establishing a stereoscopic technique for determining the kinematic properties of solar wind transients based on a generalized self-similarly expanding circular geometry. Astrophys. J. 777, 167. DOI. ADS.
Davis, C.J., Kennedy, J., Davies, J.A.: 2010, Assessing the accuracy of CME speed and trajectory estimates from STEREO observations through a comparison of independent methods. Solar Phys. 263, 209. DOI. ADS.
DeForest, C.E., Howard, T.A., Webb, D.F., Davies, J.A.: 2016, The utility of polarized heliospheric imaging for space weather monitoring. Space Weather 14, 32. DOI. ADS.
Eyles, C.J., Simnett, G.M., Cooke, M.P., Jackson, B.V., Buffington, A., Hick, P.P., Waltham, N.R., King, J.M., Anderson, P.A., Holladay, P.E.: 2003, The Solar Mass Ejection Imager (Smei). Solar Phys. 217, 319. DOI. ADS.
Eyles, C.J., Harrison, R.A., Davis, C.J., Waltham, N.R., Shaughnessy, B.M., Mapson-Menard, H.C.A., Bewsher, D., Crothers, S.R., Davies, J.A., Simnett, G.M., Howard, R.A., Moses, J.D., Newmark, J.S., Socker, D.G., Halain, J.-P., Defise, J.-M., Mazy, E., Rochus, P.: 2009, The heliospheric imagers onboard the STEREO mission. Solar Phys. 254, 387. DOI. ADS.
Fisher, R.R., Lee, R.H., MacQueen, R.M., Poland, A.I.: 1981, New Mauna Loa coronagraph systems. Appl. Opt. 20, 1094. DOI. ADS.
Gopalswamy, N.: 2010, Corona mass ejections: a summary of recent results. In: Dorotovic, I. (ed.) 20th National Sol. Phys. Meeting, 108. ADS.
Gopalswamy, N., Yashiro, S., Michalek, G., Stenborg, G., Vourlidas, A., Freeland, S., Howard, R.: 2009, The SOHO/LASCO CME catalog. Earth Moon Planets 104, 295.
Gosling, J.T., McComas, D.J., Phillips, J.L., Bame, S.J.: 1991, Geomagnetic activity associated with Earth passage of interplanetary shock disturbances and coronal mass ejections. J. Geophys. Res. 96, 7831. DOI.
Harrison, R.A., Davies, J.A., Möstl, C., Liu, Y., Temmer, M., Bisi, M.M., Eastwood, J.P., de Koning, C.A., Nitta, N., Rollett, T., Farrugia, C.J., Forsyth, R.J., Jackson, B.V., Jensen, E.A., Kilpua, E.K.J., Odstrcil, D., Webb, D.F.: 2012, An analysis of the origin and propagation of the multiple coronal mass ejections of 2010 August 1. Astrophys. J. 750, 45. DOI. ADS.
Harrison, R.A., Davies, J.A., Barnes, D., Byrne, J.P., Perry, C.H., Bothmer, V., Eastwood, J.P., Gallagher, P.T., Kilpua, E.K.J., Möstl, C., Rodriguez, L., Rouillard, A.P., Odstrčil, D.: 2018, CMEs in the heliosphere: I. A statistical analysis of the observational properties of CMEs detected in the heliosphere from 2007 to 2017 by STEREO/HI-1. Solar Phys. 293, 77. DOI. ADS (Article 1).
Hess, P., Rouillard, A.P., Kouloumvakos, A., Liewer, P.C., Zhang, J., Dhakal, S., Stenborg, G., Colaninno, R.C., Howard, R.A.: 2020, WISPR imaging of a pristine CME. Astrophys. J. Suppl. 246, 25. DOI.
Howard, R.A., Moses, J.D., Vourlidas, A., Newmark, J.S., Socker, D.G., Plunkett, S.P., Korendyke, C.M., Cook, J.W., Hurley, A., Davila, J.M., Thompson, W.T., St Cyr, O.C., Mentzell, E., Mehalick, K., Lemen, J.R., Wuelser, J.P., Duncan, D.W., Tarbell, T.D., Wolfson, C.J., Moore, A., Harrison, R.A., Waltham, N.R., Lang, J., Davis, C.J., Eyles, C.J., Mapson-Menard, H., Simnett, G.M., Halain, J.P., Defise, J.M., Mazy, E., Rochus, P., Mercier, R., Ravet, M.F., Delmotte, F., Auchere, F., Delaboudiniere, J.P., Bothmer, V., Deutsch, W., Wang, D., Rich, N., Cooper, S., Stephens, V., Maahs, G., Baugh, R., McMullin, D., Carter, T.: 2008, Sun Earth connection coronal and heliospheric investigation (SECCHI). Space Sci. Rev. 136, 67. DOI. ADS.
Howard, R., Vourlidas, A., Korendyke, C., Plunkett, S., Carter, M., Wang, D., Rich, N., Mcmullin, D., Lynch, S., Thurn, A., Clifford, G., Socker, D., Thernisien, A., Chua, D., Linton, M., Keller, D., Janesick, J., Tower, J., Grygon, M., Lamy, P.: 2013, The solar orbiter imager (SoloHi) instrument for the solar orbiter mission. Proc. SPIE 8862. DOI.
Isavnin, A., Vourlidas, A., Kilpua, E.K.J.: 2014, Three-dimensional evolution of flux-rope cmes and its relation to the local orientation of the heliospheric current sheet. Solar Phys. 289, 2141. DOI.
Kahler, S.W., Webb, D.F.: 2007, V arc interplanetary coronal mass ejections observed with the Solar Mass Ejection Imager. J. Geophys. Res. 112, A09103. DOI. ADS.
Kilpua, E.K.J., Schwenn, R., Bothmer, V., Koskinen, H.E.J.: 2005, Properties and geoeffectiveness of magnetic clouds in the rising, maximum and early declining phases of Solar Cycle 23. Ann. Geophys. 23, 4491.
Kilpua, E.K.J., Liewer, P.C., Farrugia, C., Luhmann, J.G., Möstl, C., Li, Y., Liu, Y., Lynch, B., Russel, C.T., Vourlidas, A., Acuna, M.H., Galvin, A.B., Larson, D., Sauvaud, J.A.: 2009, Multispacecraft observations of magnetic clouds and their solar origins between 19 and 23 May 2007. Solar Phys. 254, 325. DOI.
Kilpua, E.K.J., Mierla, M., Rodriguez, L., Zhukov, A.N., Srivastava, N., West, M.J.: 2012, Estimating travel times of coronal mass ejections to 1 AU using multi-spacecraft coronagraph data. Solar Phys. 279, 477. DOI.
Kilpua, E.K.J., Balogh, A., von Steiger, R., Liu, Y.D.: 2017, Geoeffective properties of solar transients and stream interaction regions. Space Sci. Rev. 212, 1271. DOI. ADS.
Kraft, S., Puschmann, K.G., Luntama, J.P.: 2017, Remote sensing optical instrumentation for enhanced space weather monitoring from the L1 and L5 Lagrange points. In: Cugny, B., Karafolas, N., Sodnik, Z. (eds.) International Conference on Space Optics – ICSO 2016, Proc. SPIE 10562, 115. DOI.
Liu, Y., Richardson, J.D., Belcher, J.W.: 2005, A statistical study of the properties of interplanetary coronal mass ejections from 0.3 to 5.4 AU. Planet. Space Sci. 53, 3. DOI.
Liu, Y., Davies, J.A., Luhmann, J.G., Vourlidas, A., Bale, S.D., Lin, R.P.: 2010, Geometric triangulation of imaging observations to track coronal mass ejections continuously out to 1 AU. Astrophys. J. Lett. 710, L82. DOI. ADS.
Liu, Y.D., Luhmann, J.G., Lugaz, N., Möstl, C., Davies, J.A., Bale, S.D., Lin, R.P.: 2013, On Sun-to-Earth propagation of coronal mass ejections. Astrophys. J. 769, 45. DOI.
Liu, Y.D., Luhmann, J.G., Kadic, P., Kilpua, E.K.J., Lugaz, N., Nitta, N.V., Möstl, C., Lavraud, B., Bale, S.D., Farrugia, C.J., Galvin, A.B.: 2014, Observations of an extreme storm in interplanetary space caused by successive coronal mass ejections. Nat. Commun. 5, 3481. DOI.
Lugaz, N.: 2010, Accuracy and limitations of fitting and stereoscopic methods to determine the direction of coronal mass ejections from Heliospheric Imagers observations. Solar Phys. 267, 411. DOI. ADS.
Lugaz, N., Vourlidas, A., Roussev, I.I.: 2009, Deriving the radial distances of wide coronal mass ejections from elongation measurements in the heliosphere – application to CME-CME interaction. Ann. Geophys. 27, 3479. DOI. ADS.
Lugaz, N., Hernandez-Charpak, J.N., Roussev, I.I., Davis, C.J., Vourlidas, A., Davies, J.A.: 2010, Determining the azimuthal properties of coronal mass ejections from multi-spacecraft remote-sensing observations with stereo secchi. Astrophys. J. 715, 493.
Lugaz, N., Downs, C., Shibata, K., Roussev, I.I., Asai, A., Gombosi, T.I.: 2011, Numerical investigation of a coronal mass ejection from an anemone active region: reconnection and deflection of the 2005 August 22 eruption. Astrophys. J. 738, 127. DOI.
Lugaz, N., Farrugia, C.J., Davies, J.A., Möstl, C., Davis, C.J., Roussev, I.I., Temmer, M.: 2012, The deflection of the two interacting coronal mass ejections of 2010 May 23-24 as revealed by combined in siyu measurements and heliospheric imaging. Astrophys. J. 759, 68. DOI.
Lugaz, N., Temmer, M., Wang, Y., Farrugia, C.J.: 2017, The interaction of successive coronal mass ejections: a review. Solar Phys. 292, 64. DOI. .
Manchester, W., Kilpua, E.K.J., Liu, Y.D., Lugaz, N., Riley, P., Török, T., Vršnak, B.: 2017, The physical processes of cme/icme evolution. Space Sci. Rev. 212, 1159. DOI.
Möstl, C., Davies, J.A.: 2013, Speeds and arrival times of solar transients approximated by self-similar expanding circular fronts. Solar Phys. 285, 411. DOI. ADS.
Möstl, C., Miklenic, C., Farrugia, C.J., Temmer, M., Veronig, A., Galvin, A.B., Vršnak, B., Biernat, H.K.: 2008, Two-spacecraft reconstruction of a magnetic cloud and comparison to its solar source. Ann. Geophys. 26, 3139. DOI.
Möstl, C., Temmer, M., Rollett, T., Farrugia, C.J., Liu, Y., Veronig, A.M., Leitner, M., Galvin, A.B., Biernat, H.K.: 2010, STEREO and wind observations of a fast ICME flank triggering a prolonged geomagnetic storm on 5-7 April 2010. Geophys. Res. Lett. 37, L24103. DOI. ADS.
Möstl, C., Rollett, T., Lugaz, N., Farrugia, C.J., Davies, J.A., Temmer, M., Veronig, A.M., Harrison, R.A., Crothers, S., Luhmann, J.G., Galvin, A.B., Zhang, T.L., Baumjohann, W., Biernat, H.K.: 2011, Arrival time calculation for interplanetary coronal mass ejections with circular fronts and application to stereo observations of the 2009 February 13 eruption. Astrophys. J. 741, 34. DOI.
Möstl, C., Rollet, T., Frahm, R.A., Liu, Y.D., Long, D.M., Colaninno, R.C., Reiss, M.A., Temmer, M., Farrugia, C.J., Posner, A., Dumbović, M., Janvier, M., Démoulin, P., Boakes, P., Devos, A., Kraaikamp, E., Mays, M.L., Vrsnak, B.: 2015, Strong coronal channelling and interplanetary evolution of a solar storm up to Earth and Mars. Nat. Commun. 6, 7135. DOI.
Möstl, C., Isavnin, A., Boakes, P.D., Kilpua, E.K.J., Davies, J.A., Harrison, R.A., Barnes, D., Krupar, V., Eastwood, J.P., Good, S.W., Forsyth, R.J., Bothmer, V., Reiss, M.A., Amerstorfer, T., Winslow, R.M., Anderson, B.J., Philpott, L.C., Rodriguez, L., Rouillard, A.P., Gallagher, P., Nieves-Chinchilla, T., Zhang, T.L.: 2017, Modeling observations of solar coronal mass ejections with heliospheric imagers verified with the Heliophysics System Observatory. Space Weather 15, 955. DOI. ADS.
Möstl, C., Amerstorfer, T., Palmerio, E., Isavnin, A., Farrugia, C.J., Lowder, C., Winslow, R.M., Donnerer, J.M., Kilpua, E.K.J., Boakes, P.D.: 2018, Forward modeling of coronal mass ejection flux ropes in the inner heliosphere with 3DCORE. Space Weather 16, 216. DOI.
Palmerio, E., Scolini, C., Barnes, D., Magdelanić, J., West, M.J., Zhukov, A.N., Rodriguez, L., Mierla, M., Good, S.W., Morosan, D.E., Kilpua, E.K.J., Pomell, J., Poedts, S.: 2019, Multipoint study of successive coronal mass ejections driving moderate disturbances at 1 AU. Astrophys. J. 878, 37. DOI. ADS.
Richardson, I., Cane, H.: 2012, Near-Earth solar wind flows and related geomagnetic activity during more than four solar cycles (1963–2011). Space Weather Space Climate 2.
Richardson, J.D., Liu, Y., Belcher, J.W.: 2005, Propagation and evolution of icmes in the solar wind. In: Sauvaud, J.-A., Němeček, Z. (eds.) Multiscale Processes in the Earth’s Magnetosphere: From Interball to Cluster NATO Science Series 178, Springer, Dordrecht, 1. DOI.
Robbrecht, E., Berghmans, D., der Linden, R.A.M.V.: 2009, Automated LASCO CME catalogue for solar cycle 23: are CMEs scale invariant? Astrophys. J. 691, 1222. DOI.
Rollett, T., Möstl, C., Temmer, M., Frahm, R.A., Davies, J.A., Veronig, A.M., Vršnak, B., Amerstorfer, U.V., Farrugia, C.J., Žic, T., Zhang, T.L.: 2014, Combined multipoint remote and in situ observations of the asymmetric evolution of a fast solar coronal mass ejection. Astrophys. J. Lett. 790, L6. DOI. ADS.
Rollett, T., Möstl, C., Isavnin, A., Davies, J.A., Kubicka, M., Amerstorfer, U.V., Harrison, R.A.: 2016, ElEvoHI: a novel CME prediction tool for heliospheric imaging combining an elliptical front with drag-based model fitting. Astrophys. J. 824, 131. DOI. ADS.
Rouillard, A.P., Davies, J.A., Forsyth, R.J., Rees, A., Davis, C.J., Harrison, R.A., Lockwood, M., Bewsher, D., Crothers, S.R., Eyles, C.J., Hapgood, M., Perry, C.H.: 2008, First imaging of corotating interaction regions using the STEREO spacecraft. Geophys. Res. Lett. 35, L10110. DOI. ADS.
Sachdeva, N., Subramanian, P., Vourlidas, A., Bothmer, V.: 2017, CME dynamics using STEREO and LASCO observations: the relative importance of Lorentz forces and solar wind drag. Solar Phys. 292, 118. DOI. ADS.
Savani, N.P., Rouillard, A.P., Davies, J.A., Owens, M.J., Forsyth, R.J., Davis, C.J., Harrison, R.A.: 2009, The radial width of a coronal mass ejection between 0.1 and 0.4 AU estimated from the heliospheric imager on STEREO. Ann. Geophys. 27, 4349. DOI. ADS.
Savani, N.P., Owens, M.J., Rouillard, A.P., Forsyth, R.J., Davies, J.A.: 2010, Observational evidence of a coronal mass ejection distortion directly attributable to a structured solar wind. Astrophys. J. 714, L128. DOI.
Savani, N.P., Owens, M.J., Rouillard, A.P., Forsyth, R.J., Kusano, K., Shiota, D., Kataoka, R., Jian, L., Bothmer, V.: 2011, Evolution of coronal mass ejection morphology with increasing heliocentric distance. II. In situ observations. Astrophys. J. 732, 117. DOI.
Savani, N.P., Davies, J.A., Davis, C.J., Shiota, D., Rouillard, A.P., Owens, M.J., Kusano, K., Bothmer, V., Bamford, S.P., Lintott, C.J., Smith, A.: 2012, Observational tracking of the 2D structure of coronal mass ejections between the Sun and 1 AU. Solar Phys. 279, 517. DOI. ADS.
Sheeley, N.R. Jr., Herbst, A.D., Palatchi, C.A., Wang, Y.-M., Howard, R.A., Moses, J.D., Vourlidas, A., Newmark, J.S., Socker, D.G., Plunkett, S.P., Korendyke, C.M., Burlaga, L.F., Davila, J.M., Thompson, W.T., St Cyr, O.C., Harrison, R.A., Davis, C.J., Eyles, C.J., Halain, J.P., Wang, D., Rich, N.B., Battams, K., Esfandiari, E., Stenborg, G.: 2008, Heliospheric images of the solar wind at Earth. Astrophys. J. 675, 853. DOI. ADS.
Sheeley, N.R., Walters, J.H., Wang, Y.-M., Howard, R.A.: 1999, Continuous tracking of coronal outflows: two kinds of coronal mass ejections. J. Geophys. Res. 104, 24739. DOI. ADS.
St. Cyr, O.C., Burkepile, J.T., Hundhausen, A.J., Lecinski, A.R.: 1999, A comparison of ground-based and spacecraft observations of coronal mass ejections from 1980-1989. J. Geophys. Res. 104, 12493. DOI. ADS.
St. Cyr, O.C., Plunkett, S.P., Michels, D.J., Paswaters, S.E., Koomen, M.J., Simnett, G.M., Thompson, B.J., Gurman, J.B., Schwenn, R., Webb, D.F., Hildner, E., Lamy, P.L.: 2000, Properties of coronal mass ejections: SOHO LASCO observations from January 1996 to June 1998. J. Geophys. Res. 105, 18169. DOI. ADS.
Tappin, S.J., Howard, T.A.: 2009, Interplanetary coronal mass ejections observed in the heliosphere: 1. Review of theory. Space Sci. Rev. 147, 31. DOI. ADS.
Temmer, M., Veronig, A.M., Peinhart, V., Vršnak, B.: 2014, Asymmetry in the CME-CME interaction process for the events from 2011 February 14-15. Astrophys. J. 785, 85. DOI. ADS.
Thernisien, A.F.R., Howard, R.A., Vourlidas, A.: 2006, Modeling of flux rope coronal mass ejections. Astrophys. J. 652, 763. DOI.
Tousey, R., Howard, R.A., Koomen, M.J.: 1974, The frequency and nature of coronal transient events observed by OSO-7*. In: Bull. Am. Astron. Soc. 6, 295. ADS.
Volpes, L., Bothmer, V.: 2015, An application of the stereoscopic self-similar-expansion model to the determination of cme-driven shock parameters. Solar Phys. 290, 3005. DOI.
Vourlidas, A., Colaninno, R., Nieves-Chinchilla, T., Stenborg, G.: 2011, The first observation of a rapidly rotating coronal mass ejection in the middle corona. Astrophys. J. 733, L23. DOI.
Vourlidas, A., Howard, R.A., Plunkett, S.P., Korendyke, C.M., Thernisien, A.F.R., Wang, D., Rich, N., Carter, M.T., Chua, D.H., Socker, D.G., Linton, M.G., Morrill, J.S., Lynch, S., Thurn, A., Van Duyne, P., Hagood, R., Clifford, G., Grey, P.J., Velli, M., Liewer, P.C., Hall, J.R., DeJong, E.M., Mikic, Z., Rochus, P., Mazy, E., Bothmer, V., Rodmann, J.: 2016, The Wide-field Imager for Solar Probe Plus (WISPR). Space Sci. Rev. 204, 83. DOI. ADS.
Vourlidas, A., Balmaceda, L.A., Stenborg, G., Lago, A.D.: 2017, Multi-viewpoint coronal mass ejection catalog based on STEREO COR2 observations. Astrophys. J. 838, 141.
Wang, Y., Shen, C., Wang, S., Ye, P.: 2004, Deflection of coronal mass ejection in the interplanetary medium. Solar Phys. 222, 329. DOI.
Wang, Y., Wang, B., Shen, C., Shen, F., Lugaz, N.: 2014, Deflected propagation of a coronal mass ejection from the corona to interplanetary space. J. Geophys. Res. 119, 5117. DOI.
Webb, D.F., Howard, T.A.: 2012, Coronal mass ejections: observations. Liv. Rev. Solar Phys. 9, 3. DOI.
Yashiro, S., Gopalswamy, N., Michalek, G., St. Cyr, O.C., Plunkett, S.P., Rich, N.B., Howard, R.A.: 2004, A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. 109, A07105. DOI. ADS.
Zhang, J., Dere, K.P., Howard, R.A., Kundu, M.R., White, S.M.: 2001, On the temporal relationship between coronal mass ejections and flares. Astrophys. J. 559, 452. DOI. ADS.
Zhang, J., Dere, K.P., Howard, R.A., Vourlidas, A.: 2004, A study of the kinematic evolution of coronal mass ejections. Astrophys. J. 604, 420. DOI. ADS.
Zhang, J., Richardson, I.G., Webb, D.F., Gopalswamy, N., Huttunen, E., Kasper, J.C., Nitta, N.V., Poomvises, W., Thompson, B.J., Wu, C.-C., Yashiro, S., Zhukov, A.N.: 2007, Solar and interplanetary sources of major geomagnetic storms (\(\mathit{Dst} \leq -100\) nT) during 1996–2005. J. Geophys. Res. 112, A10102. DOI.
Acknowledgements
This work was carried out as part of the EU FP7 HELCATS (Heliospheric Cataloguing, Analysis and Techniques Service) project (www.helcats-fp7.eu/). We acknowledge support from the European Union FP7–SPACE–2013–1 programme for the HELCATS project (#606692). The HI instruments on STEREO were developed by a consortium that comprised the Rutherford Appleton Laboratory (UK), the University of Birmingham (UK), Centre Spatial de Liège (CSL, Belgium), and the Naval Research Laboratory (NRL, USA). The STEREO/SECCHI project, of which HI is a part, is an international consortium led by NRL. We recognise the support of the UK Space Agency for funding STEREO/HI operations in the UK. C. Möstl thanks the Austrian Science Fund (FWF): P31521-N27, P31659-N27.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure of Potential Conflicts of Interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barnes, D., Davies, J.A., Harrison, R.A. et al. CMEs in the Heliosphere: III. A Statistical Analysis of the Kinematic Properties Derived from Stereoscopic Geometrical Modelling Techniques Applied to CMEs Detected in the Heliosphere from 2008 to 2014 by STEREO/HI-1. Sol Phys 295, 150 (2020). https://doi.org/10.1007/s11207-020-01717-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-020-01717-w