1 Introduction

Prominences are dense and cold solar coronal magnetic structures, which are highly complex, as shown for instance by their long and thin threads (Tandeberg-Hanssen 1974). The average prominence temperature is about two hundred times lower and the mass density approximately two hundred times higher than the ambient coronal values. Prominences are linked to the underlying photosphere by several footpoints and lie along the polarity inversion line. The length of prominences is in the range of \(50\,\mbox{--}\,500~\mbox{Mm}\), their height is between \(10\,\mbox{--}\,100~\mbox{Mm}\), and their average thickness is \(15~\mbox{Mm}\) (Priest 1989).

Solar prominences can be classified into two groups: i) active prominences and ii) quiescent prominences (Zirin 1988). Active prominences have life-times of no more than a few days, undergoing dramatic changes in plasma motions and magnetic activity. They are often associated with solar flares. Quiescent prominences can live for months; they form over a magnetic neutral line that separates the regions of opposite magnetic polarities on the photosphere.

The first quiescent prominence models were devised about 60 years ago (Menzel 1951). Two classical models are commonly accepted, which are known as the Kippenhahn and Schlüter (1957) and Kuperus and Raadu (1974) models. In these models the cool and dense plasma is maintained against gravity by the magnetic tension at the local dip of the magnetic arcade. The distribution of magnetic polarity in this arcade prominence is the same as in the underlying photosphere, i.e. direct polarity. Kuperus and Raadu (1974) proposed a model in which the prominence, taking the form of a magnetic-flux rope, is maintained in a vertical current-sheet with open magnetic-field lines. Below this current-sheet the \(X\)-point is present, and the prominence exhibits inverse polarity. Currently, there are two well-accepted 3D prominence models with inverse polarity: the sheared arcade and the flux-rope magnetic structures (Labrosse et al. 2010, and references cited therein).

While these classical models reveal the equilibrium magnetic configurations of quiescent prominences, a recent trend is emerging with the observational and theoretical reports that led to the foundation of plasma and wave dynamics within such stable magnetic configurations of the prominence system. Luna and Karpen (2012) and Luna, Díaz, and Karpen (2012) have found that the observed large-amplitude longitudinal prominence oscillations (\({>}\,20~\mbox{km}\,\mbox{s}^{-1}\)) are driven by the projected gravity along the flux tubes and are strongly influenced by the curvature of the dips of the magnetic field in which the prominence threads reside. These oscillations reported by both Luna and Karpen (2012) and Luna, Díaz, and Karpen (2012) for slow magnetoacoustic–gravity modes are the symmetric longitudinal oscillations. Terradas et al. (2013) have studied the excitation of fast and slow antisymmetric magnetoacoustic–gravity modes of a prominence; they also considered magnetostatic (MHS) equilibrium and performed linear MHD normal mode analysis. Small-amplitude longitudinal (slow) and fast transverse prominence oscillations either as a collective motion or as an individual thread (\({\approx}\,2\, \mbox{--}\,3~\mbox{km}\,\mbox{s}^{-1}\)) are well observed and modeled in the solar atmosphere (Arregui, Oliver, and Ballester 2012, and references cited therein). Terradas, Oliver, and Ballester (2001) have reported that slow magnetoacoustic–gravity longitudinal oscillations of the quiescent prominences can be damped by the radiation and Newtonian cooling. Longitudinal prominence oscillations were observed and modeled by Li and Zhang (2012), Zhang et al. (2012), Shen et al. (2014), Bi et al. (2014), and Chen, Harra, and Fang (2014).

While a number of generalizations to the seminal models of Kippenhahn and Schlüter (1957) and Kuperus and Raadu (1974) were constructed in the past, we propose an arcade model of normal polarity as sketched by Pikelner (1971). Pikelner (1971) only sketched the model, but he did not support it by any analytical expression. Our aim is to devise an analytical arcade model of a prominence by presenting the stringent mathematical expressions for the equilibrium prominence quantities. Our devised analytical model of prominence is relevant for the bounded prominence structures that exhibit collective wave motions and plasma dynamics. Additionally, our goal is to implement this analytical model into the FLASH numerical code (Lee 2013) and develop a numerical model. This numerical model allows us to study a number of plasma phenomena. As a particular application of this model, we here simulate magnetoacoustic–gravity waves in the prominence that result from a localized pressure pulse. This is the first article describing our newly developed analytical model in detail. We also present one numerical experiment on long-period prominence oscillations to shed light on the driving physical mechanism of these waves. The derived results can be applied to understand the physical processes of the prominence during evolved nonlinear oscillations and are thereby useful for prominence seismology and related observations.

This article is organized as follows: Section 2 describes the analytical model of a quiescent prominence that is based on Pikelner’s model. The results of numerical simulations are outlined in Section 3. In the last section we present the discussion and conclusions.

2 Analytical Model of Quiescent Prominence

2.1 MHD Equations

We consider a gravitationally stratified and magnetically confined plasma, which is described by ideal two-dimensional (2D) magnetohydrodynamic (MHD) equations:

$$\begin{aligned} {{\partial\varrho}\over {\partial t}}+\nabla \cdot (\varrho\boldsymbol{V}) =&0, \end{aligned}$$
(1)
$$\begin{aligned} \varrho{{\partial\boldsymbol{V}}\over {\partial t}}+ \varrho(\boldsymbol{V} \cdot \nabla) \boldsymbol{V} =& -\nabla p+ \frac{1}{\mu} (\nabla \times \boldsymbol{B})\times\boldsymbol{B} +\varrho \boldsymbol{g}, \end{aligned}$$
(2)
$$\begin{aligned} {{\partial\boldsymbol{B}}\over {\partial t}} =& \nabla\times(\boldsymbol{V} \times\boldsymbol{B}), \end{aligned}$$
(3)
$$\begin{aligned} \nabla\cdot\boldsymbol{B} =& 0, \end{aligned}$$
(4)
$$\begin{aligned} {\partial p\over \partial t} + \boldsymbol{V}\cdot\nabla p =& - \gamma p \nabla\cdot\boldsymbol{V}, \end{aligned}$$
(5)
$$\begin{aligned} p =& \frac{k_{\mathrm{B}}}{m} \varrho T. \end{aligned}$$
(6)

Here \({\varrho}\) is the mass density, \(p\) the gas pressure, \(\boldsymbol{V}=[V_{x}, V_{y}, 0]\), \(\boldsymbol{B}=[B_{x}, B_{y}, 0]\), and \(\boldsymbol{g}=[0,-g,0]\) represent the plasma velocity, the magnetic field, and gravitational acceleration, respectively. The value of \(g\) is equal to \(274~\mbox{m}\,\mbox{s}^{-2}\). In addition, \(T\) is the plasma temperature, \(\gamma=5/3\) is the adiabatic index, \(\mu\) is the magnetic permeability of the plasma, and \(m\) is a particle mass that is specified by a mean molecular weight of 0.6. Although this value is valid for a fully ionized plasma of the corona, its higher value will probably not qualitatively change the response of the system. We assumed that \(z\) is an invariant coordinate (\(\partial/\partial z=0\)), and we set the \(z\)-components of velocity and magnetic field equal to zero. This assumption removes Alfvén waves from the system in which magnetoacoustic–gravity waves are able to propagate.

2.2 Equilibrium Configuration

We assume that the solar atmosphere is in static equilibrium [\({\boldsymbol{V}}_{\mathrm{e}}=\mathbf{0}\)]. It follows from Equations (1) – (5) that in such a model this equilibrium is described by

$$\begin{aligned} -\nabla p_{\mathrm{e}}+\frac{1}{\mu}(\nabla\times {\boldsymbol{B}}_{\mathrm{e}})\times\boldsymbol{B}_{\mathrm{e}}+ \varrho_{\mathrm{e}} \boldsymbol{g} = \boldsymbol{0}, \end{aligned}$$
(7)
$$\begin{aligned} \nabla\cdot\boldsymbol{B}_{\mathrm{e}}= 0. \end{aligned}$$
(8)

Here the subscript e corresponds to the equilibrium quantities.

As a result of Equation (8), the magnetic field [\(\boldsymbol{B}_{\mathrm{e}}\)] can be expressed with the use of the magnetic-flux function [\(A(x,y)\)] as

$$ \boldsymbol{B}_{\mathrm{e}}(x,y)=\nabla\times(A\hat{\boldsymbol{z}} ) , $$
(9)

with \(\hat{\boldsymbol{z}}\) being a unit vector along the \(z\)-direction. As a result, the \(x\)- and \(y\)-components of the magnetic field are

$$ B_{\mathrm{ex}}=\frac{\partial A}{\partial y},\quad \quad B_{\mathrm {ey}}=- \frac{\partial A}{\partial x}. $$
(10)

Under the above assumptions, Equations (6) and (7) are reduced to the following expressions (Low 1975, 1980):

$$\begin{aligned} \nabla^{2} A(x,y) =& -\mu\frac{\partial p_{\mathrm {e}}(A,y)}{\partial A}, \end{aligned}$$
(11)
$$\begin{aligned} \varrho_{\mathrm{e}} (x,y) g =& - \frac{\partial p_{\mathrm{e}}(A,y)}{\partial y}. \end{aligned}$$
(12)

Now, we can specify the right-hand-side of Equation (11) and thereafter proceed to solve this equation for the magnetic field; however, this is a formidable nonlinear Dirichlet problem to solve (Low 1975, 1980). Here we adopt the approach proposed by Low (1980, 1981, 1982), who reversed the mathematical problem by specifying the magnetic field first and then deriving the equilibrium conditions for the mass density and gas pressure. By defining the magnetic flux function [\(A(x, y)\)] we can in general integrate Equation (11) to find the formula for the equilibrium gas pressure and then calculate the mass density using Equation (12). Following this idea, we integrate Equation (11) regarding \(y\)-coordinate as a fixed parameter (Solov’ev 2010). Then, a variation of \(A\) is

$$\begin{aligned} {\mathrm {d}}A=\frac{\partial A}{\partial x} {\mathrm {d}}x+\frac {\partial A}{\partial y} {\mathrm {d}}y+ \frac{\partial A}{\partial z} {\mathrm {d}}z=\frac{\partial A}{\partial x} \mathrm{d}x, \end{aligned}$$
(13)

as a result of \(\partial A/\partial z=0\) and \({\mathrm {d}}y=0\).

Using this expression in Equation (11), we obtain

$$ \mu p_{\mathrm{e}}=- \int\biggl(\frac{\partial^{2} A}{\partial x^{2}} +\frac {\partial^{2} A}{\partial y^{2}} \biggr) \frac{\partial A}{\partial x} {\mathrm {d}}x + \mu C(y), $$
(14)

where \(C(y)\) is an integration function. As the integration over the first integrand can be performed explicitly, we obtain

$$ \mu p_{\mathrm{e}}= - \frac{1}{2} \biggl( \frac{\partial A}{\partial x} \biggr)^{2}- \int\frac{\partial^{2} A}{\partial y^{2}}\frac{\partial A}{\partial x} {\mathrm {d}}x+ \mu C(y). $$
(15)

As the magnetic field tends to zero at \(x\to\pm\infty\) and \(p_{\mathrm{e}}=p_{\mathrm{h}}(y)\), we find

$$\begin{aligned} C(y)=p_{\mathrm{h}}(y), \end{aligned}$$
(16)

where \(p_{\mathrm{h}}(y)\) is the hydrostatic pressure of the magnetic-free solar atmosphere with

$$ -\frac{\partial p_{\mathrm{h}}}{\partial y}=\varrho_{\mathrm{h}} (y) g, $$
(17)

which is specified by a temperature profile \(T_{\mathrm{e}}(y)\). In this case we adopt the temperature model of Avrett and Loeser (2008). We note that the temperature reaches its minimum of 4300 K at \({\approx}\,0.6~\mbox{Mm}\) (Figure 1). At higher altitudes, the temperature rises with \(y\). At the transition region that is located at \(y\approx2.1~\mbox{Mm}\), the temperature abruptly increases by about 0.8 MK in the solar corona at \(y=10~\mbox{Mm}\). The temperature profile uniquely determines the hydrostatic mass density and gas pressure, which fall off with \(y\) (not shown here). For a recent implementation of \(p_{\mathrm{h}}(y)\) see Murawski et al. (2013). From Equation (15) we derive

$$ p_{\mathrm{e}}(x,y)=p_{\mathrm{h}}(y)-\frac{1}{\mu} \biggl( \int\frac {\partial^{2}\! A}{\partial y^{2}}\frac{\partial A}{\partial x} \,\mathrm{d}x + \frac{1}{2} \biggl(\frac{\partial A}{\partial x} \biggr)^{\!2} \biggr). $$
(18)
Figure 1
figure 1

Vertical hydrostatic temperature profile from the data of Avrett and Loeser (2008).

Full size image

From Equation (12) it follows that to find the distribution of the mass density [\(\varrho_{\mathrm{e}}(x,y)\)] we need to calculate \(\partial p_{\mathrm{e}}(A,y)/\partial y\). To execute this action, we perform the following analysis. Let \(A(x,y)\) be a function of independent variables \((x, y)\). Then we can express any differentiable function [\(S(x,y)\)] as \(S(y,A(x,y))\) and the following equation is derived:

$$\begin{aligned} \frac{\partial S(x,y)}{\partial y}=\frac{\partial S(y,A)}{\partial y}+\frac{\partial A}{\partial y} \frac{\partial S(y,A)}{\partial A}. \end{aligned}$$
(19)

Then

$$ \frac{\partial S(y,A)}{\partial y}=\frac{\partial S(x,y)}{\partial y}-\frac{\partial A}{\partial y} \frac{\partial S(y,A)}{\partial A}. $$
(20)

Replacing \(S(y,A)\) by \(p_{\mathrm{e}}(y,A)\) and using Equation (11), we find

$$ \frac{\partial p_{\mathrm{e}}(y,A)}{\partial y}=\frac{\partial p_{\mathrm{e}}(x,y)}{\partial y}- \frac{\partial A}{\partial y} \nabla^{2} A, $$
(21)

and then expressing \(p_{\mathrm{e}}(y,A)\) by Equation (18), we find the formula for the equilibrium mass density,

$$ \varrho_{\mathrm{e}} (x,y) g=\varrho_{\mathrm{h}} (y) g+ \frac {1}{\mu} \biggl[\frac{\partial}{\partial y} \biggl( \int\frac{\partial^{2} \! A}{\partial y^{2}}\frac{\partial A}{\partial x} \,\mathrm{d}x +\frac{1}{2} \biggl(\frac {\partial A}{\partial x} \biggr)^{\!2} \biggr)-\frac{\partial A}{\partial y}\nabla ^{2} A \biggr]. $$
(22)

We note that \(p_{\mathrm{e}}\) and \(\varrho_{\mathrm{e}}\) are specified by Equations (18) and (22), respectively. These equations are general in nature. Specific forms of \(p_{\mathrm{e}}\) and \(\varrho_{\mathrm{e}}\) are obtained after estimating \(A(x,y)\), which is a free function. This function must be chosen based on some physical reasons. In the following, we present this function for a solar prominence.

2.3 Pikelner’s Prominence Model

For the solar prominence model of Pikelner (1971) we adopt the following expression for the flux function:

$$ A(x,y) = \frac{B_{0}}{k}\bigl(1 + a_{1} k^{2} x^{2}\bigr)\exp\bigl[-k^{2} \bigl(a_{2} (y-y_{\mathrm {ref}})^{2}+x^{2}\bigr) \bigr], $$
(23)

where \(a_{1}\) and \(a_{2}\) are some positive constants, \(k\) denotes the inverse length, which determines the spatial scale of the structure, and \(B_{0}\) is the magnetic-field strength at the reference point, (\(x=0, y=y_{\mathrm{ref}}\)). We choose and hold fixed \(y_{\mathrm{ref}}=10~\mbox{Mm}\), \(k=1/50~(\mbox{Mm})^{-1}\), and \(B_{0}\approx 6~\mbox{Gauss}\). This choice of \(A(x,y)\) leads to magnetic-field lines that are characteristic for a prominence, and the equilibrium mass density and gas pressure can be given by relatively simple expressions.

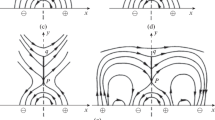
The magnetic field resulting from Equations (23) and (10) is illustrated in Figure 2. The dip in the magnetic-field vectors is discernible along the vertical line \(x=0\), and this dip grows with \(a_{1}\) as magnetic lines are more tilted for a high value of \(a_{1}\) (Figure 2). After specifying \(A(x,y)\) by Equation (23), we express the equilibrium gas pressure and the mass density for the Pikelner’s model with Equations (18) and (22) as

$$\begin{aligned} p_{\mathrm{e}}(x,y) =& p_{\mathrm{h}}(y) - 0.5 \, \bigl[ \bigl(p_{3} x^{4}+p_{4} x^{2}+p_{7} \bigr) y^{2}+p_{9} x^{4} x^{2}+p_{1} x^{4}+ p_{2} x^{2}-2 a_{2}^{2} \bigr] \\ &{}\exp \bigl[p_{10} (y-y_{\mathrm{ref}})^{2}+p_{11} x^{2} \bigr] B_{0}, \end{aligned}$$
(24)
$$\begin{aligned} \varrho_{\mathrm{e}}(x,y) =& \varrho_{\mathrm{h}}(y) + 4 \, \bigl(p_{5} x^{4}+p_{6} x^{2}+p_{8} \bigr) (y-y_{\mathrm{ref}}) \\ &{}\exp\bigl[p_{10} (y-y_{\mathrm{ref}})^{2}+p_{11}x^{2} \bigr] B_{0}/g, \end{aligned}$$
(25)

where

$$\begin{aligned} \textstyle\begin{array}{l@{\qquad}l} p_{1} =k^{4}\bigl(-2 a_{1}^{2} a_{2}-8 a_{1}^{2}+8 a_{1}\bigr), & p_{2} =k^{2}\bigl(-4 a_{1} a_{2}+4 a_{1}^{2}-8 a_{1}+4 \bigr), \\ p_{3} =4 k^{6} a_{1}^{2} a_{2}^{2}, & p_{4}=8 k^{4} a_{1} a_{2}^{2}, \\ p_{5} =k^{6}\bigl(a_{1}^{2} a_{2}^{2}-a_{1}^{2} a_{2} \bigr), & p_{6} =k^{4}\bigl[2 a_{1} a_{2}^{2}+\bigl(-a_{1}^{2}-2 a_{1}\bigr) a_{2}\bigr], \\ p_{7} =4 k^{2} a_{2}^{2}, & p_{8} =k^{2}\bigl[a_{2}^{2}+(a_{1}-1) a_{2}\bigr], \\ p_{9} =4 k^{6} a_{1}^{2}, & p_{10} =-2 k^{2} a_{2}, \; p_{11} =-2 k^{2}. \end{array}\displaystyle \end{aligned}$$
Figure 2
figure 2

Spatial profiles of magnetic-field lines in Pikelner’s prominence model for \(a_{2}=1.5\), \(a_{1}=1.6\) (dashed lines) and \(a_{1}=2.0\) (solid lines). Only the right-hand (\(x\geq0\)) side of the prominence is displayed.

Full size image

The prominence equilibrium mass-density and temperature profiles that result from Equations (24), (25), and (6) are displayed in Figure 3. We note that the prominence plasma occupies the dense (at \(x=0\), \(y\approx20~\mbox{Mm}\)) and cold (at \(y\approx35~\mbox{Mm}\)) region. While the classical models of a prominence exhibit a single cold region that is centrally located, Pikelner’s model reveals the central cold region and two cold side regions (Figure 3c and d). These side regions result from faster fall-off in gas pressure than in mass density.

Figure 3
figure 3

Spatial profiles of \(\log(\varrho_{\mathrm{e}}(x,y))\) for \(a_{2} = 1.5\), \(a_{1} = 1.6\) (a) and \(a_{1} = 2.0\) (b). Temperature profiles \(\log(T_{\mathrm{e}}(x,y))\) for \(a_{1} = 1.6\) (c) and \(a_{1} = 2.0\) (d).

Full size image

3 Results of Numerical Simulations

Equations (1) – (6) are solved numerically using the FLASH code (Lee and Deane 2009; Lee 2013). This code implements a third-order, unsplit Godunov solver with various slope limiters and Riemann solvers (e.g. Tóth 2000) and also includes an adaptive mesh refinement (MacNeice et al. 2000). We use the minmod slope limiter and the Roe Riemann solver. For all cases considered we set the simulation box as \((-110,110)~\mbox{Mm} \times(1,111)~\mbox{Mm}\) and impose boundary conditions by fixing in time all plasma quantities at all four boundaries to their equilibrium values. In all of our studies we use a static grid with the lowest (highest) level of refinement set to 3 (9). The whole computational region is covered by a set of blocks with different grid-cell sizes, which are organized in a hierarchical fashion using a tree data structure (Figure 4). The blocks at the first or top level of the tree consist of the largest cells, while their children have a factor of two smaller cells. As a result, at level 3 (9) the block size contains cells that are smaller by a factor of \(2^{2}\) (\(2^{8}\)) than the top-level cells. In this way, we attain the effective finest spatial resolution of about 20 km below the transition region, \(y=2.1~\mbox{Mm}\). The total number of grid cells implemented at \(t=0~\mbox{seconds}\) in the model is almost \(10^{6}\). The typical computation time is 48 hours, and the computations were performed with 32 CPUs.

Figure 4
figure 4

Block system used in the simulation studies.

Full size image

3.1 Perturbations in Pikelner’s Prominence

We initially perturb the above-described equilibrium impulsively by adding a Gaussian pulse in a gas pressure, viz

$$ p(x,y,t=0) = p_{\mathrm{e}}(x,y) \biggl[1+A_{\mathrm{p}} \exp \biggl( -\frac {x^{2}+(y-y_{\mathrm{0}})^{2}}{w^{2}} \biggr) \biggr]. $$
(26)

Here \(A_{\mathrm{p}}\) denotes the amplitude of the initial pulse, \(y_{\mathrm{0}}\) its initial position, and \(w\) its width. The relative amplitude of the initial pressure pulse, i.e. \(A_{\mathrm{p}} = -0.95\) means that we consider large-amplitude oscillations. We set and hold fixed \(A_{\mathrm{p}}=-0.95\), \(w=4~\mbox{Mm}\), and \(y_{\mathrm{0}}=35~\mbox{Mm}\), where \(y_{\mathrm{0}}\) corresponds to the position at the bottom of the magnetic dip. The negative value of \(A_{\mathrm{p}}\) mimics rapid cooling of the plasma, which was recently studied by Murawski, Zaqarashvili, and Nakariakov (2011). The sudden, spatially localized decrease in the gas pressure around the null point sucks the plasma in, creating a region of the density enhancement around the X-point. The compression of mass density is subject to the buoyancy force, and its influence is expressed by changing the blob shape.

3.2 Dynamics of the Perturbed Plasma

Figure 5 displays \(\log(\varrho_{\mathrm {e}}(x,y,t))\) at four consecutive moments of time. As a result of the initial perturbation, magnetoacoustic–gravity waves, which propagate in the system, are essentially excited within Pikelner’s prominence. However, these waves quickly leave the prominence domain. Later the under-pressure that settles at the launching place results in slow magnetoacoustic–gravity waves, which propagate essentially along the magnetic-field lines (Figure 5b). This under-pressure region brought some extra plasma from the ambient region into the launching place (Figure 5c and d).

Figure 5
figure 5

Spatial profiles of \(\log(\varrho(x,y))\) for \(a_{1} = 1.6\) and \(a_{2} = 1.5\) at \(t=1000~\mbox{seconds}\) (a), \(t=2500~\mbox{seconds}\) (b), \(t=4000~\mbox{seconds}\) (c), and \(t=5500~\mbox{seconds}\) (d). The vectors denote the velocity of the perturbed plasma. Only the \(x\geq0~\mbox{Mm}\) region is displayed.

Full size image

Figure 6 illustrates the relative mass [\(M_{\mathrm{r}}\)] of the prominence. This mass is evaluated within the region \(|x| \leq 20~\mbox{Mm}\), \(20~\mbox{Mm} \leq y \leq 45~\mbox{Mm}\). Indeed, according to our expectations, this mass grows in time; at \(t = 0~\mbox{seconds}\), \(M_{\mathrm{r}}=1\) while at \(t=4000~\mbox{seconds}\), \(M_{\mathrm{r}}\) reaches a magnitude of 1.13.

Figure 6
figure 6

The relative mass of the prominence vs. time.

Full size image

Figure 7 shows temperature profiles at four instants of time. Plasma at the top of Pikelner’s arcade becomes colder than in the ambient medium. As we are considering adiabatic equations, the cooling plasma results from the inflow of plasma, which is caused by the initial depression in the gas pressure there. As a result of this depression, plasma is attracted by the pressure gradient force into the launching place.

Figure 7
figure 7

Spatial profiles of \(\log(T(x,y))\) for \(a_{1} = 1.6\) and \(a_{2} = 1.5\) at \(t=1000~\mbox{seconds}\) (a), \(t=2500~\mbox{seconds}\) (b), \(t=4000~\mbox{seconds}\) (c), and \(t=5500~\mbox{seconds}\) (d). The velocity vectors are denoted by arrows.

Full size image

We do not include any dissipation mechanism in our model, such as radiation or thermal conduction. The initial negative pressure imbalance produces an increase of the mass density at the dip of the model prominence because it produces an inflow there mainly from chromospheric plasma, which is seen in Figure 8 after the first 250 seconds of the simulation. As the dip is a potential well, some part of the inflowing plasma is trapped there and the mass density grows there. A similar physical explanation can be applied to the temperature field of the prominence. The plasma flows from the foot-points of the prominence along its field lines, which is colder than the plasma in the dip at \(t=0~\mbox{seconds}\).

Figure 8
figure 8

Spatial profiles of \(\log(\varrho(x,y))\) for \(a_{1} = 1.6\) at \(t=250~\mbox{seconds}\). The vectors denote the velocity of the perturbed plasma.

Full size image

Figure 9 displays the temporal signatures that are drawn by collecting wave signals in the mass density at the point \((x=0, y=35)~\mbox{Mm}\), which corresponds to the location of the prominence dip. These time-signatures reveal an initial phase with strong mass-density variations. This initial phase lasts until \(t \approx1500~\mbox{seconds}\). The oscillations are later of lower amplitude, indicating a strong attenuation. The attenuation may result from energy leakage through the foot-points of the prominence that are located at the transition region, and also from the dip in magnetic-field lines. We discuss below some estimates to support the inherent wave-leakage process to dissipate the magnetoacoustic oscillations. The temporal evolution of the mass density exhibits a clear nonlinear behavior because the initial mass density, i.e. the equilibrium value, is lower than the end value, which remains almost constant. The velocity field also oscillates according to the mass-density perturbations.

Figure 9
figure 9

Time-signatures of \(\varrho(x=0~\mbox{Mm},y=35~\mbox{Mm})\) vs. time for \(a_{1} = 1.6\) (dashed line) and \(a_{1} = 2.0\) (solid line).

Full size image

Figure 10 shows the velocity oscillation near the maximum of the prominence at \((x= 20, y=35)~\mbox{Mm}\). The velocity-field perturbations are aligned with the magnetic-field lines, indicating that the motions are associated with slow modes.

Figure 10
figure 10

Time-signatures of velocity \(V_{x}(x=20~\mbox{Mm},y=35~\mbox{Mm})~\mbox{km}\,\mbox{s}^{-1}\) (the left panel) and \(V_{y}(x=20~\mbox{Mm},y=35~\mbox{Mm})~\mbox{km}\,\mbox{s}^{-1}\) (the right panel) vs. time for \(a_{1} = 2.0\).

Full size image

These oscillations for \(a_{1}=2.0\), which represent the slow magnetoacoustic–gravity oscillations along the arcade, are analyzed by the Fast Fourier Transform (FFT) and wavelet methods. They exhibit a main period of \(1577~\mbox{seconds}\), as is shown in Figures 11 and 12.

Figure 11
figure 11

The wavelet spectrum of velocity \(V_{x}(x=20~\mbox{Mm},y=35~\mbox{Mm})~\mbox{km}\,\mbox{s}^{-1}\) (the left panel) and \(V_{y}(x=20~\mbox{Mm},y=35~\mbox{Mm})~\mbox{km}\,\mbox{s}^{-1}\) (the right panel) for \(a_{1} = 2.0\).

Full size image
Figure 12
figure 12

The Fast Fourier Transform (FFT) (the left panel) and wavelet spectra (the right panel) of time-signatures of mass density for \(a_{1} = 2.0\).

Full size image

Figure 13 shows that the maximum of the mass density [\(\varrho_{\mathrm{max}}\)] grows with \(a_{\mathrm{1}}\). A higher value of \(a_{\mathrm{1}}\) corresponds to a larger depth of the dips in the magnetic-field lines; the prominence with a larger depth of the dips, shows a larger amplitude of the slow magnetoacoustic–gravity oscillations after it has been perturbed and departed from equilibrium. As a result, more plasma can be trapped in the dips and the mass density there increases, which explains the growing trend exhibited in Figure 13.

Figure 13
figure 13

Maximum of the mass density taken from the left panel of Figure 9 vs. \(a_{\mathrm{1}}\).

Full size image

From Figure 9 we infer that a larger depth of the dips in the magnetic-field lines of a prominence leads to more oscillations in the mass density. Compare the solid line drawn for the larger depth in the dip with the dashed line, which corresponds to the case of the shallower dip.

The decay of the slow magnetoacoustic–gravity oscillations clearly decreases with the depth of the magnetic dip of a prominence. Figure 9 shows the fast attenuation and almost no oscillatory motion in the case of a shallower depth of the magnetic dip (dashed line). Figure 14 illustrates how attenuation time [\(\tau\)] grows with \(a_{1}\). This means that a prominence with a larger dip (larger \(a_{1}\)) has a longer attenuation time (i.e. longer decay) and vice versa.

Figure 14
figure 14

Variation of attenuation time \(\tau\) vs. \(a_{1}\).

Full size image

Terradas et al. (2013) also found longer oscillation wave periods for massive prominences and shorter period waves for light prominences.

Our model considers the prominence and its ambient medium within the framework of the analytical technique of Solov’ev (2010), in which all forces acting on the plasma are taken into account. The oscillations excited in the system are not pure gravity or gas pressure, which is a different aspect compared to the previous model. The results in our article are associated with the antisymmetric longitudinal oscillations, which is a case study of our developed prominence model, and they match the results obtained by Terradas et al. (2013). However, it should be noted that the present model is based on nonlinear full MHD, while the model by Terradas et al. (2013) considered magnetostatic equilibrium and linear MHD normal-mode analysis. In the context of the model description, these two cases are therefore not very relevant. As stated above, the most likely dissipation mechanism of the excited oscillations is a wave leakage. This can result from energy leakage through the footpoints of the prominence, which are located at the transition region, and also from energy leakage through the dip in magnetic-field lines. Figure 15 shows the ratio of kinetic energy of the plasma just below the footpoints to the total kinetic energy above the footpoints, i.e. above the transition region. This ratio grows with time, which indicates the leakage of energy from the prominence. Figure 16 also shows some leakage of energy below and above the prominence in the form of side streams of fast-moving plasma. Therefore, we quantify the wave-leakage process as the dissipative agent for the evolved antisymmetric magnetoacoustic–gravity oscillations in Pikelner’s model prominence.

Figure 15
figure 15

The ratio of the energy below the footpoints to the total energy.

Full size image
Figure 16
figure 16

Total velocity in \(\mbox{km}\,\mbox{s}^{-1}\) (color scale and vectors) for \(a_{1}=1.6\) at time \(t=6000~\mbox{seconds}\).

Full size image

We infer from Figure 16 that the highest pulse velocity is about \(50~\mbox{km}\,\mbox{s}^{-1}\). This magnitude of the flow matches the typical observational data. For a large amplitude of the initial pulse, nonlinear effects would become more important. However, we have verified by running the appropriate cases that the general scenario of the system evolution remains similar.

4 Summary

We adopted the analytical methods of Solov’ev (2010) to derive Pikelner’s model (Pikelner 1971) of a normal-polarity solar prominence. We implemented our analytical model in the publicly available FLASH code (Lee and Deane 2009) and demonstrated the feasibility of fluid simulations in obtaining quantitative features in weakly magnetized and gravitationally stratified prominence plasma. In particular, we focused on the perturbation of the developed normal-polarity prominence model and its subsequent evolution. This perturbation was triggered by launching the initial pulse in gas pressure, which excited fast and slow magnetoacoustic–gravity waves. Fast waves were present at the initial stage of the prominence evolution, while slow waves developed later on. They led to an accumulation of plasma at the launching place, which corresponds to location of the magnetic dip. The parametric studies that we performed revealed that this accumulation varies with the depth of the dip; for a shallower dip there is less accumulated plasma and smaller oscillations at the magnetic dip.

These large-amplitude oscillations consist of motions with observed velocities greater than \(20~\mbox{km}\,\mbox{s}^{-1}\) (Arregui, Oliver, and Ballester 2012), which is also evident in our model results. Large-amplitude longitudinal oscillations can be excited by impulsive events, e.g. microflares that are due to impulsive heating (e.g. Zhang et al. 2012). In our model we therefore considered the gas-pressure perturbation as a physical initial trigger mechanism of the oscillations that excite longitudinal fast and slow magnetoacoustic–gravity waves.

Our new analytical prominence model with realistic temperature distribution shows a reasonable physical behavior of the typical slow acoustic oscillations in these quiescent prominences, which also matches the numerical results of Terradas et al. (2013). However, it should be noted that Terradas et al. (2013) considered magnetostatic (MHS) equilibrium and linear MHD normal-mode analysis, while our model is based on nonlinear full MHD equations. The general damping mechanism most likely is radiative cooling, as invoked by many analytical and numerical investigations (e.g. Terradas, Oliver, and Ballester 2001; Terradas et al. 2013), which is related to the slow acoustic oscillations of the quiescent prominences. The fast dissipation of large-amplitude prominence oscillations is clearly evident in the observational data (e.g. Terradas et al. 2002; Arregui, Oliver, and Ballester 2012, and references cited therein). In the present case, we specifically found and quantified that the wave-leakage process is the dissipative agent for the antisymmetric magnetoacoustic–gravity oscillations in Pikelner’s model prominence. Since in our model we did not invoke any non-adiabatic thermodynamical effects, e.g. radiative cooling, for the dissipation of such oscillations, even then the wave-leakage is a very effective mechanism for the dissipation of asymmetric oscillations. The relative significance of various dissipative agents on the magnetoacoustic–gravity mode oscillations, e.g. wave-leakage, radiative cooling, etc. is an important task that we will study in a future project.

In conclusion, we have tested our new analytical prominence model numerically and excited the slow magnetoacoustic–gravity oscillations along its magnetic dip by perturbing a gas pressure within the prominence. Our model will be further used in a more detailed study of prominence dynamics and to constrain its oscillations to exploit prominence seismology with the aim to deduce local plasma conditions.