Nonlinear Resonant Excitation of Fast Sausage Waves in Current-Carrying Coronal Loops

Abstract

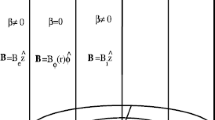
We consider a model of a coronal loop that is a cylindrical magnetic tube with two surface electric currents. Its principal sausage mode has no cut-off in the long-wavelength limit. For typical coronal conditions, the period of the mode is between one and a few minutes. The sausage mode of flaring loops could cause long-period pulsations observed in microwave and hard X-ray ranges. There are other examples of coronal oscillations: long-period pulsations of active-region quiet loops in the soft X-ray emission are observed. We assume that these can also be caused by sausage waves. The question arises of how the sausage waves are generated in quiet loops. We assume that they can be generated by torsional oscillations. This process can be described in the framework of the nonlinear three-wave interaction formalism. The periods of interacting torsional waves are similar to the periods of torsional oscillations observed in the solar atmosphere. The timescale of the sausage-wave excitation is not much longer than the periods of interacting waves, so that the sausage wave is excited before torsional waves are damped.

Appendix

The dispersion equation for the sausage mode has the form

$$\begin{aligned} & WZ - XY = 0, \end{aligned}$$

(59)

$$\begin{aligned} &W = J_0(\kappa b)I_0(\lambda b) - \frac{J_1(\kappa b)}{\kappa b} \biggl(I_0(\lambda b) - \frac{b\omega^2}{ \lambda V_{\mathrm{A}0}^2}I_1(\lambda b) \biggr), \end{aligned}$$

(60)

$$\begin{aligned} &X = J_0(\kappa b)K_0(\lambda b) - \frac{J_1(\kappa b)}{\kappa b} \biggl(K_0(\lambda b) + \frac{b\omega^2}{ \lambda V_{\mathrm{A}0}^2}K_1(\lambda b) \biggr), \end{aligned}$$

(61)

$$\begin{aligned} &Y = I_0(\lambda a)K_0(\lambda a) + \frac{K_1(\lambda a)}{\lambda a} \biggl(I_0(\lambda a) - \frac{a\omega^2}{ \lambda V_{\mathrm{A}0}^2}I_1( \lambda a) \biggr), \end{aligned}$$

(62)

$$\begin{aligned} &Z = K_0^2(\lambda a) + \frac{K_1(\lambda a)}{\lambda a} \biggl(K_0(\lambda a) + \frac{a\omega^2}{ \lambda V_{\mathrm{A}0}^2}K_1(\lambda a) \biggr). \end{aligned}$$

(63)

Coefficients in the nonlinear terms (41) – (42) are

$$\begin{aligned} d_j =& - \frac{(k_3 - k_j)^2}{\omega_3} W_j \frac{1}{r} \,\frac {\mathrm{d}}{\mathrm{d}r} (rJ_1) + (k_3 - k_j) \biggl( \frac{k_3}{\omega_3} - \frac{k_j}{\omega_j} \biggr) \,\frac{\mathrm{d}}{\mathrm{d}r} (J_1W_j) \\ &{}- \biggl[ \frac{\kappa^2}{\omega_3} + \biggl( \frac{k_3^2}{\omega _3} - \frac{k_j^2}{\omega_j} \biggr) + k_3k_j \biggl( \frac{1}{\omega_3} - \frac {1}{\omega_j} \biggr) \biggr] J_1 \frac{1}{r} \,\frac{\mathrm{d}}{\mathrm{d}r} (rW_j),\quad j=1, 2, \end{aligned}$$

(64)

$$\begin{aligned} d_3 =& \biggl( \frac{k_1^2}{\omega_1} + \frac{k_2^2}{\omega_2} \biggr) \frac{2}{r} W_1W_2 \\ &{}- k_1k_2 \biggl( \frac{1}{\omega_1} + \frac{1}{\omega_2} \biggr) \biggl( W_1 \frac{1}{r}\, \frac{\mathrm{d}}{\mathrm{d}r} (rW_2) + W_2 \frac{1}{r}\, \frac{\mathrm{d}}{\mathrm{d}r} (rW_1) \biggr). \end{aligned}$$

(65)

The interaction coefficients in Equations (45) – (47) are

$$\begin{aligned} C_1 =& \biggl(\frac{2\omega_1}{V_{\mathrm{Ai}}^2} \int_0^b rW_1^2(r)\mathrm {d}r \biggr)^{-1} \int _0^b rd_2W_1(r)\, \mathrm{d}r, \end{aligned}$$

(66)

$$\begin{aligned} C_2 =& \biggl(\frac{2\omega_2}{V_{\mathrm{Ai}}^2} \int_0^b rW_2^2(r)\mathrm {d}r \biggr)^{-1} \int _0^b rd_1W_2(r)\, \mathrm{d}r, \end{aligned}$$

(67)

$$\begin{aligned} C_3 =& \biggl(\frac{2\omega_3}{V_{\mathrm{Ai}}^2} \int_0^b rJ_1^2(\kappa r)\,\mathrm{d}r \biggr)^{-1} \int _0^b rd_3J_1(\kappa r)\, \mathrm{d}r. \end{aligned}$$

(68)