1 Introduction and Motivation

Quiet-Sun magnetic fields are always in motion, as new magnetic flux emerges and the two foot points of the emerging loop separate until one or both of them cancel with flux already present at the solar surface; see, e.g., Martin et al. (1985). It has been estimated from SDO/MDI magnetograms (Hagenaar 2001) that the magnetic flux in the quiet Sun’s photosphere is replaced every 14 hours, whereas Close et al. (2004, 2005) using potential-field extrapolations from MDI found a remapping time of just 1.4 hours for the quiet Sun’s coronal flux. This is remarkably short and has strong repercussions for the dynamics and heating of the solar corona.

A basic assumption of the method employed by Close et al. (2005; see their Figure 1) is that the quiet-Sun’s photospheric magnetic field is composed of a number of discrete fragments and that the quiet Sun is unmagnetized elsewhere. Consequently, the potential field in the corona was computed analytically with the help of a Green’s function method from the identified discrete sources. While such a simplification of the true nature of the quiet-Sun’s photospheric magnetic field was reasonable for magnetograms obtained with SOHO/MDI with a pixel size of 1400 km and high noise for weak fields, new observations with the balloon-borne Sunrise-mission (Solanki et al. 2010; Barthol et al. 2011) provide more detailed insights into the magnetic structure of the quiet Sun. The IMaX magnetograph (Martínez Pillet et al. 2011) on Sunrise has achieved a spatial resolution of roughly 100 km with a pixel size of 40 km and low noise level,Footnote 1 and it reveals a more detailed picture of the building blocks of the quiet-Sun’s magnetic field. Thus, in agreement with earlier observations (de Wijn et al. 2009) that internetwork regions are by no means unmagnetized and play an important role for the structure of the quiet-Sun’s atmosphere. Potential-field extrapolation from one snapshot from Sunrise/IMaX-magnetograms by Wiegelmann et al. (2010) showed that magnetic concentrations (or network elements) are frequently connected with internetwork features, as predicted in the simulation by Schrijver and Title (2003). Consequently, if we want to understand the true structure of the solar atmosphere, we have to take these connections into account also when studying the temporal evolution of the quiet-Sun’s magnetic field.

Here we investigate the evolution of the quiet-Sun’s magnetic field above the photosphere based upon numerical potential-field extrapolations starting from Sunrise/IMaX magnetograms. We structure this article as follows: In Section 2 we briefly discuss the employed data set and the method for extrapolating the photospheric field into the higher atmosphere. Section 3 is devoted to identifying network elements in the photosphere. In Section 4 we compute some statistical values about the network elements and corresponding magnetic loops. In Section 5 we discuss whether we can observe effects of magnetic reconnection and possible impact for heating processes. Finally, we draw conclusions in Section 6.

2 Extrapolation of Photospheric Magnetic Field Measurements into the Upper Solar Atmosphere

We use a 22-minute long time series of phase-diversity reconstructed Stokes vector maps in the Fe i 5250 Å spectral line of a 37×37 Mm quiet-Sun region in the photosphere recorded by Sunrise/IMaX (the data set was observed at disk center starting at 00:00 UT on 11 June 2009, with a temporal cadence of 33 seconds (Martínez Pillet et al. 2011)). The magnetic vector is obtained by inverting these data using the VFISV code described by Borrero et al. (2011). This code has been used before for the inversion of Stokes-profiles from Hinode/SP (Yang, Zhang, and Borrero 2009; Kobel, Solanki, and Borrero 2011; Borrero and Kobel 2011) and Sunrise/IMaX by Wiegelmann et al. (2010).

To get an impression of the 3D magnetic-field structure in the chromosphere and corona, we extrapolate the photospheric measurements into the atmosphere under the potential-field assumption.

(1)
(2)
(3)

where B is the magnetic-flux density. We solve Equations (1) – (3) with the help of a fast-Fourier approach (Alissandrakis 1981) with the measured vertical magnetic field as boundary condition. We refer to Wiegelmann et al. (2010) for details.

Because our field of view is small, and hence the foot-point distance for the field lines is limited, we can only investigate the magnetic field to small heights of approximately 15 Mm into the corona. This is sufficient to study the quiet-Sun coronal structure. Our extrapolation will also include the photosphere and chromosphere, where the assumption of a potential field is not justified. Because in the low parts of the atmosphere the plasma dominates the magnetic field, or equipartition is found, one should employ a full MHD model. However, we want to match the observed time-variable magnetic structure in that particular observed region, which is not (yet) possible with MHD models. Furthermore, models with a proper description of magneto-convection in the photosphere do not reach high enough in the atmosphere (e.g. Moll, Cameron, and Schüssler 2012), while models accounting for the coronal dynamics provide a rather coarse description of the photosphere and chromosphere (e.g. Peter and Bingert, 2012). Therefore, even when considering all its problems, a potential-field analysis is a valuable approach.

3 Identification of Strong-Field Magnetic Elements

First we automatically identify strong-field magnetic elements in the magnetograms. We developed the following procedure:

  • Identify all pixels above a certain threshold |B z | value, where B z is the line-of-sight photospheric magnetic-field component. Because the observations were carried out very close to the center of the solar disk, B z corresponds essentially to the vertical component of the magnetic field. We use the equipartition field strength (see Solanki et al. (1996) for details) of |B z |=300 G as threshold value.Footnote 2 Since the inversion is done for a single atmospheric component, this is the magnetic-field strength averaged over the spatial resolution of the observation. Note that the threshold is many times higher than the noise in the data, which corresponds to ≈ 10 G. Magnetic features with field strengths −300 G<B z <300 G are considered to be internetwork features.

  • Remove isolated pixels lying above the |B z | threshold. As the spatial resolution is about 100 km, any feature with an area below four pixels is spatially unresolved.

  • Use a connected-component labeling algorithm to identify and label magnetic elements (pixels above the threshold that are connected horizontally, vertically or diagonally).

  • Compute the center of gravity (x,y) for each element.

  • Different regions (magnetic elements) with same polarity which have their center of gravity close together and are separated only by a few pixels below the threshold are merged to one region.

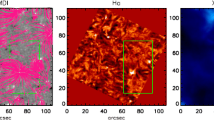
  • The magnetic elements are re-labeled by the total magnetic flux [|Φ|] they contain. Φ=dA ∑pixel B z , where dA=40 km×40 km is the area of one pixel in the photosphere.Footnote 3 The region with the most flux is labeled 1, that with the second most 2, etc. Four snapshots within the 22-minute observation interval are presented in Figure 1 and the evolution for individual regions in Figure 2. Labeled are the nine regions with the largest total magnetic flux. These nine regions are the only ones that existed without interruptions during the entire 22-minute observation period.

    Figure 1
    figure 1

    Sunrise/IMaX magnetograms and labeled network elements at the beginning of the observation period. The x- and y-axes are in Mm and the gray-scale bar shows the magnetic field in Gauss. Labeled are the nine regions that contain the most flux and exist during the entire observation period. 1 corresponds to the strongest (most unsigned flux on average over the time series), region 2 to the second strongest, etc. The labeled network elements correspond to the entries in Table 2. See Figure 2 for snapshots of the temporal evolution of selected elements and in the Electronic Supplementary Material filmmag.gif for a movie with all frames.

    Full size image
    Figure 2
    figure 2

    Temporal evolution of selected regions in the Sunrise/IMaX magnetograms at the beginning of the observation period, and after 5, 10, and 20 minutes. From left to right we show a zoom of 4×4 Mm into the magnetograms around elements 2, 3, and 8. See Figure 1 for the full FOV of Sunrise/IMaX.

    Full size image

  • For a threshold of 300 G, we identified in total 266 individual flux elements, but 100 of them can be identified only in one snapshot and we cannot estimate their lifetime. In Table 1 we present (for threshold values of 200, 300, 400 G) the number of identified elements (separately for positive- and negative-flux regions), their average and median life times, and average and median magnetic flux. The maximum magnetic-field strength in the identified regions (averaged over all regions and time) is 526, 678, 810 G for a threshold value of 200, 300, 400 G, respectively.

    Table 1 Dependence of number, average, median life time, and average and median magnetic flux of magnetic elements on the magnetic-field threshold used. In the lower part of the table (rows 7 – 12) only network elements with a magnetic flux above 1 GWb [1017 Mx] have been considered.
    Full size table

One may argue that many of the so-identified magnetic elements (first six rows in the table) are not real network elements, because the total flux that they contain is relative low. In rows 7 – 12 in Table 1 we provide the corresponding quantities, if only magnetic elements with a flux above 1 GWb [1017 Mx] are considered. Although it is clear that many of these features are not located in the network per se but rather belong to the class of strong-field internetwork features found by Lagg et al. (2010), for simplicity and in order to distinguish them from the neater internetwork fields, we refer to them as network regions in the following.

4 Time Series, Global Features

First we investigate some global features of the identified magnetic concentrations and their temporal evolution. Figure 3a shows the number of network elements. Averaged over time, 37±5 flux-regions are visible in each snapshot, with approximately half having positive and half negative polarity. However, the magnetic flux stored in positive-polarity regions is on average 2.5±0.5 times higher than in those with negative polarity. This is clearly visible in Figure 3b. We compute magnetic-field lines with one foot point located in each pixel in the identified elements. The other foot point belongs to one of the following categories:

  1. i)

    The field line connects to another (opposite polarity) network region.

  2. ii)

    The field line connects with the internetwork, defined here as regions with a magnetic-field strength below the equipartition strength of 300 G.

  3. iii)

    The other foot point lies outside the Sunrise-FOV. We cannot investigate these field lines properly.

Properties of each loop are recorded in each snapshot. Averages of some of these quantities over all loops closing in the FOV in a given snapshot are plotted in Figure 3 as a function of time at which the snapshot was recorded. Figure 3c shows the evolution of loop heights. The time-averaged value is 2.8±0.2 Mm and very little variation in time is seen. Please note that the time-averaged loop heights here are more than a factor of two higher than the averaged loop heights for one snapshot reported by Wiegelmann et al. (2010). The reason is that the leading foot points of the loops considered here are located in strong-field regions (|B z |>300 G) only, while in the previous work loops have been calculated from all pixels with significant field, i.e. with |B z |>30 G. Figure 3d displays the average field strength of the leading foot point as a solid line (from where we started the field-line integration in network elements; time-averaged |B z |=494±26 G) and the strength of the opposite foot point as a dotted line (time-averaged |B z |=243±28 G). Figure 3e depicts the fraction of field lines connecting network elements with other network elements (solid line: time-averaged 30±3 %). This fraction is, however, very different for field lines starting from positive elements (dotted line: time averaged 23±4 %) and negative ones (dashed line: time averaged 43±6 %), due to the higher magnetic flux stored in positive network elements, as seen in Figure 3b. There is just not enough flux available in negative network regions to be connected to. Consequently almost 80 % of all field lines from positive elements connect to the internetwork or leave the domain. Finally, Figure 3f reveals the fraction of magnetic field lines, that cannot reliably be traced to the opposite foot point, because of the limited FOV (solid line: time averaged 31±4 %). We also exclude unresolved loops, with a height of less than 100 km from our analysis (dotted line: the time-averaged fraction of these is only 1.6±1.4 %).

Figure 3
figure 3

Temporal evolution of various quantities. Panel a: Number of identified network regions. Panel b: Total magnetic flux in GWb in the identified regions. (Solid, dotted, and dashed lines correspond to all regions, positive-flux regions and negative-flux regions, respectively.) Panel c: Average height of magnetic loops. Panel d: Average magnetic-field strength in the foot point from which we started to trace the field line (always in a network element) and field strength of the opposite foot point (which can be anywhere in the FOV). Panel e: Fraction of all loops (closed in the Sunrise FOV and resolved) that connect network elements with other network elements. Panel f: Fraction of magnetic loops, which we cannot investigate properly, because they do not close within Sunrise-FOV (solid) or are not resolved (lower than 100 km, dotted line).

Full size image

The rather high fraction of about 30 % of loops that do not close within the Sunrise FOV is partly due to the fact that some network elements are located close to the boundary of the FOV. For some individual network regions (that preferentially lie close to the center of the FOV), this ratio is smaller, e.g. for region 2 only 12±5 % of all loops do not close within the FOV and the number of loops too small to resolve is 0.3 %, i.e. almost zero. Table 2 gives an overview of the nine strongest (i.e. with most total flux) network elements. These nine network features are also the only ones that we can trace over the entire interval of about 22 minutes. All other regions appear or disappear during the observation interval.

Table 2 Overview of long-lived network elements. The first column is an identifier for the particular region, the second column titled “pixel” contains the time-averaged area [in pixels] of each element (each pixel has an area of 40×40 km), the third column marked as ϕ NE lists the amount of magnetic flux (the polarity can be deduced from the sign), the fourth column named |ϕ c| gives the unsigned magnetic flux closing within the FOV, column 5 headed “Height” provides the average height of magnetic loops with one foot point in the particular region, column 6 marked as B z the average line-of-sight component of the magnetic field of these foot points, column 7 B z2 the average magnetic-field strength of the opposite foot point (which lies in other network areas or in the internetwork). Column 8, \(\frac{B_{z}}{B_{z2}} \) the ratio of the average foot-point strengths, Column 9, “Net”, contains the fraction of closed loops with one foot point in other network elements, column 10 “H-cut” lists the fraction of loops not closing within the FOV and column 11 “L-cut” contains the fraction of unresolved loops (height below 100 km).
Full size table

4.1 Temporal Evolution of Magnetic Elements and Magnetic Loops

To investigate further how the magnetic connectivity between network elements (network–network loops as well as network–internetwork loops) evolves in time, we trace the elements in time. We start the magnetic-field-line integration at every pixel within the nine identified network elements (we call this the lead foot point of a loop) and trace each field line to its other foot point. Unfortunately, we cannot trace those field lines that leave the Sunrise FOV. Columns 2 and 3 of Table 2 list the total magnetic flux [ϕ NE] of the network element and the part of this flux [ϕ c] that hosts foot points of closed (within the FOV) loops, respectively. A large difference between total and closed flux leads to many field lines leaving the box, which we cannot trace from one foot point to the other. We call the fraction of such field lines “High-cut”Footnote 4 and tabulate them in column 7 of Table 2. For region 1, 73 % of all field lines cannot be traced, because the region is too close to the boundary. For several other regions almost all loops close within the Sunrise-FOV, which is preferable for our analysis. We also exclude very small, unresolved loops (height below 100 km) from the further analysis, but as the last column (low-cut) shows, their number is very small for most regions (less than about 1 % for all except one region).

Column 5 of Table 2 shows the average height of loops starting in the particular element (first averaged over all loops in each snapshot and then averaged in time over 22 minutes). There is obviously considerable variation between the heights of loops emerging from different network elements, ranking from very low-lying (0.66 Mm, region 6) to an order of magnitude higher loops (6.40 Mm, region 7). Columns 6 and 7 list the (again twice averaged) line-of-sight component of the magnetic field of the lead foot point [B z ] and opposite foot point [B z2]. In column 8 we show the ratio of these two quantities, for most regions this quantity is around 1.5 with the exception of regions 1 and 2. We should not interpret the results of region 1, however, because 73 % of the pixels do not host foot points closing within the FOV. Region 2 is mainly dominated by network–internetwork connections, which explains the significantly higher ratio of the average foot-point strengths. Please note that \(\frac{B_{z}}{B_{z2}} \) refers to the average foot-point strength. For individual loops the ratio between the field strength at both foot points has a large scatter. Column 9, named “Net”, presents the fraction of closed loops that have the second foot point in another network element (any other network element, not necessarily in one of the nine stable and strong elements). The fraction of network–network loops varies significantly from region to region. From region 2 only 3 % of all loops have both foot points in network elements and consequently here almost all loops connect network to internetwork, as also seen in our first article based on Sunrise data (Wiegelmann et al. 2010). For other elements the fraction of network–network loops is significantly higher, up to about 50 %, but usually network–internetwork connections occur more often than connections between network elements. Regions with a high fraction of network–network loops have necessarily also a higher average magnetic-field strength at the second foot point B z2.

4.2 Connectivity Patterns for Selected Regions

In the following we investigate more details of the connectivity and topology change of loops starting from individual regions. Table 2 reveals that the largest region, Number 1, is not a good candidate for an in-depth analysis, because more than 70 % of all field lines emanating from this region do not close within the Sunrise-FOV (because the region is close to the boundary). Region 2 is somewhat special, as it is quite isolated (see Figure 1) and almost all (97 % on average) field lines starting in these region are connected to internetwork areas. Nonetheless, it still seems worth investigating further. Region 3 also looks like a reasonable candidate for further investigation. On average about 90 % of all field lines starting here close within the FOV (see Table 2) and with about 40 % of network–network loops the region is close to the average value of 30 %. Another suitable candidate for investigations is the negative-flux region 8, because almost all (in most snapshots all) loops with one foot point in region 8 close within the Sunrise-FOV.

We plot snapshots of magnetic-field lines starting in regions 2, 3, and 8 in Figures 4, 5, and 6, respectively. We show all loops that have one foot point in the corresponding region and close within the Sunrise-FOV. Individual panels refer to the beginning of the observation interval as well as after 5, 10, and 20 minutes, respectively. Field lines not closing in the FOV are omitted. There is a striking difference between the loops emanating from the three regions. Thus the loops starting in region 2 end in many widely distributed foot points. The temporal evolution of these field lines looks rather calm and no abrupt changes in the field-line connectivity occur. Region 2 remains basically connected with the internetwork during the entire observation interval with some wiggling around. For region 3 shown in Figure 5, long magnetic-field lines seem to dominate the picture, but they contain little flux compared with the shorter loops. These loops from region 3 show a very dynamic behavior. While the connectivity seems to be quite compact to the nearby internetwork at time zero, later connectivity to several distant network elements occurs, which are rather unstable. Finally the loops from region 8 typically end in two – six discrete magnetic features. The dynamics of loops from region 8 are not as abrupt and large scale as in region 3, but significantly more dynamic than region 2. It seems that significant changes in the field-line connectivity take place mainly for connections between network elements, while for network to internetwork connections the loop foot point in the internetwork become only slightly displaced.

Figure 4
figure 4

Snapshot of 3D loops with one foot point in region 2 at the beginning of the observation period and after 5, 10, and 20 minutes. Black field lines show connections between network elements and red field lines indicate network–internetwork connections. [See Electronic Supplementary Material filmfl2.gif for a movie with all frames.]

Full size image
Figure 5
figure 5

Snapshot of 3D loops with one foot point in region 3 at the beginning of the observation period and after 5, 10, and 20 minutes. Black field lines show connections between network elements and red field lines indicate network–internetwork connections. [See Electronic Supplementary Material filmfl3.gif for a movie with all frames.]

Full size image
Figure 6
figure 6

Snapshot of 3D loops with one foot point in region 8 at the beginning of the observation period and after 5, 10, and 20 minutes, respectively. Black field lines show connections between network elements and red field lines indicate network–internetwork connections. [See Electronic Supplementary Material filmfl8.gif for a movie with all frames.]

Full size image

5 Magnetic Reconnection

A key question for our understanding of the quiet Sun’s magnetic-field structure is whether magnetic reconnection takes place and, if it does, at what rate. Close et al. (2005) studied magnetic reconnection and thereby coronal recycling by tracking the connectivity changes between different network elements observed with MDI, while we use data taken at much higher spatial resolution with Sunrise/IMaX here.

5.1 Field Lines as Tracers for Connectivity

We use field lines as tracers of the connectivity. For a quantitative analysis of connectivity and reconnection, we should, however, use physical quantities such as the magnetic flux. To do so, we assume that every field line represents a thin fluxtube with the area dA 1 in the leading foot-point region having a strength of the vertical magnetic component B z1. The natural choice of dA 1 is the size of one pixel, here dA 1=40×40 km2. At the opposite foot point, with the vertical field strength B z2 the corresponding area of the fluxtube is dA 2=dA 1  B z1/B z2, which is in general different from a single Sunrise pixel. The connectivity (amount of connected flux in Wb, by definition a positive number or zero) is then computed by integrating (summing) over all thin flux-tubes connecting two network elements. Please note that for different absolute field strengths in both regions, the total number of field lines will depend on whether we start the field-line integration in the stronger or weaker element, while the shared flux would be the same, of course (i.e. the flux per field line is determined by the field strength of the chosen leading foot point). We compute the total flux shared by two regions with field lines independently traced from both regions. For a discrete number of magnetic-field lines, the flux will usually not be exactly the same and the difference in flux gives an approximation of the error introduced by the discretization introduced by the Sunrise pixels. For |B z | between 300 – 1500 G the flux connected by one field line is in the range 0.05 – 0.25 GWb.

5.2 Examples

Figures 7a and b show the temporal evolution of the amount of flux that region 8 shares with regions 1 and 3, respectively. These are the only two durable network regions, with which region 8 is connected. The error bars have been computed as described above from the differences in flux and, with a few exceptions, are in the range of the flux connected by one field line. Figure 7c displays the amount of flux that region 8 shares with the sum of all minor network elements (please note that none of these elements survive the entire observation period). Finally, the amount of flux in region 8, which is connected to the internetwork, is depicted in Figure 7d. It seems that region 8 is mainly connected to the internetwork at the beginning of the observation period, while network–network connections become more important with time. In the 22-minute interval we do not find any stable magnetic connectivity between region 8 and any other network element. The amount of flux connecting to other particular network regions (traced here for regions 1 and 3) varies strongly and there is no network element that the region remains connected to during the entire observation period. At the beginning of the time series, the region connects frequently with small network elements which appear and disappear in the photosphere on a time-scale of minutes. From Figure 7c we find peaks in the network–network connectivity (region 8 with minor network elements) that occur almost periodically with the maxima separated by about five minutes. The strong and rapid fluctuations in this figure indicate that it can take only about one minute for up to half of the flux connecting region 8 to other particular regions to become reconnected. The minima of the corresponding connectivity with minor elements roughly agree with the minima of connectivity with network regions 1 and 3. The flux of network–internetwork loops (panel d) has local maxima at the same time. The strong maximum of network–internetwork loops close to the beginning of the time series (at t=1 – 2 minutes) agrees also with the minima in the network-network loops shown in Figure 6b and c. A significant part of region 8 is magnetically connected to the internetwork all of the time, although the amount of flux varies by a factor of about five. The strong connection with the internetwork is also true for other network regions. For this region, we can basically ignore the amount of flux not closing within the FOV.

Figure 7
figure 7

Connectivity patterns of region 8. Panels a and b show the temporal evolution of the flux that region 8 shared with regions 1 and 3, respectively. Panel c depicts the connectivity to all other network elements and panel d to the internetwork.

Full size image

5.3 Reconnection Rate and Recycling Time

In the following we consider all network elements (86 positive and 80 negative for a threshold of |B z |≥300 G, see Table 1). We define a 86×80×40 matrix [Φpn(t)] to monitor the amount of magnetic flux that a particular positive and negative region share in a certain snapshot. Connectivities to the internetwork are monitored as well. Most of the entries in Φpn are zero. By construction, all entries are zero for combinations of positive and negative regions that are not present in the same snapshot. Positive/negative regions existing simultaneously in a particular snapshot can theoretically connect by magnetic-field lines, but only a minority of these connections actually occur. On average there are about 300 positive/negative-connectivity combinations possible, but only 21±4 of them are realized on average in a particular snapshot, so that only these have non-zero entries in Φpn. We monitor the amount of shared flux with time and sum over all entries to obtain a global reconnection rate in the form:

$$ \mathrm{Reconnection \ Rate}= \sum_{\mathrm{pn}} \biggl \vert \frac{\partial\Phi_{\mathrm{pn}}(t)}{\partial t} \biggr \vert $$
(4)

which is shown in Figure 8. Its average value is found to be 6.7±1.8 GWb minute−1. An interesting quantity is the time [Δt] needed to redistribute all of the connections of a certain snapshot [t 0].

$$ \mathrm{Flux \ Ratio}=\frac{\sum_{\mathrm{pn}} \vert \Phi_{\mathrm{pn}}(t_0 + \Delta t) - \Phi_{\mathrm{pn}}(t_0) \vert }{ \sum_{\mathrm{pn}} \Phi_{\mathrm{pn}}(t_0)} $$
(5)

The value of Δt to reach a \(\mathrm{Flux \ Ratio}\) of unity can be interpreted as the recycling time of the connections between the magnetic field present in the quiet network in the atmosphere. We call the time Δt needed for the flux ratio to reach one the connection recycling time. For the data set analyzed here, we found Δt=2.7±1.2 minutes, where we averaged over the three magnetic-threshold values used here (see second column of Table 3, for Δt computed separately with thresholds of 300, 400, and 200 G). Despite the different absolute reconnection rates for different thresholds (see Figure 8), the atmospheric recycling times (Table 3, column 2) agree within the error estimate and we do not find a systematic dependence on the threshold used. The total flux of magnetic elements depends systematically on the employed threshold for B z (see Table 1 columns 6 and 7), and this largely compensates the similar dependence on the B z threshold in the reconnection rate as expected from Equation (5).

Figure 8
figure 8

Reconnection rate as defined in Equation (4).

Full size image
Table 3 Dependence of the atmospheric recycling time, the photospheric flux weighted recycling time, and the average (not flux weighted) photospheric recycling time on the used magnetic-field threshold value. See the main text for definitions of these quantities.
Full size table

We now discuss whether this result might be biased by the use of a potential-field model. Potential fields can in principle connect any positive and negative region and connectivities are only constrained by ∇⋅B=0, so that the integrated amount of magnetic flux must be the same in the positive and negative foot-point area of a flux tube

$$ \int_{\Omega+} B_z\,\mathrm{d}A=\int _{\Omega-} B_z \, \mathrm{d}A $$
(6)

Since potential fields remain at the lowest possible magnetic energy, they often must reconfigure as soon as the foot points relocate or if the internal properties of the foot points change. This may explain the connectivity peaks separated by roughly five minutes, which corresponds to the oscillation period of the magnetic-field strength found by Martínez González et al. (2011). For current carrying fields, e.g. force-free fields ∇×B=α B, additional constraints occur, as pointed out by Aly (1989). In addition to the flux balance condition (6), the electric current has to be balanced, leading to the condition

$$ \int_{\Omega+} f(\alpha) B_z \, \mathrm{d}A = \int_{\Omega-} f(\alpha) B_z \, \mathrm{d}A $$
(7)

for any function f(α), where α is the force-free parameter; see Aly (1989) for details. To compute α one needs reliable measurements of the transverse magnetic field, which are not available in the quiet Sun. Condition (7) constrains connectivities between positive and negative regions more than if only condition (6) were valid. Consequently, connectivity changes in force-free fields are less likely than for potential fields and the connection recycling time Δt≈ three minutes deduced from a potential-field model can be considered to be a lower limit. For force-free fields we would expect a longer recycling time.

Due to the poor signal-to-noise ratio in the quiet Sun, we do not have the necessary reliable transverse-field measurements to apply a force-free model. We can, however, estimate an upper limit for the recycling time based on the life times of the magnetic elements involved. We compute the time over which two flux elements that are magnetically connected in at least one snapshot both exist simultaneously in the photosphere. If we weight the connectivities with the magnetic flux that they contain, we find (also averaged over three threshold values for the magnetic field) 11.9±3.6 minutes. If we just average over all of the connectivities without weighting, this reduces to 9.2±2.0 minutes. The flux-weighted photospheric recycling time is longer, because large magnetic features with higher magnetic flux live longer.

This method provides an upper limit, since the connectivity cannot exist if the magnetic feature forming one of the foot points ceases to exist. In columns 3 and 4 of Table 3 we provide the photospheric recycling rates calculated separately for different magnetic-threshold values. These photospheric recycling times agree well within the estimated errors for a threshold of 300 and 200 G, but are significantly shorter for a threshold of 400 G.

5.4 Energy Estimations

In the following we make a rough estimate if this amount of reconnection provides a significant contributios n to heating the chromosphere and corona. In the quiet Sun, the total energy loss rate is about \(2 \times10^{6}~\mathrm{erg\,cm}^{-2}\,\mathrm{s}^{-1}=2000~\mathrm{W\,m}^{-2}\) in the chromosphere and \(3 \times10^{5}~\mathrm{erg\,cm}^{-2}\,\mathrm{s}^{-1}=300~\mathrm{W\,m}^{-2}\) in the corona (Withbroe and Noyes 1977; Klimchuk 2006). This energy flux has to be compared with the magnetic energy [\(\int\frac{\mathbf{B}^{2}}{2 \mu_{0}} \,\mathrm{d}V \)] converted by magnetic reconnection. From our computationsFootnote 5 we can compute the energy of a potential field in the entire box (from one snapshot, to the next these integral values change only by a few percent) to E mag=14.8×1020 J of which \(E_{\mathrm{mag \, photo}}=9.5 \times10^{20}~\mathrm{J}\) is present in the photosphere, \(E_{\mathrm{mag\, chrom}}= 4.7 \times10^{20}~\mathrm{J}\) in the chromosphere and \(E_{\mathrm{mag \,corona}}= 0.6 \times10^{20}~\mathrm{J}\) in the corona. Magnetic reconnection requires free magnetic energy [E free] which is the excess energy that a field has compared to a potential field. The energy-flux density [P] produced by magnetic reconnection can be computed as:

$$ P \approx\frac{E_{\mathrm{free}}}{L_x L_y \Delta t} $$
(8)

where L x =L y =37 Mm correspond to the Sunrise-FOV, E free is the magnetic energy converted by magnetic reconnection, and Δt is the connection recycling time.

Reliable estimates of E free require more advanced atmospheric magnetic-field models, e.g. force-free fields and measurements of the transverse photospheric field, which are not available with sufficient accuracy in the quiet Sun. However, we would not expect f=E free/E pot, where E pot is the potential-field energy, to be larger in the quiet Sun than in active regions. f≈0.01…1.0 has been found by, e.g., Schrijver et al. (2008), Thalmann and Wiegelmann (2008), and Sun et al. (2012). During magnetic reconnection the entire excess energy of a force-free field is not necessarily released, however. To obtain a conservative upper limit of the energy released in the quiet Sun, we assume that it equals E free=E pot. To get an upper limit on the energy flux by reconnection, we use the short connection recycling time Δt≈ three minutes obtained from the potential field. Using the values above, we obtain the energy flux density [P].

These values are close to the published values of \(2000~\mathrm{W\,m}^{-2}\) for the chromospheric loss rate and \(300~\mathrm{W\,m}^{-2}\) for the coronal loss rate. As these approximations can be regarded as an upper limit, we expect the true value to be lower. It seems not very likely to us that the quiet-Sun’s magnetic field doubles in energy within just three minutes, i.e. less than a typical granule lifetime. Hence our analysis suggests that magnetic reconnection of the field-connecting network regions cannot be responsible for heating the quiet chromosphere and corona. Internetwork–internetwork loops are not likely to contribute significantly to coronal and chromospheric heating, because loops reaching to chromospheric and coronal heights have at least one foot point in the network (Wiegelmann et al. 2010). In principle larger energies are possible if non-force-free effects play a role, as suggested by Schrijver and van Ballegooijen (2005). Our results are valid within our assumptions. We cannot rule out heating by reconnection, but it is unlikely that the entire heating is driven by this process, unless we are missing a significant part of the quiet-Sun’s magnetic flux in Sunrise data.

Other magnetic mechanisms are consistent with our analysis as long as they do not requite a re-configuration of the magnetic field on the observable length scales. For example, Alfvén-wave turbulence as recently suggested by van Ballegooijen et al. (2011) could provide the necessary energy for the chromosphere and corona and would work for at least active-region coronal loops. Also, MHD turbulence could provide the necessary energy (e.g. Rappazzo et al., 2008). In more realistic 3D MHD models the Ohmic heating through the dissipation of induced currents would be consistent with these findings (e.g. Gudiksen and Nordlund, 2002; Bingert and Peter, 2011). There the energy input into the corona is several 100 W m−2 and higher for the chromosphere, consistent with the above-mentioned canonical values derived from observations. Furthermore these latter models produce synthetic observables close to real observations e.g. Peter, Gudiksen, and Nordlund (2004, 2006). In these as well as in the models coupling the photosphere to the low corona (Hansteen et al., 2010; Martínez-Sykora, Hansteen, and Moreno-Insertis, 2011), reconnection occurs, but does not play the major role in heating up the plasma, which is done through Ohmic heating.

In this study, which is based on Sunrise data, we estimate that energy conversion by reconnection is not likely to be sufficient to heat the chromosphere and the corona, therefore other processes, e.g. Ohmic heating, MHD turbulence, or MHD waves are likely to dominate the heat input.

One has also to consider that the observations presented here have been acquired during a really quiet phase of the solar cycle, without any active regions present. Therefore, we do not expect magnetic connections from the small network magnetic patches in our field-of-view to more active areas on the Sun through long field lines. However, such connections will exist during more active phases of the cycle, analogs to the connection of small internetwork patches to stronger network patches (Schrijver and Title 2003; Jendersie and Peter 2006). When being heated, these longer field lines could be seen as coronal loops originating in the active region reaching into surrounding quiet areas. In this case one can expect more reconnection events in the quiet-Sun regions between smaller network loops and the longer field lines to the active regions through the relentless shuffling of the network patches. Consequently the contribution of reconnection to the quiet-Sun heat input into the chromosphere and corona could be stronger at a higher global activity level than found in the present study. This hypothesis could be tested by repeating this study of the quiet-Sun with data of comparable quality during a phase of higher activity.

6 Conclusions

Within this work we analyzed the temporal evolution of a quiet-Sun area as measured with Sunrise/IMaX in the photosphere and as extrapolated in the upper solar atmosphere with the help of a potential-field model. This study confirms our earlier findings from one snapshot (see Wiegelmann et al., 2010) that magnetic connections between network elements and the internetwork are ubiquitous. For loops starting from individual network elements the fraction of network–internetwork loops varies significantly from region to region and also in time, which can be interpreted as support for the occurrence of magnetic reconnection. We estimate the time needed for the flux in the quiet Sun’s upper atmosphere to be recycled. A potential-field model gives a lower limit of three minutes, while we get an upper limit of 12 minutes from the lifetimes of magnetic elements in the quiet Sun. Within this period of time, the network elements must change their connectivity.

In earlier work using SOHO/MDI magnetograms, Close et al. (2004, 2005) found (also using a potential-field model, but ignoring the internetwork fields not resolved by MDI) an atmospheric recycling time of 1.4 hours and Hagenaar (2001) found that the magnetic flux in the quiet-Sun’s photosphere is replaced every 14 hours. While the high spatial resolution of Sunrise shows more magnetic fine structure than MDI and consequently also temporal evolution on faster scales, the field-line connectivity in the higher solar atmosphere is (from a potential-field approximation) recycled faster than the photospheric field (this is true for measurements from both instruments).

We also employ the reconnection time to obtain an upper limit on the energy-flux density becoming available for heating the gas from reconnection involving field with at least one foot point in network elements. We find that this upper limit lies just below the heating rates required for the quiet corona and quiet chromosphere. Since this upper limit assumes that the free energy in the magnetic field equals the energy in the potential field (this corresponds to the highest values found in active regions) and that this free energy is built up within the connection recycling time of three minutes, we conclude that magnetic reconnection cannot be the sole source for heating higher layers in the solar atmosphere. Our analysis does not include small-scale braiding of field lines below the 100-km resolution of IMaX, which could contribute to the global energetics of the outer layers. Such small-scale braiding (Parker 1972, 1988) can still help to have a reconnection/dissipation-driven heating scenario.

For the energy estimations, it is interesting to point out some differences from earlier works by Schrijver et al. (1997, 1998) based on MDI data, which suggest that the magnetic carpet contains enough magnetic energy for heating the upper solar atmosphere. A major difference is that the Sunrise/IMaX field of view is much smaller than MDI, and as a consequence we are missing long magnetic loops that close with distant photospheric sources outside the FOV and indeed did not include the contribution of loops leaving the computational box, which are mainly coronal. IMaX has, however, a factor of roughly 30 higher resolution than MDI and detects also weak internetwork fields. As a consequence, extrapolations from Sunrise data allow the photospheric and chromospheric layers to be resolved vertically. Our estimation of the entire change in magnetic energy density through magnetic reconection (about \(6000~\mathrm{W\,m^{-2}}\)) would be sufficient to compensate the chromospheric (about \(2000~\mathrm{W\,m^{-2}}\)) and coronal (about \(300~\mathrm{W\,m^{-2}}\)) loss rates. However, we find that 65 % of this change in magnetic energy density occurs in the (vertically resolved) photosphere and cannot contribute to the heating of higher atmospheric layers. While extrapolations from Sunrise resolve these short photospheric network–internetwork loops, this was not possible with MDI observations. Another point to consider is that the Sun was very quiet during the Sunrise observations and one needs to evaluate the energy-flux densities again during more active times, as expected for the planned re-flight of Sunrise in 2013.