1 Introduction

Portugal still compares poorly with the average European Union (EU) member state and the OECD average in several education indicators, such as educational attainment (2018: 50.2% of 25–64 year olds with only below upper secondary education in Portugal, 21.2% OECD average) or higher than average early leavers from education and training (2018: 11.8% of population aged 18–24, EU average 10.6%). Previous literature shows that, both at the micro and macroeconomic levels, education and how it is distributed plays an important role, namely in economic growth through its contribution to final goods production and innovation and imitation activities but also through its relation with income inequality, see e.g. Lucas (1988), Romer (1990), Mankiw et al. (1992), Benhabib and Spiegel (2005) and Abdullah et al. (2015). Given the dismal economic growth performance of Portugal, especially since the early 2000s, and the relatively high income inequality levels, investigating the dynamics of human capital, in the form of educational attainment levels, and its distribution can shed additional light on the causes of the recent economic hardships experienced in this country.

The objective of this paper is threefold: (i) show how the level and distribution of human capital (HC) have evolved over time in Portugal; (ii) investigate the association between HC inequality and earnings inequality; and (iii) analyse the role of returns to schooling, together with HC inequality, in the explanation of earnings inequality. We use data from Quadros de Pessoal, QP (Personnel Records) database to compute the distribution of human capital, proxied by average years of schooling of employees working in the Portuguese private labour market, as well as the distribution of the respective earnings for the period 1986–2017.

Our contribution is both descriptive and analytic: we measure inequality in educational attainment in the Portuguese economy and describe how it has evolved over the last 30 years. The focus of previous literature is on average educational attainment levels, see e.g. Pereira (2005), Teixeira (2005), Teixeira and Fortuna (2010) and Teixeira and Loureiro (2019), but little is known about its distribution, especially among employees working in the private labour market, even though De Gregorio and Lee (2002) show that although it is unclear how average educational attainment influences inequality, all else equal an increase in educational inequality leads unambiguously to greater income inequality. By measuring education inequality and describing its behaviour over time for a recent period in the Portuguese economic history we try to contribute to a better understanding of the ways through which policies can more effectively help the Portuguese economy to overcome the still relatively high inequality levels recorded and potentially promote growth. Using Mincerian earnings regressions to estimate the returns to schooling together with the Blinder-Oaxaca decomposition of hourly real earnings we also try to deepen our understanding on the possible causes of earnings inequality dynamics, fundamental for better informed policy decisions aimed at reducing inequality, a core concern across developed countries over recent decades, Nolan and Valenzuela (2019).

The remainder of the paper is organized as follows. Section 2 locates our study within the literature on educational human capital and inequality. In Sect. 3 we describe the data used and present a portrait of human capital inequality in the Portuguese private labour market. Section 4 investigates the contribution of human capital to earnings inequality through decomposition analysis. Section 5 presents the main conclusions.

2 Human Capital and Earnings Inequality: An Overview

The most often used indicator of human capital refers to educational attainment, and in particular average years of schooling of the population, such as in the pioneer work of Barro and Lee (1993), most recently updated in Barro and Lee (2013). Education is also viewed as an important determinant of income inequality, in particular through its influence on earnings inequality, Nolan and Valenzuela (2019).

Based on the theory of human capital investment initially proposed by Schultz (1961) and Becker (1964) and used by Mincer (1974) to estimate the returns to education/years of schooling, Checchi (2001) and De Gregorio and Lee (2002) show that, all else equal, an increase in education inequality results in higher earnings inequality. As the number of more educated workers increases, initially so does income inequality, but once a certain threshold is reached, the increase in the supply of more educated workers (and associated reduction in education inequality) decreases the respective wage premium and so income inequality decreases. Taking this prediction to the data, both studies confirm that a more equal distribution of education plays a significant role in making income distribution more equal. However, Lam et al. (2015) show that “While there is intuitive appeal to the notion that a more equal distribution of schooling should lead to a more equal distribution of earnings, there is clearly no theoretical reason to expect such a relationship to hold. What might be considered unambiguous improvements in the distribution of schooling (as indicated, for example, by stochastic dominance), could plausibly lead to increased inequality in earnings.” (p.5) and generalize this result to the consideration of differences in rates of return across schooling levels.

Given the importance of the distribution of human capital for economic growth and the distribution of income, Fidalgo et al. (2010) compute the distribution of average years of schooling of the working population for Portugal using data from QP for the years 1986, 1996 and 2005. The overall conclusion, based on the behaviour of different measures, is that Portugal recorded a decrease in education inequality. The authors also find evidence of a Kuznets inverted U relationship between the level of education and education inequality, based on regional data.

An initial approach to the relationship between education inequality and earnings inequality in the Portuguese economy is that of Rodrigues (1996) that decomposes adult equivalent income inequality according to years of schooling from 1980 to 1990 to determine how much of the observed inequality is due to inequality within education groups and how much is due to inequality between education groups. Applying decomposition analysis, the author concludes that 21.0% of total inequality comes from inequality between education groups in 1980, increasing to 27.2% in 1990, although most of the inequality observed comes from within-group inequality. More recently, Campos and Reis (2017) estimated returns to schooling for Portuguese workers using a modified Mincerian specification for the period 1986–2013. According to their findings, the rates of return to higher education relative to those with secondary education rose from 32.8% in 1986 to 47.7% in 2013. However, between 2010 and 2013 these returns show a decrease, which can have important implications for the relationship between the distribution in years of schooling and the earnings distribution.

Cardoso (1998), using QP data, analyses the period 1983–1992 and finds that the distribution of earnings was characterized by rising inequality, with the right tail of the distribution playing a major role in explaining this trend. Machado and Mata (2001), Machado and Mata (2005) and Hartog et al. (2001) conclude that a substantial part of the observed increase is explained by returns to education. Martins and Pereira (2004) investigate whether education reduces wage inequality based on quantile regression evidence for 16 countries. For Portugal, the authors find that schooling had a positive impact on within-group wage inequality. Possible explanations for this result are overeducation (workers with higher schooling levels accept jobs requiring lower skills), ability (the abler workers benefit more from education and the pay gap between the more and the less able is higher for higher schooling levels) and differences in schooling quality or fields of study. Carneiro (2008) also studies the relationship between education and wage inequality in Portugal for the year 2004 using data from the Labour Force Survey. He concludes that years of schooling account for 40–50% of the variance in log wages. According to Carneiro (2008,p. 24): “The increase in the returns to schooling generates an increase in inequality between individuals with different levels of education. However, there has also been an increase in inequality within education groups, which suggests that there was an increase in the return to (observed and unobserved) skill.” For a more recent period, Farinha Rodrigues et al. (2012) analyse wage inequality according to different categories of workers and firms using data from QP. Their main conclusion is that differences in schooling account for about 50% of earnings inequality, while variables such as firm location and other firm characteristics reveal no explanatory power.

Overall, previous literature that examines the relationship between educational human capital and income inequality for the Portuguese case, although highlighting the importance of education for the explanation of the observed dynamics of income inequality, seems to have neglected the contribution of education inequality. To fill this gap, the present study provides a characterization of workers’ human capital and its distribution at 10-years intervals from 1987 to 2017, based on average years of schooling of Portuguese employees in the private labour market.Footnote 1 We next make a tentative analysis of the contribution of education inequality to earnings inequality based on decomposition analysis, together with the investigation of the potential role of returns to schooling.

3 Portraits of Human Capital Distribution: Portugal 1987–2017

Quadros de Pessoal (QP) or Personnel Records is the source of data used in this study, a rich and comprehensive linked employer-employee dataset, gathered annually by the Portuguese Ministry of Labour, Solidarity and Social Security and covering all establishments having at least one wage earner. The survey does not include civil servants, self-employed, and household employees and covers almost all the workers in the manufacturing and the services sectors but the coverage of agriculture is low since the share of wage-earners in this sector is also low. For each worker, variables reported include: gender, date of birth, occupation, date of hire into the firm, hours of work (divided in regular hours and overtime), the collective bargaining agreement, the worker's job title/occupation, schooling, and monthly earnings (regular income as well as income from overtime work, before taxes). The information on schooling refers to the highest completed level of education by the worker. The wage information is collected with reference to the month of October. Information on the employer includes the industry and location. QP data covers the period 1986–2017, with no data available for the years 1990 and 2001.

We used R to perform our statistical and econometric analysis. To remove part-time workers and workers without any indication of wages amounts we have not considered workers reported as receiving base monthly earnings lower than the legal minimum wage, which in theory should not be possible unless mistakes were made by firms when inserting the requested information. We have also removed workers with monthly earnings in the top 0.5% of the distribution to mitigate the presence of outliers and again errors in the values inserted by firms. These adjustments to the database are necessary otherwise we would be facing problems of measurement error and outliers that would bias the results. We also removed all workers that lacked information for some variables such as work position or highest level of education attained. We transformed the highest level of education attained, a categorical variable, to numerical values, the respective cumulative duration in years.

We measure human capital based on educational attainment levels in the tradition of Barro and Lee (1993) corresponding to the cumulative number of years of schooling (duration) of the highest level of education attained by each worker, considering the following education categories (cumulative duration in parenthesis): (i) less than primary education (3 years); (ii) primary education (4 years); (iii) 1st cycle of lower secondary education (6 years); (iv) 2nd cycle of lower secondary education (9 years); (v) upper secondary education (12 years); (vi) post-secondary non tertiary education (13 years); (vii) short-cycle tertiary education (bacharelato), (15 years); (viii) college degree (licenciatura), (17 years); (ix) Master (19 years); and (x) Doctorate/PhD (23 years). For the post-Bologna process period (2007 onwards) we assume that individuals with tertiary education have the same number of years of schooling as their peers in the pre-Bologna period, even though the years necessary to obtain a college degree have decreased.

For the period under analysis, our dataset contains on average around 2,000,000 observations per year.

Figure 1 presents summary statistics for the distribution of human capital in the Portuguese private labour market for the years 1987, 1997, 2007 and 2017. The choice of this four data points at 10-years intervals ensures that we capture structural changes and not short-term movements. Besides corresponding to the overall time coverage of QP (1986–2017), the 30 years under analysis witnessed some important changes in Portugal in terms of education policies with important consequences for the composition of the workforce in terms of years of schooling, in particular changes in compulsory education laws (from 6 years in 1964, to 9 years in 1986 and to 12 years in 2009). In 1987, the distribution of human capital was heavily concentrated around 4 years of schooling, the duration of primary education, with the first and second quartiles of the distribution recording this value. Over the subsequent decade, it is clear the change in the shape of the distribution, with the second quartile now corresponding to 6 years of schooling (4 years of primary education plus 2 years of lower secondary education) and the third quartile increasing from 6 to 9 years of schooling (corresponding to the completion of lower secondary education). This change corresponds to a shift to the right in the median due to an increase in the number of workers with a higher number of years of schooling and thus higher levels of education. In the following decades human capital continued to record a positive trend, with the median of the distribution increasing from 6 to 9 years of schooling and the third quartile increasing from 9 to 12 years of schooling (the duration of upper secondary education) while the maximum years of schooling of employees increased from 17 years in 1997 to 23 years in 2007. In 2017, the second quartile increased from 9 to 12 years of schooling although there were no changes in the third quartile, that remained at 12 years of schooling.

Fig. 1
figure 1

Source: Authors’ based on data from Quadros de Pessoal

Summary statistics for human capital in the Portuguese private labour market, 1987–2017 (years of schooling).

Full size image

Overall, according to the data presented in Fig. 1, from 1987 to 2017 the average worker in the private labour market recorded a substantial increase in years of schooling, from 4 years of formal education in 1987 to 12 years in 2017. The trend of the first and third quartiles is also positive, with the first quartile increasing from 4 to 9 years of schooling and the second quartile from 6 to 12 years of schooling. As to the shape of the distribution, there was a monotonic shift to the right of the middle of the distribution so that workers in the subset defined by the interquartile range experienced important increases in the respective levels of education. Portugal started with a probability mass of the distribution of human capital concentrated around 4 years of schooling, the left tail of the distribution, and ended up with the distribution concentrated around 12 years of schooling, the right tail of the distribution.

A simple and straightforward way of assessing inequality is looking at the interquartile range, i.e. the difference between the third and first quartiles of a given distribution. As shown in Fig. 2, the interquartile range for the distribution of human capital in the Portuguese private labour market goes from 2 years of schooling in 1987, to 5 years in 1997, it reaches a maximum of 6 years in 2007 and decreases to 3 years of schooling in 2017. Computing other frequently used inequality indicators such as the Gini coefficient, the Atkinson index, the Theil T index or the mean error for the logarithmic distribution (Theil N)Footnote 2 reveals the same positive trend until 2007 followed by a decrease until 2017.Footnote 3

Fig. 2
figure 2

Source: Authors’ based on data from Quadros de Pessoal

Interquartile range for the distribution of human capital in the Portuguese private labour market, 1987–2007 (years of schooling).

Full size image

As for the causes of the behaviour over time of inequality in the distribution of human capital, the initial increase in the median of years of schooling resulted in an increase in inequality since it was initially very concentrated around 4 year of schooling. The median and the third quartile of the distribution increased at a faster pace during the initial period, widening the difference between the middle and the top of the distribution relative to the bottom of the distribution. This trend continued until around 2007. In 2017, on the contrary, inequality records a decrease relative to the previous decade with the distribution of years of schooling concentrating in the right part of the distribution, around 12 years of schooling. During this last decade there is a clear catching up effect, with the first quartile getting closer to the median, and the median catching up with the third quartile, pushing inequality downwards.

The dynamics of the main statistical moments of the distribution of human capital also suggest the existence of an educational Kuznets curve for Portugal, an inverted U relationship between the average level of human capital/education and inequality in the distribution of human capital/education in the Portuguese private labour market: as the average level of educational attainment increases, initially so thus inequality in its distribution, but as a substantial part of the population gets more educated inequality decreases, Lim and Tang (2008), Morrisson and Murtin (2010), Meschi and Scervini (2013) and Shukla and Mishra (2019).This inverted U relationship tends to be associated with the age composition of the workforce. Due to the increase in the duration of compulsory education, from 6 years of formal schooling since 1964 to 9 years in 1986 and to 12 years in 2009, the inflows of workers with higher levels of education started to drive human capital inequality upwards, up to the point where the distribution became more homogenous due to older workers leaving the labour market. This in turn resulted in smaller intergenerational differences in years of schooling.

4 Levels of Schooling and Earnings Inequality: A Decomposition Analysis

In this section we perform a decomposition analysis of earnings inequality according to levels of schooling based first on Theil’s N index of earnings inequality for the years 1987, 1997, 2007 and 2017 followed by an analysis based on the Blinder-Oaxaca decomposition. The latter involves the prior estimation of returns to schooling using Mincerian regressions. The original data used in this section was retrieved from QP (see the previous section).

4.1 Decomposition of Earnings Inequality by Levels of Schooling Using Theil’s N

To compute the distribution of earnings we first calculate hourly earnings corresponding to the actual overall monthly earnings (including base wage and other regularly paid components) over total monthly hours worked. Earnings were deflated using the consumer price index (base 2010).

It is only possible to additively decompose indexes that belong to the class of Generalized Entropy Indexes (GEI), such as Theil's N, also known as the Logarithmic Mean Error, given by Eq. (1):

$$Theil~N = \left( {\frac{1}{n}} \right)\mathop \sum \limits_{{i = 1}}^{n} \ln \left( {\frac{{y_{i} }}{\mu }} \right)~$$
(1)

where \({y}_{i}\) is real earnings of individual i, n is the number of individuals in the population and \(\mu\) is the average real earnings across individuals. Theil’s N gives more weight to inequality on the left tail of the distribution.

Figure 3 presents the dynamics of the Theil N index of the distribution of earnings in the Portuguese private labour market over the period 1987–2017: earnings inequality increases from 1987 until 2007 and then decreases during the last decade under analysis. We next decompose the Theil N of the earnings distribution to determine how much of the observed overall earnings inequality comes from human capital inequality (between-groups differences) and how much comes from other factors (within-groups differences).

Fig. 3
figure 3

Source: Authors based on data from Quadros de Pessoal

Theil N index of the earnings distribution in the Portuguese private labour market, 1987–2017.

Full size image

Unlike other inequality measures, Theil’s N satisfies the property of strict additive decomposability that allows for the decomposition of earnings inequality into an intra/within-group component and a between-group component in an exact way. According to Cowell (2011) it is possible in this way to analyse the behaviour of inequality over time according to three components/sources: within group inequality, between group inequality and population composition. Following Rodrigues (1996) we want to determine how much of earnings inequality is due to human capital inequality. According to the right-hand-side (RHS) of Eq. (2), Theil’s N can be separated in two components:

$$Theil{\text{~}}N = {\text{~}}\mathop \sum \limits_{{i = 1}}^{\gamma } \left( {\frac{{n_{\gamma } }}{n}} \right)N_{\gamma } + \mathop \sum \limits_{{i = 1}}^{\gamma } \left( {\frac{{n_{\gamma } }}{n}} \right){\text{ln}}\left( {\frac{{n_{\gamma } }}{n}} \right){\text{~}}$$
(2)

Dividing the population in \(\gamma\) different groups, in our case years of schooling/levels of education of the workforce (see the previous section), the first component on the RHS of Eq. (2) corresponds to within group inequality, which is the weighted average (percentage of the population obeying a specific criteria, \(\frac{{n}_{\gamma }}{n}\)) of Theil’s N earnings inequality for each group (\({N}_{\gamma })\); the second component corresponds to between group inequality, the level of inequality in the distribution of averages conditional on the criteria defined. This decomposition of Theil’s N tells us how much of the observed overall inequality in earnings in a given year comes from differences in earnings within a certain education group (e.g. the variability in earnings for workers with secondary education) and how much comes from differences between mean earnings across different education groups.

Figure 4 presents the relative amount of within and between group inequality in the Theil N index of earnings inequality computed based on Eq. (2). In all four years under analysis, 1987, 1997, 2007 and 2017, most of earnings inequality comes from within group inequality, ranging from 78.7% in 1987 to 81.9% in 1997, indicating that factors other than differences in educational attainment have an important influence on earnings inequality, as already noted by Rodrigues (1996). Between group differences in educational attainment contribute a minimum of 18.1% (1997) and a maximum of 28.2% (2007) to earnings inequality, still an important part of observed earnings inequality.

Fig. 4
figure 4

Source: Authors’ using Schulenberg (2018) and data from Quadros de Pessoal

Additive decomposition of Theil’s N index of earnings inequality conditioned by differences in human capital, 1986–2017.

Full size image

As far as the dynamics of the former different contributions to earnings inequality are concerned, we concluded that from 1987 to 1997 approximately 92.5% of the increase in earnings inequality came from changes in the within group component, while the other 7.5% came from changes in between group inequality. In this period, the contribution of human capital inequality to earnings inequality decreased from 21.3% to 18.1%. However, from 1997 to 2007, the opposite applies, with the between group component accounting for most of the increase in earnings inequality. The within group component even presented a negative contribution, although not very important. For that same decade, the contribution of human capital inequality to earnings inequality rose to 28.2%. From 2007 to 2017 the decrease in earnings inequality can be attributed in a more balanced way to both within and between groups inequality. The within group component explains almost 57% of the decrease, while the latter explains 43%.

Based on the previous evidence it is not possible to identify a trend for the contribution of between-group differences to earnings inequality since this contribution fluctuates from one decade to the next. In any case, it is possible to conclude that differences in human capital explain more of earnings inequality in the last two years under analysis, although from 2007 to 2017 the contribution of human capital inequality to earnings inequality decreased (from 28.2% in 2007 to 25% in 2017). To better understand these earnings inequality dynamics it is useful to investigate another important factor affecting the link between human capital inequality and earnings inequality, returns to schooling.

4.2 Returns to Schooling by Decade, 1986–2017

In his most influential work, Mincer (1974) states that potential gross income of a worker in a given period depends on the initial level of potential income determined by exogenous innate ability, an exogenous rate of return to human capital (\(r)\) and net investments in human capital. A standard empirical specification according to Mincer’s theory is given by Eq. (3):

$$y_{i} = \alpha + \mathop \sum \limits_{{j = 2}}^{5} \beta _{j} S_{{j,i}} + \theta _{1} Exp_{i} + \theta _{2} Exp_{i} ^{2} + \theta _{3} Tenure_{i} + \theta _{4} Tenure_{i} ^{2} + \theta _{5} Firm\_size_{i} + {\text{~}}\theta _{6} Gender_{i} + ~\varepsilon _{i} {\text{~}}$$
(3)

In Eq. (3), \({y}_{i}\) stands for the logarithm of hourly real earnings, \({S}_{j,i}\) = 1,…,5 is a dummy variable that takes the value one when individuals: 1) have less than 9 years of schooling; 2) have exactly 9 years of schooling; 3) have exactly 12 years of schooling; 4) have more than 12 but less than17 years of schooling; and 5) have 17 or more years of schooling, and zero otherwise. Individuals with less than 9 years of schooling are not considered since this would generate collinearity problems constituting the reference group for calculating the returns to other schooling levels. The estimated coefficients correspond to the respective returns relative to those of workers with less than 9 years of schooling. As in Campos and Reis (2017), the variable schooling (S) is treated as a categorical variable to account for different private returns to education depending on the maximum level of education attained by individual i. This specification allows for returns to schooling to vary across different levels of schooling and thus it is possible to account for the importance of human capital distribution to earnings inequality through a different channel. The variable \({Exp}_{i}\) corresponds to potential experience of individual i and is calculated, following Lemieux (2006), by subtracting from the individual’s age the number of years of formal schooling and six (years), the age at which individuals usually start school. Following Campos and Reis (2017), we add as explanatory variables: \({Tenure}_{i}\) corresponding to the number of years individual i has worked for his/her current employer/firm; \({Firm\_size}_{i}\), the logarithm of real revenues of the firm in which individual i works; and \({Gender}_{i}\) that takes the value one if the individual is male and zero otherwise.

The econometric problems associated with the estimation of Mincerian earnings regression are well established in the literature. Because the variance of the logarithm of real hourly earnings is not constant across years of schooling, heteroscedasticity in the distribution of the error terms is expected. To overcome this problem, we estimate a regression with robust standard errors using R package sandwich developed by Zeileis (2004). Another problem emphasized by Campos and Reis (2017) is omitted variable bias when unobserved characteristics of the individuals, such as ability or the individual discount rate, are correlated with years of schooling. However, since we are not interested in determining causation this does not pose major problems to our analysis. Nonetheless, it still remains that OLS estimation in the presence of correlations between the error term and the explanatory variables leads to biased estimators, which in the case of returns to schooling could be either positive or negative, Dickson (2013). To overcome this problem, we would need to find an instrumental variable (IV) that is correlated with years of schooling but not with the error term in Eq. (3). However, since we are working with cross-sectional individual data it is not possible to find such an IV in our database. In any case, we are mostly interested in determining how returns to schooling have changed over time and not on its exact value and with OLS the dynamics of the returns remain the same, as shown in Sousa et al. (2015), since the unobserved characteristics correlated with years of schooling are likely to keep affecting earnings over the whole period under analysis.

The estimation of Eq. (3) allows us to compute the relative rates of return to education for each schooling level as follows: i) those with 9 years of schooling relative to those with less than 9 years (\({\beta }_{2})\); ii) those with secondary education relative to those with 9 years of schooling (\({\beta }_{3}-{\beta }_{2})\); iii) those with post-secondary education relative to those with secondary education (\({\beta }_{4}-{\beta }_{3})\); and iv) those with a college degree or more relative to those with secondary education (\({\beta }_{5}-{\beta }_{3})\).

Table 1 presents the results of the estimation of Eq. (3) with data for all the employees in the Portuguese private labour market for each year under analysis 1986, 1996, 2007 and 2017, using the OLS estimator with robust standard errors, since the null hypothesis of the Breusch-Pagan and the White tests (homoscedasticity) was always rejected at the 1% significance level, Breusch and Pagan (1979) andWhite (1980).Footnote 4 All the estimated coefficients have the expected signs and are statistically significant at the 1% level, confirming the existence of positive but diminishing returns to one additional year of experience and tenure. The returns associated with each level of schooling follow the same behaviour as that found in Campos and Reis (2017), with returns to higher education decreasing in 2017 relative to the previous years.

Table 1 Results for the earnings regressions (OLS with robust standard errors).
Full size table

Table 2 contains information on the relative returns to each education level, computed using the results presented in Table 1, according to which in 1986 workers with a college degree or more get the highest return (50.4%) followed by workers with only nine years of schooling (41.1%). During the first decade (1986–1996), workers with more than secondary education saw their returns increase by more than 49%, especially those with post-secondary education (increase of 51.2%, from 31.4.% to 47.5%), while workers with less than secondary education recorded a decrease, more intense for those with 9 years of schooling (−26.5%). By 1996, those with higher than secondary education still record the highest relative returns. During the second decade (1996–2007), we witness the beginning of the downward trend of the returns to those with a college degree or more, while the drop continued for those with 9 years of education. The only group of workers that saw their relative returns increase was the one with secondary education (an increase of 31.8% from 17.3% to 22.8%). During the last decade (2007–2017), although workers with more than secondary education still record the highest relative returns, workers with post-secondary education record an increase in the respective relative returns (+ 14.8% from 41.9% to 48.1%), while workers with a college degree record a decrease in the relative returns (−5.9% from 67.9% to 63.9%); the returns to secondary education also decrease and by an even higher amount (−20.6% from 22.8% to 18.1%).

Table 2 Relative returns to education (%).
Full size table

Overall, there is evidence of a negative trend in returns to college education in recent decades, both relative to returns to secondary education and to returns to post-secondary education. One candidate explanation is educational mismatches with individuals with a college education possessing skills that are not valued by the labour market and/or employed in jobs that require them to perform tasks that do not demand the use of their acquired knowledge and competences (overeducation). However, Pimenta and Pereira (2019, p.54), using QP data on employees’ occupation and education for the period 1995–2013 conclude that in Portugal “(…) overeducation remains a rather unimportant phenomenon throughout, rising from negligible values at the beginning of the sample to around 5% at the end.” Digging deeper into overeducation among college graduates, the authors find that the share of overeducated college graduates in the total number of college graduates increased from around 20% to 30% in the first decade but then stabilized, although it has become more prevalent among the new generations of college graduates. According to the authors, these overeducated college graduates are mainly from Economics, Social Sciences and Law and work predominantly in the services sector. Additionally, using pooled data for the period 2000–2002 from the Portuguese Labour Force Survey, Budría (2011, p.430), concludes that it is possible to “(…) reject the hypothesis that the higher wage dispersion among the educated is due to the prevalence of (different types and degrees of) educational mismatches in the labour market.”

4.3 Threefold Blinder-Oaxaca Decomposition of the log of Real Hourly Earnings

In this section we use the information on years of schooling of workers and returns to education to decompose the change in average real hourly earnings for the periods 1986–1996, 1996–2007 and 2007–2017 according to the contribution of changes in the averages of the explanatory variables included in Eq. (3) and the changes in the respective estimated coefficients. One widely used method of decomposition of the mean values of the dependent variable is the Blinder-Oaxaca decomposition, Blinder (1973), Oaxaca (1973) and Jann (2008). Following Hlavac (2018), the difference in the average values of the same variable between two distinct groups of data (e.g. for different years) can be expressed as in Eq. (4), where \({\stackrel{-}{Y}}_{A}\) is the mean value for group A and \({\stackrel{-}{Y}}_{B}\) is the mean value for group B:

$$\Delta \bar{Y} = {\text{~}}\bar{Y}_{A} - \bar{Y}_{B} {\text{~}}$$
(4)

We know from standard econometrics that the mean value of a variable is a function of the mean value of a vector of variables and, by assumption, the mean value of the error term is zero. Thus, it is possible to write Eq. (4) as in Eq. (5), where \(\bar{X}_{A}^{T} ~\) and \(\bar{X}_{B}^{T}\) are the mean values of the explanatory variables of each group and \(\hat{\beta }_{A} ~\) and \(\hat{\beta }_{B}\) are the respective estimated coefficients:

$$\Delta \bar{Y} = {\text{~}}\bar{X}_{A}^{T} \hat{\beta }_{A} - \bar{X}_{B}^{T} \hat{\beta }_{B} {\text{~}}$$
(5)

Equation (5) can be further decomposed into differences in the mean value of the vector of explanatory variables and differences in the estimated coefficients between the two groups, as in Eq. (6):

$$\Delta \bar{Y} = {\text{~}}(\bar{X}_{A} - \bar{X}_{B} )^{T} \hat{\beta }^{*} + \bar{X}_{A}^{T} \left( {\hat{\beta }_{A} - \hat{\beta }^{*} } \right) + {\text{~}}\bar{X}_{B}^{T} \left( {{\text{~}}\hat{\beta }^{*} - \hat{\beta }_{B} } \right)$$
(6)

where \({\widehat{\beta }}^{*}\) is the weighted average between \({\widehat{\beta }}_{A}\) and \({\widehat{\beta }}_{B}\), given the number of observations in each group.

According to Eq. (6), the variation in the mean value of the dependent variable is decomposed into: i) differences between the mean values of the vector of explanatory variables for each group; ii) differences in the estimated coefficients for each group; and iii) an interaction term between the previous differences. Using this decomposition method, it is possible to pinpoint the sources of the variation in the logarithm of real hourly earnings and how much each explanatory variable (in particular schooling levels), and the respective estimated coefficients (in particular returns to each level of education) contributed to the observed changes in earnings.

In what follows we present and discuss the main results from the threefold Blinder-Oaxaca decomposition of the log of real hourly earnings using the results from Mincerian earnings regressions estimated with both OLS and pooled OLS. The latter method of estimation is used, as argued in Hlavac (2018), in order to conduct a counter-factual analysis that generates a value for \({\widehat{\beta }}^{*}\) in Eq. (6) that is neither the coefficient estimated for group A nor for group B using OLS with cross section data.

The first threefold decomposition was conducted for the decade 1986–1996. Table 3 presents the contributions to the change in average real hourly earnings of endowments, coefficients and the interaction of the two for each variable. Overall, the results show an increase of 27.3% in average real hourly earnings, with 4.1 percentage points (p.p.) coming from variations in the average levels (in the case of numerical variables) and composition (in the case of categorical variables) of endowments and 23.5 p.p. from variations in the estimated coefficients. The remaining variation is explained by the interaction of both, which accounts for roughly −0.4 p.p of the total change. Looking at the contribution of each variable, from the perspective of endowments there are positive contributions from increases in the relative participation of better educated workers, especially those with secondary education, with a contribution of 5.9 p.p. to average real hourly earnings. Even with the average level of experience of the workforce decreasing throughout the period, improvements in education were able to counteract this negative effect. Regarding the behaviour of the estimated coefficients, that account for most of the change in earnings, the (decreasing) returns to experience played a major role, along with changes in the intercept, which captures movements in more fundamental aspects of the economy, such as institutional factors. Changes in the returns to all levels of education played a less important role. Nonetheless, it is already possible to see that decreasing returns to those with 9 years of schooling is influencing negatively the dynamics of earnings. The positive impact stemming from the increase in returns to secondary education is starting to show up but is still very subtle.

Table 3 Threefold blinder-oaxaca decomposition of the log of real hourly earnings using the mincerian regressions results (1986–1996).
Full size table

For the second decade under analysis, 1996–2007, the results presented in Table 4 show that average real hourly earnings rose by 14.4%, with the variation of the average levels of endowments contributing, ceteris paribus, with 34.8 p.p. and the change in the estimated coefficients with −22.7 p.p. Considering the results for the different variables, from the perspective of endowments there are two important contributions coming from the increase in average tenure (25 p.p.) and increased participation of workers with a college degree (8.9 p.p.). For the first time in this period higher education appears to have a leading role in explaining earnings dynamics. When we look at the contribution of changes in the estimated coefficients, again the intercept is a major source of fluctuations in average earnings. However, now the influence is negative, and the same applies to the contribution of decreasing returns to experience. Additionally, the negative contribution of the fall in the returns to education becomes more important. Again, the change in returns to those with nine years of education had the most adverse effect on earnings, followed by the drop in the returns to those with secondary education. It is also important to highlight the negative contribution of the drop in the returns to higher education.

Table 4 Threefold blinder-oaxaca decomposition of the log of real hourly earnings using the mincerian regressions results (1996–2007).
Full size table

For the third and last decade under analysis, 2007–2017, the results presented in Table 5 correspond to an increase in average real hourly earnings of 10.5%, where −17.4 p.p. came from changes in the average levels of endowments, 19.8 p.p. from changes in the estimated coefficients and 8 p.p. from the interaction. The contribution of endowments was negative due to an important decline in average experience and tenure, that surpassed the positive contributions of a better educated workforce. Similar to the previous decade, the major positive contribution came from a higher participation of workers with a college degree. Looking at the changes in the estimated coefficients, again the differences in the fundamentals, proxied by the intercept, are a major source of earnings variation, with a positive contribution in this period. The contribution of the change in the intercept more than compensated the more intense negative contribution of the fall in the returns to education, in particular for college and secondary education.

Table 5 Threefold blinder-oaxaca decomposition of the log of real hourly earnings using the mincerian regressions results (2007–2017).
Full size table

Looking at the overall changes that occurred during the 30 years under analysis, from 1986 to 2017, it is possible to conclude that factors other than those considered as explanatory variables in the Mincerian earnings regressions played an important role in the dynamics of real hourly earnings, which we called fundamentals. Fluctuations in the average level of experience are also important in explaining changes in earnings and the increased participation of better educated workers is positively correlated with changes in earnings. On the other hand, falling returns to education, in particular for those with higher than secondary education, have consistently impaired average earnings growth, acting in the opposite direction of the former and almost making the respective positive impact vanish.

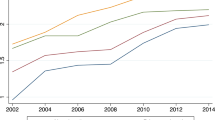
Comparing the contributions of endowments and coefficients to the variations of changes in average real hourly earnings from 1986 to 2017, policies aimed at reducing human capital inequality are a possible explanation of the decline in returns to education based on a supply side effect in the labour market. With technological driven demand for labour (skill-biased technological change) increasing at a slower pace than the supply of more educated workers, a fall in equilibrium earnings is expected, as shown in M. Centeno and Á. Novo (2014). As an illustration of this candidate explanation, Fig. 5 contains the percentage change of real hourly earnings for the different deciles of the earnings distribution in each decade. We can see that returns to college education relative to secondary education have been trending downwards since at least the late 2000’s, which together with increased participation of highly educated workers puts a downward pressure on average earnings. Comparing earnings growth for each decile of the distribution it is possible to see that the right part of the distribution, that tends to be associated with higher levels of education, has experienced the lowest growth rates promoting earnings convergence betwixt the different education groups.

Fig. 5
figure 5

Source: Authors’ calculations using R and data from Quadros de Pessoal

10-years change in real hourly earnings across deciles of the earnings distribution (%).

Full size image

To illustrate further the previous candidate explanation for the decrease in returns to higher education, Fig. 6 compares the evolution of returns to college and post-secondary education with the evolution of the relative supply of highly skilled workers (share of employees with post-secondary and college education) in the Portuguese private labour market from 1986 to 2017. As can be seen, the behaviour of the returns to education series shows opposite movements to that of the supply series indeed suggesting that all else equal an increase in the relative supply of workers with higher education resulted in a decrease in the respective wage premium.

Fig. 6
figure 6

Source: Authors’ calculations using R and data from Quadros de Pessoal

Rates of return to college and post-secondary education (relative to secondary education) and relative supply of highly skilled workers (%), Portugal 1986–2017.

Full size image

Although testing candidate explanations of the changes observed in the shape of the earnings distribution and returns to education in Portugal over the period 1987–2017 is beyond the scope of this study, another possible explanation relates to changes in labour market institutions (LMI), such as the minimum wage, collective wage bargaining regimes or employment protection legislation (EPL), albeit previous literature has reached no definite conclusions on the sign of these different contributions, see e.g. Checci and García-Peñalosa (2010) and Fortuna and Neto (2020).

As stated by Centeno and Novo (2014), the real minimum wage increased by 12% from 1984 to 1995 and by 21% between 1995 and 2009. In 2011, the freezing of the nominal minimum wage due to the economic and financial assistance programme signed between the Portuguese government and the Troika (IMF, ECB and the European Commission) that lasted from May 2011 until June 2014, resulted in a decrease of its real value, but from 2014 onwards the minimum wage was again updated in January of each year and resumed the respective positive trend, OECD (2017). Cardoso (1998) analyses earnings inequality in Portugal for the period 1983–1992 and concludes that the increase in the minimum wage played an equalizing role at the bottom of the earnings distribution from 1983 until 1986, but this effect disappeared from 1986 to 1992. Centeno and Novo (2014) conclude that from 1995 to 2009 polarisation and the minimum wage were responsible for a decrease/stagnation in wage inequality at the left tail since workers with intermediate-skills jobs saw their wages decrease relative to low-skills jobs.

Centralized collective (wage) bargaining also contributed to less earnings inequality at the bottom between 1983 and 1986, as per Cardoso (1998), but from 1986 to 1992 firms used the wage drift mechanism to overcome the former. Since 2011 collective bargaining became much less centralised and representative and firm level agreements are now allowed for firms with at least 150 workers (500 previously), features that can result in more wage dispersion; also collective bargaining was suspended during the 2009–2013 crisis up to 2015.

Notwithstanding some recent changes, there is in Portugal an established gap in EPL between permanent and temporary contracts, e.g. quite lower severance pay for the latter, resulting in a segmented labour market that may promote wage inequality, Fortuna and Neto (2020). For instance, Silva (2016) studied the effect of the 2004 reform, corresponding to the extension of the maximum legal duration of temporary contracts, on the distribution of the within-firm wage gap between permanent and temporary workers and found evidence of an increase in this gap at the median and at percentile 75. Previously, as regards the EPL reform of 1989 that limited the causes for dismissing workers in small firms, Martins (2009) does not find robust significant effects on workers’ flows but concluded for negative effects in firms’ profitability. The EPL reform of 2003 extended the causes for dismissing workers to small firms; Centeno and Novo (2012) and Centeno and Novo (2013) studied the effects of the former on labour market composition concluding for an increasing share of temporary contracts and more protection for permanent workers. Concerning the major changes in EPL under the Troika intervention period (lower severance pay for permanent workers, workers dismissal facilitation and unemployment benefits reduction), Carneiro et al. (2014) explored the “credit constraints”, “wage rigidity” and “segmentation” channels and conclude that they contributed to amplify the negative response of employment to the 2007–08 crisis resulting in massive job destruction.

5 Conclusion

Despite still recording relatively low levels of educational attainment when compared to its European counterparts, Portugal has been successfully raising the level of education of its population. This paper computes and analyses the distribution of human capital (average years of schooling) of employees in the Portuguese private labour market for the period 1986–2017 and investigates its contribution for earnings inequality dynamics.

Over the period under analysis, the average level of education of the Portuguese employees increased from 4 years of schooling in 1986 to 12 years in 2017. This increase was first accompanied by an increase in inequality in the respective distribution, that started to decrease over the last decade reflecting changes in the age composition of the workforce, with newcomers/younger workers having on average more years of schooling than the older workers, mostly a result of the change in compulsory schooling laws (from 6 years in 1964 to 9 years in 1986 and to 12 years of schooling in 2009). This behaviour also suggests that a Kuznets inverted U curve of education applies to Portugal. Our findings additionally indicate that the contribution of human capital inequality to earnings inequality varies between 18.2% (1997) and 28.1% (2007) but with no clear trend in terms of the evolution of its contribution. We also examined the potential role of changes in returns to different schooling levels, estimated based on Mincerian regressions, to the dynamics of earnings inequality since the increase in average years of schooling, if accompanied by higher average earnings will result, all else equal, in a decrease in earnings inequality. The results obtained show that the returns to post-secondary non tertiary education and also to college education or higher recorded important decreases in the last two decades, a candidate explanation for the decrease in the importance of human capital inequality for the explanation of earnings inequality. In any case, our findings are supportive of the idea that educational policies that promote the reduction of human capital inequality by increasing average levels of educational attainment can be an effective strategy to address earnings inequality. The recent expansion to 12 years of compulsory schooling is an example of such an educational policy. Other policies that can decrease further human capital inequality include preventing early school leaving (decreasing the percentage of the population aged 18–24 with at most lower secondary education not in further education or training) and promoting adult participation in learning/education (increasing the share of people aged 25 to 64 that receive education). Another possibility is providing wider access to education participation in early childhood (pre-primary education).

To better understand the relationship between education inequality and earnings inequality we next considered both the dynamics of the educational composition of the workforce and of the returns to different schooling levels. Returns to schooling changed across the distribution of education in Portugal, with returns at the top decreasing in the last decade. The policy of universal access to education at increasingly higher levels steadily pursued in Portugal and the expansion in tertiary education seems to be resulting in a more equitable earnings distribution, but this raises other important questions that deserve further investigation. If lower rates of return to tertiary education are the driving force of the observed decrease in earnings inequality this might imply, as documented in the literature, the existence of a mismatch in the labour market between workers’ skills and those demanded by employers, see e.g. Lin (2007), Almeida et al. (2017) and Pimenta and Pereira (2019). Further investigation is needed to understand if the mismatch is coming from the supply side. For instance, the increase in years of schooling, especially at the tertiary education level, may not correspond to education of sufficient quality or students are not graduating in the areas required by employers resulting in overeducation or even unemployment. This represents a waste of scarce resources and should not be overlooked by policy makers, especially as far as tertiary education is concerned. But it can also originate in the demand side if Portuguese firms are not incorporating the technological know-how that requires more educated workers (skill-biased technological change), lagging behind firms from technological leaders and hampering aggregate productivity growth. If this is the case, Portugal needs to implement an industrial policy that targets structural change of the productive fabric towards modern progressive sectors that can absorb and utilize the full potential of the increased supply of more educated workers. Modernizing the existing productive fabric through technological improvement of all activities and sectors could also contribute to limit mismatches.