The Trade-off Between Poverty Reduction and Carbon Emissions, and the Role of Economic Growth and Inequality: An Empirical Cross-Country Analysis Using a Novel Indicator

Abstract

Is it possible for countries to eradicate poverty while also meeting environmental goals? Despite the passage of international agreements calling for these issues to be addressed simultaneously, little is known about the direct relationship between them. This study addresses this gap by proposing a new and composite indicator that integrates measures for both poverty and environmental outcomes (carbon emissions) into a single variable, the carbon intensity of poverty reduction (CIPR). This variable defines the trade-off between the proportional changes of emissions per capita and of the share of the population above the poverty line. In parallel an analytic framework is developed to formulate propositions concerning the possible effects of growth and inequality on the CIPR. The propositions are tested empirically using data from 135 countries across a 30-year time period (1981–2012). The findings confirm that the carbon intensity of poverty reduction is heterogeneous across countries. This heterogeneity is partly explained by economic growth, which is found to have a negative effect on the CIPR up to a certain income level, defined here as a “turning point”. Above that turning point, economic growth increases the CIPR. By contrast, inequality reduction is shown to have a significant negative effect on the CIPR. This study contributes to the literature on sustainable development by analytically and quantitatively linking its three dimensions (social, economic and environmental) and by employing a composite indicator that directly measures the trade-off between poverty reduction and emission levels across countries.

1 Introduction

Is it possible for countries to eradicate poverty while also meeting environmental goals? Does economic growth make poverty reduction more environmentally sustainable? These questions are critical as global poverty and climate change are two of the most pressing issues of our time. Despite a significant reduction in poverty levels over the last decades, one billion people still live in extreme poverty (Sumner 2016). At the same time, emission levels are crossing dangerous boundaries (Steffen et al. 2015). Recent international agreements, such as the Sustainable Development Goals (SDGs) and the Paris Agreement, underline the urgency and relevance of both poverty eradication and environmental goals. These agreements also imply that these goals need to be achieved simultaneously (Hubacek et al. 2017).

Two of the main drivers of both poverty reduction and emission levels have been identified as economic growth and inequality, both of which are central policy issues (Freistein and Mahlert 2016; Schmelzer 2015). Overall, empirical evidence shows that, over the past two centuries, economic development has resulted in a sharp decrease in absolute poverty worldwide. Yet it has also lead to a significant increase in global emissions. Scholarship suggests, therefore, that a trade-off exists between reductions in poverty and increases in emissions if economic growth is pursued. In parallel, reductions in inequality, while decreasing poverty, have been shown to have an ambiguous effect on emission levels. Yet these conclusions are drawn from studies that examine poverty and environmental degradation as separate issues. Little has been done to date to analyze explicitly the trade-off between these two phenomena directly, or to understand whether or not it is feasible to eradicate poverty within sustainable emission levels. This leaves important research questions unanswered. If the general pattern that emerges is one in which global emissions increase as poverty decreases, is this pattern consistent across all countries and across all types of development? What role do economic growth and inequality play in shaping this pattern? Can the pursuit of economic growth alone work to achieve both poverty eradication and climate mitigation or is it necessary to focus on inequality reduction and redistribution?

This study starts from a premise, confirmed from the data that will be presented in Sect. 2, that the trade-off between poverty reduction and emissions is heterogeneous across countries. In many cases, reductions in poverty are, as commonly expected, accompanied by increases in emission levels. Some countries, however, have been able to achieve reductions in poverty while maintaining, or even decreasing, emission levels. These findings are consistent with comparable research documenting the heterogeneity in the relationship between CO₂ emissions and well-being, measured with indicators such as life expectancy (Jorgenson 2014). A deeper understanding of these patterns is therefore needed to understand the factors that might explain such heterogeneity.

This study addresses the research questions presented above in two steps. The first step, and the first contribution of the study, consists in the development of a composite measure that integrates emissions and poverty into a single variable, the carbon intensity of poverty reduction (CIPR). This variable can be defined as the proportional change in the ratio between per capita emissions and the proportion of the population above the poverty line (defined as non-poverty). In parallel an analytic framework is also developed to formulate hypotheses concerning the possible effects of growth and inequality on the CIPR. Their effect is positive when emission levels increase proportionally more than well-being, in the form of non-poverty. In this case, poverty reduction becomes more carbon intensive. The second step involves an empirical test of the framework through an econometric analysis. Data has been collected from multiple sources on 135 countries, representing the majority of both global emissions and populations in poverty. The data covers the period between 1981 and 2012.

In particular, the aim of the econometric analysis is to estimate the effects of economic growth and inequality on the CIPR. More specifically, the analysis seeks to understand whether these relationships are non-linear and may, therefore, be represented by a (inverted) Kuznets curve (Stern 2017). In the case of non-linearity in relation to economic growth, the analysis also seeks to identify the turning point of the curve, defined as the income level above which a further rise in mean income would reverse its effect on the carbon intensity of poverty reduction.

The empirical estimation, based on the proposed analytical framework, confirms that, at the country level, the effect of economic growth on the CIPR is non-linear: up to a certain income level, further growth has a negative effect (reduces the carbon intensity), while after a turning point, the effect becomes positive. This confirms previous studies that analyze other well-being indicators other than poverty (Dietz et al. 2012). By contrast, the results also present a novel finding in that reductions in inequality consistently reduce the CIPR. The results are robust for different poverty lines and different model specifications. Overall, the study provides an initial analysis of the effects of economic development and income inequality on the direct trade-off between poverty reduction and environmental degradation. The study concludes by discussing these findings in the context of both social and economic policy; in particular, the study suggests that the pursuit of economic growth in richer countries is not an environmentally sustainable solution to eradicate poverty (Kallis et al. 2018). The results also highlights the tension between national and global sustainable development goals (Steffen et al. 2015).

The article is organized as follows. Section 2 presents a preliminary analysis of the current and past trends of poverty and emission levels. In Sect. 3 the extant literature on the factors that impact poverty and emissions is reviewed, with particular emphasis on economic development and inequality. Section 4 develops an analytical framework unifying the literatures previously examined. Section 5 then presents the data and the estimation methods used for the econometric analysis. The results of the estimations are presented in Sect. 6, while the conclusions and policy implications are discussed in Sect. 7.

2 Current and Recent Trends in Global Poverty and Emissions

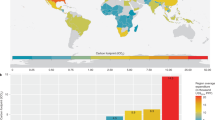
Much progress has been made in the fight to eradicate income poverty over the past decades.¹ Extreme poverty (US$ 1.90 a day in 2011 PPPs) decreased globally from over 40% at the beginning of the 1980s to an estimated 10.9% in 2013 (World Bank 2016). It is important to note that the global decrease in poverty becomes less remarkable when higher poverty lines (US$ 3.10 and US$ 5) are considered. Yet it is argued that such progress has been achieved at the expense of the environment, as measured by CO₂ emissions per capita.² Estimated annual CO₂ emissions per capita have, in fact, risen globally from 4.2 to 5 metric tons, representing a 19.7% increase, over the last 30 years (1981 to 2013) (World Bank 2016).³

Still, these changes show significant variations by region, as shown by the elasticities presented in Table 1. Although South Asia and the Latin American and Caribbean region experienced similar decreases in their poverty headcounts, their results for emissions were quite different. South Asia witnessed a significant jump in emissions, while the Latin America and Caribbean region experienced only a slight increase. This means that poverty reduction has been achieved in a more “environmentally efficient” way (i.e. with fewer emissions) in Latin America than in South Asia. By contrast, in Sub-Saharan Africa poverty has been reduced over the last decade in the presence of a nearly constant volume of per capita emissions. These trends show that, over the long run, while decreases in poverty are commonly accompanied by increases in emissions, the elasticities between poverty reduction and changes in emission levels are not homogeneous across regions. Such results suggest that there may be important lessons to be learned about how different countries and regions address these challenges.⁴

Table 1 Percentage changes in CO₂ emissions per capita and poverty headcount (US$ 1.90 a day) from 1993 to 2013, by region.

Such heterogeneity in the relationship between changes in poverty and emissions across regions over the long term is even more pronounced across countries over the short-term. This can be seen by looking at spells, defined as intervals of time between two comparable and consecutive data points. In this study a total of 609 spells are identified across countries and time (see the data section for a full explanation of the methodology used). In Table 2 these 609 spells are divided according to the sign of the changes of both the poverty headcount (using the US$ 3.10 a day poverty line) and CO₂ emissions per capita levels. The resulting 2 × 2 matrix shows that, among the four possibilities [(a), (b), (c) and (d)], the largest group (272 out of 609 spells, around 45%) is the one identifying spells with increasing emissions and decreasing poverty [category (b)]. This is expected, especially in the context of low- and middle-income countries (LMICs, which represent the majority of countries in the sample). In fact, recent achievements in terms of poverty reduction were largely accompanied by economic growth and an increased importance of the manufacturing sector, closely linked to increases in emissions (Ravallion 2016). Nonetheless the other categories [(a), (c) and (d)] also contain significant shares of the total spells. One category of particular interest is (d), which contains 125 (21% of total) spells where both poverty and emissions have decreased. Almost all of these 125 spells, moreover, belong to one of three groups: (1) high-income European countries, which are decreasing emissions through the transition to service economies⁵; (2) sub-Saharan African countries, which have decreased emissions per capita due to significant population growth and an underdeveloped manufacturing sector; (3) Latin American countries. It is interesting to note that for the first two groups, the cases of category (d) are associated with economic growth. On the other hand, 23 of the 32 cases of category (d) for Latin America, present decreases in inequality. Therefore, it seems that for this region, compared to the European and African examples previously mentioned, simultaneous decreases in poverty and emissions have been achieved through a reduction in inequality.

Table 2 Changes in poverty and per capita emissions, frequency.

In summary, the data provides initial evidence of the presence of significant, yet puzzling, differences in the relationship between changes in poverty and emissions per capita across both time and regions. While part of the heterogeneity in this relationship might depend on the starting points of countries in terms of both poverty and emission levels, other factors may also contribute to create these differences. If the goal is to make poverty eradication less carbon intensive, it is important to gain a better understanding of which factors are at work, and how these factors influence the relationship between poverty and emissions.

It is important to note that the focus on elasticities and proportional changes in this study means that the main quantitative analysis does not directly address planetary boundaries (Rockström et al. 2009) and carbon budgets, defined by the absolute levels of carbon emitted. For example, despite having comparable proportional changes in emissions per capita, East Asia and South Asia present significant differences in terms of their absolute changes in total emissions. In fact, annual emissions in East Asia increased by 8830 Mtons (million tons; equal to a change of 3.5 tons in per capita terms) between 1993 and 2013, while the increase for South Asia was of 1477 Mtons (0.7 tons per capita) in the same time period. While it is indeed recognized that global environmental boundaries are crucial, this paper focuses on the heterogeneity between countries. A discussion of their relevance is left to the conclusions of the article concerning the policy implications of the findings.

3 Review of the Literature Linking the Three Pillars of Sustainable Development

Sustainable development is a balance between economic, social and ecological goals (Redclift 1991). To date, empirical research at the macro level has addressed only marginally the direct links between poverty (defined as the social dimension) and environmental goals, such as emission levels. Some work has been done, however, to address these links through studies on the relationship between environmental pressures and well-being, with the latter measured by indicators such as the average life expectancy at birth. The use of such indicators may be explained by the availability of data for such measures as compared to direct data on poverty (Jean et al. 2016). These studies define the ratio between an environmental variable (such as the mean ecological footprint or carbon emissions) and a well-being indicator as the environmental (carbon) intensity of well-being.⁶ This literature shows how, for low levels of income, economic growth decreases the environmental intensity of well-being while, at higher income levels, the effect of further economic growth is reversed (Dietz et al. 2012). Jorgenson et al. (2014) also show that the carbon intensity of well-being has changed over time, indicating that differences between regions may be linked to economic development. Finally, focusing on a different driver, Knight and Rosa (2011) find that higher levels of inequality have a negative impact on the environmental efficiency of well-being.

Still, despite the fact that the aforementioned indicators of well-being (such as life expectancy) may correlate with poverty, and may even share some of the same drivers, they do not measure poverty directly. Research is therefore needed to examine the direct relationship between poverty and the environment, and to explore the economic dimensions of this relationship. In the following section, a critical review of the separate literatures in which economic development is linked directly either with emissions or with poverty is presented. This review serves as a starting point for the development of a framework that links emissions and poverty directly.

3.1 The Environmental Kuznets Curve: Emissions, Income and Inequality

Much of the empirical research on the determinants of carbon emissions focuses on the relationship between income and emissions per capita across countries. Most prominent in this literature is the analysis of the environmental Kuznets curve (EKC), which depicts the relationship between income per capita and environmental degradation (as defined mainly by CO₂ emissions per capita and other GHG concentrations). The EKC theorizes that environmental impacts are an inverted U-shaped function of mean income (Stern 2004). For most local pollutants, this U-shaped function is confirmed by empirical evidence. This means that, once a certain income threshold has been reached, emissions per capita actually decrease with increasing income per capita. For CO₂ emissions, however, empirical research finds that the relationship between income and CO₂ levels increases monotonically, albeit not according to a strictly linear relationship (Stern 2017).

Despite these distinctions, the literature on the EKC is useful for identifying a number of different mechanisms to explain the relationship between income and emissions. Andreoni and Levinson (2001) suggest that declines in emission rates at higher income levels are due to changes in the composition of production and consumption. Changes in the composition of production may occur due to factors such as the scale of production, the composition effect (the output mix), the input mix, technology, and international reallocation (Copeland and Taylor 2004; Stern 2017). Changes in the composition of consumption, by contrast, may be caused by shifts in preferences and individual behavior that favor the environment or by the introduction of institutions that internalize external diseconomies (Dasgupta and Mäler 1995). In the economic growth literature, Brock and Taylor (2010) and Ordás Criado et al. (2011) also develop sustainable growth models to emphasize that technological progress in pollution abatement and investments in clean technologies are key to the shaping of sustainable growth dynamics.

Empirical research has also begun to investigate the relationship between inequality and emission levels (Grunewald et al. 2017; Ravallion et al. 2000). This research is closely linked to studies of political economy (Boyce 1994; Torras and Boyce 1998) in which it is postulated that greater power inequality leads to higher pollution levels due to a preference for short-term policies. This research suggests, in fact, that greater levels of inequality may reduce the ability of societies to reach political agreements that concern long-term environmental goals or that consider the environment as a public good to be protected. Other studies, by contrast, suggest that higher inequality results in greater levels of exclusion from the carbon economy and, hence, lower emissions (Ravallion et al. 2000). According to this view, greater inequality means a larger share of population in poverty, lacking access to modern energy and leading largely carbon-neutral lives. Such arguments are mirrored by those related to the aggregation bias put forward by Heerink et al. (2001). These authors propose that lower levels of inequality may result in higher levels of emissions due to the redistribution of income and the marginal propensity to emit.

Some of the aforementioned studies also examine the interaction effects between income and inequality on emissions. Grunewald et al. (2017) and Ravallion et al. (2000), for example, conclude that, for low- and middle-income countries, higher inequality decreases per capita emissions, while the opposite is true for high-income countries. Therefore, for poor countries, there is a trade-off between inequality and emissions as mean incomes increase. Overall, these streams of research suggest that significant trade-offs exist between income and inequality regarding emission levels.

3.2 The Poverty–Growth–Inequality Triangle

The poverty–growth–inequality triangle analyses inequality and growth as determinants of poverty (Michálek and Výbošťok 2019). This literature has been summarized in depth by other authors (Ravallion 2016). Some of the major findings of this scholarship, however, are relevant for the present study. Much of the empirical research on poverty reduction, in fact, indicates growth as the main determinant of poverty reduction (Dollar et al. 2016). This is true even when different measures of poverty are used.⁷ Estimates of the growth elasticity of poverty reduction are found to be in the range between minus 2 and minus 3, meaning that a 10% income growth decreases poverty by between 20% and 30% (Adams 2004; Ravallion and Chen 1997).

However, economic growth is not the only determinant of poverty reduction. In fact, it is common to decompose poverty reduction into changes in income and inequality (Datt and Ravallion 1992; Fosu 2017), making it possible to quantify the effects of changes in inequality. Studies find that, while growth remains the main determinant of poverty reduction, changes in inequality also play a statistically significant role in decreasing poverty levels (Datt and Ravallion 1992; Kraay 2006).

Further, as in the literature on the Environmental Kuznets Curve, the interaction between growth and inequality has been found to be relevant for poverty reduction (Bourguignon 2003; Kalwij and Verschoor 2007). Studies on the growth elasticity of poverty find, in fact, that the growth elasticity of poverty reduction is heterogeneous and varies by country.⁸ One of the main explanations for such heterogeneity relates to the initial levels of inequality across countries: it is shown that high initial levels of inequality may act as impediments to growth and may hinder the effects of growth on poverty.⁹

4 A Model Linking Changes in Poverty, Emissions and Their Determinants

4.1 Carbon Intensity of Poverty Reduction and Trade-offs

Let’s consider a policymaker who wants both to reduce poverty and to address environmental degradation, defined as emissions levels per capita (E). Poverty (P) is conceptualized as “a pronounced deprivation in well-being” (Barrientos 2013).¹⁰ The policy-maker addresses poverty and emission levels as simultaneous goals, ideally seeking to eradicate (reduce) poverty and decrease emissions at the same time. In practice, however, this is problematic, especially in the short-term, and the policy maker will confront a trade-off between the two goals. As noted above, in fact, research shows that poverty reduction is most often accompanied by increases in emissions.

Previous studies on the relationship between well-being and emissions (Dietz et al. 2012; Jorgenson 2014; Jorgenson et al. 2014; Knight and Rosa 2011) use an indicator called the environmental intensity of well-being, defined as the ratio between emissions per capita and well-being (WB): therefore $\frac{E}{WB}$. In this study, a new metric is needed for three main reasons. First, the objective here is to link emissions with direct indicators of poverty. As a result, this study employs the proportion of population above the poverty line (1 − P), also defined as non-poverty, as the measure of national well-being. The ratio $\frac{E}{1 - P}$, therefore, represents the amount of emissions per capita for the percentage of the population above the poverty line. Second, policy-makers are interested in changes in poverty and emissions over time and the previous indicator does not focus on changes. Third, compared to the use of a simple ratio between indicators, the use of proportional changes allows the analysis to overcome methodological issues (which will be explained in more detail in the data section). To address these points, a specific measure is developed here to measure the relationship between emissions and poverty over time. This measure is called the carbon intensity of poverty reduction (CIPR). This measure represents the proportional change of the ratio between per capita emissions and non-poverty between periods $t$ and $t - 1$.¹¹

$$CIPR_{t,t - 1} = \left( {\frac{{\left( {\frac{{E_{t} }}{{1 - P_{t} }}} \right)}}{{\left( {\frac{{E_{t - 1} }}{{1 - P_{t - 1} }}} \right)}}} \right) - 1 \approx \ln \left( {\frac{{E_{t} }}{{1 - P_{t} }}} \right) - \ln \left( {\frac{{E_{t - 1} }}{{1 - P_{t - 1} }}} \right)$$

(1)

A negative value for the CIPR means that the amount of per capita emissions per each percentage point of non-poverty has decreased, indicating greater carbon efficiency in poverty reduction.

Rearranging the terms, the CIPR can also be described as the trade-off ($Tr$) between proportional changes ($\Delta$) in emission levels and non-poverty. In fact:

$$CIPR_{t,t - 1} = \ln \left( {\frac{{E_{t} }}{{1 - P_{t} }}} \right) - \ln \left( {\frac{{E_{t - 1} }}{{1 - P_{t - 1} }}} \right) = \left( {\ln \left( {E_{t} } \right) - \ln (E_{t - 1} } \right)) - \left( {\ln \left( {1 - P_{t} } \right) - \ln \left( {1 - P_{t - 1} } \right)} \right) = \Delta_{t,t - 1} E - \Delta_{t,t - 1} \left( {1 - P} \right) = Tr\left( {E_{t,t - 1} ,1 - P_{t, t - 1} } \right)$$

(2)

$Tr\left( {E_{t,t - 1} ,1 - P_{t, t - 1} } \right)$ is therefore the difference between the proportional changes of per capita emissions ($\Delta_{t,t - 1} E$) and non-poverty ($\Delta_{t,t - 1} \left( {1 - P} \right))$. Employing the concept of trade-off also provides a better understanding of the three different cases in which the CIPR is negative (see Fig. 2). The first, straightforward, case is represented when non-poverty increases and emissions decrease.¹² In the second case, the carbon intensity of poverty reduction decreases when non-poverty and emissions both increase, but the former increases proportionally more than the latter. Finally, the CIPR is negative when non-poverty and emissions both decrease, but the former decreases less in proportional terms compared to the latter. The last two cases underline the concept of trade-off, as the CIPR can be negative even if non-poverty decreases (or emissions increase), as long as the decrease in emissions (increase in non-poverty) is proportionally larger. This means that the CIPR is negative even if one of the indicators worsens (lower non-poverty or higher emissions), as long as this negative outcome is offset by improvement in the other indicator, and the overall trade-off is still positive. Therefore, the concept of trade-off is used interchangeably with the carbon intensity of poverty reduction (CIPR) to convey the same relationship.

4.2 Growth and Inequality as Drivers of Poverty Reduction and Emissions: An Analytical Representation

As noted above, previous research suggests that country indicators for both poverty and emission levels (measured in terms of both absolute amounts and changes over time) may be represented as a function of mean income and inequality. Integrating mean income and inequality into Eqs. (1) and (2), the CIPR for country i between $t$ and $t - 1$ may be re-written as:

$$CIPR_{i,t,t - 1} = Tr\left( {E_{i,t,t - 1} ,1 - P_{i,t, t - 1} , } \right) = \left( {\ln \left( {E_{i,t} \left( {x_{i,t} ,\emptyset_{i,t} } \right)} \right) - \ln \left( {E_{i,t - 1} \left( {x_{i,t - 1} ,\emptyset_{i,t - 1} } \right)} \right)} \right) - \left( {\ln \left( {1 - P_{i,t} \left( {x_{i,t} ,\emptyset_{i,t} } \right)} \right) - \ln \left( {1 - P_{i, t - 1} \left( {x_{i,t - 1} ,\emptyset_{i,t - 1} } \right)} \right)} \right) = f\left( {x_{i,t} ,\emptyset_{i,t} ,x_{i,t - 1} ,\emptyset_{i,t - 1} } \right)$$

(3)

where $x_{i,t}$ and $\emptyset_{i,t}$ are the average income and the inequality in country i at time $t$.¹³

Equation (3) formally defines the CIPR as a function of mean income and inequality. Equation (3) can be expressed extensively to outline the possible non-linearities and interactions, as suggested by the previous review of the literature concerning poverty and emission levels (Zaman and Shamsuddin 2018). Starting with mean income, as shown in studies on the poverty–growth–inequality triangle, the growth-elasticity of poverty reduction is heterogeneous across countries (Sumner (2016), among many others). One explanation for this is the non-linear relationship between income and poverty: increases in income present diminishing returns for poverty reduction (non-poverty increases). At the same time, it has been shown that the relationship between income and CO₂ emissions is represented by a monotonically increasing, but slightly concave, curve.¹⁴

In terms of inequality, although the issue of non-linearity has not been addressed in previous research, it is interesting to test for non-linearity in the relationship between inequality and the trade-off between poverty and emissions, especially given the use in this study of a new and composite dependent variable (CIPR).

Finally, the model developed includes the interactions between the levels (changes) of income inequality and changes (levels) of mean income. This is important since it has been shown that these interactions are crucial for both emission levels and poverty. The interaction between changes of income and inequality is not included in the present model as it has not been found to be significant in the literature (Dollar et al. (2016).

Following the above considerations concerning the issues of non-linearity and interaction effects of economic growth and inequality, Eq. (3) may be written extensively as:

$$\begin{aligned} CIPR_{i,t,t - 1} &= \beta_{0} + \beta_{1} \hat{x}_{i,t} + \beta_{2} \hat{x}_{i,t} \left( {x_{i,t - 1} } \right) + \beta_{3} (x_{i,t - 1} ) + \beta_{4} \hat{\emptyset }_{i,t}\\&\quad + \beta_{5} \hat{\emptyset }_{i,t} (\emptyset_{i,t - 1} ) + \beta_{6} (\emptyset_{i,t - 1} ) + \beta_{7} \hat{x}_{i,t} (\emptyset_{i,t - 1} ) + \beta_{8} \hat{\emptyset }_{i,t} \left( {x_{i,t - 1} } \right) \end{aligned}$$

(4)

where $\hat{x}_{i,t}$ and $\hat{\emptyset }_{i,t}$ are the annualized proportional changes (growth rates) of mean incomes and inequality between periods $t - 1$ and $t$. Following from Eq. (4), the marginal effects of economic growth and changes in inequality on the CIPR can be derived. The former may be represented by

$$\frac{{\partial CIPR_{i,t,t - 1} }}{{\partial \hat{x}_{i,t} }} \approx \beta_{1} + \beta_{2} \left( {x_{i,t - 1} } \right) + \beta_{7} (\emptyset_{i,t - 1} )$$

(5)

From the previous discussion of the literature, $\upbeta_{1}$ is expected to be negative, while $\upbeta_{2}$ is expected to be positive. This follows the fact that the concavity of the relationship between income and non-poverty should be stronger than the relationship between income and CO₂ emissions.¹⁵ Empirical evidence has shown, in fact, that, for LMICs, the poverty–growth elasticity is higher than the growth emissions elasticity (Adams 2004; Narayan and Narayan 2010; Stern 2017).¹⁶ Therefore, at lower levels of income, economic growth is expected to increase non-poverty more than emissions. By contrast, the sign of $\upbeta_{7}$ which indicates the interaction between economic growth and the initial level of inequality, is uncertain. While the interaction effect can be predicted for poverty (economic growth has a much higher poverty reduction capacity if initial inequality is lower), the same cannot be done for emissions. In fact, the sign of the interaction depends on the level of income. Therefore, the first proposition to test is:

Economic growth decreases the carbon intensity of poverty reduction (CIPR) for low income levels. After a turning point in mean income, further economic growth has a positive effect on the CIPR.

In parallel, the marginal effects of inequality on the CIPR may be represented by

$$\frac{{\partial CIPR_{{i,t,t - 1}} }}{{\partial \hat{\emptyset }_{{i,t}} }} \approx \beta _{4} + \beta _{5} (\emptyset _{{i,t - 1}} ) + \beta _{8} \left( {x_{{i,t - 1}} } \right) .$$

(6)

Both $\upbeta_{4}$ and $\upbeta_{5}$ are expected to be positive. Empirical research has shown that lower levels of inequality are associated with lower poverty headcount values (for the same level of income). In addition, $\upbeta_{8}$ is expected to be positive since, at higher levels of income, it is proposed that increases in inequality will increase emissions. Thus, the second proposition to test is:

Decreasing inequality decreases the carbon intensity of poverty reduction (CIPR), especially at higher income levels.

5 Data and Methodology

5.1 Data

The data used in the analysis is drawn from two main sources. The main estimates concerning poverty, inequality and mean income (presented in US$ using 2011 PPPs) are sourced from PovcalNet.¹⁷ This source was selected as the most comprehensive collection of household surveys. This data is regarded as reliable and is employed by the majority of studies on cross-country poverty in the literature. The data format allows the estimation of alternative inequality measures and poverty estimates according to different absolute poverty lines.¹⁸

Emissions data come from the Climate Analysis Indicators Tool (CAIT) (WRI 2017).¹⁹ This source was chosen since the database includes estimates for historical CO₂ emissions; and the estimates employed include emissions from different sources (electricity production, heat, manufacturing/construction, transportation, fugitive emissions and other fuel combustion), sectors (energy, industrial processes, waste), and pollutants. The estimates represent territorial emissions. Additional variables are used as covariates in the regressions (see Table 7).

The final dataset consists of 609 spells from 135 countries, where percentage changes are calculated as the average annual difference between logarithms.²⁰ Spells, following the poverty–growth–inequality literature, are defined as intervals of time between consecutive and comparable data points. This definition and use of spells is especially relevant when performing econometric analysis using a panel of cross-country poverty estimates, as it will be further explained in Sect. 5..3. In fact, household surveys are different in nature between countries, and are not available for all years and for all countries. The comparability of poverty estimates between countries may therefore be problematic. To improve the robustness of the estimations, the use of spells has been complemented by a trimming of the original data following the literature. First, spells have been kept if the same welfare indicator (income or consumption) was used at both ends (initial and final year of the spell). Second, only spells of at least two years have been considered. Finally, the spells for which the annual proportional and absolute changes in the poverty headcounts, per capita emissions, and mean incomes are excessively large, are considered as outliers and dropped.²¹

5.2 Summary Statistics

Table 3 shows the unweighted averages of the annual proportional changes in the main variables for all spells. Annual average (compound) growth rates for each variable are calculated as the difference between logarithmic values of two consecutive points in time, divided by the length of the spell in years. Income per capita has increased on average by 1.9% annually. Poverty headcounts decreased on average for all poverty lines. For the poverty estimates, different poverty lines have been considered, based on Hoy and Sumner (2016). Each line represents a different concept of poverty. Considering the poverty lines of US$ 1.90, US$ 3.10, US$ 5 and US$ 10 a day, the annual average decrease has been of 4.9%, 3%, 2.1% and 1% respectively. Inequality, represented by the Gini index, exhibits an average decrease of 0.2%. Finally, emissions per capita increased annually by 1.2% on average.

Table 3 Average annual percentage change of the main variables.

In addition, Fig. 1 in the “Appendix” shows the relationships between the values of non-poverty (top two graphs), emissions (bottom two graphs), and mean income (the horizontal axes). The data displayed in this figure seem to provide initial evidence of the relationships proposed above.²²

5.3 Econometric Strategy

The aim of the econometric analysis is to estimate the effects of a selected set of dependent variables on the CIPR as defined in Eq. (1), which can also be expressed as the trade-off between proportional changes in emissions and non-poverty. In this analysis, the use of spells is employed to overcome several methodological limitations (Bourguignon 2003; Dollar et al. 2016; Sanchez and Stern 2016). This methodology is consistent with the empirical literature on poverty reduction and its determinants. Moreover, although the use of panel data is still dominant in the literature on the EKC (Uchiyama 2016), the use of spells has recently been introduced in empirical studies in this research stream (Sanchez and Stern 2016; Stern et al. 2017).²³

A number of possible estimation issues related to analyses employing composite dependent variables, such as CIPR, have been identified in previous studies (Dietz et al. 2012; Jorgenson 2014; Knight and Rosa 2011). In this study, however, the use of proportional changes addresses the aforementioned comparability issues.

The estimation model starts with Eq. (4), and includes a number of control variables.²⁴ The final equation to be estimated is:

$$\begin{aligned} CIPR_{i,t,t - 1} &= \beta_{0} + \beta_{1} \hat{x}_{i,t} + \beta_{2} \hat{x}_{i,t} \left( {x_{i,t - 1} } \right) + \beta_{3} (x_{i,t - 1} ) + \beta_{4} \hat{\emptyset }_{i,t} + \beta_{5} \hat{\emptyset }_{i,t} (\emptyset_{i,t - 1} ) + \beta_{6} (\emptyset_{i,t - 1} ) + \beta_{7} \hat{x}_{i,t} (\emptyset_{i,t - 1} ) \\&\quad+ \beta_{8} \hat{\emptyset }_{i,t} \left( {x_{i,t - 1} } \right) + \beta_{9} EI_{i,t - 1} + \beta_{10} \left( {1 - P_{i,t - 1} } \right) + \mathop \sum \limits_{j = 11}^{J} \beta_{j} \pi_{i,t - 1} + \varepsilon_{i,t} \end{aligned}$$

(7)

where $CIPR_{i,t,t - 1} = Tr\left( {E_{i,t,t - 1} ,1 - P_{i, t, t - 1} } \right)$ is the annualized CIPR between times t and t − 1 for country i; $\hat{x}_{i,t}$ and $\hat{\emptyset }_{i,t}$ are the annual average growth rates in mean income and inequality (Gini Index); $x_{i,t - 1}$ and $\emptyset_{i,t - 1}$ are the natural logarithms of the mean income and the Gini coefficient at time $t - 1$; $EI_{i,t - 1}$ and $\left( {1 - P_{i,t - 1} } \right)$ are the logarithms of emission intensity and of the non-poverty rate at time t − 1; and $\mathop \sum \nolimits_{j = 11}^{J} \pi_{i,t - 1}$ is the set of additional control variables. Finally, $\varepsilon_{i,t}$ is the error term. Turning to the coefficients, $\beta_{1}$ represents the income growth elasticity of the CIPR. The interactions between income growth rates and initial mean income ($\beta_{2}$), and between the annual percentage change in the Gini coefficient and the initial Gini coefficient ($\beta_{5}$) capture the non-linear effect of economic growth and inequality changes on the CIPR. On the other hand $\beta_{7}$ and $\beta_{8}$ represent the interaction between growth and initial inequality, and between the initial income level and the change in inequality. Following Stern et al. (2017) all of continuous variables in levels are demeaned to simplify the interpretation of the coefficients. For example, $\beta_{1}$ is the growth elasticity of the CIPR when all continuous variables are at their sample mean, and inequality does not change. A positive value of a coefficient thus indicates that an increase of the variable has a positive effect on the CIPR.

If $\beta_{1}$ is positive and $\beta_{2}$ is negative (or viceversa), a turning point related to income, calculated as $\mu = \exp \left( {\frac{{ - \beta_{1} }}{{\beta_{2} }}} \right)$, is present.²⁵ This would mean that increases in income levels do not always have the same effect on the dependent variable.²⁶

Following the empirical literature on poverty reduction, an Ordinary Least Squares (OLS) regression is the main method employed to estimate Eq. (7). The use of robust standard errors is also employed to take into account heteroscedasticity.²⁷ Despite some advantages, fixed effects are used as robustness checks (Table 8; Table 9 presents random effects estimations) due to possible relevant drawbacks in the context of this analysis (Hauk and Wacziarg 2009; Ravallion 2016). Moreover, in relation to the exogeneity of the regressors and causality claims, limited evidence exists concerning causality running from emissions to income, except for the case of high-income countries.²⁸ But because these countries represent a small share of the sample, simultaneity between income, inequality, and emissions should not be a concern in the present estimations (Grunewald et al. 2017; Stern 2004). In addition, regressions control for the initial level of poverty, as suggested by Ravallion (2012).²⁹

6 Results

6.1 Regression Results

Table 4 presents the estimations of Eq. (7) for different poverty lines.³⁰ Model (I) uses the US$ 3.10 a day poverty line. This model is the focus of the study since the US$ 3.10 value represents the international poverty line. Alternative poverty lines are used to test the robustness of the results and to analyze the dynamics associated with different definitions of poverty. More specifically, Models (II), (III) and (IV) employ poverty lines of US$ 1.90 (the international extreme poverty line), US$ 5 and US$ 10 a day respectively.

Table 4 Regression results using all poverty lines, final model.

The results of Model (I) show that growth in mean income decreases, on average, the CIPR with a statistically significant coefficient ($\beta_{1}$) of − 0.24. This means that, for the average country in the sample, economic growth makes poverty reduction less carbon intensive. By contrast, the interaction with income level is positive and significant. This means that, for higher incomes, the effect of income growth is higher and will turn positive after a certain income value. This indicates the presence of a turning point, which will be addressed in greater detail in the subsequent section. The effect of economic growth on the CIPR might also depend on its interaction with the initial level of inequality [the interaction is represented by coefficient $\beta_{7}$ in Eq. (7)]. The coefficient is positive but not significant. Therefore, in general terms, the results confirm the first proposition outlined above that economic growth reduces the carbon intensity of poverty reduction for lower income levels, and that, after a turning point, at higher income levels, the effect becomes positive.

Model (I) shows that the effect of decreasing inequality is negative. The coefficients for both the proportional change and the interaction between the level and the proportional change are all positive and statistically significant. This confirms the second preposition derived from the framework that lower inequality decreases the CIPR. Model (I) also shows that the interaction between the proportional change in inequality and the level of mean income is negative, but statistically insignificant.

The initial (at time t − 1) values of non-poverty and emission intensity are both statistically significant, as expected. More specifically, higher initial non-poverty has a positive effect while higher initial emissions intensity has a negative effect. It is interesting to note that, contrary to the arguments advanced in Ravallion (2012), the coefficients for both initial inequality and initial poverty are significant, although the significance of the former is much lower.

Few of the control variables have statistically significant effects. From the full regression table presented in the “Appendix” (Table 10), it is interesting to note that the coefficient related to the share of the labor force in the services sector is positive and significant. This may be due to the fact that growth in the services sector tends to have a lower impact on poverty reduction (Ravallion 2016; Sumner 2016).

The other three models of Table 4 present the results of the estimations using alternative poverty lines. These results broadly confirm the non-linearity of the effects of income growth. The size of the coefficients changes between models using different poverty lines, but the significance and the sign of the coefficients related to income growth and its interaction with the logarithm of the initial income level remain the same. A similar reasoning may be made for the coefficients related to inequality changes. Three exceptions may be noted. First, the coefficient for income growth in Model (II), when the US$ 1.90 a day poverty line is employed, is not significant. This is due to the use of demeaned level variables, as the sample mean is relatively high compared to the income level (turning point), after which economic growth has a small effect on poverty.³¹ Second, the effect of inequality is non-linear in the case of the highest poverty line (US$ 10 a day) in Model (IV). In fact, the coefficient of the growth for the Gini index is significant and negative, while its interaction with the level of inequality is positive. This is likely due to the fact that the baseline of US$ 10 a day is a much higher poverty line, closely linked to the concept of middle class (Hoy and Sumner 2016). Therefore, different dynamics might be in place compared to the lower poverty lines considered. Third, different results are found in the interactions between economic growth and initial inequality, and between changes in inequality and the initial income, compared to the benchmark Model (I). In fact, both interactions are positive and significant when the two highest poverty lines (US$ 5 and US$ 10 a day) are used. Again, this is most likely due to differences in the dynamics at higher poverty lines.

Table 5 shows detailed results for the econometric estimation of Eq. (7) when the poverty line of US$ 3.10 a day in 2011 PPPs is used. This table presents multiple models that gradually include additional variables in order to test the significance of their inclusion. Model (V) includes only the growth in mean income as a regressor. This gives an initial indication of the average effect of growth on the CIPR. Model (VI) considers the non-linearity of the effect of economic growth, through the inclusion of the interaction between the growth rate and the level of mean incomes (in logarithmic terms), as well as the level of mean income on its own. In Model (VII) variables related to inequality are added. Model (VIII) includes the interactions between initial inequality levels and income growth, as well as the interaction between changes in inequality and the initial level of income. Model (IX) contains the initial levels of poverty and emissions intensity as further controls. Finally, in Model (X) additional control variables are added (equal to Model (I) in the previous table).

Table 5 Regression results using the US$ 3.10 a day poverty line, all models.

Two main findings emerge from Table 5. First, the final Model (X) exhibits the highest adjusted R-squared value, equal to 49%. This means that the final model is the one with the highest explanatory power. Second, it is important to note that the sign and the significance of the coefficients related to economic growth and its interaction with the level of income do not change throughout the models. This suggests that the effects of economic growth are robust to the inclusion of control variables as well as to the interaction with the inequality variables. Similarly, the coefficients of income inequality are robust, with one exception related to the level of inequality: this coefficient becomes statistically insignificant when the initial level of non-poverty is added. This result is consistent with the finding presented in Ravallion (2012). Finally, no important difference in the significance and size of the coefficients between Models (IX) and (X) can be found. This indicates that the addition of the control variables changes the point estimates only slightly.

6.2 Turning Points

Turning points identify the level after which the effect of a variable on the outcome of interest switches from positive to negative or from negative to positive. For example, in the case of the EKC, the turning point indicates the income level below which further economic growth increases emissions.

The analysis presented here shows the existence of turning points in the relationship between economic growth and the carbon intensity of poverty reduction. Table 6 presents the estimated turning points for the different gradual models seen in Table 5, for all four poverty lines. The results of the different models are similar and the turning points increase at higher poverty lines. For example, from the last column of Table 6 that considers the final Eq. (7)³² and the US$ 3.10 a day poverty line, it can be seen that the turning point is approximately US$ 5000. This means that countries in which income per capita is below US$ 5000 a year, economic growth would, on average, decrease the carbon intensity of poverty reduction for this poverty line. The turning points for the other poverty lines above US$ 3.10 a day are higher, reaching a value of around US$ 17,700 a year at the US$ 10 a day poverty line. At the other end, if we move to the international extreme poverty line (US$ 1.90 a day), the turning point is lower, at a value of US$ 3542.

Table 6 Turning points, income per capita (US$ 2011 PPPs).

How do these results relate to the sample at hand with respect to the trade-off between poverty and emissions? At a turning point of US$ 5000 a year, 66% of the countries in the sample fall below the threshold. The mean income of the sample, in fact, is US$ 5700 a year; while the median is US$ 3269.³³ This indicates that, for the majority of countries, economic growth reduces the carbon intensity of poverty reduction.

These findings are consistent with those of related studies. Dietz et al. (2012), for example, examine the trade-off between life expectancy as an indicator of well-being and the ecological footprint as an indicator of environmental efficiency. They estimate a turning point of around US$ 2500. While this specific estimate is not fully comparable to the turning points identified in this study due to methodological differences, their general results lead to the same type of conclusion.³⁴ They suggest, in fact, that the relationship between environmental efficiency and economic growth, just like that between non-poverty and economic growth, is non-linear in nature.

7 Conclusions and Policy Implications

This paper examines the trade-off between poverty reduction and environmental goals as measured by changes in emission levels. It does so through the construction of a composite indicator of the carbon intensity of poverty reduction (CIPR). The paper also explores the potential drivers of this trade-off, namely economic growth and inequality. The findings show that the degree of the trade-off between the two goals of poverty reduction and emission levels varies significantly across countries. The findings also show that the relationship between economic growth and the CIPR is non-linear, presenting a U-shaped form. These findings add a complementary perspective to studies on sustainable development. While the EKC finds an inverted U-shaped relationship when using (local) environmental indicators alone (Stern 2017), this study finds the opposite effect when a composite indicator of sustainable development is employed. This suggests that, differently from the propositions put forward in the EKC, in the case of sustainable development, economic growth has a positive affect up to a certain value. This confirms previous studies on the environmental efficiency of well-being (Dietz et al. 2012). The second main finding is that reductions in inequality consistently result in decreases in the carbon intensity of poverty reduction. This suggests that addressing inequality may be an effective way to deal with the trade-off between poverty reduction and emissions.

In terms of policy implications, the current study reveals the potential use of composite indicators to disentangle the trade-offs between different dimensions of sustainable development (Campagnolo et al. 2018; Cracolici et al. 2009; Michalos 1997). The findings presented in this study strongly support the arguments of the degrowth (Kallis et al. 2018) and agrowth (van den Bergh 2017) movements, especially for high- and upper middle-income countries. These movements and their related policies aim at shifting attention away from economic growth towards a better redistribution of resources (Steinberger and Roberts 2010). This viewpoint is reinforced by studies that show that high- and middle-income countries potentially have the fiscal capacity necessary to implement appropriate policies, such as the eradication of poverty through the use of financial resources obtained from the removal of fossil fuel subsidies (Hoy and Sumner 2016). Greater focus on policies aimed at redistribution and structural change is also supported by evidence that shows that these countries are witnessing a low growth elasticity of poverty reduction due to increasing inequality, an insufficient structural transformation of their economies and spatial poverty traps (Sumner 2016). In the case of India, for example, Murthy et al. (1997) show that eradicating poverty through redistributive programs is more efficient than addressing poverty through growth. These issues may be further exacerbated if environmental issues are considered.

The results presented here also support the possibility of green growth (defined in its broader sense as relative decoupling between economic growth and environmental pressures) for lower-middle and low-income countries. Green economic development may represent an opportunity for many poorer countries that are not locked into polluting industries. On the other hand, green growth may not be feasible in high-income countries. In fact, given their emissions-intensive economic structures, over the past decades only few richer countries have achieved decarbonisation rates that are close to the established global targets (4.4% annual reductions in emissions; Hubacek et al. (2017)), while pursuing economic growth. Nonetheless the green growth model in lower income countries may face some critical issues. Most importantly, its ability to address the challenge of poverty reduction is still uncertain and will depend on how such green growth is achieved (Dercon 2014).

Given the challenges presented by such general policy approaches and the urgency to eradicate poverty and address climate goals, this study suggests that, especially in the short term, policy makers should focus on specific policies that directly address the trade-offs between social and environmental goals. Understanding how and when climate change mitigation and antipoverty policies are not mutually exclusive is critical as governments in many LMICs prioritize social goals over climate goals. The literature has already identified examples of policies that could achieve both goals, such as the recycling of revenues from carbon taxes and the elimination of fossil fuel subsidies (which are regressive and have negative health effects) to address the needs of the poor segments of the population (Ojha 2009), to build social infrastructure (such as modern energy in rural areas), and to implement progressive policies in relation to agriculture and transport (Jakob et al. 2014).

This study presents several limitations that also represent interesting avenues for future research. First, more research is needed to understand the kinds of structural transformation and development paths needed to improve the trade-off between social and environmental policies. This will require the further employment of interdisciplinary and holistic approaches to these issues in order to bring together the three dimensions (economic, social and environmental) of sustainable development. Second, this study highlights several tensions between national level policies and global goals for sustainable development that will need to be addressed in future research. The findings indicate that, for many low- and middle-income countries, economic growth may lead to an improvement in the trade-off between poverty and emissions and may reduce the national carbon intensity of poverty reduction (as defined by CIPR). However, such growth may also have a significant impact on global emissions in absolute terms if it occurs in some of the large economies in these categories. China and India, for example, lie below the lowest turning point (US$ 3542) in terms of mean income. Yet, because they are among the highest polluters in absolute terms, their further economic growth will result in even higher levels of global emissions. Thus tensions between the national carbon intensity of poverty reduction and the global environmental boundaries exist. Future research is needed to understand if and how the development paths followed by these countries might be designed to reduce this tension.

Of course it is crucial to underline that richer countries play a critical role in the tensions concerning global emission levels. To remain within planetary boundaries, high-income economies will need to decrease their emission levels drastically. This needs to be argued on both on equity and sufficiency grounds (Peters et al. 2015; Raupach et al. 2014). Still, it is also important for future research to examine potential growth paths for LMICs that differ from the ones followed by advanced economies. If lower income countries follow the same path of high-income ones, global emissions will continue to increase and will pass dangerous thresholds (Steffen et al. 2015).

Appendix

See Tables 7, 8, 9 and 10 and Figs. 1 and 2.

Table 7 Description of control variables used in the regressions.

Table 8 Regression results using all poverty lines, final model: fixed effects.

Table 9 Regression results using all poverty lines, final model: random effects.

Table 10 Full regression results using all poverty lines, final model.

Fig. 1

Relationship between poverty, emissions and mean income (color figure online)

Fig. 2

Different cases of the CIPR