Trade-Offs in a Multidimensional Human Development Index

Abstract

This paper deals with the issue of trade-offs in an aggregate measure of well-being and argues for a simple multi-dimensional human development measure which allows no substitutability among the dimensions. From a theoretical point of view, our index is shown to satisfy desirable normative and statistical properties highlighted by the literature as well as the practical requirements of user-friendliness and simplicity. An alternative that is less stringent for policy is also analysed from the point of view of trade-offs, including a comparison of ‘social’ trade-offs with market trade-offs when the latter are available. We end the paper with two empirical illustrations, at macro and micro levels, comparing our index with other commonly used indices in each context.

Appendices

Appendix 1: A Closer Look at CIA and a New Proposal—A Generalised CIA (GCIA)

A close look at the definition of CIA shows that it means that the index obtained using the sum of two transformed normalised (component) measures is equal to the sum of the indices obtained using the transformed normalised indices of the components.

Suppose we have two components (of a single measure) say $x_j$ and $y_j$ and let us call their sum $S_j$. The sum of the transformed normalised component measures is:

$$\begin{aligned} a_j+b_j = \left( \frac{x_j - m_j}{M_j - m_j} \right) ^r + \left( \frac{y_j - \tilde{m}_j}{\tilde{M}_j - \tilde{m}_j} \right) ^r \end{aligned}$$

Thus $a_j+b_j$ is NOT the transformed normalised version of the sum $S_j$. Because it is easily seen that

$$\begin{aligned} \left( \frac{S_j-{ min}_s}{{ Max}_s-{ min}_s}\right) ^r \ne \left( \frac{x_j - m_j}{M_j - m_j} \right) ^r + \left( \frac{y_j - \tilde{m}_j}{\tilde{M}_j - \tilde{m}_j} \right) ^r \end{aligned}$$

where ${ min}_s$ and ${ Max}_s$ are the minimum and maximum values respectively of the sum (which are the sum of the corresponding component minima and maxima). So the components are already normalised and transformed before summing. In fact it is by construction that CIA is satisfied. Taking the example of two dimensions $j=1,2$, what CIA says is

$$\begin{aligned} I(a_1+b_1, a_2+b_2) = I(a_1, a_2) + I(b_1,b_2) \end{aligned}$$

but $I(a_1+b_1, a_2+b_2)$ is exactly the mean of the two arguments which are already normalised and transformed (see Chakravarty 2003) i.e.

$$\begin{aligned} \frac{1}{2}\left[ \left( \frac{x_1- m_1}{M_1 - m_1} \right) ^r+\left( \frac{y_1 - \tilde{m}_1}{\tilde{M}_1 - \tilde{m}_1} \right) ^r \right] + \frac{1}{2}\left[ \left( \frac{x_2 - m_2}{M_2 - m_2} \right) ^r + \left( \frac{y_2 - \tilde{m}_2}{\tilde{M}_2 - \tilde{m}_2} \right) ^r \right] \end{aligned}$$

and hence is equal to the sum of the mean of the first two transformed normalised components and the mean of the second two transformed normalised components. Thus CIA is satisfied by construction but its economic content is not clear as there is no obvious substantive interpretation attached to the aggregation $a_j+b_j$.

We now define another aggregation property which is a generalised version of consistency in aggregation (G-CIA) but which has a more interesting substantive interpretation. Then we will show that there are aggregate indices that have an economic interpretation and satisfy this G-CIA.

We call the new property a generalised CIA as it is defined for general aggregation functions which are not necessarily additive in transformed normalised values (like Chakravarty’s (2003) generalised HDI). This property is defined as:

$$\begin{aligned} I\left[ I(a_1,b_1),\ldots , I(a_J,b_J)\right] = I\left[ I(a_1,\ldots ,a_J), I(b_1,\ldots , b_J)\right] \end{aligned}$$

(5)

In other words, the function that is used to aggregate dimensions is the same as that used to aggregate components of a dimension. If the aggregate is a sum then the components are added whereas if the aggregate is another function like the generalised mean then the components should also be aggregated using a generalised mean. Having defined our G-CIA property let us now go back to the generalised mean.

This generalised mean satisfies G-CIA. We have

$$\begin{aligned} I(I(a_1,\ldots ,a_J),I(b_1,\ldots ,b_J))= & {} \left[ \left\{ \left[ \sum _{j=1}^J a_j \right] ^{\frac{1}{r}}\right\} ^r + \left\{ \left[ \sum _{j=1}^J b_j \right] ^{\frac{1}{r}}\right\} ^r \right] ^{\frac{1}{r}}\\= & {} \left[ \sum _{j=1}^J a_j + \sum _{j=1}^J b_j \right] ^{\frac{1}{r}} \end{aligned}$$

G-CIA is also satisfied by the weighted generalised mean.

$$\begin{aligned} I(I(w_1 a_1,\ldots ,w_J a_J),I(w_1 b_1,\ldots ,w_J b_J)) = I(I(a_1,b_1),\ldots ,I(a_J,b_J)) \end{aligned}$$

as

$$\begin{aligned} I(I(a_1,\ldots ,a_J),I(b_1,\ldots ,b_J))= & {} \left[ \left\{ \left[ \sum _{j=1}^J w_j a_j \right] ^{\frac{1}{r}}\right\} ^r + \left\{ \left[ \sum _{j=1}^J w_j b_j \right] ^{\frac{1}{r}}\right\} ^r \right] ^{\frac{1}{r}}\\= & {} \left[ \sum _{j=1}^J w_j a_j + \sum _{j=1}^J w_j b_j \right] ^{\frac{1}{r}} \end{aligned}$$

and

$$\begin{aligned} I(I(a_1,b_1),\ldots ,I(a_J,b_J))= & \,{} \left\{ \left( \left[ w_1 a_1 + w_1 b_1 \right] ^{\frac{1}{r}}\right) ^r+ \left( \left[ w_2 a_2 + w_2 b_2 \right] ^{\frac{1}{r}}\right) ^r\right. \\&+\cdots + \left. \left( \left[ w_J a_J + w_J b_J \right] ^{\frac{1}{r}} \right) ^r \right\} ^{\frac{1}{r}} \\= &\, {} \left\{ \left[ w_1 a_1 + w_1 b_1 \right] + \left[ w_2 a_2 + w_2 b_2 \right] +\cdots +\left[ w_J a_J + w_J b_J \right] \right\} ^{\frac{1}{r}} \end{aligned}$$

Finally, the min index also satisfies our generalised version G-CIA. Since our index is not additive in $z_j$, the consistency in aggregation cannot work with a ‘sum’ function but should be defined using the same aggregation function as the one used for constructing the index. Hence the G-CIA property is given by:

$$\begin{aligned} I(I(z_1,\ldots ,z_J),I(y_1,\ldots ,y_J)) = I(I(z_1,y_1),\ldots ,I(z_J,y_J)) \end{aligned}$$

that is

$$\begin{aligned} \min \left( \min (z_1,\ldots ,z_J),\min (y_1,\ldots ,y_J)\right) ) = \min \left( \min (z_1,y_1),\ldots ,\min (z_J,y_J)\right) \end{aligned}$$

where $y_j$ and $z_j$ are the normalised values of two component indicators.

Thus the aggregation rule itself is the ‘min’ here, in line with our definition of the G-CIA property, and similarly to the example of the generalised mean index in which the generalised mean was taken the aggregation function for verifying consistency. That is, in general, the two components of a measure have to be ‘aggregated’ according to the same function that is chosen for aggregating the dimensions, in order to show ‘generalised’ consistency.

PROOF of G-CIA for ‘min’ index:

We outline the proof for $J=4$ as the reasoning is exactly the same for any J. Let us assume that the different values $y_j$ and $z_j$, $j=1,\ldots ,4,$ can be ordered from the smallest to the biggest as follows: $y_2 \, z_3 \, z_2 \, y_4 \, y_1 \, z_1 \, z_4 \, y_3$

Looking at the sequence above, it is easily seen that $\min \{y_1,y_2,y_3,y_4\} = y_2.$ Similarly $\min \{z_1,z_2,z_3,z_4\} = z_3.$ Finally $\min \{y_2,z_3\} = y_2$.

On the other side, $\min \{y_1,z_1\}= y_1$, $\min \{y_2,z_2\}= y_2$, $\min \{y_3,z_3\}= z_3$, $\min \{y_4,z_4\}= y_4$. And $\min \{y_1, y_2, z_3, y_4\} = y_2$.

Thus we see that both $\min \left( \min (z_1,\ldots ,z_4),\min (y_1,\ldots ,y_4)\right)$ and $\min \left( \min (z_1,y_1),\ldots ,\min (z_4,y_4)\right)$ give the same answer in the above example. Now, it is easy to see that one will obtain the same result for any J and any ordering of the values.

Appendix 2: Market Prices as Trade-Offs?

There is a considerable discussion in the literature on how to set the weights of different dimensions in an aggregate index with no general consensus on what the best choice is. Both ‘normative’ weights and ‘data-driven’ weights are widely employed in empirical applications. It is beyond the scope of this study to go into this debate. One can find a good review on weighting schemes in multi-dimensional indices in Decancq and Lugo (2013). Here we would like to focus on one particular issue in this connection namely the use of ‘market prices’ as weights when available. As most of the dimensions, such as health, education, political freedom, do not have market weights, one can only use ‘social’ weights either fixed normatively or derived statistically. But for a moment let us imagine we have ‘market prices’ for our dimensions⁷ and we use them as weights. Then the ‘market’ trade off will be given by

$$\begin{aligned} MRS^m_{j,k} = \frac{p_j}{p_k} \end{aligned}$$

How does this ‘market’ marginal rate of substitution compare with the ‘social’ marginal rate of substitution? The latter is given by:

$$\begin{aligned} MRS^s_{j,k} = -\left( \frac{z_j }{z_k } \right) ^{r-1} \frac{w_j}{w_k} = -\left( \frac{z_k }{z_j } \right) ^{1-r} \frac{w_j}{w_k} \end{aligned}$$

• If $r=1$ and $w_j=p_j, \, \forall j$ then they are both the same.

• If $r \ne 1$ but $w_j=p_j, \, \forall j$, then

  $$\begin{aligned} MRS_{j,k} = -\left( \frac{z_j }{z_k } \right) ^{r-1} \frac{p_j}{p_k} = -\left( \frac{z_k }{z_j } \right) ^{1-r} \frac{p_j}{p_k} \end{aligned}$$

  and we have the following cases.

  • 1. $0<r<1$

    • If $z_j > z_k$ then $\left( \frac{z_j }{z_k } \right) ^{r-1} \frac{p_j}{p_k} < \frac{p_j}{p_k}$ i.e. social MRS is less than the market trade-off. Society values $z_j$ less than $z_k$ because it has more of $z_j$ compared to $z_k$ (and because they are not so substitutable) and hence the relative social value is less than the relative market value.

    • If $z_j < z_k$ then the opposite happens and the social MRS is more than the market trade-off as $z_j$ being the more deprived dimension in the society, a unit loss in $z_j$ has a bigger social value (loss) and more than the market trade-off is needed to compensate for it.

  • 2. $r>1$

    • If $z_j > z_k$, $\left( \frac{z_j }{z_k } \right) ^{r-1} \frac{p_j}{p_k} > \frac{p_j}{p_k}$. Social MRS is greater than the market trade-off.

    • If $z_j < z_k$ then the opposite happens and the social MRS is less than the market trade-off.

Appendix 3: HDI–MIN Comparisons Table

See Tables 1 and 2.

Table 1 Comparison of min index with HDI

Table 2 Comparison of min index with HDI—contd

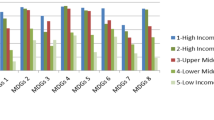
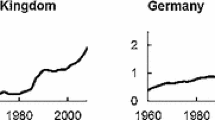
Appendix 4: NFHS Data Graphs

See Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10.

Fig. 2

Distribution of RankAM–RankMin

Fig. 3

Distribution of RankGM–RankMin

Fig. 4

Distribution of RankAM–RankGM

Fig. 5

Min index versus arithmetic mean index

Fig. 6

Min index versus geometric mean index

Fig. 7

Arithmetic mean index versus geometric mean index

Fig. 8

QQ plot RankAM/RankMin

Fig. 9

QQ plot RankGM/RankMin

Fig. 10

QQ plot RankAM/RankGM