Detection and identification of changes of hidden Markov chains: asymptotic theory

Abstract

This paper revisits a unified framework of sequential change-point detection and hypothesis testing modeled using hidden Markov chains and develops its asymptotic theory. Given a sequence of observations whose distributions are dependent on a hidden Markov chain, the objective is to quickly detect critical events, modeled by the first time the Markov chain leaves a specific set of states, and to accurately identify the class of states that the Markov chain enters. We propose computationally tractable sequential detection and identification strategies and obtain sufficient conditions for the asymptotic optimality in two Bayesian formulations. Numerical examples are provided to confirm the asymptotic optimality.

1 Introduction

In this paper, we revisit the joint problem of sequential change-point detection and hypothesis testing generalized in terms of hidden Markov chains. For a sequence of random variables whose distributions are functionals of a hidden Markov chain, the objective is to quickly detect the disorder, described by the event in which the hidden Markov chain leaves a specific set of states, and to accurately identify its cause, as represented by the class of states into which the Markov chain is absorbed. The problem reduces to solving the trade-off between minimizing the expected detection delay and the false alarm and misdiagnosis probabilities. A Bayesian formulation was studied in Dayanik and Goulding (2009).

The sequential change-point detection, hypothesis testing, and their combinations are applied in a wide array of fields. Classic examples include signal, speech, and image processing; radio astronomy; finance/economics; and seismology. Their methodologies are often essential in the control of epidemics; see, e.g., (Baron 2004; Yu et al. 2013), which explores the detection of an influenza outbreak. The common objective in these applications is to derive efficient stopping rules that minimize the required observation size and the false alarm/misidentification probabilities. For a comprehensive review of this subject, see, e.g., (Poor 2013; Tartakovsky et al. 2014; Tartakovsky 2020).

While classical formulations have focused on settings with i.i.d. (independently and identically distributed) observations and simple (usually binary) decision rules, real-life decision-making is often more complex. Therefore, most of the past research on this subject has extended the classical settings to accommodate more realistic scenarios – typically by relaxing the i.i.d. assumptions and allowing for more complex (multiary) decision rules. This paper discusses one way to generalize using hidden Markov chains.

Fig. 1

Transition of the status of a contagious disease. The node $( \text {H}_i, \alpha )$, $i = 0,1$ and $\alpha =$ A,B,C,B&C, corresponds to the state where the hypothesis $\text {H}_i$ is true and County $\alpha$ is infected. The node $( \text {H}_i, \text {extinct})$ is where $\text {H}_i$ is true and the disease has become extinct before reaching A

To motivate the Markov chain model studied in this paper, consider the following problem, as graphically illustrated in Fig. 1. There are three counties A, B, and C facing an infectious disease. Suppose a case of infections is reported in County B, and the agency of County A must promptly detect the event of the infection transmission to County A. Initially, two hypotheses exist regarding the disease: human-to-human transmission possible ($\text {H}_1$) and its negation ($\text {H}_0$). Suppose Counties A, B and C are adjacent to each other and transmission can occur between these counties, except for the route from County C to A under $\text {H}_0$. The agency wants to quickly detect two events: transmission to County A and the disease becoming extinct before reaching County A. Hypothesis $\text {H}_1$ versus $\text {H}_0$ must also be identified to take suitable actions. Note that this formulation can be applied more widely outside of epidemic control; for example, rather than disease, computer viruses can be studied, or rumors that tend to change forms through social networks can be analyzed.

These dynamics can be efficiently modeled via a Markov chain, say $Y=(Y_n)_{n \ge 0}$: the decision-maker wants to detect the first time Y enters one of the four shaded nodes and to identify which node is entered. However, Y is not directly observable, and one must make a guess through indirect observations, say $X=(X_n)_{n \ge 0}$.

This problem includes the features of both change-point detection and sequential hypothesis testing. The decision-maker must select the time to detect critical events and identify the true status of the disease (Y) to take appropriate actions. More precisely, one observes a sequence of random variables whose distributions are functionals of a hidden Markov chain Y. The objective is to as quickly as possible detect the event that the hidden Markov chain leaves a specific set of states and to accurately identify the class of states into which the Markov chain is absorbed.

The scenario in Fig. 1 is merely one example, but the expanded Markov chain is capable of modeling various decision-making problems in various fields. The classical change-point detection with geometrically distributed disorder time and binary hypothesis testing under i.i.d. observations can be modeled by two-state Markov chains. Additional states to the Markov chain enable the modeling of the sequential change diagnosis (detection/isolation) problem, which was first studied in Nikiforov (1995) for the non-Bayesian (minimax) formulation and was further elaborated by, e.g., (Lai 2000; Nikiforov 2000, 2003; Oskiper and Poor 2002; Tartakovsky 2008); the Bayesian model has been studied in Dayanik et al. (2008). In fact, the range of problems the hidden Markov model encompasses is broad. For example, the geometrically distributed disorder time can be generalized to a phase-type distribution (the distribution of the absorption time of a Markov chain); see the examples described in Sections 1 and 2 of Dayanik and Goulding (2009).

There are two main research approaches of this subject – (i) to find the means to compute an optimal solution and (ii) to design asymptotically optimal solutions that are easy to compute and implement. In the first direction, the problem can typically be expressed in terms of the optimal stopping of the posterior probability process of each alternative hypothesis. However, few examples admit analytical solutions, and in practice, one needs to rely on numerical approximations, for example, via value iteration in combination with the discretization of the space of the posterior probability process. The computational burden and nontrivial computer representation of the optimal solution hinder the application of the findings of this first direction in practice. The second direction pursues a strategy that provides simple and scalable implementation but gives only near-optimal solutions. The asymptotic optimality as a certain parameter of the problem approaches an ideal value is commonly used as a proxy for the near-optimality.

Asymptotically optimal strategies are in most cases derived via renewal and nonlinear renewal theories (see Tartakovsky et al. 2014 for a comprehensive reference).

In the sequential (multiple) hypothesis testing with i.i.d. observations, the log-likelihood ratio (LLR) processes become conditional random walks. By utilizing the ordinary renewal theory, the asymptotic behaviors of the expected sample size and the misidentification costs can be approximated; see, for example, (Baum and Veeravalli 1994). Similar approaches are possible for change-point detection. In particular, when the disorder time is geometrically distributed and the observations are conditionally i.i.d., ordinary renewal theory can be applied to the LLR processes, which are conditional random walks.

On the other hand, when the observed random variables are not i.i.d. or when the change-point is not geometrically distributed, the asymptotic optimality is in general not guaranteed; instead, the existing literature typically shows that the r-quick convergence of Lai (1977, 1981) of a certain LLR process is a sufficient condition for asymptotic optimality. Tartakovsky (1998) and Dragalin et al. (2000) generalized Lai’s results to multi-hypothesis sequential tests and for more general models; Dragalin et al. (2000) further obtained higher-order approximations by taking into account the overshoots at up-crossing times of the LLR processes. As for the change-point detection, Tartakovsky and Veeravalli (2004b) consider the non-i.i.d. case and show the asymptotic optimality of the Shiryaev procedure under the r-quick convergence. Its continuous-time version is studied (Baron and Tartakovsky 2006). Dayanik et al. (2013) obtained asymptotically optimal strategies for sequential change diagnosis, showing that the r-quick convergence is again a sufficient condition for asymptotic optimality.

Recently, Tartakovsky (2017) successfully obtained a weaker alternative sufficient condition, known as the r-complete convergence, for the non-i.i.d. case of the change-point detection. The r-quick convergence condition can be replaced by the r-complete convergence condition for a more general class of problems. For a comprehensive account on both analytical and asymptotic optimality of the change-point detection and sequential hypothesis testing, we refer the reader to Tartakovsky et al. (2014); Tartakovsky (2020). For up-to-date results on the general detection-identification problem for non-i.i.d. data, see (Tartakovsky 2021).

This paper presents an asymptotic analysis of the detection and identification problem in terms of the hidden Markov chains described above and derives asymptotically optimal strategies, focusing on the following two Bayesian formulations:

• The minimum Bayes risk formulation minimization of the sum of the expected detection delay time and the false alarm and misdiagnosis probabilities (known as the Bayes risk).

• The Bayesian fixed-error-probability formulation minimization of the expected detection delay time subject to certain upper bounds on the false alarm and misdiagnosis probabilities.

The optimal strategy of the former was derived in Dayanik and Goulding (2009). The latter is usually solved through its Lagrange relaxation, which is a minimum Bayes risk problem where the costs are the Lagrange multipliers of the constraints on the false alarm and misdiagnosis probabilities. In theory, by employing a hidden Markov chain of an arbitrary number of states, a wide range of realistic models can result. However, the implementation is computationally feasible only for simple cases. The problem dimension is proportional to the number of states of the Markov chain, and the computation complexity increases exponentially, which hinders the applications of the hidden Markov model. In practice, obtaining exact optimal strategies is still limited to simple and classical examples.

We propose simple and asymptotically optimal strategies for both the minimum Bayes risk and the Bayesian fixed-error-probability formulations. The asymptotic analysis is similar for both formulations and can be conducted almost simultaneously. Similar to Dayanik et al. (2013), we show that the r-complete convergence for an appropriate choice of the LLR processes is a sufficient condition for asymptotic optimality. This is of particular importance because it was recently verified in Pergamenchtchikov and Tartakovsky (2018), Pergamenchtchikov and Tartakovsky (2019) that the r-complete convergence holds for a large class of Markov processes. We also show in certain cases that the limit can be analytically derived in terms of the Kullback-Leibler divergence. Through a sequence of numerical experiments, we further acknowledge the convergence results of the LLR processes and the asymptotic optimality of the proposed strategies.

The remainder of the paper is organized as follows. In Sect. 2, the two Bayesian formulations are defined. Section 3 presents strategies and the derivation of sufficient conditions for asymptotic optimality in terms of the r-complete convergence of the LLR processes. In Sect. 4, we present examples where the limits of the LLR processes can be analytically obtained via the Kullback-Leibler divergence. Section 5 concludes the paper with numerical results. Long proofs are deferred to the appendix.

2 Problem formulations

In this section, we define two Bayesian formulations: the minimum Bayes risk formulation (Problem 2.1) and the Bayesian fixed-error probability formulation (Problem 2.2). In particular, the former has been studied and its non-asymptotic solution has been derived in Dayanik and Goulding (2009).

Consider a probability space $(\Omega , {\mathcal {F}}, {\mathbb {P}})$ hosting a time-homogeneous Markov chain $Y = (Y_n)_{n \ge 0}$ with some finite state space ${\mathcal {Y}}$, initial state distribution $\eta = \{ \eta (y) \in [0,1], y \in {\mathcal {Y}}\}$, and one-step transition matrix $P = \{ P(y, y') \in [0,1], y, y' \in {\mathcal {Y}} \}$. Suppose that ${\mathcal {Y}}_1,\ldots , {\mathcal {Y}}_M$ are M closed (but not necessarily irreducible) mutually disjoint subsets of the state space ${\mathcal {Y}}$, and let ${\mathcal {Y}}_0 := {\mathcal {Y}} \setminus \bigcup _{k=1}^M {\mathcal {Y}}_k$. In other words, ${\mathcal {Y}}_0$ is transient and the Markov chain Y eventually gets absorbed into one of the M closed sets. Let us define

$$\begin{aligned} \theta := \min \left\{ t \ge 0: Y_t \notin {\mathcal {Y}}_0 \right\} \quad \text {and} \quad \mu := \arg \left\{ 1 \le j \le M: Y_\theta \in {\mathcal {Y}}_j \right\} \end{aligned}$$

as the absorption time and the closed set that absorbs Y, respectively. Here because ${\mathcal {Y}}_0$ is transient (i.e. $\theta < \infty$ a.s.), the random variable $\mu$ is well-defined. We also define ${\mathcal {M}}:= \left\{ 1,\ldots ,M \right\}$ and ${\mathcal {M}}_0 := {\mathcal {M}}\cup \{0\}$.

Remark 2.1

In the example of Fig.  1, ${\mathcal {Y}}_1 = \{ (\text {H}_1, \text {A}) \}$, ${\mathcal {Y}}_2 = \{ (\text {H}_0, \text {A}) \}$, ${\mathcal {Y}}_3 = \{ (\text {H}_1, \text {extinct}) \}$, ${\mathcal {Y}}_4 = \{ (\text {H}_0, \text {extinct}) \}$, and ${\mathcal {Y}}_0$ consists of the other nodes; the absorption time $\theta$ models the first time when the disease arrives in County A if $\mu = 1,2$ and when it is extinct when $\mu =3,4$.

The Markov chain Y can be indirectly observed through another stochastic process $X = (X_n)_{n \ge 1}$ defined on the same probability space $(\Omega , {\mathcal {F}}, {\mathbb {P}})$. We assume that there exists a set of probability measures $\left\{ {\mathbb {P}}(y, {\mathrm{d}}x); y \in {\mathcal {Y}}\right\}$ defined on some common measurable space $(E,{\mathcal {E}})$ such that

$$\begin{aligned} {\mathbb {P}}\left\{ Y_0 = y_0, \ldots , Y_t = y_t, X_1 \in E_1, \ldots , X_t \in E_t \right\} = \eta (y_0) \prod _{n=1}^t P(y_{n-1},y_n) {\mathbb {P}}(y_n, E_n) \end{aligned}$$

for every $(y_n)_{0 \le n \le t} \in {\mathcal {Y}}^{t+1}, (E_n)_{1 \le n \le t} \in {\mathcal {E}}^t, t \ge 1$. For every $y \in {\mathcal {Y}}$, we assume that ${\mathbb {P}}(y, {\mathrm{d}}x)$ admits a density function f(y, x) with respect to some $\sigma$-finite measure $\mathrm {m}$ on $(E,{\mathcal {E}})$; namely,

$$\begin{aligned} f (y,x) \mathrm {m} ({\mathrm{d}}x) = {\mathbb {P}}(y, {\mathrm{d}}x). \end{aligned}$$

Remark 2.2

In this paper, we focus on the case the distribution of X is only dependent on the (unobservable) state of Y. However, in many applications such as the detection of the autoregressive (AR) process, the distribution of observation is also dependent on the past observations. For a hidden Markov model that encompasses this general setting, see (Fuh and Tartakovsky 2018) (see also Remark 2.5).

Remark 2.3

In practical applications, the parameters of the post-change observation distributions are unknown (composite hypothesis). The considered model assumes to know more concrete information on the post-change observation distribution and it does not cover the composite hypothesis cases existing in the literature. In general, the parameter set is not a finite set and one natural way to handle, as in many of the existing literature, is to consider the robust version using the worst-case error probabilities. We refer the reader to, for example, (Tartakovsky 2020, Chapter 7) for the Beyesian formulation of the composite case. One potential extension of the current hidden Markov model is to consider the composite version where the observation is further dependent on additional unknown parameter as well as the state of the Markov chain.

Remark 2.4

It is common in the literature to use X for the hidden Markov chain and Y for the observation process. In this paper, however, we follow the notations in Dayanik and Goulding (2009) and use Y for the hidden Markov chain and X for the observation process.

Let ${\mathbb {F}}= ({\mathcal {F}}_n)_{n \ge 0}$ denote the filtration generated by the stochastic process X; namely,

$$\begin{aligned} {\mathcal {F}}_0 = \{\varnothing , \Omega \} \quad \text {and} \quad {\mathcal {F}}_n = \sigma (X_1,\dots ,X_n), \quad n \ge 1. \end{aligned}$$

A (sequential decision) strategy $(\tau ,d)$ is a pair of an ${\mathbb {F}}$-stopping time $\tau$ (in short, $\tau \in {\mathbb {F}}$) and a random variable $d: \Omega \rightarrow {\mathcal {M}}$ that is measurable with respect to the observation history ${\mathcal {F}}_\tau$ up to the stopping time $\tau$ (namely, $d \in {\mathcal {F}}_{\tau }$). Let

$$\begin{aligned} \Delta := \left\{ (\tau ,d) : \tau \in {\mathbb {F}}\; \text {and} \; d \in {\mathcal {F}}_\tau \; \text {is an }{\mathcal {M}}\text {-valued random variable}\right\} \end{aligned}$$

be the set of strategies.

Our objective is to obtain a strategy $(\tau ,d)$ that minimizes the m-th moment of the detection delay cost

$$\begin{aligned} D^{(c,m)}(\tau ) := {\mathbb {E}}\Big [ \Big (\sum _{t=0}^\infty c(Y_t) 1_{\{t < \tau \}} \Big )^m \Big ] \end{aligned}$$

(2.1)

for some $m \ge 1$ and deterministic nonnegative and bounded function $c: {\mathcal {Y}} \rightarrow [0,\infty )$, as well as the terminal decision losses (TDLs)

$$\begin{aligned} R_{yi}(\tau ,d) := {\mathbb {P}}\left\{ d=i, Y_\tau = y, \tau < \infty \right\} , \quad i \in {\mathcal {M}}, \, y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i. \end{aligned}$$

(2.2)

Regarding the function c, if we set $c(y) = 0$ for $y \in {\mathcal {Y}}_0$ and $c(y)=$ const for $y \notin {\mathcal {Y}}_0$, then it can model a classical expected detection delay ${\mathbb {E}}[((\tau - \theta )_+)^m ]$. By allowing c to be state-dependent, it gives more flexibility in modeling; see, e.g., the examples given in Dayanik and Goulding (2009).

The Bayes risk is a linear combination of all of these losses,

$$\begin{aligned} u^{(c,a,m)}(\tau ,d) := D^{(c,m)}(\tau ) + \sum _{i \in {\mathcal {M}}} \sum _{y \in {\mathcal {Y}} \setminus {\mathcal {Y}}_i} a_{yi} R_{yi} (\tau ,d) \end{aligned}$$

(2.3)

for some $m \ge 1$, c, and a set of strictly positive constants $a= (a_{yi})_{i \in {\mathcal {M}}, y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i }$. In (2.1), while it is natural to assume $c(y)=0$ for $y \in {\mathcal {Y}}_0$, we allow c(y) to take any nonnegative values for $y \in {\mathcal {Y}}_0$. On the other hand, in (2.2) and (2.3), we assume that any correct terminal decision (i.e., $\{d=i, Y_\tau \in {\mathcal {Y}}_i, \tau < \infty \}$) is not penalized because otherwise the terminal decision loss (2.2) cannot be bounded by small numbers and Problem 2.2 (defined subsequently) would not make sense.

Problem 2.1

(Minimum Bayes risk formulation) Fix $m \ge 1$, c, and a set of strictly positive constants $a= (a_{yi})_{i \in {\mathcal {M}}, y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i }$, we want to calculate the minimum Bayes risk

$$\begin{aligned} \inf _{(\tau ,d) \in \Delta } u^{(c,a,m)}(\tau ,d) \end{aligned}$$

and find a strategy $(\tau ^*,d^*)$ that attains it, if such a strategy exists.

Problem 2.2

(Bayesian fixed-error probability formulation) Fix $m\ge 1$, c, and a set of strictly positive constants ${\overline{R}} = ({\overline{R}}_{yi})_{i \in {\mathcal {M}}, y \in {\mathcal {Y}} \setminus {\mathcal {Y}}_i}$, we want to calculate the minimum m-th moment of the detection delay cost

$$\begin{aligned} \inf _{(\tau ,d) \in \Delta ({\overline{R}})} D^{(c,m)}(\tau ) \end{aligned}$$

over the set of strategies

$$\begin{aligned} \Delta ({\overline{R}}) := \left\{ (\tau ,d) \in \Delta : R_{yi}(\tau ,d) \le {\overline{R}}_{yi}, \; i \in {\mathcal {M}}, y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i \right\} , \end{aligned}$$

and find a strategy $(\tau ^*,d^*)\in \Delta ({\overline{R}})$ that attains it, if such a strategy exists.

Remark 2.5

(Connection with the hidden Markov model of Fuh and Tartakovsky (2018)) Problem 2.2 in our setting and the problem considered in Fuh and Tartakovsky (2018) complement each other. In Fuh and Tartakovsky (2018), they considered a version of change point detection (without identification) using a hidden Markov chain that changes its dynamics at an unobservable time $\theta$, whose initial distribution is independent of the observation process.

In Fuh and Tartakovsky (2018), the distribution of the observation $X_{t}$ at time t is a function of both the state of the hidden Markov chain $Y_t$ as well as the previous observation $X_{t-1}$, such that the conditional probability given the change has occurred and has not occurred can be written

$$\begin{aligned} {\mathbb {P}}^{(j)} \left\{ Y_1 \in A, X_1 \in B | Y_0 = y_0, X_0 = x_0 \right\} = \sum _{y' \in A} \int _{x' \in B} P^{(j)}(y_0,y') f^{(j)}(y',x'; x_0) \mathrm {m}({\mathrm{d}}x'), \end{aligned}$$

with ${\mathbb {P}}^{(j)}(y, {\mathrm{d}}x; x_0) = f^{(j)}(y, x; x_0) \mathrm {m} ({\mathrm{d}}x)$ for $j = 0$ (pre-change) and 1 (post-change).

When $f^{(j)}(y, x; x_0)$ is invariant of $x_0$ (i.e. the distribution of observation only depends on the current state of the Markov chain), it can be modeled as a special case of Problem 2.2 with $M=1$. To see this, consider the case when $\theta \sim Geom(p)$ and the state space of the Markov chain Y is ${\tilde{E}}$. Construct two Markov chains on ${\mathcal {Y}}_j = \{(i,j); i \in {\tilde{E}} \}$, $j = 0,1$ with corresponding transition matrices $P^{(j)}$. Then, the model of Fuh and Tartakovsky (2018) corresponds to Problem 2.2 with a new Markov chain with state space ${\mathcal {Y}} = {\mathcal {Y}}_0 \cup {\mathcal {Y}}_1$ with the new transition matrix P given by, for $i,i' \in {\tilde{E}}$,

$$\begin{aligned} P((i,0), (i',0))&= (1-p) P^{(0)} (i,i'), \\ P((i,1), (i',1))&= P^{(1)} (i,i'), \\ P((i,0), (i',1))&= p 1_{\{i = i' \}}. \end{aligned}$$

This can be generalized by considering the case $\theta$ is phase-type (see Example 1 of Dayanik and Goulding (2009)) and modeling ${\mathcal {Y}}_0$ in an analogous way using N copies of the Markov chain where N is the number of states necessary to describe the phase-type distribution.

With the framework of Dayanik and Goulding (2009), we can consider various generalizations such as the case with identification ($M \ge 2$) and also the case when the disorder time $\theta$ depends on $\mu$ (see Example 2 of Dayanik and Goulding (2009)).

For every $i \in {\mathcal {M}}$, define

$$\begin{aligned} {\widetilde{R}}_{ji}(\tau ,d) := \sum _{y \in {\mathcal {Y}}_j} R_{yi}(\tau ,d) = \left\{ \begin{array}{ll} {\mathbb {P}}\left\{ d=i, \tau< \theta \right\} , &{} j = 0, \\ {\mathbb {P}}\left\{ d=i, \mu =j, \theta \le \tau < \infty \right\} , &{} j \in {\mathcal {M}}\setminus \{i\}. \end{array} \right. \end{aligned}$$

(2.4)

Remark 2.6

Fix a set of positive constants ${\overline{R}}$. We have

$$\begin{aligned} \Delta ({\overline{R}})&\subset \Big \{ (\tau ,d) \in \Delta : {\widetilde{R}}_{ji}(\tau ,d) \le \sum _{y \in {\mathcal {Y}}_j }{\overline{R}}_{yi}, \; i \in {\mathcal {M}}, j \in {\mathcal {M}}_0 \setminus \{ i \} \Big \} =: {\overline{\Delta }} ({\overline{R}}),\\ \Delta ({\overline{R}})&\supset \Big \{ (\tau ,d) \in \Delta : {\widetilde{R}}_{ji}(\tau ,d) \le \min _{y \in {\mathcal {Y}}_j }{\overline{R}}_{yi}, \; i \in {\mathcal {M}}, j \in {\mathcal {M}}_0 \setminus \{ i \} \Big \} =: {\underline{\Delta }} ({\overline{R}}). \end{aligned}$$

In our analysis, we will need to reformulate the problem in terms of the conditional probabilities

$$\begin{aligned} {\mathbb {P}}_i \left\{ X_1 \in E_1,...,X_n \in E_n\right\}&:= {\mathbb {P}}\left\{ \left. X_1 \in E_1,...,X_n \in E_n \right| \mu = i\right\} , \\ {\mathbb {P}}_i^{(t)} \left\{ X_1 \in E_1,...,X_n \in E_n\right\}&:= {\mathbb {P}}\left\{ \left. X_1 \in E_1,...,X_n \in E_n \right| \mu = i, \theta = t\right\} , \quad t \ge 0, \end{aligned}$$

defined for every $i \in {\mathcal {M}}$, $n \ge 1$ and $(E_1 \times \cdots \times E_n) \in {\mathcal {E}}^n$. Let ${\mathbb {E}}_i$ and ${\mathbb {E}}_i^{(t)}$ be the expectations with respect to ${\mathbb {P}}_i$ and ${\mathbb {P}}_i^{(t)}$, respectively. We also let

$$\begin{aligned} \nu _i&:= {\mathbb {P}}\left\{ \mu = i\right\} , \quad i \in {\mathcal {M}}, \end{aligned}$$

be the unconditional probability of the event that Y is absorbed by ${\mathcal {Y}}_i$. Because ${\mathcal {Y}}_0$ is transient, we must have $\sum _{i \in {\mathcal {M}}} \nu _i =1$. Without loss of generality, we assume

$$\begin{aligned} \nu _i > 0, \quad i \in {\mathcal {M}}\end{aligned}$$

because otherwise we can disregard ${\mathcal {Y}}_i$ and consider the Markov chain on ${\mathcal {Y}}\setminus {\mathcal {Y}}_i$.

In terms of those conditional probabilities, we have $D^{(c,m)}(\tau ) = \sum _{i \in {\mathcal {M}}} \nu _i D_i^{(c,m)}(\tau )$, where

$$\begin{aligned} D_i^{(c,m)}(\tau ) := {\mathbb {E}}_i \Big [\Big (\sum _{t=0}^\infty c(Y_t) 1_{\{t < \tau \}} \Big )^m \Big ], \quad i \in {\mathcal {M}}, \; (\tau ,d) \in \Delta . \end{aligned}$$

We decompose the Bayes risk such that

$$\begin{aligned} u^{(c,a,m)}(\tau ,d) = \sum _{i \in {\mathcal {M}}} \nu _i u_i^{(c,a,m)}(\tau ,d) \end{aligned}$$

where we define

$$\begin{aligned} u_i^{(c,a,m)}(\tau ,d)&:= D_i^{(c,m)} (\tau ) + R_i^{(a)} (\tau ,d), \end{aligned}$$

(2.5)

$$\begin{aligned} R_i^{(a)} (\tau ,d)&:= \frac{1}{\nu _i} \sum _{y \in {\mathcal {Y}} \setminus {\mathcal {Y}}_i} a_{yi} R_{yi} (\tau ,d) \end{aligned}$$

(2.6)

for every $(\tau ,d) \in \Delta$. In particular, if we set $a_{yi} = 1$ for all $y \in {\mathcal {Y}}\backslash {\mathcal {Y}}_i$, using (2.4),

$$\begin{aligned} R_i^{(1)} (\tau ,d) := \frac{1}{\nu _i} \sum _{y \in {\mathcal {Y}} \setminus {\mathcal {Y}}_i} R_{yi} (\tau ,d) = \frac{1}{\nu _i} \sum _{j \in {\mathcal {M}}_0 \setminus \{i\}} {\widetilde{R}}_{ji} (\tau ,d), \quad (\tau ,d) \in \Delta . \end{aligned}$$

(2.7)

3 Asymptotically optimal strategies

We now introduce two strategies. The first strategy triggers an alarm when the posterior probability of the event that Y has been absorbed by a certain closed set exceeds some threshold for the first time, and will be later proposed as an asymptotically optimal solution for Problem 2.1. The second strategy is its variant, expressed in terms of the log-likelihood ratio (LLR) processes and will be proposed as an asymptotically optimal solution for Problem 2.2.

For all $y \in {\mathcal {Y}}$, let $(\Pi _n(y))_{n \ge 0}$ be the posterior probability process defined by

$$\begin{aligned} \Pi _n(y) := {\mathbb {P}}\left\{ \left. Y_n = y \right| {\mathcal {F}}_n \right\} , \quad y \in {\mathcal {Y}}. \end{aligned}$$

Then, for $y \in {\mathcal {Y}}$, $\Pi _0(y) = \eta (y)$ and for $n \ge 1$

$$\begin{aligned} \Pi _n(y) = \frac{\alpha _n(X_1,\ldots ,X_n,y)}{\sum _{y' \in {\mathcal {Y}}}\alpha _n(X_1,\ldots ,X_n,y')} \end{aligned}$$

where

$$\begin{aligned} \alpha _n (x_1,\ldots , x_n,y) := \sum _{(y_0,\ldots , y_{n-1}) \in {\mathcal {Y}}^n} \left( \eta (y_0) \prod _{k=1}^{n-1} P(y_{k-1},y_k) f(y_k,x_k)\right) P(y_{n-1},y) f(y,x_n); \end{aligned}$$

(3.1)

see Dayanik and Goulding (2009) for how these can be derived. Also define

$$\begin{aligned} {\widetilde{\Pi }}_n^{(i)} := {\mathbb {P}}\left\{ \left. Y_n \in {\mathcal {Y}}_i \right| {\mathcal {F}}_n \right\} = \left\{ \begin{array}{ll} {\mathbb {P}}\left\{ \left. \theta > n \right| {\mathcal {F}}_n \right\} , &{} i=0 \\ {\mathbb {P}}\left\{ \left. \theta \le n, \mu =i \right| {\mathcal {F}}_n \right\} , &{} i \in {\mathcal {M}}\end{array}\right\} . \end{aligned}$$

Then ${\widetilde{\Pi }}_0^{(i)} = \sum _{y \in {\mathcal {Y}}_i}\Pi _0(y) = \sum _{y \in {\mathcal {Y}}_i} \eta (y)$, $i \in {\mathcal {M}}_0$, and for $n \ge 1$

$$\begin{aligned} {\widetilde{\Pi }}_n^{(i)} = \sum _{y \in {\mathcal {Y}}_i}\Pi _n(y) = \frac{{\widetilde{\alpha }}_n^{(i)}(X_1,\ldots ,X_n) }{\sum _{j \in {\mathcal {M}}_0}{\widetilde{\alpha }}_n^{(j)}(X_1,\ldots ,X_n) }, \end{aligned}$$

where

$$\begin{aligned} {\widetilde{\alpha }}_n^{(i)}(x_1,\ldots ,x_n) := \sum _{y \in {\mathcal {Y}}_i} \alpha _n(x_1,\ldots ,x_n,y), \quad i \in {\mathcal {M}}_0, \, (x_1,\ldots , x_n) \in E^n. \end{aligned}$$

(3.2)

For the rest of the paper, we use the short-hand notations: ${\widetilde{\alpha }}_n^{(i)}:= {\widetilde{\alpha }}_n^{(i)}(X_1,\ldots ,X_n)$ for $n \ge 1$ and $i \in {\mathcal {M}}_0$. We also assume the following, which is imposed so that the LLR process is well-defined. Note, however, that this naturally holds except for pathological (and non-interesting) cases. This fails for example when $\theta$ is a deterministic constant (which can be modeled by using the transition matrix with elements 0 and 1) and $M = 1$.

Assumption 3.1

We assume, there exists T such that $0< {\widetilde{\Pi }}_n^{(i)} < 1$ a.s. for every finite $n \ge T$ and $i\in {\mathcal {M}}$.

Let $\Lambda (i,j) = \left( \Lambda _n(i,j) \right) _{n \ge 1}$ be the LLR processes;

$$\begin{aligned} \Lambda _n(i,j) := \log \frac{{\widetilde{\Pi }}_n^{(i)}}{{\widetilde{\Pi }}_n^{(j)}} = \log \frac{{\widetilde{\alpha }}_n^{(i)}}{{\widetilde{\alpha }}_n^{(j)}}, \quad n \ge 1, \; i \in {\mathcal {M}}, \; j \in {\mathcal {M}}_0\setminus \{i\}. \end{aligned}$$

(3.3)

Definition 3.1

($(\tau _A,d_A)$-strategy for the minimum Bayes risk formulation) Fix a set of strictly positive constants $A = (A_i)_{i \in {\mathcal {M}}}$, define strategy $(\tau _A,d_A)$ by

$$\begin{aligned} \tau _A = \min _{i \in {\mathcal {M}}}\; \tau _A^{(i)} \quad \text {and} \quad d_A \in {{\,\mathrm{\arg \min }\,}}_{i \in {\mathcal {M}}} \tau _A^{(i)}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} \tau _A^{(i)} := \inf \left\{ n \ge 1: {\widetilde{\Pi }}_n^{(i)} > \frac{1}{1+A_i}\right\} , \quad i \in {\mathcal {M}}. \end{aligned}$$

(3.5)

Define the logarithm of the odds-ratio process

$$\begin{aligned} \Phi _n^{(i)}&:= \log \frac{{\widetilde{\Pi }}_n^{(i)}}{1-{\widetilde{\Pi }}_n^{(i)}}= - \log \Big [ \sum _{j \in {\mathcal {M}}_0 \setminus \{i\}} \exp \left( -\Lambda _n(i,j) \right) \Big ]\nonumber \\&= \log \frac{{\widetilde{\alpha }}_n^{(i)}}{\sum _{j \in {\mathcal {M}}_0 \setminus \{i\}}{\widetilde{\alpha }}_n^{(j)}}, \quad i \in {\mathcal {M}}, \; n \ge 1. \end{aligned}$$

(3.6)

Then, (3.5) can be rewritten as

$$\begin{aligned} \tau _A^{(i)} = \inf \left\{ n \ge 1 : \frac{1-{\widetilde{\Pi }}_n^{(i)}}{{\widetilde{\Pi }}_n^{(i)}} < A_i \right\} = \inf \left\{ n \ge 1: \Phi _n^{(i)} > - \log A_i \right\} , \quad i \in {\mathcal {M}}. \end{aligned}$$

(3.7)

Definition 3.2

($(\upsilon _B,d_B)$-strategy for the Bayesian fixed-error-probability formulation) Fix a set of strictly positive constants $B = (B_{ij})_{i \in {\mathcal {M}}, \; j \in {\mathcal {M}}_0 \setminus \{i\}}$, define

$$\begin{aligned} \upsilon _B := \min _{i \in {\mathcal {M}}} \upsilon _B^{(i)} \quad \text {and} \quad d_B \in \arg \min _{i \in {\mathcal {M}}} \upsilon _B^{(i)} \end{aligned}$$

(3.8)

where

$$\begin{aligned} \upsilon _B^{(i)} := \inf \left\{ n \ge 1: \Lambda _n(i,j) > - \log B_{ij} \hbox { for every}\ j \in {\mathcal {M}}_0 \setminus \{i\}\right\} , \quad i \in {\mathcal {M}}. \end{aligned}$$

(3.9)

Remark 3.1

In (3.4) and (3.8), when the minimizer is not unique, $d_A$ and $d_B$ can be selected arbitrarily among the minimizers.

Fix $i \in {\mathcal {M}}$. Define

$$\begin{aligned} {\overline{B}}_i := \max _{j \in {\mathcal {M}}_0 \setminus \{i\}} B_{ij} \quad \text {and} \quad {\underline{B}}_i := \min _{j \in {\mathcal {M}}_0 \setminus \{i\}} B_{ij}, \end{aligned}$$

and the minimum of the LLR processes,

$$\begin{aligned} \Psi ^{(i)}_n := \min _{j \in {\mathcal {M}}_0 \setminus \{i\}} \Lambda _n(i,j), \quad n \ge 1. \end{aligned}$$

Then we have

$$\begin{aligned} {\underline{\upsilon }}_B^{(i)} \le \upsilon _B^{(i)} \le {\overline{\upsilon }}_B^{(i)}, \end{aligned}$$

where

$$\begin{aligned} {\underline{\upsilon }}_B^{(i)} := \inf \left\{ n \ge 1: \Psi ^{(i)}_n> - \log {\overline{B}}_{i} \right\} \quad \text {and} \quad {\overline{\upsilon }}_B^{(i)} := \inf \left\{ n \ge 1: \Psi ^{(i)}_n > - \log {\underline{B}}_{i} \right\} . \end{aligned}$$

Notice, by (3.6), that $\Phi _n^{(i)} \le \Lambda _n(i,j)$ for every $n \ge 1$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$, and hence

$$\begin{aligned} \Psi ^{(i)}_n \ge \Phi _n^{(i)}, \quad n \ge 1. \end{aligned}$$

(3.10)

We will show that, by adjusting the values of A and B, the strategy $(\tau _A,d_A)$ is asymptotically optimal in Problem 2.1 as

$$\begin{aligned} \Vert c\Vert := \max _{y \in {\mathcal {Y}}} c (y) \downarrow 0 \end{aligned}$$

for fixed a, and the strategy $(\upsilon _B,d_B)$ is asymptotically optimal in Problem 2.2 as

$$\begin{aligned} \Vert {\overline{R}}\Vert := \max _{i \in {\mathcal {M}}, \; y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i } {\overline{R}}_{yi} \downarrow 0 \end{aligned}$$

for fixed c. For the latter, we assume that, in taking limits, ${\overline{R}}_i := ({\overline{R}}_{yi})_{y \in {\mathcal {Y}}\backslash {\mathcal {Y}}_i}$ satisfy

$$\begin{aligned} \frac{\min _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i} {\overline{R}}_{yi}}{\max _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i} {\overline{R}}_{yi}} > \beta _i, \quad i \in {\mathcal {M}}, \end{aligned}$$

(3.11)

for some strictly positive constants $(\beta _i)_{i \in {\mathcal {M}}}$. This limit mode will still be denoted by “$\Vert {\overline{R}}\Vert \downarrow 0$” for brevity. We assume (3.11) for our asymptotic optimality results. We choose the values of the barriers B as functions of ${\overline{R}}$, and, for our strategies to be asymptotically optimal, it is necessary to assume that ${\overline{R}}_{yi}$ for each y needs to decrease at a similar speed (see Remark 3.4 and (3.22)).

We will find functions A(c) and $B({\overline{R}})$ so that

$$\begin{aligned} u^{(c,a,m)}(\tau _{A(c)},d_{A(c)})&\sim \inf _{(\tau ,d) \in \Delta } u^{(c,a,m)}(\tau ,d) \quad \text {as } \Vert c \Vert \downarrow 0, \end{aligned}$$

(3.12)

$$\begin{aligned} D^{(c,m)}(\upsilon _{B({\overline{R}})})&\sim \inf _{(\tau ,d) \in \Delta ({\overline{R}})} D^{(c,m)} (\tau ) \quad \text {as } \Vert {\overline{R}} \Vert \downarrow 0, \end{aligned}$$

(3.13)

where

$$\begin{aligned} x_{\gamma } \sim y_\gamma \text { as } \gamma \rightarrow \gamma _0 \Longleftrightarrow \lim _{\gamma \rightarrow \gamma _0} \frac{x_\gamma }{y_\gamma } = 1. \end{aligned}$$

In fact, we will obtain results stronger than (3.12) and (3.13); we will show

$$\begin{aligned} u_i^{(c,a,m)}(\tau _{A(c)},d_{A(c)})&\sim \inf _{(\tau ,d) \in \Delta } u_i^{(c,a,m)}(\tau ,d) \quad \text {as } \Vert c\Vert \downarrow 0, \end{aligned}$$

(3.14)

$$\begin{aligned} D^{(c,m)}_i(\upsilon _{B({\overline{R}})})&\sim \inf _{(\tau ,d) \in \Delta ({\overline{R}})} D^{(c,m)}_i (\tau ) \quad \text {as } \Vert {\overline{R}} \Vert \downarrow 0, \end{aligned}$$

(3.15)

for every $i \in {\mathcal {M}}$.

3.1 Convergence of terminal decision losses and detection delay

As c and ${\overline{R}}$ decrease in Problems 2.1 and 2.2 , respectively, the optimal stopping regions shrink and one should expect to wait longer. In Problem 2.1, when the unit sampling cost is small, one should take more advantage of it and sample more. In Problem 2.2, when the upper bounds on the TDLs are small, one expects to wait longer to collect more information in order to satisfy the constraints. On the other hand, the size of the stopping regions for $(\tau _A,d_A)$ and $(\upsilon _B,d_B)$ decrease monotonically as A and B decrease. Therefore, functions A(c) and $B({\overline{R}})$ should be monotonically decreasing as c and ${\overline{R}}$ decrease, respectively. We explore the asymptotic behaviors of the detection delay cost and the TDL as $A \downarrow 0$ and $B \downarrow 0$.

Define

$$\begin{aligned} \Vert A \Vert := \max _{i \in {\mathcal {M}}} A_i \quad \text {and} \quad \Vert B \Vert := \max _{i \in {\mathcal {M}}, \, j \in {\mathcal {M}}_0 \setminus \{i\}} B_{ij}. \end{aligned}$$

Moreover, assume, while taking limits $\Vert B\Vert \downarrow 0$, that the ratio ${\underline{B}}_i/{\overline{B}}_i$ for every $i \in {\mathcal {M}}$ is bounded from below by some strictly positive number so that it is consistent with how $\Vert {\overline{R}}\Vert$ decreases to 0 as we assumed in (3.11).

We first obtain bounds on the TDLs that are shown to converge to zero in the limit. The LLR processes can be used as Radon-Nikodym derivatives to change measures as the following lemma shows. The proof only requires the change of measure and the same result holds more generally. For the proof, see, e.g., Lemma 2.3 of Dayanik et al. (2013).

Lemma 3.1

(Changing Measures) Fix $i \in {\mathcal {M}}$, an ${\mathbb {F}}$-stopping time $\tau$, and an ${\mathcal {F}}_\tau$-measurable event F. We have

$$\begin{aligned} {\mathbb {P}}\left( F \cap \left\{ \mu =j, \theta \le \tau< \infty \right\} \right)&= \nu _i\, {\mathbb {E}}_i \left[ 1_{F \cap \{\theta \le \tau< \infty \}} e^{-\Lambda _\tau (i,j)}\right] , \quad j \in {\mathcal {M}}\setminus \{i\}, \\ {\mathbb {P}}\left( F \cap \left\{ \tau< \theta \right\} \right)&= \nu _i\, {\mathbb {E}}_i \left[ 1_{F \cap \left\{ \theta \le \tau < \infty \right\} } e^{-\Lambda _\tau (i,0)}\right] . \end{aligned}$$

The next proposition can be obtained by setting $F:= \{d=i\} \in {\mathcal {F}}_{\tau }$ in Lemma 3.1.

Proposition 3.1

For every strategy $(\tau ,d) \in \Delta$, we have

$$\begin{aligned} {\widetilde{R}}_{ji}(\tau ,d)&= \nu _i\, {\mathbb {E}}_i \left[ 1_{\{d=i, \; \theta \le \tau < \infty \}} e^{-\Lambda _\tau (i,j)}\right] , \quad i \in {\mathcal {M}}, \; j \in {\mathcal {M}}_0\setminus \{i\}. \end{aligned}$$

In particular, (2.7) can be rewritten

$$\begin{aligned} R_i^{(1)}(\tau ,d)&= {\mathbb {E}}_i \Big [ 1_{\left\{ d=i, \; \theta \le \tau < \infty \right\} } \sum _{j \in {\mathcal {M}}_0 \setminus \{i\}} e^{-\Lambda _{\tau } (i,j)} \Big ], \quad i \in {\mathcal {M}}, \; (\tau ,d) \in \Delta . \end{aligned}$$

(3.16)

Remark 3.2

Fix $i \in {\mathcal {M}}$. Let

$$\begin{aligned} {\overline{a}}_i := \max _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i} a_{yi}. \end{aligned}$$

By (2.6), (2.7) and (3.16),

$$\begin{aligned}&R_i^{(a)} (\tau ,d) \le \frac{1}{\nu _i} \sum _{j \in {\mathcal {M}}_0 \setminus \{i\}} (\max _{y \in {\mathcal {Y}}_j} a_{yi}) {\widetilde{R}}_{ji} (\tau ,d) \le {\overline{a}}_i R_{i}^{(1)} (\tau ,d) \\&\quad = {\overline{a}}_i {\mathbb {E}}_i \Big [ 1_{\left\{ d=i, \; \theta \le \tau < \infty \right\} } \sum _{j \in {\mathcal {M}}_0 \setminus \{i\}} e^{-\Lambda _{\tau } (i,j)} \Big ]. \end{aligned}$$

With this remark and Definitions 3.1 and 3.2 and (3.7), we attain a slight modification of Proposition 3.4 of Dayanik et al. (2013).

Proposition 3.2

(Bounds on the TDL) We can obtain the following bounds on the TDLs.

• (i) For every fixed $A = (A_i)_{i \in {\mathcal {M}}}$ and $a = (a_{yi})_{i \in {\mathcal {M}}, y \in {\mathcal {Y}} \setminus {\mathcal {Y}}_i}$, we have

  $$\begin{aligned} R_i^{(a)}(\tau _A,d_A)&\le {\overline{a}}_i A_i, \quad i \in {\mathcal {M}}. \end{aligned}$$

• (ii) For every $B = (B_{ij})_{i \in {\mathcal {M}}, j \in {\mathcal {M}}\setminus \{i\}}$, we have

  $$\begin{aligned} {\widetilde{R}}_{ji} (\upsilon _B, d_B)&\le \nu _i B_{ij}, \quad i \in {\mathcal {M}}, \, j \in {\mathcal {M}}_0 \setminus \{i\}. \end{aligned}$$

Using the bounds in Proposition 3.2 and Remark 2.6, we can obtain feasible strategies by choosing the values of A and B accordingly.

Proposition 3.3

(Feasible Strategies for Problem 2.2) Fix a set of strictly positive constants ${\overline{R}} = (R_{yi})_{i \in {\mathcal {M}}, y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i}$. If $B_{ij} ({\overline{R}}) \le {\min _{y \in {\mathcal {Y}}_j} {\overline{R}}_{yi}/\nu _i}$ for every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$, then $(\upsilon _{B({\overline{R}})}, d_{B({\overline{R}})}) \in \Delta ({\overline{R}})$.

We now analyze the asymptotic behavior of the detection delay. The next remark allows us to use $\tau ^{(i)}_A \uparrow \infty$ (resp. $\upsilon ^{(i)}_B \uparrow \infty$) and $A_i \downarrow 0$ (resp. $B_i \downarrow 0$ where $B_i := (B_{ij})_{j \in {\mathcal {M}}_0 \setminus \{i\}}$) interchangeably for every $i \in {\mathcal {M}}$. Its proof is the same as that of Proposition 3.6 of Dayanik et al. (2013).

Remark 3.3

Fix $i \in {\mathcal {M}}$. We have ${\mathbb {P}}_i$-a.s.,

• (i) $\tau _A^{(i)} \rightarrow \infty$ as $A_i \downarrow 0$ and $\tau _A \rightarrow \infty$ as $\Vert A\Vert \downarrow 0$,

• (ii) $\upsilon _B^{(i)} \rightarrow \infty$ as ${\overline{B}}_i \downarrow 0$ and $\upsilon _B \rightarrow \infty$ as $\Vert B\Vert \downarrow 0$.

The posterior probability process $({\widetilde{\Pi }}^{(i)}_n)_{i \in {\mathcal {M}}_0}$ has been shown to converge a.s. in Dayanik and Goulding (2009). Moreover, because the posterior probability of the correct hypothesis should tend to increase in the long run, on the event $\{\mu =i\}$, $i \in {\mathcal {M}}$, it is expected that ${\widetilde{\Pi }}_n^{(i)}$ converges to 1 and that ${\widetilde{\Pi }}_n^{(j)}$ converges to 0 for every $j \in {\mathcal {M}}_0 \setminus \{i\}$ with probability one. This suggests the a.s.-convergence of $\Lambda _n(i,j)$ to infinity given $\mu =i$ for every $j \in {\mathcal {M}}_0 \setminus \{i\}$. For the rest of this section, we further assume that the average increment converges to some strictly positive value.

Assumption 3.2

For every $i \in {\mathcal {M}}$, we assume that

$$\begin{aligned} \Lambda _n(i,j)/n \xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i-a.s.} l(i,j), \end{aligned}$$

for some $l(i,j) \in (0,\infty ]$ for every $j \in {\mathcal {M}}_0 \setminus \{i\}$, and

$$\begin{aligned} \min _{j \in {\mathcal {M}}_0 \setminus \{i\}} l(i,j) < \infty . \end{aligned}$$

This is indeed satisfied in the i.i.d. case (Dayanik et al. 2013). For the case $|{\mathcal {M}}| = 1$, stronger convergence results (for a more general hidden Markov setting) beyond Assumption 3.2 hold as shown by (Fuh and Tartakovsky 2018, Lemma 1). In Sect. 4, we will show that this is also satisfied in certain settings and that the limit can be expressed in terms of the Kullback-Leibler divergence.

Let us fix $i \in {\mathcal {M}}$. We show that, for small values of A and B, the stopping times $\tau _A^{(i)}$ and $\upsilon _B^{(i)}$ in (3.4) and (3.9) are essentially determined by the process $\Lambda (i,j(i))$, where

$$\begin{aligned}&j(i) \in {{\,\mathrm{\arg \min }\,}}_{j \in {\mathcal {M}}_0 \setminus \{i\}} l(i,j) \quad \text {is any index in }{\mathcal {M}}_0 \setminus \{i\} \text { that attains}\\&l(i) := \min _{j \in {\mathcal {M}}_0 \setminus \{i\}} l(i,j) > 0, \end{aligned}$$

and ${\mathbb {P}}_i$-a.s. $\Lambda _n(i,j(i))/n \approx \Phi _n^{(i)}/n \approx \Psi ^{(i)}_n/n \approx l(i)$ for sufficiently large n as the next proposition implies.

Proposition 3.4

For every $i \in {\mathcal {M}}$, we have ${\mathbb {P}}_i$-a.s. (i) $\Phi _n^{(i)}/n \rightarrow l(i)$ and (ii) $\Psi _n^{(i)}/n \rightarrow l(i)$ as $n \uparrow \infty$.

For the proof of Proposition 3.4 above, (ii) follows immediately by Assumption 3.2 and (i) follows from the next lemma after replacing $Y^{(j)}_n$, ${\mathbb {P}}$, and $(\mu _j)_{j \in {\mathcal {M}}_0 \setminus \{i\}}$ in the lemma with $\Lambda _n(i,j)/n$, ${\mathbb {P}}_i$, and $(l(i,j))_{j \in {\mathcal {M}}_0 \setminus \{i\}}$, respectively, for every fixed $i\in {\mathcal {M}}$.

Lemma 3.2

For every $j=1,\dots ,m$, let $Y^{(j)}=(Y_n^{(j)})_{n \ge 1}$ be a sequence of random variables defined on a common probability space $(\Omega , {\mathcal {E}},{\mathbb {P}})$, and suppose that $Y_n^{(j)}$ converges a.s. to some constant $\mu _j \in [-\infty ,\infty ]$ for every $j=1,\dots ,m$. Then $- \frac{1}{n} \log \sum _{j=1}^m e^{-n Y_n^{(j)}} \xrightarrow [n \uparrow \infty ]{a.s.} \min _{1 \le k \le m} \mu _k$.

Lemma 3.2 is a straightforward extension of Lemma 5.2 of Baum and Veeravalli (1994) and hence its proof is omitted.

The following lemma can be derived from Proposition 3.4. The proof is the same as that of Lemma 3.9 of Dayanik et al. (2013).

Lemma 3.3

For every $i \in {\mathcal {M}}$ and any $j(i) \in {{\,\mathrm{\arg \min }\,}}_{j\in {\mathcal {M}}_0\setminus \{i\}} l(i,j)$, we have ${\mathbb {P}}_i$-a.s.

$$\begin{aligned} \text { (i)}&\quad -\frac{\tau _A^{(i)}}{\log A_i} \xrightarrow {A_i \downarrow 0} \frac{1}{l(i)},&\text { (ii)} \quad - \frac{(\tau _A^{(i)}-\theta )_+}{\log A_i} \xrightarrow {A_i \downarrow 0} \frac{1}{l(i)},\\ \text { (iii)}&\quad -\frac{\upsilon _B^{(i)}}{\log B_{ij(i)}} \xrightarrow {{\overline{B}}_i \downarrow 0} \frac{1}{l(i)},&\text { (iv)} \quad -\frac{(\upsilon _B^{(i)}-\theta )_+}{\log B_{ij(i)}} \xrightarrow {{\overline{B}}_i \downarrow 0} \frac{1}{l(i)}. \end{aligned}$$

Remark 3.4

Without loss of generality, we shall assume that $0< B_{ij}<1$ (i.e. $-\infty<\log B_{ij}<0$) for all $i \in {\mathcal {M}}$ and $j\in {\mathcal {M}}_0 \setminus \{i\}$ as we are interested in the limits of certain quantities as $\Vert B\Vert \downarrow 0$. Recall also that the ratio ${\underline{B}}_i/{\overline{B}}_i$ for every $i \in {\mathcal {M}}$ is bounded from below by some strictly positive number. Hence

$$\begin{aligned} 1=\lim _{{\overline{B}}_i \downarrow 0} \; \frac{\log B_{ij}}{\log {\overline{B}}_i} = \lim _{{\overline{B}}_i \downarrow 0} \; \frac{\log {\underline{B}}_i}{\log {\overline{B}}_i} = \lim _{{\overline{B}}_i \downarrow 0} \; \frac{\log B_{ij}}{\log {\underline{B}}_i} \quad \text {for every }i\in {\mathcal {M}}, j\in {\mathcal {M}}_0\setminus \{i\}. \end{aligned}$$

Here, the last equality follows from the first two equalities.

For every $i \in {\mathcal {M}}$, conditionally on $\{Y_0 \in {\mathcal {Y}}_i\}$, the finite-state Markov chain Y always admits a unique distribution $w_i(y)$, $y \in {\mathcal {Y}}_i$, such that

$$\begin{aligned} \frac{1}{n+1} \sum _{m=0}^n 1_{\{y\}} (Y_m) \xrightarrow {n \uparrow \infty } w_i(y), \quad \text { a.s. on } \{ Y_0 \in {\mathcal {Y}}_i\}; \end{aligned}$$

see, e.g., (Tijms 2003). Then

$$\begin{aligned} \frac{1}{n+1} \sum _{m=0}^n c(Y_m) \xrightarrow {n \uparrow \infty } c_i : = \sum _{y \in {\mathcal {Y}}_i} c(y) w_i(y), \quad \text {a.s. on } \{ Y_0 \in {\mathcal {Y}}_i\}. \end{aligned}$$

This and the a.s. finiteness of $\theta$ together with Lemma 3.3 prove the next lemma.

Lemma 3.4

For every $i \in {\mathcal {M}}$ and any $j(i) \in {{\,\mathrm{\arg \min }\,}}_{j\in {\mathcal {M}}_0\setminus \{i\}} l(i,j)$, we have ${\mathbb {P}}_i$-a.s.

$$\begin{aligned} \text { (i)}&\quad -\frac{\sum _{m=0}^{\tau _A^{(i)}} c(Y_m)}{\log A_i} \xrightarrow {A_i \downarrow 0} \frac{c_i}{l(i)},&\text { (ii)} \quad - \frac{\sum _{m=\theta }^{\tau _A^{(i)} \vee \theta } c(Y_m)}{\log A_i} \xrightarrow {A_i \downarrow 0} \frac{c_i}{l(i)},\\ \text {(iii)}&\quad -\frac{\sum _{m=0}^{v_B^{(i)}} c(Y_m)}{\log B_{ij(i)}} \xrightarrow {{\overline{B}}_i \downarrow 0} \frac{c_i}{l(i)},&\text { (iv)} \quad -\frac{\sum _{m=\theta }^{v_B^{(i)} \vee \theta } c(Y_m)}{\log B_{ij(i)}} \xrightarrow {{\overline{B}}_i \downarrow 0} \frac{c_i}{l(i)}. \end{aligned}$$

Because we want to minimize the $m^{th}$ moment of the detection delay time for any $m\ge 1$, we will strengthen the convergence results of Lemma 3.3. We require Condition 3.1 below for some $r \ge m$.

Condition 3.1

(Uniform Integrability) For given $r \ge 1$, we assume that

• (i) $(\tau _A^{(i)}/(-\log A_i))^r_{A_i > 0}$ is ${\mathbb {P}}_i$-uniformly integrable for every $i \in {\mathcal {M}}$,

• (ii) $(\upsilon _B^{(i)}/(-\log B_{ij(i)}))^r_{B_i > 0}$ is ${\mathbb {P}}_i$-uniformly integrable for every $i \in {\mathcal {M}}$.

Because $c(\cdot )$ is bounded, this also implies the following.

Lemma 3.5

For every $i \in {\mathcal {M}}$, we have the followings.

• (i) Under Condition 3.1 (i) for some $r \ge 1$, $\big ( (\sum _{m=0}^{\tau _A^{(i)}} c(Y_m))/(-\log A_i) \big )_{A_i > 0}^{r}$ is ${\mathbb {P}}_i$-uniformly integrable.

• (ii) Under Condition 3.1 (ii) for some $r \ge 1$, $\big ( (\sum _{m=0}^{\upsilon _B^{(i)}} c(Y_m))/(-\log B_{ij(i)}) \big )_{B_i > 0}^{r}$ is ${\mathbb {P}}_i$-uniformly integrable.

Hence, Condition 3.1 for some $r \ge m$ is sufficient for the $L^m$-convergence.

Lemma 3.6

For every $i \in {\mathcal {M}}$ and $m \ge 1$, we have the following.

• (i) If Condition 3.1 (i) holds for some $r \ge m$, then we have

  $$\begin{aligned} {\tau _A^{(i)}} /(-\log A_i) \xrightarrow [A_i \downarrow 0]{\hbox { in}\ L^m({\mathbb {P}}_i)} {l(i)}^{-1} \; \text {and} \; {D_i^{(c,m)}(\tau _A)} /(-\log A_i) \xrightarrow {A_i \downarrow 0} (c_i/l(i))^m. \end{aligned}$$

  (3.17)

• (ii) If Condition 3.1 (ii) holds for some $r \ge m$, then we have

  $$\begin{aligned} {\upsilon _B^{(i)}} /(-\log B_{ij(i)}) \xrightarrow [{\overline{B}}_i \downarrow 0]{\hbox { in}\ L^m({\mathbb {P}}_i)} {l(i)}^{-1} \; \text {and} \; {D_i^{(c,m)}(\upsilon _B)} /(-\log B_{ij(i)}) \xrightarrow {{\overline{B}}_i \downarrow 0} (c_i/l(i))^m. \end{aligned}$$

  (3.18)

Alternatively to Condition 3.1, it can be shown that the r-quick convergence is a sufficient condition as in (Baron and Tartakovsky 2006; Dragalin et al. 2000; Lai 1981; Tartakovsky and Veeravalli 2004b). However, here we obtain a weaker sufficient condition known as the r-complete convergence recently verified to act as a sufficient condition for a related problem in Tartakovsky (2017).

Lemma 3.7

Fix $i \in {\mathcal {M}}$. (i) If

$$\begin{aligned} \sum _{n = 1}^\infty n^{m-1} {\mathbb {P}}_i \Big \{ {\Phi _n(i)} /n< l(i) - \varepsilon \Big \} < \infty , \end{aligned}$$

for all $\varepsilon > 0$, we have ${\tau _A^{(i)}} /(-\log A_i) \xrightarrow [A_i \downarrow 0]{\hbox { in}\ L^m({\mathbb {P}}_i)} {l(i)}^{-1}$. (ii) If

$$\begin{aligned} \sum _{n = 1}^\infty n^{m-1} {\mathbb {P}}_i \Big \{ {\Psi _n(i)} /n< l(i) - \varepsilon \Big \} < \infty , \end{aligned}$$

for all $\varepsilon > 0$, we have ${\upsilon _B^{(i)}} /(-\log {\underline{B}}_i) \xrightarrow [{\overline{B}}_i \downarrow 0]{\hbox { in}\ L^m({\mathbb {P}}_i)} {l(i)}^{-1}$.

Proof

We only prove (ii). The proof for (i) is similar and slightly simpler.

First, Fatou’s lemma and Lemma 3.3 give the lower bound: $l(i)^{-m} \le \liminf _{{\underline{B}}_i \downarrow 0} {\mathbb {E}}_i [(\upsilon _B^{(i)})^m] / (-\log {\underline{B}}_i)^m$, and hence it suffices to obtain the upper bound.

By following (A.5) of Tartakovsky (2017), we have a bound: for $0< \varepsilon < l(i)$,

$$\begin{aligned} {\mathbb {E}}_i [(\upsilon _B^{(i)})^m] \le N_B(\varepsilon )^m + m 2^{m-1} \sum _{n = N_B(\varepsilon )}^\infty n^{m-1} {\mathbb {P}}_i \{\upsilon _B^{(i)} > n \} \end{aligned}$$

where

$$\begin{aligned} N_B(\varepsilon ) := 1 + \left\lfloor \frac{- \log {\underline{B}}_i}{l(i) - \varepsilon } \right\rfloor . \end{aligned}$$

(3.19)

For all $n \ge N_B(\varepsilon )$ (so that $(l(i) - \varepsilon ) n > - \log {\underline{B}}_i$),

$$\begin{aligned} {\mathbb {P}}_i \{ \upsilon _B^{(i)} > n \} \le {\mathbb {P}}_i \left\{ \Psi _{n} (i) \le - \log {\underline{B}}_{i} \right\} \le {\mathbb {P}}_i \big \{ {\Psi _n(i)} / n < l(i) - \varepsilon \big \}. \end{aligned}$$

Therefore, by (3.19) and the assumption,

$$\begin{aligned} \limsup _{{\overline{B}}_i \downarrow 0}\frac{{\mathbb {E}}_i [(\upsilon _B^{(i)})^m] }{(-\log {\underline{B}}_i)^m}&\le \limsup _{{\overline{B}}_i \downarrow 0} \frac{N_B(\varepsilon )^m + m 2^{m-1} \sum _{n = 1}^\infty n^{m-1} {\mathbb {P}}_i \Big \{ \frac{\Psi _n(i)}{n} < l(i) - \varepsilon \Big \}}{(-\log {\underline{B}}_i)^m} \\&= \Big (\frac{1}{l(i) - \varepsilon } \Big )^m. \end{aligned}$$

Because $\varepsilon > 0$ is arbitrary, we have the result. $\square$

Corollary 3.1

Fix $i \in {\mathcal {M}}$. Suppose ($C_1$) for all $j \in {{\,\mathrm{\arg \min }\,}}_{k \in {\mathcal {M}}_0 \setminus \{i\}} l(i,k)$ (such that $l(i,j) = l(i)$),

$$\begin{aligned} \sum _{n = 1}^\infty n^{m-1} {\mathbb {P}}_i \big \{ {\Lambda _n(i,j)} / n< l(i) - \varepsilon \big \} < \infty , \end{aligned}$$

for all $\varepsilon > 0$, and ($C_2$) for all $j \in {\mathcal {M}}_0 \backslash (\{i\} \cup {{\,\mathrm{\arg \min }\,}}_{k \in {\mathcal {M}}_0 \setminus \{i\}} l(i,k))$ (such that $l(i,j) > l(i)$),

$$\begin{aligned} \sum _{n = 1}^\infty n^{m-1} {\mathbb {P}}_i \big \{ \Lambda _n(i,j) / n< l(i) \big \} < \infty . \end{aligned}$$

Then, we have (i) ${\tau _A^{(i)}} /(-\log A_i) \xrightarrow [A_i \downarrow 0]{\hbox { in}\ L^m({\mathbb {P}}_i)} {l(i)}^{-1}$ and (ii) ${\upsilon _B^{(i)}} /(-\log {\underline{B}}_i) \xrightarrow [{\overline{B}}_i \downarrow 0]{{\text {in}}L^m({\mathbb {P}}_i)} {l(i)}^{-1}$.

Proof

The claim (ii) holds by Lemma 3.7 because, for $0< \varepsilon < \min _{j \in {\mathcal {M}}_0 \backslash \{i\}: l(i,j) > l(i)} (l(i,j) - l(i))$ and $n \ge 1$,

$$\begin{aligned} {\mathbb {P}}_i \big \{ {\Psi _n(i)} / n< l(i) - \varepsilon \big \}&\le \sum _{{j \in {\mathcal {M}}_0 \backslash \{i \}}} {\mathbb {P}}_i \big \{ {\Lambda _n(i,j)} / n< l(i) - \varepsilon \big \} \\&\le \sum _{j \in {\mathcal {M}}_0 \backslash \{i \}: l(i,j) = l(i)} {\mathbb {P}}_i \big \{ {\Lambda _n(i,j)} / n< l(i) - \varepsilon \big \}\\&\quad + \sum _{j \in {\mathcal {M}}_0 \backslash \{i \}: l(i,j) > l(i)} {\mathbb {P}}_i \big \{ \Lambda _n(i,j) /n < l(i) \big \}. \end{aligned}$$

On the other hand, as in the proof of Remark 3.16 of Dayanik et al. (2013), we have, for all $\varepsilon > 0$ and $n > 2 \log M / \varepsilon$,

$$\begin{aligned} \{ \Phi _n^{(i)} / n \ge l(i) - \varepsilon \} \supset \{\Lambda _n(i,j) / n \ge l(i,j) - \varepsilon /2, \quad \forall j \in {\mathcal {M}}_0 \backslash \{i\} \}, \end{aligned}$$

and hence, for sufficiently small $\varepsilon$,

$$\begin{aligned} {\mathbb {P}}_i \left\{ \Phi _n^{(i)} / n< l(i) - \varepsilon \right\}&\le {\mathbb {P}}_i \left\{ \Lambda _n^{(i,j)} / n< l(i,j) - \varepsilon / 2 \; \text {for some } j \in {\mathcal {M}}_0 \backslash \{i\} \right\} \\&\le \sum _{ j \in {\mathcal {M}}_0 \backslash \{i\}}{\mathbb {P}}_i \left\{ \Lambda _n^{(i,j)} / n< l(i,j) - {\varepsilon } / 2 \right\} \\&\le \sum _{j \in {\mathcal {M}}_0 \backslash \{i \}: l(i,j) = l(i)} {\mathbb {P}}_i \Big \{ {\Lambda _n(i,j)} / n< l(i) - \varepsilon / 2 \Big \} \\&\qquad \quad + \sum _{j \in {\mathcal {M}}_0 \backslash \{i \}: l(i,j) > l(i)} {\mathbb {P}}_i \Big \{ {\Lambda _n(i,j)} / n < l(i) \Big \}. \end{aligned}$$

Hence, (i) holds as well under $C_1$ and $C_2$. $\square$

Proposition 3.5

Fix $i \in {\mathcal {M}}$. Suppose conditions $C_1$ and $C_2$ of Corollary 3.1 hold. Then, (3.17) and (3.18) hold.

Proof

Fix $i \in {\mathcal {M}}$. (i) Because ${\mathbb {E}}_i (\tau _A ^{(i)})^m \sim (-\log A_i/l(i))^m$, $(\frac{\tau _A^{(i)}}{-\log A_i})_{A_i > 0}^m$ is ${\mathbb {P}}_i$-uniformly integrable. In addition, because $\frac{\sum _{t = 1}^{\tau _A^{(i)}} c(Y_t) }{\tau _A^{(i)}}$ is bounded, $\Big ( \frac{ \sum _{t = 1}^{\tau _A^{(i)}} c(Y_t) }{\tau _A^{(i)}} \frac{\tau _A^{(i)}}{-\log A_i} \Big )_{A_i > 0}^m$ is also ${\mathbb {P}}_i$-uniformly integrable and converge to $(c_i/l(i))^m$, and hence we have

$$\begin{aligned} \lim _{A_i \downarrow 0}\frac{{\mathbb {E}}_i [(\sum _{t= 1}^{\tau _A^{(i)}} c(Y_t))^m]}{{\mathbb {E}}_i [(\tau _A^{(i)})^m]} = {\mathbb {E}}_i \Big [ \lim _{A_i\downarrow 0} \Big ( \frac{ \sum _{t = 1}^{\tau _A^{(i)}} c(Y_t) }{\tau _A^{(i)}} \frac{\tau _A^{(i)}}{-\log A_i} \Big )^m \Big ] \lim _{A_i \downarrow 0} \frac{(-\log A_i)^m}{{\mathbb {E}}_i [(\tau _A^{(i)})^m]} = c_i^m. \end{aligned}$$

This and Corollary 3.1 show (3.18). The proof of (3.17) is similar. $\square$

3.2 Asymptotic optimality

We now prove the asymptotic optimality of $(\tau _A,d_A)$ and $(\upsilon _B,d_B)$ for Problems 2.1 and 2.2 under Conditions 3.1 (i) and (ii), respectively.

We first derive a lower bound on the expected detection delay under the optimal strategy (see Lemma  3.8). The lower bound on the expected detection delay under the optimal strategy can be obtained similarly to CPD and SMHT (see Baron and Tartakovsky 2006; Baum and Veeravalli 1994; Dragalin et al. 1999, 2000; Lai 2000; Tartakovsky and Veeravalli 2004a). This lower bound and Lemma 3.6/Proposition 3.5 can be combined to obtain asymptotic optimality for both Problems 2.1 and 2.2 .

Lemma 3.8

For every $i \in {\mathcal {M}}$ and $j(i) \in {{\,\mathrm{\arg \min }\,}}_{j \in {\mathcal {M}}_0 \setminus \{i\}} l(i,j)$, we have

$$\begin{aligned}&\liminf _{{\overline{R}}_i \downarrow 0} \inf _{(\tau ,d) \in {\overline{\Delta }} ({\overline{R}})} \frac{D_i^{(c,m)}(\tau )}{\left( { \frac{c_i}{l(i)} \left| \log \left( \frac{1}{\nu _i}{\sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| } \right) ^m} \ge 1. \end{aligned}$$

We now study how to set A in terms of c in order to achieve asymptotic optimality in Problem 2.1. We see from Proposition 3.2 and Lemma 3.6 that the TDLs decrease faster than the detection delay cost and are negligible when A and B are small. Indeed, we have, with ${\tilde{c}}_i := c_i^m$, in view of the definition of the Bayes risk in (2.5), by Proposition 3.2 and Lemma 3.6, for every $i \in {\mathcal {M}}$,

$$\begin{aligned} u^{(c,a,m)}_{i} (\tau _{A},d_{A}) \sim {\tilde{c}}_i \left( \frac{-\log A_i}{ l(i)} \right) ^m + A_i \sim {\tilde{c}}_i \left( \frac{-\log A_i}{ l(i)} \right) ^m, \quad \text {as } A_i \downarrow 0. \end{aligned}$$

(3.20)

Following the same idea of Baron and Tartakovsky (2006) for the change detection problem, we choose the value of $A_i$ as the minimizer of the mapping

$$\begin{aligned} x \mapsto g^{( {\tilde{c}}_i )}_i(x) := {\tilde{c}}_i \left( \frac{-\log x}{ l(i)} \right) ^m + x \end{aligned}$$

(3.21)

over $x \in (0,\infty )$. In other words,

$$\begin{aligned} A_i (c_i) \in {{\,\mathrm{\arg \min }\,}}_{x \in (0,\infty )}g_i^{( {\tilde{c}}_i )}(x), \quad {\tilde{c}}_i> 0. \end{aligned}$$

In particular, when $m=1$, $A_i(c_i) = c_i / l(i)$.

The proof of the following is similar to that of Proposition 3.18 of Dayanik et al. (2013) and is hence omitted.

Proposition 3.6

(Asymptotic optimality of $(\tau _A,d_A)$ in Problem 2.1) Fix $m \ge 1$ and a set of strictly positive constants a. Under Conditions 3.1 (i) or $C_1$ and $C_2$ of Corollary 3.1 for the given m, the strategy $(\tau _{A(c)},d_{A(c)})$ is asymptotically optimal as $\Vert c\Vert \downarrow 0$; that is, (3.14) holds for every $i \in {\mathcal {M}}$.

We now show that the strategy $(\upsilon _B,d_B)$ is asymptotically optimal for Problem 2.2. It follows from Proposition 3.3 that, if we set

$$\begin{aligned} B_{ij} ({\overline{R}}) := \frac{\min _{y \in {\mathcal {Y}}_j}{\overline{R}}_{yi}}{\nu _i}, \; \text {for every } i \in {\mathcal {M}}, j \in {\mathcal {M}}_0 \setminus \{i\}, \end{aligned}$$

then we have $(\upsilon _{B({\overline{R}})}, d_{B({\overline{R}})}) \in \Delta ({\overline{R}})$ for every fixed positive constants ${\overline{R}} = (R_{yi})_{i \in {\mathcal {M}}, \, y \in {\mathcal {Y}}\backslash {\mathcal {Y}}_i }$. Assuming the conditions in Lemma 3.6 (ii) or Proposition 3.5 hold, because $\upsilon _{B({\overline{R}})} \le \upsilon ^{(i)}_{B({\overline{R}})}$ and $\min _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi} \downarrow 0$ is equivalent to $B_{ij(i)} ({\overline{R}}) \downarrow 0$, we have

$$\begin{aligned} \limsup _{{\overline{R}}_i \downarrow 0} \frac{D_i^{(c,m)}(\upsilon _{B({\overline{R}})})}{\left( {\frac{c_i}{l(i)} |\log \left( \min _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi} / \nu _i \right) |} \right) ^m} = \limsup _{{\overline{R}}_i \downarrow 0} \frac{D_i^{(c,m)}(\upsilon _{B({\overline{R}})})}{\left( { \frac{c_i}{l(i)}|\log B_{ij(i)} ({\overline{R}})|}\right) ^m} \le 1. \end{aligned}$$

(3.22)

This together with Lemma 3.8 shows asymptotic optimality.

Proposition 3.7

(Asymptotic optimality of $(\upsilon _B, d_B)$ in Problem 2.2) Fix $m \ge 1$. Under Condition 3.1 (ii) or $C_1$ and $C_2$ of Corollary 3.1 for the given m, the strategy $(\upsilon _{B({\overline{R}})},d_{B({\overline{R}})})$ is asymptotically optimal as $\Vert {\overline{R}}\Vert \downarrow 0$; that is, (3.15) holds for every $i \in {\mathcal {M}}$.

4 Convergence results of LLR processes

In this section, we consider two particular cases where Assumption 3.2 holds with l(i, j) expressed in terms of the Kullback-Leibler divergence. We assume that $X_\theta , X_{\theta +1},\ldots$ are identically distributed on $\{\mu = i\}$ given $\theta$, for every $i \in {\mathcal {M}}$. For the purpose of determining the limit l(i, j), because each class is closed, we can assume without loss of generality that ${\mathcal {Y}}_{i}$ consists of a single state, say,

$$\begin{aligned} {\mathcal {Y}}_{i} = \{i\} \text { with } f_i(\cdot ) \equiv f(i, \cdot ), \end{aligned}$$

(4.1)

for every $i \in {\mathcal {M}}$.

The conditional probability of the event that Y is absorbed by ${\mathcal {Y}}_i = \{i\}$ at time $t \ge 0$, given $\{ \mu = i \}$, is

$$\begin{aligned} \rho _t^{(i)} := {\mathbb {P}}\{ \theta = t | \mu = i\} = \left\{ \begin{array}{ll} \frac{\eta (i)}{\nu _i}, &{} t=0, \\ \frac{1}{\nu _i}\sum _{(y_0,\ldots , y_{t-1}) \in {\mathcal {Y}}_{0}^t} \eta (y_0) \prod _{k=1}^{t-1} P(y_{k-1}, y_k) P(y_{t-1},i), &{} t\ge 1. \end{array} \right. \end{aligned}$$

(4.2)

We assume the following throughout this section.

Assumption 4.1

For every $i \in {\mathcal {M}}$, we assume that

$$\begin{aligned} \varrho ^{(i)} := - \lim _{t \rightarrow \infty }\frac{\log \rho _t^{(i)}}{t} = - \lim _{t \rightarrow \infty }\frac{\log (1-\sum _{k=0}^t \rho _k^{(i)})}{t} \end{aligned}$$

(4.3)

exists and $\varrho ^{(i)} \in (0, \infty ]$.

Here, $\varrho ^{(i)} = \infty$ holds for example when ${\mathbb {P}}_i \left\{ \theta < M \right\} = 1$ for some $M <\infty$. On the other hand, we must have $\varrho ^{(i)} > 0$. To see this, because $\theta$ is the exit time from a set of transient states, using the facts on absorption probabilities (see e.g. Çınlar 2013, Chapters 5 and 6), it can be shown that ${\mathbb {P}}\{ \theta > t\} = o(z^t)$ as $t \rightarrow \infty$ for some $z < 1$. Now, fix $i \in {\mathcal {M}}$. Because ${\mathbb {P}}\{ \theta> t\} = \sum _{j \in {\mathcal {M}}} \nu _j {\mathbb {P}}\{ \theta> t | \mu = j \} \ge \nu _i {\mathbb {P}}\{ \theta > t | \mu = i \}$, we have ${\mathbb {P}}\{ \theta> t | \mu = i \} \le {\mathbb {P}}\{ \theta > t\} / \nu _i$. Hence,

$$\begin{aligned} \liminf _{t \rightarrow \infty } \Big (- \frac{\log {\mathbb {P}}\{ \theta> t | \mu = i \}}{t} \Big ) \ge \liminf _{t \rightarrow \infty } \Big ( - \frac{\log {\mathbb {P}}\{ \theta> t\} - \log \nu _i }{t} \Big ) \ge - \log z > 0. \end{aligned}$$

In a special case where the change time is geometric with parameter $p > 0$ as in Dayanik et al. (2013), this is satisfied with $\varrho ^{(i)} = |\log (1-p)|$. Assumption 4.1 also holds, for example, when $\theta$ is a mixture or a sum of geometric random variables; see the examples given in Sect. 5.1.

4.1 Example 1

Suppose that the distribution of X given Y is identical in the transient set ${\mathcal {Y}}_{0}$; namely,

$$\begin{aligned} f(y,\cdot ) = f(z, \cdot ) =: f_0(\cdot ), \quad y,z \in {\mathcal {Y}}_{0}. \end{aligned}$$

This models, for example, the case the change point $\theta$ is phase-type. See Example 1 of Dayanik and Goulding (2009).

We denote the Kullback-Leibler divergence of $f_i(\cdot )$ from $f_j(\cdot )$ by

$$\begin{aligned} q(i,j) := \int _E \left( \log \frac{f_i(x)}{f_j(x)}\right) f_i(x) \mathrm {m}({\mathrm{d}}x), \quad i\in {\mathcal {M}},\;j \in {\mathcal {M}}_0 \setminus \{i\}, \end{aligned}$$

(4.4)

which always exists and is nonnegative.

We assume $f_i(\cdot )$ and $f_j(\cdot )$ as in (4.1) for any $i \ne j$ are distinguishable; namely, we assume the following.

Assumption 4.2

We assume $\int _{\{x\in E: f_i(x) \not = f_j(x)\}} f_i(x) \mathrm {m} ({\mathrm{d}}x)> 0$ for every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$. This ensures that

$$\begin{aligned} q(i,j) > 0, \quad i\in {\mathcal {M}},\; j \in {\mathcal {M}}_0 \setminus \{i\}. \end{aligned}$$

(4.5)

To ensure that $\int _E \big ( \log \frac{f_0(x)}{f_j(x)} \big ) f_i(x) \mathrm {m}({\mathrm{d}}x)$ exists for every $i\in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$, we further assume the following.

Assumption 4.3

For every $i \in {\mathcal {M}}$, we assume that $q(i,0) < \infty$.

Indeed, since $\int _E (\log \frac{f_i(x)}{f_j(x)})_- f_i(x) \mathrm {m} ({\mathrm{d}}x)\le 1$ for every $i\in {\mathcal {M}}$ and $j\in {\mathcal {M}}_0\setminus \{i\}$,

$$\begin{aligned}&\int _E \left( \log \frac{f_0(x)}{f_j(x)} \right) f_i(x) \mathrm {m} ({\mathrm{d}}x)= \int _E \left( \log \frac{f_i(x)}{f_j(x)} \right) f_i(x) \mathrm {m} ({\mathrm{d}}x) \nonumber \\&\quad - \int _E \left( \log \frac{f_i(x)}{f_0(x)} \right) f_i(x) \mathrm {m} ({\mathrm{d}}x) = q(i,j)-q(i,0), \end{aligned}$$

(4.6)

exists by Assumption 4.3. Here, we allow (4.6) to be $+\infty$ but we assume the following.

Assumption 4.4

For every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}\setminus \{i\}$, we assume $\min \{ \varrho ^{(j)}, q(i,j) \} < \infty$.

We shall prove the following under Assumptions 4.1-4.4.

Proposition 4.1

(Limits of LLR processes in Example 1) For every $i \in {\mathcal {M}}$, Assumption 3.2 holds with the limits

$$\begin{aligned} l(i,j)&:= \left\{ \begin{aligned}&q(i,0)+ \min _{k \in {\mathcal {M}}} \varrho ^{(k)},&j=0 \\&\min \big \{q(i,j),q(i,0) + \varrho ^{(j)} \big \},&j \in {\mathcal {M}}\setminus \{i\} \end{aligned} \right\} \nonumber \\&\quad \equiv \left\{ \begin{aligned}&q(i,0)+ \min _{k \in {\mathcal {M}}} \varrho ^{(k)},&j=0 \\&q(i,j),&j \in \Gamma _i \\&q(i,0) + \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \end{aligned}$$

(4.7)

where $\Gamma _i := \{ j \in {\mathcal {M}}\setminus \{i\}: q(i,j) < q(i,0) + \varrho ^{(j)} \}$.

Remark 4.1

• (1) Assumptions  4.3 and 4.4 ensure that

  $$\begin{aligned} q(i,j)&< \infty , \quad j \in \Gamma _i, \\ q(i,0) + \varrho ^{(j)}&< \infty , \quad j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}). \end{aligned}$$

• (2) Assumption 4.2 guarantees that $l(i,j) > 0$ for every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$. In particular, (1) ensures $0< l(i,j) < \infty$ for any $j \in {\mathcal {M}}\setminus \{i\}$. Hence, $0< l(i) < \infty$.

• (3) By (4.7), we can choose $j(i) \in \{0\} \cup \Gamma _i$. If $j(i) = 0$, we must have $\min _{k \in {\mathcal {M}}} \varrho ^{(k)} < \infty$.

In order to show Proposition 4.1, we first simplify the LLR process as in (3.3). Define, for each $j \in {\mathcal {M}}$,

$$\begin{aligned} \begin{aligned} L_n^{(j)}&:= \log \left( \rho _0^{(j)} + \sum _{k=1}^n \rho _k^{(j)} \prod _{l=1}^{k-1} \frac{f_0(X_l)}{f_j(X_l)} \right) , \\ K_n^{(j)}&:= \log \left( \frac{\rho _0^{(j)}}{\rho _n^{(j)}} \prod _{k=1}^n \frac{f_j(X_k)}{f_0(X_k)} + \sum _{k=1}^n \frac{\rho _k^{(j)}}{\rho _n^{(j)}} \prod _{m=k}^n \frac{f_j (X_m)}{f_0(X_m)} \right) \\&= -\log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{f_j(X_k)}{f_0(X_k)} + L_n^{(j)}. \end{aligned} \end{aligned}$$

(4.8)

Lemma 4.1

Fix $i \in {\mathcal {M}}$. For any $n \ge 1$,

$$\begin{aligned} \Lambda _n(i,0)&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_0(X_k)} + L_n^{(i)} - \log \Big [ \sum _{j \in {\mathcal {M}}} \nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \Big ] + \log \nu _i \end{aligned}$$

and for $j \in {\mathcal {M}}\backslash \{i\}$

$$\begin{aligned} \Lambda _n(i,j)&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j(X_k)} + L_n^{(i)} - L_n^{(j)} + \log \nu _i - \log \nu _j \\&= -\log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_0(X_k)} + L_n^{(i)} - K_n^{(j)} +\log \nu _i - \log \nu _j . \end{aligned}$$

By this lemma, each LLR process admits a decomposition

$$\begin{aligned} \Lambda _n(i,j)= \sum _{l=1}^n h_{ij}(X_l) + \epsilon _n(i,j), \quad j\in {\mathcal {M}}_0\setminus \{i\}, \end{aligned}$$

where

$$\begin{aligned} h_{ij}(x)&:= \left\{ \begin{aligned}&\log \frac{f_i(x)}{f_0(x)} + \min _{k \in {\mathcal {M}}} \varrho ^{(k)},&j = 0\\&\log \frac{f_i(x)}{f_j(x)},&j \in \Gamma _i \\&\log \frac{f_i(x)}{f_0(x)} + \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \quad x \in E, \nonumber \\ \epsilon _n(i,j)&:= \left\{ \begin{aligned}&L^{(i)}_n - \log \Big [ \sum _{j \in {\mathcal {M}}} \nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \Big ] - n \min _{k \in {\mathcal {M}}} \varrho ^{(k)}+ \log \nu _i,&j=0 \\&L_n^{(i)} - L_n^{(j)}+\log \nu _i - \log \nu _j,&j \in \Gamma _i \\&L_n^{(i)} - K_n^{(j)}+ \log \nu _i - \log \nu _j - \log \rho ^{(j)}_n - n \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \nonumber \\&\quad n\ge 1. \end{aligned}$$

(4.9)

Here notice that $\varrho ^{(j)} < \infty$ for $j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$ by Remark 4.1(1).

We explore the convergence for ${(\sum _{l=1}^n h_{ij}(X_l))}/n$ and $\epsilon _n(i,j)/n$ separately. For $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$, because $\theta$ is an a.s. finite random variable (so that $n^{-1}\sum _{l=1}^{n \wedge (\theta -1)} h_{ij} (X_l) \xrightarrow {n \uparrow \infty } 0$), a direct application of the strong law of large number (SLLN) leads to

$$\begin{aligned} \frac{1}{n} {\sum _{l=1}^n h_{ij}(X_l)} \xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i{\text {-a.s.}}} l(i,j). \end{aligned}$$

(4.10)

We now show that $\epsilon _n(i,j) /n$ in (4.9) converges almost surely to zero.

Lemma 4.2

For every $i \in {\mathcal {M}}$, we have the followings under ${\mathbb {P}}_i$.

• (i) $L_n^{(i)}/n \xrightarrow {n \uparrow \infty } 0$ a.s.

• (ii) $L_n^{(j)}/n \xrightarrow {n \uparrow \infty } \left[ q(i,j)-q(i,0)-\varrho ^{(j)} \right] _+$ a.s. for every $j \in {\mathcal {M}}\setminus \{i\}$.

• (iii) $K_n^{(j)}/n \xrightarrow {n \uparrow \infty } \left[ q(i,j)-q(i,0)-\varrho ^{(j)} \right] _-$ a.s. for every $j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$.

• (iv) $L_n^{(i)}$ converges a.s. as $n \uparrow \infty$ to an a.s. finite random variable $L_\infty ^{(i)}$.

• (v) $L_n^{(j)}$ converges a.s. as $n \uparrow \infty$ to an a.s. finite random variable $L_\infty ^{(j)}$ for every $j \in \Gamma _i$.

• (vi) For every $j\in {\mathcal {M}}$, $(|L^{(j)}_n/n|^r)_{n\ge 1}$ is uniformly integrable for every $r\ge 1$, if

  $$\begin{aligned} \int _{E}\frac{f_0(x)}{f_j(x)} f_0(x) \mathrm {m} ({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _{E}\frac{f_0(x)}{f_j(x)} f_i(x) \mathrm {m} ({\mathrm{d}}x) <\infty . \end{aligned}$$

  (4.11)

• (vii) For every $j\in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$, $(|K^{(j)}_n/n|^q)_{n\ge 1}$ is uniformly integrable for every $0\le q \le r$, if (vi) holds, and

  $$\begin{aligned} \int _{E}\left| \frac{f_j(x)}{f_0(x)}\right| ^r f_0(x) \mathrm {m} ({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _{E}\left| \frac{f_j(x)}{f_0(x)}\right| ^r f_i(x) \mathrm {m} ({\mathrm{d}}x) <\infty , \quad \text {for some } r \ge 1. \end{aligned}$$

  (4.12)

By the characterization of $\epsilon _n(i,j)$ in (4.9) and Lemma 4.2 (i)-(iii),

$$\begin{aligned} {\epsilon _n(i,j)} /n \xrightarrow {{\mathbb {P}}_i-a.s.} 0, \quad i \in {\mathcal {M}}, j\in {\mathcal {M}}\setminus \{i\}. \end{aligned}$$

This also holds when $j = 0$ because

$$\begin{aligned} - \frac{1}{n} \log \Big [ \sum _{j \in {\mathcal {M}}} \nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)}\big ) \Big ] \xrightarrow {n \uparrow \infty } \min _{j \in {\mathcal {M}}} \varrho ^{(j)}. \end{aligned}$$

(4.13)

Indeed, the left-hand side of (4.13) equals

$$\begin{aligned} - \frac{1}{n} \log \big [ \sum _{j \in {\mathcal {M}}} \exp \big ( \log \nu _j + \log \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \big ) \big ] = - \frac{1}{n} \log \big ( \sum _{j \in {\mathcal {M}}}e^{-n A_j(n)} \big ), \end{aligned}$$

where $A_j(n) := - \frac{1}{n} \big ( \log \nu _j + \log \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \big )$. Because $A_j(n) \rightarrow \varrho ^{(j)}$ by Assumption 4.1 and by Lemma 3.2, we have (4.13). This together with (4.10) shows Proposition 4.1.

The a.s. convergence can be extended to the $L^r ({\mathbb {P}}_i)$-convergence for $r \ge 1$ as well, under additional integrability conditions. Firstly, as in Lemma 4.3 of Dayanik et al. (2013), for every $i \in {\mathcal {M}}$, $j \in {\mathcal {M}}_0 \setminus \{i\}$ and $r \ge 1$, we have $n^{-1} {\sum _{l=1}^n h_{ij}(X_l)} \xrightarrow [n \uparrow \infty ]{L^r({\mathbb {P}}_i)} l(i,j)$, if

$$\begin{aligned} \int _E \left| h_{ij}(x) \right| ^r f_0(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| h_{ij}(x) \right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x)<\infty . \end{aligned}$$

(4.14)

Here, (4.14) holds if the following condition holds.

Condition 4.1

Given $i \in {\mathcal {M}}$, $j\in {\mathcal {M}}_0\setminus \{i\}$, and $r \ge 1$, suppose that

$$\begin{aligned} \begin{aligned}&\int _E \left| \log \frac{f_i(x)}{f_j(x)}\right| ^r f_0(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| \log \frac{f_i(x)}{f_j(x)}\right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x)<\infty&\text {if}\quad j\in \Gamma _i,\\&\int _E \left| \log \frac{f_i(x)}{f_0(x)}\right| ^r f_0(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| \log \frac{f_i(x)}{f_0(x)}\right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x) <\infty&\text {if} \quad j \in {\mathcal {M}}_0 \backslash \Gamma _i. \end{aligned} \end{aligned}$$

In addition, when $j = 0$, we assume $\min _{j \in {\mathcal {M}}}\varrho ^{(j)} < \infty$.

On the other hand, by Lemma 4.2, $\epsilon _n(i,j)/n \rightarrow 0$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ under the following condition (Condition 4.2). Notice in Lemma 4.2 (vi) when $j = i$ that in order for $L_n^{(i)}/n$ to converge in $L^r({\mathbb {P}}_i)$ to zero, it is sufficient to have

$$\begin{aligned} \int _E \frac{f_0 (x)}{f_i(x)} f_0(x) \mathrm {m} ({\mathrm{d}}x) < \infty , \end{aligned}$$

(4.15)

because $\int _E \frac{f_0 (x)}{f_i(x)} f_i(x) \mathrm {m} ({\mathrm{d}}x) = \int _E f_0 (x) \mathrm {m} ({\mathrm{d}}x)= 1 < \infty$.

Condition 4.2

Given $i \in {\mathcal {M}}$, $j\in {\mathcal {M}}\setminus \{i\}$ and $r \ge 1$, we suppose that (4.11) and (4.15) hold, and, if $j \in {\mathcal {M}}\setminus \Gamma _i$, (4.12) holds for the given r.

In summary, we have the following $L^r$-convergence results.

Proposition 4.2

For every $i \in {\mathcal {M}}$ and $j\in {\mathcal {M}}_0\setminus \{i\}$, we have $\Lambda _n(i,j)/n \rightarrow l(i,j)$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ for some $r \ge 1$ if Conditions 4.1 and 4.2 hold for the given r.

4.2 Example 2

As a variant of Example 1, we consider the case X is not necessarily identically distributed when Y is in ${\mathcal {Y}}_0$. Suppose ${\mathcal {Y}}_0 = {\mathcal {Y}}^{(1)}_{0} \sqcup \cdots \sqcup {\mathcal {Y}}^{(M)}_{0}$ and ${\mathcal {Y}}_{0}^{(i)}$ is absorbed with probability one by ${\mathcal {Y}}_i = \{ i\}$ for each $i \in {\mathcal {M}}$. This implies that

$$\begin{aligned} {\mathbb {P}}\big \{ \mu = i | Y_0 \in {\mathcal {Y}}_0^{(i)}\big \}=1, \quad i \in {\mathcal {M}}. \end{aligned}$$

Also let

$$\begin{aligned} f(y,\cdot ) \equiv f(z, \cdot ) =: f^{(0)}_i(\cdot ), \quad y,z \in {\mathcal {Y}}_{0}^{(i)}, i \in {\mathcal {M}}. \end{aligned}$$

This can model the case when the distribution of X and $\theta$ depends on $\mu$. See Sect.  5.1 for an example.

Because, given $\mu = i$, $Y_0, \ldots , Y_{\theta -1} \in {\mathcal {Y}}_0^{(i)}$ and $Y_\theta = i$, the conditional probability of $\theta = t$ given $\{ \mu = i\}$ as in (4.2) can be written

$$\begin{aligned} \rho _t^{(i)} = \left\{ \begin{array}{ll} \frac{\eta (i)}{\nu _i}, &{} t=0, \\ \frac{1}{\nu _i} \sum _{y_0,\ldots , y_{t-1} \in {\mathcal {Y}}_{0}^{(i)}} \eta (y_0) \prod _{k=1}^{t-1} P(y_{k-1}, y_k) P(y_{t-1},i), &{} t\ge 1. \end{array} \right. \end{aligned}$$

Assumption 4.5

For every $i \in {\mathcal {M}}$, we assume $f_i(\cdot )$ is distinguishable from $f_j(\cdot )$ for $j \in {\mathcal {M}}\setminus \{i\}$ and from $f^{(0)}_j(\cdot )$ for every $i \in {\mathcal {M}}$: $\int _{\{x\in E: f_i(x) \not = f_j(x)\}} f_i(x) \mathrm {m} ({\mathrm{d}}x)> 0$ and $\int _{\{x\in E: f_i(x) \not = f^{(0)}_j(x)\}} f_i(x) \mathrm {m} ({\mathrm{d}}x)> 0$. This ensures that $q(i,j) > 0$ and $q^{(0)}(i, j) > 0$ where we use (4.4) and define

$$\begin{aligned} q^{(0)}(i,j) := \int _E \Big ( \log \frac{f_i(x)}{f_j^{(0)}(x)} \Big ) f_i(x) \mathrm {m}({\mathrm{d}}x), \quad i, j \in {\mathcal {M}}. \end{aligned}$$

We assume the following to ensure that $\int _E \big ( \log \frac{f^{(0)}_j(x)}{f_j(x)} \big ) f_i(x) \mathrm {m}({\mathrm{d}}x)$ exists for every $i, j \in {\mathcal {M}}$.

Assumption 4.6

For every $i, j\in {\mathcal {M}}$, we assume that $q^{(0)}(i,j) < \infty$.

We shall show the following under Assumptions 4.1, 4.4, 4.5, and 4.6 .

Proposition 4.3

(Limits of LLR processes in Example 2) Assumption 3.2 holds with the limits

$$\begin{aligned} l(i,j)&:= \left\{ \begin{aligned}&\min _{k \in {\mathcal {M}}} \big \{ q^{(0)}(i,k)+\varrho ^{(k)} \big \},&j=0 \\&\min \big \{q(i,j),q^{(0)}(i,j) + \varrho ^{(j)} \big \},&j \in {\mathcal {M}}\setminus \{i\} \end{aligned} \right\} \nonumber \\&\quad \equiv \left\{ \begin{aligned}&\min _{k \in {\mathcal {M}}} \big \{ q^{(0)}(i,k)+\varrho ^{(k)} \big \},&j=0 \\&q(i,j),&j \in \Gamma _i \\&q^{(0)}(i,j) + \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \end{aligned}$$

(4.16)

where $\Gamma _i := \big \{ j \in {\mathcal {M}}\setminus \{i\}: q(i,j) < q^{(0)}(i,j) + \varrho ^{(j)} \big \}$ for every $i\in {\mathcal {M}}$.

Remark 4.2

• (1) Assumptions 4.4 and 4.6 ensure that

  $$\begin{aligned} q(i,j)&< \infty , \quad j \in \Gamma _i, \\ q^{(0)}(i,j) + \varrho ^{(j)}&< \infty , \quad j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}). \end{aligned}$$

• (2) Assumption 4.5 guarantees that $l(i,j) > 0$ for every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$. In particular, by (1) $0< l(i,j) < \infty$ for any $j \in {\mathcal {M}}\setminus \{i\}$. Hence, $0< l(i) < \infty$.

• (3) By (4.16), we can choose $j(i) \in \{0\} \cup \Gamma _i$. If $j(i) = 0$, we must have $\min _{k \in {\mathcal {M}}} \varrho ^{(k)} < \infty$.

As we did for Example 1 of Sect.  4.1, we simplify the LLR process as follows. Define

$$\begin{aligned} \Lambda _n^{(0)}(i,j)&:= \log \frac{{\widetilde{\Pi }}_n^{(i)}}{\sum _{y \in {\mathcal {Y}}_0^{(j)}}\Pi _n(y)}, \quad i,j \in {\mathcal {M}}; \end{aligned}$$

we later show that $\Lambda _n(i,0)/n \sim \min _{j \in {\mathcal {M}}} \Lambda _n^{(0)}(i,j)/n$ as $n \rightarrow \infty$ under ${\mathbb {P}}_i$ (see (4.20)).

Lemma 4.3

For $i,j \in {\mathcal {M}}$, we have

$$\begin{aligned} \Lambda _n^{(0)}(i,j)&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f^{(0)}_j(X_k)} + L_n^{(i)} - \log \big ( 1- \sum _{t=0}^n \rho _t^{(j)} \big ) + \log \nu _i - \log \nu _j, \end{aligned}$$

and for $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}\setminus \{i\}$

$$\begin{aligned} \Lambda _n(i,j)&=\sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j(X_k)} + L_n^{(i)} - L_n^{(j)} + \log \nu _i - \log \nu _j\\&= - \log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f^{(0)}_j(X_k)} + L_n^{(i)} - K_n^{(j)} + \log \nu _i - \log \nu _j, \end{aligned}$$

where for each $j \in {\mathcal {M}}$

$$\begin{aligned} L_n^{(j)}&:= \log \left( \rho _0^{(j)} + \sum _{k=1}^n \rho _k^{(j)} \prod _{l=1}^{k-1} \frac{f^{(0)}_j(X_l)}{f_j(X_l)} \right) , \\ K_n^{(j)}&:= \log \left( \frac{\rho _0^{(j)}}{\rho _n^{(j)}} \prod _{k=1}^n \frac{f_j(X_k)}{f^{(0)}_j(X_k)} + \sum _{k=1}^n \frac{\rho _k^{(j)}}{\rho _n^{(j)}} \prod _{m=k}^n \frac{f_j (X_m)}{f^{(0)}_j(X_m)} \right) \\&= -\log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{f_j(X_k)}{f^{(0)}_j(X_k)} + L_n^{(j)}. \end{aligned}$$

As in Example 1, we decompose each LLR process for every $i\in {\mathcal {M}}$ such that

$$\begin{aligned} \Lambda _n(i,j)&= \sum _{l=1}^n h_{ij}(X_l) + \epsilon _n(i,j), \quad j \in {\mathcal {M}}\setminus \{i\},\\ \Lambda _n^{(0)}(i,j)&= \sum _{l=1}^n h^{(0)}_{ij}(X_l) + \epsilon _n^{(0)}(i,j), \quad j \in {\mathcal {M}}, \end{aligned}$$

where

$$\begin{aligned} h_{ij}(x)&:= \left\{ \begin{aligned}&\log \frac{f_i(x)}{f_j(x)},&j \in \Gamma _i \\&\log \frac{f_i(x)}{f^{(0)}_j(x)} + \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \quad x \in E, \\ h^{(0)}_{ij}(x)&:= \log \frac{f_i(x)}{f^{(0)}_j(x)} + \varrho ^{(j)}, \quad x \in E, \\ \epsilon _n(i,j)&:= \left\{ \begin{aligned}&L_n^{(i)} - L_n^{(j)}+\log \nu _i - \log \nu _j,&j \in \Gamma _i \\&L_n^{(i)} - K_n^{(j)}+ \log \nu _i - \log \nu _j - \log \rho ^{(j)}_n - n \varrho ^{(j)},&j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\}) \end{aligned} \right\} , \quad n\ge 1, \\ \epsilon _n^{(0)}(i,j)&:= L_n^{(i)} - {\log \big ( 1- \sum _{t=0}^n \rho _t^{(j)} \big )} - n \varrho ^{(j)} +\log \nu _i - \log \nu _j, \quad n \ge 1. \end{aligned}$$

By the SLLN and Assumption 4.1, for every $i \in {\mathcal {M}}$, we have ${\mathbb {P}}_i$-a.s. as $n \uparrow \infty$

$$\begin{aligned} \begin{aligned} \frac{1}{n} {\sum _{l=1}^n h_{ij}(X_l)}&\longrightarrow l(i,j), \quad j \in {\mathcal {M}}\setminus \{i\}, \\ \frac{1}{n} {\sum _{l=1}^n h_{ij}^{(0)}(X_l)}&\longrightarrow q^{(0)}(i,j)+\varrho ^{(j)}, \quad j \in {\mathcal {M}}. \end{aligned} \end{aligned}$$

(4.17)

We now show that $\epsilon _n(i,j) /n$ converges almost surely to zero as $n\rightarrow \infty$. Similar to Lemma 4.2, the following holds.

Lemma 4.4

For every $i \in {\mathcal {M}}$, we have the following under ${\mathbb {P}}_i$.

• (i) $L_n^{(i)}/n \xrightarrow {n \uparrow \infty } 0$ a.s.

• (ii) $L_n^{(j)}/n \xrightarrow {n \uparrow \infty } \left[ q(i,j)-q^{(0)}(i,j)-\varrho ^{(j)} \right] _+$ a.s. for every $j \in {\mathcal {M}}\setminus \{i\}$.

• (iii) $K_n^{(j)}/n \xrightarrow {n \uparrow \infty } \left[ q(i,j)-q^{(0)}(i,j)-\varrho ^{(j)} \right] _-$ a.s. for every $j \in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$.

• (iv) $L_n^{(i)}$ converges a.s. as $n \uparrow \infty$ to an a.s. finite random variable $L_\infty ^{(i)}$.

• (v) $L_n^{(j)}$ converges a.s. as $n \uparrow \infty$ to an a.s. finite random variable $L_\infty ^{(j)}$ for every $j \in \Gamma _i$.

• (vi) For every $j\in {\mathcal {M}}$, $(|L^{(j)}_n/n|^r)_{n\ge 1}$ is uniformly integrable for every $r\ge 1$, if

  $$\begin{aligned} \int _{E}\frac{f^{(0)}_j(x)}{f_j(x)} f^{(0)}_i(x) \mathrm {m} ({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _{E}\frac{f^{(0)}_j(x)}{f_j(x)} f_i(x) \mathrm {m} ({\mathrm{d}}x) <\infty . \end{aligned}$$

  (4.18)

• (vii) For every $j\in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$, $(|K^{(j)}_n/n|^q)_{n\ge 1}$ is uniformly integrable for every $0\le q \le r$, if (4.18) holds and

  $$\begin{aligned} \int _{E}\left| \frac{f_j(x)}{f^{(0)}_j(x)}\right| ^r f^{(0)}_i(x) \mathrm {m} ({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _{E}\left| \frac{f_j(x)}{f_j^{(0)}(x)}\right| ^r f_i(x) \mathrm {m} ({\mathrm{d}}x) <\infty , \quad \text {for some } r \ge 1. \end{aligned}$$

  (4.19)

By this lemma, for every $i \in {\mathcal {M}}$, we have $\epsilon _n(i,j)/n \rightarrow 0$ for $j\in {\mathcal {M}}\setminus \{i\}$, and $\epsilon _n^{(0)}(i,j)/n \rightarrow 0$ for $j\in {\mathcal {M}}$, as $n \uparrow \infty$ ${\mathbb {P}}_i$-a.s. By this and (4.17), the proof of Proposition 4.3 is complete once we show that

$$\begin{aligned} \frac{1}{n} \Lambda _n(i,0) \xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i\text {-a.s.}} \min _{j \in {\mathcal {M}}} \big \{ q^{(0)}(i,j)+\varrho ^{(j)} \big \}. \end{aligned}$$

(4.20)

Indeed,

$$\begin{aligned} \frac{1}{n} \Lambda _n(i,0)&= \frac{1}{n} \log \left( \frac{{\widetilde{\Pi }}_n^{(i)}}{\sum _{j \in {\mathcal {M}}} \sum _{y \in {\mathcal {Y}}_j^{(0)}}\Pi _n(y)} \right) = -\frac{1}{n} \log \left( \sum _{j \in {\mathcal {M}}} \frac{\sum _{y \in {\mathcal {Y}}_j^{(0)}}\Pi _n(y) }{{\widetilde{\Pi }}_n^{(i)}} \right) \nonumber \\&\quad = -\frac{1}{n} \log \left( \sum _{j \in {\mathcal {M}}} e^{-n A_n^{(j)}} \right) \end{aligned}$$

(4.21)

where $A_n^{(j)}:= \Lambda _n^{(0)}(i,j)/n \rightarrow q^{(0)}(i,j)+\varrho ^{(j)}$ as $n \uparrow \infty$ ${\mathbb {P}}_i$-a.s. Hence by Lemma 3.2, (4.20) holds.

We now pursue the convergence in the $L^r$-sense. In view of (4.21), we have $\Lambda _n(i,0)/n \le \Lambda _n^{(0)}(i,j)/n$ for any $j \in {\mathcal {M}}$ and

$$\begin{aligned} \frac{1}{n} \Lambda _n(i,0)&\ge -\frac{1}{n} \log \left( M \max _{j \in {\mathcal {M}}} \frac{\sum _{y \in {\mathcal {Y}}_j^{(0)}}\Pi _n(y) }{{\widetilde{\Pi }}_n^{(i)}} \right) = - \frac{\log M}{n} + \min _{j \in {\mathcal {M}}} \frac{1}{n} \Lambda _n^{(0)}(i,j) \\&\ge - \frac{\log M}{n} - \sum _{j \in {\mathcal {M}}} \frac{1}{n} (\Lambda _n^{(0)}(i,j))_-. \end{aligned}$$

Therefore, for the proof of the uniform integrability of $\Lambda _n(i,0)/n$, it is sufficient to show that of $\Lambda _n^{(0)}(i,j)/n$ for every $j \in {\mathcal {M}}$.

As in Example 1, for every $i \in {\mathcal {M}}$ and $r \ge 1$, we have $n^{-1} {\sum _{l=1}^n h_{ij}(X_l)} \xrightarrow [n \uparrow \infty ]{L^r({\mathbb {P}}_i)} l(i,j)$ for $j \in {\mathcal {M}}\setminus \{i\}$, if

$$\begin{aligned} \int _E \left| h_{ij}(x) \right| ^r f^{(0)}_i(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| h_{ij}(x) \right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x)<\infty , \end{aligned}$$

which are satisfied under the following condition.

Condition 4.3

For given $i \in {\mathcal {M}}$, $j\in {\mathcal {M}}\setminus \{i\}$, and $r \ge 1$, suppose that if $j\in \Gamma _i$

$$\begin{aligned} \int _E \left| \log \frac{f_i(x)}{f_j(x)}\right| ^r f^{(0)}_i(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| \log \frac{f_i(x)}{f_j(x)}\right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x)<\infty , \end{aligned}$$

and if $j\in {\mathcal {M}}\setminus (\Gamma _i \cup \{i\})$

$$\begin{aligned} \int _E \left| \log \frac{f_i(x)}{f_j^{(0)}(x)}\right| ^r f^{(0)}_i(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| \log \frac{f_i(x)}{f^{(0)}_j(x)}\right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x) <\infty . \end{aligned}$$

(4.22)

Moreover, $n^{-1} {\sum _{l=1}^n h_{ij}^{(0)}(X_l)} \xrightarrow [n \uparrow \infty ]{L^r({\mathbb {P}}_i)} q^{(0)}(i,j)+\varrho ^{(j)}$ for $j \in {\mathcal {M}}$, if

$$\begin{aligned} \int _E \left| h_{ij}^{(0)}(x) \right| ^r f^{(0)}_i(x) \mathrm {m}({\mathrm{d}}x)<\infty \quad \text {and} \quad \int _E \left| h_{ij}^{(0)}(x) \right| ^r f_i(x) \mathrm {m}({\mathrm{d}}x)<\infty , \end{aligned}$$

which is satisfied if $\varrho ^{(j)} < \infty$ and the following holds.

Condition 4.4

For given $i \in {\mathcal {M}}$, $j\in {\mathcal {M}}$, and $r \ge 1$, suppose that (4.22) holds.

On the other hand, by Lemma 4.2, $\epsilon _n(i,j)/n \rightarrow 0$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ under Condition 4.5 given subsequently for $j \in {\mathcal {M}}\setminus \{i\}$, and, for $j = 0$, $\epsilon _n^{(0)}(i,j)/n \rightarrow 0$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ under Condition 4.6 given subsequently for $j \in {\mathcal {M}}$. Notice as in Lemma 4.2 (vi) that in order for $L_n^{(i)}$ to converge in $L^r$ under ${\mathbb {P}}_i$ to zero, it is sufficient to have

$$\begin{aligned} \int _E \frac{f^{(0)}_i (x)}{f_i(x)} f^{(0)}_i(x) \mathrm {m} ({\mathrm{d}}x) < \infty , \end{aligned}$$

(4.23)

because $\int _E \frac{f^{(0)}_i (x)}{f_i(x)} f_i(x) \mathrm {m} ({\mathrm{d}}x) = \int _E f^{(0)}_i (x) \mathrm {m} ({\mathrm{d}}x)= 1 < \infty$.

Condition 4.5

Given $i \in {\mathcal {M}}$, $j\in {\mathcal {M}}\setminus \{i\}$ and $r \ge 1$, we suppose that (4.23) holds, and

• 1. if $j \in \Gamma _i$, (4.18) holds, and

• 2. if $j \in {\mathcal {M}}\setminus \Gamma _i$, (4.19) holds for the given r.

Condition 4.6

Given $i \in {\mathcal {M}}$, we suppose that (4.23) holds and $\max _{j \in {\mathcal {M}}}\varrho ^{(j)} < \infty$ holds.

In summary, we have the following $L^r$-convergence results.

Proposition 4.4

• (1) For every $i \in {\mathcal {M}}$ and $j\in {\mathcal {M}}\setminus \{i\}$, we have $\Lambda _n(i,j)/n \rightarrow l(i,j)$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ for some $r \ge 1$ if Conditions 4.3 and 4.5 hold for the given r,

• (2) For every $i \in {\mathcal {M}}$, we have $\Lambda _n(i,0)/n \rightarrow l(i,0)$ as $n \uparrow \infty$ in $L^r({\mathbb {P}}_i)$ for some $r \ge 1$ if Condition 4.4 holds for every $j \in {\mathcal {M}}$ and Condition 4.6 holds.

5 Numerical examples

In this section, we verify the effectiveness of the asymptotically optimal strategies through a series of numerical experiments. Because the optimality results are fundamentally relying on the existence of the limits l(i, j) as in Assumption 3.2, we first verify their existence numerically and show that they can be obtained efficiently via simulation. We then evaluate the performance of the asymptotically optimal strategies in comparison to the optimal values.

5.1 Verification of Assumption 3.2

We consider both the case when X is i.i.d. in each of the closed sets as studied in Sect.4 and also the non-i.i.d. case where each closed set may contain multiple states.

In order to verify the convergence results in Sect. 4, we consider Example 2 of Sect. 4.2 with $M=2$ and the hidden Markov chain ${\mathcal {Y}}_1 = \{1 \}$, ${\mathcal {Y}}_0^{(1)} = \{ (1,1), (1,2)\}$, ${\mathcal {Y}}_2 = \{2 \}$, and ${\mathcal {Y}}_0^{(2)} = \{ (2,1), (2,2)\}$ with

$$\begin{aligned} P = \begin{array}{c} (1,1) \\ (1,2) \\ 1 \\ (2,1) \\ (2,2) \\ 2 \end{array} \left[ \begin{array}{ll|l|ll|l} .85 &{} .15 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} .9 &{} .1 &{} 0 &{} 0 &{} 0\\ \hline 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} .8 &{} 0 &{} .2 \\ 0 &{} 0 &{} 0 &{} 0 &{} .95 &{} .05 \\ \hline 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \quad \text {and} \quad \eta = \left[ \begin{array}{c} .25 \\ .25 \\ 0\\ .25 \\ .25 \\ 0\end{array}\right] . \end{aligned}$$

(5.1)

See Fig. 2 for the diagram showing the transition of Y.

Fig. 2

Markov chain with transition matrix P in (5.1)

Under ${\mathbb {P}}_1$, Y starts at either (1, 1) or (1, 2) and gets absorbed by 1, while under ${\mathbb {P}}_2$ it starts at either (2, 1) or (2, 2) and gets absorbed by 2. Conditionally given $Y_0 = (1,1)$, the absorption time $\theta$ is a sum of two independent geometric random variables with parameters 0.15 and 0.1; conditionally on $Y_0 = (1,2)$, it is geometric with parameters 0.1. It is easy to show that the exponential tail (4.3) under ${\mathbb {P}}_1$ is $\varrho ^{(1)} = |\log (1-\min (0.1, 0.15))|$. On the other hand, regarding ${\mathcal {Y}}_2 \cup {\mathcal {Y}}_0^{(2)}$, the absorption time $\theta$ is a mixture of two geometric random variables with parameters 0.2 and 0.05. Its exponential tail is $\varrho ^{(2)} = |\log (1-\min (0.2, 0.05))|$.

For the observation process X, we assume that it is normally distributed with a common variance 1 and its conditional mean given Y is $\{ \lambda (y); y \in {\mathcal {Y}}\}$. As is assumed in Example 2, we let $\lambda ^{(0)}_1 := \lambda ((1,1)) = \lambda ((1,2))$ and $\lambda _2^{(0)} := \lambda ((2,1)) = \lambda ((2,2))$. We also let $\lambda _k := \lambda (k)$ for $k=1,2$. The Kullback-Leibler divergence is $q(i,j) = \big ( \lambda _i - \lambda _j \big )^2/2$ for every $i\in {\mathcal {M}}$, $j\in {\mathcal {M}}\setminus \{i\}$ and $q^{(0)}(i,j) = \big ( \lambda _i - \lambda ^{(0)}_j\big )^2/2$ for every $i,j\in {\mathcal {M}}$. Here we assume that $\lambda ^{(0)}_1 = 0.1$, $\lambda _1 = 0.7$, $\lambda ^{(0)}_2 = 0$ and $\lambda _2 = 0.2$. Using Proposition 4.3, the analytical limit values l(i, j) are obtained and are listed in the last column of Table 1.

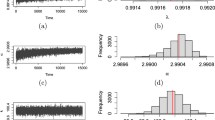
In Fig. 3, we plot sample paths of $\Lambda _n(1,\cdot )/n$ under ${\mathbb {P}}_1$ and $\Lambda _n(2,\cdot )/n$ under ${\mathbb {P}}_2$ along with the theoretical limit l(i, j). In order to verify their almost sure convergence, we show in Table 1 the statistics on the position at time $n=500, 1000, 1500$ based on 1000 samples for each. We indeed see that the mean value approaches the theoretical limit and the standard deviation diminishes as n increases, verifying the almost sure limit of the LLR processes.

Fig. 3

Sample realizations of LLR Processes: a $\Lambda _n(1,0)/n$ (red) and $\Lambda _n(1,2)/n$ (blue) under ${\mathbb {P}}_1$ and b $\Lambda _n(2,0)/n$ (red) and $\Lambda _n(2,1)/n$ (blue) under ${\mathbb {P}}_2$. The theoretical limit values $l(\cdot , \cdot )$ are also given by dotted lines

Table 1 The LLR process at time $n = 500, 1000,1500$: mean and standard deviation along with theoretical values

We now consider the non-i.i.d. case where each closed set consists of multiple states. Because this case has not been covered in Sect. 4 and the limit l(i, j) has not been derived, we shall confirm this numerically via simulation. We consider a Markov chain with $M = 2$, ${\mathcal {Y}}_0 = \{0\}$, ${\mathcal {Y}}_1 = \{(1,1),(1,2),(1,3)\}$ and ${\mathcal {Y}}_2 = \{(2,1),(2,2)\}$. We consider case 1 and case 2 with respective transition matrices:

$$\begin{aligned} P_1 := \begin{array}{c} 0\\ (1,1) \\ (1,2) \\ (1,3) \\ (2,1) \\ (2,2) \end{array} \left[ \begin{array}{l|lll|ll} .75 &{} .05 &{} .05 &{} .05 &{} .05 &{} .05 \\ \hline 0 &{} .5 &{} .2 &{} .3 &{} 0&{} 0 \\ 0&{} .3 &{}.5 &{} .2 &{} 0 &{} 0 \\ 0 &{} .3 &{} .2 &{} .5 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} 0 &{} .7 &{} .3 \\ 0 &{} 0 &{} 0 &{} 0 &{} .2 &{} .8 \end{array}\right] , \quad P_2 := \left[ \begin{array}{l|lll|ll} .75 &{} .05 &{} .05 &{} .05 &{} .05 &{} .05 \\ \hline 0 &{} 0 &{} 1 &{} 0 &{} 0&{} 0 \\ 0&{} 0 &{}0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \end{array}\right] . \end{aligned}$$

(5.2)

Here we model the acyclic case for the former and cyclic case for the latter. See Fig. 4 for the diagram showing the transition of Y. For both cases, we assume the initial distribution $\eta = \left[ 1, 0, 0, 0, 0,0 \right] ^T$ and X is again normally distributed with variance 1 and mean function $\lambda = \left[ 0, 0.2, 0.4, 0.6, -0.2, -0.4 \right] ^T$.

Fig. 4

Markov chain with transition matrix $P_1$ (left) and $P_2$ (right) in (5.2)

Fig. 5

Sample realizations of LLR processes: a $n \mapsto \Lambda _n(1,0)/n$ (red) and $n \mapsto \Lambda _n(1,2)/n$ (blue) under ${\mathbb {P}}_1$ and b $n \mapsto \Lambda _n(2,0)/n$ (red) and $n \mapsto \Lambda _n(2,1)/n$ (blue) under ${\mathbb {P}}_2$, along with the mean of $\Lambda _{1500}/1500$ given in Table 2

We plot in Fig. 5 sample paths of the LLR processes $\Lambda _n(1,\cdot )/n$ under ${\mathbb {P}}_1$ and $\Lambda _n(2,\cdot )/n$ under ${\mathbb {P}}_2$ and also show in Table 2 the statistics on their positions at $n = 500,1000,1500$ based on 1000 sample paths. We observe that these processes indeed converge to deterministic limits almost surely. It is also noted that the convergence holds regardless of the cyclic/acyclic structure of the closed sets.

5.2 Numerical results on asymptotic optimality

We now evaluate the asymptotically optimal strategy in comparison with the optimal Bayes risk focusing on Problem 2.1 with $m=1$. Dayanik and Goulding (2009) showed that the problem can be reduced to an optimal stopping problem of the posterior probability process $\Pi$, and in theory the value function can be approximated via value iteration in combination with discretization. In practice, however, the state space increases exponentially in the number of states $|{\mathcal {Y}}|$, and it is computationally feasible only when $|{\mathcal {Y}}|$ is small (typically at most three or four). Moreover, we need to deal with small detection delay costs c and hence the resulting stopping regions tend to be very small in practical applications. For this reason, the approximation is affected severely by discretization errors as well. Here in order to provide reliable approximation to the optimal Bayes risk, we consider the following simple examples.

We suppose $M = 2$, ${\mathcal {Y}}_0 = \{ (0,1), (0,2)\}$, ${\mathcal {Y}}_1 = \{1\}$ and ${\mathcal {Y}}_2 = \{2\}$ and consider Case 1 with

$$\begin{aligned} P_1 := \begin{array}{c} (0,1)\\ (0,2) \\ 1 \\ 2 \end{array} \left[ \begin{array}{llll} .95 &{} 0 &{} .05 &{} 0 \\ 0 &{} .9 &{} 0 &{} .1 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \quad \text {and} \quad \eta _1 := \left[ \begin{array}{c} .5 \\ .5 \\ 0 \\ 0 \end{array} \right] \end{aligned}$$

(5.3)

and Case 2 with

$$\begin{aligned} P_2 := \begin{array}{c} (0,1)\\ (0,2) \\ 1 \\ 2 \end{array} \left[ \begin{array}{llll} .95 &{} .05 &{} 0 &{} 0 \\ 0 &{} .85 &{} .05 &{} .1 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \quad \text {and} \quad \eta _2 := \left[ \begin{array}{c} .5 \\ .5 \\ 0 \\ 0 \end{array} \right] . \end{aligned}$$

(5.4)

Case 1 has been considered in Dayanik and Goulding (2009) where $\theta$ is geometric with parameter .05 under ${\mathbb {P}}_1$ and .1 under ${\mathbb {P}}_2$. In Case 2, it is a sum of two geometric random variables under ${\mathbb {P}}$. See Fig. 6 for the diagram showing the transition of Y for Cases 1 and 2. For X, we assume for both cases that it takes values in $E = \{1,2,3,4\}$ with probabilities ${\mathbb {P}}\{ X_1 = k | Y_1=y\}=f(y,k)$ given by

$$\begin{aligned} f = \left[ \begin{array}{llll} .25 &{} .25 &{} .25 &{} .25 \\ .25 &{} .25 &{} .25 &{} .25 \\ .4 &{} .3 &{} .2 &{} .1 \\ .1 &{} .2 &{} .3 &{} .4 \end{array}\right] . \end{aligned}$$

Table 2 The LLR process at time $n = 500, 1000,1500$: mean and standard deviation

Fig. 6

Markov chain with transition matrix $P_1$ (left) in (5.3) and $P_2$ (right) in (5.4)

Table 3 Comparison with the optimal value function

We set the detection delay function $c = [0, 0, {\bar{c}}, {\bar{c}}]$ and the terminal decision loss function $a_{yi} = 1$ for $y \notin {\mathcal {Y}}_i$ and it is zero otherwise. The limits l(i, j) can be analytically computed by Propositions 4.1 and the asymptotically optimal strategy can be constructed analytically. Here we have $A_i(c) = {\bar{c}} /l(i)$, for every $i \in {\mathcal {M}}$. In order to compute the optimal Bayes risk, we first discretize the state space of $\Pi$ (which is $|{\mathcal {Y}}|-1$-simplex) by $70^{|{\mathcal {Y}}|-1}$ mesh and then obtain the stopping regions by solving the optimality equation provided in Dayanik and Goulding (2009) via value iteration. The optimal Bayes risk is then approximated via simulation based on 10, 000 paths. The risk under the asymptotically optimal strategy is approximated based on 100, 000 paths.

Table 3 shows the results. It shows the approximated Bayes risk (with 95% confidence interval) for both strategies and also the ratio between the two. It can be seen that the ratio indeed converges to 1. In fact, the results show that the convergence is fast and it approximates the optimal Bayes risk precisely even for a moderate value of ${\bar{c}}$. The proposed strategy can be derived analytically and its corresponding Bayes risk can be computed instantaneously via simulation.

Appendix A Proofs

1.1 A.1 Proof of Lemma 3.8

The proof of Lemma 3.8 requires the following lemmas. Note that the proof is similar to that of Theorem 3.5 of Baron and Tartakovsky (2006).

Lemma 5.1

For every $i \in {\mathcal {M}}$ and $j \in {\mathcal {M}}_0 \setminus \{i\}$, $L > 0$, $\gamma > 0$ and $k > 1$, we have

$$\begin{aligned}&\inf _{(\tau ,d) \in {\overline{\Delta }}({\overline{R}})}{\mathbb {P}}_i \Big \{ \sum _{t=0}^{\tau -1} c(Y_t)> \gamma L \Big \} \\&\quad \ge 1 - \frac{\sum _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i} {\overline{R}}_{yi}}{\nu _i} - \frac{e^{k L l(i,j)}}{\nu _i} \sum _{y \in {\mathcal {Y}}_j}{\overline{R}}_{yi} \\&\quad - {\mathbb {P}}_i \Big \{ \sup _{n \le \theta + L} \Lambda _n (i,j) > k L l(i,j) \Big \} - {\mathbb {P}}_i \Big \{ \min _{n \ge L}\frac{\sum _{t=0}^{n-1} c(Y_t)}{n} < \gamma \Big \}. \end{aligned}$$

Proof

We have

$$\begin{aligned} {\mathbb {P}}_i \Big \{ {\sum _{t=0}^{\tau -1} c(Y_t)}> \gamma L \Big \}&\ge {\mathbb {P}}_i \Big \{ \frac{\sum _{t=0}^{\tau -1} c(Y_t)}{\tau } \ge \gamma , \tau> L \Big \} \\&= {\mathbb {P}}_i \left\{ \tau> L \right\} - {\mathbb {P}}_i \Big \{ \frac{\sum _{t=0}^{\tau -1} c(Y_t)}{\tau } < \gamma , \tau > L \Big \}. \end{aligned}$$

Moreover, we have

$$\begin{aligned}&{\mathbb {P}}_i \Big \{ \frac{\sum _{t=0}^{\tau -1} c(Y_t)}{\tau }< \gamma , \tau> L \Big \} \le {\mathbb {P}}_i \Big \{ \inf _{n \ge \tau }\frac{\sum _{t=0}^{n-1} c(Y_t)}{n}< \gamma , \tau> L \Big \} \\&\quad \le {\mathbb {P}}_i \Big \{ \inf _{n \ge L}\frac{\sum _{t=0}^{n-1} c(Y_t)}{n}< \gamma , \tau > L \Big \} \le {\mathbb {P}}_i \Big \{ \inf _{n \ge L}\frac{\sum _{t=0}^{n-1} c(Y_t)}{n} < \gamma \Big \}. \end{aligned}$$

As in the proof of Lemma A.1 of Dayanik et al. (2013),

$$\begin{aligned}&{\mathbb {P}}_i \left\{ \tau> L \right\} \ge {\mathbb {P}}_i \left\{ \tau -\theta> L \right\} \ge 1 - R_i^{(1)} (\tau ,d) - \frac{e^{k L l(i,j)}}{\nu _i} {\widetilde{R}}_{ji} (\tau ,d) \\&\quad - {\mathbb {P}}_i \big \{ \sup _{n \le \theta + L} \Lambda _n (i,j) > k L l(i,j) \big \}. \end{aligned}$$

Combining the above and taking infimum over ${\overline{\Delta }} ({\overline{R}})$,

$$\begin{aligned}&\inf _{(\tau ,d) \in {\overline{\Delta }}({\overline{R}})} {\mathbb {P}}_i \Big \{ \sum _{t=0}^{\tau -1} c(Y_t)> \gamma L \Big \} \ge 1 - \sup _{(\tau ,d) \in {\overline{\Delta }}({\overline{R}})}R_i^{(1)} (\tau ,d) - \frac{e^{k L l(i,j)}}{\nu _i} \sup _{(\tau ,d) \in {\overline{\Delta }}({\overline{R}})} {\widetilde{R}}_{ji} (\tau ,d) \\&\quad - {\mathbb {P}}_i \Big \{ \sup _{n \le \theta + L} \Lambda _n (i,j) > k L l(i,j) \Big \} - {\mathbb {P}}_i \Big \{ \min _{n \ge L} \frac{\sum _{t=0}^{n-1} c(Y_t)}{n} < \gamma \Big \}. \end{aligned}$$

Now, the lemma holds because $(\tau ,d) \in {\overline{\Delta }}({\overline{R}})$ implies that $R_i^{(1)}(\tau ,d) \le {\sum _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_i} {\overline{R}}_{yi}/\nu _i}$ and ${\widetilde{R}}_{ji}(\tau ,d) \le \sum _{y \in {\mathcal {Y}}_j}{\overline{R}}_{yi}$. $\square$

Lemma 5.2

Fix $0< \delta < 1$, $i \in {\mathcal {M}}$ and j(i). We have

$$\begin{aligned}&\liminf _{ {\overline{R}}_i \downarrow 0} \inf _{(\tau ,d) \in {\overline{\Delta }} ({\overline{R}})} {\mathbb {P}}_i \Big \{ \sum _{t=0}^{\tau -1} c(Y_t) \ge \delta \frac{c_i {\big |\log \big ( \frac{1}{\nu _i}{ \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \big )\big |}}{ l(i)}\Big \} =1. \end{aligned}$$

Proof

Fix ${\overline{R}}$ such that $0< \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi} < \nu _i$. Then we have $- \log ( \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}/ {\nu _i} ) = |\log ( \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}/ {\nu _i} )|$. Now in Lemma 5.1, we set $j=j(i)$,

$$\begin{aligned} L = \sqrt{\delta } \frac{\big |\log \left( \frac{1}{\nu _i}{ \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \big |}{l(i)} \quad \text {and} \quad \gamma = \sqrt{\delta } c_i, \end{aligned}$$

and choose $k > 1$ such that $0< k \sqrt{\delta } < 1$. Then we have

$$\begin{aligned}&\inf _{(\tau ,d) \in {\overline{\Delta }}({\overline{R}})} {\mathbb {P}}_i \left\{ \sum _{t=0}^{\tau -1} c(Y_t) \ge \delta \frac{ c_i {\left| \log \left( \frac{1}{\nu _i}{ \sum _{y \in {\mathcal {Y}}_{j(i)}} {\overline{R}}_{yi}} \right) \right| }}{l(i)} \right\} \\&\qquad \ge 1 - \frac{\sum _{y \in {\mathcal {Y}}\setminus {\mathcal {Y}}_{i}} {\overline{R}}_{yi}}{\nu _i} - \left( \frac{\sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}}{\nu _i} \right) ^{1-k \sqrt{\delta }} \\&\qquad - {\mathbb {P}}_i \left\{ \sup _{n \le \theta + L} \Lambda _n (i,j(i)) > kL l(i)\right\} - {\mathbb {P}}_i \left\{ \min _{n \ge L} \frac{\sum _{t=0}^{n-1} c(Y_t)}{n} < \gamma \right\} . \end{aligned}$$

The right hand side goes to 1 as ${\overline{R}}_i \downarrow 0$ because $0< 1-k \sqrt{\delta } < 1$, ${\overline{R}}_i \downarrow 0 \Longrightarrow L \uparrow \infty$, and $0< \gamma < c_i$. Indeed, by (Dayanik et al. 2013, Lemma A.2), for any $k > 1$, ${\mathbb {P}}_i \big \{ \sup _{n \le \theta + L} \Lambda _n (i,j(i)) > k L l(i)\big \} \xrightarrow {L \uparrow \infty } 0$, and because ${\sum _{t=0}^{n-1} c(Y_t)} / n$ converges ${\mathbb {P}}_i$-a.s. to $c_i$, we have ${\mathbb {P}}_i \big \{ \min _{n \ge L} \frac{\sum _{t=0}^{n-1} c(Y_t)}{n} < \gamma \big \} \xrightarrow {L \uparrow \infty } 0$, for any $0< \gamma < c_i$. $\square$

Proof of Lemma 3.8

Fix a set of positive constants ${\overline{R}}$, $0< \delta < 1$ and $(\tau ,d) \in \Delta$. We have by Markov inequality

$$\begin{aligned} \frac{D_i^{(c,m)}(\tau )}{\left( { \frac{c_i}{l(i)} \left| \log \left( \frac{1}{\nu _i}{\sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| } \right) ^m}&\ge \delta {\mathbb {P}}_i \left\{ \frac{\left( \sum _{t=0}^{\tau -1} c(Y_t)\right) ^m}{\left( { \frac{c_i}{l(i)} \left| \log \left( \frac{1}{\nu _i}{\sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| } \right) ^m} \ge \delta \right\} \\&= \delta {\mathbb {P}}_i \left\{ \sum _{t=0}^{\tau -1} c(Y_t) \ge \delta ^{\frac{1}{m}} \frac{c_i {\left| \log \left( \frac{1}{\nu _i}{ \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| }}{ l(i)} \right\} . \end{aligned}$$

By taking infimum and then limits on both sides,

$$\begin{aligned}&\liminf _{{\overline{R}}_i \downarrow 0}\inf _{({\widetilde{\tau }},{\widetilde{d}}) \in {\overline{\Delta }}({\overline{R}})} \frac{D_i^{(c,m)}({\widetilde{\tau }})}{\left( { \frac{c_i}{l(i)} \left| \log \left( \frac{1}{\nu _i}{\sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| } \right) ^m} \\&\quad \ge \delta \liminf _{{\overline{R}}_i \downarrow 0} \inf _{({\widetilde{\tau }},{\widetilde{d}}) \in {\overline{\Delta }}({\overline{R}})}{\mathbb {P}}_i \left\{ \sum _{t=0}^{{\widetilde{\tau }}-1} c(Y_t) \ge \delta ^{\frac{1}{m}} \frac{c_i {\left| \log \left( \frac{1}{\nu _i}{ \sum _{y \in {\mathcal {Y}}_{j(i)}}{\overline{R}}_{yi}} \right) \right| }}{ l(i)} \right\} , \end{aligned}$$

which is greater than or equal to $\delta$ by Lemma 5.2. Now, the claim holds because $0< \delta < 1$ is arbitrary. $\square$

1.2 A.2. Proof of Lemma 4.1

We first simplify ${\widetilde{\alpha }}_n^{(i)} (x_1,...,x_n)$ in (3.2). Corresponding to the event that Y is absorbed by ${\mathcal {Y}}_i$ at time $t \ge 0$, let the set of paths of Y until time n be denoted by ${\mathcal {S}}_{t,n}^{(i)}$ where

$$\begin{aligned} {\mathcal {S}}_{0,n}^{(i)} := \{ (i, \ldots , i)\} \quad \text {and} \quad {\mathcal {S}}_{t,n}^{(i)} :=&\{ (y_0, \ldots , y_n): y_0,\ldots , y_{t-1} \in {\mathcal {Y}}_{0}, \, y_t, \ldots , y_n = i \}, \\&1 \le t \le n, \end{aligned}$$

and by assumption

$$\begin{aligned}&f(y_0, \cdot ) \equiv \cdots \equiv f(y_{t-1}, \cdot )\equiv f_0(\cdot ) \quad \text {and} \quad f(y_t, \cdot ) \equiv \cdots \equiv f(y_n, \cdot ) \equiv f_i(\cdot ), \\&y= (y_0, \ldots , y_n) \in {\mathcal {S}}_{t,n}^{(i)}. \end{aligned}$$

Lemma 5.3

For any $n \ge 1$ and $(x_1,\ldots x_n) \in E^n$,

$$\begin{aligned} {\widetilde{\alpha }}_n^{(i)} (x_1,...,x_n)&= \left\{ \begin{array}{ll} \prod _{l=1}^n f_0(x_l) \sum _{i \in {\mathcal {M}}} \nu _i \big (1- \sum _{t=0}^n \rho _t^{(i)} \big ), &{} i = 0, \\ \nu _i \left[ \rho _0^{(i)} \prod _{k=1}^{n} f_i(x_k) + \sum _{t=1}^n \rho _t^{(i)}\prod _{k=1}^{t-1} f_0(x_k) \prod _{k=t}^n f_i(x_k) \right] , &{} i \in {\mathcal {M}}. \end{array} \right. \end{aligned}$$

Proof

Because ${\mathcal {S}}_{0,n}^{(i)}, {\mathcal {S}}_{1,n}^{(i)}, \ldots , {\mathcal {S}}_{n,n}^{(i)}$ are mutually disjoint and

$$\begin{aligned} {\mathcal {S}}_{0,n}^{(i)} \sqcup {\mathcal {S}}_{1,n}^{(i)} \sqcup \cdots \sqcup {\mathcal {S}}_{n,n}^{(i)} = \{ (y_0, \ldots , y_{n-1}, i): y_0, \ldots , y_{n-1} \in {\mathcal {Y}}_0 \cup \{i\} \} =: {\mathcal {S}}^{(i)}_n \end{aligned}$$

or the set of paths under which Y is in $\{i\}$ at time n, and because $y_n = i$ for any y in ${\mathcal {S}}_{0,n}^{(i)}, \ldots , {\mathcal {S}}_{n,n}^{(i)}$, we have

$$\begin{aligned}&{\widetilde{\alpha }}_n^{(i)} (x_1,\ldots , x_n) =\eta (i) \prod _{k=1}^{n} f_i(x_k) + \sum _{t=1}^n\sum _{y \in {\mathcal {S}}_{t,n}^{(i)}} \eta (y_0) \Big (\prod _{k=1}^{n} P(y_{k-1},y_k) f(y_k,x_k)\Big ) \\&\quad =\eta (i) \prod _{k=1}^{n} f_i(x_k) \\&\quad + \sum _{t=1}^n\sum _{y \in {\mathcal {S}}_{t,n}^{(i)}} \\&\quad \Big [ \eta (y_0) \Big (\prod _{k=1}^{t-1} P(y_{k-1},y_k) f(y_k,x_k) \Big ) P(y_{t-1},i) f_i(x_t) \prod _{k=t+1}^n f_i(x_k) \Big ] \\&\quad = \eta (i) \prod _{k=1}^{n} f_i(x_k) \\&\quad +\sum _{t=1}^n \Big ( \prod _{k=1}^{t-1} f_0(x_k) \prod _{k=t}^n f_i(x_k) \Big ) \\&\quad \sum _{y \in {\mathcal {S}}_{t,n}^{(i)}} \Big [ \eta (y_0) \prod _{k=1}^{t-1} P(y_{k-1},y_k) P(y_{t-1},i) \Big ] \\&\quad =\nu _i \Big [ \rho _0^{(i)} \prod _{k=1}^{n} f_i(x_k) + \sum _{t=1}^n \rho _t^{(i)}\prod _{k=1}^{t-1} f_0(x_k) \prod _{k=t}^n f_i(x_k) \Big ], \end{aligned}$$

by (4.2). On the other hand,

$$\begin{aligned}&{\widetilde{\alpha }}_n^{(0)} (x_1,...,x_n) = \sum _{y \in {\mathcal {Y}}_{0}}\alpha _n (x_1,...,x_n, y) \\&\quad = \prod _{l=1}^n f_0(x_l)\\&\quad \sum _{{\mathcal {Y}}^n \setminus (\cup _{i \in {\mathcal {M}}}{\mathcal {S}}_n^{(i)})} \Big ( \eta (y_0) \prod _{k=1}^{n-1} P(y_{k-1},y_k) \Big ) P(y_{n-1},y) \\&\quad = \prod _{l=1}^n f_0(x_l) \big (1- \sum _{i \in {\mathcal {M}}}\sum _{t=0}^n \nu _i \rho _t^{(i)} \big ) = \prod _{l=1}^n f_0(x_l) \sum _{i \in {\mathcal {M}}} \nu _i \big (1- \sum _{t=0}^n \rho _t^{(i)} \big ), \end{aligned}$$

as desired. $\square$

Proof

Fix $i \in {\mathcal {M}}$. By Lemma 5.3,

$$\begin{aligned} \Lambda _n(i,0)&= \log \left( \frac{ \nu _i \big [ \rho _0^{(i)} \prod _{k=1}^n f_i(X_k) + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} f_0(X_l) \prod _{m=k}^n f_i (X_m) \big ] }{\prod _{l=1}^n f_0(X_l) \sum _{j \in {\mathcal {M}}} \nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) } \right) \\&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_0(X_k)} + \log \left( \frac{ \nu _i \left[ \rho _0^{(i)} + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} \frac{f_0(X_l)}{f_i(X_l)} \right] }{\sum _{j \in {\mathcal {M}}}\nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) } \right) \\&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_0(X_k)} + L_n^{(i)} + \log \nu _i - \log \big ( \sum _{j \in {\mathcal {M}}} \nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \big ). \end{aligned}$$

For $j \in {\mathcal {M}}\backslash \{i\}$, we have

$$\begin{aligned} \Lambda _n(i,j)&= \log \frac{\nu _i}{\nu _j} +\log \left( \frac{ \rho _0^{(i)} \prod _{k=1}^n f_i(X_k) + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} f_0(X_l) \prod _{m=k}^n f_i (X_m) }{ \rho _0^{(j)} \prod _{k=1}^n f_j(X_k) + \sum _{k=1}^n \rho _k^{(j)} \prod _{l=1}^{k-1} f_0(X_l) \prod _{m=k}^n f_j (X_m) } \right) \\&= \log \frac{\nu _i}{\nu _j} +\log \left( \prod _{k=1}^n \frac{ f_i(X_k)}{ f_j(X_k)} \frac{\exp L_n^{(i)}}{\exp L_n^{(j)}} \right) \\&= \log \frac{\nu _i}{\nu _j} +\sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j(X_k)} + L_n^{(i)} - L_n^{(j)}, \end{aligned}$$

and we can also write

$$\begin{aligned} \Lambda _n(i,j)&= \log \frac{\nu _i}{\nu _j} +\log \left( \frac{1}{\rho _n^{(j)}} \prod _{k=1}^n \frac{ f_i(X_k)}{ f_0(X_k)} \frac{\rho _0^{(i)} + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} \frac{f_0(X_l)}{f_i(X_l)} }{\frac{\rho _0^{(j)}}{\rho _n^{(j)}} \prod _{k=1}^n \frac{f_j(X_k)}{f_0(X_k)} + \sum _{k=1}^n \frac{\rho _k^{(j)}}{\rho _n^{(j)}} \prod _{m=k}^n \frac{f_j (X_m)}{f_0(X_m)} } \right) \\&= \log \frac{\nu _i}{\nu _j} -\log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_0(X_k)} + L_n^{(i)} - K_n^{(j)}, \end{aligned}$$

as desired. $\square$

1.3 A.3. Proof of Lemma 4.2

The proof requires the following lemma, whose proof is similar to that of Lemma A.4 of Dayanik et al. (2013).

Lemma 5.4

Let $(\xi _n)_{n \ge 1}$ be a positive stochastic process and T an a.s. finite random time defined on the same probability space $(\Omega , {\mathcal {E}}, {\mathbb {P}})$. Given T, the random variables $(\xi _n)_{n\ge 1}$ are conditionally independent, and $(\xi _n)_{1\le n \le T-1}$ and $(\xi _n)_{n\ge T}$ have common conditional probability distributions ${\mathbb {P}}_\infty$ and ${\mathbb {P}}_0$ on $({\mathbb {R}}, {\mathscr {B}}({\mathbb {R}}))$, the expectations with respect to which are denoted by ${\mathbb {E}}_\infty$ and ${\mathbb {E}}_0$, respectively. Suppose that ${\mathbb {E}}_\infty [\log \xi _1]$ and ${\mathbb {E}}_0[\log \xi _1]$ exist, and define

$$\begin{aligned}&\lambda := {\mathbb {E}}_0[\log \xi _1], \qquad \alpha := {\mathbb {E}}_{\infty } [ \xi _1], \qquad \beta := {\mathbb {E}}_0 [ \xi _1], \qquad \gamma := \max \{\alpha ,\beta \}, \nonumber \\&\Phi _n:= \frac{1}{n} \log \prod ^n_{k=1} \xi _k, \qquad \psi _n := \log \Big (c+ \sum ^{n}_{l=1} e^{l (\Phi _l + \delta _l)} \Big ), \qquad \eta _n := \frac{\psi _n}{n}, \qquad n\ge 1,\nonumber \\ \end{aligned}$$

(5.5)

for some fixed constant $c > 0$ and deterministic sequence $\delta _l \xrightarrow {l \uparrow \infty } 0$. Then the following results hold under ${\mathbb {P}}$:

• (i) We have $\eta _n \xrightarrow {n \uparrow \infty } \lambda _+$ a.s.

• (ii) If $\lambda < 0$, then the process $\psi _n$ converges as $n \uparrow \infty$ to a finite limit a.s.

• (iii) If $\gamma <\infty$, then $(|\eta _n|^r)_{n\ge 1}$ is uniformly integrable.

• (iv) If $r\ge 1$ and $\max \{{\mathbb {E}}_{\infty }\left[ |\log \xi _1|^r\right] , {\mathbb {E}}_0\left[ |\log \xi _1|^r\right] \}<\infty$, then $(|\Phi _n|^q)_{n\ge 1}$ is uniformly integrable for every $0\le q \le r$.

With this lemma, we prove Lemma 4.2. We first suppose $\varrho ^{(j)} < \infty$. Setting in (5.5), $\xi _k := e^{-\varrho ^{(j)}} \frac{f_0(X_k)}{f_j(X_k)}$ and $c =\rho _0^{(j)} + \rho _1^{(j)} > 0$, we have

$$\begin{aligned} L_n^{(j)}&= \log \Big ( \rho _0^{(j)} + \sum _{k=1}^n {\rho _k^{(j)}} e^{(k-1) (\Phi _{k-1} + \varrho ^{(j)})}\Big ) = \log \Big ( c+ \sum _{k=2}^n {\rho _k^{(j)}} e^{(k-1) (\Phi _{k-1} + \varrho ^{(j)})}\Big ) \\&= \log \Big ( c + \sum _{k=1}^{n-1} {\rho _{k+1}^{(j)}} e^{k (\Phi _k + \varrho ^{(j)})} \Big ) \\&= \log \Big ( c + \sum _{k=1}^{n-1} \exp (\log \rho _{k+1}^{(j)} + k\varrho ^{(j)}) e^{k \Phi _k } \Big ) = \log \Big ( c + \sum _{k=1}^{n-1} e^{k (\Phi _k + \delta _k)} \Big ) \end{aligned}$$

where $\delta _k := (\log \rho _{k+1}^{(j)})/k + \varrho ^{(j)} \xrightarrow {k \uparrow \infty } 0$ by Assumption 4.1. Given that $\mu =i$ and $\theta =t$ for any fixed $i\in {\mathcal {M}}$ and $t\ge 1$, the random variables $\xi _t, \xi _{t+1},\ldots$ are conditionally i.i.d. with a common distribution independent of t; thus, the change time $\theta$ plays the role of the random time T in Lemma 5.4. Now, by Lemma 5.4 (i) and (4.6) we have $L_n^{(j)}/n \xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i-a.s.} \big [\int _E \big ( -\varrho ^{(j)} + \log \frac{f_0(x)}{f_j(x)} \big ) f_i(x) \mathrm {m} ({\mathrm{d}}x)\big ]_+ = \big [ q(i,j)-q(i,0) - \varrho ^{(j)} \big ]_+$, which proves (ii) immediately for $j\in {\mathcal {M}}\setminus \{i\}$, and (i) and (iv) by Lemma 5.4 (ii) for $j=i$ because (4.5) gives

$$\begin{aligned} \int _E \left( -\varrho ^{(i)} + \log \frac{f_0(x)}{f_i(x)} \right) f_i(x) \mathrm {m} ({\mathrm{d}}x)= q(i,i) -q(i,0) - \varrho ^{(i)} = -q(i,0) - \varrho ^{(i)} < 0. \end{aligned}$$

Similarly, for $j \in \Gamma _i$, (v) holds by Lemma 5.4 (ii), since

$$\begin{aligned} \int _E \left( -\varrho ^{(j)} + \log \frac{f_0(x)}{f_j(x)} \right) f_i(x) \mathrm {m} ({\mathrm{d}}x)= q(i,j) -q(i,0) - \varrho ^{(j)} < 0 \end{aligned}$$

by the definition of $\Gamma _i$. By (4.8), the SLLN and (ii),

$$\begin{aligned} \frac{1}{n} K_n^{(j)} = - \frac{1}{n} \log \rho _n^{(j)} + \frac{1}{n} \sum _{l=1}^{n \wedge (\theta -1)} \log \frac{f_j(X_l)}{f_0(X_l)} + \frac{1}{n} \sum _{l=\theta \wedge n}^n \log \frac{f_j(X_l)}{f_0(X_l)}+ \frac{1}{n} L_n^{(j)}\\ \xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i-a.s.} \varrho ^{(j)} +0 -q(i,j) + q(i,0) + \left[ q(i,j)-q(i,0) - \varrho ^{(j)} \right] _+, \end{aligned}$$

which equals $\left[ q(i,j)-q(i,0)-\varrho ^{(j)}\right] _-$ and proves (iii). For the proof of (vi), it holds by Lemma 5.4 (iii) and the assumption (4.11). Finally, for the proof of (vii), (4.8) implies

$$\begin{aligned}&\Big | \frac{1}{n}K^{(j)}_n\Big |^r = \Big |- \frac{1}{n} \log \rho _n^{(j)} - \varrho ^{(j)} + \frac{1}{n}\log \prod ^n_{k=1} e^{\varrho ^{(j)}} \frac{f_j(X_k)}{f_0(X_k)} +\frac{1}{n} L^{(j)}_n\Big |^r \\&\quad \le 2^{r-1}\Big ( \Big |\frac{1}{n} \log \rho _n^{(j)} + \varrho ^{(j)}\Big |^r + \Big |\frac{1}{n}\log \prod ^n_{k=1} e^{\varrho ^{(j)}}\frac{f_j(X_k)}{f_0(X_k)}\Big |^r + \Big |\frac{1}{n} L^{(j)}_n\Big |^r\Big ). \end{aligned}$$

Because (4.11) holds, $(|L^{(j)}_n/n|)_{n\ge 1}$ is uniformly integrable by (vi). If we set $\xi _k := e^{\varrho ^{(j)}}[f_j(X_k)/f_0(X_k)]$ for every $k\ge 1$ in (5.5), then (4.12) and Lemma 5.4 (iv) imply that $(|\frac{1}{n}\log \prod ^n_{k=1} (e^{\varrho ^{(j)}}\frac{f_j(X_k)}{f_0(X_k)})|^r)_{n\ge 1}$ is uniformly integrable. Therefore, $(|K^{(j)}_n/n|^r)_{n\ge 1}$ is uniformly integrable, and the proof of (vii) is complete.

By Remark 4.1 (1), it is now sufficient to prove (ii), (v) and (vi), when $\varrho ^{(j)} = \infty$ (which implies $q(i,j) < \infty$ by Assumption 4.4). For any $M > q(i,j)-q(i,0)$, $L_n^{(j)}$ is bounded by

$$\begin{aligned} L_n^{(j,M)}&:= \log \Big ( c + \sum _{k=2}^n (\rho _k^{(j)} \vee e^{-(k-1)M}) \prod _{l=1}^{k-1} \frac{f_0(X_l)}{f_j(X_l)} \Big )\\&=\log \Big ( c + \sum _{k=1}^{n-1} ({\rho _{k+1}^{(j)}} \vee e^{-kM}) \prod _{l=1}^{k} \frac{f_0(X_l)}{f_j(X_l)}\Big ) \\&=\log \Big ( c + \sum _{k=1}^{n-1} ({\rho _{k+1}^{(j)}} e^{kM}\vee 1) \prod _{l=1}^{k} e^{-M}\frac{f_0(X_l)}{f_j(X_l)}\Big ) \\&=\log \Big ( c + \sum _{k=1}^{n-1} e^{k([M + (\log \rho _{k+1}^{(j)})/k]\vee 0)} \exp \Big (\sum _{l=1}^{k} ({-M} + \log \frac{f_0(X_l)}{f_j(X_l)}) \Big ) \Big ). \end{aligned}$$

Because $[M + (\log \rho _{k+1}^{(j)})/k]\vee 0 \xrightarrow {k \uparrow \infty } 0$ by $\varrho ^{(j)}=\infty$, applying Lemma 5.4 (i) we obtain $L_n^{(j,M)} /n\xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i-a.s.} 0$. Because $L_n^{(j)}$ is bounded from below and above by $\log c$ and $L_n^{(j,M)}$ respectively, we obtain $L_n^{(j)} /n\xrightarrow [n \uparrow \infty ]{{\mathbb {P}}_i-a.s.} 0$ proving (ii). Because $L_n^{(j)}$ is increasing ${\mathbb {P}}_i$-a.s., its limit $L_\infty ^{(j)}$ exists. Moreover, because it is bounded by $L_\infty ^{(j,M)} < \infty$, $L_\infty ^{(j)}$ is finite ${\mathbb {P}}_i$-a.s., showing (v). Finally, because $L_n^{(j)}/n$ is bounded by $L_n^{(j,M)}/n$ and the latter is $L^r({\mathbb {P}}_i)$-uniformly integrable, we also have (vi).

1.4 A.4. Proof of Lemma  4.3

Fix $i \in {\mathcal {M}}$. Similar to Lemma 5.3, for any $n \ge 1$ and $(x_1,\ldots , x_n) \in E^n$, we obtain

$$\begin{aligned}&{\widetilde{\alpha }}_n^{(i)} (x_1,\ldots , x_n) = \nu _i \Big [ \rho _0^{(i)} \prod _{k=1}^n f_i(x_k) + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} f_i^{(0)}(x_l) \prod _{m=k}^n f_i(x_m) \Big ], \\&\quad \sum _{y \in {\mathcal {Y}}_{0}^{(i)}}\alpha _n (x_1,...,x_n, y) = \nu _i \big (1- \sum _{t=0}^n \rho _t^{(i)} \big ) \prod _{l=1}^n f_i^{(0)}(x_l). \end{aligned}$$

Therefore, for every $j \in {\mathcal {M}}\backslash \{i\}$,

$$\begin{aligned} \Lambda _n(i,j)&= \log \left( \frac{\nu _i \big [ \rho _0^{(i)} \prod _{k=1}^n f_i(X_k) + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} f_i^{(0)}(X_l) \prod _{m=k}^n f_i (X_m) \big ]}{\nu _j \big [ \rho _0^{(j)} \prod _{k=1}^n f_j(X_k) + \sum _{k=1}^n \rho _k^{(j)} \prod _{l=1}^{k-1} f_j^{(0)}(X_l) \prod _{m=k}^n f_j (X_m) \big ]} \right) \\&= \log \left( \frac{\nu _i}{\nu _j} \prod _{k=1}^n \frac{ f_i(X_k)}{ f_j(X_k)} \frac{\exp L_n^{(i)}}{\exp L_n^{(j)}} \right) = \log \frac{\nu _i}{\nu _j} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j(X_k)} + L_n^{(i)} - L_n^{(j)}, \end{aligned}$$

and

$$\begin{aligned} \Lambda _n(i,j)&= \log \left( \frac{\nu _i}{\nu _j} \frac{1}{\rho _n^{(j)}}\prod _{k=1}^n \frac{ f_i(X_k)}{ f_j^{(0)}(X_k)} \frac{\rho _0^{(i)} + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} \frac{f_i^{(0)}(X_l)}{f_i(X_l)} }{\frac{\rho _0^{(j)}}{\rho _n^{(j)}} \prod _{k=1}^n \frac{f_j(X_k)}{f_j^{(0)}(X_k)} + \sum _{k=1}^n \frac{\rho _k^{(j)}}{\rho _n^{(j)}} \prod _{m=k}^n \frac{f_j(X_m)}{f_j^{(0)}(X_m)} } \right) \\&= \log \frac{\nu _i}{\nu _j} - \log \rho _n^{(j)} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j^{(0)}(X_k)} + L_n^{(i)} - K_n^{(j)}. \end{aligned}$$

On the other hand, for every $j \in {\mathcal {M}}$,

$$\begin{aligned} \Lambda _n^{(0)}(i,j)&= \log \left( \frac{\nu _i \big [ \rho _0^{(i)} \prod _{k=1}^n f_i(X_k) + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} f_i^{(0)}(X_l) \prod _{m=k}^n f_i (X_m) \big ]}{\nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) \prod _{l=1}^n f_j^{(0)}(X_l)} \right) \\&= \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j^{(0)}(X_k)} + \log \left( \frac{\nu _i \Big [ \rho _0^{(i)} + \sum _{k=1}^n \rho _k^{(i)} \prod _{l=1}^{k-1} \frac{f_i^{(0)}(X_l)}{f_i(X_l)} \Big ]}{\nu _j \big (1- \sum _{t=0}^n \rho _t^{(j)} \big ) } \right) \\&= \log \frac{\nu _i}{\nu _j} + \sum _{k=1}^n \log \frac{ f_i(X_k)}{ f_j^{(0)}(X_k)} + L_n^{(i)} - \log \big ( 1- \sum _{t=0}^n \rho _t^{(j)} \big ), \end{aligned}$$

as desired.