Introduction

Diversity is not only a central concept in scientometrics (e.g., interdisciplinarity), but also in ecology (e.g., Jost, 2007) or in the social sciences (e.g., Brusco et al., 2020; Jones & Dovidio, 2018). Therefore, the measurement and operationalization of this concept is of eminent importance, which is also reflected in numerous publications on this concept especially in the field of ecology (see Foredeman et al. (2017)). A certain break in the development of this concept comes from the work of Rao and Stirling (Rao, 1982; Stirling, 2007), who developed a diversity concept based on the existing literature, which, in brief, consists of three components:

  • Variety «Variety is the number of categories into which system elements apportioned. It is the answer to the question: “How many types of things we have? … All else being equal, the greater the variety, the greater the diversity.» (Stirling, 2007, p. 709),

  • Balance «Balance is a function of the pattern of apportionment of elements across categories… All else being equal the more even is the balance, the greater the diversity.» (Stirling, 2007, p. 709),

  • Disparity “Disparity refers to the manner and degree in which the elements may be distinguished… All else being equal, the more disparate are the represented elements, the greater the diversity.” (Stirling, 2007, p. 709).

Thus, first Rao (1982) and later Stirling (2007, p. 721) developed a "general diversity heuristic" as a sum indicator of different elements j, i of a system (e.g., different research area in research proposals):

$$ D = \sum\limits_{ji(i \ne j)} {d_{ij} p_{i} p_{j} } $$
(1)

where pi and pj are proportions of elements i and j in the system (as base for balance), and dij is the is the degree of difference between the elements (disparity). Variety is the number of different elements. This concept had a strong influence not only in ecology (e.g., Rousseau et al., 1999) but also in scientometrics (e.g., Goyanes et al., 2020; Rousseau, 2018; Wang, Thijs, & Glänzel, 2015). The idea of composing an indicator multiplicatively from several individual indicators is captivating and opens up many possibilities for analysis. It is also easy to calculate.

Unfortunately, Rousseau (2018, p. 651) was able to show with a simple data example that a central assumption of the diversity indicator ("monotonicity") formulated by Stirling (2007, p. 711) does not hold. For a given variety and disparity the measure does not increase monotonically with balance. This points to fundamental problems with this concept. It is to the credit of Leydesdorff (2018) and Leydesdorff, Wagner, and Bornmann (2019b) to create an indicator that does not have these problems and continues to multiplicatively link the three individual diversity indicators, which is certainly a viable approach despite criticism and modifications (Leydesdorff et al., 2019a; Rousseau, 2019).

For i = 1 to nc and j = 1 to nc categories, the diversity is defined as follows (Leydesdorff, 2018, p. 2116):

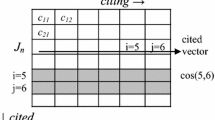
$$ Div_{c} = (n_{c} /N) \cdot GINI \cdot \left[ {\sum\limits_{\begin{subarray}{l} i = 1 \\ j = 1 \\ i \ne j \end{subarray} }^{\begin{subarray}{l} i = n_{c} \\ j = n_{c} \end{subarray} } {\frac{{d_{ij} }}{{(n_{c} \cdot (n_{c} - 1))}}} } \right], $$
(2)

where nc is the number of categories, N the total number of categories, GINI is the Gini-coefficient, dij is the disparity the Euclidean distance in terms of 1-cosine (Ahlgren et al., 2003), which is normalized by the factor (nc (nc − 1)). Unlike the classical Euclidean measure, dij in terms of 1-cosine varies between 0 and 1. The Bravais-Pearson correlation is not suitable for measuring similarity taking values between − 1 and + 1. Additionally, the cosine measure is invariant for adding zeros.

In this paper, a different path shall be taken, namely a path back to the information-theoretical roots of this concept, which is based on probabilistic foundations as already used by Shannon (1948). Although the initial work of Shannon and the entropy concept is mentioned in most publications and is also part of Stirling's concept, the probabilistic foundation and the classical entropy concept seems to have been lost or is currently not sufficiently received. For example, in a paper in Scientometrics, Shaw Jr. (1981) derives his concept of information theory from a thermodynamic representation of entropy, in which probabilities are only implicitly used. But why is probability theory for a consistent diversity concept so important? Four main reasons can be given:

  1. 1.

    Unclear theoretical basis: The theoretical basis for combining the different elements of diversity is not immediately apparent. For example, probabilities as pj or pi are linked to correlations or similarity measures (dij, Eq. 1, 2), which is not statistically derived from any probabilistic or statistical framework. Even Rao (1982, p. 7) himself says about the choice of dij: “The choice of dij is not a statistical problem and will depend on an individual's assessment of differences between qualitative categories reference to a given problem. However, one can use methods of multidimensional scaling in estimating dij by using supplementary information such as inequality relationships between dij and drs for different (i, j) and (r, s).”

  2. 2.

    Accuracy: Most diversity indicators are defined numerically, although the relative frequencies or probabilities are statistical quantities and thus have a statistical measurement error. Probabilities based on small sample sizes are far less accurate than probabilities estimated from large samples.

  3. 3.

    Interpretation of indicators: Given the large number of diversity indicators, the question remains as to how to interpret the individual indicators and what advantages one indicator has over another indicator.

  4. 4.

    Statistical analysis: Diversity indicators often have to be processed statistically, which in turn requires distributional assumptions. Therefore, the question is whether the data should not be formulated in a probabilistic form in order to apply the statistical analysis more or less directly to the raw data.

The central idea of the paper is to refer back to Shannon's concept of entropy (Leydesdorff & Ivanova, 2021), which is based on probability theory and forms the basis of today's diversity concepts, to arrive at a modified concept of diversity that firstly avoids previous inconsistencies in the diversity concept, secondly allows a simple form of interpretation in terms of uncertainty and reduction of uncertainty (entropy), and thirdly forms the basis both for new types of diversity indicators and for statistical modelling. When it comes to an application, the probabilities must be determined numerically, and that's when statistics comes into play. Probabilities are not fixed quantities but, like any statistical parameter, have estimation errors that are higher the smaller the sample size. Additionally, statistical models make it possible to include explanatory variables to explain, predict or adjust probabilities. Therefore, the information-theoretical approach is complemented by a statistical estimation approach. In the following, first the modified diversity concept and an indicator will be derived in probabilistic terms, and second a statistical approach will be outlined how to estimate these diversity components. The approach will be illustrated both with a practical application on research output data from Metrics Tide (https://responsiblemetrics.org/the-metric-tide/) and ex-ante evaluation data of projects funded by a Swiss research funding organization. The paper is an extended version (statistical approach, ex-ante evaluation data) of a paper presented at the “International Conference on Scientometrics and Informetrics” (ISSI 2021) (Mutz, 2021).

Methodological approach

Probabilistic framework of information theory and modified diversity indicator div e

Within information theory, information is defined purely syntactically without reference to semantics based on probability theory. In the following, a simple example will be taken as a starting point: The diversity of research output types of funded projects in the field of Natural Science (e.g., Mutz et al., 2012, 2014). Let us assume that project reports from 1,000 funded projects are available as part of an ex-post evaluation (synthetic data, Table 1) with two outputs. The marginal frequencies of N = 4 different output types (output 1) are shown in Table 2, on one side before the data analysis without any information (prior or expectations) and on the other side after the empirical data analysis (posterior).

Table 1 Toy example: Cross table of output 1 and output 2 for 1000 funded projects (case II dependence)
Full size table
Table 2 Marginal relative frequencies for different output types (data example) and decision tree
Full size table

We choose a step-by-step approach. First, we explain the basic concepts of Shannon's information theory using the marginal frequency table of document types (Table 2, output 1) on the assumption that a project produces only one output of a particular type at a time. However, research projects usually produce several outputs, which might be combined, e.g., output 1 "article" and output 2 "article". Therefore, in a second step, it is necessary to open the box by analyzing the combination of document types of the first versus the second output in a cross table “output 1 × output 2” (Table 1). A further information-theoretical concept will be introduced, the concept of "mutual information". A very good introduction can also be found in the works of Leydesdorff (Leydesdorff, 1991, 1995; Leydesdorff & Ivanova, 2021).

Step 1: Basic concepts

The following metaphor can be used to define information (Amann & Müller-Herold, 2011, p. 1f). If one wants to know the type of one of the four project outputs, exactly 2 binary questions are necessary to determine the type (Table 2, decision tree). With 8 output types 3 binary questions and with N = 2k types k binary questions are necessary. The information content as number of binary questions is defined as I = k = log2(N), if all events are equally likely to occur (prior, Table 2) or no empirical information is available. The maximum information content in the case of equal probabilities is I = log2(4) = 2 bits (see Table 2, code). Another definition of information is obtained from probability theory, where the output type is a random variable X with j = 1 to N possible events or occurrences (books, articles,…). Thus, the information content is log2(1/pj) or − log2(pj) with pj = 1/N if all events have the same probability (assumption log2(pj = 0) = 0). The rarer the event, the lower the probability, the higher the information. The average information over all events is then:

$$ H(X) = \sum\limits_{j = 1}^{N} { - p_{j} \log_{2} (p_{j} )} $$
(3)

and is called Shannon entropy with the assumptions that \(\sum\nolimits_{i = 1}^{N} {p_{j} = 1.0}\) and log2(pj = 0) = 0. It is assumed in a first step that the probability of occurrence of one event does not depend on the probability of occurrence of another event, an assumption which will be given up later. In research projects, the publication of proceedings papers should not depend on whether or not a journal article has also been published.

Shannon Entropy, as a measure of information, ultimately expresses the degree of uncertainty. For example, in a coin toss the uncertainty is highest when the probability of heads or tails is 0.5. A probability of 0.8 for heads, for example, reduces the uncertainty (tampered coin toss). People who bet on "heads" have a greater chance of winning than those who bet on "tails". In the above example, maximum entropy (H(X) = 2) is reached when there is equal probability (pj = 0.25) of the events. However, the actual observed frequencies as an estimate of the probabilities are not equal, the resulting entropy and thus uncertainty is reduced by 54% from 2 to 0.92 bits (see Table 2). The total entropy is the sum of − 0.1*log2(0.1) − 0.8* − log2(0.8) − 0.1*log2(0.1) − 0*log2(0) = 0.92. These considerations are in line with the idea of Bayesian statistics, in which probability is defined as uncertainty. Bayesian Inference can be defined as a statistical learning process in which an initial uncertainty about a parameter defined as a prior probability is reduced in light of the data (posterior probability). (Kruschke, 2011, p. 56f). With the entropy concept, a first measure of diversity can be derived, that is "balance". For example, the more the observed probabilities resemble an equal probability, the higher is the so-called balance, the higher is the entropy or uncertainty.

Shannon also refers to "variety": "With equally likely events there is more choice, or uncertainty, when there are more possible events." (Shannon, 1948, p. 10). Furthermore, variety could also be traced back to an entropy measure. The maximum possible variety would be N, i.e., the maximum possible number of events in a population (here N = 4 output types). Finally, the maximum variety can be defined as the maximum entropy of the system as follows:

$$ H_{{Variety_{\max } }} = \sum\limits_{j = 1}^{N} {1/N\log_{2} (1/N)} = - \log_{2} (1/N) $$
(4)

In the case of four output types, the maximum variety would be − log2(1/4). The observed variety corresponds to the number of events with nonzero probability pj > 0:

$$ H_{{Variety_{obs} }} = - \sum\limits_{j = 1}^{N} {\left( {(p_{j} > 0)\frac{1}{{\sum\limits_{j = 1}^{N} {(p_{j} > 0)} }}\log_{2} \left( {\frac{1}{{\sum\limits_{j = 1}^{N} {(p_{j} > 0)} }}} \right)} \right)} = - \log_{2} (1/\sum\limits_{j = 1}^{N} {(p_{j} > 0)} ), $$
(5)

where \(\sum\limits_{j = 1}^{N} {(p_{j} > 0)}\) is the number of units (e.g., disciplines) in use. Eventually, (pj > 0) is a 0/1-indicator variable with 1 (if pj > 0) and 0 (if pj = 0)).

For the above example, the varietyobs is − log2(1/3). Similarly, (Leydesdorff 2018, p. 2115) argues when defining a relative variety \(\sum\nolimits_{j = 1}^{N} {(p_{j} > 0)} /N\). For an common diversity indicator one could add the two entropy masses balance and diversity, although this sum does not represent a joint-distribution H(A, B) in probabilistic terms, but can still be interpreted in terms of entropy with balance and variety as independent quantities:

$$ H_{diversity} = H_{{{\text{var}} iety}} + H_{balance} $$
(6)

Step 2: “Mutual information”

To get to the last component of diversity, "disparity", the assumption of independent events has to be abandoned. For example, research outputs in a research project may be published in different output types and this may create stochastic dependencies. For example, the probability of a research article may depend on whether or not a proceedings paper has been published. For simplification, it is assumed that results of a research project are published in two research outputs with a maximum of two different output types, where it is also possible that none of the output types is published or the same output type can be chosen twice. These two research outputs can be defined as two random variables X and Y.

Table 3 presents a cross-tabulation of cell frequencies and marginal frequencies of the two outputs, where the marginal frequencies of the type of the two outputs are the same as in Table 2, but do not correspond to the cell frequencies of Table 1. It quickly becomes apparent that output 2 does not depend on output 1; the ratios of the relative frequencies across the columns remain the same across the rows. For example, for “articles” the row frequencies divided by the respective marginal frequency remains equal across columns: 0.08/0.10 = 0.64/0.80 = 0.08/0.10 = 0.80. Thus p(X|Y) = P(X) or H(X, Y) = H(X) + H(Y), the marginal frequencies are sufficient (“overall stochastic balance”).

Table 3 Case I: Independence
Full size table

For Table 4, which corresponds to the data of Table 1, the situation is different: P(X|Y) ≠ P(X), i.e., stochastic dependence is present. For example, articles in both outputs occur more frequently (p = 0.80) than expected in the case of independence of X and Y (p = 0.80*0.80 = 0.64). Two events are stochastically independent, if the probability of X AND Y equals the product of the probability of X and the probability of Y: P(X ∩ Y) = P(X) P(Y).

Table 4 Case II: Dependence
Full size table

In that case, Shannon coined the term mutual information I(X, Y), i.e. the reduction of the uncertainty of one random variable by considering another random variable. In the case of two random variables, the mutual information is (Eshima, 2020, p. 8f):

$$ I(X,Y) = H(X) + H(Y) - H(X,Y) = H(Y) - H(Y|X) $$
(7)
$$ H(X|Y) = H(X) - I(X,Y) $$

The joint entropy of X and Y is then (see Fig. 1):

$$ H(X,Y) = H(X) + H(Y) - I(X,Y) $$
(8)

The mutual information I(X, Y) can be calculated form the data using the following equation:

$$ I(X,Y) = \sum\limits_{x\varepsilon X} {\sum\limits_{y\varepsilon Y} {p(x,y)\log_{2} \left( {\frac{p(x,y)}{{p(x)p(y)}}} \right)} } , $$
(9)

where p(x, y) is the joint probability of X and Y. If the events are independent, then p(x, y) = p(x)p(y) and I(X, Y) = 0. The more the event Y depends on X, the higher the mutual information I(X, Y), the lower the total entropy H(X, Y). Mutual information represents the stochastic dependence of X and Y and is not a correlation. Regarding binary communications Pregowska, Szczepanski, and Wajnryb (2015, p. 1) conclude: “Our research shows that the mutual information cannot be replaced by sheer correlations.” With respect to Table 4 the mutual information for output 1 “article” and output 2 “article” is I(X = 2, Y = 2) = 0.80 log2(0.80/(0.80 0.80)) = 0.80 log2(1.25) = 0.258.

In Fig. 2 the relationships of the different concepts of entropy and mutual information are shown as a Venn diagram (Fig. 1).

Fig. 1
figure 1

Entropy measures

Full size image

Finally, mutual information, already mentioned by Shannon (1948, p. 12), defines the third component of diversity, "disparity", i.e. the degree of dependence of categories or events. The higher I(X, Y), the lower the disparity. If I(X, Y) is zero, then the disparity is maximal.

In the above example (Table 4), the mutual information is I(X, Y) = 0.72, the unconditional entropy of X is H(X) = 0.92, and the conditional entropy is H(X|Y) = 0.20. This reduces the uncertainty, i.e., overall diversity, by (0.92-0.20)/0.92) = 78.3% when taking into account the dependence in the data in the sense of disparity. Another measure of dependency is Cramer`s V a correlation coefficient, for categorical variables. Comparable to the mutual information I(X, Y), Cramer`s V of 0.29 shows that output 1 and output 2 are correlated.

In the case of 3 research outputs X, Y and Z, for example, the above formula, corresponding to the addition theorem of probabilities, expands as follows:

$$ H(Y,X,Z) = H(Y) + H(X) + H(Z) - I(Y,X) - I(Y,Z) - I(X,Z) + I(Y,X,Z), $$
(10)

where the last term of Eq. 10 is positive and represents a correction term in a quantity algebraic representation (i.e., subtraction of an intersection).

Unlike Stirling and Leydesdorff (Leydesdorff, 2018; Leydesdorff et al., 2019a; Stirling, 2007), the different components of the overall diversity indicator dive are now additive:

$$ div_{e} = H_{{{\text{var}} iety}} + H_{balance} - I_{disparity} , $$
(11)

where dive = 4.15 for the above example.

In summary: On the probabilistic basis of Shannon's entropy concept, a modified diversity concept was derived that is consistent, additive in nature and whose components can be empirically derived. The entropy concept gives the diversity concept a clear interpretation: the higher the diversity, the higher the information, the higher the uncertainty, the less structure there is in the data.

Statistical approach

The concept of diversity as entropy leaves unanswered how the probabilities for calculating entropy can be estimated statistically. To simply determine them by relative frequencies falls short for several reasons. bibliometric data fluctuate randomly and systematically over time because bibliographic data bases are continuously updated (journals, articles, citations, …). Furthermore, the data bases are incomplete with respect to fields and document types, for instance. Relative frequencies are only good estimates of probabilities when the sample size goes to infinity. In the case of low sample size or cell frequencies the estimation errors must be taken into account. Statistical models allow to include covariates to explain, predict or adjust probabilities (Bornmann et al., 2021, p. 9317f). Different approaches to the statistical estimation of entropy can be found in the diversity literature, especially in ecology.

In the following, the thematic focus is no longer on the diversity of output types, but on the interdisciplinary nature of projects—the content changes, the methodological concept remains the same (“disciplines” are the “outputs”). In order to conduct statistical analyses, a concrete design for the survey of interdisciplinarity is required, which will guide the statistical analyses. For instance, in the realm of the ex-ante evaluation of project proposals in funding organizations, the simplest way to assess interdisciplinarity is for the principal investigators to list the individual disciplines that are relevant to the planned project. The specified single disciplines can be further grouped into major disciplines at different levels of aggregation. Since several individual disciplines can be assigned to one main discipline, in addition to a dichotomous representation (e.g., main discipline A present or not), which is favored here, a representation can be used that distinguishes different weights of main disciplines in a project proposal (e.g., three individual disciplines from the Humanities (weight = 0.75), one individual discipline from the Natural Sciences (weight = 0.25)). A simple data analysis strategy via cross-tabulations is distinguished from a more sophisticated one via parametric models.

Basic data analysis strategy

From the perspective of probability theory, each (main) discipline then establishes a random variable. Since certain disciplines are often mentioned together in project proposals (e.g., chemistry and biology), the random variables are usually not independent of each other (similarity), which is expressed in the diversity indicator "disparity" (1-similarity). For the estimation of diversity as entropy, the so-called marginal frequency or share of a discipline is, therefore, not sufficient; cell frequencies are also required (as shown in cross-tabulation of categorical random variables). In the simplest case of 2 disciplines (named or not named in the project application), a 2 × 2-cross-tabulation (Fig. 2, above) with cell frequencies results, which can be coded by a simple data design as base for estimation of the corresponding probabilities. Eventually, with cross-tabulations, cell frequencies can already be sufficiently calculated (alternatively via log-linear models).

Fig. 2
figure 2

Cross-tabulate and data for the statistical estimation of probabilities for two disciplines: Cross-tabulate with cell frequencies (above), which can be estimated by the data design (below), where d1-d4 are the dummy-codes cells (k) of the cross-tabulate (k = cell number)

Full size image

Sophisticated analysis strategy

Here, a sophisticated analysis strategy is preferred, which offers the opportunity, not only to estimate probabilities, standard errors and confidence intervals, but also allows to include covariates to predict and explain probabilities and to derive statistically diversity measures. For example, it can be tested, whether different funding programs differ in the degree of interdisciplinarity of their funded projects. The central idea of this sophisticated strategy is to express the probabilities pij (Fig. 2.) in parameters (Eq. 15), which are statistically estimated assuming a certain distribution, here the multinomial distribution.

In order to apply this sophisticated data analysis strategy the data must be organized as in Fig. 2 (below): The different cells of a cross table are designated by k, which are transformed into k 0/1 dummy variables. In order to estimate the variety, the data set is additionally supplemented by a variable comprising the number of disciplines (NUM_DISC), mentioned in the proposal.

For this data design, a multinomial distribution is ideal as a multivariate distribution of categorical variables, which is a multivariate generalization of the binomial distribution, where k-1 cells (and dummy variables) are independent of each other. The following simple multinomial regression model applies (Hedeker, 2003). The k-dimensional vector of dummy variables d for a unit i (here project application) is multinomially distributed with the k-dimensional vector of cell probabilities p as parameters.

$$ {\mathbf{d}}_{i} \sim multinom({\mathbf{p}}_{i} ) $$
(12)

however, to allow more complex statistical analysis, the following parametric version is chosen:

$$ {\text{p}}_{k} { = }\frac{{{\text{e}}^{{\alpha_{k} }} }}{{\sum\nolimits_{k = 1}^{K} {{\text{e}}^{{\alpha_{k} }} } }}{\text{,where for k = K: }}\alpha_{K} {\text{ = 0 (e}}^{0} = 1) $$
(14)

This parameterization offers the opportunity to insert further variables into the model to explain the probabilities, for example a dichotomous variable xi indicating the funding programme (1 = ”interdisciplinary programme”, 0 = “other programmes”).

$$ {\text{p}}_{k} { = }\frac{{{\text{e}}^{{\beta_{0k} + \beta_{1k} x_{i} }} }}{{\sum\limits_{k = 1}^{K} {{\text{e}}^{{\beta_{0k} + \beta_{1k} x_{i} }} } }}{\text{,where for k = K: }}\alpha_{K} {\text{ = 0 (e}}^{0} = 1) $$
(15)

Data and methods

Data example 1: Metric tide

To answer the question of how diverse research outputs are across research areas, we drew on data from the Metric Tide Report. Metric Tide analyzed the capabilities and limitations of research metrics and indicators. "It has explored the use of metrics across different disciplines and assessed their potential contribution to the development of research excellence and impact. It has analyzed their role in processes of research assessment, including the next cycle of the Research Excellence Framework (REF).

For the analysis, data on submissions for research projects funded since 2006 (Research Excellence Framework 2014) was used. Figure 3 shows an extract of the original cross table comparable to the cross table shown in Table 1 indicating how frequently 20 output types occur in 36 units of assessments (scientific disciplines). It would have been desirable for the analysis to have data on the output types for each individual research project. Such raw data were not available. Furthermore, it is not clear whether the frequencies represent the number of research projects in a cell or the sum of research outputs across all research projects in that cell.

Fig. 3
figure 3

Extract of the table of frequencies for 23 research areas (UOA) × 6 output types (Wilsdon et al., 2015, p. 154)

Full size image

To arrive at relative frequencies or probabilities, according to the simple data analysis strategy the absolute frequencies were divided by the total number (N = 190.962). Random variable X is the “output type”, and random variable Y is the “research area” (unit of assessment, UOA).

Data example 2: Ex-ante evaluation data of a Swiss research funding organization

The statistical estimation of diversity and its components is based on data from a Swiss research funding organization. Open access data were downloaded from 11,707 projects (funding type “project funding”) that were funded in the years 2010–2020 (year of project start) (https://p3.snf.ch/Pages/DataAndDocumentation.aspx). The analyses were done for the three main disciplines based on 159 subfields: "Biology and Medicine", "Humanities and Social Sciences", "Mathematics, Natural- and Engineering Sciences”.

The funding organization does not actually want to make a statement about the interdisciplinarity of its funded projects, but nevertheless codes in the dataset the different disciplines that were relevant in a funded project.

“Researchers allocate their application to a discipline in the SNFF list of disciplines. The disciplines are subsumed under research areas, which in turn form three major research domains: humanities and social sciences; mathematics, natural and engineering sciences; biology and medicine. Although many projects are interdisciplinary in nature, we use only the main discipline (as indicated in the application) for the key figures. If an application cannot be allocated to a main discipline based on the available data, we allocate it in equal parts to each of the mentioned disciplines”. (https://data.snf.ch/key-figures/documentation).

Nevertheless, it is worth analyzing these data for research purposes in order to illustrate the approach described. However, we will refrain from drawing any further conclusions with regard to the funding organization.

The open data policy of the funding organization allows: “Downloading, printing or storage of open data from the SNSF is allowed. If any of this data is published, the source must be cited explicitly.” (https://p3.snf.ch/Pages/OpenDataPolicy.aspx). It is also allowed to processing of open data from this funding organization.

Results

Data example 1: metric tide

Different measures can be calculated for the data organized as cross table (Table 5) in order to test, whether research areas differ in their output type or whether output types depend on research areas. Thus, a statistically significant χ2-test value, a Cramer`s V of 0.24 and a mutual information of − 0.40 show that the output type (X) depends on the research area (Y). Cramer`s V is a correlation measure for categorical variables varying between 0 and 1 and is more or less an alternative measure for the mutual information. There are, as expected, significant differences of the research area in the output types of the research output beyond chance. Looking at the ratio of the unconditional entropy of "output type", H(X), and “research area”, H(Y), to the total entropy, H(X, Y), the differences in frequencies are very much determined by the differences in "research areas" than the differences between "output types". While considering the "research area" reduces about (1.20–0.80)/1.20 = 33% of the uncertainty in the "output types", conversely only about (4.96–4.56)/4.96 = 8% of uncertainty in the "research areas" is reduced.

Table 5 χ2 and entropy measures
Full size table

Overall, however, the diversity at 10.08 is very high, which is about 72.9% of the maximum possible diversity of 13.81. The maximum variety in the whole table is fully reached and the overall balance of 6.16 is 64.9% of the maximum possible balance of 9.49.

Finally, diversity measures can be derived for the "research areas", which provide information about the diversity for individual research areas. Diversity indicators for the first 11 research areas are shown in Table 6. “Computer Science and Informatics" has the highest diversity with 4.19 and "Public Health, Health Services and Primary Care" the lowest with 2.13.

Table 6 Diversity measures for a set of 11 research areas (UOA)
Full size table

"Computer Science and Informatics" has the highest variety of 4.0. "Clinical Medicine" has the highest balance (0.27) in this set of selected research areas. Among the different output types, "Journal articles" clearly shows the highest individual entropy, H(Y), i.e., the highest balance among all other output types across different research area (Table 7).

Table 7 Output types with highest individual balance values
Full size table

Data example 2: Ex-ante evaluation data

The degree of interdisciplinarity is analyzed at the level of the 3 main disciplines. Overall, almost 90% of the funded projects are disciplinary (Table 8). For the funding instrument "interdisciplinary projects" the percentage of interdisciplinary projects increases to 68.8% compared to 8.7% for the "project funding in the narrow sense". This result provides empirical evidence for the use of these data for measurement issues in the realm of interdisciplinarity. In the following analysis only projects with more than one discipline are selected (N = 1221 projects).

Table 8 Cross-tabulation of funding instruments with interdisciplinarity with respect to the 3 main disciplines (absolute frequencies, row percent)
Full size table

The statistical approach allows the testing of hypotheses formulated as statistical models. The following hypothese will be tested (Table 9): There are differences in diversity as measure of interdisciplinarity between projects funded with the funding instrument "interdisciplinary projects" and projects funded with other instruments (M1). The lower the DIC the better the model fits the data. M1 shows a lower DIC than the basic model M0. There are, actually differences in diversity between the funding instruments “interdisciplinary projects” and the other funding instruments (M1).

Table 9 Model comparison regarding the 3 research domains (N = 1,221 projects) with the deviance information criterion (DIC)
Full size table

For the basic model (M0) the different diversity components were estimated with the 95%-credible interval. Additionally, the basic model was estimated for random data, which provide for maximum and reference values of the four different components. The variety of 1 reflect that on the average 2 disciplines were indicated by the applicants (HV = − 1/log2(1/2) = 1). The balance is about 81% of the maximum possible value, very high. There is some similarity or dependency among the three disciplines, the disparity is not Zero. Diversity is about half of the maximum possible entropy (Table 10).

Table 10 Estimated overall diversity components for interdisciplinary projects regarding the 3 research domains (N = 1,221 projects) with 95% credible interval in brackets
Full size table

Discussion

Diversity is a ubiquitous term used in many disciplines (e.g., ecology, sociology, bibliometrics). A certain break in the discussion on diversity and diversity indicators was brought about by the indicator developed by Rao (1982) and Stirling (2007), which in view of its comparatively simple definition has a very wide circulation. It is to the credit of Rousseau (2019) to point out inconsistencies in this indicator, to which Leydesdorff (2018) has proposed a workable solution. Furthermore, statistical concepts such as probability and correlation/similarity are combined with each other in a way for which there is no statistical basis whatsoever, which was even noted by Rao (1982, p. 7).

Due to the problems of the Rao and Stirling indicator, the aim of this paper was to go back to Shannon's probabilistic concept of entropy (Shannon, 1948), which implicitly dealt with all three facets of diversity, in order to develop a modified concept of diversity from it, which is additive in its nature and allows for both the calculation of a diversity indicator dive as well as estimation diversity by a statistical model. Due to the fact that most interdisciplinarity indicators trace back to Shannon`s entropy, the Shannon`s concept of “mutual information” should be favored towards the concept of correlation (Pregowska et al., 2015). A statistical approach was presented how to estimate diversity and its components. In the sense of Occam's razor principle, the question arises as to why this more complex approach should be given preference in practice over the simple concept of Rao and Stirling. First of all, there is no intention to replace the existing diversity indicators, but to identify opportunities for improvement. The following four reasons could be put forward:

  1. 1.

    Inconsistencies: Concepts with obvious inconsistencies are not very convincing and reinforce the negative image of bibliometrics.

  2. 2.

    Interpretation: Diversity can be interpreted in terms of entropy as a measure of information. Diversity is at its maximum when events can no longer be predicted, as in a coin toss. The lower the diversity, the more predictable events are, the more structure is in the data.

  3. 3.

    Open the Pandorra`s box: The discussions on bibliometric concepts such as field normalization, definition of fields, fractional counting and also diversity seem to be more or less closed with some more or less workable solutions. These considerations might reopen the discussion.

  4. 4.

    Stochastic nature: If the occurrence of publications, research output, citations, etc. is assumed to base on a stochastic random process, this must be taken into account within the development of an indicator.

  5. 5.

    Statistical estimation: In principle, diversity and its various components can be statistically estimated, as shown.

The calculation of the disparity indicator requires a workable solution on how to deal with the number of components that increases when the number of units increases (e.g., research output types, number of disciplines). For example, with 3 disciplines (A, B, C), there are 4 components of disparity (AB, AC, BC, ABC), with 4 and more units the number of components strongly increases. Eventually, disparity be it mutual information or correlation reflects combinations of disciplines, which often occurs. To get rid of disparity (~ 0) different types of combinations have to distinguished with the help of a latent class analysis (Mutz & Daniel, 2013; Mutz et al., 2012, 2014). Statistically, within a latent class the different units (e.g., disciplines) are uncorrelated.