Introduction

Quantifying interdisciplinary research (IDR) is critical in developing our understanding of the conditions under which researchers integrate perspectives, concepts, theories, tools or techniques, and information or data from two or more bodies of specialized knowledge or research practice (Braun & Schubert, 2003; Chen et al., 2015; Porter et al., 2007). A dominant family of approaches in quantifying IDR uses citation data (Wagner et al., 2011; Wang et al., 2017). The most common such approach uses the list of references of any given publication (Abramo et al., 2018; Glänzel & Debackere, 2021; Leydesdorff & Goldstone, 2014; Porter et al., 2007; Zhang et al., 2018), as a coded proxy for the sources of knowledge (Mugabushaka et al., 2016; Wang et al., 2015). The references are subsequently categorized into disciplines, either by using standardized classifications such as the Web of Science (WoS) Subject Categories, by using journals as proxies for disciplines, or by using empirically defined classifications. Typically, the method also relies on some information about the similarity or cognitive distance between disciplines, such that integrating ideas from two similar disciplines will contribute less to interdisciplinary scores than from two dissimilar disciplines (Rafols, 2014). More generally, when a publication’s references are more diverse in terms of their disciplines, the publication is quantified as more interdisciplinary (Zwanenburg et al., 2022).

However, the measures of IDR that are based on references and their disciplines carry uncertainty, as they rely on assumptions that do not always hold. For example, literature may be cited for reasons other than to indicate the origin of ideas (Bornmann & Daniel, 2008), and the discipline of integrated ideas may not be derived from the included references. Further, different disciplines and journals have different citing practices, complicating the interpretation of the validity of IDR measures (Abramo et al., 2018).

Previous literature has recognized some of these limitations. For example, it has been acknowledged that the diversity of references relies on data dependent on authors’ choices in their citing behaviour and may deviate from the content of the interdisciplinary paper itself (Huutoniemi et al., 2010; Rousseau et al., 2019). Further, there have been inquiries into missing or mis-assigned category data, and its implications for IDR measurement (Calatrava Moreno et al., 2016; Moed et al., 1985). However, there has been no systematic evaluation of the assumptions of the reference-based measures of IDR, nor has there been any quantification of the uncertainty introduced by violations of these assumptions. We thus have little clue to what extent these limitations threaten the validity of measurement.

In this paper, we systematically evaluate the assumptions underlying reference-based measures of IDR, quantify IDR using the Rao Stirling index (RS index) and the Web of Science Subject Categories, and estimate the uncertainty of the RS index using bootstrapping. A better understanding of the uncertainty in reference-based IDR measures may help researchers implement and use these measures appropriately, thereby improving their ability to draw valid conclusions about interdisciplinarity.

Uncertainty in reference-based measures

Citation-based measures of the interdisciplinarity of publications rely on a number of logical sequence of steps, connecting the actual integration of knowledge from diverse disciplines (i.e. what an IDR measure should indicate) to the actual measure of it (Zwanenburg et al., 2022). Analysing these steps can help us systematically identify and discuss the sources of uncertainty associated with these measures, as shown in Fig. 1.

Fig. 1
figure 1

The process of calculating interdisciplinarity with RS index and sources of uncertainty. The workflow includes citing references by authors, collecting references and their associated journals from WoS, assigning journals into categories, and obtaining pairwise similarity. Uncertainty 1 occurs by different citation behaviour, uncertainty 2 is due to missing categorized journals for references, and uncertainty 3 is caused by allocating invalid categories to journals

Full size image

The first logical step is that authors’ integration of knowledge from diverse disciplines is codified in the cited references. Next, these cited references are captured in a bibliometric database. These captured references are then categorized into disciplines, for example by using a list of journals belonging to the Web of Science Subject Categories. Most citation-based measures of IDR are then produced using the resulting distribution of disciplines in the cited references, combined with data on the similarity of any two disciplines.

Reference-based measures of IDR thus rely on three key assumptions, namely that (1) references are in fact indicators of source disciplines, (2) references can be allocated to disciplines, and (3) that these allocations are valid.Footnote 1 As illustrated in Fig. 1, violations to these assumptions introduce uncertainty, as discussed in the next section.

Uncertainty 1: references may not indicate source disciplines

Reference-based measures of IDR implicitly assume that the references listed by authors reflect the ideas they integrate. However, it has been shown that references may be used without a direct relationship to the ideas integrated in the paper. Referencing resources is seen as a somewhat arbitrary behaviour, which can reflect an author’s inclination to a specific discipline, paper, journal, peer association or language (Silverman, 1985; Vinkler, 1987; Wagner et al., 2011; White & Wang, 1997; Zhang et al., 2018). Garfield (1965) identified 15 reasons to cite a resource, while more than half of these do not correspond to the ideas within the cited literature. Citing can help to convince reviewers and readers about the appropriateness of their techniques, theories, and results (Gilbert, 1977; Moed & Garfield, 2004), and it may help conform to the standards or regulations of publishing venues (Adams et al., 2016; Cassi et al., 2017). One review on studies on citing behaviour published from 1960 to 2005 found that of all references in papers, 10–50% of these were “perfunctory”, i.e. nonessential references without being relevant to the author’s main argument (Bornmann & Daniel, 2008). Conversely, a publication may integrate ideas without referring to the source of these ideas (MacRoberts & MacRoberts, 1988). While it is unclear if these false positives and false negatives would inflate or deflate IDR values, they are not accounted for in IDR measurement and undermine its validity.

Uncertainty 2: references may be uncategorized

Even when the cited references are reflective of the knowledge being integrated, they may not necessarily be allocatable to a discipline. Most measurements of IDR rely on databases such as Clarivate’s Web of Science or Elsevier’s Scopus which are unable to categorize all cited references into disciplines. Books, conference proceedings, and other non-journal publications are not assigned a Web of Science Subject Category or a class in Elsevier’s All Science Journal Classification. Furthermore, new, obscure, and non-English journals tend to lack a category in these databases and classifications. In past studies, the degree of missing categories of cited references has ranged from 27 to 75 percent (Porter & Rafols, 2009; Rafols et al., 2012). This missing data is more severe in disciplines that have historically published in non-journal outlets, such as the arts and humanities (Hicks, 2004; Wagner et al., 2011; Zhang et al., 2018).

Most measurements of IDR using the reference method has ignored or accepted this missing data without actively addressing it (Wang et al., 2017). This means that the measurement instance is either carried out based on a subset of the references, or not carried out at all. Several studies only quantify IDR for publications when they meet certain, largely arbitrary, criteria, such as having three (Cassi et al., 2014) or four categorized references (Yegros-Yegros et al., 2015), reducing some of the impact of missing data on IDR measurement. While some studies have added the missing data manually (Calatrava Moreno et al., 2016), this has only been done on a small scale and may be cost-prohibitive at a large scale. Some approaches allocate disciplines to cited references based on other information, such as by examining text, or evaluating the references of references recursively (Glänzel et al., 2021). Some may employ some form of clustering based on citation networks, with clusters providing a proxy for disciplines. While these alternative approaches may introduce less uncertainty, their novelty, computational expense, and issues with replicability (Klavans & Boyack, 2017; Waltman & Eck, 2012) introduce other limitations.

In sum, missing category data of cited references is clearly substantial in many studies on IDR. It introduces uncertainty, and we know little about what this means for the validity of IDR measurements.

Uncertainty 3: references may be allocated to disciplines inaccurately

Even when cited references are categorized, they may not be valid since the categorizations are normally based on the journals of the references, not the papers themselves (Moschini et al., 2020; Rafols & Leydesdorff, 2009; Zhang et al., 2018). It is possible that an individual paper is best categorised into a set of disciplines that are different from the set of disciplines allocated to its journal (Rafols & Leydesdorff, 2009). Journals often cannot be exactly matched with disciplines (Leydesdorff, 2006), and even when they are journals may cover multiple disciplines whereas individual papers may relate to only a subset of these. This last case may thus inflate measures of IDR. Although some approaches were proposed to deal with multi-category journals (Glänzel et al., 2021; Zhou et al., 2021) these methods cannot render reliable information about the subject category of the individual papers. Hence, the inheritance of the categories from the journal introduces uncertainty.

Uncertainty remains unquantified

Our evaluation indicates that reference-based measures of IDR, especially those that leverage standardized classifications, carry uncertainty due to various factors. Authors discretion in including references introduce some uncertainty. Not being able to classify, or classify correctly, the included references also introduce uncertainty in the measurement of IDR. While various studies have quantified missing data and explored some of the impacts, it is generally unclear what this means for measuring IDR, nor is it the only issue that threatens the validity of these measurements. Current practices to deal with the issues typically include papers in analysis that have a threshold of references with disciplines allocated, either absolutely or proportionally. We have little evidence in what these thresholds should be, or even if these approaches are effective. Could studies draw incorrect conclusions because of invalid measurements, or is this degree of uncertainty marginal and can we continue by ignoring these issues or applying current approaches such as using thresholds for the number of references?

To clarify this, in this paper we estimate uncertainty. The discussed sources of uncertainty will mean that the recognized share of each discipline may be over- or underrepresented. For instance, in a paper’s source disciplines, the share of one discipline may be underrepresented because of an author’s reference behaviour, because many references from this discipline are conference proceedings and thus not recognized, or because some references from this discipline are erroneously recognized as from another. Such misrepresentation mean uncertainty in the RS value to an estimable degree. By taking many random samples of the recognized set of disciplines, calculating the RS value for each, and evaluating the resulting variability of the RS value, we can estimate the degree of this uncertainty. This bootstrapping approach should produce a confidence interval that is sensitive to variations in the distribution of the recognized set of references, that are entirely conceivable given the three discussed sources of uncertainty.Footnote 2 As such, this confidence interval can form the basis for an uncertainty estimate that can then be used to filter out papers with uncertain IDR measurement. In the next sections, we demonstrate this using the Rao-Stirling diversity index as a measure for IDR.

Data and method

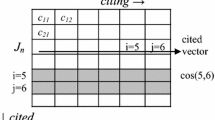
The Rao-Stirling diversity index (RS index), as applied to the disciplines of a paper’s cited references, is one of the most popular quantitative measures of IDR in the literature (Zhang et al., 2018). Appendix 1 indicates the application of RS index compared to recent measures improved based on this index. The RS index was first proposed by Rao (1982) in the context of mathematical biology. Stirling (2007) discussed it as a general measure to examine diversity in other areas of science, technology, and society (Leydesdorff et al., 2012). When applied to the categories of cited references (Porter & Rafols, 2009) the RS index, also known as the Integration score, ranges from zero, when all cited references are from a same category, to one when the cited references’ categories are maximally distant from each other. It is defined as:

$$RS index=1-{\sum }_{i,j}{S}_{ij}{P}_{i}{P}_{j}$$

where Pi is the proportion of references in each work that cite the Subject Category i, and Sij is the pair wise similarity between categories. For this paper we use the predefined similarity data developed by Rafols et al. (2010), based on the cosine similarity of any two categories’ frequencies with which they cite each category in the WoS classification. The similarity matrix was updated with 2015 publication data.

To evaluate the uncertainty of IDR across a wide range of papers, we selected all published papers in our university’s research output database with a matching record in the Web of Science database and at least one cited reference in WoS, totalling 42,660 publications. To allocate citation categories, we used a table of 29,679 journals each with one to six subject categories from the 255 WoS classification scheme, available from Web of Science.

Bootstrapping the RS index confidence interval

The non-parametric bootstrapping method (Diaconis & Efron, 1983) and bias-corrected CI (DiCiccio & Efron, 1996) were used to estimate uncertainty in IDR measurements with a 95% confidence interval. All recognized subject categories of the references for each publication were used to estimate the RS index by bootstrapping with 500 replicates using the boot() package (Banjanovic & Osborne, 2016) in RStudio version 4.2.1. The bootstrapping process, as shown in Fig. 2, takes a papers’ subject categories of size N and repeatedly resamples them with replacement to create category examples of size N. For each sample the RS index is calculated. Finally, the 95% confidence interval in the RS index was computed based on the RS index for each sample. To verify the bootstrapping output, we visually checked several example publications based on clustering of subject categories using dendrograms, as outlined in Appendix 2.

Fig. 2
figure 2

The bootstrapping process. Subject categories (size N) of cited references for a paper are repeatedly sampled with replacement to produce a new set of categories of size N. The RS index estimates from theses samples are used to estimate the range (confidence interval) estimate

Full size image

Results

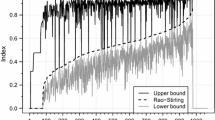
The bootstrapping process produces a lower (RSlci) and upper bound (RSuci) estimate for each paper’s RS index. Let the magnitude of the confidence interval be defined as |RSci|= RSuci–RSlci. This magnitude varies from 0.0 to about 0.6 with a distribution as shown in the results of bootstrapping in Fig. 3. The plot indicates that the highest frequency (more than 3500 papers in our sample) has a |RSci| around 0.15, which is somewhat lower than the average (0.18). The distribution of |RSci| is right-skewed normal with some values of |RSci| being exactly zero, which occurs when all cited references are in the same category.

Fig. 3
figure 3

Distribution of |RSci| calculated as RSuci—RSlci with redline showing average of |RSci|

Full size image

The highest values of the RS index (e.g., ≥ 0.8) have a very small |RSci| (~0.02), while the highest uncertainty in the RS index (|RSci|≥ 0.5) is found in low to medium interdisciplinary papers (RS index between 0.3 and 0.6), that do not have many cited references, as shown in Fig. 4. These papers have limited degrees of diversity in the reference list with references distributed in a small number of major disciplines (e.g., two to five). Based on Fig. 4, papers with few cited references may have relatively certain IDR values (|RSci|< 0.1) when the similarities of their disciplines are consistent. Alternatively, papers with a large number of references and diverse disciplines also have a small |RSci|. These properties are easily understood in terms of the resampling process of the bootstrap.

Fig. 4
figure 4

Size of confidence interval and RS value per number of citations in calculation

Full size image

While having many citations (> 75) is associated with less uncertainty, it is not a guarantee of certainty in RS values, as |RSci| ranges to 0.2 in Fig. 5. The |RSci| is large when publications contain a low number of categorized references (typically < 10). Figure 5 illustrates the confidence interval compared to the number of references used for each paper, showing that |RSci| declines with an increase in the number of references. In other words, as the number of references increase our confidence in the estimated value of the RS index increases (and therefore the uncertainty reduces).

Fig. 5
figure 5

Distribution of |RSci| per number of references

Full size image

Figure 6 shows the lower and upper bounds of RSci for papers in our dataset, ordered by RS which is indicated by the red line. The first such papers have an RS of zero, with RSlci = RSuci = 0, as these papers cite only a single discipline. Many other papers too have a lower bound of zero, which can be explained by having few references that have assigned categories. Notably, the lower bound can deviate more from RS than the upper bound, especially for papers of medium values of RS.

Fig. 6
figure 6

RS index ordered based on increasing RS value showing upper and bound for each paper

Full size image

These results indicate that uncertainty is often asymmetric and relating to the number of references in a non-linear way. It suggests that current approaches to reduce uncertainty by only including papers with a certain minimum number of references may be ineffective. However, the results also highlight the limitations of relying on the bootstrapped confidence interval. By itself, |RSci| suggests that we can be perfectly confident about IDR values of papers with very few references if all these references are in the same discipline. It ignores uncertainty due to omitted disciplines (e.g. omitted references or uncategorized references), and the number of references as an indicator of the sensitivity to this uncertainty. To illustrate, if a paper cites 50 references all within the same discipline, one is more confident of the resulting zero IDR score than if that same score was obtained from a paper with only two references, despite both having |RSci|= 0. We thus suggest that a more effective uncertainty estimate takes into account both the bootstrapped confidence interval and the number of references.

A more effective uncertainty estimate

We propose that a more effective uncertainty estimate combines a relative size of |RSci| and the log of the number of references, as follows:

$${\text{RS}}_{{{\text{unc}}}} = \, \left( {\left| {{\text{RS}}_{{{\text{ci}}}} } \right|/({\text{RS}} + {1})} \right) \, + \, \left( {{1}/{\text{log }}\left( {\left| {{\text{R}}_{{\text{i}}} } \right| + {1}} \right)} \right)$$

where for each paper RSunc refers to the uncertainty estimate, |RSci| is the confidence interval (RSuci–RSlci), RS is the Rao Stirling index, and |Ri| is the number of references used in computing RS (i.e. references published in a categorized journal). Both the denominators in this equation have one added to prevent division by zero. As shown in Fig. 7, papers vary widely on this uncertainty estimate, with most sitting between 0.25 and 0.75.

Fig. 7
figure 7

Percentage of included papers per threshold

Full size image

This variability allows us to use the measure to filter out those papers with the most uncertainty. Setting the threshold requires a trade-off between inclusivity of papers versus the confidence in their RS value. What trade-off is appropriate depends on the research context. We suggest a threshold of 0.5 for research contexts favoring middle ground between inclusivity and confidence. This threshold value means the number of references must at least be seven, even if |RSci|= 0. It includes a large majority of around 70% of papers, as shown in Fig. 7. Higher values for threshold (beyond 0.5) will mean including papers with considerably higher uncertainty, as shown in Fig. 8. Conversely, a lower threshold will mean a relatively large sacrifice in inclusivity.

Fig. 8
figure 8

Distribution of the confidence interval for papers per level of uncertainty

Full size image

To evaluate the performance of our suggested filter versus possible alternatives, we assess the ability to pick up expected variability across main disciplines. One can expect such variability to appear in valid comparisons, as applied disciplines have a stronger potential to draw from diverse disciplines than do more basic or fundamental disciplines (Van Rijnsoever & Hessels, 2011). Datasets that suffer from more uncertain measurements will carry more noise and therefore less variability across disciplines. Figure 9 compares these measurements for papers across the main subject categories in four scenarios: (a) all papers are included, (b) papers with 4 or more references are included, (c) papers with 10 or more references are included, and (d) papers with RSunc ≤ 0.5 are included. Unsurprisingly, the least variability across disciplines is picked up when including all papers (a), whereas the most is picked up when using our suggested filter (d), slightly more than a more stringent filter (c). In sum, the RSunc filtering performs relatively well in picking up expected signal.

Fig. 9
figure 9

Distribution of IDR scores across broad disciplinary categories with various filters applied: a |Ri|> 0, b |Ri|≥ 4, c |Ri|≥ 10, and d RSunc ≤ 0.5, where |Ri| refers to the number of references used in the calculation

Full size image

We performed a similar analysis of IDR variations at a finer level of disciplines, comparing high and low interdisciplinary subject categories before and after implementing different filters (Fig. 10). Within our dataset, we compared papers in Chemistry (CHEM), Mathematics (MATH), and Physics (PHY) with papers in Medicine (MED), using again the same scenarios. We found that the suggested uncertainty estimate performed most according to expectation, as papers in medicine as an applied science are on average more interdisciplinary than those in the basic science (Abramo et al., 2012; Institute of Medicine, 2005; Rijnsoever & Hessels, 2011; Rijnsoever et al., 2008). Since our sample sizes for these two groups were dissimilar (566 for the three basic sciences versus 3021 for MED) we cross-checked and found that random sampling the MED pool of papers to achieve sample size parity produced no substantially different results. This analysis showed empirically corroborates our conceptual argument that taking into account both a bootstrapped confidence interval and the number of references produces a more effective way of estimating uncertainty.

Fig. 10
figure 10

Distribution of the RS index across specific disciplines with various filters applied: (a) |Ri|> 0, 8, b |Ri|≥ 4, 8, c |Ri|≥ 10, and 8 d RSunc ≤ 0.5, where |Ri| is the number of references of a given paper

Full size image

Discussion

In this paper we have examined the uncertainty in IDR measurements, both conceptually and empirically. Both of these endeavours raise questions about the validity of IDR measures, and the research conclusions based on them. Arbitrary and non-substantive referencing practices, uncategorized references, and incorrect category assignments have all been recognized in the literature (Campbell et al., 2015; Glänzel et al., 2021; Zhang et al., 2018), and all introduce uncertainty in reference-based measures of IDR, especially when relying on standardized classifications of disciplines. Quantitatively, we believe this uncertainty can be problematic, especially for low and medium values of IDR. To illustrate, papers with a RS index of around 0.2 would typically have 0.0 ≤|RSci|≤ 0.4. This uncertainty typically goes unmeasured and unnoticed in the discussion of quantitative findings in studies on IDR, yet this level of noise suggests type 2 errors in inferring publication behaviour from patterns in RS may be common.

Many conceptually appropriate alternatives to the RS index of IDR (Zwanenburg et al., 2022), rely on similar assumptions of available and valid data on the categories of the references, and thus may suffer from similar degrees of uncertainty. However, the degree to which this uncertainty undermines research conclusions will vary across research contexts and units of analysis. Given that some of the sources of uncertainty seem to be unsystematic, it is likely that research on IDR that focuses on authors, institutions, journals, or other ‘groups’ of publications will be less at risk of drawing false inferences on IDR, as random error washes out within these groups of publications.

There are a number of possible responses to these findings. Researchers can opt to evaluate IDR not based on citations but based on other evidence, such as the full text of publications (Evans, 2016), accepting the limitations this will introduce, such as the more limited availability of full-text publications and the computational expense. Alternatively, they can continue to rely on citation-based measures. Within this approach, they could attempt to reduce uncertainty by attempting to assign a valid category to each reference, as attempted by Waltman and Eck (2012) and Klavans and Boyack (2017), for example by defining the categories based on larger citation patterns. This approach too has its merits and limitations such as the increased difficulty of interpreting research findings from study to study.

Researchers who wish to continue to rely on citations and standardized classifications of disciplines can also remove those observations that do not inspire confidence. While previous practices have adopted a threshold for the number of references (Cassi et al., 2014; Yegros-Yegros et al., 2015) or completeness (Calatrava Moreno et al., 2016), we suggest that taking into account the structure of the cited categories per paper is conceptually and empirically desirable.

Conceptually, we have developed that uncertainty is introduced by a variety of factors that are difficult to control for, raising the importance of quantifying uncertainty and acting on this information, such as by filtering out all uncertain measurements. Empirically, we have shown empirically that the RSunc filter is a promising approach, which reveals expected variability in IDR across five broad subject categories and across specific categories. All in all, we see clearer results when applying the filter, and researchers can expect it would reduce the likelihood of type 2 errors.

We also posit that this filter is more desirable than simply relying on completeness or number of references. Two papers can have the same number of references or relative completeness, and still differ markedly in their IDR certainty due to differences in the distribution of cited categories, such as the number of ‘outliers’, i.e. the number of categories dissimilar from a cluster of similar categories. The relationship between |RSci| and number of references and completeness is shown in Fig. 11a and b respectively, underscoring the differences empirically. Since |RSci| is unreliable as a proxy for uncertainty for low numbers of references, our suggested filter RSunc is a composite of |RSci| and the number of references. Figure 11c shows the difference of this composite with |RSci|.

Fig. 11
figure 11

Relationships between a |RSci| and number of references in calculation; b |RSci| and completeness; and c RSunc and |RSci|

Full size image

Indeed, when adopting our filter with the suggested threshold of 0.5 we obtain a rather different set than if the number of references, |Ri| alone were used as a filter. This difference in size, for different thresholds of the number of references is shown in Fig. 12. Here, the black line indicates the size of the set using the |Ri| threshold, the dotted blue line indicates the size of the set using the RSunc ≤ 0.5 filter, and the red line showing how many papers the latter filter accepts that the former does not. While our analysis presented in Figs. 9 and 10 suggests that using higher levels of the |Ri| threshold results in more confidence in IDR measurement, this clearly comes at the cost of inclusivity, and we thus do not see this as a good alternative to our approach.

Fig. 12
figure 12

A comparison of the inclusivity of two filters, using the suggested RSunc threshold (dotted blue line) and using a variable number of references, |Ri|, as a filter (black line). The red line indicates the number of accepted papers the former accepts that the latter rejects

Full size image

Hence, the evaluation of |RSci| and RSunc allows a more effective filter than using just the RS index and a reference count threshold, is simple to assess, and is grounded in the theory of non-parametric assessment of uncertainty. It provides for a promising basis for a more confident measurement of interdisciplinarity using references and standard classifications of disciplines. It also can be used to indicate the need to adopt different approaches to the measurement, if a particular set proves too uncertain for a given research context.

While our demonstration has focused on the RS index, similar results would be expected for measures derived from the RS, such as DIVc (Leydesdorff et al., 2019), Refined diversity indicator, DIV* (Rousseau, 2019), and Overall diversity indicator, dive (Mutz, 2022) as these too do rely on the discussed assumptions that are associated with uncertainty. Similarly, we expect similar results when employing different standard classifications that too assign disciplines to journals, such as the All Journal Science Index. Future work could confirm these expectations.

This paper has ignored any potential uncertainty stemming from the data on the similarity of disciplines. Arguably, uncertainty stems from the data not reflecting changes in this similarity, being particularly of interest when comparing the interdisciplinarity of papers historically. Future studies could quantify this particular uncertainty by comparing similarity matrices over time, for instance, as a complement to the study of similarity matrices by Huang et al. (2021). Another more focused endeavour could examine the problem of uncertainty stemming from papers ‘inheriting’ the disciplines of their journals. Such examinations could give further guidelines in how or when we can rely on journal disciplines being a good proxy for paper disciplines, and how we best deal with multiple categories for a given journal.

In sum, there are many non-negligible sources of uncertainty in common measures of IDR that rely on cited references and standard classifications of disciplines. These sources of uncertainty are difficult to account for without in-depth analyses. This paper has discussed these sources and demonstrated how a bootstrapping approach helps quantify their impact. We posit that a combination of the magnitude of the bootstrapped confidence interval with the number of references yields an effective estimate for uncertainty. Using a large dataset, we have demonstrated the performance of this estimate when used as a filter, both in terms of the validity of measurement and the inclusivity compared to other inclusion criteria. We hope that these results help researchers quantify the uncertainty in their IDR measurement, reduce it, and ultimately improve the likelihood of drawing valid research conclusions.