The dynamics of collaboration networks and the history of general relativity, 1925–1970

Scientometrics volume 122, pages 1129–1170 (2020)Cite this article

2541 Accesses
4 Citations
Metrics details

Abstract

This paper presents a novel methodology for defining and analyzing the dynamics of the collaboration networks of scientists working on general relativity from the mid-1920s–1970. During these four and a half decades the status of the theory underwent a radical transformation: from a marginal theory before the mid-1950s to a pillar of modern physics. To investigate this passage—known as the renaissance of general relativity—we used a definition of collaboration networks broader than the co-authorship relations retrievable from online datasets. We constructed a multilayer network, in which each layer represents a different kind of collaboration. After having analyzed the evolution over time of specific parameters of the co-authorship network, we investigated the effects of adding one type of collaboration edge at a time, in a cumulative fashion, on the values of these parameters and on the topology of the collaboration network through time, including rapid shifts in the dynamic evolution of the largest component. This analysis provides robust quantitative evidence that a shift in the structure of the relativity collaboration network occurred between the late 1950s and the early 1960s, when a giant component started forming. We interpret this shift as the central social dynamic of the renaissance process and then identify its central actors. Our analysis disproves common explanations of the renaissance process. It shows that this phenomenon was not a consequence of astrophysical discoveries in the 1960s, nor was it a simple by-product of socio-economic transformations in the physics landscape after World War II.

Introduction

The status of general relativity underwent a radical transformation between the mid-1920s and 1970. From the mid-1920s until the mid-1950s, the theory had a marginal status within theoretical physics, leading historian of physics Jean Eisenstaedt to label this stage the “low-water mark” of general relativity (Eisenstaedt 1986, 1989). After the mid-1950s the theory gradually returned to the mainstream of physics. This transformation of the theory from a mathematical curiosity in the mid-1950s to “one of the most exciting branches of physics” in 1970 has been called the “renaissance of general relativity” by physicist Clifford Will (1986, 1989, p. 7). This paper aims at investigating this historical passage from the “low-water mark” to the “renaissance” by analyzing the changing social structure of scientists working on the theory of general relativity between 1925 and 1970.

One of the authors (RL) has investigated, together with A. Blum and J. Renn, the social and intellectual dynamics of such a big historical shift (Blum et al. 2015, 2016, 2017, 2018). The major hypothesis developed in these studies is that during the “low-water-mark” phase, the field of general relativity was greatly dispersed across a variety of different research agendas, pursued by isolated groups or individuals. In contrast, during the renaissance period a more uniform research field related to the physical predictions of general relativity was established. These studies also suggest that the major shift occurred between 1955 and the early 1960s, before the serendipitous discovery of quasars in 1963, which is often credited as the major external event that sparked the renaissance process. The present paper proposes a methodology to test this hypothesis by investigating the dynamics of the collaboration networks of scientists working on general relativity in the period under investigation and by identifying a few indicators in these dynamics that can be related to the change of the status of the theory. Using different measures of centrality, we also identify those actors who might have played a particularly relevant role in crucial moments of the renaissance process, at least as far as the structure of the social network is concerned.^{Footnote 1}

The main methodological issue we tackle in this paper is how to define and analyze the meaningful collaboration network of scientists working on general relativity in a long period during which co-authorship relations were sparse. Since the path-breaking contribution of De Solla Price and Beaver (1967) studies of complex and longitudinal collaboration networks in the sciences have been traditionally restricted to co-authorship networks. Usually based on information automatically retrieved from online scholarly repositories such as Web of Science (WoS) and PubMed, these studies have used theoretical advances in network theory (see, e.g., Barabási et al. 2006) to produce insights on different aspects of scientific co-authorship networks, including structure (Newman 2001a, b, 2004; Fatt et al. 2010), dynamical evolution (Barabási et al. 2002; Moody 2004; González-Alcaide et al. 2012; Uddin et al. 2013), community detection (Girvan and Newman 2002), measures of the relevance and performance of specific actors (Abbasi et al. 2011) and the relationship between the dynamics of co-authorship networks and the establishment of scientific fields (Bettencourt et al. 2008, 2009).

While it is commonly accepted that, despite various kinds of uncertainty, co-authorship networks are a fair proxy of scientific collaboration networks in recent scientific endeavors (Melin and Persson 1996), when it comes to historical studies, one has to take into account historically changing collaboration and co-authorship practices as well as missing data in online datasets. This problem becomes even more troubling when one is trying to address the changing landscape of a research field such as that of general relativity, which we suppose to be historically constituted and composed of many different research strands.^{Footnote 2} Besides the radical change of status during the renaissance phase, in the period between 1925 and 1970 research on general relativity took place on various research agendas including: unified field theory, quantization of Einstein’s equation, cosmology, mathematical methods and astronomical observations. In addition, research was published within different disciplinary domains, spanning from physics and astronomy to mathematics and philosophy. All these limitations, taken together, make it difficult to apply the methodologies of keyword search and citation analysis usually employed to retrieve a reliable dataset of papers and authors in a specific field. The question is, then, whether and how we can apply the advances in the study of co-authorship networks to the field of general relativity over four and a half decades of scientific enquiry, from 1925 to 1970.

The method we propose is to consider a range of collaboration relations in addition to co-authorship relations retrieved in online repositories. The dynamic of the enlarged collaboration networks thus created by imposing additional layers of collaboration data will then be compared with purely co-authorship networks in order to identify possible transformations in the topologies of the network. While this approach might embed biases in the manually retrieved data on involved social actors, it will be shown that the evolution of a more complex collaboration network is much richer and more historically informative than that acquired through the study of the co-authorship network alone. We will argue that this methodology allows for a robust quantitative interpretation of the renaissance of general relativity as a shift in the structure of a properly defined collaboration network. It will also be shown that each layer enriches our understanding of the historical process providing new information and leading to different historical pictures.

In the next section we describe the methodology employed to build the collaboration network, including selection criteria and definitions of collaboration edges. In the third section we introduce the methodology and clarify all criteria employed for the production of the networks analyzed in this paper. In the fourth section, we report the results of analysis with solely co-authorship edges, exploring the effects of using different data sources, as well as different assumptions on the temporal permanence of nodes and edges in the network. In the fifth section we report the results of analysis of different types of collaboration networks obtained by adding various collaboration edges to the initial co-authorship network one layer at a time in a cumulative fashion. In concluding we compare the historical interpretations following from each analysis in order to provide a robust description of the renaissance of general relativity in terms of the dynamics of social networks.

Multilayer collaboration networks: datasets and infrastructure

Actors and papers: selection criteria and datasets

In order to analyze meaningful changes in the collaboration patterns of scientists working on general relativity-related topics between 1925 and 1970, it is necessary to make a reliable selection of actors involved based on authorship of papers in the field. This is complex, however, especially in the period between the mid-1920s and the late 1950s, when the number of involved scientists was relatively low.

We carried out our analysis by combining papers retrieved using two different search strategies in the WoS online repository (Table 1). The first set was obtained using a citation search. We started from searching Einstein’s own scientific production available in WoS limited to those papers that touched topics related to general relativity, cosmology and unified field theory between 1915 and 1955 (set A). Then we retrieved all WoS indexed papers published between 1915 and 1975 that cited at least one of Einstein’s papers in set A. We have called this set of 723 WoS items set B.^{Footnote 3} A larger set of papers called set C include all those WoS items published between 1915 and 1975 that cited at least one of the 723 items in set B. Set C consists of 3181 items and together with set A and set B forms what we call Einstein’s citation space (or set D).

Table 1 Datasets of publications related to general relativity and indexed in WoS published from 1915 to 1975

Full size table

Clearly, this citation-based search cannot be considered complete, as we have to hypothesize a statistically relevant amount of missing data, especially before World War II. We therefore complemented the previous search with a keyword search across both titles and topics in the WoS search engine. Since we started from the hypothesis that general relativity had not always been a defined research field and had drawn on different research strands, we searched for papers that had any of the following keywords either in title or topic fields: “general relativity” OR gravitation* OR “allgemeine Relativitätstheorie” OR “relativité générale” OR “teoria della relatività” OR “Gravité quantique” OR “Gravità quantistica” OR “einheitliche Feldtheorie” OR Quantengravitation OR “champ unifié” OR “unified field” OR “quantum gravity” OR cosmolog* OR Kosmolog*. This second keyword-generated set consists of 5882 WoS items (set E), 1561 of which were already included in set C. The general relativity publication space (or set F) is the union of all the sets previously defined, which, after removing clearly unrelated items, included 8296 WoS indexed articles.

In order to re-construct the social network from our publications dataset we included, as the nodes of the network, all authors who have published at least two items belonging to the general relativity publication space between 1925 and 1970, which, after manual cleaning, resulted in a set of 770 authors. Under the assumption that there might be a considerable amount of missing or incorrect data in the WoS dataset, we complemented this set through historical research. A search on primary and secondary sources—such as proceedings of conferences on general relativity, reviews, datasets and completed dissertations in the Mathematics Genealogy Project until 1971^{Footnote 4}—has provided a further list of 201 names of scholars who pursued research on general relativity in the period between 1925 and 1970, but did not appear in the WoS search previously described, mostly because their publications were not indexed or their names were misspelled in the WoS data. The 971 authors thus identified are the nodes of the collaboration network who together constitute what we call the general relativity social space.

Clearly, we cannot expect that all the identified scientists were active, or even alive, during the entire timespan of our analysis. Furthermore, many switched their field of interest during this period, entering the field of general relativity or leaving it in a specific year. The duration of any scholar’s activity in general relativity is therefore restricted, lasting from the year in which the scientist began research on general relativity until the year of publication of the last paper of the author on general relativity and related subjects. This information has then been recorded as an attribute of the nodes called GR-activity timespan, allowing us to control for the presence of any given node in each network in any given year.

Collaboration edges: definition and criteria

In order to understand how the structure of the collaboration networks changed over 1925–1970, we defined five different types of collaboration edges:

1.
Co-author with The edge between two scientists having co-authored a text. While the definition is perhaps obvious, retrieving the edges involves some choices. In the present analysis we have used three different methodologies of co-authorship relation retrieval.
1. a.
  WoS-based co-authorship The first is simply the co-authorship relations in the papers contained in the general relativity publication space (set F) in the period 1925–1970. We expect that the set of co-authorship relations so retrieved is significantly incomplete.
2. b.
  ADS-based co-authorship co-authorship edges in papers published by the selected scholars and indexed in the SAO/NASA Astrophysics Data System (ADS) online database in the period between 1925 and 1970.^{Footnote 5} While this second search might also have strong limitations, the combination of both search strategies gives a fairly complete set of relations, which also includes co-authorship edges in topics not necessarily related to general relativity research, as will be showed in the next section.^{Footnote 6}
3. c.
  Manually-retrieved co-authorship other co-authorship relations that were retrieved manually through Google Scholar search and historical search on the biographical data of the authors involved.
2.
Collaborate with The second collaboration edge refers to long-lasting collaboration between two scholars that, however, did not lead to the joint publishing of indexed articles.^{Footnote 7} Evidence of these edges was retrieved manually from historical sources and includes additional information concerning the duration of such collaboration: while a co-authorship relation was assumed as created the year the co-authored paper was published, the collaboration edges occurred in specific years that had to be manually retrieved.
3.
PhD with This is the relation between a PhD student and PhD advisor when both of them are already part of our dataset, the general relativity social space. In our database we have recorded this relation independent from whether the dissertation topic is related to general relativity. As for the temporal character of the edges, the PhD edge required some additional decisions: we defined the creation of the edge either as the starting year of the PhD course or, if the previous information was not available, 3 years before the attainment of the PhD degree.
4.
Influenced by The fourth edge is the relation of influence exercised by one scientist of the dataset on another through encounters that occurred when the influenced actor was at the beginning of her or, more often, his scientific career. These kinds of edges are retrieved in two different ways: when a secondary source specifically stresses the influence of a scientist from our dataset on another scientist from the dataset and, secondly, when a scientist explicitly mentions another scientist from the dataset in the acknowledgments published in the very first paper devoted to general relativity. Even in this case we consider the starting year of the edge as the year in which the relation started. When this kind of information is not available we defined some common criteria related to the specific data source—for example, if the relation comes from an acknowledgment in a published paper, we defined the starting year of the influenced_by relations 1 year before the submission of the publication.
5.
Copresence at institution We made the assumption that our collaboration edges dataset is incomplete, as our historical sources do not contain all the relevant information about all 971 individuals. In order to reduce this bias we considered a fifth type of collaboration that is of a hypothetical character: we hypothesize that if two scientists working on general relativity were at the same institution at the same time they might have collaborated in research related to general relativity, or at least shared information with each other. Connecting individuals from our dataset to institutions over the period for which we have evidence of this affiliation, we projected the two-mode relation between persons and institutions into this fifth type of interpersonal relation.

Apart from the relations of the types 1.a and 1.b, which have been automatically retrieved from online repositories, all the other relationships have been manually retrieved using a broad variety of sources, both secondary and primary, printed and online. The database of manually retrieved relations, at the moment, consists of 1219 relations between individuals and 2257 relations between individuals and institutions.^{Footnote 8}

Construction of the multilayer social network

To test historical assumptions and adapt to changing research questions, we set up a data infrastructure which allows for the flexible creation of networks. To this end, we chose an approach that combines semantic modeling of data and network analysis.^{Footnote 9} The dataset describing the actors and their relations was created and stored using Filemaker.^{Footnote 10} Data from external databases like WoS and ADS was retrieved either by export as tabular data or using APIs offered by the services. To integrate the data, we developed an ontology based on the CIDOC-CRM (CIDOC CRM Special Interest Group 2015). This allows us to store all datasets combined as triples in a triple-store.^{Footnote 11} Structural queries can then be formulated in SPARQL (W3C 2019). To create the networks one of us (DW) developed tools that allow for the creation of networks based on these SPARQL-queries (Wintergrün 2018). A set of networks can then be combined into a multilayer network. For creating, visualizing and analyzing these, a python package has been developed called “network-extension.”^{Footnote 12}

The multilayer network we are analyzing in the following is composed of four distinct layers constructed out of the five collaboration relations defined in “Collaboration edges: definition and criteria” section. These layers are defined as follows:

1.
extended-simplified co-authorship the merged set of co-authorship edges including all edges retrieved via the three sources described in point 1 of “Collaboration edges: definition and criteria” section.
2.
collaboration this layer includes the collaboration edges in point 2 of “Collaboration edges: definition and criteria” section.
3.
influence this layer merges the collaboration edges PhD with and influenced by defined in “Collaboration edges: definition and criteria” section. Since these two relations are considered very similar and it has proved difficult to provide an unambiguous distinction between them on the basis of our historical sources, they have been merged to form the third layer of the relativity multilayer network. Both the PhD with and influenced by edges are, in principle, directed edges that go from one node to the other. However, for the present analysis we have considered them only as particular kinds of undirected collaboration edges, as our questions are related to the changing structure of collaboration networks.
4.
Copresence at institution this layer includes the collaboration relationships defined in point 5 of “Collaboration edges: definition and criteria” section.

In the definition of all above-mentioned layers, edges are included only if the relations take place when both actors have already started working on general relativity-related topics; namely, in order to be included, the relation has to occur within the GR-activity timespan (as defined in “Actors and papers: selection criteria and datasets” section) of both actors. This is particularly crucial for PhD with and copresence at institution relations, as the dataset includes many relations that might have occurred outside the relativity timespan of the actors. Dissertations on topics unrelated to general relativity are therefore almost always excluded in the layer, because in the large majority of cases students working on PhD topics unrelated to GR had not started working on general relativity yet.

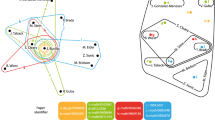
Within the comparative fashion of our methodology, one of us (DW) has created a flexible interactive framework for studying longitudinal changes of the network based on different parameters affecting the permanence of edges and nodes in the network. One of the parameters is the interval length I. This parameter describes how many years prior to the selected year are still relevant for the structure of the network of that year. As we are also researching propagation of networks into the future, we chose a negative sign for interval length when referring to an interval in the past. In the rest of the paper we report the results of two specific choices, I = − 8 and I = − 100 (see “Method of analysis” section). Since the maximum length of our analysis is 45 years (from 1925 to 1970), the 100-year value can be effectively interpreted as an interval of unlimited length. A second parameter B determines which nodes will be considered in each year. B can either be “all” or “year_only.” Each multilayer network (I, B) in year y comprises all nodes active in general relativity research between y + I and y—remembering that I in this paper is negative, being either − 8 or − 100—and all edges which existed for at least 1 year in this interval.^{Footnote 13} If B = “year_only”, all actors not active in the year y are excluded (Fig. 1).^{Footnote 14}

Method of analysis

We compared the dynamics of the collaboration network based on the different definitions of collaboration edges listed in “Construction of the multilayer social network” section. We will first report the results obtained when one uses only the WoS-based co-authorship edges. We will then show the results obtained by analyzing the collaboration network given first by the extended-simplified co-authorship and then by the networks obtained by adding the other layers of the multilayer social network in “Construction of the multilayer social network” section one layer at a time.^{Footnote 15} In all phases of our study, we do not weight edges based on the number of relations. We use a uniform weight because in this analysis we are interested in understanding how the network structure changes over time as we cumulatively add different types of relations, rather then giving an artificial numerical value to an instance of scientific collaboration. This implies that in all co-authorship networks, nodes are connected with an edge of weight one independently of the number of papers written together. And for the multilayer networks we use the basic flattening approach: all layers are projected onto a final layer in which multiple instances and types of collaboration are rendered as a single link (see Dickison et al. 2016, p. 74). That is, an edge between nodes in any additional layer only contributes to the final layer if they were not previously connected in the other layers.

Contrary to many studies on co-authorship networks, our analysis is inherently dynamic and ranges over a long period, during which the topology of the network changed considerably, both in terms of the number of elements, nodes and edges, and related topological features. The specificity of our study thus poses a number of problems that are less relevant to studies of more recent co-authorship networks or periods ranging over only a few years. The first problem concerns how long edges should stay in the network after the publication of papers. This problem usually does not arise in studies of co-authorship networks, as they are mostly static or addressing changes occurring during a timespan of a few years. When longer periods are analyzed, one usually compares different temporal sets to provide an analysis of temporal evolution over a few decades (see e.g., González-Alcaide et al. 2012; Bornmann 2016; Medina 2018). In order to identify possible specific moments as turning points in the network topology, our (rolling samples) approach instead investigates the continuous change of network parameters. This has involved a decision on how long one should consider an edge’s trace in existence after the publication of a co-authored paper.

To justify our decision at this point, we tested different rules to observe the effect on network structure and dynamic. We finally settled on two values: an 8-year and 100-year timespan. The latter is effectively permanent since the maximum number of years considered in our analysis is 45 years (see rules in “Construction of the multilayer social network” section). The networks constructed under the assumption of this unlimited edge length might give indicators that go considerably beyond actual social relations, as they include relations occurring far in the past. By filtering out older relations a shorter timespan for the length of edges indicates actual social groups created by more recent collaborations. We settled on 8 years as an intermediate value between the unstable networks produced by immediate social connections (1 or 2 years), and longer lengths (e.g. 20 years) that would approach unlimited edge length and therefore not provide a meaningful comparison. Finally, we also compared the structure and dynamic of collaboration networks resulting from different assumptions about the existence of nodes in the year-graphs, employing either the all_node or the only_node rule introduced in “Construction of the multilayer social network” section.

In this paper we report the analysis of the following networks:

1.
Co-authorship network
1. a.
  WoS_AllNodes_UnlimitedLength (“WoS-based co-authorship [all_nodes – edges of unlimited length] ” section)
2. b.
  Co-authorExtended_AllNodes_ UnlimitedLength (“Co-authorship extended [all_nodes – edges of unlimited length]” section)
3. c.
  Co-authorExtended_OnlyNodes_ UnlimitedLength (“Co-authorship extended [only_nodes – edges of unlimited length]” section)
4. d.
  Co-authorExtended_AllNodes_8Years (“Co-authorship extended [all_nodes – 8-year length edges]” section)
2.
Collaboration_AllNodes_8Years (“Collaboration+ExtendedCo-author network [all_nodes – 8-year length edges]” section)
3.
Influence_AllNodes_8Years (“Influence+Collaboration+ExtendedCo-author network [all_nodes – 8-year length edges]” section)
4.
AllRelations_OnlyNodes_8Years (“Copresence at institution+Influence+Collaboration+ExtendedCo-author network [only_nodes – 8-year length edges]” section)

We have studied the development of various parameters of the multilayer network over time in order to identify meaningful changes in the topology of the network, with special reference to the formation of a giant component as a possible indicator of the formation of a connected general relativity research field (Bettencourt et al. 2008, 2009). The network measures we have investigated are: the total number of nodes and edges, the number of nodes and edges of the largest connected component, the diameter of the largest connected component, as well as the average path length and the clustering coefficients that might be possible indicators of small-world network behavior (Watts and Strogatz 1998; Newman 2001a, 2004). These measures are also compared with values from two different random graph models: The Erdős-Rényi model and the Barabàsi-Albert (BA) model.^{Footnote 16} We used the algorithms implemented in igraph and applied them for each year and each layer in the multi-layer network.^{Footnote 17} The comparison of our real networks with the simulated graphs helped to identify specific developments in the social networks beyond a random formation of the social sphere.^{Footnote 18}

Finally, we have studied the change over time of centrality values of most central actors, using various definitions of centrality. One particular challenge is how to make the role of any individual actor in different years comparable. To answer this question, we compared, next to absolute numbers, the relative position of an actor ranked by the value of these centrality measures. In more detail, we calculated the histogram of the distribution and chose bins holding on average 3 actors in one group. We then created a rank function r(y) to run for each actor. The value is given by 20—(number of bins containing the author), where the bins are ordered such that the bin covering the highest values has the number 0.^{Footnote 19} This was carried out with a twofold target: firstly, the evolution over time of centrality measures might give a second indication of relevant changes occurring in the network at the level of individual influence over the structure of the network; secondly, by looking at the centrality of actors at specific moments that looked particularly relevant for the topological change of the networks, we can identify which actors’ actions may have sparked such changes.

The dynamics of the co-authorship network

WoS-based co-authorship [all_nodes – edges of unlimited length]

As a first step we here show the analysis of the co-authorship network between 1925 and 1970 created by considering only the WoS-generated set of papers in Set F, which we call the general relativity publications space (see Table 1). We report the results of this analysis considering that all nodes and edges remain permanently after they first entered the network, as is usually assumed in most studies of dynamical co-authorship networks (the unlimited edge length and all_nodes criteria in “Construction of the multilayer social network” section). The network thus created is labeled WoS_AllNodes_UnlimitedLength.^{Footnote 20}

The edges of this quite dispersed network remain fewer than nodes over the entire period. The dimension of the network steadily increases without any major shift, aside from rapid growth in the total number of nodes and edges after World War II, and more precisely after 1950 (Fig. 2a). In spite of the growth in the number of connections, the largest connected component remains always significantly smaller than the entire network. A possible major development in the formation of the largest connected component seems to occur between 1964 and 1965, when both the numbers of nodes and edges of the largest components increase rapidly and considerably. This pattern appears more evident in the diagram of the percentage of the nodes and edges of the largest component over the respectively total number of nodes and edges: in 1965 there is a clear reversal in the trend of relative number of edges of the largest connected component, which constantly decreases from the late 1940s. This change, however, does not seem to have a strong impact on connectivity, as the dimension of the largest component remains significantly lower than the dimension of the network, less than 20% at its apex in 1970 (Fig. 2b).

The picture that emerges from the analysis of WoS co-authorship network is that scholars working on general relativity formed a very small network, which remained weakly connected. In spite of its smallness, the diameter of the largest component grows monotonically in this period, which is a further indicator of the dispersion of the network and its instability (Fig. 2c).

Co-authorship extended [all_nodes—edges of unlimited length]

The second step involved analyzing the co-authorship network generated by considering the extended-simplified co-authorship edges—described in “Construction of the multilayer social network” section as the merged set of three different co-authorship record sources, and not just of the WoS-derived co-authorship edges—and using the same criteria adopted in the previous section: edges are considered to be of unlimited length, and the nodes are not restricted to those still active at the specific year of the analysis. We call this network Co-authorExtended_AllNodes_UnlimitedLength.

This network contains a greater number of nodes and edges, but still represents a small and disconnected network where the number of nodes remains always greater than the number of edges. However, the network also clearly displays change in structure and trend, contrary to what could be seen in the analysis of the WoS-based co-authorship network in “WoS-based co-authorship [all_nodes – edges of unlimited length]” section. There are some moments of rapid change in the slopes of the curves of nodes and edges of the largest connected component that did not appear in the previous analysis (Fig. 3a). What is relevant from a historical perspective is the identification of these moments of change and the lag between the change in the slope of the total number of nodes over time and that of the edges of the largest component over time. To analyze and visualize these shifts we calculated the discrete first derivative of the total number of nodes and edges of the largest component with respect to year.^{Footnote 21} The increased rate of growth in the number of nodes starts right at the end of World War II and continues at an ever-increasing rate until the early 1960s, after which the rate seems to slow down. This does not correspond to any similar modification in the largest connected component, as identified by the first derivative of the curve of the edges of the largest connected component. That transformation starts later, after 1958, and continues growing up to the end of the period under consideration, with a first major peak in 1964 (Fig. 3c, d). Following the hypothesis put forward by Bettencourt et al. (2008, 2009) that the formation of a scientific field is related to the stabilization of the diameter of the largest component, while the number of nodes in the components continues growing, one sees that, a few years after the drastic change between 1961 and 1962, the largest component stabilizes and the diameter stops growing in 1963 (Fig. 3b).^{Footnote 22}

The stabilization does not seem to represent, however, the formation of a small-world network. The size of the largest connected component reaches 329 units at its peak in 1970, corresponding only to about 40% of the dimension of the network, significantly smaller than giant components identified in the scientific literature, both in relative and absolute terms (Newman 2004). The evolution of the average path length and of the clustering coefficient shows no robust sign of small-world network behavior either. If one, however, compares these values with random graph models such as the Erdős-Rényi model or the Barabási–Albert model, some kind of small-world behavior of this network seems to emerge (see “Appendix 1”, Fig. 22).

To better understand the change occurring between 1961 and 1962 with a sudden increase in the size of the largest connected component, we have closely analyzed the networks in these 2 years. This scrutiny shows that the transformation is due to the creation in 1962 of new edges between the largest connected component of the 1961 network and a smaller component mostly composed of West German scientists. This connection was established by the career move toward the United States of one scholar. In 1961, West German astronomer and physicist Engelbert Schucking started working as a research associate at Syracuse University with Peter Bergmann, who had established a center focusing on general relativity research back in 1947 (Fig. 4). The two scientists published a paper together with mathematician Ivor Robinson in 1962 (Bergmann et al. 1962). Schucking might then have played the role of broker between previously separated research groups (Granovetter 1973).

The last indicator we used to understand relevant historical changes in the network structure is the pattern of the centrality measures of particularly relevant scientists. As is very easily seen in the network images, Einstein is still present in our analysis of the early 1960s network in spite of the fact that he had already passed away in 1955. This is a consequence of our choice of having considered a node in the network as lasting forever. While this is questionable for obvious reasons, this choice gives the possibility to see how scientists continued to be intellectually relevant in shaping the structure of the developing social network of authors. In the Co-authorExtended_AllNodes_UnlimitedLength, in spite of the fact that Einstein did not publish any co-authored paper since the late 1940s, he still maintained the highest betweenness centrality, as well as the highest degree and closeness centrality, well after his death.

Figure 5 shows the ranked diagram of Einstein’s closeness centrality for the co-authorship network here analyzed (see “Method of analysis” section). The diagram shows that Einstein reached a high level of centrality only after his move to Princeton in 1933 when he started publishing co-authored papers with his assistants at the Institute for Advanced Study. Einstein was clearly in a dominant position in the largest connected component that started slowly growing after mid-1930s, and he maintained this central position thanks to some of his close associates in the 1930s, such as Peter Bergmann and Leopold Infeld, who played a major role in general relativity research in the 1950s and 1960s and both helped increase the largest connected component with their students. The pattern of Einstein’s closeness centrality again suggests that the period between 1961 and 1964 was particularly important for the structure of the network.^{Footnote 23} We have already shown that the period around 1961–1962 appears as the moment in which the largest connected component started growing at a more rapid pace. Exactly at the same time, in 1962, Einstein lost his place as the most central actor in the network. This might mean that the network started taking shape around actors who gradually became more and more emancipated from Einstein’s intellectual influence, as shown by the comparisons of the ranked closeness centrality measures of some of the most central actors in that period. In 1962, former Einstein’s assistant, Bergmann took the highest value, especially thanks to the dominant position of the Syracuse University research center on general relativity in attracting postdocs, and a strong collaborative connection with other centers of growing relevance, such as King’s College London around Hermann Bondi, who also became a central actor in the 1960s (Fig. 5).

The increasing intellectual distance from Einstein is visible in changes in the centrality measures of John A. Wheeler. He started a research group on general relativity before the mid-1950s at Princeton University, and Wheeler’s center has come to be considered a posteriori a major center in the renaissance phenomenon (Thorne 1994; Misner 2010; Rickles 2018; Blum and Brill 2019). In fact, all through the 1950s, Wheeler and his co-authors remained disconnected from the largest connected component up to the mid-1960s, forming an increasingly larger separated connected component. As a consequence, Wheeler had very low-ranked closeness centrality until the late 1960s (Fig. 5), when he rapidly became the most central actor. Figure 6 shows the network in 1969 when Wheeler and his co-authors have been included in the giant component and Wheeler immediately reached a central position. Not only did he have the second highest betweenness and degree centrality measures in 1969 (after Bergmann), but he is also the most central figure in the largest, purple cluster, as identified by the Girvan–Newman algorithm (see “Appendix 2”, Table 2).

Table 2 Centrality measures of the seven scholars who have the five highest centrality measures of one of the three following centrality measures: betweenness centrality (%), closeness centrality (%) and degree in the Co-authorExtended_AllNodes_UnlimitedLength network in 1969

Full size table

Co-authorship extended [only_nodes—edges of unlimited length]

Assuming that edges have unlimited length results in the unlimited persistence of the nodes, which is highly unrealistic in long-lasting networks. In order to focus on active scientists, we have analyzed the co-authorship network using the only_nodes criteria (see “Construction of the multilayer social network” section), which gives a more realistic picture of the scientists working on general relativity in a specific period. While the previous network might be interpreted as providing measures of who contributed to the intellectual base of the field in a given period, the present network shows the actors in a given time and their connections with other active. We call this network the Co-authorExtended_OnlyNodes_UnlimitedLength.

The analysis of the network of active nodes connected by edges of unlimited temporal length leads to very similar results as in the previous analysis, while revealing moments of historical change more clearly. Figure 7a, b show clearly the radical shift occurring between 1961 and 1962 in the process of the creation of a social network working on general relativity research agendas. The increasing rate of growth of both the nodes and edges in the largest connected component between 1961 and 1962 and the tendency of the component to become more and more connected (number of edges over number of nodes) appear with particular evidence. While it remains a disconnected network with only 40 percent of the authors belonging to the largest connected component at its apex, the dynamic of this network shows a pattern similar to that found without excluding inactive scientists in the year-graphs in “Co-authorship extended [all_nodes – edges of unlimited length]” section. The only_node choice only makes more evident particularly disruptive changes, such as the death of Einstein in 1955, which clearly disrupted the largest component (see the drop in the number of nodes and edges between 1955 and 1956 in Fig. 7a)

A close study of the networks shows that the rapid increase occurs between 1961 and 1962 because different large connected components of the network, including the two largest ones, merge. In 1961, there is no clear giant component. The three largest connected components are grouped around central figures, whom we call research leaders. The three largest components center on three figures with the highest degree centrality: Hermann Bondi, leader of the relativity group at King’s College London since 1955; Bergmann at Syracuse University; and John Wheeler at Princeton University. The change between 1961 and 1962 is due to the merging of two of these largest components (Bondi’s and Bergmann’s) as well as other smaller components. Besides Schucking, already identified in the previous analysis, a central position is held here by the mathematician Ivor Robinson as he connects the active groups formed around Peter Bergmann at the Syracuse University with the UK-based group where Bondi had a central position (see Fig. 8).^{Footnote 24}

Co-authorship extended [all_nodes—8-year length edges]

In previous sections we hypothesized that the edges, once created, would remain forever, a highly problematic assumption that may not capture the rapidity with which social groups of co-authors form in historical dynamics. As a final step of the co-authorship analysis, we have analyzed the effect of posing a limit to the temporal length of edges on the simplified-extended co-authorship network, hypothesizing that each edge lasted 8 years (see “Construction of the multilayer social network” section). In this case we report only the result of the all_nodes, because the 8-year rule gradually eliminates all those nodes that were no longer active in the field, with no further need to put more constraints for the presence of the nodes in the year-graphs. We call this network the Co-authorExtended_AllNodes_8Years.

The picture is very similar to the one offered in the previous analysis apart from the fact that the edges are fewer and the network much less stable as edges between any two authors disappear 8 years after not having co-authored any paper in the meantime. This assumption makes even more evident the radical change occurring between 1961 and 1962, shown with great clarity by the first derivative of the number of nodes and edges of the largest connected component (Fig. 9).

However, the 8-year rule produces a significant difference if one looks at those indicators that might show a stabilization of the field in the 1960s. The 8-year network, in fact, shows no sign of stabilization during the 1960s, as the diameter continues growing until 1969 (Fig. 10).^{Footnote 25}

The 8-year rule, moreover, allows a study of the centrality of scientists in a changing scientific environment. It shows, for example, the predominant role Wheeler, and one of his former PhD students, Charles Misner, come to occupy in the last years of the 1960s in the Co-authorExtended_AllNodes_8Years network with respect to the other central figures of the network, such as Bondi and Bergmann (Fig. 11).

Discussion on the dynamics of co-authorship networks

The four co-authorship networks above discussed have some commonalities and, also, significant differences, which might also lead to different historical interpretations. Compared to other scientific co-authorship networks analyzed in the scientometric literature, the relativity co-authorship network remained small and sparse in all four analyses (see, e.g., Barabási et al. 2002; Newman 2004; Mele et al. 2006; Fatt et al. 2010). Average degree remains less than one in all these networks throughout the entire period, which results in great uncertainty on the insights obtained with in this analysis.

In spite of this sparseness, the methodology here applied to look at the dynamics of different kinds of co-authorship relations with different hypotheses on the permanence of nodes and edges in the network provides, on the one hand, some tentative insights on the development of the field of general relativity and, on the other, allows for a comparison of the impacts of different analytical assumptions on the historical interpretations. The co-authorship network retrieved automatically from WoS (WoS_AllNodes_UnlimitedLength) shows a relevant shift only in 1965. One might then be tempted to interpret the small but evident change in the trend occurring in 1965 as the result of the discovery of quasars. This would support the common view that general relativity started to coalesce into a more defined physical discipline as a consequence of astrophysical discoveries in the 1960s, starting from the discovery of quasars (Schmidt 1963). Accordingly, the so-called renaissance of general relativity could be interpreted as a result of the establishment of the field of relativistic astrophysics. As a final finding, there is no quantitative signature of the establishment of a scientific field before 1970, as the diameter continues growing all through the timeframe of our analysis.

The adding of other co-authorship relations changes this perspective and makes this interpretation untenable. The analysis of Co-authorExtended_AllNodes_UnlimitedLength shows that the end of World War II clearly has a strong quantitative influence on the growth of the network with a sudden increase of the total number of nodes and edges, but this does not lead immediately or directly to the formation of a giant component. This starts to happen more than 15 years later. A first, small change occurs only between 1958 and 1959, but a more evident shift happens between 1961 and 1962. Many of the indicators employed show that a giant component starts forming at a rapid pace around 1962, while at the same time Einstein is displaced as the most central actor. At the same time the diameter of the largest component stabilizes, which might be interpreted as the formation of a more closely connected field of enquiry with respect to a previous dispersion in different agendas. This means that there was a meaningful change in the network structure at the beginning of the 1960s, before the astrophysical discoveries starting form 1963. Finally, while the structure of the co-authorship network does not follow the preferential attachment model, it is also considerably different from an Erdős-Rényi graph, as it has a very high clustering coefficient showing, at least in part, small-world features. This analysis seems to allow the identification of a particularly relevant passage in the topology of the network and therefore also for the identification of particularly central actors in this passage.

Imposing some restrictions on the co-authorship network created two new networks: in the first only nodes active in the year of the analysis are included; the second modifies the temporal length of the edges. In spite of these restrictions, the historical picture concerning the moment of the shift in the network structure is not affected. Rather, the restriction to active nodes makes this shift even more evident and also shows the specific connections that modify the social collaboration structure of active scientists. Einstein’s death clearly disrupts this network and the shift in the largest connected component between 1961 and 1962 emerges more clearly. In this case, a study of centrality measures cannot be used to evaluate Einstein’s later influence in the structure of the largest component as the node suddenly disappears in 1955, but it gives a more realistic perception of the role of authors in their social network. The co-authorship network in 1962 shows the first meetings of various groups or components as the result of early-career scientists moving from one place to another, an effect studied by historian of science David Kaiser (2005), who terms the phenomenon “postdoc cascade.” Centrality measures of betweenness centrality and closeness centrality here have also a striking predictive power. In 1963, Robinson, Schucking and Peter Bergmann would be three of the four organizers of the first conference on the newly born relativistic astrophysics, which the meeting itself helped establish: the Texas Symposium on Relativistic Astrophysics (Robinson et al. 1965; Schucking 2008). The three above-mentioned scientists were the only US-based scientists at the time who were within the first five highest values of both betweenness centrality and closeness centrality measures in the recently established largest connected component in 1962 (see Table 3 in “Appendix 2”). This provides further ground to the thesis that, contrary to the idea that the conference itself and the field of relativistic astrophysics created the basis for the explosion of the general relativity field, an already established group in general relativity embedded the new discovery within a field that was already being formed by other means and around other topics.

Table 3 Centrality measures of the nine scholars who have the five highest centrality measures of one of the three following centrality measures: betweenness centrality (%), closeness centrality (%) and degree in the Co-authorExtended_OnlyNodes_UnlimitedLength network in 1962

Full size table

While providing the same general picture of the previous two co-authorship networks, the temporal restriction on the length of edges provides some granularity in the comprehension of the historical changes by more clearly distinguishing relevant and sudden processes, and identifying well the most central figures in these processes. However, contrary to the second case, the restrictions on the nodes and the temporal length of edges result in the diameter not stabilizing.

The dynamics of the extended collaboration networks

So far, we have limited our study of the relativity collaboration network to the co-authorship networks, using different criteria for the choice of co-authorship edges, length of the edges and the permanence of nodes in the network. This section will add, one layer at a time, the three other kinds of collaboration edges of our multilayer network, which have been retrieved through the historical analysis of biographical data: collaboration, influence and copresence at institution edges (see “Collaboration edges: definition and criteria” section).

Collaboration + ExtendedCo-author network [all_nodes—8-year length edges]

The first layer we added is that formed by collaboration edges as described in “Collaboration edges: definition and criteria” section. Since we are interested in historically relevant transformations that might be visualized in sudden changes in network parameters, in the following analyses we will consider that all edges last only 8 years and discuss only what the different edge types add to our previous studies in a cumulative fashion. As far as the nodes are concerned, we will not filter out those inactive in the specific year of the year-graphs, for the reasons explained in “Co-authorship extended [all_nodes – 8-year length edges]” section. We call the flattened multilayer network including the extended co-authorship and the collaboration relations with the all-nodes and 8-year rules the Collaboration_AllNodes_8Years.

Introducing a new kind of edge manually retrieved from biographical data has the obvious effect of significantly increasing the number of edges with respect to the Co-authorExtended_AllNodes_8Years network analyzed in “Co-authorship extended [all_nodes – 8-year length edges]” section. Most interestingly, however, adding a new layer provides a different periodization of a sudden shift in the network topology toward the formation of a giant component. The number of nodes and edges of the largest connected component of the new collaboration graph shows a radical transformation occurring a few years before it becomes evident in the co-authorship network (Fig. 12a). The relevance of this shift is clearly visible if one looks at the first derivative of the number of edges of the largest component over time, which shows the first high peak in 1960 (Fig. 12b). Various indicators of the dynamics of the Collaboration_AllNodes_8Years network show, then, that a change occurred between 1959 and 1960, suggesting a different dynamic which does not appear in the co-authorship network. This seems to be confirmed also by the comparison of various parameters of the Collaboration_AllNodes_8Years network to the random-graph and scale-free models (See Fig. 23 in “Appendix 1”).

As was the case in the previous section, the 8-year rule does not lead to the stabilization of the largest component, while the assumption that the edges stay permanently in the network does (Fig. 13). The 8-year rule allows for sudden social changes to become visible, while the assumption of unlimited length for the edge might provide some insight on the intellectual stability of the field.^{Footnote 26}

The networks in Fig. 14 show that the transformation can be interpreted as driven by specific movements of scientists. In 1959 the collaboration network has three large components, similar to the ones identified as separate components in the 1961 co-authorship network in Fig. 8: the UK-based group mostly centered around Bondi at King’s College London; the US-based group mostly connected to John Wheeler at Princeton University; and the US-based group mostly connected with Peter Bergmann at Syracuse University, which in this network is already connected with Jordan’s group by 1959. Contrary to the co-authorship network in Fig. 8, the shift between 1959 and 1960 corresponds to the merging of all these three components.

The degree centrality measures in the Collaboration_AllNodes_8Years network in 1960 reveal at least two junior scholars together with research center leaders Bergmann, Bondi and Wheeler as the most central actors in shaping the network structure. These junior scholars are German physicist Rainer Kurt Sachs and British physicist Felix Pirani. Notice that these scientists are different from those identified as central in the previous co-authorship analyses. The closeness centrality measures give an even greater relative central position to those scholars connecting various groups such as Pirani, Robinson, Sachs and the senior relativity expert John L. Synge, who at the time was a leader of a smaller group at the Dublin Institute for Advanced Studies (see Table 4 in “Appendix 2”). Bondi and Pirani reach a high betweenness centrality in the early 1950s, displacing Einstein as the major figure already by the mid-1950s, together with Bergmann, who, however, is not attached to the largest component until 1960 (Fig. 15).

Table 4 Centrality measures of the nine scholars who have the five highest centrality measures of one of the three following centrality measures: betweenness centrality (%), closeness centrality (%) and degree in the Collaboration_AllNodes_8Years network in 1960

Full size table

Influence + Collaboration + ExtendedCo-author network [all_nodes—8-year length edges]

We then added the third layer of “Construction of the multilayer social network” section: influence, which includes the two relations PhD with and influenced by described in “Collaboration edges: definition and criteria” section. We use the same criteria for the permanence of nodes and the length of edges, and call this network the Influence_AllNodes_8Years.

In spite of the fact that adding a new layer necessarily implies more connections than in the previous analysis in “Collaboration+ExtendedCo-author network [all_nodes – 8-year length edges]” section, the general picture concerning the relevant changes in the topology of the network and the formation of a giant component remains essentially unaltered. The number of edges and nodes in the largest component is greater than in the Collaboration_AllNodes_8Years from the early 1950s and these values more than double already by 1957. The radical change in the structure, however, occurs again the same year, between 1959 and 1960 (Fig. 16).

While the general picture is not modified in any substantial way by including relations of influence, this analysis shows more clearly the effect of the war on the topology of the network: the number of nodes and edges in the last years of the 1930s is significantly greater than in the previous analysis. It is possible to identify the increase of the largest component as a social group based on influence relations, more than collaborations, but this group is disrupted by World War II and never materializes into a more connected network. After the disruption one has to wait until 1955 to see the same number of edges in the largest component as before World War II. After 20 years, however, those scholars belonging to the largest connected component have changed significantly.

The influence edges alter the interpretation of the connection between the different groups in the collaboration network before and after the major shift occurred. According to this new picture, in 1959 there are only two, rather than three, major components. The largest one was centered on scientists based at Cambridge University and at King’s College London, but also includes Leopold Infeld’s group in Poland and Synge’s in Dublin. The second group is mostly based out of American universities and grows from an early connection between Wheeler’s group and Bergman’s group, which in our previous analysis did not appear at all (Fig. 17). This edge was created by physicist Arthur Komar’s going from Princeton, where he was a PhD student of John Wheeler’s, to Syracuse University as a junior associate of Peter Bergmann in 1957. In this picture the role of junior researchers around 1959 is especially evident as Komar and Pirani have a particularly high betweenness centrality comparable, or even higher than, those of research group leaders at the time (3th and 4th highest values, see Table 5 in “Appendix 2”).

Table 5 The ten scholars with the highest betweenness centrality measures in Influence_AllNodes_8Years network in 1959

Full size table

The sudden change between 1959 and 1960 is, in this case, due to the merging of these two previously disconnected largest components, which makes Sachs and Robinson emerge as the brokers of this dynamic, as suggested in the previous analysis and as easily seen by their closeness and betweenness centrality measures (Table 6 in “Appendix 2”). The analysis also indicates the presence of other large groups, such as the French groups in Paris around mathematician André Lichnerowicz and theoretical physicist Marie-Antoinette Tonnelat, who, however, remain significantly isolated, separated from both each other and the largest component. Both Lichnerowicz and Tonnelat have, in 1960, a high degree centrality (2nd and 4th respectively) but their complete disjunction from the largest component clearly conveys their marginalization within the relativity community that was being established. Only in 1965 do both Lichnerowicz and Tonnelat enter the largest connected component. However, while they maintain a relatively high degree centrality, and assume a high betweenness centrality in 1965, their distance from the center of the network is made evident by the low closeness centrality, which indicates, that while having many students, they remain marginal to the community that was being established around other major centers and scientists (see Table 7 in “Appendix 2”).

Table 6 Centrality measures of the seven scholars who have the five highest centrality measures of at least one of the three following centrality measures: betweenness centrality (%), closeness centrality (%) and degree in Influence_AllNodes_8Years network in 1960

Full size table

Table 7 Centrality measures of the scholars with the five highest degree centrality measures in Influence_AllNodes_8Years network in 1966, ordered by degree centrality

Full size table

Copresence at institution + Influence + Collaboration + ExtendedCo-author network [only_nodes—8-year length edges]

We completed our analysis by including the fourth layer of our multilayer network introduced in “Construction of the multilayer social network” section copresence at institution. This kind of edge is, as discussed in more detail in “Collaboration edges: definition and criteria” section, purely hypothetical, but has the potential to reveal some hidden connections that were not accessible from other collaboration edges. It constitutes the space of possible collaborations and, as such, is of great utility for historical studies. While we are here taking into consideration hypothetical collaboration edges in addition to those previously analyzed, there is substantial evidence that, in a field still as small as relativity research, practitioners tended to meet and discuss with persons working in the same or geographically closer institutions. In this section, we report the result of the analysis using the 8-year rule for the length of edges. As far as the nodes are concerned, we report the results obtained using the only_nodes rule, excluding thereby those who were not active in general relativity research in that year. This was done to limit the bias created by the large increase of uncertain connections between scientists. This choice implies that the only_nodes rule is consistently applied to all the four layers forming the merged network. We call this network AllRelations_OnlyNodes_8Years.

The number of edges increased enormously, as one might expect in view of the fact that we are including a new layer of connections to the pre-existing three layers and in spite of the fact that the number of nodes is slightly less than in previous analyses (as we are using only_nodes rather than the all_nodes rule). The comparison between the total number of nodes and edges of the AllRelations_OnlyNodes_8Years network with respect to the previous three layers of collaboration edges (Influence_AllNodes_8Years) shows both the effect of the war in disrupting existing institutional connections and the relevant impact of post-WWII changes in the physics landscape and career practices. The general image is of a two-step change occurring in the 1950s. The first step occurs in 1951, when the total number of edges becomes greater than the total number of nodes, and the second one occurs in 1958 when the pace of increase of edges quickens (Figs. 18a, b).

A comparison between the largest connected component in the influence and all-layers networks displays similar post-1950s growth, with a first major shift between 1950 and 1951, a second one between 1956 and 1958 and a third one between 1961 and 1962. The number of nodes in the largest component also shows a similar pattern after 1950. Even Einstein’s disappearance from the network in 1955 does not provoke a major disruption in the largest component of AllRelations_OnlyNodes_8Years. This is interpreted as a measure of how robust the socio-institutional network had become by the mid-1950s (Fig. 19a). The number of nodes and edges of the largest connected component over the total number of nodes and edges conveys even more clearly the picture that a giant component started forming between 1950 and 1951 and continued growing, as far as the number of nodes are concerned, while remaining stable as far as the relative number of edges of the largest connected component over the total number of edges is concerned (Fig. 19b).

In the case of the AllRelations_OnlyNodes_8Years network, we can also see more indications of small-world network behavior. Between 1957 and 1962 the average path length of the largest connected component stops growing and after 1962 starts decreasing in spite of the growth of the number of nodes (Fig. 20a). Secondly, in spite of the 8-year rule this network does show a stabilization of the field at the end of the 1950s (more specifically from 1958), when the diameter stops growing and starts decreasing in spite of the large growth of nodes in the largest component, contrary to what occurred in all the other networks that used the 8-year rule (see Fig. 20b). This picture is confirmed by comparing the AllRelations_OnlyNodes_8Years network with the values of the Erdős-Rényi and BA models (see Fig. 24 in “Appendix 1”).

The analysis of centrality measures in the period of major topological changes in the structure of this network identifies a younger scholar who seems to have played a particularly relevant role in connecting different parts of the network in the moment when the giant component started forming in the early 1950s. British physicist Felix Pirani emerges exactly in that period as a possible broker between different national communities, American and British, and more importantly between two different research topics, quantum gravity avant la lettre and the steady-state cosmology developed at Cambridge University. After having received his PhD with a dissertation on the quantization of Einstein’s field equations in 1951, he moved to Cambridge to do a second PhD with Hermann Bondi, one of the proponents of the steady-state cosmological model, an alternative to the evolving universe model. In 1951, Pirani became an early broker in the network, as shown by his high betweenness centrality, and he also maintained this particularly central position in the next few years, until 1960, anticipating other major actors who would gradually become more central in the 1960s. Centrality measures in this 4-layer network also give more relevance to Dennis Sciama at Cambridge, who appears as a central actor much earlier than in our analysis of previous networks (Fig. 21 and Table 8 in “Appendix 2”).

Table 8 Betweenness centrality measures of the scholars with the five highest measures in the AllRelations_OnlyNodes_8Years network in 1951

Full size table

Discussion on the dynamics of flattened multilayer collaboration networks

The results presented in the co-authorship networks analyzed in “The dynamics of the co-authorship network” section were strongly disputable, as all the co-authorship networks remained very sparse all through the period of analysis, with an average degree lower than one until 1970. The inclusion of more layers with different kinds of collaborations significantly increased the density of the networks and allowed for a more robust analysis. The first two layers, collaboration and influence, provide similar historical pictures of the shift in the topology of the network (Fig. 16). Strikingly, the Influence_AllNodes_8Years network precisely matches the year in which the shift occurred in Collaboration_AllNodes_8Years (1959–1960). This result was contrary to our expectations, as we anticipated that by including many more edges the formation of the giant component would have started earlier. We interpret this result as a sign of the robustness of the finding that historically relevant changes occurred precisely between 1959 and 1960

We interpreted Fig. 16 in the following way. While the number of scholars working on general relativity started increasing soon after the end of World War II, this increment did not lead immediately, nor straightforwardly, to a change in the structure of the network. A topological shift occurred only about 15 years after the end of World War II, when a giant component started forming at a very rapid pace. The addition of other types of collaboration data backdates this topological shift by a few years with respect to the co-authorship networks. The delay with respect to the end of World War II undermines the view that the renaissance of general relativity was simply a by-product of the increase of the number of physicists. By taking into consideration the collaboration and influence layers it emerges more clearly that post-doc movements between research groups were essential to the formation of the giant component and that this preceded the astrophysical discoveries, thus undermining the historical narrative that sees in these discoveries the major moving force beyond the renaissance of general relativity.

Apart from a more detailed and robust analysis of the structural dynamics of the relativity collaboration network, the new layers offer also a richer understanding of the process of the renaissance of general relativity, confirming the relevance of particular groups and specifying which kinds of movement increase the connectivity of the network. Collaboration and influence edges not only anticipate relations that later appear as co-authorship relations, but effectively show connections that were not available in our previous analysis, such as those between Wheeler and his students or junior associates with the largest component built around Bondi and other European groups in the collaboration layer (Fig. 14). This implies that Wheeler might have been more influential in the forming relativity community before it becomes evident in the co-authorship network, as in the extended co-authorship networks he becomes part of the largest connected component only in 1964, namely, after the discovery of quasars.

Various parameters of the influence layer, such as the diameter of the largest component, the clustering coefficient and the average path length, also do not provide any new results concerning the topology of the network with respect to the collaboration layer. The same can be said for the comparison of the parameters of the Influence_AllNodes_8Years network with the Erdős-Rényi and BA models, which does not show any relevant new insights with respect to the previous analysis. The influence network, however, reveals some central persons, and entire groups, such as the French groups of students of Lichnerowicz and Tonnelat, which were completely absent in our previous analyses, most probably because of different national or disciplinary traditions of co-authorship between PhD supervisor and students, as well as a different research environment as concerns the career path of relativity experts.

The AllRelations_OnlyNodes_8Years provides, instead, a somewhat different picture, as should be expected by the fact that the number of edges more than doubles with respect to the Influence_AllNodes_8Years. The emergence of a giant component appears much earlier, in the early 1950s, only a few years after the end of World War II. Further, the diameter and other parameters stabilize by the late 1950s, in any case before 1962.^{Footnote 27} The effect of World War II appears quite distinctly in this network both as a disruption of the socio-institutional network emerging in the 1930s and in the fact that a giant component started forming early after the war contrary to all our previous analyses. All these elements seem to indicate the establishment of the giant component started after the war and stabilized by the late 1950s—a foundation that might be called the socio-institutional preconditions of the renaissance of general relativity, where institutional relations clearly preceded, and most probably favored, actual collaborations. The introduction of this layer in the analysis also gives a different indication of who might have been particularly central individuals, leading to the evaluation of Felix Pirani as a particularly central scientist in this early phase of the construction of a giant component.

Conclusion

In this paper we have compared various approaches for employing social network theory to the evolution of collaborative groups working on general relativity over a long time period spanning from 1925 to 1970. These different approaches were based on different definitions of collaboration relations as well as different assumptions on the length of permanence and on the presence of nodes. Our aim was threefold. First, we wanted to find a methodology to analyze collaboration networks in the history of science in periods when co-authorship networks are sparse. The second was to test the impact of different network analytical assumptions on the interpretation of historical data. The third was historical, namely to find a more robust definition and periodization of the so-called renaissance of general relativity based on data-driven computational methods.

From the methodological perspective, besides a deepening of insight into structural dynamics and the role of specific individuals in the evolution of this structure, the comparative approach has showed how the historical interpretation might depend crucially on assumptions about the length of edges, the permanence of nodes and the type of relations taken into consideration. Adding more layers not only deepens the analysis, but in historical cases such as this one can also make an analysis possible at all, as shown by the striking difference between the results obtained from using co-authorship data from WoS alone and those obtained after more edges had been added. Likewise the stabilization of the largest component diameter crucially depended on assumptions regarding temporal edge length.

Adding other sources besides WoS edges for co-authorship relations resulted in a richer network and shows sudden processes that might be interpreted as the emergence of a giant component by the early 1960s. This is roughly in line with what occurs when one adds other relationship layers, such as manually retrieved collaboration and influence relations. However, even the combined co-authorship network remained quite sparse for the entire period of the analysis, which made the insights obtained hardly reliable.

Adding the collaboration and influence layers increased the number of edges and make the analysis much more robust. The inclusion of these layers shifts back the periodization of the forming of a giant component to the late 1950s. This analysis of the various layers leads us to conclude that a more connected scientific community of relativity experts was emerging well after the end of World War II, but before the discovery of quasars. In this process a particularly relevant role was played by the movements of scholars in their post-doc career stage. This result is considered very robust, as it is independent from the various types of collaboration relations as well as from the various hypotheses about the length of edges and permanence of nodes. While this general picture remained largely the same, each successive layer brought new findings about the network structure and, especially, about the relevant persons and relations in the structure of the network as well as the relevance of specific events such as the start of World War II, its conclusion, the death of Einstein and so on. Our approach has been useful for historical analysis in that it provides a complex picture of the renaissance process, its causes and its major actors.

The inclusion of the layer of possible connections from the copresence at institution layer gives, instead, a quite different picture with respect to the previous analyses. In this case, relevant changes in the topology of the network occurred much earlier than in the other networks: in the early 1950s, rather than around 1960. Besides the fact that from this analysis emerge those actors who might have had an early influence on the development of the network, such as Felix Pirani, the result might be interpreted as the strength of the institutional structure that would constitute the basis for making the collaboration network between individuals emerge.

The present analysis on the dynamics of the social network of general relativity will be followed by further analyses extending the multilayer methodology of adding layers with different types of nodes and relations, including co-citation networks and networks of topics mentioned in the titles and abstracts of the published papers. Our aim is to complement research on the passage between the “low-water mark” period and the renaissance of general relativity with the range of relevant approaches network analysis offers, including both social relations and conceptual changes in an integrated manner. The analysis here proposed is the first step of this program.

Notes

The result of this analysis of the social network is being combined with the study of co-citation networks and topics network to provide a full picture of the renaissance of general relativity process (Lalli et al. Socio-Epistemic Networks of General Relativity, 1925–1970, in The Renaissance of General Relativity in Context, ed. by A. Blum, R. Lalli and J. Renn, Springer, forthcoming) that takes into account both social and epistemic networks (Renn et al. 2016).
For a critique of the uncritical use of co-authorship network as a proxy of collaboration networks, see (Katz and Martin 1997; Laudel 2002).
We have consistently excluded book reviews, biographical items and items about individuals.
Math subject Class 83- Relativity and Gravitation Theory in https://www.genealogy.math.ndsu.nodak.edu/results.php? Accessed 12 December 2018.
https://ui.adsabs.harvard.edu/. Accessed 12 October 2018.
The NASA ADS repository contains a number of false co-authorship edges, such as the relation between the author of a book and the reviewer of the same book, or the relations between those who published abstracts assembled together in journals. We have manually excluded these false edges.
Collaborate with hereafter refers to this second type of collaboration edge, not to all kinds of collaboration.
Historical sources for each collaboration edge of types 1.c, 2, 3, 4, and the edges between scientists and institutions necessary to retrieve the collaboration edge of type 5 are reported in (Wintergrün et al. 2019a). These include, but are not limited to: reviews, historical monographs, textbooks, biographies, oral interviews, obituaries, encyclopedia articles, online webpages, bulletins (such as the Bulletin on General Relativity and Gravitation published form 1962 to 1969), bibliographical dictionaries (such as American Men & Women of Science), university records, online databases (such as The Mathematics Genealogy Project) and acknowledgments in research papers. The process of manual acquisition of data from this broad variety of sources has been time-consuming, having required about 1200 h. The automatic retrieval of data of types 1.a and 1.b has required minor work of name disambiguation, which was mainly dealing with the problem of initials of first and middle names.
See Dirk Wintergrün’s dissertation for an introduction into network analysis and model-based description of historical knowledge structures Wintergrün (2019a).
See (FileMaker 2019).
In our case we use blazegraph (SYSTAP 2019) as triple-store and metaphactory (metaphacts 2019) for simple visualizations and queries.
A first version of this package has been published (Wintergrün 2019b). See the ipython-Notebooks Create multilayer network with corrections from SPARQL.ipynb and Create co-author network - persons - ads and WoS based on TripleStore for details on how the queries are constructed. The dataset we are referring to in this article can be found at (Wintergrün et al. 2019) Version 3.
A more complex model will take different lengths of the interaction interval into account. For this study we have restricted ourselves to the choice of one parameter for every form of interaction.
Hereafter, networks are referred to as either “all_node” or “only_node” depending on the choice of B.
To the best of our knowledge this approach is new for what concerns collaboration network studies and the employment of network analysis in the history of science. However, the cumulative approach to studying the impact of different layers of data on parameters is common in the sciences. See, for instance, studies on the observational determination of cosmological parameters pursued through the adding of different layers of observation, such as gravitational lensing, Microwave Background anisotropies, supernova, etc. (e.g., Serjeant 2010).
In the Erdős-Rényi model, the number of nodes und edges is kept (Erdös and Rényi 1959). In the Barabàsi-Albert (BA) model, the number of nodes and the degree distribution is fixed (Albert and Barabási 2002). The creation of the network using this model can be understood as forming a social network by using preferential attachment (see, e.g., Jackson 2008).
See https://igraph.org/python/doc/igraph.GraphBase-class.html#Barabasi and https://igraph.org/python/doc/igraph.GraphBase-class.html#Erdos_Renyi (igraph 2019).
Methods for comparing real graphs with simulated graphs are also part of the network_extension Python package (Wintergrün 2019b).
The number 20 was chosen because we started our research with a fixed number of bins of 20 for each year and wanted a visualization which would give the highest values to the most important actors. However, it turned out that we need a flexible adaptation of the bin sizes for each year to more adequately represent processes where the network becomes more homogeneous.
As explained in “Method of analysis” section, the weight of the edge, once established, will be one independently of the number of co-authored papers.
As derivative we are using the symmetric difference quotient for each point, see standard textbooks on numerical analysis (e.g., Kress 1998).
We identified a similar turning point in the development of the average path length, which also reached a maximum in 1963, after which it started decreasing. The hypothesis of the stabilization of the diameter around 1963 has been tested also by plotting the diameter of the largest component over the dimension of the largest component, which is the same methodology as in Bettencourt et al. (2008, 2009). This plot fully confirms the stabilization process that might mistakenly appear as a transient phenomenon in Fig. 3.b due to the closeness between 1963 and 1970. We still prefer to show the yearly plot because we are interested in the historical interpretation of such plots.
Other centrality measures, such as betweenness centrality and degree centrality provide similar results.
Robinson appears here much more relevant because in 1962 he connects groups that in the previous analysis are joined by nodes no longer active this year (such as Einstein for example).
The rapid decrease of the diameter of the 8-year network in 1970 is most probably an artifact of how the scientists have been chosen, as those who completed their PhD after 1971 and did not publish any paper on the subject before 1971 have been excluded.
Notice that Bettencourt et al. (2008, 2009) and most dynamic analyses of collaboration network assume edge on unlimited length, but usually focus on a shorter range of years.
In 1959 the international community of relativity researchers established the first institutional body aimed at promoting the field at the international level, which was called International Committee on General Relativity and Gravitation (Lalli 2017). The connection between the stabilization of the socio-institutional network and the establishment of this institution might have been related, but no quantitative analysis has been so far performed to establish the connection.

References

Abbasi, A., Altmann, J., & Hossain, L. (2011). Identifying the effects of co-authorship networks on the performance of scholars: A correlation and regression analysis of performance measures and social network analysis measures. Journal of Informetrics,5, 594–607. https://doi.org/10.1016/j.joi.2011.05.007.
Article Google Scholar
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74(1), 47–97. https://doi.org/10.1103/RevModPhys.74.47.
MathSciNet Article Google Scholar
Barabási, A. L., Jeong, H., Néda, Z., Ravasz, E., Schubert, A., & Vicsek, T. (2002). Evolution of the social network of scientific collaborations. Physica A: Statistical Mechanics and its Applications,311(3), 590–614. https://doi.org/10.1016/S0378-4371(02)00736-7.
MathSciNet Article MATH Google Scholar
Barabási, A.-L., Watts, D. J., & Newman, M. E. J. (2006). The structure and dynamics of networks., Princeton studies in complexity Princeton, N.J.: Princeton University Press.
MATH Google Scholar
Bergmann, P. G., Robinson, I., & Schücking, E. (1962). Asymptotic properties of a system with nonzero total mass. Physical Review,126, 1227–1231. https://doi.org/10.1103/PhysRev.126.1227.
MathSciNet Article Google Scholar
Bettencourt, L. M. A., Kaiser, D. I., & Kaur, J. (2009). Scientific discovery and topological transitions in collaboration networks. Journal of Informetrics,3, 210–221. https://doi.org/10.1016/j.joi.2009.03.001.
Article Google Scholar
Bettencourt, L. M. A., Kaiser, D. I., Kaur, J., Castillo-Chávez, C., & Wojick, D. E. (2008). Population modeling of the emergence and development of scientific fields. Scientometrics,75, 495–518. https://doi.org/10.1007/s11192-007-1888-4.
Article Google Scholar
Blum, A., & Brill, D. (2019). Tokyo wheeler or the epistemic preconditions of the renaissance of relativity. arXiv:1905.05988 [gr-qc, physics:physics].
Blum, A., Giulini, D., Lalli, R., & Renn, J. (2017). Editorial introduction to the special issue “The Renaissance of Einstein’s Theory of Gravitation”. The European Physical Journal H,42, 95–105. https://doi.org/10.1140/epjh/e2017-80023-3.
Article Google Scholar
Blum, A., Lalli, R., & Renn, J. (2015). The reinvention of general relativity: A historiographical framework for assessing one hundred years of curved space-time. Isis,106, 598–620.
MathSciNet Article Google Scholar
Blum, A., Lalli, R., & Renn, J. (2016). The renaissance of general relativity: How and why it happened. Annalen der Physik,528, 344–349.
MathSciNet Article Google Scholar
Blum, A., Lalli, R., & Renn, J. (2018). Gravitational waves and the long relativity revolution. Nature Astronomy,2, 534–543. https://doi.org/10.1038/s41550-018-0472-6.
Article Google Scholar
Bornmann, L. (2016). Is the promotion of research reflected in bibliometric data? A network analysis of highly cited papers on the clusters of excellence supported under the excellence initiative in Germany. Scientometrics,107, 1041–1061. https://doi.org/10.1007/s11192-016-1925-2.
Article Google Scholar
Brandes, U., & Wagner, D. (2004). Visone—Analysis and visualization of social networks. In M. Jünger & P. Mutzel (Eds.), Graph drawing software (pp. 321–340). Berlin: Springer. https://doi.org/10.1007/s11192-016-1925-2.
Chapter Google Scholar
CIDOC CRM Special Interest Group. (2015). CIDOC CRM.
De Solla Price, D. J., & Beaver, D. (1967). Collaboration in an invisible college. American Psychologist,21, 1011–1018. https://doi.org/10.1037/h0024051.
Article Google Scholar
Dickison, M. E., Magnani, M., & Rossi, Luca. (2016). Multilayer social networks. Cambridge: Cambridge University Press.
Book Google Scholar
Eisenstaedt, J. (1986). La relativité générale à l’étiage: 1925–1955. Archive for History of Exact Sciences,35, 115–185.
MathSciNet Article Google Scholar
Eisenstaedt, J. (1989). The low water mark of general relativity, 1925–1955. In D. Howard & J. Stachel (Eds.), Einstein and the history of general relativity (pp. 1–277). Boston: Birkhäuser.
Google Scholar
Fatt, C. K., Ujum, E. A., & Ratnavelu, K. (2010). The structure of collaboration in the Journal of Finance. Scientometrics,85, 849–860. https://doi.org/10.1007/s11192-010-0254-0.
Article Google Scholar
FileMaker. (2019). Innovation in the workplace—filemaker, An Apple subsidiary. Retrieved June 27, 2019, from https://www.filemaker.com/.
Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences,99, 7821–7826. https://doi.org/10.1073/pnas.122653799.
MathSciNet Article MATH Google Scholar
González-Alcaide, G., Park, J., Huamaní, C., Gascón, J., & Ramos, J. M. (2012). Scientific authorships and collaboration network analysis on Chagas disease: Papers indexed in PubMed (1940–2009). Revista do Instituto de Medicina Tropical de São Paulo,54, 219–228. https://doi.org/10.1590/S0036-46652012000400007.
Article Google Scholar
Granovetter, M. S. (1973). The strength of weak ties. American Journal of Sociology,78, 1360–1380.
Article Google Scholar
igraph. (2019). python-igraph. Retrieved June 27, 2019, from https://igraph.org/python/.
Jackson, M. O. (2008). Social and economic networks. Princeton, NJ: Princeton University Press.
Book Google Scholar
Kaiser, D. (2005). Drawing theories apart: The dispersion of Feynman diagrams in postwar physics. Chicago: University of Chicago Press.
Book Google Scholar
Katz, J. S., & Martin, B. R. (1997). What is research collaboration? Research Policy,26, 1–18. https://doi.org/10.1016/S0048-7333(96)00917-1.
Article Google Scholar
Kress, R. (1998). Numerical analysis. New York: Springer.
Book Google Scholar
Lalli, R. (2017). Building the general relativity and gravitation community during the cold war. Cham: Springer International.
Book Google Scholar
Laudel, G. (2002). What do we measure by co-authorships? Research Evaluation,11, 3–15. https://doi.org/10.3152/147154402781776961.
Article Google Scholar
Medina, A. M. (2018). Why do ecologists search for co-authorships? Patterns of co-authorship networks in ecology (1977–2016). Scientometrics,116, 1853–1865. https://doi.org/10.1007/s11192-018-2835-2.
Article Google Scholar
Mele, S., Dallman, D., Vigen, J., & Yeomans, J. (2006). Quantitative analysis of the publishing landscape in high-energy physics. Journal of High Energy Physics,2006, S01. https://doi.org/10.1088/1126-6708/2006/12/S01.
Article MATH Google Scholar
Melin, G., & Persson, O. (1996). Studying research collaboration using co-authorships. Scientometrics,36, 363–377. https://doi.org/10.1007/BF02129600.
Article Google Scholar
metaphacts. (2019). metaphactory. Retrived June 27, from https://metaphacts.com/product.
Misner, C. W. (2010). John Wheeler and the recertification of general relativity as true physics. In I. Ciufolini & R. A. Matzner (Eds.), General relativity and John Archibald Wheeler (pp. 9–27). Dordrecht: Springer. https://doi.org/10.1007/978-90-481-3735-0_2.
Chapter MATH Google Scholar
Moody, J. (2004). The structure of a social science collaboration network: Disciplinary cohesion from 1963 to 1999. American Sociological Review,69, 213–238. https://doi.org/10.1177/000312240406900204.
Article Google Scholar
Newman, M. E. J. (2001a). The structure of scientific collaboration networks. Proceedings of the National Academy of Sciences,98, 404–409. https://doi.org/10.1073/pnas.98.2.404.
MathSciNet Article MATH Google Scholar
Newman, M. E. J. (2001b). Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physical Review E,64, 016132. https://doi.org/10.1103/physreve.64.016132.
Article Google Scholar
Newman, M. E. J. (2004). Coauthorship networks and patterns of scientific collaboration. Proceedings of the National Academy of Sciences,101, 5200–5205. https://doi.org/10.1073/pnas.0307545100.
Article Google Scholar
Renn, J., Wintergrün, D., Lalli, D., Laubichler, M., & Valleriani, M. (2016). Netzwerke als Wissensspeicher. In J. Mittelstraß & U. Rüdiger (Eds.), Die Zukunft der Wissensspeicher : Forschen, Sammeln und Vermitteln im 21. Jahrhundert (pp. 35–79). München: UVK Verlagsgesellschaft Konstanz.
Google Scholar
Rickles, D. (2018). Geon wheeler: From nuclear to spacetime physicist. The European Physical Journal H,43, 243–265. https://doi.org/10.1140/epjh/e2018-80053-x.
Article Google Scholar
Robinson, I., Schild, A., & Schucking, E. L. (Eds.). (1965). Quasi-stellar sources and gravitational collapse, including the proceedings of the First Texas symposium on relativistic astrophysics. Chicago: University of Chicago Press.
Google Scholar
Schmidt, M. (1963). 3C 273: A star-like object with large red-shift. Nature,197, 1040.
Article Google Scholar
Schucking, E. L. (2008). The first Texas symposium on relativistic astrophysics. Physics Today,42, 46–52. https://doi.org/10.1063/1.881214.
Article Google Scholar
Serjeant, S. (2010). Observational cosmology. Cambridge: Cambridge University Press.
Google Scholar
SYSTAP. (2019). Graph database & application download. Blazegraph. Retrieved June 27, 2019, from https://www.blazegraph.com/.
Thorne, K. S. (1994). Black holes and time warps: Einstein’s outrageous legacy. New York: WWNorton.
MATH Google Scholar
Uddin, S., Hossain, L., & Rasmussen, K. (2013). Network effects on scientific collaborations. PLoS ONE,8, e57546. https://doi.org/10.1371/journal.pone.0057546.
Article Google Scholar
W3C. (2019). SPARQL query language for RDF. Retrived June 27, 2019, from https://www.w3.org/TR/rdf-sparql-query/.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature,393, 440–442. https://doi.org/10.1038/30918.
Article MATH Google Scholar
Will, C. M. (1986). Was Einstein right? Putting general relativity to the test. New York: Basic Books.
Google Scholar
Will, C. M. (1989). The renaissance of general relativity. In P. Davies (Ed.), The new physics (pp. 7–33). Cambridge: Cambridge University Press.
Google Scholar
Wintergrün, D. (2018). SPARQLGraph. GitLab. Retrieved August 10, 2019, from https://gitlab.gwdg.de/dirk.wintergruen/SPARQLGraph.
Wintergrün, D. (2019a). Netzwerkanalysen und semantische Datenmodellierung als heuristische Instrumente für die historische Forschung. Erlangen: Friedrich-Alexander-Universität Erlangen-Nürnberg.
Google Scholar
Wintergrün, D. (2019b). Network-extensions: Managing multilayer graphs with igraph (version 0.9.5.0). Retrieved June 27, 2019, from https://pypi.org/project/network-extensions/.
Wintergrün, D., Lalli, R., & Howey, R. (2019). History of general relativity/data input- filemaker. Retrieved August 10, 2019, from https://hdl.handle.net/21.11103/FK2.5XQP2X.

Download references

Acknowledgements

Open access funding provided by Max Planck Society. This research is supported by Department 1 of the Max Planck Institute for the History of Science and by the Berlin Center for Machine Learning (www.bzml.de) (01IS18037), funded by the Federal Ministry for Education and Research of Germany. We are indebted to Dept. 1 director Jürgen Renn for his institutional support and intellectual engagement with the project. Earlier version of this research has been discussed with many colleagues, including Alexander Blum, Jürgen Jost, Manfred Laubichler, Matteo Valleriani, as well as the participants of the International Workshop on Graphs, Networks and Digital Humanities in Bucharest, the Workshop Network Science in the Humanities at the Max Planck Institute for Mathematics in Leipzig, the Historical Network Research panel at the Sunbelt 2018 Conference, Utrecht. We are wholeheartedly grateful to them all as well as to the two referees for the many insightful comments we have received.

Author information

Authors and Affiliations

Max Planck Institute for the History of Science, Berlin, Germany
Roberto Lalli, Riaz Howey & Dirk Wintergrün

Authors

Roberto Lalli
View author publications
You can also search for this author in PubMed Google Scholar
Riaz Howey
View author publications
You can also search for this author in PubMed Google Scholar
Dirk Wintergrün
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

Roberto Lalli and Dirk Wintergrün prepared the study conception, design and developed the methodology. The digital infrastructure for data acquisition and analysis was designed and prepared by Dirk Wintergrün. Data collection was performed by Riaz Howey and supervised by Roberto Lalli. Historical interpretations were put forward by Roberto Lalli. The first draft of the manuscript was written by Roberto Lalli and all authors commented on previous versions of the manuscript. The final version was reviewed by Riaz Howey. Riaz Howey contributed to the tables, images and diagrams. All authors have read and approved the final manuscript.

Corresponding author

Correspondence to Roberto Lalli.

Appendices

Appendix 1 Comparison with random models

See Figs. 22, 23, and 24.

The comparison with random models captures the dynamical characteristics of the Co-authorExtended_AllNodes_UnlimitedLength network and its possible similarity with small-network behaviors. This is shown by the sudden drop in the plot of the fraction of both the radius and the average path length of the largest components of Co-authorExtended_AllNodes_UnlimitedLength over the same parameters in the Erdős-Rényi model calculated as explained in “Method of analysis” section. While our network does not seem to follow the pattern of the preferential attachment model, it is significantly more connected than an Erdős-Rényi random graph. As far as the clustering coefficient is concerned, it shows considerable signs of increasing clusterization behavior after 1950, with a strong increase between 1963 and 1964, which is also considerably larger than the clustering coefficient calculated with the BA model (Fig. 22).

The comparison between radius and average path length of the largest component of Collaboration_AllNodes_8Years and values of the same parameters in the Erdős-Rényi model conveys the idea that a large component forming in 1960 became significantly more connected than a random graph in the following years. By the same token, while the clustering coefficient of the largest component of the network was always quite large, it became even greater in the 1960s, as is shown by the comparison with the BA model (Fig. 23).

Before 1950 the AllRelations_OnlyNodes_8Years network was more connected than the kinds of collaboration network previously analyzed. Beginning in the 1950s, there was an increase in diameter and average path length that became greater than the corresponding values of random graphs. By the end of the 1950s, there was a stabilization and, gradually, a decrease of these parameters with respect to the corresponding values of the Erdős-Rényi model. The clustering coefficient was greater than the values of both models over the entire timespan, but the relative difference was less than those of the collaboration networks previously analyzed. Even in the case of the clustering coefficient, there are noticeable shifts in the 1950s and the 1960s, signaling a different clustering behavior and structure of the AllRelations_OnlyNodes_8Years network (Fig. 24).

Appendix 2

Tables with centrality measures in the year of shift in the formation of the giant component

See Tables 2, 3, 4, 5, 6, 7 and 8.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Cite this article

Lalli, R., Howey, R. & Wintergrün, D. The dynamics of collaboration networks and the history of general relativity, 1925–1970. Scientometrics 122, 1129–1170 (2020). https://doi.org/10.1007/s11192-019-03327-1

Download citation

Received: 08 July 2019
Published: 16 December 2019
Issue Date: February 2020
DOI: https://doi.org/10.1007/s11192-019-03327-1

Keywords

Collaboration networks
Co-authorship networks
Multilayer graph
General relativity
Einstein
Historical methodology

Abstract

Introduction

Multilayer collaboration networks: datasets and infrastructure

Actors and papers: selection criteria and datasets

Collaboration edges: definition and criteria

Construction of the multilayer social network

Method of analysis

The dynamics of the co-authorship network

WoS-based co-authorship [all_nodes – edges of unlimited length]

Co-authorship extended [all_nodes—edges of unlimited length]

Co-authorship extended [only_nodes—edges of unlimited length]

Co-authorship extended [all_nodes—8-year length edges]

Discussion on the dynamics of co-authorship networks

The dynamics of the extended collaboration networks

Collaboration + ExtendedCo-author network [all_nodes—8-year length edges]

Influence + Collaboration + ExtendedCo-author network [all_nodes—8-year length edges]

Copresence at institution + Influence + Collaboration + ExtendedCo-author network [only_nodes—8-year length edges]

Discussion on the dynamics of flattened multilayer collaboration networks

Conclusion

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding author

Appendices

Appendix 1

Comparison with random models

Appendix 2

Rights and permissions

About this article

Cite this article

Share this article

Keywords