The interaction of a size-dependent tax policy and financial frictions: evidence from a tax reform in Japan

Abstract

This study examines the effects of the interaction of a size-dependent tax policy that exempts firms whose stated capital is at or below a certain threshold from taxation and financial frictions on firm growth and financing. Our empirical findings can be summarized as follows: First, firms with lower productivity, a positive potential tax benefit, and smaller stated capital are more likely to conduct the cash-out capital reduction to or below the threshold in response to the policy. Second, this capital reduction causes ex-post lower firm growth and fewer debt. Third, such causal effects are observed for firms with less cash flow ratios. These results indicate that the interaction between a size-dependent tax policy and financial constraints deters firm growth.

Plain English Summary

The interaction of a size-dependent tax policy that exempts firms whose stated capital is at or below a certain threshold from taxation and financial frictions deters firm growth. We use the introduction of the pro forma standard taxation system in Japan that exempts firms (SMEs), whose stated capital is at or below a threshold, from taxation to empirically examine how firms react to this institutional change and how such a reaction systematically affects their financing and real outcomes. We show that size-dependent tax policies can have a significant effect on firms’ growth and financing through financial constraints. It indicates that firms decide whether to obtain an SME status by considering the trade-off between a more severe borrowing constraint and a smaller tax payment. The results obtained in this study indicate that such indirect effects of a size-dependent tax policy on firm dynamics should be considered when designing the policy. Moreover, governments should understand that an institutional change in their tax systems generates a heterogeneous reaction from firms and thus has heterogeneous effects on their dynamics.

1 Introduction

Many countries provide tax preferences, subsidies, regulation relaxations, and other benefits to small and medium enterprises (SMEs) by defining SMEs using size thresholds in terms of, e.g., sales, employment, and assets. Recent studies have shown that such size-dependent policies provide disincentives to grow beyond the threshold and therefore cause distorted size distribution and inefficient resource allocation.¹

When the threshold for SMEs is defined in terms of the variables measuring firm size (e.g., sales, employment, and assets), such policies have apparent negative effects on firm growth beyond the threshold simply because firms have incentives to keep their size below the threshold to receive benefits as SMEs. Here, in addition to this “direct” effect, those firms that obtain an SME status by reducing their size in terms of the relevant threshold may face financial constraints, which may further impede growth. In this paper, we explore how a size-dependent policy “indirectly” affects firm growth through such an interaction of the policy and financial constraints.

In general, it is difficult to identify the indirect effects of financial constraints originating from a size-dependent policy on firm growth as such a policy could generate both the aforementioned direct and indirect effects. Suppose a SME policy defines a threshold in terms of assets. Then, ceteris paribus, firms that reduce assets to obtain an SME status may face tighter financial constraints if the net assets of debt (i.e., net worth) also decrease. This is because the net assets often serve as collateral for borrowing (e.g., Bernanke & Gertler, 1989; Bernanke et al., 1999; Kiyotaki & Moore, 1997; Matsuyama, 2008). In this case, such policies impede firm growth not only due to firms’ incentives to receive benefits as SMEs but also due to tighter financial constraints associated with smaller assets.

Against this empirical difficultly, the threshold for SMEs defined in terms of financial indicators such as stated capital, which we focus on in this paper, helps us to examine the indirect financial constraint effect because the policy has no direct effect deterring firm growth. Moreover, when firms are not facing financial constraints, the sized-dependent policy based on those financial indicators has no indirect effect deterring firm growth. In fact, tax incentive for capital investment that SMEs obtain could even positively contribute to their growth. However, if financial constraints are binding, firms that reduce their net assets to obtain an SME status, for example, by reducing stated capital, might not be able to secure enough external funds when hit by a positive productivity shock. If such an interaction between a size-dependent tax policy and financial constraints overwhelms the contribution of benefits from the SME policy, this interaction could indirectly deter the growth of financially constrained firms. These illustrations motivate us to theoretically and empirically investigate the effects on firm growth of the size-dependent policy that uses stated capital as the eligibility criteria for SMEs.²

Motivated by the above discussion, we examine the introduction of the pro forma standard tax that the Japanese government announced in December 2002 and made it a part of corporate enterprise tax (a local government tax) in 2004. The government imposed this new tax on firms’ paid-up capital (the sum of stated capital and capital reserves) and value added, but it exempted firms with stated capital at or below 100 million JPY from taxation. To exploit this tax reform, we first build a theoretical model based on the literature on tax policies³ while incorporating the trade-off between tax savings and financial constraints to hypothesize a firm’s responses to the pro forma standard tax. Then, we use a firm-level panel dataset that covers the period before and after the announcement and introduction of the tax reform to test the derived hypotheses.

Specifically, we first examine whether firms reduce their stated capital to reduce tax burdens in response to the new tax and, if so, what are their ex-ante characteristics that reduce their capital.⁴ Then, we investigate how firms that reduce capital grow and finance afterward. Ex-post financing is relevant because weaker financial indicators such as the reduction of stated capital potentially have negative effects on external financing and real activities if firms face financial constraints. We further examine how the ex-post growth and financing vary depending on the ex-ante degree of financial constraints. As our theoretical model shows, constrained firms should grow and borrow less than unconstrained firms. Thus, this study provides a better understanding of how such policies affect the behavior of firms through financial constraints.

The present study contributes to the broad literature on how size-dependent policies distort the firm size. Some theoretical studies show that such a policy-induced distortion of firm size reduces aggregate productivity through inefficient resource allocations (Garicano et al., 2016; Gourio & Roys, 2014; Guner et al., 2008; Keen & Mintz, 2004). Recent empirical studies have investigated the effects of discrete tax schemes on the size distribution of firms by using disaggregated data. Onji (2009), Liu et al. (2021), and Harju et al. (2019) investigate the VAT in Japan, the UK, and Finland, respectively, Devereux et al. (2014) investigate the corporate income tax in the UK, and Almunia and Lopez-Rodriguez (2018) investigate the monitoring system of tax payments in Spain. They all find that these size-dependent tax policies create bunching in the distribution of sizes at the threshold (e.g., sales and income) that indicates that firms respond to such policies by obtaining SME status to reduce their tax payments and compliance costs. Apart from tax policies, size-dependent regulations on firing and entry restrictions have also been shown to distort the distribution of firm size (Gourio & Roys, 2014; Garicano et al, 2016; Schivardi & Torrini, 2008; Guner et al. 2008; Garcia-Santana & Pijoan-Mas, 2014). Most of these studies examine the size distribution near the threshold that implicitly suggests that some firms restrict their size to obtain benefits from an SME status. On the contrary, we focus on firms that obtain SME status and explicitly examine the effects of the firms’ reactions to the change in tax policy, that is, capital reduction in this study, on their ex-post dynamics through a proper consideration of the selection bias associated with their heterogeneous reactions to the tax reform. Specifically, we use propensity score matching (PSM) and difference-in-differences (DID) to examine such effects. Such causal inferences provide clear and reliable evidence about the effects of a size-dependent tax policy on the various measures of a firm’s activities.⁵

As the most closely related study to ours, Tsuruta (2020) examines the effects of size-dependent policies based on stated capital on firm growth as we do. Examining the change in the SME Basic Act in Japan that raised the thresholds in terms of stated capital for various SME policies, he finds that the SMEs that had increased stated capital in response to the policy reform increased total assets, tangible fixed assets, and inventories. He further finds that among the firms that increase stated capital, relatively large firms also increase debt. Here, besides the difference of the specific policy reforms that Tsuruta (2020) and we focus on, Tsuruta (2020) does not explicitly explore the mechanism through which a change in stated capital leads to changes in assets and debt while we do. Namely, we theoretically analyze the trade-off between tax benefits and financial constraints and empirically examine how changes in stated capital affect size and financing and how such effects differ depending on the degree of financial constraints based on our theoretical predictions. To explicitly explore the mechanism, we further classify capital reductions into those with the reduction in net assets through the reimbursement of cash to shareholders and those without. Then, we obtain evidence that only the cash-out capital reductions have substantial negative effects on growth and debt financing, confirming the effects of financial constraints on them.

The rest of this paper is organized as follows: Section 2 provides a brief background on the new tax system and the practical procedure of capital reduction by firms in Japan. Section 3 presents the theoretical model and the testable hypotheses derived from the model. In Section 4, we discuss the data and method used in our analysis and present the empirical results in Section 5. Section 6 concludes the paper and includes potential avenues for future research.

2 Background information

2.1 Pro forma standard taxation system in Japan

The Japanese government first announced the pro forma standard taxation system on December 13, 2002, and then introduced it in the Japanese fiscal year that started on April 1, 2004. This system was set up as part of the corporate enterprise tax, which is a local government tax at the prefecture level. Before its system’s introduction, the corporate enterprise tax was levied only on corporate income and exempted firms with losses, which raised concerns about the inequality in tax burdens between profit and loss firms. Thus, to remedy such inequality, the new system required firms to pay a tax of 0.2% on their capital and capital reserve when their capital exceeded 100 million JPY, regardless of whether they were generating profits.⁶ Furthermore, these firms were also required to pay 0.48% of their value added (see Table 1).⁷ As the most important feature of this tax system, SMEs with capital equal to or less than 100 million JPY (about 900,000 USD) were exempted from paying these taxes. Under the new tax system, the tax rate on SMEs’ income was slightly higher than that on non-SMEs’ income (44.79% for SMEs vs. 42.39% for non-SMEs).

Table 1 The pro forma standard taxation system

While the pro forma standard taxation with tax exemption for SMEs was a newly introduced size-dependent tax policy in 2004, it was not the first size-dependent tax policy introduced in the corporate tax system in Japan. Earlier, the central government had already provided SMEs with some types of tax preferences such as a reduced tax rate on income, a tax credit associated with investment in physical capital and R&D, and a tax-loss carryback. During our sample period from 1996 to 2006, the central government lowered the reduced tax rate applied to the part of SMEs’ income twice in 1998 and 1999.⁸ However, because it lowered the regular tax rate applied to the income of non-SMEs simultaneously at that time, the difference between the regular tax rate and the reduced tax rate changed little. Therefore, the reduction in the tax rate on SMEs’ income likely did not affect the incentive to reduce capital to a level at or below the threshold.

To estimate the amount of taxes that a firm can save by reducing its capital from above the threshold to at or below it, we assume that the corporate income tax base does not change between before and after the capital reduction. Table 2 shows the mean difference in such hypothetical tax payments between under non-SME and SME statuses for each class of corporate income tax base and each period before and after the introduction of the pro forma standard taxation.⁹ When we calculate the hypothetical tax payment, we only consider the taxes shown in Table 1 and the reduced corporate tax rate applied to the part of SME’s income and assume that the corporate income tax base does not change if a firm selects either tax status.

Table 2 Mean difference in tax payment between non-SME and SME statuses by class of corporate income tax base (unit: 1 M JPY)

Table 2 shows that, before the introduction of the pro forma standard tax system (in the period 1996–2003), the mean difference in the tax payment is zero when the income tax base is zero and then increases slightly as the income tax base becomes larger. It is about 0.8 million JPY even when the income tax base is larger than 1000 million JPY. This value indicates that firms could on average save little on their tax payment by reducing their capital. However, after the introduction of the new tax system (in the period 2004–2006), the mean difference in tax payments is positive and larger than before for firms whose income tax base is 100 million JPY or less. It is the largest (about 14.8 million JYP) when the income tax base is zero and then decreases as the income tax base becomes larger. This value indicates that firms with a relatively small income tax base could on average save more on their tax payment by decreasing their capital.

2.2 Capital reduction in Japan

According to the Companies Act of Japan, to reduce capital, firms must first obtain agreement at a general shareholder meeting (Article 447 Paragraph 1). They must also announce the planned capital reduction to all creditors at least 1 month prior to starting because it might be a disadvantage to creditors. If no creditor opposes the reduction, firms can officially register it. However, if some creditors oppose the move, firms have to repay their debts or provide security to them to overcome their objection. As such, a series of official procedures are required to reduce capital, and the process takes substantial time and cost to complete.

The creditors whose consent firms must obtain to reduce capital usually include banks and other financial institutions. As traditionally modeled in the theoretical literature and examined in empirical analyses (see, e.g., Bernanke & Gertler, 1989; Kiyotaki & Moore, 1997; Bernanke et al., 1999; Matsuyama, 2008), these institutions consider the level of net assets as an important measure of debtors’ creditworthiness. Thus, we presume that capital reduction leads to tighter financial constraints on firms.

As an important detail regarding the way to reduce capital, there are two types of capital reduction that do not involve cash payouts to shareholders and thus do not affect the size of net assets. First, if firms hold accumulated losses in their balance sheet, they can offset those losses by reducing their stated capital (loss-offsetting capital reduction). In this case, there is no actual effect on the size of the firm’s balance sheet because the net assets (the sum of paid-up capital and accumulated losses) do not change. Second, firms can also reduce capital and increase their capital surplus by the same amount without changing the size of the firm’s balance sheet (item-changing capital reduction). In both cases, firms do not pay out any cash but only experience a reduction in the capital on the books.

To reduce capital without loss-offsetting or item-changing, the firm must pay cash to shareholders with dividends or must repurchase shares and thereby decrease their net assets. Consequently, to conduct such a capital reduction, the firm must sell its assets or increase its debt by an amount equal to or more than the cash paid out to shareholders. We call this reduction a “cash-out” capital reduction, and our empirical analysis mainly addresses this type of reduction, which presumably leads to tighter financial constraints on firms.¹⁰ Among the 1006 capital reductions to a level at or below the threshold (i.e., 100 million JYP) in our sample from 1996 to 2006, the share of cash-out capital reduction is 29% while that of loss-offsetting and item-changing capital reduction is 32% and 31%, respectively.¹¹

Some firms reduce capital to or below the threshold to avoid taxes by selling a part of their assets to the affiliated firms that they create or already have.¹² It is important for our purpose to exclude capital reductions associated with such company splits because such a “masquerade” of capital reduction may induce substantially different growths from what real capital reduction induces.¹³ The share of capital reductions that involve company splits is about 2.7% of all cash-out capital reductions across the threshold.

3 Theoretical underpinnings and hypotheses

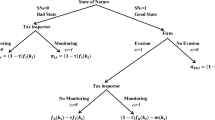
To derive some testable hypotheses, we build a theoretical model that examines the reactions of firms to changes in the tax scheme. Specifically, we consider a firm that first decides whether to reduce its capital to the threshold level in response to the new tax system and then produces output to maximize its after-tax profits given the size of its capital. A crucial feature of the model is that the firm faces a borrowing constraint that depends on its capital, which corresponds to the net assets at the beginning of the period because we do not consider capital reserves and retained earnings for simplicity. Specifically, we assume that the maximal amount of funds that the firm can borrow to rent physical capital depends on its capital. As a result, the borrowing constraint binds if the firm’s demand for physical capital is high and/or the amount of its capital is small. Thus, given that capital reduction is conducted by paying out cash to shareholders in the model, the firm decides to reduce capital if higher tax savings outweigh tighter borrowing constraints.

We first assume that the borrowing constraint depends only on the firm’s capital and analytically solve the model. Then, we extend the model in two ways: first by allowing for the borrowing constraint to depend on cash flow as well as capital and second by considering the possibility that the firm runs deficits due to fixed operating costs. We numerically solve for this extended model under plausible parameters to confirm the robustness of the main theoretical results obtained from the basic model. In this section, we present the basic model and the testable hypotheses derived from the model. We leave all the discussion based on the extended model and the proofs to the Online Appendix B.

3.1 Setup

3.1.1 Timeline and technology

First, a firm that has inherited capital knows that the government has introduced a pro forma standard tax system.¹⁴ After observing its productivity (A), the firm decides whether to keep the size of its inherited capital (e) or reduce it to the threshold level ($\overline{e }$), above which the firm incurs a pro forma standard tax payment, where$e>\overline{e }$¹⁵$.$ Then, the firm produces output (y) from the physical capital (k), labor (l), and intermediate goods (m) according to the production technology in Eq. (1):

$$\begin{array}{cc}y=A{k}^{\alpha }{l}^{\beta }{m}^{\gamma },& \alpha +\beta +\gamma <1.\end{array}$$

(1)

The firm sells the output in a competitive market at a unit price. We assume decreasing returns to scale.¹⁶

3.1.2 Borrowing constraint

We assume that the firm has access to competitive financial intermediaries that receive deposits from the firm and rent physical capital k at rate R to the firm. The rental rate of physical capital (R) is equal to $(r+\delta )$ under the competitive intermediation market in which $\delta$ and r denote the depreciation rate and the interest rate, respectively. Following Buera and Shin (2013), we assume that, after production has taken place, the firm can renege on the contracts and keep the fraction $\left(1-\phi \right)$ of the undepreciated physical capital ($0<\phi \le 1$) and all the revenue net of labor payments, intermediate payments, and taxes ($y-wl-pm-T$, where $w$, $p$, and $T$ denote the wage rate, the price of intermediate goods, and taxes, respectively). If the firm reneges on the contracts, the intermediary punishes it by garnishing the financial assets the firm has deposited with the financial intermediary, which is represented by e. For the rental contracts of physical capital to be incentive-compatible, the following inequality must hold:

$$\left(1+r\right)e-\left(r+\delta \right)k\ge (1-\phi )\left(1-\delta \right)k.$$

Rearranging the inequality yields

$$\lambda e\ge k$$

(2)

where $\lambda =\frac{1}{1-\frac{(1-\delta )}{1+r}\phi }$, and $1<\lambda \le \frac{1+r}{r+\delta }$.

The borrowing constraint in Eq. (2) means it is tightened if the firm reduces its capital or $\lambda$ is smaller. If the firm reduces capital from e to $\overline{e }$, then the relevant borrowing constraint is the same as in Eq. (2) with e replaced by $\overline{e }$.

The parameter $\phi$ (and hence $\lambda$) depends on the degree of contract enforcement in an economy. It may also depend on the type of physical capital; if the physical capital can be easily pledged as collateral, $\phi$ is likely to be high. As such, $\phi$ may differ across industries that use different kinds of physical capital.

3.1.3 Taxes

We construct a tax system that mimics the post-reform corporate tax system in Japan as much as possible. Therefore, we define the tax base of corporate income as follows:

$${\pi }^{\mathrm{pre}}=A{k}^{\alpha }{l}^{\beta }{m}^{\gamma }-\delta k-r\left(k-e\right)-wl-pm.$$

(3)

The term $(k-e)$ denotes net borrowings for physical capital if positive and net savings if negative. Equation (3) contains the negative of $r\left(k-e\right)$, as the tax rule allows borrowing costs to be deductible while interest earnings are taxable. The post-reform corporate tax system can be represented as shown in Eq. (4):

$$T=\left\{\begin{array}{l}\tau_LI\left(\pi^{\mathrm{pre}}>0\right)\pi^{\mathrm{pre}}+\tau_V\left(y-pm\right)+\tau_Ee\;if\;e>\overline e\\\tau_HI\left(\pi^{\mathrm{pre}}>0\right)\pi^{\mathrm{pre}},\;otherwise,\end{array}\right.$$

(4)

where ${\tau }_{L}$, ${\tau }_{V}$, and ${\tau }_{E}$ denote the corporate income tax rate, the tax rate on value added, and the tax rate on capital when the pro forma standard taxation is applied and ${\tau }_{H}$ denotes the corporate income tax rate when the pro forma standard taxation is avoided, respectively. I denotes an indicator function equal to one if the argument is met.¹⁷ The threshold $\overline{e }$ denotes the level of capital above which the pro forma standard tax is levied. We assume that $0<{\tau }_{L}, {\tau }_{V},{\tau }_{E},{\tau }_{H}<1$ and ${\tau }_{L}<{\tau }_{H}$ based on the post-reform tax system in Japan. We also impose the following assumption that ensures the tax rate on value added (${\tau }_{V}$) is sufficiently low relative to the tax rate on income applied to the firm that reduces capital (${\tau }_{H}$). This assumption is consistent with the Japanese post-reform tax system.

Assumption 1: ${\left(1-{\tau }_{L}-{\tau }_{V}\right)}^{1-\gamma }>{(1- {\tau }_{L})}^{\alpha +\beta }{(1- {\tau }_{H})}^{1-\alpha -\beta -\gamma }$

3.1.4 Profit maximization and capital reduction

The firm’s problem can be solved backward in two steps. First, for a given level of capital, e or $\overline{e }$, the firm chooses l, m, and k to maximize after-tax profit $\pi$ under the borrowing constraint. Second, given the solution to the optimization problem, the firm decides whether to keep its initial capital at e or reduce it to $\overline{e }$. In step 1, given the factor prices of the wage rate (w), the rental rate of physical capital ($R=r+\delta$), and the intermediate good price (p), the firm chooses (k, l, m) to maximize the profit net of tax payments (T) in Eq. (5) under the borrowing constraint in Eq. (2):

$$\pi =A{k}^{\alpha }{l}^{\beta }{m}^{\gamma }-(r+\delta )k-wl-pm-T$$

(5)

Then, in step 2, by comparing the after-tax profits for e and $\overline{e }$, the firm chooses the one that yields the higher after-tax profit.

3.1.5 Analytical solutions

We first examine the types of firms that are likely to reduce capital by classifying firms into borrowing-constrained and unconstrained firms and then show how the effects of capital reduction on firms’ size and debt depend on whether the borrowing constraint is binding or not. Some supplementary propositions and all the proofs are placed in Online Appendix B.

First, we analyze the types of firms that are likely to reduce capital based on whether the firm is financially constrained or not. If the borrowing constraint is not binding regardless of whether the firm reduces capital or not, the following proposition holds.¹⁸

Proposition 1A: Suppose that the borrowing constraint is not binding regardless of whether the firm reduces capital.

• (i) Suppose that $\left({\tau }_{L}r+{\tau }_{E}\right)e>{\tau }_{H}r\overline{e }$; then, the firm reduces capital if and only if $A<\widehat{A}(e, \overline{e })$, where $\widehat{A}(e, \overline{e })$ increases with e.

• (ii) Suppose that $\left({\tau }_{L}r+{\tau }_{E}\right)e\le {\tau }_{H}r\overline{e }$; then, the firm never reduces capital.

Proposition 1A (i) argues that when the borrowing constraint is not binding regardless of whether the firm reduces capital, low-productivity firms are more likely to reduce capital given the size of their initial capital. By reducing capital, a firm can avoid taxes on value added and capital but incurs more taxes on income. However, such an increase in taxes on income is relatively small for a low productivity and hence low-profit firm. Moreover, the fact that $\widehat{A}(e, \overline{e })$ increases with e shows that, given its productivity, a firm with more capital is more likely to decrease capital because the benefits of avoiding taxes on capital are greater for such firms. Proposition 1A (ii) posits that the firm never reduces capital if the initial capital is very low because the benefit from not paying taxes is small.

If the borrowing constraint is binding regardless of whether the firm reduces capital or not, the following proposition holds.¹⁹

Proposition 1B: Suppose that the borrowing constraint is binding regardless of whether the firm reduces capital.

• (i) Suppose that $\left({\tau }_{L}r+{\tau }_{E}\right)e>{\tau }_{H}r\overline{e }$; then, the firm reduces capital if and only if $A<\widetilde{A}(e, \overline{e })$, where $\widetilde{A}(e, \overline{e })$ either increases or decreases with e. $\widetilde{A}(e, \overline{e })$ is more likely to decrease with $e$ as $\phi$ (and hence $\lambda$) is larger.

• (ii) Suppose that $\left({\tau }_{L}r+{\tau }_{E}\right)e\le {\tau }_{H}r\overline{e }$; then, the firm never reduces capital.

Proposition 1B (i) argues that when the borrowing constraint is binding regardless of whether the firm reduces capital, low-productivity firms are more likely to reduce capital given their initial capital. This is not only because their increase in taxes on income is small, but also because they incur fewer opportunity costs from the tighter borrowing constraint that is associated with a smaller amount of capital. In contrast to the unbinding constraint case in Proposition 1A, $\widetilde{A}(e,\boldsymbol{ }\overline{e })$ can decrease or increase with e which means, given productivity, a firm with more capital is more or less likely to decrease capital. To provide intuition for this result, we compare firms with the same productivity ($A)$ but different amounts of initial capital ($e$). On the one hand, the benefits from avoiding taxes on capital by capital reduction are greater for firms with more capital (a tax-saving effect). On the other hand, because the physical capital available to firms depends on their capital due to the borrowing constraint (Eq. (2)), firms with more capital have more physical capital and hence earn more profits before capital reduction but have the same capital ($\overline{e }$) and hence earn the same profits afterward as compared to firms with less capital. This means that firms with more capital incur larger losses from capital reduction as far as such a borrowing constraint effect is concerned. Therefore, whether firms with more capital are more or less likely to reduce capital depends on which effect is larger. Because the borrowing constraint effect is larger as $\phi$ (and hence $\lambda$) is larger (Eq. (2)), firms with more capital are less likely to reduce capital (i.e., $\widetilde{A}(e, \overline{e })$ decreases with e) in such a case.

Propositions 1A (i) and 1B (i) show that given capital ($e$), a firm with lower productivity ($A$) is more likely to reduce capital under the pro forma taxation system regardless of whether the borrowing constraint is binding or not. This result leads to our Hypothesis 1.

• Hypothesis 1: Compared to a high-productivity firm, a low-productivity firm is more likely to reduce capital in response to the pro forma standard taxation given the firm’s capital.

Propositions 1A and 1B predict different effects of a firm’s capital ($e$) to the likelihood of capital reduction in response to the pro forma taxation system for a given level of the firm’s productivity ($A$). On the one hand, if the borrowing constraint is very weak and thus not binding, the firms with more capital are more likely to reduce their capital (Proposition 1A (i)). This theoretical property leads to our Hypothesis 2A. On the other hand, a binding borrowing constraint can flip this relationship. Namely, if the borrowing constraint is binding and not too tight, a firm with less capital is more likely to reduce capital in response to the pro forma standard taxation given its productivity (Proposition 1B (i)), which leads to our Hypothesis 2B.

• Hypothesis 2A: If the borrowing constraint is not binding either before or after reducing capital, then a firm with more capital is more likely to reduce capital in response to the pro forma standard taxation given its productivity.

• Hypothesis 2B: If the borrowing constraint is binding but not too tight both before and after reducing capital, then a firm with less capital is more likely to reduce capital in response to the pro forma standard taxation given its productivity.

Next, we analyze the effects of capital reduction on a firm’s size in terms of physical capital (k), output (y), and debt ($k-e$), which depends on whether the borrowing constraint is binding.

Proposition 2A: Suppose that the borrowing constraint is not binding regardless of whether the firm reduces capital. Then, if the firm reduces its capital, its physical capital, output, and debt increase.

For unconstrained firms, the result for physical capital is natural given that under Assumption 1, the relevant marginal tax rate on physical capital becomes lower after the firm reduces capital. An increase in physical capital leads to an increase in output for two reasons. First, more capital directly increases output. Second, a lower marginal tax rate on labor and intermediate goods increases these inputs and hence output. An increase in physical capital that represents an asset, coupled with a decrease in capital, also leads to an increase in debt.

Proposition 2B: Suppose that the borrowing constraint is binding regardless of whether the firm reduces capital. Then.

• (i) If a firm reduces capital, its physical capital and debt decrease. Output decreases after capital reduction if and only if ${\left(\frac{1-{\tau }_{L}-{\tau }_{V}}{1-{\tau }_{L}}\right)}^{\beta }>{\left(\frac{\overline{e}}{e }\right)}^{\alpha }$, and

• (ii) As $e$ is larger, the negative effects of reducing capital on physical capital and debt are larger, and its negative effect on output is also larger if ${\left(\frac{1-{\tau }_{L}-{\tau }_{V}}{1-{\tau }_{L}}\right)}^{\beta }>{\left(\frac{\overline{e}}{e }\right)}^{\alpha }$.

For constrained firms, reducing capital leads to a tighter borrowing constraint and, hence, less physical capital. In addition, debt also decreases. Proposition 2B is in sharp contrast to Proposition 2A; whether a firm’s physical capital and debt decrease after capital reduction depends on whether the borrowing constraint is binding. Proposition 2B (i) also shows that output decreases after capital reduction unless the initial capital is close to the threshold. If the initial capital is close to the threshold, the decrease in physical capital is small. As a result, increases in labor and intermediate goods due to a lower marginal tax on them more than offset the effect of smaller physical capital on output. The second part of Proposition 2B is straightforward because the decrease in physical capital is proportional to the decrease in capital when the borrowing constraint (Eq. (2)) is binding both before and after the capital reduction.

Propositions 2A and 2B show that the impacts of capital reduction on firm growth depend on whether the borrowing constraint is binding or not. Namely, if the borrowing constraint is (not) binding, then the firm’s capital reduction in response to the pro forma standard taxation tends to decrease (increase) its physical capital, output, and debt. These propositions mean that a size-dependent tax policy based on a financial indicator can deter firm growth when it interacts with financial constraints, which is an indirect financial effect of the policy on firm size. This theoretical property leads to Hypotheses 3A and 3B.

• Hypothesis 3A: If the borrowing constraint is not binding either before or after reducing capital, then the firm’s capital reduction in response to the pro forma standard taxation increases its physical capital, output, and debt.

• Hypothesis 3B: If the borrowing constraint is binding both before and after reducing capital, then the firm’s capital reduction in response to the pro forma standard taxation decreases its physical capital, output, and debt.

4 Data and method

4.1 Data and sample selection

The dataset for this study is provided by Tokyo Shoko Research Ltd. (TSR), which is one of the largest Japanese credit reporting agencies. The dataset covers more than one million listed and unlisted firms in Japan and comprises their basic characteristics, such as yearly sales. Among these firms, around 100,000 have detailed annual financial statements that contain the stated capital, capital reserve, and earned surplus carried forward. All the data are for commercial use and are only available to the public at a cost. We obtained the data directly from TSR because of a joint research contract between Waseda University and TSR.

The data we use range from 1996 to 2006, which is 6 years before and 4 years after the announcement of the tax reform in 2002. We exclude the financial crisis that started in 2007 from our analysis; thus, our estimates are not contaminated by its effects.

In our empirical analysis, we exclude bankrupt firms after the year of bankruptcy. We also exclude firms that belong to the financial industry because they are subject to a minimum capital requirement and other regulations. In addition, we exclude firms that belong to the electricity and gas industries because the pro forma standard taxation does not apply to them. We further exclude firms that belong to the industries containing public interest corporations because almost all of them are exempted from the pro forma standard taxation even if their capital is above the threshold.²⁰ For all analyses except for the bunching estimation in the Online Appendix C, we focus on firms with capital above the threshold of 100 million JPY. For each year, we exclude firms whose capital in the previous year was smaller than or equal to the threshold, because the tax reform had virtually no effect on these firms. We also exclude firms that reduce their capital within a range above the threshold, while we use a part of these firms as a placebo test. Further, we exclude firms that reduce their capital across the threshold by company splits and the two types of capital reductions that do not involve cash payouts (i.e., loss-offsetting and item-changing capital reductions) as already mentioned. After we exclude firms whose data for the determinants of the capital reduction are not available, the total number of firm-year observations is 104,126 over the sample period. The industry composition in our sample is roughly consistent with that of the population of corporate firms.²¹ Note that at the end of Section 5, we also use the sample of firms that conducted loss-offsetting or item-changing capital reduction to compare the effects of cash-out capital reduction and that of non-cash-out capital reduction on firm growth and financing.

4.2 Method

4.2.1 Reaction to the introduction of the new tax system

The probability that firms reduce capital

In this subsection, we focus on firms whose capital at the end of year t − 1 (t = 1996, 1997,…, 2006) is above the threshold and examine how the probability of those firms reducing their capital to a level at or below the threshold in year t varies over the sample periods. We do so first by not controlling for any firm-level characteristics and later by controlling for them.Thus, we define the variable, ${\mathrm{CAPRED}}_{it}$ as follows:

$${\mathrm{CAPRED}}_{it}=\left\{\begin{array}{l} 1\;if\;{\mathrm{\;Capital}}_{\mathrm{t}}\le\;100\;million\;yen\\ 0\;if{\mathrm{\;Capital}}_{\mathrm{t}}\ge {\mathrm{ Capital}}_{\mathrm{t}-1}\end{array}\right..$$

Figure 1 summarizes the definitions of CAPRED.

Fig. 1

Definition of CAPRED

The transition of this unconditional probability of capital reduction is obtained by estimating firm-level Eq. (6):

$${\mathrm{CAPRED}}_{it} ={\sum }_{j=1996}^{2006}{\beta }_{j} {\mathrm{YEAR}}_{j}+{\varepsilon }_{it}.$$

(6)

In this equation, ${\beta }_{j}$ indicates the coefficient for year dummy j (${\mathrm{YEAR}}_{j}$). If firms reduce capital to avoid the new tax, then the estimated value of ${\beta }_{j}$ (the probability of ${\mathrm{CAPRED}}_{it}=1$) should increase after the announcement of the tax system in 2002.

Ex-ante characteristics of firms that reduce capital

We further augment Eq. (6) with firm characteristics to identify a more detailed mechanism that induces firms to save taxes through a capital reduction. We use the same sample selection criteria for Eq. (6) and estimate Eq. (7) that incorporates the firm i’s observable lagged characteristics, ${X}_{it-1}$, and unobservable fixed effects, ${\eta }_{i}$:

$${\mathrm{CAPRED}}_{it} ={\sum }_{j=1996}^{2006}{\beta }_{j} {\mathrm{YEAR}}_{j}+{\sum }_{j=1996}^{2006}{\gamma }_{j} {\mathrm{ YEAR}}_{j}\times {X}_{it-1}+{\eta }_{i}+{\varepsilon }_{it},$$

(7)

For this estimation, we consider the following firm characteristics: First, we use labor productivity as the primary determinant of capital reductions in our theoretical analysis (Hypothesis 1). Specifically, we define ${\mathrm{VAPE}}_{it-1}$ as a dummy variable equal to one if firm i’s labor productivity in year t − 1 is above the overall median value for the whole sample and zero otherwise.²² Firm i’s labor productivity is calculated as its value added per the number of employees.²³ We calculate value added as the sum of operating profit and wages. Second, we use their ex-ante capital. As Hypotheses 2A and 2B show, the firm’s capital can significantly affect its decision on whether to reduce capital or not. We define ${\mathrm{CAPITAL}}_{it-1}$ as the natural logarithm of firm i’s capital at the end of year t − 1. Third, to consider whether a firm can save taxes by reducing capital, we define ${\mathrm{TAXSAVE}}_{it-1}$ as a dummy variable equal to one if a capital reduction reduces firm i’s hypothetical tax payment based on year t − 1 data and zero otherwise. As we have shown in Section 2.1, the difference in the hypothetical tax payments is computed as the difference between the amounts a firm pays under its non-SME and SME statuses. Although to estimate ${\mathrm{TAXSAVE}}_{it-1}$, we assume that taxable income does not change due to the capital reduction, the reduction is likely to decrease taxable income if the borrowing constraint is binding. In this case, the hypothetical tax payment under the tax exemptions in the pro forma standard tax for SMEs is likely to be overestimated. With this caveat in mind, we use ${\mathrm{TAXSAVE}}_{it-1}$ as an explanatory variable for analyzing the capital reduction because this variable is likely to be correlated with the real tax benefits from the capital reduction across firms.

We further add various control variables. First, to account for size, we define ${\mathrm{EMP}}_{it-1}$ as the natural logarithm of the number of firm i’s employees at the end of year t − 1. Second, to account for a long-term growth opportunity, we use ${\mathrm{\Delta TAN}}_{it-1}$ that denotes the change in the natural logarithm of tangible fixed assets between year t − 1 and year t − 2. Third, to account for firms’ capital structure, we use ${\mathrm{DEBTRATIO}}_{it-1}$ that denotes the change in the ratio of total debt to total assets at the end of year t − 1. Fourth, to account for firms’ internal financing ability to conduct a cash-out capital reduction, we use ${\mathrm{CFRATIO}}_{it-1}$ that denotes the ratio of firm i’s cash flow to total assets at the end of year t − 1. Firm i’s cash flow is calculated as the sum of ordinary profit and depreciation cost. To remove the effect of outliers, we winsorize the top and bottom 1% for ${\mathrm{\Delta TAN}}_{it-1}$, ${\mathrm{DEBTRATIO}}_{it-1}$, and ${\mathrm{CFRATIO}}_{it-1}$.

We test whether these firm characteristics have a significant and greater effect on ${\mathrm{CAPRED}}_{it}$ after the announcement of the pro forma standard taxation than before.

4.2.2 Effects of reducing capital on firm growth and finance

Average effects

We conduct a standard PSM-DID estimation using firms that reduced capital as the treated group and those that did not as the control group to investigate how a tax-induced capital reduction affects firms’ subsequent growth and financing. The DID analysis enables us to remove a macroeconomic trend from the effects of capital reduction subsequent to the tax reform announcement by comparing the change in the dynamics and performance of the two groups.

Whether a firm is treated (i.e., whether a firm reduces capital) is not randomly assigned but depends on its characteristics, as our hypotheses predict. To remove the bias that arises from such selection, we match the control firms with the treated firms by using the propensity score matching (PSM) procedure. Specifically, we estimate propensity scores and construct the matched treated and control firms by means of the nearest neighbor matching. As the sample period for our PSM-DID estimation, we focus on t = 2002, 2003, 2004, 2005, and 2006 as the years when the treated firms reduce their capital in response to the new tax system. We estimate the probit model in Eq. (8) for each year during the sample period:

$$\mathrm{Pr}\left({\mathrm{CAPRED}}_{it}=1\right)=\mathrm{Pr}\left(\beta {X}_{it-1}>{-\varepsilon }_{it}\right), {\varepsilon }_{it}\sim N\left(0, 1\right)\mathrm{\;for\;each\;}t=2002, \dots ,2006,$$

(8)

where the vector of firm characteristic variables, ${X}_{it-1}$ consists of ${\mathrm{VAPE}}_{it-1}$, ${\mathrm{TAXSAVE}}_{it-1}$, ${\mathrm{CAPITAL}}_{it-1}$, ${\mathrm{EMP}}_{it-1}$, ${\mathrm{\Delta TAN}}_{it-1}$, ${\mathrm{DEBTRATIO}}_{it-1}$, ${\mathrm{CFRATIO}}_{it-1}$, and industry dummy variables based on major division.²⁴ Then, using the estimated conditional probabilities of capital reduction as propensity scores, we construct the matched control firms so that the propensity score of each one is the nearest to that of the corresponding treated firm among the unmatched control firms in the same year (nearest neighbor matching).

Next, using the matched treated and control firms, we estimate the following DID of the three groups of 7 outcome variables (Y) between the treated (T) and control groups (C) over the pre-event period (t − 1) and post-event periods (t, t + 1, and t + 2):

$$\mathrm{DI}{\mathrm D(Y)}_s=\frac1N\sum\nolimits_{i\in T}\left(Y_{i,t+s}-Y_{i,t-1}\right)-\frac1N\sum\nolimits_{j\in C}\left(Y_{j,t+s}-Y_{j,t-1}\right)\mathrm{for}\;s=0,1,2,$$

(9)

Here, $N$ is the number of observations in each of the T and C groups. To track the change in the DID effect over multiple periods, we restrict our sample to firms that survive up to t + 2.²⁵

To measure growth in terms of firm size as the first group of the outcome variables, we use the natural logarithms of total assets (${\mathrm{ASSET}}_{it}$), the number of employees (${\mathrm{EMP}}_{it}$), and sales (${\mathrm{SALES}}_{it}$). The second group of variables accounts for firms’ financing activities as measured by the natural logarithm of net assets (${\mathrm{NETASSET}}_{it}$), the natural logarithm of total debt (${\mathrm{DEBT}}_{it}$) and the ratio of total debt to total assets (${\mathrm{DEBTRATIO}}_{it}$).²⁶ The third group of variables accounts for the composition of their asset portfolios as measured by the ratio of cash holdings to total assets (${\mathrm{CASHRATIO}}_{it}$) and the ratio of tangible fixed assets to total assets (${\mathrm{TANRATIO}}_{it}$).²⁷

For each outcome variable, we estimate the difference between the treatment and control groups with regard to the change in a variable from year t − 1 to year t, t + 1, and t + 2 (i.e., three DID estimates with different periods). We also estimate the difference between both groups with regard to the change in each outcome variable from year t − 2 to year t − 1 to examine whether they have the same trend before the capital reduction or not. To remove the effects of outliers, we winsorize the top and bottom 1% for the difference in all variables.²⁸

Heterogeneous effects

The effects of capital reduction on firms’ growth and financing are likely to vary due to the existence or absence of financial constraints.

Hypotheses 3A and 3B state that the effects of reducing capital to at or below the threshold on size and debt are negative if and only if a firm faces financial constraints. To test these hypotheses, we follow Maffini et al. (2019) who use cash flow scaled by assets as a proxy for a financial constraint. Specifically, we first divide sample firms in each year into two subsamples based on whether their cash flow-to-assets ratio in year t − 1 is higher or lower than the median value of all firms including SMEs (firms with a capital of less than or equal to 100 million JPY) in year t − 1. The firms with lower (higher) cash flow-to-asset ratios are more (less) likely to be financially constrained. Then, for each subsample, we estimate propensity scores and construct the matched treated and control firms by means of the nearest neighbor matching.

5 Empirical results

5.1 Reaction to the introduction of the new tax system: univariate analysis

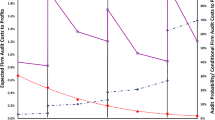
As detailed in the Online Appendix C, we start from investigating whether and to what extent the new tax policy affects the distribution of capital around the threshold. We use the method developed by Chetty et al. (2011) and Kleven and Waseem (2013) and estimate the degrees of bunching that correspond to each year over the sample period.

Figure C1 in the Online Appendix C shows that bunching exists at or just below the threshold in the year 2004 when Japan introduced the new taxation. To confirm that the bunching in 2004 was caused at least partly by the new tax, we calculate the bunching estimators for each year over the sample period by deducting the estimated round number bunching from the actual bunching. We show the time-series of bunching estimators over the sample period in Figure C2. It shows that the bunching estimator increases significantly after the introduction. In the six panels of Figure C3, we also depict the actual distributions of the stated capital (solid line) and the counterfactual distributions (dashed line) separately for the years 2001–2006. Consistent with the result reported in Figure C2, those figures show that the spike at the threshold becomes larger over time, which indicates the response of firms’ capita reduction to the tax reform.

Given the results of the bunching estimator in the Online Appendix C, we specifically examine whether and what types of firms reduce their capital in response to the new tax system. Table 3 presents the summary statistics of the variables used in estimating Eqs. (6) and (7). While Table 3 shows that the mean value of ${\mathrm{CAPRED}}_{it}$ is 0.2%, it increases fourfold after the announcement of the new policy from about 0.1% (in the period from 1996–2001) to 0.4% (in the period from 2002–2006). Table 3 also shows the mean values of the variables for the subsamples classified by ${\mathrm{CAPRED}}_{it}$. Firms that reduce their capital to a level at or below the threshold (${\mathrm{CAPRED}}_{it}=1$) have a smaller mean value of ${\mathrm{VAPE}}_{it-1}$, ${\mathrm{CAPITAL}}_{it-1}$, ${\mathrm{EMP}}_{it-1}$, ${\Delta TAN}_{it-1}$, and ${\mathrm{CFRATIO}}_{it-1}$ than firms that do not reduce their capital (${\mathrm{CAPRED}}_{it}=0$). Furthermore, the former firms have a larger mean value of ${\mathrm{TAXSAVE}}_{it-1}$ than the latter that indicates they are more likely to save tax payments than the latter. There is almost no difference in ${\mathrm{DEBTRATIO}}_{it-1}$ between the two groups. These univariate analyses show that firms with lower labor productivity, less capital, smaller size, positive tax benefits, and lower growth in tangible fixed assets as well as a lower cashflow ratio are more likely to reduce their capital.

Table 3 Summary statistics

5.2 Reaction to the introduction of the new tax system: probit analysis

5.2.1 Did more firms reduce capital in response to the new tax system?

Figure 2 illustrates the estimated ${\beta }_{j}$ (the probability of capital reduction in year j) for j = 1996–2006 from Eq. (6). Here, we use the estimated coefficient for j = 2001 ( ${\beta }_{2001}$) as a benchmark for the estimates in the other years. Thus, the estimate in each year is measured as the difference from ${\beta }_{2001}$, and the confidence interval is constructed for $({\beta }_{j}-{\beta }_{2001})$. Figure 2 shows that there is no specific trend in the estimated $({\beta }_{j}-{\beta }_{2001})$ prior to j = 2001. This finding means that firms experienced no systematic change in the probability of reducing their capital before the announcement of the new tax system. Notably, the estimated $({\beta }_{j}-{\beta }_{2001})$ after j = 2001 is positive and significantly different from zero.²⁹³⁰

Fig. 2

Estimated response of capital reduction: differences from the level in 2001. Notes: lower limit of 95CI and upper limit of 95%CI denote the lower and upper limit values of the 95% confidence interval, respectively. All the standard errors are clustered at the firm level

Here, we might be worried that the responses of capital reduction right after the introduction of the new pro forma standard taxation system were confounded by other concurrent factors. Thus, it is worth checking if we can clearly see such a pattern for the firms that find it beneficial to reduce their capital under the newly introduced pro forma taxation system, while we find little responses for the firms that do not find large benefits of capita reduction. If we can confirm these heterogeneous responses, we can be more certain about the causal relationship running from the introduction of the pro forma taxation system to a higher probability of firms to reduce capital.

In Fig. 3a, b, we depict the estimated responses of firms’ capital reduction in the same format as in Fig. 2 by dividing the firms into two subsamples based on their income tax bases. Firms with less income tax bases are likely to save more taxes by reducing capital (Table 2). Moreover, they are likely to have lower productivity and hence more likely to reduce capital (Hypothesis 1).

Fig. 3

a, b The estimated responses of capital reduction. Notes: lower limit of 95CI and upper limit of 95%CI denote the lower and upper limit values of the 95% confidence interval, respectively. All the standard errors are clustered at the firm level

First, as we present in Fig. 3a, the firms finding it beneficial to reduce the capital under the pro forma taxation (i.e., firms with lower income tax base) responded to the introduction of the system by increasing the probability of capital reduction. Second, as we present in Fig. 3b, it is apparent that the firms finding little benefit to reduce their capital (i.e., the firms with higher income tax base) did not largely increase their probability to reduce capital after the introduction of the pro forma taxation system.

To further see if the difference between those two panels is statistically significantly away from zero or not, we run the regression which incorporates the dummy variable (${\mathrm{LOWINC}}_{it-1}$) taking a value of one if a firm has a lower income tax base in the previous year and zero otherwise. To implement a DID analysis, in which we compare the changes of probabilities to reduce capital between the firms with lower and higher income tax base, we interact this dummy variable with the variables ${\mathrm{YEAR}}_{j}$ in Eq. (6). Specifically, we estimate Eq. (10) so that we can formally test that the difference between the two panels in Fig. 3 is statistically significantly away from zero.

$${\mathrm{CAPRED}}_{it} ={\sum }_{j=1996}^{2006}{\beta }_{j} {\mathrm{YEAR}}_{j}+{\sum }_{j=1996}^{2006}{\gamma }_{j} {\mathrm{ YEAR}}_{j}\times {\mathrm{LOWINC}}_{it-1}+{\eta }_{i}+{\varepsilon }_{it},$$

(10)

Figure 4 depicts the estimated ${\gamma }_{j}$ as normalized by the difference from the estimated ${\gamma }_{j}$ as of 2001 for the difference of the probabilities of capital reduction between firms with lower and higher tax income. We confirm the statistically significant difference in the probabilities of capital reduction between them after the introduction of the pro forma taxation system. These results based on the analyses taking care of potential confounding factors suggest the causal effect of the policy.

Fig. 4

The difference in the estimated responses of capital reduction between firms with lower and higher income tax bases. Notes: lower limit of 95CI and upper limit of 95%CI denote the lower and upper limit values of the 95% confidence interval, respectively. All the standard errors are clustered at the firm level

5.2.2 Which firms were more incentivized to reduce capital?

Figure 5a–c shows the estimated ${\gamma }_{j}$ associated with ${\mathrm{VAPE}}_{it-1}$, ${\mathrm{CAPITAL}}_{it-1}$, and ${\mathrm{TAXSAVE}}_{it-1}$, respectively, for j = 1996–2006 in Eq. (7). As in the previous subsection, we use the estimated coefficient ${\gamma }_{2001}$ as a benchmark for the estimates in the other years. First, we find that there is no specific trend prior to the announcement in Eq. (7) in the estimated (${\gamma }_{j}-{\gamma }_{2001})$ that is associated with these three characteristics.

Fig. 5

a–g The coefficients of firms’ attributes in capital reduction regression: differences from the 2001 levels. Notes: lower limit of 95CI and upper limit of 95CI denote the lower and upper limit values of the 95% confidence interval, respectively. All the standard errors are clustered at the firm level

Second, however, the estimated $({\gamma }_{j}-{\gamma }_{2001})$ that is associated with these three variables shows a significant change after 2001. That is, firms with lower labor productivity (${\mathrm{VAPE}}_{it-1}$), smaller capital (${\mathrm{CAPITAL}}_{it-1}$), and a positive potential tax benefit (${\mathrm{TAXSAVE}}_{it-1}$) in year t − 1 reduce their capital.³¹ The negative effect of ${\mathrm{VAPE}}_{it-1}$ is consistent with Hypothesis 1. Given that we control for ${\mathrm{TAXSAVE}}_{it-1}$, the result shows that low-productivity firms are more likely to reduce capital because they have fewer investment opportunities and do not need to keep a large amount of capital which helps in raising external financing. The negative coefficients for ${\mathrm{CAPITAL}}_{it-1}$ are also consistent with the case of financial constraints (Hypothesis 2B) but are inconsistent with the case of no financial constraints (Hypothesis 2A).

Figure 5d–g shows the estimated ${\gamma }_{j}$ associated with ${\mathrm{EMP}}_{it-1}$, ${\mathrm{\Delta TAN}}_{it-1}$, ${\mathrm{DEBTRATIO}}_{it-1}$, and ${\mathrm{CFRATIO}}_{it-1}$ for j = 1996–2006 in the case of Eq. (7). As expected, there is no specific trend in the estimated (${\gamma }_{j}-{\gamma }_{2001})$ that is associated with these four characteristics before 2001. The estimated $({\gamma }_{j}-{\gamma }_{2001})$ for these four variables does not show a significant change in ${\mathrm{CAPRED}}_{it}$ after 2001 except for ${\mathrm{EMP}}_{it-1}$ in 2006, ${\Delta TAN}_{it-1}$ in 2003, and ${\mathrm{DEBTRATIO}}_{it-1}$ in 2002.

5.2.3 A placebo test

Our results above indicate that more firms reduced capital in response to the introduction of the pro forma standard taxation and that firms with lower labor productivity, smaller capital, and a positive potential tax benefit were more likely to do so. However, firms may reduce capital in the same period to achieve an objective other than avoiding the new tax. In such a case, firms would reduce capital to various levels, not just to the tax threshold. Therefore, we conduct a placebo test by arbitrarily setting a counterfactual threshold above the actual level to see whether non-tax-related motives drive firms to reduce capital. Specifically, we set a counterfactual threshold at 300 million JPY and redo the regressions in Eqs. (6) and (7) but replace the dependent variable with the dummy that is associated with this counterfactual threshold.

The detailed method and results are provided in Online Appendix E. We confirm that the estimated ${\beta }_{j}$ s in the counterpart of Eq. (6) or ${\gamma }_{j}$ in that of Eq. (7) have no specific trend either before or after 2001. This finding clearly shows that the hike in $({\beta }_{j}-{\beta }_{2001})$ and the significant change in the coefficients of the three characteristics (${\mathrm{VAPE}}_{it-1}$,${\mathrm{TAX}}_{it-1}$, and ${\mathrm{CAPITAL}}_{it-1}$) in the case of ${\mathrm{CAPRED}}_{it}$ are not related to a macrotrend but reflect the firms’ intention to avoid the new tax.

5.3 Effect on firm growth and financing

5.3.1 Average effects

Table 4 shows the results of the probit estimations for each year. We use these estimates to compute the propensity score and to match the treated firms with the control firms. From the estimated coefficients for ${\mathrm{VAPE}}_{it-1}$, ${\mathrm{TAXSAVE}}_{it-1}$, and ${\mathrm{CAPITAL}}_{it-1}$, we can confirm that firms with lower labor productivity, a positive tax benefit, and less capital are more likely to reduce their capital, which is consistent with the findings presented in the previous subsection.³²

Table 4 Probit estimation

Table 5 summarizes the balancing property before and after the matching. After matching, differences in the mean values of the characteristics in year t − 1 between the treated and control firms are statistically insignificant. These results show that the matched firms are well balanced in terms of their ex-ante characteristics.³³

Table 5 Balancing property

Table 6 summarizes the DID estimation results. Each panel shows the DID estimates for firms’ size, financing, and asset portfolio. Table 6 also shows the difference in the pre-trend (i.e., the difference from t − 2 to t − 1) of each outcome variable between the treated and control groups. We find that there is no significant difference between both groups in terms of the pre-trend for any outcome variable.

Table 6 DID estimations

First, Table 6A shows that the capital reduction during 2002–2006 resulted in lower subsequent growth and shrinkage in various dimensions of size. This shrinkage means that this capital reduction, which was largely induced by the new taxation, has a negative effect on growth. This result supports Hypothesis 3B and indicates the presence of the borrowing constraint. Notably, regardless of the size measure, the negative effects of capital reduction on size tend to increase over time. This finding indicates that these negative effects are not mechanical because of the payment of a one-shot dividend at the time of the capital reduction. Moreover, the quantitative effects of a capital reduction on size are substantial. Firms that reduce their capital decrease their assets (ASSET), the number of employees (EMP), and sales (SALES) by 18.6%pts, 9.8%pts, and 12.3%pts, respectively, for the 3 years (from year t − 1 to t + 2) more than those that do not reduce their capital, although these numbers are relatively small compared with the average rate of decrease in capital for the treated group of 43.8%. Firms may take more than 3 years to make downward adjustments. Moreover, avoiding taxation likely results in a larger after-tax cash flow that may partly offset the shrinking effect of the capital reduction.

Second, Table 6B shows that a capital reduction causes a significant decrease in net asset (NETASSET). This is not surprising as we focus on cash-out capital reduction. More importantly, a capital reduction significantly decreases total debt (DEBT) and that the magnitude of the decrease in debt for the 3 years is comparable to the decrease in total assets (16.0%pts and 18.6%pts for DEBT and ASSET, respectively). Consistent with the similar responses of assets and debt to capital reduction, the ratio of total debt to total assets (DEBTRATIO) does not change significantly.³⁴

Third, Table 6C shows that the shares of cash holdings and tangible assets in total assets (CASHRATIO and TANRATIO, respectively) do not change significantly after the capital reduction. These results show that capital reduction does not affect the asset structures of firms because every type of asset decreases almost proportionately to total assets.³⁵

5.3.2 Cross-sectional heterogeneity with respect to the effect on firm growth and financing

In this subsection, we show the results of the DID estimation for the subsamples of firms divided by a proxy for financial constraints. As the proxy, we use the ratio of cash flow to total assets.

Table 7 shows the results of DID estimates from dividing the sample by whether the cashflow ratio is above or below the median of all firms including SMEs in the previous years of capital reduction of the treated firms. Firms with lower cashflow ratios are supposed to face tighter financial constraints. Table 7A shows that firms with lower cashflow ratios decrease total assets and sales significantly, while firms with higher cashflow ratios decrease them only marginally significantly or insignificantly. Moreover, the estimated magnitudes of the decreases in assets and sales are larger for firms with lower cashflow ratios. The effects on employment are either insignificantly or only marginally significant for both types of firms.

Table 7 DID estimation by the degree of cash flow ratio

In Table 7, we also show whether the differences between the DID estimates (i.e., DIDID estimates) for the firms with higher and lower cashflow ratios are statistically away from zero. In Table 7A, we find that the DIDID estimates are away from zero in the case of total assets. Table 7B also shows that for both types of firms, net asset significantly decreases but that the degree of the decrease is larger for firms with lower cashflow ratios. Total debt significantly decreases only for firms with lower cashflow ratios. While the debt ratio does not virtually change for firms with lower cashflow ratios, it significantly increases for firms with higher cashflow ratios. The latter result reflects the combination of the significant decrease in net assets and little changes in total debt. Table 7C shows that neither the cash ratio nor the tangible asset ratio significantly changes for both types of firms.³⁶

5.3.3 Non-cash-out capital reductions

Thus far, we have focused on the effects of cash-out capital reduction. In this subsection, we examine the effects of the non-cash-out capital reduction induced by the tax reform.³⁷ If financial constraints associated with cash outs that are involved with capital reduction play a pivotal role in ex-post firm growth and financing, we should observe no significant effects for non-cash-out capital reduction.

Table 8 shows the DID results for the two types of non-cash-out capital reductions conducted after the announcement of the tax reform: loss-offsetting and item-changing capital reductions. For each type of capital reduction, we have selected control groups using the same approach as in the baseline DID estimation, i.e., the Propensity Score Matching based on the probit estimation for each year.³⁸ Table 8A shows that although total assets significantly decrease in year $t$ in the case of loss-offsetting capital reduction, its magnitude is substantially smaller than for cash-out capital reduction (− 5.2% vs. − 9.9%). Moreover, the significant negative effects on total assets disappear in year $t+2$ in the case of loss-offsetting capital reduction. No significant effects on employment and sales are observed for both types of non-cash-out reductions. Table 8B shows that net assets do not significantly change, which supports our classification into cash-out and non-cash-out capital reductions. Although debt significantly decreases in year $t+1$ in the case of item-changing capital reductions, its magnitude is slightly smaller than that of cash-out capital reductions (− 7.3% vs. − 8.7%), and the negative effect becomes smaller and only marginally significant in year $t+2$. The debt ratio significantly increases rather than decreases in year $t$ in the case of loss-offsetting capital reduction. Table 8C shows no significant changes in asset structure.

Table 8 DID estimation for the non-cash-out capital reductions

In sum, in the cases of non-cash-out capital reductions, we observe only small or temporary negative effects, if any, on assets and debt. These results support the importance of financial constraints associated with cash-out capital reductions.

6 Conclusion

As an example of the interaction of a size-dependent policy and financial constraints, we use the introduction of the pro forma standard taxation system in Japan that exempts firms (SMEs) whose stated capital is at or below a threshold from taxation. We empirically examine how firms react to this institutional change and how such a reaction systematically affects their financing and real outcomes.

The empirical analyses guided by our theoretical model, which features the firms’ borrowing constraint, provide the following results. First, firms that originally held capital above the threshold become more likely to reduce their capital to or below the threshold by refunding cash to the stockholders after the announcement of the new tax system. Second, firms with lower labor productivity, smaller capital, and positive potential tax benefits are more likely to do so. Third, firms that conduct cash-out capital reductions show lower ex-post growth in asset size, number of employees, and sales, the magnitudes of which become larger over time. Quantitatively, firms that reduce their capital and yet survive for at least 2 years subsequent to the reduction on average decrease their assets, number of employees, and sales by 18.6%pts, 9.8%pts, and 12.3%pts, respectively, more than those that do not decrease their capital. Fourth, cash-out capital reduction has negative effects on total debt as well as net assets. Meanwhile, there are almost no significant effects on the cash-to-total asset ratio, debt-to-asset ratio, and ratio of tangible fixed assets to total assets. Fifth, firms with lower cash flow ratios show more significant decreases in their size and debt. Finally, the negative effects of capital reduction on assets and debt are small or only temporary, if any, in the case of non-cash-out capital reductions that do not change the net assets. These results are consistent with the hypothesis that borrowing constraints are affected by net assets. Overall, our results show that the size-dependent tax policy induces firms’ capital reductions that have substantial negative effects on firm growth and distorts financing due to financial constraints.

This study shows that size-dependent tax policies can have a significant effect on firms’ growth and financing through financial constraints. It indicates that firms decide whether to obtain an SME status by considering the trade-off between a more severe borrowing constraint and a smaller tax payment. The results obtained in this study indicate that such indirect effects of a size-dependent tax policy on firm dynamics should be considered when designing the policy. Moreover, governments should understand that an institutional change in their tax systems generates a heterogeneous reaction from firms and thus has heterogeneous effects on their dynamics.

An important future research question would be to check the external validity of our results by focusing on other size-dependent policies in Japan and other countries. We should also note that while we shed new light on a dark side of size-dependent tax policies, we do not evaluate their effects on saving compliance costs and enhancing the productivity of SMEs, which are also left to future research.