Abstract
We evaluate how country-level entrepreneurship—measured via the national system of entrepreneurship—triggers total factor productivity (TFP) by increasing the effects of Kirznerian and Schumpeterian entrepreneurship. Using a database for 45 developed and developing countries during 2002–2013, we employ non-parametric techniques to build a world technology frontier and compute TFP estimates. The results of the common factor models reveal that the national system of entrepreneurship is a relevant conduit of TFP, and that this effect is heterogeneous across countries. Policies supporting Kirznerian entrepreneurship—e.g., increased business formation rates—may promote the creation of low value-adding businesses which is not associated with higher TFP rates. Policy interventions targeting Schumpeterian entrepreneurship objectives—e.g., innovative entrepreneurship and the development of new technologies—are conducive to technical change by promoting upward shifts in the countries’ production function and, consequently, productivity growth.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
What explains the large disparities in productivity across economies? Furthermore, to what extent can these productivity gaps be explained by reasons other than the countries’ factor endowments? Productivity growth—for example, resulting from enhanced resource allocation policies or technological advances—has been invoked as a critical component of economic development (Acemoglu and Zilibotti 2001; Barro 1991). Echoing the seminal work by Solow (1957), economists have devoted a great deal of effort to evaluating the sources of productivity growth between and within countries over time. Prior studies have documented significant differences in total factor productivity (TFP) across economies (e.g., Caselli and Coleman II 2006; Griffith et al. 2004; Kumar and Russell 2002). Various reasons have been proposed to explain productivity discrepancies at country level, including slow diffusion of technology or barriers to technology transfer (Barro and Sala-i-Martin 1997; Mankiw et al. 1992; Parente and Prescott 1994), differences in endogenous technical change associated with the limited access to technological knowledge and human capital (Lucas 1988; Prescott 1998; Romer 1990; Young 1998), or underdeveloped financial markets (Moll 2014).
This literature often assumes that commercialization and diffusion are more or less costless and autonomous processes. What is frequently overlooked is the empirically well-established heterogeneity in the quality and quantity of entrepreneurship across countries as well as the arguably large differences in terms of resource exploitation across economies. Both aspects can be linked to the quality of the entrepreneurial ecosystem.
Following the seminal contribution of Schumpeter (1934), in this study we evaluate the role of entrepreneurship on the economic performance of countries. This is the core of our analysis. Positioning our work in the emerging literature dealing with the connection between entrepreneurship and economic growth (Acs et al. 2014; Atkinson and Lind 2018; Baumol and Strom 2007; Lafuente et al. 2016; Prieger et al. 2016), we argue that, besides the differences in technology and the allocation of production factors (i.e., capital and labor), the national system of entrepreneurship—i.e., the institutional setting backing entrepreneurship at country level—plays a decisive role in shaping TFP across countries. More concretely, we evaluate if the national system of entrepreneurship is conducive to productivity growth by enabling and enhancing different types of entrepreneurship which we link to different sources of productivity growth.
Underlying our approach to the relationship between country-level entrepreneurship and productivity are three elements that constitute the cornerstones upon which we built the study. The first critical aspect deals with the definition of entrepreneurship at the country level. Entrepreneurship is an attractive concept that has been analyzed mostly from the perspective of the individual (Acs et al. 2016). At the national level, entrepreneurship is much more than mere business formation rates and its operationalization should incorporate the regulating effect of context-related factors on individual actions (Acs et al. 2014). Countries cover a range of different institutional settings (Acemoglu et al. 2005), which suggests that entrepreneurial entry decisions are governed by complex interactions. Thus, a systemic approach to entrepreneurship seems appropriate to obtain a more realistic picture of country-level entrepreneurship and its effects on TFP. Therefore, we adopt the concept of the “national system of entrepreneurship” developed by Acs et al. (2014). The national system of entrepreneurship provides a richer framework that contributes to better understand how entrepreneurship fuels national productivity through innovation and a more efficient allocation of resources to the economy (Acs et al. 2014; Lafuente et al. 2016).
Entrepreneurship is not only heterogeneous between countries but also in terms of its effects on TFP. Thus, the second cornerstone of our study distinguishes between the effects on TFP of Kirznerian and Schumpeterian entrepreneurship. By scrutinizing how the national system of entrepreneurship triggers different sources of TFP growth, we can assess if a healthy entrepreneurial ecosystem yields to a more efficient mobilization of resources and exploitation of available opportunities—a process that we link to Kirznerian entrepreneurship (Kirzner 1973, p. 74)—and, consequently, to higher output levels. Also, our analysis allows us to evaluate whether the national system of entrepreneurship enhances the role of the entrepreneurs responsible for the “creative destruction” (Aghion and Howitt 1992; Schumpeter 1934) on productivity by introducing “new combinations” that lead to create new products (or produce old products in new ways) and to enhance production methods (Schumpeter 1934, p. 66).Footnote 1 These innovations shift technology curves that translate in higher rates of technical change (Kirzner 1973, p. 81).
The distinction between Kirznerian and Schumpeterian entrepreneurship pushes us to rethink the way we establish the link between entrepreneurship and TFP. The third key element of this study—closely related to the second one—therefore deals with the computation of total factor productivity and the modeling of the relationship between entrepreneurship and TFP. Building on Solow’s standard model (Solow 1957) and subsequent contributions by, among others, Barro (1991) and Mankiw et al. (1992), underlying most research is the assumption of a homogeneous set of benchmark economies common to all countries. In this tradition, research emphasizes production variations across countries (between variation) and implicitly assumes that processes and policies driving input utilization are homogeneous in developed and underdeveloped countries, and that the latter group of economies have the potential to reach the input exploitation level of the former group to achieve similar development levels (see, e.g., Caselli and Coleman II 2006; Griffith et al. 2004). Nevertheless, development is more than benchmarking the record of other more developed peers. The production technology of countries is heterogeneous and besides the analysis of productive differences between countries, our analysis focuses on the evolutionary path of countries’ TFP over time (within variation).
To accurately model countries’ TFP and capture the effects of Kirznerian and Schumpeterian entrepreneurship on productivity, we employ non-parametric techniques to compute TFP measures based on observed input–output vectors without imposing any restriction on the functional form (Färe et al. 1994; Kumar and Russell 2002). Besides generating country-specific TFP variables, this approach allows us to separate the effect of changes in the countries’ position relative to the technology frontier from the shifts of the world frontier. We can then evaluate if the national system of entrepreneurship promotes Kirznerian entrepreneurship by helping economies to move closer to the technology frontier. Also, we can test if the national system of entrepreneurship is more conducive to technical change by increasing the effect of disruptive technologies—which we link to Schumpeterian entrepreneurship—on TFP.
By using common factor models (Kapetanios et al. 2011; Pesaran 2006), our econometric strategy allows us to generate estimators that accommodate the interplay of endogeneity arising from common factors and panel heterogeneity to provide evidence on the role of the national system of entrepreneurship in explaining TFP variations across countries and across time. Also, the proposed common factor approach is particularly suitable to analyze how country-level entrepreneurship has a differentiating effect on TFP across economies in the presence of cross-sectional correlations (Pesaran 2006), which are typical in macro panels and may arise from common shocks—such as the global crisis of 2007–2008—or more local time-varying or fixed effects (e.g., policy development or cultural differences). Results corroborate that the quality of the national system of entrepreneurship is positively associated with changes in TFP at the country level. Our findings reveal that the effect of the entrepreneurial ecosystem on TFP exclusively originates from the capacity of the former to promote Schumpeterian entrepreneurship that translates into upward shifts of the countries’ production function (technical progress). On the contrary, the entrepreneurial ecosystem does not contribute to efficiency changes that move a country closer to the global technology frontier.
The following section presents the theory that underpins this work. Section 3 describes the data and the methodological approach. Section 4 presents the results. The discussion and implications are offered in Section 5, while Section 6 concludes.
2 Background theory
2.1 Kirznerian and Schumpeterian entrepreneurship
In the economic literature, there are two dominant approaches dealing with the role of entrepreneurship on national performance, namely Kirznerian and Schumpeterian entrepreneurship. The first approach theorizing the role of entrepreneurship comes from the work of “Austrian” economists such as Von Mises, Hayek, and Kirzner. This approach underlines the relevance of market processes over economic equilibrium analysis. Kirzner (1973, 1997) emphasized the function of entrepreneurship as a market discovery process in which entrepreneurs—defined as “entrepreneurially alert” individuals—discover and exploit failures in the market pricing mechanisms by reacting to others’ competitive actions (Kirzner 1997, p. 71). All entrepreneurs—productive and unproductive—fall in the conception of entrepreneurship proposed by Kirzner, and these entrepreneurs create market profits by using available technologies in the context of the existing production function. Instead of the creation of new opportunities that may shift the country’s production function, Kirznerian entrepreneurship primarily focuses on the identification and exploitation of existing business opportunities under given technology restrictions (Kirzner 1973, p. 74). Thus, the contribution of Kirznerian entrepreneurship to national performance mostly comes from enhanced market efficiency. That is, the efficient mobilization and allocation of resources to achieve superior output levels. In this case, Kirznerian entrepreneurship helps economies to move closer to equilibrium under the best technology frontier available.
The second approach is rooted in the Schumpeterian system (Schumpeter 1934) that stresses how disruptive entrepreneurs introduce new input combinations and products into the market that may promote upward shifts in the countries’ production function. Under this line of thought, entrepreneurship is a critical factor that sparks economic development by creating disequilibrium. Due to the close connection between the entrepreneurial function and disruptive innovations, Schumpeterian entrepreneurs should not be confused with business owners or self-employed, in general. For Schumpeter, entrepreneurs introduce radical innovations to the market that create new combinations of inputs and outputs (Schumpeter 1934, p. 66). Within the Schumpeterian system, entrepreneurship is a special economic function, not a statistical category. Entrepreneurs then primarily spark economic development by promoting innovations that result in the shift of production curves (Kirzner 1973, p. 81). Schumpeterian entrepreneurship—which constitutes the driving force of innovation—will materialize in upward shifts of the technology frontier—i.e., technical change—if the institutional mechanisms governing the selection and commercialization of knowledge by entrepreneurs promote such behavior and ensure they are and remain profitable.
Both the Kirznerian and Schumpeterian function are conducive to higher productivity levels in the aggregate (given/more output for less/given input), and confounding these functions may well obscure the true effects of entrepreneurship on TFP. For example, let us consider the case of the commercialization of semiconductors. This technological development—which is a clear act of Schumpeterian entrepreneurship—generated productivity effects rippling from Silicon Valley to the rest of the USA and throughout the world in ways one could never imagine to be traced back to the quality of the Silicon Valley’s entrepreneurial ecosystem. This technological advance is a relevant component of technical change in the USA that contributed to improve many production processes and develop a wide array of consumer goods. However, the speed at which other countries absorbed this new technology once it was made available (technology diffusion or catch-up effect) most likely depended on how the local entrepreneurial ecosystem contributed to the effective exploitation of the new market opportunities (Kirznerian entrepreneurship).
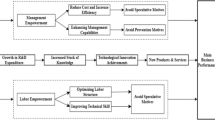
Figure 1 illustrates the effect of both types of entrepreneurship on national performance. The figure shows a standard production frontier (W) in which one output (y)—e.g., GDP per worker (y = Y/L)—is produced by two inputs: capital (K) and labor (L). The described technology in the figure represents the maximum output that can be produced for given input levels.
Following our argument line, Kirznerian entrepreneurship will contribute to national performance if entrepreneurs adopt existing technologies and/or efficiently (re)allocate resources in the economy. Countries can at any time operate below their maximum efficiency level (Griffith et al. 2004) and for a fictitious economy (C) Kirznerian entrepreneurship would translate in higher efficiency levels if, as a result of the exploitation of market opportunities, the country moves closer to the technology frontier in subsequent periods (Ct + 1). The effect of Kirznerian entrepreneurship on TFP is closely related to the catch-up effect (convergence) analyzed from an economic perspective by, among others, Färe et al. (1994) and Kumar and Russell (2002). Given that efficiency cannot be pushed beyond 100%, however, this source of TFP growth runs into strong diminishing returns and eventually cannot explain GDP growth in the long run.
Alternatively, the productivity of countries may be shaped by actions linked to the development of innovations that expand the countries’ production possibilities set via technical change. Literature addressing the role of technical change on productivity includes, among others, the work by Romer (1990), Acemoglu and Zilibotti (2001), Acemoglu (2002), and Caselli and Coleman II (2006).
It should be kept in mind that Schumpeter (1934, 1947) noted that entrepreneurship is potentially conducive to technical change. For Schumpeter, the entrepreneurship function is strictly linked to the introduction of new combinations, often faced with fierce resistance from established actors (Schumpeter 1947, p. 152). The full implementation of disruptive technologies—referred to as “the carrying out of new combination” by Schumpeter (1934, p. 66)—in the economy helps to create new value-adding combinations of inputs that enhance the countries’ productive capacity. In this case, such innovative entrepreneurship will be beneficial to the economy (country “S” in Fig. 1) if we observe an upward shift in the country’s technology function between two periods (in Fig. 1—from St to St + 1), that is, Schumpeterian entrepreneurship contributes to technical change. Therefore, in the long run, the ultimate source of productivity growth is Schumpeterian entrepreneurship which, for example, can be fueled by knowledge generation processes (Romer 1990). In the short run, however, Kirznerian entrepreneurship may be more beneficial and effective in improving countries’ efficiency level by reducing the countries’ distance to the technology frontier. This may be especially relevant for developing countries.
At this point, it is worth noting that the notion that entrepreneurship is good for the economy is widely accepted among economists (see, e.g., Acs and Audretsch 1988; Parker 2009); however, the debate on how to accurately measure entrepreneurship at the country level is still open. Entrepreneurship as a national phenomenon is much more than the mere rate of business formation, and it should embrace the capacity of the entrepreneurial activity to dynamically optimize the allocation of resources in the economy (Acs et al. 2014; Lafuente et al. 2018). Regardless of the level of economic development, the rate of business formation is heterogeneous across economies. This suggests that complex interactions govern the economic effects of the business formation rate, which is often considered a measure of country-level entrepreneurship. Thus, a systemic approach to country-level entrepreneurship seems appropriate to obtain a more holistic picture of entrepreneurship at the country level and its effects on total factor productivity.
From the perspective of the national system of entrepreneurship (Acs et al. 2014), the essential aspect of entrepreneurship is not the number of new businesses created in the economy, but how entrepreneurial activity contributes to channel resources to the economy. By connecting the quality of countries’ entrepreneurial ecosystem to its different sources of productivity change (operating efficiency and technical change), we can gauge the relative importance of Kirznerian and Schumpeterian entrepreneurship for TFP.
2.2 Decomposing country-level total factor productivity
A relevant question in macroeconomics is how to accurately describe the relationship between inputs and outputs—i.e., the aggregate production function—at the country level. Following the discussion in Section 2.1, in this section we present a simple decomposition of total factor productivity that is consistent with our objective of identifying two different sources of productivity growth, namely efficiency changes (that we loosely link to Kirznerian entrepreneurship) and technical change (that we loosely link to Schumpeterian entrepreneurship). Most research addresses this issue by employing the standard Solow–Swan model:
where Y denotes gross domestic product, K is physical capital, L is labor, 0 < α < 1 is the output elasticity of capital, and A is an index of labor augmenting productivity. The production function in (1) is allowed to vary across countries via the total factor productivity (TFP) term A1 − α.
Additionally, the term A can be expressed as A = E × W, where W ≥ 0 is the current state of technology, often linked to longitudinal technical change (TC) (Caselli and Coleman II 2006), and 0 ≤ E ≤ 1 is the country’s inefficiency level with respect to the global technology frontier. The change in efficiency over time will be represented by EC.
It should be highlighted that our approach to TFP implicitly assumes that productivity changes result from efficiency changes (EC ≥ 0) and from technical change (TC ≥ 0).
By allowing for the possibility that efficiency changes and technical change drive TFP over time, our model attributes productivity growth to genuine technical progress associated with innovation development (Schumpeterian entrepreneurship) and to efficiency changes that we connect to the capacity of countries to improve input utilization and exploitation for a given state of technology (Kirznerian entrepreneurship). Therefore, a model that allows for inefficiency permits the accurate analysis of the role of both Kirznerian and Schumpeterian entrepreneurship on country-specific productivity changes.
We can use the described production function to directly derive total factor productivity (TFP) as follows:
Similar to prior economic work (e.g., Caselli and Coleman II 2006; Eberhardt et al. 2013; Griffith et al. 2004), note that in Eq. (3) productivity is defined as the ratio between output (GDP) and measured inputs (in our case, capital and labor), and the production technology is assumed to exhibit constant returns to scale. These properties are included in the non-parametric model used to compute countries’ TFP (for applications with a similar TFP specification, see the work by Färe et al. 1994 and Kumar and Russell 2002). Details on the computation of the TFP variable are presented in Section 3.2.
Additionally, Eq. (3) shows that TFP is explained by efficiency level (E) and the state of the technology (W). In line with our arguments in Section 2.1, both efficiency change \( \left( EC=\dot{E}(t)/E(t)\right) \) and technical change \( \left( TC=\dot{W}(t)/W(t)\right) \) are modeled as functions of Kirznerian and Schumpeterian entrepreneurship, respectively (a dot over the variable indicates the time derivate).
This is the core innovation in our study. By decomposing TFP changes into efficiency change (EC) and technical change (TC), our contribution relies on the analysis of how entrepreneurship—measured by the national system of entrepreneurship—acts as a conduit of different sources of productivity growth that we link to Kirznerian and Schumpeterian entrepreneurship.
3 Data, estimation strategy, and time-series properties
3.1 Data
The data used in this study come from two sources of information. First, macroeconomic data for the analyzed countries was obtained from the International Financial Statistics available from the International Monetary Fund (IMF) datasets. Second, variables related to the country’s demographic, educational, and economic conditions, as well as to the entrepreneurial activity used to estimate the Global Entrepreneurship Index (GEI), were obtained from different sources, including the Global Entrepreneurship Monitor (GEM) adult population surveys, the Global Competitiveness Index (GCI), and the Doing Business Index.
We compute TFP growth and its components on a sample of 45 economies at all stages of development over the period 2002–2013. Given our interest in evaluating productivity patterns at the world scale, we work with an unbalanced panel so that the final analyzed sample comprises 448 country–year observations. The group of analyzed countries (see Table 8 of the Appendix) includes 25 European countries (Belgium, Bosnia and Herzegovina, Croatia, Denmark, Finland, France, Germany, Greece, Hungary, Iceland, Ireland, Israel, Italy, Latvia, Macedonia, Netherlands, Norway, Romania, Russia, Slovenia, Spain, Sweden, Switzerland, Turkey, and UK), 11 American countries, including both North America and Latin America as well as the Caribbean islands (Argentina, Brazil, Chile, Colombia, Ecuador, Jamaica, Mexico, Peru, USA, Uruguay, and Venezuela), seven Asian economies (six countries—China, Iran, Japan, South Korea, Malaysia, and Singapore—and one territory (special administrative region), namely Hong Kong), one African country (South Africa), and one Oceania economy (Australia).
According to the figures made available by the IMF, for 2013 our sample of 45 countries represents 71.59% of the world’s economic output, in terms of GDP.
3.2 The dependent variable: total factor productivity
The approach adopted in this study to construct the world production frontier and associated inefficiency levels of each analyzed economy is non-parametric. When dealing with multiple inputs yielding multiple outputs, the efficiency literature often makes use of data envelopment analysis (DEA) frontier methods (Cooper et al. 2011). This data-driven method approximates the true technology through linear programming without imposing any restrictions on the sample distribution (Grifell-Tatjé and Lovell 2015). DEA models yield a production possibilities set where efficient units—in our case, countries—positioned on the efficient surface shape the frontier. For the rest of the countries, the DEA computes an inefficiency score indicating the countries’ distance to the best practice frontier. The fundamental technological assumption of our DEA model is that, in a focal period (t), countries (i) use two inputs (x)—capital (K) and labor (L) (x = K, L)—to produce one output, namely gross domestic product (GDP); and that this input–output set forms the technology (W): W = {(x, GDP, t) : x can produce GDP at time t}. Our technology design is in line with previous studies evaluating country-level productivity (see, e.g., Boussemart et al. 2003; Färe et al. 1994; Kumar and Russell 2002; Lafuente et al. 2016).
Concerning the variables used to build the technology frontier, the GDP is expressed at 2011 prices in billions of PPP international dollars. Labor is measured as the country’s number of employees (expressed in millions of workers). Similar to prior studies (Caselli and Coleman II 2006; Kumar and Russell 2002), capital is defined as the private capital stock which is computed through the perpetual-inventory method. This variable is expressed at 2011 prices in billions of PPP international dollars. Table 1 presents the descriptive statistics for the input–output set.
The technology (W) is modeled for each country (i) in the sample (N) via an output distance function Dt(xt, GDPt) = inf(θ > 0 : (xt, GDPt/θ) ∈ Wt) = (sup(θ > 0 : (xt, θGPDt) ∈ Wt))−1. The drawn technology exhibits constant returns to scale, is homogeneous of degree + 1, and is convex in the output (GDP). The following linear program models the described technology and computes, for each country (i) and each period (t), the output distance function (Dt(xt, GDPt)):
The solution value of θ in Eq. (4) is the inefficiency score computed for the country i at time t. Note that for efficient countries θ = 1, while for inefficient countries θ > 1 and 1 − θ points to the degree of inefficiency. The term \( {\lambda}_i^t \) is the intensity weight used to form the linear combinations of the sampled countries (N). It should be kept in mind that the (Shephard) output distance function (Dt(xt, yt)) is the inverse of the Farrell’s inefficiency score (TE = θy/y) (Bogetoft and Otto 2011, p. 30). Therefore, in the specific context of the output distance function used in this study, it turns out that Dt(xt, GDPt)−1 = TEt = θyt/yt ∀ TEt ≥ 1 (Färe et al. 1994, equation (2) on page 69).
Next, the output distance functions can be used to compute changes in total factor productivity (TFP) through the Malmquist index (M (·)). The Malmquist TFP index—first introduced by Malmquist (1953) and formally developed in the pioneering work by Caves et al. (1982)—measures TFP variations between two periods. In a multiple input–output setting, this index reflects changes (progress or regress) in productivity along with changes (progress or regress) of the frontier technology over time. By using output distance functions, the output-oriented Malmquist TFP index (M(xt − 1, GDPt − 1, xt, GDPt)) is computed for each country (i) on the benchmark technologies in periods t − 1 and t as follows (Färe et al. 1989):
In Eq. (5), productivity growth (progress) yields a TFP index greater than unity, while values lower than one point to productivity decline. Analogous interpretations hold for the components of the TFP index. The term inside the first square bracket measures the effect of efficiency changes (EC), that is, whether the efficiency level of a focal country is moving closer (catching-up) or farther from the technology frontier between periods t − 1 and t. The geometric mean of the term inside the second square bracket captures the effect of technical change (TC), that is, the shift in the country-specific technology function between the two periods. Improvements in the technical-change component are considered to be evidence of innovation (Färe et al. 1994; Kumar and Russell 2002). In line with our theory, we link efficiency changes (EC) to Kirznerian entrepreneurship, while technical change (TC) is associated with the effect of Schumpeterian entrepreneurship.
Table 2 presents the summary statistics of the TFP measure and its components, while Fig. 2 plots the TFP index during the study period. The data reveal that, on average and per year, the analyzed economies experienced a productivity progress of 1.04% between 2003 and 2013 (Fig. 2). The reported productivity growth was mainly driven by efficiency improvements (EC) which were, on average, 0.91% per year. The average yearly rate of technical change (TC) was 0.13%; however, this result is explained by the drastic fall associated with the economic downturn that hit most economies: average technical change was 0.78% during the 2003–2007 period, while the average technical change between 2008 and 2013 was, on average, − 0.27% (Table 2).
For illustrative purposes, Fig. 3 displays the empirically constructed global technology frontier for three periods (2005, 2009, and 2013) along with scatterplots of labor productivity and the capital–labor ratio. Because of the large disparities in the input–output values, there would be a poor visual resolution in the figure at low levels of the capital–labor ratio. Thus, to ease the readability of the figure, we only plotted the results for efficient countries on the frontier in each of the selected periods and for three complementary cases (Germany, Singapore, and UK). Three are the main results that can be drawn from Fig. 3. First, two developed economies consistently shape the technology frontier (Norway and USA) in the selected periods, and highly capitalized countries—i.e., high values for the capital–labor ratio—tend to show high output levels. Additionally, the downward shift in the technology reported for 2009, relative to 2005, only confirms the technological degradation that followed the economic downturn that hit most economies after 2008. Technological deterioration may have been caused by efficiency declines linked to poor resource exploitation or by technical regress associated with underutilization or antiquation of available technologies.
Second, at low values of the capital–labor ratio, a group of developing economies is positioned on the frontier (Chile, 2005; China, 2005; Iran, 2009, 2013). Although it may seem puzzling, this result is consistent with the notion that efficient resource utilization is compatible with differences in factor endowments across economies (Caselli and Coleman II 2006; Lafuente et al. 2016). In other words, the presence of developing (undercapitalized) countries on the frontier in a focal year does not necessarily imply that these economies cannot efficiently use their limited resources (Kumar and Russell 2002).
Third, the results in Fig. 3 strongly support that global technical change between 2002 and 2013 has been non-homothetic (non-neutral). Following Solow (1957, p. 312), Hicks-neutral technical change is associated with a constant marginal rate of substitution between inputs that simply increase or decrease the output level.Footnote 2 The shift in the global technology is also inconsistent with the Harrod-neutral (labor-dependent) definition of technical change, which is the change in the countries’ output along a constant capital–output path. By comparing the global technology in 2009 and 2013, we note that the greater technological expansion—i.e., technical change—occurred in those areas of the hyperplane characterized by low and mid levels of the capital–labor ratio. For countries positioned in this part of the technology surface, technical change is labor-using (capital-saving). The technology choices of countries are heterogeneous over time, and this result pointing to a non-homothetic technical change is in line with Samuelson and Swamy (1974, p. 592) who argued that “the Santa Claus hypothesis of homotheticity in tastes and in technical change is quite unrealistic.”
In practical terms, various considerations may explain non-homothetic shifts in the production function. Countries will take advantage of technological innovations that optimize the use of locally abundant production factors. It follows that countries better able to introduce technologies that match the local conditions of factor markets should show better productivity results than countries that have put less effort in shaping technologies according to the relative availability of production factors. Also, countries have different productive and economic priorities and the successful implementation of technologies in one country might prove itself ineffective in other contexts with different local conditions of factor markets. This technology heterogeneity is a central aspect of our empirical design as we motivate below in Section 3.4.
3.3 Independent variables
National system of entrepreneurship (NSE)
To achieve the core objective of this study—the analysis of the relationship between productivity and country level entrepreneurship—we need a good proxy for the quality of the entrepreneurial ecosystem at the national level. We use the Global Entrepreneurship Index (GEI), developed by Acs et al. (2014), to capture the multidimensional nature of the National System of Entrepreneurship. The GEI measures the dynamic and institutionally embedded interaction between entrepreneurial attitudes, entrepreneurial abilities, and entrepreneurial aspirations by individuals, which drive resource allocation through new business venturing (Acs et al. 2014). The GEI, which ranges between 0 and 100, is built on 14 pillars which result from 14 individual-level variables properly matched with selected institutional variables related to the country’s entrepreneurship ecosystem.
The novelty of the GEI lies on the systemic view of countries’ entrepreneurship in which the harmonization (configuration) of the analyzed pillars through the penalty for bottleneck (PFB) determines the country’s systems of entrepreneurship (Acs et al. 2014). Through the PFB method, the system performance is mainly determined by the weakest element (bottleneck) in the system. The magnitude of the country-specific penalty depends on the absolute difference between each pillar and the weakest pillar. Also, pillars cannot be fully substituted through the PFB method, i.e., a poorly performing pillar can only be partially compensated by a better performing pillar. More details on the methodology and data used to build the GEI can be found in Acs et al. (2014). Table 3 presents summary statistics and correlations for the variables used in our study.
Capital-to-labor ratio
Similar to prior economic work evaluating the effect of capital accumulation on TFP (e.g., Eberhardt et al. 2013; Kumar and Russell 2002), our models include the capital-to-labor ratio, defined as the ratio of the capital stock (K) divided by the number of workers (L). Keep in mind that inputs used to compute the TFP values (capital and labor) are introduced individually. Furthermore, in DEA models, more or less of one input or output does not imply higher or lower inefficiency. In this case, the capital-to-labor variable only captures the effect on TFP of movements of this ratio along the isoquant.
Control variables
We control for country size, access to credit, time, and country-specific time trends in all model specifications. Country size—measured as the log value of the GDP—accounts for potential aggregate scale effects that may positively impact productivity (Melitz and Ottaviano 2008). Schumpeter (1934) stressed that financial intermediaries are crucial agents for technological innovation and economic growth. Therefore, similar to King and Levine (1993), we introduce the ratio of domestic credit to the private sector divided by GDP to measure the capacity of financial systems to channel financial resources that contribute to funding the growth of new and incumbent firms. Finally, fixed-effects models include two sources of time-related heterogeneity. First, we introduce a set of (T − 1) time dummies to control for year effects linked to unobserved changes in economic and environmental conditions that are common to all countries. Second, similar to Friedberg (1998) and Raphael and Winter-Ebmer (2001), we added country-specific time trends (interaction terms between a time trend and country dummies) to rule out productivity variations caused by country-specific factors that vary over time (Wooldridge 2002, section 11.2). By allowing for country-specific time slopes, we estimate a more flexible fixed-effects model that accounts for country-specific unobserved heterogeneity, time-invariant unobserved factors, and time-varying country-specific effects.
3.4 Estimation strategy
In line with the arguments that underpin this study—which propose a relationship between TFP and entrepreneurship at the country level—the model used to test the study propositions empirically has the following form:
The proposed regression models countries’ performance—i.e., TFP, EC, and TC (Eq. (5))—as a function of the national system of entrepreneurship (GEI), the capital-to-labor ratio, and the set of control variables (country size, domestic credit divided by GDP, time, and country-specific time trends). Note that our productivity measures (TFP, EC, and TC) are based on discrete time estimations and, for each country, their values are computed for every adjacent pair of years (t − 1 and t). Also, all time-varying independent variables are lagged one period to avoid potential endogeneity related to reverse causality. In Eq. (6) βj are coefficients for the jth independent variable, η is the time-invariant effect controlling for country-specific (i) unobserved heterogeneity and that is uncorrelated with parameters, and ε is the normally distributed error that varies cross-countries and cross-time (t).
To compute parameters, we follow a strategy based on the use of two estimation methods. First, we employ fixed-effects models to obtain a set of baseline results. By construction, coefficients estimated via fixed effects (and GMM estimation methods) are homogeneous for all countries in the sample (Wooldridge 2002).
Nevertheless, in models like ours—in which we study a group of (heterogeneous) developed and underdeveloped economies using longitudinal data that includes periods of growth and recession—the question often raises as to whether the distorting effect of economic cycles can affect the quality of estimations (Durlauf et al. 2005) or whether regression coefficients remain consistent if technology heterogeneity is allowed.
Thus, in the second stage, we estimate Eq. (6) using the Common Correlated Effects Mean Group (CCEMG) approach proposed by Pesaran (2006). This method accounts for heterogeneous unobserved common factors by introducing cross-section averages for the dependent and independent variables into the model (Pesaran 2006). The common factor model approach is particularly suitable to analyze the determinants of productivity across countries (Bai 2009; Eberhardt and Teal 2013). In the context of this study, the proposed CCE estimator deals with variations in the economic cycle, whether they originate from country-specific effects (e.g., adoption of different policies or local spillovers) common to a small number of economies or from changes in the economic cycle at the global scale with a heterogeneous impact on the study countries (Kapetanios et al. 2011). The CCEMG method accommodates these aspects and yields consistent estimates for the means of heterogeneous slopes that are robust to datasets with a relatively small number of cross-section units (N), cross-section dependence of errors, non-stationary variables that can be co-integrated or not, and in the presence of unobserved common factors or changes in the economic cycle that affect countries’ productivity (Chudik et al. 2011; Pesaran and Tosetti 2011).
Based on Eq. (6), in this study, the CCE mean group model is generated according to the following heterogeneous panel data model:
In Eq. (7), Zit − 1 is the vector of observed explanatory variables described in Eq. (6), with their parameters allowed to vary across countries \( \left({\beta}_i^{\prime}\ne \beta \forall i\right) \). The error term has a multifactor structure that includes country-specific intercepts (αi), a vector of unobserved common factors ft with country-specific “factor loadings” \( \left({\gamma}_i^{\prime}\right) \) that account for the evolution of unobserved TFP, and a country-specific error (εit) that is independently distributed of (αi, Zit − 1). Also, in Eq. (7), the vector of observed factors (Zit) is modeled as a function of a set of unobserved common factors connected (ft) and unconnected (gt) to the independent variable and noise (νit) such that\( {\mathbf{Z}}_{it}={\gamma}_i^{\prime }{\mathbf{f}}_t+{\phi}_i^{\prime }{\mathbf{g}}_t+{\nu}_{it} \). This definition of Z introduces endogeneity in Eq. (7). Pesaran (2006) shows that Eq. (7) can be consistently estimated by approximating the unobserved common factors with strictly exogenous cross-section means of the dependent and independent variables.
The CCEMG coefficients are computed as the average of the individual CCE estimators, such that the parameter associated to any focal variable (j) is \( {\hat{\boldsymbol{\upbeta}}}_j^{MG}={N}^{-1}\sum \limits_{i=1}^N{\boldsymbol{\upbeta}}_{ij} \) (Pesaran 2006, p. 982). Note that the estimated coefficients are time invariant and can be heterogeneous across countries. Also, the proposed CCE estimation assumes equal weights for all countries (N−1), which from an economic perspective suggests that the unobserved common factors affecting TFP are common to all countries.
Various properties of the CCEMG model are worth mentioning. First, canonical fixed-effects (FE) and GMM estimators work on the crucial assumption that coefficients are homogeneous across countries (i.e.,\( {\beta}_i^{\prime }=\beta \forall i \)), while the CCEMG model adopted in this study relaxes this assumption and allows parameters to vary across countries \( \left({\beta}_i^{\prime}\ne \beta \forall i\right) \). In the context of this study, this relevant property allows to capture the heterogeneous capacity of countries to use their inputs (capital and labor) as well as the capacity of their entrepreneurial ecosystem to generate TFP (i.e., technology heterogeneity).
Second, input endogeneity is an aspect highlighted in the economic growth literature, which implies that the inputs of our production function (i.e., capital and labor) are correlated with unobservable productivity. Existing literature often proposes to achieve efficient identification through instrumentation, that is, by employing GMM estimators (Arellano and Bond 1991; Blundell and Bond 1998). Nevertheless, GMM estimators assume common technology (homogeneous coefficients), stationary variables, as well as cross-section independence. Thus, this identification strategy is invalid if any of these assumptions are violated (Pesaran and Smith 1995). The CCEMG estimator deals with this endogeneity problem in that it employs unobserved common factors (ft) which induce a correlation with observable inputs. Eberhardt et al. (2013) offer an interesting discussion on the properties of common factor models viz.-à-viz. other homogeneous parameter models (e.g., fixed-effects and GMM estimators).
In summary, the CCEMG model offers a flexible framework that is robust to endogeneity, allows technology heterogeneity across countries which translates into heterogeneous (country-specific) coefficients, and addresses concerns about data properties related to non-stationarity and cross-section correlation (Kapetanios et al. 2011; Pesaran 2006).
3.5 Time series properties: test of unit root, cross-section dependence, and cointegration
Before reporting the estimation results, we ran a series of tests—non-stationarity, cross-country correlation, and cointegration—to evaluate pertinent properties of the study data. For each variable used in the paper, the results of these diagnostic tests are reported in Tables 4, 5, and 6.
Table 4 shows the results for the first generation (Maddala and Wu 1999) and second generation (Pesaran 2007) panel unit root tests. For both tests, the CADF regressions include an intercept and a linear trend. Results indicate that the null hypothesis of non-stationarity (against the alternative of trend stationarity) cannot be rejected for any of the study variables. This suggests that, in our data, TFP (and its components) as well as the key study variables are persistent and they can be represented by non-stationary processes.Footnote 3
The results of the cross-section dependence test are presented in Table 5. Based on the CD test (Pesaran 2004), the findings strongly confirm the presence of cross-section correlation within the sampled countries.
Given that the series of the variables are non-stationary, the next step is to test for the existence of a long-run relationship between them. Thus, we perform the battery of seven panel data cointegration tests based on different statistics described in Pedroni (1999). Results for the tests based on Eq. (6) are reported in Table 6. For the three dependent variables, the seven tests reject the null of no cointegration at 1% level. Also, by analyzing the sample size properties of these tests, Pedroni (2004, p. 614–615) shows how in small panels the results for the group-rho statistics tend to have the best power because it is slightly undersized and empirically the most conservative of the tests.
Taken together, the tests strongly support that the analyzed variables are persistent (non-stationary), cross-sectionally dependent, and cointegrated. Instead of employing homogeneous parameter estimators (fixed-effects or GMM models), these results further validate the proposed analysis based on a common factor model (CCEMG).
4 Results
4.1 The connection between the national system of entrepreneurship and TFP
Table 7 presents the results for the proposed model emphasizing the relationship between the national system of entrepreneurship and country-level productivity. For both the fixed-effects and the common factor model specifications, the dependent variables are the changes in the TFP index and its components (Eq. (5)), namely efficiency change, which we link to the catch-up effect, and technical change more related to the effect of innovations. Also, we tested stationarity and cross-section dependence for model residuals. For each model, results for these diagnostic tests are presented in Table 7.
First, we present estimates for the control variables and the results of the diagnostic tests for the error terms. When the dependent variable is TFP and efficiency change, the size coefficients are relatively stable across the fixed-effects and common factor specifications (parameters range between − 0.48 and − 0.29). By comparing the fixed-effects and the CCEMG models, we observe that the coefficients for the capital/labor ratio show similar effects on efficiency change (negative) and technical change (positive); however, different results are reported when the dependent variable is TFP (fixed-effects model, not significant; CCEMG, negative). Finally, for both the fixed-effects and the CCEMG model, the variable relating domestic credit to GDP is not significant across the different specifications.
Looking at the residual diagnostics, the errors generated by the fixed-effects models are non-stationary, while the results of the unit root test indicate that the CCE models generate stationary errors (Table 7). Additionally, for comparison purposes, we also computed Eq. (6) using the system GMM estimator. Results in Table 9 of the Appendix indicate that the errors produced by the system GMM models are stationary and cross-sectionally dependent. The presence of non-stationary errors creates inaccurate standard errors that translate in overrated estimations (Eberhardt and Bond 2009; Kao 1999), which in our case renders fixed-effects and GMM results inconsistent. The CD test shows that, contrary to the case of the fixed-effects and GMM residuals, errors generated by the CCEMG models are cross-section independent. These results suggest that in our case, the commonly used fixed-effects and GMM estimators produce inaccurate estimations with non-stationary, cross-section correlated errors, while the CCEMG estimations offer more convincing results.
We now discuss the results of the common factor models. It should be noted that figures in Table 7 represent the robust coefficient mean of the country-specific parameters and that, following Pesaran and Smith (1995, p. 82), t-statistics test if average coefficients are significantly different from zero.
Concerning the average coefficient for the control variables, the CCEMG model indicates that country size measured via GDP is negatively associated with TFP and efficiency change. However, in the case of the technical change variable, the lack of significance in the average coefficient suggests that countries can experience technical progress irrespective of their size, in terms of GDP. Technical change, which embraces different aspects related to the countries’ capacity to generate and channel value-adding innovations to the market, may well not be affected by the size of the economy.
The key finding of the study indicates that the GEI measuring the quality of the system of entrepreneurship at country level is positively associated with TFP changes. In terms of coefficients, results for the TFP model show that a 10% improvement in the national system of entrepreneurship would increase TFP by 1.38 percentage points (ln(ΔGEI) × βGEI = ln(1.1) × 0.1452). This result is consistent with our argument that the national system of entrepreneurship is positively associated with changes in TFP.
The CCEMG model that uses efficiency changes (EC) as dependent variable evaluates if the national system of entrepreneurship is conducive to mostly Kirznerian entrepreneurship by moving countries closer to the global frontier. Contrary to the case of the coefficient in the fixed-effects model, the CCEMG estimator shows that the system of entrepreneurship does not impact TFP via efficiency change in a significant way (Kirznerian entrepreneurship).
Technical change is an accurate measure of the countries’ capacity to develop and introduce innovations that enhance their production function (Kumar and Russell 2002). The result for the average coefficient in Table 7 indicates that the national system of entrepreneurship enhances technical change, an effect that we link to Schumpeterian entrepreneurship. Based on the CCEMG model, the result for the average coefficient suggests that increasing the GEI score by 10% is associated with an improvement in technical change of 0.91 percentage points(ln(ΔGEI) × βGEI = ln(1.1) × 0.0954). This result is in line with our argument that the national system of entrepreneurship may increase the positive effect of Schumpeterian entrepreneurship on TFP via higher rates of technical change.
In summary, our analysis suggests that canonical fixed-effects and system GMM models produce non-stationary, cross-sectional dependent error terms that question the validity of parameters, while the CCEMG models offer more reliable estimations of the true effect of the system of entrepreneurship on TFP. The discrepancies in the estimations indicate that a model that accounts for technology heterogeneity—which translates into country-specific parameter estimates—plays a decisive role in the analysis of TFP determinants across countries.
In the case of the effect of the Kirznerian entrepreneurship, the CCEMG estimators are not significant. This result suggests that many entrepreneurs run low-quality firms with little market value, which dilutes the effect of entrepreneurship on efficiency improvements (Atkinson and Lind 2018; Kirchhoff 1994). Concerning technical change, we find that the positive effect of the GEI variable on TFP exclusively originates from the capacity of the entrepreneurship systems to promote effective innovations that trigger upward shifts in the technology function, an effect that we link to Schumpeterian entrepreneurship. In our interpretation, this finding indicates that a healthier entrepreneurial system may facilitate the introduction and commercialization of inventions that are conducive to more efficient input–output combinations and, ultimately, to technical progress.
4.2 Robustness checks
This sub-section presents the results of a number of robustness checks evaluating the suitability of the GEI to measure country-level entrepreneurship compared to alternative variables, the role of influential (efficient) observations on our results, and the direction of causality of the analyzed relationships.
Alternative definitions of country-level entrepreneurship
We first considered the possibility that our estimates based on the GEI are similar to results using other, more traditional, measures of country-level entrepreneurship. Existing studies on the relationship between entrepreneurship and performance at the country level often employ the rates of business creation or aggregate business ownership rates to operationalize country-level entrepreneurship (see, e.g., Koellinger and Thurik 2012; Parker 2009). In line with these studies, one would be tempted to question whether the capacity of the variable linked to the national system of entrepreneurship to explain differences in TFP across countries is different to that of conventional entrepreneurship metrics.
To further corroborate the appropriateness of the GEI as a measure of country-level entrepreneurship, we first estimated Eq. (7) using two variables obtained from the Global Entrepreneurship Monitor (GEM) adult population surveys that are commonly employed as proxies of country-level entrepreneurship: the rate of new businesses with less than 42 months of market experience (Prieger et al. 2016), and the opportunity-led entrepreneurial activity (opportunity TEA) rate which identifies whether entrepreneurial activity is initiated to pursue a business opportunity (Reynolds et al. 2005; Wong et al. 2005). Also, we use a third entrepreneurship proxy variable based on the rate of self-employment relative to total employment made available by the World Bank.
Results in Table 10 of the Appendix reveal that, for all dependent variables, the coefficients linked to the three analyzed entrepreneurship proxies do not have a significantly positive impact on country-level TFP. The only significant result emerges between the rate of self-employment and technical change. The negative relationship between the rate of self-employment and technical change suggests that, in many countries, high rates of self-employment may be evidence of the presence of a large group of entrepreneurs running firms that add little value to the economy (Atkinson and Lind 2018).
The results of the CCEMG models confirm not only that firm formation rates are merely quantity figures that do not have the capacity to explain variations in TFP across economies but also that the proposed GEI—which is a proxy metric of the national system of entrepreneurship—embraces relevant properties of (multidimensional) entrepreneurship systems that contribute to explain TFP differences across countries and across time.
The role of influential (efficient) countries
Second, we dealt with the possibility that the results are driven by country-specific effects not captured by the common factor model and correlated with total factor productivity. More concretely, we evaluated if the relationship between TFP and country-level entrepreneurship is primarily determined by the effects of efficient countries positioned on the global technology frontier. Equation (4) is used to compute, for each country, the distance to the efficiency frontier (see Section 3.2). In our sample, USA is consistently efficient during the whole analyzed period (2003–2013), while Norway is efficient in all time periods excepting 2007, 2008, and 2010. Also, four countries are efficient—i.e., positioned on the efficiency frontier—in at least one of the analyzed years (2003–2013): Australia (efficient in the period 2003–2005), Chile (2004 and 2005), China (period 2003–2008), and Iran (period 2009–2013). The remaining 39 countries in the sample are inefficient in all time periods. For the purposes of this robustness check, the six efficient countries were removed from the sample to ensure the validity of CCEMG estimators.
Table 11 in the Appendix presents regression results based on Eq. (7) for the sample of inefficient countries. The estimated coefficients for the GEI are robust to this exercise, thus confirming that the positive effect of the national system of entrepreneurship on TFP—and primarily on technical change—is not driven by efficient countries positioned on the global technology frontier.
Direction of causality
Finally, provided that the study variables are non-stationary and that they are cointegrated, we apply a causality test to further corroborate that the results presented in Section 4.1 can be interpreted as causal evidence. The Dumitrescu and Hurlin (2012) heterogeneous panel causality test was used to evaluate the direction of the causal relationships between the analyzed variables. In line with the arguments that support our econometric strategy (Section 3), this procedure adapts the Granger causality test to unbalanced panels and different lag orders in the panel autoregressive process, accounts for cross-sectional dependence, and allows for parameter heterogeneity in the autoregressive parameter linked to the lagged dependent variable as well as in the slopes of regression coefficients. Because the dependent variables represent productivity changes, we applied the causality test on the first difference of the data series.
The key result of the heterogeneous panel causality test in Table 12 (Appendix) reveals a unidirectional causality from the national system of entrepreneurship variable (ln GEI) to the three dependent variables (TFP, efficiency change, and technical change), and that there is no reverse causality from the productivity variables to GEI in the short run. Similar results were found for the variables measuring country size and the domestic credit/GDP ratio.
Finally, a bi-directional causality is found between the three dependent variables and the capital/labor ratio. This means that the capital-to-labor ratio and TFP (and its components) stimulate each other in the short run, which is consistent with our approach to modeling TFP. Because capital and labor are the inputs used to produce GDP in our technology function, this finding only indicates that variations in the capital/labor ratio explain productivity differences, which in turn causes changes in the capital-to-labor ratio, that is, input choices are conditioned by past productivity results.Footnote 4
The objective of this analysis was to show that our empirical results reasonably present a causal relationship from the analyzed variables to TFP, and not vice versa. The core findings of this exercise—unidirectional causality from most variables to TFP—further validate the interpretations in the CCEMG models presented above in Section 4.1.
4.3 Discussion and policy implications
What is the contribution of our study relative to prior research dealing with the effect of entrepreneurship on country-level productivity? Since the contribution of Schumpeter (1934), the role of innovation has been central to the analysis of economic growth and development; however, entrepreneurship has not fared as well on national performance analyses. Entrepreneurship has been shown to be important for countries’ economic performance, but what exactly is entrepreneurship other than innovation has been sidestepped. In this sense, the main contribution of this study relies on the comprehensive analysis of the relationship between country-level entrepreneurship and total factor productivity (distinguishing efficiency change from technical change). Entrepreneurship is not only heterogeneous between countries but also in terms of its effects on productivity. We argue that the entrepreneurial ecosystem is a relevant transmission channel that contributes to national TFP by promoting different types of entrepreneurship, namely Kirznerian and Schumpeterian.
By scrutinizing how the national system of entrepreneurship triggers different sources of TFP, we assess how the entrepreneurial ecosystem yields to higher output levels via a more efficient resource mobilization of available opportunities, a process that we link to Kirznerian entrepreneurship (Kirzner 1973, p. 74). Also, our analysis permits to assess if the national system of entrepreneurship is conducive to superior TFP levels by enhancing the economic role of the entrepreneurs responsible for the “creative destruction” (Aghion and Howitt 1992; Schumpeter 1934). These innovative actions shift technology curves and translate into higher rates of technical change (Kirzner 1973, p. 81).
In this paper, we have been able to put both types of entrepreneurship that have eluded scholars for a generation into a common framework to advance policy. We present novel empirical evidence on the sources of productivity at country level suggesting that the entrepreneurial ecosystem is conducive to total factor productivity. Instead of improving TFP via increased output levels resulting from a more efficient mobilization of resources (Kirznerian entrepreneurship), the results indicate that the national systems of entrepreneurship triggers productivity by promoting Schumpeterian entrepreneurship. Schumpeterian entrepreneurship—which we link to the introduction of disruptive technologies or, as defined by Schumpeter, “the carrying out of new combinations” (Schumpeter 1934, p. 66)—is a special case of economic function critical for achieving higher rates of technical change that lead to upward shifts in technology curves (Kirzner 1973, p. 81). Our findings show how countries with a solid entrepreneurial ecosystem are better able to generate outcomes linked to Schumpeterian entrepreneurship—e.g., development and commercialization of innovations—which in turn translate into technical progress and, ultimately, higher rates of total factor productivity.
In light of the contribution of this study, what policy lessons can be drawn from the proposed analysis of the relationship between country-level entrepreneurship and productivity growth? Scholars increasingly acknowledge the need to harmonize the definition and operationalization of country-level entrepreneurship (Acs et al. 2014). In this sense, the debate is still open and our study provides evidence on the value of the national system of entrepreneurship as a reliable variable to measure country-level entrepreneurship by incorporating in the analysis the complex and systemic interactions that govern entrepreneurial actions.
Policy-makers often allocate large sums of public money in policies excessively oriented toward the stimulation of employment, capital accumulation, and knowledge generation in the economy, such as subsidies to support self-employment and human capital formation as well as investments in research and development. These policies—rooted in the endogenous growth theory—are conducive to economic performance and undoubtedly have translated into significant economic outcomes linked to increased levels of employment and education (Aghion and Howitt 1992). Nevertheless, our comprehensive analysis fuels the notion that policy should shift from a focus on capital and labor toward designs that match knowledge and capital formation programs with policy interventions aimed at enhancing the national systems of entrepreneurship.
From a policy perspective, entrepreneurship support programs would become sterile if entrepreneurs navigate in contexts that do not guarantee the effective exploitation of their knowledge. Thus, policy-makers need to turn their attention to the development of an appropriate national system of entrepreneurship; and prioritize policies that promote the ‘interconnector’ role of the national systems of entrepreneurship so that the knowledge generated is efficiently channeled to the economy, which in turn has the potential to create economic growth. Additionally, in the long run, successful productivity growth should be grounded in the creation and/or consolidation of policies that support Schumpeterian entrepreneurship, such as the development of mechanisms to finance innovations and incentives to develop new technologies (Baumol and Strom 2007; Prieger et al. 2016).
Finally, many developed and developing countries implement policies to stimulate economic growth based on the mere formation of new businesses (Atkinson and Lind 2018). However, the effects of such policies vary across countries with different levels of development. On the one hand, the strong growth effect of the entrepreneurial ecosystem on TFP through technical change suggests that for advanced countries—i.e., those responsible of most innovations—explicit policies designed to improve the entrepreneurial ecosystem may prove themselves effective in promoting productivity, even if such policies discourage entrepreneurship indirectly (Litan et al. 2009). On the other hand, countries with a limited capacity to develop innovations that try to increase efficiency might benefit more from an investment policy that seeks to accommodate their existing resources to new technologies, rather than an entrepreneurial policy focused on the improvement of their entrepreneurial ecosystem. This argument is in line with Acemoglu et al. (2005) who stress that the optimal growth strategy is country specific and it depends upon the development process.
5 Concluding remarks
This study has produced novel economic evidence on the importance of the national system of entrepreneurship for countries’ TFP. Building on economic and institutional frames (Acs et al. 2014; Baumol 1990; Bjørnskov and Foss 2016), prior work on the relationship between entrepreneurship and productivity growth (mostly using homogeneous parameter methods) offers inconclusive results (e.g., Acs et al. 2012; Bjørnskov and Foss 2013; Lafuente et al. 2018; Prieger et al. 2016; Shane 2009; Van Stel et al. 2005). In contrast, by employing a common factor model that allows for technology heterogeneity, we propose that, besides technology and the availability of production factors, the entrepreneurial ecosystem plays a decisive channeling role that contributes to spur TFP.
Overall, our results provide strong evidence for the positive effect of the national system of entrepreneurship on countries’ TFP. This effect is conditional on the type of entrepreneurship promoted by the entrepreneurial ecosystem. The findings reveal that the effect of the entrepreneurial ecosystem on TFP exclusively originates from the capacity of the former to promote upward shifts in the countries’ production function (technical progress). On the contrary, the entrepreneurial ecosystem—measured by the GEI—does not lead to movements toward the technology frontier (efficiency change). This latter result suggests that large self-employment rates—often found in underdeveloped economies (Prieger et al. 2016)—may well result from poor labor market conditions, and that the relatively high business entry rates in these countries can be detrimental to TFP due to the creation of too small and low value-adding firms.
Productivity results from technological progress, which in turn emerges from the capacity of (new and incumbent) economic agents to generate and commercialize innovations. Innovation is the main conduit of entrepreneurship attitudes, and our results indicate that the main transmission mechanism through which the entrepreneurial ecosystem impacts countries’ TFP is technical change. This finding helps to reconcile the results in theoretical models with the conflicting empirical results. Also, the systemic approach adopted in this study to measure country-level entrepreneurship appears to provide a better measure of entrepreneurship than metrics based on individual-level or business-level data.
The findings presented in this study have a strong intuitive and conceptual appeal, and are open to future verification. In this sense, it would be valuable to extend the analysis in several directions, such as evaluating the connection between TFP and the patterns of basic and major innovations in order to determine the effect of different types of innovations on TFP as well as the role of the entrepreneurial ecosystem in these processes. Also, the proposed analysis would gain richness if future studies assess the relationship between country-level entrepreneurship and TFP using alternative production functions that, besides labor and capital, include other equally relevant inputs and outputs into the technology. The inclusion of inputs capturing the dissimilar levels of human capital among the working population (Caselli and Coleman II 2006) or countries’ absorptive capacity (Griffith et al. 2004), as well as outputs connected to other policy objectives (e.g. environmental goals, as discussed in Acemoglu et al. (2012)) constitute interesting directions for future research. Supported by our results, the scrutiny of the national system of entrepreneurship is a relevant aspect that should enter the research agenda of scholars and policy-makers, and future work should evaluate the effectiveness of different policies designed to improve weak spots in the national system of entrepreneurship.
Change history
11 March 2021
A Correction to this paper has been published: https://doi.org/10.1007/s11187-021-00467-8
Notes
The Romer (1990) and Grossman and Helpman (1991) expanding variety models are in that sense more Schumpeterian in nature. In these models, the introduction of new ideas erodes the profitability of the incumbent businesses. Also, the creative destruction process is not explicit in these models as they do not incorporate the possibility of business exit.
For Sollow (1957), neutral technical change occurs if the marginal rate of substitution (MRS) between two inputs (x1, x2) is constant and only increase or decrease the output in period t and t + 1: x2t + 1/x1t + 1 = x2t/x1t. Mathematically, neutrality can be written as \( \mathrm{d}/\mathrm{d}t\mathrm{MRS}=\mathrm{d}/\mathrm{d}t\left({F}_1^t/{F}_2^t\right)=-\mathrm{d}/\mathrm{d}t\left(\mathrm{d}x2/\mathrm{d}x1\right)=0 \), where\( {F}_1^t \) and \( {F}_2^t \) are the marginal products and x2/x1 is held constant. Neutrality implies a homothetic inward shift on the unit isoquant (Binswanger 1974).
Note that we also ran these tests for country-specific time series. Results, available on request, mostly confirm the persistence of the study variables. At the country level, the result of the Maddala and Wu test rejects the null hypothesis of non-stationarity only for six data series of the GEI variable (Argentina, Greece, Jamaica, Norway, Sweden, and the USA), for three data series of the capital/labor ratio variable (Brazil, Iran, and Romania), for two data series of the GDP variable (Greece and Sweden), and for one data series of the TFP index (Norway). In the case of the CIPS test (Pesaran 2007) results indicate that, for all analyzed countries and all variables, the null hypothesis of non-stationarity cannot be rejected at standard levels of significance.
As we indicated in Section 3, the input variables (capital stock and labor) used to compute the TFP index and its components are introduced individually. Thus, the capital-to-labor variable only captures the effect on productivity of movements of this ratio along the isoquant.
References
Acemoglu, D. (2002). Directed technical change. Review of Economic Studies, 69(4), 781–809.
Acemoglu, D., Aghion, P., Bursztyn, L., & Hemous, D. (2012). The environment and directed technical change. American Economic Review, 102(1), 131–166.
Acemoglu, D., Johnson, S., & Robinson, J. A. (2005). Institutions as the fundamental cause of long-run growth. In P. Aghion & S. Durlauf, Handbook of Economic Growth (pp. 385–472). Amsterdam: North-Holland.
Acemoglu, D., & Zilibotti, F. (2001). Productivity differences. Quarterly Journal of Economics, 116(2), 563–606.
Acs, Z. J., & Audretsch, D. B. (1988). Innovation in large and small firms—an empirical analysis. American Economic Review, 78, 678–690.
Acs, Z. J., Audretsch, D. B., Braunerhjelm, P., & Carlsson, B. (2012). Growth and entrepreneurship. Small Business Economics, 39(2), 289–300.
Acs, Z. J., Audretsch, D. B., Lehmann, E. E., & Licht, G. (2016). National systems of entrepreneurship. Small Business Economics, 46(4), 527–535.
Acs, Z. J., Autio, E., & Szerb, L. (2014). National systems of entrepreneurship: measurement issues and policy implications. Research Policy, 43(3), 476–494.
Aghion, P., & Howitt, P. (1992). A model of growth through creative destruction. Econometrica, 60(2), 323–351.
Arellano, M., & Bond, S. R. (1991). Some tests of specification for panel data. Review of Economic Studies, 58(2), 277–297.
Atkinson, R. D., & Lind, M. (2018). Big is beautiful: debunking the myth of small business. Cambridge, MA: The MIT Press.
Bai, J. (2009). Panel data models with interactive fixed effects. Econometrica, 77, 1229–1279.
Barro, R. (1991). Economic growth in a cross section of countries. Quarterly Journal of Economics, 106(2), 407–443.
Barro, R., & Sala-i-Martin, X. (1997). Technological diffusion, convergence, and growth. Journal of Economic Growth, 2, 1–26.
Baumol, W. J. (1990). Entrepreneurship: productive, unproductive and destructive. Journal of Political Economy, 98(5), 893–921.
Baumol, W. J., & Strom, R. J. (2007). Entrepreneurship and economic growth. Strategic Entrepreneurship Journal, 1, 233–237.
Binswanger, H. P. (1974). The measurement of technical change bias with many factors of production. American Economic Review, 64, 964–976.
Bjørnskov, C., & Foss, N. J. (2013). How strategic entrepreneurship and the institutional context drive economic growth. Strategic Entrepreneurship Journal, 7, 50–69.
Bjørnskov, C., & Foss, N. J. (2016). Institutions, entrepreneurship, and economic growth: what do we know and what do we still need to know? Academy of Management Perspectives, 30(3), 292–315.
Blundell, R., & Bond, S. R. (1998). Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics, 87(1), 115–143.
Bogetoft, P., & Otto, L. (2011). Benchmarking with DEA, SFA, and R. New York: Springer.
Boussemart, J.-P., Briec, W., Kerstens, K., & Poutineau, J.-C. (2003). Luenberger and Malmquist productivity indices: theoretical comparisons and empirical illustration. Bulletin of Economic Research, 55(4), 391–405.
Caselli, F., & Coleman, W. J., II. (2006). The world technology frontier. American Economic Review, 96(3), 499–522.
Caves, D. W., Christensen, L. R., & Diewert, W. E. (1982). The economic theory of index numbers and the measurement of input, output, and productivity. Econometrica, 50, 1393–1414.
Chudik, A., Pesaran, M. H., & Tosetti, E. (2011). Weak and strong cross-section dependence and estimation of large panels. The Econometrics Journal, 14(1), C45–C90.
Cooper, W. W., Seiford, L. M., & Zhu, J. (2011). Handbook on data envelopment analysis (2nd ed.). New York: Springer.
Dumitrescu, E.-I., & Hurlin, C. (2012). Testing for Granger non-causality in heterogeneous panels. Economic Modelling, 29, 1450–1460.
Durlauf, S., Johnson, P.A., & Temple, J.R.W. (2005). Growth econometrics. In P. Aghion & S. Durlauf, Handbook of economic growth (pp. 555–677). Amsterdam: North Holland.
Eberhardt, M., & Bond, S. (2009). Cross-section dependence in nonstationary panel models: a novel estimator. In MPRA Paper 17692. Germany: University Library of Munich.
Eberhardt, M., Helmers, C., & Strauss, H. (2013). Do spillovers matter when estimating private returns to R&D? Review of Economics and Statistics, 95(2), 436–448.
Eberhardt, M., & Teal, F. (2013). No mangoes in the tundra: spatial heterogeneity in agricultural productivity analysis. Oxford Bulletin of Economics and Statistics, 75(6), 914–939.
Färe, R., Grosskopf, S., Lindgren, B., & Roos, P. (1989). Productivity developments in Swedish hospitals: a Malmquist output index approach. In A. Charnes, W.W. Cooper, A.Y. Lewin, & L.M. Seiford, Data envelopment analysis: theory, methodology and applications. Boston: Kluwer Academic Publishers.
Färe, R., Grosskopf, S., Norris, M., & Zhang, Z. (1994). Productivity growth, technical progress, and efficiency change in industrialized countries. American Economic Review, 84(1), 66–83.
Friedberg, L. (1998). Did unilateral divorce raise divorce rates? Evidence from panel data. American Economic Review, 88(3), 608–627.
Grifell-Tatjé, E., & Lovell, C. A. K. (2015). Productivity accounting: the economics of business performance. New York: Cambridge University Press.
Griffith, R., Redding, S., & Van Reenen, J. (2004). Mapping the two faces of R&D: productivity growth in a panel of OECD industries. Review of Economics and Statistics, 86(4), 883–895.
Grossman, G. M., & Helpman, E. (1991). Quality ladders in the theory of growth. Review of Economic Studies, 58(1), 43–61.
Kao, C. (1999). Spurious regression and residual-based tests for cointegration in panel data. Journal of Econometrics, 65, 9–15.
Kapetanios, G., Pesaran, M. H., & Yamagata, T. (2011). Panels with non-stationary multifactor error structures. Journal of Econometrics, 160(2), 326–348.
King, R. G., & Levine, R. (1993). Finance and growth: Schumpeter might be right. Quarterly Journal of Economics, 108(3), 717–737.
Kirchhoff, B. A. (1994). Entrepreneurship and dynamic capitalism. Westport CT: Praeger.
Kirzner, I. M. (1973). Competition and entrepreneurship. Chicago: University of Chicago Press.
Kirzner, I. M. (1997). Entrepreneurial discovery and the competitive market process: an Austrian approach. Journal of Economic Literature, 35(1), 60–85.
Koellinger, P. D., & Thurik, A. R. (2012). Entrepreneurship and the business cycle. Review of Economics and Statistics, 94(4), 1143–1156.
Kumar, S., & Russell, R. R. (2002). Technological change, technological catch-up, and capital deepening: relative contributions to growth and convergence. American Economic Review, 92(3), 527–548.
Lafuente, E., Acs, Z. J., & Szerb, L. (2018). The entrepreneurship paradox: more entrepreneurs are not always good for the economy—the role of the entrepreneurial ecosystem on economic performance in Africa. In SSRN working paper available at https://ssrn.com/abstract=3307617.
Lafuente, E., Szerb, L., & Acs, Z. J. (2016). Country level efficiency and national systems of entrepreneurship: a data envelopment analysis approach. Journal of Technology Transfer, 41(6), 1260–1283.
Litan, R., Baumol, W., & Schramm, C. J. (2009). Good capitalism, bad capitalism, and the economics of growth and prosperity. New Haven: Yale University Press.
Lucas, R. E. (1988). On the mechanics of economic development. Journal of Monetary Economics, 22(1), 3–42.
Maddala, G. S., & Wu, S. (1999). A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics, 61, 631–652.
Malmquist, S. (1953). Index numbers and indifference surfaces. Trabajos de Estadistica, 4, 209–242.
Mankiw, N. G., Romer, D., & Weil, D. N. (1992). A contribution to the empirics of economic growth. Quarterly Journal of Economics, 107, 407–437.
Melitz, M. J., & Ottaviano, G. I. (2008). Market size, trade, and productivity. Review of Economic Studies, 75(1), 295–316.
Moll, B. (2014). Productivity losses from financial frictions: can self-financing undo capital misallocation? American Economic Review, 104(10), 3186–3221.
Parente, S. L., & Prescott, E. C. (1994). Barriers to technology adoption and development. Journal of Political Economy, 102, 298–321.
Parker, S. C. (2009). The economics of entrepreneurship. New York: Cambridge University Press.
Pedroni, P. (1999). Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxford Bulletin of Economics and Statistics, 61, 653–670.
Pedroni, P. (2004). Panel cointegration: asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econometric Theory, 20, 597–625.
Pesaran, M.H. (2004). General diagnostic tests for cross section dependence in panels. IZA Discussion Paper No. 1240.
Pesaran, M. H. (2006). Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica, 74(4), 967–1012.
Pesaran, M. H. (2007). A simple panel unit root test in the presence of cross-section dependence. Journal of Applied Econometrics, 22, 265–312.
Pesaran, M. H., & Smith, R. (1995). Estimating long-run relationships from dynamic heterogeneous panels. Journal of Econometrics, 68(1), 79–113.
Pesaran, M. H., & Tosetti, E. (2011). Large panels with common factors and spatial correlations. Journal of Econometrics, 161, 182–202.
Prescott, E. C. (1998). Needed: a theory of total factor productivity. International Economic Review, 49, 525–553.
Prieger, J. E., Bampoky, C., Blanco, L. R., & Liu, A. (2016). Economic growth and the optimal level of entrepreneurship. World Development, 82, 95–109.
Raphael, S., & Winter-Ebmer, R. (2001). Identifying the effect of unemployment on crime. Journal of Law and Economics, 44(1), 259–283.
Reynolds, P., Bosma, N., Autio, E., Hunt, S., De Bono, N., Servais, I., Lopez-Garcia, P., & Chin, N. (2005). Global entrepreneurship monitor: data collection design and implementation 1998–2003. Small Business Economics, 24(3), 205–231.
Romer, P. M. (1990). Endogenous technological change. Journal of Political Economy, 98, S71–S102.
Samuelson, P. A., & Swamy, S. (1974). Invariant economic index numbers and canonical duality: survey and synthesis. American Economic Review, 64(4), 566–593.
Shane, S. (2009). Why encouraging more people to become entrepreneurs is bad public policy. Small Business Economics, 33(2), 141–149.
Schumpeter, J. A. (1934). The theory of economic development: an inquiry into profits, capital, credit, interest, and the business cycle. Cambridge, MA: Harvard University Press.
Schumpeter, J. A. (1947). The creative response in economic history. Journal of Economic History, 7(2), 149–159.
Solow, R. M. (1957). Technical change and the aggregate production function. Review of Economics and Statistics, 39(3), 312–320.
Van Stel, A., Carree, M., & Thurik, R. (2005). The effect of entrepreneurial activity on national economic growth. Small Business Economics, 24(3), 311–321.
Wong, P. K., Ho, Y. P., & Autio, E. (2005). Entrepreneurship, innovation and economic growth: evidence from GEM data. Small Business Economics, 24(3), 335–350.
Wooldridge, J.M. (2002). Econometric analysis of cross section and panel data. Cambridge, MA: The MIT Press.
Young, A. (1998). Growth without scale effects. Journal of Political Economy, 106(1), 41–63.
Acknowledgements
Esteban Lafuente acknowledges financial support by the Spanish Ministry of Economy, Industry and Competitiveness (grant no. ECO2017-86305-C4-2-R). Mark Sanders received financial support from the European Union through the Horizon2020 project “Financial and Institutional Reforms to build an Entrepreneurial Society” (FIRES) (grant no. 649378). László Szerb acknowledges financial support by the Higher Education Institutional Excellence Program of the Hungarian Ministry of Human Capacities, within the framework of the 4th thematic program ‘Enhancing the Role of Domestic Companies in the Reindustrialization of Hungary’ of the University of Pécs (reference number of the contract: 20765-3/2018/FEKUTSTRAT); and by the Hungarian National Foundation for Scientific Research (project: OTKA-K-120289 titled ‘Entrepreneurship and competitiveness investigations in Hungary based on the Global Entrepreneurship Monitor surveys 2017-2019’).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: The article “The global technology frontier: productivity growth and the relevance of Kirznerian and Schumpeterian entrepreneurship”, written by Esteban Lafuente, Zoltan J. Acs, Mark Sanders, and László Szerb, was originally published Online First without Open Access. After publication in volume 55, issue 1, page 153–178 the author decided to opt for Open Choice and to make the article an Open Access publication.
Appendix
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lafuente, E., Acs, Z.J., Sanders, M. et al. The global technology frontier: productivity growth and the relevance of Kirznerian and Schumpeterian entrepreneurship. Small Bus Econ 55, 153–178 (2020). https://doi.org/10.1007/s11187-019-00140-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11187-019-00140-1
Keywords
- National system of entrepreneurship
- Total factor productivity
- Technical change
- Parameter heterogeneity
- Common factor model
- International