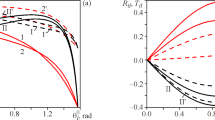
The deformed state at the interface between the solids is studied under the boundary conditions of an ideal contact and slip. These boundary conditions are implemented at the interfaces between the multiphase and structurally inhomogeneous elastic solids during friction and surface wave propagation and are used in solving a number of problems. The study is carried out in the framework of the problem of elastic wave propagation through the interface. The analytical expressions obtained for the Fresnel coefficients make it possible to calculate the curves of their dependence and those of the strain amplitude dependence on the angle of wave incidence on the interface under the conditions of a perfect contact and slip between the contacting solids. The influence of the boundary conditions, the properties of the contacting solids and the character of the external action, determined by the incident wave type, on the deformed state at the interface is analyzed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
T. W. Clyne and P. J. Withers, An Introduction to Metal Matrix Composites, Cambridge University Press (1993).
B. E. Pobedrya, Mekhanika Komp. Mater., 108, Iss. 1, 3 (1996).
L. I. Manevitch, I. V. Andrianov, and V. G. Oshmyan, Mechanics of Periodically Heterogeneous Structures, Springer (2002).
I. E. Golovnev, E. I. Golovneva, and V. M. Fomin, Phys. Mesomech., 24, No. 1, 14 (2021).
L. Deng, Z. Liu, B. Wang, et al., Mater. Characterizat., 150, 62 (2019).
N. N. Belov, A. S. Plyaskin, N. T. Yugov, et al., Russ. Phys. J., 64, No. 10, 1997 (2021).
S. I. Rokhlin and Y. J. Wang, J. Accoust. Soc. Am., 89, 503 (1991).
M. G. Krinitsyn, Yu. V. Dontsov, and V. A. Yurkina, Russ. Phys. J., 64, No. 6, 1086 (2021).
Y. Zare and K. Y. Rhee, Phys. Mesomech., 23, No. 2, 176 (2020).
H. F. Cooper, J. Accoust. Soc. Am., 42, No. 5, 1064 (1967).
L. D. Landau and E. M Lifshitz, Theory of Elasticity, Elsevier (1986).
N. V. Chertova and Yu. V. Grinyaev, Zh. Fizich. Mesomekh., 21, No. 2, 56 (2018).
N. V. Chertova and Yu. V. Grinyaev, Tech. Phys. Lett., 44, Iss. 5, 404 (2018).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Fizika, No. 4, pp. 53–61, April, 2022.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chertova, N.V., Grinyaev, Y.V. An Analysis of the Deformed State in Elastic Solids at the Interface Under the Conditions of an Ideal Contact And Slip. Russ Phys J 65, 643–653 (2022). https://doi.org/10.1007/s11182-022-02680-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11182-022-02680-8