Reference-dependent discounting

Abstract

Reference-dependence has become a widely established phenomenon in decision making under risk, not only for monetary outcomes but also for other outcomes, e.g., related to health. However, when the prospects involve risk about timing (the time of receipt of outcomes), rather than the outcomes themselves, much less is known about reference-dependence. This study extends discounted utility to incorporate reference-dependence and is the first to test it in timing prospects. We are also the first to estimate the probability weighting function for timing prospects. For both timing and outcome risk tasks, we replicate the typical fourfold pattern of risk attitudes: risk seeking for low-probability gains, risk aversion for high-probability gains, risk aversion for low-probability losses and risk seeking for high-probability losses. In other words, we find substantial pessimism with regard to high probabilities in the gain domain and low probabilities in the loss domain, and probabilistic optimism for low probabilities in the gain domain and high probabilities in the loss domain. Furthermore, we report loss aversion for outcome risks, while for timing risks, we find the opposite result, which we term earliness seeking. In sum, we find substantial empirical support for reference-dependent discounting. Our results show that psychological biases are also important when timing is risky, although the direction of bias may differ.

1 Introduction

Studies on decision under uncertainty usually consider trade-offs at a given point in time (for a review see Starmer (2000)), while studies on intertemporal choice tend to focus on trading off earlier and later gains under certainty (for a review see Frederick et al. (2002) and Cohen et al. (2020)). There have also been several studies combining risk with time. Particularly, one popular stream of literature studies the effect of uncertainty on time preference and suggests that future outcomes are discounted because the future bears uncertainty (Halevy, 2008), while another stream studies the effect of timing on risk preferences, suggesting attitudes toward risk are less pronounced when risks are resolved in the future rather than in the present (Abdellaoui et al., 2011; Baucells & Heukamp, 2010, 2012; Keren & Roelofsma, 1995; Noussair & Wu, 2006; Öncüler & Onay, 2009; Weber & Chapman, 2005). By contrast, there has been much less work for the case where the outcomes are certain, but there is uncertainty of the timing of outcomes. Only a handful of studies have addressed this topic (Chesson & Viscusi, 2003; DeJarnette et al., 2020; Ebert, 2020, 2021; Fishburn & Rubinstein, 1982; Onay & Öncüler, 2007; Schneider, 2016). This is unfortunate, because variability in the timing of outcomes is highly relevant to many real-world decisions, such as waiting for public transport and vaccinations. Another example originating from the COVID-19 pandemic is the recent occurrence of supply chain shortages causing a highly uncertain delivery timing (Ivanov, 2024; Ye et al., 2022). This paper aims to directly study how decision makers behave when there is risk concerning the time of receiving the outcome, compared to the standard risky choice where the risk is associated with the outcome. In particular, we are the first to propose a reference-dependent discount function, where speedups and delays are framed as gains and losses in waiting time, respectively, and where delays may be penalized more heavily than speedups in case of loss aversion over waiting time (or gains may be valued more strongly in case of gain seeking over waiting time).

Loss aversion, the phenomenon that losses with regard to a reference point loom larger than commensurate gains (Kahneman & Tversky, 1979), has been considered to be the core idea of prospect theory by Kahneman (2003), who wrote that “[t]he concept of loss aversion was, I believe, our [Tversky & Kahneman] most useful contribution to the study of decision making” (p.726). In addition to reference points for amounts of outcomes, people also form reference points with regard to the timing of outcomes, and—in case of favorable outcomes—perceive a delay as a loss compared to this reference point, and a speedup as a gain. This has been found to result in higher discount rates for delayed outcomes than for expedited outcomes, known as the delay-speedup asymmetry (Attema, 2012; Frederick et al., 2002; Loewenstein, 1988; Loewenstein & Prelec, 1992; Scholten & Read, 2013; Shelley, 1993). For example, when some good is due to be delivered in 1 week, then receiving it now already is seen as gain, increasing its value, but not as much as the value reduction in case of a delay. This gain-loss asymmetry is relevant in many economic applications. For one thing, it implies that if managers manipulate decision makers’ reference points with regard to the timing of cash bonuses and penalties, the optimal design of compensation schemes can be substantially affected (Shelley, 1993; Shelley & Omer, 1996). Furthermore, in a health context, individuals may have a particular period in mind in which to receive a COVID-19 vaccination. If this is then delayed due to unexpectedly low supplies, it will be regarded as a loss, causing disproportionally more disutility than any positive utility resulting from an unexpected windfall in the supply of vaccines.

Loewenstein and Prelec (1992) explained the asymmetry by means of a reference-dependent value function. For instance, a delay in receipt of a reward is modeled as a loss of the outcome now and a gain of the outcome later. This paper proposes a new model that brings in reference-dependence and loss aversion in the discount function and that is able to capture the delay-speedup asymmetry in the dimension of time. The discount function we propose is similar in spirit to the reference-dependent utility function in prospect theory for outcomes (Kahneman & Tversky, 1979). In an experiment, we study our model for waiting time for money, eliciting the parameters of this model: discounting and probability weighting for both delay and speedup as well as loss aversion for delays relative to speedups, which we will refer to as lateness aversion in this paper. In addition, for comparison we include regular outcome lotteries, again for gains as well as losses.

Our results show strong evidence of the fourfold pattern of risk attitudes for both outcome and timing risks: risk attitudes are highly affected by the probabilities used, with more risk seeking (aversion) for small (large) probabilities of the best outcome. Moreover, we observe a modest amount of risk aversion in the mixed prospects. Finally, some differences in parameter estimates are found between the timing prospects and the outcome prospects. Most interestingly, the lateness aversion index is smaller than 1 for timing prospects, while the loss aversion index is around 2 for all outcome prospects. In both prospects, we observe probabilistic pessimism for gains and strong probabilistic optimism for losses.

2 Related literature

As in Onay and Öncüler (2007), we study prospects with fixed outcomes and a risky timing of these outcomes. Onay and Öncüler showed that, due to the convex shape of the discount function, discounted expected utility (DEU) predicts respondents to prefer a lottery over the timing of a fixed outcome over the expected value of this lottery’s timings. In other words, agents are predicted to be risk seeking over timing lotteries. However, empirical tests produced the opposite result (Chesson & Viscusi, 2003; DeJarnette et al., 2020; Onay & Öncüler, 2007). Onay and Öncüler (2007) and Schneider (2016) suggested that this finding may be caused by probability weighting. Instead, DeJarnette et al. (2020) argued that probability weighting nevertheless cannot explain risk aversion for timing lotteries. They suggested an alternative property, called “stochastic impatience”, as the fundamental property to be rejected when someone is risk averse for timing lotteries. That is, someone with these preferences necessarily violates stochastic impatience, but need not violate expected utility or discounted utility. Hence, risk aversion for timing lotteries is only possible if one drops the stochastic impatience property, for which DeJarnette et al. (2020) reported substantial support. If this is indeed the case, another class of models is needed, for instance one with a (partly) concave discount function, compatible with a future bias (Sayman & Öncüler, 2009; Takeuchi, 2011).

Abdellaoui et al., (2010, 2013) separately measured the discounting of gains and losses of money, and found significant differences, with losses being discounted at a lower rate than gains. Their studies differ from ours because the gain-loss distinction was not in time itself, but in the traditional way: in outcomes. They compared waiting time for gain outcomes with waiting time for loss outcomes, but waiting time was always framed neutrally, as distance from the present. We consider cases with only gain outcomes but with a reference point in the time dimension, so that some waiting times are gains and others are losses. This brings reference-dependence directly in the time dimension and discounting, deviating more fundamentally from traditional cases.

Pan et al. (2015) proposed the concept of two-stage exponential discounting, which is able to model present-biased preference without a quasi-hyperbolic discounting model. They introduce a switch point, with the discount rate being allowed to change at the switch point, but it is constant before and after it. This switch point might be considered similar to our reference point in that we allow for different discount rates above and below this time point. However, our model also incorporates loss aversion for delays, which is not modelled by Pan et al. (2015).

Recently, an increasing interest in the elicitation of utility for waiting time has emerged (Abdellaoui et al., 2018; Abdellaoui & Kemel, 2014; Ebert & van de Kuilen, 2015; Festjens et al., 2015; Kemel & Travers, 2016). These studies use gambles with time (e.g., traveling time or waiting time) as the outcome that directly generates utility. Our design is different in that time does not generate utility but discounting. Utility is generated by the gain outcome received, and time adds a discount factor. We investigate reference-dependence in the discounting of time rather than in the utility of time.

Some other studies explored time-dependency of prospect theory preferences for outcome prospects (Abdellaoui et al., 2011, 2022; Pan et al., 2019). The findings of Abdellaoui et al. (2011) revealed more risk tolerance for delayed prospects than for non-delayed prospects, which was fully reflected by time-dependent probability weighting, whereas utility was time invariant. Abdellaoui et al. (2022) show that individuals become less sensitive and more pessimistic with respect to winning probabilities when prospects are resolved later rather than immediately. Pan et al. (2019) proposed general discounted prospect theory. Our study differs from theirs as it does from Abdellaoui et al. (2010, 2013) in the sense that we have reference-dependence in discounting whereas they have it the traditional way, in outcomes. Further, we only study outcome risks at one time point (i.e., t = 0) and hence, we can take the usual prospect theory specification for outcome risks. In the risky timing prospects, there is no outcome risk because we have a fixed reward z > 0 and only vary its timing. Contrary to these studies, apart from considering risky timing, we do not consider the effect of the timing of the resolution of uncertainty, since all uncertainties are resolved immediately after the experiment.

A number of preceding studies have already demonstrated that probability weighting functions as modelled by prospect theory can play a large role in explaining intertemporal choices. For instance, Halevy (2008) put forward an axiomatisation of discounted utility with nonlinear probability weighting, showing that probability weighting might explain the present bias, without the need for a (quasi-)hyperbolic discount function. Empirical support for this theory was presented by Epper et al. (2011). Moreover, Baucells and Heukamp (2012) have integrated time and risk distance and derived a preference model that is able to explain the common ratio and common difference effects for decision under risk, and the magnitude effect for intertemporal choice, which was supported by experimental data (Baucells & Heukamp, 2010). However, these studies all investigated outcome risks, whereas in this paper we address reference-dependent discounting in the case of timing risks. Finally, Qiu and Weitzel (2012) and Viscusi and Huber (2012) extended reference-dependence and loss aversion from pay-offs to probabilities. However, we could not find any studies proposing reference-dependent discounting.

3 Method

In our experiment, described in Sect. 4, outcomes were money amounts.¹ We implemented two types of prospects, (atemporal) outcome prospects and timing prospects. In all tasks, we assume that a decision maker’s preference relation is a weak order $\succcurlyeq$ (transitive and complete). Strict preference and indifference are denoted by $\succ$ and $\sim$, respectively.

3.1 Outcome prospects

For outcome prospects, we use ${x}_{P}y$ to denote the prospect that gives outcome $x$ with probability $p$ and outcome $y$ with probability $1-p$. The outcomes $x$, $y$ and $r$ are real numbers standing for the amount of money. Throughout this paper, we use the notation ${x}_{P}y$ if $x\ge y\ge 0 [x\le y\le 0,\text{ or } x>0>y]$ for gain [loss, or mixed] prospects.

We assume that preferences for outcomes x, y are reference-dependent. Commonly,

$$U(x)= u(x)\;if\;x\ge 0 (gains),$$

$$U(x)= \lambda u\left(x\right)\;if\;x\le 0 (losses),$$

(1)

where U(x) is the utility function with the requirement $U\left(r\right)=0$, and $\lambda >0$ is the loss aversion index, with $\lambda >1$ ($\lambda <1$) reflecting loss aversion (gain seeking). For later purposes, we give below the extension that does not need this requirement. For outcome prospects ${x}_{P}y$, we assume that all outcomes occur at t = 0. They are evaluated as follows (Wakker, 2010):

$$\text{PT}\left({x}_{P}y\right)={\text{w}}_{x}^{+}\left(\text{p}\right)\cdot \left(\text{U}\left(\text{x}\right)-\text{U}\left(\text{y}\right)\right)+\text{U}(\text{y})$$

(2a)

for gain prospects, ${\text{w}}_{x}^{+}$ the decision weight of x;

$$\text{PT}\left({x}_{P}y\right)={\text{w}}_{x}^{-}\left(\text{p}\right)\cdot \left(\text{U}\left(\text{x}\right)-\text{U}\left(\text{y}\right)\right)+\text{U}(\text{y})$$

(2b)

for loss prospects, ${\text{w}}_{x}^{-}$ the decision weight of x; and, when assuming U(r) = 0

$$\text{PT}\left({x}_{P}y\right)={\text{w}}_{x}^{+}\left(\text{p}\right)\cdot \text{U}\left(\text{x}\right)+{\text{w}}_{x}^{-}\left(1-\text{p}\right)\cdot \text{U}\left(\text{y}\right)$$

(2c)

for mixed prospects.

For utility, we assume the usual power shape, i.e., ${u}^{+}(x)={x}^{\alpha }$ for gains and ${u}^{-}(x)=-(-{x)}^{\beta }$ for losses. For probability weighting, we used Prelec’s two parameter weighting family $w\left(p\right)={e}^{-g{(-\mathit{ln}p)}^{d}}$ where $d$ reflects a decision maker’s sensitivity to changes in probability, with higher values representing more sensitivity, while $g$ reflects the elevation, where higher values represent more weight being attached to the higher outcome in a gamble (Prelec, 1998; Wu & Gonzalez, 1999).

In total, there are seven unknown parameters $(\alpha , \beta , {d}_{x}^{+}, {d}_{x}^{-},{g}_{x}^{+}, {g}_{x}^{-}, \lambda )$. In each set of choices among outcome prospects, each subject completed 24 choice lists 10 in the gain domain, 10 in the loss domain and 4 in the mixed domain.

The choice probability of choosing a prospect $X$ over a prospect $Y$ is given by $(X,Y,W)=\varnothing(\frac{PT\left(X\right)-PT\left(Y\right)}e)$, where $\varnothing$ is the cumulative normal distribution, $e$ is a ‘noise’ term, and $W$ represents the set of preference parameters to be estimated. To estimate the parameters $\alpha$, $\beta ,$ ${\omega }_{x}^{+},$ ${\omega }_{x}^{-}$ and $\lambda$ for each subject, we aggregate all the choices in the 48 choice lists each subject made in the gain, loss and mixed domain, and look for the best fitting parameters that maximize the likelihood function $L(X, Y,W)$ which is obtained with:

$$\prod\nolimits_{k=1}^{90}\left\{P\left(X,Y,W\right)\times I_{s_{i,k}=1}+\left[1-P\left(X,Y,W\right)\right]\times I_{s_{i,k}=-1}\right\},\;$$

(3)

where s_i,k denotes the k-th choice of subject i, which is equal to 1 when subject i chooses option X; otherwise, it is $-1$.

3.2 Timing prospects

For the timing prospects, we denote absolute time by capital letters, such as $T$ and $R$. $T=0$ designates the present. We assume one special reference time, denoted $R$. In the experiment, this is induced by framing. We use small letters to designate distances from $R$, such as $t$. Specifically, $t=T-R$ refers to the same timepoint as $T$. We usually implicitly assume $t=T-R$. Usually, $R>0$ and $t$ can take both positive values (delay relative to $R$; losses) and negative values (speedups relative to $R$; gains). We could write $r=0$. Note that by this definition, a gain (i.e., speedup) is of the opposite sign than in the outcome prospects. This allows the discount function to increase (decrease) with the amount of the gain (loss), which will be convenient when relating to utility functions in prospect theory, with gains positive arguments and losses negative arguments.

We use ${a}_{P}b$ to denote the prospect speeding-up the outcome $z$ by $a$ with probability $p$ and speeding-up the outcome z by $b$ with probability$1-p$, relative to the reference time point $R$, with the outcome $z$ often suppressed. The outcome $z$ is a constant gain. Similarly, we use the notation ${a}_{P}b$ if $a\le b\le 0$ for speedup prospects and $a\ge b\ge 0$ for delay prospects. A prospect is mixed, containing both a delay and a speedup, if $b>0>a.$

We assume a discount function $D(t)$ with $D\left(0\right)=1$. Reference-dependent discounting with reference point $R$ is defined as follows. There exists a strictly increasing continuous function $d$, and a lateness aversion index $\lambda >0$, such that:²

$$D\left(t\right)=d\left(t\right)if t\le 0 \left(gains\right),$$

$$D\left(t\right)=d\left(0\right)\times {\left(\frac{d\left(t\right)}{d\left(0\right)}\right)}^{\lambda }\text{ if }t\ge 0(\text{losses}).$$

(2c)

One other change is that we impose $d\left(0\right)\ne 0$. It cannot be 0 at reference point $R$, because that would imply that a reward received at the reference time would have no value. This change is unimportant and only a matter of convenient scaling, to impose $d\left(0\right)=1$. A brief preference foundation of this model is provided in Appendix A.

We assume that timing prospects ${a}_{P}b$ are evaluated by:

$$\text{PT}\left({a}_{P}b\right)={w}_{t}^{early}(\text{p})\cdot \left(\text{d}\left(\text{a}\right)-\text{d}\left(\text{b}\right)\right)+\text{d}(\text{b})$$

(5a)

for gain/speedup prospects where $a\le b\le 0$, and where ${w}_{t}^{early}$ is the decision weight of a and

$$\text{PT}\left({a}_{P}b\right)={w}_{t}^{late}\left(\text{p}\right)\cdot \left(d\left(0\right)\times {\left(\frac{d\left(a\right)}{d\left(0\right)}\right)}^{\lambda }-d\left(0\right)\times {\left(\frac{d\left(b\right)}{d\left(0\right)}\right)}^{\lambda }\right)+d\left(0\right)\times {\left(\frac{d\left(b\right)}{d\left(0\right)}\right)}^{\lambda }$$

(5b)

for loss/delay prospects where $a\ge b\ge 0$ and ${w}_{t}^{late}$ the decision weight of a. It is clear that U(z) cancels out, and that the equations are not affected by the scaling of d(0). Finally, mixed prospects ($b>0>a$) are evaluated by:

$$\text{PT}\left({a}_{P}b\right)=\text{d}\left(0\right)+{w}_{t}^{early}\left(\text{p}\right)\cdot \left(\text{d}\left(\text{a}\right)-\text{d}\left(0\right)\right)+{w}_{t}^{late}\left(1-\text{p}\right)\cdot \left(\text{d}\left(\text{b}\right)-\text{d}\left(0\right)\right).$$

(5c)

These formulas provide an extension of discounted utility toward reference-dependent discounted utility. We are not aware of any previous efforts in this regard, but these formulas provide the proper extensions. Note that preferences do not change after adding a constant to the function D.

In terms of the specific functional form of the discount function, we estimated the exponential discounting function: d $\left(t\right)=$ ${\delta }^{t}$. This function is increasing in gains in waiting time and decreasing in losses in waiting time if 0< $\delta$  < 1.

To test if our general reference-dependent discounting framework works with different discounting functions, we also estimate the dual exponential discount function (Prelec & Rohde, 2016).

$$Dual discounting: d\left(t\right)= {0.5e}^{-\delta t}-{0.5e}^{\delta t}+1.$$

(6)

At the reference point, we have $d(t=0)=1$ for all the discount functions. The probability weighting function is the same as in the outcome prospects.

A graphical illustration may help explaining our model. Consider a mixed prospect with a being a gain in time and b a loss in time. Figure 1 shows how this prospect would be evaluated under DEU with a positive discount rate as captured by the convex shape, while Fig. 2 illustrates what changes in case of reference-dependent discounting. Under DEU, only the timing itself matters and the difference compared to the reference timing would be irrelevant. The reference-dependent discount function instead allows for both a different shape of the discount function and a kink at t = 0 due to loss aversion. In Fig. 2, the shapes differ between gains and losses, representing the possibility of reference-dependent discount factors. Figure 2 only illustrates the case of lateness aversion where delay weighs more heavily than speedup. More specifically, the kink at t_r indicates timing losses loom larger than timing gains. The figures make clear that under DEU, we would need a large value of b to compensate for the smaller delay a, whilst this value of b is lower under reference-dependent discounting. The reason is that b is regarded as a loss in the latter, which gets more weight, and hence giving the same loss in discounted utility for a lower value of b.

Fig. 1

Graphical representation of a mixed prospect under DEU

Fig. 2

Graphical representation of a mixed prospect under reference-dependent discounting

The number of choices in each domain and the econometric approach to estimate the parameters $({\delta }_{t}^{early}, {\delta }_{t}^{late}, {d}_{t}^{early}, {g}_{t}^{early}, {d}_{t}^{late}, {g}_{t}^{late} ,\lambda )$ is the same as for the outcome prospects.³ A complication for timing prospects is that losses in timing still generate a positive addition to total discounted utility.

Table 1 summarizes the resulting variables and parameters that we elicited from the experiment.

Table 1 Overview of experimental design

4 Experiment

Two experiments were conducted. The first experiment tested the outcome prospects and timing prospects not only in the monetary context but also in the health context. The health context was hypothetical and the prospects in the first experiment fixed the probabilities at 50%-50%. The second experiment improved the first experiment by extending the probabilities to a wider range from 10% to 90% so that we could estimate a more complete probability weighting function. Moreover, the health context was removed in the second experiment because it yielded similar results as the money context in the first experiment and because the health treatment generated several complications due to the special nature of health. Hence, we decided to focus on the monetary context and fully incentivized the second experiment with real money. Overall, the results of the second experiment are consistent with the first experiment, so we only report the second experiment in the main paper and the details of the first experiment can be found in the online appendix.

4.1 Procedure

We conducted the experiment at the Experimental Economics lab at Dongbei University of Finance and Economics, Dalian, China. Students at this university were voluntarily recruited to participate in the experiment through eight different sessions across two days. The experiment was conducted in Chinese. The participant pool included students of different levels (undergraduate, postgraduate, PhD) and of different studies (business, science, etc.). Upon entering the lab, each subject was randomly assigned with an ID number, which was used for identification throughout the experiment. Subjects were introduced to the basic lab rules before they could enter their ID number in the experiment program and start the experiment. The general instructions of the experiment were presented at the very beginning of the experiment program as well as on a hard copy handout on each subject’s desk. Subjects were also presented with one practice choice list task and could only proceed to the actual experimental tasks after successfully answering three test questions based on the practice task.

From the general instructions, subjects were informed that the experiment consisted of two parts (outcome prospects and timing prospects) and each part had its own instructions (all instructions can be found in the online appendix).

The two parts were presented in a random order. Within each part, the gain, loss, and mixed questions were completely randomized. Subjects could take as much time as they wished when completing the choice task and on average, they completed the experiment in 30 min. When the subjects had completed the experiment, they were asked some socio-demographic questions.

4.2 Subjects

N = 183 subjects completed the experiment. The average age of the subjects is 21.6 years old, and 69% of them are female. All students are Chinese. The amount of money the subjects could receive depends on their answer to one randomly selected experimental question.

The probability of each choice in both parts to be selected for payment was equal. If a randomly selected question resulted in a monetary payment in the future, the experimenter set up a standing order through the online banking in front of the subject and signed a guarantee slip which entitled the subject’s right to claim the payment if not received at the agreed time. The average payment was about 125 RMB (= 13 GBP, 17 USD or 15 EUR at the time of the experiment).

4.3 Choice list

Data were administered using a computerized choice list design. Each row of the choice list presented a binary choice between two options. The binary choice was always between a sure option and a risky option. In the choices involving the mixed prospects, the sure option was the status quo—neither a gain nor a loss. Figure 3 presents one example of the choice list of the risky monetary prospects in the gain domain. Subjects were required to click on one radio button on each row. They could change their answers as many times as they wanted before clicking on the submit button to move on to the next question. The only restriction was that subjects could switch only once in the choice list. After switching, all other options were automatically filled to save effort for subjects and to avoid any multiple switches. Such a procedure has also been used in previous preference elicitations, e.g., Bleichrodt et al. (2016) for intertemporal choices and Gerhardt et al. (2017) for outcome risks. We would infer the mid-point of the two rows where switching occurred as the indifference value. If there was no switch made in the choice list, we took the boundary value in the list as the indifferent value. For instance, in Fig. 3, if option B is chosen all the time in the list, we would infer the indifferent value of option B is 6 EUR. In this case, we also mark the decision made in this choice list as a weak violation of stochastic dominance. Details of the violation of stochastic dominance in the experiment are in Sect. 5.4.

Fig. 3

An example of the choice list implemented in the experiment

4.4 Tasks

Each of the tasks is explained below.

4.4.1 Outcome risk

Subjects by default got 150 RMB in the Outcome risk task, and could get more in the gain part, where they had to choose between a sure additional amount and a lottery giving either a higher or a lower gain. For losses they again got 150 RMB by default, and now had to choose between a sure loss and a gamble generating either a higher or a lower loss. The maximum loss amount was 105 RMB, so the subjects never had to pay anything out of their own pockets. Finally, in the mixed part, the default was 150 RMB again and the subject had to choose between an amount of gain or loss for sure and a lottery giving either a gain on top of this default or a loss.

4.4.2 Timing risk

The Timing risk task here stands for waiting for money, where subjects were told to get 100 RMB in 50 days by default. They were presented with the chance to expedite the payment to today in the mixed prospect, but concurrently facing the possibility of further postponement in the future. For gains, there was an option with a fixed amount of speeding up and an option that could speed up the 100 RMB either more or less than this fixed amount, but delivery would always be within 50 days. For losses, there was an option with a fixed amount of postponement and an option that could postpone reception of the 100 RMB by either more or less than this fixed amount, whilst delivery would always be in at least 50 days.

4.5 Analysis

In each gain and loss choice list, the ranges of the sure amount were determined by the outcomes in the prospect ${x}_{P}y$. This was done in such a way that the lower range was always smaller than the smallest outcome in the prospect and the upper range was always larger than the greatest outcome in the prospect. For instance, to elicit the Certainty Equivalent (CE) of the outcome prospect ${100}_{0.1}20$, the sure amount in the list was a series of 15, 20, 25, … 0.100, 105. From Table 2, we can see the stimuli in the Outcome risk task and the Timing risk task.

Table 2 Stimuli

Traditionally, the difference between the Expected Value (EV) of a risky prospect and its CE (the risk premium) is taken as a measure of risk aversion/seeking. However, this measure does not directly apply to the timing prospects, because the outcome waiting period differs from the way monetary outcomes are calculated or processed in decision models. However, we argue we can similarly take the difference of CE and EV as an indication of the risk attitudes for timing. EV indicates linear utility and linear probability weighting in outcome prospects and linear discounting in timing prospects, hence giving a benchmark of neutrality. Concave utility will make CE smaller than EV; CE < EV is then commonly taken as risk aversion for outcome prospects. The discount function often takes a reverse convex shape. In a similar way, such convex discounting will make CE smaller than EV, so we can also take CE < EV as risk aversion for timing prospects.

5 Results

5.1 Aggregate analysis

We computed the difference between the EV and CE to infer the risk attitudes revealed in the data. The following figures are all based on the data where we calculated the EV and CE difference and normalized the EV-CE difference based on the formula:

$$\frac{EV-CE}{p\left(High\right)*High-p\left(Low\right)*Low}.$$

(7)

The aggregate (normalized) EV-CE difference of each choice is shown in the following plot (Fig. 4). The red bars indicate the gain choices, green the loss choices, and blue the mixed choices. The aggregate results show different risk attitudes emerging from different choices within the gain or loss domain. In mixed choices, we observe risk aversion in general.

Fig. 4

Mean EV-CE differences*

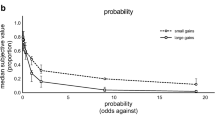
In addition, we present median instead of mean data in Fig. 5, showing that the overall pattern is still the same.

Fig. 5

Median EV-CE differences *

If we look at the distribution of the EV-CE differences within each question, the error bars in Fig. 6 suggest great individual heterogeneity.

Fig. 6

Mean EV-CE difference by gain/loss for each question domain*

5.2 Individual analysis

For each subject, we try to capture their risk attitudes for each type of choice in each domain; that is, (Outcome risk; Timing risk) x (Gain; Loss), constituting four sub-categories. For each domain and each type of task, we categorized subjects as risk neutral, risk averse or risk seeking. For the prospects with the same absolute values but in different sign domains (gain vs. loss), we compare the size of the EV-CE difference and take that as the indication of how risk attitudes differ in the gain and loss domain.

First, we simply classify individuals’ risk attitude as risk averse if the majority of EV-CE differences is positive out of ten choices, risk seeking if the majority is negative, risk neutral if the majority is zero and otherwise as mixed. From Table 3 and Table 4, we can see that a great proportion of subjects exhibit variability in their answers and are categorized as the mixed type. Furthermore, there are more subjects exhibiting mixed risk attitudes in losses than in gains. Instead, risk aversion is the dominant classification in gains for both outcome and timing risk. Finally, the variability of risk attitudes is larger for timing risk than outcome risk.

Table 3 Individual risk attitudes in gains versus losses for each treatment

Table 4 Individual risk attitudes comparison between Outcome risk and Timing risk

Since there is much heterogeneity within the risk attitudes for the gain and loss domain, it helps to look at the risk attitude distribution for each choice, because it is likely that the risk attitudes are influenced by the probability levels in each different choice.

As Fig. 7 shows, risk seeking becomes weaker as the probability level increases in gain choices, with the colour changes from red to blue showing a downward trend. For losses, the trend is the opposite, with more risk seeking when the probability level goes up, forming an upward trend in the figure. This confirms the fourfold pattern for gain and loss. Moreover, we observe strong risk aversion, similar as in the first experiment (details in online appendix). Interestingly, we also observe some risk neutral behavior for choices with moderate probabilities in both gain and loss choices.

Fig. 7

Risk attitudes for each choice

5.3 Parametric analysis

We ran aggregate estimations to get the best fitting parameters. We summarize the estimation results for each treatment in Table 5. The analysis was performed on the dataset where the occurrences (not the subjects) of both weak and strict violations of stochastic dominance are removed.⁴ To better present the estimation results, the estimated functional forms are also shown graphically in Fig. 8.

Table 5 Aggregate parameter estimates

Fig. 8

Graphs of utility and discount functions and probability weighting, with and without loss aversion

Table 5 shows that the power coefficients for outcome prospects are slightly larger than 1, suggesting convexity for gains and concavity for losses. The coefficients of the exponential discounting model for timing risks suggest a moderate amount of discounting (i.e., less than 1% per day), and more discounting for losses than for gains. The estimates of Prelec’s probability weighting functions are similar for outcome and timing risks and comparable to those of previous studies (Abdellaoui et al., 2010; Bleichrodt & Pinto, 2000; van de Kuilen & Wakker, 2011). They indicate elevation and insensitivity to changes in probabilities. Moreover, the probability weighting function is more elevated for losses, which means subjects also assign a higher weight to the same probability in losses than in gains, indicating more optimism in losses than in gains.⁵

Finally, the lateness aversion coefficient is smaller than 1, indicating earliness seeking. This contrasts with the results for the outcome prospects, where the estimated loss aversion index is around 2, in accordance with previous findings (e.g., Tversky & Kahneman, 1992). However, because we took the exponent of the discount factor to be the product of delay and the lateness aversion coefficient, it is hard to disentangle lateness aversion/earliness seeking from the discount rate of delays. As such, we face identification issues in the estimation process, and we cannot draw any strong conclusions from the estimate of the lateness aversion index.

We see that utility curvature is close to linearity, similar to what is reported in the literature when the curvature of the utility is corrected for probability weighting. If we force linear probability in the estimation, the estimated utility parameter for gains becomes more concave. Table 6 presents the estimation results when we assume linear probability. Utility curvature for gains has become concave, but for losses it has become less concave. This suggests that if we do not allow for probability weighting, utility curvature is reflecting additional risk attitudes. With probability weighting, utility curvature cleanly shows how people evaluate money, i.e., much closer to linearity for small amounts of money. Additionally, the loss aversion parameter becomes smaller than 1. This suggests that if we do not use probability weighting to correct for strong optimism for losses, the loss aversion will become less prominent to compensate the optimism for loss.

Table 6 Parameter estimates with linear probability for outcome prospects

5.4 Violation of stochastic dominance

In the experiment, the 183 subjects each completed 48 choice lists, totalling 8784 choice lists. For each choice list, we checked whether there was a violation of stochastic dominance. In the choice list of gain and loss prospects ${x}_{P}y$ (x > y), the value of sure amounts for eliciting the CE ranges from y – one unit of increment to x + one unit of increment. For instance, if the increment between the rows in the choice list is 5 and the prospect is ${50}_{0.1}(-5)$, the range of the sure amounts will be [–10, 55]. For anyone who did not switch at all in the list, there is for sure a strict violation of stochastic dominance. However, there may be individuals who choose x over ${x}_{P}y$, or ${x}_{P}y$ over y, in those cases, we determine those people weakly violating stochastic dominance.

In the choice list of mixed prospects, at the boundary of the list, there are prospects that become pure gains or pure losses. In this case, there is a possibility for subjects to choose the status quo over pure gains, or to choose pure losses over the status quo, which we classify as strictly violating stochastic dominance.

Among the total of 8784 choice lists, 3.6% of the choice lists suggests weak stochastic dominance and only 1.3% of the choices strictly violated stochastic dominance. If we allow violation of weak dominance, 136 out of 183 did not violate stochastic dominance at all in the 48 choices, and only 6 subjects violated it in more than 5 choices. We also conducted the above analysis without subjects violating strict and weak stochastic dominance. The overall pattern remains unchanged from the above results and, hence, we do not report them.

6 Discussion

This paper has reported the first study of reference-dependent timing prospects. We have extended the study of timing prospects to a larger set of probabilities than only p = 0.5 and distinguished between gains and losses in timing. The experiment generated several noteworthy results. First, we observed the fourfold pattern of risk attitudes (Harbaugh et al., 2010; Tversky & Kahneman, 1992): risk aversion was strongly influenced by the probabilities used in the prospects, with a majority of risk averse choices for larger (smaller) probabilities in gains (losses) and a majority of risk seeking choices for smaller (larger) probabilities in gains (losses). Related to this, there was substantial probability weighting. For timing prospects, this result supports the conclusion of Onay and Öncüler (2007) that risk averse behavior for timing prospects can be attributed to probability weighting, and extends the typical finding of inverse-S shaped probability functions to timing prospects. This suggests for future studies examining risk attitudes, it is worth including a full range of probability to gain a complete picture.

Also, subjects were loss averse in outcome prospects, but earliness seeking (being the timing equivalent of gain seeking) in timing prospects, in spite of similar amounts of risk aversion for both gains, losses and mixed prospects in both tasks. This is also manifested in subjects’ feedback to our experiment, such as:

• “50 天接近两个月, 跟假期时间差不多。按50天作为参照” (50 days is about the same as the summer holiday. I take it as if by default waiting for a holiday to receive the payment.)

• “提前时间多比较好, 如果没提前多少就都一把; 把50天当作参考” (50 days as reference. It is better if I can speed up. If there is not much chance of speeding-up, I am willing to take risks.)

• “50 天本来已是一段较长的时间, 经过50天后推迟一点时间对我个人而言影响已经较小, 但相反如果能超乎预期地提前支付我会很高兴” (50 days is quite a long time, further delay makes less impact to me. On the other hand, I will be extra happy if I can get it earlier.)

The difference in λ may instead be due to a loss in timing still giving a positive monetary reward and, hence, a delayed reward still adding a positive amount to the discounted utility of a prospect. Another reason for earliness seeking could be that the reference points used in the timing prospects were perceived negatively, because subjects had to wait for their reward in most cases, and it has been shown that painful reference points may evoke gain seeking behavior (Mellers et al., 2021). Theoretically, the earliness seeking in our study may also be caused by increasing impatience (Bleichrodt et al., 2016; Lipman & Attema, 2020), instead of the constant impatience as assumed in our constant discounting model. However, the dual exponential model that we fitted to the data—which allows for decreasing and increasing impatience—did not converge and performed worse than the exponential discounting. This suggests that this possibility is not likely, although more research explicitly isolating the effects of decreasing and increasing impatience from reference-dependence is encouraged and is called for to draw stronger conclusions. Finally, because of the identification issues outlined above, the lateness aversion index was correlated with the other parameter estimates; hence, we could not uniquely identify this index, such that no strong claims about the presence of earliness seeking can be made. Future research could test the robustness of our finding of earliness seeking by eliciting the lateness aversion index separately from the other parameters, although as explained earlier this may necessitate to take this index outside of the time dimension.

Our results on timing risks lend partial support to the gain-loss asymmetry. We observed that subjects were overall risk averse regarding mixed timing prospects, suggesting that they tended to avoid timing losses. However, our finding of earliness seeking suggests that this cannot be attributed to losses in timing receiving more weight than timing gains, although one should keep in mind the caveat discussed in the previous paragraph. Instead, the original explanation of the gain-loss asymmetry (which is typically found in situations where subjects are asked for their willingness to pay for speedups or willingness to accept for delays) offered by Loewenstein and Prelec (1992), cannot be refuted by our findings. This explanation states that not receiving an outcome now but later is regarded as a loss of this outcome now and a gain of the outcome in the future. Vice versa, receiving an outcome earlier rather than later is seen as a gain now and a loss later. Because of loss aversion in the outcome domain, this results in the delay-speedup asymmetry.

As we have shown in this study, making the discount function reference-dependent generates substantial econometric complications. First, capturing lateness aversion in time perception requires to include the lateness aversion parameter in the exponent of the discount factor. As a result, lateness aversion does not cancel out for losses, and one has to estimate this parameter jointly with the other ones. Second, apart from causing a more laborious estimation process, this also leads to collinearity issues, making it hard to attribute risk attitudes to the different components of reference-dependent discounting (i.e., amount of discounting, probability weighting and lateness aversion). Third, in order to facilitate a valid comparison with the outcome prospects, we had to use the same laborious estimation process for the latter, which would not have been necessary in a stand-alone analysis. One could avoid these problems by including lateness aversion as a factor to be multiplied with the loss in discounted utility, but then one would simply be using the original prospect theory specification in gambles with varying delays and fixed rewards. Our contribution instead provides a novelty by modeling loss aversion in time perception (i.e., lateness aversion), which is fundamentally different from loss aversion in discounted utility.

Several previous studies have investigated risk preferences for time dedicated to particular tasks in a prospect theory framework, separating gains and losses. However, because we considered a situation where one could still perform other activities while waiting for the reward, the results are hard to compare. Abdellaoui and Kemel (2014) obtained less concave utility and smaller loss aversion for time dedicated to a specific task than for money. Furthermore, they found more probabilistic optimism [pessimism] for time gains [losses] than money gains [losses]. Because we elicited a discount function for the timing prospects, we could not compare utility for time and outcomes. Our lateness/loss aversion estimates were lower for timing than for outcome prospects. With regard to probability weighting, we found similar results as Abdellaoui and Kemel (2014) with slightly more pessimism for timing gains than outcome gains, and less sensitivity for timing losses than outcome losses. Festjens et al. (2015) reported more concave utility for small money losses than small time losses, and the opposite for large money and time losses. Again, we could not make such a comparison.

A limitation of this study is the use of a student sample, which is younger and higher educated than a sample representative of the general public. Consequently, replications in more heterogenous samples are of interest.

In the timing prospects, a drawback of this study is that we only considered acceleration and postponement of positive outcomes (i.e., receiving money). An interesting venue for future research would be to replicate this study with negative outcomes, such as paying money, incurring a disease, or a deteriorating health state. Another limitation of the timing risks task is the use of exogenous reference points occurring in the future. Not all subjects may have adopted this time point as their reference point, but rather some other time, like the present. To test this, we added a debriefing question at the end of the experiment to verify if they took 50 days as their reference point. A majority indicated that they indeed took this as their reference point, lending some support to our assumption. Still, future research is encouraged to test this assumption more thoroughly, or to use endogenous reference points.

Furthermore, our design did not enable a perfect comparison between the parameters obtained with the outcome prospects and those obtained with the timing prospects. Apart from their different nature, a distorting factor was that the reference point was occurring in the future for the timing prospects, but not for the outcome prospects. Even though this comparison was not the primary aim of our study, it would be interesting to compare the parameters of outcome and timing prospects in the case of an identical timing of the reference point in future research, because prior literature suggests the individuals exhibit different attitudes for prospects resolved and paid in the future (Abdellaoui et al., 2011, 2022).

Finally, a problem of most methods used to assess prospect theory preferences, including our method, is that there tends to be collinearity between utility and probability weighting (Zeisberger et al., 2012). Future work applying a nonparametric elicitation method (e.g., Abdellaoui et al., 2016; Wakker & Deneffe, 1996) can address these limitations. In particular, further research separating the effects of probability weighting and reference-dependence from discounting preferences is of interest.

Our study raises many new questions. For example, to what extent can loss aversion in time perception (i.e., lateness aversion) replace the usual prospect theory loss aversion, where the loss aversion coefficient is multiplied with the loss in (discounted) utility? And to what extent can we combine this lateness aversion with a separate prospect theory loss aversion coefficient? Will these be different when changing the fixed outcome amounts Z or when including more than one of such nonzero outcomes? Our paper has proposed a new concept and performed a first pragmatic empirical test, but these and many other questions still need to be addressed in future research.

7 Conclusion

This study has been the first to incorporate reference-dependence in the discount function, and applied it in an experiment. We compared prospect theory’s parameters for timing lotteries to those obtained by regular outcome lotteries. The results indicated that the fourfold pattern of risk attitudes, as well as more risk aversion in mixed prospects than in gains are robust for both tasks, in accordance with the predictions from prospect theory. However, we also showed that extending discounting to allow for reference-dependence has several conceptual and econometric caveats, and that the parameter estimates of the reference-dependent discounting model are less stable than for reference-dependent utility. Altogether, these findings suggest that reference-dependence is influential for time discounting, while at the same time raising many challenges.

Appendix A: Preference foundation of reference-dependent discounting

In this introductory and experimental paper, we will abstain from elaborated axiomatic work. We nevertheless briefly sketch how a preference foundation can be obtained. We first use preference conditions to obtain the general discounting representation $D(T)u(x)$, similar to Fishburn and Rubinstein (1982). We next consider axioms that reduce the general $D$ to a desired special form $f$, such as in Koopmans (1960, 1972) for constant discounting, Olea and Strzalecki (2014) for quasi-hyperbolic discounting, Loewenstein and Prelec (1992) for generalized hyperbolic discounting, and Bleichrodt et al. (2009) for unit invariance. In Section 3 we assume constant discounting, which is axiomatized by stationarity. However, we only impose those conditions on the gain domain $T\le R$ and, separately, on the loss domain $T\ge R$. The representations usually leave an exponent unspecified. We thus get a discount function ${f}^{\alpha }$ on the first domain and ${f}^{\beta }$ on the second domain. We can fix the exponent by taking $\alpha =1$ and replacing $\beta$ by $\lambda =\beta /\alpha$. We then define $d\left(t\right)=f(T-R)$, to obtain the desired reference-dependent discount function. We next bring in the axioms of the desired risk model, such as expected utility or prospect theory, ensuring that ordinal representations of time preferences end up at the right cardinal level for the risk theory considered.

The novelty in the above axiomatization is the separate treatment of the gain and loss domain, where gains here are not specified by outcomes but by time points.