Predicting expected idiosyncratic volatility: Empirical evidence from ARFIMA, HAR, and EGARCH models

Abstract

We investigate the performances of the ARFIMA, HAR, and EGARCH models in capturing the time-varying property of idiosyncratic volatility (IVOL). We find that the expected IVOL predictions by HAR are superior. In diverse portfolio scenarios, a greater degree of judgment is required to assess the pricing ability of expected IVOLs. For the lowest value-weighted quintiles and the expected IVOL estimated by the HAR model, the IVOL-return relationship is negative. Conversely, the IVOL-return relationship is positive for the expected IVOL estimated by the EGARCH model. Further evidence suggests a complicated and mixed relationship between the expected IVOL estimated by the ARFIMA model and stock returns.

1 Introduction

Contradictory results stem from the time-varying nature of idiosyncratic volatility (IVOL), which inherently reflects firm-specific activities such as periodical disclosures and seasonal variations in operating activities. Ang et al. (2006) [AHXZ (2006) hereafter] propose one path of a negative relationship, known as the IVOL puzzle, using the IVOL from the current month as a proxy for the next month. Another route, following Fu (2009), supports a positive IVOL-return relationship by adopting the expected IVOL from Exponential Generalized Autoregressive Conditional Heteroskedasticity (EGARCH) models. Consequently, predicting the future value for a non-stationary random walk series, as described by AHXZ (2006), is deemed inappropriate, given the persistent impact of a random shock from a faraway time to the present (Fu 2009).

Recognizing the critical role of the time-series property of IVOL in examining its relationship with stock and market returns, as well as in selecting the approximate value for expected IVOL, we are motivated to compare the performances of other, unexplored dynamic models in catching the time-variation of IVOL and examine the relationship between the expected IVOL and stock returns. Beyond the EGARCH model, our paper also resorts to the Autoregressive Fractionally Integrated Moving Average (ARFIMA) model and calibrates the Heterogenous Autoregressive (HAR) model to capture the time-series property in IVOL. In particular, the ARFIMA model, enhancing the Autoregressive Moving Average (ARMA) model and ARIMA model, incorporates the conversion between factional integration and fractional difference, demonstrating clear performance in capturing long-run dependence in realized volatility prediction (Koop et al. 1997; Andersen et al. 2003; Bhardwaj and Swanson 2006). The HAR model reproduces the decay of autocorrelations over various horizons (Corsi et al. 2008; Corsi 2009). The HAR model treats the time series as immediately observable and is also straightforward to estimate (Bollerslev et al. 2016). Despite their frequent use in the realized volatility literature,¹ the ARFIMA and HAR models are surprisingly absent from IVOL literature.²

Meanwhile, we revisit the IVOL-return relationship on both the stock and portfolio levels using expected IVOLs from ARFIMA, HAR, and EGARCH models. The IVOL puzzle, stating that lower IVOL should be compensated by higher returns, has been contested under various model specifications. Notably, the one-month-lagged IVOL in AHXZ (2006) and Ang et al. (2009) [AHXZ (2009) hereafter] is questioned due to its unreliable nature and its autocorrelation of 0.33, contradicting their underlying random walk assumption. For instance, the IVOL predicted by the EGARCH model shows a positive relationship with future stock returns (Fu 2009). Chua et al. (2010) document a positive relationship conditioning on the unexpected aspect of IVOL, decomposing IVOL from AR(2) processes into expected and unexpected components. However, the positive IVOL-return relationship modeled by the ARIMA model is reversed due to short-term return reversals (Huang et al. 2010) or January effects (Peterson and Smedema 2011).

Previous studies have taken into account the time-series nature of financial variables, for instance, the time-varying expected business conditions (Campbell and Diebold 2009). However, there is no consensus in the relevant literature on the most appropriate model for capturing the time-series characteristics of IVOL. For instance, when estimating the conditional IVOL, Spiegel and Wang (2005), Fu (2009), and Guo et al. (2014) adopt an EGARCH model in light of its relaxation of the symmetry requirement in the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model examined by Xu and Malkiel (2003). Fu’s empirical findings demonstrate a positive relationship between expected stock returns and the EGARCH-estimated IVOL. Others, such as Diavatopoulos et al. (2008), Chua et al. (2010), and Bekaert et al. (2012), utilize the Autoregressive (AR) model, while some, including Huang et al. (2010) and Peterson and Smedema (2011), go further to test the Autoregressive Integrated Moving Average (ARIMA) model. Khovansky and Zhylyevskyy (2013) first apply the Gaussian Mixed Models (GMM).

Our sample includes stocks with share codes 10 and 11 traded on the NYSE, AMEX, and NASDAQ from CRSP during the period from July 1965 to December 2020. We calculate IVOL as the standard deviation of residuals with respect to the Fama–French three-factor model scaled by the number of trading days. Initially, we assess the long memory property of IVOL through unit root tests and graphical analyses (line graph, density graph, and autocorrelogram). Significant Augmented Dickey-Fuller (ADF) results are documented for both IVOL series and sorted portfolios, indicating that recent IVOLs are still impacted by past IVOLs. Subsequently, we select the best-fitting models. For the EGARCH model, we test nine permutations among its autoregressive parameter (1 ≤ p ≤ 3) and the moving average parameter (1 ≤ q ≤ 3). For the ARFIMA model, we test 16 permutations among its autoregressive parameter (0 ≤ p ≤ 3), and the moving average parameter (0 ≤ q ≤ 3), and estimate the long memory parameter d. For the HAR model, we identify the most significant autoregressive lags based on ACF (Autoregressive Function), PACF (Partial Autoregressive Function), and AIC (Akaike Information Criterion). All models are run recursively using IVOLs up to month t to predict IVOL in month t + 1. We use notations such as Exp_IVOL^ARFIMA, Exp_IVOL^HAR, and Exp_IVOL^EGARCH to refer to IVOLs predicted by the ARFIMA, HAR and EGARCH models, respectively. The original IVOL is denoted as Actual_IVOL.

To assess each model’s predictive ability, we compare all expected IVOLs to Actual_IVOL. Later, to examine the pricing ability in the IVOL-return relationship, we regress stock returns on each expected IVOL individually and collectively with controls. On the stock level, we begin by recursively estimating expected IVOLs using value-weighted and equal-weighted series. Autocorrelograms and ADF tests suggest long-term reliance in both series, where previous IVOLs continue to impact current IVOL. We find that the HAR model more accurately reproduces the time-variation of Actual_IVOL with 1-month, 3-month, and 9-month lags for value-weighted series and with 1-month, 2-month, 3-month, and 12-month lags for equal-weighted series. Notably, the IVOL puzzle is observed only for Exp_IVOL^HAR in value-weighted series, while the IVOL-return relationship for Exp_IVOL^ARFIMA remains positive, unaffected by the weighting scheme.

On the portfolio level, we employ the portfolio-sorting approach, frequently used in the relevant literature for examining relationships between variables and generally performing well for nonlinear relationships.³ In the main section, we sort the data using three different methods: IVOL-sorting, size-sorting, and book-to-market ratio-sorting, respectively. Generally, we observe the existence of the IVOL puzzle in the lowest value-weighted portfolios, in contrast to the positive relationship in the lowest equal-weighted portfolios, across all sorting approaches. Furthermore, the IVOL puzzle exists when the HAR model outperforms. Positive IVOL-return relationships are found when the EGARCH model surpasses the other two models, but only in the two lowest quintiles. However, the precise direction of the IVOL-return relationship is inconclusive when the ARFIMA model outcompetes its rivals. Only the lowest two value-weighted quintiles show a concentration of the negative relationship; the other quintiles have a positive relationship. In the robustness check, we discover a similar pattern for quintile portfolios sorted by BETA as well as for various exclusion schemes of the IVOL building under 10-day and 11-day. We discover that the IVOL explanation for the BETA anomaly put forth by Liu et al. (2018) depends on the model applied for the IVOL prediction. We further include analysis for portfolios sorted by the sentimentalized IVOL. The previously described pattern becomes confused when the joint factor is included, and a positive Exp_IVOL^HAR-return relationship is first noticed.

Overall, our study contributes to the comprehensive investigation of the time-varying property of IVOL and addresses the IVOL puzzle under various model specifications as well as stock compositions within the portfolio. We expand the toolkit with the ARFIMA and HAR models to the discussion on the IVOL puzzle.⁴ Our empirical results unfold attention on lower portfolios across various sorted contexts., underscoring the importance of carefully assessing the risk and return dynamics when making investment decisions. However, it is inconclusive which model outperforms in predicting IVOL and capturing its time-varying feature. By merely using the EGARCH model for the prediction, we are unable to refute the existence of the IVOL puzzle. The inclusion of the ARFIMA and HAR models emphasizes the need for careful consideration of the IVOL-return relationship.

The remainder of this paper is organized as follows. Section 2 reviews related literature on the IVOL puzzle and the time-series properties of IVOL. Section 3 describes data and introduces the calculation of IVOL and the mechanisms of EGARCH, ARFIMA, and HAR models. The empirical findings for the IVOL series and sorted portfolios are presented in Section 4. We discuss robustness in Section 5 and include a further analysis in Section 6. Section 7 concludes.

2 Related literature

2.1 The IVOL puzzle

AHXZ (2006) point out a considerable difference in the monthly average returns between the quintiles with the highest idiosyncratic volatility and the lowest idiosyncratic volatility. As indicated by this anomalous negative correlation, the difference of 1.06% is substantial at the portfolio level. At the firm level, the negative coefficient stands. The subsequent work by AHXZ (2009), investigates further by extending the IVOL puzzle findings made by AHXZ (2006) in the U.S. market to international stock markets such as those in G7 countries, even while contending with the effects of size, value, momentum, volume, liquidity, market frictions, and information asymmetry (see Jiang et al. 2009; Babenko et al. 2016; Chen and Strebulaev 2019, for more negative relationship). However, Fu (2009) illustrates a positive relationship between future stock returns and their IVOL measure using an EGARCH model and emphasizes the IVOL measure in their ability to capture the time-variant characteristic. Bergbrant and Kassa (2021) suggest the use of various out-of-sample EGARCH models dynamically and find the IVOL-return relationship to be positive after ruling out the noise brought by using just one out-of-sample EGARCH model. From Brockman et al. (2022), the IVOL premium is present in 57 different countries worldwide (see Malkiel and Xu 2002; Spiegel and Wang 2005; Boehme et al. 2009; Chua et al. 2010; Brockman et al. 2022, for more positive relationship). The positive relationship appears to be more inclined to the under-diversification argument offered by classical theories (Levy 1978; Merton 1987), while the negative relationship is explained within the context of mispricing (Shleifer and Vishny 1997; Brav et al. 2010).

Mixed relationships between IVOL and stock returns have been documented in other studies. For instance, Guo and Savickas (2006) find that when combined with the aggregate market realized volatility, the negligible forecasting power from value-weighted IVOL becomes significantly negative. Duan et al. (2010) discover a significant monthly return difference between the stocks with the highest and lowest IVOL quintiles while the negative IVOL-return relationship clusters among stocks with a high short interest. Huang et al. (2010) ascribe the negative relationship to return reversals and demonstrate that the magnitude of this bias depends on the IVOL estimation approach used. As shown in Rachwalski and Wen (2016), stocks with high idiosyncratic volatility earn lower returns initially for a few temporary months (during the previous six months), but subsequently see continuously higher returns. The lower return over a short period reflects the delay in incorporating risk news. The IVOL puzzle is more substantial when receiving a lower attention from sophisticated investors and is concentrated in the first half of the month following portfolio formation (see, for instance, Bali and Cakici 2008; Khovansky and Zhylyevskyy 2013; Cao and Han 2016 for more details).

2.2 The time-series properties of IVOL

The current body of research employs various techniques in an effort to dynamically capture the time variation exhibited in the IVOL series. According to earlier investigations, IVOL decays slowly and has a strong first-order autocorrelation (Amihud and Hurvich 2004; Lewellen 2004; Campbell and Yogo 2006). As a result, the approach of regressing the lagged IVOL on stock returns to gauge their relationship may prove unproductive (Jiang and Lee 2006). The recent research most frequently uses the EGARCH model, which is selected as a natural estimator for IVOL (Spiegel and Wang 2005; Fu 2009; Huang et al. 2010; Peterson and Smedema 2011; Fink et al. 2012; Guo et al. 2014; Cao and Han 2016; Bergbrant and Kassa 2021; Brockman et al. 2022). Fu (2009) explicitly elaborates on the adoption of the EGARCH model and finds a positive IVOL-return relationship with the constraint that stocks have a minimum of 15 trading days in a month in the pooled sample. Because the autocorrelation of 0.33 during Fu (2009)’s sample period deviates from the underlying implication of random walk in AHXZ (2006, 2009), which is reaffirmed by the Dickey-Fuller test result, Fu (2009) contends that the one-month lagged IVOL in AHXZ (2006,2009) is not necessarily a proper proxy for the expected IVOL. The advantage of the EGARCH model in relaxing the non-negative parameter restrictions makes it able to reflect the asymmetry of volatilities. Fu (2009) evaluates nine permutations of the EGARCH model with the auto-regressive parameter p to be between 1 to 3 and the moving average parameter q to also be between 1 to 3 and then chooses the best-fitting model based on the lowest AIC with an expanding window of the previous 30 months.

Due to its reflection of the time-series features and its reduction of the majority of serial autocorrelation, Diavatopoulos et al. (2008) and Chua et al. (2010) decide to employ the AR(2) model based on AIC. Bekaert et al. (2012) describe IVOL at the aggregate level by AR(1) and AR(3) processes. In accordance with the time-series characteristics of IVOL, Huang et al. (2010) and Peterson and Smedema (2011) implement the ARIMA model over a 24-month rolling window. The direction of the IVOL-return relationship is dependent on the estimation windows, following Khovansky and Zhylyevskyy (2013), who initially implement the GMM procedure to estimate IVOL. The GMM approach frees the previous two-pass method in that it immediately makes an estimation without being affected by the duration of available stock returns and does not require estimating IVOL as the first step based on the Fama–French model. Nevertheless, this GMM approach is parametrically constrained and has distributional restrictions. Aslanidis et al. (2019) extend Boyer et al. (2010)’s methodology for calculating expected idiosyncratic skewness, to obtain the expected IVOL throughout regressions on the one-period lagged IVOL with a 240-month rolling window.

Overall, the existence of the IVOL puzzle is currently being researched and the best-fitting model for IVOL estimation is inclusive. By utilizing the novel ARFIMA model and HAR model to capture the time-series evolution of IVOL and to explore the IVOL puzzle with a comparison to the EGARCH model, our paper adds to the field.

3 Data and methodology

3.1 Data and IVOL calculation

The sample period is from July 1965 to December 2020, with a total of 666 months. Daily stock returns including all the ordinary common equities (share code 10 or 11) on the NYSE, AMEX, and NASDAQ (exchange code 1, 2, or 3) are collected from CRSP. There are overall 28,523 stocks identified by the unique PERMNO during the sample period without any exclusion. We include common time-series control variables in the regressions (AHXZ, 2006; Peterson and Smedema 2011). Monthly excess market return (MKT), HML, SMB, MOM, LMW, and risk-free rate are from Professor Kenneth French’s website.⁵ The risk-free rate is the monthly T-bill return compounded from the simple daily rate from Ibbotson and Associates Inc. Excess market return MKT is calculated by subtracting the risk-free rate. HML stands for high book-to-market ratio minus low book-to-market ratio while SMB stands for small market capitalization minus big market capitalization. MOM stands for the momentum factor, which is the difference between the average return on the two high prior (2–12 month) return portfolios and the two low prior (2–12 month) return portfolios. ST_Rev is the short-term reversal factor, which is the difference between the average return on the two high prior (1 month) return portfolios and the two low prior (1 month) return portfolios. We also include the liquidity factor (PS) of Pástor and Stambaugh (2003), which is available from Professor Stambaugh’s website.⁶

To be consistent with previous studies and for a better comparison, we adopt the prevalent measurement of computing the standard deviation of the residuals from the Fama and French (1993) three-factor model⁷ as follows:

$${XRET}_{i,n}={\alpha }_{i}+{\beta }_{i}{RET}_{M,n}+{h}_{i}{HML}_{n}+{s}_{i}{SMB}_{n}+{\epsilon }_{i,n},$$

(1)

where XRET_i,n is the excess return for stock i in day n and RET_M,n, HML_n, and SMB_n are the three Fama–French factors in day n. The standard deviation of the residual series on stock i and day n will be computed each month for stock i following the estimate in order to indicate the stock i’s monthly IVOL. In particular, IVOL is scaled by the square root of the number of trading days inside the corresponding month and is estimated monthly using daily data. The exclusion applies to stocks with less than 5 trading days in a month (different exclusions of days will be carried out in the robust tests).

3.2 Unit root test and long memory

To determine whether the time series of IVOL has a long memory, the Augmented Dickey-Fuller test (ADF test) and autocorrelogram are used. The null hypothesis of the ADF test is that there exists a unit root in the time-series sample. The null hypothesis is rejected when the P-value is below the predetermined significance level, proving that the time series sample does not have a unit root and is therefore stationary. In this case, we can state that this time series sample has a long memory if the autocorrelogram demonstrates that lagged terms continue to lay influence on present terms. A forecast of the future IVOL is possible, in a sense, for instance, if the time series of IVOL has a long memory, and historical IVOLs are still influencing future IVOLs. As stated by Fu (2009), by capturing the time-varying characteristic of IVOL, we can predict expected IVOL using the EGARCH model. We can then examine the relationship between the predicted expected IVOL and the stock return. Similarly, we may also predict the expected IVOL using the ARFIMA and HAR models, both of which are established on the principle of long memory.

3.3 The EGARCH model

The EGARCH model, which Nelson (1991) extended based on Engel (1982)’s ARCH model and Bollerslev (1986)’s GARCH model, accommodates the asymmetry in volatility, known as the leverage effect, where the return volatility increases more after stock price declines due to the increase of leverage ratio, and relaxes the parameter restriction of non-negative variance in the earlier two models. Assuming that the IVOL estimation process’s residuals from the Fama–French three-factor model (Eq. (1)) follow a normal distribution and are serially independent,

$${\epsilon }_{i,n}\sim N\left(0,{\sigma }_{i,n}^{2}\right),$$

(2)

and the conditional variance ${\sigma }_{i,n}^{2}$ follows the EGARCH (p,q) process,

$${\text{ln}}{\sigma }_{i,n}^{2}={\alpha }_{i}+\sum_{l=1}^{p}{b}_{i,l}ln{\sigma }_{i,n-1}^{2}+\sum_{k=1}^{q}{\gamma }_{i,k}\left\{\theta \left(\frac{{\varepsilon }_{i,n-k}}{{\sigma }_{i,n-k}}\right)+\gamma \left[\left|\frac{{\varepsilon }_{i,n-k}}{{\sigma }_{i,n-k}}\right|-\left(\frac{2}{{\pi }^\frac{1}{2}}\right)\right]\right\},$$

(3)

where the conditional variance ${\sigma }_{i,n}^{2}$ has the past p periods and return shocks have the past q periods.

The EGARCH model has already been applied in the IVOL prediction (for further information on how to use EGARCH models, see Spiegel and Wang 2005; Fu 2009). It has been proven that the expected IVOL, as calculated by the EGARCH model, is robustly and positively correlated with stock returns.

3.4 The ARFIMA model

The fractal market hypothesis, which takes into account the nonlinear causal relationship between irrational investor expectations and the market’s response to information, presenting the market structure and characteristics under normal circumstances, serves as the rationale of the ARFIMA model. The long memory is represented by parameter d in the ARFIMA model, and the short-term first-order property of time series is represented by parameters p and q. Following Granger and Joyeux (1980), the ARFIMA model can be expressed as in the following Eq. (4),

$$\varnothing \left(L\right){\left(1-L\right)}^{d}{X}_{t}=\theta \left(L\right){\epsilon }_{t},$$

(4)

where ϕ(L) and θ(L) are lag polynomials of finite orders. ϵ_t, which is only defined for the integer value of d, is a stationary noise series. L is the lag operator and is generalized to fractional differences using binomial expansion. The long memory parameter d is a real number in the range [-0.5,0.5] within which the time series will be stable, and more weight is given to older data. The ARFIMA model is a development of the ARIMA model to non-integer values of d. As the ARFIMA(p,d,q) model degrades into the ARMA(p,q) model, the time series will specifically have long memory in the region [0,0.5], medium memory in the region [-0.5,0] and short memory when d = 0.

It is widely acknowledged that the ARFIMA model can demonstrate the first-order long-term and short-term correlation of time series and can depict the fractional feature via parameter d, making it superior to other models that only take into consideration short or long memories as well as the autocorrelogram, which relies on intuition and subjective judgment (Granger and Joyeux 1980).

3.5 The HAR model

The fat-tailed, leptokurtic, and scaling characteristics of time series cannot be replicated by the standard GARCH model and other stochastic models. Corsi (2009) also disputes factional integrated models such as the ARFIMA model for their complexity and information loss. Then the HAR model is raised with the addictive autoregressive cascade with the goal of easily and parsimoniously capturing and forecasting the long-memory feature of time series. Based on Müller et al. (1993)’s Heterogeneous Market Hypothesis, the HAR model incorporates information from diverse time scales of different market participants as shown in Eq. (5),

$${V}_{t}=\alpha +{\beta }_{1}{V}_{t-1}+{\beta }_{2}{V}_{t-5}+{\beta }_{3}{V}_{t-22}+{\varepsilon }_{t},$$

(5)

where the time series of volatility in time t is estimated by the daily (V_t-1), weekly (V_t-5), and monthly (V_t-22) volatility.

In terms of the IVOL study, Chua et al. (2010) applied AR models to the IVOL time series and discovered that the AR(2) model fits the data best under the criterion of AIC. Their sample period is from July 1963 to December 2003. In this study, we calibrate Corsi’s HAR model and choose the autoregressive lags for the value-weighted and equal-weighted IVOL series, as well as the sorted portfolios based on AIC. We examine heterogeneous time scales and choose the significant lags rather than being constrained by the precise AR lags. Therefore, our calibrated HAR model does not require lags from short-, near- and long-term strictly but is flexible for the lags included to consider the time-variation in IVOL and at the same time absorb varied impact from different time scales.

4 Empirical results

This section first describes the basic statistical features of the time-series of value-weighted and equal-weighted Actual_IVOL for the entire sample and portfolios through the line graph, density distribution graph, autocorrelogram, and unit root test. The series will be evaluated to see if it possesses the long memory characteristic. Later, it will address how well the ARFIMA, HAR, and EGARCH models can capture time-varying traits, such as the long memory feature. Finally, we examine the IVOL-return relationship for the expected IVOLs at both stock and portfolio levels.

4.1 Time-variation in actual IVOL

4.1.1 Actual IVOL series

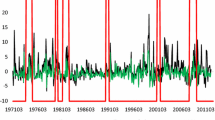
Figure 1 displays line graphs, density distribution graphs, and autocorrelograms (from top to bottom) for the monthly value-weighted Actual_IVOL (left) and equal-weighted Actual_IVOL (right), respectively. The statistical findings with the ADF test for unit root are listed in Panel A of Table 1. Both the value-weighted and equal-weighted Actual_IVOL are leptokurtic, right-skewed and have fat tails. The equal-weighted Actual_IVOL series has a higher standard deviation of 0.0374, making it more volatile. The value-weighted Actual_IVOL, however, is more right-skewed and has a higher kurtosis. Based on the ADF test, the null hypothesis that a unit root exists in the sample series is rejected at a 1% significance level by both value-weighted and equal-weighted Actual_IVOLs. The monthly time-series of value-weighted and equal-weighted Actual_IVOLs are stationary in some degree across the sample period between July 1965 to December 2020. Moreover, the autocorrelograms reveal that even 20 lags later, the long memory persists for both value-weighted and equal-weighted Actual_IVOLs, indicating that prior Actual_IVOLs continue to have a strong influence on recent Actual_IVOLs.

Fig. 1

Time-Series Properties of Actual_IVOL. This set of figures shows the line graph, the density distribution graph, and the autocorrelogram (from top to bottom) of value-weighted (left) and equal-weighted (right) Actual_IVOLs. The monthly Actual_IVOL is computed as the standard deviation of the residuals with respect to the Fama–French three-factor model of daily stock returns and is scaled by the square root of the number of trading days in each month. The value-weighted Actual_IVOL is taken monthly according to the market capitalization of each stock. The sample period is from July 1965 to December 2020. The shadow in the autocorrelogram (the bottom) is Bartlett’s formula for the MA(q) 95% confidence band

Table 1 Descriptive statistics for Actual_IVOL series and sorted portfolios

We use Actual_IVOLs from the previous t months to predict expected IVOLs through the ARFIMA, HAR, and EGARCH models in month t + 1 recursively to avoid the look-ahead bias (Guo et al. 2014; Fink et al. 2012). Fu (2009, 2010)’s approach that requiring the first 30 months to generate the initial forecast results in 636 expected IVOLs remaining in the sample.⁸ When it comes to the EGARCH model, we test nine different models following Fu (2009): EGARCH(1,1), EGARCH(1,2), EGARCH(1,3), EGARCH(2,1), EGARCH(2,2), EGARCH(2,3), EGARCH(3,1), EGARCH(3,2), and EGARCH(3,3). In other words, these nine models are permutations of the autoregressive parameter, 1 ≤ p ≤ 3, and the moving average parameter, 1 ≤ q ≤ 3. The converged model with the lowest AIC will be selected following the estimation. Each model estimating approach employs the selection procedure. The parameters of its best-fit model are used to predict expected IVOLs, denoted as Exp_IVOL^EGARCH. For example, in Panel C of Table 2, 96.23% of all estimations adopt the EGARCH(1,1) model, and the remaining 3.77% are generated by the EGARCH(2,1) model for the value-weighted Actual_IVOL series. As for the equal-weighted Actual_IVOL series, the EGARCH(1,1) model is the best-fitting for 99.06% of estimations.

Table 2 The model selection for Actual_IVOL series

The ARFIMA model is suitable to describe the time-varying characteristics in the monthly time-series of value-weighted and equal-weighted Actual_IVOL, according to the analysis of Fig. 1 and Panel A of Table 1. As indicated, the ARFIMA model depicts a long memory via the parameter d and describes the short-term first-order characteristic via parameters p and q. We test 16 permutations: ARFIMA(0,d,0), ARFIMA(0,d,1), ARFIMA(0,d,2), ARFIMA(0,d,3), ARFIMA(1,d,0), ARFIMA(1,d,1), ARFIMA(1,d,2), ARFIMA(1,d,3), ARFIMA(2,d,0), ARFIMA(2,d,1), ARFIMA(2,d,2), ARFIMA(2,d,3), ARFIMA(3,d,0), ARFIMA(3,d,1), ARFIMA(3,d,2), ARFIMA(3,d,3), with the autoregressive parameter, 0 ≤ p ≤ 3 and the moving average parameter, 0 ≤ q ≤ 3. As a result, the long memory parameter d is where the ARFIMA model estimation’s crucial point is located. We shall state that the Actual_IVOL series is stationary and has a long memory if d falls within the region [0,0.5]. Hence, by selecting the model with the lowest AIC, we will also choose the ARFIMA model that fits the data the best. The best-fitting ARFIMA model was found in Panel A of Table 2, where p = 0 and q = 0 were set for the value-weighted Actual_IVOL series (34.91% across all estimations) and p = 1 and q = 0 for the equal-weighted Actual_IVOL series (28.3% across all estimations). The long memory parameter d is estimated in this circumstance to be 0.4961 and 0.4940, respectively. Both values are inside the region [0,0.5] and significant at the 1% level. This result reconfirms that using ARFIMA models to an Actual_IVOL time series is appropriate.

We also require the first 30 months to generate the first ARFIMA prediction. Then, using the Actual_IVOL from the previous t months to forecast the Actual_IVOL in month t + 1, we estimate the parameters recursively and denote the predicted values as Exp_IVOL^ARFIMA. The best-fitted findings for the ARFIMA model differ from the relatively consistent best-fitted results for the EGARCH model, depending on the observation. As compared to the EGARCH model, we would anticipate that the more adaptable ARFIMA model will be better able to capture the time-variation in the Actual_IVOL series and provide a more precise expected IVOL forecast for the subsequent period.

For the HAR model, we examine various AR lags using partial autocorrelations and AIC statistics, and we arrive at the best-fitting model for the Actual_IVOL series. One, three and nine-month lags of the Actual_IVOL are given in Panel B of Table 2 for the value-weighted Actual_IVOL series, which is affected by the previous short-, near- and long-term periods with Actual_IVOL_t-1 contributing the most from a coefficient of 0.5362. Recent Actual_IVOLs with one, two, and three-month lags have a greater impact on the equal-weighted Actual_IVOL series. The preceding long-term Actual_IVOL_t-12 even shares a coefficient of 0.0769 with the present Actual_IVOL_t. In order to predict the expected IVOL in month t + 1, we first record the coefficients from the recursive OLS regressions of the observations up through month t and denote the predictions as Exp_IVOL^HAR. To generate the initial forecast, we also need the first 30 months’ worth of observations.

After that, we make a comparison between the Exp_IVOL^ARFIMA, Exp_IVOL^HAR,, and Exp_IVOL^EGARCH and the Actual_IVOL for the relevant month. To determine how well expected IVOLs catch the time-varying trait inside the Actual_IVOL, we regress the Actual_IVOL on expected IVOLs individually and collectively and anticipate their coefficients to be close to 1. In Table 3, whether value-weighted or equal-weighted, the mean of Exp_IVOL^HAR is closest to the mean of the Actual_IVOL. When regressed independently, all the expected IVOLs are significantly related to the Actual_IVOL. However, when regressed jointly, the direction of Exp_IVOL^EGARCH and Exp_IVOL^ARFIMA switches from positive to negative. Only the direction and significance of the Exp_IVOL^HAR coefficient remain consistent and close to 1. As it stands, the HAR model outperforms the ARFIMA and EGARCH models in terms of reflecting the time-variation inside both value-weighted and equal-weighted Actual_IVOL series.

Table 3 The comparison of expected IVOLs for Actual_IVOL series

4.1.2 Actual IVOL portfolios

We then describe the pattern for Actual_IVOL in terms of sorted portfolios. First, we sort all stocks into quintiles each month based on their Actual_IVOL. In Panel B and C of Table 1, we record the basic statistics for each value-weighted and equal-weighted Actual_IVOL quintile. The lowest Actual_IVOL quintile has the largest right-skewness and leptokurtosis but the least variation for both value-weighted and equal-weighted portfolios, while the highest Actual_IVOL quintile shows the reverse trend. Overall, value-weighted Actual_IVOL portfolios are more right-skewed and leptokurtic, aligning with the outcomes for the full sample. However, only the lowest equal-weighted Actual_IVOL quintile, which stands out from all other quintiles, has a high kurtosis of 8.8116. The stationary for Actual-IVOL-sorted portfolios is indicated by the fact that all the ADF statistics are significant at the 1% level.

The results of model selection and model comparison for each Actual_IVOL quintile are included in the Online Appendix Tables A.1 and A.2, following the same sorting and selection procedure. For both value-weighted and equal-weighted Actual_IVOL portfolios, the best-fitted EGARCH and ARFIMA models vary over a wider range, especially for the ARFIMA model. The choice for the EGARCH(1,1) model still predominates, nevertheless. For the first three quintiles, we choose the ARFIMA(0,d,0) model, and for the top two quintiles, we select the ARFIMA(0,d,3) model. Value-weighted and equal-weighted Actual_IVOLs almost always have the same AR lags for the HAR model for every quintile. The main influence is always accounted for by Actual_IVOL_t-1. Actual_IVOL_t-4 lays a negative impact on the current Actual_IVOL if it is included as an AR lag. Exp_IVOL^HAR outperforms the competition in that its coefficient is closer to 1.

The portfolio-sorting process is also done in accordance with some commonly used firm characteristics such as size and book-to-market ratio (BM ratio). Here, we sort all stocks into quintiles according to NYSE breakpoints to reduce the noise brought by small-sized stocks (Fama and French 1992; Bali and Cakici 2008). The sorting process is balanced monthly. For size-sorted quintiles, the basic statistics in Panel B and C of Table 1 demonstrate a different pattern. The three middle quintiles are more right-skewed, have higher kurtosis, and have higher ADF test statistics. In the Online Appendix A.1 and A.3, we report the selection and comparison among models in detail. First of all, the EGARCH(1,1) model remains dominant across all size-sorted quintiles, regardless of value-weighted or equal-weighted. Except for the ARFIMA(1,d,0) model of the second-lowest value-weighted size quintile and the two-lowest equal-weighted size quintiles, the ARFIMA(0,d,0) model predominates. With respect to the HAR model, almost all quintiles have lags of one, two, and three months. The lowest value-weighted quintile has lags of one, two, three, four, nine, and ten months, whereas the lowest equal-weighted quintile has lags of one, two, three, and four months. Nevertheless, the coefficient of the one-month lag of Actual_IVOL has the greatest impact on the present Actual_IVOL for all portfolios, followed by the three-month lag of Actual_IVOL. If Actual_IVOL with a four-month latency is chosen, the effect is always negative. In each quintile, when comparing expected IVOLs to the Actual_IVOL, the Exp_IVOL^HAR has the closest mean and stands out as the most prominent regressor with a close value of 1 with a consistent direction.

Next, we sort all stocks into quintiles according to their BM ratio, which is calculated following Fama and French (1992) by using the book value of equity from the previous fiscal year upon the market capitalization from the previous calendar year. This procedure is also monthly balanced. We report the basic statistics for each value-weighted and equal-weighted BM quintile in Panel B and C of Table 1. All BM-sorted portfolios are right-skewed and leptokurtic. The results of the ADF test show that previous Actual_IVOLs still have an impact on the current Actual_IVOL. The EGARCH(1,1) model is still suitable for all value-weighted and equal-weighted BM-quintiles, as described in the Online Appendix Table A.1. Here, different ARFIMA models, including the ARFIMA(0,d,0), ARFIMA(1,d,0) and ARFIMA(0,d,3) models are chosen. Except for the lowest and the highest equal-weighted BM-quintiles, the HAR model selection is dominated by one-, two-, and three-month lags. The characteristics of expected IVOLs remain the same for BM-sorted portfolios (see the Online Appendix Table A.4).

4.2 The expected IVOL-return relationship

In this section, we revisit the IVOL puzzle by using expected IVOLs from the ARFIMA, HAR, and EGARCH models at both the stock and portfolio levels.

4.2.1 Stock-level analysis

For stock-level analysis, we form both the value-weighted excess stock returns monthly according to the market capitalization as well as the equal-weighted excess stock returns. To examine whether the IVOL puzzle exists, we regress the excess stock returns on the expected IVOLs respectively and collectively in combination with additional time-series control variables. Our comparison is justified by the fact that we require the significance for each expected IVOL when regressing both individually and collectively. We also need the coefficients for each expected IVOL to point in the same direction. The model with the highest adjusted-R² and the lowest Root Mean Squared Error (RMSE) is then picked.

From Panel A of Table 4, we could observe that when regressing each expected IVOL with control variables separately (in regressions (1), (2), and (3)), the Exp_IVOL^ARFIMA and Exp_IVOL^HAR exhibit the capacity to price the value-weighted returns. The direction of Exp_IVOL^EGARCH alters from negative to positive while the Exp_IVOL^ARFIMA and Exp_IVOL^HAR remain consistent and significant when all expected IVOLs and control variables are taken into account in regression (5). The Exp_IVOL^ARFIMA has an adjusted-R² of 4.52% in regression (1) which is marginally greater than the Exp_IVOL^HAR’s in regression (2) as well as an RMSE of 0.2696 is slightly lower than the Exp_IVOL^HAR’s. All expected IVOLs in Panel B of Table 4 for the equal-weighted returns are significant whether they are regressed separately or jointly, except the direction of Exp_IVOL^HAR, which is inconsistently changing from positive to negative. Once more, Exp_IVOL^ARFIMA outperforms Exp_IVOL^EGARCH with a higher adjusted-R² of 5.77% and a lower RMSE of 0.2680. The results are not affected after comparing with the results of Actual_IVOL (in regressions (4) and (5)) as a benchmark. Given that the IVOL-return relationship depends on the model being utilized, we are unable to draw the conclusion that the IVOL puzzle exists. Specifically, the IVOL puzzle only arises for the Exp_IVOL^HAR in the value-weighted series but not for other circumstances.

Table 4 The IVOL-return relationship for Actual_IVOL series

Overall, Exp_IVOL^ARFIMA exhibits consistency, maintains positive significance, and holds the lowest RMSE and the highest adjusted-R² for pricing both value-weighted and equal-weighted Actual_IVOL series. The Exp_IVOL^EGARCH is an additional option with a positive pricing ability for the equal-weighted Actual_IVOL series. Only the value-weighted Actual_IVOL series employing the HAR model with one-, three-, and nine-month lags could reveal the IVOL puzzle.

4.2.2 Sorted portfolios analysis

We further expand our results to value-weighted and equal-weighted Actual_ IVOL-sorted, size-sorted, and BM-sorted portfolios. First, the Exp_IVOL^ARFIMA and Exp_IVOL^EGARCH have better pricing ability than Exp_IVOL^HAR across all Actual_IVOL quintiles. Table 5 shows that, although Exp_IVOL^HAR more closely resembles and fits the Actual_IVOL variation observed in earlier analyses, the Exp_IVOL^HAR is either inconsequential or inconsistent when it comes to pricing stock returns in Actual_IVOL-sorted portfolios. For example, the EGARCH model for the Actual_IVOL quintile 2 and the ARFIMA model for the Actual_IVOL quintile 3, 4, and 5 are both consistent choices within the same quintile whether weighted equally or by value. The value-weighted Actual_IVOL quintile 1 chooses the ARFIMA model in contrast to its equal-weighted equivalent, which selects the EGARCH model. It is possible that the underlying pricing feature residing in Actual_IVOL-sorted portfolios can be better captured by the ARFIMA and EGARCH models. Only the lowest value-weighted Actual_IVOL quintile for the Exp_IVOL^ARFIMA has the IVOL puzzle.

Table 5 The IVOL-return relationship for Actual_IVOL-sorted portfolios

We do observe the IVOL puzzle for all value-weighted portfolios as well as for equal-weighted portfolios 4 and 5 concerning size quintiles. In Table 6, all of these IVOL puzzles, except for the value-weighted portfolio 2 by the Exp_ IVOL^ARFIMA, are discovered to be predicted by the Exp_IVOL^HAR. The lowest three equal-weighted quintiles include only two positive Exp_IVOL^EGARCH-return relationships. The two smallest size quintiles, like Actual_IVOL quintiles, are appropriate for various models and have coefficients that point in opposite directions.

Table 6 The IVOL-return relationship for size-sorted portfolios

When it comes to quintiles that are sorted using the BM ratio, the pattern is distinct from previously sorted portfolios. As reported in Table 7, excluding quintile 2, value-weighted BM-quintiles generally exhibit an IVOL puzzle, whereas all equal-weighted BM-quintiles present a positive IVOL-return relationship. Nevertheless, only quintile 2, which is either value-weighted or equal-weighted, chooses the EGARCH model with a positive coefficient.

Table 7 The IVOL-return relationship for BM-sorted portfolios

In conclusion, we could notice that the IVOL puzzle always exists in the lowest value-weighted portfolios from the aforementioned Actual-IVOL-, size-, and BM-sorted approaches. In contrast, the two lowest equal-weighted quintiles always show a positive IVOL-return relationship. Furthermore, focusing on the individual model, we also observe the negative IVOL-return relationship across all HAR-predicted quintiles, regardless of how the data are sorted (Actual_IVOL, size, or BM), whether they are value- or equal-weighted. Although the EGARCH model only outperforms in the bottom two quintiles, we also confirm that the Exp_IVOL^EGARCH-return relationship is positive. The IVOL puzzle brought by the Exp_IVOL^ARFIMA, on the other hand, is only present in the lowest two value-weighted quintiles and is more circumstantial. It is difficult to pinpoint the precise choice of models for predicting expected IVOLs as it depends on the stock composition within the portfolio.

5 Robustness checks

5.1 Results for BETA-sorted portfolios

We estimate BETA following Liu et al. (2018)’s explanation of the beta anomaly, which states that stocks with low beta have higher earnings than stocks with high beta. They argue that the beta anomaly is caused by the interaction between the positive beta-IVOL correlation and the negative IVOL-return relationship among overpriced stocks. In our sample, we expect that the coefficient of the best expected IVOL in explaining stock returns will also be negative.

To reconcile non-synchronous trading effects, we regress the monthly excess stock return of i in month t on the monthly market excess return in both month t and month t-1 with a 60-month rolling window. We require stocks to have at least 36 months of returns and the excess return is computed by subtracting the one-month US treasury bill. We denote the sum of coefficients of the current market excess return and the one-month lagged market excess return as β_i (Dimson 1979). Then following Vasicek (1973), we compute BETA by shrinking β_i with weight ω_i as in Eq. (6),

$${BETA}_{i}={\omega }_{i}*{\beta }_{i}+\left(1-{\omega }_{i}\right)*1,$$

(6)

where weight ω_i is defined as,

$${\omega }_{i}=\frac{\frac{1}{{\sigma }^{2}\left({\beta }_{i}\right)}}{\frac{1}{{\sigma }^{2}\left({\beta }_{i}\right)}+\frac{1}{{\widehat{\sigma }}^{2}\left(\beta \right)}}.$$

(7)

Specifically, in the above Eq. (7), σ²(β_i) is the variance of β_i; ${\widehat{\sigma }}^{2}\left(\beta \right)$ is the estimate of the cross-sectional variance of true betas, computed by taking the difference between the cross-sectional variance of β_i and the cross-sectional mean of σ²(β_i).

We include the results for BETA-quintiles in the Online Appendix (Tables A.5, A.6, and A.7). Similar to the general characteristics observed in the previous sorted approaches, the lowest two equal-weighted quintiles still reveal a positive IVOL-return relationship. However, the relationship is positive rather than negative for the lowest value-weighted quintile. Regarding the beta anomaly, we could only find negative relationships for the Exp_IVOL^HAR in value-weighted portfolios, whereas positive relationships are presented from the Exp_IVOL^ARFIMA and Exp_IVOL^EGARCH.

5.2 Different exclusion schemes for IVOL

In the main section above, we have excluded stocks having less than 5 trading days in a month. As noted in Bali and Cakici (2008), however, there is no consensus in the extant literature about the exclusion of stocks. Different ways of applying the data collection criteria such as selecting from monthly, daily, or even intra-day data, weighting equally or by value, or excluding small-sized, low-priced, or illiquid stocks, lead to positive, negative, or compromised conclusions for the investigation of the IVOL-return relationship. By implementing two additional exclusion strategies during the IVOL construction process, we corroborate our findings. Since the exact number of stocks excluded between the 10-day scheme and 11-day scheme is significant, we choose to exclude both stocks with less than 10 trading days in a month and stocks with less than 11 trading days in a month. Although unreported, it is noteworthy that our main findings are not affected by the exclusion scheme.

6 Further analysis

We further take into account portfolios that are sorted on the sentimentalized idiosyncratic volatility [hereafter sentimentalized IVOL], which is the product between the investor sentiment index aligned by Huang et al. (2015) and IVOL. We find a significant pricing effect, shifting from negative to positive with the growth of the sentimentalized IVOL itself, on the cross-section of stock returns.

Both value-weighted and equal-weighted portfolios show novel patterns within sentimentalized IVOL quintiles when the IVOL-return relationship is examined (see the Online Appendix Table A.8). Previously, all Exp_IVOL^HAR always displayed the IVOL puzzle. In quintiles sorted on the sentimentalized IVOL, the lowest value-weighted quintile and the two bottom equal-weighted quintiles have a positive coefficient with Exp_IVOL^HAR. Value-weighted quintiles 4 even have no discernible IVOL-return association. We might locate the IVOL puzzle for the Exp_IVOL^HAR in quintiles 4 and 5 when equally weighted.

7 Conclusion

The time-varying property of IVOL is crucial in examining the relationship between IVOL and stock returns and selecting the appropriate model for estimating IVOL. In this paper, we evaluate the three expected IVOLs from the ARFIMA, HAR, and EGARCH models for their capacity to replicate and capture the time-variation property within the Actual_IVOL series and portfolios. We also look at how the three expected IVOLs and stock returns are related. Empirically, we find that the Exp_IVOL^HAR beats its two counterparts by a wide margin when it comes to simulating the variation in both the Actual_IVOL series and portfolios. This benefit cannot, however, be extended to the pricing ability. There is no all-encompassing model that can estimate expected IVOLs and reproduce its time-variation simultaneously. As a result, the performance of expected IVOLs in the IVOL-return relationship varies depending on the model used.

Our findings add to the ongoing debate over the IVOL puzzle. Under the EGARCH model, in which the best-fitted model is selected recursively, the IVOL-return relationship is consistently positive. The findings of Fu (2009) are likewise consistent with this positive relationship. The advantage of the HAR model in capturing the time-varying property suggests that different models might yield varying insights into the IVOL-return relationship. We discover the presence of the IVOL puzzle for Exp_IVOL^HAR in our sample period of July 1965 to December 2020, where the best-fitted HAR model is calibrated under the particular value-weighted and equal-weighted series or portfolios. The direction of the relationship between the Exp_IVOL^ARFIMA and stock returns is undetermined, so each case must be separately examined. Overall, there is not a universally recognized and standardized model that can effectively capture the dynamic time-dependency of IVOL and duplicate it. Therefore, if we solely rely on the expected IVOL derived from a single model, we would be unable to challenge the IVOL puzzle of AHXZ (2006). Continuous scrutiny of model assumptions and methodologies is still essential. While the inconclusive IVOL puzzle is still under investigation and depends on the sample composition, our findings imply some unique portfolios for the puzzle and call for more cautionary portfolio construction and decision-making. By recognizing the limitations of relying on one certain model, practitioners need to refine their risk management practices, with higher awareness of lower portfolios.