Option pricing with random risk aversion

Abstract

Based on a standard general equilibrium economy, we develop a framework for pricing European options where the risk aversion parameter is state dependent, and aggregate wealth and the underlying asset have a bivariate transformed-normal distribution. Our results show that the volatility and the skewness of the risk aversion parameter change the slope of the pricing kernel, and that, as the volatility of the risk aversion parameter increases, the (Black and Scholes) implied volatility shifts upwards but its shape remains the same, which implies that the volatility of the risk aversion parameter does not change the shape of the risk neutral distribution. Also, we demonstrate that the pricing kernel may become non-monotonic for high levels of volatility and low levels of skewness of the risk aversion parameter. An empirical example shows that the estimated volatility of the risk aversion parameter tends to be low in periods of high market volatility and vice-versa.

1 Introduction

Recent research suggests that the level of risk aversion of investors is not constant (Barseghyan et al. 2011; Guiso et al. 2018), possibly due to changing inflation rates, equity premium, long-term bond risk premia, and credit spread amongst others (Brandt and Wang 2003; Danthine et al. 2004; Bekaert et al. 2010, 2019). Attempts to estimate the (implicit) level of risk aversion using the option markets suggest a non-constant level of risk aversion (Jackwerth 2000; Bliss and Panigirtzoglou 2004 amongst others). However, when it comes to option pricing, the assumption that the risk aversion parameter is constant is still standard in the general equilibrium option pricing framework.¹

In this paper we relax this assumption by deriving a general equilibrium European option pricing model where the risk aversion parameter (the curvature of the utility function) is stochastic.² Thus, an investor faces uncertainty not only about the future payoff of a given security but also about the level of risk aversion.³ In this sense, our economy is similar to the ones proposed by Karni (1983), Karni et al. (1983), and Gordon and St-Amour (2000, 2004) amongst others.

Apart from a state dependent risk aversion assumption, the distributional assumptions employed here are very general, as we let wealth and the underlying asset have a joint transformed-normal distribution. The resulting option pricing formulae derived here do not depend on the expected values of wealth, the risk aversion parameter or the underlying asset—the formulae depend only on their volatilities and on the correlation between wealth and the underlying asset.

We show that, for a fixed level of the risk aversion parameter, the volatility and the skewness of the risk aversion parameter change the slope of the pricing kernel. Therefore, this result complements the one obtained by Gordon and St-Amour (2000), who show that the level of the risk aversion parameter changes the slope of the pricing kernel. We also show that a high level of volatility or a low level of skewness may result in a non-monotonic pricing kernel.⁴

We provide examples to show that the level of volatility of the risk aversion parameter affects the level of implied volatility but not its shape. Hence, the volatility of the risk aversion parameter does not change the shape of the risk neutral distribution. In addition, we provide an empirical example which shows that the estimated volatility of the risk aversion parameter and the market volatility present a negative relationship. That is, in periods of high market volatility the estimated risk aversion volatility is low and vice-versa. Our results are consistent with the ones obtained by Bakshi and Madan (2006), and Bekaert et al. (2010, 2019), for instance. However, as our model depends on the volatility of the risk aversion parameter and not on its level, their results and ours are not directly comparable.

The remainder of this paper is organized as follows: in the next section the economy is introduced. The third section introduces the distributional assumptions and obtains a general form for the pricing kernel. The fourth section obtains new option pricing models and provides a simple empirical application. Finally, the last section concludes.

2 The basic set up

Suppose the representative investor maximises her future time t expected utility function of aggregate wealth, w, while her level of risk aversion is state dependent. The problem she faces can be written as

$$\begin{aligned} \max \underset{i}{E}\underset{s}{E}\left[ u\left( w_{i},s\right) \right] , \end{aligned}$$

(1)

where $\underset{i}{E}$ is the expectation of w over i outcomes, $\underset{s}{E}$ is the expectation of occurrence of state s, and $u\left( \cdot \right)$ is the utility function.

Assuming the existence of a riskless asset with a rate of return r per period, the agent will invest in a combination of risky and riskless assets in order to maximise the expected utility of aggregate wealth so that, at equilibrium, the current price $v_{0}$ of any given asset can be obtained according to the following equation

$$\begin{aligned} v_{0}=e^{-r}\underset{i}{E}\left[ M\left( w_{i}\right) v_{i}\right] , \end{aligned}$$

(2)

where

$$\begin{aligned} M\left( w_{i}\right) =\frac{\underset{s}{E}u'\left( w_{i},s\right) }{\underset{i}{E}\underset{s}{E}u'\left( w_{i},s\right) } \end{aligned}$$

(3)

is defined as the pricing kernel, $v_{0}$ and $v_{i}$ are the prices of a risky asset at time 0 and t respectively. It is important to highlight that one can price any asset in this economy by applying Eqs. (2) and (3), provided that the investor’s utility function and the distribution followed by the relevant random variables are specified. These are provided in the next section, where we discuss two different scenarios: one where the distribution of the risk aversion parameter is not specified whilst in the second scenario we let the risk aversion parameter have a transformed-normal distribution.

3 The pricing kernel

In this section we obtain the pricing kernel and discuss the impact that the state-dependent risk aversion parameter has on it. We start with the definition of a transformed-normal distribution and then we discuss two specific cases.

Definition 1

(The transformed-normal distribution) A random variable x is said to have a transformed-normal distribution if $x=h_{x}^{-1}\left( \mu +\sigma z\right)$, where $h_{x}\left( \cdot \right)$ is a strictly monotonic differentiable function, $z\sim N\left( 0,1\right)$, and $\mu$ and $\sigma$ are the location and the scale parameters respectively.

The transformation is a technique for generating distributions with levels of skewness and kurtosis that differ from the normal distribution (see for instance Johnson 1949). The family of transformed-normal distributions was introduced to the option pricing literature by Camara (2003).

Definition 2

(The distribution of aggregate wealth and the underlying asset) The time t aggregate wealth, w, and the underlying asset price, v, have a bivariate transformed-normal distribution with correlation parameter $\rho$. Their transformed-normal marginal densities are, respectively, $h_{w}\left( w\right) \sim N\left( \mu _{w},\sigma _{w}^{2}\right)$ and $h_{v}\left( v\right) \sim N\left( \mu _{v},\sigma _{v}^{2}\right)$, where $\mu _{w}$ and $\mu _{v}$ are location parameters and $\sigma _{w}$ and $\sigma _{v}$ are scale parameters.

The transformed-normal distribution provides great flexibility in terms of the choice of distribution for the relevant random variables. Functions $h_{w}$ and $h_{v}$ need not be the same and the transformed-normal family include several types of distributions that have been used extensively in option pricing e.g. the log-normal distribution used by Black and Scholes (1973), the normal distribution used by Brennan (1979), the displaced log-normal distribution used by Rubinstein (1983), the inverse cosh-normal and the $S_{u}$ distributions used by Camara (2001, 2003), and the g-distribution used by Vitiello and Poon (2008) amongst others.

3.1 When the distribution of the risk aversion parameter is not specified

As the distribution of the risk aversion parameter is not specified, we assume that there is a probability $p_{s}$ that state s will occur and that the risk aversion parameter will have a value of $\gamma _{s}$, as in Gordon and St-Amour (2000). The main result of this subsection is presented below.

Proposition 3

(The pricing kernel) Suppose that the representative investor has a marginal utility function of aggregate wealth of the following form

$$\begin{aligned} u'\left( w,s\right) =\exp \left[ -\gamma _{s}\left( h_{w}\left( w\right) -\ln \lambda \right) \right] , \end{aligned}$$

(4)

where $\gamma _{s}$ is the level of risk aversion in state s, $\lambda >0$ is a constant preference parameter, w is the wealth at time t, and $h_{w}\left( \cdot \right)$ is a function of w, as per Definitions 1and 2. Let $p_{s}$ be the probability of occurrence of state s, for $s=1,\ldots ,N$ with $\sum _{s}p_{s}=1$. Then, the pricing kernel in Eq. (3) is given by

$$\begin{aligned} M\left( w\right) =\frac{\sum _{s}p_{s}\exp \left[ -\gamma _{s}\left( h_{w}\left( w\right) -\ln \lambda \right) \right] }{\sum _{s}p_{s}\exp \left( \gamma _{s}\ln \lambda -\mu _{w}\gamma _{s}+0.5\gamma _{s}^{2}\sigma _{w}^{2}\right) }. \end{aligned}$$

(5)

Proof

See “Appendix”. $\square$

The above proposition leads to the corollary below.

Corollary 4

If the investor’s risk aversion parameter is constant, $\gamma _{s}$ $=-\gamma \;\forall s$, and $\lambda =1$ then Eq. (5) reduces to $M^{*}\left( w\right) =\exp \left( \gamma _{s}h_{w}\left( w\right) -\gamma _{s}\mu _{w}-0.5\gamma _{s}^{2}\sigma _{w}^{2}\right)$, which is the same pricing kernel obtained by Camara (2003).

To guarantee non-satiation and risk-aversion, the results from Proposition 3 require, in general, that $\gamma _{s}>0$ $\forall s$ and that $h_{w}\left( \cdot \right)$ is a strictly increasing monotonic differentiable function.⁵ As that the denominator of Eq. (5) is a constant, any non-linearity in the pricing kernel is driven by the marginal utility function in Eq. (4).

It is possible to see from Eq. (4) that if $h_{w}\left( w\right) =w$ the investor will have an exponential marginal utility, $u'\left( w,s\right) =\lambda ^{\gamma _{s}}\exp \left( -\gamma _{s}w\right)$. If $h_{w}\left( w\right) =\ln \left( w\right)$ the investor will have a power marginal utility, $u'\left( w\right) =\lambda ^{\gamma _{s}}w^{-\gamma _{s}}$, which is consistent with the utility function used by Gordon and St-Amour (2000), given by $u\left( w,s\right) =\lambda ^{\gamma _{s}}w^{1-\gamma _{s}}/\left( 1-\gamma _{s}\right) .$ In this case, using the definition of the expected value of a log-normal random variable, the pricing kernel in Eq. (5) becomes

$$\begin{aligned} M\left( w\right) =\frac{\sum _{s}p_{s}\lambda ^{\gamma _{s}}\exp \left( -\gamma _{s}\ln w\right) }{\sum _{s}p_{s}\lambda ^{\gamma _{s}}\exp \left( -\mu _{w}\gamma _{s}+0.5\gamma _{s}^{2}\sigma _{w}^{2}\right) }. \end{aligned}$$

(6)

To illustrate the impact of $\gamma$ on the pricing kernel, assume that there are only three states of nature, i.e. $s=1,2,3$, and that $\mu _{w}=0.9$, $\sigma _{w}=0.25$, $p_{s}=1/3$, and $\lambda =1.5$. Also, let the mean, the standard deviation, and the skewness of the risk aversion parameter be $\mu _{\gamma }$, $\sigma _{\gamma }$, and $skew_{\gamma }$ respectively.

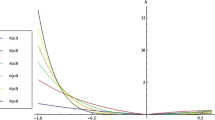
Figure 1 shows the pricing kernel in Eq. (6) for three different values of $\sigma _{\gamma }$ and keeping the mean $\left( \mu _{\gamma }=1\right)$ and the skewness $\left( skew_{\gamma }=0\right)$ of the risk aversion parameter constant.⁶ The figure shows that changes in $\sigma _{\gamma }$ lead to a change in the slope of the pricing kernel and that, considering the values of wealth given in the picture, the pricing kernel is a monotonic decreasing function of wealth.

Of the three curves presented in Fig. 1, the pricing kernel with $\sigma _{\gamma }=0.05$ is closest to having a constant elasticity (see Franke et al. 1999). As the expected value of the pricing kernel must be equal to one, i.e., $E[M(w)=1]$, one curve cannot dominate the other. When $\sigma _{\gamma }=0.5$ or $\sigma _{\gamma }=0.8$, investors value extreme observations more than the case when $\sigma _{\gamma }=0.05.$

It is important to note, however, that for high values of $\sigma _{\gamma }$ the pricing kernel may become non-monotonic. This is driven by the fact that for high values of $\sigma _{\gamma }$ and w the probability-weighted marginal utility function becomes convex. Based on the values used in this example, in order to obtain a high $\sigma _{\gamma }$ some of the $\gamma _{s}$ must be negative, which leads to a non-concave marginal utility function.

Figure 2 shows the pricing kernel for $\mu _{\gamma }=1$, $\sigma {}_{\gamma }=0.8$, and different values of $skew_{\gamma }$. It can be seen that, just like $\sigma _{\gamma }$, skewness changes the slope of the pricing kernel.⁷

Fig. 1

The pricing kernel for different values of $\sigma _{\gamma }$. The pricing kernel obtained from Eq. (6) for $\mu _{\gamma }=1$, $skew_{\gamma }=0$, $\mu _{w}=0.9$, $\sigma _{w}=0.25$, $\lambda =1.5$, $p_{s}=1/3$ with $s=1,2,3$, and different values of $\sigma _{\gamma }$

Fig. 2

The pricing kernel for different values of $skew_{\gamma }$. The pricing kernel obtained from Eq. (6) for $\mu _{\gamma }=1$, $\sigma _{\gamma }=0.8$, $\mu _{w}=0.9$, $\sigma _{w}=0.25$, $\lambda =1.5$, $p_{s}=1/3$ with $s=1,2,3$, and different values of $skew_{\gamma }$

3.2 When the risk aversion parameter has a transformed-normal distribution

If we make the additional assumptions that $\gamma$ has a transformed-normal distribution and that it is correlated to the states of nature, s, it is possible to explicitly incorporate the distributional parameters of $\gamma$ into the pricing kernel. The proposition below introduces such a case.

Proposition 5

(The pricing kernel when $\gamma$ has a transformed-normal distribution). Suppose that the representative investor has a marginal utility function of aggregate wealth of the following form

$$\begin{aligned} u'\left( w,s\right) =\exp \left[ -h_{\gamma }\left( \gamma \right) \left( h_{w}\left( w\right) -\ln \lambda \right) \right] , \end{aligned}$$

(7)

where $\lambda >0$ is a constant preference parameter, $h_{\gamma }\left( \gamma \right) \sim N\left( \mu _{\gamma },\sigma _{\gamma }^{2}\right)$ and $h_{w}\left( w\right) \sim N\left( \mu _{w},\sigma _{w}^{2}\right)$ are independent and are functions of the risk aversion parameter $\gamma$ and wealth w, respectively. Then, the pricing kernel in Eq. (3) is given by

$$\begin{aligned} M\left( w\right)&=\frac{\int _{\gamma }\exp \left[ -h_{\gamma }\left( \gamma \right) \left( h_{w}\left( w\right) -\ln \lambda \right) \right] f_{TN}\left( \gamma \right) d\gamma }{\int _{\gamma }\int _{w}\exp \left[ -h_{\gamma }\left( \gamma \right) \left( h_{w}\left( w\right) -\ln \lambda \right) \right] f_{TN}\left( w\right) f_{TN}\left( \gamma \right) dwd\gamma }, \\&=\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}\exp \left[ \frac{1}{2}\sigma _{\gamma }^{2}A^{2}-\mu _{\gamma }A+\frac{1}{2\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) }\left( 2\mu _{\gamma }B-\sigma _{\gamma }^{2}B^{2}-\mu _{\gamma }^{2}\sigma _{w}^{2}\right) \right] , \end{aligned}$$

(8)

where $f_{TN}\left( \cdot \right)$ is the transformed-normal density, $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$, $A=h_{w}\left( w\right) -\ln \lambda$, and $B=\mu _{w}-\ln \lambda$.

Proof

See “Appendix”. $\square$

Corollary 6

If the risk aversion parameter is constant, with $\mu _{\gamma }=-\gamma$ and $\lambda =1$, then the pricing kernel in Eq. (8) collapses into $M\left( w\right) =\exp \left( -\gamma h_{w}\left( w\right) +\gamma \mu _{w}-0.5\gamma ^{2}\sigma _{w}^{2}\right)$, which is the same pricing kernel obtained by Camara (2003).

Similar to the previous section, to guarantee non-satiation and risk-aversion, the results from Proposition 5 require, in general, that $h_{\gamma }\left( \gamma \right) >0$ and that $h_{w}\left( \cdot \right)$ is a strictly increasing monotonic differentiable function. As an example, let w be log-normally distributed, i.e. $h_{w}=\ln \left( w\right)$ as per Definition 2, and let $\gamma$ be normally distributed, $h_{\gamma }\left( \gamma \right) =\gamma$,⁸ with location and scale parameters $\mu _{\gamma }$ and $\sigma _{\gamma }$ respectively, and independent of wealth.⁹ Given these assumptions, the pricing kernel in Eq. (8) becomes

$$\begin{aligned} M\left( w\right)&=\frac{\int _{\gamma }\lambda ^{\gamma }\exp \left( -\gamma \ln w\right) f_{N}\left( \gamma \right) d\gamma }{\int _{\gamma }\int _{w}\lambda ^{\gamma }\exp \left( -\gamma \ln w\right) f_{\Lambda }\left( w\right) f_{N}\left( \gamma \right) dwd\gamma } \\&=\frac{\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}\exp \left[ -\mu _{\gamma }\left( \ln w-\ln \lambda \right) +0.5\sigma _{\gamma }^{2}\left( \ln w-\ln \lambda \right) ^{2}\right] }{\exp \left[ \left( 2-2\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{-1}\left( \sigma _{\gamma }^{2}\left( \mu _{w}-\ln \lambda \right) ^{2}+\mu _{\gamma }^{2}\sigma _{w}^{2}-2\mu _{\gamma }\left( \mu _{w}-\ln \lambda \right) \right) \right] }, \end{aligned}$$

(9)

where $f_{N}\left( \cdot \right)$ is the normal density function, $f_{\Lambda }\left( \cdot \right)$ is the log-normal density function, and $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$.

As w is not correlated to $\gamma$, Eq. (9) does not have a correlation coefficient, but it contains both the location and the scale parameter of $\gamma$. For $\mu _{\gamma }=1$, $\mu _{w}=0.9$, $\sigma _{w}=0.25$, and $\lambda =1.5$, Fig. 3 shows that changing the value of $\sigma _{\gamma }$ leads to a change in the slope of the pricing kernel. As discussed in the previous subsection, the pricing kernel will become non-monotonic for high values of $\sigma _{\gamma }$ since, considering our distributional assumption, a high $\sigma _{\gamma }$ increases the probability of a negative $\gamma$.¹⁰

Fig. 3

The pricing kernel for different values of $\sigma _{\gamma }$. The pricing kernel obtained from Eq. (9) with $\mu _{\gamma }=1$, $\mu _{w}=0.9$, $\sigma _{w}=0.25$, $\lambda =1.5$, and different values of $\sigma _{\gamma }$

In the next section we apply Proposition 5 to obtain a framework for the pricing of options and provide applications of this framework.

4 Asset prices in equilibrium

Given the equilibrium relation in Eq. (2), and a non-satiated and risk-averse investor, the price at time 0 of an underlying asset with a terminal payoff v is given by the following market equilibrium relationship

$$\begin{aligned} v_{0}&=e^{-r}\int \int vM\left( w\right) f_{TN}\left( w,v\right) dwdv, \end{aligned}$$

(10)

where $f_{TN}\left( \cdot ,\cdot \right)$ is a bivariate transformed-normal density function. Similarly, the price at time 0 of a derivative with payoff $\kappa \left( v\right)$ is given by

$$\begin{aligned} c_{0}=e^{-r}\int \int \kappa \left( v\right) M\left( w\right) f_{TN}\left( w,v\right) dwdv. \end{aligned}$$

(11)

As Camara (2003) and Heston (1993) point out, if the expectation in Eq. (10) is given in closed-form and if it can be expressed in terms of one of the distributional parameters, then it may be possible to replace the investor’s preference parameter and/or some of the distributional parameters in Eq. (11) with marketable securities.¹¹

We demonstrate the applicability of our framework in the subsections below. The examples are based on standard assumptions used in discrete-time general equilibrium models (see Brennan 1979; Camara 2003), except that we allow the risk aversion parameter to be random.

4.1 The Black and Scholes model when $\gamma$ has a normal distribution

Using the results in Proposition 5, and Eqs. (10) and (11), the current prices of the underlying asset, $v_{0}$, and of an option written on it, $c_{0}$, are obtained in the two propositions below.

Proposition 7

(The underlying asset price equilibrium relationship) Let the risk aversion parameter have a normal distribution so that $h_{\gamma }\left( \gamma \right) =\gamma .$ Then, given Definitions 1and 2with $h_{w}\left( w\right) =\ln w$ and $h_{v}\left( v\right) =\ln v_{t}$, Eq. (10), and Proposition 5, the equilibrium price of the underlying asset at time 0 is given by

$$\begin{aligned} v_{0}=\exp \left[ \mu _{v}-r+\frac{\sigma _{v}^{2}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }-\frac{\sigma _{v}\sigma _{w}\rho \left( \mu _{\gamma }-\sigma _{\gamma }^{2}\left( \mu _{w}-\ln \lambda \right) \right) }{1-\sigma _{\gamma }^{2}\sigma _{w}^{2}}\right] , \end{aligned}$$

(12)

where $1-\sigma _{\gamma }^{2}\sigma _{w}^{2}>0$.

Proof

See “Appendix”. $\square$

Proposition 8

(The random-risk-aversion Black–Scholes equation—RRA-BS) Given Eq. (11), and Propositions 5and 7, the prices of a call option with payoff $k\left( v\right) =\max \left( v-k,0\right)$, and of a put option with payoff $k\left( v\right) =\max \left( k-v,0\right)$ where k is the strike price, are given respectively by

$$\begin{aligned} call_{0}=v_{0}N\left( d_{1}\right) -ke^{-r}N\left( d_{2}\right) , \end{aligned}$$

(13)

$$\begin{aligned} put_{0}=ke^{-r}N\left( -d_{2}\right) -v_{0}N\left( -d_{1}\right) , \end{aligned}$$

(14)

where

$$\begin{aligned} d_{1}&= \left[ \frac{1}{\sigma _{v}}\left( \ln \left( \frac{v_{0}}{k}\right) +r\right) +\frac{\sigma _{v}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }\right] \frac{\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}{\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}},\\ d_{2}&= d_{1}-\frac{\sigma _{v}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}{\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}, \end{aligned}$$

with $1-\sigma _{\gamma }^{2}\sigma _{w}^{2}>0$.

Proof

See “Appendix”. $\square$

Corollary 9

If the investor’s risk aversion parameter is constant then Eq. (12) becomes $v_{0}=\exp \left( \mu _{v}-r-\gamma \rho \sigma _{v}\sigma _{w}+0.5\sigma _{v}^{2}\right)$, which is the same market equilibrium relationship obtained by Brennan (1979). Applying this equilibrium relationship to Eqs. (13) and (14) leads to the Black and Scholes (1973) call and put option pricing models respectively.

As discussed earlier in this section, we use the market equilibrium relationship in Eq. (12) to replace some of the distributional parameters, and thus Eqs. (13) and (14) do not depend on the mean values of the underlying asset return, risk aversion parameter or wealth.

An example of the shape of the implied volatility of put options obtained from the random-risk-aversion Black and Scholes (RRA-BS) in Eq. (14) is provided in Fig. 4, with $\sigma _{v}=0.5$, $\sigma _{w}=0.25$, $\rho =0.85$, $r=10\%$, and different values of $\sigma _{\gamma }$.¹² As in the Black and Scholes model, the implied volatility in Fig. 4 is constant, and when $\sigma _{\gamma }$ is zero the implied volatility is at its lowest value, which corresponds to the implied volatility obtained from the Black and Scholes model, as per Corollary 9. However, as $\sigma _{\gamma }$ increases, the level of implied volatility shifts parallel upwards, without changing its shape.

Fig. 4

The volatility smile of the RRA-BS model for different values of $\sigma _{\gamma }$. Simulated option prices obtained from Eq. (14) with $\sigma _{v}=0.5$, $\sigma _{w}=0.25$, $\rho =0.85$, $r=10\%$, and different values of $\sigma _{\gamma }$

4.2 The g-option pricing model when $\gamma$ has a normal distribution

In this example, it is assumed that the underlying asset has a g-distribution. This transformation was introduced by Tukey (1977) and has been applied, for instance, to the calibration of option prices to risk neutral densities by Dutta and Babbel (2002) and to option prices by Vitiello and Poon (2008). The g-distribution is defined below.

Definition 10

(The g-distribution) The underlying asset is said to have a g-distribution if $v=g^{-1}\left[ \exp \left( gy\right) -1\right] ,$ where $y\sim N\left( 0,1\right)$ and $\left( gv+1\right) >0$. In this case the density function of the underlying asset has the following form

$$\begin{aligned} f\left( v\right) =\frac{1}{\sigma _{v}\left( gv+1\right) \sqrt{2\pi }}\exp \left[ -\frac{1}{2\sigma _{v}^{2}}\left( \frac{1}{g}\ln \left( gv+1\right) -\mu _{v}\right) ^{2}\right] . \end{aligned}$$

(15)

Following the steps taken in the previous subsection, the equilibrium price of the underlying asset is given by the proposition below. Note that, as the distributional assumptions related to w and $\gamma$ are the same as the ones used in Proposition 7, the pricing kernel is also the same. The only difference is the distribution of v.

Proposition 11

(The underlying asset price equilibrium relationship under a g-distribution) Let wealth have a log-normal distribution, the risk aversion parameter have a normal distribution, and the underlying asset have a g-distribution as per Definition 10. Then, given Eq. (10) and Proposition 5, the equilibrium price of the underlying asset at time 0 is given by

$$\begin{aligned} v_{0}=\frac{e^{-r}}{g}\left[ \exp \left( g\mu _{v}+\frac{g^{2}\sigma _{v}^{2}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) }-\frac{g\sigma _{v}\sigma _{w}\rho \left( \mu _{\gamma }-\sigma _{\gamma }^{2}\left( \mu _{w}-\ln \lambda \right) \right) }{1-\sigma _{\gamma }^{2}\sigma _{w}^{2}}\right) -1\right] . \end{aligned}$$

(16)

Proof

See “Appendix”. $\square$

Using the equilibrium relationship above, the g-distributed option pricing model with random $\gamma$ is provided below.

Proposition 12

(The random-risk-aversion g-distributed option pricing equation—RRA-g) Given Eq.  (11), and Propositions 5and 16, the prices of a call option with payoff $\kappa \left( v\right) =\max \left( v-k,0\right)$, and of a put option with payoff $\kappa \left( v\right) =\max \left( k-v,0\right) ,$ where k is the strike price, are given respectively by

$$\begin{aligned} call_{0}=\left( gv_{0}+e^{-r}\right) g^{-1}N\left( d_{1}\right) -\left( g^{-1}+k\right) e^{-r}N\left( d_{2}\right) , \end{aligned}$$

(17)

$$\begin{aligned} put_{0}=\left( g^{-1}+k\right) e^{-r}N\left( -d_{2}\right) -\left( gv_{0}+e^{-r}\right) g^{-1}N\left( -d_{1}\right) , \end{aligned}$$

(18)

where

$$\begin{aligned} d_{1}&= \frac{1}{g\sigma _{v}}\ln \left( \frac{gv_{0}e^{r}+1}{gk+1}\right) \frac{\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}{\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}+\frac{g\sigma _{v}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}},\\ d_{2}&= d_{1}-\frac{g\sigma _{v}\left( 1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}{\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) ^{1/2}}, \end{aligned}$$

with $1-\sigma _{\gamma }^{2}\sigma _{w}^{2}>0$.

Proof

See “Appendix”. $\square$

Corollary 13

If the investor’s risk aversion parameter is constant then Eqs. (17) and (18) reduce to the g-option pricing model of Vitiello and Poon (2008).

The implied volatility of the random risk aversion g-distributed option pricing model is shown in Fig. 5, with $g=0.5$ and keeping all other variables with the same values as in the previous figures. Similarly to what happened to the RRA-BS model in Fig. 4, as $\sigma _{\gamma }$ increases, the implied volatility also increases, shifting parallel upwards but retaining the same shape.

Fig. 5

The volatility smile of the RRA-g option pricing model for different values of $\sigma _{\gamma }$. Simulated option prices obtained from Eq. (18) with $g=0.5,$ $\sigma _{v}=0.5$, $\sigma _{w}=0.25$, $\rho =0.85$, $r=10\%$, and different values of $\sigma _{\gamma }$

4.3 A simple empirical application

In this subsection we estimate empirically¹³ the value of $\sigma _{\gamma }$ by using S&P500 put options using the random risk aversion g-distributed option pricing model (RRA-g) from Proposition 12.¹⁴ We use daily prices of 30-day-to-maturity options obtained from OptionMetrics for the period of January 2000 to December 2017. The main reason for using 30-day to maturity options is to avoid issues with different time values of options. The zero-coupon yield and the dividend-yield were also obtained from OptionMetrics, and the value of the S&P 500 index was obtained from CRSP.

As we are pricing options on the market index S&P500, the index and the asset distributions are the same, hence $v=w$, $\sigma _{v}=\sigma _{w}$, and $\rho =1.$ In this case, the RRA-g put option formula in Eq. (18) becomes

$$\begin{aligned} put_{0}=\left( \frac{1}{g}+k\right) e^{-rt}N\left( -d_{2}\right) -\left( \frac{1}{g}\left( gv_{0}e^{-\delta t}+e^{-rt}\right) \right) N\left( -d_{1}\right) , \end{aligned}$$

(19)

where $\delta$ is the dividend yield,

$$\begin{aligned} d_{1}= & {} \ln \left( \frac{gv_{0}e^{\left( r-\delta \right) t}+1}{gk+1}\right) \frac{\left( 1-\sigma _{\gamma }^{2}\sigma _{v}^{2}t^{2}\right) ^{1/2}}{\sigma _{v}\sqrt{t}}+\frac{g\sigma _{v}\sqrt{t}}{2\left( 1-\sigma _{\gamma }^{2}\sigma _{v}^{2}t^{2}\right) },\\ d_{2}= & {} d_{1}-g\sigma _{v}\sqrt{t}\left( 1-\sigma _{\gamma }^{2}\sigma _{v}^{2}t^{2}\right) ^{-1/2}. \end{aligned}$$

Note that here we are using annualised values for the risk free rate, dividends, $\sigma _{v}$, and $\sigma _{\gamma }$ so that Eq. (19) is comparable to the Black and Scholes (1973) model and the g-option model of Vitiello and Poon (2008).

Since our interest here is to estimate $\sigma _{\gamma }$, we use the 5-minute realised volatility obtained from the Oxford-Man Institute of Quantitative Finance as a proxy for $\sigma _{v}$.

The average (mean), the standard deviation (s.d.), and maximum and minimum values for $\sigma _{\gamma }$, and g are presented in Table 1.¹⁵ The average value for g is 1.396, which implies a longer right tail than the log-normal distribution. This is in line with Bakshi and Madan (2006), who obtained a right skewed distribution for risk aversion for both 28 and 56 days (skewness of 2.77 and 2.17 respectively). The mean value $\sigma _{\gamma }=11.57$ seems to be sufficiently high to explain the values of risk aversion simulated by Bekaert et al. (2010), who found that the 95 percentile of risk aversion is equal to 18.8, and that risk aversion exceeds 100 in less than 1% of the cases.

Table 1 Summary of estimated values

We gauge the impact of high values of $\sigma _{\gamma }$ on the implied volatility by calculating the difference between $\sigma _{\gamma }=93.056$, the highest estimated value, and $\sigma _{\gamma }=0$, the case of a constant risk aversion parameter. We calculate theoretical option prices using Eq. (19) with the estimated $\sigma _{\gamma }=93.056$ and then repeat the calculations with $\sigma _{\gamma }=0$, for the 25th of November of 2016, which is the day the highest $\sigma _{\gamma }$ was observed. Based on these theoretical prices, we calculate the implied volatility of an ATM option, obtaining 10.91% for $\sigma _{\gamma }=93.056$, and 8.87% for $\sigma _{\gamma }=0$.¹⁶ That is, an increase from 0 to 93 in $\sigma _{\gamma }$ leads to a change of approximately 2 percentage points in the implied volatility.

The daily estimated values of g, $\sigma _{\gamma }$ and $\sigma _{v}$ obtained from daily put option prices are presented in Fig. 6, panels a, b and c, respectively. The parameters g and $\sigma _{\gamma }$ move approximately together and, as Fig. 7 confirms, high levels of $\sigma _{\gamma }$ tend to be related to high positive levels of skewness of the risk adjusted distribution.

The relationship between parameters $\sigma _{\gamma }$ and $\sigma _{v}$ is presented in Fig. 8, which shows that in periods of low market volatility, $\sigma _{\gamma }$ is high, suggesting a higher dispersion of risk aversion. On the other hand, in periods of high market volatility, the volatility of the risk aversion parameter gets closer to zero. These findings complement, for instance, the ones obtained by Bekaert et al. (2019), who found that risk aversion has a positive relationship with implied volatility and a negative relationship with realised volatility—recall that the theoretical results obtained in Sect. 3 show a positive relationship between the volatility of the risk aversion parameter and implied volatility whilst the results obtained in this section show a negative relationship between the estimated volatility of the risk aversion parameter and realised volatility. Hence, considering our results and the ones by Bekaert et al. (2019) together, when implied volatility increases, risk aversion also increases, but the volatility of the risk aversion parameter decreases.

Fig. 6

Daily estimates of g, $\sigma _{\gamma }$ and $\sigma _{v}$. Estimated values of g, $\sigma _{\gamma }$ and $\sigma _{v}$ obtained from Eq. (19) for daily S&P500 put option prices from January 2000 to December 2017

Fig. 7

The estimated relationship between $\sigma _{\gamma }$ and g. Scatter plot from estimated values of the volatility of the risk aversion parameter, $\sigma _{\gamma }$, and distributional parameter g

Fig. 8

The relationship between $\sigma _{\gamma }$ and $\sigma _{v}$. Scatter plot of $\sigma _{v}$ against estimated values of $\sigma _{\gamma }$

5 Discussion

This article develops a general equilibrium framework for pricing European options when risk aversion is random while aggregate wealth and the underlying asset have a bivariate transformed-normal distribution. The resulting option pricing models depend on the correlation between wealth and the underlying asset, and on the volatility of the underlying asset, wealth and the risk aversion parameter—they do not depend on their means.

We show that the volatility of the risk aversion parameter raises the level of the implied volatility but does not change its shape i.e. the volatility of the risk aversion parameter does not change the shape of the risk neutral distribution. This means that random risk aversion does not alter the relative expensiveness of options, regardless of it being call or put. As the increase in implied volatility is the same for all options, the price impact is the highest for at-the-money calls and puts.

We also show that the volatility and the skewness of the risk aversion parameter change the slope of the pricing kernel. In particular, the slope of the pricing kernel changes when we keep the mean value of the risk aversion parameter constant and change its volatility or skewness. This result complements the ones obtained by Gordon and St-Amour (2000), who show that the level of the risk aversion parameter changes the slope of the pricing kernel.

It is important to highlight that random risk aversion may lead to a non-zero probability that the risk aversion parameter becomes negative, resulting in a non-monotonic pricing kernel. Hence, a risk aversion parameter with low mean and high volatility can make the investor risk averse at low wealth levels and risk seeking at high wealth levels. Similarly, low values of skewness can also lead to a non-monotonic pricing kernel.

Finally, we show that the empirically estimated volatility of the risk aversion parameter and the market volatility display a negative relationship. The estimated volatility of the risk aversion parameter is very small (tends to zero) when the market volatility is high and vice-versa.

Appendix

Proof

(Proposition 3) Solving the denominator of Eq. (3) first, leads to

$$\begin{aligned} \sum _{s}p_{s}Eu'\left( w,s\right)&=\sum _{s}p_{s}E\left[ \lambda ^{\gamma _{s}}e^{-\gamma _{s}h_{w}\left( w\right) }\right] \\&=p_{1}E\left[ \lambda ^{\gamma _{1}}e^{-\gamma _{1}h_{w}\left( w\right) }\right] +\cdots +p_{N}E\left[ \lambda ^{\gamma _{N}}e^{-\gamma _{N}h_{w}\left( w\right) }\right] \\&=p_{1}\lambda ^{\gamma _{1}}e^{-\mu _{w}\gamma _{1}+0.5\gamma _{1}^{2}\sigma _{w}^{2}}+\cdots +p_{N}\lambda e^{-\mu _{w}\gamma _{N}+0.5\gamma _{N}^{2}\sigma _{w}^{2}} \\&=\sum _{s}p_{s}\lambda ^{\gamma _{s}}\exp \left( -\mu _{w}\gamma _{s}+0.5\gamma _{s}^{2}\sigma _{w}^{2}\right) , \end{aligned}$$

(A.1)

where each one of the expectations in the second row can be solved as follows (note that the expectations are independent)

$$\begin{aligned} E\left[ \lambda ^{\gamma _{s}}e^{-\gamma _{s}h_{w}\left( w\right) }\right]&=\int _{-\infty }^{\infty }\frac{\lambda ^{\gamma _{s}}e^{-\gamma _{s}h_{w}\left( w\right) }}{\sigma _{s}\sqrt{2\pi }}\left| h_{w}'\left( w\right) \right| e^{-0.5\sigma _{w}^{-2}\left( h_{w}\left( w\right) -u_{w}\right) ^{2}}dw\\ &=\lambda ^{\gamma _{s}}\exp \left( -\mu _{w}\gamma _{s}+0.5\gamma _{s}^{2}\sigma _{w}^{2}\right) . \end{aligned}$$

Considering Eq. (4) and summing it over all N states gives the numerator of Eq. (3), which can be written as $\sum _{s}p_{s}\lambda ^{\gamma _{s}}\exp \left( -\gamma _{s}h\left( w\right) \right)$. Dividing this expression by Eq. (A.1) leads to Eq. (5). $\square$

Proof

(Proposition 5). The pricing kernel in Eq. (8) can be obtained from (3). As $\gamma$ and w are independent, the denominator can be obtained by solving $\int \int \exp \left[ -h_{\gamma }\left( \gamma \right) h_{w}\left( w\right) \right] f_{TN}(w)f_{TN}(\gamma )dwd\gamma$, which leads to

$$\begin{aligned} E\left[ U'\left( w\right) \right]& = \left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{-1/2}\exp \left[ \frac{1}{2\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) }\left( \sigma _{\gamma }^{2}B^{2}-2\mu _{\gamma }B+\mu _{\gamma }^{2}\sigma _{w}^{2}\right) \right] , \end{aligned}$$

(A.2)

where $f_{TN}\left( \cdot \right)$ is a transformed-normal density function, $B=\mu _{w}-\ln \lambda$, and $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$. Dividing (7) by (A.2) yields Eq. (8). $\square$

Proof

(Proposition 7) Given Eq. (8) and the fact that wealth and the underlying asset have a bivariate log-normal distribution, we can write equation (10) as

$$\begin{aligned} v_{0}=e^{-r}\int \int v\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}e^{\frac{1}{2}\sigma _{\gamma }^{2}A^{2}-\mu _{\gamma }A+\frac{1}{2\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) }\left( 2\mu _{\gamma }B-\sigma _{\gamma }^{2}B^{2}-\mu _{\gamma }^{2}\sigma _{w}^{2}\right) }f_{\Lambda }\left( w,v\right) dwdv, \end{aligned}$$

(A.3)

where $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$,$A=h_{w}\left( w\right) -\ln \lambda$, $B=\mu _{w}-\ln \lambda$, and

$$\begin{aligned} f_{\Lambda }\left( w,v\right) =\frac{\exp \left[ -\frac{1}{2\left( 1-\rho ^{2}\right) }\left[ \left( \frac{\ln w-\mu _{w}}{\sigma _{w}}\right) ^{2}+\left( \frac{\ln v-\mu _{v}}{\sigma _{v}}\right) ^{2}-2\rho \left( \frac{\ln w-\mu _{w}}{\sigma _{w}}\right) \left( \frac{\ln v-\mu _{v}}{\sigma _{v}}\right) \right] \right] }{2\pi vw\sigma _{v}\sigma _{w}\sqrt{1-\rho ^{2}}} \end{aligned}$$

(A.4)

is the bivariate log-normal density.

The solution to Eq. (A.3) is a matter of algebra, where Eq. (12) can be obtained by means of changing variables and then simplifying the resulting equation. $\square$

Proof

(Proposition 8) Using the results from Proposition 5, Eq. (11), and the bivariate log-normal density in Eq. (A.4) we obtain

$$\begin{aligned} call_{0}=e^{-rt}\int \int \max \left( v-k,0\right) \left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}e^{\frac{1}{2}\sigma _{\gamma }^{2}A^{2}-\mu _{\gamma }A+\frac{2\mu _{\gamma }B-\sigma _{\gamma }^{2}B^{2}-\mu _{\gamma }^{2}\sigma _{w}^{2}}{2\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) }}f_{\Lambda }\left( w,v\right) dwdv, \end{aligned}$$

where $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$, $A=h_{w}\left( w\right) -\ln \lambda$, and $B=\mu _{w}-\ln \lambda$.

Changing variables, solving the inner integral and simplifying yields,

$$\begin{aligned} call_{0}&=e^{-rt}\int \frac{\max \left( \exp \left( v\sigma _{v}+\mu _{v}\right) -k,0\right) \left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}}{\sqrt{2\pi }\sqrt{1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}}}\\&\times \exp \left[ -\frac{\left( v\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) +\sigma _{w}\rho \left( \mu _{\gamma }-\sigma _{\gamma }^{2}\left( \mu _{w}-\ln \lambda \right) \right) \right) ^{2}}{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) \left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\left( 1-\rho ^{2}\right) \right) }\right] dv. \end{aligned}$$

Expanding the expression above and using the market equilibrium relationship from Eq. (12) leads to Eq. (14). The put option equation can be obtained in a similar way. $\square$

Proof

(Proposition 11) This proof is similar to the one to Proposition 7. Given Eq. (8) and the fact that wealth and the underlying asset have a bivariate g-log-normal distribution, we obtain an equation similar to (A.3), but the expectation is taken with respect to the bivariate g-log-normal distribution. That is, in Eq. (A.3) we replace $f_{\Lambda }\left( w,v\right)$ with the following density

$$\begin{aligned} f_{g-\Lambda }\left( w,v\right) =\frac{\exp \left[ -\frac{1}{2\left( 1-\rho ^{2}\right) }\left[ \left( \frac{\ln w-\mu _{w}}{\sigma _{w}}\right) ^{2}+\left( \frac{\ln \left(gv+1 \right) - g\mu _{v}}{g \sigma _{v}}\right) ^{2}-2\rho \left( \frac{\ln w-\mu _{w}}{\sigma _{w}}\right) \left( \frac{ \ln \left(gv+1 \right) - g\mu _{v}}{g \sigma _{v}}\right) \right] \right] }{2\pi \left(gv+1 \right) w\sigma _{v}\sigma _{w}\sqrt{1-\rho ^{2}}}. \end{aligned}$$

(A.5)

Changing variables and simplifying the resulting equation proves the proposition. $\square$

Proof

(Proposition 12) This proof is similar to the one to Proposition 8. Using the results from Proposition 5, Eq. (11), and the bivariate g-log-normal density in Eq. (A.5) we obtain

$$\begin{aligned} call_{0}=e^{-rt}\int \int \max \left( v-k,0\right) \left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}e^{\frac{1}{2}\sigma _{\gamma }^{2}A^{2}-\mu _{\gamma }A+\frac{2\mu _{\gamma }B-\sigma _{\gamma }^{2}B^{2}-\mu _{\gamma }^{2}\sigma _{w}^{2}}{2\left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) }}f_{g-\Lambda }\left( w,v\right) dwdv, \end{aligned}$$

where $1-\sigma _{w}^{2}\sigma _{\gamma }^{2}>0$, $A=h_{w}\left( w\right) -\ln \lambda$, and $B=\mu _{w}-\ln \lambda$.

Changing variables, solving the inner integral and simplifying yields,

$$\begin{aligned} call_{0}&=e^{-rt}sign(g)\int _{-sign(g)\infty }^{sign(g)\infty }\frac{\max \left( \exp \left( gv\sigma _{v}+g\mu _{v}\right) -k,0\right) \left( 1-\sigma _{w}^{2}\sigma _{\gamma }^{2}\right) ^{1/2}}{\sqrt{2\pi }\sqrt{1-\left( 1-\rho ^{2}\right) \sigma _{\gamma }^{2}\sigma _{w}^{2}}}\\&\times \exp \left[ -\frac{\left( v\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) +\sigma _{w}\rho \left( \mu _{\gamma }-\sigma _{\gamma }^{2}\left( \mu _{w}-\ln \lambda \right) \right) \right) ^{2}}{2\left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\right) \left( 1-\sigma _{\gamma }^{2}\sigma _{w}^{2}\left( 1-\rho ^{2}\right) \right) }\right] dv. \end{aligned}$$

Expanding the expression above and using the market equilibrium relationship from Eq. (16) leads to Eq. (17). The put option equation can be obtained in a similar way. $\square$