Skip to main content
SpringerLink
Log in

The pricing kernel puzzle: survey and outlook

  • Research Article
  • Published:
Annals of Finance Aims and scope Submit manuscript

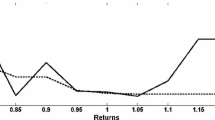
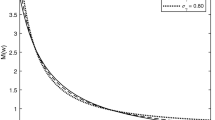
Abstract

It has been a while since the literature on the pricing kernel puzzle was summarized in Jackwerth (Option-implied risk-neutral distributions and risk-aversion, The Research Foundation of AIMR, Charlotteville, 2004). That older survey also covered the topic of risk-neutral distributions, which was itself already surveyed in Jackwerth (J Deriv 2:66–82, 1999). Much has happened in those years and estimation of risk-neutral distributions has moved from new and exciting in the last half of the 1990s to becoming a well-understood technology. Thus, the present survey will focus on the pricing kernel puzzle, which was first discussed around 2000. We document the pricing kernel puzzle in several markets and present the latest evidence concerning its (non-)existence. Econometric studies are detailed which test for the pricing kernel puzzle. The present work adds much breadth in terms of economic explanations of the puzzle. New challenges for the field are described in the process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. For the fit of a continuous time Levy-processes see Carr et al. (2002).

  2. Note that Friedman and Savage (1948) introduced their utility function for individuals and not for the representative investor. In particular, their concern was with small stakes gambling such as buying a lottery ticket. Chetty and Szeidl (2007) provide a microeconomic motivation for Friedman–Savage utility via consumption commitments (e.g. housing), for which the spending cannot easily be adjusted. Again, this is a model of individual investors, and it is not obvious that the convexities would survive aggregation to a representative investor. See Ingersoll (2014) for related results on another partially convex utility function, namely cumulative prospect theory.

  3. Zdorovenin and Pezier (2011) use a close variant, too, and are subject to the same critique as Kostakis et al. (2011).

  4. See also Lioui and Malka (2004) for reported differences due to using either only call or only put options.

  5. Compare Linn et al. (2014), who can only establish the pricing kernel puzzle for the FTSE 100 but not for the S&P 500. Cuesdeanu and Jackwerth (2017) attribute this result to (i) a lack of scaling so that the physical distributions of Linn et al. (2014) are not integrating to one and (ii) a mismatch in their optimization (based on moments of the uniform distribution via GMM) and their measurement of fit (based on the Cramer van Mises statistic).

  6. In particular, they find that the empirical volatility pricing kernel is u-shaped; a fact that is not captured by any option pricing model so far. A related observation by Boes et al. (2007) is that that the risk-neutral distribution, conditional on a low spot volatility, does not exhibit negative skewness.

  7. For a study on forecasting option returns, see Israelov and Kelly (2017).

  8. Branger et al. (2011) do not confirm their result in more recent data, thus documenting the presence of the pricing kernel puzzle in the data. They further argue that stochastic volatility, stochastic jump option pricing models, which also have jumps in the volatility process, can explain those call option returns.

  9. The empirical evidence is consistent with Branger et al. (2011); compare for the theoretical results also Chaudhuri and Schroder (2015).

  10. Carr and Yu (2012) replace the assumptions on the utility function of a representative investor by assuming that the dynamics of the numeraire portfolio under the physical measure are being driven by a bounded diffusion. Walden (2017) extends Ross (2015) recovery to unbounded diffusion processes and Huang and Shaliastovich (2014) to the state dependent, recursive preferences of Epstein and Zin (1989). Schneider and Trojani (2015) suggest recovery based on assumptions on the signs of risk premia on different moments of market returns.

  11. This point is also made in Borovicka et al. (2015) who attribute these problems to “misspecified recovery,” which happens when the pricing kernel has non-trivial martingale components.

  12. In such setting, Shefrin (2008a, b) coins the term sentiment for the ratio of the mixture of the different subjective distributions and the physical distribution. His ideas become clearer when one assumes that the shapes of the subjective distributions and the physical distributions remain the same but the mean is low for the pessimists, high for the optimists, and in between for the physical distribution, see Shefrin (2008b, Fig. 1).

  13. Although the model captures stochastic volatility and jumps, the risk-aversion functions turn negative for high return states, implying a u-shaped pricing kernel. Such behavior contradicts the standard assumption of a risk-averse representative investor. This leads to the question, if stochastic volatility, stochastic jump models are typically incapable of fitting the historical risk-neutral and physical distribution simultaneously, or if the assumptions on the functional form of the risk-premium parameters are mis-specified in such models.

  14. A number of papers show that such additional state variables seem to be empirically needed in order to explain option prices, see for example Buraschi and Jackwerth (2001), Coval and Shumway (2001), and Constantinides et al. (2013).

  15. Benzoni et al. (2011) offer a similar model but do not show the model pricing kernel in the return dimension, and one cannot easily determine if it exhibits the pricing kernel puzzle; the pricing kernel in the dimension of consumption is monotonically decreasing by assumption.

  16. For a survey of ambiguity aversion and its relevance for asset pricing, see Epstein and Schneider (2010). For an alternative formulation of ambiguity aversion through Choquet expected utility, see Bassett et al. (2004).

  17. Unfortunately, we cannot easily analyze the derivative of the pricing kernel with respect to returns. The resulting expressions are intractable and cannot be nicely segregated into, say, an income and a substitution effect.

  18. Note that alternatively, one could also use \(U(x)=\frac{x^{1-\gamma }-1}{1-\gamma }\) with \(\gamma \in (0,1)\) but the above formulation allows for a great range of risk aversion coefficients.

  19. Marroquin-Martinez and Moreno (2013) extend Cochrane and Saa-Requejo (2000) and Bernardo and Ledoit (2000) to settings with stochastic volatility and find the resulting bounds to be tighter than in the original papers.

References

  • Ait-Sahalia, Y., Lo, A.W.: Nonparametric estimation of state-price densities implicit in financial asset prices. J Finance 53, 499–547 (1998)

    Google Scholar 

  • Ait-Sahalia, Y., Lo, A.W.: Nonparametric risk management and implied risk aversion. J Econom 94, 9–51 (2000)

    Google Scholar 

  • Ait-Sahalia, Y., Duarte, J.: Nonparametric option pricing under shape restrictions. J Econom 116, 9–47 (2003)

    Google Scholar 

  • Alcock, J., Smith, G.: Testing alternative measure changes in nonparametric pricing and hedging of European options. J Futures Mark 34, 320–345 (2014)

    Google Scholar 

  • Andreou, P.C., Kagkadis, A., Philip, D.: Investor sentiments, rational beliefs, and option prices. Working paper, Lancaster University (2014)

  • Audrino, F., Meier, P.: Empirical pricing kernel estimation using a functional gradient descent algorithm based on splines. Working paper, University of St. Gallen (2012)

  • Audrino, F., Huitema, R., Ludwig, M.: An empirical analysis of the Ross recovery. Working paper, University of St. Gallen (2015)

  • Babaoglu, K., Christoffersen, P., Heston, S., Jacobs, K.: Option valuation with volatility components, fat tails, and non-monotonic pricing kernels. Working paper, University of Toronto (2016)

  • Backus, D., Chernov, M., Martin, I.: Disasters implied by equity index options. J Finance 66, 1969–2012 (2011)

    Google Scholar 

  • Bahra, B.: Implied risk-neutral probability density functions from option prices: theory and application. Working paper, Bank of England, no. 66 (1997)

  • Bakshi, G., Madan, D.: Investor heterogeneity, aggregation, and the non-monotonicity of the aggregate marginal rate of substitution in the price of market-equity. Working paper, University of Maryland (2007)

  • Bakshi, G., Madan, D.B., Panayotov, G.: Returns of claims on the upside and the viability of u-shaped pricing kernels. J Financ Econ 97, 130–154 (2010)

    Google Scholar 

  • Bakshi, G., Madan, D.B., Panayotov, G.: Heterogeneity in beliefs and volatility tail behavior. J Financ Quant Anal 50, 1389–1414 (2015)

    Google Scholar 

  • Bali, T.G., Cakici, N., Chabi-Yo, F., Murray, M.: The Risk-Neutral Distribution of Option Returns. Georgetown University (2017)

  • Barone-Adesi, G., Dall’O, H.: Is the price kernel monotone? Working paper, Swiss Finance Institute (2010)

  • Barone-Adesi, G., Mancini, L., Shefrin, H.: A tale of two investors: estimating optimism and overconfidence. Working paper, Swiss Finance Institute (2013)

  • Barone-Adesi, G., Engle, R., Mancini, L.: A GARCH option pricing model with filtered historical simulation. Rev Financ Stud 21, 1223–1258 (2008)

    Google Scholar 

  • Bartunek, K.S., Chowdhury, M.: Implied risk aversion parameter from option prices. Financ Rev 32, 107–124 (1997)

    Google Scholar 

  • Bassett, G.W., Koenker, R., Kordas, G.: Pessimistic portfolio allocation and Choquet expected utility. J Financ Econom 2, 477–492 (2004)

    Google Scholar 

  • Bates, D.: Post-’87 crash fears in S&P 500 futures options. J Econom 94, 181–238 (2000)

    Google Scholar 

  • Bates, D.: U.S. stock market crash risk, 1926–2010. J Financ Econ 105, 229–259 (2012)

    Google Scholar 

  • Bates, D.: Testing option pricing models. In: Maddala, G.S., Rao, C. R. (eds.) Statistical Methods in Finance (Handbook of Statistics, vol. 14, Chapter 20), pp. 567–611. Elsevier Science, Amsterdam (1996a)

  • Bates, D.: Jumps and stochastic volatility: exchange rate processes implicit in Deutsche mark options. Rev Financ Stud 9, 69–107 (1996b)

    Google Scholar 

  • Bates, D.: The market for crash risk. J Econ Dyn Control 32, 2291–2321 (2008)

    Google Scholar 

  • Beare, B.K.: Measure preserving derivatives and the pricing kernel puzzle. J Math Econ 47, 689–697 (2011)

    Google Scholar 

  • Beare, B.K., Schmidt, L.: An empirical test of pricing kernel monotonicity. J Appl Econom 31, 338–356 (2014)

    Google Scholar 

  • Beare, B.K., Schmidt, L.: Empirical implications of the pricing kernel puzzle for the return on contingent claims. Working paper, UC San Diego (2015)

  • Belomestny, D., Haerdle, W., Krymova, E.: Sieve estimation of the minimal entropy martingale marginal density with application to pricing kernel estimation. Int J Theor Appl Finance 20, 1750041 (2017)

    Google Scholar 

  • Benth, F.E., Groth, M., Lindberg, C.: The implied risk aversion from utility indifference option pricing in a stochastic volatility model. Int J Appl Math Stat 16, 11–37 (2010)

    Google Scholar 

  • Benzoni, L., Collin-Dufresne, P., Goldstein, R.: Explaining asset pricing puzzles associated with the 1987 market crash. J Financ Econ 101, 552–573 (2011)

    Google Scholar 

  • Berkowitz, J.: Testing density Forecasts with applications to risk management. J Bus Econ Stat 19, 465–474 (2001)

    Google Scholar 

  • Bernardo, A., Ledoit, O.: Gain, loss, and asset pricing. J Polit Econ 108, 144–172 (2000)

    Google Scholar 

  • Bliss, R., Panigirtzoglou, N.: Testing the stability of implied probability density functions. J Bank Finance 26, 381–422 (2002)

    Google Scholar 

  • Bliss, R., Panigirtzoglou, N.: Option-implied risk aversion estimates. J Finance 59, 407–446 (2004)

    Google Scholar 

  • Boes, M.J., Drost, F.C., Werker, B.J.M.: Nonparametric risk-neutral joint return and volatility distributions. Working paper, VU University Amsterdam and Tilburg University (2007)

  • Bollen, N., Whaley, R.: Does net buying pressure affect the shape of implied volatility functions? J Finance 59, 711–754 (2004)

    Google Scholar 

  • Bollerslev, T., Todorov, V.: Tails, fears and risk premia. J Finance 66, 2165–2211 (2011)

    Google Scholar 

  • Borovicka, J., Hansen, L.P., Scheinkman, J.A.: Misspecified recovery. Working paper, NBER (2015)

  • Branger, N., Hansis, A., Schlag, C.: The impact of risk premia on expected option returns. Working paper, University of Muenster (2011)

  • Breeden, D.T., Litzenberger, R.H.: Prices of state-contingent claims implicit in options prices. J Bus 51, 621–651 (1978)

    Google Scholar 

  • Broadie, M., Chernov, M., Johannes, M.: Understanding index option returns. Rev Financ Stud 22, 4493–4529 (2009)

    Google Scholar 

  • Brown, D., Jackwerth, J.C.: The pricing kernel puzzle: reconciling index option data and economic theory. In: Batten, J.A., Wagner, N. (eds.) Contemporary Studies in Economics and Financial Analysis: Derivative Securities Pricing and Modelling, vol. 94, pp. 155–183. Bingley: Emerald Group (2012)

  • Buraschi, A., Jackwerth, J.C.: The price of a smile: hedging and spanning in option markets. Rev Financ Stud 14, 495–527 (2001)

    Google Scholar 

  • Campbell, J., Cochrane, J.: By force of habit: a consumption-based explanation of aggregate stock market behavior. J Polit Econ 107, 205–251 (1999)

    Google Scholar 

  • Carr, P., Yu, J.: Risk, return, and Ross recovery. J Deriv 20, 38–59 (2012)

    Google Scholar 

  • Carr, P., Geman, H., Madan, D.P., Yor, M.: The fine structure of asset returns: an empirical investigation. J Bus 75, 305–332 (2002)

    Google Scholar 

  • Chabi-Yo, F.: Pricing kernels with stochastic skewness and volatility risk. Manag Sci 58, 624–640 (2012)

    Google Scholar 

  • Chabi-Yo, F., Song, Z.: Recovering the probability weights of tail events with volatility risk from option prices. Working paper, Ohio State (2013)

  • Chabi-Yo, F., Garcia, R., Renault, E.: State dependence can explain the risk aversion puzzle. Rev Financ Stud 21, 973–1011 (2008)

    Google Scholar 

  • Chaudhuri, R., Schroder, M.D.: Monotonicity of the stochastic discount factor and expected option returns. Rev Financ Stud 28, 1462–1505 (2015)

    Google Scholar 

  • Chernov, M.: Empirical reverse engineering of the pricing kernel. J Econom 116, 329–364 (2003)

    Google Scholar 

  • Chernov, M., Ghysels, E.: A study towards a unified approach to the joint estimation of objective and risk-neutral measures for the purpose of options valuation. J Financ Econ 56, 207–458 (2000)

    Google Scholar 

  • Chetty, R., Szeidl, A.: Consumption commitments and risk preferences. Q J Econ 122, 831–877 (2007)

    Google Scholar 

  • Christoffersen, P., Heston, S., Jacobs, K.: Capturing option anomalies with a variance-dependent pricing kernel. Rev Financ Stud 26, 1962–2006 (2013)

    Google Scholar 

  • Christoffersen, P., Heston, S., Jacobs, K.: The shape and term structure of the index option smirk: why multifactor stochastic volatility models work so well. Manag Sci 55, 1914–1932 (2009)

    Google Scholar 

  • Christoffersen, P., Jacobs, K., Chang, B.Y.: Forecasting with option-implied information. In: Elliot, G., Timmermann, A. (eds.) Handbook of Economic Forecasting, vol. 2, pp. 581–656. Amsterdam: North-Holland (2013)

  • Cochrane, J.H., Saa-Requejo, J.: Beyond arbitrage: good-deal asset price bounds in incomplete markets. J Polit Econ 108, 79–119 (2000)

    Google Scholar 

  • Constantinides, G.M., Perrakis, S.: Stochastic dominance bounds on derivative prices in a multiperiod economy with proportional transaction costs. J Econ Dyn Control 26, 1323–1352 (2002)

    Google Scholar 

  • Constantinides, G.M., Perrakis, S.: Stochastic dominance bounds on American option prices in markets with frictions. Rev Finance 11, 71–115 (2007)

    Google Scholar 

  • Constantinides, G.M., Jackwerth, J.C., Savov, A.: The puzzle of index option returns. Rev Asset Pricing Stud 3, 229–257 (2013)

    Google Scholar 

  • Constantinides, G.M., Jackwerth, J.C., Perrakis, S.: Option pricing: real and risk-neutral distributions. In: Birge, J.R., Linetsky, V. (eds.) Handbooks in Operations Research and Management Science: Financial Engineering, vol. 15, pp. 565–591. Amsterdam: Elsevier (2008)

  • Constantinides, G.M., Jackwerth, J.C., Stylianos Perrakis, S.: Mispricing of S&P 500 index options. Rev Financ Stud 22, 1247–1277 (2009)

    Google Scholar 

  • Constantinides, G.M., Czerwonko, M., Jackwerth, J.C., Perrakis, S.: Are options on index futures profitable for risk averse investors? Empirical evidence. J Finance 66, 1401–1431 (2011)

    Google Scholar 

  • Coutant, S.: Implied risk aversion in option prices using Hermite polynomials. Working paper, Banque de France (1999)

  • Coutant, S.: Time-varying implied risk aversion in option prices using Hermite polynomials. Working paper, Banque de France (2000)

  • Coval, J.D., Shumway, T.: Expected option returns. J Finance 56, 983–1009 (2001)

    Google Scholar 

  • Cuesdeanu, H.: Empirical pricing kernels: a tale of two tails and volatility. Working paper, University of Konstanz (2016)

  • Cuesdeanu, H., Jackwerth, J.C.: The pricing kernel puzzle in forward looking data. Rev. Deriv. Res. (2017). https://doi.org/10.1007/s11147-017-9140-8

  • David, A., Veronesi, P.: Investors’ and central bank’s uncertainty embedded in index options. Rev Financ Stud 27, 1661–1716 (2014)

    Google Scholar 

  • Detlefsen, K., Haerdle, W., Moro, R.: Empirical pricing kernels and investor preferences. J Math Methods Econ Finance 3, 19–48 (2010)

    Google Scholar 

  • Diebold, F.X., Tay, A.S., Wallis, K.F.: Evaluating density forecasts of inflation: the survey of professional forecasters. In: Engle, R.F., White, H. (eds.) Cointegration, Causality, and Forecasting: A Festschrift in Honour of Clive W. J. Granger, pp. 76–90. New York: Oxford University Press (1999)

  • Diebold, F.X., Gunther, T.A., Tay, A.S.: Evaluating density forecasts with applications to financial risk management. Int Econ Rev 39, 863–883 (1998)

    Google Scholar 

  • Dierkes, M.: Probability weighting and asset prices. Working paper, University of Muenster (2013)

  • Dimson, E., Marsh, P., Staunton, M.: Equity premiums around the world. In: Hammond, B., Leibowitz, M., Siegel, L. (eds.) Rethinking the Equity Premium, Chapter 4, pp. 32–52. Charlottesville: Research Foundation of the CFA Institute (2012)

  • Dittmar, R.F.: Nonlinear pricing kernels, kurtosis preference, and evidence from the cross section of equity returns. J Finance 57, 369–403 (2002)

    Google Scholar 

  • Drechsler, I.: Uncertainty, time-varying fear, and asset prices. J Finance 68, 1843–1889 (2013)

    Google Scholar 

  • Duan, J.C., Zhang, W.: Forward-looking market risk premium. Manag Sci 60, 521–538 (2014)

    Google Scholar 

  • Dybvig, P.H.: Distributional analysis of portfolio choice. J Bus 61, 369–93 (1988)

    Google Scholar 

  • Epstein, L.G., Schneider, M.: Ambiguity and asset markets. Annu Rev Financ Econ 2, 315–346 (2010)

    Google Scholar 

  • Epstein, L.G., Zin, S.: Substitution, risk aversion, and the temporal behavior of consumption and asset returns: a theoretical framework. Econometrica 57, 937–969 (1989)

    Google Scholar 

  • EZB: Der Informationsgehalt von Optionspreisen während der Finanzkrise. Monatsbericht, EZB Februar (2011)

  • Fengler, M., Hin, L.Y.: Semi-nonparametric estimation of the call price surface under no-arbitrage constraints. J Econom 184, 242–261 (2015)

    Google Scholar 

  • Figlewski, S.: Estimating the implied risk-neutral density for the U.S. market portfolio. In: Bollerslev, T., Russell, J., Watson, M. (eds.) Volatility and Time Series Econometrics: Essays in Honor of Robert F. Engle, pp. 323–353. Oxford: Oxford University Press (2010)

  • Figlewski, S., Malik, F.M.: Options on leveraged ETFs: a window on investor heterogeneity. Working paper, New York University (2014)

  • Friedman, M., Savage, L.J.: Utility analysis of choices involving risk. J Polit Econ 56, 279–304 (1948)

    Google Scholar 

  • Garcia, R., Luger, R., Renault, E.: Empirical assessment of an intertemporal option pricing model with latent variables. J Econom 116, 49–83 (2003)

    Google Scholar 

  • Garleanu, N., Pedersen, L.H., Poteshman, A.M.: Demand-based option pricing. Rev Financ Stud 22, 4259–4299 (2009)

    Google Scholar 

  • Gemmill, G., Shackleton, M.B.: Prospect theory and option prices: evidence from S&P 500 index options. Working paper, Warwick University (2005)

  • Giacomini, E., Haerdle, W.: Dynamic semiparametric factor models in pricing kernel estimation. In: Dabo-Niang, S., Ferraty, F. (eds.) Functional and Operational Statistics, Contributions to Statistics, pp. 181–187. Heidelberg: Springer (2008)

  • Giacomini, E., Handel, M., Haerdle, W.: Time dependent relative risk aversion. In: Bol, G., Rachev, S.T., Würth, R. (eds.) Risk Assessment: Decisions in Banking and Finance, pp. 15–46. Heidelberg: Physica (2008)

  • Glosten, L.R., Jagannathan, R., Runkle, D.E.: On the relation between the expected value and the volatility of the nominal excess return on stocks. J Finance 48, 1779–1801 (1993)

    Google Scholar 

  • Gollier, C.: Portfolio choices and asset prices: the comparative statics of ambiguity aversion. Rev Econ Stud 78, 1329–1344 (2011)

    Google Scholar 

  • Golubev, Y., Haerdle, W., Timofeev, R.: Testing monotonicity of pricing kernels. AStA Adv Stat Anal 98, 305–32 (2014)

    Google Scholar 

  • Grith, M., Haerdle, W., Park, J.: Shape invariant modeling pricing kernels and risk aversion. J Financ Econom 11, 370–399 (2013)

    Google Scholar 

  • Grith, M., Haerdle, W., Kraetschmer, V.: Reference dependent preferences and the EPK puzzle. Rev Finance 21, 269–298 (2017)

    Google Scholar 

  • Haas, J.R., Fajardo Barbachan, J.S., Rocha de Farias, A.: Estimating relative risk aversion, risk-neutral and real-world densities using Brazilian real currency options. Econ Apl 16, 567–577 (2012)

    Google Scholar 

  • Haerdle, W., Grith, M., Mihoci, A.: Cross country evidence for the EPK paradox. Working paper, Humboldt University (2014)

  • Haerdle, W., Kraetschmer, V., Moro, R.: A microeconomic explanation of the EPK paradox. Working paper, Humboldt University (2009)

  • Haerdle, W., Okhrin, Y., Wang, W.: Uniform confidence bands for pricing kernels. J Financ Econom 13, 376–413 (2015)

    Google Scholar 

  • Haley, M.R., Walker, T.: Alternative tilts for nonparametric option pricing. J Futures Mark 30, 983–1006 (2010)

    Google Scholar 

  • Han, B.: Investor sentiment and option prices. Rev Financ Stud 21, 387–414 (2008)

    Google Scholar 

  • Han, Q., Turvey, C.G.: Equilibrium market prices for risks and market risk aversion in a complete stochastic volatility model with habit formation. Working paper, Cornell University (2010)

  • Hens, T., Reichlin, C.: Three solutions to the pricing kernel puzzle. Rev Finance 17, 1065–1098 (2013)

    Google Scholar 

  • Heston, S.L.: A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev Financ Stud 6, 327–343 (1993)

    Google Scholar 

  • Heston, S., Nandi, S.: A closed-form GARCH option pricing model. Rev Financ Stud 13, 585–626 (2000)

    Google Scholar 

  • Hill, S.I.: Tracking value at risk through derivative prices. J Comput Finance 16, 79–121 (2013)

    Google Scholar 

  • Hodges, S.D., Tompkins, R.G., Ziemba, W.T.: The favorite-longshot bias in S&P 500 and FTSE 100 index futures options: the return to bets and the cost of insurance. In: Hausch, D.B., Ziemba, W.T. (eds.) Handbook of Sports and Lottery Markets. Amsterdam: Elsevier (2008)

  • Huang, D., Shaliastovich, I.: Risk adjustment and the temporal resolution of uncertainty: evidence from options markets. Working paper, University of Pennsylvania (2014)

  • Ingersoll, J.E.: Cumulative prospect theory, aggregation, and pricing. Crit Finance Rev 4, 1–55 (2014)

    Google Scholar 

  • Israelov, R., Kelly, B.: Forecasting the distribution of option returns. Working paper, University of Chicago (2017)

  • Jackwerth, J.C.: Option-implied risk-neutral distributions and implied binomial trees: a literature review. J Deriv 2, 66–82 (1999)

    Google Scholar 

  • Jackwerth, J.C.: Recovering risk aversion from option prices and realized returns. Rev Financ Stud 13, 433–467 (2000)

    Google Scholar 

  • Jackwerth, J.C.: Option-implied risk-neutral distributions and risk-aversion. Charlotteville: The Research Foundation of AIMR (2004)

  • Jackwerth, J.C., Vilkov, G.: Asymmetric volatility risk: evidence from option markets. Working paper, University of Konstanz (2017)

  • Jackwerth, J.C., Rubinstein, M.: Recovering probability distributions from option prices. J Finance 51, 1611–1631 (1996)

    Google Scholar 

  • Jackwerth, J.C., Menner, M.: Does the Ross recovery theorem work empirically? Working paper, University of Konstanz (2015)

  • Jensen, C.S., Lando, D., Pedersen, L.H.: Generalized recovery. Working paper, Copenhagen Business School (2016)

  • Kang, B.J., Kim, T.S.: Option-implied risk preferences: an extension to wider classes of utility functions. J Financ Mark 9, 180–198 (2006)

    Google Scholar 

  • Kang, B.J., Kim, T.S., Lee, H.S.: Option-implied preferences with model uncertainty. J Futures Mark 34, 498–515 (2014)

    Google Scholar 

  • Kiesel, R., Rahe, F.: Option pricing under time-varying risk-aversion with applications to risk forecasting. J Bank Finance 76, 120–138 (2017)

    Google Scholar 

  • Kitsul, Y., Wright, J.H.: The economics of options-implied inflation probability density functions. J Financ Econ 110, 696–711 (2013)

    Google Scholar 

  • Klibanoff, P., Marinacci, M., Mukerji, S.: A smooth model of decision making under ambiguity. Econometrica 73, 1849–1892 (2005)

    Google Scholar 

  • Kliger, D., Levy, O.: Theories of choice under risk: insights from financial markets. J Econ Behav Organ 71, 330–346 (2009)

    Google Scholar 

  • Kocherlakota, N.R.: The equity premium: it’s still a puzzle. J Econ Lit 34, 42–71 (1996)

    Google Scholar 

  • Kostakis, A., Panigirtzoglou, N., Skiadopoulos, G.: Market timing with option-implied distributions: a forward-looking approach. Manag Sci 57, 1231–1249 (2011)

    Google Scholar 

  • Leisen, D.: Small sample bias in pricing kernel estimations. Working paper, University of Mainz (2014)

  • Li, H., Zhao, F.: Nonparametric estimation of state-price densities implicit in interest rate cap prices. Rev Financ Stud 22, 4335–4376 (2009)

    Google Scholar 

  • Linn, M., Shive, S., Shumway, T.: Pricing kernel monotonicity and conditional information. Working paper, University of Michigan (2014)

  • Lioui, A., Malka, R.: Revealing the parameter of risk-aversion from option prices when markets are incomplete: theory and evidence. Working paper, Bar Ilan University (2004)

  • Liu, J., Pan, J., Wang, T.: An equilibrium model of rare-event premia and its implication for option smirks. Rev Financ Stud 18, 131–164 (2005)

    Google Scholar 

  • Liu, X., Kuo, J.M., Coakley, J.: A pricing kernel approach to valuing options on interest rate futures. Eur J Finance 21, 93–110 (2015)

    Google Scholar 

  • Liu, X., Shackleton, M.B., Taylor, S.J., Xu, X.: Empirical pricing kernels obtained from the UK index options market. Appl Econ Lett 16, 989–993 (2009)

    Google Scholar 

  • Liu, X., Shackleton, M.B., Taylor, S.J., Xu, X.: Closed-form transformations from risk-neutral to real-world distributions. J Bank Finance 31, 1501–1520 (2007)

    Google Scholar 

  • Ludwig, M.: Robust estimation of shape-constrained state price density surfaces. J Deriv 22, 56–72 (2015)

    Google Scholar 

  • Lundtofte, F.: Implied volatility and risk aversion in a simple model with uncertain growth. Econ Bull 30, 182–191 (2010)

    Google Scholar 

  • Marroquin-Martinez, N., Moreno, M.: Optimizing bounds on security prices in incomplete markets. Does stochastic volatility specification matter? Eur J Oper Res 225, 429–442 (2013)

    Google Scholar 

  • Martin, I.: What is the expected return on the market? Q J Econ 132, 367–433 (2017)

    Google Scholar 

  • Mehra, R., Prescott, E.C.: The equity premium: a puzzle. J Monet Econ 15, 145–161 (1985)

    Google Scholar 

  • Mehra, R.: The equity premium puzzle: a review. Found Trends Finance 2, 1–81 (2008)

    Google Scholar 

  • Melick, W.R., Thomas, C.P.: Recovering an asset’s implied pdf from option prices: an application to crude oil during the gulf crisis. J Financ Quant Anal 32, 91–115 (1997)

    Google Scholar 

  • Merton, R.C.: Option pricing when underlying stock returns are discontinuous. J Financ Econ 3, 125–144 (1976)

    Google Scholar 

  • Ni, S.X.: Stock option returns: a puzzle. Working paper, Hong Kong University of Science and Technology (2009)

  • Pan, J.: The jump-risk premia implicit in options: evidence from an integrated time-series study. J Financ Econ 63, 3–50 (2002)

    Google Scholar 

  • Patton, A.J., Timmermann, A.: Monotonicity in asset returns: new tests with applications to the term structure, the CAPM, and portfolio sorts. J Financ Econ 98, 605–625 (2010)

    Google Scholar 

  • Perignon, C., Villa, C.: Extracting information from options markets: smiles, state-price densities and risk aversion. Eur Financ Manag 8, 495–513 (2002)

    Google Scholar 

  • Perrakis, S., Ryan, P.: Option pricing bounds in discrete time. J Finance 39(2), 519–525 (1984)

    Google Scholar 

  • Polkovnichenko, V., Zhao, F.: Probability weighting functions implied by options prices. J Financ Econ 107, 580–609 (2013)

    Google Scholar 

  • Pozzi, L.C.G., de Vries, C.G., Zenhorst, J.: World equity premium based risk aversion estimates. Working paper, Tinbergen Institute 2010-007/2 (2010)

  • Prelec, D.: The probability weighting function. Econometrica 66, 497–527 (1998)

    Google Scholar 

  • Pyo, U.: Minmax price bounds in incomplete markets. J Econ Finance 35(3), 274–295 (2011)

    Google Scholar 

  • Rieger, M.O.: Co-monotonicity of optimal investments and the design of structured financial products. Math Stat 15, 27–55 (2011)

    Google Scholar 

  • Rosenberg, J.V., Engle, R.F.: Empirical pricing kernels. J Financ Econ 64, 341–372 (2002)

    Google Scholar 

  • Ross, S.: The recovery theorem. J Finance 70, 615–648 (2015)

    Google Scholar 

  • Rubinstein, M.: Implied binomial trees. J Finance 49, 771–818 (1994)

    Google Scholar 

  • Sala, C., Barone-Adesi, G.: Sentiment lost: the effect of projecting the empirical pricing kernel onto a smaller filtration set. Working paper, Swiss Finance Institute (2016)

  • Sala, C.: Does the pricing kernel anomaly reflect forward-looking beliefs? Working paper, ESADE Business School (2016)

  • Santa-Clara, P., Yan, S.: Crashes, volatility, and the equity premium: lessons from S&P 500 options. Rev Econ Stat 92, 435–451 (2010)

    Google Scholar 

  • Schneider, P., Trojani, F.: (Almost) model free recovery. Working paper, Swiss Finance Institute (2015)

  • Schweri, U.: Is the pricing kernel u-shaped? Working paper, University of Zurich (2010)

  • Shefrin, H.: A Behavioral Approach to Asset Pricing, 2nd edn. Amsterdam: Elsevier (2008a)

  • Shefrin, H.: Risk and return in behavioral SDF-based asset pricing models. J Invest Manag 6, 1–18 (2008b)

    Google Scholar 

  • Shimko, D.C.: Bounds of probability. Risk Mag 6, 33–37 (1993)

    Google Scholar 

  • Shive, S.: On the shape of the option-implied stochastic discount factor. Working paper, University of Michigan (2003)

  • Shive, S., Shumway, T.: A non-decreasing pricing kernel: evidence and implications. Working paper, University of Michigan (2004)

  • Shive, S., Shumway, T.: Is the pricing kernel monotonic? Working paper, University of Notre Dame (2009)

  • Siddiqi, H., Quiggin, J.: Differential awareness and the pricing kernel puzzle. Working paper, University of Queensland (2016)

  • Silverman, B.: Density Estimation. London: Chapman & Hall (1986)

  • Song, Z.: Expected VIX option returns. Working paper, Federal Reserve Board (2012)

  • Song, Z., Xiu, D.: A tale of two option markets: state-price densities and volatility risk. J Econom 190, 176–196 (2016)

    Google Scholar 

  • Stutzer, M.: A simple nonparametric approach to derivative security valuation. J Finance 51, 1633–1652 (1996)

    Google Scholar 

  • Tversky, A., Kahneman, D.: Advances in prospect theory: cumulative representation of uncertainty. J Risk Uncertain 5, 297–323 (1992)

    Google Scholar 

  • Veronesi, P.: Belief-dependent utilities, aversion to state-uncertainty, and asset prices. Working paper, University of Chicago (2004)

  • Walden, J.: Recovery with unbounded diffusion processes. Rev Finance 21, 1403–1444 (2017)

    Google Scholar 

  • Wallmeier, M.: Mispricing of index options with respect to stochastic dominance bounds? Working paper, University of Fribourg (2015)

  • Weber, T.: Estimating risk aversion in the European CDO market. Working paper, University of Konstanz, Germany (2006)

  • Wu, L.: Dampened power law: reconciling the tail behavior of financial security returns. J Bus 79, 1445–1473 (2006)

    Google Scholar 

  • Yamazaki, A.: A dynamic equilibrium model for u-shaped pricing kernels. Working paper, Hosei University (2017)

  • Yang, J.: Semiparametric estimation of asset pricing kernel. Appl Financ Econ 19, 257–272 (2009)

    Google Scholar 

  • Zdorovenin, V., Pezier, J.: Does information content of option prices add value for asset allocation? Working paper, University of Reading, UK (2011)

  • Ziegler, A.: State-price densities under heterogeneous beliefs, the smile effect, and implied risk aversion. Eur Econ Rev 46, 1539–1557 (2002)

    Google Scholar 

  • Ziegler, A.: Why does implied risk aversion smile? Rev Financ Stud 20, 859–904 (2007)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Konstanz, PO Box 134, 78457, Constance, Germany

    Horatio Cuesdeanu & Jens Carsten Jackwerth

Authors
  1. Horatio Cuesdeanu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jens Carsten Jackwerth
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jens Carsten Jackwerth.

Additional information

We would like to thank George Constantinides, Maria Grith, and Alexandros Kostakis for helpful comments.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (docx 38 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cuesdeanu, H., Jackwerth, J.C. The pricing kernel puzzle: survey and outlook. Ann Finance 14, 289–329 (2018). https://doi.org/10.1007/s10436-017-0317-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10436-017-0317-9

Keywords

JEL Classification

Search

Navigation