Sources of time varying return comovements during different economic regimes: evidence from the emerging Indian equity market

Abstract

We study the economic and non-economic sources of stock return comovements of the emerging Indian equity market and the developed equity markets of the US, UK, Germany, France, Canada and Japan. Our findings show that the probability of extreme comovements in the economic contraction regime is relatively higher than in the economic expansion regime. We show that international interest rates, inflation uncertainty and dividend yields are the main drivers of the asymmetric return comovements. Findings reported in the paper imply that the impact of interest rates and inflation on return comovements could be used for anticipating financial contagion and/or spillover effects. This is particularly critical since during extreme market conditions, the tail return comovements can potentially reveal critical information for active portfolio management.

1 Introduction

Globalisation of financial markets has created both opportunities and challenges for international investors. Whilst it has led to greater opportunities for portfolio diversification, the risk of contagion among financial markets has also increased. It is therefore critical to estimate accurately return comovements and more importantly, to identify the factors which drive these comovements. This paper examines the asymmetric stock return comovements of the emerging Indian market and selected developed markets in different economic regimes. The paper also provides evidence of the key economic and non-economic sources of stock return comovements.

The existing evidence on return comovements largely focuses on developed markets. Research on the key sources of extreme return comovements between emerging and developed markets is relatively sparse. Identification of the key sources of asymmetric comovements during bearish and bullish economic conditions will be highly useful for policymakers and international investors. If return comovements are positive during periods of economic turbulence, then an understanding of the key determinants will enable appropriate policy interventions for containing contagion risks. Likewise, knowledge of the sources of return comovements will help international investors in their portfolio asset allocation decisions.

It is widely acknowledged that emerging markets in general and India in particular are playing an ever increasing role in driving world economic growth. India with its large and educated human capital, access to natural resources, and growing markets for goods and services offers an attractive destination for international investors. Among the BRIC (Brazil, Russia, India and China) nations, India’s well established global trade links are next only to China (Aloui et al. 2011). Further, since the economic liberalisation in 1992, the cumulative annual Foreign Institutional Investments (FIIs) in the Indian equity markets have surged from a mere $4 million in 1992–1993 to approximately $125 billion in 2012 (SEBI 2012). However, during the US-led subprime crisis in 2008–2009, India experienced an outflow of $12 billion (SEBI 2011). Such volatility of the international portfolio flows particularly during the recent global economic crisis has triggered serious macroeconomic challenges for emerging economies such as India since the stock markets are considered as a leading indicator of a country’s economic well-being. Consequently, an understanding of the causes of extreme stock return comovements will be extremely valuable to both policy makers in emerging markets and international investors. In this context, our paper makes two significant contributions. First we investigate both the probability and magnitude of asymmetric return comovements between the Indian emerging market and six developed stock markets. Second, we provide evidence of how the sources of extreme return comovements differ when the developed economies are in economic expansion and economic contraction regimes.

We report several interesting and relevant findings. First, we show that the probability of extreme comovements in the economic contraction regime is relatively higher. Second, we find that both Indian and international inflation uncertainty are likely to adversely affect portfolio risk diversification. Third, we discover that an increase in international interest rates increases the asymmetric return comovements. While an increase in the Indian interest rates negatively affects its stock market, it has no impact on the international equity markets. Finally, we find that Indian dividend yield and price-to-earnings ratios influence the return comovements more in the economic expansion regime than in the economic contraction regime of the developed economies. However, an increase in international dividend yield during the economic contraction regime increases the return comovements, suggesting that it fails to uplift the investors’ sentiments in both international and Indian equity markets.

The rest of the paper is presented as follows: Sect. 2 discusses the relevant literature on the dependence structure of return comovements. Section 3 presents the methodology. Section 4 discusses the data and empirical findings and finally Sect. 5 concludes the paper.

2 Literature review

Understanding the asset market linkages, especially during periods of economic contraction, will be highly useful in predicting the probability of a financial contagion. For investors, understanding the key drivers of financial contagion will help them manage their risk exposure to foreign assets. Further, understanding the influence of various economic and financial sources on return comovements will enable the policy makers to initiate appropriate interventions. Existing studies have investigated the financial contagion from a market integration perspective, i.e. if financial markets are segmented, financial contagion cannot occur. In this regard, though the past studies report significant linkages between emerging and developed equity markets [see, Ghosh et al. (1999) for Asian emerging markets; Fujii (2005) for Latin American emerging markets], research on extreme comovements is sparse.

In examining financial contagion, one body of literature examines volatility spillover which characterizes the structure of asset return relationships across markets. However, from an empirical point of view, methodologies vary considerably. For instance, Asgharian and Nossman (2013) use stochastic volatility models with jumps to examine the volatility spillover effects from the US and regional stock markets on the local markets of the Pacific Basin region and China. They report significant spillovers for all the countries, except for China. However, the stochastic volatility models with jumps are exposed to potential misspecifications. Specifically, (1) jumps in the returns can generate large comovements, but their impact may be temporary, (2) the diffusive stochastic volatility process may be persistent thus violating the assumption of normally distributed increments as per the Brownian motion and (3) often instead of jumps, smooth diffusion processes with clusters are observed. Li (2007) examines the volatility linkages between Chinese stock exchanges and the US stock market using a multivariate GARCH framework. Similarly, using GARCH framework Cheng and Glascock (2005) examine the stock market linkages between Mainland China, Hong Kong, and Taiwan and two developed markets, Japan and the United States. They show that the stock markets of the Greater China Economic Area (GCEA) are not cointegrated with the either US or Japan and there exists a weak non-linear relation between the markets. In a similar vein, Chiang and Doong (2001) investigate the time-series behavior of Asian stock markets. Employing Threshold GARCH model they show that there is an asymmetric relationship between the Asian stock markets. However, these studies do not explore the relationship during economic expansion and economic contraction regimes. Further, these studies do not examine that factors that drive the return comovements between the developed and the emerging economies.

Moreover, since the GARCH process assumes equal weights for small and large changes in returns, it fails to account for the differential impact caused by abnormal returns (Zhang et al. 2009). While Zhang et al. (2009) account for these differential impacts, their study is restricted to Shanghai and Hong Kong stock markets. Further, they do not consider the evolutionary process of the return comovements. Additionally, far fewer studies consider the asymmetric nature of the comovements in modelling market interdependence (see de Melo and Mendes 2005). Consequently, our research differs from the previous studies in the following two aspects. First, we allow the marginal distributions of the equity returns to follow an appropriate conditional heteroskedastic process that accommodates for risk-return tradeoff. Second, our analytical framework takes into account the autoregressive evolutionary process and asymmetric nature of the return comovements.

Another body of literature examines contagion using cross-market return correlations during stable and crisis periods. For example King and Wadhwani (1990) and Lee and Kim (1993) provide evidence of contagion when the correlation during the crisis period is relatively higher. They find that the likelihood of contagion increases during highly volatile periods; however, this approach has several limitations. Forbes and Rigobon (2002) argue that the presence of volatility clustering during periods of economic turmoil causes biased linear correlation estimates. Pesaran and Pick (2007) suggest that contagion involves a dynamic increase in return correlation rather than a static estimate. Cheng and Glascock (2006) examine the stock market linkages between US and the GCEA before and after the Asian Financial Crisis. Using Granger causality test they provide evidence of increased market linkage post financial crisis, indicating harmonious market comovements post 1997 Asian financial crisis. Further, Chiang et al. (2007) highlight the potential issues of omitted variable bias in estimating cross-market correlations. Several other studies therefore use Vector Autoregressive (VAR) and Autoregressive Conditional Heteroskedastic (ARCH)-type of models to study cross-market return comovements but report inconclusive findings. For example, Baele (2005) finds evidence of contagion between the US and several European stock markets during periods of high market volatility. In contrast, Bekaert et al. (2005) report no contagion between the US and the countries in Europe, Asia and Latin America during the Mexican crisis. Using Vector Error Correction Model (VECM), Masih and Masih (2001) examine the stock market interdependencies between Australian and four Asian markets, namely Taiwan, South Korea, Singapore and Hong Kong. They show that Hong Kong market plays a dominant role in influencing the other Asian and the Australian stock market. More recently, Pesaran and Pesaran (2010) show that movements in asset return volatilities are shared across markets during the global financial crisis of 2008. Samarakoon (2011) reports similar findings which suggest that the decline in stock prices in the emerging markets during the crisis periods reflects their high dependency on the US market.

The extant research on stock returns comovements primarily rely on using linear measures of comovements. While techniques which assume linear correlations are easy to use, they fail to accurately capture the return comovements if the returns are not normally distributed. Poon et al. (2004) confirm that the linear measures of correlations fail to distinguish extreme positive and negative returns. Further, the asymmetric correlation between the stock returns during periods of economic expansion and contraction cannot be explained by the conventional measure of comovements (Beine et al. 2008). Several research papers have shown that multivariate Generalized Autoregressive Conditional Heteroskedastic (GARCH) models (ŞErban et al. 2007) and/or the use of copula functions (Longin and Solnik 2001) are highly effective in modelling non-normal return comovements (see Cherubini et al. 2004; Patton 2006). While the multivariate GARCH is suitable for non-normally distributed stock returns, it assumes that the error term is independently and normally distributed. Unlike GARCH, copula models do not require normal distribution assumption and are particularly effective in capturing extreme return comovements. Using the copula approach, Jondeau and Rockinger (2006) show that dependence is higher and more persistent in the European markets than other stock markets. Similarly, Kenourgios et al. (2011) and Yang and Hamori (2013) provide evidence of increased comovements during the crisis periods between emerging and developed markets. In contrast to the return-based volatility studies, Chiang and Wang (2011) use a time-varying logarithmic conditional autoregressive range model with the lognormal distribution (TVLCARR) and examine the volatility contagion of the G7 stock markets. They use smooth transition copula functions to detect the volatility contagion. They show that contagion did occur from the US to other developed nations including France, the UK, Italy and Japan during the subprime crisis.

In the Indian context, the empirical evidence of stock market linkages is mixed. For example, in one of the early studies, Sharma and Kennedy (1977) examine the equity return comovements of the Indian with the London and New York stock markets. They report no significant comovements of asset returns. Their results could be attributed to the fact that in the 1970s the Indian economy was a closed economy. In contrast, Kumar and Mukhopadyay (2002) using the GARCH framework provide evidence of volatility spillover between the US and the Indian equity market for the period 1999–2001. Similarly, Wong et al. (2005) use weekly data for the period 1991–2003 in examining the relationship between the Indian equity market and the US, UK and Japan stock markets. They show that (1) all of the developed equity markets are cointegrated with the Indian stock market and (2) there is evidence of unidirectional causality from only the US and the Japan stock markets. On the other hand, Kolluri and Wahab (2010) show that during the period 1997–2009, the UK stock market influences the Indian market much more than the US stock market. Further, though Gupta and Donleavy (2009) provide evidence of time varying return comovements, they neither examine the dependence structures nor the factors influencing the return comovements of Indian and global stock markets. Finally, whilst Poshakwale and Thapa (2009) document evidence of the increased integration of Indian equity markets with global markets and attribute this to the rapid growth of foreign equity portfolio investment flows, they do not explicitly model asymmetric stock return comovements.

Our paper therefore uses a time-varying conditional copula and Markov switching (MS) stochastic volatility model for investigating the economic and non-economic sources of stock return comovements of the emerging Indian equity market and the developed equity markets of US, UK, Germany, France, Canada and Japan. Our paper makes two distinct contributions to the existing literature. First we investigate both the probability and magnitude of asymmetric return comovements between the Indian emerging market and six developed stock markets. Second, we provide evidence of how the sources of extreme return comovements differ when the developed economies are in economic expansion and economic contraction regimes.

3 Methodology

We model return comovements based on the copula theory. Copula (C) is defined as a function that couples multiple distribution functions of Random Variables (RV) to their unidimensional unit-dimensional distribution function. Application of this cumulative distribution function (CDF) is derived from the Sklar Theorem (Sklar 1959). The theorem states that for a joint distribution function H _X,Y (x, y) for all x, y a function, copula C(u, v), can be characterized in $\bar{R} \in \left( { - \infty ,\infty } \right)$ such that $H_{XY} \left( {x, y} \right) = C\left( {F_{X} (x), F_{Y} (y)} \right)$, where F _X (x) and F _Y (y) are the marginal distribution functions.

3.1 Conditional copula

Let the conditional CDF of two RV (X and Y) and a given conditioning vector K be $H_{{\left( {XY|K} \right)}} \left( {x, y|K} \right)$ and the marginal distributions be $F_{{\left( {x|K} \right)}} \left( {x|K} \right)$ and $F_{{\left( {y|K} \right)}} \left( {y|K} \right)$. Then there exists a copula C, such that

$$H_{XY\left| K \right.} \left( {x, y|k} \right) = C\left( {F_{X\left| K \right.} \left( {x|k} \right), F_{Y\left| K \right.} \left( {y|k} \right)} \right) = C(u, v)$$

(1)

where $\left( {x, y|K} \right) = k$ and $(x,y) \in \bar{R} \times \bar{R}$. In Eq. (1), u and v are the realizations of $U \equiv F_{{X\left| K \right.\left( {x|k} \right)}}$ and $V \equiv F_{{Y\left| K \right.\left( {y|k} \right)}}$, given K = k. U and V are the conditional probability integrals of the RV, X and Y (Sklar 1959).

Tail dependence allows us to capture the behaviour of the RV during periods of extreme events. It measures the probability of occurrence of extreme movements in one variable, given that the other variable witnesses an extreme deviation from the mean. In this study, we examine the tail dependence using the Modified Joe-Clayton (MJC) copula. Using MJC instead of a normal Joe-Clayton copula allows us to model the asymmetry of the tail dependence irrespective of the functional form of the copula used. The Joe-Clayton copula is defined as:

$$C_{JC} \left( {u,v|\tau^{U} ,\tau^{L} } \right) = 1 - \left( {\left\{ {\left[ {1 - \left( {1 - u} \right)^{\theta } } \right]^{ - \delta } + \left[ {1 - \left( {1 - v} \right)^{\theta } } \right]^{ - \delta } - 1} \right\}^{ - 1/\delta } } \right)^{1/\theta }$$

(2)

where $\tau^{L} \;{\text{and}}\;\tau^{U}$ are the probability of the RV in lower or upper joint tails respectively, θ = 1/log₂(2 − τ ^U), δ = −1/log₂(τ ^L) and $\tau^{U} \in \left[ {0, 1} \right],\;\tau^{L} \in \left[ {0, 1} \right]$. A key limitation of the Joe-Clayton copula is that there is some level of asymmetry due to its functional form, even though the two tail dependence measures are equal. In order to overcome this limitation, we use MJC which is characterized as:

$$C_{MJC} \left( {u,v|\tau^{U} ,\tau^{L} } \right) = \frac{1}{2} \times \left( {C_{JC} \left( {u,v|\tau^{U} ,\tau^{L} } \right) + C_{JC} \left( {1 - u,1 - v|\tau^{U} ,\tau^{L} } \right) + u + v - 1} \right)$$

(3)

The above modification of the Joe-Clayton copula ensures that the tail dependence is not asymmetric when $\tau^{U} = \tau^{L}$. Next, we discuss the copula model specifications.

3.2 Copula model specifications

It is well established that financial returns generally do not follow a normal distribution but rather adhere to Student’s t distribution (Hu 2010). Building on this, we model each marginal distribution of the asset returns employing an Autoregressive Moving Average ARMA (p, q)-Exponential Generalized Autoregressive Conditional Heteroskedastic EGARCH (1, 1)-t model to accommodate for differential impacts in return volatility clustering. Then, we estimate the scale-free measure of dependence, which preserves the dependence structure during the simulation of the RV.

3.2.1 Marginal model

We assume that the distributions of the equity returns follow an ARMA (p, q)-EGARCH (1, 1)-t process (Nelson 1991). The model is characterized as

$$X_{i,t} = \theta_{i} + \sum\limits_{j = 1}^{p} {\beta_{j} X_{i,t - j} } + \sum\limits_{k = 1}^{q} {\alpha_{k} \varepsilon_{t - k} } + \varepsilon_{i,t}$$

(4)

$$\log \left( {\sigma_{t}^{2} } \right) = a_{0} + \sum\limits_{j = 1}^{p} {a_{i1} \log \left( {\sigma_{t - j}^{2} } \right)} + \sum\limits_{i = 1}^{q} {\alpha_{2j} \left| {\frac{{e_{t - i} }}{{\sigma_{t - i} }}} \right|} + \sum\limits_{j = 1}^{q} {\alpha_{3j} \left( {\frac{{\varepsilon_{t - j} }}{{\sigma_{t - j} }}} \right)}$$

(5)

$$\sqrt {\frac{d}{{\sigma_{i,t}^{2} \left( {d - 2} \right)}}} \cdot \varepsilon_{i,t} \left| {I_{t - 1} \sim\,i.i.d.t_{di} } \right.$$

(6)

where X _i,t is the asset return series, θ _i and ε _i,t−1 are the conditional mean and error term, which is the news relating to the volatility from one lag period. β _j is the autoregressive component and α _k is the moving average parameter. The noise process ε _t represented in Eq. 4 follows a skewed Student’s-t distribution with (d) degrees of freedom and (σ ² _t ) conditional variance. (σ ² _t−j ) is the GARCH component and the leverage effect is captured by a ₃. The information contained about the volatility of the lagged period is captured by ɛ _t−1 which represents the ARCH component. The information set is considered as the condition vector ‘k’. The order of the ARMA term ‘p’ is determined using Akaike Information Criteria (AIC).

In our study, we estimate ARMA (p, q)—EGARCH (1, 1) model for each of the financial return time-series. We select the most appropriate lag orders for each of the return series using the AIC, observing the conditional variance equation as an EGARCH (1, 1)-t process. The mean equations of the equity returns of India, US, UK, Germany, France, Canada and Japan follow ARMA (1, 1), ARMA (3, 3), ARMA (4, 4), ARMA (1, 1), ARMA (1, 1), ARMA (1, 1) and ARMA (3, 3) processes, respectively. We confirm that the marginal models are free from autocorrelation and heteroskedastic effects (results are not reported here but can be provided on request). To evaluate the adequacy of the marginal estimations, we conduct misspecification tests following Diebold et al. (1998). We examine the correlograms of $\left( {\hat{u}_{t} - \bar{u}} \right)^{l}$ and $\left( {\hat{v}_{t} - \bar{v}} \right)^{l}$ for ‘l’ ranging from one to four. The values u and v are the probability integral transformations of the estimates of the marginal models. The correlograms confirm the absence of any serial correlation in the first four moments, which indicates that our marginal models are correctly specified.

3.2.2 Tail dependence measure

The tail dependence measure is another property of the copula that is very useful in analyzing the joint tail dependence of bivariate distributions. Tail dependence estimates the probability of the RV in lower or upper joint tails. Intuitively, this measures the tendency of the asset returns to co-move up and down together.

$$\tau^{U} = Lt_{{u\text{}1}} P\left[{X \ge F_{X}^{- 1} (u)/Y \ge F_{Y}^{- 1} (u)} \right] = Lt_{{u\text{}1}} \frac{{1 - 2u - C\left({u,v} \right)}}{1 - u}$$

(7)

$$\tau^{L} = Lt_{{u\text{}0}} P\left[{X \ge F_{X}^{- 1} (u)/Y \le F_{Y}^{- 1} (u)} \right] = Lt_{{u\text{}0}} \frac{C(u,v)}{u}$$

(8)

where $\tau^{U} ,\tau^{L} \in \left[ {0,1} \right]$ and F ⁻¹ _x and F ⁻¹ _Y are the marginal density functions of the RV series. If the tail dependence measures are positive then upper or lower tail dependence exists, i.e. τ ^U(τ ^L) measures the probability of the RV-X being above (below) a high (low) quantile, given that the RV-Y is above (below) a high (low) quantile.

We allow for the tail dependence estimate to follow an evolution process that captures the level changes. We define the evolution process as

$$\tau_{t}^{U/L} = \varTheta \left( {\beta_{0}^{U/L} + \beta_{1}^{U/L} \cdot \tau_{t - 1}^{U/L} + \beta_{2}^{U/L} \cdot \frac{1}{q}\sum\limits_{i = 1}^{q} {\left| {u_{t - i} - v_{t - i} } \right|} + \beta_{3}^{U/L} D} \right)$$

(9)

where $\varTheta = \frac{1}{{1 + e^{ - x} }}$ is a logistic transformation that is used to keep $\tau_{t}^{U/L}$ in [0, 1] at all times. The dependence parameter follows an ARMA (1, q) process, characterized by β ₁, the autoregressive term, and β ₂, the forcing variable. While the former term accounts for the persistence effect, the latter term captures the variation effect of the dependence parameter. We add a dummy variable term β ₃ D to allow for level variation in the dependence. The dummy variable takes the value ‘0’ for economic expansion regime and ‘1’ otherwise. We obtain the dependence parameter of the Student-t and MJC copula models using the maximum likelihood (ML) method (see the estimation process in “Appendix 1”).

We examine the performance of the copula models based on AIC, and Bayesian information criteria (BIC). The former is adjusted for small sample bias (Rodriguez 2007) and the latter is a goodness-of-fit test for the copula models to compare the different dependence structures.

3.3 The dynamic model to examine dependence structures

We employ an MS framework in investigating the dependence structures. Further, this study allows each state variable to follow an evolutionary process which is presented in the following section. Although autoregressive conditional heteroskedasticity (ARCH) models can be employed to tackle this issue (Bollerslev et al. 1988; Engle 1982), the standard normally and independently distributed (NID) assumption of the error term is often violated in practice. We, therefore, specify a model for the state variables that allows each of the vectors to follow an independent stochastic volatility (ISV) process. The stochastic volatility (SV) specification builds in a time-varying variance process for each of the elements of the structural factors, by allowing the variance to be a latent process.

We specify the MS model, which defines the dependence structure (y _t ) as

$$y_{t} = \sum\limits_{l = 1}^{L} {\varphi_{l} S_{t} x_{l,t}^{S} } + \varepsilon_{t}$$

(10)

where L denotes the number of switching coefficients, x _l,t represents the explanatory state variables, S _t represents the regime of the variable at time t, and $\varepsilon_{t} \sim\,P\left( {\phi_{{S_{t} }} } \right)$ with p(ϕ) as the probability density function of the innovations, defined by the vector (ϕ). Each of the independent state variables follows a Markov switching stochastic volatility (MSSV) process, which we discuss next.

Our main motive is to make the model parsimonious and yet flexible. Therefore, in contrast to the ARCH-type models, we allow the log volatility of the state variables to evolve stochastically over time. Following the discrete type convention (Ball and Torous 1999; Shephard 1996), we characterize the SV model as an extension of the time-diffusion process

$$\varDelta x_{t} = a + bx_{t - 1} + \sigma_{t} x_{t - 1}^{\gamma } \varepsilon_{t}$$

(11)

where γ represents the diffusion term, $\varDelta x_{t} = x_{t} + x_{t - 1}$ and ɛ _t is the standard normal random variable. The residual of the above equation is $e_{t} = \sigma_{t} x_{t - 1}^{\gamma } \varepsilon_{t}$. The model allows the volatility (σ) to evolve stochastically, following a first-order autoregressive process

$$\log \sigma_{t}^{2} = \omega + \varphi \log \sigma_{t - 1}^{2} + \eta_{t}$$

(12)

where $\eta_{t} \sim N\left( {0,\sigma_{\eta }^{2} } \right),i.i.d.$ is the disturbance term. It makes the variance subject to random shocks, making the process stochastic. We transform the residuals in Eq. (11) to $e_{t} = \varDelta x_{t} - a - bx_{t - 1}$, which allows us to formulate a quasi-likelihood function by employing Kalman filtering. The log of the squared residuals is

$$\log e_{t}^{2} = \log \sigma_{t}^{2} + 2\gamma \log x_{t - 1} + \log \varepsilon_{t}^{2}$$

(13)

Considering $z_{t} = \log e_{t}^{2}$ and $g_{t} = \log \sigma_{t}^{2}$ Eq. (13) reduces to

$$z_{t} = g_{t} + 2\gamma \log x_{t - 1} + \log \varepsilon_{t}^{2}$$

(14)

where g _t  = ω + φg _t−1 + η _t . Next, we discuss the MSSV model, which is employed to examine the dynamics of the dependence structure.

This is a generalization of the SV and the MS model. This model allows the volatility to vary across different regimes. Assuming constant volatility in the regimes will yield either underestimation or overestimation of the volatility. Thus, the motivation to use MSSV is that it allows different estimates of the elasticity of variance (γ). In this study the MSSV model is characterized as

$$\begin{aligned} z_{t} & = g_{t} + 2\gamma \log x_{t - 1} + \log \varepsilon_{t}^{2} \\ g_{t} & = \omega_{m} + \varphi g_{t - 1} + \eta_{t} \\ \end{aligned}$$

(15)

In contrast to Eq. (14), Eq. (15) defines $\omega_{m} = \log \sigma_{m}^{2}$, which allows us to capture the different regimes at a particular point in time. Duffee (1993) provides evidence for structural breaks with a monetarist experiment and shows that even the SV models lack in analyzing these effects in the economy. With the regimes governing the dynamic behaviour of the estimated state variables, we condition a particular regime and calibrate the density of the variable of interest. In this parameterization of the MS model, the transition probabilities from state m to state n in time t are defined as $p_{mn} = \Pr \left[ {\left. {S_{t} = m} \right|S_{t - 1} = n} \right]$. It should be noted that for $m = 1, \ldots ,M$, only $M(M - 1)$ needs to be specified as $p_{mn} = \Pr \left[ {\left. {S_{t} = M} \right|S_{t - 1} = n} \right] = 1 - \sum\nolimits_{m = 1}^{M - 1} {\Pr \left[ {\left. {S_{t} = m} \right|S_{t - 1} = n} \right]}$. In our model we allow the unconditional volatility to change between different states by allowing (σ _i ) in Eq. (11) to take values of $m \in \left\{ {1, \ldots , M} \right\}$ at time t. The corresponding equation transforms to

$$\varDelta x_{t} = a + bx_{t - 1} + \sigma_{m} x_{t - 1}^{\gamma } \varepsilon_{t}$$

(16)

An important component of the structure of the MS model is that the switching of the states follows a stochastic process. Thus, identifying states based on distributional characteristics of the regime switching variable, such as $(\mu \pm \sigma )$, i.e. mean plus or minus standard deviation, would lead to a restricted form of the switching model failing to capture the true dynamics of the dependence structure. However, a weak regime classification will imply that the model is unable to successfully distinguish between the regimes from the behaviour of the data, leading to misspecification. In order to address this issue, we identify the regimes based on regime switching classification. An ideal switching model should classify the regimes sharply, i.e. the regime transition probabilities (p _mn ) should be close to 0 or 1. Based on Ang and Bekaert (2002) we construct the regime classification statistic (RCS) for M states as

$$RCS\left( M \right) = 100M^{2} \frac{1}{T}\sum\limits_{t = 1}^{T} {\left( {\prod\limits_{m = 1}^{M} {p_{mt} } } \right)}$$

where $p_{mt} = \Pr \left( {S_{t} = m\left| {I_{T} } \right.} \right)$ indicating the regime transition probabilities and 100 M ² serves as a normalizing constant to keep the statistic between 0 and 100. A value of 0 signifies perfect regime classification, whereas a value of 100 implies that the regimes are not capable of distinguishing the behaviour of the data, i.e. dependence structure, across the defined regimes and hence they are irrelevant.

We use Kalman filter for estimating the MSSV model. However, the above procedures make the process exclusively path dependent. Hence, to remove the path dependence we compute the conditional expectation of the log-volatility forecast by taking the weighted average output of the previous iteration. We then calculate the regime probabilities based on Smith’s (2002) modification of Hamilton’s (1989) filter (the estimation process is explained in “Appendix 2”).

4 Empirical results

4.1 Data description

We use monthly data from April 1997 to March 2013 for examining the dependence structure of stock return comovements of Indian and developed equity markets. Our sample includes (1) Standard and Poor’s (S&P) CNX Nifty Index of the National Stock Exchange of India, (2) US S&P 500 composite index, (3) Financial Times Stock Exchange (FTSE)—100 index of UK, (4) DAX-30 index of Germany, (5) CAC all-tradable index of France, (6) S&P composite index of Canada and (7) Tokyo Stock Exchange Index (TOPIX) of Japan. The price indexes are obtained from DataStream. We compute returns on a continuous compounding basis, calculated as 100 times the logarithmic difference of the dollar adjusted index/price values.

Previous studies show that changing economic conditions affect asset returns (Fama and French 1988). Consequently, we examine the return comovements in different economic cycles. We obtained data from the National Bureau of Economic Research (NBER) for the US and from the Economic Cycle Research Institute (ECRI) for the UK, Germany, France, Canada and Japan. The analysis of the stock return comovements for the economic cycle regimes is based on the economic expansion and contraction periods of the respective developed economies.¹ “Appendix 3” shows economic regimes for the developed economies included in our sample. We classify every month as either an economic expansion or an economic contraction month. This is based on the turning point, i.e. trough to peak dates, as specified by the NBER’s and ECRI’s Economic cycle dating committee.² Thus, we create two sub-samples, the economic expansion (E) regime and the economic contraction (C) regime. In Table 1 we provide the summary statistics of the stock returns.

Table 1 Summary statistics of asset returns

Panel A of Table 1 presents the annualized dollar-adjusted stock returns and standard deviations including the summary statistics for the expansion and contraction periods and for the whole period from April 1997 to March 2013. The economic sub-periods show significant variations in average returns compared to the returns for the whole sample period. As expected, equity returns are positive during the expansionary regime and negative during the contractionary regime. Germany reports the highest annualized returns of 14.63 % followed by India (11.64 %) during the expansionary regime. Whereas in the contraction period, France records lowest returns of −30.84 % followed by US (−25.64 %). Standard deviations of average returns confirm that returns during the economic expansion period are more stable compared to the contractionary period. The summary statistics confirm the presence of excessive skewness and kurtosis relative to Gaussian distribution, which suggests that the return distributions have fatter tails, indicating that extreme variances are highly probable.

Panel B of Table 1 shows the Jarque–Bera test results which strongly reject the normality assumption. The Lagrangian Multiplier (LM) test confirms the presence of ARCH effects. Further, the Breusch-Godfrey (BG) LM tests suggest that stock returns for most markets are serially correlated for at least one of the lag orders. These results violate Gaussian distribution assumptions which imply that linear measures of comovements are not likely to provide an accurate estimation of return comovements. We, therefore, use the copula function approach as an alternative method for estimating returns comovements.

4.2 Dependence structure dynamics

Table 2 reports the copula parameter estimates of the time-varying MJC copula models for the Indian and international stock returns pairs. Panel A reports the probability of extreme comovements during economic expansion, i.e. the lower tail $(\tau_{L} )$, and economic contraction, i.e. the upper tail $(\tau_{U} )$. The results show a higher likelihood of extreme comovements during the economic contraction regime than in the economic expansion regime. Results in Panel B confirm that the return comovements of the Indian stock market and the stock return of developed markets are higher in the contractionary than in the expansionary regime (see Panel B). For example in the case of India–US, the dependence measure during the contraction period is 0.831 whereas during the expansion period it is 0.517. Further, the difference in the comovements between the contractionary and expansion periods is statistically significant. The results have major economic implications since higher comovements during the contractionary period would diminish the portfolio diversification benefits for international investors.

Table 2 Parameter estimates of copula models

The beta values in Panel A capture the persistence and variation effects in the dependence structure of the asset return comovements. The significant beta values confirm the importance of using an evolutionary model for estimating return comovements. As the static case is a restricted approximation of the time-varying evolution of dependence parameters, we conduct a Likelihood Ratio (LR) test to confirm the suitability of the time-varying conditional copula model. Statistically significant LRs suggest that the time-varying copula model is more appropriate than the static model. Since the findings confirm that stock return comovements of the Indian and international markets are both time-varying and asymmetric in nature, it is therefore appropriate that we should use time varying copula models for examining return comovements during different economic conditions.

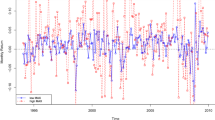
Figure 1 presents the time path of the dependence structure of the five different combinations of the Indian and international equity return pairs. We show the lower and upper tail dependence structures along with the time-varying Student-t copula models for each pair. For all models, the dependence measure of upper tail is higher than the lower tail (see notes provided under Fig. 1 for explanation). For instance, the average upper dependence measure is highest for the Indian-Canadian equity pair, i.e. 0.534, and lowest for the Indian-German pair, i.e. 0.372 (see Panels E and C of Fig. 1). This suggests that in terms of risk diversification during economic contraction, the German investors would be relatively less affected compared to their Canadian counterparts.

Fig. 1

Time path of Indian and foreign equity dependence structures. a Dependence structure of Indian equity-US equity copula pair. b Dependence structure of Indian equity-UK equity copula pair. c Dependence structure of Indian equity-German equity copula pair. d Dependence structure of Indian equity-French equity copula pair. e Dependence structure of Indian equity-Canadian equity copula pair. f Dependence structure of Indian equity-Japanese equity copula pair. Notes In the figure, a–f The time path of the time-varying dependence structure of Indian and foreign equity return-pairs. The average dependence measures for the period 1987–2012 of the different asset pairs are: In/US = 0.524, In/UK = 0.504, In/G = 0.545, In/F = 0.528, In/C = 0.619 and In/J = 0.456. The lower tail corresponds to the extreme movements in the economic expansionary regime and the upper tail corresponds to the extreme movements in the economic contractionary regime. The x axis prepresents the number of months. The period of study is from April 1997 to March 2013

4.3 Economic factor contributions

Thus far, we have the overall picture of how the stock returns move in tandem. In this subsection, we examine the factors that drive the forward-looking dependence structure during the economic expansion and contraction regimes using the MSSV model. Specifically, we examine the extent to which Indian-international equity market linkages are related to financial market development indicators, country-specific macroeconomic variables and associated stock market measures. Existing literature reports that financial market development is closely related to market integration. In particular, previous studies show that financial market development measures have a significant association with stock market integration (Bekaert and Harvey 2000; Carrieri et al. 2007; Panchenko and Wu 2009). Thus, similar to De Jong and De Roon (2005), we consider Indian Market Openness (MO) as a proxy for the financial development measure of the Indian market. MO is computed as a ratio of total market capitalization of the S&P Investable Index and the S&P Global Index for only the Indian emerging economy. We also include stock traded turnover ratio (TR) of the Indian market as a control variable that may reflect its stage of development, information costs and transaction costs associated with trading equity in the market. For macroeconomic variables, we consider variables based on existing studies. Chui and Yang (2012) show that federal rates and Producer Price Index (PPI) have a significant influence on the US, UK and German markets. Further, consistent with the Modigliani-Cohn hypothesis, Campbell and Vuolteenaho (2004) show that inflation significantly affects stock markets. We therefore include these three macroeconomic factors, i.e. PPI, interest rate (IR) and inflation uncertainty (IU). Inflation uncertainty (iu _t measured as $(\pi_{u} )$) is estimated as the fractional uncertainty measure of inflation $\left[ {\frac{{\pi_{e} - \pi }}{\pi }} \right]$. We measure Inflation (i _t measured as π) as the log difference of the Consumer Price Index for all items for urban consumers. We calculate expected inflation (π _e ) by subtracting returns on Treasury Inflation Protected notes from the returns of 10-year Treasury notes. Increase in IU has an unfavorable effect on the stock markets. Further, inflationary pressures impact the stock prices through the discounted cash flow framework. Likewise, IR is expected to have a significant influence on both the economic contractionary and expansionary regimes. During the economic expansion regime the increase in aggregate demand leads to an increase in the real income and inflation. This leads to a demand-pull inflation which is counter-balanced by an increase in the real IR by the central bank. Whereas, during the economic contractionary regime, the government increases spending through expansionary fiscal policy. With rising IRs, investments tend to fall due to the higher cost of borrowing. This hampers economic recovery and unfavorably impacts on the equity markets. Similarly, since higher than expected price inflation has a negative impact on the stock markets, an increase in the level of PPI is viewed as unfavorable by investors. Thus, these three variables are important as they would capture the dynamics of the macroeconomic conditions.

As a proxy for the stock market volatility (SV), we use the VIX index for India, US, Canada and Japan and for the European markets we use DVAX. We include two stock market indicators, i.e. dividend yields (DY) and price to earnings ratio (PE) since Fama and French (1988) and Panchenko and Wu (2009) have shown that DY and PE are important factors for explaining expected stock returns. Following Panchenko and Wu (2009), we also include market capitalization (MC) as a stock market indicator because an increase in MC value suggests improved market sentiments.

Tables 3 and 4 presents the impact of Indian and international factors on the stock return comovements. The findings show evidence of two regimes of the dependence structure, i.e. Regimes (1) and (2), corresponding to the economic contraction (EC) regime and economic expansion (EE) regime, respectively. Here, it is important to note that the economic regimes relate only to the developed markets. Our findings reveal several interesting insights. The results show that MO is positive and statistically significant in both the regimes of the economy for all the international markets. This suggests that an increase in stock MO increases the likelihood of extreme comovements across Indian and international equity market returns. The significant effect of MO on stock market linkages can be explained by De Jong and De Roon’s (2005) segmentation risk premia phenomenon. A high segmentation risk is priced in the risk premium for emerging markets when they are partially segmented with the rest of the international financial markets. However, as the emerging markets open up, the segmentation risk premia declines, decreasing the equity risk premia. This occurs because of greater risk sharing amongst domestic and international investors, which increases the concordance between domestic and foreign stock markets. The positive and significant influence of MO also implies that increased equity market integration post Indian market liberalization has led to increased return comovements. Consistent with the existing literature on emerging market linkages (Bekaert and Harvey 2000; Carrieri et al. 2007), we find that the Indian financial market development control variable, i.e. stock traded TR is a significant factor in explaining the return comovements for most markets.

Table 3 Impact of Indian and international variables

Table 4 Impact of Indian and international variables

Further, the findings reveal the significant and positive influence of IU on return comovements during the economic expansion periods. This suggests that an increase in IU has a direct impact on the returns comovements. Interestingly, IR has a significantly negative influence on both the economic contractionary and expansionary regimes. This has significant economic significance. The negative influence of IR during the economic contraction regime suggests that an increase in the Indian IR attracts international capital flows which provide a boost to the Indian stock market while the international stock markets are still in a bearish regime. In contrast, the negative impact of IR on the economic expansion regime shows evidence of a crowding effect in the Indian market. Likewise, PPI has a negative influence on both the regimes of the economy, though it is only significant for the Indian-US and Indian-Canadian markets. Considering the stock market indicators, DY and PE have a greater positive impact during the economic expansion regimes. This suggests that higher DY and PE positively impact the Indian equity market, bringing in international capital flows and thereby increasing return comovements during periods of economic expansion. While similar findings are reported by some recent research on international market linkages (Aloui et al. 2011; Bracker et al. 1999; Panchenko and Wu 2009), they do not specifically show the influence of the domestic and international factors on the dependence measure during the expansion and contraction regimes of the economy. The stock market indicator, MC, bears the same sign as the other market indicator, TR. However, MC is not statistically significant. Finally, it is worth noting that Indian stock market volatility is only significant for the Indian-US market during the contraction regime.

Considering the international factors, the results reveal several interesting insights. The IU variable shows a similar influence to the Indian IU factor, indicating that IU in the international markets triggers an increase in return comovements. Though statistically insignificant, the negative sign of IU can be attributed to the fact that stock market investors are subjected to inflation illusion (Modigliani and Cohn 1979), where the investors fail to understand the effect of inflation on nominal dividend growth. In contrast to the Indian IR factor, the international IR variable has a positive impact. This implies that the increase in return comovements due to an increase in international IRs can be attributed to the reduction in investments as IR rises. The results suggest that both return comovements are directly affected by the changes in international IRs. However, while an increase in the Indian IRs negatively affects its stock market, it has no impact on the international equity markets. The impact of DY varies across the regimes and is country-specific. This suggests that during periods of economic contraction high DY fails to uplift the investors’ sentiments in the developed markets. Similar results are observed for the other stock market indicator, i.e. PE, during the economic contraction regime. Surprisingly, the influence of SV on return comovements is negative and is significant during the economic contraction regime. This suggests that an increase in stock market volatility in the developed markets during the economic contraction regime does not adversely impact the Indian stock market returns. Finally, we find that the impact of international stock Market Capitalisation (MC) is negative. This indicates that high MC reflects positive investor sentiments and hence contributes towards a reduction in the return comovements.

4.4 Panelled quantile regressions

We estimate the quantile regression to further investigate the factors that drive the forward-looking return comovements during the economic expansion and contraction regimes. Though this approach permits estimating various quantile regressions (Koenker and Bassett 1978), we rely on least absolute deviation regression to overcome the low-power problem of the ordinary least square regressions (see Connolly 1989). Further, the results from the different quantile regressions help us to provide robust testing of the factors that drive the return comovements.

We estimate the coefficients of the quantile regression, θ (which denotes the quartiles for which the relation between the dependence structures and the explanatory variables is estimated) for values ranging from 0.05 to 0.95 with an increment³ of 0.05. We also include two additional extreme percentiles at 0.99 and 0.01 levels to observe the changes in the forward-looking return comovements when large deviations are present. The statistical inferences from these regression models are drawn by the bootstrapping method (for details see Andrews and Buchinsky 2000; Angelis et al. 1993). Here, it is necessary to state that lower θ values indicate the economic expansion regime and the higher θ values indicate the economic contraction regime.

In Table 5 we report the regression results from the quantile method. Several interesting findings are apparent here. First, MO plays a more dominant role during periods of extreme economic expansion. This suggests that during periods of economic expansion, an increase in MO results in higher return comovements. This is consistent with the findings of Poshakwale and Thapa (2009), who report an increase in Indian stock market linkages following the increase in international portfolio flows.

Table 5 Quantile regression estimates examining the impact of Indian and international variables

Second, the Indian variables, IR and PPI, show a significant negative influence. In contrast, IU has a positive influence only during periods of economic expansion. Further, the Indian stock market volatility is only significantly positively related during extreme periods of economic contraction.

Third, considering the international factors, in particular, IR and dividend yield, these have a significant influence on return comovements. More interestingly, in contrast to the Indian IR variable, the international IR variable shows a positive significant influence during periods of extreme economic expansion and contraction. This suggests that the changes in the international IR have a direct impact on return comovements. With regard to international DY, the signs are negative during the economic expansion regime (though only significant at 0.01 quantile) and positive during the economic contraction regime. This possibly suggests that even if firms pay dividends during economic recession signaling high levels of earning potential in the future, they fail to significantly impact the investors’ sentiments during economic turmoil.

Finally, it is worth nothing that both the Indian and international stock market volatility factors are only significant during the extreme economic contraction regime; however, the impacts are different. While an increase in Indian stock market volatility increases the return comovements, an increase in international stock market volatility reduces them. This suggests that while high stock volatility in the Indian market reflects a global economic downturn, high stock market volatility in international markets fails to severely impact the Indian stock markets during regimes of economic contraction.

5 Conclusions

The paper provides evidence of the key sources of time-varying asymmetric return comovements. Using data from April 1997 to March 2013 for India and the six major developed economies of the US, the UK, Germany, France, Canada and Japan, the paper examines the regime switching behavior of the asymmetric return comovements during economic contraction and expansion regimes and the factors which drive these comovements. Robust estimation of extreme comovements is important for two main reasons. First, international investors seeking diversification of portfolio risk by investing in emerging markets, such as India, will require an understanding of the key sources of return comovements for asset allocation decisions. Second, understanding of the factors which drive international equity market linkages would provide richer insights for policy makers for initiating timely interventions to prevent financial contagion.

We report several interesting findings. We show that the likelihood of extreme comovements in the economic contractionary regime is relatively higher than in the expansionary regime. This has profound implications for international investors since historically the low correlation of emerging markets offered huge potential for risk diversification for investors from developed markets. Further, we show that both Indian and international IU directly affects the return comovements. International IRs also positively impact the return comovements which imply that both international and Indian equity markets would be adversely affected by an increase in IRs. On the other hand, while an increase in the Indian IRs seems to negatively affect India’s equity market, it has no impact on the international equity markets. An increase in stock market volatility in the developed markets during the economic contraction regime does not adversely impact the Indian stock market returns. Finally, we show that Indian dividend yield (DY) and price-to-earnings (PE) ratios have a higher impact on return comovements during the economic expansion regime than in the economic contraction regime. However, an increase in international dividend yield during the economic contraction regime increases the return comovements, suggesting that it fails to improve the investors’ sentiments in both the Indian and international equity markets.

Findings reported in the paper have significant implications both for policy makers in emerging economies, such as India, and international investors seeking to diversify portfolio risk. First, for the policy makers, the impact of IRs and inflation on return comovements could be used for anticipating financial contagion and/or spillover effects. For international investors, reliable and accurate estimation of the return comovements will enable them to achieve better asset allocation and risk diversification. This is particularly critical since during extreme market conditions, the tail return comovements can potentially reveal critical information for active portfolio management.

Appendices

Appendix 1: Copula estimation

We obtain the dependence parameter of the Student-t and MJC using ML method. Referring to Eq. (1) we have $C\left( {u,v,\delta } \right) = C\left( {F_{X\left| k \right.} \left( {x|k;\theta_{1} } \right),F_{y\left| k \right.} \left( {y|k;\theta_{1} } \right);\delta } \right)$, where θ ₁ and θ ₂ are the coefficients of the conditioning vector k. Therefore, the joint density of an instance $(x_{t} ,y_{t} )$ is written as

$$\begin{aligned} & c\left( {x_{t} ,y_{t} ;\delta } \right) = \frac{{\partial^{2} C\left( {u_{t} ,v_{t} ;\delta } \right)}}{{\partial u_{t} v_{t} }} \cdot \frac{{\partial u_{t} }}{{\partial x_{t} }} \cdot \frac{\partial v}{{\partial y_{t} }} \\ & \Rightarrow c\left( {x_{t} ,y_{t} ;\delta } \right) = c\left( {u_{t} ,v_{t} ;\delta } \right) \cdot f_{X\left| k \right.} \left( {x_{t} |k;\theta_{1} } \right) \cdot f_{Y\left| k \right.} \left( {y_{t} |k;\theta_{2} } \right) \\ \end{aligned}$$

(17)

From the above equation, we write the log-likelihood of the sample $\left( {x_{1t} ,y_{1t} } \right)$ as

$$\begin{aligned} & L(\varPhi ) = \sum\limits_{t = 1}^{T} {\ln \left[ {c\left( {u_{t} ,v_{t} ;\delta } \right) \cdot f_{X\left| k \right.} \left( {x_{t} |k;\theta_{1} } \right) \cdot f_{Y\left| k \right.} \left( {y_{t} |k;\theta_{2} } \right)} \right]} \\ & \Rightarrow L(\varPhi ) = \sum\limits_{t = 1}^{T} {\ln \left[ {c\left( {F_{X\left| k \right.} \left( {x_{t} |k;\theta_{1} \delta } \right) \times F_{Y\left| k \right.} \left( {y_{t} |k;\theta_{2} \delta } \right)} \right) \cdot f_{X\left| k \right.} \left( {x_{t} |k;\theta_{1} } \right) \cdot f_{Y\left| k \right.} \left( {y_{t} |k;\theta_{2} } \right)} \right]} \\ & \Rightarrow L(\varPhi ) = L_{C} + L_{X} + L_{Y} \\ \end{aligned}$$

(18)

The ML estimation may be difficult to compute if the number of unknown parameters is large (Jondeau and Rockinger 2006), in which case only numerical gradients can be computed instead of having an analytical expression of the likelihood gradients. This leads to considerable slowing down of the numerical estimation. We, therefore, compute the ML estimation using Inverse Function of Margins. This is a two-step estimation process. First, the marginal distribution parameters are estimated employing an ARMA (p, q)-EGARCH (1, 1)-t process as discussed above. We also capture the time variation of the dependence structure which further increases the number of unknown parameters to be estimated. We use the following estimation equation for computing the values of $\hat{\theta }_{1}$ and $\hat{\theta }_{2}$.

$$\hat{\theta }_{K} = \arg \mathop {Max}\limits_{\theta } L_{XY} \left( {x_{t} ,y_{t} ;\theta_{1} ,\theta_{2} } \right);\quad for\;k = 1, 2$$

(19)

Next, we estimate the copula parameter $(\hat{\delta })$ using the following equation.

$$\hat{\delta } = \arg \mathop {Max}\limits_{\delta } L_{C} \left( {x_{t} ,y_{t} ;\delta , \hat{\theta }_{1} ,\hat{\theta }_{2} } \right)$$

(20)

In this second step the marginal densities do not influence the copula estimation parameter as the marginal parameters are computed using Eq. (19). Therefore, the second remains unchanged and computes asymptotically efficient and normal estimates of the copula parameter (Cherubini et al. 2004).

Appendix 2: Estimation filter for the MSSV model

The Kalman filter employed for projection is an iterative process. It forecasts the state variable at the ‘t + 1’ period and updates it when z _t is observable in the Eq. (10). For deriving the filtering equations we denote:

$$\begin{aligned} g_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} & = E\left[ {g_{t} \left| {S_{t} = m,S_{t - 1} = n,\psi_{t - 1} } \right.} \right],\;p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} = E\left[ {\left( {g_{t} - g_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} } \right)\left| {S_{t} = m,S_{t - 1} = n,\psi_{t - 1} } \right.} \right] \\ g_{{t\left| {t - 1} \right.}}^{m} & = E\left[ {g_{t} \left| {S_{t} = m,\psi_{t - 1} } \right.} \right],\;p_{{t\left| {t - 1} \right.}}^{m} = E\left[ {\left( {g_{t} - g_{{t\left| {t - 1} \right.}}^{m} } \right)\left| {S_{t} = m,\psi_{t - 1} } \right.} \right] \\ \end{aligned}$$

Following Smith (2002), we first forecast log-volatility and then update the previous forecasted estimate. The sequential steps are:

• Step 1: The log-volatility is forecast using:

  $$g_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} = \omega_{m} + \varphi_{m} g_{{t\left| {t - 1} \right.}}^{n}$$

  (21)
  $$p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} = \varphi_{m}^{2} p_{{t\left| {t - 1} \right.}}^{n} + \sigma_{m}^{2}$$

  (22)

• Step 2: The forecasted estimate is updated using

  $$g_{t\left| t \right.}^{{\left( {m,n} \right)}} = g_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} + p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} \left( {p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} + \frac{{\pi^{2} }}{2}} \right)^{ - 1} \left( {Z_{t} - Z_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} } \right)$$

  (23)
  $$p_{t\left| t \right.}^{{\left( {m,n} \right)}} = p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} - p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} \left( {p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} + \frac{{\pi^{2} }}{2}} \right)^{ - 1} p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}}$$

  (24)

The conditional densities are computed using the following equation

$$f\left( {Z_{t} \left| {S_{t} = m,} \right.S_{t - 1} = n,\psi_{t - 1} } \right) = \frac{1}{{\sqrt {2\pi \left( {p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} + \frac{{\pi^{2} }}{2}} \right)} }} - \exp \left( {\frac{{ - \left( {Z_{t} - Z_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} } \right)^{2} }}{{2\left( {p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}} + \frac{{\pi^{2} }}{2}} \right)}}} \right)^{ - 1} p_{{t\left| {t - 1} \right.}}^{{\left( {m,n} \right)}}$$

(25)

It can be noted that the above procedures make our process exclusively path dependent. Hence, to remove the path dependence we rely on Kim (1994) as cited in Smith (2002). We compute the conditional expectation of the log-volatility forecast by taking the weighted average output of the previous iteration using the formulations stated below.

$$g_{t\left| t \right.}^{m} = \frac{{\sum\nolimits_{n = 1}^{N} {\Pr \left[ {S_{t} = m,S_{t - 1} = n\left| {\psi_{t} } \right.} \right]} g_{t\left| t \right.}^{{\left( {m,n} \right)}} }}{{\Pr \left[ {S_{t} = m\left| {\psi_{t} } \right.} \right]}}$$

(26)

$$p_{t\left| t \right.}^{m} = \frac{{\sum\nolimits_{n = 1}^{N} {\Pr \left[ {S_{t} = m,S_{t - 1} = n\left| {\psi_{t} } \right.} \right]} \left( {p_{t\left| t \right.}^{{\left( {m,n} \right)}} + \left( {g_{t\left| t \right.}^{n} - g_{t\left| t \right.}^{{\left( {m,n} \right)}} } \right)^{2} } \right)}}{{\Pr \left[ {S_{t} = m\left| {\psi_{t} } \right.} \right]}}$$

(27)

We calculate the regime probabilities based on Smith’s (2002) modification of Hamilton’s (1989) filter. First, we estimate the regime probabilities using

$$\Pr \left[ {S_{t} = m,S_{t - 1} = n\left| {\psi_{t} } \right.} \right] = \Pr \left[ {S_{t} = m\left| {S_{t - 1} = n} \right.} \right] \times \Pr \left[ {S_{t - 1} = m\left| {\psi_{t - 1} } \right.} \right]$$

(28)

The term Pr[S _t−1 = m|ψ _t−1] in the Eq. (28) is the previous iteration filter output. Next we calibrate the joint density using

$$f\left( {Z_{t} ,S_{t} = m,S_{t - 1} = n\left| {\psi_{t - 1} } \right.} \right) = f\left( {Z_{t} \left| {S_{t} = m} \right.,S_{t - 1} = n,\psi_{t - 1} } \right) \times \Pr \left[ {S_{t - 1} = m\left| {\psi_{t - 1} } \right.} \right]$$

(29)

where f(Z _t |S _t  = m, S _t−1 = n, ψ _t−1) is defined previously in Eq. (25). In step three we integrate the regimes to calculate the unconditional density as given in Eq. (30) and then we update the probability of the regimes in state ‘t’ using Eq. (31).

$$f\left( {Z_{t} \left| {\psi_{t - 1} } \right.} \right) = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {f\left( {Z_{t} \left| {S_{t} = m} \right.,S_{t - 1} = n,\psi_{t - 1} } \right)} }$$

(30)

$$\Pr \left[ {S_{t} = m,S_{t - 1} = n\left| {\psi_{t - 1} } \right.} \right] = \frac{{f\left( {Z_{t} \left| {S_{t} = m} \right.,S_{t - 1} = n,\psi_{t - 1} } \right)}}{{f\left( {Z_{t} \left| {\psi_{t - 1} } \right.} \right)}}$$

(31)

Appendix 3: Turning points in the economic cycle

Turning point	Date	Expansion (E)/contraction (C)	Months in regime
Panel A: US
0	4/1997	E1	47
1	3/2001	C1	8
2	11/2001	E2	73
3	12/2007	C2	18
4	6/2009	E3	46
Panel B: UK
0	4/1997	E1	133
1	5/2008	C1	20
2	1/2010	E2	7
3	8/2010	C2	18
4	2/2012	E3	14
Panel C: Germany
0	4/1997	E1	45
1	1/2001	C1	31
2	8/2003	E2	56
3	4/2008	C2	9
4	1/2009	E3	51
Panel D: France
0	4/1997	E1	64
1	8/2002	C1	9
2	5/2003	E2	57
3	2/2008	C2	12
4	2/2009	E3	50
Panel E: Canada
0	4/1997	E1	129
1	1/2008	C1	18
2	7/2009	E2	45
Panel F: Japan
0	4/1997	C1	28
1	7/1999	E1	13
2	8/2000	C2	32
3	4/2003	E2	58
4	2/2008	C3	13
5	3/2009	E3	17
6	8/2010	C4	8
7	4/2011	E4	13
8	5/2012	C5	8
9	1/2013	E5	2

The turning points of the economic cycle are based on the National Bureau of Economic Research (NBER) official dates of troughs and peaks for the US and the Economic Cycle Research Institute (ECRI) for the UK, Germany, France, Canada and Japan (ECRI 2014; NBER 2013). The sample period is from April 1997 to March 2013, yielding 192 monthly observations. Each month in the sample is divided into either an expansionary regime or a contractionary regime based on the turning point.