Introduction

The durability, fixity and heterogeneity of dwellings imply that transactions costs are significant in the housing market. In comparison to financial markets, and in comparison to the markets for most consumer goods, housing purchases require costly search to uncover the prices and attributes of commodities. Given the many frictions associated with the purchase of housing, it is hardly surprising that observed price behavior deviates from that predicted by simple models of economic markets.

Inertia in the price adjustment process in the housing market has been well-documented; many studies have concluded that returns in housing markets are predictable by demonstrating that time series estimates of aggregate prices exhibit inertia (Hosios and Pesando 1991; Guntermann and Norrbin 1991; Gatzlaff 1994; and Malpezzi 1999).

Persistence in housing returns has been found recently at the level of individual dwellings—in eight regional markets in Sweden (Englund et al. 1999) and in four U.S. cities (Hill et al. 1999). These analyses reject the random walk hypothesis, which underlies the Case and Shiller model (1989), in favor of a first-order serial correlation process for housing prices. But in this geographical market, price signals exist in space as well as time. Many of the features which can lead to slow diffusion in the time domain may have analogous effects over space. Price information diffuses over space as well as time, and information costs alone can cause prices to deviate from random fluctuations.

Disentangling a diffusion process in the time domain and a diffusion process over space is not straightforward. Our analysis concludes that it is important to take explicit account of these diffusion processes—since shocks and signals tend to be substantially more persistent when individual dwelling returns are correlated over time and over space. Our analysis shows that, due to this persistence, conventional procedures for estimating price series are quite likely to generate misleading estimates of aggregate housing returns.

In this paper, we develop a model of price diffusion, and we incorporate a more general and more appropriate structure of the price discovery process at the level of the individual dwelling. We explicitly incorporate spatial and temporal dependence of idiosyncratic housing prices into a repeat transactions model. We construct a repeat transactions index of prices by estimating this model using a body of data almost uniquely suited to the analysis: the prices of condominium dwellings in Singapore using all transactions reported in the entire country during an eleven-year period. Multiple transactions of the same condominium unit are observed, and all dwellings with market transactions are geocoded. We compare the properties of aggregate housing price indexes and returns computed from our more general model with indexes computed from conventional models. We find that when aggregate investment returns are estimated from models permitting housing prices to follow a random walk and that they be spatially independent, aggregate housing returns are strongly predictable. However, when aggregate returns are estimated from more general models permitting mean revision and spatial correlation, predictability in aggregate investment returns is completely absent. We show that this arises from two sources; the illiquid nature of housing transactions and the persistent shocks to individual housing prices in time and over space. With these two factors present, the estimated predictability in aggregate housing returns is biased. In principle, even with persistent shocks on individual housing prices, if there were enough transactions at a given point in time, then this small sample bias would disappear. However, we also find that having more observations over time, while maintaining a constant transaction frequency, exacerbates this bias. Only higher transactions frequencies would reduce the bias. For the bias to disappear, however, the frequency of transactions would need to be about as high in the housing market is as it is in the stock market.

We then analyze the economic implications of these statistical findings for investment in housing markets. In particular, we simulate the investment outcomes for an investor fully informed about spatial and temporal dynamics with the outcomes for an uninformed investor. Presumably, better information about housing market dynamics will lead to better investment performance in the housing market. We find that the investor with better knowledge of price diffusion over time and space outperforms the uninformed investor, capitalizing on this informational advantage. However, her superior performance appears to be bounded by relatively short holding periods and low transactions costs.

“A Micro Model of House Prices” develops a general model of housing prices that supports explicit tests for the spatial and temporal pattern of price movements. This section links our model to the widely employed method for measuring housing prices proposed more than 40 years ago by Bailey et al. (1963), as well as its subsequent extensions (e.g., Case and Shiller 1987). The data are described tersely in “Data”. Our empirical results are presented in “The Diffusion of House Price Innovations”, “The Course of Housing Prices, Investment Returns and Their Predictability”, “Investment Performance” and “Conclusion”. We test for random walks in space and time against the alternative of mean reversion, and we examine the link between pricing deviations at the individual level and aggregate price movements. We reconcile the puzzle of autocorrelated estimates of prices and returns. We also investigate investor behavior and housing market illiquidity in some detail.

A Micro Model of House Prices

The objects of exchange in the housing market are imperfect substitutes for one another. Indeed, dwellings with identical physical attributes may differ in market price simply because the price incorporates a complex set of site-specific amenities and access costs. But few dwellings have identical physical characteristics; thus comparison-shopping is more difficult and more expensive than in most other markets.

Moreover, housing transactions are made only infrequently, so households must consciously invest in information to participate in this market. As a result, the market is characterized by a costly matching process. Market agents, buyers, and sellers are heterogeneous, and they differ in information and motivation; commodities are themselves heterogeneous. Consequently an observed transaction price for a specific unit may deviate from the price ordained in a simpler environment.

Buyers, sellers, appraisers, and real estate agents estimate the “market price” of a dwelling by utilizing the information embodied in the set of previously sold dwellings. The usefulness of these transactions as a reference depends upon their similarity across several dimensions: physical, spatial, and temporal. Inferences about the “market price” of the dwelling can be drawn only imperfectly from a set of past transactions, because dwellings differ structurally, enjoy different locational attributes, and are valued under different market conditions by different actors over time. Because dwellings trade infrequently, the arrival of new information about market values is slow. From an informational standpoint, the closest comparable transaction across these various dimensions may be the last transaction of the same dwelling. Alternatively, the most comparable transaction may be the contemporaneous selling price of another dwelling in close physical proximity.

An attempt to uncover the market value of a dwelling is further complicated by the fact that a transactions price is not only a function of observable physical characteristics, but also of unobserved buyer and seller characteristics such as their urgency to conclude a transaction (Quan and Quigley 1991). For any given transaction, all that is known is that an offer was made by a specific buyer that was higher than a specific seller’s reservation price.

We develop a model with spatially and temporally correlated errors in a repeat transactions framework. Innovations in housing prices are assumed to take place continually, but transactions are observed sporadically. At any point in time, the prices of houses are dependent over space. In the determination of the price of a house, the weights attributable to neighboring houses depend upon their proximity to the house. But the prices of neighboring houses are also observed only infrequently.

Let the log transaction price of dwelling i at time t be

$$ {V_{it}} = {P_t} + {Q_{it}} + {e_{it}} = {P_t} + {X_{it}}\beta + {e_{it}}, $$
(1)

where V it is the log of the observed transactions price of dwelling i at t, and P t is the log of aggregate housing prices. Q it is the log of housing quality, and can be parameterized by X it , the set of housing attributes and by a set of coefficients, β, which price those attributes. If a transaction is observed at two points in time, t and τ, and if the quality of the dwelling remains constant during the interval, then

$$ \begin{array}{*{20}{c}} {{V_{it}} - {V_{i\tau }} = {P_t} - {P_\tau } + \left( {{X_{it}} - {X_{i\tau }}} \right)\beta + {e_{it}} - {e_{i\tau }}} \\ { = {P_t} - {P_\tau } + {e_{it}} - {e_{i\tau }}} \\ \end{array} $$
(2)

With constant quality, (2) identifies price change in the market. Equation 2 also shows that the return on an individual dwelling can be decomposed into an aggregate return \( \left( {{P_t} - {P_\tau }} \right) \) and an idiosyncratic return \( \left( {{e_{it}} - {e_{i\tau }}} \right) \).

Let the idiosyncratic part of the house price (or the error term), e it , consist of two components that are realized for each individual dwelling at the time of transaction: η it , an idiosyncratic innovation without persistence; and ε it , an idiosyncratic innovation with persistence, \( {\varepsilon_{it}} = \lambda {\varepsilon_{it}} + {\mu_{it}} \). In addition, assume that the value of any particular dwelling depends also on innovations that occur to other dwellings contemporaneously. We assume this spatial correlation depends on the distance between units.

$$ {e_{it}} = \rho \sum\limits_{j = 1}^N {{w_{ij}}{e_{jt}} + {\xi_{it}} = \rho \sum\limits_{j = 1}^N {{w_{ij}}{e_{jt}} + {\varepsilon_{it}} + {\eta_{it}} = \rho \sum\limits_{j = 1}^N {{w_{ij}}{e_{jt}} + \lambda {\varepsilon_{i,t - 1}} + {\eta_{it}} + {\mu_{it}},} } } $$
(3)

where w ij is some function of the distance between unit i and j and N is the number of dwellings in the economy. Let \( E\left( {{\eta_{it}}{\eta_{jt}}} \right) = 0,E\left( {{\varepsilon_{it}}{\varepsilon_{jt}}} \right) = 0,E\left( {\eta_{it}^2} \right) = \sigma_\eta^2 \) and \( E\left( {\mu_{it}^2} \right) = \sigma_\mu^2 \). The value of a particular dwelling depends, not only on its own past and contemporaneous innovations, but also on innovations of other dwellings, past and contemporaneous.

In vector notation, expression (3) is

$$ {{\mathbf{e}}_t} = \rho {\mathbf{W}} {{\mathbf{e}}_t} + {{\mathbf{\xi }}_t}, $$
(4)

where e t is a vector of e it for all the dwellings at time t, \( _{{{\mathbf{e}}_t} = \left[ {{e_{1t}},{e_{2t}}, \cdots, {e_{Nt}}} \right]\prime } \), W is a weight matrix, some measure of the distance between dwellings, and \( {{\mathbf{\xi }}_t} \) a vector of ξ it where \( {{\mathbf{\xi }}_t} = \left[ {{\xi_{1t}},{\xi_{2t}}, \cdots, {\xi_{Nt}}} \right]\prime \), for all dwellings. By solving for e t and taking the difference between two transactions at times t and s, we have

$$ {{\mathbf{e}}_t} - {{\mathbf{e}}_s} = {\left( {{\mathbf{I}} - \rho {\mathbf{W}}} \right)^{ - 1}}\left( {{{\mathbf{\xi }}_t} - {\xi_s}} \right). $$
(5)

The variance-covariance matrix of (5) is

$$ E\left[ {\left( {{{\mathbf{e}}_t} - {{\mathbf{e}}_s}} \right)\left( {{{\mathbf{e}}_t} - {{\mathbf{e}}_s}} \right)\prime } \right] = {\left( {{\mathbf{I}} - \rho {\mathbf{W}}} \right)^{ - 1}}E\left[ {\left( {{{\mathbf{\xi }}_t} - {{\mathbf{\xi }}_s}} \right)\left( {{{\mathbf{\xi }}_t} - {{\mathbf{\xi }}_s}} \right)\prime } \right]{\left( {{\mathbf{I}} - \rho {\mathbf{W}}} \right)^{ - 1}}. $$
(6)

Equations 5 and 6 indicate that when the prices of dwellings are autocorrelated over time and space, the price of any unit in the market at any period will be predictably related to those of other units at other periods.

Transactions on dwellings occur only infrequently. First, consider the covariance in errors between a dwelling i sold at t and s and another dwelling k sold at τ and ς, \( E\left[ {\left( {{e_{it}} - {e_{is}}} \right)\left( {{e_{k\tau }} - {e_{k\varsigma }}} \right)} \right] \). From Equation 6, and letting \( {\mathbf{\Pi }} = {\left( {{\mathbf{I}} - \rho {\mathbf{W}}} \right)^{ - 1}} = \left[ {{{\mathbf{\pi }}_1},{{\mathbf{\pi }}_2}, \cdots, {{\mathbf{\pi }}_2}} \right] \), we have

$$ E\left[ {\left( {{e_t} - {e_s}} \right)\left( {{e_\tau } - {e_\varsigma }} \right)\prime } \right] = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\pi }}_1^\prime } \\ {{\mathbf{\pi }}_2^\prime } \\ \vdots \\ {{\mathbf{\pi }}_{\text{N}}^\prime } \\ \end{array} } \right]\left\{ {E\left[ {\left( {{\xi_t} - {\xi_s}} \right)\left( {{\xi_\tau } - {\xi_\varsigma }} \right)\prime } \right]} \right\}\left[ {{{\mathbf{\pi }}_1},{{\mathbf{\pi }}_2}, \cdots, {{\mathbf{\pi }}_N}} \right]. $$
(7)

The elements of this expression are,

$$ E\left[ {\left( {{e_{it}} - {e_{is}}} \right)\left( {{e_{k\tau }} - {e_{k\varsigma }}} \right)} \right] = {\mathbf{\pi }}_i^\prime \left\{ {E\left[ {\left( {{\xi_\tau } - {\xi_s}} \right)\left( {{\xi_\tau } - {\xi_\varsigma }} \right)\prime } \right]} \right\}{{\mathbf{\pi }}_k}. $$
(8)

Since \( E\left( {{\xi_{it}}{\xi_{js}}} \right) = 0\;{\text{for}}\;i \ne j,E\left[ {\left( {{\xi_t} - {\xi_s}} \right)\left( {{\xi_\tau } - {\xi_\varsigma }} \right)\prime } \right] \) is a diagonal matrix such that

$$ E\left[ {\left( {{\xi_t} - {\xi_s}} \right)\left( {{\xi_\tau } - {\xi_\varsigma }} \right)\prime } \right] = E\left[ {\left( {{\xi_{it}} - {\xi_{is}}} \right)\left( {{\xi_{i\tau }} - {\xi_{i\varsigma }}} \right)} \right] \times {\mathbf{I}}. $$
(9)

It is straightforward to show that

$$ E\left( {{\xi_{it}}{\xi_{i\tau }}} \right) = {\lambda^{\left| {t - \tau } \right|}}\left( {\frac{{\sigma_\mu^2}}{{1 - {\lambda^2}}}} \right) + 1\left( {t = \tau } \right)\sigma_\eta^2, $$
(10)

which implies

$$ E\left[ {\left( {{\xi_{it}} - {\xi_{is}}} \right)\left( {{\xi_{i\tau }} - {\xi_{i\varsigma }}} \right)} \right] = \left( {{\lambda^{\left| {t - \tau } \right|}} - {\lambda^{\left| {t - \varsigma } \right|}} - {\lambda^{\left| {s - \varsigma } \right|}}} \right)\left( {\frac{{\sigma_\mu^2}}{{1 - {\lambda^2}}}} \right) + \left[ {1\left( {t = \tau } \right) - 1\left( {t = \varsigma } \right) - 1\left( {s = \tau } \right) + 1\left( {s = \varsigma } \right)} \right]\sigma_\eta^2. $$
(11)

Therefore, the variance-covariance matrix of innovations between a dwelling i sold at t and s and another dwelling k sold at τ and ς is

$$ E\left[ {\left( {{e_{it}} - {e_{is}}} \right)\left( {{e_{k\tau }} - {e_{k\varsigma }}} \right)} \right] = {\mathbf{\pi }}_i^\prime \left\{ {E\left[ {\left( {{\xi_{it}} - {\xi_{is}}} \right)\left( {{\xi_{i\tau }} - {\xi_{i\varsigma }}} \right)} \right] \times {\mathbf{I}}} \right\}{{\mathbf{\pi }}_k} = \left\{ {\left( {{\lambda^{\left| {t - \tau } \right|}} - {\lambda^{\left| {t - \varsigma } \right|}} - {\lambda^{\left| {s - \tau } \right|}} + {\lambda^{\left| {s - \varsigma } \right|}}} \right)\left( {\frac{{\sigma_\mu^2}}{{1 - {\lambda^2}}}} \right) + \left[ {1\left( {t = \tau } \right) - 1\left( {t = \varsigma } \right) - 1\left( {s = \tau } \right) + 1\left( {s = \varsigma } \right)} \right]\sigma_\eta^2} \right\}{\mathbf{\pi }}_\eta^\prime {{\mathbf{\pi }}_k} $$
(12)

Equation 12 indicates how the variance-covariance matrix of residuals from the regression specified in (2) can be used to identify the temporal and spatial components of house price persistence, λ and ρ, respectively. Identification requires observing at least two transactions for each dwelling and observing the distance of each dwelling from all others in the market.

Note that this model of housing prices specializes to that of Bailey et al. (1963) when λ = ρ = 0, to that of Case and Schiller (1987) when λ = 1, ρ = 0 and to those of Hill et al. (1999) and Englund et al. (1999) when ρ = 0. When, ρ = 0 so that no spatial correlation is present, the variance of the return on an individual dwelling between t and s is

$$ var\left( {{V_{it}} - {V_{is}}} \right) = \frac{{2\sigma_\mu^2}}{{1 - {\lambda^2}}}\left( {1 - {\lambda^{t - s}}} \right) + 2\sigma_\eta^2, $$
(13)

which is concave in the transaction interval.

In Case and Shiller’s (1989) model, with λ = 1 and ρ = 0, the error term in individual housing price follows \( {e_{it}} = {\varepsilon_{it}} + {\eta_{it}} \) where \( {\varepsilon_{it}} = {\varepsilon_{i,t - 1}} + {\mu_{it}} \). Then, the variance of the return on an individual dwelling is

$$ var\left( {{V_{it}} - {V_{is}}} \right) = \left( {t - s} \right)\sigma_\mu^2 + 2\sigma_\mu^2. $$
(14)

The variance increases linearly with the length of the time interval between transactions. Thus, with mean reversion in the data, a model based on a random walk assumption underestimates the return variances for housing transactions over short intervals, but overestimates the variances for housing transactions over long intervals.Footnote 1 The housing price indexes published by U.S. government agencies (e.g., the OFHEO, now FHFA, price indices for metropolitan areas) are based upon the repeat transactions model developed above with λ = 1 and ρ = 0. But the computation procedures do include a second order term in the variance estimation (See Abraham and Schauman 1991; Calhoun 1996), so that the variance increases at a diminishing rate with the time interval between transactions (A < 0).

$$ var\left( {{V_{it}} - {V_{is}}} \right) = A{\left( {t - s} \right)^2} + B\left( {t - s} \right) + C $$
(14′)

Data

The analysis below is based upon all private condominium transactions in Singapore during an eleven-year period. Non-landed properties (apartments and condominiums) account for roughly two-thirds of the Singapore housing stock, and units in condominiums account for almost 40% of private residential housing in land-scarce Singapore.Footnote 2

The data include all transactions involving condominium dwellings during the period from January 1, 1990 to December 31, 2000.Footnote 3 An extensive set of physical characteristics of the dwellings is recorded. The date of the transaction is recorded as well as the date of completion of construction. In addition, the address, including the postal code, is reported. The postal code identifies the physical location—the block of flats or, quite often, the specific building. A matrix of distances among Singapore’s fifteen hundred postal codes permits each dwelling to be located spatially. The data set includes transactions among dwellings in the standing stock, sales of newly constructed dwellings, and presales of dwellings under construction (where transactions may be consummated several months before the date construction is actually completed).

The panel nature of the data permits us to distinguish dwellings sold more than once, and this identifies the models specified in “A Micro Model of House Prices.” By confining the sample to dwellings in multifamily properties, we eliminate the types of dwellings for which additions and major renovations are feasible. The sample of multifamily dwellings is thus less likely to include those for which the assumption of constant quality between transactions (see Eq. 2) is seriously violated.

Singapore data offer another advantage in estimating the model of housing prices, namely a spatial homogeneity of local public services (e.g., police protection, neighborhood schools), especially when compared to cities of comparable size in North America. During the decade of the 1990s, there was no discernible trend in the quality of neighborhood attributes of the bundle of housing services.Footnote 4

Table 1 presents a summary of the repeat sales data used in the empirical analysis reported below. There are several points worth noting. First, confirming the infrequency of housing transactions, the number of dwellings sold more than once is less than 20% of the population of dwellings sold during the eleven-year period. Only 3% of the 52,337 dwellings were sold more than twice in the eleven-year period.

Table 1 Summary of Transactions Data on Singapore Condominiums 1990–2000
Full size table

Second, the average selling prices tend to be higher for dwellings sold more frequently. The rate of appreciation is also higher. On average, dwellings sold five times appreciate almost twice as fast as dwellings sold only twice. For the dwellings sold more frequently, price appreciation tends to be more volatile. Transactions involving high-turnover dwellings are apparently riskier, but this risk is compensated by higher returns.

Third, the intervals between transactions are longer for dwellings sold infrequently. In part, this is an artifact of the fixed sampling framework. For presold dwellings, the average elapsed time between transaction and completion of construction is largest for those sold least frequently, which is not consistent with the popular belief in Singapore that presales are associated with “speculation” in the housing market.

Fourth, there are some differences in the characteristics of the dwellings sold more frequently. They tend to be larger in area, contain more rooms, and they are more centrally located. Their transit access is similar to that of dwellings sold less frequently.

The data on condominium transactions supports a price index regression model of the form of Eq. 2,

$$ {V_{it}} - {V_{is}} = {P_t}{D_{it}} - {P_s}{D_{is}} + \gamma {\kappa_{it}} - \gamma {\kappa_{it}} + {e_{it}} - {e_{is}}, $$
(15)

where D ij is a variable with a value of 1 for the month j in which condominium i is sold and zero in other months, and P j is the estimated coefficient for this variable. There are 132 of these time variables, one for each month between 1990 and 2000. If dwelling i has been presold, κ it is the time interval between the transaction date and the completion of construction.Footnote 5 For dwellings sold after completion of construction, κ it is zero. Thus, the estimated coefficient γ measures the monthly discount rate for presold dwellings, i.e., the discount for unrealized service flows from dwellings which have been purchased but which are not yet available for occupancy. The purchase of a dwelling before completion, or even before construction, is not unique to Singapore and has become rather common in condominium transactions, for example in vacation properties in the U.S. Pre-sale contracts provide liquidity to developers and insurance to consumers against unanticipated price increases in the market.Footnote 6 Of the 11,883 pairs of transactions noted in Table 1, 305 consist of presale pairs. For another 5,204 pairs, the first transaction was made sometime before the property was completed.

The Diffusion of House Price Innovations

We assume the error terms in Eq. 3, η it and μ it , are normally distributed. The log likelihood function for the observed sample of condominium transactions is thus

$$ \log L\left( {P,\gamma, \lambda, \rho, \sigma_\eta^2,\sigma_\mu^2} \right) = - \frac{T}{2}\log \left( {2\pi } \right) + \frac{1}{2}\left\{ {\log \left( {{{\left| {\mathbf{\Omega }} \right|}^{ - 1}}} \right) - \left( {{\mathbf{\delta }}\prime {{\mathbf{\Omega }}^{ - 1}}{\mathbf{\delta }}} \right)} \right\}, $$
(16)

where \( {\mathbf{\delta }} = \left[ {{V_{it}} - {V_{is}} - {P_t}{D_{it}} + {P_s}{D_{is}} - \gamma {\kappa_{it}} + \gamma {\kappa_{it}}} \right],{\mathbf{\Omega }} = \left[ {{\omega_{ij}}} \right] \), and \( {\omega_{ij}} = E\left[ {\left( {{e_{it}} - {e_{is}}} \right)\left( {{e_{j\tau }} - {e_{j\varsigma }}} \right)} \right] \) defined in (15). We estimate the parameters, λ, ρ, γ, P t , σ η and σ μ , by maximizing the log likelihood (16), based on 11,883 observations of repeat sales of 10,288 dwellings sold two or more times. In (3), the weights are assumed to be inversely related to distance, up to 250 m.Footnote 7 The influence of any transaction extends for roughly 200,000 square meters in the surrounding area.

Table 2 reports the estimated error structure when it is assumed that the price of an individual dwelling follows a spatio-temporal correlation process, a mean reverting process, and a random walk process, respectively. In the most general model, Column A, the estimated serial correlation coefficient, ρ, implies a large persistence in individual housing prices, with a half life of more than 6 months. The estimated spatial correlation coefficient, 0.55, implies a slow spatial diffusion. These coefficients are quite precisely estimated; the estimated value for ρ, 0.89, is significantly different from one by a wide margin. The estimated coefficient for γ, the discount for the period between transaction and dwelling completion (for presold units), is 14 basis points. This represents a 1.7% annual discount for a dwelling unit sold today for occupancy a year hence. The magnitude of the discount is not trivial. During this period aggregate housing prices rose, on average, by 0.4% monthly; thus, the discount for presold units reduced the net price appreciation for consumers by one third.Footnote 8

Table 2 Estimated Error Structure and Price Dynamics, Singapore condominium 1990–2000. (t-statistics in parentheses)
Full size table

The second column reports parameter estimates for the model when individual house prices are allowed to follow a mean reverting process, but with ρ assumed to be zero. The estimated serial correlation coefficient, λ, is 0.72, somewhat smaller than the estimate in Column A. Likelihood ratio tests reject a random walk in house prices (λ = 1) and serially uncorrelated house prices (λ = 0) by wide margins, χ 2 = 16,564, and χ 2 = 1,670.6 respectively. The estimated value of λ suggests that the half-life of a one-unit shock to housing prices is about 2 months.

The third column reports parameter estimates for a model in which individual house prices are assumed to follow a random walk process without spatial autocorrelation. Following OFHEO, the table reports the model with a quadratic term, as in (14′), which also fits the data better. These results suggest that the variance in house prices increases with transaction intervals up to 37 months.

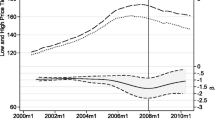
Figure 1 presents estimated monthly price indexes derived from the three models reported in Table 2. The estimated price index from the model with a mean reverting process and the index from the model with a spatio-temporal correlation process appear to move quite closely. The estimated price index from the random walk model is consistently lower than that implied by the other two models.

Fig. 1
figure 1

Singapore Condominium Price Indices 1990–2000 (The figure graphs the monthly index values \( {I_t} = \exp \left[ {\sum\limits_{j = 1}^t {{P_j}} } \right] \) where the values of P are estimated from models reported in Table 2 by maximizing the likelihood function in Eq. (16))

Full size image

The Course of Housing Prices, Investment Returns and Their Predictability

Predictability of Housing Returns

Although Fig. 1 reports similar patterns for the course of housing prices of Singapore dwellings, the investment returns implied by these aggregate indices are quite different. Ignoring transactions costs and leverage, the return in any period, R t , is the change in the asset value plus the dividend (i.e., the rental stream, S t , enjoyed during the period).

$$ {R_t} = \left( {\frac{{{P_t} + {S_t}}}{{{P_{t - 1}}}}} \right)\left( {\frac{{{I_{t - 1}}}}{{{I_t}}}} \right), $$
(17)

where I t is an index of the cost of living, less housing.

Figure 2 uses the non-housing component of the CPI for Singapore to chart the course of real investment returns in logarithms during the eleven-year period, from the three models.Footnote 9 Although the mean returns differ by less than five basis points per month, the patterns of estimated returns and the estimated volatility from the three models are strikingly different.

Fig. 2
figure 2

Monthly Returns to Investment in Singapore Condominiums 1990–2000

Full size image

Table 3 reports tests of the predictability of estimated monthly returns for the three indexes. We investigate the forecastability of returns based upon one-month and three-month lags. There is a consistent disparity in the predictability of investment returns implied by models based upon the three price generating processes. When spatial and serial correlations are recognized in the estimation of housing prices (Column A), there is no evidence that aggregate returns to housing investment are predictable. However, when housing returns are estimated from a mean reverting process without spatial correlation (Column B), standard tests reject the null hypothesis of no predictability in returns. Finally, when returns are estimated from the conventional random walk model, they are strongly predictable. The p-values for both tests are less than 0.5%. These results are consistent for both a one-period and a three-period distributed lag.Footnote 10 Indeed, the nonparametric kernel-based test (Hong 1996), reported in the last row, shows that the result does not rely upon any parametric specification of lag structure.

Table 3 Forecastability of Investment Returns, Singapore Condominiums, 1990–2000 (p-values in parentheses) \( {\hat R_t} = {\beta_o} + \sum\limits_i^n {{\beta_i}{{\hat R}_{t - i}} + {v_t}} \)
Full size table

The most striking feature of the table is that the predictability of the aggregate housing returns gradually disappears as restrictive assumptions on the individual housing price generating process are relaxed. When the assumption of the random walk with no spatial diffusion is maintained, p-values of the test statistics are very small. When the random walk assumption is relaxed (but spatial diffusion is not allowed), p-values are larger; the null hypothesis of no predictability in aggregate housing returns is still rejected at least for some of the tests. When returns on individual dwellings are allowed to be dependent over time and over space, p-values of the test statistics are all large enough that the null hypothesis of no predictability in aggregate housing returns is not rejected in any of the tests. This implies that the well known predictability in housing returns may arise simply because the underlying price index is inaccurately estimated due to restrictive assumptions about the price generation process.

Why does the aggregate return, when estimated with the random walk and no spatial diffusion assumption, appear to be significantly predictable while it exhibits no predictability when it is estimated without such restrictions?

To understand this, let \( {\hat R_t} = R_t^* + {\zeta_t} \), where \( {\hat R_t} \) is a regression-based estimate of the aggregate return, \( R_t^* \) is the true (unobserved) return, and \( {\zeta_t} \) is the estimation error. Consider a regression of the estimated aggregate return on its lagged term, \( {\hat R_{t + 1}} = {\beta_0} + {\beta_1}{\hat R_t} + {v_t} \). The value of the AR(1) coefficient, β 1, is

$$ {\beta_1} = \frac{{{\rm cov} \left( {R_t^*, R_{t + 1}^* } \right) + {\rm cov} \left( {{\zeta_t},{\zeta_{t + 1}}} \right)}}{{{\rm var} \left( {R_t^* } \right) + {\rm var} \left( {{\zeta_t}} \right)}} $$
(18)

For the autocorrelation coefficient, β 1, to be zero, it is required that: the true aggregate return be unpredictable, \( {\rm cov} \left( {R_t^*, R_{t + 1}^* } \right) = 0 \); and the estimation error be not persistent, \( {\rm cov} \left( {{\zeta_t},{\zeta_{t + 1}}} \right) = 0 \). Conversely, a non-zero estimate of the AR(1) coefficient, β 1, need not imply predictability in returns at all; it can arise from persistent forecast errors. This implies that the well-known findings that housing prices and housing returns are predictable may arise, simply by construction, if \( {\rm cov} \left( {{\zeta_t},{\zeta_{t + 1}}} \right) \) is not equal to zero.

The properties of \( {\zeta_t} \) determine estimated autocorrelation coefficient, β 1. Suppose we have a sample of M houses transacted in each of T periods. If \( {\rm cov} \left( {R_t^*, R_{t + 1}^* } \right) = 0 \), it can be shown that

$$ {\text{E}}\left( {{{\hat \beta }_1}} \right) = \frac{{E\left( {{\zeta_t}{\zeta_{t + 1}}} \right) + 0\left( {\frac{1}{T}} \right)}}{{\sigma_r^2 + \sigma_\varepsilon^2 + 0\left( {\frac{1}{T}} \right)}} + \frac{{\left\{ {E\left( {{\zeta_t}{\zeta_{t + 1}}} \right) + 0\left( {\frac{1}{T}} \right)} \right\}0\left( {\frac{1}{T}} \right)}}{{{{\left\{ {\sigma_r^2 + \sigma_\varepsilon^2 + 0\left( {\frac{1}{T}} \right)} \right\}}^3}}} - \frac{{\sigma_\varepsilon^2E\left( {{\zeta_t}{\zeta_{t + 1}}} \right) + 0\left( {\frac{1}{T}} \right)}}{{{{\left\{ {\sigma_r^2 + \sigma_\varepsilon^2 + 0\left( {\frac{1}{T}} \right)} \right\}}^2}}}, $$
(19)

where \( E\left( {{\zeta_t}{\zeta_{t + 1}}} \right) \to 0 \) for large M.

Equation 19 shows that \( E\left( {{{\hat \beta }_1}} \right) \) will converge to zero only if T is large enough and M is also large enough. The convergence of \( E\left( {{\zeta_t}{\zeta_{t + 1}}} \right) \) depends on the spatial structure of the housing market, and convergence is slow when prices of individual dwelling units are more correlated.Footnote 11

We can evaluate the impacts of the sample sizes of T and M by simulation. Using Singapore’s spatial structure, the previously estimated parameters, and assuming unpredictable aggregate returns, β 1 = 0, we simulate the Singapore private condominium market in two different dimensions, M and T. First, we simulate the price of each house in the sample each month for 10 years. We then randomly select some fixed number of houses each month, reflecting an underlying liquidity level or “transactions frequency.” We use the transactions so sampled to compute a repeat sales housing price index (Eq. 2), incorrectly assuming a random walk and no spatial diffusion. These estimates are used to compute the index-based returns, the first order autocorrelation coefficient of housing returns, \( {\hat \beta_1} \), and its t-ratio. We construct the base case of 1% transactions probability, i.e., for each month 1% of total dwellings are randomly selected for trading. Then we extend the base case, first with a higher transactions frequency of 5%, and second with a longer time series of 50 years and a one-percent transactions frequency. Note that these two cases will generate the same number of observations.

Figure 3 summarizes these simulations, replicated 100 times. The figure reports the distributions of the estimated coefficient \( \left( {{{\hat \beta }_1}} \right) \) and the corresponding t-statistics. It reports three distributions, the first with one-percent transactions frequency and monthly observations for 10 years, the second with the one-percent transactions frequency but monthly observations for 50 years, and the third with five-percent transactions frequency and monthly observations for 10 years.

Fig. 3
figure 3

Empirical Distribution of AR(1) Coefficient and t-statistics With different transactions probabilities, in Singapore private condominium market

Full size image

A transactions frequency of 1% per month is much higher than the turnover rate observed in virtually all housing markets.Footnote 12 A transactions frequency of 5% per month is close to the turnover rate observed in the U.S. stock market.Footnote 13 Thus, the 1% figure represents an illiquid market, and a 5% figure represents a very liquid market.

The probability distribution of \( {\hat \beta_1} \) with 1% transactions frequency and 120 monthly observations is sharply skewed to the left, centered around −0.3, quite far from the true value of 0. The distribution of t-statistics shows that usual t-tests are highly misleading. Among the 100 simulations, there are only fifteen instances where the t-statistic is larger than −2. This indicates that when the housing market has low transactions frequencies, even though aggregate housing returns are not predictable, it is very likely that the estimated returns will be highly predictable. This apparent predictability persists for low values of the monthly transactions frequency, and it is not eliminated until the monthly turnover rate reaches 5% level. When the transactions probability is 5%, the distribution is substantially further to the right, and the center of the distribution is quite close to zero; the t-statistics are between −2 and 2 for 90 instances out of 100, and the null hypothesis of no predictability is rarely rejected using conventional tests.

However, when the sample period extends to 50 years (five times the original 10 years) with the transactions frequency kept at 1%, the results are quite different. The distribution moves to the right only by a small margin, and the center of the distribution is still well below −0.2. At the same time, dispersion of the distribution is reduced. In this instance, a small change in mean and a large reduction in variance shifts the distribution of t-statistics further to the left. Therefore, if the transactions probability remains low, but the sample period is extended, the analyst is considerably more likely to reject the null hypothesis of no predictability. In fact, there is no instance out of 100 simulations where the t-statistics is larger than −2.

This simulation indicates how important it is to have enough observations cross sectionally (M) in testing for the predictability of aggregate returns. At the same time, it also shows how difficult it is to test for the predictability of returns since the low frequency of housing transactions is not due to inadequate data collection, but arises as an inherent feature of housing markets.

Investment Performance

The previous results show that persistent shocks in returns to individual dwellings over time and in space, coupled with infrequent housing transactions, leads to substantial small sample bias in the predictability of aggregate housing returns when measured under conventional repeat sales models. Is this economically important? How seriously do these biased forecasts affect investment decisions?

First, it is clear that the results noted above have separate implications for aggregate housing returns and for individual housing returns. Table 3 indicates that the aggregate housing return \( \left( {{R_t} = {P_t} - {P_{t - 1}}} \right) \) is not predictable at the level of the aggregate housing index, but the idiosyncratic housing return \( \left( {{e_{it}} - {e_{it - 1}} = \left[ {{V_{it}} - {V_{it - 1}}} \right] - \left[ {{P_t} - {P_{t - 1}}} \right]} \right) \) is still predictable. Let φ denote the serial correlation of monthly returns in an individual dwelling. It is straightforward to show, from (12), that

$$ \phi = - \frac{{\left( {1 - \lambda } \right)\sigma_\mu^2 + \left( {1 + \lambda } \right)\sigma_\eta^2}}{{2\sigma_\mu^2 + 2\left( {1 + \lambda } \right)\sigma_\eta^2}}. $$
(21)

For the Singapore housing market, the results in Table 3 indicate that an individual housing return is substantially persistent, and its monthly serial correlation is −0.29. This has significant implications for investment in the local housing market. A better knowledge of the price process for individual dwellings can lead to superior investment decisions in two ways. First, improvement may arise through better estimates of aggregate housing price trends. Different assumptions about the price generating process have small effects on the large-sample properties of slope coefficients, but, as shown above, they do have substantial effects on the efficiency of the estimated aggregate returns when transaction frequencies are low. An investor who relies on random walk and no spatial diffusion would conclude that the aggregate housing return is predictable. She would base her investment decision on the “pseudo-predictability,” which will likely lead to sub par performance. Second, improved performance will arise from basing investment decisions on more complete information. For example, when housing prices are spatially and serially correlated, knowledge of past and present innovations in nearby dwellings provides information valuable for predicting the future course of prices for any house that the investor considers for investment. The investor who believes in a random walk and no spatial diffusion in individual housing returns would simply ignore those signals. The empirical issue is whether these signals are economically important.

To explore this, we conduct a second simulation of investor activity which utilizes the structure of a hypothetical “Grid City.” In this hypothetical city, dwellings are located on a square grid with 41 points on a side, and a house at each interior point is separated by 50 m from its four nearest neighbors. Assume that the price of each dwelling follows the spatial and temporal correlation process, as reported in Table 2 Column A (i.e., ρ = 0.55 and λ = 0.89). We simulate the price of each house in the Grid City each month for 10 years. In the simulation, the true aggregate housing return is not predictable, β 1 = 0. We then analyze the results of investment rules which depend upon forecasts of future housing returns. The investment rule applied here is quite simple. Given assumptions on the price process and the consequent parameter values governing the processes, an investor makes forecasts for housing returns using all the available transactions information. The investor is instructed to “buy” if the forecasted return is greater than some preset threshold. When the investor decides not to buy, she is assumed to invest in some alternative asset that generates a risk free return. The threshold may be interpreted as some known transactions costs in the housing market. We set the risk free rate equal to zero for these simulations.

Transactions costs vary with housing market characteristics, financial market characteristics and tax systems, so it is difficult to specify a precise level.Footnote 14 We use 0%, 6% and 12% as investment thresholds, comparable with a wide range of plausible transactions and opportunity costs.Footnote 15

The simulation of housing returns is performed in a similar manner to the previous section. The investment holding period is set at 24 months, 48 months, and 96 months. We assume that the investor observes the market and collects transactions information during an initial observation period. We set the observation period at 24 months, 48 months, 72 months and 96 months. For simplicity, we concentrate on the dwelling unit located at the center of the grid. A price for each of 1,681 dwelling units is generated for every month of the observation period and the holding period. From the simulated prices, a sample of houses is selected each month with the preset transactions probability of 1%. Using the observations on the houses in the sample, together with her estimates of the parameters (λ and ρ), the investor makes a price forecast for the next 24, 48, or 96 months. If the forecasted return exceeds the threshold, she will invest. The price at the end of the holding period is then used to evaluate the return on her investment. We consider two investors with differing information. The fully informed investor is armed with the full knowledge of housing price dynamics which follows the correlation process reported in Table 2, column A, ρ = 0.55 and λ = 0.89. The uninformed investor forms her own forecasts in a similar manner. However, she assumes ρ = 0 and λ = 1, and does not recognize the serial and spatial correlation of prices. It is assumed that the transactions cost is paid when the house is sold, so the net performance of the investment is the capital gain less transactions cost.

Table 4 summarizes the forecast performance of the two investors. The table reports the average percent difference between the true price at the end of the holding period and the forecast made by the two investors. Each investor uses the information available in the observation period to make a forecast of the price at the end of the holding period. The forecast is compared to the actual price, and the average (absolute) percent deviations are reported in the table. The table reports the results of 2500 replications of this comparison using an underlying transactions probability of 1%.

Table 4 Difference in Forecasts by Fully Informed Investors and Uninformed Investors for Different Observation Periods and Holding Periods (2500 replications with transactions probabilities of 1% per month)
Full size table

Clearly the percentage errors are larger when the forecast is for prices further in the future (that is, when the assumed holding period is longer). The percentage errors are likewise smaller when the forecast is based upon more information (that is, when the forecasts are based upon a longer period of observing property transactions).

The results clearly establish that the informed investor makes better forecasts of future prices. For 15 out of 16 comparisons, the average error in the forecasts is less for the informed than for the uninformed investor. The difference is larger for shorter holding periods, but this advantage extends up to a holding period of 8 years.

The economic significance of the small, but systematic, advantage of the informed investor in forecasting is analyzed in Table 5. Table 5 reports the increased returns, in percentage points, to the informed investor as a function of the observation period and the holding period. The average increased return to the informed investor is reported for 2500 replications with an underlying transactions frequency of 1%. Results are reported for transactions costs of 0, 6, and 12%.

Table 5 Economic Advantage of Fully Informed Investor over Uninformed Investors in Percentage Points. (2500 replications with transactions probabilities of 1% per month)
Full size table

With no transactions costs, the informed investor earns a return that is about 200 basis points higher than the uninformed investor. Even with high transactions costs, the fully informed investor outperforms the uninformed investor by one to four percentage points. Only when transactions costs are very high (12%) and holding periods are very short (6 months), does the uninformed investor perform almost as well as the informed investor.

Conclusion

For the past 15 years, it has been widely accepted that investment returns in housing are predictable. It is also widely believed that, due to high transactions costs, it is difficult to take advantage of this predictability. This paper develops a model of housing price determination that considers spatial correlation and serial correlation concurrently. Using comprehensive data on all Singapore condominium transactions, we estimate the extent of predictability in aggregate housing returns and in individual housing returns. The analysis supports a general model of price discovery, rejecting a simple random walk model as well as a model with the mean reversion without spatial correlation. More importantly, we find that assumptions about the underlying price process for individual dwellings affect the predictability in aggregate housing returns. There is no evidence of strong predictable aggregate housing returns when the appropriate price process—persistent idiosyncratic returns over time and space—is taken into account. This need not necessarily imply that housing market is efficient; individual housing returns are still persistent. The results indicate that the housing return is only predictable at the level of the individual asset, not at the aggregate level. In contrast, when the aggregate housing price index is estimated from a random walk model without spatial diffusion, the estimated aggregate housing return shows substantial predictability. We show that this arises from two sources; the illiquid nature of housing transactions and the persistent shocks on individual housing prices in time and over space. With these two factors present, the estimated predictability in aggregate housing returns contains substantial small sample bias. We show that the bias cannot be removed by extending time periods in the sample. More observations over time at the same transactions frequency only exacerbate this bias. The bias disappears only when the transactions frequency is high enough. However, for the bias to disappear, the transactions frequencies in the housing market would have to be as liquid as the transactions frequencies in stock markets.

Our simulation results suggest that an investor with enough information about the individual housing price process can, in fact, enjoy higher returns to housing investment. Our simulation results show that the investment performance of the fully informed investor is indeed superior to that of the naïve investor, even though her performance is bounded by holding periods and transactions costs.