Abstract
To writing anything on a keyboard at all requires us to know first what to type, then to activate motor programmes for finger movements, and execute these. An interruption in the information flow at any of these stages leads to disfluencies. To capture this combination of fluent typing and typing hesitations, researchers calculate different measures from keystroke-latency data—such as mean inter-keystroke interval and pause frequencies. There are two fundamental problems with this: first, summary statistics ignore important information in the data and frequently result in biased estimates; second, pauses and pause-related measures are defined using threshold values which are, in principle, arbitrary. We implemented a series of Bayesian models that aimed to address both issues while providing reliable estimates for individual typing speed and statistically inferred process disfluencies. We tested these models on a random sample of 250 copy-task recordings. Our results illustrate that we can model copy typing as a mixture process of fluent and disfluent key transitions. We conclude that mixture models (1) map onto the information cascade that generate keystrokes, and (2) provide a principled approach to detect disfluencies in keyboard typing.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
Introduction
Hesitations in keyboard typing are indicative of process delays on higher levels of activation. For example, imagine you are asked to copy the word “piobaireachd.” Unless you are familiar with Scottish Gaelic this is difficult: even though you know which word to write and how to spell it, you will probably pause at least once in the middle of the word. The maximum fluency when copying and composing text is restricted by how fast we can move our fingers—plan and execute motor codes. However, sometimes upstream processes have to catch up—when double-checking the target word’s spelling or when deciding what to say next—meaning that the output speed decreases. These hesitations are typically referred to as disfluencies and are invaluable to develop a theoretical understanding of an individual’s writing dynamics.
Whether or not or how often we hesitate when copying a word gives insight into our ability to translate visual input into motor plans (and execute these). In spontaneous production disfluencies allow insight into the information cascade that underlies language production from the mental generation of a message, into grammatical processing, and finally the generation and execution of motor codes. In particular disfluencies are indicators of process demands that arise on higher levels of mental representation (Christiansen & Chater, 2016; Olive, 2014); for example when preplanning syntactic dependencies (Roeser et al., 2019) or retrieving the lexical entry of a word or its spelling (Torrance et al., 2016). This idea can be found in theoretical models of spoken language production (Bock & Ferreira, 2014), handwriting (Van Galen, 1991) and keyboard typing (Hayes, 2012). Copy-typing, in contrast to free text production, does not require the generation and linguistic translation of contents (Leijten & Van Waes, 2013; Van Waes et al., 2019, 2021). Hesitations, however, arise during both copy-typing and unconstrained text production. Consequently, data from keyboard typing involves a combination of two processes: (1) a smooth information flow from higher into lower levels of activation and (2) hesitations at the execution stage resulting from inhibitions on higher levels of activation. At present there is no principled way to detect keystroke intervals that can be considered disfluencies. In this paper we present a series of statistical models that aim to capture this theoretical process underlying keyboard typing as a combination of fluent and disfluent keystroke transitions.
These two processes—fluent and disfluent information flow into lower levels of activation—are typically distinguished by writing researchers in the analysis of keystroke transitions as those keystroke intervals that constitute a pause and those that do not. Keystroke-logging captures this information. From these logs, researchers calculate different process measures including measures of writing fluency (Chukharev-Hudilainen et al., 2019; Medimorec et al., 2017; Medimorec & Risko, 2016; Van Waes & Leijten, 2015), means, medians and standard deviations of inter-keystroke intervals (the latency between two consecutive keystrokes), and writing hesitations such as the number of pauses or pause duration (for an overview of frequently used keystroke measures see Conijn et al., 2019a). Indeed, Conijn et al. (2019a) suggested that these aggregates are sensitive to processing difficulty that arises on different levels of mental representation. However, there are two substantial problems tight to the use of such summary statistics to inform theories of how cognitive processes are coordinated throughout the writing timecourse.
First, pause frequencies, writing bursts and related measures are used to assess writing performance (e.g. Alves & Limpo, 2015; Beers et al., 2017; Zhang et al., 2019). These measures require a definition of what passes as a pause (Van Waes et al., 2016; Wengelin, 2006), i.e. a pause criterion threshold often set to 2 secs (Chanquoy et al., 1996; Kaufer et al., 1986; Sullivan & Lindgren, 2002; Wengelin, 2002) or some other lower bound (Chukharev-Hudilainen, 2014; Connelly et al., 2012; Leijten & Van Waes, 2013). Researchers have stipulated pause thresholds specific to their research purposes and based on thresholds stipulated by prior research. However, ideally, these thresholds would need to be specific to factors such as location of the keystroke transition in the text, writing task, and writing skills / experience of the typist (Wengelin, 2006). For example, pauses are more common before sentences than within words: writers are more likely to plan what to say next before they start a new sentence than at the middle of a word; pauses within words are likely to be related to difficulty with activating spelling. Also, when comparing the frequency of pauses larger than 2 secs for dyslexic and normal typists, one might observe more pauses for dyslexic individuals merely because writing execution unfolds generally more slowly than for proficient typists; indeed pauses shorter than 2 secs for proficient typists would be neglected entirely (Wengelin, 2001). In other words, a difference in typing-execution speed would create the illusion of a larger number of pauses in dyslexic typists. The same principle applies to the interpretation of pausing in L2 typists and the use of other threshold criteria (Van Waes & Leijten, 2015).
Second, data aggregation results in the loss of information of timecourse variations such as disfluencies. Even if this variation is not of interest to the research question, parametric aggregates such as mean and standard deviation, and even non-parametric quantities such as median and interquartile range, are biased estimates for keystroke data. This is because summary statistics capture some aspects of the data but neglect others. For example, both mean and median represent the centre of a normal distribution. However, for non-normally distributed data, the mean represents the average—extreme values pull the mean away from the center of the distribution—but does not capture where majority of data are located; the latter is captured by the median. This is a problem for keystroke data. Typing speed is restricted by the time it takes to plan and execute motor programs.Footnote 1 Yet, writers can slow down typing execution and pause as long as they wish; hence keystroke intervals have, in principle, no upper bound. The combination of these two factors renders a distribution that has a strong positive skew. Consequently the normal distribution implied by parametric summary statistics does not match the empirical distribution of keystroke data. Figure 1 illustrates this mismatch between. The figure shows a sample taken from the copy-task log of two participants (from the copy-task data reported below). For the keystroke intervals of both participant, we contrast the density function of the empirical data (dashed line) and the normal density function (solid line). The normal density function is based on the observed mean (dotted vertical line) and standard deviation (see figure caption). Panel A shows the untransformed inter-keystroke intervals; Panel B shows the log-transformed data.
Example for mean as biased estimator for the inter-keystroke intervals (IKIs) for two participants (participant 72 in the top panels; participant 75 in the bottom panels). All panels show the empirical density of the data and the normal-density function entailed by the observed mean (represented as dotted vertical line) and the standard deviation (SD): participant 72: mean = 431 (SD = 448), participant 75: mean = 256 (SD = 98). The untransformed IKIs are shown in plot A and the log-scaled IKIs are shown in plot B
Figure 1 shows a poor match between the parametric summary measures of both the untransformed and the log-scaled keystroke data of participants 72 and 75 and the normal distribution. Importantly, this mismatch is not only due to the positive skew in the keystroke data but is related to a bimodal tendency that can be seen best in the log-scaled keystroke-intervals shown in Fig. 1b; the empirical-density function shows two peaks in both participants. This mixture of short and long keystroke intervals is going to influence what the obtained summary statistics represent.
Therefore, data aggregation may lead to incorrect inference about the writing process (Baaijen & Galbraith, 2018). To address biases in these estimates researchers have used data transformation, and data trimming (Hoaglin & Iglewicz, 1987) to remove data that were considered outliers, or separated disfluencies (or pauses) from short keystroke transitions. However log-transformation may account for positive skew but does not address the bimodality, as illustrated in Fig. 1b. From existing research we know that keystroke data are not merely positively skewed, which can be addressed with log-normal transformations, but heavily right tailed (Almond et al., 2012; Baaijen et al., 2012; Chukharev-Hudilainen, 2014; Guo et al., 2018). Further, using fixed threshold values to distinguish between normal and delayed typing intervals will inevitably impact more on struggling writers but also learners and dyslexic individuals more generally leading to larger data loss, less reliable typing estimates and therefore incorrect conclusions about the hypothesis tested. A pause threshold would need to be participant-specific (Wengelin, 2006) but is more difficult to determine for individuals with a larger variability (e.g. participant 72 in Fig. 1a).
Our overall aim was to provide a statistical model that captures data from keyboard typing and fits its underlying cognitive process. The challenge in developing such a model is to distinguish fluent keystroke transition from typing hesitations that resulted from upstream delays and, at the same time, accounting for sample-specific properties of the data (e.g. individual typing style, key-pair identity). Importantly, for reasons discussed above, modelling keystroke data as two independent processes should by-pass data aggregation, data trimming, and threshold criteria. Such a model, that allows the statistical estimation of writing disfluencies as independent of fluent keystroke transitions, has implications for writing research (Hayes, 2012; Kaufer et al., 1986; Van Waes et al., 2016; Wengelin, 2006).
To test the models that we describe in the following section we use data from two copy-tasks that are part of the default Dutch Inputlog copy task (Van Waes et al., 2019). Using a constrained writing context such as a copy task rather than data from spontaneous text production was fundamentally important. This is because, first, we can reduce the influence of higher level processes: text production involves the generation of content and its linguistic encoding but copy-typing does not. In other words, the cognitive source of keystroke hesitations is less ambiguous. Second, spontaneous text production comes with a considerable variability between what participants write. In a copy task we can largely control this variability. Using data from a copy task can therefore, reduce the number of confounding factors. Opportunities for future research to apply the presented models to data from free writing tasks are discussed.
Method
Modelling the copy-typing process
As a guiding principle, we aim to produce a statistical model that can represent the mental process that generates the keystroke data. Keystrokes, in copy-typing and free text production, are the end of a cascade of mental processes. Latencies between subsequent keypresses, for example, the transitions c\(^{\wedge }\)a\(^{\wedge }\)t for the word cat, where \(^{\wedge }\) indicates the inter-keystroke intervals (IKI) between pressing <c> and <a>, and <a> and <t>, increase when the information flow into motor execution was interrupted at a higher level. Keystroke intervals reflect at minimum two states of this information flow: (1) either activation can flow into motor plans and keystroke transitions are maximal fluent; (2) activation flow was inhibited at a higher level and therefore the time between two keystrokes increased.
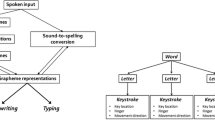
For example, writing a word involves the retrieval of its name and, then, its spelling. If the writer knows both, activation can flow smoothly into the execution of the corresponding motor codes. However if the writer struggles to retrieve the spelling or the lexical entry of a word, the activation flow is interrupted. Inhibition is then resulting in process disfluencies expressed in a larger lag between adjacent keystrokes. In copy-typing tasks we can constrain the underlying cognitive process by removing higher-level processes such as lexical planning and orthographic retrieval (Grabowski, 2008; Wallot & Grabowski, 2013). Figure 2 illustrates a basic model of the copy-typing process (Logan & Crump, 2011; Salthouse, 1984; see also Yamaguchi & Logan, 2014).Footnote 2 At the top level, some chunk of letters has to be visually encoded. The size of this chunk is to some extent specific to task, target string, individual typing skill / style, but mainly constrained the verbal working memory of the participant. The visually encoded sequence has to be buffered and, then, corresponding motor codes have to be activated. If there are no more motor codes that can be generated from the buffered information, visual encoding is required to update the buffer.
The consequence of buffer updates is a slowdown in keystroke intervals (i.e. a pause, a hesitation) that cannot necessarily be explained on the basis of difficulty with specific bigrams. Figure 3 shows the by-bigram IKIs of three participants copy-typing the (Dutch equivalent of the) phrase a chaotic cowboy. These example data illustrate disfluencies are not bigram specific. Participant 241 shows a longer IKI for <c> and <h> but no other notable slowdown; participant 105 shows a large IKI for <o> and <t>; participant 232 shows a smaller and a larger peak in IKIs. Importantly, although to-be-copied words were the same, the number, location, and size of the slowdown varied across participants. Our statistical model should provide a systematic way of capturing process disfluencies, even though their occurrence is, to some extent, non-deterministic—disfluent keystroke transitions within a sequence of letters that cannot be predicted on the basis of letter identity or bigram location.
Statistical models can be used to characterize the theoretically assumed data-generating process as a function of parameters. For example, if we assume that the data come from a single underlying process—as in linear-regression models—we can describe this process with a normal distribution that takes two parameters, the mean \(\mu \) and the variance \(\sigma ^2\). The values of the parameters \(\mu \) and \(\sigma ^2\) are unknown and typically used to represent and compare task and population-specific (typing) performance. This model can be written as \(y \sim Normal(\mu , \sigma ^2)\); i.e. the data y come from a single process that follows a normal distribution with an unknown mean \(\mu \) and an error variance \(\sigma ^2\). We can then feed data into our statistical model to estimate the model’s parameter values. The resulting parameter estimates can then be interpreted in the realm of the assumed data-generating (cognitive) process; i.e. a single process that generates normal distributed data.
Log-normal mixed-effects model of typing
For the first model, the baseline model, we will assume that IKIs follow a log-normal distribution (e.g. Almond et al., 2012; Guo et al., 2018) because IKIs are positively skewed.Footnote 3 This model is characterising the information cascade that generates keystroke intervals as a single process with a population mean-keystroke transition.
To estimate the mean we need to be able to account for variability related to the sampling process. This can be achieved with log-normal (linear) mixed-effects models (LMM) which have been used in the literature to model keystroke data (Leijten et al., 2011; Quené & Van den Bergh, 2004; Van Waes et al., 2010, 2021). The LMM in Eq. 1 is an extension of the simple example above. We know that some participants are faster typists than other participants and some bigrams can be typed faster than others. Writers vary generally in how fast they type, or how quickly they are performing in the given task. Further, more frequent bigrams (as part of words with a large number of occurrences in a corpus or bigrams that occur in many different words) are typically typed faster than low frequency bigrams; bigrams that are part of words are typed faster than novel bigrams; bigrams within morphological boundaries are typed faster than bigrams that cross morphological boundaries with similar effects for syllable boundaries (Feldman et al., 2019; Gentner et al., 1988; Nottbusch et al., 2005; Pinet et al., 2016; Sahel et al., 2008; Weingarten et al., 2004).
In other words, IKIs for participants and bigrams are varying around a common (population) mean. These sources of random-error variance as captured by u for participants and w for keystroke bigrams in Eq. 1. The population mean is then captured by the parameter \(\beta \) after accounting for variance associated with participants and bigrams.
Each participant i has keystroke latency, expressed as \(u_i\), different from the population mean \(\beta \) with some participants being faster than average (i.e. \(<0\)) and other are being slower than average (i.e. \(>0\)); these differences should be normally distributed with a between-participants variance \(\sigma _u^2\) with \(i = 1, \dots , I\), where I is the number of participants (see 2). Because \(\sigma _u^2\) is a variance it can not be negative so we can cut off the normal distribution at zero—constrain the prior distribution to be larger than zero. This type of distribution is known as a half-normal. We used a prior of 2.5 for the variance of the variance \(\sigma _u^2\) to regulate the random intercepts for participants to be normal distributed around the population average (Gelman, 2006). This is because the majority of participants should have, by definition, an average IKI close to the population estimate with fewer participants being much faster or slower than the average. A variance of 2.5 is an informative prior that ensures that the variability across participants is approximately normal.
Similar to variability between participants we can model variation between keystroke pairs (i.e. letter bigrams) as random-intercepts term; w in Eq. 1 (Van Waes et al., 2019, 2021). IKIs of bigrams differ due to factors such as bigram frequency, position of keys on keyboard, and hand combination. These factors are not independent but affect keystroke latencies in combination. To account for these factors that render some bigrams faster than others we included a difference \(w_j\) for each bigram j with \(j = 1, \dots , J\), where J is the total number of bigrams. Similar to random participant intercepts, the difference for random bigram intercepts \(w_j\) is distributed around 0 with a between-bigram variance \(\sigma _w^2\) (Eq. 3).
The parameter of interest, the mean \(\beta \) in Eq. 1, is the marginalised value after taking into account random variation between participants and bigrams. In all models we parameterised the mean \(\beta \) as non-centered with regulating priors (Eq. 4; following Gelman et al., 2014; Papaspiliopoulos et al., 2007). Non-centering parameters can be used to aid sampling efficiency of the model by adding additional parameters that capture uncertainty (i.e. the scale \(\epsilon \) and the variance \(\sigma _\beta \)). In other words, a more reliable parameter estimate can be achieved with the same number of iterations. This can be helpful for small data sets. For the mean \(\mu _\beta \) of the population mean \(\beta \), we used a prior that is normally distributed around a value of 5 log msecs (i.e. \(\approx \) 150 msecs) with a variance of 2 log msecs which is putting the majority of prior probability of the true parameter for fluent key transitions between \(\approx \) 80 msecs and \(\approx \) 215 msecs (i.e. \(e^{5} \pm 1.96 \cdot \sqrt{e^{5 + 2}}\) because for a normal distribution 95% are \(\pm 1.96\) standard deviations from the mean) which are plausible estimates for fluent keystroke typing given existing analyses (Van Waes et al., 2021).
For the unexplained residual variance \(\sigma _e^2\), we used an uninformative half-Cauchy prior (Eq. 5; as mentioned in Gelman et al., 2014). The Cauchy is a heavy tailed distribution; a centre of 0 indicates that the residual variance should be close to 0 and a scale of 2.5 makes the prior uninformative by allowing larger values. As the residual variance must be positive, we constrained \(\sigma _e\) to be larger than 0, and therefore the prior to be half-Cauchy.
Typing as autoregressive process
The previous model captures variation associated with bigrams but implies that bigrams are independent and thus their locations in the string are, in principle, exchangeable. In other words, keystroke intervals depend on the identity of the associated bigram but are not affected by preceding keystroke interval.Footnote 4
IKIs are not necessarily independent of preceding keystroke intervals; an IKI \(y_{i}\) might be related to the IKI \(y_{i-1}\) preceding it. For example, disfluencies might impacts on neighbouring keystroke intervals (Conijn et al., 2019b). The relationship between subsequent keystrokes can be captured by predicting an IKI with the IKI preceding it. This is called an autoregressive process (Eltahir et al., 2004); in Eq. 6 the relationship between subsequent IKIs is captured by the parameter \(\phi \). As the degree of autocorrelation might vary with typing skill, we assumed that the autocorrelation varies between participants \(\phi _i\) with a centered mean \(\mu _\phi \) and a variance \(\eta \). The prior on \(\mu _\phi \) is centred around 0 (no autocorrelation) with a large weakly-informative variance of 1 as autocorrelation is ranging between –1 (speedup in keystrokes intervals) and 1 (slowdown in keystroke intervals). The variance \(\eta \) is a half-Cauchy constrained as \(>0\): this prior favours positive values close to 0 but also allows for more extreme values.
Typing as mixture process
So far we constructed models that account for the keystroke-interval differences associated with different typists, bigrams and that accounts for autocorrelation between subsequent keystroke intervals. Next we model keystroke intervals as the result of a combination of two independent processes. For this purpose we used a finite mixture-process model.
Mixture models are a straight-forwarded tool of representing data that come from a combination of different processes (e.g. Farrell & Lewandowsky, 2018; Gelman et al., 2014). Finite-mixture models have been used to represent cognitive processes in which larger values—process inhibitions—arise probabilistically (see e.g. Vasishth et al., 2017a, 2017b). Keystroke disfluencies in writing can be represented in a similar way. For keystroke data, the assumed process is a combination of two processes: (1) normal typing, when activation flows smoothly from higher into lower levels; (2) typing disfluencies, when activation flow is interrupted at higher levels (e.g. for a buffer update). In other words, we fixed the number of underlying distributions to two, namely 2 log-Gaussian (log-normal) distributions, of which one represents fluent typing—shorter IKIs—and the other represents disfluencies—longer IKIs.
This model can be parameterised as in Eq. 7, following Vasishth et al. (2017a). The first and second line express that the data y are modelled as the sum of two weighted log-normal distributions: The first distribution has a weight—called mixing proportion—of \(\theta \) and the other distribution receives a weight of \(1-\theta \). The mixing proportion of both distributions must sum to 1. In this parameterisation, \(\theta \) represents the unknown probability of process disfluencies. This was achieved by using an identical mean \(\beta \) for both distributions but adding a parameter \(\delta \), that was constrained to be positive, to the first distribution. As prior on \(\delta \) we used a normal distribution with a mean of 0 and a variance of 1, thus favouring hesitations that are close to \(\beta \)—the population mean of fluent key transitions. In other words the population mean of the first distribution is \(\beta + \delta \) but only \(\beta \) for the second distribution. The \(\delta \) parameter is therefore capturing the hesitation size of process disfluencies with \(\theta \) indicating the probability of disfluencies to occur. The probability of disfluent IKIs was allowed to vary across participants i and stored in \(\theta _i\). This is because the probability to exhibit disfluencies can be assumed to depend on individual typing style (and skills).
To increase sampling efficiency we placed a continuous prior on the logit of the individual mixing proportions \(\alpha _i\), which was transformed to range between 0 and 1, using the inverse-logit function, and stored in \(\theta _i\). This is shown in Eq. 8. We used a normal prior for the logit of individual mixing proportions \(\alpha _i\) with a mean \(\mu _{\alpha }\) that captures the logit of the population disfluency-probability (with an error variance \(\tau \)). The hyper-prior on the population mixing-proportion \(\mu _{\alpha }\) was assumed to have a mean of logit 0 and a variance of logit 1. On the proportion scale this means that the mixing proportion favours a \(\theta \) of 0.5 (both fluent and hesitant keystrokes are equally likely) and a variance of \(\approx \) 0.73 (logit 1); thus the prior is weakly informative.
As longer latencies are known to be associated with a larger variances for both response-time data in particular (Wagenmakers & Brown, 2007) and human motor behaviour in general (Schöner, 2002; Wing & Kristofferson, 1973), we constrained the variance \(\sigma _{e'}\) associated with the distribution of typing disfluencies to be larger than the variance for normal typing \(\sigma _e\); see Eq. 9 (see Vasishth et al., 2017a, 2017b). This was achieved by introducing a parameter \(\sigma _\text {diff}\) that was constrained to be positive. This parameter is centred around 0 with a variance of 1 so that \(\sigma _{e'}\), the variance of the first mixture component, is larger than \(\sigma \) and \(\sigma _{e}\), the variance of the second mixture component, is smaller than \(\sigma \).
Typing as autoregressive mixture process
The mixture model, as well as the LMM, assumes that lags between subsequent letter bigrams are independent of each other; the argument against this was introduced above for autoregressive models. We implemented another mixture model that is largely equivalent to the model presented in the previous section but includes an autoregressor as in Eq. 6; see Eq. 10 for the autoregressive mixture-process model.
Copy-task data
To test which model captures the typing process best, we applied the four models described in the previous section to data from a subset of the Dutch copy-task corpus (Leijten & Van Waes, 2013; Van Waes et al., 2019, 2021). An overview of all models can be found in Table 1.
The copy-task corpus consists of keystroke data collected via a Javascript-based web application as part of Inputlog 8 (available on www.inputlog.net) with the source code released on github.com/lvanwaes/Inputlog-Copy-Task and zenodo.org/record/2908966. In a set of different subtasks participants had to produce keyboard-typed responses. We used a random sample of 250 participants (175 females, 71 males, 4 unknown) from the age range of 18 to 25 years (median age = 22 years). In this analysis we focus on the difference between key-down presses rather than key lifts or combinations of key presses and lifts. Before analysis we excluded spaces and editing operations from the data. Spaces were removed from the analysis as hesitations at string edges are more common than within strings and should be modelled as an additional factor.Footnote 5 In contrast, hesitations within strings / words are to some extent probabilistic and cannot always be predicted from bigram-specific properties.
In this analysis we focus on the consonants task and the low-frequency (LF) bigrams task. In the consonants task, participants saw and copy-typed a single time four blocks of six consonants; i.e. “tjxgfl pgkfkq dtdrgt npwdvf.” This task is intended to measure typing skills in a non-lexical environment (Grabowski et al., 2010). The consonants task is an extreme test case of a typing task that is ridden by disfluencies: because this is a relative unnatural typing task, typists are likely to hesitate more than usual. Therefore, this task provides scope for our models to detect typing disfluencies. We repeated the analysis for the LF-bigrams task to contrast the non-lexical consonants task and a more natural lexical copy task. In the LF-bigram task, participants typed three-word combinations seven times (een chaotische cowboy “a chaotic cowboy” in the Dutch version) of which four bigrams are low frequent.Footnote 6 For comparability to the consonants task, we removed all repetitions after the first time the three-word sequence was copied.
Importantly for the present purpose, fluent copying and pausing may be thought of as a function of (1) the familiarity with the letter sequences (or lexicality) and (2) the participant’s memory span and typing skill; for example touch-typists may depend less on memory representation of the to-be typed bigrams for fluent copying than hunt-and-peck typists. Indeed these—relying on memory and hunt-and-pecking—might be two distinct processes that both could affect typing fluency relatively independent. For both these possibilities, the resulting keystroke intervals are a combination of fluent typing and typing interruptions. In other words, for these tasks we need to be able to disentangle fluent and disfluent IKIs.
Bayesian models, as used in this paper, are ideal for the estimation of parameter values: Bayesian parameter estimation goes beyond point estimates and expresses the uncertainty associated with parameter values as probability distribution (Farrell & Lewandowsky, 2018; Gelman et al., 2014; Lee & Wagenmakers, 2014). To achieve this, Bayesian models require the explicit inclusion of prior information, i.e. existing knowledge about parameter values. For small data sets priors influence the inferred parameter estimates (known as posterior); for larger data sets weakly informative and vague priors are quickly overcome by the data (i.e. automatic Ockham’s razor, Jefferys & Berger, 1992). In other words the choice of priors values has less impact on the posterior. In the present paper, we use weakly informative priors to aid model convergence by constraining the parameter space (see e.g. Lambert, 2018; McElreath, 2016). The predictive performance (i.e. fit) of these models is compared in the “Results” section using leave-one-out cross-validation.
Results
Data overview
The IKI data for the LF-bigrams task and the consonants task are visualized in Fig. 4. The upper panels of the LF-bigrams task and the consonants task in Fig. 4a show the data for each participant. In the lower panels of Fig. 4a, different measures of central tendency are shown. The density function of the IKI data are shown in Fig. 4b with vertical lines corresponding to the central tendency measures in Fig. 4a.
Data overview. Plot a illustrates IKIs over bigram position (time-course) by participant in the upper rows and as different measures of central tendency (with standard error) in the lower rows for each the LF-bigrams task and the consonants task. Plot b shows the density distribution of IKI data with the same central-tendency descriptors as in plot a
These visualisations highlight two points for the present data that were discussed in the “Introduction” section: (1) aggregating data neglects individual time-course variability in the data; (2) the choice of central-tendency measure leads to different conclusions about the data. As for the first point, Fig. 4a shows that participants slowdowns and speedups throughout the trial but do not show consistent patterns for the same letter bigrams as might be concluded from the corresponding summary statistics. If we disregard by-participant variability, central-tendency measures in the lower panels of Fig. 4a suggest that some slowdowns and speedups might be bigram specific. For example, in the LF-bigrams task, the first bigram is followed by a faster IKI; in the consonants task, the first bigram is followed by a slowdown. Importantly though, there is a substantial variability between participants.
As for the second point, the choice of central-tendency measure might affect whether we consider an observation a disfluency, or a participant to be prone to disfluent typing. In particular, means are systematically longer than the median and mode. Figure 4b illustrates why this is the case. Shown are the density functions for the LF-bigrams and the consonants task. Even log-scaled data show skewed distributions with a heavy right tail. While in a normal distribution the mean, median and mode have identical values, the conceptual differences between these three measures of central tendency lead to different values in non-normal distributed data. In particular, means are known to be sensitive to extreme values; these are inevitable for zero-bound IKIs with, in principle, no upper bound. For keystroke data, large means might be the consequence of a few larger IKIs that over-shadow largely normal typing behaviour. Means are closer to the horizontal middle of the data space which, for right-skewed distributions, is on the right of the distribution’s peak (the value with the highest kernel density). The latter is being represented by the mode. Regardless of which measure is used, all three central tendency indicators ignore important properties of the distribution. That is, measures of central tendency neglect the variability in the data; keystroke data might indeed represent a combination of processes; e.g. normal typing and disfluencies. Central tendency measures do not allow us to distinguish between IKIs that are the results of fluent typing and IKIs that reflect process lags.
For our data, aggregation does not just neglect participant-specific typing patterns but the choice of central-tendency measure leads to different conclusions about the data (e.g. which IKIs can be considered pauses). To ensure accurate statistical inference, we need to be able to account for participant-specific typing patterns as expressed across the typing time-course.
Model fit
All models were implemented as Bayesian models (see e.g. Gelman et al., 2014; Lambert, 2018; McElreath, 2016) in the probabilistic programming language Stan (Carpenter et al., 2016; Hoffman & Gelman, 2014; Stan Development Team, 2015a, 2015b). Data, R scripts and Stan code are available on OSF (osf.io/y3p4d). A detailed walkthrough document shows how R can be used to apply the Stan code of a mixture model to copy-task data (rpubs.com/jensroes/765467). Models were fitted with 30,000 iterations (15,000 warm-up) on 3 MCMC chains. Convergence was tested via the Rubin-Gelman statistic (Gelman & Rubin, 1992), trace plots and cross-validation (Vehtari et al., 2015, 2017).
The predictive performance of the models was established using leave-one-out cross-validation. Cross-validation, in contrast to more conventional model-comparison metrics such as \(R^2\), are not subject to model overfitting: models with more parameters do not necessarily render a better fit to the data (see Farrell & Lewandowsky, 2018; Lambert, 2018; Lee & Wagenmakers, 2014; McElreath, 2016). The out-of-sample predictive performance was determined via Pareto smoothed importance-sampling (Vehtari et al., 2015, 2017). To compare the predictive quality of our models we used the sum of the expected log predictive density (\({\widehat{elpd}}\)). Model comparisons can be found in Table 2. Model comparisons revealed higher predictive performance for both mixture models M3 and M4 for both copy-task components. The increase in predictive performance is larger for the LF bigrams task compared to the consonants task. The differences in predictive performance of all models shows the same pattern in both copy-task components. For both tasks, the combination of the mixture model and the autoregressive-process model as implemented in model M4 (see Eq. 7) revealed the highest predictive performance with a small advantage over mixture model M3 (see Eq. 10). We therefore chose model M4 for parameter evaluation of both copy-task components.
Parameter evaluation
The copy-typing process can be characterized by the posterior of the mixture model’s parameter values. These parameters values are summarised in Table 3 and in Fig. 5. Table 3 summarises the population and variance estimates as posterior mean with 95% probability intervals (PI). Estimates are shown for the LF-bigrams task and the consonants task. After accounting for process disfluencies, keystroke intervals were longer for the consonants task (429 msecs, PI: 356–515) compared to the LF-bigrams task (158 msecs, PI: 139–180). The slowdown for disfluencies was about four times longer for the consonants task. For the LF-bigrams task, the model determined a slowdown of 95 msecs (PI: 76–116) with a probability of 0.34 (PI: 0.31–0.38); for the consonants task we found a slowdown of 414 msecs (PI: 333–509) with a probability of 0.73 (PI: 0.66–0.80). In other words, in the consonants disfluent keystroke transitions were three times more likely to occur than fluent transitions; in the LF-bigrams task, only one out of three transitions constitutes a disfluency. The size of the slowdown in the consonants task suggest higher level processes such as reading of the target string. This is unlikely to be the case for the short slowdown in the LF-bigrams task. Instead, the slowdown in the LF-bigrams task might be a bigram-frequency effect. Four out of 16 bigrams in the LF-bigrams have a low frequency (i.e. \(\frac{4}{16}\approx 0.19\)). In other words, the magnitude for disfluencies and hence their cognitive source in the typing process is task-specific. Further autocorrelation between subsequent keystrokes was non-different from zero in the LF-bigrams task; keystroke transitions in the consonants task were in general followed by a –0.08 times faster keystroke transition; PI: –0.10 to –0.05. Variance components are reported for completeness.
Figure 5 summarises by-participant model estimates. The modelled IKIs for fluent typing are shown in Fig. 5a. This figure shows the estimated typing speed of each participant (i.e. a random sample of 75 participants for visualisation) after accounting for typing disfluencies. Each horizontal line represents the statistically inferred estimate for a participant. The vertical dotted line shows the estimated population mean. Figure 5b shows the disfluency probabilities, i.e. the probability to exhibit a typing disfluency for each participant. For each participant the model captures varying pausing probabilities that express individual but also task-specific typing difficulty. Although, on the population level, disfluencies are likely to occur in the consonants task, not all all participants show a more disfluent than fluent keystrokes (as indicated by individual estimates below 0.5 in Fig. 5b representing a larger probability of fluent keystroke transitions) or more disfluencies in the consonants task than in the LF-bigrams task. In fact, some participants paused more often in the LF-bigrams task than in the consonants task (see Fig. 5e).
By-participant parameter values for LF-bigrams and consonants task. Plot a and Plot b show the average IKIs for fluent typing and disfluency probabilities, respectively, for each participant (for a random subset of 75 participants for illustration); error bars indicate 95% PIs, dotted vertical line shows the posterior population mean. Plot c–e show correlations (red line) between by-participant mean-posterior estimates of the consonants task and the LF-bigrams task for fluent typing (c), the autoregressor (d), and the disfluency probability (e)
Figure 5c–e show between LF bigrams and consonants correlations for the by-participant estimates of the fluent-typing interval duration (C), the autocorrelation between subsequent keystroke intervals (D), and the disfluency probability. The correlations show that individuals with longer keystroke intervals for the LF-bigrams task also show longer keystroke intervals in the consonants task (Fig. 5c); a similar relationship can be seen for autoregression although in the consonants task participants generally show faster keystroke intervals across bigrams while for the LF bigrams task some participants speedup and other slowdown (Fig. 5d). No such correlation was found for the disfluency probability (Fig. 5e). Participants that exhibit many disfluencies in the consonants task do not necessarily show more disfluencies in the LF-bigrams task. In other words, the model parameters do not just capture individual differences but also task-specific differences with regards to typing speed and pausing behaviour.
Faster participants might, in principle, show larger disfluency magnitudes; i.e. the size of the disfluency magnitude may vary by participant. To test this possibility we also implemented two models that are largely identical to model M3 (see Eq. 7): first, we allowed both the disfluency probability \(\theta \) and the disfluency magnitude \(\delta \) to vary by participant; second, \(\delta \) but not \(\theta \) was allowed to vary by participant. We compared the predictive performance of either model to model M3. Neither model was convincingly better than model M3, neither for the consonants task nor for the LF-bigrams task. For the consonants data, allowing \(\delta \) and \(\theta \) to vary by participant resulted in negligibly better predictive performance compared to model M3 (\(\Delta {\widehat{elpd}}\)=7, SE=4); holding the disfluency probability \(\theta \) constant while allowing the disfluency magnitude \(\delta \) to vary by participant revealed a lower predictive performance (\(\Delta {\widehat{elpd}}\)= −100, SE=50). The same patterns was found for LF bigrams: allowing \(\delta \) to vary rendered no predictive gain (\(\Delta {\widehat{elpd}}\)=−1, SE=0.5); fixing \(\theta \) and allowing \(\delta \) to vary showed a decrease in predictive performance (\(\Delta {\widehat{elpd}}\)=−30, SE=8). This comparison suggests that it is not the magnitude of the disfluencies (\(\delta \)) that varies across participants but the disfluency probability (mixing proportion \(\theta \)).
Overall, the values of the three process-central model parameters—fluent typing speed, disfluency probability, and slowdown magnitude for disfluencies—were found to be task sensitive. The LF-bigrams task shows shorter typing intervals, a lower disfluency probability compared to the consonants task and a shorter slowdown magnitude for typing disfluencies. Individual typing style was characterized by random variation in typing speed and in the probability but not in the magnitude of process disfluencies.
Discussion
Our aim was to provide a statistical model that allows to account for process disfluencies in keyboard-typing data. To address this aim we tested a series of Bayesian models on a lexical and a non-lexical copy-typing task. Model comparisons revealed that finite mixture models provided a better fit to inter-keystroke intervals of both copy-tasks compared to standard linear mixed-effects models. In other words, we showed that, among the models tested, data from copy-typing can be modelled best as a combination of fluent and disfluent typing intervals by means of an unknown individual mixing weight. We demonstrated how the model posterior can be used to infer estimates for three typing characteristics for individual participants and on the population level.
The best fitting model summarizes the typing process as a function of three process-relevant parameter values. Those are: (1) the population-level and by-participant keystroke transitions for fluent typing after accounting for process disfluencies; (2) population-level and by-participant mixing proportions indicating the probability of disfluent keystroke transitions; (3) the population-level disfluency magnitude, i.e. slowdown in keystroke transitions. These parameter estimates are interesting for two reasons: first, they allow us to characterize the writing task at hand as a mixture of fluent and disfluent keystroke transitions as represented in Fig. 6;Footnote 7 second, by-participant parameter estimates allow us to extract characteristics for individual typists. On the basis of the population-level and individual parameter estimates, we can determine whether an individual is a fast / slow typist or has unusually high / low probability to exhibit disfluencies compared to the population estimates. Thus, the model can be used diagnostically to identify participants with larger disfluency probabilities or to compare pausing across groups of participants.
Basic model of copy typing with mixture-model parameters. Disfluencies are the sum of \(\alpha \) and \(\delta \), where \(\delta \) is the additional time that results from updating the letters buffered for motor encoding. The probability of disfluencies is indicated as \(\theta \) mapping onto looks to the target string
The strength of this model is that it allows us to characterize the writing process and detect disfluencies in a principled way in line with what we know about keyboard typing. In particular, keyboard typing can be thought of as a process in which information cascades from higher to lower levels of activation; process inhibition on higher levels causes lags downstream. We have captured this process by characterizing the typing process as a mixture of fluent and disfluent keystroke transitions. Typing speed and the proportion of disfluent transitions depend on each typist’s copying style. This is important because not distinguishing between between fluent and disfluent keystroke transitions can lead to incorrect inference about fluent typing. For example, collapsing across fluent and disfluent transitions might lead to the conclusion that task-related difficulty impacts on the execution of keystrokes even though the overall increased keystroke-transition duration was in fact the results of more frequent and longer pauses while typing speed itself may remain constant. From the present analysis we know that merely one-quarter of the data from the consonants task and two-thirds of the data from the LF-bigrams task were found to correspond to fluent keystroke transitions. Even after accounting for disfluent keystroke transitions, fluent typing was found to be two times slower in the consonants task compared to the LF-bigrams task. Not accounting for task-specific disfluency probabilities would result in biased estimates and, therefore, affect conclusions about task-related difference in typing speed.
Our results suggest that the probability and size of disfluencies are sensitive to task related factors. In the consonants task, disfluencies are indeed more probable than fluent transitions. This was not the case in the LF-bigrams task. Across participants the probability of typing disfluencies was relatively homogeneous in the LF-bigrams task but showed a larger variability in the consonants task. Similarly the average by-participant typing speed was more diverse in the consonants task compared to the LF-bigrams task. This contrast might be the result of a larger range of strategies that participants applied to copy consonant sequences than when copying the word triplet in the LF-bigrams task. For example, participants may have used n-grams (one letter at a time or more) or spaces to chunk consonants before generating motor codes; in the lexical LF-bigrams task, word(s) or the entire phrase are better candidates for chunking than individual letters.
The variability in typing strategies across the sample may be understood as a function of typing skills and cognitive factors. For example, non-touch typists depend on memory resources to correctly copy the target string. This is because participants with poor typing skills have to shift gaze between keyboard and text more often than touch typists. Consequently, memory resources are more important for poor typists such that participants with a shorter memory span might update their memory representation of the target string more frequently than participants with a long memory span expressed as an increased disfluency probability. This might be less important for the typing performance of touch typists to the extent that touch typists have less need to search for keys corresponding to target letters. In contrast, the lower variability found for the LF-bigrams task can be understood as a more uniform use of copy-typing strategies across participants. Copy-typing strategies might have been more consistent for the LF-bigrams task because participants, especially those with poor typing skills, can make use existing knowledge (e.g. lexical meaning of words, motor codes for bigrams) to relief memory demands. This is not possible for the consonants task. However, our results did not support a trade-off between typing speed and disfluency probability. This might be because disfluencies are not merely the result of a memory-representation update but are also related to difficulty finding the correct key and individual memory-span differences. Therefore the disfluency probability can be understood as an estimate for all non-typing related activities. As such the disfluency probability may be an indicator of memory span (Grabowski et al., 2010; Olive, 2014), low level reading skill (De Smet et al., 2018) and individual typing skills. To evaluate to what extent memory resources involved in copy-typing in combination with typing skills (touch typists) impact on the model parameters one would need to model these as additional factors. The prediction is that individuals with access to more memory resources would display lower disfluency-probability values.
A central advantage of using a mixture model to account for typing disfluencies is that we can by-pass pause threshold-values and instead by-participant pausing proportions and fluent typing speed; this can then be used as individual typing-skill characteristic. Our mixture model provides estimates for fluent typing while accounting for disfluencies by modelling fluent and disfluent typing as a mixture process. At the same time, the model provides disfluency estimates as expression for individual and task-specific typing difficulty. Stipulating threshold values ignores that some participants are generally slower typists and some tasks are more difficult. Mixture models allow us to capture disfluencies as a latent process in a principled manner. This is important because disfluencies must be understood as relative to an individuals’ typing speed given the task at hand (Wengelin, 2006). In the context of the copy task that aims to measure typing skills (Van Waes et al., 2019, 2021), researchers could use mixture models to obtain by-participant estimates of typing speed and pause frequencies. These estimates can be used as individual-differences indicators or to identify individuals that struggle with those skills assessed in the components of the copy task; this information can then be carried forward into the analysis of data from a free writing task to, for example, compare different groups of typists or to controll for typing skills as model covarietes.
Because mixture models do not require us to stipulate pause thresholds, they allow us to test predictions about typing disfluencies in certain populations such as learning typists, L2 typists and individuals with genuine typing difficulty after account for individual differences in typing speed or vice versa. For example, some individuals that might be classified as having typing problems might not have excessive numbers of pauses but merely longer key transitions, while proficient typists use pauses to prepare larger linguistic units. In other words, the presented model can be used to test hypotheses about psychological factors (e.g. memory demands, writing experience, proficiency in writing in a second language) that might affect the ratio of disfluencies in the writing process. If disfluencies are crucial to identify poor typists in a sample, mixture models might be used as diagnostic tool. Also, mixture models allow us to directly test whether the number of disfluencies can be changed as response to a keyboard-typing intervention. As an avenue for future research, mixture models as presented in this paper can be used for different types of writing tasks and particular populations.
We demonstrated how keystroke data can be modelled as a mixture processes distinguishing between keystroke transitions that are resulting from (1) a smooth information flow into motor processes and (2) delays on higher levels of activation. We focused on key transitions from within string / word bigram pairs collected in a copy task. However, it is possible that our results do not generalise to free text production—hesitations cannot be modelled as mixture process. There is some research that has used a mixture-model framework in the context of spontaneous text production (Almond et al., 2012; Baaijen et al., 2012; Guo et al., 2018; Roeser et al., 2020). Therefore is scope for future research to apply the mixture models presented in this paper to model hesitations in free text production. For example, one could model the disfluency probability and magnitude for different locations in the text: this is because hesitations within words might be smaller and less frequent than hesitations before words, or before sentences. In our mixture-model walkthroughFootnote 8 we describe how researchers can model and compare the mixture process across different factors. We are confident that mixture models will prove useful for data from free text production. This is because mixture models can capture long latencies as the the consequences of a processing delay in the information cascade which affects both copy typing and free text production (Olive, 2014; Van Waes et al., 2021).
For spontaneous text production, there is scope to extent the models we presented in this paper. Text production as opposed to copy typing involves processing on various levels. A delay on any of these levels causes disfluencies. For copy typing process can be described using a binary distinction between fluent and disfluent typing. However for text production lags on different levels of activation might be associated with different disfluency magnitudes and might be cumulative. If the size of the disfluency is assumed to depend on the inhibited process upstream or combination of processes, this can be implemented as additional mixture component(s) (similar to Baaijen et al., 2012; see also Almond et al., 2012) to address different types of disfluencies (Medimorec et al., 2017; Medimorec & Risko, 2016; Wengelin, 2001). In other words extensions of mixture models allow us to test different hypotheses about the cascade of processes involved in writing and language production.
Notes
And in fact keyboard polling.
This flowchart is a simplification of the basic components involved in copy typing and ignores that both copy typing (Van Waes et al., 2021) and free text production (Olive, 2014) involve a cascading information flow that operates in parallel for subsequent planning units. This means that planning of unit \(n+1\) can begin as soon as a processing level is free for input, i.e. when planning unit n was submitted to the next processing level.
We discussed above that the heavy tail associated with keystroke data is not necessarily fitting a log-normal distribution. We use a log-normal models as this is equivalent to the standard statistical method used in the field (e.g. fitting parametric models to log-transformed data).
The independence of bigrams is not merely a problem of model choice but related to within-word bigrams more generally. Typing random combinations of letters can be thought of as independent if we randomise their locations across participants. However, this is not easily possible for bigrams within a syllable, morpheme, word, and even phrase.
This walkthrough gives an example how other factors can be added to a mixture model: rpubs.com/jensroes/765467.
Note, we refer to this task as LF-bigrams task as in Van Waes et al. (2019). The majority of bigrams in the target-word group are highly frequent.
This model is just one possibility of how the mixture-model parameters map onto copy-typing. Disfluencies might as well arise on a lower level, for example, when the typist is struggling to find the correct key.
References
Almond, R., Deane, P., Quinlan, T., Wagner, M., & Sydorenko, T. (2012). A preliminary analysis of keystroke log data from a timed writing task (Research Report No. RR-12-23). Educational Testing Service.
Alves, R. A., & Limpo, T. (2015). Progress in written language bursts, pauses, transcription, and written composition across schooling. Scientific Studies of Reading, 19(5), 374–391. https://doi.org/10.1080/10888438.2015.1059838
Baaijen, V. M., & Galbraith, D. (2018). Discovery through writing: Relationships with writing processes and text quality. Cognition and Instruction, 36(3), 199–223. https://doi.org/10.1080/07370008.2018.1456431
Baaijen, V. M., Galbraith, D., & de Glopper, K. (2012). Keystroke analysis: Reflections on procedures and measures. Written Communication, 29(3), 246–277. https://doi.org/10.1177/0741088312451108
Beers, S. F., Mickail, T., Abbott, R., & Berninger, V. (2017). Effects of transcription ability and transcription mode on translation: Evidence from written compositions, language bursts and pauses when students in grades 4 to 9, with and without persisting dyslexia or dysgraphia, compose by pen or by keyboard. Journal of Writing Research, 9(1), 1–25. https://doi.org/10.17239/jowr-2017.09.01.01
Bock, J. K., & Ferreira, V. S. (2014). Syntactically speaking. In M. Goldrick, V. S. Ferreira, & M. Miozzo (Eds.), The Oxford Handbook of Language Production (pp. 21–46). Oxford University Press.
Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M. A., Guo, J., Li, P., & Riddell, A. (2016). Stan: A probabilistic programming language. Journal of Statistical Software, 20. https://doi.org/10.18637/jss.v076.i01
Chanquoy, L., Foulin, J.-N., & Fayol, M. (1996). Writing in adults: A real-time approach. In G. Rijlaarsdam, H. Van den Bergh, & M. Couzijn (Eds.), Theories, models and methodology in writing research (pp. 36–44). Amsterdam University Press.
Christiansen, M. H., & Chater, N. (2016). The now-or-never bottleneck: A fundamental constraint on language. Behavioral and Brain Sciences, 39, 1–72. https://doi.org/10.1017/S0140525X1500031X
Chukharev-Hudilainen, E. (2014). Pauses in spontaneous written communication: A keystroke logging study. Journal of Writing Research, 6(1), 61–84. https://doi.org/10.17239/jowr-2014.06.01.3t
Chukharev-Hudilainen, E., Saricaoglu, A., Torrance, M., & Feng, H.-H. (2019). Combined deployable keystroke logging and eyetracking for investigating L2 writing fluency. Studies in Second Language Acquisition, 41(3), 583–604. https://doi.org/10.1017/S027226311900007X
Conijn, R., Roeser, J., & van Zaanen, M. (2019). Understanding the keystroke log: The effect of writing task on keystroke features. Reading and Writing, 32(9), 2353–2374. https://doi.org/10.1007/s11145-019-09953-8
Conijn, R., Van Zaanen, M., Leijten, M., & Van Waes, L. (2019). How to typo? Building a process-based model of typographic error revisions. The Journal of Writing Analytics, 3, 69–95.
Connelly, V., Dockrell, J. E., Walter, K., & Critten, S. (2012). Predicting the quality of composition and written language bursts from oral language, spelling, and handwriting skills in children with and without specific language impairment. Written Communication, 29(3), 278–302. https://doi.org/10.1177/0741088312451109
De Smet, M. J. R., Leijten, M., & Van Waes, L. (2018). Exploring the process of reading during writing using eye tracking and keystroke logging. Written Communication, 35(4), 411–447. https://doi.org/10.1177/0741088318788070
Eltahir, W. E., Salami, M. J. E., Ismail, A. F., & Lai, W. K. (2004). Dynamic keystroke analysis using AR model. IEEE International Conference on Industrial Technology, 3, 1555–1560. https://doi.org/10.1109/ICIT.2004.1490798
Farrell, S., & Lewandowsky, S. (2018). Computational modeling of cognition and behavior. Cambridge University Press.
Feldman, L. B., Dale, R., & van Rij, J. (2019). Lexical and frequency effects on keystroke timing: Challenges to a lexical search account from a type-to-copy task. Frontiers in Communication, 4, 17. https://doi.org/10.3389/fcomm.2019.00017
Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis, 1(3), 515–533. https://doi.org/10.1214/06-BA117A
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2014). Bayesian data analysis (3rd edn). Chapman.
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7(4), 457–472. https://doi.org/10.1214/ss/1177011136
Gentner, D. R., Larochelle, S., & Grudin, J. (1988). Lexical, sublexical, and peripheral effects in skilled typewriting. Cognitive Psychology, 20(4), 524–548. https://doi.org/10.1016/0010-0285(88)90015-1
Grabowski, J. (2008). The internal structure of university students’ keyboard skills. Journal of Writing Research, 1(1), 25–52.
Grabowski, J., Weinzierl, C., & Schmitt, M. (2010). Second and fourth graders’ copying ability: From graphical to linguistic processing. Journal of Research in Reading, 33(1), 39–53. https://doi.org/10.1111/j.1467-9817.2009.01431.x.
Guo, H., Deane, P. D., van Rijn, P. W., Zhang, M., & Bennett, R. E. (2018). Modeling basic writing processes from keystroke logs. Journal of Educational Measurement, 55(2), 194–216. https://doi.org/10.1111/jedm.12172.
Hayes, J. R. (2012). Evidence from language bursts, revision, and transcription for translation and its relation to other writing processes. In M. Fayol, D. Alamargot, & V. Berninger (Eds.), Translation of thought to written text while composing (pp. 15–25). Psychology Press.
Hoaglin, D. C., & Iglewicz, B. (1987). Fine-tuning some resistant rules for outlier labeling. Journal of the American Statistical Association, 82(400), 1147–1149. https://doi.org/10.1080/01621459.1987.10478551
Hoffman, M. D., & Gelman, A. (2014). The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15(1), 1593–1623.
Jefferys, W. H., & Berger, J. O. (1992). Ockham’s razor and Bayesian analysis. American Scientist, 80(1), 64–72. http://www.jstor.org/stable/29774559
Kaufer, D. S., Hayes, J. R., & Flower, L. (1986). Composing written sentences. Research in the Teaching of English, 20(2), 121–140. https://www.jstor.org/stable/40171073
Lambert, B. (2018). A student’s guide to Bayesian statistics. Sage.
Lee, M. D., & Wagenmakers, E.-J. (2014). Bayesian cognitive modeling: A practical course. Cambridge University Press.
Leijten, M., De Maeyer, S., & Van Waes, L. (2011). Coordinating sentence composition with error correction: A multilevel analysis. Journal of Writing Research, 2(3), 331–363. https://doi.org/10.1177/0741088313491692
Leijten, M., & Van Waes, L. (2013). Keystroke logging in writing research: Using Inputlog to analyze and visualize writing processes. Written Communication, 30(3), 358–392.
Logan, G. D., & Crump, M. J. C. (2011). Hierarchical control of cognitive processes: The case for skilled typewriting. In B. Ross (Ed.), Psychology of learning and motivation (Vol. 54, pp. 1–27). Academic Press.
McElreath, R. (2016). Statistical rethinking: A Bayesian course with examples in R and Stan. CRC Press.
Medimorec, S., & Risko, E. F. (2016). Effects of disfluency in writing. British Journal of Psychology, 107(4), 625–650. https://doi.org/10.1111/bjop.12177
Medimorec, S., Young, T. P., & Risko, E. F. (2017). Disfluency effects on lexical selection. Cognition, 158, 28–32. https://doi.org/10.1016/j.cognition.2016.10.008
Nottbusch, G., Grimm, A., Weingarten, R., & Will, U. (2005). Syllabic sructures in typing: Evidence from deaf writers. Reading & Writing, 18(6), 497–526. https://doi.org/10.1007/s11145-005-3178-y
Olive, T. (2014). Toward a parallel and cascading model of the writing system: A review of research on writing processes coordination. Journal of Writing Research, 6(2), 173–194.
Papaspiliopoulos, O., Roberts, G. O., & Sköld, M. (2007). A general framework for the parametrization of hierarchical models. Statistical Science, 22(1), 59–73. https://www.jstor.org/stable/27645805
Pinet, S., Ziegler, J. C., & Alario, F.-X. (2016). Typing is writing: Linguistic properties modulate typing execution. Psychonomic Bulletin & Review, 23(6), 1898–1906. https://doi.org/10.3758/s13423-016-1044-3
Quené, H., & Van den Bergh, H. (2004). On multi-level modeling of data from repeated measures designs: A tutorial. Speech Communication, 43(1–2), 103–121. https://doi.org/10.1016/j.specom.2004.02.004
Roeser, J., Torrance, M., Andrews, M., & Baguley, T. (2020). No scope for planning—language pre-planning as mixture process. In 26th architectures and mechanisms for language processing (AMLaP). https://amlap2020.github.io/.
Roeser, J., Torrance, M., & Baguley, T. (2019). Advance planning in written and spoken sentence production. Journal of Experimental Psychology: Learning, Memory, and Cognition, 45(11), 1983–2009. https://doi.org/10.1037/xlm0000685
Sahel, S., Nottbusch, G., Grimm, A., & Weingarten, R. (2008). Written production of german compounds: Effects of lexical frequency and semantic transparency. Written Language & Literacy, 11(2), 211–228. https://doi.org/10.1075/wll.11.2.06sah
Salthouse, T. A. (1984). Effects of age and skill in typing. Journal of Experimental Psychology: General, 113(3), 345–371. https://doi.org/10.1037/0096-3445.113.3.345
Schöner, G. (2002). Timing, clocks, and dynamical systems. Brain and Cognition, 48(1), 31–51. https://doi.org/10.1006/brcg.2001.1302
Stan Development Team. (2015a). Stan: A C++ library for probability and sampling. http://mc-stan.org/.
Stan Development Team. (2015b). Stan modeling language user’s guide and reference manual. http://mc-stan.org/.
Sullivan, K. P. H., & Lindgren, E. (2002). Self-assessment in autonomous computer-aided second language writing. ELT Journal, 56(3), 258–266. https://doi.org/10.1093/elt/56.3.258
Torrance, M., Rønneberg, V., Johansson, C., & Uppstad, P. H. (2016). Adolescent weak decoders writing in a shallow orthography: Process and product. Scientific Studies of Reading, 20(5), 375–388. https://doi.org/10.1080/10888438.2016.1205071
Van Galen, G. P. (1991). Handwriting: Issues for a psychomotor theory. Human Movement Science, 10(2), 165–191. https://doi.org/10.1016/0167-9457(91)90003-G
Van Waes, L., & Leijten, M. (2015). Fluency in writing: A multidimensional perspective on writing fluency applied to L1 and L2. Computers and Composition, 38, 79–95. https://doi.org/10.1016/j.compcom.2015.09.012
Van Waes, L., Leijten, M., Lindgren, E., & Wengelin, Å. (2016). Keystroke logging in writing research: Analyzing online writing processes. In C. A. MacArthur, S. Graham, & J. Fitzgerald (Eds.), Handbook of writing research (pp. 410–426). The Guilford Press.
Van Waes, L., Leijten, M., Pauwaert, T., & Van Horenbeeck, E. (2019). A multilingual copy task: Measuring typing and motor skills in writing with inputlog. Journal of Open Research Software, 7(30), 1–8. https://doi.org/10.5334/jors.234
Van Waes, L., Leijten, M., & Quinlan, T. (2010). Reading during sentence composing and error correction: A multilevel analysis of the influences of task complexity. Reading and Writing, 23(7), 803–834. https://doi.org/10.1007/s11145-009-9190-x
Van Waes, L., Leijten, M., Roeser, J., Olive, T., & Grabowski, J. (2021). Measuring and assessing typing skills in writing research. Journal of Writing Research, 13(1), 107–153. https://doi.org/10.17239/jowr-2021.13.01.04
Vasishth, S., Chopin, N., Ryder, R., & Nicenboim, B. (2017a). Modelling dependency completion in sentence comprehension as a Bayesian hierarchical mixture process: A case study involving Chinese relative clauses. arXiv Preprint arXiv:1702.00564
Vasishth, S., Jäger, L. A., & Nicenboim, B. (2017b). Feature overwriting as a finite mixture process: Evidence from comprehension data. arXiv Preprint arXiv:1703.04081.
Vehtari, A., Gelman, A., & Gabry, J. (2015). Pareto smoothed importance sampling. arXiv Preprint arXiv:1507.02646.
Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27(5), 1413–1432. https://doi.org/10.1007/s11222-016-9696-4
Wagenmakers, E.-J., & Brown, S. (2007). On the linear relation between the mean and the standard deviation of a response time distribution. Psychological Review, 114(3), 830–841. https://doi.org/10.1037/0033-295X.114.3.830
Wallot, S., & Grabowski, J. (2013). Typewriting dynamics: What distinguishes simple from complex writing tasks? Ecological Psychology, 25(3), 267–280. https://doi.org/10.1080/10407413.2013.810512
Weingarten, R., Nottbusch, G., & Will, U. (2004). Morphemes, syllables, and graphemes in written word production. In T. Pechmann & C. Habel (Eds.), Multidisciplinary approaches to language production (Vol. 157, pp. 529–572). Mouton de Gruyter.
Wengelin, Å. (2001). Disfluencies in writing—Are they like in speaking? in ISCA Tutorial and Research Workshop (ITRW) on Disfluency in Spontaneous Speech.
Wengelin, Å. (2002). Text production in adults with reading and writing difficulties. PhD thesis. Göteborg University.
Wengelin, Å. (2006). Examining pauses in writing: Theory, methods and empirical data. In K. P. H. Sullivan & E. Lindgren (Eds.), Computer keystroke logging and writing: Methods and applications (Vol. 18, pp. 107–130). Elsevier.
Wing, A. M., & Kristofferson, A. B. (1973). Response delays and the timing of discrete motor responses. Perception & Psychophysics, 14(1), 5–12. https://doi.org/10.3758/BF03198607
Yamaguchi, M., & Logan, G. D. (2014). Pushing typists back on the learning curve: Revealing chunking in skilled typewriting. Journal of Experimental Psychology: Human Perception and Performance, 40(2), 592–612. https://doi.org/10.1037/a0033809.
Zhang, M., Bennett, R. E., Deane, P., & van Rijn, P. W. (2019). Are there gender differences in how students write their essays? An analysis of writing processes. Educational Measurement: Issues and Practice, 38(2), 14–26. https://doi.org/10.1111/emip.12249
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roeser, J., De Maeyer, S., Leijten, M. et al. Modelling typing disfluencies as finite mixture process. Read Writ 37, 359–384 (2024). https://doi.org/10.1007/s11145-021-10203-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11145-021-10203-z