Introduction

Language therapists, clinical linguists and scientists who work with children with developmental language disorder (DLD) have long been interested in understanding the cognitive mechanisms underlying the language problems seen in these children. Children with DLD have deficits in language that cannot be attributed to neurological damage, hearing impairment, intellectual disability, or unfavourable psycho-social/educational conditions. The difficulties with language manifest themselves across multiple areas such as the lexicon, morphology, (morpho)syntax, discourse (Leonard, 2014), reading (McArthur, Hogben, Edwards, Heath, & Mengler, 2000) and spelling (Joye, Broc, Olive, & Dockrell, 2018). Also, they frequently co-occur with difficulties in other cognitive domains such as attention, working memory (e.g., Ebert & Kohnert 2011; Montgomery, Evans, & Gilliam, 2018) and motor skills (Hill, 2001). This wide range of observed difficulties makes it difficult to point to a core underlying (cognitive) deficit for the disorder and thus far the observed language problems in children with DLD have been explained from language-specific deficits (see Leonard, 2014, chapter 9 for an overview) as well as from deficits in more general learning or processing mechanisms that contribute to language development (e.g, auditory perception deficits: Tallal, Stark, & Mellits, 1985; slower processing (of spoken language): Miller, Kail, Leonard, & Tomblin, 2001; limited short-term memory and working memory capacities: Archibald, & Gathercole, 2006; Montgomery et al., 2018). In the present paper, we seek evidence for one of these more general accounts, namely that the problems observed in children with DLD stem from a general cognitive statistical learning deficit (Evans, Saffran & Robe-Torres, 2009; Hsu and Bishop, 2014; Lammertink, Boersma, Wijnen & Rispens, 2017; Obeid, Brooks, Powers, Gillespie-Lynch & Lum 2016; Wijnen, 2013). Before we turn into explaining why the study of visual statistical learning in DLD is interesting, we first outline how sensitivity to structural regularities in the input (i.e., statistical learning) may play a role in children’s language development.

Language learning through statistics

Natural languages reflect structural regularities at the sound, word and sentence level. The ability to detect and learn these regularities may be crucial for language development as it has been proposed to underlie word segmentation (Saffran & Graf Estes, 2006) and the construction of linguistic categories and dependencies (e.g., Mintz, 2003; Wijnen, 2013). Indeed, there seems to be a predictive relation between detecting and learning regularities from linguistic input (statistical learning) and different aspects of language (e.g., vocabulary knowledge: e.g, Spencer, Kaschak, Jones, & Lonigan, 2015; Shafto, Conway, Field, & Houston, 2012; morphology/grammar: Hamrick, Lum, & Ulman, 2017 and syntactic processing: Kidd, 2012; Kidd & Arciuli, 2016; Wilson et al., 2018). Another source of evidence for a link between statistical learning and language ability comes from studies in people with DLD: these studies have shown that people with DLD are less sensitive to statistical regularities in auditorily presented verbal stimuli than people without DLD (meta-analyses: Lammertink et al., 2017; Obeid et al., 2016). In these studies participants typically listen to a continuous stream of auditorily presented nonsense syllables, either presented in a continuous manner (e.g., bupadadutaba; Saffran, Newport, Aslin, Tunick, & Barrueco, 1997) or with short pauses in between (e.g. tep wadim lut; Gómez, 2002). Unbeknowst to the participants the nonsense syllables form words (the example above consists of two words: bupada and dutaba) or their order of appearance in the utterance is govered by rules (in the second example above, tep and lut always co-occur). These words and rules can be learned if participants are sensitive to the transitional probabilities or nonadjacent dependencies that underlie them. When people with and without DLD are tested on their knowledge of these words and rules, it has been shown that people without DLD outperform people with DLD. Hence, people with DLD show an auditory verbal statistical learning deficit as compared to people without DLD.

Statistical learning outside the language domain

Structure is not unique to language, however (e.g., “like language, music can be viewed as a system of structure regularities”; Leonard, 2014, p. 213), and therefore it has been hypothesised that humans may have a domain-general statistical learning mechanism. The hypothesis that a domain-general statistical learning mechanism, rather than a domain-specific learning mechanism (i.e., sensitivity to statistical patterns solely in the linguistic input), is important for successful language acquisition, leads to two predictions. Firstly, one would expect to observe correlations between people’s ability to detect statistical regularities in other domains than language and their performance on language tasks. Secondly, the hypothesis also predicts that the statistical learning deficit observed in children with DLD is domain-general and should thus also be present outside the auditory verbal domain. As for the first prediction, there is evidence that in typically developing (TD) children and in children with dyslexia, statistical learning of regularities between non-linguistic elements in the visual domain (e.g., unfamiliar cartoon-like characters, meaningless shapes or symbols) and visuomotor domain (e.g., a sequence of computer screen locations in which a cartoon or shape appears) correlates with reading performance (Arciuli & Simpson, 2012; Hedenius et al., 2013; Steacy et al., 2019; Vakil, Lowe, & Goldfus, 2015; van der Kleij, Groen, Segers, & Verhoeven, 2018; von Koss Torkildsen, Arciuli, & Wie, 2019) and grammar ability (meta-analysis by Hamrick et al., 2017). As for the second prediction, there is also evidence that children with DLD perform worse on statistical learning tasks with non-linguistic stimuli in the visuomotor domain than typically developing children (Lum, Conti-Ramsden, Morgan, & Ullman, 2014). Such visuomotor non-linguistic statistical learning deficit has also been observed in children with dyslexia (Lum, Ullman, & Conti-Ramsden, 2013), but see recent studies reporting no evidence for or against such deficit in dyslexia: Henderson & Warmington (2017), Schmalz, Altoè, & Mulatti (2017), van der Kleij et al. (2018), van Witteloostuijn, Boersma, Wijnen, & Rispens (2019a). Children with dyslexia also perform more poorly in their detection of non-linguistic regularities (geometrical shapes or unfamiliar symbols) in the visual domain, hence they show a visual statistical learning (VSL) deficit (Pavlidou & Williams, 2014; Sigurdardottir et al., 2017). In this light, it should also be noted, however, that two different research groups concluded that the magnitude of the VSL deficit in dyslexia may be inflated as a result of publication bias (Schmalz et al., 2017; van Witteloostuijn, Boersma, Wijnen, & Rispens, 2017).

A visual non-linguistic statistical learning deficit in DLD

Interestingly, while there are some studies on VSL in children with dyslexia, studies on VSL in children with DLD are scarce. To the best of our knowledge only one study has thus far used a non-linguistic VSL task to compare children with and without DLD (Noonan, 2018). Noonan found no evidence for or against a difference in VSL performance between children with and without DLD, but note that neither of the groups in her study showed evidence of learning or not learning the non-linguistic regularities. Thus, it is still unknown whether the difficulties with language (and literacy) in children with DLD relate to a VSL deficit.

Investigating visual non-linguistic statistical learning abilities in children with DLD is important for several reasons. Firstly, in the statistical learning literature on typical learners it has recently been claimed that—as opposed to being fully domain-general—the statistical learning mechanism is in part domain- or stimulus dependent (Siegelman, Bogaerts, Elazar, Arciuli, & Frost, 2018). More specifically, Siegelman et al. observed a dissociation between people’s statistical learning of linguistic materials versus their learning of non-linguistic materials. From this, Siegelman et al. claim that differences in prior knowledge of statistical structure may impact behaviour on linguistic statistical learning tasks differently from behaviour on non-linguistic statistical learning tasks. They argue that the tabula rasa assumption (i.e., that learners have no expectations or prior knowledge regarding the underlying statistical structure) holds for non-linguistic tasks but not for linguistic tasks. With linguistic materials, participants may always have expectations of the underlying structure based on their native language experience (Siegelman et al. refer to this as “linguistic entrenchment”). If this claim is true, this may mean that children with DLD are worse in detecting statistical regularities in linguistic materials than their typically developing peers, not because they are less sensitive to the statistical regularities, but because they have less expectations of the underlying structure due to their language deficit. Only if the children with DLD also show a deficit in their detection of regularities in a non-linguistic statistical learning task, one could conclude that reduced sensitivity to domain-general structural regularities contributes to the observed language problems in this group of children.

Secondly, on the basis of studies on typically developing children and those in children with dyslexia, it has been claimed that visual and visuomotor statistical learning of non-linguistic materials relates to literacy skills (see “Statistical Learning Outside The Language Domain” section). While children learn to read and write, they need to detect which graphemes correspond to which phonemes and vice versa. In many orthographies, graphemes may correspond to multiple phonemes. Which phoneme should be used is then dependent on the context in which it appears. For example, in English, the grapheme ‘c’ may correspond to either /k/ as in can’t or to /s/ as in cent. The statistical regularity to be learned is that the vowel that follows the ‘c’ determines its phoneme. When ‘c’ is followed by ‘a’,’o’ or ‘u’ it is usually pronounced as /k/; when it is followed by ‘e’, ‘i’ or ‘y’ it is usually pronounced as /s/. Children may use a statistical learning mechanism to detect these (context-dependent) regularities in grapheme–phoneme correspondences (Arciuli, 2017; 2018, Treiman, 2018). Interestingly, children with DLD exhibit large individual differences in literacy performance; approximately half of the children with DLD have problems with reading and/or spelling (McArthur et al., 2000). In the present study, we will explore whether these large individual differences in literacy performance among children with DLD can be explained by individual differences in visual statistical learning—as has also been claimed for typically developing children and children with dyslexia.

Thirdly, a methodological reason for conducting the present study is that the evidence for a domain-general non-linguistic statistical learning deficit comes mostly from studies using the serial reaction time task (Nissen & Bullemer, 1987). Although the serial reaction time task is widely used as a measure of people’s visuomotor non-linguistic statistical learning ability, the validity of the task has been questioned (West, Vadillo, Shanks, & Hulme, 2017). Also, children with DLD often have subtle motor deficits (Hill, 2001) that may impact their performance on this visuomotor task. In the present study, we therefore use a non-linguistic statistical learning task in the visual (rather than visuomotor) domain to investigate the domain-generality of the statistical learning deficit in DLD. The reliability of the VSL task has been questioned as well, but recent modifications to the set-up of the task are promising and seem to detect learning—in both adults (Siegelman, Bogaerts, & Frost, 2017; Siegelman, Bogaerts, Kronenfeld, & Frost, 2017) and children (van Witteloostijn, Lammertink, Boersma, Wijnen, & Rispens, 2019c).

Fitfthly, the present study follows one of the research directions put forward in Arciuli and Conway (2018). In this review paper, Arciuli and Conway conclude that it is important to further investigate under what conditions children with developmental disabilities can and cannot learn statistical regularities. As outcomes of studies like the present study may identify relative strengths and weaknesses of these children, they may be helpful in developing intervention studies that aim to support language learning in children with language difficulties.

The visual statistical learning paradigm

In the present study, we use a triplet learning paradigm to investigate children’s sensitivity to statistical regularities in the visual non-linguistic domain. In this paradigm, participants are visually exposed to a sequence of individual non-linguistic elements (unique cartoon drawings or meaningless shapes) that appear one by one on a computer screen. Unbeknownst to the participants, the individual elements are distributed into fixed groups of three (triplets). Within these triplets, the transitional probability (TP) between elements is 1.0, but across triplets the TP is lower. After exposure to a series of elements, participants’ knowledge of the triplets is assessed with an offline recognition test. Several research groups raised concerns on the use of a recognition task as the only measure of statistical learning performance (Karuza, Farmer, Fine, Smith, & Jaeger, 2014; Siegelman, Bogaerts and Frost, 2017; Siegelman, Bogaerts, Kronenfeld, et al., 2017). In response to these concerns, these groups made the exposure phase self-paced (Karuza et al., 2014; Siegelman, Bogaerts, Kronenfeld et al., 2017) or turned this phase into a target detection task (Qi, Sanchez, Georgan, Gabrieli, & Arciuli, 2019) such that response times (RTs) can serve as an additional, and online, index of VSL. In the self-paced familiarization phase designs, learners show a predictability advantage such that their RTs to predictable elements (e.g., the second element and third element of the triplets) are faster than their RTs to unpredictable elements (e.g., the first element of a triplet). Siegelman, Bogaerts, Kronenfeld et al., detected such predictability advantage using a self-paced VSL in adults. van Witteloostuijn et al. (2019c) detected it using a self-paced VSL task in children aged between five and eight years old. In the target detection task, learning of the triplets is observed as learners (both children and adults) become faster at detecting the target (which is always the third element of a triplet, and thus predictable if one is sensitive to the triplet structure) over time (see Qi et al., 2019). Finally, Siegelman, Bogaerts, & Frost (2017) also gave recommendations on how to expand the offline test phase with different types of test items. van Witteloostuijn et al. (2019c) implemented both the recommended online measure and offline measure in a child-friendly version of the task, and we use their task in the present study.

The present study

The aim of the present study is thus to investigate whether children with DLD have a domain-general statistical learning deficit. In doing so, we compare VSL performance between children with DLD and their TD peers, using a self-paced online measure of learning (Siegelman, Bogaerts, Kronenfeld et al., 2017; van Witteloostuijn et al., 2017) and two offline measures of learning (Siegelman, Bogaerts, & Frost, 2017). Our first research question is whether children with DLD have a non-linguistic VSL deficit as compared to their TD peers. We expect to observe such a deficit, since we hypothesize that a domain-general statistical learning deficit underlies the language problems in these children. Our second research question concerns the putative association between VSL and literacy in DLD. As van der Keij et al. (2018) report that growth in pseudoword reading, but not word reading, is associated with serial reaction time performance in children with dyslexia, we will explore the correlations between VSL and reading words and reading pseudowords separately.

Method

Participants

The present study is part of a larger research project on the relation between statistical learning, grammar and literacy acquisition in children (see “Procedure” section), and consequently our sample of participants overlaps with those reported on in other studies with different research questions (Lammertink, Boersma, Wijnen, & Rispens, 2019, submitted; van Witteloostuijn, Boersma, Wijnen, & Rispens, 2019a, b, submitted). The data reported on in this study has not been submitted elsewhether or published previously.

The two groups of children that participated in the present study—children with DLD and TD children—are matched on gender, age (maximal difference of 3 months), non-verbal intelligence and socioeconomic status (SES). A combined score that takes the average education level, average income and average working status of the people living in a particular district (defined per zip code) is used as a proxy for SES (Sociaal Cultureel Planbureau, 2016). The score has been designed to have a Dutch average of 0 and higher scores indicate higher SES. SES estimates for the children with DLD are based on either their home address (N = 22) or school address (N = 14). SES estimates for the TD children are based on their school address (four different schools across the Netherlands). Ethical approval for this study was obtained from the ethical review committee of the University of Amsterdam, Faculty of Humanities. For the children with DLD, informed consent was given by the children’s parents or caregivers prior to participating in the study. Typically developing children were enrolled on an opt-out basis.

Children with DLD

As also described in Lammertink et al. (2019) and in Lammertink et al. (submitted), 37 children with DLD, aged seven to eleven years old, took part in the study. The children with DLD were recruited via four national organizations in the Netherlands, via an association for parents with children with DLD and self-employed speech therapists. Children had to be diagnosed with DLD by a licensed clinician, taking the following criteria into account: (1) a proficiency score 1.5 SD below the norm on two out of four subscales (speech production, auditory processing, grammatical knowledge, lexical semantic knowledge) of a standardized language assessment test battery, (2) they had at least one parent who is a native speaker of Dutch and (3) they had not been diagnosed with Autism Spectrum Disorder, Attention Deficit Hyperactivity Disorder (ADHD), or other (neuro)psychological problems. In addition to these criteria, children had to obtain a percentile score of at least 17 on the Raven Coloured Progressive Matrices (RCPM; Raven, Raven, & Court 2003)—a standardized measure of nonverbal intelligence that was administered as part of our own test battery. After testing, we had to exclude one child with DLD as it turned out that this child had hearing problems in addition to the diagnosis of DLD. This left us with a sample of 36 children with DLD (8 female, 28 male, Mage = 9;1. Age range = 7;8–10;4). At the start of the project, we contacted different professionals working with children with DLD in the Netherlands (see above). We informed all the professionals who were involved in the recruitment process that recruitment and testing had to take place within a pre-determined testing period that ran from January 2017 to March 2018. We tested as many children as possible in this period. The widths of the confidence intervals for our confirmatory and exploratory research questions will tell us whether the power of the experiment was sufficient to detect a medium-sized effect size. As the number of participants per group (N = 36) is relatively large for this type of study (see “Discussion” section), we expect that this should not be a problem, however.

TD children

Fifty-nine TD children, aged seven to 11 years, also took part in the study. The TD children were recruited via four different primary schools across the Netherlands. Five of the 59 TD children that participated were excluded because their RCPM-score was lower than 17 and/or because they scored below the normal range (norm score < 8; percentile score < 17) on at least two of the following language tasks: 1-min word reading (Brus & Voeten, 1979), 2-min pseudoword reading (Klepel; van den Bos, Spelberg, Scheepstra, & De Vries, 1994), spelling (Schoolvaardigheidstoets spelling; Braams & de Vos, 2015) or sentence recall (CELF-4-NL; Semel, Wiig, & Secord, 2010). Additionally, one TD child was excluded, because this child reported having been diagnosed with ADHD. From the remaining 53 children, we selected 36 children (9 female, 27 male, Mage = 9;1. Age range = 7;8–10;4) that matched best with our DLD sample, taking age, gender, SES and non-verbal intelligence into account.

Visual statistical learning task

The VSL task used in the present study is also described in van Witteloostijn et al. (2019c) and modelled after previous studies (Arciuli & Simpson, 2012; Siegelman, Bogaerts, & Frost, 2017; Siegelman, Bogaerts, & Kronenfeld et al., 2017). The present VSL task differs from the one described by van Witteloostuijn et al. (2019c) on four points: (1) we made the task instructions more explicit (see “Appendix 1”); (2) There were two sets of alien triplets, instead of one; (3) All children performed a cover task, and this cover task is different from the one described in van Witteloostuijn et al. (2019c); (4) In the offline test phase, the order of tasks was reversed: the triplet completion task was first, the triplet recognition task second.

Online Familiarization Phase

At the start of the experiment, we told children that they were going to play a game in which they would send aliens off to a spaceship (“Appendix 1”). The aliens appeared on the screen, one-by-one, and were sent into the spaceship by pressing the space bar. Every time the child pressed the space bar, the current alien disappeared and the next alien appeared. Each alien was part of a triplet of three aliens that always occurred in the same order (thus in the triplet ABC, B always followed A and C always followed B). There were four such triplets (ABC, DEF, GHI, JKL, see “Appendix 2”). Children were not informed about these triplets, but they were told that some of the aliens really liked each other and therefore stood together in line. Children were asked to watch each alien closely and to try and figure out which aliens belonged together.

Each triplet occured 24 times in the familiarization phase, divided over four blocks of six repetitions of each triplet. Between every two successive blocks, there was a small break in which children were awarded a sticker. The predictability of appearance of individual aliens was dependent on the position of the alien within the triplet: the appearance of the second and third aliens is fully predictable from the appearance of the preceding alien(s) (TP = 1.0). The transitional probability when crossing a triplet boundary, thus going from the third alien to the first element of another triplet is lower (each first alien can be preceded by the third alien from either of the two other triplets), making the appearance of each first alien less predictable (Fig. 1, Figure adapted from van Witteloostuijn et al., 2019c, p.5). There were two constraints on the order of appearance of the triplets: (1) the same tripet never appeared twice in a row (e.g., ABC, ABC), and (2) repetitions of pairs of triplets (e.g., ABC, JKL, ABC, JKL) were ruled out.

Fig. 1
figure 1

Note that we adopted this Figure from van Witteloostuijn et al. (2019c), p.5

The Transitional Probability (TP) structure in the visual statistical learning task

Full size image

There were two experiment versions that differed with respect to which set of individual aliens comprised a triplet (“Appendix 2”). In each experiment version, there were two randomized orders. We decided to work with two experiment versions and two randomized orders to control for any potential effects of single stimuli, triplets or order of appearance. Finally, the familiarization phase had a cover task: children were instructed that occasionally the exact same alien appeared twice in a row. If this happened, the child had to touch the repeated alien with his/her finger on the screen. In each block, such a repetition occurred three times (e.g., AABC, DEEF and GHII) and we ensured that every individual alien was repeated once over the complete course of the familiarization phase.

Offline test phase

The offline test phase consisted of 40 trials (16 triplet completion trials and 24 triplet recognition trials) to test children’s knowledge of the triplets that they were familiarized with (the “base triplets”). The base triplets were contrasted with “foil triplets”: four triplets that were created from the same set of twelve aliens, but had never appeared as a triplet during the familiarization phase. We tested children’s knowledge of complete base triplets (e.g., ABC; triplet completion: N = 8; triplet recognition: N = 8) as well as their knowledge of “base pairs” from within the base triplets (e.g., AB, BC; triplet completion: N = 8; triplet recognition: N = 16; Fig. 2; “Appendix 3”). In the triplet completion trials, children either completed the missing alien in a base triplet or base pair. The correct answer was always one out of three aliens (three-alternative forced choice task). In the triplet recognition items children were presented with either two complete triplets (the base triplet and one foil triplet: e.g., ABC versus DHL) or two pairs (a base pair and a foil pair: e.g., AB versus DH) and we asked the children to pick the triplet or pair that appeared most familiar to them (two-alternative forced choice). In both the triplet competion and triplet recognition trials, we controlled for the position of the correct alien on the screen and for the frequency of foil triplets, pairs and single aliens to avoid continued learning during the triplet recognition trials (Arciuli & Simpson, 2012).

Fig. 2
figure 2

a Two examples (left: one base triplet; right: one base pair) from the triplet completion trials. Children are asked to replace the question mark with one of the three aliens at the bottom. b Two examples (upper row: one base triplet; bottom row: one base pair) from the triplet recognition trials. Children are asked to pick the group of aliens that looks most familiar to them

Full size image

Literacy tasks

Word reading test

In this task children had 1 minute to read aloud as many (existing) Dutch words as they could (EMT; Brus, & Voeten, 1979). The raw score was the total number of words read, with a maximum of 116 words. Age-appropiate norm scores were derived from the raw scores. A norm score of 10 corresponds to a percentile score of 50. Norm scores below 8 are interpreted as below average whereas norm scores above 12 are interpreted as above average.

Pseudoword reading test

Similarly, as in the word reading task, children were asked to read pseudowords aloud. This time, however, they had 2 minutes to read as many pseudowords as they could (Klepel; van den Bos et al., 1994). Again, the maximum number of words to read was 116, and norm scores were derived from the raw scores.

Spelling test

In the spelling task (schoolvaardigheidstoets spelling; Braams & de Vos, 2015), the experimenter read aloud a sentence to the child and then instructed the child to write down one word from this sentence. There were 30 items. For each correct written form, children received one point. Age-appropiate percentile scores were derived from the raw scores. Percentile scores below 17 are interpreted as below average whereas scores above 85 are interpreted as above average (Table 1).

Table 1 Summary of the group characteristics
Full size table

Other cognitive measures

We also took a measure of children’s visual spatial short-term memory, their visual spatial working memory and their sustained attention (Table 2).

Table 2 Description of the cognitive tasks
Full size table

Procedure

As described earlier, the present study is part of a larger research project. The total task battery contained more tasks than reported here. All children that participated in the present study completed the full task battery, and this took two to four sessions (each lasting approximately 1 hour) per child. The results on the other tasks of our battery, but with the same group children, are reported in Lammertink et al. (2019, submitted). Furthermore, a number of the TD participants from the same group of 59 TD children are also reported on in studies by van Witteloostuijn et al. (2019a, b) and van Witteloostuijn et al. (submitted). In her studies, van Witteloostuijn and colleagues uses the performance of the TD children to evaluate statistical learning in children with dyslexia.

Data analysis and hypotheses

We made our data, and the scripts that we used for data analysis available at our Open Science Framework (OSF) page: https://osf.io/8gpjt/.

Online measures of VSL

During the online self-paced familiarization phase, we measured children’s RTs to each individual alien (i.e., time between the appearance of the alien on the screen and the child’s space bar press) in milliseconds (ms). Prior to analysis, we removed all responses to the three aliens of the first triplet of each block (i.e. four triplets, 12 individual aliens per child). Also, we removed all RTs shorter than 50 ms (DLD; 0.42% of the total observations; TD: 0.22% of the total observations). Finally, we normalized the RTs, such that they can be interpreted as optimally distributed z-values. These normalized RTs were obtained by first ranking all N raw RT observations, sorting them in increasing order, labelling them with a ranking number r (Baguley, 2012, p. 254-358) and then replacing all observations by the (r – 0.5)/N quantile of the unit normal distribution. We decided a priori to normalize the raw RTs as with this procedure, we take the data closer to satisfying the assumption of normally distributed model residuals, which is a central assumption of linear mixed effects model analysis (package lme4; Version 1.1.17, Bates, Maechler, Bolker, & Walker 2015; R programming language: R Core Team, 2018). Furthermore, the advantage of working with transformed RT data (in general) is that one can include all observations and thus not have to apply an arbitrary criterion in removing outlier observations (Simmons, Nelson, & Simonsohn, 2011). As a sanity check we visually inspected the model residuals from the raw RT model and normalized RT model and indeed observe that the residuals of the model with normalized RTs are more symmetrically distributed than the residuals of the model with raw RTs (see histograms on our OSF page).

The normalized RTs were analysed using a linear mixed effects model that fitted normalized RT as a function of the ternary within-subject predictor Predictability (alien 1, alien 2, alien 3), the binary between-subjects predictors Group (DLD, TD), TripletVersion (Triplets A, Triplets B) and TripletOrder (Order 1, Order 2), and the continuous within-subject predictor Time (repetition of triplets, originally ranging from 1 to 24, after centering and scaling ranging from − 1.68 to + 1.65). All predictors were included in interaction with each other, and the random-effects structure of the model contained by-subject (N = 72) and by-item (N = 12; individual alien) random intercepts and by-subject random slopes for the main effects of Predictability and Time and for their interaction. If children are sensitive to the TPs, then their RTs to predictable aliens (alien 2 and 3) should be faster than their RTs to unpredictable aliens (alien 1). We will refer to this as the “predictability advantage”. The size of the predictability advantage is estimated by the first contrast of the predictor Predictability (with alien 1 coded as \(- \frac{2}{3}\) and both alien 2 and alien 3 coded as \(+ \frac{1}{3}\)). A difference in learning between children with DLD and TD children may be observed in two ways: either we observe a difference in the average predictability advantage (interaction between Predictability and Group) or in the emergence of a difference in predictability advantage over time (interaction between Time, Predictability and Group). The predictor Group is coded with DLD as \(- \frac{1}{2}\) and TD coded as \(+ \frac{1}{2}\). Finally, we included the predictors TripletVersion (coded as \(- \frac{1}{2}\) and \(+ \frac{1}{2}\).) and TripletOrder (coded as \(- \frac{1}{2}\) and \(+ \frac{1}{2}\).) as they potentially influence learning. These predictors were not of interest to our research question.

Statistical significance of the predictors that estimate the difference in size of the predictability advantage between children with DLD and TD children (online measure 1), and the difference in the effect of time on the predictability advantage between both groups of children (online measure 2; i.e., our confirmatory predictors) is assessed via 98.75% profile confidence intervals. These confidence intervals are Bonferroni-corrected for multiple testing as we assess the VSL difference with a total of four measures: two online measures and two offline measures.

Offline measures of VSL

Responses in the triplet recognition task and triplet completion task were coded as 1 (correct) or 0 (incorrect), with a maximum score of 24 on the triplet recognition task and a maximum of 16 on the triplet completion task. If children are sensitive to the TPs between the elements, then their correctness probabilities on the offline tasks should exceed chance level (33.3% and 50% respectively). The offline accuracy scores were analysed using generalized linear mixed effects models (package lme4, Bates et al., 2015). For both offline tasks, correctness probability was fitted as a function of the binary predictors Group, TripletVersion and TripletOrder. All predictors were added in interaction with each other and the random effects structure of the model contained a by-subject (N = 72) random intercept. We will conclude that children with DLD have a visual statistical learning deficit if their correctness probabilities are significantly lower than those of our TD children (main effect of Group). Statistical significance of the confirmatory predictors is assessed via 98.75% profile confidence intervals.

Results

Background measures

Table 3 presents the raw scores and—when available—the standardized scores on the cognitive and literacy tasks for both groups of children. Between-group t-tests show that children with DLD have lower (raw) scores on all three literacy tasks: word reading (t(70) = − 8.60, p = 1.6 × 10−12); pseudoword reading (t(70) = − 9.34, p = 8.7 × 10−14); and spelling (t(70) = − 12.45, p = 5.0 × 10−19). With a norm score > 7 being interpreted as “average” performance, we observe that 42% of the children with DLD can be classified as “average” readers (i.e., they score > 7 on both the (pseudo)word reading tests). For the spelling task, 31% percent of the children with DLD had a percentile score of 17% or higher, indicating that they may be classified as “average” spellers. Finally, we have no evidence that the children with DLD perform differently from the TD children on the tasks that measured visuospatial short-term memory (t(69) = − 1.83, p = 0.072), visuospatial working memory (t(69) = − 1.02, p = 0.31) and sustained attention (t(70) = − 0.78, p = 0.44). Therefore, we decided not to control for these measures when comparing VSL in children with DLD and TD children. Please note that we have missing data on the visuospatial short-term memory and visuospatial working memory for one child with DLD.

Table 3 Summary of Children’s Relevant Raw and—when available—norm or percentile scores
Full size table

Visual statistical learning in DLD

In the sections that present the results of our confirmatory research question (online and offline visual statistical learing) we only present the model estimates for the predictors that are relevant for our hypothesis testing or data checks. The full model outcomes are available on our OSF page.

Descriptives

Children’s mean RTs to all three alien positions (alien 1, alien 2, alien 3) across the 24 repetitions of each triplet are visualized for the children with DLD and the TD children separately in Fig. 3. Descriptively and pooled over the 24 repetitions, children with DLD respond fastest to the second alien (M = 807 ms, SD = 624 ms), followed by the third alien (M = 812 ms, SD = 588 ms), followed by the first alien (M = 819 ms, SD = 611 ms). TD children respond fastest to the second alien (M = 858 ms, SD = 555 ms), followed by the first alien (M = 859 ms, SD = 555 ms), followed by the third alien (M = 864 ms, SD = 554 ms).

Fig. 3
figure 3

Visualization (descriptive) of children’s raw (i.e. unnormalized) mean RTs (in ms) to the aliens in first position (black circles), in second position (orange triangles) and third position (blue squares). The left graph shows the RTs of children with DLD, the right graph shows the RTs of TD children. Please note that these raw RTs are only displayed for ease of exposition and that they do not represent the outcome of our confirmatory hypothesis testing. Therefore, (descriptive) differences in these raw RTs cannot be used to interpret the strength of the effects reported later in this paper or to draw any conclusions on our confirmatory research question. (Color figure online)

Full size image

Confirmatory results I: online measures of VSL

If children are sensitive to the TPs in the VSL task, we expect to observe a predictability advantage. The model estimated that, pooled over the groups, the children responded faster to predictable than to unpredictable aliens (main effect of Predictability: Δz = − 0.011), but this estimate was not significantly different from zero (t = − 0.95, 98.75% profile CI [− 0.041, + 0.019], p = 0.34; Table 4). The two-way interaction between Predictability and Group estimated that the predictability advantage was larger in our children with DLD than in our TD children (ΔΔz = + 0.020), but this estimate was not significantly different from zero (t = + 0.96, 98.75% profile CI [− 0.032, + 0.072], p = 0.34; Table 4). To obtain an estimate of the maximal standardized effect size (i.e., the maximal standardized difference between both groups of children), we divided the maximal absolute raw effect size (i.e., the greater absolute bound of the confidence interval) by the residual standard deviation (SD) of the model (residual SD = 0.68). The estimate of the maximal standardized effect size is 0.11 (0.072/0.68). This effect size can be interpreted as a Cohen’s d effect size (Cohen, 1988) and as it is < 0.20, it means that if a DLD-TD differences exists at all, the difference will be small.

Table 4 Outcome of the Relevant Estimates from the Linear Mixed Effects Model (RT data; 19807 observations)
Full size table

We also looked at the model estimate of children’s predictability advantage unfolding over time (interaction between Predictability and Time). Unexpectedly, the model estimated that the predictability advantage decreased over time (ΔΔz = + 0.011). This decrease was larger for the children with DLD than for the TD children (ΔΔΔz = − 0.015). Both the two-way interaction between Predictability and Time and the three-way interaction between Predictability, Time and Group were not significantly different from zero, however (two-way interaction: t = + 1.12, 98.75% profile CI [− 0.014, + 0.037], p = 0.26; three-way interaction: t = − 0.73, 98.75% profile CI [− 0.067, + 0.036], p = 0.46; Table 4). The estimate of the maximal standardized effect size for a difference in the emergence of a predictability advantage over time between children with DLD and TD children is 0.098 (0.067/0.68). Again, the maximal standardized effect size is < 0.20 and thus, if a DLD-TD difference exists, the difference will be small.

Taken together, the online measures of VSL provide no evidence that children are sensitive or insensitive to the TPs or that sensitivity to the TPs emerges or does not emerge over time. Also, we have no evidence for or against a DLD–TD difference.

Confirmatory results II: offline measures of VSL

For both offline tasks (triplet completion and triplet recognition), the criterion for learning was that the correctness probabilities (i.e., model intercepts) exceed chance level (0.333 for triplet completion and 0.50 for triplet recognition). The intercepts for both offline models estimated that, pooled over both groups of children, children picked the correct answer more than one would expect on the basis of chance (triplet completion: log-odds = + 0.099, odds = 0.91, probability = 47%; triplet recognition: log-odds = + 0.53; odds = 1.7, probability = 63%). Both estimates are statistically significantly different from chance probability (triplet completion: p = 5.9 × 10−7, 98.75% CI [41%, 0.55%]; triplet recognition: p = 3.9 × 10−7; 98.75% CI [57%, 0.69%]).

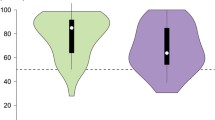
If children with DLD learn fewer triplets than the TD children, then their correctness probabilities on both tasks should be lower than those of the TD children. Indeed, on the triplet completion task, the model estimated that the ratio by which children picked the correct missing alien was 1.1 higher in the TD children than in the children with DLD. This odds ratio was not significantly different from 1, however (z = + 0.66; p = 0.51; 98.75% CI odds ratio [0.67, 2.0], Fig. 4, Table 5).

Fig. 4
figure 4

Children’s individual correctness probabilities on the triplet completion task (left) and triplet recognition task (right). The dashed lines represent chance probability (33.3% for the triplet completion task and 50% for the triplet recognition task). The crosses indicate the mean correctness probabilities per group (DLD and TD). Please note that we did not obtain these correctness probabilities from the statistical model. These descriptive data are only displayed for ease of exposition and do not represent the outcome of the generalized linear mixed model. Therefore, (descriptive) differences in this plot cannot be used to interpret the strength of the effects reported later in this paper or to draw any conclusions with respect to our confirmatory research question

Full size image
Table 5 Outcomes of the relevant estimates from the triplet completion generalized linear mixed effects models (accuracy data; 1152 observations)
Full size table

For the triplet recognition task, the model estimated that the ratio by which children picked the correct group of aliens was 0.9 times higher (and thus 1.1 times worse) in the TD children than in children with DLD. This odds ratio was not significantly different from 1, however (z = − 0.66; p = 0.51; 98.75% CI odds ratio [0.54, 1.5], Fig. 4, Table 6).

Table 6 Outcomes of the Relevant Estimates from the Triplet Recognition Generalized Linear Mixed Effects Models (accuracy data; 1728 observations)
Full size table

To check whether the groups separately showed correctness probabilities that exceed chance expectations, we fitted two additional models for both tasks in which we re-referenced the contrast-coding for the predictor of Group such that we obtained estimates for the children with DLD (with contrasts set as DLD 0; TD + 1) and the TD children (DLD + 1; TD: 0) separately. For both groups of children, and for both tasks, the estimates were significantly different from chance (Tables 5, 6).

Taken together, for both populations of children, and for both tasks we conclude that children can learn which aliens belong together. We have no evidence for or against a DLD–TD difference either the completion task or the recognition task.

Exploratory results: the link between literacy and VSL

To see if there is an association between VSL and literacy in children with DLD, we averaged children’s offline VSL measures (triplet completion and triplet recognition), as children’s scores on these tasks were positively correlated, and significantly different from zero (Pearson’s r (34) = + 0.67, p = 6.6 × 10−6; 95% CI [+ 0.44, + 0.82].

None of the correlations between VSL and literacy were significantly different from zero (word reading: Pearson’s r (34) = + 0.070, p = 0.68, 95% CI [− 0.26, + 0.39; pseudoword reading: Pearson’s r (34) = − 0.014, p = 0.93, 95% CI [− 0.34, + 0.32]; spelling: Pearson’s r (34) = + 0.13, p = 0.44, 95% CI [− 0.20, + 0.44]; Fig. 5). Although not part of our hypothesis testing, we also explored the correlations between VSL and literacy in the TD children. None of the explored correlations in the TD children were significantly different from zero (see output at our OSF page).

Fig. 5
figure 5

Descriptive visualization of the correlation between visual statistical learning correctness probability (accuracy offline VSL: triplet completion and triplet recognition combined) and A. Word reading, B. Pseudoword reading, and C. Spelling in children with DLD (N = 36)

Full size image

Taken together, we cannot conclude that offline VSL associates (or does not associate) with individual differences in literacy performance in children with DLD.

Discussion

The main aim of the present study was to assess whether children with DLD have a non-linguistic visual statistical learning deficit as compared to their TD peers. We had expected to observe such deficit, since we hypothesized that a domain-general statistical learning deficit underlies te language problems observed in chidren with DLD. The outcomes of this study provides no evidence for or against such domain-general visual statistical learning deficit in children with DLD, as compared to typically developing children, however. Neither with the online VSL measures nor with the offline VSL measures did we detect a difference in learning between both populations. Null results, however, can never be used to prove that an effect is absent. Therefore, we can only assign meaning to our findings by showing that, if a difference would exist at all, this difference would be small. We estimated the magnitude of the DLD–TD differences using estimates of the maximal standardized effect sizes (see Results), and found that the maximal standardized effect sizes for both our online measures are below 0.20, meaning that if a DLD–TD difference existed at all, this difference would be small (Cohen, 1988). With the offline measures, we observe that children with DLD either perform maximally 2.0 times worse (upper bound CI) or 1.5 times better (lower bound CI) than the TD children on the triplet completion task, and maximally 1.5 times worse or 2.0 times better on the triplet recognition task. As there is no general consensus on how to interpret the magnitude of odds ratio effect sizes, we refrain from calling these effect sizes small, medium or large (but see Chen, Cohen, & Chen, 2010).

A limitation of the present study is that the online measures could not detect children’s learning of the visual regularities. Therefore, even if a DLD–TD difference exists, it is the question whether such a difference will be meaningful. Our small (and statistically non-significant) result for the online measure (pooled over groups) of Δz = − 0.011 falls within the (statistically significant) predictability advantage found (for TD children) by van Witteloostuijn et al. (2019c) which ranged from Δz = − 0.114 to Δz = − 0.002. van Witteloostuijn et al. (2019c) already concluded that the predictability advantage effect can be called small, meaning that if it could be detected at all, the effect may be too small to be reliably detected across studies or between different participant groups. As such the outcomes of the present study fit within a series of recently published papers that investigate the psychometric properties of statistical learning designs. These studies address 1) the reliability of statistical learning tasks in their ability to capture individual differences in children’s (language) learning ability (Arnon, 2019), but also 2) the validity of the tasks in measuring the construct of statistical learning (West et al., 2017). As the present study was not designed to assess the psychometric properties (i.e., split-half reliability and test–retest reliability) of our visual task we cannot draw any conclusions with respect to this reliability/validity issue. Nevertheless we deem it important to place our study within this debate and to refer the interested reader to relevant papers on this issue (e.g., Arnon, 2019; Siegelman, Bogaerts, & Frost, 2017, West et al., 2017).

Interestingly, our offline measures of VSL indicate that both groups of children were sensitive to the transitional probabilities between the aliens. Both children with DLD and TD children completed and recognized the triplets with correctness probabilities that exceed chance expectation. This may be a preliminary indication that children with DLD are sensitive to TPs in the non-linguistic visual domain. This conclusion could not be drawn in Noonan (2018), who also studied VSL in children with DLD, because Noonan could not detect a learning effect in children with and without DLD. It may thus be illuminating to highlight some differences between both studies. Firstly, as we used a self-paced familiarization phase, children were exposed to the stimuli at their own pace. This is different from the Noonan study in which the children were presented with the stimuli at a fixed presentation rate. Secondly, in line with the task instructions given by Siegelman, Bogaerts, Kronenfeld et al. (2017), we instructed the children to pay attention to the order in which the aliens appeared. Even though with these instructions we gave no information about the triplet patterns, our instructions are likely to be more explicit than the “deliberately vague (Noonan, 2018, p. 84)” instructions given by Noonan. Thirdly, the stimuli that we used were more colorfol, less abstract and thus easier to verbalize than the black, abstract shapes used in Noonan her study. Finally, the present study contained fewer triplets (four triplets) than the study by Noonan (five triplets). We speculate that the abovementioned differences made learning of the structure in present study easier or more explicit than in the study by Noonan. As offline measures of statistical learning are proposed to measure more explicit representations of acquired knowledge (Franco, Eberlen, Destrebecqz, Cleeremans, & Bertels, 2015), this may be one of the reasons that we did detect a learning effect in the offline measures.

For the children with DLD, we also investigated the link between their VSL performance and literacy skills, but found no evidence for or against the existence of such a link. The confidence intervals for the association between VSL and our literacy measures ranged from r = − 0.26 to + 0.39 (reading), r = − 0.34 to + 0.32 (pseudoword reading) and from r = − 0.20 to + 0.44 (spelling). The estimated upper bounds of the “standardized” effect sizes for these associations are R2 = 0.15 (0.392), R2 = 0.10 (0.322) and R2 = 0.19 (0.442) respectively, indicating that if associations exist, these may be small in size (as all standardized effect sizes are < 0.20 Cohen, 1988). Null results for the relationship between VSL and literacy have recently been reported in other studies with TD children (e.g., Schmalz, Moll, Mulatti, & Schulte-Körne, 2018) and in children with DLD (Noonan, 2018).

Given these small effects, the only notable—and probably unsatisfactory—conclusion that we can draw is that the currently available measures of VSL are not sensitive enough to detect differences in VSL between children with DLD and TD children (see Arnon, 2019; Arciuli & Conway, 2018; Noonan, 2018; Schmalz et al., 2018, and West et al., 2017, for similar conclusions). We do believe that publication of our null results is important, however. Null results should be published to overcome existing publication biases (van Witteloostuijn et al., 2017; Schmalz et al., 2017) and because the data should be available for researchers who wish to conduct meta-analyses on this topic.

We have reasons to believe that our null results are not the result of the power of our study being too low to detect the effects under examination: Firstly, in comparison to serial reaction time studies, the number of children with DLD tested for the present study is relatively large (only two out of the eleven published serial reaction time studies tested more than 36 children, Hsu and Bishop, 2014; Conti-Ramsden, Ullman, & Lum, 2015). Secondly, looking at our outcomes we observe (A) a learning effect with our offline measures of learning, (B) a small DLD-TD difference in online visual statistical learning and (C) small correlations between visual statistical learning and literacy in children with DLD. The detection of an effect (A) indicates that we tested sufficiently children to detect offline visual statistical learning. As for (B) and (C), the confidence intervals of the standardized effect sizes for these effects indicate that if the effects exist, the true effects lie between 0 and small; that’s a small range. In an underpowered study this range would have been large. Finally, as we selected our children with DLD according to strict in- and exclusion criteria, we do not think that our results are driven by the use of an unrepresentative group of children with DLD. This claim is supported by our background measures in which children with DLD show impairments in sentence recall, receptive vocabulary knowledge (clinical markers of the disorder) and reading performance, as compared to their TD peers.

At this point we would also like to reiterate that the theoretical question on the domain-generality of the statistical learning deficit is important (Elleman, Steacy, & Compton, 2019; Arciuli and Conway, 2018). Results of the present study provide preliminary evidence that children with DLD are sensitive to non-linguistic regularities in the visual domain. From this we tentatively conclude that if children with DLD have a statistical learning deficit, this deficit may not be domain-general. Furthermore, in light of the linguistic entrenchment hypothesis as put forward by Siegelman et al. (2018) another possibility is that the statistical learning deficit with linguistic materials observed in children with DLD (for an overview of two meta-analysis supporting this claim see: Lammertink et al., 2017; Obeid et al., 2016) does not necessarily reflects reduced sensitivity to statistical regularities, but that—due to their language deficit—children with DLD have fewer expectations on the underlying structure than typically developing children. Following this line of reasoning, in order to test the hypothesis that children with DLD are less sensitive to statistical regularities, we need to show that it is not their reduced prior knowledge of structure that impacts their statistical learning performance. The challenge is thus to develop tasks that are able to detect learning of statistical regularities in linguistic and non-linguistic materials while controlling for prior knowledge and individual differences of such knowledge.