Spectral moments of the real Ginibre ensemble

Abstract

The moments of the real eigenvalues of real Ginibre matrices are investigated from the viewpoint of explicit formulas, differential and difference equations, and large N expansions. These topics are inter-related. For example, a third-order differential equation can be derived for the density of the real eigenvalues, and this can be used to deduce a second-order difference equation for the general complex moments $M_{2p}^\textrm{r}$. The latter are expressed in terms of the ${}_3 F_2$ hypergeometric functions, with a simplification to the ${}_2 F_1$ hypergeometric function possible for $p=0$ and $p=1$, allowing for the large N expansion of these moments to be obtained. The large N expansion involves both integer and half-integer powers of 1/N. The three-term recurrence then provides the large N expansion of the full sequence $\{ M_{2p}^\textrm{r} \}_{p=0}^\infty$. Fourth- and third-order linear differential equations are obtained for the moment generating function and for the Stieltjes transform of the real density, respectively, and the properties of the large N expansion of these quantities are determined.

1 Introduction

1.1 Context

The study of moments of the spectral density for random matrix ensembles hold a special place in the development of random matrix theory. One landmark was Wigner’s [30, 31] introduction of what is now referred to as the moment method as a strategy to prove that a large class of symmetric random matrices have the same scaled spectral density $\rho ^\textrm{W}(x):= {2 \over \pi } (1 - x^2) \chi _{|x|<1}$. The functional form $\rho ^\textrm{W}(x)$ is now known as the Wigner semi-circle. An essential point is that the 2p-th even moment $m_{2p}$ of $\rho ^\textrm{W}(x)$ is equal to $2^{-2p} C_p$, where $C_p$ denotes the p-th Catalan number, and moreover, this moment sequence uniquely determines $\rho ^\textrm{W}(x)$. Wigner then used the fact that in the random matrix setting $m_{2p} = \lim _{N \rightarrow \infty } (\sigma ^2/2^2N)^p\mathbb {E} (\textrm{Tr} \, X^{2p})$ as the starting point for the computation of limiting scaled moments of the spectral density (here $\sigma ^2$ is the variance of the off-diagonal entries of X, which are assumed too to have mean zero). Subsequent to Wigner’s work, the method of moments, and its generalisation to cumulants, has been used extensively in questions beyond the spectral density such as for the Gaussian fluctuations of linear statistics and pair counting statistics; see the recent review [29].

Specialise now to complex Hermitian matrices from the Gaussian unitary ensemble, with unit variance of the modulus of the off-diagonal entries so that the joint element distribution is proportional to $e^{-\textrm{Tr} \, X^2/2}$. Another landmark has been in relation to the interpretation of the coefficients in the large N of $M_{2p}^\textrm{GUE}:= \mathbb {E} \, \textrm{Tr} \, X^{2p}$. This expansion is a terminating series in $1/N^2$,

$$\begin{aligned} N^{-p-1} M_{2p}^\textrm{GUE} = \sum _{g=0}^{\lfloor p/2 \rfloor } {\nu _{p,g}^\textrm{GUE} \over N^{2g}}. \end{aligned}$$

(1.1)

The result of Wigner gives that $\nu _{p,0} = C_p$. Using a diagrammatic interpretation of non-zero terms in the computation of $\textrm{Tr} \, X^{2p}$ as implied by Wick’s theorem, it was shown by Brézin et al. [3] that the $\nu _{p,g}$ counts the number of pairings of the sides of a 2p-gon which are dual to a map on a compact orientable Riemann surface of genus g. Equivalently, after the sides are identified in pairs, it is required that a surface of genus g results. The case $g=0$ is referred to as planar and represents the leading order in (1.1).

Motivated by this topological interpretation, Harer and Zagier [22] further investigated the sequences $\{ M_{2p}^\textrm{GUE} \}$ and $\{ \nu _{p,g}^\textrm{GUE} \}$.¹ In particular, they obtained that $\{ M_{2p}^\textrm{GUE} \}$ obeys the three-term recurrence

$$\begin{aligned} (p+1) M_{2p}^\textrm{GUE} = (4p - 2) N M_{2p-2}^\textrm{GUE} + (p-1) (2p-1) (2p - 3) M_{2p-4}^\textrm{GUE} \end{aligned}$$

(1.2)

subject to the initial conditions $M_{0}^\textrm{GUE}= N$, $M_{2}^\textrm{GUE} = N^2$. From this, it was shown that $\{ \nu _{p,g} \}$ obeys the two-variable recurrence

$$\begin{aligned} (p+2) \nu _{p+1,g}^\textrm{GUE} = p(2p+1) (2p-1) \nu _{p-1,g-1}^\textrm{GUE} +2 (2p+1) \nu _{p,g}^\textrm{GUE}, \end{aligned}$$

(1.3)

subject to the initial condition $\nu _{0,0}^\textrm{GUE} = 1$, and boundary conditions $\nu _{p,g}^\textrm{GUE} = 0$ for any of the conditions $k<0, g<0$ or $g > \lfloor p/2 \rfloor$. For instance, the first few values are given by

$$\begin{aligned} \nu _{p,0}^{ \mathrm GUE }&= C_p , \\ \qquad \nu _{p,1}^{ \mathrm GUE }&= C_p \, \frac{(p+1)!}{(p-2)!} \frac{ 1}{12}, \\ \qquad \nu _{p,2}^{ \mathrm GUE }&= C_p \, \frac{(p+1)!}{(p-4)!} \frac{ 5p-2 }{1440}, \end{aligned}$$

see, e.g. [32, Theorem 7].

The focus of our study relating to random matrix spectral moments in the present work is an outgrowth of theory underlying and relating the three-term recurrence (1.2), combined with the results from the recent paper [4] by one of us. The question addressed in [4] is to identify a recurrence relation for the spectral moments of the real eigenvalues of elliptic GinOE matrices. The latter is the ensemble of asymmetric real Gaussian matrices defined by

$$\begin{aligned} \sqrt{1 + \tau \over 2} S_+ + \sqrt{1 - \tau \over 2} S_-, \end{aligned}$$

(1.4)

where $S_{\pm }$ are independent random real symmetric and skew-symmetric GOE matrices, and $0 \le \tau \le 1$ is a parameter. For $\tau = 1$, one sees that elliptic GinOE reduces to GOE. Earlier, the work of Ledoux [24] had found a fifth-order linear recurrence for $\{ M_{2p}^\textrm{GOE} \}$. Existing literature due to Goulden and Jackson [20], extending the work of Harer and Zagier, has given an interpretation of the $M_{2p}^\textrm{GOE}$ in terms of pairings which lead to both nonoriented and orientable surfaces. The analogue of (1.1) is now

$$\begin{aligned} N^{-p-1} M_{2p}^\textrm{GOE} = \sum _{l=0}^{p} {\nu _{p,l}^\textrm{GOE} \over N^{l}}, \end{aligned}$$

(1.5)

which in particular involves both odd and even powers of 1/N. In keeping with the universality of the Wigner semi-circle law, one again has for the leading contribution $\nu _{p,0}^\textrm{GOE} = C_p$.

The other extreme of (1.4) is $\tau = 0$, when each entry is identically distributed as an independent standard real Gaussian, this giving rise to a random matrix from GinOE. See [5, 6] for recent reviews on the Ginibre ensembles. Here, there was no previous literature on the moment sequence of the real eigenvalues. The $\tau = 0$ limiting case of the in general 11-term linear recurrence found in [4] for the moments of the density of real eigenvalues was found to reduce to just a three-term recurrence

$$\begin{aligned} 2 (2p+1) M_{2p}^\textrm{r, GinOE}= & {} (2p-1) (6p+4N - 5) M_{2p-2}^\textrm{r, GinOE}\nonumber \\{} & {} \quad - (2p-3) (2p+N - 4) (2p+2N - 3) M_{2p-4}^\textrm{r, GinOE}.\qquad \end{aligned}$$

(1.6)

Motivated by the relative simplicity of (1.6), and its similarity with the GUE moment recurrence (1.2), in this work, we will carry out a study of the moments $\{ M_{2p}^\textrm{r, GinOE} \}$ as a stand-alone sequence, not viewed as a limit of moments for the real eigenvalues of elliptic GinOE. In the case of the recurrence (1.2), it has been known since the work of Haagerup and Thorbjørnsen [21] that there is a tie in with certain higher-order differential equation and also with certain special function functions, in particular hypergeometric polynomials. In fact such structures have been shown to also be features of the spectral moments in a broad range of settings [2, 8, 9, 13, 17,18,19, 24, 25, 27]. However, GinOE is distinct from the ensembles in these earlier studies since only a fluctuating fraction of eigenvalues are real.

1.2 Some known results

Let G be a real Ginibre matrix (GinOE) of size N, defined by the requirement that all entries are independent standard Gaussians. By making use of knowledge of the Schur function average with respect to GinOE matrices, it was shown in [16, 28] that for any positive integer $p \ge 1$,

$$\begin{aligned} \mathbb {E} \Big [ {\text {Tr}}G^{2p} \Big ] = 2^p \frac{ \Gamma (N/2+p) }{ \Gamma (N/2) } = N(N+2)\dots (N+2p-2). \end{aligned}$$

(1.7)

But with the eigenvalues of GinOE matrices being in general both real and complex, this is a result which combines moments relating to the real eigenvalues and moments relating to the complex eigenvalues. Specifically, let $\mathcal {N}_\mathbb {R}$ be the number of real eigenvalues and define

$$\begin{aligned} M_{2p,N}^{ \mathrm r }:= \mathbb {E} \bigg [ \sum _{j=1}^{ \mathcal {N}_\mathbb {R}} x_j^{2p} \bigg ], \qquad M_{2p,N}^{ \mathrm c }:= & {} \mathbb {E} \bigg [ \sum _{j=1}^{ N-\mathcal {N}_\mathbb {R}} z_j^{2p} \bigg ] \nonumber \\= & {} 2 \, \mathbb {E} \bigg [ \sum _{j=1}^{ (N-\mathcal {N}_\mathbb {R})/2 } {\text {Re}}z_j^{2p} \bigg ], \end{aligned}$$

(1.8)

where $x_j$ $(j=1,\dots , \mathcal {N}_\mathbb {R})$ and $z_j$ ($j=1,\dots , N-\mathcal {N}_\mathbb {R}$) are real and complex eigenvalues of G, respectively. Here and in the sequel, we drop the superscript “GinOE”, cf. (1.6). We have used the convention $z_{j+(N-\mathcal {N}_\mathbb {R})/2}=\bar{z}_j.$ Note that by definition,

$$\begin{aligned} M_{2p,N}^{ \mathrm r }+ M_{2p,N}^{ \mathrm c } = \mathbb {E} \Big [ {\text {Tr}}G^{2p} \Big ]. \end{aligned}$$

(1.9)

It has been known for some time [10, 11] that the average densities of real and complex eigenvalues of the GinOE are given by

$$\begin{aligned} \rho _N^{ \mathrm r }(x)&= \frac{1}{\sqrt{2\pi }(N-2)! } \bigg ( \Gamma (N-1,x^2) \nonumber \\&\quad + 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } |x|^{N-1} \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big ) \bigg ), \end{aligned}$$

(1.10)

$$\begin{aligned} \rho _N^{ \mathrm c }(x+iy)&= \sqrt{ \frac{2}{\pi } } |y| {\text {erfc}}(\sqrt{2}|y|) e^{2y^2} \frac{ \Gamma (N-1,x^2+y^2) }{ \Gamma (N-1) }. \end{aligned}$$

(1.11)

Here,

$$ \gamma (a,z):= \int _0^z e^{a-1} e^{-t}\,dt, \qquad \Gamma (a,z):= \int _z^\infty e^{a-1} e^{-t}\,dt =\Gamma (a)- \gamma (a,z) $$

are lower and upper incomplete gamma functions and

$$ {\text {erfc}}(z):= \frac{2}{ \sqrt{\pi } } \int _z^\infty e^{-t^2} \,dt $$

is the complementary error function. The densities relate to the even integer moments of the real and complex eigenvalues by

$$\begin{aligned} M_{2p,N}^{ \mathrm r }= & {} \int _\mathbb {R}x^{2p} \rho _N^{ \mathrm r }(x) \,dx, \nonumber \\ M_{2p,N}^{ \mathrm c }= & {} \int _{\mathbb {R}^2} (x+iy)^{2p} \rho _N^{ \mathrm c }(x+iy) \,dx\,dy. \end{aligned}$$

(1.12)

The pioneering work [11] relating to the real eigenvalues of GinOE has provided both an exact evaluation and an asymptotic expansion, for

$$ M_{0,N}^{ \mathrm r } = N- M_{0,N}^{ \mathrm c } = \mathbb {E} \mathcal {N}_\mathbb {R}. $$

Thus, from [11, Cor. 5.1], we have the expression in terms of a particular Gauss hypergeometric function

$$\begin{aligned} M_{0,N}^{ \mathrm r } = \frac{1}{2} + \sqrt{ \frac{2}{\pi } } \frac{ \Gamma (N+\frac{1}{2}) }{ (N-1)! } {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{1}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) . \end{aligned}$$

(1.13)

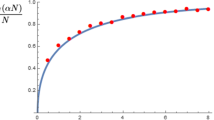
As an application of this formula, it is shown in [11, Cor. 5.2] that for $N \rightarrow \infty$

$$\begin{aligned} M_{0,N}^{ \mathrm r }= & {} \sqrt{2N \over \pi } \bigg ( 1 - {3 \over 8 N} - {3 \over 128 N^2} + {27 \over 1024 N^3} \!+\! {499 \over 32768 N^4} \!+\! \textrm{O} \Big ( {1 \over N^5} \Big ) \bigg )\! +\! {1 \over 2}.\qquad \qquad \end{aligned}$$

(1.14)

As a series, the Gauss hypergeometric function in (1.13) is not terminating. Nonetheless, by considering the recurrence in N implied by this formula, such terminating forms were obtained [11, Cor. 5.3]

$$\begin{aligned} M_{0,N}^{ \mathrm r } = {\left\{ \begin{array}{ll} \displaystyle 1+ \sqrt{2} \sum _{k=1}^{(N-1)/2} \frac{(4k-3)!!}{ (4k-2)!! } &{}N odd , \\ \displaystyle \sqrt{2} \sum _{k=0}^{N/2-1} \frac{(4k-1)!!}{ (4k)!! } &{}N even . \end{array}\right. } \end{aligned}$$

(1.15)

(See also [1, Prop. 2.1].) As a consequence, one reads off that for N even, $M_{0,N}^{ \mathrm r }$ is equal to $\sqrt{2}$ times a rational number, while for N odd, it is equal to 1 plus $\sqrt{2}$ times a rational number. As an aside, we remark that an arithmetic result of this type is also known for the expected number of real eigenvalues in the case of the product of two size N GinOE matrices, where it is shown in [14, §4.2] to be of the form $\pi$ times a rational number for N even, and 1 plus $\pi$ times a rational number for N odd. The special function that appears here is not the Gauss hypergeometric function but rather a particular Meijer G-function, which was simplified to a finite series by Kumar [23].

1.3 New results

Our first new result generalises (1.14).

Theorem 1.1

Let m be any positive integer. Then as $N \rightarrow \infty$, we have

$$\begin{aligned} M_{0,N}^{ \mathrm r } = \sqrt{ \frac{2}{\pi } N } \bigg ( 1+ \sum _{ l=1 }^{m-1} \frac{ a_l }{ N^l } +\textrm{O}( N^{-m} ) \bigg )+\frac{1}{2}, \end{aligned}$$

(1.16)

where

$$\begin{aligned} a_l= - \frac{1}{ \sqrt{\pi } } \frac{ \Gamma (l-\frac{1}{2}) }{ l! } \frac{d^l }{dt^l} \bigg [ \Big ( \frac{e^t-1}{t} \Big )^{-\frac{3}{2}} \frac{ e^{ 2t } }{ e^t+1 } \bigg ]_{t=0}. \end{aligned}$$

(1.17)

Furthermore, as $N \rightarrow \infty$, we have

$$\begin{aligned} N^{-1} M_{2,N}^{ \mathrm r } = \sqrt{ \frac{2}{\pi } N } \bigg ( \frac{1}{3}+ \sum _{l=1}^{m-1} \frac{b_l}{N^l} +\textrm{O}( N^{-m} ) \bigg ) + \frac{1}{2}, \end{aligned}$$

(1.18)

where

$$\begin{aligned} b_l=-\frac{1}{2\sqrt{\pi } } \frac{ \Gamma (l-\frac{3}{2}) }{ l! } \frac{ d^l }{ dt^l } \bigg [ \Big ( \frac{e^t-1}{t} \Big )^{-\frac{5}{2} } \frac{ e^{2t}(e^t-3) }{ (e^t+1)^2 } \bigg ]_{t=0}. \end{aligned}$$

(1.19)

This gives for the first few terms

$$\begin{aligned} N^{-1} M_{2,N}^{ \mathrm r }= & {} \sqrt{ \frac{2}{\pi } N } \bigg ( \frac{1}{3} \!+\! \frac{3}{8N} -\frac{43}{384N^2} \!+\! \frac{29}{1024N^3} \!+\! \frac{1859}{ 98304N^4 } +\textrm{O} \Big (\frac{1}{N^5} \Big ) \bigg ) +\frac{1}{2}.\nonumber \\ \end{aligned}$$

(1.20)

The three-term recurrence (1.6) then gives that for all $p \ge 0$,

$$\begin{aligned} N^{-p} M_{2p,N}^{ \mathrm r } = \sqrt{ \frac{2}{\pi } N } \bigg ( {1 \over 2p + 1} + \sum _{l=1}^{m-1} {b_{l,p} \over N^l} + \textrm{O}(N^{-m}) \bigg ) + {1 \over 2} + \sum _{l=1}^{p-1} {c_{l,p} \over N^l} \qquad \end{aligned}$$

(1.21)

for certain coefficients $b_{l,p}$ and $c_{l,p}.$

We remark that a generalisation of the asymptotic formula (1.16) for the elliptic GinOE can also be found in [7, Prop. 2.2]. The terminating series $\sum _{l=1}^{p-1} c_{l,p} N^{-l}$ for the first $p=2,3,4,5$ are given by

$$\begin{aligned} \frac{1}{N}, \qquad \frac{3}{N} + \frac{4}{N^2}, \qquad \frac{6}{N} + \frac{22}{N^2} + \frac{24}{N^3}, \qquad \frac{10}{N} +\frac{70}{N^2} + \frac{200}{N^3} + \frac{192}{N^4}, \end{aligned}$$

(1.22)

, respectively. These coefficients can also be derived from the moment generating function, see (3.25) and (3.26).

Recall that the generalised hypergeometric function is given by the Gauss series

$$\begin{aligned} {_{r}F_{s}}\left( \begin{array}{c}c_1,\dots ,c_r\\ d_1, \dots ,d_s\end{array}\Bigg |z\right) := \sum _{k=0}^\infty \frac{(c_1)_k \dots (c_r)_k }{ (d_1)_k \dots (d_s)_k } \frac{z^k}{k!}; \end{aligned}$$

(1.23)

see, e.g. [26, Chapter 16], where it is assumed that the parameters are such that the series converges. Using this function with $r=3$ and $s=2$, we next give an explicit formula for the even 2p-th moments of both the real and complex eigenvalue densities. In earlier work, the hypergeometric function ${}_3F_2$ has appeared in the evaluation of spectral moments of certain Hermitian unitary ensembles—see [9, Eqs.(3.9),(3.10)]—although there with extra structure of being terminating and furthermore identifiable in terms of certain orthogonal polynomials in the Askey scheme.

Theorem 1.2

For all positive integers N and p, we have

$$\begin{aligned} \begin{aligned} M_{2p,N}^{ \mathrm r }&= \frac{1}{ \sqrt{2\pi } } \frac{ 2 }{ 2p+1 } \frac{ \Gamma (N+p-\frac{1}{2}) }{ (N-2)! } {_{3}F_{2}}\left( \begin{array}{c}1,-\frac{1}{2}-p,\frac{1}{2}+p\\ \frac{1}{2}, \frac{3}{2}-N-p \end{array}\Bigg |\frac{1}{2}\right) \\&\quad + 2^p \frac{ \Gamma (p+N/2) }{ \Gamma (N/2) } \mathbbm {1}_{ \{ N: odd \} } \end{aligned} \end{aligned}$$

(1.24)

and

$$\begin{aligned} M_{2p,N}^{ \mathrm c }&= -\frac{1}{ \sqrt{2\pi } } \frac{ 2 }{ 2p+1 } \frac{ \Gamma (N+p-\frac{1}{2}) }{ (N-2)! } {_{3}F_{2}}\left( \begin{array}{c}1,-\frac{1}{2}-p,\frac{1}{2}+p\\ \frac{1}{2}, \frac{3}{2}-N-p \end{array}\Bigg |\frac{1}{2}\right) \nonumber \\&\quad + 2^p \frac{ \Gamma (p+N/2) }{ \Gamma (N/2) } \mathbbm {1}_{ \{ N: even \} }. \end{aligned}$$

(1.25)

The definition (1.12) of the even integer moment $M_{2p,N}^\textrm{r}$ can be extended to all complex p with Re$(p) > - 1/2$ by rewriting $M_{2p,N}^\textrm{r}$ as

$$\begin{aligned} M_{2p,N}^\textrm{r} = \int _{\mathbb {R}} |x|^{2p} \rho _N^\textrm{r}(x) \, dx = 2 \int _0^\infty x^{2p} \rho _N^\textrm{r}(x) \, dx. \end{aligned}$$

(1.26)

The evaluation formula (1.24) again remains valid.

Proposition 1.3

Define $M_{2p,N}^\textrm{r}$ for general ${\text {Re}}(p) > - 1/2$ by (1.26). The evaluation formula (1.24) can be continued off the positive integers to remain valid throughout this region of the complex plane.

Remark 1.4

Let $p=q+1/2$ for $q \ge 0$ a non-negative integer. The series (1.23) defining the ${}_3F_2$ function in (1.24) is ill defined as the parameters are such that the indeterminant zero divided by zero occurs. For the series to be well defined, the limit q approaches a non-negative integer must be taken.

It is possible to deduce that the three-term recurrence (1.6) for the moments is valid not just for the even integer moments, but the complex moments too, and to use this to deduce a three-term recurrence specifically for the ${}_3F_2$ function appearing in (1.24). To this end, we make use of a third-order differential equation satisfied by $\rho _N^\textrm{r}(x)$, which is of independent interest.

Proposition 1.5

The density $\rho _N^{ \mathrm r }$ of real eigenvalues given in (1.10) satisfies the differential equation

$$\begin{aligned} \mathcal {A}_N[x] \rho _N^{ \mathrm r } (x)=0, \quad \mathcal {A}_N[x]:= & {} \Big ( x^2 \partial _x^3 + x ( 3 x^2-3N+4) \partial _x^2 \nonumber \\{} & {} + ( 2 x^2-2N+1 ) ( x^2-N+2 ) \partial _x \Big ). \end{aligned}$$

(1.27)

Corollary 1.6

The three-term recurrence (1.6) remains valid for complex values of p such the terms are well defined. Also, as a function of complex p

$$\begin{aligned}{} & {} (2N+2p-1) (2N+2p+1) {_{3}F_{2}}\left( \begin{array}{c}1,-\frac{5}{2}-p,\frac{5}{2}+p\\ \frac{1}{2}, -\frac{1}{2}-N-p \end{array}\Bigg |\frac{1}{2}\right) \nonumber \\{} & {} \quad = (6p+4N+7) (2N+2p-1) {_{3}F_{2}}\left( \begin{array}{c}1,-\frac{3}{2}-p,\frac{3}{2}+p\\ \frac{1}{2}, \frac{1}{2}-N-p \end{array}\Bigg |\frac{1}{2}\right) \nonumber \\{} & {} \quad \quad - 2 (2p+N)(2N+2p+1) {_{3}F_{2}}\left( \begin{array}{c}1,-\frac{1}{2}-p,\frac{1}{2}+p\\ \frac{1}{2}, \frac{3}{2}-N-p \end{array}\Bigg |\frac{1}{2}\right) . \end{aligned}$$

(1.28)

Another consequence of (1.27) is related to the differential equation for the Fourier-Laplace, or equivalently for the (positive integer) moment generating function, as well as for the Stieltjes transform.

Corollary 1.7

Let

$$\begin{aligned} u(t):= \int _\mathbb {R}e^{tx} \rho _N^{ \mathrm r }(x)\,dx. \end{aligned}$$

(1.29)

This satisfies the fourth-order linear differential equation

$$\begin{aligned} D_N[t]\, u(t)=0, \end{aligned}$$

(1.30)

where

$$\begin{aligned} D_N[t]:= & {} 2t \, \partial _t^4 - ( 3 t^2-8 ) \, \partial _t^3 + t(t^2 - 4 N -13 ) \, \partial _t^2 \nonumber \\{} & {} + ( (3 N+2) t^2 -8N-8 )\, \partial _t +(2N^2+N)t. \end{aligned}$$

(1.31)

Furthermore, introduce the Stieltjes transform of the density

$$\begin{aligned} W(t):= \int _\mathbb {R}{ \rho _N^{ \mathrm r }(x) \over t - x} \,dx, \qquad t \notin \mathbb {R}. \end{aligned}$$

(1.32)

With $\mathcal {A}_N[t]$ the differential operator specified in (1.27), but with respect to t rather than x, we have that W(t) satisfies the inhomogeneous differential equation

$$\begin{aligned} \mathcal {A}_N[t] W(t) = (1 + 4 N - 2 t^2) M_{0,N}^\textrm{r} - 6 M_{N,2}^\textrm{r}. \end{aligned}$$

(1.33)

Remark 1.8

In [4, Cor. 1.5], it was found that the moment generating function u(t) satisfies a seventh-order differential equation. Indeed, it can be observed that the differential equation in [4, Cor. 1.5] can be further simplified to

$$\begin{aligned} 0= & {} (t^3\,\partial _t^3-6t^2\,\partial _t^2+15t\,\partial _t-15) \circ \,D_N[t] u (t) \nonumber \\= & {} (t \,\partial _t-a)\circ (t \,\partial _t-b)\circ (t \,\partial _t-c) \circ D_N[t] \, u (t) , \end{aligned}$$

(1.34)

where (a, b, c) is a permutation of (1, 3, 5).

The proofs of the above results are given in Sect. 2. In Sect. 3, we link up the large N asymptotic expansion of the moments Theorem 1.1 with large N asymptotic expansions that can be deduced for the Fourier-Laplace transform u(t) and the Stieltjes transform W(t).

2 Proofs

2.1 Proof of Theorem 1.1

To begin we recall a particular asymptotic formula of ${}_2F_1$, telling us that as $\lambda \rightarrow \infty$ ($\lambda \in \mathbb {R}$),

$$\begin{aligned} {_{2}F_{1}}\left( \begin{array}{c}a,b\\ c+\lambda \end{array}\Bigg |z\right) = \frac{ \Gamma (c+\lambda ) }{ \Gamma (c-b+\lambda ) } \sum _{s=0}^{m-1} q_s(z) \frac{\Gamma (b+s)}{\Gamma (b)} \,\lambda ^{-s-b}+\textrm{O}(\lambda ^{-m-b}); \end{aligned}$$

(2.1)

see [26, Eq. (15.12.3)]. Here $q_0(z)=1$ and $q_s(z)$ when $s=1,2,\ldots$ are defined by the generating function

$$\begin{aligned} \Big ( \frac{e^t-1}{t} \Big )^{b-1} e^{t (1-c) } (1-z+ze^{-t})^{-a} =\sum _{s=0}^\infty q_s(z) \, t^s. \end{aligned}$$

(2.2)

Using this with $a=1,b=-1/2, c=0$ and $\lambda =N$ in (1.13) gives (1.16).

In preparation for deducing the large N asymptotic form of $M_{2,N}^\textrm{r}$, an evaluation formula analogous to (1.13) is required.

Proposition 2.1

We have

$$\begin{aligned} \begin{aligned} M_{2,N}^{ \mathrm r }&= \sqrt{ \frac{2}{\pi } } \frac{\Gamma (N+\frac{3}{2})}{(N-1)!} \bigg ( \frac{1}{2N} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right) + \frac{1}{3} {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) \bigg ) + \frac{N}{2}. \end{aligned} \end{aligned}$$

(2.3)

Proof

We will assume temporarily the validity of the evaluation formula given by the $p=1$ case of $M_{2p,N}^\textrm{r}$ in Theorem 1.2 (this will be proved for all non-negative p in the next section). This gives

$$\begin{aligned} \begin{aligned} M_{2,N}^{ \mathrm r } = \frac{1}{(N-2)!} \sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ \Gamma (k+\frac{3}{2}) \Gamma (N-k+\frac{1}{2}) }{ \Gamma (k+\frac{1}{2}) \, \Gamma (-k+\frac{5}{2}) } + N\, \mathbbm {1}_{ \{ N: odd \} }. \end{aligned} \end{aligned}$$

(2.4)

We note that

$$\begin{aligned}&\sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ \Gamma (k+\frac{3}{2}) \Gamma (N-k+\frac{1}{2}) }{ \Gamma (k+\frac{1}{2}) \, \Gamma (-k+\frac{5}{2}) } = \sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ (k+\frac{1}{2}) \Gamma (N-k+\frac{1}{2}) }{ \Gamma (-k+\frac{5}{2}) } \\&\quad = \sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ (k+\frac{1}{2}) \Gamma (N-k+\frac{1}{2}) }{ \Gamma (-k+\frac{5}{2}) } = \sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ ( (k+\frac{3}{2})-1) \Gamma (N-k+\frac{1}{2}) }{ \Gamma (-k+\frac{5}{2}) } \\&\quad = \frac{\Gamma (N+\tfrac{1}{2})}{ 6\sqrt{\pi } } {_{2}F_{1}}\left( \begin{array}{c} -\frac{3}{2}, -N-\frac{1}{2} \\ -N+\frac{1}{2} \end{array}\Bigg |-1\right) +\frac{ \Gamma (N-\tfrac{1}{2}) }{ 2\sqrt{\pi } } {_{2}F_{1}}\left( \begin{array}{c} -\frac{1}{2}, -N-\frac{1}{2} \\ -N+\frac{3}{2} \end{array}\Bigg |-1\right) \\&\quad = \frac{ \sqrt{\pi } (-1)^N }{ 6 \, \Gamma (-N+\frac{1}{2}) } {_{2}F_{1}}\left( \begin{array}{c} -\frac{3}{2}, -N-\frac{1}{2} \\ -N+\frac{1}{2} \end{array}\Bigg |-1\right) - \frac{ \sqrt{\pi }(-1)^N }{ 2\, \Gamma (-N+\tfrac{3}{2}) } {_{2}F_{1}}\left( \begin{array}{c} -\frac{1}{2}, -N-\frac{1}{2} \\ -N+\frac{3}{2} \end{array}\Bigg |-1\right) . \end{aligned}$$

Recall the linear transformation [26, Eq. (15.8.5)]

$$\begin{aligned}{} & {} \frac{ \sin (\pi ( c-a-b ) ) }{ \pi \,\Gamma (c) } {_{2}F_{1}}\left( \begin{array}{c}a,b\\ c\end{array}\Bigg |z\right) \nonumber \\ {}{} & {} \quad = \frac{ z^{-a} }{ \Gamma (c-a)\Gamma (c-b) \Gamma (a+b-c+1) }{_{2}F_{1}}\left( \begin{array}{c}a,a-c+1\\ a+b-c+1\end{array}\Bigg |1- \frac{1}{z} \right) \nonumber \\{} & {} \quad \quad - \frac{(1-z)^{ c-a-b }z^{a-c} }{ \Gamma (a)\Gamma (b) \Gamma ( c-a-b+1) } {_{2}F_{1}}\left( \begin{array}{c}c-a,1-a\\ c-a-b+1\end{array}\Bigg |1-\frac{1}{z}\right) . \end{aligned}$$

(2.5)

Here, let us mention that the regularised hypergeometric function ${}_2 {\textbf {F}}_1$ in [26, Eq. (15.8.5)] is given by

$$ {}_2 {\textbf {F}}_1 (a,b;c;z)= \frac{1}{\Gamma (c)} {}_2 F_1(a,b;c;z). $$

Using (2.5) with $a=-N-1/2, b=-3/2,c=-N+1/2$, we have

$$\begin{aligned}&\frac{ 1 }{ \pi \Gamma (-N+\frac{1}{2}) } {_{2}F_{1}}\left( \begin{array}{c} -N-\frac{1}{2} , -\frac{3}{2} \\ -N+\frac{1}{2} \end{array}\Bigg |-1\right) \\&\quad = \frac{ 2^{ 5/2 } }{ \Gamma (-N-\frac{1}{2})\Gamma (-\frac{3}{2}) \Gamma ( \frac{7}{2}) } {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) \\&\quad = -\frac{(-1)^{N} 2^{ 5/2 } \Gamma (N+\frac{3}{2}) }{ \pi \Gamma (-\frac{3}{2}) \Gamma ( \frac{7}{2}) } {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) \\&\quad = -\frac{(-1)^{N} 2^{ 7/2 } \Gamma (N+\frac{3}{2}) }{ 5 \pi ^2 } {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) , \end{aligned}$$

which leads to

$$ \frac{ \sqrt{\pi } (-1)^N }{ 6 \, \Gamma (-N+\frac{1}{2}) } {_{2}F_{1}}\left( \begin{array}{c} -N-\frac{1}{2}, -\frac{3}{2} \\ -N+\frac{1}{2} \end{array}\Bigg |-1\right) = - \frac{4}{15}\sqrt{ \frac{2}{\pi } } \Gamma (N+\tfrac{3}{2}) {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) . $$

Here, we have used $1/\Gamma (-N+2)=0$, the reflection formula of Gamma function

$$\begin{aligned} \Gamma (z)\Gamma (1-z)=\pi /\sin (\pi z) \end{aligned}$$

(2.6)

and

$$ \Gamma (-\tfrac{3}{2})= \frac{4\sqrt{\pi }}{3}, \qquad \Gamma ( \tfrac{7}{2} )= \frac{15 \sqrt{\pi }}{8} $$

in each identity. Similarly, we have

$$\begin{aligned} \frac{ \sqrt{\pi }(-1)^N }{ 2\, \Gamma (-N+\tfrac{3}{2}) } {_{2}F_{1}}\left( \begin{array}{c} -N-\frac{1}{2},-\frac{1}{2} \\ -N+\frac{3}{2} \end{array}\Bigg |-1\right)&= - \frac{8}{15}\sqrt{ \frac{2}{\pi } } \Gamma (N+\tfrac{3}{2}) {_{2}F_{1}}\left( \begin{array}{c}2,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) . \end{aligned}$$

Furthermore, again using (2.5) after removing the removable singularities, it follows that

$$\begin{aligned}&- \frac{4}{15}\sqrt{ \frac{2}{\pi } } \Gamma (N+\tfrac{3}{2}) {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) = -\frac{1}{ \sqrt{2} } \frac{ \Gamma (N+\tfrac{3}{2}) }{ \Gamma (\frac{7}{2}) } {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) \\&\quad = \sqrt{ \frac{2}{\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{3 (N-1) } {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) + \frac{(-1)^N (N-2)! }{ 8 }{_{2}F_{1}}\left( \begin{array}{c} \frac{5}{2},0 \\ 2-N \end{array}\Bigg |\frac{1}{2}\right) \\&\quad = \sqrt{ \frac{2}{\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{3 (N-1) } {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) + \frac{(-1)^N (N-2)! }{ 8 } \end{aligned}$$

and

$$\begin{aligned}&\frac{8}{15}\sqrt{ \frac{2}{\pi } } \Gamma (N+\tfrac{3}{2}) {_{2}F_{1}}\left( \begin{array}{c}2,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) = \sqrt{2} \frac{ \Gamma (N+\tfrac{3}{2}) }{ \Gamma (\frac{7}{2}) } {_{2}F_{1}}\left( \begin{array}{c}2,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) \\&\quad = \frac{1}{ \sqrt{2\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{N(N-1)} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right) +\frac{ (-1)^N (N-1)!}{2} {_{2}F_{1}}\left( \begin{array}{c}\frac{3}{2},-1\\ 1-N\end{array}\Bigg |\frac{1}{2}\right) \\&\quad = \frac{1}{ \sqrt{2\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{N(N-1)} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right) +\frac{ (-1)^N (4N-1)\, (N-2)!}{8}. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned}&\sqrt{ \frac{2}{\pi } } \frac{4}{15} \frac{\Gamma (N+\tfrac{3}{2}) }{(N-2)!} \bigg ( 2\,{_{2}F_{1}}\left( \begin{array}{c}2,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) - {_{2}F_{1}}\left( \begin{array}{c}1,N+\frac{3}{2}\\ \frac{7}{2} \end{array}\Bigg |2\right) \bigg ) \\&\quad = \frac{1}{ \sqrt{2\pi } } \frac{ \Gamma (N\!+\!\frac{3}{2}) }{N!} {_{2}F_{1}}\left( \begin{array}{c}2,\!-\frac{1}{2}\\ N\!+\!1\end{array}\Bigg |\frac{1}{2}\right) \!+\! \sqrt{ \frac{2}{\pi } } \frac{ \Gamma (N\!+\!\frac{3}{2}) }{3 (N-1)! } {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) \!+\! (-1)^N\frac{N}{2} \\&\quad = \sqrt{ \frac{2}{\pi } } \frac{\Gamma (N+\frac{3}{2})}{(N-1)!} \bigg ( \frac{1}{2N} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right) + \frac{1}{3} {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) \bigg ) + (-1)^N\frac{N}{2}, \end{aligned}$$

which completes the proof. $\square$

Focusing now on (2.3), we note from (2.1) with $a=2,b=-1/2, c=1$ that

$$\begin{aligned} \frac{1}{ \sqrt{2\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{N!} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right)&\sim N\sqrt{ \frac{2}{\pi } N } \sum _{s=1}^{m-1} \frac{\alpha _{s-1}}{2} \frac{ \Gamma (-3/2+s) }{ \Gamma (-1/2) } N^{-s}, \end{aligned}$$

where

$$\begin{aligned} 4\Big ( \frac{e^t-1}{t} \Big )^{-3/2} (1+e^{-t})^{-2} =\sum _{s=0}^\infty \alpha _s\, t^s. \end{aligned}$$

(2.7)

Also, using (2.1) with $a=1,b=-3/2,c=0$, we have

$$\begin{aligned} \sqrt{ \frac{2}{\pi } } \frac{ \Gamma (N+\frac{3}{2}) }{3 (N-1)! } {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) \sim N \sqrt{ \frac{2}{\pi } N } \sum _{s=0}^{m-1} \frac{\beta _s}{3} \frac{ \Gamma (-3/2+s) }{ \Gamma (-3/2) } N^{-s} \end{aligned}$$

where

$$\begin{aligned} 2\Big ( \frac{e^t-1}{t} \Big )^{-5/2} e^{t } (1+e^{-t})^{-1} =\sum _{s=0}^\infty \beta _s \, t^s. \end{aligned}$$

(2.8)

Therefore, we have shown that

$$\begin{aligned}&\sqrt{ \frac{2}{\pi } } \frac{\Gamma (N+\frac{3}{2})}{(N-1)!} \bigg ( \frac{1}{2N} {_{2}F_{1}}\left( \begin{array}{c}2,-\frac{1}{2}\\ N+1\end{array}\Bigg |\frac{1}{2}\right) + \frac{1}{3} {_{2}F_{1}}\left( \begin{array}{c}1,-\frac{3}{2}\\ N\end{array}\Bigg |\frac{1}{2}\right) \bigg ) \\&\quad \sim N \sqrt{ \frac{2}{\pi } N } \bigg ( \frac{\beta _0}{3}+ \sum _{s=1}^{m-1} \frac{ \beta _s-\alpha _{s-1} }{ 3 } \frac{ \Gamma (-3/2+s) }{ \Gamma (-3/2) } N^{-s} \bigg ). \end{aligned}$$

Substituting in (2.3) the expansion (1.18) follows. $\square$

2.2 Proof of Theorem 1.2

In relation to Theorem 1.2, note that the spectral moments (1.25) of complex eigenvalues follow from (1.7), (1.9) and their real counterparts (1.24). Thus, it suffices to show (1.24). The more general setting of Proposition 1.3 we will be assumed requires only that $\textrm{Re} \, p > -1/2$.

By using [11, Cor. 4.1], we have

$$\begin{aligned} \sum _{ N=1 }^\infty \rho _N^{ \mathrm r }(x) z^N = \mathcal {F}(z,x), \end{aligned}$$

(2.9)

where

$$\begin{aligned} \mathcal {F}(z,x):= & {} \frac{z }{ \sqrt{2\pi } } \bigg ( e^{ -\frac{x^2}{2} } +\frac{z}{1-z} e^{ (z-1) x^2 } \bigg ) + \frac{ z^2 |x| }{ 2 } e^{ \frac{(z^2-1)x^2}{2} } \bigg ( {\text {erf}}\Big ( \frac{ z |x| }{ \sqrt{2} } \Big ) \nonumber \\{} & {} \quad + {\text {erf}}\Big ( \frac{ (1-z) |x| }{ \sqrt{2} } \Big ) \bigg ). \end{aligned}$$

(2.10)

It then follows that

$$\begin{aligned} \sum _{ N=0 }^\infty M_{2p,N}^{ \mathrm r } \, z^N = \int _\mathbb {R}|x|^{2p} \mathcal {F}(z,x)\,dx. \end{aligned}$$

(2.11)

Since

$$\begin{aligned} \int _\mathbb {R}|x|^{2p} e^{-\frac{x^2}{2} }\,dx= & {} 2^{ p+\frac{1}{2} } \, \Gamma \Big (p+\frac{1}{2} \Big ), \qquad \\ \int _\mathbb {R}|x|^{2p} e^{ (z-1)x^2 }\,dx= & {} (1-z)^{ -p-\frac{1}{2} } \Gamma \Big (p+\frac{1}{2} \Big ), \end{aligned}$$

where in the second integral it is assumed $|z|<1$, we have

$$\begin{aligned}&\frac{z }{ \sqrt{2\pi } } \int _\mathbb {R}|x|^{2p} \bigg ( e^{ -\frac{x^2}{2} } +\frac{z}{1-z} e^{ (z-1) x^2 } \bigg )\,dx\nonumber \\&\quad = \frac{z }{ \sqrt{2\pi } } \bigg ( 2^{ p+\frac{1}{2} } + \frac{z}{(1-z)^{ p+\frac{3}{2} }} \bigg ) \Gamma \Big (p+\frac{1}{2} \Big ). \end{aligned}$$

(2.12)

On the other hand, by using the expansion [26, Eq. (7.6.2)]

$$\begin{aligned} {\text {erf}}(z) = \frac{2}{ \sqrt{\pi } } e^{-z^2} \sum _{k=0}^\infty \frac{ 2^k z^{2k+1} }{ (2k+1)!! }, \end{aligned}$$

(2.13)

we have

$$\begin{aligned} \begin{aligned}&\int _\mathbb {R}|x|^{2p} \frac{ z^2 |x| }{ 2 } e^{ \frac{(z^2-1)x^2}{2} } \bigg ( {\text {erf}}\Big ( \frac{ z |x| }{ \sqrt{2} } \Big ) + {\text {erf}}\Big ( \frac{ (1-z) |x| }{ \sqrt{2} } \Big ) \bigg ) \,dx \\&\qquad = \frac{z^2}{2} \sqrt{ \frac{2}{\pi } } \sum _{k=0}^\infty \int _\mathbb {R}\frac{ |x|^{2p+2k+2} }{ (2k+1)!! } \bigg ( z^{2k+1} e^{ -\frac{x^2}{2} } +(1-z)^{2k+1} e^{ (z-1)x^2 } \bigg ) \,dx \\&\qquad = \frac{z^2}{2} \sqrt{ \frac{2}{\pi } } \sum _{k=0}^\infty \frac{1}{(2k+1)!!} \bigg ( z^{2k+1} 2^{ p+k+\frac{3}{2} } + (1-z)^{ k -p-\frac{1}{2} } \bigg ) \Gamma \Big ( p+k+\frac{3}{2} \Big ). \end{aligned} \end{aligned}$$

(2.14)

Combining the above, we have

$$\begin{aligned} \int _\mathbb {R}|x|^{2p} \mathcal {F}(z,x)\,dx&= \frac{z }{ \sqrt{2\pi } } \bigg ( 2^{ p+\frac{1}{2} } + \frac{z}{(1-z)^{ p+\frac{3}{2} }} \bigg ) \Gamma \Big (p+\frac{1}{2} \Big ) \\&\quad + \frac{z^2}{ \sqrt{2\pi } } \sum _{k=0}^\infty \frac{1}{(2k+1)!!} \bigg ( z^{2k+1} 2^{ p+k+\frac{3}{2} }+ (1-z)^{ k -p-\frac{1}{2} } \bigg ) \\&\quad \Gamma \Big ( p+k+\frac{3}{2} \Big ) , \end{aligned}$$

which can be written as

$$\begin{aligned} \int _\mathbb {R}|x|^{2p} \mathcal {F}(z,x)\,dx= & {} \frac{z^2}{ \sqrt{2\pi } } \sum _{k=0}^\infty \frac{1}{(2k-1)!!} \bigg ( z^{2k-1} 2^{ p+k+\frac{1}{2} }+ (1-z)^{ k -p-\frac{3}{2} } \bigg ) \nonumber \\{} & {} \quad \Gamma \Big ( p+k+\frac{1}{2} \Big ). \end{aligned}$$

(2.15)

By using

$$\begin{aligned} (1-z)^{k-p-\frac{3}{2}} = \sum _{l=0}^\infty \left( {\begin{array}{c}k-p-3/2\\ l\end{array}}\right) (-z)^{l} = \sum _{l=0}^\infty \frac{ \Gamma (k-p-\frac{1}{2}) }{ l! \, \Gamma (k-p-l-\frac{1}{2}) } (-z)^{l}, \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned} \int _\mathbb {R}|x|^{2p} \mathcal {F}(z,x)\,dx&= \frac{1}{\sqrt{2\pi }} \sum _{k=0}^\infty \frac{ \Gamma (k+p+\frac{1}{2}) 2^{p+k+\frac{1}{2}} }{ (2k-1)!! } z^{2k+1} \\&\quad + \frac{1}{\sqrt{2\pi }} \sum _{N=0}^\infty \bigg ( \sum _{k=0}^\infty \frac{ (-1)^{N} \Gamma (k+p+\frac{1}{2}) \Gamma (k-p-\frac{1}{2}) }{(2k-1)!!\,(N-2)!\, \Gamma (k-p-N+\frac{3}{2})} \bigg ) z^{N}. \end{aligned} \end{aligned}$$

(2.16)

This gives rise to

$$\begin{aligned} M_{2p,N}^{ \mathrm r }= & {} \frac{1}{\sqrt{2\pi }} \frac{(-1)^N}{(N-2)!} \sum _{k=0}^\infty \frac{ \Gamma (k+p+\frac{1}{2}) \Gamma (k-p-\frac{1}{2}) }{(2k-1)!! \, \Gamma (k-p-N+\frac{3}{2})} \nonumber \\{} & {} +\frac{1}{\sqrt{2\pi }} \frac{ \Gamma (p+N/2) 2^{p+N/2} }{ (N-2)!! } \mathbbm {1}_{ \{ N: odd \} } \nonumber \\= & {} \frac{1}{(N-2)!} \sum _{k=0}^\infty \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ \Gamma (k+p+\frac{1}{2}) \Gamma (N+p-k-\frac{1}{2}) }{ \Gamma (k+\frac{1}{2}) \, \Gamma (p-k+\frac{3}{2}) } \nonumber \\{} & {} + 2^p \frac{ \Gamma (p+N/2) }{ \Gamma (N/2) } \mathbbm {1}_{ \{ N: odd \} }. \end{aligned}$$

(2.17)

Note here that

$$\begin{aligned} \frac{1}{\sqrt{2\pi }} \frac{ \Gamma (p+N/2) 2^{p+N/2} }{ (N-2)!! }&= \frac{ \Gamma (p+N/2) 2^{p} }{ \Gamma (N/2) } \end{aligned}$$

and that

$$\begin{aligned} \frac{1}{\sqrt{2\pi }} \frac{ \Gamma (k+p+\frac{1}{2}) \Gamma (k-p-\frac{1}{2}) }{(2k-1)!! \, \Gamma (k-p-N+\frac{3}{2})}&= \frac{1}{ 2^{k+\frac{1}{2}} } \frac{ \Gamma (k+p+\frac{1}{2}) \Gamma (k-p-\frac{1}{2}) }{ \Gamma (k+\frac{1}{2}) \, \Gamma (k-p-N+\frac{3}{2})} \\&= \frac{ (-1)^{N} }{ 2^{k+\frac{1}{2}} } \frac{ \Gamma (k+p+\frac{1}{2}) \Gamma (N+p-k-\frac{1}{2}) }{ \Gamma (k+\frac{1}{2}) \, \Gamma (p-k+\frac{3}{2}) }, \end{aligned}$$

where to obtain the final line use has been made of (2.6). Now the expression (1.24) follows from the definition (1.23) of the generalised hypergeometric function. $\square$

2.3 Proof of Proposition 1.5

We follow a strategy introduced in [32, Proofs of Thms. 4 and 9] in relation to the differential equations satisfied by the eigenvalue density for the GUE and GOE. Due to the symmetry $x \mapsto -x$, it suffices to consider the case $x>0.$ Let

$$\begin{aligned} f(x) = \frac{d}{dx} \bigg [ \Gamma (N-1,x^2) + 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } x^{N-1} \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big ) \bigg ], \end{aligned}$$

so that according to (1.10), the function f(x) is proportional to $\frac{d}{dx}\rho _N(x)$. In terms of f(x), the differential equation of the proposition reads

$$\begin{aligned} x^2 f''(x) + x ( 3 x^2-3N+4) f'(x) + ( 2 x^2-2N+1 ) ( x^2-N+2 ) f(x)=0.\nonumber \\ \end{aligned}$$

(2.18)

Using

$$\begin{aligned} \frac{d}{dx} \Gamma (N-1,x^2) = -2\, x^{2N-3} e^{-x^2} ,\qquad 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } \frac{d}{dx} \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big ) = x^{N-2} e^{-x^2}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} f(x)&= - x^{2N-3} e^{-x^2} + 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } x^{N-2} \Big ( -x^2+ N-1 \Big ) \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big ) \\&=: - a(x) + (-x^2 + N - 1) b(x). \end{aligned} \end{aligned}$$

(2.19)

Similarly, it follows that

$$\begin{aligned} f'(x)= & {} x^{2N-3} \Big ( x -\frac{ N-2 }{ x } \Big ) e^{-x^2}\nonumber \\{} & {} + 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } x^{N-2} \Big ( x^{3}-(2N-1)x+\frac{(N-1)(N-2)}{x} \Big ) \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big ) \nonumber \\= & {} \Big ( x -\frac{ N-2 }{ x } \Big ) a(x) + \Big ( x^{3}-(2N-1)x+\frac{(N-1)(N-2)}{x}\Big ) b(x), \end{aligned}$$

(2.20)

and

$$\begin{aligned} f''(x)= & {} x^{2N-3} \Big ( -x^{2} +(2N-5) -\frac{(N-2)(N-3)}{x^2} \Big ) e^{-x^2}\nonumber \\{} & {} + 2^{(N-3)/2} e^{ -\frac{x^2 }{2} } x^{N-2} \Big ( -x^{4}+3N\,x^{2}-3(N-1)^2 \nonumber \\{} & {} +\frac{(N-1) (N-2)(N-3)}{x^2} \Big ) \gamma \Big ( \frac{N-1}{2}, \frac{x^2}{2} \Big )\nonumber \\= & {} \Big ( -x^{2} +(2N-5) -\frac{(N-2)(N-3)}{x^2} \Big ) a(x)\nonumber \\{} & {} + \Big ( -x^{4}+3N\,x^{2}-3(N-1)^2 +\frac{(N-1) (N-2)(N-3)}{x^2}\Big ) b(x).\nonumber \\ \end{aligned}$$

(2.21)

Combining all of the above, the desired differential equation (2.18) follows. The intermediate working is best carried out using computer algebra for efficiency and accuracy. $\square$

We mention that at the beginning, the way to derive the exact form of the differential equation (2.18) is to use (2.19) and (2.20) regarded as a linear system to solve for a(x), b(x) in terms of f(x) and $f'(x)$. With this done, substituting in (2.21) gives (2.18).

2.4 Proof of Corollary 1.6

To deduce the three-term recurrence (1.6) with p in general complex, we multiply the differential equation by $x^p$ and integrate over $x \in (0,\infty )$. Carrying out the integration using integration by parts gives (1.6), provided ${\text {Re}}(p)$ is large enough so that all terms requiring evaluation at $x=0$ vanish. Analytic continuation removes the need for such a restriction.

In relation to the three-term recurrence for the ${}_3F_2$ function (1.28), we notice by direct computations that

$$\begin{aligned} 2(2p+5) 2^{p+2}\frac{ \Gamma (p+2+N/2) }{ \Gamma (N/2) }&= (2p+3) (6p+4N+7) 2^{p+1} \frac{ \Gamma (p+1+N/2) }{ \Gamma (N/2) }\\&\quad - (2p+1) (2p+N)(2p+2N+1) 2^{p} \frac{ \Gamma (p+N/2) }{ \Gamma (N/2) }. \end{aligned}$$

Therefore by (1.24), one can observe that the recursion formula (1.6) implies (1.28). $\square$

2.5 Proof of Corollary 1.7

Note that

$$\begin{aligned} \frac{d^k}{dt^k}u(t) = \int _\mathbb {R}e^{tx} x^k \rho _N^{ \mathrm r }(x)\,dx. \end{aligned}$$

Then the differential equation (1.30) follows from Proposition 1.3, after multiplying by $e^{tx}$ and integrating over $x \in \mathbb {R}$ using integrating by parts. For the latter, we note

$$\begin{aligned}&\frac{d}{dx} \Big [ ( 2 x^2-2N+1 ) ( x^2-N+2 ) e^{tx} \Big ] -\frac{d^2}{dx^2} \Big [ x(3x^2-3N+4) e^{tx} \Big ] + \frac{d^3}{dx^3}\Big [ x^2e^{tx} \Big ] \\&\quad = \Big ( 2 t x^4 - ( 3 t^2-8 ) x^3 + t(t^2 - 4 N -13 ) x^2 \\&\quad \quad + ( (3 N+2) t^2 -8N-8 ) x + (2N^2+N)t \Big ) e^{tx}. \end{aligned}$$

In relation to the Stieltjes transform, we first separate out the coefficients of $\partial _x^2$ and $\partial _x$ in $\mathcal {A}_N[x]$ so that the differential equation (1.27) reads

$$ \Big ( x^2 \partial _x^3 + R(x) \partial _x^2 + S(x) \partial _x \big ) \rho _N^\textrm{r}(x) = 0, $$

with

$$ R(x) = x (3 x^2 - 3N + 4), \qquad S(x) = (2 x^2 - 2N + 1) (x^2 - N + 2). $$

Next we manipulate this equation so that it takes the form

$$\begin{aligned}{} & {} \Big ( t^2 \partial _x^3 + R(t) \partial _x^2 + S(t) \partial _x \Big ) \rho _N^\textrm{r}(x)\\{} & {} = \Big ( (t^2 - x^2) \partial _x^3 + (R(t) - R(x)) \partial _x^2 + (S(t) - S(x)) \partial _x \Big ) \rho _N^\textrm{r}(x). \end{aligned}$$

Multiplying through by $1/(t-x)$ and integrating over $x \in \mathbb {R}$, the LHS is readily identified as $\mathcal {A}_N[t]$ after integration by parts. On the RHS, the term $1/(t-x)$ can be cancelled with factors in the coefficients, which then reduce to polynomials symmetric in t and x. Integration by parts requires that these polynomials be differentiated with respect to x a suitable number of times, with the result giving the RHS of (1.33). $\square$

3 Links between large N expansions

3.1 Asymptotic expansion of the moment generating function

Let us define the rescaled moment generating function

$$\begin{aligned} \widetilde{u}(t):= \frac{1}{\sqrt{N}} u \Big (\frac{t}{\sqrt{N}}\Big ) = \int _\mathbb {R}e^{tx} \rho _N^{ \mathrm r }( \sqrt{N} x) \,dx. \end{aligned}$$

(3.1)

Then (1.30) gives rise to

$$\begin{aligned} \bigg ( \mathcal {D}_0[t] + \frac{\mathcal {D}_1[t]}{N}+ \frac{\mathcal {D}_2[t]}{N^2} \bigg ) \widetilde{u}(t)=0, \end{aligned}$$

(3.2)

where

$$\begin{aligned} \mathcal {D}_0[t]&:= 2 t \, \partial _t^4 + 8 \, \partial _t^3 -4t \, \partial _t^2 -8 \, \partial _t + 2t \end{aligned}$$

(3.3)

$$\begin{aligned} \mathcal {D}_1[t]&:= -3t^2 \, \partial _t^3 -13 t \, \partial _t^2 +( 3t^2-8 ) \, \partial _t +t, \end{aligned}$$

(3.4)

$$\begin{aligned} \mathcal {D}_2[t]&:= t^3 \, \partial _t^2+2t^2 \, \partial _t . \end{aligned}$$

(3.5)

As is consistent with the expansion of the even integer moments Theorem 1.1, introduce the large N expansion

$$\begin{aligned} \widetilde{u}(t)= \sum _{k=0}^\infty \bigg ( \frac{ \widetilde{u}_{ (k) }(t) }{ N^k } + \frac{ \widetilde{u}_{ (k+1/2) }(t) }{ N^{k+1/2} } \bigg ). \end{aligned}$$

(3.6)

Use the expansion coefficients therein to introduce a sequence of smoothed densities $\{ r_{(k)}(x), r_{(k+1/2)}(x) \}$ by the requirement that

$$\begin{aligned} \widetilde{u}_{ (k) }(t) = \int _{\mathbb {R}} e^{tx} r_{(k)}(x) \, dx, \qquad \widetilde{u}_{ (k+1/2) }(t) = \int _{\mathbb {R}} e^{tx} r_{(k+1/2)}(x) \, dx. \end{aligned}$$

(3.7)

Note that then, in a formal sense, and with the LHS interpreted as being always begin integrated against a smooth function, we then have

$$\begin{aligned} \rho _N^{ \mathrm r }(\sqrt{N}x) = \sum _{k=0}^\infty \bigg ( \frac{ {r}_{ (k) }(x) }{ N^k } + \frac{ {r}_{ (k+1/2) }(x) }{ N^{k+1/2} } \bigg ). \end{aligned}$$

(3.8)

We know from [6, displayed equation below Eqs. (3.5) and (3.8)] that

$$\begin{aligned} r_{(0)}(x) = \frac{1}{\sqrt{2\pi }} \, \mathbbm {1}_{(-1,1)}(x), \qquad r_{(1/2)}(x) = \frac{1}{4}\Big ( \delta (x-1)+\delta (x+1) \Big ), \end{aligned}$$

(3.9)

and so

$$\begin{aligned} \widetilde{u}_{(0)}(t):= \sqrt{ \frac{2}{\pi } } \frac{ \sinh (t) }{t}, \qquad \widetilde{u}_{(1/2)}(t):= \frac{\cosh (t)}{2}. \end{aligned}$$

(3.10)

Note also that by (1.16) and (1.18), for $k \ge 1$,

$$\begin{aligned} \widetilde{u}_{(k)}(0)= \sqrt{ \frac{2}{\pi } } \, a_k, \qquad \widetilde{u}''_{(k)}(0)= \sqrt{ \frac{2}{\pi } } \, b_k \end{aligned}$$

(3.11)

and

$$\begin{aligned} \widetilde{u}_{(k+1/2)}(0)= \widetilde{u}''_{(k+1/2)}(0)= 0. \end{aligned}$$

(3.12)

Scaling (3.2), $t \mapsto t/\sqrt{N}$, and substituting (3.6) shows

$$\begin{aligned} \mathcal {D}_0[t]\, \widetilde{u}_{ (k) }(t) + \mathcal {D}_1[t]\, \widetilde{u}_{ (k-1) }(t) + \mathcal {D}_2[t]\, \widetilde{u}_{ (k-2) }(t) =0 \end{aligned}$$

(3.13)

and

$$\begin{aligned} \mathcal {D}_0[t]\, \widetilde{u}_{ (k+1/2) }(t) + \mathcal {D}_1[t]\, \widetilde{u}_{ (k-1/2) }(t) + \mathcal {D}_2[t]\, \widetilde{u}_{ (k-3/2) }(t) =0, \end{aligned}$$

(3.14)

with the convention that $\widetilde{u}_j \equiv 0$ if $j <0.$ One observes that the differential operator $\mathcal {D}_0[t]$ has the factorisations

$$\begin{aligned} \mathcal {D}_0[t] =2 ( t \, \partial _t^2+4\, \partial _t -t ) \circ (\partial _t^2-1)=2 ( \partial _t^2-1 ) \circ ( t\,\partial _t^2+2\, \partial _t-t ). \end{aligned}$$

(3.15)

From the explicit functional forms of $\widetilde{u}_{(0)}(t)$ and $\widetilde{u}_{(1/2)}(t)$ (3.10), it is observed that both are annihilated by $\mathcal {D}_0[t]$. Indeed, the general even solution to $\mathcal {D}_0[t] f(t)=0$ is of the form

$$ f(t) = c_0 \cosh (t) + c_1 \frac{\sinh (t)}{t}, \qquad c_0,c_1 \in \mathbb {R}. $$

By taking $k=1$ in (3.13),

$$\begin{aligned} \mathcal {D}_0[t] \,\widetilde{u}_1(t)+ \mathcal {D}_1[t] \,\widetilde{u}_0(t) = \mathcal {D}_0[t] \,\widetilde{u}_1(t) - 6 \sqrt{ \frac{2}{\pi } } \sinh (t) =0. \end{aligned}$$

By solving this differential equation with the initial condition (3.11), we have

$$\begin{aligned} \widetilde{u}_{(1)}(t) = \sqrt{ \frac{2}{\pi } } \frac{3}{8} \bigg ( t \sinh (t) - \cosh (t) \bigg ) . \end{aligned}$$

(3.16)

Similarly, it follows that

$$\begin{aligned} \widetilde{u}_{(2)}(t)&= \sqrt{ \frac{2}{\pi } } \frac{1}{384} \bigg ( (23t^2+9)\,t\, \sinh (t)-(26t^2+9) \cosh (t) \bigg ), \end{aligned}$$

(3.17)

$$\begin{aligned} \widetilde{u}_{(3)}(t)&= \sqrt{ \frac{2}{\pi } } \frac{1}{15360} \bigg ( ( 91 t^4- 285 t^2 -405) \,t\,\sinh (t) -5 ( t^4- 84 t^2 -81) \cosh (t) \bigg ). \end{aligned}$$

(3.18)

In general, one can observe that $\widetilde{u}_k$ is of the form

$$\begin{aligned} \widetilde{u}_{(k)}(t)= \sqrt{ \frac{2}{\pi } } \bigg ( P_{k,1}(t)\,t\, \sinh (t) + P_{k,2}(t) \,\cosh (t) \bigg ), \end{aligned}$$

(3.19)

where $P_{k,1}$ and $P_{k,2}$ are some even polynomials of degree $k+1.$ The corresponding quantities in the expansion (3.6) are then

$$\begin{aligned} {r}_{(k)}(x)= & {} \frac{1}{ \sqrt{2 \pi } } \bigg ( P_{k,1}(-\partial _x)(-\partial _x) \Big ( \delta (x-1) - \delta (x+1) \Big ) \nonumber \\{} & {} \quad +P_{k,2}(-\partial _x) \Big ( \delta (x-1) + \delta (x+1) \Big ) \bigg ) \end{aligned}$$

(3.20)

as can be checked from (3.7).

Regarding the half-integer coefficients in (3.6), we also have

$$\begin{aligned} \widetilde{u}_{(3/2)}(t)&= \frac{1}{8} \bigg ( t^2\, \cosh (t) -t \, \sinh (t) \bigg ), \end{aligned}$$

(3.21)

$$\begin{aligned} \widetilde{u}_{(5/2)}(t)&= \frac{1}{192} \bigg (3 t^2 (t^2-1) \cosh (t) - t( 2 t^2-3) \sinh (t) \bigg ). \end{aligned}$$

(3.22)

For general k,  we have

$$\begin{aligned} \widetilde{u}_{(k+1/2)}(t)= \widehat{P}_{k,1}(t)\,t\, \cosh (t) + \widehat{P}_{k,2}(t) \,\sinh (t), \end{aligned}$$

(3.23)

where $\widehat{P}_{k,1}$ and $\widehat{P}_{k,2}$ are certain odd polynomials of degree $k+1$, from which it follows

$$\begin{aligned} {r}_{(k+1/2)}(x)= & {} \frac{1}{2} \bigg ( \widehat{P}_{k,1}(-\partial _x)(-\partial _x) \Big ( \delta (x-1) + \delta (x+1) \Big ) \nonumber \\{} & {} \quad +\widehat{P}_{k,2}(-\partial _x) \Big ( \delta (x-1) - \delta (x+1) \Big ) \bigg ); \end{aligned}$$

(3.24)

cf. (3.20). Notice also that

$$\begin{aligned}&\widetilde{u}_{(3/2)}(0)= \widetilde{u}_{(3/2)}''(0)=0, \qquad \widetilde{u}_{(3/2)}''''(0)=1, \qquad \widetilde{u}_{(3/2)}^{(6)}(0)=3, \nonumber \\&\widetilde{u}_{(3/2)}^{(8)}(0)=6, \qquad \widetilde{u}_{(3/2)}^{(10)}(0)=10. \end{aligned}$$

(3.25)

These coincide with the coefficients of the $\textrm{O}(1/N)$ term in (1.22). Along the same lines, we have

$$\begin{aligned}&\widetilde{u}_{(5/2)}(0)= \widetilde{u}_{(5/2)}''(0)= \widetilde{u}_{(5/2)}''''(0)=0, \qquad \widetilde{u}_{(5/2)}^{(6)}(0)=4, \nonumber \\&\widetilde{u}_{(5/2)}^{(8)}(0)=22, \qquad \widetilde{u}_{(5/2)}^{(10)}(0)=70 \end{aligned}$$

(3.26)

which also correspond to the coefficients of the $\textrm{O}(1/N^2)$ term in (1.22). To be consistent with the fact that the final sum in (1.21) terminates, for general k, we must have ${\partial _t^{2j} } \tilde{u}_{(k+1/2)}(t) |_{t=0}=0$ for $j=0,\dots ,k$.

3.2 Asymptotic expansion of the Stieltjes transform

Let us write

$$\begin{aligned} \widetilde{W}(t):= \int _\mathbb {R}\frac{ \rho _N^{ \mathrm r }(\sqrt{N}x) }{ t-x }\,dx= W(\sqrt{N}t) \end{aligned}$$

(3.27)

for the Stieltjes transform of the rescaled density. Then (1.33) can be rewritten as

$$\begin{aligned} \bigg ( \widehat{\mathcal {D}}_0[t] + \frac{\widehat{\mathcal {D}}_1[t]}{N}+ \frac{ \widehat{\mathcal {D}}_2[t]}{N^2} \bigg ) \widetilde{W}(t)= \Big ( 4 - 2 t^2 + \frac{1}{N} \Big ) \frac{ M_{0,N}^\textrm{r} }{ N^{1/2} } - 6 \frac{ M_{N,2}^\textrm{r} }{ N^{3/2} }, \end{aligned}$$

(3.28)

where

$$\begin{aligned}&\widehat{\mathcal {D}}_0[t]:= 2(t^2-1)^2 \partial _t, \end{aligned}$$

(3.29)

$$\begin{aligned}&\widehat{\mathcal {D}}_1[t]:= (t^2-1) ( 3t\,\partial _t^2+5 \,\partial _t ), \end{aligned}$$

(3.30)

$$\begin{aligned}&\widehat{\mathcal {D}}_2[t]:= t^2 \, \partial _t^3+4 t\,\partial _t^2+2 \,\partial _t . \end{aligned}$$

(3.31)

On the other hand, by Theorem 1.1,

$$\begin{aligned}{} & {} \Big ( 4 - 2 t^2 + \frac{1}{N} \Big ) \frac{ M_{0,N}^\textrm{r} }{ N^{1/2} } - 6 \frac{ M_{N,2}^\textrm{r} }{ N^{3/2} } \sim \sqrt{ \frac{2}{\pi } } \bigg ( 2-2t^2 + \sum _{l=1}^{\infty } \frac{ (4-2t^2)a_l+ a_{l-1} -6 b_l }{N^l} \bigg )\nonumber \\{} & {} \quad - \frac{t^2+1}{ N^{1/2} } +\frac{1}{2N^{3/2}}. \end{aligned}$$

(3.32)

Then as before, by recursively solving this system of differential equations with the initial condition $\widetilde{W}(t)=\textrm{O}(1/t)$ as $t \rightarrow \infty$, one can derive the expansion

$$\begin{aligned} \widetilde{W}(t)= \sum _{k=0}^\infty \bigg ( \frac{ \widetilde{W}_{ (k) }(t) }{ N^k } + \frac{ \widetilde{W}_{ (k+1/2) }(t) }{ N^{k+1/2} } \bigg ). \end{aligned}$$

(3.33)

For instance, we have

$$\begin{aligned} \widetilde{W}_{ (0) }(t) = \frac{1}{ \sqrt{2\pi } } \log \Big ( \frac{t+1}{t-1} \Big ), \qquad \widetilde{W}_{ (1/2) }(t) = \frac{t}{2(t^2-1)}, \end{aligned}$$

(3.34)

which are consistent with (3.9), and

$$\begin{aligned} \widetilde{W}_{ (1) }(t) = -\frac{1}{ \sqrt{2\pi } } \frac{3t(t^2-3)}{ 4(t^2-1)^2 }, \qquad \widetilde{W}_{ (3/2) }(t)= \frac{t}{(t^2-1)^3}. \end{aligned}$$

(3.35)

In particular, one reads off that as $t \rightarrow \infty$, $\widetilde{W}_{(1)}(t) \asymp t^{-1}$, whereas $\widetilde{W}_{(3/2)}(t) \asymp t^{-3}$. Generally, it is required that for $t\! \rightarrow \! \infty$, $\widetilde{W}_{(k)}(t) \!\asymp \! t^{-1}$, whereas $\widetilde{W}_{(2k+1)/2}(t)\! \asymp \!{t^{-2k-1}}$, so as to be consistent with (1.21).