Skip to main content
SpringerLink
Log in

The Real Ginibre Ensemble with \(k=O(n)\) Real Eigenvalues

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

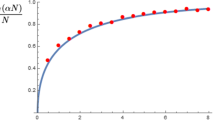
We consider the ensemble of real Ginibre matrices conditioned to have positive fraction \(\alpha >0\) of real eigenvalues. We demonstrate a large deviations principle for the joint eigenvalue density of such matrices and introduce a two phase log-gas whose stationary distribution coincides with the spectral measure of the ensemble. Using these tools we provide an asymptotic expansion for the probability \(p^n_{\alpha n}\) that an \(n\times n\) Ginibre matrix has \(k=\alpha n\) real eigenvalues and we characterize the spectral measures of these matrices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. For the sake of completeness, we recall that the distance between two probability measures \((\mu ,\nu )\) on \(\mathbbm {C}\) is defined as:

    $$\begin{aligned} d_L(\mu ,\nu )=\inf \left\{ \delta >0\,;\,\mu (A)\le \nu (A^\delta ) \text{ and } \nu (A)\le \mu (A^\delta )\quad \forall A\in \mathcal {B}(\mathbb {C})\right\} \end{aligned}$$

    where \(\mathcal {B}(\mathbb {C}\) is the Borel algebra of \(\mathbbm {C}\) and for \(A\in \mathcal {B}(\mathbbm {C})\), \(A^\delta =\{x;d(x,A)\le \delta \}\).

References

  1. Forrester, P.J.: London Mathematical Society Monographs. Princeton University Press, Princeton (2010)

    Google Scholar 

  2. Tao, T.: Topics in Ramdom Matrix Theory. American Mathematical Society, Providence (2012)

    Book  Google Scholar 

  3. Bordenave, C., Chafai, D.: Around the circular law. Probab. Surv. 93, 1–89 (2012)

    MathSciNet  MATH  Google Scholar 

  4. Wigner, E.P.: Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 98(1), 145–147 (1955)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Auffinger, A., Ben Arous, G., Černỳ, J.: Random matrices and complexity of spin glasses. Commun. Pure Appl. Math. 66(2), 165–201 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. May, R.M.: Will a large complex system be stable? Nature 238, 413–414 (1972)

    Article  ADS  Google Scholar 

  7. Wainrib, G., Touboul, J.: Topological and dynamical complexity of random neural networks. Phys. Rev. Lett. 110(11), 118101 (2013)

    Article  ADS  Google Scholar 

  8. del Molino, L.C.G., Pakdaman, K., Touboul, J., Wainrib, G.: Synchronization in random balanced networks. Phys. Rev. E 88(4), 042824 (2013)

    Article  ADS  Google Scholar 

  9. Couillet, R., Debbah, M., et al.: Random Matrix Methods for Wireless Communications. Cambridge University Press, Cambridge (2011)

    Book  MATH  Google Scholar 

  10. Jaeger, H., Haas, H.: Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304(5667), 78–80 (2004)

    Article  ADS  Google Scholar 

  11. Donoho, D.L.: Compressed sensing. IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  12. Lehmann, N., Sommers, H.J.: Eigenvalue statistics of random real matrices. Phys. Rev. Lett. 67, 941–944 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Edelman, A.: The probability that a random real Gaussian matrix has k real Eigenvalues, related distributions, and the circular law. J. Multivar. Anal. 60, 203–232 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  14. Forrester, P.J., Nagao, T.: Eigenvalue statistics of the real Ginibre enesmble. Phys. Rev. Lett. 99, 050603 (2007)

    Article  ADS  Google Scholar 

  15. Sommers, H.J.: Symplectic structure of the real Ginibre ensemble. J. Phys. A 40(29), F671 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Forrester, P.J., Nagao, T.: Skew orthogonal polynomials and the partly symmetric real Ginibre ensemble. J. Phys. A 41(37), 375003 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Forrester, P.J., Mays, A.: A method to calculate correlation functions for \(\beta =1\) random matrices of odd size. J. Phys. A 134(3), 443–462 (2009)

    MathSciNet  MATH  Google Scholar 

  18. Sinclair, C.: Correlation functions for \(\beta =1\) ensembles of matrices of odd size. J. Stat. Phys. 136(1), 17–33 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Sommers, H.J., Wieczorek, W.: General eigenvalue correlations for the real Ginibre ensemble. J. Phys. A 41(40), 405003 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Borodin, A., Sinclair, C.: The Ginibre ensemble of real random matrices and its scaling limits. Commun. Math. Phys. 291(1), 177–224 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Rider, B., Sinclair, C.D., et al.: Extremal laws for the real ginibre ensemble. Ann. Appl. Probab. 24(4), 1621–1651 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tao, T., Vu, V.: Random matrices: universality of ESD and the circular law. Ann. Probab. 38(5), 2023–2065 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Tao, T., Vu, V.: Random matrices: universality of local spectral statistics of non-hermitian matrices (2012). arXiv:1206.1893

  24. Bourgade, P., Erdos, L., Yau, H.: Universality of general \( beta \)-ensembles. Duke Mathematical Journal 163(6), 1127–1190 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Bourgade P., Erdos, L., Yau, H., Yin, J.: Fixed energy universality for generalized Wigner matrices (2014). arXiv:1407.5606

  26. Erdös, L., Yau, H.-T., Yin, J.: Rigidity of eigenvalues of generalized wigner matrices. Adv. Math. 229(3), 1435–1515 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  27. Bourgade, P., Erdös, L., Yau, H.-T.: Bulk universality of general \(\beta \)-ensembles with non-convex potential. J. Math. Phys. 53(9), 095221 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Bourgade, P., Erdös, L., Yau, H.-T.: Edge universality of beta ensembles. Commun. Math. Phys. 332(1), 261–353 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Bourgade, P., Yau, H.-T., Yin, J.: Local circular law for random matrices. Probab. Theory Relat. Fields 159(3–4), 545–595 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Bourgade, P., Yau, H.-T., Yin, J.: The local circular law ii: the edge case. Probab. Theory Relat. Fields 159(3–4), 619–660 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ben Arous, G., Guionnet, A.: Large deviations for Wigner’s law and Voiculescu’s non-commutative entropy. Probab. Theory Relat. Fields 108, 517–542 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  32. Ben Arous, G., Zeitouni, O.: Large Deviations from the circular law. ESAIM: Probab. Stat. 2, 123–134 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  33. Edelman, A., Kostlan, E., Shub, M.: How many Eigenvalues of a random matrix are real? J. Am. Math. Soc. 7, 247–267 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ginibre, J.: Statistical ensembles of complex, quaternion, and real matrices. J. Math. Phys. 6, 440–449 (1965)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. Sommers, H.J., Crisanti, A., Sompolinsky, H.: Spectrum of large random asymmetric matrices. Phys. Rev. Lett. 60, 1895 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  36. Tribe, R., Zaboronski, O.: Pfaffian formulae for one dimensional coalescing and annihilating systems. Electron. J. Probab. 163(76), 2080–2103 (2011)

    MathSciNet  MATH  Google Scholar 

  37. Forrester, P.J.: Diffusion processes and the asymptotic bulk gap probability for the real Ginibre ensemble. arXiv:1306.4106

  38. Beenakker, C.: Random-matrix theory of majorana fermions and topological superconductors (2014). arXiv:1407.2131

  39. Kanzieper, E., Akemann, G.: Statistics of real eigenvalues in Ginibre’s ensemble of random real matrices. Phys. Rev. Lett. 95(23), 230201 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  40. Akemann, G., Kanzieper, E.: Integrable structure of Ginibre’s ensemble of real random matrices and a Pfaffian integration theorem. J. Stat. Phys. 129(5–6), 1159–1231 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Kanzieper, E., Poplavskyi, M., Timm, C., Tribe, R., Zaboronski, O.: What is the probability that a large random matrix has no real eigenvalues? (2015). arXiv:1503.07926

  42. Dyson, F.J.: A Brownian-motion model for the Eigenvalues of a random matrix. J. Math. Phys. 3, 1191–1198 (1962)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  43. Majumdar, S.N., Nadal, C., Scardicchio, A., Vivo, P.: Index distribution of gaussian random matrices. Phys. Rev. Lett. 103(22), 220603 (2009)

    Article  ADS  Google Scholar 

  44. Majumdar, S.N., Vivo, P.: Number of relevant directions in principal component analysis and wishart random matrices. Phys. Rev. Lett. 108(20), 200601 (2012)

    Article  ADS  Google Scholar 

  45. Rogers, L., Shi, Z.: Interacting Brownian particles and the Wigner law. Probab. Theory Relat. Fields 95, 555–570 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  46. Cepa, E., Lepingle, D.: Diffusing particles with electrostatic repulsion. Probab. Theory Relat. Fields 107, 429–449 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  47. Anderson, W., Guionnet, A., Zeitouni, O.: An Introduction to Random Matrices. Cambridge University Press, Cambridge (2009)

    Book  MATH  Google Scholar 

  48. Sandier, E., Serfaty, S.: 1d log gases and the renormalized energy: crystallization at vanishing temperature. Probab. Theory Relat Fields 162, 1–52 (2014)

    MathSciNet  MATH  Google Scholar 

  49. Sandier, E., Serfaty, S.: 2d coulomb gases and the renormalized energy (2012). arXiv:1201.3503

  50. Rougerie, N., Serfaty, S.: Higher dimensional coulomb gases and renormalized energy functionals (2013). arXiv:1307.2805

  51. Allez, R., Touboul, J., Wainrib, G.: Index distribution of the Ginibre ensemble. J. Phys. A 47(4), 042001 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. Braides, A.: Gamma-convergence for Beginners. Oxford University Press, Oxford (2002)

    Book  MATH  Google Scholar 

  53. Armstrong, S.N., Serfaty, S., Zeitouni, O.: Remarks on a constrained optimization problem for the ginibre ensemble. Potential Anal. 41(3), 945–958 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  54. Abrikosov, A.A.: On the magnetic properties of superconductors of the second type. Sov. Phys. JETP 5, 1174–1182 (1957)

    Google Scholar 

  55. Chafaï, D., Gozlan, N., Zitt, P.-A.: First order global asymptotics for confined particles with singular pair repulsion (2013). arXiv:1304.7569

  56. del Molino, L.C.G., Pakdaman, K., Touboul, J.: The heterogeneous gas with singular interaction: generalized circular law and heterogeneous renormalized energy. J. Phys. A 48(4), 045208 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  57. Vivo, P., Majumdar, S.N., Bohigas, O.: Large deviations and random matrices. Acta Phys. Pol. B 38(13), 4139 (2007)

    ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We thank an anonymous referee for his suggestions on the proof of Theorem 1.

Author information

Authors and Affiliations

  1. Institut Jacques Monod, CNRS UMR 7592, Université Paris Diderot, Paris Cité Sorbonne, 750205, Paris, France

    Luis Carlos García del Molino & Khashayar Pakdaman

  2. Mathematical neuroscience Team, CIRB-Collège de France (CNRS UMR 7241, INSERM U1050, UPMC ED 158, MEMOLIFE PSL), 11 place Marcelin Berthelot, 75005, Paris, France

    Luis Carlos García del Molino & Jonathan Touboul

  3. MYCENAE Team, INRIA Paris-Rocquencourt, 11 place Marcelin Berthelot, 75005, Paris, France

    Jonathan Touboul

  4. Département d’Informatique (DATA), Ecole Normale Supérieure, 45 rue d’Ulm, 75005, Paris, France

    Gilles Wainrib

Authors
  1. Luis Carlos García del Molino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Khashayar Pakdaman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jonathan Touboul
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Gilles Wainrib
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luis Carlos García del Molino.

Appendices

Appendix

Monte Carlo Algorithm for the Eigenvalues

An efficient method to approximate numerically the minimizer \(\mu _{\alpha }\) and the probability distribution of the proportion of real eigenvalues is to use the Metropolis–Hastings Monte Carlo algorithm. This method consists in constructing an ergodic Markov chain whose stationary distribution is given by (1). Here, we evolve a n-particles system \(z_t\), but in contrast to the log-gas, the dynamics is now discrete, and the transition probability is based on the pdf (1): a new configuration \(z^*\) is drawn by modifying one of the eigenvalues at random and the Markov chain has a transition towards \(z^*\) if \(Q^n(z^*)>Q^n(z_t)\), and otherwise according to a Bernoulli variable of parameter \(\frac{Q^n(z^*)}{Q^n(z_t)}\).

When conditioning on very rare events, (here for instance, a fixed number of real eigenvalues), cases satisfying the constraints have an extremely low probability of being explored, and more refined methods need to be developed in order to access these probabilities. In the present case, the problem is considerably simplified since we dispose of an explicit form of the distribution of the eigenvalues under our constraint. Indeed, the joint probability distribution of Ginibre matrices of size n constrained on having k real eigenvalues \((\lambda _i\;;\; i=1\ldots k)\) (and therefore \(l=(n-k)/2\) pairs of complex eigenvalues \((z_i, i=1\ldots n-k)\)) is given by:

$$\begin{aligned}&\mathbb {P}\big [\lambda _1\ldots \lambda _k, z_1,\ldots ,z_{n-k}\big ]=\tilde{C}_n \prod _{i>j}\vert \lambda _i-\lambda _j\vert \prod _{i>j} \vert z_i-z_j\vert \prod _{i,j}\vert \lambda _i-z_j\vert \\&\qquad \qquad \qquad \times \left( \prod _{i=1}^k\exp (-\lambda _i^2)\prod _{i=1}^{n-k} \exp (-z_i^2)\text {erfc}(\vert z_i-z_i^*\vert /\sqrt{2})\right) ^{1/2}, \end{aligned}$$

where the coefficient \(C_n\) can be found in [14].

Classical Metropolis–Hastings algorithm with Gaussian transitions preserving the nature of the system therefore allow to access directly the distribution of eigenvalues and the probability p(n, k) of the event considered.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

del Molino, L.C.G., Pakdaman, K., Touboul, J. et al. The Real Ginibre Ensemble with \(k=O(n)\) Real Eigenvalues. J Stat Phys 163, 303–323 (2016). https://doi.org/10.1007/s10955-016-1485-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-016-1485-0

Keywords

Search

Navigation