Financial networks of cryptocurrency prices in time-frequency domains

Abstract

This paper explores financial networks of cryptocurrency prices in both time and frequency domains. We complement the generalized forecast error variance decomposition method based on a large VAR model with network theory to analyze the dynamic network structure and the shock propagation mechanisms across a set of 40 cryptocurrency prices. Results show that the evolving network topology of spillovers in both time and frequency domains helps towards a more comprehensive understanding of the interactions among cryptocurrencies, and that overall spillovers in the cryptocurrency market have significantly increased in the aftermath of COVID-19. Our findings indicate that a significant portion of these spillovers dissipate in the short-run (1–5 days), highlighting the need to consider the frequency persistence of shocks in the network for effective risk management at different target horizons.

1 Introduction

Connectedness is crucial in many fields and kind of real-world networks, such as telecommunication, computer science, transportation, economic, financial and social networks ( see,among others, Lauritzen and Wermuth 1989; Billio et al. 2012; Chinazzi and Fagiolo 2015; Pecora and Spelta 2017; Chen et al. 2021; Giudici et al. 2023; Spelta et al. 2023; Pagnottoni 2023). A highly connected network might offer key benefits, such a high degree of efficiency, and greater resilience; although this, in many contexts such as financial time series, translates into increased risk. Understanding network connectedness is crucial for optimal network design, enhancing the performance of networks, and predicting network behavior.

Network science is a powerful tool in finance for analyzing the stability and resilience of a financial system, as well as for identifying potential risks and contagion effects. The configurations, i.e. topologies, of financial networks are constantly evolving, especially in highly dynamic systems like financial markets, and particularly in nascent markets such as the cryptocurrency one. The study of cryptocurrency interconnectedness is determinant to a better understanding the basic functioning and stability of the cryptocurrency market as a whole. It might shed light on the potential spillover effects of changes in one cryptocurrency price or volatility on others and on the overall market, and the importance of considering interconnections when analyzing the performance of individual securities has become indisputably relevant in finance. Therefore, the area of research of cryptocurrency market linkages is gaining increasing attention as the cryptocurrency market continues to evolve and mature.

The extant literature focuses on various aspects of cryptocurrencies, their performance and market dynamics. Park and Park (2020) explores the connection between web traffic and social network attributes and cryptocurrency performance, finding that these two can serve as indicators for performance. In Singh et al. (2022), the authors propose a new grey system approach for predicting the closing prices of several cryptocurrencies and finds it to be effective. de Senna and Souza (2022) study the impact of cryptocurrencies on stock exchange indexes in both the short and long term. Nadarajah et al. (2021) investigates the dependence between the price of bitcoin and African currencies and finds a strong correlation. Li et al. (2021) introduces a Generalized Superior Augmented Dickey-Fuller (GSADF) procedure to identify price bubble periods in the Bitcoin market and finds it successfully timestamps bubbles. Overall, these papers offer insight into the relationships between cryptocurrencies and various factors and provide effective methods for forecasting prices and identifying bubble periods.

Within this context, a growing strand of research has analyzed cryptocurrency spillovers, both across cryptocurrencies themselves and with different asset classes (Corbet et al. 2018; Katsiampa et al. 2019; Pogudin et al. 2019; Pagnottoni and Dimpfl 2019; Qureshi et al. 2020; Giudici and Pagnottoni 2020; Chaudhari and Crane 2020; Assaf et al. 2022; Caferra 2022; Balcilar et al. 2022; Giudici et al. 2022; Agosto et al. 2022). Ugolini et al. (2023) examines return spillovers within and between different Decentralized Finance (DeFi), cryptocurrency, stock, and safe-haven assets by using the block aggregation procedure of Greenwood-Nimmo et al. (2016, 2021), based on the connectedness approach of Diebold and Yılmaz (2014). It shows that DeFi and cryptocurrency asset markets exhibit strong within-market and between-market return spillovers, that stock and safe-haven markets show weak connectedness.

The concept of time series network connectedness can be characterized by the Generalized Forecast Error Variance Decomposition (GFEVD) method, which is based on Vector Autoregressive (VAR) models. This method allows for the measurement of spillovers, or cross-variance shares, between individual securities in terms of returns or return volatilities. The GFEVD approach can be used to analyze the spillover network in the time domain and represents it in terms of network topology (Diebold and Yilmaz 2012; Diebold and Yılmaz 2014). Baruník and Křehlík (2018) then expanded on this method by proposing a new approach for measuring frequency connectedness among securities, enabling the evaluation of connectedness at different time horizons.

Against this background we investigate, from the standpoint of network theory, the topological structure of short and long-run shock transmission networks of a set of 40 cryptocurrency prices derived from large multivariate autoregressive models. Our approach combines time series analysis and network theory to produce novel evidence of network systemic risk built upon robust multivariate autoregressive models. The foundation of our approach is that the decomposition of forecast error variance of multivariate time series models creates weighted, directed spillover networks, and that the interconnectedness measures stemming from econometrics are closely tied to centrality measures commonly used in network analysis (as discussed in Diebold and Yılmaz, 2014). This enables to investigate time series connectedness through the lens of network theory, and leverage the potential of the spectral representation of VAR processes to quantify shock transmission impacts at different time horizons.

Our results show that the analysis of cryptocurrency interactions in the frequency domain reveals a more in-depth understanding of their relationships in terms of frequency persistence of shock propagation and sensitivity to large shocks affecting the system. We find that the COVID-19 pandemic has had a substantial impact on the cryptocurrency market, leading to increased spillovers. However, our estimates further highlight that a very relevant portion of spillovers (roughly 80%) fades out within a few days (approximately 5), emphasizing the importance of accounting for the persistence of shocks in the network of cryptocurrencies when managing risk.

The remainder of this paper proceeds as follows. Section 2 presents the methodology. Section 3 illustrates the results of the method to the set of selected cryptocurrency prices. Section 4 concludes.

2 Methodology

The framework employed for characterizing time series connectedness is founded on the Generalized Forecast Error Variance Decomposition (GFEVD) of multivariate time series systems, which has been expounded upon in the works of Diebold and Yilmaz (2012); Diebold and Yılmaz (2014). The study by Diebold and Yılmaz (2014) proposes a weighted and directed network model that incorporates measures of time series connectedness that are consistent with commonly used centrality indicators in network research. The Generalized Forecast Error Variance Decomposition (GFEVD) is a technique that is obtained from Vector Autoregressive (VAR) models. It forms the foundation for the connectedness methodology that has been suggested by Diebold and Yılmaz (2014), which measures the directional connectedness within the time domain. The methodology is enhanced by Baruník and Křehlík (2018) through the utilization of the spectral representation of the GFEVD to evaluate the connectedness in the frequency domain, which includes both short and long-term cycles. The utilization of GFEVD for the characterization of multivariate time series networks enables the prompt computation of network centrality metrics, including node degree, centrality, and strength, within a weighted and directed network structure.

The present section is structured in the following procedure. Initially, we will analyze the connectedness metrics that are obtained from the Granger-causality-based forecast error variance decomposition (GFEVD) in the temporal domain. Next, we will analyze the frequency decomposition of connectedness in order to assess the immediate and prolonged effects of disturbances on the variables within the system. Subsequently, we demonstrate the correlation between connectedness metrics obtained through Granger causality-based functional empirical vector autoregressive models and the principles of network theory.

2.1 Time-dependent connectedness

The measures of connectedness are derived from the variance decomposition of a Vector Autoregressive (VAR) approximation model. The focus is on a N-dimensional process ${\textbf{x}}_{t}=\left( x_{1, t}, \ldots , x_{N, t}\right) ^{\prime }$, which is covariance-stationary and observed at discrete time points $t=1, \ldots , T$. This process is modeled using a Vector Autoregressive (VAR) model of order p

$$\begin{aligned} {\textbf{x}}_{t}={\varvec{\Phi }}_{1} {\textbf{x}}_{t-1}+{\varvec{\Phi }}_{2} {\textbf{x}}_{t-2}+\cdots +{\varvec{\Phi }}_{p} {\textbf{x}}_{t-p}+\varvec{\epsilon }_{t} \end{aligned}$$

(1)

with $\varvec{\Phi }_{1}, \ldots , \varvec{\Phi }_{p}$ and the white noise process $\varvec{\epsilon }_{t}$, which is characterized by a covariance matrix denoted as $\varvec{\Sigma }$. In the VAR setting, each variable is not only regressed on its own p lags but also on the lags of all other variables. Consequently, the matrices of coefficients contain comprehensive information on the autoregressive impacts among variables. The $(N \times N)$ matrix lag-polynomial, represented as $\varvec{\Phi }(L)=\left[ {\varvec{I}}_{N}-\varvec{\Phi }_{1} L-\cdots -\varvec{\Phi }_{p} L^{p}\right]$ where ${\varvec{I}}_{N}$ is the identity matrix, can be conveniently expressed in the model as $\varvec{\Phi }(L) {\textbf{x}}_{t}=\varvec{\epsilon }_{t}$.

If the roots of $|\Phi (z)|$ are located outside the unit circle, the VAR process has a vector moving average - i.e., MA $(\infty )$ - representation as ${\textbf{x}}_{t}=\varvec{\varvec{\Psi }}(L) \varvec{\epsilon }_{t}$, where the matrix of infinite lag polynomials $\varvec{\Psi }(L)$ is computed recursively from $\varvec{\Phi }(L)=[\varvec{\Psi }(L)]^{-1}$ and is critical to understanding the system’s dynamics. Since $\varvec{\Psi }(L)$ includes an infinite number of lags, it must be approximated using moving average coefficients $\varvec{\Psi }_{h}$ computed at $h=1, \ldots , H$ horizons. The connectedness measures are developed through variance decompositions, which are transformations of $\varvec{\Psi }_{h}$ and enable the evaluation of the effects of shocks on the system.

The VMA representation of the system is fundamental to evaluate the effect of a shock in one system variable on the others thanks to the impulse response functions and variance decomposition tools. In particular, the variance decomposition allows to decompose the H-step-ahead error variance in predicting $x_{i}$ due to shocks to $x_{j}$, $\forall j \ne i$ and $\forall i=1,..., n$.

The VAR model, as expressed in equation (1), involves N endogenous variables and p lags. The estimation of coefficients in this model amounts to $N^2 \times p$, a value that exhibits quadratic growth with respect to the number of variables. The effective management of the curse of dimensionality is of utmost importance when dealing with a large number of variables ($N=40$ variables in our case) and employing dynamic rolling window estimation, which involves estimation over samples of fewer observations. LASSO, a shrinkage and selection technique, is a popular solution for handling high-dimensional models. In high-dimensional scenarios, connectedness can be assessed through dimensionality reduction methods, such as LASSO-VAR models, as demonstrated in the literature (e.g. Diebold et al. (2017); Bostanci and Yilmaz (2020)). In this study, we use a LASSO-VAR model with a basic penalty, and the objective function is specified as follows:

$$\begin{aligned} \min _{\Phi } \sum _{t=1}^T\left\| {\textbf{x}}_t-\sum _{i=1}^p \varvec{\Phi }_i {\textbf{x}}_{t-i}\right\| _2^2+\lambda \Vert \varvec{\Phi }\Vert _1 \end{aligned}$$

where $\Phi =\left[ \Phi _1, \ldots , \Phi _p\right]$ and the penalty parameter $\lambda \ge 0$ being selected via sequential cross-validation. The LASSO estimator employs a penalty parameter to diminish the magnitude of the estimated coefficients with the smallest values, thereby achieving both shrinkage and selection of the most relevant variables. Although the coefficient between variables j and k has been chosen as zero, it is still plausible for the innovation linked with equation j to have an effect on the future development of variable k. This implies that despite the selection of coefficients, it is still very likely that the spillover matrix will retain elements that are not equal to zero.

Given a shock in a variable may not occur independently and orthogonally from shocks in other variables, identification is key for correctly quantifying the variance decomposition. Cholesky factorization and other traditional methods alike impose strict constraints and are dependent on the arrangement of the variables. Pesaran and Shin (1998) provide an identification approach of variance decompositions that is independent of the order of the variables. Generalized variance decompositions can be written in the form

$$\begin{aligned} {\text {GFEVD}}\left( x_{j,t}; \epsilon _{k,t}, H\right) =\left( {\varvec{\theta }}\right) _{j,k}^{(H)}&=\ \frac{\sigma _{k k}^{-1} \sum _{h=0}^{H}\left( \left( {\varvec{\Psi }}_{h} {\varvec{\Sigma }}\right) _{j, k}\right) ^{2}}{\sum _{h=0}^{H}\left( {\varvec{\Psi }}_{h} {\varvec{\Sigma }} {\varvec{\Psi }}_{h}^{\prime }\right) _{i, j}} \end{aligned}$$

where ${\varvec{\Psi }}_{h}$ is a $(N \times N)$ matrix of moving average coefficients at lag h, and $\sigma _{k k}=(\varvec{\Sigma })_{k, k}$ is the variance of the innovation process of the k-th variable. The $(\varvec{\theta })_{j,k}^{(H)}$ represents the contribution of the k-th variable to the variance of the forecast error of element j, at horizon H. For a comprehensive explanation of the formula, we refer the readers to Diebold and Yilmaz (2012). As the matrix $\varvec{\Sigma }$ has a non-diagonal form, the elements of ${\text {GFEVD}}(\cdot )$ across j may not add up to 1. Thus, the sum of the variance shares may exceed $100 \%$. To address this issue, Diebold and Yılmaz (2014) introduces normalized GFEVDs, which are defined as:

$$\begin{aligned} \left( \tilde{\varvec{\theta }}_{H}\right) _{j, k}=\left( \varvec{\theta }_{H}\right) _{j, k} / \sum _{k=1}^{N}\left( \varvec{\theta }_{H}\right) _{j, k} \end{aligned}$$

Now the $\sum _{j=1}^{N}\left( \tilde{\theta }_{H}\right) _{j, k}=1$ and the sum of all elements in $\tilde{\theta }_{H}$ is equal to N, by construction.

At a given horizon H, the generic element (j, k) within the matrix denotes the pairwise connectedness between variable j and variable k. The generic diagonal element (k, k) of the matrix denotes the impact of the shock on the k-th variable in isolation. The element located off the diagonal, specifically at the intersection of row j and column k, denotes the extent to which variable j contributes to the variance of the forecast error of variable k at a given time horizon H. The aforementioned components possess the capability to be consolidated in order to evaluate the overall interconnectedness of the system. Diebold and Yılmaz (2014) discusses the perspective of the matrix as a weighted directed network, where edges are represented by variables and links are represented by forecast error variance contributions.

2.2 Frequency-dependent connectedness

In order to examine the frequency dynamics of spillovers, a spectral representation of the variance decompositions is employed, with a specific emphasis on frequency responses to shocks. The work of Baruník and Křehlík (2018) defines the spectral representation of the generalized forecast error variance decomposition (GFEVD). The authors employ the Fourier transform of the impulse response functions to capture the frequency responses. The aim is to estimate the fraction of the forecast error variance that can be attributed to exogenous shocks in other variables within a specified frequency band.

Consider the frequency response function $\varvec{\Psi }\left( \textrm{e}^{-\textrm{i} \omega }\right) =\sum _{h} \textrm{e}^{-\textrm{i} \omega h} \varvec{\Psi }_{h}$ through a Fourier transformation of the coefficients $\varvec{\Psi }_{h}$. The spectral density of ${\textbf{x}}_{t}$ at frequency $\omega$ can be defined as a Fourier transform of MA($\infty$) filtered series as:

$$\begin{aligned} S_{{\textbf{x}}}(\omega )=\sum _{h=-\infty }^{\infty } E\left( {\textbf{x}}_{t} {\textbf{x}}_{t-h}^{\prime }\right) \textrm{e}^{-\textrm{i} \omega h}=\varvec{\Psi }\left( \textrm{e}^{-\textrm{i} \omega }\right) \varvec{\omega } \varvec{\Psi }^{\prime }\left( \textrm{e}^{+\textrm{i} \omega }\right) \end{aligned}$$

(2)

The understanding of frequency dynamics is reliant on the power spectrum $S_{{\textbf{x}}}(\omega )$, as it serves as a crucial component in equation (2). The spectrum represents how the variance of ${\textbf{x}}_{t}$ is divided among the frequency components $\omega$. By employing the spectral representation of covariance, which is expressed as $E\left( {\textbf{x}}_{t} {\textbf{x}}_{t-h}^{\prime }\right) =\int {-\pi }^{\pi } S_{{\textbf{x}}}(\omega ) \textrm{e}^{\textrm{i} \omega h} \mathrm {~d} \omega$, the subsequent definition establishes the frequency domain equivalents of variance decomposition. The generalized causation spectrum across frequencies $\omega$ within the interval $(-\pi , \pi )$ is mathematically represented as follows:

$$\begin{aligned} (f(\omega ))_{j, k} \equiv \frac{\sigma _{k k}^{-1}\left| \left( \varvec{\Psi }\left( e^{-i w}\right) \varvec{\Sigma }\right) _{j, k}\right| ^{2}}{\left( \varvec{\Psi }\left( \omega ^{-i w}\right) \varvec{\omega } \varvec{\Psi }^{\prime }\left( e^{+i w}\right) \right) _{j, j}} \end{aligned}$$

where the Fourier transform of the impulse response is denoted by $\varvec{\Psi }\left( e^{-i w}\right)$, $\varvec{\Psi }$ denotes a matrix, where each element $(f(\omega ))_{j, k}$ represents the fraction of the spectral density of the j-th variable at a given frequency $\omega$ that can be attributed to disturbances in the k-th variable. Consequently, the aforementioned quantity is construed as a form of causation within the frequency domain. This interpretation is derived from the fact that the denominator encompasses the spectrum of the j-th variable, which corresponds to the diagonal elements of the cross-spectral density of $x_j$ at a given frequency $\omega$.

In order to derive a frequency-based intuitive decomposition of the initial GFEVD, $(f(\omega ))_{j, k}$ can be weighted by the frequency proportion of variance of the j-th variable. The weighting function is defined as follows:

$$\begin{aligned} \Gamma _{j}(\omega )=\frac{\left( \varvec{\Psi }\left( e^{-i w}\right) \varvec{\Sigma } \varvec{\Psi }^{\prime }\left( e^{+i w}\right) \right) _{j, j}}{\frac{1}{2 \pi } \int _{-\pi }^{\pi }\left( \varvec{\Psi }\left( e^{-i \lambda }\right) \varvec{\Sigma } \varvec{\Psi }^{\prime }\left( e^{+i \lambda }\right) \right) _{j, j} d \lambda } \end{aligned}$$

The power of the j-th variable at a specific frequency is represented by $\Gamma _{j}(\omega )$, and it adds to a constant value of $2 \pi$ across all frequencies. This enables the definition of the GFEVD in frequency domain:

$$\begin{aligned} {\text {GFEVD}}\left( x_{j,t}; \epsilon _{k,t}, d\right) = \left( \varvec{\theta }\right) _{j,k}^{(d)}&=\frac{1}{2 \pi } \int _{d} \Gamma _{j}(\Sigma )(f(\Sigma ))_{j, k} d \Sigma \end{aligned}$$

Furthermore, it is possible to apply the standard normalization technique to the GFEVD in order to derive its normalized equivalent. Moreover, the spillover indices, as delineated in Diebold and Yilmaz (2012), can be conveniently obtained from the Global Forecast Error Variance Decomposition (GFEVD).

2.3 GFEVD network topology

The GFEVD can be conceptualized as a network that is both directed and weighted. Consequently, the metrics of connectedness designed in multivariate time series exhibit a significant association with the centrality indicators that are commonly employed in network analysis (see Diebold and Yılmaz, 2014). A very relevant example to be taken into account in this direction is the matrix of the connectedness of the normalized GFEVD

$$\begin{aligned} {\tilde{\varvec{\theta }}_{H}}=\left[ \begin{array}{cccc} \tilde{\theta }_{1,1}^{(H)} &{} \tilde{\theta }_{1,2}^{(H)} &{} \cdots &{} \tilde{\theta }_{1,N}^{(H)} \\ \tilde{\theta }_{2,1}^{(H)} &{} \tilde{\theta }_{2,2}^{(H)} &{} \cdots &{} \tilde{\theta }_{2,N}^{(H)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \tilde{\theta }_{N,1}^{(H)} &{} \tilde{\theta }_{N,2}^{(H)} &{} \cdots &{} \tilde{\theta }_{N,N}^{(H)} \end{array}\right] \end{aligned}$$

(3)

The matrix in (3) defines a weighted network adjacency matrix denoted by $\tilde{\varvec{\theta }}_{H}$, which is commonly known as "variance decomposition matrix". This matrix exhibits a number of desirable characteristics. First of all, the components of the matrix represent the magnitude of the connection. Additionally, it should be noted that links possess a directionality which typically renders the matrix asymmetric in nature. Thirdly, it can be observed that the summation of every row in the matrix is equivalent to 1, given that the individual elements are proportion of variance. Consequently, the values located on the diagonal of matrix A can be expressed as $(\tilde{\varvec{\theta }}_{H})_{i,i}=1-\sum {\begin{array}{c} j=1 \\ j \ne i \end{array}}^{N} (\tilde{\varvec{\theta }}_{H})_{i,j}$. Furthermore, it is common for the diagonal elements of matrix $\tilde{\varvec{\theta }}_{H}$ to be non-zero, indicating the presence of self-loops in network terms.

The weighted directed network established by the GFEVD permits the straightforward computation of centralities, such as node degree and strength, and the application of network science techniques to analyze multivariate time series networks. The computation of degrees can be achieved by performing either a row or column summation of the binarized adjacency matrix denoted as $\tilde{\varvec{\theta }}_{H}$. The magnitude of the force can be obtained by computing the summation of the constituent elements of matrix $\tilde{\varvec{\theta }}_{H}$. The in-strength and out-strength of matrix $\tilde{\varvec{\theta }}_{H}$, which are equivalent to the summation of rows and columns, respectively, are analogous to the directional connectedness metrics to and from as elaborated in Diebold and Yilmaz (2012). The out-strength of a given node, denoted as i, is mathematically defined as $\delta _{i}^{\text{ from } }=\sum _{\begin{array}{c} j=1 \\ j \ne i \end{array}}^{N} (\tilde{\varvec{\theta }}_{H})_{i,j}$. Similarly, the in-strength of a node, denoted as j, is defined as $\delta {i}^{to}=\sum _{\begin{array}{c} i=1 \\ i \ne j \end{array}}^{N} (\tilde{\varvec{\theta }}_{H})_{i,j}$.

2.3.1 Minimum spanning tree

The Minimum Spanning Tree (MST) representation can be used to simplify the relationships presented by the spillover matrix and derive shortest paths of shock transmission. Kruskal’s algorithm is a method for obtaining the minimum spanning tree from adjacency matrices. This algorithm effectively decreases the number of links connecting nodes by establishing a link between each node and its nearest neighbor. Through this approach, one can visualize most relevant links and shortest path channels where the time series shocks tend to get through.

The Minimum Spanning Tree (MST) is based on the methodological premise that a weighted graph $G=[V,E]$ exists, where V represents the vertices and E represents the weighted edges. It is possible to consider the weights as the expense required to reach vertex $v_j$ from vertex $v_i$, without any loss of generality.

Our objective is to identify a subgraph ${\tilde{G}}$ of G that has the same set of nodes as G (i.e., $V(G)=V({\tilde{G}})$), while minimizing the total cost of the subgraph. The cost to reach $v_j$ from $v_i$ is epitomized by the weights of the edges in the graph. We are interested in finding a subgraph ${\tilde{G}}$ of G such that $V(G)=V({\tilde{G}})$, roughly speaking such that they span the same nodes, with the minimum aggregate cost, which can be conceived as the sum of the entirety of graph weights.

Define ST(G) as the set spanning trees spanned by G. ${\hat{G}}\in ST(G)$ is a MST if the sum of the edge weights of ${\hat{G}}$ is not higher than the sum for any other spanning tree of G. Kruskal’s algorithm can be summarized as follows. Given a weighted, connected graph G:

• 1. Find in the graph the minimum weight edge, and mark it.

• 2. Choose a minimum weight edge across the unmarked edge not forming any cycles with any of the marked ones.

• 3. If a panning tree of G is formed from the set of marked edges, stop the algorithm, otherwise repeat 2.

2.3.2 Community detection

The community structure, which refers to the prevalence of clusters of nodes, is an essential characteristic of complex networks. Each group contains a set of nodes, and the edge density within each group is greater than that between groups. Community detection algorithms help in clustering network nodes may disclose the concealed connections between them. The primary goal of the Louvain method is to identify a partition of the set of vertices that maximizes the modularity of the graph under consideration. This function compares the existence of an edge between two vertices in an undirected network to the probability of having such an edge in a random model.

Modularity is a metric used to evaluate the structure of networks, indicating the extent to which a network is divided into distinct clusters or subgroups. A network exhibiting high modularity is characterized by a significant density of links among nodes within the same community while displaying a low density of links between nodes belonging to distinct communities. This holds significance in the study of financial and economic spillover networks, as it provides insight into the groups participating in the transmission of risk, as well as the entities that are resilient. The modularity Q of a partition ${\mathcal {C}}$ of an undirected graph $G=(V, E)$ is formally defined as follows:

$$\begin{aligned} Q=\frac{1}{2 m} \sum _{i, j}\left[ (\tilde{\varvec{\theta }}_{H})_{i,j}-\frac{d_{i} d_{j}}{2 m}\right] \delta \left( c_{i}, c_{j}\right) \end{aligned}$$

(4)

with m being the number of edges of G, $d_{i}$ represents the degree of i, $c_{i}$ represents the community to which i belongs, and $\delta$ is the Kronecker delta function, namely $\delta (u,v)=1$ if $u=v$, and 0 elsewhere.

The algorithm of Louvain is built upon on a greedy procedure. Initially, every individual node is allocated to its respective community. Subsequently, the algorithm has the objective to enhance the modularity value through the relocation of nodes to the neighboring community. Stated in a different way, the algorithm calculates the modularity gain resulting from the inclusion of vertex i into community C by means of the following procedure:

$$\begin{aligned} \Delta _{Q}&=\left[ \frac{\sum _{i n}+d_{i}^{C}}{2 m}-\left( \frac{\sum _{t o t}+d_{i}}{2 m}\right) ^{2}\right] -\left[ \frac{\sum _{i n}}{2 m}-\left( \frac{\sum _{t o t}}{2 m}\right) ^{2}-\left( \frac{d_{i}}{2 m}\right) ^{2}\right] \end{aligned}$$

(5)

where $d_{i}^{C}$ is node i’s degree in community C, $\sum _{i n}$ represents the number of edges in community C and $\sum _{\text{ tot } }$ the total number of edges incident to C.

After computing the aforementioned value for all communities that are linked to community i, the placement of community i is determined based on the maximum value of modularity. In the absence of any potential improve, the variable denoted by i will stay in its initial community. The procedure is iteratively and consecutively executed on all nodes until no further actions can enhance the modularity value.

3 Empirical application

3.1 Data and preliminary analysis

We apply our methodology to study the spillover network of a set of cryptocurrency prices. We select, among the top 50 cryptocurrencies in terms of market capitalization to date, those whose data are available to ensure at least a three-year timespan. Our sample selection ends up with 40 cryptocurrencies, i.e. Ampleforth (AMPL), Aragon (ANT), Binance Coin (BNB), BitTorrent (BTT), Bitcoin (BTC), Bitcoin Cash (BCH), Cardano (ADA), Celsius (CEL), Chainlink (LINK), Crypto.com Coin (CRO), Decentraland (MANA), Enjin Coin (ENJ), Ethereum (ETH), Fantom (FTM), Gas (GAS), Litecoin (LTC), LinkedMinds (LM), Loopring (LRC), Maker (MKR), Nexo (NEXO), Numeraire (NMR), Ocean Protocol (OCEAN), Polygon (MATIC), Qtum (QTUM), Ren (REN), Rupiah Token (RP), RSR (RSR), THETA (THETA), THORChain (RUNE), Tezos (TZ), Tether (USDT), TRON (TRX), 0x (ZRX), Basic Attention Token (BAT), Band Protocol (BAND), Chiliz (CHZ), Orbs (ORBS), Synthetix (SNX), USD Coin (USDC), VeChain (VET). The analyzed sample period ranges from 18 September 2019 to 9 February 2023.

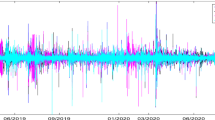
We start by presenting in Fig. 1 the evolution of the selected cryptocurrency price series over the analyzed period. It is clear that cryptocurrencies experience different volatility regimes over the sample. In particular, prices tend to generally grow from the beginning of 2021 onwards, experience several fluctuations until the end of the second quarter of 2022 when they become more steady. Few exceptions are USDT, USDC and AMPL which are US dollar-pegged stablecoins and thereby just gently swing around their mean.

Fig. 1

Price time series. The figure shows the evolution of the natural logarithm of the time series of prices related to the selected cryptocurrencies over the sample period

Before the estimation of the VAR model, we check for stationarity via the Augmented Dickey-Fuller (ADF) test. Results are presented in Table 1.

Table 1 Stationarity Test

It is noteworthy to observe that many of the analyzed time series in levels exhibit non-stationary behavior throughout the entire sample. There are a few cryptocurrencies (AMPL, BTT, ORBS, LRC, RUNE) for which the p-value of the test is lower than the conventional level of 10% already in levels. It is worth noting that the considered time series are stationary in log returns, and thereby we can proceed with the estimation of the LASSO-VAR model.

3.2 Network connectedness analysis

The focus of our empirical application is to analyze the transmission of shocks in the network of cryptocurrency prices via time series connectedness measures. To this aim, we estimate a vector autoregression (VAR) model in a full sample fashion as well as with a rolling window approach, to evaluate the dynamic nature of spillovers over time. The optimal lag order for the VAR model is determined using the Bayes-Schwarz information criterion (BIC), and the width of the rolling window is set to 100. Additionally, we define two frequency bands for the generalized frequency-domain causality (GFEVD) estimations: a short-term band (ranging from 1 to 5 days) and a long-run band (from 5 days onwards).

We present as a preliminary analysis the results of the estimation of the LASSO-VAR model in Fig. 2, where the estimated autoregressive coefficients are depicted. The LASSO shrinkage and selection procedure with cross-validation selects fewer than 10% of the coefficients in the final specification of the model, with as much as 90.31% of the coefficients set to zero. The largest negative autoregressive impact recorded is that of BTT on NMR, whereas the largest positive impact is that of ORBS in the equation of CHZ. These coefficients, together with the variance-covariance matrix of innovations, concur to the determination of the spillover network.

Fig. 2

LASSO VAR coefficient estimates. The figure illustrates the LASSO VAR coefficient estimates across the selected cryptocurrencies over the full sample period

The full sample connectedness matrix with spillover contributions between each variable is shown in Fig. 3 with regard to the full sample LASSO-VAR estimation. We observe that own variance shares (diagonal elements) concur to a larger extent to the development of spillovers when compared to cross variance shares (cross-diagonal elements). We can further notice that stablecoins such as USDT, USDC, AMPL and a few others are relatively isolated and do not exchange much information with the other cryptocurrencies in terms of transmitted forecast error variance. Despite that, two of them share the largest cross-variance contributions, i.e. USDC and USDT, with that of USDC on USDT being of larger magnitude. These findings as confirmed by Fig. 4, the own variance shares, or the individual contributions to the spillovers as indicated by the diagonal of the spillover matrix, are depicted over the entire sample period. Indeed, US dollar-pegged stablecoins are those whose own dynamics contribute to a larger portion to their future development and, particularly, USDC and USDT. Moreover, also BitTorrent (BTT) seems to remain relatively uninfluenced by shocks in the others.

Fig. 3

GFEVD spillover network. The figure illustrates the estimated GFEVD spillover network across the selected cryptocurrencies over the full sample period

Fig. 4

Own variance shares. The figure shows the estimated own variance shares, i.e. the diagonal elements of the GFEVD spillover network across the selected cryptocurrencies over the full sample period

In Fig. 5 we show the short-run and long-run GFEVD spillover networks resulting from the frequency decomposition of forecast error variance. The figure refers to the full sample, and short-run spillovers denote impacts of shocks from 1 to 5 days, whereas long-run spillovers denote impacts of shocks from 5 days onwards. A first prominent insight is that short-run spillovers are higher in magnitude than long-run spillovers. In other words, shock transmission is more vigorous in the short-term, and then tends to dissipate over the long run. Another interesting finding is that principal actors in the network, tend to remain stable, despite the different magnitude of shock transmitted over the different horizons.

Fig. 5

Frequency decomposition of spillover network (full sample). The figure shows the GFEVD spillover network across cryptocurrencies over the full sample period. The left panel represents short-run spillovers (1 to 5 days), whereas the right panel illustrates long-run spillovers (from 5 days onwards)

The study of full sample interconnectedness provides a static, average estimation of the impacts of spillovers among cryptocurrencies. However, market changes may alter these relationships over time, making a static model of interconnectedness poor of dynamic insights. While the full sample analysis gives a useful snapshot of the overall system’s behavior, a single model with fixed parameters may not be effective for the entire sample. To address this, we calculate dynamic interconnectedness based on rolling samples to gauge the variations in spillovers over time by analyzing the corresponding spillover time series, both in the short and long-term.

The derivation of connectedness measures in the time domain using dynamic estimation results in the Total Spillover Index shown in Fig. 6. There is a noticeable fluctuation in the total spillover of the system over time, with the highest overall spillover recorded following the initial outbreak of the COVID-19 pandemic. Additionally, the overall spillovers have been rising in the latter part of the sample period, signifying increased synchronicity of security returns starting around mid-2021. The proportion of long-run spillovers over the short-run ones is fairly constant, with the short-run spillovers being predominant (roughly five times the long-run ones).

Fig. 6

Frequency decomposition of total spillover. The figure shows the estimated dynamic total spillover across the selected cryptocurrencies over the analyzed period. “Short” corresponds to the total spillover on the frequency band from 1 to 5 days (short run), while “Long” represents the total spillover on the frequency band from 5 days onwards (long run)

To further investigate the nature of short and long-term total spillovers, we represent their normal kernel probability density estimates in Fig. 7. Firstly, the figure confirms the fact that short-run spillovers are considerably higher than long-run ones. Secondly, the figure highlights the fact that the distributions of the two are dissimilar. The long-run spillovers seem to be more concentrated around their median value, whereas the short-run ones appear more dispersed. Furthermore, there is a hint of bi-modality in the short-run spillover distribution.

Fig. 7

Kernel density estimates of total spillover. The figure shows the normal kernel probability density estimates of the dynamic total spillover across the selected cryptocurrencies over the analyzed period. “Short” corresponds to the total spillover on the frequency band from 1 to 5 days (short run), while “Long” represents the total spillover on the frequency band from 5 days onwards (long run)

In this context, we present in Fig. 8 the distribution of pairwise network linkages between all analyzed cryptocurrencies over time. Bivariate network linkages exhibit quite strong fluctuations over time. Large values of pairwise spillovers start being recorded in the midst of the outbreak of COVID-19. Moreover, after a quieter period at the end of 2020, pairwise spillovers start to rise with the beginning of 2021, to then gradually diminish until the end of the sample. It is interesting to notice that few pairwise relationships (in particular that existing between USDC and USDT) are sensibly higher in magnitude than the rest of spillovers transmitted by/to other cryptocurrencies.

Fig. 8

Distribution of pairwise network linkages over time. The figure shows the distribution of bivariate network linkages across cryptocurrencies over time. The x-axis represent the bivariate network linkages, the y-axis time, whereas the z-axis represents the magnitude of pairwise directional spillovers

Fig. 9

Frequency decomposition of own variance shares over time. The figure shows the distribution of own variance shares across cryptocurrencies over time. The x-axis represent cryptocurrencies, the y-axis time, whereas the z-axis represents the magnitude of own variance share

The previous findings are confirmed by the analysis of Fig. 9, which depicts the frequency decomposition of own variance shares for each cryptocurrency over time. Even own variance shares are relatively higher in magnitude for the two stablecoins mentioned (USDC and USDT), although with a lower difference. Own variance shares are also dynamic over time, and their effect is also much more prominent in the short-term rather than in the long-term.

We now turn to the complex analysis of cryptocurrency return spillover networks. In particular, we assess the “minimal” structure of cryptocurrency forecast error variance decomposition networks via their MST representation, which depicts the shortest paths of risk transmission. The MST of the cryptocurrency spillover network related to the whole sample period is depicted in Fig. 10.

Fig. 10

Minimal Spanning Tree (MST) of spillover network. The figure shows the Minimal Spanning Tree (MST) of spillover network of cryptocurrency price returns over the full sample period

The analysis of Fig. 10 sheds some light on the shortest path mechanisms of shock transmission across cryptocurrency prices. In particular, it is clear how USDC, followed by BTC, are central nodes in the MST network as far as shock transmission is concerned. While the centrality of Bitcoin might have been an expected outcome, the one of USDC is not trivial. This can be connected to the role of USD as medium of exchange and store of value for investors. Being it pegged to the US dollar and, thereby being reliable and of relatively low volatility, it has become widely employed in the crypto-community over recent times.

We further perform community detection through the Louvain clustering algorithm to identify major clusters of cryptocurrencies influencing each other. Results related to the application of the Louvain community detection algorithm to the cryptocurrency spillover network over the full sample period are represented in Fig. 11. We use different colors to label the clusters, and additionally represent the clustered network where only links exceeding the 0.9-percentile of the distribution are retained, so to highlight the most relevant links.

Fig. 11

Louvain clustering of spillover network. The figure shows the results of the Louvain community detection algorithm applied to the spillover network connectivity matrix over. Colors represent the clusters identified by the algorithm. The upper panel refer to the full network representation, whereas the lower panel depict networks where only links exceeding the 0.9-percentile of the distribution are retained

The figure shows that as much as three clusters emerge. The three clusters are very different in terms of numbers: the first one contains 24 nodes, the second one 12, and the third one just 4 elements. Two mature cryptocurrencies (BTC and LTC) belong to the same cluster, the one with 12 elements, whereas ETH, for instance, belongs to the most numerous one. USDC and USDT, instead, belong to the smallest cluster to which the algorithm assigns also two relatively recent cryptocurrencies (MKR and MAN). However, it is evident how the most relevant linkage within such cluster is the one between USDC and USDT, clearly due to the fact they are both pegged to the dollar. Despite that notice that while USDC has emerged as central from the MST analysis, this is partially due to the effect of the many connections, rather than to their magnitude. Indeed, USDT seems to exhibit more relevant links in terms of magnitude with respect to USDC.

4 Concluding remarks

We aimed at examining the financial network structures of cryptocurrency prices in both time and frequency domains. The approach has combined time series analysis and network theory to produce novel evidence of network systemic risk built upon robust multivariate autoregressive models. We analyzed the generalized forecast error variance decomposition (GFEVD) method, in time and frequency domains, through the lens of network science to study the topological structure of shock transmission among a set of top 40 cryptocurrency prices. The findings revealed that the frequency domain network structure provides a more comprehensive understanding of the interactions among cryptocurrencies, that the COVID-19 pandemic had a significant effect on the cryptocurrency market, resulting in increased spillovers, but also that a significant portion of spillovers dissipates, in general, within the short-term (1 to 5 days).

As a consequence, results emphasize the relevance of taking the frequency persistence of shocks into account when managing risk in the cryptocurrency market. Tracking the evolution of financial networks of cryptocurrency shock transmission could be useful to investors and policymakers in making informed decisions in the rapidly growing and ever-changing cryptocurrency market. By monitoring time-frequency spillovers and their network structure, risk managers can better understand the relationships between different cryptocurrencies and identify any potential transmissions of risks. Such information can be of high relevance in the implementation of risk management strategies which are better suited to the either short or long term horizon of the investor and tackle specific risks affecting the cryptocurrency markets.

This field has potential for further empirical and methodological advancements. Future research could explore the practical applications of field intersecting multivariate time series and network science for asset allocation and portfolio management, as for instance in Ko and Lin (2008); Spelta et al. (2022). It could also examine the impact of significant exogenous shocks, such as the COVID-19 pandemic or climate shocks, on financial markets, as demonstrated in Zhang et al. (2020); Pagnottoni et al. (2021); Akyildirim et al. (2022). Furthermore, the proposed method can be applied to the connectedness between DeFi, cryptocurrency, stock, and safe-haven assets.