New directions in pass-and-swap queues

Abstract

Recently, driven by redundancy systems and matching systems, there has been renewed interest in models with product form stationary distributions. By a “product form,” we mean that the stationary distribution can be expressed as a product of terms, each of which corresponds to a job in the system. Given the recent discovery of many such systems, it is natural to ask: how broad is this class of systems? In this paper, we consider extensions and generalizations of the recently-proposed pass-and-swap queue, which has a product-form stationary distribution. We make three main contributions. First, we identify sufficient conditions under which pass-and-swap queues can be connected in a closed network, while still preserving the product form. Second, we identify dimensions along which the pass-and-swap system can be extended while preserving the product-form stationary distribution. At the same time, we also identify cases in which generalizing the pass-and-swap queue causes the product-form nature of the stationary distribution to break. Finally, we identify questions that remain open and present a road map for future study.

1 Introduction

Identifying a closed-form expression for the stationary distribution of the system state is of paramount importance in the analysis of queueing systems. Determining the stationary distribution often is the first step in deriving performance metrics of interest, including the mean or distribution of the number of jobs in system and the response time; it is also a key factor in identifying necessary and sufficient conditions for stability. In some cases, having a closed-form expression for the stationary distribution has allowed researchers to establish that seemingly unrelated systems are in fact equivalent [1]. Many existing closed-form results for performance metrics in queueing systems stem from a product-form stationary distribution. In this paper, we use the phrase “product-form stationary distribution” to refer to the fact that the stationary distribution of the queue state can be expressed as a product of terms, where there is one term corresponding to each job in the queue. Clearly, the stationary distributions for the M/M/1 and M/M/k queues exhibit this structure. Yet the class of systems that admit a product-form stationary distribution is far broader than these simple examples. We note that alternative interpretations of the phrase “product-form” characterize the network models of Jackson and Kelly [22,23,24], queueing systems with negative customers [19, 20] and signals [10], and other systems; these notions of product forms are further away from our work.

In this paper we examine the pass-and-swap queue, or in short the P &S queue, recently introduced by Comte and Dorsman [12], which represents a fundamentally new mechanism that yields a product-form stationary distribution. The key feature of the P &S queue is that it allows for job routing within the queue: that is, the jobs in the queue no longer necessarily appear in first-come first-served order. Intra-queue routing occurs via the pass-and-swap mechanism, wherein, upon the service completion of a job, that job may take the place of a later job in the queue. That job may in turn take the place of another job that appears even later in the queue; this process continues until finally some job—not necessarily the one that completed service—is ejected from the system. Thus, a service completion results not only in the departure of some job from the system, but also possibly in a reordering of the queue. The P &S queue is so named because of this mechanism: after leaving its current position in the queue, a job scans the rest of the queue, passes over some jobs, and eventually swaps positions with some later job (or leaves the system). Each job belongs to some job class, and whether a job can take the place of another job in the queue depends on the classes of these jobs. In particular, the P &S mechanism is governed by a swapping graph, the vertices of which coincide with the job classes in the system: two jobs are swappable if there is an edge between the corresponding classes in the swapping graph. As we will see, the P &S queue generalizes several known product-form systems that have been of considerable interest in recent literature. In the remainder of this section we describe several such systems; later, in Sect. 2.1, we discuss in detail how each of these other systems can be cast as a P &S queue.

1.1 Order independent queues

The Order Independent (OI) queue, first introduced in the seminal work of Berezner and Krzesinski [7], represents the foundation of much of the recent work on product forms. In an OI queue, jobs are stored in first-come first-served order, and any job present in the system may receive service subject to two conditions. First, the service rate allocated to a job can depend only on the jobs that arrived earlier than it. Second, the total service rate allocated to the first i jobs in the queue cannot depend on the order in which those jobs appear. This definition is quite broad: it allows for multiple jobs to be in service at the same time, and for the total service rate to depend on both the number and types of jobs in the system. The M/M/1 and M/M/k queues both satisfy the OI conditions, as do many other systems, including, for example, the Multiserver Station with Concurrent Classes of Customers [14] and the Multiserver Center with Hierarchical Concurrency Constraints [25]. The OI queue was later extended to include loss queues [8], networks of OI queues with negative customers [28], and OI queues with abandonment [16]; see also [26] for further details. The P &S queue represents a direct generalization of the OI queue, as the P &S queue augments the OI service process with the intra-queue routing mechanism described above. Any system that can be described as an OI queue is thus also a P &S queue with an empty swapping graph, and can be further generalized by introducing a non-empty swapping graph.

1.2 Redundancy and matching models

Within the past decade, there has been considerable interest in two particular applications: redundancy models and stochastic matching models. Both of these types of systems consist of multiple servers and multiple classes of jobs and are characterized by a graph that defines a compatibility structure between job classes and servers. In a redundancy system, an arriving job joins the queue at all servers with which it is compatible and waits to be served by any one of those servers. In a stochastic matching model, one may think of jobs and servers more broadly as being “items,” where an arriving item will wait in the queue until it can be matched with a compatible item, at which point both items depart from the system. A wealth of papers show that innumerable variations on these types of models exhibit product-form stationary distributions [2, 3, 9, 11, 13, 15, 17, 27]; see also [16] for a more detailed overview. Typically, the analysis presented in these papers applies only to the specific system under consideration, meaning that while all of these results contribute to the discourse on product-forms, most do not do so in a systematic and generalizable manner. Furthermore, some of these variations are special cases of the OI queue, while others are not. For example, the cancel-on-complete variation of redundancy fits within the OI framework, whereas the cancel-on-start variation, using the state space of Visschers et al. [29], does not. This indicates that the OI conditions are not sufficiently broad to capture the full space of systems that admit product-form stationary distributions.

As we have seen, the OI queue is itself a P &S queue; hence, so is the cancel-on-complete redundancy system. We will see in Sect. 3.2.2 that the cancel-on-start redundancy system also can be interpreted as a P &S queue by reframing the system as a closed network of two P &S queues in tandem, in which both “jobs” and “servers” in the redundancy system are viewed as items present in the P &S queues.

1.3 Token models

Motivated by a desire to systematically identify the conditions under which a system will admit a product-form stationary distribution, several recent works have proposed frameworks that encompass some subset of the above results. Ayesta et al. [6] show that the cancel-on-start and cancel-on-complete variations of redundancy systems—which previously were analyzed independently—can in fact be studied using the same state space and analytical approach. In effect, the results of Ayesta et al. demonstrate that, by considering an alternative state space, one can reframe the cancel-on-start variation as a system that does adhere to the OI conditions. In later work, Ayesta et al. [5] propose a new token-based model that generalizes both the OI framework and the Visschers et al. framework [29]. The token-based model allows for the study of systems that fall within neither category, thereby identifying a new class of systems that admit a product-form stationary distribution. As we will see in Sect. 3.2, the P &S queue in turn generalizes the token-based model.

1.4 Our contributions

The fact that the P &S mechanism preserves the product-form stationary distribution—while also representing a significant generalization of the dynamics governing other product-form systems—suggests that the pass-and-swap mechanism is a promising starting point for further innovation. In this paper we aim to expand the discussion of what is possible in the space of product-form results by exploring possible extensions to the P &S queue. Our three major contributions are as follows.

First, we present a detailed analysis of closed networks of P &S queues (Sect. 3). We begin by reviewing existing results from [12] that pertain to a closed network of two P &S queues in tandem. We provide a comprehensive discussion of how such a closed network can be used to model many systems of practical interest. We then present new results on larger and more general closed networks. We find that, while closed tandems of any even number of P &S queues readily admit a product-form stationary distribution, the story is more complicated for odd tandems and general topologies. Our results lay the groundwork for further study in this area.

Second, we identify ways in which the P &S queue can—and cannot—be extended while preserving the product-form stationary distribution. In Sect. 4 we consider a setting where the swapping graph is not fixed, but instead is modulated by a exogenous continuous-time Markov chain. We show that this extension also allows for a product-form stationary distribution in both open and closed P &S systems. In fact, we find that the stationary distribution of the queue state remains unaffected, revealing that the stationary distribution is independent of the swapping graph. In Sect. 5 we study an extension of another key feature of the P &S graph, namely the number of swaps involved in a pass-and-swap transition. In particular, we introduce a limit on the number of swaps that can occur during a single transition. We find that in open P &S queues the stationary distribution no longer has a product form; in contrast, in closed networks there are conditions under which it does still exhibit a product form.

Finally, we identify several important questions that remain open and present a road map for future study. Our analysis reveals surprising intricacies that offer new insights about the conditions required for product forms. Hence, we conclude this paper with Sect. 6, in which we discuss questions that we leave open for future study and potential approaches to solving these problems.

2 Model and preliminaries

In this section we give an overview of several key results that motivate the work of this paper. We begin with Order Independent (OI) queues [7, 8, 26], which represent an important class of queues that exhibit a product-form stationary distribution (Sect. 2.2). We then turn to the P &S queue [12], which extends the OI queue by introducing a mechanism by which jobs may be routed within the queue upon a service completion (Sect. 2.3), and provide a brief survey of the main results on the single (open) P &S queue (Sect. 2.4).

2.1 Model and notation

We consider a system with multiple job classes, where we denote the set of all job classes by $\mathcal {I}=\{1,2,\dots ,I\}$. For all $i\in \mathcal {I}$, jobs of class i arrive to the system according to a Poisson process with rate $\lambda _i$. Upon arrival, jobs join a queue. The queue is ordered by arrival time, so that the job at the front of the queue has been in the system the longest and the job at the back of the queue is the most recent arrival. We assume that the queue has an unlimited capacity.

The state of the system is given by $c = (c_1,\dots ,c_n)$, where n is the total number of jobs present in the system and $c_i\in \mathcal {I}$ is the class of the i-th oldest job. If there are no jobs present in the system, the state is given by $\emptyset$. The state space is then the set of all finite sequences consisting of elements of $\mathcal {I}$; we note that this set is the Kleene closure of $\mathcal {I}$, denoted by $\mathcal {I}^*$.

We assume that the system is work-conserving, meaning that the rate at which there is a departure from the system is strictly positive whenever the system is non-empty. We also assume that service is allocated in such a way that the evolution of the state of the system over time exhibits a memoryless property (and thus represents a Markov process). In particular, we assume throughout this paper that the total available service rate is allocated among jobs in the system in accordance with the Order Independence conditions, detailed in the next section.

2.2 Order independent queues

In an Order Independent queue, or in short an OI queue, the total service rate is allocated among jobs such that (i) the rate allocated to a particular job depends only on the set of jobs that are in front of it in the queue (i.e., those jobs that arrived earlier), and (ii) this rate is independent of the order in which the jobs ahead of it appear in the queue. Any job that is allocated a nonzero service rate may complete service, at which time the job departs immediately from the system.

Formally, given a state $c=(c_1, \ldots , c_n)$, let $\mu (c)$ or $\mu (c_1, \ldots , c_n)$ denote the total available service rate of the queue when it is in state c. Note that this total rate may depend on both the number and classes of jobs in the system. Furthermore, we define $\varDelta \mu (c_1, \ldots , c_n):= \mu (c_1, \ldots , c_n) - \mu (c_1, \ldots , c_{n-1})$ to be the service rate allocated to the final job in position n. The service rate function is now said to satisfy the order independence conditions, or in short the OI conditions, when the following definition applies.

Definition 1

An Order Independent queue is one in which, in all states $c\in \mathcal {I}^*$, the service rate allocation satisfies the following properties:

• 1. For all $i<n$, the service rate allocated to the job in position i is given by $\varDelta \mu (c_1, \ldots , c_i)$.

• 2. For all permutations $\sigma (c_1, \ldots , c_n)$ of $c=(c_1, \ldots , c_n)$, $\mu (\sigma (c_1, \ldots , c_n)) = \mu (c_1, \ldots , c_n)$.

• 3. For all classes $c\in \mathcal {I}$, $\mu (c)>0$.

Property (i) ensures that a job’s service rate depends only on the jobs ahead of it, as the number and classes of jobs behind position i are disregarded. Furthermore, properties (i) and (ii) ensure that the order of those jobs is immaterial. Finally, property (iii) ensures that the system is indeed work-conserving. Even stronger, properties (i) and (iii) combined ensure that the first job in an OI queue always has a positive service rate.

Remark 1

The definition of Order Independent queues given in [26] allows for the service rate to be multiplied by an additional factor that can depend on the number of jobs in the system. This state-dependent service rate enables one to model, e.g., the Processor Sharing service discipline using an OI queue.

Example 1

Consider a system with five classes of jobs, so that $\mathcal {I}=\{1,2,3,4,5\}$, and three servers, each operating at rate $\mu =1$. Each job class is compatible with some subset of the servers, as shown in Fig. 1. At each moment in time, each server processes the first job in the queue with which it is compatible; multiple servers are permitted to process the same job at once, in which case the job receives service at the sum of the servers’ rates.

Suppose that the system is in state (4, 1, 2, 3, 4, 5, 2). In this case, servers 1 and 2 are both processing the class-4 job at the head of the queue, hence this job receives service at rate $\varDelta \mu (4) = 2$. The class-1 and class-2 jobs immediately behind this job do not receive any service, so $\varDelta \mu (4,1) = \varDelta \mu (4,1,2) = 0$. Server 3 is processing the class-3 job, which thus receives service at rate $\varDelta \mu (4,1,2,3) = 1$. All remaining jobs behind this class-3 job receive service at rate 0.

The service rate function imposed by the above system dynamics can readily be seen to satisfy the OI conditions given in Definition 1. Each server works on the first compatible job in the queue, meaning that a job can only be “blocked” from receiving service by jobs that are ahead of it in the queue (property (i)). Furthermore, the total rate of service allocated to the jobs in positions $1,\dots ,i$, $\mu (c_1,\dots ,c_i)$, is simply the sum of the rates of all servers compatible with any jobs in this set; hence, this rate depends only on the classes of these jobs and not on their order (property (ii)).

Fig. 1

A compatibility structure between job classes and servers, which, in combination with the first-come-first-served service discipline, gives rise to an OI queue

The key result of [7] is that all OI queues exhibit a product-form stationary distribution. This result is restated in Theorem 1 below.

Theorem 1

Consider an order independent queue with job classes $\mathcal {I}=\{1,\dots ,I\}$, per-class arrival rates $\lambda _1,\dots ,\lambda _I$, and service rate function $\mu (\cdot )$. Let

$$\begin{aligned} G \equiv \sum _{c\in \mathcal {I}^*} \prod _{j=1}^{n} \frac{\lambda _{c_j}}{\mu (c_1, \ldots , c_j)}. \end{aligned}$$

(1)

Then the system is stable if and only if $G < \infty$. If the system is stable, then the queue is quasi-reversible and the stationary distribution $\pi (\cdot )$ satisfies:

$$\begin{aligned} \pi (c) = \pi (\emptyset ) \prod _{j=1}^{n} \frac{\lambda _{c_j}}{\mu (c_1, \ldots , c_j)}, \end{aligned}$$

(2)

where $\pi (\emptyset ) = 1/G$.

The result of Theorem 1 has been extended to OI queues with abandonment [16], OI loss models (including, e.g., OI queues with a buffer of fixed finite size) [8], and networks of OI queues [28]. In the following section, we discuss in detail one particular extension: the pass-and-swap queue.

2.3 The pass-and-swap mechanism

A Pass-and-Swap queue, or in short a P &S queue, follows the service allocation rules of the OI queue. However, one key assumption of the OI queue is relaxed: we no longer require the job that completes service to be the job that departs from the system. Instead, a different job may depart; this job is determined based on the pass-and-swap mechanism.

In order to define the pass-and-swap mechanism, we must first introduce an auxiliary graph called the swapping graph. The swapping graph includes a vertex for each job class in the system and may include an undirected edge between any pair of job classes. We denote an edge between vertex i and vertex j (i.e., job classes i and j) by (i, j). Note that self-loops are also permissible; a self-loop from vertex (job class) i to itself is denoted by (i, i). The interpretation of an edge in the swapping graph is as follows: upon service completion of a class-i job, the class-i job may take the place of a class-j job in the queue if and only if edge (i, j) exists in the swapping graph. In this case, we say that classes i and j are swappable.

Example 2

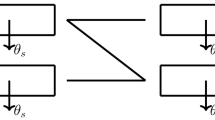
Consider the same system as described in Example 1, which consists of five job classes and three servers with the compatibility structure depicted in Fig. 1. We now introduce to this system the swapping graph shown in Fig. 2a. The swapping graph has vertex set $V=\{1,2,3,4,5\}$, where each vertex corresponds to a job class, and edge set $E=\{(1,3),(1,5),(2,4),(3,4),(4,5)\}$. This indicates that, for example, when a class-1 job completes service it may take the place of either a class-3 job or a class-5 job in the queue.

Fig. 2

The swapping graph and state transition described in Examples 2 and 3

We are now ready to define the pass-and-swap mechanism, which is triggered by a service completion. In this mechanism, the job that completes service does not immediately depart from the system, but instead scans the queue, beginning at its own position and moving backwards in the queue. As soon as it finds the first job with a class that is swappable with its own, it takes the place of this job, which is ejected from the queue. The ejected job in turn scans backwards in the queue, taking the place of and ejecting the first job with which it is swappable. This process continues until an ejected job finds no swappable job in the remainder of the queue; at this point, this final ejected job departs from the system. In the remainder of this paper, we will also refer to the combination of a service completion and the resulting execution of the pass-and-swap mechanism as a pass-and-swap transition. First, however, we illustrate the pass-and-swap mechanism through an example.

Example 3

Consider again the system with the job-server compatibility graph shown in Fig. 1 and the swapping graph shown in Fig. 2a. Suppose that the system is in state (4, 1, 2, 3, 4, 5, 2); as we have seen in Example 1, this means that the class-4 job at the head of the queue is being processed at rate 2 and the class-3 job is being processed at rate 1.

Figure 2b shows the transition that occurs when the class-4 job completes service. At this point, the class-4 job scans the queue to find the first job with which it is swappable, according to the swapping graph; this is the class-2 job. The class-4 job then takes the place of the class-2 job, which in turn begins to scan backwards in the queue in search of a job with which it is swappable. The first such job is the class-4 job in position 5 of the queue; hence the class-2 job takes the place of this job. This process continues, resulting in the class-4 job taking the place of the class-5 job immediately behind it. At this point, there are no jobs behind the class-5 job with which it is compatible, so the class-5 job departs from the system. The resulting state is (1, 4, 3, 2, 4, 2).

2.4 The open pass-and-swap queue

The main result of [12] is that the P &S queue admits the same product-form stationary distribution as the original OI queue. Many of our results in the sections that follow involve extending the proof of Theorem 2 to incorporate generalizations of the P &S queue. In other cases, we will identify scenarios in which the product-form no longer holds. Throughout, it will be instructive to refer back to the proof of Theorem 2, which we restate in its entirety in Appendix A.

Theorem 2

(Reproduced from Theorem 2 in [12]) Consider a P &S queue with job classes $\mathcal {I}=\{1,\dots ,I\}$, per-class arrival rates $\lambda _1,\dots ,\lambda _I$, and service rate function $\mu (\cdot )$. Let

$$\begin{aligned} G \equiv \sum _{c\in \mathcal {I}^*} \prod _{j=1}^{n} \frac{\lambda _{c_j}}{\mu (c_1, \ldots , c_j)}. \end{aligned}$$

(3)

Then the system is stable if and only if $G < \infty$. If the system is stable, then the queue is quasi-reversible and the stationary distribution $\pi (\cdot )$ satisfies:

$$\begin{aligned} \pi (c) = \pi (\emptyset ) \prod _{j=1}^{n} \frac{\lambda _{c_j}}{\mu (c_1, \ldots , c_j)}, \end{aligned}$$

(4)

where $\pi (\emptyset ) = 1/G$.

The proof of Theorem 2 involves establishing a set of partial balance equations that capture the dynamics of the system, then showing that the form given in (4) satisfies those equations. We will state the partial balance equations here because their form—and the notation used to define them—will be useful in the sections that follow; we defer the verification of the partial balance equations to Appendix A.

Before we give the partial balance equations, it will be helpful to define some additional notation. For any state $c=(c_1,\dots ,c_n)\in \mathcal {I}^*$ and any positions $p,q\in \{1,\dots ,n\}$ with $p\le q$, let $c_{p,\dots ,q} = (c_p,\dots ,c_q)$; if $p>q$ we define $c_{p,\dots ,q}\equiv \emptyset$.

For all states $c\in \mathcal {I}^*$ we will need to identify the set of states d such that it is possible to move from state d into state c due to a departure of a class-i job. Let u denote the maximum number of jobs that can be involved in the pass-and-swap transition that results in entering state c; note that this number u includes the class-i job that departs from the system. Furthermore, we denote by $\mathcal {I}_i$ the set of job classes that are swappable with job class i. Then, let $q_0,q_1,\dots ,q_u$ denote the sequence of positions that can be involved with the transition, where

$$\begin{aligned} q_v = {\left\{ \begin{array}{ll} n+1 &{} v=0 \\ \max \{q\le q_{v-1}-1~:~c_q\in \mathcal {I}_{i_{v-1}}\} &{} 0<v<u \\ 0 &{} v=u, \end{array}\right. } \end{aligned}$$

where $u = \textrm{argmin}_v\{ \{q\le q_{v-1}-1~:~c_q\in \mathcal {I}_{i_{v-1}}\} = \emptyset \}$.

We find that we can enter state c due to a departure of a class-i job from any state d of the form:

$$\begin{aligned} d= & {} c_{1,\dots ,p-1},i_v,c_{p,\dots ,q_v-1},i_{v-1},c_{q_v+1,\dots ,q_{v-1}-1},\dots ,c_{q_3+1,\dots ,q_2-1},i_1,\nonumber \\ {}{} & {} \quad c_{q_2+1,\dots ,q_1-1},i_0,c_{q_1+1,\dots ,n}, \end{aligned}$$

(5)

where $v\in \{0,\dots ,u-1\}$ denotes the number of jobs that are involved with the transition, and $p\in \{q_{v+1}+1,q_{v+1}+2,\dots ,q_v\}$ denotes the position of the job whose service completion initiated the pass-and-swap transition. Finally, we let $\delta _p(d) = (c,i)$ if, starting in state d, a service completion at position p causes the system to transition to state c, with a class-i job departing.

Example 4

Continuing with our running example, we now consider the state $c=(4,1,2,3,4,5,2)$ and $i=i_0=3$; we seek to identify the states d from which we can enter state c due to the departure of a class-3 job. Due to the swapping graph shown in Fig. 2a, we have $\mathcal {I}_3 = \{1,4\}$. By the definition of $q_v$ given above, we have $q_0=8$. We then have $q_1 = \max \{q\le q_0-1=7~:~ c_q\in \mathcal {I}_3=\{1,4\}\}$. That is, $q_1$ is the last position in the queue that contains either a class-1 or a class-4 job, thus $q_1 = 5$ and $i_1=4$. Continuing in this manner, $q_2$ is the last position before position 5 that contains a class-2, 3, or 5 job (because $\mathcal {I}_4 = \{2,3,5\}$; we thus have $q_2=4$ and $i_2=3$. By similar reasoning, we obtain $q_3=2$ and $i_3=1$. Finally, there are no jobs earlier than position 2 that are in $\mathcal {I}_1=\{3,5\}$, so we conclude that $u=3$ is the maximum number of swaps that can occur in a transition that results in state c due to a class-3 departure, and that $(q_3,q_2,q_1)=(2,4,5)$ gives the sequence of positions that could be involved in such a transition.

Following equation (5), the possible states d from which we can enter state c with a class-3 job departing from the system and for which $v=3$ have the form:

$$\begin{aligned} d = c_{1,\dots ,p-1},1,c_{p,\dots ,1},3,c_{3},4,3,c_{6,\dots ,7}. \end{aligned}$$

There are two states satisfying this form, namely states $d'=(4,1,3,2,4,3,5,2)$ and $d''=(1,4,3,2,4,3,5,2)$. In the latter case, one can easily verify that the service completion of the class-1 job will trigger a pass-and-swap transition that indeed results in state (4, 1, 2, 3, 4, 5, 2), with a class-3 job departing from the system. In the former case, the class-1 job does not receive any service due to the job-server compatibility structure described in Example 1; in this case, while the form of state $d'$ allows for the possibility of the desired transition, this transition in fact will never occur.

One can similarly enumerate the possible states d from which we can enter state c with a class-3 job departing from the system for $v=0, 1,$ and 2.

The partial balance equations used to show the result of Theorem 2 are as follows:

• For states $c\in \mathcal {I}^*\backslash \emptyset$, the flow out of state c due to a service completion equals the flow into state c due to a job arrival:

  $$\begin{aligned} \pi (c)\mu (c) = \pi (c_1,\dots ,c_{n-1})\lambda _{c_n}. \end{aligned}$$

  (6)

• For states $c\in \mathcal {I}^*$ and for each $i\in \mathcal {I}$, the flow out of state c due to a class-i arrival equals the flow into state c due to a class-i departure:

  $$\begin{aligned} \pi (c)\lambda _i = \sum _{d\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _p(d)=(c,i) \end{array}}^{n+1} \pi (d)\varDelta \mu (d_1,\dots ,d_p). \end{aligned}$$

  (7)

3 Closed networks of pass-and-swap queues

We now turn to closed networks of P &S queues. In Sect. 3.1 we present the model and briefly survey some results from [12], which will provide a starting point for the generalizations and counterexamples that we present in the sections that follow. In Sect. 3.2, we illustrate how a closed tandem of two P &S queues can be used to model many systems for which a product-form stationary distribution previously has been established, thereby motivating the two-queue closed tandem as a useful starting point for further study. Even though the two-queue network suffices for many applications, in Sect. 3.3 we extend the results of [12] to a many-queue network.

3.1 Closed network of two pass-and-swap queues in tandem

We consider a closed network consisting of two P &S queues in tandem, adopting the model and notation in Sect. 5.2 of [12]. In this setting both queues adhere to the same swapping graph, and a job that departs from one queue immediately joins the end of the other queue.

There is no external arrival process and there are no departures from the network as a whole; jobs simply move between the two queues. Each queue may operate according to its own service rate function; this function must satisfy the OI conditions given in Definition 1. The service rate function of the upper queue is given by $\mu (\cdot )$, while that of the lower queue is given by $\nu (\cdot )$. The state of the upper (respectively, lower) queue is denoted by $c = (c_1, \ldots , c_n)$ (respectively, $d = (d_1, \ldots , d_m)$), where n (respectively, m) denotes the number of jobs in the queue. We refer to the state of the system as a whole by (c; d). Let $|c|=(n_1,\dots ,n_I)$ (respectively, $|d|=(m_1,\dots ,m_I)$), where $n_i$ ($m_i$) denotes the number of class-i jobs in the upper (lower) queue, and define the macrostate of the system as $\ell =|c|+|d|=(\ell _1,\dots ,\ell _I)$. Observe that, because the system is closed, the macrostate $\ell$ is constant over time.

Fig. 3

The evolution of a closed network of two P &S queues, as described in Example 5

Example 5

Fig. 3 shows an example of a closed network consisting of two pass-and-swap queues in tandem. Both of the queues adhere to the swapping graph depicted in Fig. 2a. The initial state is $((5,1,4,3,2);\emptyset )$ as depicted in Fig. 3a. Suppose that the class-5 job at the head of the upper queue completes service. This triggers a pass-and-swap transition in which the class-5 job swaps with the class-1 job, which in turn swaps with the class-3 job. The class-3 job then leaves the upper queue and immediately joins the lower queue. The new system state is thus ((5, 4, 1, 2); (3)) (see Fig. 3b). Now suppose there is another service completion at the head of the upper queue; that is, the class-5 job again completes service. This time, a pass-and-swap transition occurs in which the class-5 job swaps with the class-4 job, which in turn swaps with the class-2 job, which leaves the upper queue and joins the back of the lower queue. The new system state is thus ((5, 1, 4); (3, 2)) (see Fig. 3c). Observe that, in all states depicted in Fig. 3, the class-5 job precedes the class-1 job in the upper queue. It is not hard to see that, by the virtue of both queues adhering to the swapping graph in Fig. 2a, no matter the order of the service completions in the sequel, this remains the case whenever both the class-5 job and the class-1 job are in the upper queue. Conversely, when both jobs will reside in the lower queue, the class-1 job will always be closer to the front of the lower queue than the class-5 job.

Example 5 draws attention to a key feature of the closed tandem of pass-and-swap queues: in general, there may be certain states that are not reachable given the initial state and the swapping graph. This is due to the placement order imposed by the initial state. A placement order can be interpreted as a partial order of job classes. In particular, this partial order is determined by assigning an orientation to each edge in the swapping graph to obtain a directed acyclic graph (DAG); we call this DAG a placement graph. For two job classes i and j, we write a $i \prec _A j$ if there is a directed path from i to j in placement graph A. We say that the network state $(c;d) = ((c_1, \ldots , c_n); (d_1, \ldots , d_m))$ adheres to a placement order A if and only if (1) $c_j \nprec _A c_i$ and $d_k \nprec _A d_l$ for $1 \le i < j \le n$ and $1 \le k < l \le m$, and (2) $d_j \nprec _A c_i$ for any $i \in \{1, \ldots , n\}$ and $j\in \{1, \ldots , m\}$. Proposition 4 in [12] tells us that when the initial network state adheres to the placement order A, then any state reached by applying the pass-and-swap mechanism to either of the two queues also adheres to this placement order. Furthermore, under certain assumptions, Proposition 5 in [12] implies that the set of states that adhere to the same placement order form a closed communicating class in the associated Markov chain. In the sequel, we will use $\varSigma _A$ to denote the set of all states (c; d) that adhere to a given placement order A.

Fig. 4

The directed acyclic placement graph depicting the placement order of the network states in Example 5

Observe that in Example 5, the initial state and the subsequent states in Fig. 3, as well as any other states that may follow, adhere to the placement order A depicted in Fig. 4.

We close this section by giving the stationary distribution of the closed tandem of two pass-and-swap queues, as derived in [12], and a related lemma. Several of our results in the sections that follow build upon the proof of Theorem 3, which is deferred to Appendix B.

Lemma 1

[12, Propositions 2 and 4] In a closed single P &S queue or a closed tandem of two P &S queues, it holds that if the initial state adheres to a placement order A, then any state reached by applying the P &S mechanism after any service completion also adheres to placement order A.

Theorem 3

[12, Theorem 5] Consider a closed network consisting of two pass-and-swap queues in tandem, and assume that the Markov process associated with the state space $\varSigma _A$ is irreducible for a given placement order A. Let $\varPhi (c)$ and $\varLambda (d)$ denote respectively the balance functions for the upper and lower queues. Then, for all states $(c;d)\in \varSigma _A$, the stationary probability that the system is in state (c; d) is given by:

$$\begin{aligned} \pi (c;d)&= \frac{1}{G}\varPhi (c)\varLambda (d), \end{aligned}$$

(8)

where G is a normalization constant given by:

$$\begin{aligned} G&= \sum _{(c;d)\in \varSigma _A} \varPhi (c)\varLambda (d). \end{aligned}$$

3.2 Applications of pass-and-swap queues

In the remainder of this paper, when considering extensions to the P &S queue in closed networks we will generally restrict attention to closed tandems of two P &S queues as regarded in the previous section. The primary rationale behind this focus is that the closed tandem of two P &S queues can be used to model many systems that are already known to have product-form stationary distributions. Hence, identifying extensions for the closed tandem of two P &S queues also yields possible extensions for these related product-form systems and the applications that they model. Below, we provide an overview of how several existing systems can be interpreted as P &S queues.

3.2.1 OI queues with rejections

In Sects. 2.2 and 2.4, we assume that the OI queue and the P &S queue have Poisson arrival processes. The product-form nature of the stationary distribution is in some cases retained when relaxing this assumption. For example, the OI queue continues to exhibit a product form when arrivals are rejected according the so-called truncation property [8]. In particular, let $\mathcal {C}$ comprise the set of states $c=(c_1, \ldots , c_n)$ such that an arriving class-i job is accepted when the system is in a state $c\in \mathcal {C}$ and rejected otherwise, and assume that the truncation property holds:

• (i) When $(c_1, \ldots , c_n) \in \mathcal {C}$, it holds for any permutation $c'$ of $(c_1, \ldots , c_n)$ that $c' \in \mathcal {C}$.

• (ii) When $(c_1, \ldots , c_n) \in \mathcal {C}$, we also have that $(c_1, \ldots , c_{n-1}) \in \mathcal {C}$.

The truncation property implies that if a job would be accepted with a given set of jobs in the queue, it will still be accepted if any job is removed from that set.

The OI queue with rejections can be modeled as a closed tandem of P &S queues, where the swapping graph is assumed to have no edges. In this view, the “upper” queue represents the OI queue with job rejections, while the “lower” queue represents the arrival process, as follows. We define the service process at the upper queue to be the same as that of the OI queue with rejections. When a job departs from the upper queue (due to a service completion), it joins the back of the lower queue. Similarly, the job departures from the lower queue form the arrivals to the upper queue, and hence govern the “net arrival stream” to the OI queue with rejections.

Recall that $\ell _i$ denotes the number of class-i jobs present in the closed network of P &S queues. For each class $i\in \mathcal {I}$, we will set $\ell _i = \max \{|c|_i: c \in \mathcal {C}\}$; that is, the number of class-i jobs present in the closed tandem is equal to the maximum number of class-i jobs that can be present in the OI queue with rejections. In this way, a class-i rejection from the OI queue because there are already $\ell _i$ class-i jobs present is now represented in the closed tandem by the scenario where all $\ell _i$ class-i jobs are present in the upper queue. In this case there are no class-i jobs in the lower queue, hence, a service completion in the lower queue cannot result in the arrival of an additional class-i job to the upper queue.

Observe that the lower queue contains exactly those jobs that could be accepted by the OI queue, given the state of the upper queue. To model the arrival process to the OI queue with rejections, we set the service process at the lower queue as follows. For all $i \in \mathcal {I}$, the service completion rate of the class-i job closest to the front of the queue is $\lambda _i$, and all other class-i jobs in the lower queue receive no service. Thus, $\varDelta \nu _i(d_1, \ldots , d_i) = \lambda _{d_i}\mathbb {1}_{\{d_i \notin \cap _{j=1}^{i-1}d_j\}}$. These service rates are easily verified to satisfy the order-independent conditions given in Definition 1, and are tantamount to each class i departing from the lower queue according to a Poisson process if and only if class-i jobs can be accepted to the OI queue whose state matches that of the upper queue. Indeed, the truncation property given above is equivalent to the dynamics of this tandem. Condition (i) is equivalent to the service process at the lower queue being independent of the order of jobs in the upper queue. Condition (ii) is a consequence of the fact that if the upper queue can have state $(c_1, \ldots , c_n)$, then it also can have state $(c_1, \ldots c_{n-1})$ with $c_n$ in the lower queue.

Having established a mapping from the OI queue with rejections to the closed tandem of two P &S queues, we can now apply Theorem 3 to obtain the stationary distribution of the OI queue with rejections:

$$\begin{aligned} \pi ((c_1, \ldots , c_n); (d_1, \ldots d_m))= & {} \frac{1}{G}\prod _{i=1}^n \frac{1}{\mu (c_1, \ldots , c_i)}\\ {}{} & {} \quad \prod _{j=1}^m \frac{1}{\sum _{k=1}^j \lambda _{d_k}\mathbb {1}_{\{d_i \notin \cap _{j=1}^{i-1}d_j\}}}. \end{aligned}$$

By aggregating over all permutations of $d=(d_1, \ldots , d_m)$, one recovers the expression derived in [8, Theorem 1] for the OI queue with rejections:

$$\begin{aligned} \pi ((c_1, \ldots , c_n)) = \frac{1}{G_{OI}}\prod _{i=1}^n \frac{\lambda _{c_i}}{\mu (c_1, \ldots , c_i)}, \end{aligned}$$

where $G_{OI}$ is a normalizing constant.

Example 6

Regard the closed tandem in Example 5, where the service rate function in the lower queue is given by $\nu _i(d_1, \ldots , d_i) = \lambda _i \mathbb {1}_{\{d_i \notin \cap _{j=1}^{i-1}d_j\}}$. Then, the upper queue behaves stochastically the same as an open OI queue with five job classes with arrival rates $\lambda _i$ and service rate function $\mu (\cdot )$, where jobs of any given class are rejected when there is already a job of the same class in the queue.

3.2.2 The noncollaborative service model with the ALIS policy

We next turn to the redundancy system with cancel-on-start service, which is equivalent to the so-called noncollaborative model [16] and also has been studied in the context of manufacturing and service systems, e.g. [29]. In this model, there are multiple machines $M_1, \ldots , M_J$ and multiple job classes $k=1, \ldots K$. Define $\mathcal {C}(M_j)$ to be the set of job classes that can be handled by machine $M_j$. When a job arrives, if it finds multiple idle compatible servers it must be assigned to exactly one of them. We consider the assign-longest-idle-server policy (ALIS), which was first studied in [3], but we will present it with a slightly different state descriptor and again add a rejection mechanism.

Each machine $M_j$, $j=1, \ldots , J$ provides service at rate $\mu _j$ and is able to serve jobs whose classes are in the set $\mathcal {C}(M_j)$. Class-k jobs arrive according to a Poisson process with rate $\lambda _k$. The system is permitted to contain at most $\mathcal {K}_k$ class-k jobs; hence, an arriving class-k job is accepted only if there are fewer than $\mathcal {K}_k$ jobs present. Once the arriving job is accepted, it checks whether there is any idle machine $M_j$ available such that $k \in \mathcal {C}(M_j)$. If so, it immediately enters service on whichever such machine has been idle the longest. If there are no such machines, the class-k job waits in the queue. When a machine $M_j$ completes service, it begins serving the compatible job that has been waiting the longest. If there are no such jobs, the machine becomes idle.

The state descriptor includes information about both the jobs present in the system as well as the status of the machines. We use $M_j$ to denote the corresponding machine, and we use $f_k$ to denote a job of class k. The state of the system can now be described by two-queue states. The main queue contains all busy machines and all jobs waiting for service, where the machines and jobs are collectively recorded in arrival order (for machines, we use the arrival time of the job currently in service). The auxiliary queue contains all idle machines and class-specific “slots” corresponding to jobs that would be accepted to the main queue given its current state; the machines and jobs are collectively ordered based on the order in which the machines became idle and the job slots became available. Note that the former must indeed be recorded to implement the ALIS mechanism described above.

We now illustrate the above state description and its evolution via an example.

Example 7

Consider a system with three machines, $M_1$, $M_2$ and $M_3$, and two different job classes, 1 and 2. Jobs of class 1 can be served by $M_1$ and $M_2$, while jobs of class 2 are compatible with $M_2$ and $M_3$: $\mathcal {C}(M_1) = \{1\}$, $\mathcal {C}(M_2) = \{1,2\}$ and $\mathcal {C}(M_3) = \{2\}$. Furthermore, the system can at most hold $\mathcal {K}_1=\mathcal {K}_2=2$ waiting jobs of each class (independent of how many jobs of each class are in service).

Figure 5 shows a possible state in this system. The main queue is depicted as the upper queue, and the auxiliary queue is the lower queue. In the initial state shown in Fig. 5a, the main (upper) queue has state $(M_2,M_1,f_1,f_1)$. This indicates that both servers $M_2$ and $M_1$ are busy processing jobs, and that the job in service at $M_2$ arrived to the system before the job in service at $M_1$; the state does not disclose the classes of the jobs in service. The state does disclose the classes of the waiting jobs: in this case, both waiting jobs are of class 1, and both arrived after those jobs that are in service on $M_1$ and $M_2$. The auxiliary (lower) queue has state $(f_2,f_2,M_3)$, indicating that machine $M_3$ is idle and up to two class-2 jobs could be accepted to the upper queue.

Suppose that $M_2$ now completes service; the state that results from this service completion is shown in Fig. 5b. In particular, the main queue enters state $(M_1, M_2, f_1)$ because the longest-waiting class-1 job enters service on machine $M_2$. This means that a slot opens up in the queue for an additional class-1 job, as indicated by the presence of $f_1$ in the auxiliary queue. Observe that, in the main queue, $f_1$ can never precede $M_1$ or $M_2$ due to the FCFS service order: it cannot be the case that $M_1$ or $M_2$, both of which are compatible with job class 1, would skip over the $f_1$ job to begin serving a job that arrived later. Similarly, $M_3$ (or, indeed, $M_2$) cannot precede $f_2$ in the auxiliary queue, as this would indicate that the machine started idling while a compatible job was still present in the main queue.

Now suppose that a class-2 job arrives to the system; the resulting state is shown in Fig. 5c. Because $M_3$ is the longest-idling machine that is compatible with class 2, the arriving job will immediately enter service on $M_3$. Meanwhile, the waiting slot for a class-2 job remains available. The auxiliary queue state thus becomes $(f_2, f_2, f_1)$, while $M_3$ moves to the back of the main queue. Note that if $M_2$ and $M_3$ were already in the main queue when a class-2 job arrived, there would be no idle compatible machine, so the arriving job would claim the waiting class-2 job slot, resulting in $f_2$ moving to the back of the main queue.

Fig. 5

The tandem of P &S queues modeling Example 7

Observe that the above example, and, in general, the noncollaborative ALIS system with job rejections, can be interpreted as a closed tandem of P &S queues. The swapping graph is a bipartite graph $G=(V,E)$ equivalent to the compatibility graph in the noncollaborative system. In particular, $V=V_{M} \cup V_{f}$, where $V_M = \{M_1, \ldots , M_J\}$ is the set of all machines and $V_{f} = \{f_1, \ldots , f_K\}$ is the set of all jobs (slots). The edge set E reflects the compatibilities between machines and job classes: there exists an edge between $M\in V_M$ and $f_i\in V_f$ if and only if $i \in \mathcal {C}(M)$. Figure 6 depicts the swapping graph, as well as the orientation representing the placement order, associated with Example 7. Observe that, consistent with Example 7, the placement order is such that in the upper queue machines always precede the jobs of compatible classes, while in the lower queue the idling machines always succeed available job slots of compatible classes.

Fig. 6

The placement graph belonging to the closed tandem of P &S queues in Fig. 5

The closed tandem of P &S queues that models the noncollaborative ALIS system contains $J+\sum _{i=1}^K \mathcal {K}_k$ “jobs”: J of these are the machines $M_1, \ldots , M_J$, and the remainder represent, for each class $k=1,\ldots ,K$, the $\mathcal {K}_k$ waiting class-k job slots labeled $f_k$. The service rate function $\mu (\cdot )$ in the upper queue is such that $M_i$ completes at rate $\mu _i$, and the service rate allocated to any f-job (representing a waiting job) is zero. A transition in the upper queue where a machine $M_i$ takes the place of a waiting class-j job $f_j$ represents the completion of a service by machine $M_i$ such that $M_i$ begins serving the waiting class-j job, and the class-j job slot becomes available (i.e., $f_j$ moves to the lower queue). If machine $M_i$ completes service and finds no compatible waiting jobs in the upper queue, then no swaps will occur and $M_i$ begins an idle period in the lower queue.

At the same time, the service rate function $\nu (\cdot )$ in the lower queue is such that, for each job class j, the first job slot $f_j$ to appear in the queue receives service at rate $\lambda _j$, while all machines $M_i$ and all f-jobs that are not the first of their class receive no service. A transition in the lower queue where a class-j job slot $f_j$ takes the place of a machine $M_i$ represents the arrival of a class-j job that immediately begins service on machine $M_i$, so that $M_i$ moves to the upper queue and the class-j job slot remains available for class-j arrivals.

Having established that the noncollaborative service model with the ALIS mechanism and job rejections can be modeled as a closed tandem of P &S queues, we can apply Theorem 3 to obtain the product-form stationary distribution for this model. Indeed, Theorem 3 yields

$$\begin{aligned} \pi ((c_1, \ldots , c_n);(d_1, \ldots , d_m))= & {} \frac{1}{G} \prod _{j=1}^n \frac{1}{\sum _{i \in \{1, \ldots , j\}:c_i \in V_m} \mu _{q(c_i)}}\\ {}{} & {} \quad \prod _{k=1}^m \frac{1}{\sum _{i \in \{1, \ldots , k\}:c_i \in V_f} \lambda _{q(c_i)}}, \end{aligned}$$

where $q(M_j) = j$ and $q(f_k) = k$ for all machine types $j=1, \ldots , J$ and job classes $k=1, \ldots , K$. This result is consistent with, e.g., [3, Theorem 2.1] and [16, Theorem 3.9].

Remark 2

It is worth noting that in [12], it was shown that the closed network of two pass-and-swap queues in tandem is able to model a redundancy system with a so-called cancel-on-commit regime. This redundancy system is a generalization of the noncollaborative model with an ALIS-regime, where multiple jobs may be committed to a single machine.

3.2.3 Token-based central queues with order-independent service rates

In [5], a token-based central queueing model is considered that captures redundancy models with both cancel-on-start and cancel-on-complete service, as well as several matching models. In essence, the model considered in [5] coincides with the non-collaborative model, but allows for a more general service rate function. In particular, any machine $M_i$, which in [5] is called a token, does not necessarily provide service at constant machine-specific rate $\mu _i$, but instead, the machines (or tokens) provide service at order-independent rates. In other words, in the terminology of the non-collaborative service model, when the main queue is in state $(c_1, \ldots , c_n)$ it need not be the case that $\varDelta \mu (c_1, \ldots , c_i) = \mu _{q(c_i)}$ for all $c_i$ that represent machines. Instead, any order-independent service rate function $\mu (c_1, \ldots , c_n)$ is allowed, as long as $\varDelta \mu (c_1, \ldots , c_i) = 0$ whenever $c_i$ represents a waiting job.

P &S queues allow for any service rate function $\mu (c_1, \ldots , c_n)$ that satisfies the OI conditions given in Definition 1, hence the token-based central queue model also can be modeled using a closed tandem of two P &S queues. This follows the same mapping given in Sect. 3.2.2 for the noncollaborative model, where now we simply generalize the service rate function in the upper queue accordingly.

It is worth noting that the results in [5] assume a different machine/token-assignment policy than ALIS (this alternative policy is called random-assignment-to-idle-servers (RAIS) in [16]) and incorporate no job rejections. As a result, our interpretation of the token-based central queue model as a P &S system extends the results of [5] by incorporating the ALIS mechanism (an arriving job is assigned the longest idling compatible token) and job rejections. Indeed, using similar notation as for the noncollaborative service model, the stationary distribution for this model is given by

$$\begin{aligned} \pi ((c_1, \ldots , c_n);(d_1, \ldots , d_m)) = \frac{1}{G} \prod _{j=1}^n \frac{1}{\mu (c_1, \ldots , c_j)}\prod _{k=1}^m \frac{1}{\sum _{i \in \{1, \ldots , k\}:c_i \in V_f} \lambda _{q(c_i)}}. \end{aligned}$$

Remark 3

In the noncollaborative service model and token-based central queue above, we have incorporated job rejections. Job rejections allow the number of jobs in the closed tandem to remain finite: for every waiting class-k job allowed in the system, there is a class-$f_k$ job in the closed tandem. In principle, in a system without job rejections, an infinite number of jobs in the closed tandem would be required. However, the model without job rejections can be approximated arbitrarily closely by setting the $\mathcal {K}_k$-limits large enough that the effect of state space truncation becomes negligible.

3.3 Closed networks of many pass-and-swap queues in tandem

Despite the numerous applications for the two-queue closed network, it is natural to ask whether closed networks with a larger number of queues or more general topologies still yield a product-form solution. While we conjecture that the answer to this question is affirmative in general, establishing a product-form solution for arbitrary network topologies is not straightforward. In this section, we focus on closed networks of many pass-and-swap queues in tandem. Our analysis will establish the product-form nature of the stationary distribution when the number of queues is even; we will see that the case where the number of queues is odd is more complicated.

Consider a closed network of K pass-and-swap queues in tandem, all with the same swapping graph. Queue i has service rate function $\mu ^{(i)}(c^{(i)})$, where $c^{(i)} = (c_1^{(i)}, \ldots , c_{n^{(i)}}^{(i)})$ is the state of queue i, $i=1, \ldots , K$. The number $n^{(i)}$ thus reflects the number of jobs present in queue i. The complete state of the network is given by $\vec {c} = (c^{(1)}; \ldots ; c^{(K)})$. For $i=1, \ldots , K$, the macrostate of queue i is given by $|c^{(i)}|$. Furthermore, we define, with a slight abuse of notation, the network macrostate $|\vec {c}|$ to be the elementwise sum of the macrostates associated with each queue.

We assume that the queues are connected in tandem. That is, jobs departing from queue i join the back of queue $(i \mod K)+1$. Equivalently, jobs arrive at the back of queue i when they depart queue $g(i):= (i-1) + K\mathbb {1}_{\{i=1\}}$. Furthermore, we assume that the system starts in a certain network state $\vec {c}_{start}$. Due to the closed nature of the system, the network macrostate is at all times given by $|\vec {c}_{start}|$. We let $\varSigma _{start}$ denote the recurrent set of states that the network can reach when starting in state $\vec {c}_{start}$. This set may be non-trivial to determine. For example, in case of $K=2$, we have already seen that $\varSigma _{start}$ may not necessarily consist simply of all states in $\mathcal {I}^*\times \mathcal {I}^*$ for which the associated network macrostate equals $|\vec {c}_{start}|$, cf. Sect. 3.1.

To further specify the relationship between departures from one queue and arrivals to the next, it will be helpful to define the set $\varSigma _{i,\vec {c}}$. We say that a queue state $c'\in \varSigma _{i, \vec {c}}$ if and only if the network state $\vec {c}$ can be reached by having a service completion in queue g(i), before which queue g(i) was in state $c'$. This is formalized in the following definition.

Definition 2

For any queue $i \in \{1, \ldots , K\}$ and network state $\vec {c}\in \varSigma _{start}$, the set of queue microstates $\varSigma _{i,\vec {c}} \subset \mathcal {I}^*$ corresponding to queue i is defined such that $c'\in \varSigma _{i,\vec {c}}$ if and only if the following three properties are satisfied:

• 1. the macrostate of $c'$ satisfies $|c'| = |c^{(g(i))}|+e({c_{n^{(i)}}^{(i)}})$, where e(j) is an I-dimensional vector in which the j-th element is 1 and all other elements are 0,

• 2. the set of recurrent network states $\varSigma _{start}$ contains the network state $\left( c^{(1)}; \ldots ; c'; (c_1^{(i)}, \ldots , c_{n^{(i)}-1}^{(i)}); \ldots ; c^{(K)}\right)$ when $i>1$, or the network state $\left( (c_1^{(1)}, \ldots , c_{n^{(1)}-1}^{(1)}); c^{(2)}; \ldots ; c^{(K-1)}; c'\right)$ when $i=1$, and

• 3. there exists at least one $p\in \{1, \ldots , n^{g(i)}+1\}$ so that $\delta _p(c') = \left( c^{(g(i))}, c_{n^{(i)}}^{(i)}\right)$.

Theorem 4, which establishes a product-form stationary distribution for a closed tandem network of K pass-and-swap queues, requires the following assumption:

Assumption 1

The following statements are equivalent for any queue state $c' \in \mathcal {I}^*$, any queue i in the closed tandem, and network state $\vec {c}\in \varSigma _{start}$:

• 1. $c' \in \varSigma _{i, \vec {c}}$.

• 2. If $c'$ is the queue state of an open pass-and-swap queue with the same swapping graph as that of queue g(i) in the closed network, then the open queue can directly reach state $c^{(g(i))}$ from state $c'$ by a service completion, where a job of class $c_{n^{(i)}}^{(i)}$ departs the queue.

Having stated this assumption, we are now ready to present the main result of this section.

Theorem 4

Consider a closed tandem network with K pass-and-swap queues for which Assumption 1 holds, and suppose that $\varSigma _{start}$ is an irreducible class of network states. Then, for all $\vec {c}\in \varSigma _{start}$, the stationary distribution is given by

$$\begin{aligned} \pi (c^{(1)}; \ldots ; c^{(K)}) = \frac{1}{G}\prod _{i=1}^K\varPhi ^{(i)}(c^{(i)}), \end{aligned}$$

(9)

where $\varPhi ^{(i)}(c^{(i)}) = \prod _{j=1}^{n^{(i)}} \frac{1}{\mu ^{(i)}(c_1^{(i)}, \ldots , c_j^{(i)})}$ and G is a normalization constant such that $\sum _{\vec {c}\in \varSigma _{start}}\pi (\vec {c}) = 1$.

Proof

We will begin by establishing K sets of balance equations. That is, for $i=1, \ldots K$, we equalize the flow out of state $\vec {c}=(c^{(1)}; \ldots ; c^{(K)})$ due to a service completion at queue i with the flow into state $\vec {c}=(c^{(1)}, \ldots , c^{(K)})$ due to a job arrival at queue i. Note that such a job arrival coincides with a service completion at queue $g(i) = (i-1) + K\mathbb {1}_{\{i=1\}}$. This leads to the following K partial balance equations: for $i=1, \ldots , K$,

$$\begin{aligned}&\pi (c^{(1)}; \ldots ; c^{(K)})\mu ^{(i)}(c^{(i)}) \nonumber \\&\qquad = \sum _{c'\in \varSigma _{i, \vec {c}}} \sum _{\begin{array}{c} p=1\\ \delta _p(c')=(c^{(g(i))}, c_{n^{(i)}}^{(i)}) \end{array}}^{n^{(g(i))}+1}\pi \left( c^{(1)}; \ldots ; c'; (c_1^{(i)}; \ldots ; c_{n^{(i)}-1}^{(i)}), \ldots ; c^{(K)}\right) \varDelta \mu ^{(g(i))}(c'_1, \ldots , c'_p). \end{aligned}$$

(10)

We will now show that (9) satisfies (10) for all $i=1, \ldots , K$. First, by substituting (9) in (10), noting that $\varPhi (c^{(i)})\mu ^{(i)}(c^{(i)}) = \varPhi (c_1^{(i)}, \ldots , c_{n^{(i)}-1}^{(i)})$ and simplifying the result, we obtain the equation

$$\begin{aligned} \varPhi ^{(g(i))}(c^{(g(i))}) = \sum _{c'\in \varSigma _{i, \vec {c}}} \sum _{\begin{array}{c} p=1\\ \delta _p(c')=(c^{(g(i))}, c_{n^{(i)}}^{(i)}) \end{array}} ^{n^{(g(i))}+1}\varPhi ^{(g(i))}(c')\varDelta \mu ^{(g(i))}(c'_1, \ldots , c'_p). \end{aligned}$$

(11)

It is left to show that this equation holds. Applying (29) (which is shown in the proof of Theorem 2, or equivalently in [12, Eq. below (19)]) to the balance function $\varPhi ^{(g(i))}(\cdot )$, the state $c^{(g(i))}$ and the job class $i=c_{n^{(i)}}^{(i)}$, we obtain

$$\begin{aligned} \varPhi ^{(g(i))}(c^{(g(i))}) = \sum _{c'\in \mathcal {I^*}} \sum _{\begin{array}{c} p=1\\ \delta _p(c')=(c^{(g(i))}, c_{n^{(i)}}^{(i)}) \end{array}}^{n^{(i)}+1} \varPhi ^{(g(i))}(c')\varDelta \mu ^{(g(i))}(c'_1, \ldots , c'_p). \end{aligned}$$

(12)

Due to the definition of $\delta _p(c')$ and Assumption 1, we know that states $c'\in \mathcal {I^*}\backslash \varSigma _{i, \vec {c}}$ bring a zero contribution to the outer sum in the right-hand side of (12). As such, Equation (12), which was already known to hold true, reduces to (11), completing the proof. $\square$

3.3.1 Verifying assumption 1

Theorem 4 proves that a product-form solution holds under Assumption 1. Showing that this assumption indeed holds in general, however, is non-trivial. In this section, we verify the assumption when the number of queues K is even, provided that the service rate functions are such that, at any point in time, any job in the system can complete service. We also discuss why the assumption is harder to verify when K is odd. In the remainder of this section, we assume without loss of generality that each job in the system is of a unique type, cf. Remark 4.

In the following discussion, it will prove worthwhile to extend the notion of a placement order A that we introduced in Sect. 3.1 to a larger number of queues. Recall that the placement order is a partial ordering $\prec _A$ on the job classes, so that for two job classes i and j, it holds that $i \prec _A j$ whenever there exists a directed path from i to j in the placement graph A, which is a directed acyclic graph based on the swapping graph of the queues.

Definition 3

Consider the state $\vec {c} = \left( \left( c_1^{(1)}, \ldots , c_{n^{(1)}}^{(1)}\right) ; \ldots ; \left( c_1^{(K)}, \ldots , c_{n^{(K)}}^{(K)}\right) \right)$. We say that this state adheres to the placement order A whenever

• (i) $c_j^{(k)} \nprec _A c_i^{(k)}$ for $1\le i<j\le n^{(k)}$ and odd $k\in \{1, \ldots , K\}$,

• (ii) $c_i^{(k)} \nprec _A c_j^{(k)}$ for $1\le i<j\le n^{(k)}$ and even $k\in \{1, \ldots , K\}$, and

• (iii) $c_j^{(l)} \nprec _A c_i^{(k)}$ for $i\in \{1, \ldots , n^{(k)}\}$, $j\in \{1, \ldots , n^{(l)}\}$ and $1 \le k < l \le K$.

To show that Assumption 1 holds for any even K, we will make use of two propositions. The first states that no matter how the network state evolves, its placement order remains the same.

Proposition 1

Suppose that K is even. If the initial network state adheres to the placement order A, then any subsequent state reached by applying the pass-and-swap mechanism in any of the queues also adheres to the placement order A.

Proof

We follow the same proof approach as the proof of [12, Proposition 4] for the case $K=2$.

Due to symmetry, it suffices to show that the placement order is maintained after a service completion and subsequent application of the pass-and-swap mechanism at the first queue. That is, we consider a transition from state $\vec {c} = (c^{(1)}; c^{(2)}; c^{(3)}; \ldots ; c^{(K)})$ to state $\vec {d} = (d^{(1)}; d^{(2)}; c^{(3)}; \ldots ; c^{(K)})$ due to a service completion at the first queue, and we show that if $\vec {c}$ adheres to placement order A, then $\vec {d}$ also adheres to placement order A. Our approach will be to establish that the three properties of Definition 3 hold for state $\vec {d}$, provided that the original state $\vec {c}$ satisfies all three properties.

We begin with the first two properties. Observe that for $k\ge 3$ the queue state $c^{(k)}$ does not change throughout the transition, hence properties (i) and (ii) immediately apply for $k>3$. For $k=1$, [12, Proposition 2] proves that if $c^{(1)}$ satisfies property (i), and the pass-and-swap mechanism is triggered by the service completion of the job at position $p\in \{1, \ldots , n^{(1)}\}$, then the queue state $(d_{1}^{(1)}, \ldots , d_{n^{(1)}-1}^{(1)}, c_{p}^{(1)})$ also satisfies property (i). It is hence immediate that $d^{(1)} = (d_{1}^{(1)}, \ldots , d_{n^{(1)}-1}^{(1)})$ also satisfies property (i). The fact that $d^{(2)} = \left( c_{1}^{(2)}, \ldots , c_{n^{(2)}}^{(2)}, c_{p}^{(1)}\right)$ satisfies property (ii) follows from the fact that $\vec {c}$ itself satisfies Definition 3.

It remains to check the third property for state $\vec {d}$. Because $d^{(1)}$ only contains jobs that are also present in the queue state $c^{(1)}$, property (iii) for state $\vec {d}$ and $k=1$ follows from the fact that property (iii) holds for the original state $\vec {c}$ and $k=1$. Similarly, because $d^{(2)}$ only consists of jobs that are present in $c^{(1)}$ and $c^{(2)}$, property (iii) for $\vec {d}$ and $k=2$ follows from the fact that property (iii) also holds for the original state $\vec {c}$ and $k=1,2$. Finally, the fact that property (iii) holds for $k\ge 3$ is trivial by noting that $c^{(k)}$ for $k \ge 3$ does not change throughout the application of the pass-and-swap mechanism. $\square$

We will also require that all network states that correspond to a given placement order form a single closed communicating class of the Markov process.

Proposition 2

Assume that K is even, and that, for any queue state $c\in \mathcal {I}^*$, it holds that $\varDelta \mu ^{(k)}(c) >0$ for any $k\in \{1, \ldots , K\}$; that is, any job at any queue can complete service at any given point in time. Then, all network states $\vec {c}$ that adhere to the same placement order and have the same network macrostate form a single closed communicating class of the Markov process associated with the network state of the closed tandem network of pass-and-swap queues.

Proof

To prove this proposition, we follow the lines of the proof of [12, Proposition 5]. Given Proposition 1, it suffices to show that, for all states $\vec {c} = (c^{(1)}; \ldots , c^{(K)})$ and $\vec {d} = (d^{(1)}; \ldots , d^{(K)})$ that adhere to the same placement order, say A, and satisfy $|\vec {c}| = |\vec {d}|$, state $\vec {d}$ can be reached from state $\vec {c}$ with positive probability. We will show this by construction; specifically, we will identify a path of transitions from $\vec {c}$ to $\vec {d}$. Let $n^{(i)}$ and $m^{(i)}$ denote the number of jobs present in queue i in states $\vec {c}$ and $\vec {d}$, respectively.

Step 1: There is a path from state $\vec {c}$ to state $\hat{c}$, where

$$\begin{aligned}{} & {} \hat{c}=\left( \left( c_1^{(1)}, \ldots , c_{n^{(1)}}^{(1)}, c_{n^{(2)}}^{(2)}, \ldots , c_{1}^{(2)}, \ldots , c_1^{(K-1)},\ldots , c_{n^{(K-1)}}^{(K-1)}, c_{n^{(K)}}^{(K)}, \ldots , c_{1}^{(K)}\right) ; \emptyset ; \emptyset ; \ldots ; \emptyset \right) . \end{aligned}$$

The desired path is given as follows. As long as there are jobs in queue 2, we let the job at the back of queue 2 complete service, so that it moves to the back of queue 3; observe that this is possible due to our assumption that $\varDelta \mu ^{(k)}(c)>0$ for all queues k and states c. We repeat this for $n^{(2)}$ service completions, all of the job at the back of queue 2; at the end of this process queue 2 is empty. We then have $n^{(2)}$ service completions at queue 3, again all of the job at the back of the queue. At this point, all of the jobs that were originally in queue 2 are now in queue 4. We repeat this process in turn for queues $4,5,\ldots , K$. Because K is even, this leads to the state

$$\begin{aligned} \left( \left( c_1^{(1)}, \ldots , c_{n^(1)}^{(1)}, c_{n^(2)}^{(2)}, \ldots , c_{1}^{(2)}\right) ; \emptyset ; c^{(3)}; \ldots ; c^{(K)}\right) . \end{aligned}$$

We now repeat the above procedure for queues $3,\ldots ,K$, in that order. This leads to the state $\hat{c}$ as defined above. In particular, all jobs are present in the first queue, and queues $2,\ldots ,K$ are empty. Proposition 1 guarantees that state $\hat{c}$ adheres to placement order A, as we only used valid pass-and-swap transitions.

Step 2: There is a path from state $\hat{c}$ to state $\hat{d}$, where

$$\begin{aligned}{} & {} \hat{d}=\left( \left( d_1^{(1)}, \ldots , d_{m^{(1)}}^{(1)}, d_{m^{(2)}}^{(2)}, \ldots , d_{1}^{(2)}, \ldots , d_1^{(K-1)},\ldots , d_{m^{(K-1)}}^{(K-1)}, d_{m^{(K)}}^{(K)}, \ldots , d_{1}^{(K)}\right) ; \emptyset ; \emptyset ; \ldots ; \emptyset \right) . \end{aligned}$$

Observe that in both of states $\hat{c}$ and $\hat{d}$, all of the jobs are in queue 1. We will now briefly consider a closed network with a single queue, and relate the states $\hat{c}^{(1)}$ and $\hat{d}^{(1)}$ in this single-queue network. Due to property (i) in Definition 3, the queue state $\hat{c}^{(1)}$ adheres to placement order A in the sense of [12, Section 5.1]. Proposition 3 of [12] now implies that, in the single-queue closed network, any other queue state that also satisfies placement order A and that has the same macrostate $|\hat{c}^{(1)}|$ is reachable from state $\hat{c}^{(1)}$. In particular, state $\hat{d}^{(1)}$ is reachable from $\hat{c}^{(1)}$, where we can use an argument analogous to that given in step 1 above to show that state $\hat{d}^{(1)}$ adheres to placement order A.

We are now ready to return to our original K-queue network. By applying Proposition 3 of [12] to the first queue, we can reason that one can reach the network state $\hat{d}$. In particular, we will invoke the transitions implied by [12, Proposition 3], with one modification due to the fact that, in our network with $K>1$, a job x that completes service in queue 1 joins the back of queue 2, rather than being returned to the back of queue 1. Hence, we introduce a sequence of service completions of job x at queues $2,\ldots ,K$ in that order, so that job x joins the back of queue 1 again. In this way, the first queue evolves in the same way as in the closed single-queue network. The fact that one can reach $\hat{d}^{(1)}$ from state $\hat{c}^{(1)}$ in the single-queue network therefore implies that one can reach state $\hat{d}$ from state $\hat{c}$ in the K-queue network.

Step 3: There is a path from state $\hat{d}$ to state $\vec {d}$.

It is rather straightforward to see how, finally, we can reach state $\vec {d}$ from state $\hat{d}$. We begin with $m^{(K)}$ service completions at queue 1, where in each case the last job in the queue departs. At this point, the state of queue 2 is $\left( d_{1}^{(K)}, \ldots , d_{m^{(K)}}^{(K)}\right)$. We then have $m^{(K)}$ service completions at queue 2, each of the last job in the queue; after this sequence of transitions queue 2 is empty and the state of queue 3 is $\left( d_{m^{(K)}}^{(K)}, \ldots , d_{1}^{(K)}\right)$. We repeat this process $K-3$ more times, at queues $3,\ldots ,K-1$ successively, after which the state of queue K is $d^{(K)} = \left( d_{1}^{(K)}, \ldots , d_{m^{(K)}}^{(K)}\right)$, as desired.

We now follow a similar procedure to establish the desired queue state, $d^{(K-1)}$, at queue $K-1$; this process consists of $m^{(K-1)}$ service completions of the last job in queue 1, then queue 2, and so on through queue $K-2$. Continuing in this vein, one can construct the desired queue states of queues $K-2,K-3,\ldots ,2$, after which queue 1 also has the desired state $d^{(1)} = \left( d_1^{(1)}, \ldots , d_{m^{(1)}}^{(1)}\right)$.

We have now shown that $\vec {d}$ is reachable from $\vec {c}$ by a certain sequence of transitions, each of which occurs with positive probability due to the assumption that any job in any queue can complete service at any given point in time. The proposition now follows. $\square$

Now that we have seen these two propositions, we can finally establish in the following lemma the fact that for even K, Theorem 4 may take effect.

Lemma 2

Under the conditions of Proposition 2, Assumption 1 holds and Theorem 4 takes effect.

Proof

The first statement of Assumption 1 generally implies the second. Namely, by the third property of Definition 2, $c'\in \varSigma _{i,c}$ implies $\delta _p(c') = (c^{g(i)}, c_{n^{(i)}}^{(i)})$. This in turn immediately leads to the second statement of 1 due to the definition of $\delta _p(c')$.

It remains to be seen that the second statement of Assumption 1 also implies the first, or rather, that the second statement of Assumption 1 implies the three properties of Definition 2. The first of these properties is again rather straightforward: an open queue can directly reach state $c^{(g(i))}$ from state $c'$ by having a job of class $c_{n^{(i)}}^{(i)}$ depart the queue, hence state $c'$ consists of all jobs that are present in state $c^{(g(i))}$, plus a job of class $c_{n^{(i)}}^{(i)}$. This is tantamount to the first property. By definition of $\delta _p(c')$, the third property is also easily established.

Finally, we will establish the second property of Definition 2, and it is here that Propositions 1 and 2 come into play. Suppose without loss of generality that the starting state of the network adheres to placement order A. Together, Propositions 1 and 2 tell us that $\varSigma _{start} = \varSigma _A$, where $\varSigma _A$ is the set of all network states that share the same macrostate as $\vec {c}_{start}$ and adhere to placement order A. This means that we must have $\vec {c}\in \varSigma _A$. The second statement of Assumption 1 implies that the network can transition to state $\vec {c}$ from state $\vec {c}_{prev}:= \left( c^{(1)}; \ldots ; c'; \left( c_1^{(i)}, \ldots , c_{n^{(i)}-1}^{(i)}\right) ; \ldots ; c^{(K)}\right)$ when $i>1$ (or from $\vec {c}_{prev}:= \left( \left( c_1^{(1)}, \ldots , c_{n^{(1)}-1}^{(1)}\right) ; c^{(2)}; \ldots ; c^{(K-1)}; c'\right)$ when $i=1$) by having a particular job complete service in queue g(i). Indeed, such a transition is governed by the pass-and-swap mechanism, which behaves identically in the open queue and in the closed network. It now follows from Proposition 1 that the network state $\vec {c}_{prev}$ must also adhere to placement order A. We can see this by contradiction: if $\vec {c}_{prev}$ adhered to some other placement order $A^\prime \ne A$, then due to Proposition 1 state $\vec {c}$ also would adhere to placement order $A^\prime$, contradicting the previously established fact that $\vec {c}\in \varSigma _A$. In summary, we have $\vec {c}_{prev} \in \varSigma _A = \varSigma _{start}$, implying the second property of Definition 2, completing the proof. $\square$

We now briefly turn to the case of odd K and consider why it is harder to establish that Assumption 1 holds in this case. While we make no claim that a product-form cannot be established in case K is odd, or, in particular, that Assumption 1 does not hold for odd K, verifying this assumption is considerably more difficult in this case. First, we note that we have not established that an even K is a sufficient condition for Assumption 1 to hold, as we impose the additional requirement that any job present can complete service at any point in time. Furthermore, our argument for even K hinges on the fact that we can show $\varSigma _{start}=\varSigma _A$. On the other hand, the notion of a placement order fails for odd K, meaning that there is no straightforward equivalent of Propositions 1 and 2. The same problem arises when one generalizes the network topology to something other than a tandem structure. In these cases, different methods will be necessary to identify the set $\varSigma _{start}$; we leave this for future work.

Remark 4

In this section, we assumed that each job in the closed system is unique without loss of generality. Absent this assumption, one may encounter situations with an even number of queues where the system state does not adhere to any placement order. For example, if the state of the first queue is (1, 2, 1), and an edge between job classes 1 and 2 exists in the swapping graph, then neither orientation of this edge will satisfy property (ii) in Definition 3.

Fortunately, this issue can be resolved by considering the isomorphic queue, which is a system with equivalent dynamics that introduces a unique job class for every job in the system. We defer a detailed description of the isomorphic queue to Remark 9.

4 Swapping graphs

Consider a ride-sharing system in which customers arrive to the system and request a ride from their current location to a specified destination. At any moment in time there is some set of available drivers; when a customer requests a ride she is assigned to a waiting driver. There may be compatibility restrictions that limit the drivers to whom this rider can be assigned; for example, a customer consisting of a group of people can only be assigned to a driver with a sufficiently large vehicle, a customer who is traveling a long distance can only be assigned to a driver who is willing to take a long trip, and so on. This ride-sharing model can be thought of as a noncollaborative system as described in Sect. 3.2.2, and hence can be modeling using a closed tandem of two P &S queues, yielding a product-form stationary distribution.

A notable feature of ride-sharing services is that the set of drivers need not be fixed over time. Indeed, typically drivers will enter and leave the system over time; hence, there may be periods of time when there are, e.g., very few drivers willing to take long trips, and other periods of time when there are many such drivers. Unfortunately, the P &S queue as described in [12] is not sufficiently general to model changes in the composition of the driver pool. This is because [12] imposes the restriction that the same swapping graph is utilized throughout the entire lifetime of the system. In contrast, drivers coming and going can be interpreted as the driver-rider compatibility graph—and hence, in the P &S system, the swapping graph—evolving over time.

The application of time-varying compatibility graphs motivates us to ask whether it is possible to relax the restriction that the swapping graph remain fixed without sacrificing the product-form nature of the stationary distribution. We begin by considering open systems (Sect. 4.1) and then proceed to closed systems (Sect. 4.2).

4.1 Open systems

We introduce a Markov-modulated process that evolves independently of the queue state of the system; the swapping graph that is used when a service completion occurs at time t is determined by the state of this modulating process at time t. Specifically, let $\{X(t): t \ge 0\}$ be a continuous-time Markov chain with state space $\mathcal {S}$. Its generator matrix $Q=(q_{i,j})_{i,j \in \mathcal {S}}$ is specified by its elements $q_{i,j} \ge 0$, where $q_{i,i} = -\sum _{j \in \mathcal {S}\backslash i} q_{i,j}$. We also introduce $\rho (b) = \lim _{t\rightarrow \infty } \mathbb {P}(X(t) = b)$ for $b\in \mathcal {S}$. Each state b has an associated swapping graph G(b); pass-and-swap transitions occur according to the swapping graph G(b) whenever $X(t) = b$.

The introduction of the modulating process necessitates an expansion of the state space used to describe the complete system. As specified before, the state space underlying a traditional P &S queue is the Kleene closure $\mathcal {I}^*$ of the finite set $\mathcal {I}$ of customer classes. Upon introducing the modulating process, the system state now not only includes the queue composition, but also the state of the modulating Markov chain. Therefore, the state space of the complete system now is $\mathcal {I}^* \times \mathcal {S}$. Equivalently, the state of the system is now represented by (c; b), where $c=(c_1, \ldots , c_n)\in \mathcal {I}^*$ represents the queue composition and $b\in \mathcal {S}$ represents the state of the modulating process.

We are now ready to derive the stationary distribution of the P &S queue with a Markov-modulated swapping graph.

Theorem 5

The stationary distribution $\sigma (c;b)$ of the modulated system is given by

$$\begin{aligned} \sigma (c;b) = \pi (c)\rho (b), \end{aligned}$$

(13)

where $\pi (c)$ is the stationary probability of state c in the unmodulated system.

Proof

We will modify the balance equations (6) and (7) used in the proof of Theorem 2 to account for the state of the modulating chain as well as the queue state. Let $\sigma (c_1, \ldots , c_n; b)$ be the stationary distribution of the modulated system, with $c=(c_1, \ldots , c_n)\in \mathcal {I^*}$ and $b \in \mathcal {S}$. We consider the following partial balance equations:

• 1. For all states (c; b) such that $c\in \mathcal {I}^*\backslash \emptyset , b \in \mathcal {S}$, the rate out of state (c, b) due to a departure is equal to the rate into state (c, b) due to an arrival:

  $$\begin{aligned} \sigma (c; b)\mu (c) = \sigma (c_1, \ldots , c_{n-1}; b)\lambda _{c_n}. \end{aligned}$$

  (14)

• 2. For all job classes $i\in \mathcal {I}$ and for all states (c; b) such that $c \in \mathcal {I}^*, b \in \mathcal {S}$, the rate out of state (c; b) due to the arrival of a class-i job is equal to the rate into state (c; b) due to the departure of a class-i job:

  $$\begin{aligned} \sigma (c; b)\lambda _{i} = \sum _{d \in \mathcal {I}^*}\sum _{\begin{array}{c} p=1 \\ \delta _p(d,b)=(c,i) \end{array}}^{n+1} \sigma (d;b)\varDelta \mu (d_1, \ldots , d_p). \end{aligned}$$

  (15)

  Note that we now write $\delta _p(d, b)$ where previously we wrote $\delta _p(d)$. This function still returns (c, i) if, given that the system is in state (d; b), a service completion of a job at position p will trigger a transition to state c with a job of class i departing the system. It is however worth noting that the sequence of swaps that occur upon a service completion now also depends on the modulating state b; recall that b determines the swapping graph G(b), according to which the pass-and-swap transition is made.

• 3. For all states (c; b) such that $c \in \mathcal {I}, b \in \mathcal {S}$, the rate out of state (c; b) due to a transition in the modulating chain is equal to the rate into state (c; b) due to a transition in the modulating chain:

  $$\begin{aligned} \sigma (c; b) \sum _{b'\in \mathcal {S}\backslash \{b\}} q_{b, b'}= \sum _{b' \in \mathcal {S}\backslash \{b\}} \sigma (c; b')q_{b', b}. \end{aligned}$$

  (16)

Observe that summing equation (14) over all $b \in \mathcal {S}$, equation (15) over all $i \in \mathcal {I}, b \in \mathcal {S}$, and equation (16) over all $b \in \mathcal {S}$ yields the global balance equations for the modulated system. Hence, the distribution $\sigma (c;b)$ that satisfies equations (14)-(16) represents the stationary distribution of the modulated system.

We will now show that (13) satisfies the partial balance equations (14)-(16). The fact that it satisfies equation (14) is trivial. To see that equation (15) holds, recall from the original pass-and-swap result in [12] that $\pi (c)\lambda _i = \sum _{d \in \mathcal {I}^*}\sum _{p=1; \delta _p(d) = (c,i)}^{n+1} \pi (d)\varDelta \mu (d_1, \ldots , d_p)$. Because this equation holds for any $\delta _p(d)$, it must also hold for $\delta _p(d,b)$ for any fixed b because the swapping graph (and thus also this function) remains unaltered over the course of a pass-and-swap transition. Finally, equation (16) holds because, recalling that $\rho (\cdot )$ is given to be the stationary distribution of the underlying modulating chain, we have $\rho (b)\sum _{b'\in \mathcal {S}\backslash \{b\}} q_{b, b'} = \sum _{b' \in \mathcal {S}\backslash \{b\}} \rho (c; b')q_{b', b}$. $\square$

Remark 5

From Theorem 5, it follows that the stationary distribution of the queue state is given by the distribution $\pi (\cdot )$, because $\sum _{b\in \mathcal {S}}\sigma (c;b) = \sum _{b\in \mathcal {S}}\pi (c)\rho (b) = \pi (c)$ for any $c\in \mathcal {I^*}$. This shows a remarkable independence between the stationary distribution of the state of the queue and the dynamics of the swapping graph.

Remark 6

Suppose that the swapping graph instead is chosen i.i.d. upon every service completion. From Theorem 5 and the previous remark, it immediately follows that, in this case, the queue content also has stationary distribution $\pi (\cdot )$. This result can be derived by choosing the modulating chain such that there is one state in the modulating chain corresponding to each possible swapping graph, and by choosing the stationary distribution of the modulating chain the same as the distribution according to which the swapping graph is chosen every transition. Then, we let the modulating chain run on a time scale that is infinitely faster than the time scale of the queue content, after which the claim follows.

4.2 Closed systems

We now consider closed networks of two P &S queues in tandem, as described in Sect. 3.1; similar results can be obtained for the single closed P &S queue. As was the case in the open system, we show in this section that these networks exhibit a product-form stationary distribution when the swapping graph is chosen according to an exogenous Markov modulated process. In particular, we show that the stationary distribution still exhibits a product form when the swapping graphs of both queues in the closed tandem are the same at all points in time, but are not necessarily constant. That is, we again assume that the swapping graph at both queues at time t is given by G(X(t)), where $\{X(t): t\ge 0\}$ is a continuous-time Markov chain with state $\mathcal {S}$ and generator matrix $Q = (q_{i,j})_{i,j \in {\mathcal {S}}}$ with stationary distribution $\rho (\cdot )$. We denote the complete state of the system by (c; d; b), where, as in Sect. 3, c and d denote respectively the states of the upper and lower queues, and b denotes the state of the modulating process. The following theorem now establishes the product-form nature of the stationary distribution of the complete system.

Theorem 6

For all states $(c;d;b)\in \varSigma _A\times \mathcal {S}$, the stationary distribution $\sigma (c;d;b)$ of the modulated closed system is given by:

$$\begin{aligned} \sigma (c;d;b)&= \pi (c;d)\rho (b), \end{aligned}$$

(17)

where $\pi (c;d)$ is the stationary distribution of state (c; d) in the unmodulated system; cf. Theorem 3.

Proof

We will modify the balance equations used in the proof of Theorem 3 (see Appendix B) to account for the state of the modulating chain as well as the queue states. We consider the following partial balance equations:

• 1. For all states $(c;d;b) \in \varSigma _A\times \mathcal {S}$ such that $c\ne \emptyset$, the flow out of the state due to a service completion at the upper queue equals the flow into the state due to a service completion at the lower queue:

  $$\begin{aligned} \sigma (c;d;b)\mu (c) = \sum _{d'\in \mathcal {D}_{|d| + e_{c_n}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(d')=(d,c_n) \end{array}}^{m+1} \sigma (c_1, \ldots , c_{n-1}; d';b)\varDelta \nu (d_1', \ldots , d_p'). \end{aligned}$$

  (18)

• 2. Similarly, for all states $(c;d;b) \in \varSigma _A\times \mathcal {S}$ such that $d \ne \emptyset$, the flow out of the state due to a service completion at the lower queue equals the flow into the state due to a service completion at the upper queue:

  $$\begin{aligned} \sigma (c;d;b)\nu (d) = \sum _{c'\in \mathcal {C}_{|c| + e_{d_m}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(c';b)=(c,d_m) \end{array}}^{n+1} \sigma (c'; d_1, \ldots , d_{m-1};b)\varDelta \mu (c_1', \ldots , c_p'). \end{aligned}$$

  (19)

• 3. For all states $(c;d;b)\in \varSigma _A\times \mathcal {S}$, the rate out of state (c; d; b) due to a transition in the modulating chain is equal to the rate into state (c; d; b) due to a transition in the modulating chain:

  $$\begin{aligned} \sigma (c;d;b) \sum _{b'\in \mathcal {S}\backslash \{b\}} q_{b,b'} = \sum _{b'\in \mathcal {S}\backslash \{b\}} \sigma (c;d;b') q_{b',b}. \end{aligned}$$

  (20)

We will now show that (17) satisfies the partial balance equations (18)-(20). One can see immediately that (17) satisfies (18) if and only if

$$\begin{aligned} \pi (c;d)\mu (c) = \sum _{d'\in \mathcal {D}_{|d| + e_{c_n}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(d')=(d,c_n) \end{array}}^{m+1} \pi (c_1, \ldots , c_{n-1}; d')\varDelta \nu (d_1', \ldots , d_p'). \end{aligned}$$

This is exactly equation (37), which was shown to hold in the proof of Theorem 3. That the partial balance equation (19) holds follows by a symmetric argument. Finally, equation (20) holds because $\rho (b)\sum _{b'\in \mathcal {S}\backslash \{b\}} q_{b, b'} = \sum _{b' \in \mathcal {S}\backslash \{b\}} \rho (b')q_{b', b}$, as $\rho (b)$ is the stationary distribution of the modulating Markov process. $\square$

5 Limits on the number of swaps

A major open question in the study of redundancy systems is how the scheduling policy affects performance. While [4] presents a conjecture that the stationary distribution of the cancel-on-complete redundancy system coincides under FCFS and random order of service (ROS) scheduling, [18] provides numerical evidence suggesting that this conjecture is false; to date, the question is unresolved. The challenge lies in the fact that, while the stationary distribution under FCFS is known [17], there is no existing closed-form analysis for ROS.

One could imagine studying the system under ROS by framing the ROS policy in terms of the P &S mechanism. To see how to do this, we will start by considering an M/M/1 with a single job class. Under ROS, if there are n jobs in the system then, upon a service completion, all jobs are equally likely to depart, each with probability 1/n. To model this using a P &S queue, we will use a complete swapping graph (i.e., the swapping graph has a self-loop from the one job class to itself). In order for the job in position i to depart, it must be the case that the P &S transition terminates after $i-1$ swaps. Unfortunately, the standard P &S mechanism cannot capture this behavior, as it will terminate after $n-1$ swaps when there are n jobs in the system. Instead, we will introduce a randomly-chosen, state-dependent limit on the number of swaps that can occur as part of a P &S transition. In particular, when there are n jobs in the system we set the swapping limit to i with probability 1/n, for all $0 \le i \le n-1$.

In the redundancy system, upon a service completion all jobs that are compatible with the completing server—not necessarily all jobs in the system—are equally likely to depart. Hence, in order to model ROS in the redundancy system, the state-dependent swapping limit that one needs to impose becomes more complicated. This limit now needs to depend not only on the total number of jobs in the system, but also on the number of jobs in the system that are compatible with the completing server. Nonetheless, we can still cast the redundancy system under ROS as a P &S queue with randomly-chosen, state-dependent limits on the number of swaps. A proof that one can impose such swapping limits in the P &S queue without changing the stationary distribution would thus constitute a proof that the redundancy system admits the same stationary distribution under ROS and under FCFS.

The above application motivates us to introduce the notion of a swapping limit w. We modify the original pass-and-swap mechanism as follows: As usual, a job service completion triggers the start of a pass-and-swap transition. Unlike in the original pass-and-swap queue, now this transition is permitted to involve at most w swaps. That is, the w-th job to be ejected from its original position must depart from the system, even if there are jobs in the remainder of the queue with which this job is eligible to swap according to the swapping graph.

We note two special cases. The case $w=0$ corresponds to an OI queue because, when $w=0$, a job that completes service will immediately depart from the system without swapping positions with any other job. Similarly, the case $w=\infty$ corresponds to the standard P &S queue, as this setting induces no actual swapping limit.

Example 8

Consider a P &S queue consisting of three job classes, namely 0, 1, and 2, where the vertex set of the swapping graph is $V=\{0,1,2\}$ and the edge set of the swapping graph is $E=\{(0,1),(1,2)\}$ (i.e., the swapping graph is a path on three vertices). Let the service discipline be first-come first-served, so that the first job in the queue receives service at rate $\mu$, and all other jobs receive no service (i.e., rate 0). We consider three different swapping limits.

• $w=1$. In this case only a single swap may be performed after a job completes service. Thus, when the job at the head of the queue completes service, the first job in the queue with which it is swappable, if any, will depart from the system. For example, when the queue is in state $c=(0,0,2,1,0,2,1)$ and the class-0 job at the head of the queue completes service, the first class-1 job will depart from the system, resulting in state (0, 2, 0, 0, 2, 1). Note that the pass-and-swap transition terminates at this point, even though there are other jobs in the remainder of this queue that are swappable with class-1.

• $w=2$. Suppose again that the queue begins in state $c=(0,0,2,1,0,2,1)$. When the class-0 job at the head of the queue completes service, it will swap with the first class-1 job as in the case where $w=1$. Now, one more swap is permitted, so the class-1 job will in turn swap with the class-2 job behind it. At this point the swapping limit has been reached, so this class-2 job will depart from the system (even though it is swappable with the class-1 job at the back of the queue). The new state is thus (0, 2, 0, 0, 1, 1).

• $w>2$. Here the swapping limit no longer plays a role, as the unconstrained pass-and-swap transition involves only three swaps. In this case, the class-2 job does swap with the final class-1 job, which then departs from the system, resulting in state (0, 2, 0, 0, 1, 2).

Swapping limits are a particularly intriguing area of study because, as we will see, in some cases the introduction of a swapping limit preserves the product-form stationary distribution, while in other cases it does not. In particular, in Sect. 5.1 we will show that open (networks of) pass-and-swap queues with a finite, non-degenerate swapping limit do not admit product form stationary distributions in general. On the other hand, we find in Sect. 5.2 that in closed networks product-form solutions are still feasible in some cases.

5.1 Open systems

In this section we will show that introducing a swapping limit in an open system renders the product-form solution infeasible. In particular, we will identify the step in the argument at which the partial balance approach fails. We provide a counterexample, based on Example 8, to illustrate the problem.

Counterexample 1

The system described in Example 8 with $w=1$ does not admit a product-form stationary distribution.

Proof

In general, if the open system were to admit a product-form stationary distribution, then the following partial balance equations would be satisfied for all possible states $c\in \mathcal {I}^*$:

• When $c\ne \emptyset$, the flow out of state c due to a service completion equals the flow into state c due to a job arrival:

  $$\begin{aligned} \pi (c)\mu (c) = \pi (c_1,\dots ,c_{n-1})\lambda _{c_n}. \end{aligned}$$

  (21)

• For each $i\in \mathcal {I}$, the flow out of state c due to a class-i arrival equals the flow into state c due to a class-i departure:

  $$\begin{aligned} \pi (c)\lambda _i = \sum _{d\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _{p, w}(d)=(c,i) \end{array}}^{n+1} \pi (d)\varDelta \mu (d_1,\dots ,d_p). \end{aligned}$$

  (22)

Note that these equations are the same as (6) and (7), except for the function $\delta _{p, w}(d)$ in the second equation. Akin to the “original” function $\delta _{p}(d)$, the function $\delta _{p,w}(d) = (c, i)$ if, observing the swapping limit w, a service completion of the job in position p in state d leads to the state c, with a job of class i leaving the system. The difference with the original function $\delta _{p}(d)$ is that $\delta _{p, w}(d)$ observes the swapping limit w.

We now turn to Example 8 with $w=1$ and show that there exist states $c\in \mathcal {I}^*$ for which the second partial balance equation does not necessarily hold. As before, let n denote the number of jobs present in the system in state c. For any state c, the rate of leaving c due to a class-i arrival is equal to $\pi (c)\lambda _i$. Because we assume that the queue is stable, we have that $\pi (c)>0$ for any state c, making the left-hand side of the second partial balance equation positive. We proceed to inspect the right-hand side of this equation, focusing on the case $i=0$. In this particular example $\varDelta \mu (d_1,\dots ,d_p)=0$ for $p>1$, hence any contribution to the right-hand side of the equation occurs when $p=1$. Therefore, we only need to identify the states d for which $\delta _{1, 1}(d) = (c,0)$. For a class-0 job to depart the system, there must be a job of a swappable class (i.e., a class-1 job) at the head of the queue in state d. Moreover, the first class-0 job in the queue must be the first job in the queue that is not of class 1. Hence, the system state d prior to entering state c must be of the following form, for some $j\ge 0$:

$$\begin{aligned} (1,(j~\text {class-}1~\text {jobs}),0,(n-j-2~\text {jobs of any class})). \end{aligned}$$

However, given this form of state d, we conclude that state c must be of the following form:

$$\begin{aligned} ((j+1~\text {class-}1~\text {jobs}),(n-j-2~\text {jobs of any class})). \end{aligned}$$

Clearly, there exist states c that do not satisfy this form. This is enough to conclude that the partial balance equations will not hold for all states c: for any given state c, it is always possible to leave the state due to the arrival of any class (i.e., the left-hand side of (22) is positive), but there may exist a class i such that it is not possible to enter state c due to a class-i departure (i.e., the right-hand side of (22) is 0). $\square$

While the above discussion refers to a specific example, one can readily see that the problem that arises in Counterexample 1 will also occur in practically all non-degenerate cases. In particular, any state in $\mathcal {I}^*$ is reachable due to the general arrival process and the openness of the system. This makes it possible for situations like the one described above to occur, leaving the partial balance equations (21) and (22) without a solution and hence rendering a product-form stationary distribution infeasible.

The above counterexample sheds light on a necessary condition for partial balance to hold: it must be possible to enter any state c due to the departure of any job class. This condition may seem immediately apparent, as violating this condition eliminates the possibility that the system is reversible. However, explicitly stating this condition is useful in that it allows us to identify more easily cases in which partial balance, and, hence, a product-form stationary distribution, is out of reach.

Remark 7

One might wonder at this point whether it is possible to eliminate the problem identified above by introducing a probabilistically chosen swapping limit such that, upon each service completion, the swapping limit $w = i$ with probability $\omega _i$, $0 \le i < n$. Introducing the possibility that $w=0$, in particular, means that one can always enter state c from state (i, c) due to a class-i departure, thereby eliminating the immediate problem present in Counterexample 1.

Unfortunately, the probabilistically-chosen swapping limit does not suffice to recover the product-form stationary distribution. Consider the balance equation that arises in this setting that equates the flow out of state c due to a class-i arrival with the flow into state c due to a class-i departure; this is analogous to Equation (22), and is given by the following:

$$\begin{aligned} \pi (c)\lambda _i = \sum _{w=0}^{n-1} \omega _w \sum _{d\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _{p, w}(d)=(c,i) \end{array}}^{n+1} \pi (d)\varDelta \mu (d_1,\dots ,d_p). \end{aligned}$$

Now consider again the scenario given in Example 8, and focus on the case $i=0$. Recalling that in this example we allocate service rate $\mu$ to the first job in the system and rate 0 to all other jobs, we obtain:

$$\begin{aligned} \pi (c)\lambda _0 = \sum _{w=0}^{n-1} \omega _w \sum _{\begin{array}{c} d\in \mathcal {I}^*: \\ \delta _{1, w}(d)=(c,0) \end{array}} \pi (d)\mu . \end{aligned}$$

Observe that our swapping graph—the path on class nodes $\{0,1,2\}$—is such that a class-0 job cannot depart from the system at the end of a transition with $w>0$ swaps unless there is a class-1 job present in the system. Consider, for example, state $c=(1,1)$. We can enter this state due to a class-0 departure in the following ways:

• The previous state was (0, 1, 1) and the swapping limit was chosen to be $w=0$.

• The previous state was (1, 0, 1), and the swapping limit was chosen to be $w=1$.

• The previous state was (1, 1, 0), and the swapping limit was chosen to be $w=1$ or $w=2$.

The resulting partial balance equation for state $c=(1,1)$ is thus

$$\begin{aligned} \pi (1,1)\lambda _0 = \pi (0,1,1)\mu \omega _0 + \pi (1,0,1)\mu \omega _1 + \pi (1,1,0)\mu (\omega _1+\omega _2). \end{aligned}$$

At this point, one can see without too much difficulty that the form given in (4) satisfies this balance equation if and only if $\omega _1 = 0$, which corresponds to a setting in which either no swaps are permitted ($w=0$) or there is effectively no swapping limit ($w=2=n$).

5.2 Closed tandems

We now turn to the case of a closed network of two P &S queues in tandem with fixed swapping limits. We consider the same system structure as in [12] (see Sect. 3.1); the difference is that we now impose a limit on the number of swaps per transition. We assume that this limit, which we again refer to as w, is the same for both queues in the network.

Surprisingly, this case is considerably more intricate than the open queue. The argument that we make for the open queue in Counterexample 1 no longer applies: due to the absence of an external arrival process, it is not necessarily possible to reach all conceivable queue states.

To examine the closed tandem network of two P &S queues with swapping limits, we begin by setting up the partial balance equations that correspond to the underlying Markov chain. It is immediate to verify that these are given as follows:

• 1. The rate of leaving state (c; d) due to a service completion at the upper queue is equal to the rate of entering state (c; d) due to an arrival at the upper queue (that is, a service completion at the lower queue), provided $c\ne \emptyset$:

  $$\begin{aligned} \pi (c;d)\mu (c) = \sum _{d'\in \mathcal {D}_{|d| + e_{c_n}}} \sum _{\begin{array}{c} p=1 \\ \delta _{p, w}(d')=(d,c_n) \end{array}}^{m+1} \pi (c_1, \ldots , c_{n-1}; d')\varDelta \nu (d_1', \ldots , d_p'), \end{aligned}$$

  (23)

  where $\mathcal {D}_x$ refers to the set of all states d of the lower queue such that $|d| = x$. Moreover, as before, the function $\delta _{p, w}(d')$ returns (d, i) if, observing the limit w, a service completion at position p in state $d'$ leads to the state d, with a job of class i leaving the queue.

• 2. The rate of leaving state (c; d) due to a service completion at the lower queue is equal to the rate of entering state (c; d) due to an arrival at the lower queue (that is, a service completion at the upper queue), provided $d\ne \emptyset$:

  $$\begin{aligned} \pi (c;d)\nu (d) = \sum _{c'\in \mathcal {C}_{|c| + e_{d_n}}} \sum _{\begin{array}{c} p=1 \\ \delta _{p,w}(c')=(c,d_n) \end{array}}^{n+1} \pi (c'; d_1, \ldots , d_{m-1})\varDelta \mu (d_1', \ldots , d_p'), \end{aligned}$$

  (24)

  where $\mathcal {C}_x$ refers to the set of all states c of the upper queue such that $|c| = x$.

It is worth noting that, again, the only difference between these balance equations and those of the closed tandem without swapping limits (cf. (37) and (38)) lies in the function $\delta _{p, w}(\cdot )$. That is, due to the limit w a service completion may result in a transition to a different state, ceteris paribus.

Without further assumptions, in general the partial balance equations (23) and (24) do not necessarily have a solution. We illustrate this in Sect. 5.2.1. However, in Sect. 5.2.2, we prove that under certain conditions on the swapping graph and the initial state, a product-form solution is still guaranteed.

5.2.1 Counterexample in the absence of further conditions

We now provide an example of a closed network of two P &S queues in tandem with swapping limits, the stationary distribution of which defies the partial balance equations given in (23) and (24). Specifically, we identify a particular case where the partial balance equations fail to hold. This allows us to conclude, as was the case for the open queue, that closed tandem networks of P &S queues with swapping limits do not necessarily admit a product-form solution in the absence of further conditions.

Counterexample 2

Consider a closed tandem network of two P &S queues that contains four jobs spanning three job classes. In particular, the system contains a single class-1 job, a single class-3 job, and two class-2 jobs. Therefore, at any point in time we have that $|c|+|d| = (1,2,1)$. Define the service rate functions $\mu$ and $\nu$ such that the first job in each queue receives service rate 2 and all other jobs receive service rate 0. The swapping limit is $w=1$ in both queues, and the swapping graph for both queues constitutes the complete graph with the vertex set $\{1,2,3\}$ (i.e., each job class is swappable with any other).

The system described above does not admit a product-form stationary distribution.

Proof

Before we analyze its stationary distribution, we first consider the states of the Markov chain underlying this system. The state space of this Markov chain consists of (c, d) such that $|c|+|d| = (1,2,1)$. It is easy to verify that this Markov chain is irreducible: by having the jobs in the first position of either queue complete service in the correct order, any state in the state space can be reached from any other state. As a result, because the state space is finite, the irreducibility of the Markov chain implies that all states are positive recurrent; the unique stationary distribution corresponding to this Markov chain will assign a positive probability to all of the states.

We now consider the partial balance equations (23) and (24) for this closed tandem network. The key point in this counterexample is the fact that $\delta _{p, w}(\cdot )$ depends on the limit w.

Consider this system with no swapping limit, i.e., $w=\infty$. We will write the partial balance equation (23) for the state ((1, 2); (2, 3)). The right-hand side of this partial balance equation includes a sum over states $d'$ such that $\delta _{1,\infty }(d') = ((2,3),2)$. Observe that $d'=(2,3,2)$ is the only such state with $|d'| = (0,2,1)$; in this case, the service completion of the first class-2 job will cause it to swap with the class-3 job, which in turn swaps with the second and final class-2 job. The first balance equation (23) for the state ((1, 2); (2, 3)) then becomes

$$\begin{aligned} 2\pi ((1,2); (2,3)) = 2\pi ((1); (2,3,2)), \end{aligned}$$

In contrast, when the limit $w=1$ is imposed, we have $\delta _{1, 1}((2,3,2)) = ((2,2), 3)$ because the class-3 job is forced to leave the system due to the swapping limit. Furthermore, it is easy to verify that, due to the limit $w=1$ and the structure of the swapping graph, there are no states $d'$ with $|d'| = (0,2,1)$ such that $\delta _{1,1}(d') = ((2,3), 2)$. While such states can be found for other service completion positions p, we note that in this example only the first job in the queue receives service. As a result, (23) in this example yields

$$\begin{aligned} 2\pi ((1,2); (2,3)) = 0. \end{aligned}$$

This equation contradicts the earlier observation that the stationary distribution assigns a positive probability to each state d with $|d| = (1,2,1)$. Hence, the stationary distribution does not satisfy the partial balance equations, meaning that the stationary distribution cannot have a product-form in this case. $\square$

5.2.2 Product-form stationary distributions under further conditions

Counterexample 2 shows that closed tandem networks with swapping limits do not necessarily admit product-form stationary distributions. In this section, we study a non-trivial yet sufficient condition under which the closed tandem network with swapping limits is guaranteed to admit a product-form solution. This extra condition states that the swapping graph is a $(w+1)$-partite graph, where w is the swapping limit. In other words, this condition dictates that the vertex set of the swapping graph can be divided into $w+1$ independent sets, i.e. $w+1$ sets of vertices such that there is no edge between two vertices from the same set.

The following theorem presents the stationary behavior of the closed tandem network under this condition. We formulate the corresponding proof under the added assumption that each job is of a unique job class. We make this assumption for clarity of presentation, but without loss of generality, as explained in Remark 9 below.

Theorem 7

Consider a closed network of two P &S queues in tandem, and suppose that the swapping graph is $(w+1)$-partite. Then the following statements hold:

• 1. Suppose that the initial state (c; d) adheres to a placement order A for which the longest path in the corresponding swapping graph has length at most w. Then the stationary distribution coincides with the product-form stationary distribution of the “original” closed tandem network (i.e., $w=\infty$) as given in (8):

  $$\begin{aligned} \pi _{A}(c;d) = \frac{1}{G}\varPhi (c)\varLambda (d) \qquad \forall (c;d)\in \varSigma _a, \end{aligned}$$

  (25)

  where $\varSigma _a$ consists of all states (c; d) that adhere to the placement order A. As before,

  $$\begin{aligned} \varPhi (c_1, \ldots , c_n) = \prod _{p=1}^n\frac{1}{\mu (c_1, \ldots , c_p)} \text{ and } \varLambda (d_1, \ldots , d_m) = \prod _{p=1}^m\frac{1}{\nu (d_1, \ldots , d_p)}. \end{aligned}$$

• 2. There exists at least one placement order and initial state that satisfy the previous statement.

• 3. Let $A_1, \ldots , A_I$ denote the placement orders that correspond to all $I\ge 1$ orientations of the swapping graph in which the longest path has a length of at most w. Then each convex combination of the distributions $\pi _{A_i}(\cdot ; \cdot )$ (as given in (25)), for all $i \in \{1, \ldots , I\}$, also forms a stationary distribution.

In effect, this theorem shows that, under certain conditions, it is possible for a closed tandem network of P &S queues to have a product-form stationary distribution. We present the full proof of this theorem in Appendix C.

Remark 8

While we state Theorem 7 for a closed network of two P &S queues in tandem, the theorem can be extended straightforwardly to larger tandem networks with any even number of queues, given the results presented in Sect. 3.3. We opt to limit the presentation of Theorem 7 to two queues for the sake of notational concision.

It should be noted that Theorem 7 leaves open the question of what happens when the placement order of the initial state corresponds to an orientation which allows paths of lengths exceeding w. Extensive numerical experiments support the following conjecture concerning this scenario.

Conjecture 1

Suppose that the swapping graph corresponding to the queues of the closed tandem network is $(w+1)$-partite. A state (c; d) is transient if it adheres to a placement order A that corresponds to an orientation that allows for paths with a length greater than w.

Proving this conjecture appears challenging; we comment further on a possible approach in Appendix C. Provided that this conjecture is indeed valid, it implies that if the swapping graph is $(w+1)$-partite, then no matter the initial state the system will always evolve to a state with a placement order orientation in which the longest path is at most w, since all other states are transient. Theorem 7.1 then in turn indicates that if the swapping graph is $(w+1)$-partite, then the stationary distribution of the closed tandem network is always of product form. We proceed to illustrate and provide intuition for why these findings hold by means of an example.

Fig. 7

Swapping graph and placement orders for Example 9

Example 9

We consider a closed tandem network with five job classes, where the swapping graph is a path on five vertices. That is, the swapping graph has vertex set $V=\{1,2,3,4,5\}$ and edge set $E=\{(1,2), (2,3), (3,4), (4,5)\}$, cf. Figure 7a. It is easily verified that this swapping graph is bipartite. The swapping limit in both queues is given by $w=1$, so that this closed tandem network meets the conditions posed in Theorem 7 and Conjecture 1. The service rate functions at both queues are such that at all points in time, all jobs in the system receive service at rate one.

Suppose now that the initial state is $((1,3,5,4,2); \emptyset )$. It is easily verified that this initial state corresponds to the placement order A, where we have that $1\prec _A 2$, $3 \prec _A 2$, $3\prec _A 4$ and $5 \prec _A 4$ as depicted in Fig. 7b. Theorem 7.1 applies to this initial state, as there are no paths in Fig. 7b with length larger than $w=1$. This also exemplifies the existence as claimed in Theorem 7.2. Because of this, in this state, the system will behave as if $w=\infty$. That is, if the class-1 job completes service it will swap with the class-2 job, which in turn leaves the queue because there are no jobs behind it in the queue. Similarly, if either the class-3 or the class-5 job completes service, it will swap with the class-4 job, which in turn leaves the queue because there are no jobs behind it of class i such that $4 \prec _A i$.

The above argument indicates that the first transition out of the initial state is stochastically identical to this transition in the case where $w=\infty$ as studied in [12]. As a result, Lemma 1 also applies to this transition, and therefore the next state adheres to placement order A. Furthermore, any transition out of that state will involve at most one swap, regardless of the value of w, and hence will again behave stochastically identically to the network with $w=\infty$. By repeatedly applying this argument, we conclude that, as the network state evolves, the swapping limit w is never enforced. This means that the functions $\delta _{p,1}(\cdot )$ and $\delta _{p, \infty }(\cdot )$ yield the same output, and hence the partial balance equations (23) and (24) are identical for the cases $w=1$ and $w=\infty$. Therefore, the stationary distribution of the queue state when $w=1$ is equal to the product-form stationary distribution $\pi _A$ as given in (25), as it coincides with the distribution (8) derived in [12] for the case of $w=\infty$.

We next address Conjecture 1 for this particular example. To this end, we consider the initial state $((1,2,3,4,5); \emptyset )$. This state adheres to a placement order that includes a path of length $5 > w=1$ (see Fig. 7c). In this case, the swapping limit $w=1$ does play a role. For example, if the class-1 job completes service, then the system will transition to state ((1, 3, 4, 5); (2)), as the limit forces the class-2 job to leave the queue instead of swapping with the class-3 job (which would, in turn, ultimately lead to the class-5 job leaving the queue). Now consider the following sample path: from state ((1, 3, 4, 5); (2)) the class-3 job completes service, resulting in state ((1, 3, 5); (2, 4)); then the class-4 job complete service, resulting in state ((1, 3, 5, 4); (2)); and finally the class-2 job completes service, resulting in state $((1,3,5,4,2); \emptyset )$. At this point, we have reached the state that we considered earlier in this example; recall that, once we have reached state $((1,3,5,4,2); \emptyset )$, Lemma 1 will ensure that the system will never return to state $((1,2,3,4,5); \emptyset )$. As such, the latter state is transient, exemplifying Conjecture 1.

We now turn to Theorem 7.3. Observe that from state $((1,2,3,4,5); \emptyset )$ it is possible to reach recurrent states that adhere to a placement order different from the one depicted in Fig. 7c. For example, we can also reach the state ((4, 2); (5, 1, 3)) through the following evolution of states:

$$\begin{aligned} ((1,2,3,4,5); \emptyset )&\rightarrow ((1,2,3,4); (5)) \rightarrow ((1,2,3); (5, 4))\\ {}&\rightarrow ((1,3); (5, 4, 2)) \rightarrow ((1); (5, 4, 2, 3)) \rightarrow \\ (\emptyset ; (5, 4, 2, 3, 1))&\rightarrow ((4); (5, 2, 3, 1)) \rightarrow ((4, 3); (5, 2, 1))\\ {}&\rightarrow ((4, 3, 2); (5, 1)) \rightarrow ((4, 2); (5, 1, 3)). \end{aligned}$$

The placement order of state ((4, 2); (5, 1, 3)), which we refer to as B, is similar to that depicted in Fig. 7c except that all edges are oriented in the opposite direction. Due to this symmetry, once the system reaches state ((4, 2); (5, 1, 3)) it behaves as it would in the $w=\infty$ case. Thus $\pi _B$, the limiting distribution corresponding to placement order B, also is a stationary distribution of the Markov chain underlying this example, just like $\pi _A$. By standard Markov chain theory, this implies that any convex combination of $\pi _A$ and $\pi _B$ will also form a stationary distribution. Observing that there are no other placement orders that include paths of length at most $w=1$, we have found all possible stationary distributions, in accordance with Theorem 7.2.

The proof of Theorem 7 in Appendix C follows an approach similar to the arguments presented in the above example. That is, we show that once a network state adheres to a placement order in which all paths have length at most w, the system will adopt the corresponding limiting distribution; because the limit w is irrelevant once such a state has been reached, the resulting limiting distribution must be of product form. In Appendix C we also identify particular cases in which one can prove that Conjecture 1 holds.

It is important to stress that the swapping graph being $(w+1)$-partite, as posed in Theorem 7, is by no means a necessary condition for the network to have a product-form stationary distribution. There are trivial situations in which the nature of the swapping graph does not play a role. For example, if the swapping limit w exceeds the number of jobs present in the network, then clearly the system behaves as if there is no swapping limit. As such, the stationary distribution is then of product form by the findings of [12] (see Sect. 3.1). However, there are also other, less trivial, closed tandem networks in which the swapping graph is not $(w+1)$-partite but the stationary distribution nonetheless is product-form. The following example presents such an network.

Example 10

Consider a closed tandem network of two P &S queues in which there are three jobs, all of different classes. We assume that the swapping graph is complete, i.e. the vertex set is given by $V=\{1,2,3\}$ and the edge set is given by $E = \{(1,2), (1,3), (2,3)\}$. Furthermore, all jobs in the system receive service at rate one, and the swapping limit is set to $w=1$. The swapping graph is immediately seen not to be bipartite, hence Theorem 7 and Conjecture 1 do not apply.

In this system, the state space consists of 6$\times$4$=$24 states. That is, there are six possible permutations of the set $\{1,2,3\}$, and there are four ways to divide any such permutation between the two queues.

Due to the complete symmetry of this system, it is easy to verify that for any of the 24 possible states (c; d) we have $\pi ((c;d)) = \frac{1}{24}$, independent of the initial state of the system. Similarly, it is also easily seen that this stationary distribution satisfies the partial balance equations (23) and (24) and thus has a product form. Interestingly, in contrast to Example 9, the partial balance equations for $w=1$ are not the same as those for $w=\infty$. For example, with an initial state $(c;d) = ((1,2,3);\emptyset )$, the only states that can be reached without a swapping limit are $((1,2,3); \emptyset )$, ((1, 2); (3)), ((1); (3, 2)) and $(\emptyset ; (3,2,1))$. In the case of $w=1$, all 24 states can be reached from any initial state.

It remains an open question to formulate conditions which are both necessary and sufficient for a closed tandem network with finite swapping limits to allow for a product-form solution.

Remark 9

In this section, we have only considered examples where each job in the system is of a unique class, and as such, a placement order necessarily exists. However, in the absence of this assumption, one may encounter situations where a state does not adhere to any placement order. This issue can be addressed using an isomorphic queue [12], which we now illustrate.

Consider a closed tandem network in which the swapping graph has vertex set $V=\{1, 2\}$ (i.e., there are two job classes), and edge set $E = \{(1,2)\}$ (i.e., the two job classes are swappable). Then there exist states, for example $((1,2,1); \emptyset )$, that do not adhere to any placement order. In particular, in state $((1,2,1); \emptyset )$ the class-2 job both precedes and follows a class-1 job, so the placement order A would have to satisfy $1 \prec _A 2$ and $2 \prec _A 1$; this is not possible. Therefore, one may conclude that this state is not covered by Theorem 7.

The notion of an isomorphic queue allows us to identify an equivalent system for which Theorem 7 does apply, as discussed in [12, Appendix D.1]. The idea behind an isomorphic queue is that, for each job whose class appears more than once in the system, we introduce a new job class while otherwise maintaining the dynamics of the system. For state $((1,2,1),\emptyset )$, for example, we introduce job classes $1'$ and $1''$ and define an updated swapping graph in which both of these classes have the same neighbors as the original job class 1. Thus, we now consider the swapping graph with $V=\{1', 1'', 2\}$ and $E=\{(1', 2), (1'', 2)\}$. Finally, we relabel the class-1 jobs in the original state to be of classes $1'$ and $1''$, so that we now consider the state $((1',2,1'');\emptyset )$. As long as the service rate functions in this new system treat job classes $1'$ and job class $1''$ identically to job class 1, it is immediate to verify that this new system behaves identically to the original system. The benefit of this newly defined system is that each job now has a unique job class, and so each state satisfies a placement order. Therefore, in case $w=1$, Conjecture 1 now implies that $((1', 2, 1''); \emptyset )$ is a transient state of the adapted system, and thus so is $((1,2,1); \emptyset )$ in the original system.

Because we can repeatedly relabel jobs in this fashion without altering the dynamics of the queue, we are always able to define an isomorphic queue in which there is at most one job of each class. Therefore, the assumption of unique job classes is without any loss of generality. The idea behind this relabelling technique is made more precise in [12, Appendix D].

6 Discussion of open questions

In this paper, we have identified dimensions along which known product-form systems may be extended such that their stationary distribution remains of product form. In particular, we studied the recently developed pass-and-swap queue of [12], which departs from known product-form systems in that it introduces an intricate intra-queue routing mechanism. We found that this mechanism can be extended further while still preserving the product-form nature of the stationary distribution. Our first main result shows that if the swapping graph involved with the P &S queue is modulated by an exogenous Markov process, the stationary distributions of both the open queue and the closed network of two P &S queues in tandem exhibit a product form. Even stronger, the state of the queue and that of the modulating Markov process are statistically independent in stationarity, so that the stationary distribution of the queue state is the same as that of the unmodulated version. Our second main result shows that one can introduce a limit on the number of swaps performed in the intra-queue routing mechanism without necessarily sacrificing the product form of the stationary distribution. Indeed, in certain closed networks enforcing such a limit does not break the product-form nature of the stationary distribution. Both of these findings lead to open follow-up questions, which we discuss in this section and leave for future research.

Markov modulation of other system parameters

The fact that Markov modulation of the swapping graph preserves the product-form stationary distribution begs the question of whether other system parameters may be Markov modulated as well, while still preserving the product-form stationary distribution. For the arrival rate and service rate functions, it is unlikely that Markov modulation leads to a simple, product-form stationary distribution. Indeed, even for a system as simple as the M/M/1 queue, Markov modulation of the arrival and service rates leads to an intricate stationary distribution which is hard to express in closed form; see e.g. [30]. On the other hand, numerical experiments suggest that if we were to introduce Markov modulation on the swapping limit w in the closed tandem network studied in Sect. 5.2.2, the product-form nature may be retained. For example, suppose that we introduce to Example 9 a two-state modulating Markov process, where one state corresponds to a swapping limit $w=1$ and the other state to $w=\infty$ (i.e., there is no limit on the number of swaps). In this case there is solution to the partial balance equations for this system, and hence the stationary distribution is product-form.

Conjecture 2

Consider a closed network of two P &S queues in tandem, as described in Sect. 5.2.2, and suppose that the swapping limit w is determined by the state $b\in \mathcal {S}$ of an exogenous Markov process $\{X(t): t\ge 0\}$ with state space $\mathcal {S}$. Let (c; d; b) denote the state of the system. Then the stationary distribution $\pi (c;d;b)$ is of product form.

Non-Markovian modulation of system parameters

It is conceivable that Markov modulation of the swapping graph is not the only form of modulation that leads to a product form stationary distribution. Indeed, Remark 6 suggests that an independently drawn swapping graph for every pass-and-swap transition also leads to a product-form stationary distribution. In fact, these variations on the type of modulation all lead to the same stationary distribution for the queue state, which also coincides with that derived in [12] for the original, non-modulated P &S system. Furthermore, equations (4) and (8) surprisingly reveal that the stationary distribution is independent of the swapping graph in the non-modulated setting. Hence, we expect that modulating the swapping graph in any way—including according to a non-Markovian process—will not impact the stationary distribution.

Conjecture 3

Consider the single open P &S queue (Sect. 2.4) or the closed network of two P &S queues in tandem (Sect. 3). Suppose that the swapping graph is determined by the state $b\in \mathcal {S}$ of an exogeneous non-Markovian process $\{X(t): t\ge 0\}$ with state space $\mathcal {S}$. Let (c; b) (respectively, (c; d; b)) denote the state of the open (respectively, closed) system. Then the stationary distribution $\pi (c;b)$ (respectively, $\pi ((c;d;b)$) is of product form.

State-dependent parameters

It is also natural to ask whether system parameters, such as the service rate functions, can be made state-dependent while retaining the product form stationary distribution. Unlike the case of Markov modulation, we do not expect this to hold in general without imposing additional conditions. Observe that the proofs of Sect. 4 mainly consist of adding partial balance equations to those of Sect. 2 to account for the added Markov modulating dimension: the partial balance equations of Sect. 2 corresponding to changes in the queue state are unchanged. In contrast, in the presence of state-dependent system parameters the partial balance equations of Sect. 2 would now fundamentally change, adding increased complexity to the proof. Despite this complexity, we believe that this is nonetheless a worthy avenue of exploration. We note, for example, that unlike the examples described in this paper, in the original Order Independent queue (which the P &S queue itself extends) the service rate function $\mu (\cdot )$ may incorporate an extra factor depending on the number of jobs in the queue, as this does not violate Definition 1.

Other variations to the swapping graph

In addition to modulation to determine which of multiple swapping graphs one applies for a given pass-and-swap transition, it is also worth investigating whether there are other changes that one can make to the swapping graph without compromising the product form. For example, the results in [12] and in this paper all assume that the swapping graph is undirected. It can be seen without too much difficulty that one cannot introduce a directed swapping graph in an open P &S queue and still retain the product form; the argument is similar to that given in Counterexample 1 for swapping limits in an open system. In particular, consider for example a system with two classes of jobs, a swapping graph that contains only the directed edge from class 0 to class 1, and a service process that allocates rate $\mu$ to the first job in the queue and rate 0 to all other jobs. In such a system, it is not possible to enter states of the form $(1,\ldots ,1)$ due to a class-0 departure, yet it is possible to leave such states due to a class-0 arrival; hence, the corresponding partial balance equation cannot hold. Indeed, one would not expect the product form to be retained in this system, which corresponds to a two-class preemptive priority queue. Nonetheless, it is plausible that, just as we saw in Sect. 5.2.2 for swapping limits, there may be additional conditions that one could impose in a closed network that would allow a system with a directed swapping graph to admit a product-form stationary distribution. Identifying such conditions remains an open problem for future study.

Necessary and sufficient conditions for swapping limits in closed tandem networks

Our results in Sect. 5.2 answer many questions about the circumstances under which one can introduce a swapping limit while retaining the product-form stationary distribution, yet we leave other questions open. At present, Conjecture 1 has not yet been proven; we suggest a possible proof approach in Appendix C.2. Furthermore, while we have shown that $w+1$-partiteness of the swapping graph leads to a product-form stationary distribution in a closed network of two P &S queues in tandem, this does not mean that the $w+1$-partiteness is a necessary condition, as demonstrated by Example 10. To establish the full extent of product form stationary distributions in closed systems with swapping limits, a first step may be to develop an algorithm to easily identify all states that are reachable from a given initial state; this is itself a non-trivial task.

Alternative intra-queue routing mechanisms

The original P &S queue, as described in [12], was the first time an intra-queue routing mechanism was shown to yield a product-form stationary distribution. In this paper, we show that altering the intra-queue routing mechanism, in this case by introducing a swapping limit, can preserve this product-form stationary distribution. This begs the question of whether other intra-queue routing mechanisms—perhaps entirely unrelated to the pass-and-swap mechanism—can be implemented in the OI queue and still result in a product-form stationary distribution. Preliminary numerical experiments suggest that this is indeed possible; we thus leave this question open for future research.

Conjecture 4

There exist intra-queue routing mechanisms other than the pass-and-swap mechanism that also yield a product-form stationary distribution.

Broader classes of closed systems

One can also imagine exploring directions less related to those that we have explored in this paper to identify other dimensions in which product form models may be amenable to extension. For example, we have considered only closed systems for a very specific setting with an even number of P &S queues in tandem. Other network topologies are worthy of study, as they may exhibit different behavior. Topologies that involve more complex routing among queues will interact with placement orderings in more intricate ways; one can imagine that, in a sufficiently large and highly-connected network, the placement order of the initial state may cease to be relevant. One can imagine studying such questions using analytical strategies similar to those we employ in this paper. Alternatively, one may view each queue in the closed network as a single queue with external arrivals, where the arrival rates satisfy conditions akin to the OI conditions in Definition 1. As analyzed in [16], such queues may produce a product form stationary distribution as well.

Although this paper extends the space of known product forms in several dimensions—and identifies some boundaries of this space—the above list of open questions span a large range of different unexplored directions. As a result, we conclude that it remains an open problem to completely identify the class of systems that admit a product-form stationary distribution. We hope that the conjectures and open questions that we present here will serve as a useful guide to researchers seeking to expand our understanding of the space of product forms.

Appendices

A Proof of Theorem 2

Proof

We will show that the form given in (4) satisfies the following partial balance equations:

• For states $c\in \mathcal {I}^*\backslash \emptyset$, the flow out of state c due to a service completion equals the flow into state c due to a job arrival:

  $$\begin{aligned} \pi (c)\mu (c) = \pi (c_1,\dots ,c_{n-1})\lambda _{c_n}. \end{aligned}$$

  (26)

• For states $c\in \mathcal {I}^*$ and for each $i\in \mathcal {I}$, the flow out of state c due to a class-i arrival equals the flow into state c due to a class-i departure:

  $$\begin{aligned} \pi (c)\lambda _i = \sum _{d\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _p(d)=(c,i) \end{array}}^{n+1} \pi (d)\varDelta \mu (d_1,\dots ,d_p). \end{aligned}$$

  (27)

That the first partial balance equation holds for the form given in (4) follows immediately by the same argument that holds for OI queues.

The second partial balance equation differs from the corresponding equation for OI queues and requires additional care. Let

$$\begin{aligned} \varPhi (c_1,\dots ,c_n) = \prod _{p=1}^{n} \frac{1}{\mu (c_1,\dots ,c_p)} \end{aligned}$$

(28)

denote the balance function of the P &S queue. To show that (4) satisfies (27), it suffices to show that the balance function satisfies:

where the second equality follows from (5); recall that $v\in \{0,\dots ,u-1\}$ and $p\in \{q_{v+1}+1,q_{v+1}+2,\dots ,q_v\}$. In particular, we will show that the balance function satisfies (29) for all $n\ge 0$, $u\in \{1,\dots ,n+1\}$, states $c=(c_1,\dots ,c_n)\in \mathcal {I}^*$, job classes $i\in \mathcal {I}$, and decreasing integer sequence $q_0,q_1,\dots ,q_u$ such that $q_0=n+1$ and $q_u=0$, where $i_0=i$, $i_1=c_{q_1}$, $i_2=c_{q_2},\dots ,i_{u-1}=c_{q_{u-1}}$.

The proof will proceed by induction on u. For the base case, let $u=1$; note that this case corresponds to the standard OI queue, hence (29) holds with $i=i_0$.

For the inductive step, assume that (29) holds for all $u'<u$. We will now show that (29) continues to hold for $u\ge 2$. We begin by noting that the balance function satisfies:

$$\begin{aligned} \varPhi (c) = \sum _{p=1}^{n+1} \varPhi (c_{1,\dots ,p-1},i,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i). \end{aligned}$$

(30)

This follows from the proof of Theorem 1 for the original OI queue.

We are now ready to show the inductive case. Beginning by applying (30) to state c, we have:

$$\begin{aligned} \varPhi (c)&= \sum _{p=1}^{n+1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i_0) \end{aligned}$$

(31)

$$\begin{aligned}&= \sum _{p=1}^{q_1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i_0)\nonumber \\&\quad + \sum _{p=q_1+1}^{n+1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i_0) \end{aligned}$$

(32)

$$\begin{aligned}&= \left( \prod _{p=q_1}^{n} \frac{1}{\mu (c_{1,\dots ,p},i_0)} \right) \sum _{p=1}^{q_1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,q_1-1})\varDelta \mu (c_{1,\dots ,p-1},i_0) \nonumber \\&\quad + \sum _{p=q_1+1}^{n+1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i_0) \end{aligned}$$

(33)

$$\begin{aligned}&= \left( \prod _{p=q_1}^{n} \frac{1}{\mu (c_{1,\dots ,p},i_0)} \right) \varPhi (c_{1,\dots ,q_1-1})\nonumber \\&\quad + \sum _{p=q_1+1}^{n+1} \varPhi (c_{1,\dots ,p-1},i_0,c_{p,\dots ,n})\varDelta \mu (c_{1,\dots ,p-1},i_0). \end{aligned}$$

(34)

In the above derivation, (32) follows from splitting the sum at $q_1$, (33) follows from the definition of $\varPhi$ and the OI properties of $\mu$ (cf. Definition 1), and (34) follows by applying (30) to state $c_{1,\dots ,q_1-1}$ and class $i_0$.

We will now apply the inductive hypothesis in order to rewrite $\varPhi (c_{1,\dots ,q_1-1})$. In particular, let state $c'=c_{1,\dots ,q_1-1}$, so that the number of jobs in the system is now $n'=q_1-1$. We further let $i_1$ be the class of the departing job, so that $i_0'=i_1$, $i_1'=i_2,\dots ,i'_{u'-1}=i'_{u-2} = i_{u-1}$ and $q_0'=q_1=n'+1$, $q_1'=q_2,\dots ,q_{u-2}'=q_{u-1},~q'_{u'}=q'_{u-1}=q_u=0$. Then, for state $c'$, (29) gives:

Substituting (35) into (34) gives:

We again use the definition of $\varPhi$ and the fact that $\mu$ is order independent to obtain:

which yields the desired result, noting that the second summation is the missing term $v=0$ in the first summation. $\square$

B Proof of Theorem 3

Proof

We begin by defining some notation that allows us to partition the state space $\varSigma _A$. Let $\mathcal {X}=\{x\in \mathbb {N}^I~:~|x|\le \ell \}$ denote the set of possible macrostates of the upper queue, and let $\mathcal {C}_x$ denote the set of states $c=(c_1,\dots ,c_n)\in \mathcal {I}^*$ that adhere to placement order A and satisfy $|c|=x$. Then the set of possible (detailed) states for the upper queue is given by $\mathcal {C}=\bigcup _{x\in \mathcal {X}}\mathcal {C}_x$. Define $\mathcal {Y}$ and $\mathcal {D}_y$ similarly for the lower queue, so that the set of possible (detailed) states for the lower queue is $\mathcal {D}=\bigcup _{y\in \mathcal {Y}} \mathcal {D}_y$. Observe that if the state of the upper queue is $c\in \mathcal {C}$, then the lower queue can be in any state $d\in \mathcal {D}_{\ell -|c|}$, and vice versa. Hence, we can partition the state space $\varSigma _A$ as follows:

$$\begin{aligned} \varSigma _A&= \bigcup _{x\in \mathcal {X}} \mathcal {C}_x \times \mathcal {D}_{\ell -x} = \bigcup _{y\in \mathcal {Y}} \mathcal {C}_{\ell -y} \times \mathcal {D}_y. \end{aligned}$$

We will again make use of the function $\delta _p(c')$, which outputs $(c,i)\in \mathcal {I}^*\times \mathcal {I}$ if in the equivalent single open P &S queue, a service completion of the job in position p when the system is in state $c'$ will lead to state c, with a job of class i leaving the queue.

The proof now consists of showing that (8) satisfies the following partial balance equations:

• 1. For all states $(c;d) \in \varSigma _A$ such that $c\ne \emptyset$, the flow out of the state due to a service completion at the upper queue equals the flow into the state due to a service completion at the lower queue:

  $$\begin{aligned} \pi (c;d)\mu (c) = \sum _{d'\in \mathcal {D}_{|d| + e_{c_n}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(d')=(d,c_n) \end{array}}^{m+1} \pi (c_1, \ldots , c_{n-1}; d')\varDelta \nu (d_1', \ldots , d_p'). \end{aligned}$$

  (37)

• 2. Similarly, for all states $(c;d) \in \varSigma _A$ such that $d \ne \emptyset$, the flow out of the state due to a service completion at the lower queue equals the flow into the state due to a service completion at the upper queue:

  $$\begin{aligned} \pi (c;d)\nu (d) = \sum _{c'\in \mathcal {C}_{|c| + e_{d_m}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(c')=(c,d_m) \end{array}}^{n+1} \pi (c'; d_1, \ldots , d_{m-1})\varDelta \mu (c_1', \ldots , c_p'). \end{aligned}$$

  (38)

We will begin with the partial balance equation (38). Observe that, by definition of the balance function, $\varLambda (d)\nu (d) = \varLambda (d_1, \ldots , d_{m-1})$. One can then see that (8) satisfies (38) if and only if

$$\begin{aligned} \varPhi (c)= \sum _{c'\in \mathcal {C}_{|c| + e_{d_m}}} \sum _{\begin{array}{c} p=1 \\ \delta _p(c')=(c,d_m) \end{array}}^{n+1} \varPhi (c')\varDelta \mu (c_1', \ldots , c_p'). \end{aligned}$$

Recall that we have already shown (cf. (29) in the proof of Theorem 2) that $\varPhi$ satisfies

$$\begin{aligned} \varPhi (c)&= \sum _{c'\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _p(c')=(c,i) \end{array}}^{n+1} \varPhi (c')\varDelta \mu (c'_1,\dots ,c'_p). \end{aligned}$$

Applying this form to state $(c_1,\dots ,c_{n-1})$ and class $d_m$, we obtain:

$$\begin{aligned} \varPhi (c_1, \ldots , c_{n-1}) = \sum _{c'\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1 \\ \delta _p(c')=(c_1,\dots ,c_{n-1},d_m) \end{array}}^{n} \varPhi (c')\varDelta \mu (c'_1,\dots ,c'_p). \end{aligned}$$

(39)

Next, the form of $\varPhi$ given in (28) immediately implies that $\varPhi (c)\mu (c) = \varPhi (c_1,\dots ,c_{n-1})$. Combining this with (39) leads to

$$\begin{aligned} \varPhi (c)\mu (c) = \sum _{c'\in \mathcal {I}^*} \sum _{\begin{array}{c} p=1\\ \delta _p(c')=(c_1,\dots ,c_{n-1},d_m) \end{array}}^{n} \varPhi (c')\varDelta \mu (c'_1,\dots ,c'_p). \end{aligned}$$

(40)

By dividing both the left-hand side and the right-hand side of this equation by $\sum _{c'\in \mathcal {C}} \varPhi (c')$, we have established that (8) indeed satisfies (38).

The argument for the partial balance equation (37) is symmetric and hence is omitted. $\square$

C Proof of Theorem 7 and Study of Conjecture 1

In this section, we prove Theorem 7 and more closely inspect Conjecture 1. For ease of presentation, we assume that all jobs present in the system have a unique class. This assumption is without loss of generality, as discussed in Remark 9 and [12, Appendix D]. We first provide the proof of Theorem 7, after which we turn to Conjecture 1.

1.1 C.1 Proof of Theorem 7

We consider separately each of the three statements of Theorem 7, which we will refer to as Theorems 7.1, 7.2, and 7.3.

1.1.1 C.1.1 Theorem 7.1

We formalize the approach outlined in Example 9. Let A denote the placement order to which the initial state adheres. Recall that this placement order imposes an orientation on all edges in the swapping graph (V, E) which, by construction, results in a directed acyclic graph. If a path exists from vertex $u_0\in V$ to vertex $u_n \in V$ in the placement order graph, then for job classes $u_0$ and $u_n$, we have $u_0 \prec _A u_n$. More strongly, if this path is given by $u_0 \rightarrow u_1 \rightarrow u_2 \rightarrow \ldots \rightarrow u_n$, then there exists a state adhering to this placement order in which the service completion of the job with class $u_0$ triggers a transition consisting of n swaps, ultimately resulting in the job of class $u_n$ leaving the queue. That is, the placement order may force the class-$u_0$ job to take the position of the class $u_1$-job, which then takes the position of the class-$u_2$ job, continuing the transition until the class $u_{n-1}$ job takes the position of the class-$u_n$ job, which then leaves the queue. This leads us to the following observation.

Observation 1

If $w=\infty$ (i.e., there is no swapping limit), then each path in the oriented swapping graph corresponds to a P &S transition where a service completion of a job with the class corresponding to the origin vertex of the path results in the queue departure of a job with the class corresponding to the destination vertex of the path. Hence, the length of the longest path in the oriented swapping graph provides an upper bound on the number of jobs that can be involved in any P &S transition.

This observation is the core idea behind the proof of Theorem 7.1, which includes as an assumption that the orientation corresponding to the placement order of the initial state does not include paths longer than w. By Observation 1, this in turn means that, regardless of the swapping limit, each transition can include at most w swaps. Consequently, the swapping limit w will not be enforced.

Observation 1 implies that, when leaving the initial state, the system will behave identically to a system with no swapping limit. By Lemma 1, the same placement order will apply to the new state after this first transition. At this point Observation 1 will again apply, so that the following transition will not be influenced by the presence of the swapping limit. Through the repeated application of Lemma 1 and Observation 1, it follows that the Markov chain underlying the closed tandem network with a swapping limit $w<\infty$ is the same as that for the system with $w=\infty$. As a result, the stationary distribution follows from [12, Section 5.2], which is exactly the distribution presented in Theorem 7.1.

1.1.2 C.1.2 Theorem 7.2

We now turn to Theorem 7.2, which states that there always exists at least one initial state such that the corresponding placement order imposes an oriented swapping graph in which all paths have length at most w. To this end, the following lemma based on graph-theoretical arguments turns out to be useful.

Lemma 3

A swapping graph (V, E) is $(w+1)$-partite if and only if this graph has an acyclic orientation for which the longest path has length at most w.

Proof

This lemma is a direct consequence of the Gallai–Hasse–Roy–Vitaver theorem, cf. [21, Theorem 8.5]. Alternatively, one can argue as follows. If the swapping graph is $(w+1)$-partite, then the vertex set V of this graph can be partitioned into the subsets $V_1, \ldots V_{w+1}$ such that the edge set E contains no edges between two vertices from the same subset. Therefore, all edges $(u,v)\in E$ connect a vertex $u \in V_i$ to a vertex $v \in V_j$, where $i \ne j$. Now suppose that all edges are oriented from the vertex in the lower-indexed subset to the vertex in the higher-indexed subset. In this case, there cannot exist a path with length greater than w, proving one direction of the statement.

For the reverse direction, we are given that there exists an acyclic orientation in which the longest path has length at most w. Here, we identify all vertices with no incoming oriented edges and collect them in a set $V_1$. This set is necessarily non-empty, as the orientation is acyclic. Furthermore, there are no edges $(u,v)\in E$ for which $u,v \in V_1$, since the vertices in $V_1$ have no incoming edges. We repeat this process for the graph with vertex set $V\backslash V_1$ to create a set $V_2$; similarly, $V_2$ is necessarily non-empty and there are no edges $(u,v)\in E$ for which $u,v\in V_2$. We repeat this process until all vertices have been assigned to a subset. This process yields at most $w+1$ vertex sets because the longest path in the original orientation does not exceed w. These vertex sets are by construction independent, hence that the graph (V, E) is necessarily $(w+1)$-partite. $\square$

In essence, Lemma 3 implies that if a swapping graph is $(w+1)$-partite, it is always possible to orient its edges in an acyclic fashion so that all paths have length at most w. Because an acyclic orientation on the swapping graph defines a placement order, this lemma thus establishes the existence of a placement order disallowing paths larger than w. Let A denote such a placement order.

All that remains is to show that there exists an initial state that adheres to placement order A; we will do this by construction. Recall that all jobs have a unique class and that the set of job classes is equivalent to the vertex set V of the swapping graph. Because the placement order imposes an acyclic orientation on this swapping graph, there is always a job class $i_1\in V$ such that $i_1$ has no incoming edges. Let the job with class $i_1$ be the first job present in the lower queue. We now continue this process in the spirit of the proof of Lemma 3. That is, in the subgraph with vertex set $V_1:=V\backslash \{i_1\}$, we can select a job class $i_2\in V_1$ that has no incoming edges; let the job with class $i_2$ be the second job in the lower queue. One can keep selecting job classes $i_j$ and vertex sets $V_j:= V_{j-1}\backslash \{i_j\}$ in this way n times until $V_n:= V_{n-1}\backslash \{i_n\} = \emptyset$. The initial state is then given by $(c;d) = ((i_1,\ldots , i_n);())$, which by construction adheres to placement order A.

1.1.3 C.1.3 Theorem 7.3

We now study the third and final part of Theorem 7, which states that one can obtain a new stationary distribution for the system by taking any convex combination of the (product-form) stationary distributions corresponding to all I placement orders that disallow paths longer than w.

This statement follows quite straightforwardly from Theorems 7.1 and 7.2. That is, Theorem 7.2 states that $I\ge 1$, so that $A_1, \ldots A_I$ represent one or more placement orders corresponding to oriented swapping graphs in which all path lengths are at most w. Theorem 7.1 then provides for each of these placement orders $A_i$ a stationary distribution $\pi _{A_i}(\cdot ;\cdot )$. The statement now follows from standard Markov chain theory. Namely, because the stationary distributions $\pi _{A_1}(\cdot ;\cdot ),\dots ,\pi _{A_I}(\cdot ;\cdot )$ satisfy the partial balance equations given in (23) and (24), they must also satisfy the global balance equations of the associated Markov process. That is, if Q is the generator matrix of the closed tandem network, we have, with a slight abuse of notation, that $\pi _{A_i}Q = \vec {0}$ for any $i \in \{1, \ldots , I\}$, interpreting $\pi _{A_i}$ as a vector with the same dimension as the rows or columns of Q. But if all vectors $\pi _{A_i}$ satisfy the equation $xQ = \vec {0}$, then so does any convex combination of these vectors. As a result, this convex combination is also a stationary distribution.

1.2 C.2 Proof strategy for Conjecture 1

We now study Conjecture 1, which claims that, for a $(w+1)$-partite swapping graph, a state (c; d) is transient if the oriented swapping graph corresponding to its placement order includes paths of length greater than w. One possible approach to proving this conjecture is to show that, if the system starts in such a state (c; d), then with positive probability the Markov chain reaches a state $(c';d')$ that satisfies Theorem 7.1 (recall that, by Theorem 7.2, state $(c';d')$ is guaranteed to exist). Once the system reaches state $(c';d')$, by Lemma 1 and Observation 1 the placement order will not change any further. Thus, by showing that a path exists from state (c; d) to state $(c';d')$, one has effectively shown that the Markov chain does not return to the initial state (c; d) with probability one, meaning that state (c; d) is transient.

Numerical experiments suggest that such a path indeed always exists, but designing an algorithm that constructs an appropriate sample path for any general case seems non-trivial. While this would be easy if all jobs in the system were allocated a positive service rate at all times, we note that this condition does not hold in general. The OI conditions—which the service rate functions $\mu (\cdot )$ and $\nu (\cdot )$ must satisfy—only guarantee that the first job in each queue is allocated a positive service rate. Hence, our generic algorithm must construct the required sample paths by having only the first job in each queue complete service in the correct order.

The second challenge arises in determining in which order the first jobs in the upper and lower queues should complete. In particular, observe that some edges of the swapping graph associated with the placement order change orientation every time the swapping limit is enforced. While changing the orientation of some edges is exactly what we want to achieve (we want to find a sample path to a state corresponding to an orientation that disallows paths larger than w), it is not straightforward to see which jobs must complete in which order to accomplish a certain specified change in the placement order, or equivalently, the corresponding oriented swapping graph. Relatedly, it is not straightforward to see how the length of the longest path in the oriented swapping graph induced by the placement order is affected by a service completion.

We illustrate these challenges with the following example.

Example 11

Consider a closed tandem with swapping limit $w=1$ and four job classes, where the swapping graph is a path on four vertices, i.e., it has vertex set $V=\{1,2,3,4\}$ and edge set $E=\{(1,2),(2,3),(3,4)\}$.

Suppose that the initial state is $((1,4,2,3); \emptyset )$. This state induces a placement order A where $1 \prec _A 2 \prec _A 3$, hence the length of the longest path exceeds $w=1$. Because all jobs begin in the upper queue, the first step of our sample path must be for the class-1 job to complete service; this results in the state ((4, 1, 3); (2)). This new state induces a new placement order, B, in which $3 \prec _B 2$ as opposed to $2 \prec _A 3$. However, while $1 \prec _B 2 \not \prec _B 3$ as we wish, this transition creates the path $4\prec _B 3 \prec _B 2$, which also has length 2, still exceeding the swapping limit $w=1$.

One possible sample path to follow from this point is to have the first job in the upper queue complete service, followed by another completion at the upper queue, followed by a completion at the lower queue. Following this sample path, the system visits states $\{(1,4); (2,3)\}$, $\{(1); (2,3, 4)\}$ and $\{(1, 3); (2, 4)\}$. The placement order C induced by this final state satisfies $1, 3 \prec _C 2$, and $3 \prec _C 4$; the longest path in the corresponding oriented swapping graph has length 1. Thus, we have identified a sample path that achieves the desired result for this example.

While the above example illustrates a case in which it is possible to find an appropriate sample path, the example does not reveal a generally applicable strategy that is required for the proof of Conjecture 1. We thus leave the proof of this conjecture as an open problem; we emphasize, however, that numerical experiments suggest that the conjecture holds.