Matching queues with reneging: a product form solution

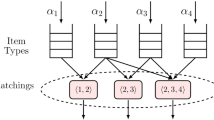
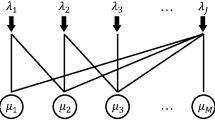
Abstract

Motivated by growing applications in two-sided markets, we study a parallel matching queue with reneging. Demand and supply units arrive to the system and are matched in an FCFS manner according to a compatibility graph specified by an N-system. If they cannot be matched upon arrival, they queue and may abandon the system as time goes by. We derive explicit product forms of the steady-state distributions of this system by identifying a partial balance condition.

Additional results

Proof of Proposition 1

The set of equilibrium equations that need to be verified are Eqs. (1)–(4), where we replace $\theta _s$ with zero. To simplify notation, define

$$\begin{aligned} x=\frac{\lambda _2}{\mu _2},\quad y=\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2}, \quad \text {and}\quad C=\frac{\mu _1}{\mu _1+\mu _2}. \end{aligned}$$

The key step is to compute

$$\begin{aligned} \sum _{k=0}^m\pi _{m-k,n+k+1}\mu _1\gamma _s(1-\gamma _s)^k\quad \text {and}\quad \sum _{k=1}^{m}\pi _{m-k,k}\mu _1(1-\gamma _s)^k. \end{aligned}$$

For the first, we have (for $n\ge 0$)

$$\begin{aligned}&\frac{1}{B}\sum _{k=0}^m\pi _{m-k,n+k+1}\mu _1\gamma _s(1-\gamma _s)^k\\&\quad = C\sum _{k=0}^{m-1} x^{m-k}y^{n+k+1}\mu _1\gamma _s(1-\gamma _s)^k+ y^{n+m+1}\mu _1\gamma _s(1-\gamma _s)^m\\&\quad = C\sum _{k=0}^{m-1} \left( \frac{x}{y}\right) ^{m-k}y^{m+n+1}\mu _1\gamma _s(1-\gamma _s)^k+ y^{n+m+1}\mu _1\gamma _s(1-\gamma _s)^m \\&\quad = y^{n+1}\mu _1\gamma _s\left( C x^m\sum _{k=0}^{m-1} \left( \frac{x}{y}\right) ^{-k}(1-\gamma _s)^k+ y^{m}(1-\gamma _s)^m\right) \\&\quad = y^{n+1}\mu _1\gamma _s\left( C x^m \frac{1-\left( \frac{y(1-\gamma _s)}{x}\right) ^m}{1-\frac{y(1-\gamma _s)}{x}}+ y^{m}(1-\gamma _s)^m\right) \\&\quad =y^{n+1}\mu _1\gamma _s x^m\\&\quad =C\lambda _1 y^{n} x^m,\\ \end{aligned}$$

where the last two equalities come from replacing the values of x, y and C. Similarly, we can verify that

$$\begin{aligned} \frac{1}{B}\sum _{k=1}^{m}\pi _{m-k,k}\mu _1(1-\gamma _s)^k=C\mu _2 x^m. \end{aligned}$$

Next, we proceed to verify the equilibrium equations. Equations (1) and (2) can be simplified by replacing the result derived above, which delivers

$$\begin{aligned} Cy^{n} x^m\left( \mu _1+\mu _2+\lambda _1+\lambda _2\right)&= Cy^{n} x^{m+1}\mu _2+Cy^{n-1} x^m(\lambda _1+\lambda _2) +C\lambda _1 y^{n} x^m,\\ C x^m(\mu _2+\lambda _1+\lambda _2)&= C y x^{m+1}\mu _2 + C\lambda _1 y x^m +C\mu _2 x^m, \end{aligned}$$

for Eqs. (1) and (2), respectively. After dividing both sides (in both equations) by $Cx^m y^n$, it is easy to see that the above relations are satisfied. Equations (3) and (4) can be verified by a similar procedure. Moreover, note that B can be explicitly computed:

$$\begin{aligned} B=\frac{(\mu _1+\mu _2-\lambda _1-\lambda _2)(\mu _2-\lambda _2)}{(\mu _1+\mu _2-\lambda _2)\mu _2}, \end{aligned}$$

Finally, note that by Proposition 6 in Visschers et al. [21] the stability conditions in the statement of the proposition guarantee ergodicity (and that B is well defined). In turn, $\pi _{m,n}$ corresponds to the steady-state probabilities. $\square$

Proof of Theorem 1

The first step in the proof is to rewrite the steady-state probabilities in the form $f(m)g(m+n)$. With this new characterization, we then proceed to verify Eqs. (1)–(4).

According to Lemma 1, we can cast $\pi _{m,n}$ as given in the statement of the proposition as

$$\begin{aligned}&\pi _{m,n} =\left( \prod _{i=1}^{m+n}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s}\right) \\&\qquad \qquad \cdot \left( \prod _{i=1}^{m}\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s}\right) B,\quad \forall m,n\ge 0. \end{aligned}$$

Now note that in the discussion after Theorem 1 we observe that the only remaining pieces that need to be verified are:

(a):

Equation (2)

(b):

Equation (1)

We begin with (a). For ease of notation, define

$$\begin{aligned} p_i&= \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s},\quad g(n)=\prod _{i=1}^np_i, \\ \quad \text {and} \quad s_i&=\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s},\quad f(m)=\prod _{i=1}^m s_i, \end{aligned}$$

observe that the definitions of g(n) and f(m) are the same as in the discussion after the statement of Theorem 1.

Thus, $\pi _{m,n}$ can then be summarized and rewritten as

$$\begin{aligned} \pi _{m,n} = g(m+n)f(m)B. \end{aligned}$$

Equation (2) then becomes

$$\begin{aligned}&g(m)f(m)(\mu _2+\lambda _1+\lambda _2 + m\theta _s)\\&\quad =g(m)f(m)p_{m+1}\theta _s + g(m)f(m)p_{m+1}s_{m+1}(\mu _2 + \theta _s(m + 1)) \\&\qquad +\sum _{k=0}^mg(m)f(m-k)p_{m+1}\mu _1\gamma _s(1-\gamma _s)^k + \sum _{k=1}^{m}g(m)f(m-k)\mu _1(1-\gamma _s)^k. \end{aligned}$$

Dividing both sides of the equation by g(m), this becomes

$$\begin{aligned}&f(m)(\mu _2+\lambda _1+\lambda _2 + m\theta _s)\nonumber \\&\quad =f(m)p_{m+1}\theta _s + f(m)p_{m+1}s_{m+1}(\mu _2 + \theta _s(m + 1))\nonumber \\&\qquad +\sum _{k=0}^mf(m-k)p_{m+1} \mu _1\gamma _s(1-\gamma _s)^{k} +\sum _{k=1}^{m}f(m-k)\mu _1(1-\gamma _s)^k\nonumber \\&\quad =f(m)p_{m+1}(\theta _s+\mu _1\gamma _s+(\mu _1+\mu _2 + m\theta _s)(1-\gamma _s))\nonumber \\&\qquad + \mu _1(\gamma _s p_{m+1}+1)\sum _{k=1}^mf(m-k)(1-\gamma _s)^{k}. \end{aligned}$$

(27)

To ease the derivation, we use the following simplification result, which is formally proved in Lemma 2:

$$\begin{aligned} \sum _{k=1}^m f(m-k)(1-\gamma _s)^{k} = \frac{f(m)(\mu _2+m\cdot \theta _s)}{\mu _1}. \end{aligned}$$

(28)

Next, we simplify Eq. (27) using Eq. (28).

$$\begin{aligned}&f(m)p_{m+1}(\theta _s+\mu _1\gamma _s+(\mu _1+\mu _2 + m\theta _s)(1-\gamma _s))\\&\qquad + \mu _1(\gamma _s p_{m+1}+1)(1-\gamma _s)^m\sum _{k=1}^m f(m-k)(1-\gamma _s)^{k-m}\\&\quad =f(m)p_{m+1}(\theta _s+\mu _1\gamma _s+(\mu _1+\mu _2 + m\theta _s)(1-\gamma _s))\\&\qquad + \mu _1(\gamma _s p_{m+1}+1)(1-\gamma _s)^mf(m)\frac{\mu _2 + m\theta _s}{\mu _1(1-\gamma _s)^m}\\&\quad =f(m)\big (p_{m+1}(\mu _1+\mu _2+(m+1)\theta _s) - \gamma _sp_{m+1}(\mu _2 + m\theta _s))\big ) \\&\qquad +f(m)\big ((\gamma _sp_{m+1}+1)(\mu _2 + m\theta _s)\big ) \\&\quad =f(m)(\lambda _1 + \lambda _2 + \mu _2 + m\theta _s); \end{aligned}$$

thus, we have verified Eq. (2).

To conclude, we move to (b) and verify Eq. (1). This is equivalent to checking that the following equation holds:

$$\begin{aligned}&g(m+n)f(m)(\mu _1+\mu _2+\lambda _1+\lambda _2 + (m+n) \theta _s )\\&\quad =g(m+n)p_{m+n+1}f(m) ((n+1)\theta +\mu _1\gamma _s)\\&\qquad +p_{m+n+1}S_{m+1}(\mu _2+(m+1)\theta _s)\\&\qquad +g(m+n)p_{m+n+1}\gamma _s\underbrace{~\sum _{k=1}^m f(m-k)\mu _1(1-\gamma _s)^k}_{ f(m)(\mu _2+m\theta _s)\text {~by Eq. (28)}} \\&\qquad +\frac{g(m+n)f(m)}{p_{m+n}}(\lambda _1+\lambda _2). \end{aligned}$$

Dividing both sides of the equation by $g(m+n)f(m)$, we get

$$\begin{aligned}&(\mu _1+\mu _2+\lambda _1+\lambda _2 + (m+n) \theta _s ) \\&\quad = p_{m+n+1} ((n+1)\theta _s+\mu _1\gamma _s) +p_{m+n+1}s_{m+1}(\mu _2+(m+1)\theta _s)\\&\qquad +p_{m+n+1}\gamma _s(\mu _2 + m\theta _s) +\frac{\lambda _1+\lambda _2}{p_{m+n}} \\&\quad =p_{m+n+1} ((n+1)\theta _s+\mu _1\gamma _s) + p_{m+n+1}(\mu _1 + \mu _2 +m\theta _s)(1-\gamma _s)\\&\qquad +p_{m+n+1}\gamma _s(\mu _2 + m\theta _s) +\mu _1 +\mu _2 +(m+n)\theta _s \\&\quad = p_{m+n+1}((m+n+1)\theta _s + \mu _1 + \mu _2) + \mu _1 + \mu _2 + (m+n)\theta _s \\&\quad =\lambda _1 + \lambda _2 + \mu _1 + \mu _2 + (m+n)\theta _s, \end{aligned}$$

which completes the verification. $\square$

Lemma 1

The expressions

$$\begin{aligned} \left\{ \begin{array}{ll}\left( \frac{\mu _1}{\mu _1 + \mu _2 + m\theta _s }\right) \left( \prod _{i=1}^m\frac{\lambda _2}{\mu _2 + i\theta _s}\right) \left( \prod _{i=1}^n\frac{\lambda _1+\lambda _2}{\mu _1 + \mu _2 + m\theta _s + i\theta _s}\right) , &{} \quad m\ge 1; \\ \prod _{i=1}^n \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i\theta _s}, &{} \quad m=0, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \left( \prod _{i=1}^{m+n}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s}\right) \cdot \left( \prod _{i=1}^{m}\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s}\right) ,\quad \forall m,n\ge 0, \end{aligned}$$

are equivalent.

Proof

Denote the first term in the statement $L_1$ and the second $L_2$. For $m\ge 1$,

$$\begin{aligned} L_1&=\bigg (\frac{\mu _1}{\mu _1 + \mu _2 + m\theta _s }\bigg )\cdot \bigg (\prod _{i=1}^m\frac{\lambda _2}{\mu _2 + i\theta _s}\bigg )\cdot \bigg (\prod _{i=1}^n\frac{\lambda _1+\lambda _2}{\mu _1 + \mu _2 + m\theta _s + i\theta _s}\bigg ) \\&=\bigg (\frac{\mu _1}{\mu _1 + \mu _2 + m\theta _s }\bigg )\cdot \bigg (\prod _{i=1}^m\frac{(\lambda _1 + \lambda _2)(1-\gamma _s)}{\mu _2 + i\theta _s}\bigg ) \cdot \bigg (\prod _{i=1}^n\frac{\lambda _1+\lambda _2}{\mu _1 + \mu _2 + m\theta _s + i\theta _s}\bigg )\\&\quad \cdot \underbrace{\bigg (\prod _{i=1}^m\frac{\mu _1+\mu _2 + i\theta _s}{\mu _1+\mu _2 + i\theta _s}\bigg )}_{=1} \\&=\bigg (\frac{\mu _1}{\mu _1 + \mu _2 + m\theta _s }\bigg )\cdot \left( \prod _{i=1}^{m+n}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s}\right) \cdot \bigg (\prod _{i=1}^m\frac{(\mu _1+\mu _2 + i\theta _s)(1-\gamma _s)}{\mu _2 + i\theta _s}\bigg ) \\&=\left( \prod _{i=1}^{m+n}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s}\right) \cdot \left( \prod _{i=1}^{m}\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s}\right) \\&=L_2. \end{aligned}$$

For $m=0$,

$$\begin{aligned} L_1 = \prod _{i=1}^n\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i\theta _s}=L_2. \end{aligned}$$

This completes the proof. $\square$

Lemma 2

Let $f:{\mathbb {N}}\rightarrow {\mathbb {R}}_+$ be a function such that $f(0)=1$ and

$$\begin{aligned} \sum _{k=1}^{m}f(m-k)(1-\gamma _s)^k=f(m)\cdot (a+m\cdot b),\quad \forall m\ge 1. \end{aligned}$$

(29)

Then

$$\begin{aligned} f(m)=\frac{(1-\gamma _s)^m}{a+b}\left( \prod _{i=2}^m \frac{1+a+(i-1)b}{a+ib}\right) ,\quad \forall m\ge 1. \end{aligned}$$

(30)

Proof

We proceed by induction. For $m=1$, since $f(0)=1$ Eq.(29) yields

$$\begin{aligned} f(1)(a+b)=(1-\gamma _s), \end{aligned}$$

(31)

which coincides with Eq. (30). For the induction step, let us compute f(m), assuming that the property holds form $f(m-1)$. From Eq. (30), we have

$$\begin{aligned}&f(m)(a+m\cdot b)\\&\quad = \sum _{k=1}^{m}f(m-k)(1-\gamma _s)^k\\&\quad =\sum _{k=0}^{m-1}f(m-1-k)(1-\gamma _s)^{k+1}\\&\quad =f(m-1)(1-\gamma _s)+(1-\gamma _s)\sum _{k=1}^{m-1}f(m-1-k)(1-\gamma _s)^{k}\\&\quad =f(m-1)(1-\gamma _s)+(1-\gamma _s)f(m-1)(a+(m-1)\cdot b)\\&\quad =f(m-1)(1-\gamma _s)(1+a+(m-1)\cdot b)\\&\quad =\frac{(1-\gamma _s)^{m-1}}{a+b}\left( \prod _{i=2}^{m-1} \frac{1+a+(i-1)b}{a+ib}\right) (1-\gamma _s)(1+a+(m-1)\cdot b)\\&\quad =\frac{(1-\gamma _s)^m}{a+b}\left( \prod _{i=2}^m \frac{1+a+(i-1)b}{a+ib}\right) \cdot (a+m\cdot b), \end{aligned}$$

where the second to last equality comes from the induction hypothesis and Eq. (30). This concludes the proof. $\square$

Proof of Theorem 2

First we rewrite the expression for the conjectured steady-state probabilities $\pi ^L_{m,n}$ and $\pi ^R_{m,n}$ in the form $\pi _{m,n}=f(m)g(m+n)B$ as follows (see Lemma 1 for a formal proof):

$$\begin{aligned} \pi _{m,n}^L&= \left( \prod _{i=1}^{m+n}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s}\right) \left( \prod _{i=1}^{m}\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s}\right) B,\\ \pi _{m,n}^R&= \left( \prod _{i=1}^{m+n}\frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+i \theta _d}\right) \left( \prod _{i=1}^{m}\frac{(\lambda _2+\lambda _1{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _d)(1-\gamma _d)}{\lambda _1+i \theta _d}\right) B. \end{aligned}$$

For ease of notation, for $\ell \in \{L,R\}$ we define

$$\begin{aligned} P^\ell _{n}=\prod _{i=1}^n p^\ell _i, \quad \text {where}\quad p^L_i = \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+i \theta _s},\quad p^R_i = \frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+i \theta _d},\quad i\ge 1. \end{aligned}$$

and

$$\begin{aligned} S^\ell _{m}=\prod _{i=1}^m s^\ell _i, \end{aligned}$$

where

$$\begin{aligned} s^L_i&=\frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s},\quad \\ s^R_i&=\frac{(\lambda _2+\lambda _1{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _d)(1-\gamma _d)}{\lambda _1+i \theta _d},\quad i\ge 1. \end{aligned}$$

This gives the following forms of $\pi ^L_{m,n}$ and $\pi ^R_{m,n}$:

$$\begin{aligned} \pi ^L_{m,n} = P^L_{m+n}S^L_m,~~\pi ^R_{m,n} = P^R_{m+n}S^R_m. \end{aligned}$$

Now we verify the equilibrium equations. To do so, we will make use of Theorem 1. Observe that from Theorem 1, Eqs. (13, 15, 16) and (18) are readily verified.

Next, we check Eq. (14). According to Theorem 1, $\pi ^L_{m,n}$ satisfies Eq. (2). Adding $\pi ^L_{m,0}\mu _1$ on both sides of Eq. (2), we have

$$\begin{aligned}&\pi ^L_{m,0}(\mu _1 + \mu _2+\lambda _1+\lambda _2 + m\theta _s) \\&\quad = \pi ^L_{m,0}\mu _1 + \pi ^L_{m,1}\theta _s + \pi ^L_{m+1,0}\left( \mu _2 + \theta _s(m + 1)\right) \\&\qquad + \sum _{k=0}^m\pi ^L_{m-k,k+1}\mu _1\gamma _s(1-\gamma _s)^k +\sum _{k=1}^{m}\pi ^L_{m-k,k}\mu _1(1-\gamma _s)^k. \end{aligned}$$

In order to verify Eq. (14), we just need to show that

$$\begin{aligned} q_{m,1}(\lambda _1 + \theta _d) = \pi ^L_{m,0}\mu _1 + \sum _{k=1}^{m}\pi ^L_{m-k,k}\mu _1(1-\gamma _s)^k. \end{aligned}$$

The left-hand side $q_{m,1}(\lambda _1 + \theta _d) = \left( \prod _{i=1}^m\frac{\lambda _2}{\mu _2+i\theta _s}\right) \mu _1B$. For the right-hand side,

$$\begin{aligned}&\pi ^L_{m,0}\mu _1 + \sum _{k=1}^{m}\pi ^L_{m-k,k}\mu _1(1-\gamma _s)^k \nonumber \\&\quad =P^L_m S^L_m\mu _1B + P^L_{m}B\underbrace{\sum _{k=1}^{m} S^L_{m-k}\mu _1(1-\gamma _s)^k}_{S^L_m(\mu _2 + m\theta _s)\text { by Lemma}~2} \nonumber \\&\quad =P_m^LS_m^LB(\mu _1+\mu _2+m\theta _s) \nonumber \\&\quad =\left( \prod _{i=1}^m \frac{\lambda _1 + \lambda _2}{\mu _1 + \mu _2 + i\theta _s}\right) \left( \prod _{i=1}^m \frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)(1-\gamma _s)}{\mu _2+i \theta _s}\right) \nonumber \\&\qquad \cdot (\mu _1+\mu _2+m\theta _s)B \nonumber \\&\quad =\left( \prod _{i=1}^m \frac{\lambda _2}{\mu _2 + i\theta _s}\right) \left( \prod _{i=1}^m \frac{(\mu _1+\mu _2{\mathbf {1}}_{\{i>1\}}+(i-1)\theta _s)}{\mu _1 + \mu _2+i \theta _s}\right) (\mu _1+\mu _2+m\theta _s)B \nonumber \\&\quad =\left( \prod _{i=1}^m \frac{\lambda _2}{\mu _2 + i\theta _s}\right) \mu _1 B, \end{aligned}$$

(32)

which completes the verification. Eq. (17) can be verified with the same technique.

We now verify equations from (19) to (22). We start with (19). For $i,j\ge 2$, dividing by $q_{i,j}$ on both sides of Eq. (19) we get the first equality of the following:

$$\begin{aligned}&(i\theta _s + j\theta _d + \mu _1 + \mu _2 + \lambda _1 + \lambda _2 ) \\&\quad = \frac{\lambda _2}{\mu _2+(i+1)\theta _s}((i+1)\theta _s + \mu _2) + \frac{{\mu _2+i\theta _s}}{\lambda _2}\lambda _2\\&\qquad + \frac{\mu _1}{\lambda _1+(j+1)\theta _d}((j+1)\theta _d + \lambda _1) +\frac{\lambda _1+j\theta _d}{\mu _1}\mu _1\\&\quad =\lambda _2 + \mu _2 + i\theta _s + \mu _1 + \lambda _1 + j\theta _d, \end{aligned}$$

which verifies Eq. (19).

For Eq. (20), replacing $\pi _{j-k,k}^R$ with $P_j^RS_{j-k}^R$ we have the first equality of the following:

$$\begin{aligned}&q_{1,j}(\theta _s + j\theta _d + \mu _1 + \mu _2 + \lambda _1 + \lambda _2)\\&\quad = q_{2,j}(2\theta _s + \mu _2) + q_{1,j+1}((j+1)\theta _d + \lambda _1) + q_{1,j-1}\mu _1\\&\qquad + BP_j^RS_j^R\lambda _2 + BP^R_j\underbrace{\sum _{k=1}^jS^R_{j-k}\lambda _2(1-\gamma _d)^k}_{S^R_j(\lambda _1 + m\theta _d)\text { by Lemma}~2} \\&\quad = q_{2,j}(2\theta _s + \mu _2) + q_{1,j+1}((j+1)\theta _d + \lambda _1) + q_{1,j-1}\mu _1\\&\qquad + BP_j^RS_j^R(\lambda _1+\lambda _2+m\theta _d) \\&\quad = q_{2,j}(2\theta _s + \mu _2) + q_{1,j+1}((j+1)\theta _d + \lambda _1) + q_{1,j-1}\mu _1\\&\qquad + B\lambda _2\left( \prod _{k=1}^j\frac{\mu _1}{\lambda _1 + k\theta _d}\right) ,\quad \text {by Eq. (32)}. \end{aligned}$$

Dividing both sides of the equation by $q_{1,j}$, we get

$$\begin{aligned}&\theta _s + j\theta _d + \mu _1 + \mu _2 + \lambda _1 + \lambda _2\\&\quad =\frac{\lambda _2}{\mu _2 + 2\theta _s}(2\theta _s + \mu _2) + \frac{\mu _1}{\lambda _1 + (j+1)\theta _d}((j+1)\theta _d + \lambda _1) \\&\qquad + \frac{\lambda _1 + j\theta _d}{\mu _1}\mu _1 + \frac{\mu _2+\theta _s}{\lambda _2}\lambda _2 \\&\quad =\lambda _2 + \mu _1 + \lambda _1 + j\theta _d + \mu _2 + \theta _s. \end{aligned}$$

This verifies Eq. (20). By symmetry, we can also conclude that (21) is verified as well.

For Eq. (22), since $q_{2,1}(2\theta _s + \mu _2) = q_{1,1}\lambda _2, q_{1,2}(2\theta _d + \lambda _1) = q_{1,1}\mu _1$, we can cancel out $q_{1,1}(\mu _1+\lambda _2)$ on both sides of Eq. (22). This gives the following equation:

$$\begin{aligned} q_{1,1}(\theta _s + \theta _d + \mu _2 + \lambda _1 )&= \pi ^R_{1,0}\lambda _2 + \pi ^R_{0,1}\lambda _2(1-\gamma _d)+ \pi ^L_{1,0}\mu _1 + \pi ^L_{0,1}\mu _1(1-\gamma _s). \end{aligned}$$

Replacing $q_{1,1}, \pi _{1,0}^R, \pi _{0,1}^R, \pi _{1,0}^L, \pi _{0,1}^L$ with their corresponding expressions, we get the first equality of the following:

$$\begin{aligned}&\frac{\lambda _2}{\mu _2+\theta _s}\frac{\mu _1}{\lambda _1+\theta _d}(\theta _s + \theta _d + \mu _2 + \lambda _1 )\\&\quad =\frac{\lambda _2(1-\gamma _d)}{\lambda _1+\theta _d} \frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d}\lambda _2 + \frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d}\lambda _2(1-\gamma _d)\\&\qquad + \frac{\mu _1(1-\gamma _s)}{\mu _2+\theta _s}\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+\theta _s}\mu _1 + \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+\theta _s}\mu _1(1-\gamma _s) \\&\quad =\frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d}\lambda _2(1-\gamma _d)\frac{\lambda _1+\lambda _2+\theta _d}{\lambda _1+\theta _d} \\&\qquad +\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+\theta _s}\mu _1(1-\gamma _s)\frac{\mu _1+\mu _2+\theta _s}{\mu _2+\theta _s} \\&\quad =\frac{\lambda _2\mu _1}{\lambda _1+\theta _d} + \frac{\lambda _2\mu _1}{\mu _2 + \theta _s}. \end{aligned}$$

This in turn verifies Eq. (22).

Finally, we verify Eq. (23). Replacing $\pi _{0,1}^L, \pi _{1,0}^L, \pi _{0,1}^R, \pi _{1,0}^R$ with their corresponding terms, we have the first equality of the following:

$$\begin{aligned}&(\lambda _1+\lambda _2+\mu _1+\mu _2) \\&\quad = \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+\theta _s}(\theta _s + \mu _1\gamma _s + \mu _2) + \frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+ \theta _s}\frac{\mu _1(1-\gamma _s)}{\mu _2+\theta _s}(\mu _2 + \theta _s)\\&\qquad +\frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d} \frac{\lambda _2(1-\gamma _d)}{\lambda _1+ \theta _d} (\theta _d+ \lambda _1)+ \frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d}(\theta _d + \lambda _1 + \lambda _2\gamma _d) \\&\quad =\frac{\lambda _1+\lambda _2}{\mu _1+\mu _2+\theta _s}(\mu _1+\mu _2+\theta _s) + \frac{\mu _1+\mu _2}{\lambda _1+\lambda _2+\theta _d}(\lambda _1 + \lambda _2 + \theta _d) \\&\quad =\lambda _1+\lambda _2+\mu _1+\mu _2, \end{aligned}$$

which verifies Eq. (23). This concludes the proof. $\square$