A coupled processor model with simultaneous arrivals and ordered service requirements

Abstract

We study a coupled processor model with simultaneous arrivals. Under the assumption of ordered input, the Laplace–Stieltjes transform of the joint stationary amount of work in the system can be explicitly calculated by relating it to the amount of work in a parallel queueing system without coupling. This relation is first exploited for the system with two coupled queues. The method is then extended to higher dimensions.

1 Introduction

In this paper we study a coupled processor model which receives service requirements at both queues simultaneously. We assume that the service requirement at, say, station 1 is always greater than the service requirement from station 2. Moreover, when server 2 is idle, it switches to process work from the first queue, if there is any. In [1], the model with simultaneous arrivals and ordered service times, but without coupled processors, was analyzed. This model has connections with tandem and priority queues, but also with a reinsurance problem with proportional reinsurance (see [1], Sect. 4.2]). Here, we extend the model to the coupled processors case.

A pioneering paper on coupled processors is Fayolle and Iasnogorodski [4], who consider two parallel M/M/1 queues with independent Poisson arrival processes, server speeds $r_i,$ $i=1,2,$ and such that as soon as queue $i$ empties, the other queue works at speed $r_j+r_j^* \ne r_j$, $i\ne j$. This system is solved for the steady-state number of customers in both queues by reducing the problem to a boundary value problem of a Riemann–Hilbert type. In Cohen and Boxma [2] this model is generalized by dropping the assumption that the service requirements are exponentially distributed. It is shown that the problem of determining the workload distribution reduces again to a Riemann–Hilbert boundary value problem. In Cohen [3], the analysis is further extended to the case when, with some probability, arriving customers may also request service simultaneously from both queues. Moreover, the service requirement of a customer is allowed to depend on whether he finds one of the queues to be empty; the so-called semi-homogeneous workload process. Both in [2, 3] the focus is on the transient problem: the study of the time-dependent amount of work/queue lengths.

The steady-state version of the functional equation for the workload vector $(V^{(1)},V^{(2)})$ from [3], p.186, (1.10)] reads:

$$\begin{aligned} K(s_1,s_2)\psi (s_1,s_2)= & {} ( r_2 s_2 - r_1^*s_1) \psi _{1}(s_1)\nonumber \\&+\,( r_1 s_1 - r_2^*s_2 )\psi _{2}(s_2) + (r_1^*s_1 + r_2^*s_2)\psi _0, \end{aligned}$$

(1)

with $\psi (s_1,s_2)$ the Laplace–Stieltjes transform (LST) of the stationary amount of work in the system and with the unknown boundary functions

$$\begin{aligned} \psi _{i}(s_i) =\mathbb {E}\left[ e^{-s_i V^{(i)}}(V^{(j)}=0)\right] , \quad \;i\ne j \in \{1,2\}, \quad \psi _0 = \mathbb {P}\left( V^{(1)}= V^{(2)}=0\right) . \end{aligned}$$

The function $K(s_1,s_2)$ is a so-called Poisson kernel. For $\phi (s_1,s_2)$ the joint transform of a generic service time vector,

$$\begin{aligned} K(s_1,s_2)= r_1 s_1 + r_2 s_2 - \lambda (1-\phi (s_1,s_2)). \end{aligned}$$

Actually, in [3] the functional equation of the time-dependent workload is given. The stationary version above is obtained by multiplying the functional equation [3], p. 186, (1.10)] with the discount factor $\rho$ of the Laplace transform over time, and then taking $\rho \rightarrow 0$, while keeping $\rho >0$.

The analysis in the above-mentioned works relies heavily on the theory of complex functions which makes it highly non-trivial, and in addition, it is difficult to recognize the probabilistic nature of the initial problem.

We will show in Sect. 2 that under an additional ordering assumption between the claims, it is possible to relate the coupled processor model to a parallel queueing system without coupling. Then the transform of the amount of work in the coupled system follows from that obtained in the decoupled parallel system, by using a result from [1]. This gives an explicit representation for the steady-state amount of work in the coupled system (Sect. 3), which can be extended to multiple coupled queues by making suitable assumptions on the coupling rates (Sect. 4).

2 Problem description

We consider two parallel $M/G/1$ queues, with simultaneous arrivals and correlated service requirements. The arrival process is a Poisson process with rate $\lambda$. We will denote by $A_n$ the time elapsed between arrival epochs $n$ and $n+1$. The service requirements at the two queues of successive customers are independent, identically distributed random vectors $(B_n^{(1)}, B_n^{(2)}), n\ge 1$. In the sequel we denote with $(B^{(1)},B^{(2)})$ a random vector with the same distribution as the vectors $(B_n^{(1)}, B_n^{(2)}), n\ge 1$. The joint Laplace–Stieltjes transform of this vector is

$$\begin{aligned} \phi (s_1,s_2) := \mathbb {E}\left( e^{-s_1B^{(1)}-s_2B^{(2)}}\right) \!. \end{aligned}$$

In addition, let $c_1$ and $c_2$ be the servers’ processing rates. An essential assumption in the model is that, after normalizing the system with the server rates, with probability one, each customer has a bigger service requirement in queue $1$ than in queue $2$, i.e.,

$$\begin{aligned} \mathbb {P}\left( B^{(1)}/c_1 \ge B^{(2)}/c_2\right) = 1. \end{aligned}$$

Moreover, the processors are coupled in the sense that as soon as server 2 becomes idle, it switches its capacity to serving work from buffer 1. We will assume that it works at rate $c^1_2$ when processing from buffer 1. We are interested in the joint stationary distribution of the amount of work in the two queues. Let us denote with $V^{(1)}$ the stationary amount of work in queue $1$ and with $V^{(2)}$ the stationary amount of work in queue $2$.

As a convention, we will denote with $V_t$ the vector representing the amount of work in the system at time $t$ and with $V_n$ the amount of work in the system just before the $n^{th}$ job arrives. Formally, $V_n$ is the left limit $V_{t(n)-}$, where $t(n)$ is the arrival instant of the $n^{th}$ customer.

Our aim is to study such a queueing system under the above assumption of ordered service times. In particular we want to find an expression for the Laplace–Stieltjes transform of the joint stationary amount of work.

3 Recursive equations for the amount of work in the coupled system

In this section we will derive stochastic recursive equations for the joint amount of work in the system.

Let $V^{(1)}_n$ be the amount of work in queue $1$ as seen by customer $n$ upon arrival, and $V^{(2)}_n$ the amount of work in queue $2$ at the same time instant. We assume that at time 0 the first customer arrives in an empty system. Then we have the following recursion for the random variables $(V^{(1)}_n,V^{(2)}_n), n\ge 1:$

$$\begin{aligned} \left( V^{(1)}_1,V^{(2)}_1\right)&= (0,0), \nonumber \\ V^{(1)}_{n+1}&= \left[ (V^{(1)}_n + B^{(1)}_{n} - c_1 A_{n})\vee 0 + \frac{c_2^1}{c_2}(V_n^{(2)} +B^{(2)}_{n} - c_2 A_{n})\wedge 0\right] \vee 0,\nonumber \\ V^{(2)}_{n+1}&= (V^{(2)}_n + B^{(2)}_{n} - c_2A_{n})\vee 0. \end{aligned}$$

(2)

We use the notation $x\wedge 0 = \min \{x,0\}$ and $x\vee 0 = \max \{x,0\}$. We remark that

$$\begin{aligned} - \frac{1}{c_2}\left[ (V_n^{(2)} +B^{(2)}_{n} - c_2 A_{n})\wedge 0\right] \end{aligned}$$

is the amount of time that server 2 has been idle between the arrival epochs $n$ and $n+1$. Then the second term in the recursion of $V^{(1)}_{n+1}$ is minus the amount of work server 2 processes at rate $c_2^1$ from buffer 1 during his idle period (if it has an idle period).

This extra term appears because the servers are coupled. It is useful to compare this with the recursion for a system without coupling between the servers. Consider two parallel queues simultaneously receiving service requirement distributed as the vector $(\tilde{B}^{(1)},\tilde{B}^{(2)})$. The servers are not coupled any more and server 1 always works at speed $\tilde{c}_1$, while server 2 always works at speed $\tilde{c}_2$. Let $(\tilde{V}^{(1)}_n,\tilde{V}^{(2)}_n)$ be the amount of work in such a system. Then the following recursion holds

$$\begin{aligned} \left( \tilde{V}^{\left( 1\right) }_1, \tilde{V}^{\left( 2\right) }_1\right)&= \left( 0,0\right) , \nonumber \\ \tilde{V}^{\left( 1\right) }_{n+1}&= \left( \tilde{V}^{\left( 1\right) }_n + \tilde{B}^{\left( 1\right) }_{n} - \tilde{c}_1 \tilde{A}_{n}\right) \vee 0,\\ \tilde{V}^{\left( 2\right) }_{n+1}&= \left( \tilde{V}^{\left( 2\right) }_n + \tilde{B}^{\left( 2\right) }_{n} - \tilde{c}_2 \tilde{A}_{n}\right) \vee 0, \nonumber \end{aligned}$$

(3)

with $\tilde{A}_{n}$ the inter-arrival time between customer $n$ and $n+1$. This is Lindley’s recursion because both queues evolve in isolation as one-dimensional systems. Notice that, marginally, queue 2 evolves as if there was no coupling in (2).

We are ready to give the main result of this section, which connects the amount of work in the coupled system to a workload process in a system without coupling between the servers. For further usage we will denote by system (C) the coupled system and by system (D) the system without coupling.

Proposition 1

Let $(V^{(1)}_n,V^{(2)}_n)_{n\ge 1}$ be the workload process at arrival epochs in system (C). Then the process $(V_n^{(1)}+ \frac{c_2^1}{c_2}V_n^{(2)}, V^{(2)}_n)_{n\ge 1}$ is the workload process in a system of type (D) with generic input $(B_n^{(1)}+\frac{c_2^1}{c_2}B_n^{(2)}, B_n^{(2)})$, where the servers have speed $(c_1+c_2^1,c_2)$ and do not interact with each other.

We will show that $(V_n^{(1)}+\frac{c_2^1}{c_2}V_n^{(2)}, V^{(2)}_n)$ has the same distribution as $(\tilde{V}^{(1)}_n,\tilde{V}^{(2)}_n)$, the solution to the recursive system (3), by using a probabilistic coupling between systems (C) and (D). That is, we will let the two systems evolve on the same probability space given by the sequences $(A_n)_{n\ge 1}$ and $(B_n^{(1)}, B_n^{(2)})_{n\ge 1}$. The choice for the input variables in system (D) is the following:

$$\begin{aligned}&\tilde{A}_n := A_n,\; \left( \tilde{B}_n^{\left( 1\right) }, \tilde{B}_n^{\left( 2\right) }\right) := \left( B_n^{\left( 1\right) }+\frac{c_2^1}{c_2}B_n^{\left( 2\right) }, B_n^{\left( 2\right) }\right) ,\nonumber \\&\tilde{c}_1 := c_1 + c^1_2,\;\;\;\; \tilde{c}_2 := c_2. \end{aligned}$$

(4)

To be more precise, start both systems empty at time $t=0$. At the $n$th arrival epoch $t_n$, system (C) receives input $(B_n^{(1)}, B_n^{(2)})$, whereas system (D) receives input $(B_n^{(1)} + \frac{c_2^1}{c_2}B^{(2)}_n, B_n^{(2)})$. Let us focus on system (D). The key idea is to partition the amount of work at queue 1 in system (D) into $V_t^{(1)}$ and $\frac{c_2^1}{c_2}V^{(2)}_t$, then during the busy periods of server 2, distribute the total capacity per time unit $c_1+c_2^1$ of server 1 in the following way: $c_1$ is dedicated to processing $V_t^{(1)}$ while $c_2^1$ is used to process the remaining $\frac{c^1_2}{c_2}V^{(2)}_t$. In this way, during the busy periods of server 2, the amount of work in queue 1 of system (C) and the work in the $c_1$-dedicated component of queue 1 in system (D) evolve in the same way.

As soon as queue 2 becomes empty (which now happens at the same moment in system (C) as in system (D) because the second queue evolves unchanged between the two systems), in both systems (C) and (D), server 1 will process work $V^{(1)}_t$ at speed $c_1+c_2^1$. Another remark is that due to the ordering between the service requirements, queue 2 will always become idle before queue 1 in any of the systems (C) or (D) (see also Remark 1 below).

We give below the formal proof of Proposition 1. The idea of the proof is to verify that $V^{(1)}_n+\frac{c_2^1}{c_2}V^{(2)}_n$ satisfies (3) with the input variables from (4).

Proof of Proposition 1

We first remark that we can drop the maximum w.r.t. $0$ in the first term of recursion (2):

$$\begin{aligned} V^{(1)}_{n+1} = \left[ V^{(1)}_n + B^{(1)}_{n} - c_1 A_{n} + \frac{c_2^1}{c_2}(V_n^{(2)} +B^{(2)}_{n} - c_2 A_{n})\wedge 0\right] \vee 0, \end{aligned}$$

(5)

the reason being that the other term is either 0 or negative as pointed out below (2), so it can only decrease the term between the square brackets in the recursion of the coupled queue 1.

Adding the term $\frac{c_2^1}{c_2}V^{(2)}_{n+1} = \frac{c_2^1}{c_2}(V^{(2)}_n + B^{(2)}_{n} - c_2A_{n})\vee 0$ to both sides of (5) gives

$$\begin{aligned} V^{(1)}_{n+1} +\frac{c_2^1}{c_2}V^{(2)}_{n+1} =&\left[ V^{(1)}_n + B^{(1)}_{n} - c_1 A_{n} + \frac{c_2^1}{c_2}(V_n^{(2)} +B^{(2)}_{n} - c_2 A_{n})\right] \\&\vee \frac{c_2^1}{c_2}(V_n^{(2)} +B^{(2)}_{n} - c_2 A_{n})\vee 0. \\ \end{aligned}$$

We used the fact that the operator $\vee$ is distributive w.r.t. addition and the obvious decomposition $x\wedge 0 + x\vee 0=x.$

There are two possible cases:

In the event that $V^{(1)}_n + B^{(1)}_{n} - c_1 A_{n}>0$, the RHS above is of the form $a\vee b\vee 0$, with $a > b$, hence $b$ can be removed. In the end we can rewrite the above as

$$\begin{aligned} V^{(1)}_{n+1} +\frac{c_2^1}{c_2}V^{(2)}_{n+1} = \left( V^{(1)}_{n} +\frac{c_2^1}{c_2}V^{(2)}_{n} + B^{(1)}_{n}+ \frac{c_2^1}{c_2}B^{(2)}_{n} - (c_1+c_2^1)A_{n} \right) \vee 0. \end{aligned}$$

This is the desired Lindley recursion for $V^{(1)}_{n} +\frac{c_2^1}{c_2}V^{(2)}_{n}$.

In the event that $V^{(1)}_n + B^{(1)}_{n} - c_1 A_{n}<0$, queue 1 would empty at epoch $n+1$ without any additional help, so that $V^{(1)}_{n+1}=0$. Then by the ordering assumption, $V^{(2)}_{n+1} = 0$ as well, and the above identity is trivially satisfied. This proof shows that the ordering between the normalized claims is an essential assumption. $\square$

Remark 1

Notice that the normalized input in the related system (D) remains ordered:

$$\begin{aligned} \frac{B_n^{(1)} + \frac{c_2^1}{c_2}B^{(2)}_n}{c_1+c_2^1} = \frac{c_1\frac{B_n^{(1)}}{c_1} + c_2^1\frac{B^{(2)}_n}{c_2}}{c_1+c_2^1} \ge \frac{B_n^{(2)}}{c_2}, \end{aligned}$$

because, by assumption, $B_n^{(1)}/c_1\ge B_n^{(2)}/c_2.$

4 The transform of the equilibrium amount of work at arrival epochs

In [1] it has been shown how to calculate the Laplace–Stieltjes transform of the joint stationary amount of work in a system of type (D) under the same ordering assumption [1], Formula (7)]. Thus, by inverting the correspondence from Proposition 1, and using Remark 1, we can recover without any additional effort the joint transform of $(V^{(1)},V^{(2)})$, the steady-state amounts of work in the coupled system, with the extra remark that, because of Poisson arrivals, we have the PASTA property, which means that in equilibrium the amount of work is the same as the workload seen by an arriving customer.

The inverse relation from Proposition 1 is

$$\begin{aligned} \left( V^{\left( 1\right) },V^{\left( 2\right) }\right) = \left( \tilde{V}^{\left( 1\right) }-\frac{c_2^1}{c_2}\tilde{V}^{\left( 2\right) },\tilde{V}^{\left( 2\right) }\right) . \end{aligned}$$

(6)

If we denote by

$$\begin{aligned} \psi _{\left( C\right) }\left( s_1,s_2\right) := \mathbb {E}\left( e^{-s_1 V^{\left( 1\right) }-s_2 V^{\left( 2\right) }}\right) ,\quad \psi _{\left( D\right) }\left( s_1,s_2\right) := \mathbb {E}\left( e^{-s_1\tilde{V}^{\left( 1\right) }-s_2 \tilde{V}^{\left( 2\right) }}\right) , \end{aligned}$$

the LST of the equilibrium amount of work in system (C) and, respectively, system (D), then via (6), the relation between the LSTs becomes:

$$\begin{aligned} \psi _{(C)}(s_1,s_2)= \psi _{(D)}\left( s_1,s_2-s_1 c_2^1/c_2\right) . \end{aligned}$$

(7)

Remark 2

Equation (1) can be adapted to describe the stationary workload $(\tilde{V}^{(1)},\tilde{V}^{(2)})$ in the decoupled system by setting the coupling rates $r^*$ equal to 0. The kernel $K(s_1,s_2)$ has to be modified as well to

$$\begin{aligned} K_{(D)}(s_1,s_2) = \left( c_1 + c_2^1\right) s_1 + c_2 s_2 - \lambda \left[ 1 - \phi \left( s_1,s_2+ s_1 c_2^1/c_2\right) \right] \end{aligned}$$

because server 1 receives the extra input $c_2^1/c_2 B^{(2)}$ and always works at speed $c_1+c_2^1$. Then (1) becomes

$$\begin{aligned} K_{(D)}(s_1,s_2) \psi _{(D)}(s_1,s_2) = c_2 s_2 \psi _{(D),1}(s_1) + (c_1+c_2^1)s_1\psi _{(D),0}, \end{aligned}$$

(8)

since by the ordering relation from Remark 1, $\psi _{(D),2}(s_2)$ is constant and equal to $\psi _{(D),0}$:

$$\begin{aligned} \psi _{(D),2}(s_2) = \mathbb {E}\left[ e^{-s_2 \tilde{V}^{(2)}}(\tilde{V}^{(1)}=0)\right] =\mathbb {P}(\tilde{V}^{(1)}=\tilde{V}^{(2)}=0) =: \psi _{(D),0}. \end{aligned}$$

On the other hand, the kernel for the coupled system (C) is

$$\begin{aligned} K_{(C)}(s_1,s_2) = c_1 s_1 + c_2 s_2 - \lambda [1-\phi (s_1,s_2)]. \end{aligned}$$

The equation that has to be satisfied by $\psi _{(C)}(s_1,s_2)$ now reads (with $\psi _{(C),2}(s_2) \equiv \psi _{(C),0}$, again because of the ordering)

$$\begin{aligned} K_{(C)}(s_1,s_2)\psi _{(C)}(s_1,s_2) = \left( c_2s_2 - c_2^1 s_1\right) \psi _{(C),1}(s_1) + \left( c_1 + c_2^1\right) s_1 \psi _{(C),0}, \end{aligned}$$

(9)

with the key remark that the two boundary functions $\psi _{(D),1}(s_1)$ and $\psi _{(C),1}(s_1)$ are identical (Proposition 1):

$$\begin{aligned} \mathbb {E}[e^{-s_1 \tilde{V}^{(1)}}( \tilde{V}^{(2)}=0)] \equiv \mathbb {E}\left[ e^{-s_1 V^{(1)}}( V^{(2)}=0)\right] \end{aligned}$$

and the same holds for $\psi _{(C),0}$ and $\psi _{(D),0}$.

Now it is easy to check that if $\psi _{(D)}(s_1,s_2)$ is the solution of (8), then $\psi _{(D)}\left( s_1,s_2- s_1 c_2^1/c_2\right)$ as in (7) is the solution of (9), and conversely, if $\psi _{(C)}(s_1,s_2)$ is the solution of (9) then $\psi _{(C)}\left( s_1,s_2+ c_2^1/c_2 s_1\right)$ is the solution of (8). In particular, it follows from [1] that the amount of work in system (C) is ergodic under the condition

$$\begin{aligned} \lim _{\mathop {s_1>0}\limits ^{s_1\rightarrow 0 }}\frac{\partial }{\partial s_1} K_{(D)}(s_1,0) >0 \Leftrightarrow \mathbb {E}\left( B^{(1)}\right) + c_2^1/c_2\mathbb {E}\left( B^{(2)}\right) < \left( c_1+c_2^1\right) \mathbb {E}(A). \end{aligned}$$

(10)

This simply means that the first queue in system $(D)$ is capable of handling the amount of input per time unit while working at speed $(c_1+c_2^1)$ and this is sufficient to ensure that the entire system is stable, because of the ordering assumption. It may happen that $\mathbb {E}(B^{(1)})> c_1 \mathbb {E}(A)$, i.e., that queue 1 of system (C) would be supercritical if it were to work only on its own. Inequality (10) together with Remark 1 implies $\mathbb {E}(B^{(2)}) < c_2 \mathbb {E}(A)$, thus queue 2 is ergodic and during its (non-degenerate) idle periods it is capable of maintaining stability in queue 1 because of the coupling.

Using the relation between $\psi _{(C)}(s_1,s_2)$ and $\psi _{(D)}(s_1,s_2)$ we obtain

Theorem 1

Under the stability condition (10), with $\tilde{\rho }_1:= \lambda \mathbb {E}(\tilde{B}^{(1)})/(c_2^1+c_1)$, the joint transform of the stationary amount of work in a system of type (C) is

$$\begin{aligned} \psi _{(C)}(s_1,s_2) = (1-\tilde{\rho }_1) \frac{\left( c_1+c^1_2\right) s_1 }{ c_1s_1+ c_2s_2-\lambda [1-\phi (s_1,s_2)]} \cdot \frac{ c_2 S_2(s_1) - c_2s_2 + s_1 c_2^1}{c_2 S_2(s_1)}. \end{aligned}$$

(11)

For each fixed $s_1$ with ${\mathcal {R}}e\,s_1>0$, $S_2(s_1)$ is the zero of the equation

$$\begin{aligned} K_{(C)}\left( s_1,S_2(s_1)+ s_1 c_2^1/c_2\right) =0, \end{aligned}$$

which is unique in the positive half of the complex plane.

Proof

The derivation for the decoupled system is known (c.f. [1], Formula (7)]). It is easy to adapt the analysis in Sect. 3 of [1] to give the transform of the workload when the servers’ speeds are not normalized. The joint transform of the stationary amount of work in the decoupled system becomes

$$\begin{aligned} \psi _{(D)}(s_1,s_2) = (1-\tilde{\rho }_1) \frac{\tilde{c}_1 s_1}{\tilde{c}_1s_1+\tilde{c}_2s_2-\lambda [1-\phi _{(D)}(s_1,s_2)]} \cdot \frac{\tilde{c}_2 S_2(s_1)-\tilde{c}_2 s_2}{\tilde{c}_2 S_2(s_1)}, \end{aligned}$$

(12)

with $\phi _{(D)}(s_1,s_2)$ the joint LST of the generic input

$$\begin{aligned} \phi _{(D)}(s_1,s_2)=\mathbb {E}\left( e^{-s_1\tilde{B}^{(1)}-s_2 \tilde{B}^{(2)}}\right) . \end{aligned}$$

The stability condition for this system is $\tilde{\rho }_1<1$, and for each fixed $s_1$ with ${\mathcal {R}}e\, s_1>0$, $S_2(s_1)$ is the zero of the equation

$$\begin{aligned} K_{(D)}(s_1, s_2)=\tilde{c}_1s_1 + \tilde{c}_2 s_2 -\lambda [1-\phi _{(D)}(s_1,s_2)]=0, \end{aligned}$$

(13)

which is unique in the positive half of the complex plane.

We have the analogous relation to (7):

$$\begin{aligned} \phi (s_1,s_2) = \phi _{(D)}\left( s_1,s_2-s_1 c_2^1/c_2\right) . \end{aligned}$$

(14)

Combining (7), (12), and (14) we obtain

$$\begin{aligned} \psi _{(C)}(s_1,s_2) = \left( 1-\tilde{\rho }_1\right) \frac{ \left( c_1+c_2^1\right) s_1}{ c_1s_1+ c_2s_2-\lambda [1-\phi (s_1,s_2)]} \cdot \frac{ c_2 S_2(s_1)- c_2 s_2 + s_1 c_2^1}{c_2 S_2(s_1)}. \end{aligned}$$

The kernel identity $K_{(D)}(s_1,s_2) = K_{(C)}(s_1,s_2+s_1 c_2^1/c_2)$ (see Remark 2) together with (13) gives that $S_2(s_1)$ is then the unique zero with positive real part of

$$\begin{aligned} K_{(C)}\left( s_1,s_2+ s_1 c_2^1/c_2\right) =0. \end{aligned}$$

This yields the desired result. $\square$

5 The $k$-dimensional model

In this section we consider multiple coupled servers in parallel which receive simultaneous requirements. It is shown that also in this case, the coupled system can be reduced to a decoupled system, upon modifying the input. However for three servers we have to specify in addition how to divide the extra service capacity of an idle server over the other queues. This was trivial for two servers since one can only assist the other during its idle periods. With such specifications in place, the formal idea of the proof for the $k$-dimensional system is analogous to the case $k=3$, and it relies on the result for two coupled queues. Thus, we can work with $k=3$, to keep formulae still accessible, without losing generality.

We extend the ordering assumption between the service requirements to

$$\begin{aligned} \mathbb {P}\left( B^{(1)}/c_1 \ge B^{(2)}/c_2 \ge B^{(3)}/c_3\right) = 1. \end{aligned}$$

In addition, while server 3 is idle and server 2 is busy, we denote by $c_3^1$ and $c_3^2$ the processing rate of server 3 into buffers 1 and 2, respectively. If also server 2 becomes idle, we denote by $c_2^1$ the processing rate of server 2 into buffer 1 during its idle time, and moreover, server 3 contributes an extra rate $\hat{c}_3^1$ into buffer 1, so that the total contribution from server 3 becomes $c_3^1 +\hat{c}_3^1$ while server 2 is idle.

Moreover we assume that $c_3^1/ c_1 \le c_3^2/c_2$ in order to ensure that the amount of work in queue 1 remains above the amount of work in queue 2 at all times. Because of this assumption, the amount of work in the system is again ordered:

$$\begin{aligned} \mathbb {P}\left( V^{(1)}/c_1 \ge V^{(2)}/c_2 \ge V^{(3)}/c_3\right) = 1. \end{aligned}$$

The Lindley-type recursion for queue 2 is similar to (5). In the sequel, we will derive the recursion for queue 1. Because of the coupling, the idle period of queue 2 plays a role in the dynamics of queue 1 so for this reason (and to keep notation short) we introduce

$$\begin{aligned} J^{(2)}_{n}:= & {} (c_3^2+ c_2)^{-1}\left[ V_{n-1}^{(2)}+B^{(2)}_{n-1} - c_2 A_{n-1}\right. \\&\left. +\,c_3^2/c_3\,\left( V_{n-1}^{(3)}+B^{(3)}_{n-1} - c_3 A_{n-1}\right) \wedge 0\right] ,\\ J^{(3)}_{n}:= & {} c_3^{-1}\left( V_{n-1}^{(3)}+B^{(3)}_{n-1} - c_3 A_{n-1} \right) . \end{aligned}$$

$-(J^{(2)}_{n}\wedge 0)$ is the idle period in queue 2 right before epoch $n$, and it follows from (2) that

$$\begin{aligned} \left( c_3^2+ c_2\right) J^{(2)}_{n}\vee 0 = V_n^{(2)}. \end{aligned}$$

(15)

Also, $-(J^{(3)}_n\wedge 0)$ is the idle period in queue 3. The fact that $-(J^{(2)}_n\wedge 0)$ is an idle period is again a consequence of the ordering, because if server 2 is idle then server 3 must also be idle and hence coupled to queue 2. We can combine the terms above into the identity

$$\begin{aligned} J^{(2)}_n = \left( c_3^2+ c_2\right) ^{-1}\left( V_{n-1}^{(2)}+B^{(2)}_{n-1} - c_2 A_{n-1} + c_3^2J^{(3)}_n\wedge 0\right) . \end{aligned}$$

(16)

Now we can write the stochastic recursion for the amount of work in queue 1 at arrival epoch $n+1$:

$$\begin{aligned} V^{(1)}_{n+1} = \left[ V_{n}^{(1)}+B^{(1)}_{n} - c_1 A_{n} + (c_2^1+\hat{c}_3^1)J^{(2)}_{n+1}\wedge 0 + c_3^1J^{(3)}_{n+1}\wedge 0\right] \vee 0. \end{aligned}$$

(17)

In addition, $-\left[ \left( c_2^1+\hat{c}_3^1\right) J^{(2)}_{n+1}\wedge 0\right]$ is the extra amount of work that server 2 and server 3 are capable of processing while working coupled to server 1 during the idle period of server 2. Similarly, $-\left( c_3^1J^{(3)}_{n+1}\wedge 0\right)$ is the amount of work that can be processed by server 3 while coupled directly to server 1.

Proposition 2

Let $\left( V_n^{(1)},V^{(2)}_n,V^{(3)}_n\right)$ be the amount of work at epoch $n$ in the coupled system (C). Then the following process defined for $n\ge 1$:

$$\begin{aligned} \tilde{V}_n^{(1)}&:= V_n^{(1)} + c_2^*/c_2V_n^{(2)} + c_3^*/c_3 V_n^{(3)},\\ \tilde{V}_n^{(2)}&:= V_n^{(2)} + c_3^2/c_3 V_n^{(3)}, \nonumber \\ \tilde{V}_n^{(3)}&:= V_n^{(3)}, \nonumber \end{aligned}$$

(18)

with

$$\begin{aligned} c_2^*:= \frac{c_2^1+\hat{c}_3^1}{c_2+ c_3^2}c_2,\quad c_3^*:= \frac{c_2^1+\hat{c}_3^1}{c_2+ c_3^2}c_3^2+ c_3^1, \end{aligned}$$

represents the amount of work at epoch $n$ in a queueing system without coupling between the servers. The service rates are $\tilde{c}_1:=c_1+ c_2^*+ c_3^*= c_1 + c_2^1+ c_3^1+\hat{c}_3^1$ for server 1, $\tilde{c}_2:= c_2 + c_3^2$ for server 2, and $\tilde{c}_3:= c_3$ for server 3. The input in the three queues at epoch $n$ is $\tilde{B}_n^{(1)} := B_n^{(1)} + c_2^*/c_2B_n^{(2)} + c_3^*/c_3 B_n^{(3)}$, $\tilde{B}_n^{(2)} := B_n^{(2)} + c_3^2/c_3 B_n^{(3)}$, and $\tilde{B}_n^{(3)} := B_n^{(3)}$, respectively.

By a similar coupling argument as in the case $k=2$, assume that all queues start empty and that the arrival epochs are the same as in the coupled system. Server 1 processes at rate $\tilde{c}_1 = c_1 + c_2^1+ c_3^1+ \hat{c}_3^1$, server 2 at rate $\tilde{c}_2 = c_2 + c_3^2$, and server 3 at the same rate $c_3$. Queue 3 evolves again unchanged. Using a bit of algebra, $\tilde{V}_n^{(1)}$ from (18) can be rewritten as

$$\begin{aligned} \tilde{V}_n^{(1)} = V_n^{(1)} + \frac{c_2^1+\hat{c}_3^1}{c_2+c_3^2}\left( V_n^{(2)} - c_2 \frac{V^{(3)}_n}{c_3}\right) + \left( c_2^1+c_3^1+ \hat{c}_3^1\right) \frac{V_n^{(3)}}{c_3}. \end{aligned}$$

Focus on the ends of the successive busy periods in the three queues. The first one to empty is queue 3. Up to the moment the third queue is empty, partition the work in queue 2 as in Sect. 3. Actually, queue 2 together with queue 3 make up precisely the two-dimensional system studied in Sect. 3.

The service rate in queue 1 can be partitioned in the following way: $c_1$ is dedicated to processing type $V_t^{(1)}$ work, and $\left( c_2^1+c_3^1+ \hat{c}_3^1\right)$ is dedicated to processing the work $\left( c_2^1+c_3^1+ \hat{c}_3^1\right) V_t^{(3)}/c_3$. We remark that $V_t^{(2)}- c_2 V_t^{(3)}/c_3$ is a.s. non-negative due to ordering. The remainder of $\tilde{V}_n^{(1)}$ is waiting in the buffer up to the moment queue 3 empties. At this point in time, work $V_t^{(2)}- c_2 V_t^{(3)}/c_3$ is still left in buffer 2, and it is processed at rate $c_2 + c_3^2$, whereas in buffer 1 the amount left equals

$$\begin{aligned} V_t^{(1)}- c_1 \frac{V_t^{(3)}}{c_3} + \frac{c_2^1+ \hat{c}_3^1}{c_2 + c_3^2}\left( V_t^{(2)} - c_2\frac{ V^{(3)}_t}{c_3}\right) . \end{aligned}$$

From this point on, partition server 1 capacity in the following way: dedicate rate $\left( c_1 + c_3^1\right)$ to process work $V_t^{(1)} - c_1 V^{(3)}_t/c_3$, and rate $\left( c_2^1+\hat{c}_3^1\right)$ to process work $\frac{c_2^1+ \hat{c}_3^1}{c_2 + c_3^2}\left( V_t^{(2)} - c_2 V^{(3)}_t/c_3\right)$. In this way, at the moment queue 2 empties, there is still work left in queue 1 that is

$$\begin{aligned} V_t^{(1)} - c_1 \frac{V_t^{(3)}}{c_3} - \frac{c_1+c_3^1}{c_2 + c_3^2}\left( V_t^{(2)} - c_2 \frac{V_t^{(3)}}{c_3}\right) , \end{aligned}$$

and this is processed at speed $c_1 + c_2^1+\hat{c}_3^1+c_3^1$ as long as there is no new arrival.

Proof of Proposition 2

The idea is to add successively the terms $\left( c_2^1+ c_3^2\right) J^{(2)}_{n+1}\vee 0$ and $c_3^* J^{(3)}_{n+1}\vee 0 = c_3^*/c_3 V^{(3)}_{n+1}$ to the recursion in (17) in order to compensate for the minima with 0 in the first bracket.

First add the term $\left( c_2^1+ \hat{c}_3^1\right) J^{(2)}_{n+1}\vee 0 = c_2^*/c_2 V^{(2)}_{n+1}$ to both sides of (17). Making use of (15) for the left-hand side and of (16) for the right-hand side, (17) becomes, after rearranging terms,

$$\begin{aligned}&V^{(1)}_{n+1} + \frac{c_2^*}{c_2} V_{n+1}^{(2)} \nonumber \\&\quad = \left[ V_{n}^{(1)}+B^{(1)}_{n} - c_1 A_{n} + \frac{c_2^*}{c_2}\left( V_{n}^{(2)}+B^{(2)}_{n} - c_2 A_{n}\right) + \frac{c_3^*}{c_3} \left( V_{n}^{(3)}+B^{(3)}_{n} - c_3 A_{n}\right) \wedge 0\right] \nonumber \\&\qquad \vee \left[ \frac{c_2^*}{c_2}\left( V_{n}^{(2)}+B^{(2)}_{n} - c_2 A_{n}\right) + \frac{c_3^*-c_3^1}{c_3}\left( V_{n}^{(3)}+B^{(3)}_{n} - c_3 A_{n}\right) \vee 0 \right] \vee 0. \end{aligned}$$

(19)

Now add the term $c_3^* J^{(3)}_{n+1}\vee 0$, which is the same as $c_3^*/c_3 V^{(3)}_{n+1}$, by Lindley’s recursion. After regrouping terms, (19) becomes

$$\begin{aligned}&V_{n+1}^{(1)} +\frac{c_2^*}{c_2} V_{n+1}^{(2)} + \frac{c_3^*}{c_3} V_{n+1}^{(3)} \nonumber \\&\quad =\left[ V_n^{(1)} + B_{n}^{(1)}- c_1 A_{n} + \frac{c^*_2}{c_2}\left( V^{(2)}_n + B_{n}^{(2)} - c_2 A_{n}\right) + \frac{c^*_3}{c_3}\left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) \right] \nonumber \\&\qquad \vee \left[ \frac{c^*_2}{c_2}\left( V^{(2)}_n + B_{n}^{(2)} - c_2 A_{n}\right) + \frac{c^*_3-c_3^1}{c_3}\left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) \right. \nonumber \\&\qquad + \left. \frac{c_3^1}{c_3} \left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) \vee 0\right] \vee \frac{c^*_3}{c_3}\left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) \vee 0. \end{aligned}$$

(20)

We show now that the two middle terms that appear in the maximum sequence above are always dominated by either one of the extremal terms. There are three cases to be considered. If

$$\begin{aligned} V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n} >0 \end{aligned}$$

then by the ordering assumption, $V_n^{(2)} + B_{n}^{(2)}- c_2 A_{n}$ and $V_n^{(1)} + B_{n}^{(1)}- c_1 A_{n}$ are also positive, and it is easy to see that the first term on the right-hand side is the largest one.

The alternative is

$$\begin{aligned} V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n} < 0, \end{aligned}$$

and there are two sub-cases to be considered: if

$$\begin{aligned} -\frac{c_3^1}{c_3}\left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) < V_n^{(1)} + B_{n}^{(1)}- c_1 A_{n}, \end{aligned}$$

then the first term dominates the second one on the right-hand side of (20) and the third term is negative by assumption, so one can ignore the intermediate terms again.

The other subcase is when

$$\begin{aligned} -\frac{c_3^1}{c_3}\left( V_n^{(3)} + B_{n}^{(3)}- c_3 A_{n}\right) > V_n^{(1)} + B_{n}^{(1)}- c_1 A_{n}, \end{aligned}$$

thus the first term on the right-hand side of (20) is smaller than the second term. We show that this second term is now negative: the above inequality means that queue 3 is able to empty queue 1 at epoch $n+1$ without the help of queue 2, so as a consequence of the ordering assumptions, queue 3 will also empty queue 2 at epoch $n+1$: $V^{(2)}_{n+1}=0$, and it is easy to see using the definitions of $c_2^*$ and $c_3^*$ and the recursion (5) for the two coupled queues, that this latter fact is equivalent to the second term being negative.

In conclusion, the intermediate terms on the right-hand side of (20) can be ignored, and this gives, after rearranging terms,

$$\begin{aligned} \tilde{V}_{n+1}^{(1)}= \left\{ \tilde{V}_n^{(1)} + \tilde{B}^{(1)}_{n} - \tilde{c}_1 A_{n} \right\} \vee 0. \end{aligned}$$

By ignoring queue 1, it follows at once from Proposition 1 that $\tilde{V}^{(2)}_n$ satisfies the corresponding Lindley recursion, and since queue 3 evolves unchanged the proof is complete. $\square$

As in Sect. 2, if we denote by $\psi _{(C)}$ and $\psi _{(D)}$ the transforms of the amount of work in the coupled and, respectively, in the related decoupled system, then the relation analogous to (7) is

$$\begin{aligned} \psi _{(C)}(s_1,s_2,s_3) = \psi _{(D)}\left( s_1,s_2-\frac{c_2^*}{c_2} s_1,s_3 - \frac{c_3^2}{c_3} s_2 - \frac{c_3^*}{c_3} s_1\right) , \end{aligned}$$

and it is easy to see that the input in the decoupled system remains ordered, which means, in principle, one can determine $\psi _{(C)}$ from the relation above using the available expression for $\psi _{(D)}$ obtained in [1] (Sect. 3, Formulae (8) and (12)).

6 Conclusions and final remarks

We have pointed out a relation between a coupled processor model and two parallel queues without coupling, under the assumption of ordered input. This relation was further used to derive the joint Laplace–Stieltjes transform of the amount of work in equilibrium.

We have also derived the relation explicitly for the case of three coupled processors. This can be used in principle to determine the joint transform of the equilibrium amount of work by using the expression derived in Proposition 2 in [1], for the queueing system with the processors not coupled.

Relation with two coupled queues in tandem There is also a relation between the coupled processor model with two queues described above and two tandem queues which are coupled. The relation is similar to the one between the systems without coupling, which was pointed out for Lévy input in Kella [5] (see also [1]).

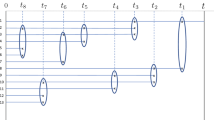
Consider two queues working in tandem, and having a compound Poisson arrival process which at epoch $n$ brings work $B_n^{(2)}$ in the first queue and work $B_n^{(1)}-B_n^{(2)}$ in the second queue (Fig. 1). Both queues work at unit speed and the output from queue 1 flows into queue 2. The queues are also coupled, which means that as soon as queue 1 is empty it switches its capacity to help queue 2, so that the processing rate of queue 2 doubles during the idle periods of queue 1. The assumption of equal rates seems to be necessary to have this model related to the coupled processor model studied in the previous sections.

Fig. 1

Tandem fluid queue

Since the amount of work does not depend on the server’s policy, one can assume that the amount of fluid coming from server 1 is processed with priority over the accumulated exogenous input into buffer 2. Then the point of the assumption of equal rates is that server 2 finishes processing the fluid at the same instant that server 1 becomes idle. For this reason, the amount of work in queue 1 together with the total amount of work in the tandem system taken as a whole is the same as the workload vector in the coupled system (C).

As a final remark, we mention that the number of jobs waiting to be served in a tandem queueing system with coupled processors has been studied in Resing and Örmeci [6] related to data transfer in cable networks. The focus is on the number of jobs at two stations which receive a Poisson input at only the first station (no exogenous arrivals) and the server distributes its capacity among the queues while both are non-empty and it switches full capacity to one queue when the other has no jobs to be served, hence the system behaves as a coupled processor model. The functional equation is solved by relating it again to a Riemann-Hilbert boundary value problem, and in van Leeuwaarden and Resing [7] it is also pointed out how to derive performance measures as the mean delay at one station, based on its solutions.