Identification in english auctions with shill bidding

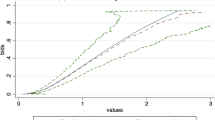
Abstract

What can we learn from auction data when the seller submits shill bids to inflate the auction price? I study identification in an incomplete model of an English auction with shill bidding in the context of independent private values. I show that the distribution of valuations is partially identified (as is the optimal reserve price), and I provide bounds for the distribution of valuations that hold even when the seller is not engaging in shill bidding. I apply these results to a sample of eBay auctions.

Appendices

Appendix A: Omitted proofs

Proof of Proposition 2

We first have that by the Glivenko-Cantelli theorem,

$$ \hat{F}^{}_{w,n+1,T}(t)=\frac{1}{T_{n+1}}\sum _{i=1}^T 1\{m_i=n+1; w_i \le t\} \overset{a.s.}{\rightarrow }\ {F}^{}_{w,n+1}(t) $$

uniformly in t, for all $n+1 \in \Omega$.

Consider $\hat{L}_{T}(t)$. Since $\phi _2^{-1}:[0,1] \rightarrow [0,1]$ is a uniformly continuous function for all n, it follows from Lemma 2 that

$$ \phi _2^{-1}(\hat{F}^{}_{n+1,T}(t-\Delta )|n) \overset{a.s.}{\rightarrow }\ \phi _2^{-1}({F}^{}_{n+1}(t-\Delta )|n) $$

uniformly in t, for all $n+1 \in \Omega$. Since the $\max$ function is continuous, it follows from the continuous mapping theorem that

$$ \hat{L}_{T}(t) \overset{a.s.}{\rightarrow }\ L(t), \; \forall t. $$

Finally, that the convergence of $L_{T}(t)$ to L(t) is a.s. uniformly in t, follows from the following inequality

$$ \sup _t |\hat{L}_{T}(t)-L(t)| \le \sum _n \sup _t |\phi _2^{-1}(\hat{F}^{}_{w,n+1,T}(t-\Delta )|n)-\phi _2^{-1}({F}^{}_{w,n+1}(t-\Delta )|n)|. $$

The rest of the proof follows by applying analogous arguments.

Proof of Proposition 3

The proof follows from the arguments provided in the text.

Proof of Proposition 4

The proof follows from arguments that are analogous to those in the proof of Proposition 1.

Proof of Proposition 5

Fix $n \in \aleph$. Define

$$\begin{aligned} \pi _n(r|v_0)=v_0 F_v(r)^n+n\int _r^{\bar{v}}(F_v(v)+vF_v'(v)-1)F_v^{n-1}(v)dv, \end{aligned}$$

where $F_v(\cdot )$ is the true but unobserved distribution of valuations, and take

$$ r_n^* \in \arg \max _{r} \pi _n(r|v_0). $$

It is true that

$$\begin{aligned} \pi _n(r_n^*)\ge & {} \sup _{ a \in [\underline{v},\bar{v}]}\pi _n^L(a) \end{aligned}$$

(12)

$$\begin{aligned} \pi _n^U(r_n^*)\ge & {} \pi _n(r_n^*) \end{aligned}$$

(13)

since $\pi _n^U(t) \ge \pi _n(t)\ge \pi _n^L(t), \forall t$.

Suppose $r_n^* \notin H[r^*]$. That implies, in particular, that $r_n^* \notin \left\{ r: \pi _n^U(r)\ge \sup _{ a \in [\underline{v},\bar{v}]}\right.$ $\left. \pi _n^L(a) \right\}$. If $r_n^* \notin \{r: \pi _n^U(r)\ge \pi _n^L(r_n^L)\}$, then

$$ \sup _{ a \in [\underline{v},\bar{v}]}\pi _n^L(a) > \pi _n^U(r_n^*). $$

But then by making use of Eqs. 12 and 13, we reach the following contradiction

$$ \sup _{ a \in [\underline{v},\bar{v}]}\pi _n^L(a) > \pi _n^U(r_n^*) \ge \sup _{ a \in [\underline{v},\bar{v}]}\pi _n^L(a). $$

Proof of Proposition 6

Part a) follows from Lemma 4 in Appendix A. Part b) follows from Proposition 5b in Manski and Tamer (2002).

Appendix B: Additional results

Lemma 1

Let $\phi _1(\cdot |n)$ and $\phi _2(\cdot |n)$ be the distribution functions of the first- and second-order statistics, defined as

$$\begin{aligned} \phi _1(x|n)=x^{n} \; \;\; \text { and } \; \; \; \phi _2(x|n)=n(n-1) \int _0^{x} u^{n-2}(1-u)du. \end{aligned}$$

The inverse functions $\phi ^{-1}_1(x|n)$ and $\phi ^{-2}_1(x|n)$ are increasing in n for $x \in (0,1)$.

Proof

I first show that $\phi _2^{-1}(x|n) \le \phi _2^{-1}(x|n+1)$ for $x\in (0,1]$. Call the left-hand side expression, $y_{n}$, and the right-hand side expression, $y_{n+1}$. From the expression for the second-order distribution function, $\phi _2(\cdot |n)$, we note that $y_n$ and $y_{n+1}$ are implicitly defined as

$$\begin{aligned} x= & {} n(y_{n}^{n-1}-y_{n}^{n})+y_{n}^{n}, \\ x= & {} n y_{n+1}( y_{n+1}^{n-1}- y_{n+1}^{n})+y_{n+1}^n. \end{aligned}$$

By setting these expressions equal, and by using the fact that $x \in [0,1]$, we obtain the following inequality

$$\begin{aligned} n(y_{n}^{n-1}-y_{n}^{n})+y_{n}^{n}= & {} n y_{n+1}( y_{n+1}^{n-1}- y_{n+1}^{n})+y_{n+1}^n \\\le & {} n( y_{n+1}^{n-1}- y_{n+1}^{n})+y_{n+1}^n, \end{aligned}$$

where the inequality follows from $y_{n+1} \in (0,1]$. The inequality can be rewritten as

$$ \phi _2(y_{n}|n) \le \phi _2(y_{n+1}(t)|n). $$

Since $\phi _2(\cdot |n)$ is a strictly increasing function, the result follows.

Consider next $\phi ^{-1}_1(x|n)$. By taking the derivative of $\phi _1^{-1}(x|n) = x^{1/n}$, one can show that the function is increasing in n for $x \in (0,1)$. $\square$

Lemma 2

Take a sequence of functions $\{g_T(\omega ,\theta )\}$, $g_T:X \rightarrow Y$, that converges to $g(\theta )$ a.s. uniformly in $\theta \in \Theta$, that is,

$$ \Pr \left[ \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | g_n(\theta )-g(\theta )|=0 \right] =1. $$

Take a uniformly continuous function $\psi :Y \rightarrow Y$. Then $\{\psi (g_T(\omega ,\theta ))\}$ converges to $\psi (g(\theta ))$ a.s. uniformly in $\theta \in \Theta$.

Proof

Fix any $\varepsilon >0$. By uniform continuity of $\psi$, $\exists \delta >0$ such that for any $x,y \in X$, $|x-y|<\delta$ implies $|\psi (x)-\psi (y)|<\varepsilon$.

By convergence a.s. uniformly of $g_T$,

$$ \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | g_T(\theta )-g(\theta )|=0 \; \; \text { a.e. }, $$

that is, $\exists \, T_{\delta }$ such that $\forall \, m \ge T_{\delta }$

$$ \sup _{\theta } |g_m(\theta )-g(\theta )| <\delta \; \; \text { a.e. }. $$

By uniform continuity of $\psi$, we conclude that $\forall m \ge T_{\delta }$

$$ \sup _{\theta } |\psi (g_m(\theta ))-\psi (g(\theta ))| <\varepsilon \; \; \text {a.e. }. $$

Since this holds for any $\varepsilon >0$,

$$ \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | g_T(\theta )-g(\theta )|=0 \; \; \text { a.e. } \; \; \Rightarrow \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | \psi (g_T(\theta ))-\psi (g(\theta ))|=0 \; \; \text { a.e. }. $$

The result follows since

$$ 1=\Pr \left[ \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | g_T(\theta )-g(\theta )|=0\right] \le \Pr \left[ \lim _{T \rightarrow \infty } \sup _{\theta \in \Theta } | \psi (g_T(\theta ))-\psi (g(\theta ))|=0 \right] . $$

$\square$

Lemma 3

$\pi _{T,n}(r) \overset{a.s.}{\rightarrow }\pi _n(r)$ uniformly in r.

Proof

Note that

$$\begin{aligned} \sup _r |\pi _{T,n}(r)-\pi _n(r)|= & {} \sup _r \left| (v_0-r)(F_{T}(r)^n-F(r)^n)\right. \\{} & {} \left. -\int _r^{\bar{v}}\left( F_T(v)^{n-1}[n(1-F_T(v))+F_T(v)]\right. \right. \\{} & {} \left. \left. -F(v)^{n-1}[ n(1-F(v))+F(v)] \right) dv\right| \\\le & {} |K_1|\cdot \sup _r|F_{T}(r)^n-F(r)^n|\\{} & {} + \sup _r \left| \int _r^{\bar{v}}\left( F_T(v)^{n-1}[n(1-F_T(v))+F_T(v)]\right. \right. \\{} & {} \left. \left. -F(v)^{n-1}[n(1-F(v))+F(v)] \right) dv \right| \\\le & {} |K_1|\cdot \sup _r|F_{T}(r)^n-F(r)^n|+|K_2| \cdot \sup _v \left| F_T(v)^{n-1}[n(1-F_T(v))\right. \\{} & {} \left. +F_T(v)]-F(v)^{n-1}[n(1-F(v))+F(v)] \right| \\= & {} |K_1|\cdot \sup _r|\psi _1(F_{T}(r))-\psi _1(F(r))|\\{} & {} +|K_2| \cdot \sup _v|\psi _2(F_{T}(r))-\psi _2(F(r))|, \end{aligned}$$

where $K_1$ and $K_2$ are constants, and $\psi _1:[0,1] \rightarrow [0,1]$ and $\psi _2:[0,1] \rightarrow [0,1]$ are uniformly continuous functions. Since $F_T(x) \overset{a.s.}{\rightarrow }F(x)$ uniformly in x, the result follows from Lemma 2. $\square$

Lemma 4

$Q_{T}(t) \overset{a.s.}{\rightarrow }Q(t)$ uniformly in t.

Proof

Note that

$$\begin{aligned} \sup _t \left| Q_{n,T}(t)-Q_n(t) \right|\!=\! & {} \sup _t \left| 1\{\sup _a \pi _{T,n}^L(a)-\pi _{T,n}^U(t)>0\}(\sup _a \pi _{T,n}^L(a)-\pi _{T,n}^U(t)) \right. \\{} & {} \left. -1\{\sup _a \pi _n^L(a)-\pi _n^U(t)>0\}(\sup _a \pi _n^L(a)-\pi _n^U(t)) \right| \\\le & {} \sup _t \left| (\sup _a \pi _{T,n}^L(a)-\pi _{T,n}^U(t))-(\sup _a\pi _n^L(a)-\pi _n^U(t)) \right| \\\le & {} \left| \sup _a \pi _{T,n}^L(a)-\sup _a \pi _n^L(a) \right| + \sup _t \left| \pi _n^U(t)-\pi _{T,n}^U(t) \right| \\\le & {} \sup _a \left| \pi _{T,n}^L(a)- \pi _n^L(a) \right| + \sup _t \left| \pi _n^U(t)-\pi _{T,n}^U(t) \right| . \end{aligned}$$

Since $\pi _{T,n}(r) \overset{a.s.}{\rightarrow }\pi _n(r)$ uniformly in r, the result follows from Lemma 2. $\square$