Abstract
Earlier work characterized pricing with switching costs as a dilemma between a short-term “harvesting” incentive to increase prices versus a long-term “investing” incentive to decrease prices. This paper shows that small switching costs may reduce firm profits and provide short-term incentives to lower rather than raise prices. We provide a simple expression which characterizes the impact of the introduction of switching costs on prices and profits for a general model. We then explore the impact of switching costs in a variety of specific examples which are special cases of our model. We emphasize the importance of a short term “compensating” effect on switching costs. When consumers switch in equilibrium, firms offset the costs of consumers that are switching into the firm. If switching costs are low, this compensating effect of switching costs causes even myopic firms to decrease prices. The incentive to decrease prices is even stronger for forward looking firms.




Similar content being viewed by others
Notes
Klemperer (1987) considers several alternative two-period models. Of these, the closest to ours is when consumer preferences are uncorrelated between the two periods. In this setting he focuses on symmetric firms and finds that the short term (second period) effect is zero and the first period (investing) effect decreases prices and profits. Our analysis generalizes this result and confirms Klemperer’s conjecture (in the conclusion there) that in asymmetric markets a firms’ reaction depends on its market share.
Pearcy (2014) shows that allowing for consumers to be forward looking can also reverse the qualitative effect of SC on symmetric markets.
Aside from small SC, the main assumption in our analysis is that the consumers’ purchasing decision is myopic. With the exception of Pearcy (2014), this assumption is common to the previous studies mentioned above, and relaxing it is an important avenue for future research.
Roughly this result requires that the firm has less than average market share.
In this paper, we consider so-called “transactional” switching costs, which are most commonly addressed in the literature. In this framework, a cost must be paid each time consumers switch products. Nilssen (1992) contrasts this type of switching costs with “learning” switching costs, where customers may costlessly switch between products they have already learned how to use.
Klemperer (1995) argues that SC are likely to play an important role in many areas of economics, including industrial organization and international trade.
Equivalently, one could normalize utility without loss of generality such a consumer in loyalty group j derives γ less utility from all goods except j.
In particular, this rules out network effects.
It is also possible to analyze alternative laws of motion that might allow for the introduction of new consumers, or experimentation by consumers who might try a new good, but remain loyal to their earlier purchase with some positive probability. Both of these extensions have the effect of reducing firms’ investment incentive, but do not change the qualitative results of our model.
This normalization is for convenience and the model can be easily generalized to accommodate firm-specific marginal costs.
Moreover, there is no reason to believe that restricting ourselves to stationary strategies will ensure a unique equilibrium as firms may detect defections from market shares.
The propositions below formalize dominance using bounds on market shares and HHI.
The exact price effect is derived for a monopolist in Section 3.4.
Note that consumers in group x are less price sensitive if \(D_{p\gamma }^{x}\geq 0\).
Similar results for the Salop demand system are provided in Appendix C.
For other demand structures, the interaction between SC and price sensitivity may not cancel when firms are symmetric. For example, switchers may become more price sensitive while the price sensitivity of loyals may not change—e.g., add a term \(-\gamma _{p} p_{jt} \mathbf {1}\left [ j\neq k\right ]\) to \(\bar {u}\) in Eq. 3.2.
While the proof relies on the quasi-linearity of utility, Appendix C provides a similar result for linear models.
We thank a referee for suggesting this.
It can be shown that with n symmetric market leaders, the same upper bound applies as \(J \to \infty \)
We focus on the case in which the SC also applies when switching to/from the outside good. Our base case is reasonable for many industries. For example, switching across cable TV, satellite, IP-TV and outside “broadcast” television requires learning the channel layout, acquiring and installing the necessary equipment, and ordering or canceling the relevant services even when switching to or from broadcast. We briefly discuss the alternative where switching to the outside good does not incur SC at the end of this section.
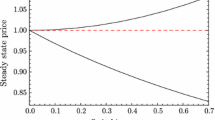
This is illustrated and discussed further using the numerical example in Fig. 1.
Consumer surplus is calculated using compensating variation (CV). In the single firm model this is:
$$CV=-\frac{1}{\alpha}\left( \log\left( e^{\delta_{0}}+e^{\delta_{1} +\alpha\cdot p-\gamma}\right) -\delta_{0}\right). $$For high switching-cost values, this method is actually a generous calculation as it assumes that all consumers can stay with the outside good “for free.” The main alternative, expenditure variation, (EV) would actually be negative for higher SC as loyal consumers are paying a very high price to keep themselves from switching.
Other symmetric specifications do not add qualitative insight. Specifically, in a symmetric duopoly, no firm can dominate the market regardless of δ. Thus, increasing δ 1 and δ 2 provides no additional insight and is not presented
We use value function iteration to approximate symmetric MPEs. The Mathematica software code is available from the authors. Our simulation used a 361 point grid for the state (share) space and process stops when the change in the value over all states is smaller than a threshold, which was set at 10−6. We verify that the optimal policy is unique by verifying that the best response function is quasi-concave and use the optimal pricing strategy to “play out” the equilibrium strategies starting at various states until a steady state is obtained. A unique steady state was obtained for all parameter values that we consider. For higher SC values, we do not expect a steady state exists as firms profit from ’invest then harvest’ cycles that take advantage of consumer myopia. Indeed, our equilibrium for high SC (roughly γ>2.7) did not converge to a steady state.
For expositional simplicity, we subtract 𝜖 in this section rather than add it as in Eq. 3.1. This is without loss of generality.
To see this note that consumers purchase the firm’s product if it offers the higher utility, that is the loyal consumer’s purchase if δ−α⋅p−𝜖 i >−γ and non-loyal consumers purchase if δ−α⋅p−γ−𝜖 i >0. Integrating these expressions over 𝜖 i leads to the demand equation.
Under the quasi-linear model, the assumption is equivalent to log concavity in Φ, i.e., \(({\Phi }^{\prime })^{2}\ge {\Phi } \cdot {\Phi }^{\prime \prime }\).
An older version of the paper derived the exact value for \(\frac {dp_{1}}{d\gamma }\):
$$ \frac{dp_{1}}{d\gamma=0} =-\frac{F^{1}_{\gamma}}{2D^{1}_{p_{1}} +p_{1} \cdot D^{1}_{p_{1} p_{1}} } $$However, this does not provide any additional insights; the proof is available from the authors. Note that the denominator must be negative by the standard second order condition.
We use steady-state non-SC market shares as a convenient proxy for the underlying firm quality
In a logit setting this requires a quality difference of five, which is over three standard deviations above the mean in the idiosyncratic term. In other words, if the firm would sell at the outside good price, it would have a share of over 0.95.
We have experimented with alternative specifications and found the results to be robust and indicative of the key insights. The upper bound of \(\bar {\gamma }=2\) reflects the upper bound for the steady state to exist. Analysis available from the authors shows that the true upper bound is slightly above \(\bar {\gamma }=2\) and decreases with δ. Reducing δ (i.e. making the market more competitive) allows increasing \(\bar {\gamma }\)
Here, because all price-setting firms are symmetric and the game is in strategic complements, can drop the strategic interaction term because we know it will only re-enforce the incentives of the leading terms.
The numerator for the derivative of the RHS wrt s J is
$$\begin{array}{@{}rcl@{}} \left(1-6s_{J}\right)\left(1+3{s_{J}^{2}}\right)-6s_{J}\left(s_{J}-3{s_{J}^{2}}\right) &=&1-6s_{J}+3{s_{J}^{2}}-18{s_{J}^{3}}-6{s_{J}^{2}}+18{s_{J}^{3}}\\ &=&1-6s_{J}-3{s_{J}^{2}}. \end{array} $$This quadratic expression is positive at s J =0 and negative at \(s_{J}=\frac {1}{3}\) (the upper bound). So need to take the maximizing point,
$$s_{J}=\frac{-6\pm\sqrt{36+12}}{6}=-1+\frac{4\sqrt{3}}{6}=-1+\frac{2}{\sqrt{3}}\;. $$By first-order effect we mean that the analysis does not consider the firm’s reaction to it’s rival price change.
A similar analysis can be applied to other models of linear demand, but the qualitative results are the same. In particular, both Rhodes (2014) and Shin et al. (2009) consider a Hotelling model. The Salop model was chosen to highlight the additional endogenous asymmetry caused by SC when there are more than two firms in the market.
References
Beggs, A., & Klemperer, P. (1992). Multi-period competition with switching costs. Econometrica, 60(3), 651–666.
Biglaiser, G., Cremer, J., Dobos, G. (2013). The value of switching costs. Journal of Economic Theory, 148(3), 935–952.
Cabral, L.M.B. (2012). Small switching costs lead to lower prices. New York: New York University.
Chen, Y. (1997). Paying customers to switch. Journal of Economics & Management Strategy, 6(4), 877–897.
Dube, J.-P., Hitsch, G.J., Rossi, P.E. (2009). Do switching costs make markets less competitive. Journal of Marketing Research, 46(5), 435–45.
Dubé, J.-P., Hitsch, G.J., Rossi, P.E. (2010). State dependence and alternative explanations for consumer inertia. RAND Journal of Economics, 41(3), 417–445.
Ellickson, B.E., & Pavlidis, P. (2014). Switching costs and market power under umbrella branding. Rochester, New York: Simon School of Business.
Farrell, J., & Shapiro, C. (1988). Dynamic competition with switching costs. The RAND Journal of Economics, 19(1), 123–137.
Farrell, J., & Klemperer, P. (2007). Coordination and Lock-In: Competition with Switching Costs and Network Effects In Armstrong, M., & Porter, R. (Eds.), Handbook of industrial organization (Vol. 3, pp. 1967–2072): Elsevier. chapter 31.
Garcia, A. (2011). Dynamic price competition, switching costs, and network effects. Charlottesville: University of Virginia.
Hotelling, H. (1929). Stability in competition. Economic Journal, 41–57.
Keane, M.P. (1997). Modeling heterogeneity and state dependence in consumer choice behavior. Journal of Business & Economic Statistics, 15(3), 310–327.
Klemperer, P. (1987). The competitiveness of markets with switching costs. The RAND Journal of Economics, 18(1), 138–150.
Klemperer, P. (1995). Competition when consumers have switching costs: an overview with applications to industrial organization, macroeconomics, and international trade. The Review of Economic Studies, 62(4), 515–539.
Nilssen, T. (1992). Two kinds of consumer switching costs. The RAND Journal of Economics, 23(4), 579–589.
Park, M. (2011). The economic impact of wireless number portability. Journal of Industrial Economics, 59(4), 714–745.
Pearcy, J. (2014). Bargains Followed by Bargains: When Switching Costs Make Markets More Competitive. Bozeman, Montana: Montana State University.
Rhodes, A. (2014). Re-examining the effects of switching costs. Economic Theory, 57(1), 161–194.
Salop, S.C. (1979). Monopolistic competition with outside goods. The Bell Journal of Economics, 10(1), 141–156.
Shcherbakov, O. (2010). Measuring consumer switching costs in the television industry: Yale University.
Shin, J., Sudhir, K., Cabral, L.M.B., Dube, J.-P., Hitsch, G.J., Rossi, P.E. (2009). Commentaries and rejoinder to do switching costs make markets less competitive. Journal of Marketing Research, 46(4), 446–552.
Shy, O. (2002). A quick-and-easy method for estimating switching costs. International Journal of Industrial Organization, 20(1), 71–87.
Somaini, P., & Einav, L. (2013). A Model of market power in customer markets. Journal of Industrial Economics, 61(4), 938–986.
Viard, V.B. (2007). Do switching costs make markets more or less competitive? The case of 800-number portability. The RAND Journal of Economics, 38(1), 146–163.
Author information
Authors and Affiliations
Corresponding author
Additional information
A previous version of this paper circulated under the title ”Do Firms Compensate Switching Consumers?”. We are very grateful to Sridhar Moorthy and two anonymous referees for many valuable suggestions. We also thank Mark Armstrong, Jonathan Eaton, Sarit Markovich, Marco Ottaviani, Rob Porter, Tim Richards, Mark Roberts, Bill Rogerson, Mark Satterthwaite, Yossi Speigel and participants in the 2009 SED meetings and 2010 IIOC for their comments and suggestions. Any remaining errors are entirely our own. Financial support from the General Motors Research Center for Strategy in Management at Kellogg School of Management is gratefully acknowledged.
Appendices
Appendix A Proofs
1.1 A.1. Proof of Lemma 2.1
The derivative of firm j’s steady-state value with respect to SC is given by
where p ∗ represents the vector of steady state prices for the equilibrium when γ=0.
Proof
For \(\frac {dV^{j}}{d\gamma }\): by construction, in any steady state equilibrium
Apply the envelope theorem \(\left (\frac {dV^{j}}{dp_{j}}=0 \right )\) to get
Using
Which simplifies to the desired result. □
1.2 A.2. Proof of Lemma 2.2
The derivative of firm j’s steady state price with respect to SC at γ=0 has the same sign as \(F^{j}_{\gamma }\), given by Eq. 2.6 (repeated here):
Where all χ j k ≥0 and p ∗ represent the vector of steady state prices for the equilibrium when γ=0. Moreover, long run incentives—i.e., \( {\sum }_{k \in J} \left (D^{j,k}_{\gamma } \cdot D^{k}_{p_{j}} \right ) \)—are always negative.
Proof
For \(F_{\gamma }^{j}\): first, derive \(\frac {dV}{d\nabla _{p_{j}}}\) by applying the envelope theorem to \(V\left (s\right )=pD^{1}+\beta V\left (s\right )\) :
Where d D is the gradient of the change in demand for all firms that resulted from the change in the started shares ∇. Next, take the total derivative with respect to λ,
At γ=0 , \(\frac {dV^{j}}{dD}=\frac {dD}{d\nabla }=0\) so the second dynamic term is zero. As we are holding price fixed, at γ=0,
Therefore
It remains to simplify the product multiplication. \(\frac {dD^{j}}{d\nabla _{p_{j}}}\) is a vector with elements \(D_{s_{i}}^{j}\). By construction
At γ=0, \(D_{s_{i}}^{j,i}=0\) and so
This identifies the elements of \(\frac {dD^{j}}{d\nabla _{p_{j}}}\). Taking the derivative w.r.t. γ on the vector \(\frac {dD^{j}}{d\nabla _{p_{j}}}\) yields elements of the form
Now perform the product multiplication:
Placing in \(F_{\gamma }^{j}\) above obtains the desired result:
To see that long run incentives are always negative, observe that \(D^{j,k}_{\gamma }\) is positive iff k=j, while \(D^{k}_{p_{j}}\) is negative iff k=j. □
1.3 A.3. Proof of Lemma 3.1
With logit demand, at γ=0:
Where all χ j k ≥0.
Proof
From Lemma 2.2 we know that,
So we can simply uses the structure of logit demand to determine each element in this equation to arrive at the second expression in the lemma. Note that the first expression of the lemma is shown in step 5 below.
-
(1)
Determine \(\frac {dD^{i}}{dp_{j}}\):
-
For i=j, the element is,
$$\frac{\partial D^{j}}{\partial p_{j}}=-\alpha D^{j}\left(1-D^{j}\right)=-\alpha s_{j}\left(1-s_{j}\right). $$ -
For i≠j, the element is,
$$\frac{\partial D^{i}}{\partial p_{j}}=\alpha D^{j}D^{i}=\alpha s_{j}s_{i}. $$ -
Observe that the irrelevant alternatives (IIA) assumption for how shares compensate is maintained,
$$\frac{\partial D^{i}}{\partial p_{j}}=\frac{\partial D^{j}}{\partial p_{j}}\cdot\left(-\frac{s_{i}}{1-s_{j}}\right). $$
-
-
(2)
Determine \(D_{\gamma }^{j,i}\) :
-
For i=j, \(D_{\gamma }^{j,j}=s_{j}\left (1-s_{j}\right )\);
-
For i≠j, \(D_{\gamma }^{j,i}=-s_{j}s_{i}\).
-
-
(3)
Determine the products,
$$D_{\gamma}^{j,j}\cdot\frac{\partial D^{j}}{\partial p_{j}}=-\alpha {s_{j}^{2}}\left(1-s_{j}\right)^{2}; $$$$D_{\gamma}^{j,i}\cdot\frac{\partial D^{i}}{\partial p_{j}}=-\alpha {s_{j}^{2}}{s_{i}^{2}}. $$ -
(4)
The sum,
$$\begin{array}{@{}rcl@{}} \beta\cdot p_{j}\cdot\left(\sum\limits_{i\in J}D_{\gamma}^{j,i}\frac{\partial D^{i}}{\partial p_{j}}\right) && =-\beta\alpha p_{j}{s_{j}^{2}}\left(\left(1-s_{j}\right)^{2}+\sum\limits_{i\neq j}{s_{i}^{2}}\right)\\ && =-\beta\alpha p_{j}{s_{j}^{2}}\left(1-2s_{j}+H\right). \end{array} $$Now use the standard first order condition at γ=0,
$$\alpha p_{j}s_{j}\left(1-s_{j}\right)=s_{j}. $$So \(\alpha p_{j}=\frac {1}{1-s_{j}}\) and the sum is,
$$ \beta\cdot p_{j}\cdot\left(\sum\limits_{i\in J}D_{\gamma}^{j,i}\frac{\partial D^{i}}{\partial p_{j}}\right)=-\beta\frac{{s_{j}^{2}}}{1-s_{j}}\left(1-2s_{j}+H\right). $$(A.1) -
(5)
Determine \(D_{\gamma }^{j}\),
$$\begin{array}{@{}rcl@{}} D_{\gamma}^{j} && =\sum\limits_{i}s_{i}D_{\gamma}^{j,i}\\ && =s_{j}s_{j}\left(1-s_{j}\right)-\sum\limits_{i\neq j}s_{i}s_{i}s_{j}\\ && ={s_{j}^{2}}-s_{j}{s_{j}^{2}}-s_{j}\sum\limits_{i\neq j}{s_{i}^{2}}\\ && ={s_{j}^{2}}-s_{j}\cdot\sum\limits_{i\in J}{s_{i}^{2}}\\ && =s_{j}\left(s_{j}-H\right). \end{array} $$This is the first statement in the lemma, but it still remains to derive the price effect.
-
(6)
Determine \(D_{p_{j}\gamma }^{j}\),
$$\begin{array}{@{}rcl@{}} D_{\gamma p_{j}}^{j,j} && =D_{p_{j}}^{j,j}\left(1-D^{j,j}\right)-D^{j,j}D_{p_{j}}^{j,j}\\ && =D_{p_{j}}^{j,j}\left(1-2D^{j,j}\right)\\ && =-\alpha s_{j}\left(1-s_{j}\right)\left(1-2s_{j}\right) \end{array} $$$$\begin{array}{@{}rcl@{}} D_{\gamma p_{j}}^{j,i\neq j} && =-D_{p_{j}}^{j,i}D^{i,i}-D^{j,i}D_{p_{j}}^{i,i}\\ && =\alpha D^{j,i}\left(1-D^{j,i}\right)D^{i,i}-\alpha D^{j,i}D^{j,i}D^{i,i}\\ && =\alpha\left[s_{j}\left(1-s_{j}\right)s_{i}-s_{j}s_{s}s_{i}\right]\\ && =\alpha s_{j}s_{i}\left(1-2s_{j}\right) \end{array} $$$$\begin{array}{@{}rcl@{}} D_{\gamma p_{j}}^{j} && =\sum\limits_{i}s_{i}D_{\gamma p_{j}}^{j,i}\\ && =-\alpha {s_{j}^{2}}\left(1-s_{j}\right)\left(1-2s_{j}\right)+\sum\limits_{i\neq j}\alpha s_{j}{s_{i}^{2}}\left(1-2s_{j}\right)\\ && =\alpha s_{j}\left(1-2s_{j}\right)\cdot\left(\sum\limits_{i\neq j}{s_{i}^{2}}-s_{j}+{s_{j}^{2}}\right)\\ && =\alpha s_{j}\left(1-2s_{j}\right)\left(H-s_{j}\right). \end{array} $$Using \(\alpha \cdot p_{j}=\frac {1}{1-s_{j}}\) (again, from the first order condition at γ=0):
$$p_{j}D_{\gamma p_{j}}^{j}=\frac{s_{j}}{1-s_{j}}\left(1-2s_{j}\right)\left(H-s_{j}\right). $$ -
(7)
Combine these to determine the price effect:
$$\begin{array}{@{}rcl@{}} F_{\gamma}^{j} &=&D_{\gamma}^{j}+p_{j}D_{\gamma p_{j}}^{j}+\beta\cdot p_{j}\cdot\left(\sum\limits_{i\in J}D_{\gamma}^{j,i}\frac{\partial D^{i}}{\partial p_{j}}\right)+\sum\limits_{k\neq j}\left(\frac{dp^{\ast}_{k}}{d\gamma} \chi_{jk}\right)\\ &=&s_{j}\left(s_{j}-H\right)+\frac{s_{j}}{1-s_{j}}\left(1-2s_{j}\right)\left(H-s_{j}\right)-\beta\frac{{s_{j}^{2}}}{1-s_{j}}\left(1-2s_{j}+H\right)\\ &&+\sum\limits_{k\neq j}\left(\frac{dp^{\ast}_{k}}{d\gamma} \chi_{jk}\right)\\ &=&\frac{s_{j}}{1-s_{j}}\left[\left(s_{j}-H\right)\left(1-s_{j}\right)+\left(H-s_{j}\right)\left(1-2s_{j} \right)-\beta s_{j}\left(1-2s_{j}+H\right)\right]\\ &&+\sum\limits_{k\neq j}\left(\frac{dp^{\ast}_{k}}{d\gamma} \chi_{jk}\right)\\ &=&\frac{s_{j}}{1-s_{j}}\left[\left(H-s_{j}\right)\left(1-2s_{j}-1+s_{j}\right)-\beta\left(1-2s_{j}+H\right)\right]\\ &&+\sum\limits_{k\neq j}\left(\frac{dp^{\ast}_{k}}{d\gamma} \chi_{jk}\right)\\ &=&\frac{{s_{j}^{2}}}{1-s_{j}}\left[-\left(H-s_{j}\right)-\beta\left(1-2s_{j}+H\right) \right] +\sum\limits_{k\neq j}\left(\frac{dp^{\ast}_{k}}{d\gamma} \chi_{jk}\right). \end{array} $$Which is the second statement in the lemma.
□
1.4 A.4. Proof of Proposition 3.1
In a random utility model with quasi-linear utility, if firms are symmetric (δ j =δ), then:
-
(1)
If firms are myopic \(\left (\beta =0\right )\), small SC have no effect on prices and profits.
-
(2)
If firms are forward looking \(\left (\beta >0\right )\), prices and profits decrease from a small SC for all firms.
Proof
With quasi-linear utility and J symmetric firms, consumers that are loyal to firm 1 purchase the firm’s product if
As all ε j are iid, this share can be described by a CDF on the first order statistic of the ε j distribution and the rival’s prices:
Where K is a (linear) function of all the firms’ rival prices. Letting ϕ denote the PDF for Φ:
Note that as \(D_{p_{1}}^{1,1}<0\) and α>0 it must be that \(\phi \left (K-\alpha p_{1}\right )>0\).
Consumers that are loyal to firm k≠1, would purchase if
Because utility is quasi-linear and the shocks are independent, this share can be described by a CDF on the first order statistic of the ε distribution, the rivals’ prices and a function \(\tau \left (\gamma \right )\) that depends only on γ:
Let \(\tau _{0}\equiv \tau ^{\prime }\left (0\right )\). The partials are:
We now prove that, at γ=0, if demand is quasi-linear, and the market is symmetric and fully covered (no outside good), then \(\tau _{0}=\frac {1}{J-1}\) and \(D_{\gamma p_{1}}^{1}=0\).
By construction, at γ=0,
By symmetry, if there’s no outside good, \(D_{\gamma }^{1}=0\), since steady state shares of all firms must remain \(\frac {1}{J}\) with and without switching costs. As \(\phi \left (K-\alpha p_{1}\right )\neq 0\), this requires that,
which proves both results.
This proves that the short term effect is zero and the price reaction depends only on the long term investment effect.
By Lemma 2.2, the investment effect only decreases prices and by strategic complementarity and symmetry prices decrease for all firms. As quantity sold does not change and prices decrease, profits decrease as well. □
1.5 A.5. Proof of Proposition 3.2
In a symmetric logit demand model with SC, if firms are forward looking \(\left (\beta >0\right )\), the effect of SC on prices strictly decreases in absolute terms when a firm is added to the market. The result applies to all quasi-linear random utility models in which equilibrium price sensitivity (\(D^{j}_{p_{j}}\)) weakly decreases in absolute terms when a firm is added to the market.
Proof
From Proposition 3.1, it is sufficient to show that the claim is true for the investment effect. The investment effect is \(\beta \cdot p_{1}\cdot {\sum }_{i}\left (D_{\gamma }^{1,i}D_{p_{1}}^{i}\right )\)
The proof of Proposition 3.1, showed that at γ=0, \(D_{p_{1}}^{1,1}=D_{p_{1}}^{1,j}=D_{p_{1}}^{1}\). Symmetry implies that 1′ s gain (or loss) is spread evenly over it’s rivals:
In addition, applying the notation and results from the proof of Proposition 3.1, at γ=0, we have that \(\tau _{0}=\frac {1}{J-1}\) and:
Thus,
Therefore,
So the investment effect is,
In any equilibrium at γ=0, the first order condition on price implies \(p_{1}D_{p_{1}}^{1}=-s_{1}\) and in the symmetric case this is \(-\frac {1}{J}\) so we obtain
An increase in J increases the denominator. Thus, it is sufficient to show that an increase in J weakly decreases the numerator. As \(D^{1}_{p_{1}} = -\alpha \cdot \phi \left (K-\alpha p_{1}\right )\), this is the condition stated in the proposition for the general quasi-linear random utility case. For the special case of the logit distribution, in any equilibrium:
And therefore,
The same investment effect can be obtained for the logit directly by plugging in \(s_{j} = \frac {1}{J}\) and \(H = \frac {1}{J}\) into the investment effect for the logit model (3.5). □
1.6 A.6. Proof of Proposition 3.3
Suppose in the logit demand model, J≥2, firm 1 has share \(s_{1} > \frac {1}{J}\) and all other firms have equal shares \(s_{j>1} = \frac {1-s_{1}}{J-1}\). A sufficient condition for all prices to decrease with SC is,
Proof
Start with deriving H:
By strategic complementarity, to prove that all prices decline, it is sufficient to show that for the strong firm (j=1), \(F_{\gamma }^{1}<0\). From Eq. 3.5 we see that this condition is,
Placing H and simplifying, the condition is,
Simplifying further, the condition is
Isolating s 1 obtains the statement in the proposition. □
1.7 A.7. Proof of Proposition 3.4
In the logit model, if all firms are symmetric, δ 1=δ 2=⋯=δ J−1, and an outside good has a share s J , then:
-
(1)
Prices and profits increase with a small SC if firms are myopic \(\left (\beta =0\right )\) and \(s_{J} < \frac {1}{J}\).
-
(2)
Prices decrease from a small SC whenever \(s_{J} > \frac {1}{J}\) or β≥0.077
Proof
In this setting, \(s_{j}=\frac {1-s_{J}}{J-1}\) and
Thus, a sufficient condition for profits to increase is that \(s_{J}<\frac {1}{J}\) (as this implies s j −H>0) and prices do not decrease. Recalling the price effect formula (3.5) at γ=0,Footnote 33
A sufficient condition for the price effect to be positive is that β=0 and s j −H>0. Thus, profits increase with a small SC if \(s_{J}<\frac {1}{J}\).
The sign of the price effect is determined by
The second term, which is subtracted, is always positive:
Therefore, a sufficient condition for price to decrease is that H−s j ≥0, which, from above, is equivalent to \(s_{J}\ge \frac {1}{J}\).
If \(s_{J}\le \frac {1}{J}\) then s j −H≥0 and,
Isolating β , price decreases if,
Simplifying:
Note that as J≥3, (the case of one firm and an outside good was handled in the previous section), the denominator is always positive. The derivative of the RHS for any s j is,
The sign follows from \(s_{J}\le \frac {1}{J}\) and J≥3. Thus, the strictest bound on β is for J=3 is,
The worse case is when \(s_{J}=\frac {2}{\sqrt {3}}-1\) (≈0.155). Footnote 34
At this point, the lower bound on β is
Thus, for any β≥.0774, prices are lower with a small SC than without. □
1.8 A.8. Proof of Proposition 3.5
For a monopolist:
Thus:
-
(1)
A small SC increases profits for a monopolist iff the monopolist share of the market is at least .5.
-
(2)
For any discount factor a small SC causes a monopolist to decrease prices if its share is lower than .5.
-
(3)
For any discount factor a small SC causes a monopolist to increase prices if in the equilibrium without SC: \(2s_{1} \cdot p_{1}D_{p_{1}\gamma }^{1,1} > D^{1,1}_{\gamma } + p_{1}D_{p_{1}\gamma }^{1,1}\).
Proof
We let the monopolist be firm 1 and the outside good firm 0. The following will be used throughout the proof:
Lemma 1.1
At γ=0:
-
(1)
D 1,1 =D 1,0
-
(2)
\(D^{1,1}_{\gamma } = -D^{1,0}_{\gamma }\)
-
(3)
\(D^{1,1}_{p_{1} \gamma } = -D^{1,0}_{p_{1} \gamma }\)
Proof
Recall that \(D^{1,1}={\Phi } \left (\delta - \alpha p_{1} + \gamma \right )\) and \(D^{1,0}={\Phi } \left (\delta - \alpha p_{1} - \gamma \right )\) The first claim follows from replacing γ = 0 in D 1,k. The second and third follow from taking the required derivatives and then placing γ=0. □
Applying Lemma 2.1:
By construction,
Applying lemma (A.1):
To derive the price effect, first write \(F^{1}_{\gamma }\) for a monopolist:
Applying Lemma 2.1 for \(D^{1,k}_{\gamma }\), \(D^{1}_{\gamma }\) and \(D^{1}_{p_{1} \gamma }\) obtains
Collecting terms and recalling that at the steady state w/o SC \(s_{1} = -p_{1} \cdot D^{1}_{p_{1}}\) obtains the desired \(F^{1}_{\gamma }\).
The qualitative statements follow directly from these two equations:
-
(1)
As \(D^{1,1}_{\gamma } \ge 0\), the sign of the profit effect depends only on 2s 1−1
-
(2)
As \(D^{1,1}_{\gamma } > 0\) and \((D^{1,1}_{\gamma } + p_{1} \cdot D^{1,1}_{p_{1} \gamma } \ge 0\), if 2s 1−1≤0 it must be that \(F^{1}_{\gamma } < 0\).
-
(3)
As \(D^{1,1}_{\gamma } \ge 0\), \(F^{1}_{\gamma }\) is lowest for β=1. Placing β=1 in \(F^{1}_{\gamma }\) yields,
$$F^{1}_{\gamma} (\beta=1) = \left( 2s_{1} -1 \right) \left( D_{\gamma}^{1,1} +p_{1}D_{p_{1}\gamma}^{1,1} \right) -2 s_{1} \cdot D_{\gamma}^{1,1}. $$Collecting terms obtains the stated result.
□
1.9 A.9. Proof of Proposition 3.6
For a monopolist facing logit demand, the introduction of a small SC changes profits by
The monopolist price increases iff \(s_{1} \ge \frac {1+2\beta }{2+2\beta }\).
Proof
The derivative of the value function with respect to switching costs can be found by substituting the logit expression for \(D_{\gamma }^{j,j}=s_{j}\left (1-s_{j}\right )\) into the general monopoly expression for \(\frac {dV^{1}}{d\gamma =0}\) found in Proposition 3.5. To show that the monopolist price increases if and only if \(s_{1} \ge \frac {1+2\beta }{2+2\beta }\), first note that under monopoly,
So
Substituting this into the first order condition for prices,
As s 1>0, the condition for prices to increase is
Isolate β:
Isolate s 1 to arrive at the expression in the Proposition:
□
Appendix B Extensions
In this appendix, we consider two extensions to the basic model and illustrate how these affect the overall impact of switching costs. Formally, the effect of each extension can be determined by evaluating the change implied on the two basic comparative static Eqs. 2.4 and 2.6. In particular, applying the framework used here, it is sufficient to evaluate the first order change in demand \(D^{j}_{\gamma }\), in price sensitivity \(D_{\gamma ^{j} p_{j}}\) and in the dynamic value of investing in consumers \(\beta \cdot D^{j,k}_{\gamma } \cdot D^{k}_{p_{j}}\).
1.1 B.1. Time-persistent consumer heterogeneity
A natural variation of the model is to assume that the same consumers that preferred good j at period t would likely prefer good j at the following period. Intuitively, as the degree of horizontal differentiation between the goods increases, the marginal consumer for each firm is more likely a loyal repeat purchaser. As a result, the firms’ short term incentive to compensate will be weaker and its incentive to harvest will be stronger, resulting in higher prices. Horizontal differentiation will also weaken the investing effect of SC – the market has less switchers to sway as more consumers choose based on their horizontal preference.
Thus, time-persistent horizontal differentiation should decrease the effects of SC that decrease profits (compensating) and prices (compensating and investing), while increasing the effect of SC that increase prices and profits (harvesting).
Formally, our derivation can be extended relatively easily to accommodate some types of time-persistent preferences. In particular, suppose that consumers are split at the start of the game into types, with ϕ n the measure of type n in the general population. Letting \(F^{j,n}_{\gamma }\) denote the first order effect of a low SC (i.e. Eq. 2.6) for firm j considering only consumers of type n, then the overall effect is simply,
To illustrate, consider the logit model with J symmetric firms and an outside good that has a lower than average market share (i.e., the outside share is less than 1/(J+1). Extend the model by allowing for J+1 consumers types. In particular, suppose that the measure of regular consumers is ϕ 0 while a consumer of type j assigns a very negative utility to purchasing any good other than good j or the outside good. That is, for ϕ 0 customers demand is as described in Eq. 3.3, while for ϕ j of the consumers, firm j is a monopoly and demand is,
As ϕ j increases, firm j’s pricing is affected more by the monopolized consumers, whose decisions are completely independent of opponents’ prices. In particular \(F^{j}_{\gamma }\) at γ=0 increases with ϕ j . As horizontal differentiation weakens competition even without considering SC. This analysis reinforces the intuition that SC should be more of a concern in industries in which competition is (or would be) weak even without SC.
1.2 B.2. Heterogeneous SC
The assumption that all customers have the same SC may not fit well in some industries. For example, Biglaiser et al. (2013) suggest that SC between online music outlets differ across customers depending on the intensity of their use of the outlet.
For small SC, heterogeneous SC across consumers are similar to an even smaller SC as long as the SC apply to all goods. If only a fraction λ of consumers are affected by the switching cost, but this fraction is the same for all consumers regardless of their previous purchase, then \(D^{j}_{\gamma }\), \(D^{j}_{\gamma p_{j}}\) and \( D^{j,k}_{\gamma } \cdot D^{k}_{p_{j}}\) are simply a fraction λ of the original homogeneous SC model. Thus, the qualitative results are unchanged, but the degree of the SC effect is smaller.
The uniformly heterogeneous SC setting also captures the effect of SC in “overlapping generations” models. In these models, a fraction λ of the consumers each period is replaced with new consumers that are not loyal to any of the goods. Economically and mathematically, the model is identical. A closely related variation is when consumers switch loyalty group only with some probability λ, and with the complementing probability retain their original loyalty, despite buying a good they are not loyal to. In this case the short run effect of SC is the same as in the basic model, while the long run investing effect is dampened by λ.
Biglaiser et al. (2013) consider heterogeneous SC that affect only consumers of a subset of the goods in the market or only consumers that have a higher consumption value. First, suppose that SC only affect consumers switching out of good 1. In this case SC clearly increase 1’s demand \((D^{1}_{\gamma } > 0)\) and decrease demand for all other goods \((D^{j\neq 1}_{\gamma } < 0)\). Thus, the first order effect of SC on profits is, as expected, positive for firm 1 and negative for all others. However, even firm 1 may decrease prices, due to the investing effect. Indeed, with logit demand, it is easy to verify that firm 1 (and thus all firms) will decrease prices whenever \(\frac {s_{1}}{1-s_{1}} \le \beta \). In all other cases, the first order effect of SC on firm 1 will be to increase prices. For all other firms, the first order effect of SC is to decrease prices.Footnote 35
Appendix C Salop Model
1.1 C.1. Salop demand
This appendix considers the implications of a small SC on the Salop (1979) circular city model.Footnote 36 The results echo the qualitative results obtained using logit demand.
Formally, the J firms are evenly spaced on a circumference, with the firm location denoted x j . Each consumer draws each period a position x i on the circumference and pays a ’travel cost’ of \(c\cdot \left |x_{j} - x_{i}\right |\) if she chooses good j. As in the previous section, firm quality is denoted δ j . Note that we do not require that the firms are symmetric. Each consumer i, loyal to good k chooses in each period t the good j that maximizes her period utility, which is given by
We assume that in the equilibrium without SC, all firms have a strictly positive market share. A direct implication of the linear structure is that there are no cross effects: \(D^{j}_{\gamma p_{j}}=0\). To illustrate the implication of SC in these settings, suppose that absent SC, a consumer is indifferent between goods 2 and 3. Add a small SC to the model, the consumer’s preference just increases for the specific good j she bought in the previous period. If that good is 2, the consumer now strictly prefers good 2, increasing 2’s equilibrium demand. The same applies for good 3. However, if the consumer is loyal to any other good, a sufficiently small SC does not affect it’s preference. The share of consumers therefore whose SC are relevant for firm 2 are only those loyal to either firm 1, 2, or 3 at the previous period. In turn, these are given respectively by s 1, s 2 and s 3. The next result summarizes the implications for this setting.
Proposition C.1
In the circular city model in which all firms have a strictly positive market share:
-
A small SC has no effect if firms are symmetric \(\left (s_{j} = s_{i} \right )\) and myopic \(\left (\beta = 0 \right )\)
-
If firms are symmetric and forward looking \(\left (\beta > 0 \right )\) , the effect of SC strictly decreases in magnitude as the number of firms in the market increases.
-
A small SC decreases prices if firms are sufficiently forward looking \(\left (\beta \ge \frac {2}{3}\right )\) , regardless of firms’ relative shares.
-
A sufficient condition for a small SC to decrease prices is that firms are sufficiently symmetric and are somewhat forward looking. Formally:
$$ \forall j: s_{j} \le \frac{s_{j-1}+s_{j+1}}{2-3\cdot\beta} $$(C.2)
Proposition C.1 provides the analogous results to Proposition 3.1 and describes the implications of asymmetry in the linear setting. If firms are symmetric, demand does not change with the SC and so the short term effect is always zero. Note that this applies to any model of linear demand with symmetric firms and a fully covered market. For the specific circular city model with symmetric firms, the relation in Eq. C.2 is an equality when firms are myopic and a strict inequality otherwise.
The economic forces are the same as those identified in the previous sections. SC alter the incentives of the marginal consumers against switching. If a firm’s share is larger than it’s relevant rivals, the effect shifts the firm’s demand up.
The return on investing in share is only relevant to those customers that in the next period would be marginal for the firm. As in the logit case, increasing the number of firms decreases the likelihood that a firm’s marginal consumer in this period would also be marginal in the next period. As a result, the return on investment is lower and the effect of SC on prices is weaker.
If firms are sufficiently patient (\(\beta \ge \frac {2}{3}\)) prices always decrease with a small SC, regardless of shares. This is because the investment effect overpowers any possible short term gains from harvesting. Finally, to illustrate the relation in Eq. C.2, observe that if in the equilibrium w/o SC no firm has a larger share than its two neighbors’ combined share, a sufficient condition for prices to decrease is that \(\beta \ge \frac {1}{3}\).
1.2 C.2. Proof of Proposition C.1
In the circular city model in which all firms have a strictly positive market share:
-
A small SC has no effect if firms are symmetric \(\left (s_{j} = s_{i} \right )\) and myopic \(\left (\beta = 0 \right )\)
-
If firms are symmetric and forward looking \(\left (\beta > 0 \right )\), the effect of SC strictly decreases in magnitude as the number of firms in the market increases.
-
A small SC decreases prices if firms are sufficiently forward looking \(\left (\beta \ge \frac {2}{3}\right )\) , regardless of firms’ relative shares.
-
A sufficient condition for a small SC to decrease prices is that firms are sufficiently symmetric and are somewhat forward looking. Formally:
$$ \forall j: s_{j} \le \frac{s_{j-1}+s_{j+1}}{2-3\cdot\beta} $$(C.3)
Proof
For notational simplicity, define \(D_{\delta _{j}}^{j}=m\). Then \(D_{\delta _{j-1}}^{j}=D_{\delta _{j+1}}^{j}=-\frac {m}{2}\) and for all remaining firms \(D_{\delta _{i}\neq j-1,j,j+1}^{j}=0\). Therefore,
and
For the investing effect we have,
And for i=j+1,j−1
Using the first order condition at γ=0, \(p_{j}=\frac {s_{j}}{\alpha }\),
Thus:
-
(1)
If firms are symmetric: \(F^{j}_{\gamma } = -m\cdot \beta \cdot \frac {3}{2J}\). This proves the first two statements.
-
(2)
If \(\beta \ge \frac {2}{3}\) prices always decrease with SC.
-
(3)
If \(\beta <\frac {2}{3}\), prices always decrease if for all j
$$s_{j}\le\frac{s_{j-1}+s_{j+1}}{2-3\beta} $$
□
Rights and permissions
About this article
Cite this article
Arie, G., E. Grieco, P.L. Who pays for switching costs?. Quant Mark Econ 12, 379–419 (2014). https://doi.org/10.1007/s11129-014-9151-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11129-014-9151-9