1 Introduction

Quantum search algorithms on graphs have a subtle relationship to the connectivity of the graph. Completely connected graphs and topologies with bridges between completely connected components provided configuration space for efficient quantum search [32] realizations. Search based on joined complete graphs can be realized with atomic systems interacting with an environment bringing such scheme closer to reality [49]. In a recent work, Pan et al., have shown that classical electric circuits perform on par with graph-based quantum search algorithm [43]. The electrical circuit-based approach can be generalized to perform search on multiple sites simultaneously[28]. In this work, we consider a different family of weighted graphs with self-similar structure for the configuration space quantum search algorithms. Advances in development of fractal configurations in physical systems suggest ways to implement quantum walk propagation on fractal graphs. For example, Fusco et al. [24] realized fractal geometries in photonic metamaterials, and on such lattices, it may be possible to implement a quantum walk protocol developed by Kitagawa et al. [31] to perform Grover’s search.

The theory of quantum algorithms has been an active area of study over the last three decades, see [16, 38, 39, 44] and references therein. In several applications, quantum algorithms have been shown to outperform their classical counterparts, hence leading to a speedup in performance [26, 46]. In this paper, we revisit Grover’s search algorithm [1, 9, 10, 17, 20, 26, 45, 48], focusing on the continuous-time quantum walk approach developed by [15, 23]. The Childs–Goldstone approach is very versatile and can be realized on quantum systems of different geometrical or topological arrangements. This feature appeared in [18, 34, 35] where it was established that a certain class of fractal-type graphs demonstrates favorable topological properties to implement perfect quantum state transfer. The feature is also present in [2], where Grover’s search algorithm was analyzed on databases with different topological arrangements. In this latter case, the (analytical and numerical) investigations of quantum walk on several graphs, such as the dual Sierpinski gaskets, T-fractals and hierarchical structures like Cayley trees, illustrate the dependency of Grover’s algorithm on the topological structure of these graphs.

In this paper, we propose an alternative optimization approach to Grover’s algorithm on graphs. In particular, instead of finding specific graph topologies convenient for the related quantum walk, we fix the graph topology and vary the underlying graph Laplacians. As a result, we search for the most appropriate analytical structure on graphs endowed with fixed topologies yielding better outcomes in Grover’s search algorithm. To describe our approach’s main ideas, we first introduce some basic terminology and notation. We perform a Grover’s search on a database modeled by a finite (possibly directed) graph \(G=(V,E)\). Let \(\{p(x,y)\}_{(x,y) \in E}\) be a sequence of weights assigned to the edges, where we regard the edge (x, y) as pointing from the vertex x to y and p(x, y) as a transition probability of a quantum walker from x to y. We impose the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \ (x,y) \in E \ \Leftrightarrow \ 0<p(x,y) \le 1 \\ \ (x,y) \notin E \ \Leftrightarrow \ p(x,y) =0 \\ \ \sum _{y :(x,y) \in E} p(x,y) = 1, \ \forall \ x \in V \end{array}\right. } \end{aligned}$$
(1)

and associate with such a sequence a probabilistic graph Laplacian on G, defined by

$$\begin{aligned} \Delta _G f (x)= f(x) \ - \sum _{y :(x,y) \in E} p(x,y) f(y). \end{aligned}$$
(2)

We assume there exists a Hilbert space \(\big ({\mathcal {H}}, \langle .,.\rangle \big )\) such that \(\Delta _{G}\) is self-adjoint (Hermitian),

$$\begin{aligned} \langle \Delta _{G} \psi ,\phi \rangle = \langle \psi , \Delta _{G} \phi \rangle , \quad \phi , \psi \in {\mathcal {H}} = \big \{ f:V \rightarrow {{\,\mathrm{{\mathbb {C}}}\,}}\big \}. \end{aligned}$$

We refer to [37] for more details and for examples of such Hilbert spaces on certain graphs. We associate each item in the database with a vertex \(x \in V\) or equivalently the corresponding normalized Dirac function

$$\begin{aligned} e_{x}:= {\delta _{x}}/ \sqrt{\langle \delta _{x}, \delta _{x} \rangle }, \quad \quad \delta _x(y) := {\left\{ \begin{array}{ll} 1, \quad x=y \\ 0, \quad x \ne y \end{array}\right. } \end{aligned}$$

and denote the target vertex in Grover’s search algorithm by \(w \in V\). Note that \(\mu : V \rightarrow (0,\infty )\), \(\mu (x):=\langle \delta _{x}, \delta _{x} \rangle \) defines a measure on the set of vertices V. The volume of the graph G is then given by

$$\begin{aligned} vol(G) := \sum _{x \in V} \mu (x), \quad \mu (x)=\langle \delta _{x}, \delta _{x} \rangle . \end{aligned}$$
(3)

To perform the search, one needs a driving Hamiltonian H of the quantum system. In this work, we use (see [2, 15])

$$\begin{aligned} {\left\{ \begin{array}{ll} \ H_{\gamma }: = \gamma \Delta _{G} - V_w, \\ \ V_w f := \langle e_w, f \rangle e_w, \quad f : V(G) \rightarrow {{\,\mathrm{{\mathbb {C}}}\,}}, \end{array}\right. } \end{aligned}$$
(4)

where \(\gamma \) is a tunable parameter in \((0,\infty )\). The potential operator \(V_w\) is also called the oracle Hamiltonian. As the initial state of the search, we choose the ground state of \(\Delta _{G}\)

$$\begin{aligned} s := \frac{1}{\sqrt{vol(G)}} \sum _{x \in V(G)} \delta _{x} \end{aligned}$$
(5)

and the goal is to evolve s continuously to the target state \(e_w\). The success probability of finding the target vertex w at the time t is then given by

$$\begin{aligned} \pi _{w}^{\gamma }(t) := \big \vert \langle e_w, \exp (-iH_{\gamma }t) s \rangle \big \vert ^2. \end{aligned}$$
(6)

Our main contribution is summarized as follows. Rather than investigating a family of Hamiltonians \(\{H_{\gamma }\}_{\gamma \in (0,\infty )}\) on graphs of different topologies, we fix the (topology on) graph G and vary the transition probabilities (1) of a quantum walker on G. By doing so, we are effectively varying \(\Delta _G\) in (2). As such, we are led to the following question: “Can we construct examples for which this approach improves Grover’s search outcomes?”. In Sect. 3, we provide an example with an easy tunable parameter to answering this question.

The rest of the paper is organized as follows: In Sect. 2, we will discuss strategies to investigate the optimality of Grover’s search algorithm. We recall that the algorithm is implemented using a family of Hamiltonians \(\{H_{\gamma }\}_{\gamma \in (0,\infty )}\) for which one is led to determine in a systematic manner the value \(\gamma _{opt}\) for which \(H_{\gamma _{opt}}\) leads to optimal search outcomes, i.e., \(\pi _{w}^{\gamma _{opt}}(t)\) is maximal in the shortest time possible (see (33) for the definition of \(\gamma _{opt}\)). In [15], Childs and Goldstone elaborated on the interplay between the success probability (6) and the overlap probabilities

$$\begin{aligned} \vert \langle s, \psi _0 \rangle \vert ^2, \ \vert \langle e_w,\psi _0\rangle \vert ^2, \ \vert \langle s, \psi _1 \rangle \vert ^2, \ \vert \langle e_w,\psi _1\rangle \vert ^2, \end{aligned}$$
(7)

where \(\psi _0\) (resp. \(\psi _1\)) refer to the ground (resp. first excited) state of \(H_{\gamma }\). As such, we focus on a better understanding of these overlap probabilities resulting in our first main contribution Theorem 2.3. This result provides conditions (15) under which we can approximate and relate the \(\psi _0\)-eigenvalue \(E_0\) (resp. \(\psi _1\)-eigenvalue \(E_1\)) with the square root of the graph’s volume, i.e.,

$$\begin{aligned} E_0 \approx -\frac{\sqrt{ \langle \delta _w, \delta _w \rangle }}{\sqrt{vol(G)}}, \quad E_1 \approx \frac{\sqrt{ \langle \delta _w, \delta _w \rangle }}{\sqrt{vol(G)}}. \end{aligned}$$
(8)

We point out that for the complete graph on N vertices the eigenvalues are given by

$$\begin{aligned} E_{0} = - \frac{1}{\sqrt{N}}, \quad E_{1} = \frac{1}{\sqrt{N}}, \end{aligned}$$
(9)

and the sufficient conditions Theorem 2.3 are satisfied. Furthermore, in this case we have \(\langle \delta _w, \delta _w \rangle =1\) for all \(w \in V\) and \(vol(G)=N\) is nothing else but the number of vertices.

In practice, it might be difficult to verify (15) for general graphs. Therefore, we introduced the parameter \(\gamma _E\) in (14) for which the corresponding success probability \(\pi _{w}^{\gamma _E}(t)\) takes the simple form (25). In fact, for a complete graph on N vertices we have \(\gamma _E=\gamma _{opt}\) holds for all N, and hence, the corresponding optimal success probability is easily computed using (25) and given by

$$\begin{aligned} \pi _{w}^{\gamma _{opt}}(t) = \Big (\frac{N-1}{N} \Big ) \sin ^2\Big (\frac{ t}{\sqrt{N}} \Big ) + \frac{1}{N}. \end{aligned}$$
(10)

These observations have led us to the second part of this work: Does the equality \(\gamma _{opt}=\gamma _E\) hold for other graphs? Or more specifically, is it possible to construct a graph such that the following properties hold:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text { A graph with variable volume} vol(G). \\ \text { The optimal success probability is well approximated by} ((25)). \\ E_1 \text { is well approximated by} \frac{\sqrt{ \langle \delta _w, \delta _w \rangle }}{\sqrt{vol(G)}}. \end{array}\right. } \end{aligned}$$
(11)

In Sect. 3, we introduce a hypercubic lattice as a Cartesian product of directed path graphs. To keep the discussion simple, we assume that the path graph has four vertices and that the transition probabilities of a quantum walker between these vertices are given via a parameter p, see Figs. 1 and 2. This parameter p can be interpreted as quantifying the database homogeneity/non-homogeneity and will play the role of the tuning parameter of the graph volume vol(G). Despite the simplicity of this model, we obtain interesting results when investigating the properties (11).

Our work is part of a long term study of mathematical physics on fractals and self-similar graphs [3,4,5,6,7,8, 21, 27, 40,41,42], in which novel features of quantum processes on fractals can be associated with the unusual spectral and geometric properties of fractals compared to regular graphs and smooth manifolds.

2 Continuous-time quantum walk on finite graphs

We start this section with some preliminary results that will be needed later for the proof of Proposition 2.2 and Theorem 2.3. Let \(E_a\) and \(\psi _a\) denote the eigenvalues and eigenvectors of \(H_{\gamma }\), respectively. We assume that \(\{\psi _a \}_{E_a \in \sigma (H_{\gamma })}\) is an orthonormal basis and in this notation, \(E_0\) and \(\psi _0\) refer to the ground state, \(E_1\) and \(\psi _1\) refer to the first excited state, and so on. For ease of discussion, we will assume in this work that \(E_0\) and \(E_1\) are non-degenerate. For \(\gamma >0\) and \(z \in \rho (\gamma \Delta _{G})\), the resolvent set of \(\gamma \Delta _{G}\), we consider the following Green function

$$\begin{aligned} G_{\gamma }(z,w,w) :=\langle e_w,(\gamma \Delta _{G}-z)^{-1} e_w \rangle . \end{aligned}$$
(12)

Let \(\{ \phi _{\lambda } \ \vert \ \lambda \in \sigma (\Delta _{G}) \ \}\) be an orthonormal basis of eigenvectors of \(\Delta _{G}\), and write

$$\begin{aligned} e_{w} = \sum _{\lambda \in \sigma (\Delta _{G})} a_{w,\lambda } \phi _{\lambda }, \quad \quad a_{w,\lambda } = \langle \phi _{\lambda },e_{w} \rangle . \end{aligned}$$
(13)

where the sum takes the eigenvalue multiplicities into account. The following result whose proof we omit is elementary.

Lemma 2.1

The following statements hold.

  1. 1.

    If \(E_a \notin \sigma (\gamma \Delta _{G})\), then \(\langle e_w,\psi _a \rangle \ne 0\).

  2. 2.

    If \(E_a \notin \sigma (\gamma \Delta _{G})\), then \(G_{\gamma }(E_a,w,w) =1\).

  3. 3.

    If \(E_a \notin \sigma (\gamma \Delta _{G})\), then \(\langle e_w, ( \gamma \Delta _{G} - E_a )^{-1} \psi _a \rangle = \frac{1}{\langle \psi _a,e_w \rangle }\).

  4. 4.

    If \(z \in \rho (\gamma \Delta _{G})\), then

    $$\begin{aligned} {\left\{ \begin{array}{ll} G_{\gamma }(z,w,w) = \sum _{\lambda \in \sigma (\Delta _{G})} \frac{\vert a_{w,\lambda }\vert ^2}{\gamma \lambda - z} \\ G_{\gamma }'(z,w,w) = \frac{d}{dz} G_{\gamma }(z,w,w) = \sum _{\lambda \in \sigma (\Delta _{G})} \frac{\vert a_{w,\lambda }\vert ^2}{(\gamma \lambda - z)^2} = \langle e_w,(\gamma \Delta _{G}-z)^{-2} e_w \rangle . \end{array}\right. } \end{aligned}$$

Next, for general finite graphs we derive formulas for the overlap probabilities.

Proposition 2.2

(Overlap probabilities) Suppose that \(E_a \notin \sigma (\gamma \Delta _{G})\). Then we have

  1. 1.

    \(\vert \langle e_w,\psi _a\rangle \vert ^2 =\frac{1}{G_{\gamma }'(E_a,w,w)}\).

  2. 2.

    \(\vert \langle s, \psi _a \rangle \vert ^2 = \frac{ \langle \delta _w, \delta _w \rangle }{vol(G) E_a^2 G_{\gamma }'(E_a,w,w)}\).

Proof

The proof uses Lemma 2.1.

  1. 1.

    Given that \(\psi _a = \langle e_w, \psi _a \rangle (\gamma \Delta _{G} - E_a )^{-1} e_w\), we have

    $$\begin{aligned} 1=\langle \psi _a, \psi _a\rangle =\overline{\langle e_w, \psi _a \rangle } \langle e_w,\psi _a \rangle \langle e_w,(\gamma \Delta _{G} - E_a )^{-2} e_w \rangle \\ =\langle e_w,(\gamma \Delta _{G} - E_a )^{-2} e_w \rangle \vert \langle e_w,\psi _a \rangle \vert ^2 \end{aligned}$$

    The statement follows by Lemma 2.1(4).

  2. 2.

    Recalling that \(\Delta _{G}s=0\), we see that

    $$\begin{aligned} - E_a \langle s,\psi _a \rangle = \langle s, ( \gamma \Delta _{G} - E_a ) \psi _a \rangle = \langle s,V_w\psi _a \rangle = \langle s,e_w \rangle \langle e_w,\psi _a \rangle . \end{aligned}$$

    Hence, \(\vert \langle s,\psi _a \rangle \vert ^2 = \frac{\vert \langle s,e_w \rangle \vert ^2 \ \vert \langle e_w,\psi _a \rangle \vert ^2}{E_a^2}\) and the result follows by \(\vert \langle s,e_w\rangle \vert ^2 = \frac{ \langle \delta _w, \delta _w \rangle }{vol(G)}\) and part (1).

\(\square \)

To study the question of which parameter \(\gamma \) the Hamiltonian \(H_{\gamma }\) leads to optimal search outcomes, we will consider the following parameters with the assumption that each of the sets below is non-empty

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma _s := \inf _{ \gamma \in (0, \infty )} \big \{ \gamma \ \big \vert \ \text { such that } \vert \langle s, \psi _0 \rangle \vert ^2 = \vert \langle s, \psi _1 \rangle \vert ^2 \big \} \\ \gamma _w := \inf _{ \gamma \in (0, \infty )} \big \{ \gamma \ \big \vert \ \text { such that } \vert \langle e_w, \psi _0 \rangle \vert ^2 = \vert \langle e_w, \psi _1 \rangle \vert ^2 \big \}. \\ \gamma _{E}:= \inf _{ \gamma \in (0, \infty )} \big \{ \gamma \ \big \vert \ \text { such that } E_0=-E_1 \big \}. \end{array}\right. } \end{aligned}$$
(14)

The following theorem establishes a relationship between the overlap probabilities and the eigenvalues \(E_0\), \(E_1\) and provides sufficient conditions to approximate these eigenvalues by the square root of the graph’s volume.

Theorem 2.3

Assume that there exist \(\gamma \in (0, \infty )\) and \(\epsilon >0\) such that

$$\begin{aligned} \Big \vert \vert \langle s, \psi _0 \rangle \vert ^2 - \vert \langle e_w, \psi _0 \rangle \vert ^2 \Big \vert \le \epsilon . \end{aligned}$$
(15)

Then

$$\begin{aligned} \Big \vert E_0^2 - \frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \Big \vert \le \epsilon . \end{aligned}$$

Similarly, if the inequality (15) holds for \(\psi _1\), then

$$\begin{aligned} \Big \vert E_1^2 - \frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \Big \vert \le \Big ( 1 + \frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \frac{\vert \vert \langle s, \psi _1 \rangle \vert ^2 - \vert \langle s, \psi _0 \rangle \vert ^2 \vert }{\vert \langle s, \psi _1 \rangle \vert ^2 \vert \langle s, \psi _0 \rangle \vert ^2} \Big ) \epsilon . \end{aligned}$$

Proof

By Proposition 2.2(2), we have

$$\begin{aligned} \Big \vert E_a^2 - \frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \Big \vert&=\frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \Big \vert \frac{ 1- G_{\gamma }'(E_a,w,w)\vert \langle s, \psi _a \rangle \vert ^2}{ G_{\gamma }'(E_a,w,w)\vert \langle s, \psi _a \rangle \vert ^2} \Big \vert \end{aligned}$$
(16)
$$\begin{aligned}&=\frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \Big \vert \frac{ \vert \langle e_w,\psi _a\rangle \vert ^2 - \vert \langle s, \psi _a \rangle \vert ^2}{ \vert \langle s, \psi _a \rangle \vert ^2} \Big \vert \end{aligned}$$
(17)
$$\begin{aligned}&=E_a^2 G_{\gamma }'(E_a,w,w) \Big \vert \vert \langle e_w,\psi _a\rangle \vert ^2 - \vert \langle s, \psi _a \rangle \vert ^2 \Big \vert , \end{aligned}$$
(18)

where in the second equality, we used \(1=G_{\gamma }'(E_a,w,w)\vert \langle e_w,\psi _a\rangle \vert ^2 \) (see Proposition 2.2(1)), and in the last equality, we used Proposition 2.2(2). The result follows from the following computations. First, we note that Lemma 2.1(4), \(E_0 <0\) and \(\sigma (\Delta _{G}) \subset [0,2]\) show

$$\begin{aligned} E_0^2 G_{\gamma }'(E_0,w,w)&=E_0^2 \sum _{\lambda \in \sigma (\Delta _{G})} \frac{\vert a_{w,\lambda }\vert ^2}{(\gamma \lambda + \vert E_0 \vert )^2} \end{aligned}$$
(19)
$$\begin{aligned}&\le \sum _{\lambda \in \sigma (\Delta _{G})} \vert \langle \phi _{\lambda },e_{w} \rangle \vert ^2 = \vert \vert e_w\vert \vert ^2 = 1. \end{aligned}$$
(20)

Moreover, Proposition 2.2 (2) shows

$$\begin{aligned} \Big \vert E_1^2 G_{\gamma }'(E_1,w,w)&- E_0^2 G_{\gamma }'(E_0,w,w) \Big \vert = \frac{\langle \delta _w, \delta _w \rangle }{vol(G)} \frac{\Big \vert \vert \langle s, \psi _1 \rangle \vert ^2 - \vert \langle s, \psi _0 \rangle \vert ^2 \Big \vert }{\vert \langle s, \psi _1 \rangle \vert ^2 \vert \langle s, \psi _0 \rangle \vert ^2}. \end{aligned}$$
(21)

\(\square \)

Complete graphs are examples for which the hypotheses of Theorem 2.3 are satisfied. In fact, if we consider the probabilistic graph Laplacian of a complete graph of N vertices

$$\begin{aligned} \Delta _G = \left( \begin{matrix}1 &{} - \frac{1}{N-1} &{} \dots &{} \dots &{} - \frac{1}{N-1}\\ - \frac{1}{N-1} &{} 1 &{} - \frac{1}{N-1} &{} \dots &{} - \frac{1}{N-1}\\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} - \frac{1}{N-1} &{} 1 &{} - \frac{1}{N-1}\\ - \frac{1}{N-1} &{} \dots &{} \dots &{} - \frac{1}{N-1} &{} 1\end{matrix}\right) , \end{aligned}$$
(22)

and set \(\gamma = \frac{N-1}{N}\), then a direct computation of the overlap probabilities gives

$$\begin{aligned} {\left\{ \begin{array}{ll} \ \vert \langle s, \psi _0 \rangle \vert ^2 = \vert \langle e_w,\psi _0\rangle \vert ^2 = \frac{\sqrt{N}+1}{2 \sqrt{N}}\\ \ \vert \langle s, \psi _1 \rangle \vert ^2 = \vert \langle e_w,\psi _1\rangle \vert ^2 = \frac{\sqrt{N}-1}{2 \sqrt{N}}. \end{array}\right. } \end{aligned}$$
(23)

It follows that (15) holds for any \(\epsilon > 0\), the eigenvalues are given by (9), and that, by definition, we have \(\gamma _E = \frac{N-1}{N}\). We remark that the Hamiltonian in [2, 15] is defined using the graph Laplacian \(D-A\), where D (resp. A) is the degree (resp. adjacency) matrix of the graph. By the regularity of complete graphs, the probabilistic graph Laplacian (22) coincides with the graph Laplacian up to a multiple constant, i.e., \((N-1)\Delta =(D-A)\). Using either operators has no impact on the analysis since

$$\begin{aligned} \gamma \Delta - V_w = {\tilde{\gamma }} (D-A) - V_w \end{aligned}$$

where \(\gamma = (N-1){\tilde{\gamma }}\). In particular, \(\gamma = \gamma _E = \frac{N-1}{N}\) if and only if \({\tilde{\gamma }}=\frac{1}{N}\), in which case, as proved in [15], a quantum search on complete graphs recovers the optimal quadratic speedup. Therefore, for complete graphs, Theorem 2.3 implies that \(E_0=-E_1\). The following result gives the consequences of assuming that \(E_0=-E_1\) for a given graph with a fixed topology.

Proposition 2.4

Suppose that there exists \(\gamma \in (0,\infty )\) such that \(E_0=-E_1\), then

$$\begin{aligned} \frac{\vert \langle e_w,\psi _1\rangle \vert ^2}{\vert \langle s,\psi _1\rangle \vert ^2} = \frac{\vert \langle e_w,\psi _0\rangle \vert ^2}{\vert \langle s,\psi _0\rangle \vert ^2}. \end{aligned}$$
(24)

Consequently, we have \( \overline{\langle \psi _1,s\rangle } \langle e_w, \psi _0 \rangle = - e^{i 2 \theta } \overline{ \langle \psi _0,s \rangle } \langle e_w, \psi _1 \rangle \) for some phase \( \theta \in [0,\pi )\). Moreover, the success probability reduces to

$$\begin{aligned} \pi _{w}^{\gamma }(t) = 4 \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \sin ^2(E_1 t + \theta ) + C + R(t) \end{aligned}$$
(25)

where C and R(t) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} C : = \vert \langle e_w, \psi _0 \rangle \vert ^2 \vert \langle s, \psi _0 \rangle \vert ^2 + \vert \langle e_w, \psi _1 \rangle \vert ^2 \vert \langle s, \psi _1 \rangle \vert ^2 - 2 \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \\ R(t) := 2 Re\big ( A(t) \overline{ r(t) } \ \big ) + \vert r(t) \vert ^2 \end{array}\right. } \end{aligned}$$
(26)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} A(t) := \langle e_w, \psi _0 \rangle \langle \psi _0,s \rangle \exp (-iE_0t) + \langle e_w, \psi _1 \rangle \langle \psi _1,s \rangle \exp (-iE_1t) \\ r(t) := \sum _{a \ge 2} \langle e_w, \psi _a \rangle \langle \psi _a,s \rangle \exp (-iE_at). \end{array}\right. } \end{aligned}$$
(27)

Proof

The first result follows by Proposition 2.2 (1) & (2). To prove the second result, we use \(\langle e_w, \exp (-itH_{\gamma }) s \rangle = A(t) + r(t)\) and compute

$$\begin{aligned} \pi _{w}^{\gamma }(t)&= \vert \langle e_w, \psi _0 \rangle \vert ^2 \vert \langle s, \psi _0 \rangle \vert ^2 + \vert \langle e_w, \psi _1 \rangle \vert ^2 \vert \langle s, \psi _1 \rangle \vert ^2 \\&\quad + \langle e_w, \psi _0 \rangle \langle \psi _0,s \rangle \overline{\langle e_w, \psi _1 \rangle } \ \overline{ \langle \psi _1 ,s \rangle } \exp (i(E_1-E_0)t) \\&\quad + \overline{ \langle e_w, \psi _0 \rangle } \ \overline{ \langle \psi _0,s \rangle } \langle e_w, \psi _1 \rangle \langle \psi _1,s \rangle \exp (-i(E_1-E_0)t) \\&\quad + A(t) \overline{r(t)} + \overline{A(t)} r(t) + r(t) \overline{r(t)}. \end{aligned}$$

Using the first result, we add the second and third terms together

$$\begin{aligned} - \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \exp (i2(E_1 t + \theta )) - \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \exp (-i2(E_1 t + \theta )) \\ = - 2 \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \cos (2(E_1 t + \theta )) \\ = 4 \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2 \sin ^2(E_1 t + \theta ) - 2 \vert \langle s, \psi _0 \rangle \vert ^2 \ \vert \langle e_w, \psi _1 \rangle \vert ^2. \end{aligned}$$

\(\square \)

3 Hypercubic lattices

In this section, we introduce a one-parameter family of Laplacians on the hypercubic lattice and investigate Grover’s search algorithm numerically when using these Laplacians. Given a finite directed path graph \(G=(V,E)\) with the vertices \(V:=\{0,1,2,3\}\) and the edges \(E: = \{(x,y) \in V \times V \ \vert \ |x-y|=1 \} \). We consider a quantum walk on G, where the transition probabilities \(\{p(x,y)\}_{(x,y) \in V \times V }\) and the corresponding probabilistic graph Laplacian \(\Delta _{G}\) are given for some \(p \in (0,1)\) in Fig. 1. Note that \(\Delta _{G}\) generates a quantum walk on G with reflecting boundaries. This class of Laplacians was first investigated in [47] and arises naturally when studying the unit interval endowed with a particular fractal measure. For more on this Laplacian and some related work, we refer to [11, 13, 14, 19, 36].

Fig. 1
figure 1

Graph G and the corresponding probabilistic graph Laplacian \(\Delta _{G}\). When \(p=1/2\), \(\Delta _{G}\) becomes the standard probabilistic graph Laplacian

Full size image
Fig. 2
figure 2

Graph \(G_2=G' \times G''\), where \(G' =G'' = G\) and G is the graph in Fig. 1. The transition probabilities are given by \(\Delta _{G_2}\)

Full size image

We equip the vertices set V with a measure, \(\mu :V \rightarrow [0,\infty )\) and assume that it satisfies the Kolmogorov’s cycle condition [22, 25, 29, 30], i.e.,

$$\begin{aligned} \mu (0)=1, \quad \mu (x) = \mu (x-1) \frac{p(x-1,x)}{p(x,x-1)}, \ \ x \in V. \end{aligned}$$
(28)

One can easily verify that \(\Delta _{G}\) is self-adjoint (Hermitian) with respect to the inner product

$$\begin{aligned} \langle f,g \rangle _G = \sum _{x \in V} \overline{f(x)} g(x) \mu (x), \end{aligned}$$
(29)

where \(f, g \in {\mathcal {H}}_G:=span\{ \ \delta _x \ \vert \ x \in V\}\). A d-dimensional hypercubic lattice is constructed as the d-fold Cartesian product of finite directed path graphs \(G_{d} = G' \times G'' \times .. \), where \(G'=G''=\hdots =G\). For simplicity, we restrict our illustration to products of two graphs as the extension to higher-dimensional products is straightforward. We follow [12] and denote by a prime anything having to do with the first graph and by a double prime anything having to do with the second graph. We recall that a Cartesian product of two graphs \(G'=(V',E')\) and \(G''=(V'',E'')\) is a graph \(G_{2} = G' \times G''\) with the set of vertices \(V(G_{2}) = \{(x', x'') \ \vert \ x' \in V', x'' \in V'' \ \}\), where two vertices \({\bar{x}}=(x', x'')\) and \({\bar{y}}=(y', y'')\) are adjacent, i.e., \(({\bar{x}},{\bar{y}}) \in E(G_{2})\) if and only if \((x',y') \in E' \ \text { and } x''=y''\) or \((x'',y'') \in E'' \ \text { and } x'=y'\). We define a Laplacian on \(G_2\) as a (normalized) Kronecker sum of \(\Delta _{G'}\) and \(\Delta _{G''}\), i.e.,

$$\begin{aligned} \Delta _{G_2} := \frac{1}{2}\big (\Delta _{G'} \otimes I + I \otimes \Delta _{G''}\big ), \end{aligned}$$
(30)

where I is an identity matrix. An example of the quantum walk generated by \(\Delta _{G_2}\) is illustrated in Fig. 2. We associate each vertex \({\bar{x}}=(x', x'') \in V(G_{2}) \) with \(\delta _{{\bar{x}}}:= \delta _{x'} \otimes \delta _{x''}\), the tensor product \( \delta _{x'} \) and \( \delta _{x''}\). It follows that \(\Delta _{G_2}\) is self-adjoint on the Hilbert space \({\mathcal {H}}_{G_2}=span\{ \ \delta _{{\bar{x}}} \vert \ {\bar{x}}=(x', x'') \in V(G_{2}) \ \}\) equipped with the inner product

$$\begin{aligned} \langle f,g \rangle = \sum _{{\bar{x}} \in V(G_2)} \overline{f({\bar{x}})} g({\bar{x}}) \mu _2({\bar{x}}), \quad {\left\{ \begin{array}{ll} \ \langle \delta _{{\bar{x}}}, \delta _{{\bar{y}}} \rangle := \langle \delta _{x'},\delta _{y'} \rangle _{G'} \langle \delta _{x''},\delta _{y''}\rangle _{G''} \\ \ \mu _2({\bar{x}}):=\langle \delta _{{\bar{x}}}, \delta _{{\bar{x}}} \rangle \end{array}\right. } \end{aligned}$$
(31)

3.1 Homogeneous versus non-homogeneous structures

When \(p=\frac{1}{2}\), then \(\Delta _{G_d}\) recovers the standard probabilistic graph Laplacian as a generator of a symmetric quantum walk on \(G_d\). In this case, it easy to compute that the symmetrizing measure (31) is the degree of the vertex, i.e.,

$$\begin{aligned} \mu _d({\bar{x}})=\langle \delta _{{\bar{x}}}, \delta _{{\bar{x}}} \rangle = \mu (x_1) \dots \mu (x_d) = 2^d, \end{aligned}$$

where \({\bar{x}}=(x_1,\dots , x_d) \in V(G_{d})\) is a non-boundary vertex. In particular, the measure is constant on the interior vertices, and as such, we say that \(G_d\) homogeneous. On the other hand, when \(p\ne \frac{1}{2}\), then \(\Delta _{G_d}\) generates an asymmetric quantum walk on \(G_d\). Consequently, the measure is vertex-dependent and varies on the interior vertices. In this case, we say \(G_d\) is non-homogeneous. For an interpretation from a physics viewpoint and the relation to fractal media, the reader is referred to the introduction of [14].

Fig. 3
figure 3

Overlap probabilities as a function of \(\gamma \) for \(G_5\): (top left) \(p=0.91\), (top right) \(p=0.5\), (bottom left) \(p=0.4\), (bottom right) \(p=0.1\)

Full size image

3.2 Numerical results

In this section, we present some numerical results on the Grover’s search algorithm on the graph \(G_5\) and provide the python codes in [33]. Note that the number of vertices is \(\vert V(G_5)\vert = 1024\). The target vertex \(w \in V(G_5)\) is assumed to be one of the corners of \(G_5\). Our focus is to analyze the search algorithm based on the homogeneity versus non-homogeneity of the database, i.e., \(p=1/2\) versus \(p\ne 1/2\). To this end, we plot the overlap probabilities and the eigenvalues \(E_0\), \(E_1\) as functions of \(\gamma \), after which we determine and discuss their intersections at the points \(\gamma _s\), \(\gamma _w\) and \(\gamma _E\). Before proceeding, it is worth mentioning that for the complete graph of N vertices, where \(N\ge 2\), we have \(\gamma _s \le \gamma _E \le \gamma _w\). When \(N=2\), we have \(\gamma _s=0\) and \(\gamma _{w}={\infty }\), while for large N, we see that

$$\begin{aligned} \gamma _s \approx \gamma _E \approx \gamma _w \approx 1. \end{aligned}$$
(32)

In the case of \(G_5\), the plots of the overlap probabilities are depicted for several p in Fig. 3. The case \(p=0.91\) (top left panel in Fig. 3) is particularly interesting and is qualitatively similar to the results for the complete graphs; see [15, Figure 1] for a comparison. We determine \(\gamma _s\), \(\gamma _w\) and \(\gamma _E\) in Table 1, and observe that in all cases

$$\begin{aligned} \gamma _s \le \gamma _E \le \gamma _w, \end{aligned}$$

where for larger p, \(\gamma _E\) is increasingly squeezed between \(\gamma _s\) and \(\gamma _w\).

Fig. 4
figure 4

Contour plot of the success probability \(\pi _{w}^{\gamma }(t)\) as a function of the time t and \(\gamma \) for \(G_5\): (top left) \(p=0.91\), (top right) \(p=0.5\), (bottom left) \(p=0.4\), (bottom right) \(p=0.1\)

Full size image
Table 1 Numerical computation of \(\gamma _s\), \(\gamma _w\), \(\gamma _E\) and \(\gamma _{opt}\) for \(G_5\) and different values of p
Full size table

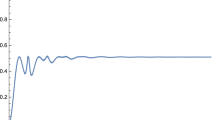
We also compute the success probability \(\pi _{w}^{\gamma }(t)\) as a function of the time t and \(\gamma \), see Fig. 4. Then we determine for which values \((t,\gamma )\) the success probability \(\pi _{w}^{\gamma }(t)\) is optimal, i.e.,

$$\begin{aligned} (t_{opt}, \gamma _{opt}) := \inf _{\gamma } \inf _{t} \big \{ (t,\gamma ) \in [0,vol(G)] \times (0,\infty ) : \pi _{w}^{\gamma }(t) \text { attains abs. max.} \big \}. \end{aligned}$$
(33)

We observe that for \(p = 0.91\), we have \(\gamma _{opt} \approx \gamma _{E} \approx \gamma _{s} \approx \gamma _{w}\), see Table 1. (Note that for the complete graph of N vertices, we have \(\gamma _{opt} = \gamma _E \) for any \(N \ge 2\).) Subsequently, we determine \(E_0\) and \(E_1\) as the eigenvalues of the ground and first excited state of \(H_{\gamma _{opt}}\). For comparison, we also compute \(\sqrt{\frac{\langle \delta _w, \delta _w \rangle }{vol(G_{5})}}\) using

$$\begin{aligned} vol(G_{5}) = \Big (2 + \frac{2}{1-p} \Big )^5. \end{aligned}$$

Note that \(\langle \delta _w, \delta _w \rangle =1\) for w located at one of the corners of \(G_5\). Again, the results for \(E_0\) and \(E_1\) are in better agreement with \(\sqrt{\frac{\langle \delta _w, \delta _w \rangle }{vol(G_{5})}}\) the larger we choose p. We plot the success probability \(\pi _{w}^{\gamma }(t)\) as a function of t, where we set \(\gamma =\gamma _{opt}\), see Fig. 5. Concerning the observation that \(\gamma _{opt} \approx \gamma _E\) for \(p=0.91\), we note that the graph in the top left panel in Fig. 5 is in very good agreement with the analytical formula (25), i.e.,

$$\begin{aligned} \pi _{w}^{\gamma _{opt}}(t) \approx 0.89 \sin ^2(E_1 t) \end{aligned}$$
(34)

where the value of \(E_1\) is given in Table 2. In contrast to the complete graphs where \(\gamma _{opt} = \gamma _E \) holds for any number of vertices, we observe in \(G_{5}\) that the deviation of \(\gamma _E\) from \(\gamma _{opt}\) increases for smaller values of p. In this case, formula (25) is less suitable for analyzing of \(\pi _{w}^{\gamma _{opt}}(t)\). Indeed, Fig. 5 (bottom right panel) illustrates how \(\pi _{w}^{\gamma _{opt}}(t)\) for \(p=0.1\) exhibits a more irregular and oscillatory behavior.

Fig. 5
figure 5

Plot of the success probability \(\pi _{w}^{\gamma }(t)\) as a function of time t for \(G_5\). We set \(\gamma =\gamma _{opt}\) in all panels: (top left) \(p=0.91\), (top right) \(p=0.5\), (bottom left) \(p=0.4\), (bottom right) \(p=0.1\)

Full size image

Finally, we observe that \(t_{opt}\) decreases with (large) p and is comparable to \(\frac{\pi }{2}\sqrt{\frac{vol(G_{5})}{\langle \delta _w, \delta _w \rangle }}\), see Table 2. For example, \(\pi _{w}^{\gamma _{opt}}(t)\) for \(p=0.91\) attains its maximum at \(t_{opt} \approx 4380\), which is not practical for searching a database of 1024 elements. On the other hand, Fig. 6 seems to suggest that choosing smaller p might improve the optimal time of Grover’s search algorithm. For example, when \(p=0.4\), we observe a slight improvement from the homogeneous case \(p=0.5\), see the corresponding \(t_{opt}\) values in Table 2. However, it seems that this improvement in Grover’s optimal time is lost when p get smaller, e.g., see the case \(p=0.1\) in Table 2.

Table 2 Numerical computation of \(E_0\), \(E_1\), \(t_{opt}\) and \(\frac{\pi }{2}\sqrt{\frac{vol(G_{5})}{\langle \delta _w, \delta _w \rangle }}\) for \(G_5\) and different values of p
Full size table
Fig. 6
figure 6

Square root of the graph volume as a function of p for \(G_5\)

Full size image

4 Conclusions

In this paper, we discussed strategies for the application of Childs–Goldstone approach [15] to Grover’s quantum walk on graphs. A database is modeled by a finite (possibly directed) graph G, and the search algorithm is implemented using the family of Hamiltonians \(\{H_{\gamma }\}_{\gamma \in (0,\infty )}\) in (4). Theorem 2.3 provides conditions (15) on the overlaps probabilities that are sufficient to approximate and relate the eigenvalues \(E_0\), \(E_1 \) with the square root of the graph’s volume. Complete graphs are examples for which the conditions (15) hold for \(\gamma = \frac{N-1}{N}\) and any \(\epsilon >0\), but this is not the case for the hypercubic lattices, see, for instance, the top right panel in Fig. 3 (the homogeneous case \(p=0.5\)). On the other hand, we were able to tune the overlap probabilities on hypercubic lattices by inducing non-homogeneity measured by the parameter p. Indeed, the top left panel in Fig. 3 evidences for \(p=0.91\) the existence of \(\gamma \) for which we have

$$\begin{aligned} \vert \langle s, \psi _0 \rangle \vert ^2 \approx \vert \langle e_w,\psi _0\rangle \vert ^2 \approx \vert \langle s, \psi _1 \rangle \vert ^2 \approx \vert \langle e_w,\psi _1\rangle \vert ^2. \end{aligned}$$

To deal with graphs for which it might be unfeasible to check (15), we introduced \(\gamma _E\)  (14) resulting in a simplified formula for the corresponding success probability \(\pi _{w}^{\gamma _E}(t)\) (25). In particular, to understand \(\pi _{w}^{\gamma _E}(t)\), we need to analyze the following quantities: \(E_1\), R(t) and the overlap probabilities

$$\begin{aligned} \vert \langle s, \psi _0 \rangle \vert ^2, \ \vert \langle e_w,\psi _0\rangle \vert ^2, \ \vert \langle s, \psi _1 \rangle \vert ^2, \ \vert \langle e_w,\psi _1\rangle \vert ^2. \end{aligned}$$

This can be done rigorously for the complete graph of N vertices, where \(\gamma _E=\frac{N-1}{N}\) and \(\pi _{w}^{\gamma _E}(t)\) is given by (10). Furthermore, complete graphs are particularly interesting as \(\gamma _E=\gamma _{opt}\), i.e., \(H_{\gamma _E}\) leads to optimal search outcomes. We then ask whether equality \(\gamma _{opt}=\gamma _E\) hold for other graphs, or whether we can construct a graph for which the properties (11) hold.

For this, we propose an approach for optimizing Grover’s algorithm on hypercubic lattice graphs. In particular, in Sect. 3, we fix the graph topology (as hypercubic lattices) and instead vary the analysis structure on these graphs; this is done by varying the considered Laplacians. The main ideas of this approach are numerically demonstrated on hypercubic lattices. We restricted our investigation on \(G_5\) and focus on graph homogeneity/non-homogeneity effects on Grover’s quantum walk. In upcoming work, we will extend our investigation to effects related to varying d and the location of the target vertex w.

In summary, we observe that the results for larger p resemble those of the complete graphs qualitatively, in particular \(\gamma _{opt} \approx \gamma _E\), and the corresponding success probability is well approximated by (25). On the other hand, Grover’s optimal times grow exponentially with p in a pattern similar to the graph volume increase in Fig. 6. Choosing smaller p, like \(p=0.4\), leads to a slight improvement in Grover’s optimal time compared to the homogeneous case \(p=0.5\). But this improvement does not continue with a further decrease of p as the case \(p=0.1\) in the bottom right panel in Fig. 5 shows.