Abstract
One of the central applications for quantum annealers is to find the solutions of Ising problems. Suitable Ising problems, however, need to be formulated such that they, on the one hand, respect the specific restrictions of the hardware and, on the other hand, represent the original problems which shall actually be solved. We evaluate sufficient requirements on such an embedded Ising problem analytically and transform them into a linear optimization problem. With an objective function aiming to minimize the maximal absolute problem parameter, the precision issues of the annealers are addressed. Due to the redundancy of several constraints, we can show that the formally exponentially large optimization problem can be reduced and finally solved in polynomial time for the standard embedding setting where the embedded vertices induce trees. This allows to formulate provably equivalent embedded Ising problems in a practical setup.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
The interest in quantum annealers, such as the devices developed by the company D-Wave Systems Inc., is still undiminished due to their ongoing fast progression. By implementing the adiabatic evolution of an Ising problem over qubits formed by overlapping superconducting loops, they promise to solve NP-hard problems. Although several physical effects prevent the ideal realization of the underlying adiabatic theorem, and optimal solutions can thus only be found with some probability, the experimental results appear to be promising for certain applications [1]. However, the advantage over classical computation is still under discussion [2].
‘Programming’ such an annealer means to provide the input parameters of the specific implemented Ising problem, that is, the weights on the vertices and the strengths on the edges of a specific hardware graph. The Chimera and Pegasus hardware architectures are currently available [3] and a new one, called Zephyr, was recently announced but is not yet released [4]. Interesting applications, however, do usually not match those graphs straightforwardly but require what is known as an embedding [5], where each vertex of the original problem is mapped to several vertices in the hardware graph to represent the desired connectivity. Unfortunately, the problem of finding such an embedding is itself an NP-hard problem [6]. Although the connectivity is increased with every new hardware release, it is apparent that all of the graphs yield some kind of locality due to physical restrictions. Therefore, the development of a completely connected hardware graph in the future is rather unlikely and the embedding problem will remain relevant in the long term. In order to circumvent this bottleneck and nevertheless enable experiments on these machines for the users, precalculated and generally applicable embedding templates provide a good starting point, such as for the complete graph [7]. Furthermore, the D-Wave API provides heuristic algorithms in the package minorminor [8], which are mainly based on an implementation of [9].
However, with only the embedding, we still cannot perform calculations on the D-Wave machine. We need to bring together the two different problems: the original one that shall be solved and the one that can be solved with the annealer. That is, we need to find suitable parameters, the weights and strengths, of an Ising problem working on the hardware subgraph induced by the embedding. The resulting embedded Ising problem should represent the original Ising problem such that the corresponding solutions can be retrieved from the output of the quantum annealer (at least in theory). If the embedded Ising problem is formulated wrongly, it either might yield optimal solutions which are suboptimal for the original problem or, even worse, the solutions might not even be ‘de-embeddable,’ which means that they have no clear correspondence to any original solution. An example for the latter is a chain of qubits where we get the solution values -1 for one half and +1 for the other. This can be addressed by applying a ‘strong coupling’ to vertices that belong to the embedding of a single original vertex to enforce that they behave collectively during the annealing process. We say they shall be synchronized. This can be achieved by large absolute strengths on the edges between the vertices. But what is ‘strong enough’? V. Choi has called this non-trivial problem of finding suitable parameters for the provable equivalence of the original and the embedded Ising problem the parameter setting problem [10].
Unfortunately, in practice, we need to take further restrictions on the parameters into account. First of all, they can only be chosen within a certain interval, where the specific boundary values might vary between the different architectures or even devices. At first sight, this might not appear to be problematic: We can simply scale the Ising problem by multiplying by a constant factor. This, however, decreases the absolute difference between the problem parameters, while the most critical restriction of D-Wave’s annealing machines is their parameter precision. Due to the transmission over the analog control circuits, the problem-defining parameters experience different perturbations [11]. This means that the actually solved problem differs slightly from the one specified by the user. Thus, problems which shall be solved with these machines need to be chosen carefully to yield some kind of ‘robustness’ in the parameter precision.
Although the programming interface allows to insert arbitrary float values within given ranges, the machine can actually realize only a limited discrete parameter range. In [12], a precision of about \(\frac{1}{30}\) was estimated for the specific annealer used in the experiments, which in turn means integer values between \(-\,30\) and 30 for a scaled problem. For problems with a higher precision, respectively, larger integer parameters, the success probability is drastically reduced because the annealing machine is not capable of resolving the parameters. In more recently released machines, the precision has probably been improved. However, the specific values and boundaries are not precisely known and can only be estimated through further experiments.
For the users, the programming of such annealing machines is only worth the effort if the machine can find the optimal solution to the provided problem in a certain number of runs, that is, if an acceptable success probability can be achieved. With the concrete restrictions on the internally implemented parameters not being specified exactly, we can therefore merely formulate some objectives aiming to improve the parameter distribution of the encoded Ising problem as much as possible, and thereby hopefully also the success probability. Because two parameters might appear too close to each other for the machine in presence of a very large parameter, a first step is therefore to keep the largest appearing parameter as small as possible (without scaling). This already concerns the encoding of an arbitrary combinatorial problem as a general Ising problem but becomes particularly important when the Ising problems shall be embedded: Such large values usually appear with the strong coupling of the embedded vertices. Therefore, the coupling strength cannot be chosen arbitrarily large.
Consequently, we do not only need to find a feasible parameter setting, ensuring the synchronization of the embedded vertices, but it also needs to be optimal in the sense that the coupling strength is as small as possible to conform with the precision of the machine. Only if this problem is solved, we can provide suitable embedded Ising problems and thus run meaningful experiments with the quantum annealers. Furthermore, this only enables to analyze the actual performance of the machines because miss-specified problems are not mixed up with the physical effects anymore, both suppressing the success probability in different ways.
1.2 Related work
The baseline for all the work around minor embedding and the corresponding parameter setting was developed by V. Choi. In [10], a first upper bound on the strengths on the coupling edges depending on the original parameters is given, achieved by providing an explicit non-uniform weighting of the vertices in the hardware graph. However, in practice, these bounds seem to be too weak and the large strengths they introduce suppress the success probability due to the necessary scaling factor. Besides that, the explicit parameter setting problem is studied less intensively than the embedding problem, in particular analytically, although the limitations are quite well examined and understood and the choice of the strengths in the single vertex embeddings was recognized early to be decisive for the success probability of the D-Wave machine [11].
By now, there is a common understanding in the quantum annealing community that the coupling strength, the single strength value that is in most cases simply applied to all coupling edges, needs to be larger than the largest absolute parameter of the original Ising problem, but should not be orders of magnitudes larger to not trigger the precision issues of the annealer. Usually, a factor of 2 is applied, as for instance is described in [13]. At the same time, the weights are in general distributed uniformly over the vertices.
Another method used in practice is determining the scaling factor empirically, see, e.g., [14]. This means that several instances of the same original problem are transferred into Ising problems, usually yielding a common structure. By successively solving the problems with certain parameters and checking the feasibility of the found solutions afterward, a specific bound or a bounding function in the input parameters is estimated and assumed to hold also for all other instances of the same problem. In [15] different coupling strength scaling is tested with several strategies to choose the weights, but none of them shows a significant advantage over the other. In any case, such scanning does not provide any provable equivalence of the embedded Ising problem but can only give some guidelines.
In the package dwave-system, D-Wave’s programming interface offers a method to set the coupling strength called ‘uniform torque compensation’ [16], which is most likely based on [13]. In the given formulation, it only applies for chains, which means if the embedding of a single vertex induces a path in the hardware graph. The method is derived from the idea that a ‘torque’ on the central edge of the chain, caused by the supposedly random influence of the neighboring chains, needs to be compensated by setting the weights and strengths accordingly. Although the results of the empirical study for certain random instances in [13] are promising, an analytical study of the equivalence of the thus obtained solutions is missing, which is why this method can also only be considered as a heuristic approach to obtain the coupling strength.
The more recent publication [17] is the first and only one after Choi’s, to our best knowledge, that provides an analytical investigation of the general parameter setting problem. Based on arbitrary, but given and fixed weights, the authors derive bounds on the coupling strength and show that their bounds are stronger than those of Choi and tight for some special cases.
1.3 Contribution
In this work, we focus on the specific programming restrictions of the annealing machines, but, apart from that, we consider the annealers as a black box without questioning their ability to actually solve the programmed problems. We aim to clearly divide the transformation steps of the problems toward the machine and close the loop to the embedded Ising problem before the annealers even are involved. Therefore, we answer a purely mathematical question here, that is interesting for itself, and thereby improve the application of quantum annealers.
We provide a mathematical description of an embedded Ising problem that holds a provable equivalence to the original Ising problem, which means both problems yield equivalent solutions. This includes embeddings that contain arbitrary embedded subgraphs rather than only chains as in previous approaches. By concentrating on synchronized solutions, we formulate general sufficient requirements. The observation of single vertices with their corresponding embeddings and certain assumptions on the thus extracted instances allow us to formulate specific constraints on the coupling strengths.
Indeed the bounds of [17] look similar to the cut constraints which we derive in Sect. 3.3. However, there is a major difference: Our constraints do not include the absolute values, which can be a decisive factor regarding the complexity of the problem. Our top-down approach, with a detailed deduction of our bounds, allows to clearly indicate why we can omit the absolute values. With this we also prove the sufficiency of more general conditions on an embedded Ising problem. We further state where we ‘lose the necessity’ but can only derive the sufficiency of our requirements. Therefore, instances for which the bounds are tight can be identified more easily.
By the choice of specific objective functions and the inclusion of a variable setting of the weights together with an additional gap parameter, we take a significant step further and extend the problem to a linear optimization problem yielding the optimal coupling strength. As such, we provide the first approach of analyzing the parameter setting problem in terms of mathematical optimization. We show by the reduction of the number of constraints that it is a problem which, in contrast to the embedding problem, can be solved easily, that is, in polynomial time if the embedded vertices induce trees [18].
1.4 Structure
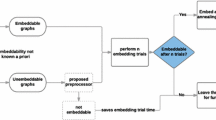
First, we introduce the basic terms and concepts in Sect. 2. After recapturing the main graph-theoretical terms used in this article in Sect. 2.1, we provide an accurate background for the two main concepts in quantum annealing, the Ising problem and the graph embedding, in Sects. 2.2 and 2.3, respectively. Combining both concepts, we can establish the notation of the embedded Ising problem and general requirements assuring that it yields solutions from which we can extract those to the original Ising problem in Sect. 2.4. Hereby, one strategy is to focus on synchronized variables, which is presented in Sect. 2.5. These steps are depicted in first three layers of Fig. 1, where we summarize all main deductions and results of this article.
In Sect. 3, we break down the full embedded Ising problem formulated over unknown parameters into smaller problems, which can be solved individually: By extracting the part concerning a single vertex, we derive sufficient requirements on the parameters concerning this vertex in Sect. 3.1. Together with an objective function aiming at minimizing the largest absolute parameter, they form the constraints of an optimization problem, which we formulate and simplify in Sects. 3.2 and 3.3. The resulting problem, named the Gapped Weight Distribution Problem, is summarized in Sect. 3.4. The individual solutions can then be recombined to a full equivalent embedded Ising problem. This is shown in the lower part of the chart in Fig. 1.
The remainder of the article then focuses on the step highlighted in green in Fig. 1 and analyzes the complexity of the deduced problem in Sect. 4. We establish a simplified description of the polyhedron over which it is defined in Sect. 4.1. By reducing the number of constraints significantly due to redundancy in Sect. 4.2, we can derive our final theorem about the polynomial-time solvability for trees. Finally, we conclude our results in Sect. 5.
2 Basic terms
2.1 General notation
First, we introduce some general notations used throughout this work. For the basic graph definitions, we generally follow the standard literature in graph theory and optimization, see, e.g., [19] or [20], and briefly recapture the main notations here: With \(G = (V, E)\) we always refer to a simple undirected finite graph with the finite set of vertices V and the set of edges \({E \subseteq \{\{v, w\}: v, w \in V\}}\). Given a graph G, V(G) and E(G) provide the vertex and the edge set, respectively, if those are not named specifically. While a subgraph of G is formed by arbitrary subsets of edges and vertices of G, G[S] refers to the vertex-induced subgraph of graph G for some vertex set \(S \subset V(G)\), where we have \(V(G[S]) = S\) and \(E(G[S]) = \{\{v, w\} \in E(G): v, w \in S\}\). For shortness, we abbreviate an edge \(\{v, w\}\) with the commutative product vw. We denote the neighbors of a vertex v in the graph G with
The incident edges are
where we use \(\delta (v)\) to abbreviate \(\delta (\{v\})\).
For indexed parameters or variables \(x \in X^I\) with the index set I and the value set X, we use \(x_J = (x_i)_{i \in J}\) for a subset \(J \subseteq I\) of the indices to refer to a subset of these parameters or variables, respectively, the corresponding vector. In turn, we ‘apply’ J by
We denote the vector containing only 1’s or 0’s by \(\mathbb {1}\) and \(\mathbb {O}\), respectively. For both, we add the subscript for the corresponding index set wherever necessary. If a set S is the disjoint union of two sets \(S_1\) and \(S_2\), that means \(S_1 \cup S_2 = S\) and \(S_1 \cap S_2 = \emptyset \), we use  . With \(2^X\), we denote the set of all subsets of a set X.
. With \(2^X\), we denote the set of all subsets of a set X.
2.2 Ising problem
In the quantum annealing processor, the magnetism of the superconducting loops and their couplings can be adjusted with user-defined input parameters. This means we can encode different quadratic functions. The term ‘Ising model’ also refers to these objective functions because they are closely related to the formulation of the physical model [10]. We use throughout this work:
Definition 1
An Ising model over a graph G with weights \(\pmb {W} \in \mathbb {R}^{V(G)}\) and strengths \({\pmb {S} \in \mathbb {R}^{E(G)}_{\ne 0}}\) is a function \(\pmb {I_{W, S}}:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}\) with
We call G the interaction graph of the Ising model.
Usually, we keep the interaction graph fixed. To be able to differ between two Ising models for the same graph, we use the symbol \(I_{W, S}\) with the corresponding weights and strengths in the subscript. In case those are clear from the context, we drop the subscript. Using this definition, we can formulate a general version of the optimization problem the quantum annealing machine can process:

D-Wave’s quantum annealer can indeed only implement float values with \(W \in [-m, m]^{V(G)}\) and \(S \in [-n, n]^{E(G)}\) for specific \(m, n \in \mathbb {N}\). For instance, for the current Chimera architecture, we have \(m=2\) and \(n=1\). However, due to possible scaling, this is not a hard restriction. A value which provides more insight into the coefficient distribution is the maximal absolute coefficient
in particular when compared with its counterpart, the minimal absolute coefficient being unequal to zero, or the minimal difference between two absolute coefficients
If we further restrict the weights and strengths to \(\mathbb {Z}\) according to the differentiation considerations explained in Sect. 1.1, which means on the integer range \(\{ -m, {-m+1},..., m\}\), respectively, \(\{-n, -n+1,..., n\}\), the latter becomes 1 after scaling. Thus, the maximal absolute coefficient \(C_{\max }\) is a decisive value to estimate whether the problem meets the parameter restrictions and is thus suitable to be solved with the annealer. According to [12], we need at least \(C_{\max } \le 30\) to achieve an acceptable success probability.
The decision problem corresponding to the Ising Problem is known to be NP-complete [21]. This means a variety of problems can be mapped to it in polynomial time [22]. In particular, it is closely related to the Quadratic Unconstrained Binary Optimization Problem (QUBO), more commonly known and well studied in combinatorial optimization. See, for example, [23] for more details.
There are preprocessing methods for directly manipulating the Ising model. One of them is applicable if the weight of a vertex exceeds the influence of the strengths of the incident edges. We recall the well-known result here because it implies the exclusion of a certain weight-strengths constellation in the following investigations. Although it is already used in [10], it is not formally proven there. Therefore, we also add the proof for completeness.
Lemma 2
For an Ising model \(I_{W, S}:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}\) over a graph G with \(W \in \mathbb {R}^{V(G)}\) and \(S \in \mathbb {R}^{E(G)}\), if we have
for some vertex \(v \in V(G)\), every optimal solution
fulfils \(s^*_v = - {{\,\textrm{sign}\,}}(W_v)\).
Proof
We extract the part of \(I_{W, S}\) containing \(s^*_v\) with
where we keep the other s-variables apart from \(s^*_v\) fixed. With the condition for vertex v, we have
and therefore can observe that
This shows that the contribution of \(s^*_v = {{\,\textrm{sign}\,}}(W_v)\) is always larger than the negated choice independently of the assignment of the other s-variables. \(\square \)
Remark: It is also easy to see that if the equality holds in the above condition for v, the optimal solution does not necessarily hold the value \(- {{\,\textrm{sign}\,}}(W_v)\) for \(s^*_v\). Still, this only happens if the last inequality in the proof collapses to an equality. Therefore, both choices yield the same optimal value and we can nevertheless choose to set \(s^*_v = - {{\,\textrm{sign}\,}}(W_v)\) in advance.
Based on this result, we could remove certain variables from our Ising problem in advance. Therefore, we assume in the following that our given Ising model is not preprocessable according to the lemma anymore, that is, we have
for all vertices \(v \in V(G)\).
However, when solving problems with D-Wave’s annealing machines, we cannot choose the interaction graph G arbitrarily. It needs to correspond to the currently operating hardware graph. Only if G is a subgraph of the hardware graph, we can directly solve the Ising Problem with the D-Wave annealer (with some probability) by setting surplus parameters to 0.
2.3 Graph embedding
D-Wave’s quantum annealers do not realize fully connected graphs, which would allow for optimizing Ising models with arbitrary interaction graphs with the same or a smaller number of vertices. They rather provide specific hardware graphs, representing the connectivity of the overlapping superconducting loops which form the qubits. For currently operating hardware, those are the Chimera and Pegasus graphs [24].
If the investigated application is not explicitly customized to fit those graphs, the interaction graph of the corresponding Ising model does in most cases not have any relation to them. Thus, to be able to calculate on such annealing machines, we always have to deal with the discrepancy between the problem graphs and the realized hardware graphs: We require what is known as an embedding. That means several hardware vertices are combined to form a logical vertex to simulate an arbitrary problem connectivity. As we base the following work on it, we repeat and slightly extend the definition of [6] here for completeness:
Definition 3
For two graphs G and H, an embedding of G in H is a map \(\pmb {\varphi }: V(G) \rightarrow 2^{V(H)}\) fulfilling the following properties, where we use \(\pmb {\varphi _v}\, {:}{=}\, \varphi (v)\) for \(v \in V(G)\) for shortness:
-
(a)
all \(\varphi _v\) for \(v \in V(G)\) induce disjoint connected subgraphs in H, more precisely
-
we have \(\varphi _v \cap \varphi _w = \emptyset \) for all \(v \ne w \in V(G)\) and
-
\(H[\varphi _v]\) is connected for all \(v \in V(G)\),
-
-
(b)
for all edges \(vw \in E(G)\), there exists at least one edge in H connecting the sets \(\varphi _v\) and \(\varphi _w\), which means we have \(\delta (\varphi _v, \varphi _w) \ne \emptyset \).
We call G embeddable into H if such an embedding function for G and H exists.
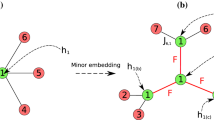
Exemplary complete graph embedding in a broken Chimera graph [7]
An example of such an embedding is shown in Fig. 2. The concept of embeddings is closely related to graph minors, which is why they are also called minor embeddings [5]. General graph minors have been intensively studied even before quantum annealing became a hot topic and the basis is formed by Robertson and Seymore, see, e.g., [25]. In the quantum annealing context, H refers to the hardware graph, such as a Chimera graph, while G is the problem graph derived from the specific application and its concrete Ising formulation, which can therefore be fully arbitrary. In the following work, we consider the embedding to be given.
Note that the above definition does not further restrict the embedded subgraphs \(H[\varphi _v]\), \(v \in V(G)\), apart from being connected. Although some embedding schemes produce only trees [9], trees forming crosses [7], like in Fig. 2, or even just paths [26], which are also called qubit chains, the subgraphs can in general form arbitrary graphs. However, we can always exclude surplus edges as long as we preserve the connectivity, by presetting their strengths to zero. This does not influence the connectivity between the subgraphs of different original vertices. Therefore, all subgraphs could be reduced to minimal connecting trees, which might be beneficial as several problems are much easier on trees. Indeed, we use this fact in our final theorem. Apart from that we deal with the most general version, with arbitrary graphs, throughout this article.
2.4 Embedded Ising problem
The Ising model as given in Definition 1 is defined over arbitrary graphs, thus also over the possible hardware graphs. As explained before, typical applications however need an embedding. Therefore, we introduce an extended definition of the Ising model in this section to combine both concepts. For this we first extend the embedding notation of Definition 3 by the following graph structures:
Definition 4
For two graphs G and H and an embedding \(\varphi : V(G) \rightarrow 2^{V(H)}\) of G in H, let the embedded graph, the subgraph of H resulting from the embedding, be

with
denoting the intra-connecting and inter-connecting edges, respectively.
Using the embedding objects of Definition 4, we can now formulate an Ising model over the given embedded graph. The following concepts are mainly well known in the quantum annealing community, see, e.g., [10] and [13], but we want to bring them into a more formal format here.
Definition 5
An embedded Ising model for two graphs G and H and an embedding \({\varphi : V(G) \rightarrow 2^{V(H)}}\) of G in H is an Ising model over \(H_\varphi \), where we have \(\pmb {\overline{I}_{\overline{W}, \overline{S}}}:\{-1, 1\}^{V(H_\varphi )} \rightarrow \mathbb {R}\) with
for the weights \(\pmb {\overline{W}} \in \mathbb {R}^{V(H_\varphi )}\) and the strengths \(\pmb {\overline{S}} \in \mathbb {R}^{E(H_\varphi )}\).
In this case, we call the corresponding Ising Problem of finding an s that solves
with the above embedded Ising model \(\overline{I}_{\overline{W}, \overline{S}}\) the Embedded Ising Problem.
With this formulation and \(H = C\) for C being a currently operating broken Chimera graph of D-Wave, we could solve the corresponding Embedded Ising Problem with the D-Wave annealer (with some probability). However, given an arbitrary Ising model whose underlying connectivity graph requires an embedding, we need to find a suitable corresponding embedded Ising model. This requires to choose the weights and strengths in a certain way such that an optimal solution of the new Ising problem corresponds to an optimal solution of the original one in the end.
In particular, as we usually do not only want to know the optimal value but also the optimal solution itself, we need a recipe how to get from an embedded to an original solution. We therefore need a ‘de-embedding’ function that can be computed easily, which means in polynomial time. This is more formally stated by the following definition, where we drop the weights and the strengths in the subscript for simplicity.
Definition 6
For two graphs G and H and an embedding \({\varphi : V(G) \rightarrow 2^{V(H)}}\) of G in H, an equivalent embedded Ising model \({\overline{I}:\{-1, 1\}^{V(H_\varphi )} \rightarrow \mathbb {R}}\) to a given Ising model \(I:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}\) fulfils the following properties:
-
(a)
The corresponding Ising problems are equivalent in the sense that we have
$$\begin{aligned} \min _{s \in \{-1,1\}^{V(H_\varphi )}} \overline{I}(s) + c = \min _{t \in \{-1,1\}^{V(G)}} I(t) \end{aligned}$$for a known constant \(c \in \mathbb {R}\) and
-
(b)
there exists a mapping from an optimal solution \(s^* \in \{-1,1\}^{V(H_\varphi )}\) of the embedded Ising problem to an optimal solution \(t^* \in \{-1,1\}^{V(G)}\) of the (unembedded) Ising problem which can be computed in polynomial time.
This would have been sufficient to use the quantum annealing machines if the underlying physical system had ideally realized the corresponding physical model. However, this is impossible in the real world and the machines thus only work heuristically providing solutions only with some unknown probability. In general, it remains unclear whether we have found the optimal solution, a sub-optimal solution or no solution at all. Thus, the user does not only need to have access to the mentioned mapping of the optimal solutions but rather needs more information to deal with the results of the machine.
In practice, we need an extended version of the above definition to overcome this issue: For each solution provided by the annealer, not only optimal ones, we want to know whether we can de-embed it to an original solution and if we can, we also want to know how to do it. We define:
Definition 7
An equivalent embedded Ising model \(\overline{I}:\{-1, 1\}^{V(H_\varphi )} \rightarrow \mathbb {R}\) to a given Ising model \(I:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}\) for two graphs G and H and an embedding \({\varphi : V(G) \rightarrow 2^{V(H)}}\) of G in H is called de-embeddable if we have two functions
and
which can both be computed in polynomial time. While
tells whether we can compute an original solution to the embedded one, the function \(\tau \) provides the corresponding de-embedded solution, where we have
for the constant \(c \in \mathbb {R}\). We call
the set of de-embeddable solutions.
Thus, for
we have by Definition 6
The most useful in practice would be if all original solutions had a corresponding embedded counterpart, which means if \(\tau \) is surjective. This in turn would mean we have \(\psi ^{-1}(1) \cong \{-1,1\}^{V(G)}\) and at least \(2^{|V(G)|}\) solutions that are de-embeddable.
To find such functions, we need to decide at some point what structure the embedded solutions should follow. Although different options might be possible due to the large number of adjustable parameters, the most straightforward way is to restrict the considerations to solutions where all variables corresponding to the embedding of a single original vertex hold the same value. This principle called synchronization is explained in the following section in more detail.
2.5 Variable synchronization
The main aspect of the equivalence of the given and the embedded Ising problem is the retrieval of the original solution from the embedded one. For this we need to be able to ‘de-embed’ the embedded solution. This in turn requires this solution to hold a certain structure. By enforcing the synchronization of all variables in the embedded Ising model that correspond to a single original variable, which means that all those variables should hold the same value, we have a simple criterion on the solutions of the embedded Ising problem. This idea was already introduced in [10] and means more formally
Definition 8
For two graphs G and H, a solution of the embedded Ising problem \({s \in \{-1, 1\}^{V(H_\varphi )}}\) is called a synchronized solution with respect to an embedding \({\varphi : V(G) \rightarrow 2^{V(H)}}\) of G in H if we have
For such a synchronized solution, we can easily provide the functions required for the de-embedding with
and
for some vertex set \(X \subseteq V(H_\varphi )\) with \(|X \cap \varphi _v| = 1\) for all \(v \in V(G)\). The vertex set X just serves as a placeholder, as we can simply choose a random vertex from \(\varphi _v\) to obtain the value of its variable because all of them hold the same value. It is easy to recognize that \(\tau \) is surjective and both functions can be computed in polynomial time.
In case the embedded variables do not hold a common value, it is unclear which value to assign to the corresponding original variable. In such cases, the common practice is to apply a post-processing on these unsynchronized solutions. A popular example is the heuristic of majority voting, where the original variable gets the value which appears in the majority of the assignments of the embedded variables [11]. Those heuristics might be useful, when considering the non-optimal solutions provided by the D-Wave machine due to its physical ‘imperfectness.’ That means, for instance, if only a few variables are flipped in the found solution compared to the optimal solution due to single-qubit failures or read-out errors.
However, if the embedded Ising model is ill-defined, which means that its optimal solution does not yield a clear correspondence to an original solution, those heuristics will not be able to extract the optimal original solution: Switching the value of an embedded variable, to the one of the majority, also changes the contribution of some edges by their strength to the objective value, which in turn influences the neighboring vertices. Thus, broken embeddings might have a global impact on the assignment of a large number of variables, which can usually not be ‘repaired locally.’ Applying such methods in these cases will therefore in general not increase the probability of finding the optimal solution. On the other hand, we do not see a way how to construct an embedded Ising model tailored to obtain the provable equivalence to the original Ising model under such ‘majority solutions’ due to the large number of possible distributions.
Therefore, we focus here on synchronized embedded solutions, which have a one-to-one correspondence to original solutions, thus can be de-embedded straightforwardly. But, how do we ensure that such an embedded Ising model based on synchronization, which means it yields the given functions of Definition 8 as a de-embedding, is also an equivalent embedded Ising model to our given one? According to Definition 6, the optimal solution of the embedded Ising problem should also be a synchronized one in this case, corresponding to the original optimal solution. The annealer could therefore find it, at least in theory, by solving the embedded problem. Note that we do not evaluate here how to deal with unsynchronized solutions, probably returned by the annealing machines due to their heuristic nature.
Obviously, the weights and the strengths of the embedded Ising model depend on the original parameters. If the weights and the strengths fulfil

and

respectively, we have for a synchronized solution s as given in Definition 8
This means, for all such synchronized solutions, we have \(\overline{I}(s) + c = I(t)\) with
Thus, the strengths \(\overline{S}_{E_\varphi }\) only introduce an offset to the overall objective value for these solutions. Furthermore, we ensure that for an optimal solution
we have \(\overline{I}(s^*) + c = I(t^*)\) for \(s^* = (t_v^* \mathbb {1}_{\varphi _v})_{v \in V(G)}\) and \(s^*\) thus also is the minimum over all synchronized solutions, which means
However, for the given \(s^*\), we do not necessarily have
which means it would also be the optimum over all solutions of the embedded Ising problem. There might be unsynchronized variable assignments yielding a lower objective value. This is the case if the contribution of the intra-connecting edges does not suffice.
As it can be seen in (II), if the variables \(s_q\) and \(s_p\) for \(pq \in E(H[\varphi _v])\) are synchronized, their product reduces to 1 and the corresponding strength \(\overline{S}_{pq}\) is added to the objective value. In turn, if the variables are assigned to different values, the product is \(-1\) and \(\overline{S}_{pq}\) is subtracted. Due to the minimization, it is therefore preferable to set \(\overline{S}_{pq}\) to a negative value. However, its contribution also needs to exceed the benefit of breaking the synchronization in the remaining part of the objective function.
To ensure the synchronization, we could, in theory, set \(\overline{S}_{pq} = - \infty \) for all \(pq \in E_\varphi \) or at least to a very large negative value, e.g., exceeding the sum of the absolute values of all coefficients in the embedded Ising model. In this case, we could also choose \(\overline{W}\) and \(\overline{S}_{E_\delta }\) arbitrarily within the sum bounds. However, these large strength values cannot be realized in practice because the annealing machines have a limited parameter precision and height due to physical restrictions. Thus, how do we need to choose the parameters \(\overline{S}_{E_\varphi }\) such that they suffice for the synchronization and how does their choice influence possible choices for \(\overline{W}\) and \(\overline{S}_{E_\delta }\) and vice versa?
3 Optimization problem extraction
For calculations on the D-Wave machine, it is essential for the user that the encoded problem indeed represents the original problem the user wants to solve. In this section, we extract and simplify the sufficient requirements on the parameters that need to be fulfilled such that the resulting embedded Ising problem provably holds equivalent solutions to those of the given problem, based on the synchronization of all variables in the embedded problem corresponding to one variable of the original one. By observing a single original vertex and adding an objective function aiming to minimize the absolute height of the parameters, we can extract a specific optimization problem respecting the physical restrictions of the machine.
We assume the two graphs \(\pmb {G}\) and \(\pmb {H}\), the embedding \(\pmb {\varphi }: V(G) \rightarrow 2^{V(H)}\) of G in H with the corresponding graph structures of Definition 4 and an Ising model \(\pmb {I_{W, S}}:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}\) with the weights \({\pmb {W} \in \mathbb {R}^{V(G)}}\) and strengths \(\pmb {S} \in \mathbb {R}^{E(G)}_{\ne 0}\) to be given and fixed in the following. Given this data, how do we find an equivalent embedded Ising model \(\overline{I}_{\overline{W}, \overline{S}}:\{-1, 1\}^{V(H_\varphi )} \rightarrow \mathbb {R}\) to \(I_{W, S}\) with weights \(\overline{W} \in \mathbb {R}^{V(H_\varphi )}\) and strengths \(\overline{S} \in \mathbb {R}^{E(H_\varphi )}\)? Note that we drop the subscripts of the Ising models in most cases for simplicity.
3.1 Single vertex evaluation
To answer the question stated at the end of Sect. 2.5, we extract the part of the embedded Ising model that concerns a single original vertex \(v \in V(G)\):
By this the remaining part \(\pmb {\overline{I}{}^{-v} (s)}\, {:}{=}\, \overline{I}(s) - \overline{I}{}^v(s)\) does only depend on the variables \({s \in \{-1, 1\}^{V(H_\varphi ) {\setminus } \varphi _v}}\). By replacing \(s \in \{-1, 1\}^{\varphi _v \cup N(\varphi _v)}\) in \(\overline{I}{}^v(s)\) with \((r, s) \in \{-1, 1\}^{\varphi _v} \times \{-1, 1\}^{N(\varphi _v)}\) we get
and can clearly indicate the different influencing parts. All variables corresponding to the embedding of vertex v, the r-variables, now only appear in \(\overline{I}{}^v\), while the s-variables form the connection to the remaining part, thus appear in both \(\overline{I}{}^{-v} = \overline{I} - \overline{I}{}^v\) and \(\overline{I}{}^v\).
In the following, we want to enforce the synchronization of the r’s independently of the influence ‘from the outside,’ which means for arbitrary s. Due to the minimization of the Ising models, this means that the minimum of the partial Ising problem should always be either \(\mathbb {1}\) or \(-\mathbb {1}\), more formally
In other words, we have
but with
Do these conditions applied to all vertices \(v \in V(G)\) ensure that the embedded problem is provably equivalent to the original one? We can indeed show their sufficiency:
Lemma 9
With
for all \(v \in V(G)\), we have for all
that \(s^* = (t_v^* \mathbb {1}_{\varphi _v})_{v \in V(G)}\) with \(t^* \in \{-1, 1\}^V\).
Proof
Assume there exists
with \(s^*_{\varphi _v} \not \in \{-\mathbb {1}, \mathbb {1}\}\) for some vertex \(v \in V(G)\). Then, we have
by the given conditions and we can further deduce
for \({\tilde{s}} \in \{-1,1\}^{V(H_\varphi )}\) with \({\tilde{s}}_{V(H_\varphi ) {\setminus } \varphi _v} = s^*_{V(H_\varphi ) {\setminus } \varphi _v}\) and \({\tilde{s}}_{\varphi _v} = r^* \mathbb {1}\) for
This contradicts to \(s^*\) being an optimal solution. \(\square \)
With this result, we can now clearly formulate the requirements on an embedded Ising model:
Theorem 10
For two graphs G and H, an embedding \(\varphi : V(G) \rightarrow 2^{V(H)}\) of G in H and an Ising model \({I_{W, S}:\{-1, 1\}^{V(G)} \rightarrow \mathbb {R}}\) with weights \(W \in \mathbb {R}^{V(G)}\) and strengths \(S \in \mathbb {R}^{E(G)}\), the Ising model \(\overline{I}_{\overline{W}, \overline{S}}:\{-1, 1\}^{V(H_\varphi )} \rightarrow \mathbb {R}\) with weights \(\overline{W} \in \mathbb {R}^{V(H_\varphi )}\) and strengths \(\overline{S} \in \mathbb {R}^{E(H_\varphi )}\) forms an equivalent embedded Ising model to \(I_{W, S}\) if we have

Proof
The optimality is clear with the deductions from the beginning of this section and Lemma 9. Furthermore, from an optimal solution
we can easily get a solution of the original Ising problem with \(t^*_v = s^*_q\) for an arbitrarily chosen \(p \in \varphi _v\) for all \(v \in V\) due to the enforced synchronization. \(\square \)
Note that this theorem only shows the sufficiency of our derived conditions. However, it does not state anything about the necessity. In the constraints for a specific vertex v, we assume the s-variables to be fully arbitrary. If we took into account that some of them are not independent from each other as they belong to the embedding of a single neighbor of v, whose embedded vertices should equivalently be synchronized, we would possibly retrieve a stronger set of constraints. This introduces another level of complexity, which we keep for future research.
Even if these variables are in turn all independent, it is still only an assumption we have made earlier that the single weights shall sum up to the original weights as well as the single strengths to the original strengths. However, based on this assumption, the constraints on the Ising model values are indeed necessary in this case. This aspect is also discussed in more detail in Sect. 3.3.
3.2 Problem instance definition
In the following, we only concentrate on a single arbitrary but fixed vertex \(\pmb {v} \in V(G)\). From the corresponding part of the embedded Ising model \({\overline{I}{}^v: \{-1, 1\}^{\varphi _v} \times \{-1, 1\}^{N(\varphi _v)} \rightarrow \mathbb {R}}\) and the constraints on the weights and strengths that concern v, we derive a specific optimization problem that needs to be solved to obtain those parameter values that ensure that the embedded vertices in \(\varphi _v\) represent the original one v.
Input
The part of the embedded graph \(\overline{I}{}^v\) is working on is the embedded subgraph structure

where we have
-
the connected inner graph \(H[\varphi _v]\, {=}{:}\,\left( {\overline{V}}, {\overline{E}}\right) \) with vertices \(\pmb {{\overline{V}}}\, {:}{=}\, \varphi _v\) and edges \(\pmb {{\overline{E}}}\, {:}{=}\, E(H[\varphi _v])\)
-
the outer neighbors \(\pmb {{\overline{N}}}\, {:}{=}\, N(\varphi _v) \subseteq \bigcup \{p \in \varphi _w: w \in N(v)\}\),
-
the set of edges to the outer neighbors \(\pmb {{\overline{D}}}\, {:}{=}\, \delta (\varphi _v)\) and
-
the edges between the outer neighbors \(E(H[N(\varphi _v)])\).
An example is shown in Fig. 3. Note that the quadratic terms for the edges between the outer neighbors of the last point do not include variables corresponding to vertices in \({\overline{V}}\). Therefore, they are not considered in the definition of \(\overline{I}{}^v\). In the following section, we nevertheless argue why we can omit these edges.
Example for an embedded subgraph structure of a single vertex with all outer neighbors, extracted from the complete graph embedding in the broken Chimera graph of Fig. 2
Although, apart from the constraints
as stated in Sect. 2.5, we are free to choose the values for the strengths on the outer edges \(\overline{S}_{pq}\) for all \(pq \in {\overline{D}}\), this introduces another level of complexity to the overall problem. Their choice does not only concern the evaluated vertex v but also its neighbors in G. We keep this additional level for future research and assume in the following that \(\overline{S}_{pq}\) is validly chosen in advance and thus given and fixed , allowing to handle all vertices v separately. Nevertheless, we discuss possible choices supporting the simplification of the problem in the following section and see that our approach can be applied in any case.
To differ between the outer edges with the given strength and the inner edges with the strength to be found, we rename them with \(\pmb {\alpha }\, {:}{=}\, \overline{S}_{\overline{D}} \in \mathbb {R}^{\overline{D}}\) and \(\pmb {\beta }\, {:}{=}\, - \overline{S}_{\overline{E}} \in \mathbb {R}^{\overline{E}}\). Note the extraction of the negative sign in the definition of \(\beta \). For simplicity of the notation, we also use for the variable weights \({\pmb {\omega }\, {:}{=}\, \overline{W}_{\varphi _v} \in \mathbb {R}^{\overline{V}}}\). With these notations and the simplifications of the previous section, we have for \(r \in \{-1, 1\}^{\overline{V}}\) and \(s \in \{-1, 1\}^{\overline{N}}\)
the Ising model \(I_{\omega , \beta }^{\alpha }: \{-1,1\}^{\overline{V}}\times \{-1,1\}^{\overline{N}}\rightarrow \mathbb {R}\), where we drop the bar and the superscript v for simplicity. All in all, we assume to be given
-
the strengths on the outer edges \(\alpha \in \mathbb {R}^{\overline{D}}\) and
-
the total weight \(\pmb {\lambda }\, {:}{=}\, W_v \in \mathbb {R}\)
and search for
-
the weights \(\omega \in \mathbb {R}^{\overline{V}}\) and
-
the strengths on the inner edges \(\beta \in \mathbb {R}^{\overline{E}}\).
Note that we could ‘cut off’ vertices from the embedded graph, where there are no outer edges incident to these vertices or all of them have zero strength, that means there is no ‘influence from outside’ on these vertices. In turn, we thus assume we always have at least one outer edge with a nonzero strength, that is, \(\{n \in {\overline{N}}: \ell n \in {\overline{D}}, \alpha _{\ell n} \ne 0\} \ne \emptyset \) for all leaves \(\ell \) of \(H[\varphi _v]\).
Output and objective
The larger we choose \(\beta _{pq}\), the stronger the vertices p and q are coupled due to the negative sign in \(I_{\omega , \beta }^{\alpha }\). As discussed in Sect. 2.2, we cannot simply set these strengths to some very large value compared to the remaining parameters due to the machine restrictions. In the literature, the coupling strength is mentioned to be decisive for the success probability; however, usually yielding the maximal absolute coefficient \(C_{\max }\) at the same time. Therefore, the question arises: How small can we set these strengths such that we can still achieve an equivalent embedded Ising? This means that a first step based on current practice would be to simply minimize \(\Vert \beta \Vert _{\infty }\).
However, by only minimizing the strengths, a corresponding suitable weighting could exceed the corresponding bound in some vertices. Hence, with the strengths on the outer edges assumed to be fixed, the more interesting objective would be the maximal absolute value of all remaining parameters of the observed part of the Ising model \(\max \{\Vert \omega \Vert _{\infty }, \Vert \beta \Vert _{\infty }\}\), which should be minimized in total.
As already mentioned before, \(H[\varphi _v]\) could be reduced to a tree by excluding possibly existing additional inner edges. We use this fact in our final theorem, as several problems are much easier on trees. However, in the following, we consider \(H[\varphi _v]\) to be an arbitrary graph to deal with the most general problem version in this regard.
Constraints
By the previous section, we can already derive the following constraints on the introduced parameters \(\omega \) and \(\beta \): The weights should sum up to the total weight with
and, from the conditions of Lemma 9, we need
to ensure that the full embedded problem is provably equivalent to original one in the end. Note that the latter condition is comprised of an exponential number of constraints, more precisely \(2^{|{\overline{N}}|} \big ( 2^{|{\overline{V}}|} - 2 \big )\) many. Although they are linear inequalities, the overall optimization problem is therefore not solvable in polynomial time in a straightforward way. Thus, it could only be used for small embedded subgraph instances \(H[\varphi _v]\) in practice.
By introducing a gap value \(\pmb {\gamma } \in \mathbb {R}_{> 0}\), we can relax the order relation to a greater or equal:
By this we can also influence how ‘far away,’ in terms of the difference of their objective values, unsynchronized variable assignments are from the synchronized ones. Breaking the synchronization introduces a penalty of at least this gap value for each original vertex, such that synchronized solutions are preferred in the minimization. In particular, this results in the optimal solution of the embedded Ising problem being also synchronized and having a distance to the next unsynchronized solution of at least \(\gamma \). Therefore, in theory, any gap value larger than 0 is sufficient to provide the provable equivalence of the problems.
However, this value might become important for the user of the actual D-Wave machine when trying to improve the success probability of finding optimal or close-to-optimal solutions, because it influences the distribution of synchronized and unsynchronized solutions: Depending on the distribution of the objective values of the original problem, the distance to the closest sub-optimal synchronized solution might be larger than \(\gamma \) and several unsynchronized solutions might therefore have an objective value in between. This could mean that the annealing machine even misses any synchronized solution, due to its heuristic nature, and instead only returns unsynchronized solutions. In this case the gap value is chosen too small and needs to be increased. However, due to the parameter restrictions of the machine, we will probably not be able to increase the gap until only synchronized solutions are preferred, as this increases the resulting coupling strength, too. In future research, we might need to evaluate the effects of the gap parameter on actual machines and could also investigate different approaches in trading off the gap against the strength. This however shall not be part of this work. In the following, we assume this value is given with the input and fixed.
In a nutshell
By the previous notations and reformulations, we can now summarize the problem. While in [18] the problem was split up in two problems with two different objective functions, this is not relevant for our hardness result here. Therefore, we concentrate on the full problem with

3.3 Simplifications
The instance defined in the previous section can be simplified due to some properties of the Ising models. We can apply several steps, which are discussed in the following.
Common strength
The \(\beta \)-variables only introduce an offset for synchronized variable assignments. As the total size of this offset is irrelevant, we can choose to set all strengths to the same maximal value. Thus, with \(\pmb {\vartheta }\, {:}{=}\, \Vert \beta \Vert _\infty \), we can set \(\beta _{pq}\) to \(\vartheta \) for all \(pq \in {\overline{E}}\) and therefore get
The constant c describing the difference to the original Ising model is now simply \(\vartheta |{\overline{E}}|\).
This also allows to further simplify the problem formulation: Instead of using \(\max \big \{\Vert \omega \Vert _\infty , \vartheta \big \}\) as the objective function to be minimized, it can be reduced to only \(\vartheta \) by introducing the additional constraint \(\vartheta \ge \Vert \omega \Vert _\infty \). This means the minimal coupling strength also serves as an upper bound for the weights which we can assign.
Non-negative input parameters due to symmetry
Furthermore, we can take advantage of the symmetry in the Ising model being defined over variables in \(\{-1, 1\}\). By replacing s with \({\bar{s}} = -s\), we can switch the sign of the strengths on the intra-coupling edges:
We can see that the different assignments of the s-variables in (IV) cover all possible sign combinations of the strengths on the outer edges \(\alpha \). Thus, we can restrict \(\alpha \) to \(\mathbb {R}_{\ge 0}^{\overline{D}}\) in the following evaluations.
Note that this does not mean that we restrict the original Ising instances which can be reformulated using our method to specific cases. We can rather handle all Ising models analogously by replacing possibly appearing negative strengths by their absolute values and proceed with the resulting Ising instance. However, in the final embedded Ising problem formulation, we need to refer to the original strengths for the corresponding quadratic terms.
Additionally, by replacing (r, s) with \(({\bar{r}}, {\bar{s}})\), we observe a symmetry for the \(\omega \)’s: We have
with
This means we can analogously restrict the total weight to \(\lambda \in \mathbb {R}_{\ge 0}\). Similar to the outer strengths as explained before, Ising instances with a negative total weight can be handled by setting \(\lambda \) to \(|\lambda |\). However, in this case, we also need to apply a transformation to the \(\omega \)-values, once we have found them, to obtain the correct embedded Ising formulation: We need to revert the sign change by replacing the found \(\omega \) with \({{\,\textrm{sign}\,}}(\lambda )\cdot \omega \) for the original total weight \(\lambda \).
Independent outer neighbors
By the embedding definition, a single edge connecting the embeddings of different vertices is sufficient. In practice, we usually have \(|\delta _{vw}| > 1\) for at least a few pairs of original vertices vw due to the symmetric structure of the Chimera. This can also be seen in Fig. 3. Here, we discuss some options how to deal with multiple inter-connecting edges and the assumptions which we base the following work on.
If there are multiple edges between the embeddings of two vertices, one possibility could simply be to choose a certain edge \({\bar{e}} \in \delta _{vw}\) and ‘ignore’ the others. This means, for the embedded Ising model, we could set
and further only deal with \(\delta _{vw} = \{{\bar{e}}\}\). This would influence the former graph structure in two ways:
-
1.
No two vertices of \({\overline{V}}\) share an outer neighbor, which means that we have \(|\{q: qn \in \delta (\varphi _v)\}| = 1\) for all \(n \in {\overline{N}}\) and thus \({\overline{D}}= \delta (\varphi _v) \cong {\overline{N}}\).
-
2.
We have \(E(H[N(\varphi _v)])) = \emptyset \), which means that no two outer neighbors are connected by an edge.
By this, on the one hand, we have already achieved a simplification of the problem and, on the other hand, we have ensured that all the outer neighbors are independent of each other because they belong to different original neighbors of v.
However, another possibility also offers advantages: By spreading the strength equally over all of the available edges as suggested in [13] with
the coefficients are decreased as much as possible. This seems to be beneficial for complying with the parameter range of the machine. As the variables corresponding to the embeddings of the other vertices shall be synchronized, too, the outer neighbors of some inner vertices are not independent of each other in this case. While in the Chimera graph no triangles exist, they might be present in other hardware graphs, such as the Pegasus graph, and might cause inner vertices that even share a common outer neighbor.
Howsoever, the strengths are distributed, we want to take advantage of both strategies. Thus, we simplify the embedded graph structure by splitting up possibly existing shared vertices and simply considering all outer vertices to be pairwise independent of each other as if they would belong to different neighbors of the original vertex. Thus, for the following considerations in this work, we assume that we have \({\overline{D}}\cong {\overline{N}}\) and that \(\pmb {\alpha } \in \mathbb {R}_{\ge 0}^{\overline{D}}= \mathbb {R}_{\ge 0}^{\overline{N}}\) are given and fixed strengths yielding the points 1 and 2 from above.
These assumptions become relevant in the following section, where we estimate the worst cases of the ‘outer influence,’ the contribution of the strengths on the edges to the outer neighbors multiplied by the s-variables, to further simplify \(\overline{I}{}^v\). If there exist two variables \(s_n\) and \(s_m\) corresponding to two outer neighbors \(n,m \in {\overline{N}}\) that belong to the same embedding \(\varphi _w\) of an original neighboring vertex w, those variables would get the same value in a synchronized solution of the overall problem. As we however assume they can be chosen arbitrarily and independently, the worst case might be overestimated. This means our derived bounds still hold, but the found strength might be larger than actually necessary in this case. Additionally, the actual minimal gap between a synchronized and an unsynchronized solution might be larger than intended by the user. This is another point where we can only derive the sufficiency but not the necessity of our conditions.
In turn, if the given embedding does not contain any multiple inter-connecting edges, we do not have the choice to split the strength of the original edge but rather need to assign it to the single corresponding edge in the hardware graph. Thus, in this case, our bounds are tight in this regard and we would not lose the necessity here.
Single outer neighbor
Finally, we further reduce the problem such that the given graph instance does only have a single outer neighbor for each vertex \(q \in {\overline{V}}\). This would mean we had \({\overline{N}}\cong {\overline{V}}\). If this is not the case, which means there are at least two outer neighbors for a single inner vertex, the following lemma shows that a synchronization of the variables over these outer neighbors suffices to also cover those cases where the strengths on the outer edges get different signs.
Lemma 11
For \(I_{\omega , \vartheta }^\alpha : \{-1, 1\}^{\overline{V}}\times \{-1, 1\}^{\overline{N}}\) as given in (V) with \(\alpha \in R_{\ge 0}^{\overline{D}}\), the gap value \(\gamma \in \mathbb {R}_{\ge 0}\), a vertex \(q \in {\overline{V}}\) and its neighbors \(n, m \in {\overline{N}}\) with \(qn, qm \in {\overline{D}}\), we have
for all \(r \in \{-1, 1\}^{\overline{V}}\) and all \(s_{{\overline{N}}{\setminus } \{m, n\}} \in \{-1, 1\}^{{\overline{N}}{\setminus } \{m, n\}}\).
Proof
In the following proof, we drop the sub- and superscripts on I for simplicity. With
and
the functions A, B and C are independent of \(r_q\), \(s_n\) and \(s_m\). By the condition of the lemma, we know

and it remains to show that from this follows

More simply, this means to show that, for any fixed \(A, B, C \in \mathbb {R}\) and \(X, Y \in \mathbb {R}_{\ge 0}\) with
it follows that
This can be achieved by the following two case distinctions. By inserting \(s=-1\) and \(r=1\) in inequality (i), we obtain due to \(X, Y \ge 0\)
-
for \(C \le X + Y\)

-
and for \(C > X + Y\)

Thus, we have shown the implication of inequality (ii) for r = 1 and arbitrary s. By inserting \(s=1\) and \(r=-1\) in inequality (i), we obtain in turn
-
for \(C \ge -X - Y\)

-
and for \(C < -X - Y\)

This means we have also shown implication of inequality (ii) for \(r = -1\) and arbitrary s, which completes the proof. \(\square \)
With the conditions of the lemma, we can replace the single occurrence of \(s_m\) with \(s_n\) in \(I_{\omega , \vartheta }^\alpha (r, s)\). This way \(s_n\) gets the coefficient \(\alpha _{qn} + \alpha _{qm}\) and we have reduced the outer neighbors by 1 by removing m. We can apply this lemma iteratively to all outer neighbors that share an inner vertex. Hence, by the lemma, we can say that the synchronization of the variables corresponding to the outer neighbors forms the ‘worst case’ with respect to the outer influence. Note that this step only reduces the number of cases which need to be considered but does not lead to weaker bounds, even if the ‘merged’ outer neighbors have not been independent before.
By defining the weighting \(\pmb {\sigma } \in \mathbb {R}_{\ge 0}^{\overline{V}}\) with
we can therefore reduce the Ising model to
where we reindexed the s-variables accordingly, that is \(s \in \{-1, 1\}^{{\overline{V}}}\). Thus, only \(\sigma \in \mathbb {R}_{\ge 0}^{\overline{V}}\) is considered in the following as an input for the weight distribution problem and we do not require the outer neighbors \({\overline{N}}\) and the edges to them \({\overline{D}}\) anymore.
Graph cuts
With the former simplifications, we can now further evaluate the condition
for fixed parameters and reformulate it using graph cuts. Inserting the full formulation for \(I_{\omega , \vartheta }^\sigma \) in the above inequality, we have for all \(s \in \{-1,1\}^{\overline{V}}\) and for all \(r \in \{-1,1\}^{\overline{V}}\setminus \{-\mathbb {1}, \mathbb {1}\}\):
which is equivalent to

By combining all the lower bounds, we can further deduce stronger conditions, where we have for all \(r\in \{-1,1\}^{\overline{V}}\,{\setminus }\, \{-\mathbb {1}, \mathbb {1}\}\)

It is easy to recognize that the maximum in the former relation is achieved when setting \(s_q\) to \(-r_q\) for all \(q \in {\overline{V}}\), leading to the last equality. Note that we already reduced the number of constraints to \(2^{|{\overline{V}}|} - 2\) with this step.
With the vertex set definition of \(S = \{q \in {\overline{V}}: r_q = -1\}\) for a specific assignment of the r-variables and
we can equivalently formulate for all \(\emptyset \ne S \subsetneq {\overline{V}}\):
Note that the empty set and the full vertex set are excluded because the r-variables cannot get all the value 1 or all the value \(-1\). As furthermore the graph \(H[\varphi _v]\) is connected by the embedding definition, we have \(|\delta (S)| > 0\) for all non-trivial cuts S. As \(\vartheta \) is the objective function, we can reformulate the conditions to lower bounds on the optimal value with
We refer to them as cut inequalities in the following. They can equivalently be combined all in one with
Note that, according to the preprocessing step based on Lemma 2 of Sect. 2.2, there are instances for which the weight of the original vertex predominates all outer influences caused by its incident edges. The variable corresponding to such a vertex can be preprocessed before the embedding anyway by setting it according to the sign of the weight. This case appears if we have \(\lambda \ge \sigma ({\overline{V}})\). Thus, we also only consider instances with \(\sigma ({\overline{V}}) > \lambda \) in the following. We summarize the resulting problem in the next section.
3.4 The problem
In this section, we briefly summarize the problem that is derived from the Gapped Parameter Setting Problem, where the sufficient requirements on the embedded Ising Problem are combined. Previously, we have considered a more complex objective function, which has now been reduced to simply optimize \(\vartheta \) while distributing the weights \(\omega \). Therefore, we have

Note that we have now switched to the standard notation of a graph \({G = (V, E)}\) as the input for the Gapped Weight Distribution Problem for simplification. This graph G does however not correspond to the interaction graph of the original Ising problem, which we introduced in the beginning of this article. By solving the above problem with \(G = H[\varphi _v]\),
and \(\lambda = |W_v|\) as explained in Sect. 3.3, we can find the corresponding optimal strength and weights for vertex v in the embedded problem. Thus, to get the full embedded Ising problem, we need to repeat the optimization for all vertices and their corresponding subgraph structures and combine the results into a full embedded Ising model according to equation (III). Remembering the simplification steps of Sects. 3.2 and 3.3, we set
for each original vertex v and its corresponding optimal solution \((\vartheta ^*, \omega ^*)\) of the above problem. The strengths on the inter-connecting edges \(\overline{S}_{E_\delta }\) remain as chosen in advance.
Additionally, we have also substituted \(\tfrac{1}{2}\gamma \) with \(\gamma \) in the problem for simplicity. This means that the actual distance between a synchronized and a non-synchronized solution is \(2\gamma \) in the end. Furthermore, note the restriction \(\lambda < \sigma (V)\), which results from Lemma 2 and is the reformulation of (I) with the new notation. It is important in the next section.
Just considering the cut constraints, we can see a relation to a graph property called the edge expansion of the graph [27]. In our case, we additionally have a weighting \(\sigma \) on the vertices, rather than just counting the number of vertices. This is in turn closely related to the minimum cut density as introduced in [28]. There the authors show that, in case of trees, the minimum cut density can be solved by just evaluating those partitions which are derived from cutting at each edge. Thus, the problem can be solved in a time quadratically in the number of vertices if the examined graph is a tree. Although our problem formulation is slightly different to both mentioned ones, we can establish a similar results for our problem.
4 Analysis
As \(\delta (S)\) is constant for every set S, we only have linear functions and the Gapped Weight Distribution Problem thus belongs to the class of linear optimization problems (LPs). Although we have already reduced and simplified the requirements on the embedded Ising problem, we still have to take every possible constellation of the signs of the outer influences on the embedded vertices into account. This is results in a constraint for every non-trivial subset of the vertices of \(H[\varphi _v]\). Their number is exponentially large and we therefore have exponentially large LPs, which cannot be solved in polynomial time in a straightforward way. We need to analyze the problem in more detail.
4.1 Polyhedral description
In the following, let the graph \(\pmb {G} = (\pmb {V}, \pmb {E})\), the strengths \(\pmb {\sigma } \in \mathbb {R}_{\ge 0}^V\), the total weight \(\pmb {\lambda } \in \mathbb {R}_{\ge 0}\) with \(\lambda < \sigma (V)\) and the gap \(\pmb {\gamma } \in \mathbb {R}_{> 0}\) be given and fixed. For \(\emptyset \ne S_1 \subseteq S_2 \subseteq V\), we see the \(\sigma \)-sums are monotonic over the partial ordering of the subset relation with
due to \(\sigma \ge \mathbb {O}\). Furthermore, we have
for arbitrary \(\emptyset \ne S \subseteq V\). With

and
for \(\lambda \ge 0\), we get by the resolution of the minimum the constraint
for all \(\emptyset \ne S \subsetneq V\). This can be used for the following polyhedra and other helpful definitions:
Definition 12
Let
We have
if \(\sigma (S) < \vartheta _{\!\tiny {\frac{1}{2}}}\) and
otherwise by the given relations and due to
Note that, with \(\lambda < \sigma (V)\), we always have \(\vartheta _{\!\tiny {\frac{1}{2}}}> 0\).
Now we can reformulate the problem:
Corollary 13
The Gapped Weight Distribution Problem can be written as the LP
With these definitions, we can easily see that \(\Theta \) is an unbounded, |V|-dimensional polyhedron described by an exponential number of inequalities. The domain of the Gapped Weight Distribution Problem is then the intersection of \(\Theta \) with the cone \(\Phi \), which is defined by only 2|V| constraints since \(\vartheta \ge \Vert \omega \Vert _\infty \) is equivalent to
or without any absolute value also to
4.2 Connected vertex sets
Note that we restrict our considerations to \(0 \le \lambda < \sigma (V)\) to focus on the cases that are not preprocessable according to Lemma 2. This implies \(\vartheta _{\!\tiny {\frac{1}{2}}}> 0\), which is indeed necessary for the constructions. We further assume \(\pmb {G}\) and \(\pmb {\sigma } \in \mathbb {R}^V_{\ge 0}\) to be given and fixed again.
To reduce the complexity of the description of \(\Theta \) from Definition 12, we need to reduce the number of inequalities. By the following result, we can indeed show that some inequalities describing \(\Theta \) are redundant due to the monotonicity of the \(\sigma \)-sums:
Theorem 14
We have
for \({\pmb {\mathfrak {C}}\, {:}{=}\, \big \{\emptyset \ne S \subsetneq V: G[S] \text { connected and } {G[V\, {\setminus }\, S]} \text { connected} \big \}}\).
Proof
Due to the reduction of the number of constraints, the left-hand side is contained in the right-hand side. In the following, we show the reverse direction by establishing the redundancy of the constraints associated with sets in \(2^V \setminus \{\emptyset , V\}\) that are not included in \(\mathfrak {C}\). For this we introduce the type t(S) of a vertex set \(\emptyset \ne S \subsetneq V\) denoting the number of connected components of the corresponding induced subgraph G[S]. Note that every non-empty vertex set has at least a type of 1 and we only have \(t(S) = 1\) if G[S] is connected. As the equality \(\omega (V) = \lambda \) is important for the following derivations, we furthermore work on the hyperplane \(\Theta _\lambda \) but do not explicitly mention it for simplicity.
The first step is to show the sufficiency of the restriction to vertex sets that induce connected subgraphs, which means
with \(\pmb {\mathfrak {C}'} = \big \{\emptyset \ne S \subsetneq V: G[S]\text { connected} \big \} = \big \{\emptyset \ne S \subsetneq V: t(S) = 1\big \}\). Suppose this does not hold. Let \(S^* \in 2^V\, {\setminus }\, (\mathfrak {C}' \cup \{\emptyset , V\}) = \big \{\emptyset \ne S \subsetneq V: t(S) > 1\big \}\) be a vertex set with
having minimal type. Then there exist two non-empty vertex sets \(S_1\) and \(S_2\) with  and \(\delta (S_1, S_2) = \delta (S_1) \cap \delta (S_2) = \emptyset \). Due to \(t(S_1) + t(S_2) = t(S^*)\) and the minimality of \(S^*\), we have \(t(S_1) = t(S_2) = 1\) and therefore \(S_1, S_2 \in \mathfrak {C}'\) with
and \(\delta (S_1, S_2) = \delta (S_1) \cap \delta (S_2) = \emptyset \). Due to \(t(S_1) + t(S_2) = t(S^*)\) and the minimality of \(S^*\), we have \(t(S_1) = t(S_2) = 1\) and therefore \(S_1, S_2 \in \mathfrak {C}'\) with
In the following, we show that the inequality defining \(\Theta (S^*)\) can be derived from the inequalities defining \(\Theta (S_1)\) and \(\Theta (S_2)\) by summation. Because
holds for arbitrary domains X and functions \(f,g: X \rightarrow \mathbb {R}\), this results in
which is, together with (ii), a contradiction to (i). This is supported by the additivity of \(\sigma \) and \(\omega \) with
and
We have two different cases concerning \(S^*\):
-
(A)
\(\sigma (S^*) < \vartheta _{\!\tiny {\frac{1}{2}}}\): Due to the monotonicity of \(\sigma \), we have \({\sigma (S_1), \sigma (S_2) \le \sigma (S^*) < \vartheta _{\!\tiny {\frac{1}{2}}}}\). From the inequalities defining \(\Theta (S_i)\),
$$\begin{aligned} \vartheta |\delta (S_i)| \ge \sigma (S_i) + \omega (S_i) + \gamma \end{aligned}$$for \(i=1,2\), we get
$$\begin{aligned} \begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (S_1)| + \vartheta |\delta (S_2)| \\&\ge \sigma (S_1) + \omega (S_1) + \sigma (S_2) + \omega (S_2) + 2\gamma \\&= \sigma (S^*) + \omega (S^*) + 2\gamma \\&\ge \sigma (S^*) + \omega (S^*) + \gamma \end{aligned} \end{aligned}$$with \(\gamma > 0\), which provides the constraint defining \(\Theta (S^*)\).
-
(B)
\(\sigma (S^*) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\): In this case, we cannot derive conditions on \(\sigma (S_1)\) and \(\sigma (S_2)\). Thus, there are three possibilities, which follow the same construction as in case (A):
-
(a)
\(\sigma (S_1), \sigma (S_2) < \vartheta _{\!\tiny {\frac{1}{2}}}\): From
$$\begin{aligned} \vartheta |\delta (S_i)| \ge \sigma (S_i) + \omega (S_i) + \gamma \end{aligned}$$for \(i=1,2\), we get
$$\begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (S_1)| + \vartheta |\delta (S_2)| \\&\ge \sigma (S_1) + \omega (S_1) + \sigma (S_2) + \omega (S_2) + 2\gamma \\&\ge \sigma (S^*) + \omega (S^*) + \gamma \end{aligned}$$analogously to (A) and further by ‘adding 0’
$$\begin{aligned}&= 2\sigma (S^*) - \sigma (S^*) + \omega (S^*) + \gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S^*) + \omega (S^*) + \gamma . \end{aligned}$$Thus, we obtained the inequality of \(\Theta (S^*)\) in this case.
-
(b)
\(\sigma (S_1), \sigma (S_2) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\): From
$$\begin{aligned} \vartheta |\delta (S_i)| \ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S_i) + \omega (S_i) + \gamma \end{aligned}$$for \(i=1,2\) and \(\vartheta _{\!\tiny {\frac{1}{2}}}> 0\) for \(\lambda < \sigma (V)\), we get
$$\begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (S_1)| + \vartheta |\delta (S_2)| \\&\ge 4\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S_1) + \omega (S_1) - \sigma (S_2) + \omega (S_2) + 2\gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S^*) + \omega (S^*) + \gamma . \end{aligned}$$ -
(c)
\(\sigma (S_1) < \vartheta _{\!\tiny {\frac{1}{2}}}\) and \(\sigma (S_2) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\) w.l.o.g.: From
$$\begin{aligned} \begin{aligned} \vartheta |\delta (S_1)|&\ge \sigma (S_1) + \omega (S_1) + \gamma , \\ \vartheta |\delta (S_2)|&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S_2) + \omega (S_2) + \gamma , \end{aligned} \end{aligned}$$we get
$$\begin{aligned} \begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (S_1)| + \vartheta |\delta (S_2)| \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}+ \sigma (S_1) + \omega (S_1) - \sigma (S_2) + \omega (S_2) + 2\gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S_1) + \omega (S_1) - \sigma (S_2) + \omega (S_2) + 2\gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S^*) + \omega (S^*) + \gamma \end{aligned} \end{aligned}$$due to \(\sigma (S_1) \ge 0 \ge - \sigma (S_1)\).
-
(a)
Therefore, the constraint associated with \(S^*\) is redundant if \(S^*\) does not induce a connected subgraph.
Next we show that the vertex sets whose complement also does not induce a connected subgraph are unnecessary, too, hence
Note that, with the former definition of \(\mathfrak {C}'\), we have \(\mathfrak {C}= \big \{S \in \mathfrak {C}': t(V\, {\setminus }\, S) = 1\big \}\). We derive an analogous contradiction as before and therefore assume the above relation does not hold. Let \(S^*\in \mathfrak {C}' {\setminus } \mathfrak {C}= \big \{\emptyset \ne S \subsetneq V: t(S) = 1, t(V\, {\setminus }\, S) > 1\big \}\) be a vertex set with
whose complement \(V \setminus S^*\) has minimal type. We can derive analogously to the first part that \(G[V \setminus S^*]\) needs to consist of only two connected components induced by vertex sets in \(\mathfrak {C}\). However, we need a minor additional step: Let

with \(t(X_i) = 1\) for all \(i=1,..., k\) and \(|\delta (X_i, X_j)| = \emptyset \) for all \(i \ne j \in \{1,..., k\}\), be a partition of \(V \setminus S^*\) into the vertex sets inducing the connected components of \(G[V \setminus S^*]\) for \(t(V \setminus S^*) = k > 1\). Since the graph G is connected, the complement of two of the above vertex sets, w.l.o.g. \(X_1\) and \(X_2\), induces a graph, \(G[V\, {\setminus }\, (X_1 \cup X_2)]\), which needs to be connected, too. Then we have \(t(V \setminus (X_1 \cup X_2)) = 2\), which would contradict the choice of \(S^*\) if we had \(k>2\). This means we have  with \(X_1, X_2 \in \mathfrak {C}\) and symmetrically also \(V \setminus X_1, V \setminus X_2 \in \mathfrak {C}\). This is illustrated in Fig. 4.
with \(X_1, X_2 \in \mathfrak {C}\) and symmetrically also \(V \setminus X_1, V \setminus X_2 \in \mathfrak {C}\). This is illustrated in Fig. 4.
The construction follows the same structure as in the first part, only with a slight deviation, because we use the complements in the following relations:
In order to establish the desired contradiction to (iii), the first relation remains to be shown. Remember, due to the additivity, we have
Analogously to before, we need to distinguish between different cases. However, the different possibilities for \(S^*\) ‘arise naturally’ and we therefore only consider the sets \(X_1\) and \(X_2\):
-
(a)
\(\sigma (V \setminus X_1), \sigma (V \setminus X_2) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\): From the inequalities which define \(\Theta (V \setminus X_1)\) and \({\Theta (V \setminus X_2)}\),
$$\begin{aligned} \vartheta |\delta (X_i)| = \vartheta |\delta (V \setminus X_i)| \ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (V \setminus X_i) + \omega (V \setminus X_i) + \gamma \end{aligned}$$for \(i=1,2\), we get
$$\begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (X_1)| + \vartheta |\delta (X_2)| \\&\ge 4\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (V \setminus X_1) + \omega (V \setminus X_1) - \sigma (V \setminus X_2) + \omega (V \setminus X_2) + 2\gamma \\&= 4\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (V \setminus X_1) + \omega (V \setminus X_1) - \sigma (S^* \cup X_1) + \omega (S^* \cup X_1) + 2\gamma \\&= 4\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (V) + \sigma (X_1) + \lambda - \omega (X_1) \\&\quad - \sigma (S^*) - \sigma (X_1) + \omega (S^*) + \omega (X_1) + 2\gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S^*) + \omega (S^*) + \gamma , \end{aligned}$$which is the inequality defining \(\Theta (S^*)\) in case of \(\sigma (S^*) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\). For \(\sigma (S^*) < \vartheta _{\!\tiny {\frac{1}{2}}}\), we can extend the chain of relations by
$$\begin{aligned}&> 2\sigma (S^*) - \sigma (S^*) + \omega (S^*) + \gamma \\&= \sigma (S^*) + \omega (S^*) + \gamma , \end{aligned}$$which provides the inequality defining \(\Theta (S^*)\) in this case.
-
(b)
\(\sigma (V \setminus X_1), \sigma (V \setminus X_2) < \vartheta _{\!\tiny {\frac{1}{2}}}\): These conditions contradict each other due to
$$\begin{aligned} \sigma (X_1) = \sigma (V) - \sigma (V \setminus X_1) > \sigma (V) - \tfrac{1}{2}\big (\sigma (V) - \lambda \big ) = \tfrac{1}{2}\big (\sigma (V) + \lambda \big ) \ge \vartheta _{\!\tiny {\frac{1}{2}}}, \end{aligned}$$while we require at the same time \(\sigma (V\, {\setminus }\, X_2) = \sigma (X_1) + \sigma (S^*) < \vartheta _{\!\tiny {\frac{1}{2}}}.\)
-
(c)
\(\sigma (V\, {\setminus }\, X_1) < \vartheta _{\!\tiny {\frac{1}{2}}}\) and \(\sigma (V\, {\setminus }\, X_2) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\) w.l.o.g.: From
$$\begin{aligned} \begin{aligned} \vartheta |\delta (X_1)| = \vartheta |\delta (V \setminus X_1)|&\ge \sigma (V \setminus X_1) + \omega (V \setminus X_1) + \gamma \\ \vartheta |\delta (X_2)| = \vartheta |\delta (V \setminus X_2)|&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (V \setminus X_2) + \omega (V \setminus X_2) + \gamma \end{aligned} \end{aligned}$$for \(i=1,2\), we get with
$$\begin{aligned} \vartheta |\delta (S^*)|&= \vartheta |\delta (X_1)| + \vartheta |\delta (X_2)| \\&= 2\vartheta _{\!\tiny {\frac{1}{2}}}+ \sigma (V \setminus X_1) + \omega (V \setminus X_1) - \sigma (V \setminus X_2) + \omega (V \setminus X_2) + 2\gamma \\&= 2\vartheta _{\!\tiny {\frac{1}{2}}}+ \sigma (S^* \cup X_2) + \omega (S^* \cup X_2) - \sigma (V \setminus X_2) + \omega (V \setminus X_2) + 2\gamma \\&= 2\vartheta _{\!\tiny {\frac{1}{2}}}+ \sigma (S^*) + \sigma (X_2) + \omega (S^*) + \omega (X_2) \\&\quad - \sigma (V) + \sigma (X_2) + \lambda - \omega (X_2) + 2\gamma \\&= \sigma (S^*) + 2\sigma (X_2) + \omega (S^*) + 2\gamma \\&\ge \sigma (S^*) + \omega (S^*) + \gamma \end{aligned}$$the inequality defining \(\Theta (S^*)\) in case of \(\sigma (S^*) < \vartheta _{\!\tiny {\frac{1}{2}}}\) or by extending
$$\begin{aligned}&= 2\sigma (S^*) - \sigma (S^*) + \omega (S^*) + \gamma \\&\ge 2\vartheta _{\!\tiny {\frac{1}{2}}}- \sigma (S^*) + \omega (S^*) + \gamma \end{aligned}$$the inequality defining \(\Theta (S^*)\) in the other case where \(\sigma (S^*) \ge \vartheta _{\!\tiny {\frac{1}{2}}}\).
Therefore, the constraint for \(S^*\) is also redundant if \(V\, {\setminus }\, S^*\) is not connected. \(\square \)
Although the \(\Theta \)-polyhedron can now be described with less inequalities, their number might still be exponential in an arbitrary graph. This means that expanding the whole optimization problem to provide it to the optimizer would already take exponential time and we thus cannot solve this problem as such in less than exponential time, which is of course intractable for problem instances above a certain size.
By the requirements of an embedding, however, we can always restrict ourselves to trees by simply ignoring surplus edges in the graph, as explained in Sect. 2.3. For a lot of problems, it is known that trees yield better solvability because of their much simpler structure. This also holds in our case, and we can finally state:
Theorem 15
If G is a tree, the Gapped Weight Distribution Problem can be solved in polynomial time.
Proof
For G being a tree, it is easy to see that the set of cuts \(\mathfrak {C}\) of Theorem 14 is only formed by cutting at single edges of the tree. More formally, this means
where \((S_e, V \setminus S_e)\) denotes the partitions derived from cutting the tree at edge e. Thus, we have \(|\mathfrak {C}| = 2|E| = 2|V| - 2\). Together with the single inequality for \(\Theta _\lambda \) and the 2|V| additional inequalities describing \(\Phi \), the LP for the Gapped Weight Distribution Problem has a linear size in the number of vertices. Therefore, we can derive the stated result due to the general solvability of polynomial LPs. \(\square \)
This means, with the restriction to trees, which is always feasible in the embedding setup as stated before, the formerly exponentially large optimization problem can be significantly reduced, finally yielding only a linear number of constraints. Therefore, we can now provide it to a standard LP solver to get the optimal solution to the problem in a practically feasible time. To obtain all weights and strengths which are needed to formulate a provably equivalent embedded Ising model to a given one, our approach requires to solve a Gapped Weight Distribution Problem for each vertex of the original graph and its corresponding embedded subgraph. This means that the total runtime to obtain the final full embedded Ising model can be estimated in the worst case by the number of vertices of the original graph times a polynomial over the largest number of embedded vertices in a subgraph.
In particular, the above result also shows that the additional weight bounds, restricting the weights to be smaller than or equal to the coupling strength, do not increase the complexity of the problem. But, the thus found weights are optimized regarding the height of the final coefficients of the embedded Ising model and therefore promise a better performance of the quantum annealing machines.
5 Conclusion
Whether the quantum annealers, in particular those built by D-Wave, show an advantage over classical computers is still under discussion and will only reveal with the further development of such machines. To evaluate the great potential of this technology however, we need to design our experiments carefully. If the architecture does not change drastically, the two programming steps, minor embedding and parameter setting, will remain relevant in the long term. They are critical when it comes to providing meaningful input for the annealing machines. While the necessary minor embedding can prevent calculations on the machine at all, that is, if no embedding can be found, the specific parameter setting decisively influences the success in solving the actual problem.
We provide the first polynomial but rigorous description to find the parameters of the embedded Ising problem for a given problem and its corresponding embedding such that both problems are provably equivalent. Due to the structure of the embeddings, the restriction on trees, required for the solvability proof, is a condition which can always be established, e.g., by ignoring surplus edges in the embedded subgraphs. Furthermore, while the embedding problem is strongly related to the specific hardware graphs of D-Wave, our weight distribution approach is applicable for all hardware which implements an Ising problem over graphs that do not yield an all-to-all connectivity and thus require an embedding. Although our formulation makes several assumptions on the structure of the problem, Sect. 3.3 clearly shows where they come from and in which cases they might deviate from the actual bound. In turn, we can deduce that there are several instances for which our bounds are tight.
Thinking ahead, the parameter precision issues support the assumption that it is preferable to have as few different values for the parameters of the Ising model as possible, while those should have the largest possible pairwise absolute difference, to achieve an acceptable success probability. If our original Ising problem is already defined only over integer parameters, a possible approach would be to also allow only integer parameters for the embedded Ising problem rather than dealing with rational parameters. This fixes the distance of the parameters to at least 1, which might increase the success probability. Minimizing the largest absolute integer parameter however increases the complexity of the problem significantly, as it is the step from an LP to an ILP. The evaluation of this problem will be the next step in our research.
Another interesting research direction might be to extend the approach of [13]: Rather than evaluating the worst case scenario, as we do in this publication, where the embedded vertices must be synchronized for all possible neighboring constellations, the average case, where they ‘only’ must hold for most of the cases, might also suffice in practice but yield an even smaller coupling strength.
Apart from that, with our results, the formulated Ising problems can now directly be transferred to the D-Wave machines. This means, the computational properties of these machines can now be investigated even further: Do the theoretically optimal coupling strengths also hold under the perturbations of the machine, that is, do they suffice to enforce the synchronization of the variables in practice? While, in theory, any positive gap is sufficient for the equivalence of the problems, an ideal quantum annealer should thus indeed return the optimal solution after a sufficiently long annealing time, the gap value most likely needs to be increased for any physical annealing machine. This gap parameter is a tool which provides different but, most importantly, equivalent encodings of the same problem and thus allows to study the difference between the theoretical and the effective coupling strength, which means the one which is necessary for the real machine to return the optimal value with an acceptable success probability. With this we will get a deeper understanding of the problem-independent behavior of such machines, supporting their further development.
Data availability
The manuscript has no associated data.
References
Stollenwerk, T., Michaud, V., Lobe, E., Picard, M., Basermann, A., Botter, T.: Agile earth observation satellite scheduling with a quantum annealer. IEEE Trans. Aerosp. Electron. Syst. 57(5), 3520–3528 (2021). https://doi.org/10.1109/TAES.2021.3088490
Jünger, M., Lobe, E., Mutzel, P., Reinelt, G., Rendl, F., Rinaldi, G., Stollenwerk, T.: Quantum annealing versus digital computing: an experimental comparison. ACM J. Exp. Algorithm. 26, 1–30 (2021). https://doi.org/10.1145/3459606
Boothby, K., Bunyk, P., Raymond, J., Roy, A.: Next-generation topology of D-Wave quantum processors. Preprint (2020) arXiv:2003.00133 [quant-ph]
Boothby, K., King, A., Raymond, J.: Zephyr topology of D-Wave quantum processors. Technical report, D-Wave Systems Inc. (2021). https://www.dwavesys.com/media/2uznec4s/14-1056a-a_zephyr_topology_of_d-wave_quantum_processors.pdf
Choi, V.: Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Inf. Process. 10(3), 343–353 (2011). https://doi.org/10.1007/s11128-010-0200-3
Lobe, E., Lutz, A.: Minor embedding in broken Chimera and Pegasus graphs is NP-complete. Preprint (2021) arXiv:2110.08325 [quant-ph]
Lobe, E., Schürmann, L., Stollenwerk, T.: Embedding of complete graphs in broken Chimera graphs. Quantum Inf. Process. 20(7), 1–27 (2021). https://doi.org/10.1007/s11128-021-03168-z
D-Wave Systems Inc.: minorminor. GitHub. version 0.2.11 (2023). https://github.com/dwavesystems/minorminer/releases/tag/0.2.11
Cai, J., Macready, W.G., Roy, A.: A practical heuristic for finding graph minors. Preprint (2014) arXiv:1406.2741 [quant-ph]
Choi, V.: Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process. 7(5), 193–209 (2008). https://doi.org/10.1007/s11128-008-0082-9
King, A.D., McGeoch, C.C.: Algorithm engineering for a quantum annealing platform. Preprint (2014) arXiv:1410.2628 [cs.DS]
Stollenwerk, T., O’Gorman, B., Venturelli, D., Mandrà, S., Rodionova, O., Ng, H., Sridhar, B., Rieffel, E.G., Biswas, R.: Quantum annealing applied to de-conflicting optimal trajectories for air traffic management. IEEE Trans. Intell. Transp. Syst. 21(1), 285–297 (2019). https://doi.org/10.1109/TITS.2019.2891235
Raymond, J., Ndiaye, N., Rayaprolu, G., King, A.D.: Improving performance of logical qubits by parameter tuning and topology compensation. In: 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), pp. 295–305. IEEE (2020). https://doi.org/10.1109/QCE49297.2020.00044
Venturelli, D., Marchand, D.J., Rojo, G.: Quantum annealing implementation of job-shop scheduling. Preprint (2015) arXiv:1506.08479 [quant-ph]
Pudenz, K.L.: Parameter setting for quantum annealers. In: 2016 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1–6. IEEE (2016). https://doi.org/10.1109/HPEC.2016.7761619
D-Wave Systems Inc.: dwave-system. GitHub. version 1.19.0 (2023). https://github.com/dwavesystems/dwave-system/blob/1.19.0/dwave/embedding/chain_strength.py
Fang, Y.-L., Warburton, P.: Minimizing minor embedding energy: an application in quantum annealing. Quantum Inf. Process. 19(7), 1–29 (2020). https://doi.org/10.1007/s11128-020-02681-x
Lobe, E.: Combinatorial problems in programming quantum annealers. PhD thesis, Otto-von-Guericke-Universität Magdeburg, Fakultät für Mathematik (2022). https://doi.org/10.25673/89443
Diestel, R.: Graph Theory. Graduate Texts in Mathematics, vol. 173, 5th edn. Springer, Berlin (2017). https://doi.org/10.1007/978-3-662-53622-3
Korte, B., Vygen, J.: Combinatorial Optimization: Theory and Algorithms. Algorithms and Combinatorics, vol. 21, 6th edn. Springer, Berlin (2018). https://doi.org/10.1007/978-3-662-56039-6
Barahona, F.: On the computational complexity of Ising spin glass models. J. Phys. A: Math. Gen. 15(10), 3241–3253 (1982). https://doi.org/10.1088/0305-4470/15/10/028
Lucas, A.: Ising formulations of many NP problems. Front. Phys. 2, 5 (2014). https://doi.org/10.3389/fphy.2014.00005
Kochenberger, G., Hao, J.-K., Glover, F., Lewis, M., Lü, Z., Wang, H., Wang, Y.: The unconstrained binary quadratic programming problem: a survey. J. Comb. Optim. 28(1), 58–81 (2014). https://doi.org/10.1007/s10878-014-9734-0
D-Wave Systems Inc.: D-Wave System Documentation. Visited 2023-06-09. https://docs.dwavesys.com/docs/latest/index.html
Robertson, N., Seymour, P.D.: Graph minors. XIII. The disjoint paths problem. J. Comb. Theory Ser. B 63(1), 65–110 (1995). https://doi.org/10.1006/jctb.1995.1006
Boothby, T., King, A.D., Roy, A.: Fast clique minor generation in chimera qubit connectivity graphs. Quantum Inf. Process. 15(1), 495–508 (2016). https://doi.org/10.1007/s11128-015-1150-6
Hoory, S., Linial, N., Wigderson, A.: Expander graphs and their applications. Bull. Am. Math. Soc. 43(4), 439–561 (2006). https://doi.org/10.1090/S0273-0979-06-01126-8
Matula, D.W., Shahrokhi, F.: Sparsest cuts and bottlenecks in graphs. Discrete Appl. Math. 27(1–2), 113–123 (1990). https://doi.org/10.1016/0166-218X(90)90133-W
Funding
Open Access funding enabled and organized by Projekt DEAL. The underlying research project is part of the project ‘Algorithms for quantum computer development in hardware-software codesign’ (ALQU), which was made possible by the DLR Quantum Computing Initiative (QCI) and the Federal Ministry for Economic Affairs and Climate Action (BMWK); https://qci.dlr.de/alqu.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lobe, E., Kaibel, V. Optimal sufficient requirements on the embedded Ising problem in polynomial time. Quantum Inf Process 22, 305 (2023). https://doi.org/10.1007/s11128-023-04058-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-023-04058-2