1 Introduction

Quantum steering was first proposed by Schrödinger in 1936 [1] in response to the EPR paradox [2]. However, it did not attract much attentions until 2007, when Wiseman et al. reinterpreted quantum steering strictly from the operational view and even proposed some experimental criteria [3]. Ever since, the research of quantum steering has made great progress both in theory [4, 5] and experiment [6,7,8,9,10]. In Wiseman’s definition, quantum steering that logically intermediates between quantum entanglement and Bell nonlocality, describes the ability of one party, Alice, to nonlocally control the state of another party, Bob, even when Bob does not trust Alice’s measurement apparatus, exhibiting unique asymmetric behavior [11,12,13,14]. As an essential type of quantum correlations, quantum steering has great applications in quantum key distribution [15, 16], subchannel discrimination [17], asymmetric quantum network [18], randomness generation [19, 20] and randomness certification [21]. In the standard EPR steering tasks, N entangled particles are separately distributed to N different observers and each observer performs some projective (sharp) measurements to demonstrate her or his steerability. Since each observer is spatially separated, the non-signaling condition is strictly satisfied between different observers, i.e., the marginal probability distribution of each observer does not depend on the measurements of any other observers [22]. Due to the monogamy constraints, the number of observers who share quantum correlation via sharp measurement is limited [23,24,25,26]. Recently, a surprising result was reported by Silva et al. that the number of observers sharing non-locality can be increased if the sequential weak (unsharp) measurement was employed, where the non-signaling condition is dropped [27]. Their result later is confirmed by theoretical [28,29,30] as well as experimental works [31, 32], and the sequential unsharp measurement strategy has been extended to study other types of quantum correlation [33,34,35]. It has shown that the maximum number of Alices who can simultaneously share steering with a single Bob can also beat the steering monogamy limits [36,37,38].

However, all the steering sharing scenarios [36, 38] investigated till now have the following commonalities: the initial shared state is restricted to be the maximum entangled state, the sequential unsharp measurement is only adopted by one side, and the number of measurement settings is not more than 3. Thus, some interesting questions raise: whether or not the steering correlation can be kept when the shared state is not pure any more? If there exist multiple observers on both sides, can multiple Alices steer multiple Bobs simultaneously? Compared to the single Bob case, do multiple Bobs make a difference? And how many observers can share steering simultaneously if the number of measurement settings increases?

In this work, we consider a more general sequential steering scenario featuring that unsharp measurements are sequentially performed on both sides. We investigate how many pairs of Alice and Bob can sequentially demonstrate steering in the above scenario when each party performs N-setting equal sharpness measurements. With the N-setting linear steering criterion [39], we find no more than 5 Alices can steer a single Bob for a Werner state when N increases from 2 to 16. Then, we show how such sequential steering sharing scenarios tolerate the environmental noise and experimental imperfections by analyzing the useful sharpness measurement range of each observer and the minimum purity bound of the initial state. Furthermore, we explore the case when multiple Bobs involved in, reporting a counterintuitive result that at most 2 Alices can steer 2 Bobs even the number of steering sharing observers larger than 4 in the single Bob case. Finally, we show that our scenario can be used to simulate quantum decoherence channels to effectively change the ability and direction of quantum steering. Our results not only reveal the rich structure of steering sharing but also can be applied to more general scenarios involving high dimension or genuine multipartite quantum steering [12].

2 The both-sides sequential steering sharing scenario

Fig. 1
figure 1

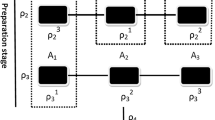
The scenario of steering sharing with multiple observers on both sides. A two-qubit entangled state is initially shared between a sequence of Alices and Bobs. Multiple Alices implement unsharp measurements on one part of the state successively, and multiple Bobs do similar operations on the other part

Full size image

A schematic of steering sharing scenario with both sides sequential unsharp measurements is shown in Fig. 1. A pair of two-qubit entangled state \(\rho _{AB} \) is sent to multiple pairs of spatially separated observers. One of the qubits is accessed by m Alices, say, \(A_{1}\), \(A_{2}\),..., \(A_{m}\), while the other qubit is possessed by n Bobs, say, \(B_{1} \), \(B_{2} \),..., \(B_{n}\). To demonstrate the steering between multiple Alices and Bobs at the same time, all observers except the last Alice and Bob should perform unsharp measurements; otherwise, the steerability will be completely destroyed. For convenience, we assume that the sharpness of the N-setting measurements that each observer used is equal, which is denoted as \(\lambda _{i}\) and \(\eta _{p}\) for the i-th Alice and the p-th Bob, respectively. Thus, their corresponding N-setting measurements can be represented by \(\lbrace {\hat{\Pi }}^{\lambda _{i}}_{\mathbf {m}_{1}}, {\hat{\Pi }}^{\lambda _{i}}_{\mathbf {m}_{2}}\),..., \( {\hat{\Pi }}^{\lambda _{i}}_{\mathbf {m}_{N}}\rbrace \) and \(\lbrace {\hat{\Lambda }}^{\eta _{p}}_{\mathbf {n}_{1}}, {\hat{\Lambda }}^{\eta _{p}}_{\mathbf {n}_{2}}\),..., \( {\hat{\Lambda }}^{\eta _{p}}_{\mathbf {n}_{N}}\rbrace \), where \(\mathbf {m}_{k}\) and \(\mathbf {n}_{k}\) represent the measurement directions with \(k\in \lbrace 1 ,\ldots ,\, N \rbrace \), \(i\in \lbrace 1 ,\ldots ,\, m \rbrace \), \(p\in \lbrace 1 ,\ldots , \, n \rbrace \), \(\lambda _{i} \in [0,1]\) and \(\eta _{p} \in [0,1]\). \(\lambda _{i} (\eta _{p})\!=\!0\) corresponds to no measurement, \(\lambda _{i} (\eta _{p})\!=\!1\) implies the measurement is sharp, and \(\lambda _{i} (\eta _{p})\in (0,1)\) means it is unsharp. It has been demonstrated that an unsharp measurement is optimal when quality factor F and the precision G of the measurement satisfy the trade-off relation \( F^{2}+G^{2}=1 \) [27]. Here, each observer adopts the optimal measurement strategy.

In the first step, suppose \(A_{1}\) wants to convince \(B_{1}\) that she can remotely affect his state through local measurements. However, \(B_{1}\) does not trust her, so he asks \(A_{1}\) to perform a measurement along \(\mathbf {m}_{k}\). After each run of experiment, \(A_{1}\) sends \(B_{1}\) the corresponding outcome \( a_{k}\in \lbrace 0,1 \rbrace \) and sends \(A_{2}\) the post-measurement state, which can be described by the Lüders ruler [40]

$$\begin{aligned} \rho _{AB}\rightarrow (\!K^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}} \otimes I_{B} )\rho _{AB}(K^{\lambda _{1}\dagger }_{a_{k}\mid \mathbf {m}_{k}} \otimes I_{B}), \end{aligned}$$
(1)

where \(K^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}} K^{\lambda _{1}\dagger }_{a_{k}\mid \mathbf {m}_{k}}\!=\!{\hat{\Pi }}^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}}\!=\!(I_{A}+(-1)^{a_{k}} \lambda _{1}\,\mathbf {m}_{k}\cdot \varvec{\sigma })/2\), \(\varvec{\sigma }\!=\!\{\sigma _x, \sigma _y, \sigma _z\}\) is the Pauli matrix, and \(I_{A}\) \((I_{B})\) is the identity matrix. Repeating the process many times, when \(A_{1}\) finishes all the N-setting measurements, \(B_{1}\) will obtain 2N conditional states. Then, \(B_{1}\) performs some measurements along \(\lbrace \mathbf {n}_{1}, \mathbf {n}_{2},\ldots ,\mathbf {n}_{N} \rbrace \) to analyze whether these conditional states can be described by a local hidden variable state (LHS) model. If they cannot, \(B_{1}\) is convinced that \(A_{1}\) can steer his state, and vice versa. Here, we certify the steering sharing by violating the most widely used N-setting linear steering inequality [39], which is defined as \(S_N^{1,1} \le C_N\) for \(A_{1}\) and \(B_{1}\), where \(S_N^{1,1}\equiv \frac{1}{N}\sum _{k=1}^N\langle {\hat{\Pi }}^{\lambda _{1}}_{\mathbf {m}_{k}}{\hat{\Lambda }}^{\eta _{1}}_{\mathbf {n}_{k}}\rangle =\mathrm {Tr} [\rho _{AB}\,( {\hat{\Pi }}^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}}\otimes {\hat{\Lambda }}^{\eta _{1}}_{b_{k}\mid \mathbf {n}_{k}})] \), \(b_k\) is \(B_{1}\)’s measurement result, \(C_N\) is the maximum value of \(S_N\), which can have if the LHS model exists. On the other hand, as \(A_{1}\) is assumed to act independently, thus the state shared between \(A_{2}\) and \(B_{1}\) should be averaged over \(A_{1}\)’s outputs, i.e.,

$$\begin{aligned} \rho ^{2,1}_{N}\!=\!\sum _{k=1}^{N} \sum _{a_{k}=0}^{1}(\!K^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}} \otimes I_{B} )\rho _{AB}(K^{\lambda _{1}\dagger }_{a_{k}\mid \mathbf {m}_{k}} \otimes I_{B}). \end{aligned}$$
(2)

Similarly, the state shared between \(A_{1}\) and \(B_{2}\) can be described by

$$\begin{aligned} \rho ^{1,2}_{N}\!=\!\sum _{k=1}^{N} \sum _{b_{k}=0}^{1}(\! I_{A} \otimes K^{\eta _{1}}_{b_{k}\mid \mathbf {n}_{k}})\rho _{AB}(\! I_{A}\otimes K^{\eta _{1}\dagger }_{b_{k}\mid \mathbf {n}_{k}}). \end{aligned}$$
(3)

Suppose \(B_{1}\) wants to show steering with \(A_{2}\) in the next step. They can verify it by calculating the steering parameter \(S_N^{2,1}\!\equiv \!\frac{1}{N}\sum _{k=1}^N\langle {\hat{\Pi }}^{\lambda _{2}}_{\mathbf {m}_{k}}{\hat{\Lambda }}^{\eta _{1}}_{\mathbf {n}_{k}}\rangle \!=\!\mathrm {Tr} [\rho ^{2,1}\,( {\hat{\Pi }}^{\lambda _{2}}_{a_{k}\mid \mathbf {m}_{k}}\otimes {\hat{\Lambda }}^{\eta _{1}}_{b_{k}\mid \mathbf {n}_{k}})]\). If it is larger than \(C_N\), then \(B_{1}\) succeeds; otherwise, he fails. Considering the first pair Alice and Bob (\(A_{1}\) and \(B_{1}\)) have implemented the matched measurement (when \(A_{1}\) performs a measurement along \(\mathbf {m}_{k}\), and \(B_{1}\) should measure along the \(\mathbf {n}_{k}\)), the average state shared between \(A_{2}\) and \(B_{2}\) can be expressed as:

$$\begin{aligned} \begin{aligned} \rho ^{2,2}_{N}=\!\sum _{k=1}^{N} \sum _{\begin{array}{c} a_{k}=0 \\ b_{k}=0 \end{array}}^{1}\!(K^{\lambda _{1}}_{a_{k}\mid \mathbf {m}_{k}}\!\otimes \!K^{\eta _{1}}_{b_{k}\mid \mathbf {n}_{k}}) \rho _{AB}(K^{\lambda _{1}\dagger }_{a_{k}\mid \mathbf {m}_{k}}\!\otimes \!K^{\eta _{1}\dagger }_{b_{k}\mid \mathbf {n}_{k}}). \end{aligned} \end{aligned}$$
(4)

Acting in analogy with the above process, at any step the state \( \rho ^{i,p}_{N} \) shared between the i-th Alice and the p-th Bob can be obtained by averaging over the previous observers’ measurements with the help of the Lüders transformation rule. The corresponding steering criterion can be written as:

$$\begin{aligned} S_N^{i,p}\equiv \frac{1}{N}\sum _{k=1}^N\langle {\hat{\Pi }}^{\lambda _{i}}_{\mathbf {m}_{k}}{\hat{\Lambda }}^{\eta _{p}}_{\mathbf {n}_{k}}\rangle \le C_N, \end{aligned}$$
(5)

where \( \langle {\hat{\Pi }}^{\lambda _{i}}_{\mathbf {m}_{k}}{\hat{\Lambda }}^{\eta _{p}}_{\mathbf {n}_{k}}\rangle =\mathrm {Tr}[\rho ^{i,p }\,( {\hat{\Pi }}^{\lambda _{i}}_{a_{k}\mid \mathbf {m}_{k}}\otimes {\hat{\Lambda }}^{\eta _{p}}_{b_{k}\mid \mathbf {n}_{k}})]\). Thus, we can investigate the behavior of quantum steering under sequential measurements by comparing the steering parameter with the classical bound in the same measurement setting.

3 Sharing the steering of an initial Werner state

Noting that the environmental effects may turn a pure state into a mixed one and considering the imperfection of the experimental device, one cannot prepare a maximum entangled pure state. Here, we take Werner state, the best-known class of mixed entangled states, as an example to investigate the steering sharing among multiple Alices and Bobs with the aid of steering criterion shown in Eq. (5). For qubits, the Werner state is given by [41]

$$\begin{aligned} \rho \left( \mu \right) =\mu \vert \psi \rangle \langle \psi \vert +(1-\mu ) \frac{I}{4}, \end{aligned}$$
(6)

where \(\vert \psi \rangle \!=\!\frac{1}{\sqrt{2}}(\vert 01\rangle -\vert 10\rangle )\) is the singlet state, I is the identity matrix and \(\mu \in [0,1]\).

According to the symmetrical property of the state, it has been demonstrated that the optimal measurement settings for any Alice and Bob are defined by the directions through antipodal pairs of vertices of a regular polyhedron [42]. Thus, we can get 2, 3, 4, 6, 10 measurement settings from the square, octahedron, cube, icosahedron, and dodecahedron, respectively. And it can be further increased by combining the measurement directions from above five regular polyhedrons. In combination with the measurement directions of the icosahedron and dodecahedron, the 16 measurement settings can be obtained [43].

For the case of multiple Alices and a single Bob, the state sharing among the i-th Alice and the single Bob in the case of \(N=2\) settings becomes

$$\begin{aligned} \rho _2^{i,1}=\left( \begin{array}{cccc}\frac{1-x}{4} &{}\quad 0 &{}\quad 0 &{}\quad \frac{-x+z}{4}\\ 0 &{}\quad \frac{1+x}{4} &{}\quad -\frac{x+z}{4} &{}\quad 0\\ 0 &{}\quad -\frac{x+z}{4} &{}\quad \frac{1+x}{4} &{}\quad 0\\ \frac{-x+z}{4} &{}\quad 0 &{}\quad 0 &{}\quad \frac{1-x}{4}\end{array} \right) , \end{aligned}$$
(7)

where \(x\!=\!\frac{1}{2^{i\!\!-\!1}}\mu \!\prod \nolimits _{1\le j\le i\!-\!1}(1\!+\!\sqrt{1\!-\!{\lambda _j}^2})\in [0,1]\) and \(z\!=\!\mu \prod \nolimits _{1 \le j\le i\!-\!1}(\sqrt{1\!-\!{\lambda _j}^2})\in [0,1]\), \( i\in \lbrace 1,2,\ldots ,m\rbrace \). The j is positive integer, and its minimum value is 1, while the shared state for \(N\ge 3\) settings keeps the Werner state’s form:

$$\begin{aligned} \rho _N^{i,1}=\mu '\vert \psi \rangle \langle \psi \vert +(1-\mu ') \frac{I}{4}, \end{aligned}$$
(8)

where \(\mu '\!=\!\frac{1}{3^{i\!-\!1}}\mu \prod \nolimits _{1\le j\le i\!-\!1}(1\!+2\!\sqrt{1\!-\!{\lambda _j}^2})\) \(\in [0,1]\). Obviously, the shared state of each step remains symmetrical; thus, the N-setting steering inequality Eq. (5) is a sufficient and necessary criterion, which can be rewritten as:

$$\begin{aligned} S_2^{i, 1}\!=\!\frac{1}{2^{i\!-\!1}}\mu \lambda _i\eta _1\prod \limits _{1\le j\le i\!-\!1}(1\!+\!F_{\lambda _j}), \end{aligned}$$
(9)

for \(N\!=\!2\) settings and

$$\begin{aligned} S_N^{i,1}\!=\!\frac{1}{3^{i\!-\!1}}\mu \lambda _i\eta _1\!\prod \limits _{1\le j\le i\!-\!1}(1\!+2F_{\lambda _j})\!, \end{aligned}$$
(10)

for \(N\!\ge \!3\) settings. \(F_{\lambda _j}\)=\(\sqrt{1\!-\!{\lambda _j}^2}\) represents the quality factors of related measurements. Similarly, the case of a single Alice and multiple Bobs can also be calculated.

For the case of multiple Alices and Bobs, considering the previous pair of observers adopting the matched measurements (if the Alice performs a measurement along \(\mathbf {m}_{k}\), the Bob should measure along the \(\mathbf {n}_{k}\)) to verify their state’s steering ability; here, we choose the optimal method to calculate the state shared by the i-th Alice and the p-th Bob, which can maximize the value of the steering parameter. We take the case that \( i\ge p>1\) for example, the shared state among the current i-th Alice and p-th Bob for \(N\!=\!2\) settings is same as the form of Eq. (7), while the values of x, z change to \(\frac{1}{2^{i\!-\!1}}\mu \prod \nolimits _{1\le j \le p\!-\!1}(1\!+\!F_{\lambda _{j\!+\!i\!-\!p}}\!F_{\eta _j})\prod \nolimits _{1\le l \le i\!\!-p}(1\!+\!F_{\lambda _l}) \in [0,1], \!\mu \prod \nolimits _{1\le j \le p\!-\!1}F_{\lambda _{j\!+\!i\!-\!p}}\!F_{\eta _j}\prod \nolimits _{1\le l \le i\!-\!p}F_{\lambda _l} \in [0,1]\), respectively. Then, the steering parameter can be written as:

$$\begin{aligned} S_2^{i,p}\!=\!\frac{1}{2^{i\!-\!1}}\mu \lambda _i\eta _p\!\prod \limits _{1\le j \le p\!-\!1}(1\!+\!F_{\lambda _{j\!+\!i\!-\!p}}\!F_{\eta _j})\!\prod \limits _{1\le l \le i\!-\!p}(1\!+\!F_{\lambda _l}), \end{aligned}$$
(11)

where the l is positive integer.

When \(N\!\ge \!3\), their shared state still follows the Werner state’s form of Eq. (8), where \(\mu '\!=\!\frac{1}{3^{i\!-\!1}}\mu \prod \nolimits _{1\le j \le p\!-\!1}(1\!+\!2\!F_{\lambda _{j\!+\!i\!-\!p}}\!F_{\eta _j})\prod \nolimits _{1\le l \le i\!-\!p}(1\!+\!2\!F_{\lambda _l})\) \(\in [0,1]\). And the steering parameter becomes

$$\begin{aligned} S_N^{i,p}\!=\!\frac{1}{3^{i\!-\!1}}\mu \lambda _i\eta _p\prod \limits _{1\le j \le p\!-\!1}(1\!+\!2\!F_{\lambda _{j\!+\!i\!-\!p}}\!F_{\eta _j})\prod \limits _{1\le l \le i\!-\!p}(1\!+\!2\!F_{\lambda _l}). \end{aligned}$$
(12)

The other case that \( p\ge i>1\) can be obtained with the same method.

Obviously, the unsharp measurement strategy used here is optimal. For Werner state, the classical bound \(C_N\!=\!\lbrace 1/\sqrt{2},\,1/\sqrt{3},\,1/\sqrt{3},\,0.5393,\,0.5236,\,0.503,\,0.5\rbrace \) when \(N\!=\!\lbrace 2,3,4,6,10,16,\infty \rbrace \), respectively [42, 44]. Since the classical bound of \(N\!=\!16\) is very close to that of infinite measurement settings, we implement \(N\!=\!\lbrace 2,3,4,6,10,16 \rbrace \) to investigate the behavior of quantum steering in this work.

3.1 Multiple Alices and a single Bob

Fig. 2
figure 2

The relationship between the maximum number of Alices \(N_A^\mathrm {max}\) who can share steering with a single Bob and the number of measurement settings N

Full size image

Firstly, we take multiple Alices and a single Bob as an example to explore how many observers in one part can simultaneously steer the state of a single observer in the other part in different settings. It is obvious that the steering parameter increases with the increase in current measurement sharpness and the decrease in previous measurement sharpness. Since the previous measurement may decrease the steerability of the current shared state, the measurement sharpness of the latter Alices would be increased to obtain enough information to show their steerability, i.e., \(\lambda _1<\lambda _2<,\cdots ,<\lambda _m\). And the steering sharing process can continue, with each latter Alice and Bob being able to violate steering inequality with the average shared state obtained from the previous stage, as long as \(\lambda _i\!<\!1\) and \(\eta _1\!<\!1\). From this condition, one can obtain the maximum number of Alices \(N_A^\mathrm {max}\) who can share steering simultaneously with a single Bob. The result is presented in Fig. 2. It is obvious that as the number of measurement settings N increases, the overall tendency of \(N_A^\mathrm {max}\) rises. We find at most 5 Alices can simultaneously steer Bob’s state when the number of measurement setting reaches 16. Interestingly, for some special case \(N_A^\mathrm {max}\) remains the same even if N increases (such as \(N\!=\!3,4\), or \(N\!=\!6,10\)). Note that it was conjectured in Ref. [36] that at most N Alices can exhibit steering with a single Bob by the violation of N-setting linear inequality. From our results, it seems that this conjecture is not true.

We further calculate the useful sharpness parameter regions for all possible sharing scenarios with the maximally entangled initial state. The results are summarized in Table 1. Here, we assume Bob performs sharp measurements when \(N_A\ge 3\) and the final Alice also performs sharp measurements when \(N_A\ge 2\), while in other cases, the observer’s measurements are unsharp. It clearly indicates that the useful measurement sharpness interval of these observers decreases with the number of Alices increasing and the number of the measurement settings decreasing. For the case of 2 Alices and a single Bob, we find the ranges of the first Alice’s sharpness \(\lambda _1\) and the first Bob’s sharpness \(\eta _1\) are, respectively, expanded about 2.3 and 2.9 times, as the number of measurement settings increases from 2 to 16, making it easier to apply directly to experiments.

Table 1 The range of different measurement sharpness, \(\lambda _{1}, \lambda _{2}, \lambda _{3}\) and \(\lambda _{4}\), when steering sharing is achieved for the pure initial shared state (\(\mu =1\)), where N is the number of measurement settings, and \(N_{A}\), \(N_{B}\) represent the number of Alices and Bob, respectively
Full size table

It should be noted that all the above results are restricted to a pure initial shared state. Considering the decoherence effect of environmental noise and the imperfection of the experimental device, we further investigate whether or not the steering correlation can be kept when the shared state is not pure any more. We find that it can be kept indeed. The minimum purity bound of the initial state \(\mu _\mathrm {min}\) is presented in the last column of Table 1. Obviously, for any possible steering sharing scenarios, there exist a finite continuous range of purity such that these Alices can share steering with Bob. And for a fixed number of observers, the more measurement settings, the greater the purity range and the stronger the robustness.

3.2 Multiple Alices and Bobs

Fig. 3
figure 3

a The schematic diagram for the 2 Alices and 2 Bobs is displayed via 3 or more settings measurement. Here, the arrow indicates the steering direction. b Steering parameters \(S_3^{i,p}\) (\(i\!=\!1,2\), and \(p\!=\!1,2\)) are presented for 3-setting measurements as a function of \(\lambda _{1}\) and \(\eta _{1}\). \(\lambda _{2}=1\) and \(\eta _{2}=1\) indicates that \(A_2\) and \(B_2\) implement the sharp measurements. The green, blue, red, and purple lines correspond to \(S_3^{1,1}\!=\!C_3\), \(S_3^{1,2}\!=\!C_3\), \(S_3^{2,1}\!=\!C_3\), and \(S_3^{2,2}\!=\!C_3\), respectively. The regions where the corresponding colored arrows point to indicate that the \(S_3^{1,1}\), \(S_3^{1,2}\), \(S_3^{2,1}\), and \(S_3^{2,2}\) exceed \(C_3\), respectively. c Displaying the steering parameters \(S_{16}^{i,p}\) (\(i\!=\!1,2\), and \(p\!=\!1,2\)) for 16-setting measurements versus \(\lambda _{1}\) and \(\eta _{1}\). Similarly, the regions where the corresponding colored arrows point to mean that the violation of linear inequality between \(A_1\)-\(B_1\), \(A_1\)-\(B_2\), \(A_2\)-\(B_1\), \(A_2\)-\(B_2\), respectively. The overlapping regions in b and c colored in yellow demonstrate the steering sharing among 2 Alices and 2 Bobs (Color figure online)

Full size image

In the previous section, we get the number limitation of Alice who can demonstrate steering with a single Bob. Now, we address the question of whether these Alices can further share steering with more Bobs. We find that it is not possible to increase the number of Bobs when the number of Alices reaches the maximum value in the single Bob scenario. However, we can reduce the number of observers on the one side to increase that on the other side and then make it possible that multiple Alices show steering with multiple Bobs. Counterintuitively, we find that at most 2 Alices can be simultaneously steered by 2 Bobs in the multiple Alices and Bobs scenario even if the total number of steering shared observers in the single Bob scenario is greater than 4 (see “Appendix” for more details).

Taking the first two Alices and Bobs as an example, the 2 Alices and 2 Bobs successful steering sharing scenario is depicted Fig. 3a and the relationship between the steering parameters and sharpness parameters in the case of 3-setting measurements and 16-setting measurements is presented Fig. 3b and c. The yellow region represents the valid ranges of \(\lambda _{1}\) and \(\eta _{1}\) where 2 Alices and 2 Bobs share steering at the same time. Due to the symmetrical property of the state, \(\lambda _{1}\) and \(\eta _{1}\) have the same ranges. For the 3-setting measurements, they both are [0.756(1), 0.802(5)] which is much smaller than the valid ranges of \(\lambda _{1}\) and \(\lambda _{2}\) in the case of 3 Alices and a single Bob with the same measurement settings, indicating it is harder to sharing quantum steering between multiple Alices and Bobs. However, one can improve its robustness by adding the measurement settings. Figure 3b and c shows that the useful ranges of \(\lambda _{1}\) and \(\lambda _{2}\) can be expanded more than 10 times as the measurement settings increase from 3 to 16.

4 Application

Note that if the disturbance caused by the former observer’s measurement is regarded as noise, our steering sharing protocol can also be applied to investigate the dynamic of steering in the presence of decoherence [44], such as steering sudden death and revival [45]. Especially, our 3 settings unsharp measurement strategy is essentially equivalent to the depolarizing channel. By changing the former observer’s measurement sharpness, the steering ability and direction of the current observers can be controlled. For example, in our 2 Alices and 2 Bobs steering sharing scenario, \(A_2\) and \(B_2\) can share steering if \(\lbrace \lambda _{1}, \eta _{1} \rbrace \) locates in left side of purple line (\(S_3^{2,2}=C_3\) ) in Fig. 3b, otherwise they cannot. If the initial Werner state is replaced by an asymmetric state [13] or \(A_1\) and \(B_1\) adopt some asymmetric measurements, a tunable \(\lbrace \lambda _{1}, \eta _{1} \rbrace \) further allows \(A_2\) and \(B_2\) to exhibit their steerabilities from both directions to only one direction.

5 Conclusion and discussion

In this work, we discuss a new steering sharing scenario, where half of an entangled pair is accessed by a sequence of Alices, and the other half is distributed to multiple Bobs. We address the question of how many pairs of Alice and Bob can demonstrate quantum steering by violating the N-setting steering inequality where \(N=2,3,4,6,10,16\). Contrary to the conjectured proposed by Sasmal et al. [36], we find at most 5 Alices can steer a single Bob and no more than 2 observers can be steered in the multiple Alices and Bobs scenario when the sharpness of the N-setting measurements that each Alice and Bob used is equal. We also provide the useful sharpness parameter ranges and the minimum purity of the initial state for different steering sharing cases and give evidence that they increase as the number of observers decreases and the number of measurement settings increases. The noise robustness of our sharing scenario makes our results applicable to the experimental demonstration. On the other hand, we show that our protocol can also be applied to investigate the dynamic of steering in a noise channel and even control the steering direction.

The shareable steering is a primary resource for some practical and commercial quantum information processing tasks where the general consumers may not want to trust their providers, such as, in the context of quantum internet [46], secret sharing [47], and random number generation [48]. It is thus of importance to further increase the shareable observers to utilize it for many times which could be realized by adopting multipartite entangled states [49] or allow the sequential observers in the above scenario to share some classical information. We will carry out some researches in these directions in the near future.