Rectangular surface code under biased noise

Abstract

To date, the surface code has become a promising candidate for quantum error correcting codes because it achieves a high threshold and is composed of only the nearest gate operations and low-weight stabilizers. Here, we have exhibited that the logical failure rate can be enhanced by manipulating the lattice size of surface codes that they can show an enormous improvement in the number of physical qubits for a noise model where dephasing errors dominate over relaxation errors. We estimated the logical error rate in terms of the lattice size and physical error rate. When the physical error rate was high, the parameter estimation method was applied, and when it was low, the most frequently occurring logical error cases were considered. By using the minimum weight perfect matching decoding algorithm, we obtained the optimal lattice size by minimizing the number of qubits to achieve the required failure rates when physical error rates and bias are provided .

1 Introduction

For the realization of quantum computing, errors that are induced when interacted with the environment should be detected using quantum error correction (QEC) codes. Two types of QEC codes such as circuit-based codes (Shor code, Steane code, RM codes, etc.) [1,2,3] and topological codes have been developed to protect the quantum states. In particular, because of the lower stabilizer weight than circuit-based codes and the nearest stabilizer measurement operation of topological codes, surface codes such as toric codes and color codes have become the main topics in several researches.

The earlier topological codes of Kitaev called toric codes have periodic boundaries and qubits that are located on the torus [4]. Surface codes with non-periodic boundaries which allow planar qubit location have been developed [5, 6]. The toric code can encode two logical qubits, and surface codes with non-periodic boundaries can encode one logical qubit using physical qubits. In both cases, the number of physical qubits scales as O($L^2$).

Recent QEC research focuses on the implementation and construction of the QEC codes [7, 8] by considering a biased noise error channel and other channels [9], by designing the efficient decoder using the machine learning [10, 11] techniques, and by improving the threshold below which the logical failure rate can be decreased. A framework that applies machine learning techniques for decoding and improves the logical error rate in the depolarizing noise channel is also proposed in [12]. Previous work by Panos et al. proposed a concatenated phase flip QEC code [13]. By employing the phase flip code as an inner code, the number of Z errors that induce logical Z error increases, and the logical operation can be performed with an outer code, such as an RM code or a topological code [14,15,16]. Tuckett et al. proposed an effective machine learning decoder in the surface code under a biased noise error channel by using X, Y stabilizer instead of X, Z stabilizer and thus obtained more information regarding Z errors [17,18,19]. This kind of biased error arises in superconducting qubits, quantum dots, and trapped-ion qubit systems.

In this study, we first explored a method for reducing the logical failure rate of the surface code with a non-periodic boundary when the noise was biased. In other words, Pauli Z errors occurred at a higher rate than Pauli X errors. We have proposed a larger weight of logical Z operator than logical X operator because logical Z(X) error occurs only due to Z(X) physical error. Thereafter, we analyzed the impact of the large weight of the logical Z operator on logical X error. We scaled the reduced logical failure rate using the lattice size and the physical error rate as parameters.

Secondly, we analyzed an overhead as a function of the single-qubit physical error rate and the logical failure rate. The number of qubits for rectangular surface code was calculated to minimize the overhead. As a result, the optimal lattice size for the required logical error rate could be derived. We simulated the performance of the optimal lattice size surface code to verify whether the code has achieved a given logical failure.

We applied the Edmonds’ minimum weight perfect matching (MWPM) algorithm [20, 21] to decode the surface codes; however, the expected alternative algorithms such as the machine learning (ML) decoder could be applied. Edmonds’ MWPM algorithm counts the weight of noise that causes the observed syndrome and performs error correction using the minimum weight error chain.

The remainder of this paper is organized as follows: In Sect. 2, we review some backgrounds of the surface code and introduce the noise model. In Sect. 3, we present the rectangular surface codes. Section 4 describes the simulation results, and we conclude in Sect. 5.

Fig. 1

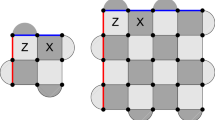
Representation of a $d=5$ surface code with boundaries, where d is the code distance. The edges represent data qubits. Vertexes($A_v$) and plaquettes($B_p$) represent the measurement qubits. Each vertex and plaquettes stabilizers are composed of X and Z operators, respectively. Rough boundaries are the upper and lower boundaries, and smooth boundaries are the right and left boundaries, respectively. a $L \times L$ square surface code, b $(L+1) \times L$ square surface code

2 Surface code and biased noise

2.1 Surface code

The surface code with boundaries is defined on the $L \times L$ square lattice or $(L+1) \times L$ square lattice having the data qubits on the edges, the Z-stabilizers on the vertexes, and the X stabilizers on the plaquettes as shown in Fig. 1. The $(L+1) \times L$ lattice can be interpreted as the square lattice because it has the same number of qubits between boundaries. We consider $L \times L$ square lattice as the square lattice in this paper. Stabilizers that are located at the boundaries operate on the three nearest data qubits, but otherwise on the four qubits, and detect X, Z errors, respectively,

$$\begin{aligned} A_v = \otimes _{i \in v} X_i, B_p = \otimes _{j \in p} Z_i. \end{aligned}$$

(1)

Boundaries adjacent to the X-stabilizers (Z-stabilizers) are defined as smooth (rough) boundaries. We denote the logical state of the surface code by $\big |\varPsi \big \rangle _L$ and stabilizers by $S = \{ A_v,B_p \}$.

$$\begin{aligned} S_i \big |\varPsi \big \rangle _L= \big |\varPsi \big \rangle _L. \end{aligned}$$

(2)

Logical operators that are homologically non-trivial chains are operators that connect smooth or rough boundaries. Logical X (Logical Z) connects smooth (rough) boundaries. By applying physical X(Z) operation on the edges in logical operators, logical operators can be performed. Let us denote Logical X by $X_L$ and Logical Z by $Z_L$. The minimum weight of the logical operator defines the code distance (d), and $d=5$ surface code with boundaries is shown in Fig. 1.

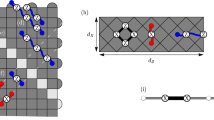
X(Z) physical errors were detected via Z(X) stabilizer measurement, and the measurement outcome is referred to as syndromes. If an even number of errors occur at the qubits around certain stabilizers, then the measurement outcome is zero; else, the measurement outcome is one. The set of all errors on the lattice is called chain E, and the MWPM algorithm searches for the minimum weight error chain $E'$, where $C=E+E'$ is a cycle. Decoding is successful if C is homologically trivial (Fig. 2a), and it fails if C is homologically non-trivial (Fig. 2b).

Fig. 2

E is the error chain, and $E'$ is the minimum weight error chain that is obtained from the decoder. a chain $C=E+E'$ is homologically trivial, and errors are properly corrected. b chain $C=E+E'$ is homologically non-trivial, and the physical error causes logical Z error

2.2 Biased noise

One of the commonly used single-qubit noise models supposes the probability of X error, and that of Z error is equal. Y error occurs when X, Z errors occur simultaneously. However, in many qubit systems, the dephasing error arises more frequently than the relaxation error [22,23,24]. Therefore, this study considers the Z error biased noise channel. Let us denote the Z(X) error probability by $p_Z$($p_X$). For a biased channel,

$$\begin{aligned} p_Z>p_X. \end{aligned}$$

The physical error probability is the sum of both Z and X error probabilities,

$$\begin{aligned} p_{phy}=p_Z+p_X, \end{aligned}$$

(3)

and Bias($\eta$) is the ratio of $p_Z$ to $p_X$

$$\begin{aligned} \eta = {{p_Z}\over {p_X}}. \end{aligned}$$

(4)

This paper presents the logical error and overhead reduction in the biased error channel schemes without any ML decoders or concatenation.

Fig. 3

$7 \times 5$ rectangular surface code. Logical Z(X) operator is defined by connecting rough (smooth) boundaries. The weight of logical Z is 7, and the weight of logical X is 5

3 Rectangular surface code

The rectangular surface code is defined on the $L_1 \times L_2$ lattice with data qubits on edges and the stabilizers on vertexes and plaquettes. Figure 3 is an example of a $7\times 5$ rectangular surface code. Similar to the square surface code (Fig. 1), the logical operator is a chain that connects the same boundaries. However, the weight of the logical Z operator that connects the rough boundaries differs from that of the logical X operator that connects the smooth boundaries. In other words, the minimum weight of the logical Z relies on the vertical length of the lattice and is $L_1$, and the minimum weight of the logical X relies on the horizontal length of the lattice and is $L_2$.

The higher weight of the logical Z operator than that of the logical X operator contributes to the robustness of a logical Z error because the number of the physical Z errors that cause the logical error increases, while this code is weaker to the logical X error than the square $L_2 \times L_2$ surface code. For $5 \times 5$ square surface codes, the minimum number of the Z errors, which leads to a logical Z error, is three. For $7 \times 5$ rectangular surface codes, three physical Z errors can be corrected, and four physical Z errors are required to introduce logical Z errors.

Figure 4 depicts a $1 \times 3$ surface code which is equivalent to 3 qubit bit-flip code and $2 \times 3$ surface codes. Although the $1 \times 3$ code cannot correct any two physical X errors, and the $2 \times 3$ code can correct some of them, more paths for logical X error exist in a $2 \times 3$ rectangular code. Because any X errors with a weight two introduce the logical error in $1 \times 3$ surface code, the logical X error rate for the $1 \times 3$ surface code can be estimated as

$$\begin{aligned} P_{L_{x,1 \times 3}} = _{3}\mathrm {C}_{2} p^2(1-p) + _{3}\mathrm {C}_{3} p^3. \end{aligned}$$

For the $2 \times 3$ surface code, Fig. 4b depicts all two physical X error patterns and the first two patterns conclusively lead to logical errors after decoding. The number of paths includes the symmetry of error cases. The logical X error rate for a $2 \times 3$ surface code is larger than the rate estimated by considering only two physical X errors: $P_{L_{x,2 \times 3}} > 6 p^2(1-p)^6$. For $p_X < 0.12$,

$$\begin{aligned} P_{L_{X,1 \times 3}} < P_{L_{X,2 \times 3}} \end{aligned}$$

which means that below the threshold, $P_{L_X}$ worsens as $L_2$ increases. Thus, under a biased error channel, manipulation of the lattice size can decrease the logical failure rate using the same number of data and measurement qubits. When an error is biased to dephasing, the probability of the logical X error is considerably smaller than that of the logical Z error, and the rectangular surface code that has a longer vertical length than the horizontal length can perform better than a square surface code.

Fig. 4

a Error pattern that a $1 \times 3$ rectangular surface code can have from two physical X errors and the number of error path. b Error pattern that a $2 \times 3$ rectangular surface code can have from two physical X errors. By considering symmetry, each pattern includes at most four different error paths. The total number of paths is $_{8}\mathrm {C}_{2}$, and six paths lead to logical X errors

The number of qubits required to encode information depends on the lattice size. $L \times L$ square surface codes require $4L^2-4L+1$ qubits, where there exist $2L^2-2L+1$ data qubits and $2L^2-2L$ stabilizer measurement qubits, and $L_1 \times L_2$ rectangular surface codes require $4L_1 L_2-2L_1-2L_2+1$ qubits, where there exist $2L_1 L_2-L_1-L_2+1$ data qubits and $2L_1 L_2-L_1-L_2$ stabilizer measurement qubits. In some lattice sizes, the number of physical qubits comprising square and rectangular lattices is equal or similar. For example, both $5 \times 25$ rectangular surface code and $11 \times 11$ square surface code require 441 physical qubits.

We determined the value of $L_1$ and $L_2$ by considering the total logical failure rate and bias in this study.

3.1 Failure rate estimation

Let us denote the logical Z error rate as $P_{L_Z}$, logical X error rate as $P_{L_X}$, and failure rate as $P_{fail}$. The failure rate contains cases that have any logical error. Because we consider physical X errors and physical Z errors as independently occurring errors, $P_{L_Z}$ and $P_{L_X}$ are also independent. Therefore, $P_{fail}$ can be written as

$$\begin{aligned} \begin{aligned} P_\text {{fail}}&= 1- (1-P_{L_Z} )(1-P_{L_X} )\\&= P_{L_Z}+P_{L_X}-P_{L_Z} P_{L_X}. \end{aligned} \end{aligned}$$

(5)

3.2 Logical error rate estimation

The logical error rate for square surface code is known to be affected by the lattice size and the physical qubit error rate. Similarly, the logical error rate of rectangular surface code can be represented as a function of lattice sizes $L_1$, $L_2$, and the physical error rate, $p_{phy}$.

As in [25], we estimated the logical error rate in the two regions. The first is the region where the physical X(Z) error rate is significantly low, ($p_X(p_Z) < p_{X,low}(p_{Z,low})$), so that most of the logical X(Z) error is caused by $\lceil L_1/2 \rceil$($\lceil L_2/2 \rceil$) errors. As a result, the logical error rate can be approximated as

$$\begin{aligned} \begin{aligned} P_{L_X}&= L_2 {L_1! \over {{\lceil L_1/2 \rceil }!{\lfloor L_1/2 \rfloor }!}}p_X^{\lceil L_1/2 \rceil }\\ P_{L_Z}&= L_1 {L_2! \over {{\lceil L_2/2 \rceil }!{\lfloor L_2/2 \rfloor }!}}p_Z^{\lceil L_2/2 \rceil }. \end{aligned} \end{aligned}$$

(6)

The first factor $L_2(L_1)$ is the number of the minimum weight logical X(Z) operators. The second factor is the binomial coefficient, which counts the number of weight $\lceil L_1/2 \rceil$($\lceil L_2/2 \rceil$) error patterns along with the minimum weight logical X(Z) operators. By using Stirling’s approximation, $n! \approx \sqrt{2\pi n} ({{n} \over {e}})^n$, the logical error rate can be modified to

$$\begin{aligned} \begin{aligned} P_{L_X}&\approx L_2 \sqrt{{{2L_1} \over {\pi (L_1+1)^2}} \times ({{4L_1^2} \over {L_1^2-1} })^{L_1}}p_X^{\lceil L_1/2 \rceil }\\ P_{L_Z}&\approx L_1 \sqrt{{{2L_2} \over {\pi (L_2+1)^2}} \times ({{4L_2^2} \over {L_2^2-1} })^{L_2}}p_Z^{\lceil L_2/2 \rceil }. \end{aligned} \end{aligned}$$

(7)

The second region is the high physical error rate region ($p_X(p_Z) > p_{X,high} (p_{Z,high}$), but below the threshold that is between 0.1 and 0.11. The estimation is based on a simulation using polynomial, exponential, and log functions. We estimated the logical Z error rate first, and thereafter, analogously estimated logical X error rate. Below the threshold, the logical error rate depends exponentially on the vertical lattice size [25, 26] and can be expressed as

$$\begin{aligned} \begin{aligned} ln(P_{L_Z}) = \alpha _Z(L_1,p_Z) \times L_2 + \beta _Z(L_1,p_Z) \end{aligned} \end{aligned}$$

(8)

where $\alpha _Z(L_1,p_Z)$ and $\beta _Z(L_1,p_Z)$ are the functions of $L_1$ and $p_Z$. At the same time, the logical error rate linearly depends on the horizontal lattice size (Fig. 5). Therefore, we assume that

$$\begin{aligned} \begin{aligned} \alpha _{Z}(L_1,p_Z)&= \alpha _{Z}(p_Z) \\ \beta _{Z}(L_1,p_Z)&= log(\beta _{Z1}(p_Z)\times L_1+ \beta _{Z2}(p_Z))\\ ln(P_{L_Z})&= \alpha _{Z}(p_Z)L_2 + log(\beta _{Z1}(p_Z)\times L_1+ \beta _{Z2}(p_Z)) \end{aligned} \end{aligned}$$

(9)

where $\alpha _{Z}(p_Z)$, $\beta _{Z1}(p_Z)$, and $\beta _{Z2}(p_Z)$ are functions of $p_Z$.

Fig. 5

Dependence of the logical error rate $P_{L_Z}$ on $L_1$ for $p_Z=0.05,0.07,0.09,0.11$. Color infers vertical lattice sizes.a $p_Z$ = 0.05 b $p_Z$ = 0.07 c $p_Z$ = 0.09 d $p_Z$ = 0.11

$\alpha _{Z}(p_Z), \beta _{Z1}(p_Z)$, and $\beta _{Z2}(p_Z)$ can be acquired via a numerical fitting over a wide range of $L_1$, $L_2$, and we assumed that

$$\begin{aligned} \begin{aligned} \alpha _{Z}(p_Z)&= \alpha _{Z11}(p_Z - \alpha _{Z12})^2 + \alpha _{Z13} \\ \beta _{Z1}(p_Z)&= \beta _{Z11}p_Z + \beta _{Z12}\\ \beta _{Z2}(p_Z))&= \beta _{Z21}(p_Z - \beta _{Z22})^2 + \beta _{Z23} \end{aligned} \end{aligned}$$

(10)

where $\alpha _{Z11}$, $\alpha _{Z12}$, $\alpha _ {Z13}$, $\beta _{Z11}$, $\beta _ {Z12}$, $\beta _{Z21}$, $\beta _{Z22}$, $\beta _{Z23}$ are constants.

$\alpha _{Z11}$, $\alpha _{Z12}$, $\alpha _ {Z13}$, $\beta _{Z11}$, $\beta _ {Z12}$, $\beta _{Z21}$, $\beta _{Z22}$, $\beta _{Z23}$ can be acquired via numerical fitting over a wide range of $L_1$, $L_2$, and $p_Z$. Consequently, the logical Z error rate can be approximated as

$$\begin{aligned} \begin{aligned} ln(P_{L_Z})&= (c_1(p_Z-c_2)^2+c_3)L_2 +ln((c_4p_Z+c_5)L_1 \\&\quad + c_6(p_Z-c_7)^2+c_8)) \end{aligned} \end{aligned}$$

(11)

where $c_i, 1 \le i \le 8$ are constants in Eq. (10) and are determined via parameter estimation. The logical X error rate can be estimated analogously to the logical Z error rate.

$$\begin{aligned} \begin{aligned} ln(P_{L_X})&= (c_1(p_X-c_2)^2+c_3)L_1 +ln((c_4p_X+c_5)L_2 \\&\quad + c_6(p_X-c_7)^2+c_8)). \end{aligned} \end{aligned}$$

(12)

We generated $0.05 \le p_Z \le 0.11$ at the intervals of 0.01, and odd lattice sizes in the range of $9 \le L_1$, $L_2 \le 21$ data set. Each data set is performed $N = 10^5$ times, and the logical error rate is $N_f \over N,$ where $N_f$ is the number of trials that the logical error occurs. These data sets are employed for the parameter $c_i, 1 \le i \le 8$ estimation. The detailed process is presented in Appendix 1.

Figure 6 shows the estimated $P_{L_Z}$ plot. X-axis is the physical Z error rate, and Z-axis is the logical Z error rate. The solid line is the estimated logical error rate function, and each circle is the simulation data set. The color infers vertical lattice sizes.

Given $p_{phy}$ and $\eta$, the physical X and Z error rates can be written as

$$\begin{aligned} \begin{aligned} p_X&= {{1} \over {\eta +1}} p_{phy}\\ p_Z&= {{\eta } \over {\eta +1}} p_{phy} \end{aligned} \end{aligned}$$

(13)

from Eq. (3-4). Substituting $p_X$ and $p_Z$, given by Eq. (13) into Eq.(7,11-12), yields an expression for $P_{L_X}$ and $P_{L_Z}$ in terms of lattice size, physical error rate, and bias.

$$\begin{aligned} \begin{array}{ll} P_{L_X} &{}=\left\{ \begin{array}{ll} L_2 \sqrt{{{2L_1} \over {\pi (L_1+1)^2}} \times ({{4L_1^2} \over {L_1^2-1} })^{L_1}}({{1} \over {\eta +1}} p_{phy})^{\lceil L_1/2 \rceil } &{} {for} \quad {p_X< p_{X,low}}, \\ \\ \text {exp}[{(c_1({{1} \over {\eta +1}} p_{phy}-c_2)^2+c_3)L_1}] \\ \times [({{c_4} \over {\eta +1}} p_{phy}+c_5)L_2 + c_6({{1} \over {\eta +1}} p_{phy}-c_7)^2+c_8)] &{} {for} \quad {p_X> p_{X,high} }. \end{array}\right. \\ \\ P_{L_Z}&{}=\left\{ \begin{array}{ll} L_1 \sqrt{{{2L_2} \over {\pi (L_2+1)^2}} \times ({{4L_2^2} \over {L_2^2-1} })^{L_2}}( {{\eta } \over {\eta +1}} p_{phy})^{\lceil L_2/2 \rceil } &{} {for} \quad {{p_Z < p_{Z,low} }}, \\ \\ \text {exp}[{(c_1({{\eta } \over {\eta +1}}p_{phy}-c_2)^2+c_3)L_2}]\\ \times [({{c_4\eta } \over {\eta +1}} p_{phy}+c_5)L_1 + c_6({{\eta } \over {\eta +1}} p_{phy}-c_7)^2+c_8)] &{} {for} \quad {p_Z > p_{Z,high} }. \end{array}\right. \end{array}\nonumber \\ \end{aligned}$$

(14)

3.3 The validity of the two regimes

The logical error rate is estimated in two regions: a low error rate region and a high error rate region. The dividing physical error rate can be calculated by considering the distribution of the number of errors [25]. Let us denote the weight of the error chains as $\left| E \right|$. $\mu$ and $\sigma$ denote the expected value and deviation of $\left| E \right|$, respectively,

$$\begin{aligned} \begin{aligned} \mu&= 2L_1L_2 - L_1 - L_2 \approx 2L_1L_2,\\ \sigma ^2&= \mu p(1-p) \approx 2L_1L_2p(1-p) \end{aligned} \end{aligned}$$

(15)

where p is $p_z$ and $p_x$ for $P_{L_Z}$ and $P_{L_X}$ region validation, respectively. Assuming that the mean number of errors on the lattice must be two standard deviations below $\lceil L_2/2 \rceil$($\lceil L_1/2 \rceil$) leads to a low error rate region.

$$\begin{aligned} \begin{aligned} \mu + \sigma< {\lceil { L_2 \over 2}\rceil } \\ \mu + \sigma < {\lceil { L_1 \over 2}\rceil }. \end{aligned} \end{aligned}$$

(16)

$p_{Z,low}$ is extracted from the first formula in Eq.(16), and $p_{X,low}$ is extracted from the second formula in Eq.(17). By substituting Eq.(15) into Eq.(16), the low error region $p_Z< p_{Z,low}$, $p_X< p_{X,low}$ can be defined as

$$\begin{aligned} \begin{aligned} p_{Z,low}&= {{2L_1L_2+4L_1-\sqrt{8L_1^2L_2-2L_1L_2}} \over {8L_1^2L_2}}\\ p_{X,low}&= {{2L_1L_2+4L_2-\sqrt{8L_1L_2^2-2L_1L_2}} \over {8L_1L_2^2}}. \end{aligned} \end{aligned}$$

(17)

Similar to the low error rate regime, the high error rate regime can be defined by $\mu - \sigma> {\lceil { L_2 \over 2}\rceil }, \mu - \sigma > {\lceil { L_1 \over 2}\rceil }$ which leads to

$$\begin{aligned} \begin{aligned} p_{Z,high}&= {{2L_1L_2+4L_1+\sqrt{8L_1^2L_2-2L_1L_2}} \over {8L_1^2L_2}}\\ p_{X,high}&= {{2L_1L_2+4L_2+\sqrt{8L_1L_2^2-2L_1L_2}} \over {8L_1L_2^2}}. \end{aligned} \end{aligned}$$

(18)

By identifying which region the physical X, Z error rates are included, the logical error rate is to be estimated.

Fig. 6

Estimated logical error rate $P_{L_z}$ plot for the high error rate region. The circles are $N = 10^5$ simulation data set. Solid line is estimated logical Z error rate. Color infers vertical lattice sizes. a $L_1$ = 15 b $L_1$ = 17 c $L_1$ = 19 d $L_1$ = 21

3.4 Optimal lattice size based on logical failure rate

To obtain the optimal lattice size($L_{1,opt}, L_{2,opt}$) when the target logical failure rate($P_{f,target}$) and the physical error rate have been provided, we solve the following optimizing problem:

$$\begin{aligned} \begin{aligned}&\underset{L_1,L_2}{\arg \min }&4L_1L_2 - 2L_1 - 2L_2 +1 \\&\text {s.t.}&P_{fail} \le P_{f,target} \end{aligned} \end{aligned}$$

(19)

where $P_{fail}$ can be formulated from Eq. (5, 14). The optimizing function is the number of total qubits, and the constraint is to ensure that the estimated failure rate of the surface code is below the target failure rate. For diverse $P_{f,target}$, $\eta$, and $p_{phy}$, the optimal lattice sizes, $L_{1,opt}$ and $L_{2,opt}$, are listed in Table 1. For $10^{-2}$ target failure rate, $p_x$ and $p_z$ are in the high error rate region. For $10^{-16}$ target failure rate, $p_x$ and $p_z$ are in the low error rate region.

Table 1 Estimated optimal lattice sizes for the various target failure rate, bias, and physical error rates. The optimal lattice size is obtained from solving optimization problem Eq. (19). $P_{f,target}$ is the target logical failure rate. $L_{1,opt}$ and $L_{2,opt}$ are the optimal horizontal and vertical lattice size

4 Numerics

We first ran $N=10^6$ simulation and compared the rectangular and square lattice surface code’s failure rate using a similar number of qubits as shown in Table 2. We set that the number of qubits used in square surface codes is slightly larger than that used in rectangular surface codes for the $\eta$ and $p_{phy}$. $P_{f, rect}$ is the rectangular lattice surface code’s failure rate when $N=10^6$ trial is performed, and $P_{f, square}$ is the square lattice surface code’s failure rate. The results show that the rectangular surface codes perform better than square surface codes in terms of logical failure rate under the biased noise channel, although the rectangular surface codes consume more resources. When $\eta = 2.5$ and $p_{phy} = 0.11$, the ratio of the square surface code’s failure rate to the rectangular code’s failure rate, $P_{f,square}/P_{f,rect}$, is 4.37. This ratio is larger than 6 when $\eta = 2.5$ and $p_{phy} = 0.08$, which is the maximum value in Table 2.

Second, we compared the number of qubits to achieve the target error rate for rectangular and square lattice surface codes. The optimized lattice sizes of rectangular and square surface codes are extracted from Eq.(19) to perform the simulation. It is verified whether the optimal lattice size surface code achieves target error rate by performing $N=10^6$ simulations in Table 3. We set $10^{-2}$, $10^{-3}$ as target failure rates, 2.5, 2 as bias, and 0.1, 0.08 as physical error rates. We ran $N = 10^6$ simulations for the estimated optimal lattice size surface codes and verified that the failure rates of the optimal lattice size surface codes are below the target failure rates. The physical error rates are within the high error rate region for the extracted optimal lattice size. By adopting the rectangular surface codes, the number of total qubits decreases significantly. To achieve $10^{-2}$ logical failure rate under $\eta =2$ and $p_{phy}=0.1$, the rectangular surface code requires 493 qubits, whereas the square surface code requires 1369 qubits, resulting in 64% resource reduction. In other cases, the rectangular surface codes decrease qubit resources 36% to 54% times compared to square lattice surface codes.

Table 2 $N = 10^{6}$

Table 3 $N = 10^{6}$

5 Conclusion

We have demonstrated a method for constructing a rectangular surface code when the noise is biased. Enlarging the minimum weight of logical Z operator and shortening the weight of logical X operator reduce the failure rate compared to the square structure for the same or similar number of physical qubits by exploiting noise bias. The estimation of the logical failure rates of rectangular surface codes was performed based on the simulations when the physical error rate was high. When the physical error rate was low, it was calculated by considering the most frequently occurring cases of logical errors. This estimation is the upper bound for logical error rate because only parts of the logical error occurring cases are considered. Therefore, we expect that using the larger lattice size achieves the target error rate under the low error rate region. Each error rate region has been expressed in terms of the lattice sizes.

By $N=10^6$ simulation data set, we have provided strong evidence for our proposal that improves the failure rate using fewer number of qubits. In the case that $p_{phy}$ = 0.08 and $\eta = 2.5$, the failure rate of our proposal is 6.3 times lower than that of the previous $L \times L$ square surface code. For the other cases, the failure rate of our scheme is from 2.1 to 4.4 times lower than that of the square lattice surface codes.

Secondly, we have presented the optimal lattice size for given logical error rates and the physical error rate by calculating the overhead to encode logical information. The estimation was verified over a wide range of physical error rates in the high error rate region and lattice sizes with $N=10^6$ simulation data set. To obtain $P_{fail}=10^{-2}$ under $\eta = 2.5$ and $p_{phy} = 0.1$, 493 qubits are required for the rectangular surface code, whereas 1369 qubits are used for the square surface codes. For other cases, our scheme requires 36% to 54% number of qubits compared to the square surface codes to achieve diverse target failure rates.

We have employed the MWPM decoder to obtain our failure rate; however, it is not the most efficient decoder. We anticipate that using a different decoder [10, 11] such as the machine learning decoder can achieve the lower failure rate, and therefore, the number of physical qubits can decrease further.

Appendix 1. Logical error rate estimation for high physical error rate

In Sect. 3.2, we estimated the logical error rate for the high physical error rate as in Eq. (12,13). This appendix exhibits how these equations are obtained from $N = 10^5$ data set.

Fig. 7

Dependence of $\alpha _Z(L_1,p_Z)$ on $L_1$. $\alpha _Z(L_1,p_Z)$ was assumed to be independent on $L_1$

Fig. 8

Dependence of $\alpha _Z(p_Z),\beta _{z_1}(p_z),\beta _{z_2}(p_z)$ on $p_z$. $\alpha _Z(p_Z)$ and $\beta _{z_2}(p_z)$ were assumed to be quadratic functions, and $\beta _{z_1}(p_z)$ was assumed to be a linear function

To determine the logical error rate $P_{L_Z}$, we numerically simulated the error correction protocol using the MWPM decoder for p in the range of $0.05 \le p \le 0.11$, and for $L_1$ and $L_2$ in the range of $9 \le L_1,L_2 \le 21$. It is known that the logical error rate depends exponentially on the vertical lattice size, and thus, Eq. (8) has been formulated. Figure 7 shows dependence of $\alpha _Z(L_1,p_Z)$ on $L_1$ for various $p_Z$. Considering linear dependence of $P_{L_Z}$ on $L_1$, we assumed that $\alpha _Z(L_1,p_Z)$ is independent on $L_1$.

$$\begin{aligned} \begin{aligned} ln(P_{L_Z})&= \alpha _Z(p_Z)L_2 + \beta _Z(L_1,p_Z)\\&= \alpha _Z(p_Z)L_2 + log(\beta _{Z1}(p_Z)L_1 + \beta _{Z2}(p_Z)) \end{aligned} \end{aligned}$$

(20)

Figure 8 shows the estimated values of $\alpha _Z(p_Z)$, $\beta _{Z1}(p_Z)$, and $\beta _{Z2}(p_Z)$, where these values were obtained by parameter estimation using $L_1$,$L_2$, and simulated logical error rate data set as input data. These parameters were estimated using linear and quadratic functions in Eq. (10), and Eq. (11) is derived from Eq. (10). Each constant $c_1 = -65.727, c_2 = 0.122, c_3 = -0.0682, c_4 = -0.172, c_5 = 0.065, c_6 = 0.190, c_7 = -6.070, c_8 = -7.407$ has been acquired by the parameter estimation using $L_1, L_2, p_Z$, and the logical error rate simulation data set as input data. Solid line in Fig. 6 is plotted by substituting these constants to Eq. (11).