1 Introduction

Nonlocality is one of the most fundamental properties of quantum theory. In recent years, nonlocal correlations were found to be useful in many applications in quantum information theory; see, e.g., [3, 5, 6, 9,10,11, 13, 21, 24]. Initially, nonlocality was considered in a bipartite case. In this scenario, violation of Bell’s inequalities is treated as an argument that the quantum world is nonlocal. The analysis of nonlocal correlations was extended to multipartite case by Mermin [17]. However, in this case, the structure of nonlocal correlation is much more interesting than in a bipartite case. Indeed, for example in the tripartite case, one can distinguish in the set of all nonlocal correlations the subset of genuine tripartite nonlocal correlations, i.e., such nonlocal correlations that cannot be reduced to bipartite ones. Svetlichny inequality was introduced to study genuine tripartite nonlocality [23]. This inequality gives an upper bound to the linear combination of the correlation of eight quantities measured by three independent observers. The violation of the Svetlichny inequality is a sufficient condition of genuine tripartite nonlocality.

In 1994, Popescu [20] discovered that the lack of nonlocality can be detected using sequential measurements for one copy of the states, while Peres in 1996 [19] gave an alternative solution by detecting violation Bell inequalities by means of collective measurements on several identical copies of the same quantum state. The second approach with time began to be called activation of quantum nonlocality. We deal with activation when the lack of a certain property of each component is accompanied by the presence of this property in a system that includes both components as elements of a certain whole.

The activation of the Svetlichny inequality means that a single copy of a given state does not violate the inequality for any measurement setting while two copies of this state violate the inequality. Therefore, one has to find a class of states for which a single copy does not violate the Svetlichny inequality while two copies of this state violate it.

It is worth to stress here that the determination of the maximal value of the Svetlichny operator with the help of numerical methods is a very delicate problem, especially in the context of the activation of the Svetlichny inequality. The reason is that when we find a maximum by means of numerical procedure, it is very hard to prove that this maximum is the global one. Therefore, when we show numerically that the maximal value of the Svetlichny operator is less than 4 for one copy of a state, we can usually treat it only as an indication of the fact that the Svetlichny inequality is not violated in this state for any measurement setting, but not as a proof. On the other hand, to prove that two copies of the state violate the Svetlichny inequality, it is enough to find only one instance, numerical procedures are very well suited for this purpose.

Taking the above considerations into account in our previous paper [7, 8], we have shown that the violation of the Svetlichny inequality can be activated for a class of GHZ states. We considered GHZ states because for these states the maximum value of the Svetlichny operator for a single copy of the state was determined analytically in [1]. Moreover, due to the very simple form of the white noise, we were able to show that noisy GHZ states of the form \((1-p)\rho _\mathrm{GHZ}+p I\) can also be activated for nonzero values of p [8]. We could not analyze different types of noise because of the difficulties described above. However, in the recent paper [15], Li et al. proposed the general method of determining the maximal value of the Svetlichny operator for arbitrary three-qubit state. Using their results in this paper, we extend the analysis of the noise resistance of activation of the violation of the Svetlichny inequality in GHZ states for various kinds of noise. In particular, we will analyze bit flip channels, phase flip channels, depolarizing channels and amplitude damping channels.

Let us notice here that the influence of noise on the violation of various tripartite Bell-type inequalities was investigated in the literature (see, e.g., [2, 14, 16, 22]). All of these authors consider one copy of a noisy tripartite state. For example, in the most recent paper [22], Singh and Kumar considered the effect of phase damping and depolarizing noise acting on two qubits from the three-qubit GHZ state. They established an analytical relation between the maximum expectation value of the Svetlichny operator, state parameter and noise parameter.Footnote 1

In our work, we consider a different problem and show that the violation of the Svetlichny inequality can be activated for a class of noisy GHZ states. We consider bit flip, phase flip, depolarizing and amplitude damping noise acting on one, two or three qubits. To solve this problem, it is necessary to analyze the violation of the Svetlichny inequality for two copies of the three-qubit noisy GHZ state.

2 The Svetlichny inequality

Let us remind first the notion and meaning of the Svetlichny inequality. We follow the notation used in our previous paper [7]. Let Alice, Bob and Charlie be three independent and distant observers who perform measurements on a tripartite system in a state \(\rho \). Alice can measure observables \(X_{1}\), \(X_{2}\), Bob \(Y_{1}\), \(Y_{2}\), and Charlie \(Z_{1}\) and \(Z_{2}\). Each of the observables \(X_{1}\), \(X_{2}\), \(Y_{1}\), \(Y_{2}\), \(Z_{1}\), \(Z_{2}\) has eigenvalues \(\pm 1\). Let P(abc|XYZ) denote the probability that observers obtain outcomes a, b and c provided that they measure observables X, Y and Z, respectively. Then, a tripartite correlation function is given by

$$\begin{aligned} E_{\rho }(XYZ)=\sum _{a,b,c}abcP(abc|XYZ)={{\,\mathrm{Tr}\,}}(\rho X\otimes Y\otimes Z). \end{aligned}$$
(1)

If probabilities P(abc|XYZ) cannot be written in the form

$$\begin{aligned} P(abc|XYZ)=\sum _{\lambda } f(\lambda )P_{\lambda }(a|X) P_{\lambda }(b|Y) P_{\lambda }(c|Z), \end{aligned}$$
(2)

where \(\lambda \) is a hidden variable with the probability distribution \(f(\lambda )\), \([f(\lambda )\in [0,1],\sum _{\lambda }f(\lambda )=1]\) and \(P_{\lambda }(a|X)\), \(P_{\lambda }(b|Y)\), \(P_{\lambda }(c|Z)\) are one-partite probability distributions, then the correlation function (1) is called nonlocal.

Bell’s inequalities are a necessary and sufficient condition for detecting two-partite nonlocality. In a tripartite case, situation is more complicated. As it was shown in [17], local correlation functions in a three-qubit state fulfill so-called Mermin inequality (its explicit form will be given below).

However, it is easy to see that probabilities that factorize into a product (one-party probability) \(\times \) (joint probability of two parties) are nonlocal although this nonlocality is purely two-partite. This observation leads us to the concept of a genuine tripartite nonlocality [23]. Namely, probabilities (and corresponding correlation functions) are called genuinely tripartite nonlocal if they cannot be written in the following form

$$\begin{aligned} \begin{aligned} P(abc|XYZ)=&\sum _{\lambda }f(\lambda )P_{\lambda }(a|X)P_{\lambda }(bc|YZ) +\sum _{\sigma }f(\sigma )P_{\sigma }(b|Y)P_{\sigma }(ac|XZ)\\&+\sum _{\tau }f(\tau )P_{\tau }(c|Z)P_{\tau }(ab|XY), \end{aligned} \end{aligned}$$
(3)

where \(f(\lambda ), f(\sigma ), f(\tau ) \in [0,1]\) and \(\sum _{\lambda }f(\lambda )+\sum _{\sigma }f(\sigma ) +\sum _{\tau }f(\tau )=1\). Correlation functions which arise from probabilities of the above form fulfill the Svetlichny inequality [23]. Therefore, the violation of the Svetlichny inequality is a sufficient condition of a genuine tripartite nonlocality.

Let us notice here that in recent years other definition of genuine tripartite nonlocality was introduced in [4, 12]. Activation of such a defined nonlocality was considered in [18]. In this paper, we restrict our attention to the standard Svetlichny notion of genuine tripartite nonlocality.

Let us introduce the following operator

$$\begin{aligned} M_{X_{1}X_{2}Y_{1}Y_{2}Z_{1}Z_{2}}(\rho )= {{\,\mathrm{Tr}\,}}[\rho (X_{2}Y_{1}Z_{1} + X_{1}Y_{2}Z_{1} + X_{1}Y_{1}Z_{2} -X_{2}Y_{2}Z_{2})], \end{aligned}$$
(4)

where \(X_{i},Y_{j},Z_{k}\) (\(i,j,k\in \left\{ 1,2\right\} \)) denote observables used by Alice, Bob and Charlie, respectively, and \(\rho \) is a three-qubit state defined in the Hilbert space \(\mathcal {H_{A}}\otimes \mathcal {H_{B}}\otimes \mathcal {H_{C}}= \mathbb {C}^{2}\otimes \mathbb {C}^{2}\otimes \mathbb {C}^{2}\). The explicit form of the Mermin and the Svetlichny inequalities is the following:

Mermin inequality:

$$\begin{aligned} M_{X_{1}X_{2}Y_{1}Y_{2}Z_{1}Z_{2}}(\rho )\le 2, \end{aligned}$$
(5)

Svetlichny inequality:

$$\begin{aligned} |S_{X_{1}X_{2}Y_{1}Y_{2}Z_{1}Z_{2}}(\rho )|\equiv |M_{X_{1}X_{2}Y_{1}Y_{2}Z_{1}Z_{2}}(\rho )+ M_{X_{2}X_{1}Y_{2}Y_{1}Z_{2}Z_{1}}(\rho )|\le 4. \end{aligned}$$
(6)

As we have described it in Introduction, to analyze the activation of the violation of the Svetlichny inequality for a given class of states, we should be able to determine analytically the maximal value of the Svetlichny operator (6), (5) for his class of states. Publication of the work [15] made it possible to determine the maximum value of the Svetlichny operator for a single copy of any three-qubit state.

Li et al. in [15] proved that for any three-qubit quantum state \(\rho \), the maximum quantum value of the Svetlichny inequality satisfies

$$\begin{aligned} \max |S_{X_{1},X_{2},Y_{1},Y_{2},Z_{1},Z_{2}}(\rho )|\le 4\lambda _{1}, \end{aligned}$$
(7)

where the maximum is taken over all \(2\times 2\) observables \(X_{1},X_{2},Y_{1},Y_{2},Z_{1},Z_{2}\) with eigenvalues \(\left\{ 1,-1\right\} \), \(\lambda _{1}\) is the maximum singular value of the matrix \(M=(M_{j,ik})\) with \(M_{ijk}={{\,\mathrm{Tr}\,}}[\rho (\sigma _{i}\otimes \sigma _{j}\otimes \sigma _{k})], i,j,k=1,2,3\).

3 Analysis of the superactivation of the Svetlichny inequality in the presence of noise

In this chapter, we analyze the activation of the violation of the Svetlichny inequality for the class of GHZ states in the presence of noise. We consider the GHZ states in the following form \(\rho _\mathrm{GHZ}=|\psi _\mathrm{GHZ}\rangle \langle \psi _\mathrm{GHZ}|\), where

$$\begin{aligned} |\psi _\mathrm{GHZ}\rangle =\cos \theta |000\rangle +\sin \theta \cos \theta _{3}|110\rangle +\sin \theta \sin \theta _{3}|111\rangle . \end{aligned}$$
(8)

Let us denote the maximum value of the Svetlichny operator in one copy of a given three-qubit state \(\rho \) by \(S^{(1)}_\mathrm{max}(\rho )\) (the maximum is taken over all possible observables used by Alice, Bob and Charlie) and by \(S_\mathrm{max}^{(2)}(\rho ^{\otimes 2})\) the maximum value of the Svetlichny operator attained in the state \(\rho ^{\otimes 2}=\rho \otimes \rho \). The analytical formula for \(S^{(1)}_\mathrm{max}(\rho _\mathrm{GHZ})\) as a function of parameters was found in [1]. In our previous papers [7, 8], we have shown that there exist such GHZ states for which \(S^{(1)}_\mathrm{max}(\rho _\mathrm{GHZ})<4\) while \(S_\mathrm{max}^{(2)}(\rho ^{\otimes 2}_\mathrm{GHZ})>4\). Moreover, due to the very simple form of white noise, we were able to find \(S^{(1)}_\mathrm{max}(\rho _\mathrm{wnGHZ})\) where

$$\begin{aligned} \rho _\mathrm{wnGHZ}=p \rho _\mathrm{GHZ}+\frac{1-p}{8} I_{8},\quad p\in [0,1]. \end{aligned}$$
(9)

Using this formula for \(S^{(1)}_\mathrm{max}(\rho _\mathrm{wnGHZ})\), we have shown that for some GHZ states mixed with white noise \(S^{(1)}_\mathrm{max}(\rho _\mathrm{wnGHZ})<4\) while \(S_\mathrm{max}^{(2)}(\rho ^{\otimes 2}_\mathrm{wnGHZ})>4\). In other words, we have shown that the activation of the violation of the Svetlichny inequality is resistant to white noise. We could not consider other kinds of noise due to the lack of analytical formula for arbitrary noisy GHZ state. Publication of the paper [15] opened the possibility of analyzing noise resistance of the violation of the Svetlichny inequality to various types of noise. Now, to establish the notation, we briefly describe noise models utilized in our paper.

3.1 Models of noise

Let \(\rho \) be a density matrix of a one-qubit state. Then, the noisy counterpart of the state \(\rho \) in the Kraus representation reads

$$\begin{aligned} \rho _{n}=\sum _{i=1}^{k} E_{i}\rho E_{i}^{\dagger }, \end{aligned}$$
(10)

where Kraus operators \(E_{i}\) obey the condition

$$\begin{aligned} \sum _{i=1}^{k}E_{i}^{\dagger }E_{i}=I_{2}, \end{aligned}$$
(11)

with \(1\le k\le 4\).

We model various types of noise by different choices of Kraus operators. The transformation (10) is also called a quantum channel. We will apply the following one-qubit noisy quantum channels:

  1. 1.

    Bit flip

    $$\begin{aligned} E_{1}=\sqrt{1-p} I,\quad E_{2}=\sqrt{p}\sigma _{1}. \end{aligned}$$
    (12)
  2. 2.

    Phase flip

    $$\begin{aligned} E_{1}=\sqrt{1-p} I,\quad E_{2}=\sqrt{p}\sigma _{3}. \end{aligned}$$
    (13)
  3. 3.

    Depolarizing

    $$\begin{aligned} E_{1}=\sqrt{1-3p/4} I,\quad E_{2}=\sqrt{p/4}\sigma _{1},\quad E_{3}=\sqrt{p/4}\sigma _{2},\quad E_{4}=\sqrt{p/4}\sigma _{3}.\nonumber \\ \end{aligned}$$
    (14)
  4. 4.

    Amplitude damping

    $$\begin{aligned} E_{1}=\left( \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} \sqrt{1-p} \\ \end{array} \right) ,\quad E_{2}=\left( \begin{array}{c@{\quad }c} 0 &{} \sqrt{p} \\ 0 &{}0 \\ \end{array} \right) . \end{aligned}$$
    (15)

In all of the above formulas \(p\in [0,1]\), \(\sigma _{i}\), \(i=1,2,3\) are the standard Pauli matrices.

Now, one-qubit noisy quantum channels can be generalized to three-qubit noisy channels in the following way:

$$\begin{aligned} \rho _{n ABC}= \sum _{i=1}^{n_{A}} \sum _{j=1}^{n_{B}} \sum _{k=1}^{n_{C}} E_{ijk}(p_{A},p_{B},p_{C}) \rho _{ABC} E_{ijk}^{\dag }(p_{A},p_{B},p_{C}), \end{aligned}$$
(16)

where \(\rho _{ABC}\) is a three-qubit state and

$$\begin{aligned} E_{ijk}(p_{A},p_{B},p_{C}) = E_{i}(p_{A})\otimes F_{j}(p_{B}) \otimes G_{k}(p_C). \end{aligned}$$
(17)

Various scenarios of noise we want to consider correspond to different choices of \(E_{i}\), \(F_{j}\) and \(G_{k}\). We have the following possibilities:

Noise acting on one qubit (let say qubit A) corresponds to the choice \(n_{B}=1\), \(n_{C}=1\), \(F_{1}(p_{B})=I\), \(G_{1}(p_{C})=I\) and consequently

$$\begin{aligned} E_{i11}^{A}(p_{A},p_{B},p_{C})=E_{i}(p_{A})\otimes I\otimes I \end{aligned}$$
(18)

where \(E_{i}(p_{A})\) are one-qubit Kraus operators related to bit flip or phase flip or depolarizing or amplitude damping channel. Similarly, noise acting on qubit B corresponds to the choice

$$\begin{aligned} E_{1i1}^{B}(p_{A},p_{B},p_{C})=I\otimes E_{i}(p_{B})\otimes I \end{aligned}$$
(19)

and analogously for the noise acting on qubit C.

Noise acting on two qubits (let say A and B) corresponds to the choice \(n_{C}=1\), \(G_{1}(p_{C})=I\) and consequently

$$\begin{aligned} E_{ij1}^{AB}(p_{A},p_{B},p_{C})=E_{i}(p_{A})\otimes E_{j}(p_{B})\otimes I, \end{aligned}$$
(20)

where \(E_{i}(p_{A})\) and \(E_{j}(p_{B})\) are Kraus operators related to one-qubit noisy channels. Similarly, noise acting on qubits AC or BC corresponds to the following choices:

$$\begin{aligned} E_{i1j}^{AC}(p_{A},p_{B},p_{C})=E_{i}(p_{A})\otimes I\otimes E_{j}(p_{C}) \end{aligned}$$
(21)

and

$$\begin{aligned} E_{1ij}^{BC}(p_{A},p_{B},p_{C})=I\otimes E_{i}(p_{B})\otimes E_{j}(p_{C}), \end{aligned}$$
(22)

respectively.

And finally, noise acting on all of the three qubits can be modeled by the channel with the following Kraus operators:

$$\begin{aligned} E_{ijk}^{ABC}(p_{A},p_{B},p_{C}) = E_{i}(p_{A})\otimes E_{j}(p_{B})\otimes E_{k}(p_{C}), \end{aligned}$$
(23)

where, as previously, \(E_{i}(p_{A})\), \(E_{j}(p_{B})\), \(E_{k}(p_{C})\) are Kraus operators related to one-qubit noisy channels.

3.2 Noise acting on one qubit

In this subsection, we assume that noise acts on one qubit only, i.e., Kraus operators defining a noisy channel are of form (18) (or analogous if a noise acts on qubit B or C). We consider bit flip, phase flip, depolarizing and amplitude damping noisy quantum channels acting on qubit A or C. The maximum value attained by a Svetlichny operator for one copy of a noisy GHZ state can be calculated with the help of Eq. (7).

Fig. 1
figure 1

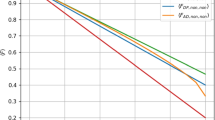
Bit flip on qubit A, optimization approach. The maximum of Svetlichny inequality for one \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}}\) and two copies \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}\) of the noisy states GHZ state as a function of p, for \(\theta _{3}=\frac{\pi }{2}\). The maximum value of Svetlichny inequality for a single copy of this state is 3.9 for \(p = 0\) and \(p=1\). \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}=4\) for \(p=0.97137\)

Full size image
Fig. 2
figure 2

Bit flip on qubit A, continuity approach. The maximum of Svetlichny inequality for one \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}}\) and two copies \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}\) of the noisy GHZ state as a function of p, for \(\theta _{3}=\frac{\pi }{2}\). The maximum value of Svetlichny inequality for a single copy of this state is 3.9 for \(p = 0\). \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}=4\) for \(p=0.02863\)

Full size image

Unfortunately, we cannot use this formula for two copies of the state. In this case, we have at our disposal two approaches: Firstly, we can try to apply the numerical optimization procedure similarly as we have done it in [7] (optimization approach). Secondly, we can use observables found to prove the activation of the violation of the Svetlichny inequality for pure GHZ state [7] and check whether they violate the Svetlichny inequality for two copies of a noisy GHZ state (continuity approach). In each of the considered cases, we tried both approaches; however, the optimization one was successful only in the case of the bit flip noisy channel acting on qubit A. The results obtained with the help of optimization approach are presented in Fig. 1. Observables for which the maximal value of the Svetlichny operator is attained are given in “Appendix.” For other kinds of noise, the numerical optimization procedure failed to find maximum value of the Svetlichny operator greater than 4. However, in these cases, we were able to show the activation of the violation of the Svetlichny inequality using continuity approach. As we have mentioned above, in this approach, we use the same observables (Svetlichny operator) which give the violation of the Svetlichny inequality for pure GHZ state and check for what values of a noise parameter they violate the inequality for two copies of a noisy state. Results obtained in this manner for bit flip noise are presented in Fig. 2. Similar plots for phase flip, amplitude damping and depolarizing noisy channels can be easily obtained with the help of observables we have given in “Appendix.” What is interesting, the range of noise parameter p for which activation of the violation of the Svetlichny inequality occurs is slightly bigger for observables found in optimization approach than for observables we apply in continuity approach. As we can see from the plots, the activation survives up to \(p=0.97137\) and \(p=0.02863\) for bit flip, \(p=0.04719\) and \(p=0.95281\) for phase flip, \(p=0.03316\) for amplitude damping, \(p=0.04400\) for depolarizing noisy channel.

3.3 Noise acting on two and three qubits

Fig. 3
figure 3

Bit flip on two qubits A and C, continuity approach. The maximum of Svetlichny inequality for one \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}}\) and two copies \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}\) of the noisy GHZ state as a function of p, for \(\theta _{3}=\frac{\pi }{2}\). The maximum value of Svetlichny inequality for a single copy of this state is 3.9 for \(p = 0\). \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}=4\) for \(p=0.01449\)

Full size image

In this subsection, we consider the situation when noise acts on two and three qubits. In the case of two qubits, we assume that noise acts on qubits A and C. In such a case, Kraus operators are of form (21). We considered a case when noise acting on both qubits is of the same type as well as a case when on each of the qubits act different types of noise. We have also tried to apply both approaches: optimization and continuity one. Unfortunately, only the continuity approach was successful. The results for bit flip noisy channel acting on qubits A and C are presented in Fig. 3; the results for bit flip channel acting on qubit A and phase flip channel acting on qubit C are presented in Fig. 4. Plots for other noisy channels acting on qubits A and C can be obtained with the help of observables we have given in “Appendix”.

Fig. 4
figure 4

Bit flip–phase flip on qubits A and C, continuity approach. The maximum of Svetlichny inequality for one \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}}\) and two copies \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}\) of the noisy GHZ state as a function of p, for \(\theta _{3}=\frac{\pi }{2}\). The maximum value of Svetlichny inequality for a single copy of this state is 3.9 for \(p = 0\). \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}=4\) for \(p=0.01784\)

Full size image

In the case of noise acting on three qubits, Kraus operators are of form (23). Similarly, like in previous cases, we tried to apply optimization as well as continuity approach but only the continuity one was successful. The results for bit flip channel acting on all of the three qubits are presented in Fig. 5. Plots for other noisy channels acting on three qubits including the case when different types of noise act on different qubits can be obtained with the help of observables we have given in “Appendix.” The results are summarized in Tables 1 and 2.

Fig. 5
figure 5

Bit flip on three qubits A, B and C, continuity approach. The maximum of Svetlichny inequality for one \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}}\) and two copies \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}\) of the noisy GHZ state as a function of p, for \(\theta _{3}=\frac{\pi }{2}\). The maximum value of Svetlichny inequality for a single copy of this state is 3.9 for \(p = 0\). \(S^{\max }_{\rho ^{n}_\mathrm{GHZ}\otimes \rho ^{n}_\mathrm{GHZ}}=4\) for \(\hbox {p}=0.00970\)

Full size image
Table 1 Range of noise parameter for which activation of the violation of the Svetlichny inequality for noisy GHZ states occurs
Full size table
Table 2 Range of noise parameter for which activation of the violation of the Svetlichny inequality for noisy GHZ states occurs in the case of noise acting on two and three qubits
Full size table

4 Conclusions

In our paper, we have analyzed the noise resistance of activation of the violation of the Svetlichny inequality. We have considered bit flip, phase flip, depolarizing and amplitude damping noisy quantum channels acting on one, two and three qubits from the pure GHZ state. The results, i.e., the ranges of noise parameters for which activation survives under noisy quantum channels, are summarized in Tables 1 and 2. From those tables, we see that noise resistance of the activation of the violation of the Svetlichny inequality is different for different kinds of noise. For noise acting on one qubit, the activation is most robust in the case of phase flip channel while most fragile in the case of amplitude damping channel. For noise acting on two and three qubits, the activation is again most robust in the case of phase flip channel but most fragile in the case of depolarizing channel.

The noise is an inevitable component of any real experiment; therefore, we hope that our results might be useful in experimental study on activation of the violation of the Svetlichny inequality.

Experimental investigation of the robustness against noise for different Bell-type inequalities in one copy of three-qubit GHZ states has been carried out in [16]. Theoretical analysis of the influence of noise on violation of different Bell-type inequalities in tripartite GHZ states has been also performed in [2, 14, 22].