Abstract
By combining quantum renormalization group approach and critical theory, we investigate the performance of global entanglement and Bell nonlocality in quantum phase transition (QPT) that occurred in Ising model with a transverse field (ITF). After several iterations, both of them gradually develop two different saturated values relevant to the Ising phase and paramagnetic phase. Moreover, we proved that the inherent block–block correlation is strong enough to violate the quantum nonlocality. What is more, we derive an exact relation between global entanglement and Bell nonlocality for the given case. To serve further insight, the nonanalytic and scaling behaviors are analyzed.




Similar content being viewed by others
References
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935)
Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)
Bell, J.: On the einstein podolsky rosen paradox. Physics 1, 195 (1964)
Genovese, M.: Research on hidden variable theories: a review of recent progresses. Phys. Rep. 413, 319 (2005)
Vidal, G., Latorre, J.I., Rico, E., Kitaev, A.: Entanglement in quantum critical phenomena. Phys. Rev. Lett. 90, 227902 (2003)
Amico, L., Fazio, R., Osterloh, A., Vedral, V.: Entanglement in many-body systems. Rev. Mod. Phys. 80, 517 (2008)
Verstraete, F., Popp, M., Cirac, J.I.: Entanglement versus correlations in spin systems. Phys. Rev. Lett. 92, 027901 (2004)
Li, Y.C., Lin, H.Q.: Thermal quantum and classical correlations and entanglement in the XY spin model with three-spin interaction. Phys. Rev. A 83, 052323 (2011)
Rulli, C.C., Sarandy, M.S.: Global quantum discord in multipartite systems. Phys. Rev. A 84, 042109 (2011)
Werlang, T., Ribeiro, G.A.P., Rigolin, G.: Spotlighting quantum critical points via quantum correlations at finite temperatures. Phys. Rev. A 83, 062334 (2011)
Boschi, D., Branca, S., De Martini, F., Hardy, L., Popescu, S.: Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 80, 1121 (1998)
Peres, A., Terno, D.R.: Quantum information and relativity theory. Rev. Mod. Phys. 76, 93 (2004)
Hu, T.T., Xue, K., Sun, C.F., Wang, G.C., Ren, H.: Quantum teleportation and dense coding via topological basis. Quantum Inf. Process. 12, 3369–3381 (2013)
Harrow, A., Hayden, P., Leung, D.: Superdense coding of quantum states. Phys. Rev. Lett. 92, 187901 (2004)
Sachdev, S.: Quantum Phase Transitions. Cambridge University Press, Cambridge (2001)
Werlang, T., Trippe, C., Ribeiro, G.A.P., Rigolin, G.: Quantum correlations in spin chains at finite temperatures and quantum phase transitions. Phys. Rev. Lett. 105, 095702 (2010)
Osterloh, A., Amico, L., Falci, G., Fazio, R.: Scaling of entanglement close to a quantum phase transition. Nature 416, 608 (2002)
Wu, L.A., Sarandy, M.S., Lidar, D.A.: Quantum phase transitions and bipartite entanglement. Phys. Rev. Lett. 93, 250404 (2004)
Jafari, R., Kargarian, M., Langari, A., Siahatgar, M.: Phase diagram and entanglement of the Ising model with Dzyaloshinskii–Moriya interaction. Phys. Rev. B 78, 214414 (2008)
Qin, M., Ren, Z.Z., Zhang, X.: Universal quantum correlation close to quantum critical phenomena. Sci. Rep. 6, 26042 (2016)
Langari, A., Pollmann, F., Siahatgar, M.: Ground-state fidelity of the spin-1 Heisenberg chain with single ion anisotropy: quantum renormalization group and exact diagonalization approaches. J. Phys. Condens. Matter 25, 406002 (2013)
Kargarian, M., Jafari, R., Langari, A.: Renormalization of concurrence: the application of the quantum renormalization group to quantum-information systems. Phys. Rev. A 76, 060304(R) (2007)
Liu, C.C., Shi, J.D., Ding, Z.Y., Ye, L.: Exploring the renormalization of quantum discord and Bell non-locality in the one-dimensional transverse Ising model. Quantum Inf. Process. 15, 3209–3221 (2016)
Vidal, J., Palacios, G., Mosseri, R.: Entanglement in a second-order quantum phase transition. Phys. Rev. A 69, 022107 (2004)
Lambert, N., Emary, C., Brandes, T.: Entanglement and the phase transition in single-mode superradiance. Phys. Rev. Lett. 92, 073602 (2004)
Ma, F.W., Liu, S.X., Kong, X.M.: Entanglement and quantum phase transition in the one-dimensional anisotropic XY model. Phys. Rev. A 83, 062309 (2011)
Song, X.K., Wu, T., Ye, L.: Negativity and quantum phase transition in the anisotropic XXZ model. Eur. Phys. J. D 67, 96 (2013)
Song, X.K., Wu, T., Xu, S., He, J., Ye, L.: Renormalization of quantum discord and Bell nonlocality in the XXZ model with Dzyaloshinskii–Moriya interaction. Ann. Phys. 349, 220 (2014)
Zanardi, P., Paunkovic, N.: Ground state overlap and quantum phase transitions. Phys. Rev. E 74, 031123 (2006)
Cheng, W.W., Liu, J.M.: Fidelity susceptibility approach to quantum phase transitions in the XY spin chain with multisite interactions. Phys. Rev. A 82, 012308 (2010)
Kargarian, M., Jafari, R., Langari, A.: Dzyaloshinskii–Moriya interaction and anisotropy effects on the entanglement of the Heisenberg model. Phys. Rev. A 79, 042319 (2009)
Pan, J.W., Bouwmeester, D., Matthew, D., Harald, W., Zeilinger, A.: Experimental test of quantum nonlocality in three-photon Greenberger–Horne–Zeilinger entanglement. Nature 403, 515 (2000)
Mandel, O., Greiner, M., Widera, A., et al.: Controlled collisions for multiparticle entanglement of optically trapped atoms. Nature 425, 937 (2003)
Sackett, C.A., Kielpinski, D., King, B.E., et al.: Experimental entanglement of four particles. Nature 404, 256 (2000)
Roos, C.F., Riebe, M., Haffner, H., et al.: Control and measurement of three-qubit entangled states. Science 304, 1478 (2004)
Rauschenbeutel, A., Nogues, G., Osnaghi, S., et al.: Step-by-step engineered multiparticle entanglement. Science 288, 2024 (2000)
Qin, M., Ren, Z.Z., Zhang, X.: Renormalization of the global quantum correlation and monogamy relation in the anisotropic Heisenberg XXZ model. Quantum Inf. Process. 15, 255–267 (2016)
Shi, J.D., Wang, D., Ye, L.: Genuine multipartite entanglement as the indicator of quantum phase transition in spin systems. Quantum Inf. Process. 15, 4629–4640 (2016)
Batle, J., Casas, M.: Nonlocality and entanglement in the XY model. Phys. Rev. A 82, 062101 (2010)
Justino, L., de Oliveira, T.R.: Bell inequalities and entanglement at quantum phase transitions in the XXZ model. Phys. Rev. A 85, 052128 (2012)
Bartkiewicz, K., Horst, B., Lemr, K., Miranowicz, A.: Entanglement estimation from Bell inequality violation. Phys. Rev. A 88, 052105 (2013)
Verstraete, F., Wolf, M.M.: Entanglement versus bell violations and their behavior under local filtering operations. Phys. Rev. Lett. 89, 170401 (2002)
Horst, B., Bartkiewicz, K., Miranowicz, A.: Two-qubit mixed states more entangled than pure states: comparison of the relative entropy of entanglement for a given nonlocality. Phys. Rev. A 87, 042108 (2013)
Miranowicz, A., Horst, B., Koper, A.: Paradoxes of measures of quantum entanglement and Bell’s inequality violation in two-qubit systems. J. Comput. Methods Sci. Eng. 10, 501 (2010)
Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)
Meyer, D.A., Wallach, N.R.: Global entanglement in multiparticle systems. J. Math. Phys. 43, 4273 (2002)
Brennen, G.K.: An observable measure of entanglement for pure states of multi-qubit systems. Quantum Inf. Comput. 3, 619 (2003)
Horodecki, R., Horodecki, P., Horodecki, M.: Violating Bell inequality by mixed spin-1/2 states: necessary and sufficient condition. Phys. Lett. A 200, 340 (1995)
Yao, Y., Li, H.W., Li, M., Yin, Z.Q., Chen, W., Han, Z.F.: Bell violation versus geometric measure of quantum discord and their dynamical behavior. Eur. Phys. J. D 66, 295 (2012)
Acknowledgements
This work was supported by National Science Foundation of China under Grant No. 11605028, the Natural Science Research Project of Education Department of Anhui Province of China under Grant No. KJ2016A547, the Open Foundation for CAS Key Laboratory of Quantum Information under Grant No. KQI201702, the Key Program of Excellent Youth Talent Project of the Education Department of Anhui Province of China (Grant No. gxyqZD2016190), the Key Research Foundation of Education Department of Anhui Province of China (Grant No. KJ2013A205), the Teaching Research Program of Fuyang Normal University (Grant Nos. 2014JYXM18 and 2015JYXM34), the Research Center for Quantum Information Technology of Fuyang Normal University under Grant No. kytd201706 and the Doctoral Foundation of Fuyang Normal University under Grant No. FYNU1602.
Author information
Authors and Affiliations
Corresponding authors
Appendix
Appendix
In this appendix, we will first detail how the ITF model is renormalized by exploiting the QRG method. The Hamiltonian of the ITF model in the z direction on a periodic chain of N site is
By implementing the Kadanoff’s block method, Hamiltonian (A1) can be rewritten as
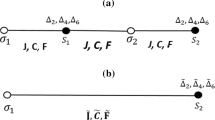
where \(H^\mathrm{B}\) is the block Hamiltonian and \(H^\mathrm{BB}\) is the interblock Hamiltonian. Here, we choose two sites as a block and the decomposition is shown in Fig. 5.
Simultaneously, the specific forms of Hamiltonian \(H^\mathrm{B}\) and \(H^\mathrm{BB}\) are
with \(h_L^A =-J\left[ {\sigma _{L,1}^x \sigma _{L,2}^x +g\sigma L^z } \right] \) is the Lth block Hamiltonian. A remark is in order; choosing two-site block is essential here to get a self-similarity Hamiltonian after each iterative step.
In terms of the matrix product states, the Lth block Hamiltonian can be exactly diagonalized and solved. Then, we can obtain two degenerate ground states which are used to construct the projection operators. With \(\left| \uparrow \right\rangle \) and \(\left| \downarrow \right\rangle \) defined as the eigenstates of operator \(\sigma ^{z}\), both degenerate ground states are
To eliminate the higher energy of the system and retain the lower, the projection operator \(P_0 \) is composed of its lowest energy eigenstates. Then, the effective Hamiltonian \(H^\mathrm{eff}\) and original Hamiltonian H have in common the low-lying spectrum, which can be given by the projection operator, i.e., \(H^\mathrm{eff}=P_0^\dagger HP_0 \) wherein \(P_0^\dagger \) is the Hermitian operator of \(P_0 \). In the effective Hamiltonian, we consider only the first-order correction in the perturbation theory, which is
At the same time, the projection operator \(P_0 \) can be put in a factorized form
where the specific form of \(P_0^L\) is
with \(\left| \Uparrow \right\rangle _L \) and \(\left| \Downarrow \right\rangle _L \) are the renamed states of the Lth block to represent the effective site degrees of freedom. Then, the effective Hamiltonian of the renormalized ITF model can be cast into with the scaled couplings.
Now, we analytically present the derivation of global entanglement for the pure state \(\rho \). Explicitly, in the orthonormal product basis \(\left\{ {\left| {\downarrow \downarrow } \right\rangle ,\left| {\downarrow \uparrow } \right\rangle ,\left| {\uparrow \downarrow } \right\rangle ,\left| {\uparrow \uparrow } \right\rangle } \right\} \), the state \(\rho \) can be rewritten in the matrix form
Then, the reduced density matrices \(\rho _k \) for the subsystem k are
Correspondingly,
Based on Eq. (A12), we can readily calculate the global entanglement.
Rights and permissions
About this article
Cite this article
Shi, J., Ding, Z., He, J. et al. Renormalization of global entanglement and Bell nonlocality in the Ising model with a transverse field. Quantum Inf Process 16, 311 (2017). https://doi.org/10.1007/s11128-017-1745-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-017-1745-1