1 Introduction

A key question of the solid-state quantum information processing is whether an engineered system could display multipartite states with designed quantum properties necessary for many spectacular phenomena of quantum world, such as quantum teleportation [1,2,3,4,5], quantum cryptography [6, 7] or in general, indicating for the quantumness of physical systems [8]. In particular, the multi-qudit entanglement (which starts at the tripartite entanglement) necessary for quantum error correction effect has been recently gaining increasing attention. As it has been shown, entangled qudits are less affected by noise than entangled qubits [9, 10], and in quantum cryptography it is more secure to apply entangled qutrits or qudits against eavesdropping attacks, than to use qubits [11,12,13]. For these reasons, the creation of higher-dimensional (i.e., containing more than two internal states) multipartite entangled states is not only a fundamental scientific endeavor itself, but is also the way to improve the technology of quantum information processing.

Recently, an impressive progress in the field of quantum states engineering has been made. Models involving ultra-cold atoms trapped in optical lattices [14, 15], ultra-cold quantum gates [16], or coupled quantum dots [17,18,19] etc., are considered as toolboxes for experimental realization and probing many-particle systems and their static and dynamical properties. For instance, ultra-cold atomic systems offer unique freedom allowing to engineer and manipulate quantum states. They can be tuned with a very high degree of accuracy and versatility at single lattice sites, as well as collectively within the whole lattice. Therefore, contrary to the ”classical” solid-state physics, it becomes possible to manage all relevant parameters almost adiabatically, even in the vicinity of the phase transitions [20, 21], or controlling an atomic localization along a lattice. This opportunity permits ultra-cold atomic systems to serve as quantum simulators and opens completely new possibilities of answering fundamental questions of quantum information theory related to transitions from the product to entangled states. Consequently, some phenomena, which are very difficult or even impossible to study in their natural appearance and environment of the canonical quantum solid-state physics, can be explicitly reconstructed and modeled in ultra-cold atomic systems.

Based on all those facts, Huang et al. [22] have presented a very interesting example of generation of bipartite total hyperfine-zero-singlet states using hyperfine-spin-1 particles confined in an optical lattice. In that paper, authors dealt with the ground state of bosons confined in an one-dimensional lattice with one atom per site, when the system was remaining in the Mott-insulator phase. For such a case, one can treat the tunneling between two neighboring sites as a virtual process in the second order of the perturbation theory [23] and hence describe the system by the Heisenberg spin model with an additional biquadratic term (such model is called quadratic–biquadratic Heisenberg (QBH) model [24,25,26,27]). As it was shown in [25, 28], thanks to the proper choice of the interaction between bosons, the lattice translational symmetry is spontaneously broken. In consequence, the ground state of the system is expected to be in the dimerized phase, and it can be considered as a collection of isolated singlet pairs. For such a system, a scheme allowing for the generation of the qutrit singlet state, starting from completely unentangled states, was presented in [22]. Such scheme can be summarized in the following way. It is known that for certain conditions (see [22]) singlet state becomes a ground state of the system. For such situation, the initial product state which is characterized by the zero value of the total \(S^z\), automatically becomes the singlet state (this process requires adiabatic changes of the external magnetic field). However, this simple mechanism does not work properly for more general cases. Therefore, Huang et al. have exploited the idea of spin-changing dynamics of two interacting bosons in the presence of a quadratic Zeeman field. They have shown that with a proper choice of the strength of magnetic field, the pure singlet state can be prepared at some moment of time. Their result is especially important as a spin-singlet state is considered to be one of the most entangled states of biqutrit systems.

In this paper, we would like to extend the bipartite model analyzed in [22] to that involving three sites. Considering the three-site QBH model describing three particles trapped in an optical lattice, which can be treated as dedicated quantum simulator of a spin system, we will concentrate on the wave function evolution leading to the generation of tripartite entangled states with specifically designed quantum properties. In particular, we shall discuss the sensitivity of the bipartite system to the weak interaction with the third (ancilla) particle. Our motivation arises from the fact that whereas the entanglement of pure bipartite systems is well understood, apparently the entanglement of pure tripartite quantum states is not a trivial extension of the entanglement of bipartite systems [29, 30]. Some results concerning the entanglement of pure tripartite systems have been presented in [30,31,32] (and the references therein). In these papers it was shown that for such systems a new kind of entanglement which cannot be captured by the bipartite measurements can be detected. This type was referred to as a genuine tripartite entanglement. At this point we would like to emphasize that it is not our aim to present the analysis of the dynamics of various types of entanglements in this paper. Instead, we shall show that even a weak disturbance of the bipartite system can lead to the appearance of a genuine tripartite entanglement. This means that one can design an experimental setup so that translational symmetry of the wave function is reached despite strong asymmetry of the system and interatomic interactions. In this sense the system can be recognized as homogeneous. Therefore, we would also like to present our proposal allowing to extract bipartite singlet qutrit states from the tripartite wave function describing our system.

Even if we ultimately cannot obtain experimentally a strongly asymmetric system by fulfilling the condition of homogeneity, we believe that the studies of three-site dynamics (and its potential relations with two-site evolution) will be helpful not only in effective generation of the entangled states but also to better understanding various quantum magnetism phenomena. It is known that for the low energy limit, the interatomic interactions can be characterized by the s-wave scattering length which (in general) depends on the spin states in the incoming and outcoming scattering channels. Such spin-dependent interactions favor various relative orientation of the atomic spins, i.e., various spin configurations (for the spin-1 system, see for instance [33]). Therefore, gaining information concerning the values of coupling parameters allows to determine the nature of a ground state. Precise measurements of spin-dependent interaction strength have been presented for example in [34]. In that paper the Rabi-type oscillations between two spin states of an ultra-cold pair of atoms trapped in optical lattices were studied, which allowed for a direct determination of coupling parameters and hence the differences in scattering lengths. By comparing them to theoretical predictions, the experimental accuracy has been estimated at more than 80%.

Since our model can be recognized as spin-1 bosons (for example, 23-sodium or 87-rubidium alkali atoms) confined in an optical trimerized superlattice, we believe that the dynamics discussed in this paper could be useful for further analysis of nontrivial tripartite cases (especially in a context of proper choice of the values of spin-dependent coupling parameters) and their experimental investigation. The trimerized superlattice can be implemented by strong trimerized Kagomé latices [35,36,37], which are characterized by a structure involving weakly coupled three-well potentials. Therefore, such systems could be quite good arena for studying three-site dynamics. An alternative approach for creation of replicated three-well systems has been proposed in [38]. In the framework of that proposition, the laser beams propagate at angles \(2\pi /3\) to a bichromatic lattices profile in the x–y plane, and all of them are polarized in the z direction. As a result, one can receive a two-dimensional array of triangular rings.

2 Tripartite hyperfine-spin-1 system

2.1 Model

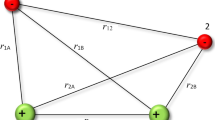
Analogously as in [22, 34] we assume that two particles are confined in double-well potentials and each of them are in the state \(\mid S,S^z \rangle = \mid 1, 0 \rangle \). Both atoms remain in the ground states of external potential throughout the whole process evolution. In consequence, S is conserved and those particles have just one degree of freedom: \(S^z\). In other words, such system’s dynamics is related only to the changes of projection of hyperfine spins. Thus, to simplify the notation the label S will be omitted here and then the initial state \(\mid 0, 0\rangle \) will denote the situation when particles on both sites (further labeled as L and R) are characterized by \(S^z = 0\). The dynamics of such a system has already been studied (also experimentally) in order to generate the maximally entangled singlet state by changing the external magnetic field strength [22] and to extract the spin-dependent interaction parameters (the spin-dependent s-wave scattering lengths) [34].

Now, let us consider a situation when both particles can interact (in the same way) with a third (ancilla) particle located at site A. We assume here that the whole system’s dynamics is limited within a single triple-well superlattice. In other words, we assume that tunneling amplitudes between potential trimers are weakened completely to zero. In the Mott-insulator phase the interactions among bosons in such triple-wall lattice can be described with the QBH model of the form [22, 25, 26]:

$$\begin{aligned} \hat{H} = \hat{H}_0 + \hat{H}_A, \end{aligned}$$
(1)

where

$$\begin{aligned} \hat{H}_0 = J \hat{\varvec{S}}_{L}\hat{\varvec{S}}_{R} + K (\hat{\varvec{S}}_{L}\hat{\varvec{S}}_{R})^2 + q \bigg ( (\hat{S}^z_L)^2+(\hat{S}^z_R)^2\bigg ) \end{aligned}$$
(2)

and

$$\begin{aligned} \hat{H}_A =&J' \bigg (\hat{\varvec{S}}_{L}\hat{\varvec{S}}_{A} + \hat{\varvec{S}}_{R}\hat{\varvec{S}}_{A} \bigg ) \nonumber \\&+ K' \bigg ( (\hat{\varvec{S}}_{L}\hat{\varvec{S}}_{A})^2 + (\hat{\varvec{S}}_{R}\hat{\varvec{S}}_{A})^2 \bigg ) + q (\hat{S}^z_A)^2, \end{aligned}$$
(3)

with L, R, and A denoting lattice sites and \(\hat{\varvec{S}}_i = (\hat{S}^x_i, \hat{S}^y_i, \hat{S}^z_i)\) for a spin \(S=1\) operator. The parameters J and \(J'\) refer to exchange interaction constants, while K and \(K'\) describe biquadratic interactions. Since the values of the both couplings are related to the optical lattice’s parameters (they depend on the strength and shape of analyzed optical potential) and the kind of trapped atoms, a general formula for coupling constants cannot be written in a direct form. An example of the exact formula determining such constants for a simple homogeneous cubic lattice has been presented in [25, 26]. It was shown there that their values are proportional to s-wave scattering lengths \(a_{0}\) and \(a_{2}\), where \(a_{0}\) and \(a_{2}\) correspond to scattering channels with a total spin of colliding two particles equal \(S=0\) and \(S=2\), respectively. On the other hand, for the bipartite case discussed in [22], the authors assumed arbitrary energy levels \(E_0\) and \(E_2\) (the lowest and the highest ones) of the Hamiltonian (2) with \(q=0\) rather than J and K—the appropriate relation can be written as follows: \(E_2-E_0 = 3 (J-K)\). Furthermore, if one defines the spatial wave function as \(\phi _0 (\mathbf {r})\), then energies \(E_S= \frac{4 \pi a_S}{M_a} \int d^3 \mathbf {r} |\phi _0 (\mathbf {r})|^4=a_S \tilde{U}\), where \(M_a\) is the mass of one atom and \(\tilde{U}\) was defined as in [34]. So, the coupling parameters can be considered as related to the spin-dependent interactions in the sense mentioned before.

Regardless of a suitable form of all interaction constants, one can introduce the standard parameterization \(J= J_0 \cos \theta \), \(K= J_0 \sin \theta \) (\(J'= J'_0 \cos \varphi \), \(K'= J'_0 \sin \varphi \)), where \(J_0=\sqrt{J^2 + K^2}\) (\(J'_0=\sqrt{(J')^2 + (K')^2}\)), for the Hamiltonian (1). From the model point of view, the angle \(\theta \) (\(\varphi \)) is confined within the interval \((-\pi ,\pi )\) and the experimental scheme where a whole range of \(\theta \) (\(\varphi \)) can be obtained was also proposed. It can be done directly (for instance by using optical Feshbach resonances [39, 40]) or by performing some kind of “quantum simulation” technique for which the system is initially prepared in its excited state (as it was proposed in [24, 33]). Therefore, in contrast to the usual condensed matter systems, for ultra-cold atoms systems it becomes possible to engineer experimental setups for which biquadratic coupling is stronger than a quadratic one. For a one-dimensional chain of trapped atoms, the dimer phase (discussed in the introduction) is expected for \(-3 \pi /4< \theta =\varphi < -\pi /4\). In this article we will focus on the regime of the weak interactions between subsystem LR and the additional site A. Therefore, we will assume here that the ratio

$$\begin{aligned} J_0'/J_0 \ll 1. \end{aligned}$$
(4)

Finally, the parameter q appearing in the Hamiltonian (1) refers to the magnitude of the quadratic Zeeman shift given by \(q=q_0 B^2\), where B is external magnetic field and \(q_0\) is a coefficient depending on the atom under consideration. As we see, the sign of q is directly related to \(q_0\). However, it is important to mention that there are experimental techniques allowing to alter the sign of the quadratic Zeeman shift [41].

2.2 System’s dynamics

As it is known, the Hamiltonian (1) exhibits the U(1) symmetry (conserves total \(S^z\)). Thus, the Hilbert space of our system can be divided into mutually orthogonal subspaces with respect to the total \(S^z\). Since the initial bipartite state of subsystem LR is \(\mid 0, 0 \rangle _{\textit{LR}}\) so it exhibits total \(S^z\) equal to 0, the appropriate Hilbert subspace for tripartite system is designed by the value of \(S^z_A\) that can be \(-1,0,1\). On the other hand, in the absence of the linear Zeeman shift the results obtained for \(S^z_A = 1\) have their counterparts for \(S^z_A= -1\). Therefore, without loss of generality, our analysis focuses on two tripartite initial states \(|\varPsi _0(0) \rangle = \mid 0, 0, 0 \rangle \) and \(|\varPsi _1(0) \rangle = \mid 0, 0, 1 \rangle \).

The time-dependent wave function of the three spin-1 bosons can be written as

$$\begin{aligned} \mid \varPsi (t) \rangle = \sum _{\alpha , \beta , \gamma \in \{-1,0,1\}} a_{\alpha , \beta , \gamma }(t) \mid \alpha , \beta , \gamma \rangle , \end{aligned}$$
(5)

where \(a_{\alpha , \beta , \gamma }(t)\) are complex probability amplitudes related to the situation when all particles are in the states when \(S^z_L=\alpha \), \(S^z_R=\beta \) and \(S^z_A=\gamma \).

Time-evolution of the wave function (5) and hence probability amplitudes can be found with use of standard procedure applying Schrödinger equation written in the form (we use units \(\hbar =1\)):

$$\begin{aligned} \langle \alpha , \beta , \gamma \mid i \frac{\mathrm{d}}{\mathrm{d}t} \mid \varPsi (t) \rangle = \langle \alpha , \beta , \gamma \mid \hat{H} \mid \varPsi (t) \rangle , \end{aligned}$$
(6)

where \(\alpha , \beta , \gamma \in \{-1,0,1\}\) as before.

For instance, if one considers \(|\varPsi _0(0) \rangle \) to be the initial state and puts \(q=0\), the following set of independent equations can be derived (see “Appendix 1” for details):

$$\begin{aligned} i a_{1,0,-1}'(t)= & {} (J + K - J' + 4 K')~a_{1,0,-1}(t) \nonumber \\&+\,J'~a_{1,-1,0}(t) + (J'-K')~a_{0,0,0}(t), \nonumber \\ i a_{1,-1,0}'(t)= & {} 2 J'~a_{1,0,-1}(t) - (J - 3 K - 2 K')a_{1,-1,0}(t) \nonumber \\&+\,(J - K)~a_{0,0,0}(t), \nonumber \\ i a_{0,0,0}'(t)= & {} 4 (J'-K')~a_{1,0,-1}(t) + 2 (J - K)a_{1,-1,0}(t) \nonumber \\&+\,2 (K + 2 K')~a_{0,0,0}(t). \end{aligned}$$
(7)

Then, the solutions for all nonzero probability amplitudes can be written as follows

$$\begin{aligned} a_{1,0,-1}(t)= & {} -\frac{\mathrm{e}^{-2 i K t}}{10}\bigg (-2~\mathrm{e}^{-i \omega _1 t} +\big (1-A_1\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 + \mathcal {Z})}\nonumber \\&+\,\big (1+A_1\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 - \mathcal {Z})} \bigg ), \nonumber \\ a_{1,-1,0}(t)= & {} -\frac{\mathrm{e}^{-2 i K t}}{10}\bigg (-2~\mathrm{e}^{-i \omega _1 t} +\big (1-A_2\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 + \mathcal {Z})}\nonumber \\&+\,\big (1+ A_2\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 - \mathcal {Z})}\bigg ), \nonumber \\ a_{0,0,0}(t)= & {} \frac{\mathrm{e}^{-2 i K t}}{10}\bigg (4~\mathrm{e}^{-i \omega _1 t} +\big (3 -A_4\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 + \mathcal {Z})}\nonumber \\&+\,\big (3 + A_4\big )~\mathrm{e}^{\frac{i t}{2} (\omega _2 - \mathcal {Z})}\bigg ), \end{aligned}$$
(8)

and

$$\begin{aligned} a_{1,0,-1}(t)= & {} a_{0,1,-1}(t) = a_{-1,0,1}(t) = a_{0,-1,1}(t), \nonumber \\ a_{1,-1,0}(t)= & {} a_{-1,1,0}(t), \end{aligned}$$
(9)

where the amplitudes \(A_i\) and frequencies \(\omega _i\) are given by

$$\begin{aligned} \omega _1= & {} J - K +2 (J' + K'),\nonumber \\ \omega _2= & {} J - K + 3 J' - 8 K',\nonumber \\ A_1= & {} 3 (J - K - J' + 2 K')/\mathcal {Z},\nonumber \\ A_2= & {} (-7 (J - K) +7 J' -4 K')/\mathcal {Z},\nonumber \\ A_4= & {} (-J + K + J' + 8 K')/\mathcal {Z}, \end{aligned}$$
(10)

and \(\mathcal {Z}= \big (9 (J - K)^2 + 2 (8 K' - 9 J') (J - K) + 9 (J')^2 - 16 K' J' + 16 (K')^2~ \big )^{1/2}\).

Although we have presented here exact analytical results, one should keep in mind that for other more general cases the analytical solutions can take a much more complicated form, and therefore, they will not be presented in the text. For such cases the results considered here can be derived with use of numerical calculations. In order to do this, an unitary evolution operator \(\hat{U}(t)= \exp (-i \hat{H} t)\) should be created, where the Hamiltonian (1) is used. Then, the time-dependent wave function \(\mid \varPsi (t) \rangle \) can be found according to equation

$$\begin{aligned} \mid \varPsi (t) \rangle = \hat{U}(t) \mid \varPsi _k(0)\rangle , \end{aligned}$$
(11)

where \(\mid \varPsi _k(0)\rangle \) is one of the initial states mentioned earlier.

3 Results and discussion

3.1 Weak interaction \(J_0'/J_0\) limit

To understand the impact of weak interaction between the bipartite subsystem and the ancilla particle, described by the Hamiltonian (3), it is useful to start by considering a two-site problem, i.e., when the interaction is suppressed to zero. Such a situation has been well described in [22, 34]. In our model it can be achieved by putting \(J'=K'=0\) (alternatively \(J_0'=0\)) to the general equations (29) and (32). In this subsection we are going to focus on the \(|\varPsi _0(0) \rangle \) initial states, although similar results can be obtained for \(|\varPsi _1(0) \rangle \), too.

In the case of a suppressed interaction, the value of the projection of \(S_A\) remains constant during the whole process. Therefore, the wave function (27) can be factorized as \(\mid \varPsi (t) \rangle =\mid \varPsi (t) \rangle _{\textit{LR}} \otimes \mid 0 \rangle _A\), where the time-dependent part related to the bipartite subsystem LR takes form:

$$\begin{aligned} \mid \varPsi (t) \rangle _{\textit{LR}} = \frac{1}{N(t)} (\mid 1, -1\rangle + \varLambda (t) \mid 0, 0\rangle + \mid -1, 1 \rangle ). \end{aligned}$$
(12)

Appearing here \(N(t)=(2+\varLambda (t) \bar{\varLambda }(t))^{1/2}\) is appropriate norm constant, whereas the probability amplitude \(\varLambda (t)\) is given by

$$\begin{aligned} \varLambda (t) = \frac{J - K - 2 q + i \varOmega \cot (\varOmega t/2)}{2 (J - K)} \end{aligned}$$
(13)

with the Rabi frequency

$$\begin{aligned} \varOmega = \sqrt{9 (J-K)^2 - 4 (J - K) q + 4 q^2}. \end{aligned}$$
(14)

It is straightforward to show that for \(t_0 = 0, \frac{2 \pi }{\varOmega }, \ldots \), we have \(\mid \varPsi (t_0) \rangle _{\textit{LR}} \approx \mid 0, 0\rangle \). Moreover, with a suitable choice of \(q=q^{*}\), where

$$\begin{aligned} q^{*}=\frac{3(J-K)}{2} \end{aligned}$$
(15)

(and only this one) we can find that \(\varOmega = \frac{6 |J-K|}{\sqrt{3}}\), and hence, at time \(t^{*} = \frac{\pi (2 k+1)}{\varOmega }\) the singlet state is generated

$$\begin{aligned} \mid \varPsi (t^{*}) \rangle _{\textit{LR}} = \frac{1}{\sqrt{3}} (\mid 1, -1\rangle - \mid 0, 0\rangle + \mid -1, 1 \rangle ). \end{aligned}$$
(16)

Presented here results are consistent with those derived in [22], and they represent a vary useful scenario for creating singlet states when adiabatic processes cannot be involved. However, it is important to mention that the above procedure of generation the total hyperfine-spin-singlet state requires the same signs of q and \((J-K)\).

Fig. 1
figure 1

Results for \(J=1\) and \(K=0.98\). The interactions with ancilla site have been parameterized as follows: \(J'=J_0' \cos ( \varphi )\) and \(K'=J_0' \sin ( \varphi )\), where \(\phi =-0.358\pi \) and a \(J_0'=0\), b \(J_0'=0.001\), c \(J_0'=0.005\), d \(J_0'=0.015\), e \(J_0'=0.02\), f \(J_0'=0.05\). Black lines refer to time-dependent fidelity \(F(\rho , \sigma )\), whereas red lines denote trace distance \(D(\rho , \sigma )\). The matrices \(\rho \) and \(\sigma \) refer to the three- and two-site systems, respectively (Color figure online)

Full size image

Now, let us introduce an interaction with the ancilla site A and verify how it can influence the dynamics of the subsystem LR. To do this, we define the reduced density matrix \(\sigma (t) = \big [\mathrm{Tr}_A |\varPsi (t) \rangle \langle \varPsi (t)| \big ]_{J_0'=0}\), which describes the time-evolution of the subsystem LR. This matrix will be treated as a reference point in our analysis. We expect that if the presence of site A can be treated as a tiny perturbation (for \( J_0'/ J_0 \ll 1 \)) then the dynamics of subsystem LR should be carried out in the way almost identical as previously described (for the two-site case), and considerable differences should appear for time t longer than one period (or even several periods) \(T_0 = 2 \pi / \varOmega \). In other words, if \( t \le T_0\) the state described by the reduced density matrix, \(\rho (t) = \mathrm{Tr} _A | \varPsi (t) \rangle \langle \varPsi (t) |_{J_0'\ne 0}\), should not differ significantly from the state \(\sigma (t)\).

There are many methods to determine the distance between quantum states [42]. One of them is based on fidelity F between two states \( \rho \) and \( \sigma \) given by

$$\begin{aligned} F(\rho , \sigma )= & {} \mathrm{Tr} (\sqrt{\sqrt{\rho } \sigma \sqrt{\rho }})^2. \end{aligned}$$
(17)

It can be shown that \(0 \le F(\rho , \sigma ) \le 1\), and \(F(\rho , \sigma )=1 \) if and only if \(\rho =\sigma \). Thus, the fidelity is not a metric as such, but serves rather as a generalized measure of the overlap between two quantum states. The fidelity is also symmetric in its inputs, \(F(\rho , \sigma ) = F(\sigma , \rho )\).

Another good measure of distance between quantum states is a trace distance [43]. The trace distance between density matrices \(\rho \) and \(\sigma \) is defined by

$$\begin{aligned} D(\rho , \sigma ) = \frac{1}{2} ||\rho - \sigma ||_1, \end{aligned}$$
(18)

where \(||A||_1 = \mathrm{Tr}(\sqrt{A^{\dagger } A})\) is a trace norm. According to this definition, the trace distance is a genuine metric on quantum states, with \(0 \le D(\rho , \sigma ) \le 1\). The trace distance has a compelling physical interpretation as a measure of state distinguishability, so \(D(\rho , \sigma ) = 0\) if and only if \(\rho =\sigma \).

In Fig. 1 the results for some exemplary set of the parameters are shown. We have assumed there that \(J=1\) and \(K=0.98\) (causing the \(J_0=1.4\)). The weak interaction has been parameterized as \(J'=J_0' \cos ( \varphi )\) i \(K'=J_0' \sin ( \varphi )\), where \(\varphi =-0.358\pi \) and \(J_0'\) turns into the range 0–0.05. For simplicity, we have assumed that \(q=0\), and hence, the wave function \(\mid \varPsi (t) \rangle \) is fully described by the probability amplitudes (8) and (9). For the chosen here values of the parameters, it is easy to find the period \(T_0\) which is given by \(T_0=2 \pi /(3 |J-K|)\approx 105\). As we can see, even for \(J_0'=0.001\), the fidelity \(F(\rho , \sigma )\) decreases by \(\sim \)10% at time \(t=T_0\) (similarly the trace distance \(D(\rho , \sigma )\) increases by \(\sim \)10% at time \(t=T_0\)). When \(J_0'\) grows to 0.005 it results in decreasing (increasing) of the fidelity (trace distance) to about 50%. Such behavior is a result of the fact that the presence of even a weak interaction described by \(J_0'\) leads to the appearance of additional “magnetic” states of the subsystem LR (such as \([\mid 1, 0\rangle - \mid 0, 1\rangle ]_{\textit{LR}}\)). For such states the nonzero total spin (\(S^z_L+S^z_R \ne 0\)) is compensated by the particle at site A so that the conservation of total \(S^z\) is fulfilled. From the presence of rapidly decreasing fidelity (rapidly increasing trace distance), we can conclude that those states become so important that they cannot be neglected. Moreover, further growth of \(J_0'\) causes even faster (often irregular) oscillations of \( F(\rho ,\sigma )\) and \( D(\rho , \sigma )\). It suggests significant changes of the Rabi frequency for the state \(\rho \), so both states \(\rho \) and \(\sigma \) exhibit considerable different oscillations’ periods. Since the ratio between them is not a rational number, the irregular oscillations are observed. Therefore, we can say that even for a small values of the interaction parameter \(J_0'\), our system’s dynamics cannot be regarded as close to its bipartite counterpart.

Now, we want to show how important the “magnetic” states are, so we reverse the previous question and ask how far the state \(\rho (t)\) is from the state coming from the tripartite homogeneous system, \(\sigma '(t) = \big [\mathrm{Tr}_A |\varPsi (t) \rangle \langle \varPsi (t)| \big ]_{J=J',K=K'}\). As we see from Fig. 2, the fast irregular oscillations of \(F(\rho , \sigma ')\) and \(D(\rho , \sigma ')\) are also present there. However, with a suitable choice of \(J_0'\) (Fig. 2d) one can find such situations when \(F(\rho , \sigma ')=1\) and \(D(\rho , \sigma ')=0\) for any time t. So, both states are identical, \(\rho (t)=\sigma '(t)\). This outcome can be observed whenever the following condition is satisfied:

$$\begin{aligned} J-K= J'-K'. \end{aligned}$$
(19)

The above equality is a generalized condition of homogeneity (by contrast to the standard one, \(J=J'\) and \(K=K'\)). It shows that the closer both interactions J and K are, the weaker interactions \(J'\) and \(K'\) are necessary to make the tripartite system’s dynamics similar to that for the homogeneous system case. If one parameterizes all interactions as it was done before, Eq. (19) can be written in the form \(J_0(\cos \theta - \sin \theta ) = J'_0 (\cos \varphi - \sin \varphi )\). Now, it is easy to see that the left side of this equality tends to zero for \(\theta =\ldots , -\frac{3\pi }{4}, \frac{\pi }{4}, \ldots , \) so when angle \(\theta \) becomes close to the dimer phase borders.

It should also be emphasized that the generalized condition (19) determining homogeneity of the system is not unambiguous and it can be fulfilled for various sets of parameters, even if one of its sides is fixed. Moreover, it does not require a specific relationships between various types of interactions, such as \(K'/K\). Thus, the same results (with the precision up to the phase factor) can be obtained even for the extreme cases when one of the parameters was eliminated. It is enough if the remaining parameters still satisfy the above condition of homogeneity.

Fig. 2
figure 2

Results for the same sample set of parameters as in Fig. 1. As previously, black lines refer to the fidelity \(F(\rho , \sigma ')\), whereas the red lines denote trace distance \(D(\rho , \sigma ')\). As a reference point the tripartite homogeneous system (described by the reduced density matrix \(\sigma '\)) has been taken (Color figure online)

Full size image

Finally, it is important to mention that the above results are also true for other sets of parameters, also for \(q \ne 0\). Therefore, the procedure described in [22] cannot be successfully used even in the weak interaction \(J_0'/J_0\) limit. Moreover, one can reach the generalized condition of the homogeneity not only for initial states \(|\varPsi _0 (0) \rangle \) and \(|\varPsi _1 (0) \rangle \) but also for other states demonstrating the indistinguishability between sites L and R.

3.2 Preparation of the singlet state for the initial state \(|\varPsi _0 (0) \rangle \)

As it was shown in the previous subsection, for the model considered here even a small interaction can lead to the homogeneous tripartite system’s behavior. Therefore, both three-site dynamics and possibility of generating maximally entangled states in the framework of a homogeneous system seem to be worth discussing. Below we present a procedure to extract various types of bipartite maximally entangled states from the wave function describing our system, in particular the singlet state.

Due to the presence of symmetry between sites L and R, both sites become indistinguishable, and hence, the wave function (27) describing the tripartite system (for the initial state \(| \varPsi _0 (0) \rangle \)) can be written as follows:

$$\begin{aligned} \mid \varPsi (t) \rangle= & {} \alpha (t)~(\mid 0,-1 \rangle + \mid -1,0 \rangle )_{\textit{LR}}~\otimes \mid 1\rangle _A \nonumber \\&+\,\beta (t)(\mid 1,-1 \rangle +\vartheta (t) \mid 0,0 \rangle + \mid -1,1 \rangle )_{\textit{LR}}~\otimes \mid 0 \rangle _A \nonumber \\&+\,\gamma (t)~(\mid 1,0 \rangle + \mid 0,1 \rangle )_{\textit{LR}}~\otimes \mid -1 \rangle _A, \end{aligned}$$
(20)

where the parameters, \(\alpha (t)=a_{0,-1,1}(t)=a_{-1,0,1}(t)\), \(\gamma (t)=a_{0,1,-1}(t)=a_{1,0,-1}(t)\), \(\beta (t)=a_{1,-1,0}(t)=a_{-1,1,0}(t)\) and \(\vartheta (t)=\frac{a_{0,0,0}(t)}{\beta (t)}\), are functions of both time and the Zeeman shift q.

After some straightforward calculations (see “Appendix 1”) for the homogeneous system one can find that

$$\begin{aligned} \vartheta (t)=-\frac{J'-K' + 2 q - i \mathcal {D} \cot (\frac{1}{2} \mathcal {D} t)}{2 (J'-K')}, \end{aligned}$$
(21)

with \(\mathcal {D}=\sqrt{25 (J'-K')^2 + 4 (J'-K') q + 4 q^2}\). Moreover, all probability amplitudes are equal to each other \(\alpha (t)=\beta (t)=\gamma (t)\), where

$$\begin{aligned} \gamma (t)=\frac{-2 (J' - K') \sin \left( \frac{1}{2} \mathcal {D} t\right) \left( 1 - i \tan \left( \frac{J'+11 K'+ 2 q}{4} t\right) \right) }{\mathcal {D} \left( -i + \tan \left( \frac{J'+11 K'+ 2 q}{4} t\right) \right) }. \end{aligned}$$
(22)

The last equality of three probability amplitudes implies that Eq. (20) can be rewritten in the same form while taking the site L or R as a focus point instead of site A. This means that for such a case, the same reduced density matrices will be achieved regardless which site is traced out, \(\big [\mathrm{Tr}_A |\varPsi (t) \rangle \langle \varPsi (t)| = \mathrm{Tr}_L |\varPsi (t) \rangle \langle \varPsi (t)| = \mathrm{Tr}_R |\varPsi (t) \rangle \langle \varPsi (t)| \big ]_{J=J',K=K'}\), and hence, the two-site dynamics will be identical for all bipartite subsystems. Since the homogeneous system can be created even for a strong asymmetry of the internal interactions [Eq. (19)], we can see that for such situation the wave function conserves the translational symmetry despite the couplings asymmetry.

In order to create the singlet states, first we require that \(\vartheta (t) = -1\). This particular condition can be achieved if one puts \(q=q'\)

$$\begin{aligned} q'=\frac{J'-K'}{2}. \end{aligned}$$
(23)

Then, the above requirement is satisfied when the time

$$\begin{aligned} t'=\frac{\pi (1 + 2 k)}{2 \sqrt{7} |J'- K'|}. \end{aligned}$$
(24)

If we put \(q'\) and \(t'\) to Eqs. (20)–(22), we will find that the subsystem LR can be in one of the three maximally entangled states depending on the \(S^z_A\) state: triplet qubit states if \(S^z_A=\pm 1\) and singlet qutrit state for \(S^z_A=0\). In other words, by measuring the state of site A at time \(t'\), we can predict what type of the state is generated in the subsystem LR. Moreover, if we could set \(S^z_A=0\) and simultaneously switch off the external field in z direction (to “freeze” the eigenstate of the system), the stable hyperfine-singlet state will be achieved in deterministic way. Such procedure could be done in analogous way as that applied for the preparation of the initial state, i.e., by applying some ultrashort interaction with an external and local magnetic field. In consequence, \(S^z_A\) can be transformed such a way that it become equal to 0.

Applying expressions (15) and (23) to the generalized condition of homogeneity (19), one can find that \(q'=q^{*}/3\). In the same way the moments of time when the singlet state is produced can be written as \(t'=\sqrt{\frac{3}{7}}~t^{*}\). So, in comparison to the two-site system, for tripartite systems the weaker field and a shorter time are necessary for the creation of the singlet state. Moreover, based on those relations, we can see that it becomes possible to deduce the values of \(q'\) (hence, the required magnetic field denoted as \(B'\)), as well as the time \(t'\) which would be suitable in the potential experimental implementations of the tripartite homogeneous case, despite the lack of exact form for \(J'\) and \(K'\). It becomes sufficient to determine the appropriate values for \(q^{*}\) and \(t^{*}\). As an example let us consider \(^{23}\)Na atoms in their hyperfine-spin-1 state. By analogy to [22], we can replace \(J-K\) by the relevant energy levels \((E_2-E_0)/3\). Moreover, if we use the relation \(E_i=a_i \tilde{U}\), we immediately obtain that \(J-K = \tilde{U} (a_2-a_1)/3\). Given that for \(^{23}\)Na atoms \(a_2-a_1 = 3.5\,a_B\), where \(a_B\) is the Bohr radius and \(q_0=278\) Hz/G\(^2\), if one chooses \(\tilde{U} = 2 \pi \times 30\) Hz/\(a_B\) (see [34]), then the required magnetic field is \(B'=(\frac{J-K}{6 q_0})^{1/2} = 0.628\) G. The shortest possible time of creating the singlet state is equal \(t'=2.7\) ms.

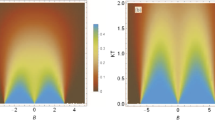
It should be noted that the procedure of the singlet state extraction can be also done for inhomogeneous systems. It is enough to obtain the state \(|0 \rangle \) for the ancilla when \(\vartheta (t) = -1\). For such situation the probability amplitudes of Eq. (20) for inhomogeneous case have been found numerically, and the values of q and t leading to the singlet state generation have been estimated for various coupling parameters. The results are presented in Fig. 3, where variable j refers to the dimensionless interaction distributions, i.e., \(j=J_0'\cdot \frac{(\cos \varphi - \sin \varphi )}{J-K}\), with fixed values of both angle \(\varphi \) and difference \(J-K\). In particular, \(j=0\) refers to the two-site system (when \(J_0'=0\)). Such situation is discussed in [22] and is denoted in Fig. 3 by \(q^*\) and \(t^*\). From other side, points corresponding to \(j=1\) and indicated by \(q'\) and \(t'\) refer to the three-site homogeneous system. For such a case, from Eq. (19) we have \(J_0'=\frac{J-K}{(\cos \varphi - \sin \varphi )}\). As we can see, a dimensionless Zeeman shift (\(q/|J-K|\)) and time (\(t\cdot |J-K|\)) as a function of j exhibit an universal angle-dependent behavior. Depending on whether \( \cos \varphi > \sin \varphi \), i.e., \(J'> K'\) or not (\( \cos \varphi < \sin \varphi \) what is equivalent to \(J'< K'\) ), both dimensionless quantities tend toward more round (flat) changes, regardless of the J and K values themselves. Moreover, all curves overlap at \(j=1\) as it can be concluded from Eq. (23).

Fig. 3
figure 3

Sets of solutions for q and t as a function of the interaction distributions \(j=J_0'\cdot \frac{(\cos \varphi - \sin \varphi )}{J-K}\). Lines and symbols correspond to various J and K giving \((J-K)\) equal to 0.02 and 0.0133(3), respectively. Squares (red line) refer to \(\varphi =-0.5 \pi \), circles (black line) to \(\varphi =-0.358 \pi \), diamonds (green line) to \(\varphi =-0.142 \pi \) and triangles (blue line) to \(\varphi =0\) (Color figure online)

Full size image

3.3 Other initial states

Additionally, one can consider the possibility of the singlet state generation for the cases when \(|\varPsi _1 (0) \rangle \) is assumed as the initial state. For such situation the system’s dynamics is confined within the Hilbert subspace corresponding to the total \(S^z=1\). Thus, the appropriate wave function can be written as:

$$\begin{aligned} \mid \varPsi (t) \rangle= & {} b_{1,0,0}(t)~(\mid 1,0 \rangle + \mid 0,1 \rangle )_{\textit{LR}}~\otimes \mid 0 \rangle _A \nonumber \\&+\,b_{1,-1,1}(t)(\mid 1,-1 \rangle + \chi (t) \mid 0,0 \rangle + \mid -1,1 \rangle )_{\textit{LR}}~\otimes \mid 1 \rangle _A \nonumber \\&+\,b_{1,1,-1}(t)~\mid 1,1\rangle )_{\textit{LR}}~\otimes \mid -1 \rangle _A, \end{aligned}$$
(25)

where \(\chi (t) = \frac{b_{0,0,1}(t)}{b_{1,-1,1}(t)}\). For the special case when \(q=0\), the analytical formulas corresponding to the probability amplitudes are given by Eqs. (33) and (34) (see “Appendix 2”). However, for more general cases, the numerical calculations should be performed.

Similarly to the scenario discussed before, in order to create a singlet state, we need to prepare the state (25) with \(\chi (t)=-1\). In Fig. 4 the possible solutions for q and t as functions of j meeting the above requirements are shown. As we can see, contrary to the previously discussed results (see Fig. 3), various curves do not converge each other for \(j = 1\), which is especially evident for \(t|J-K|\) (see Fig. 4, right). This means that for the homogeneous case the expected values of q and t are not just functions of \((J-K)\) (or equivalently \((J'-K')\)), but they depend on the accurate values of coupling constants. To proof this fact, let us consider the homogeneous system and rewrite the condition \(\chi (t) =-1\) in the equivalent form as:

$$\begin{aligned}&(\mathrm{e}^{i t \mathcal {Q}} (3 (J'- K') - 2 q + \mathcal {D})~\mathcal {Q} \nonumber \\&\qquad -\,\mathrm{e}^{i t (\mathcal {D} + \mathcal {Q})} (3 (J'- K') - 2 q - \mathcal {D})~\mathcal {Q} \nonumber \\&\qquad +\,2 \mathrm{e}^{\frac{3}{2} i t (J' + K')} \big ((\mathcal {Q} - q)~\mathcal {D}+ \mathrm{e}^{2 i t \mathcal {Q}} (\mathcal {Q}+q) \big )~\mathcal {D} \nonumber \\&\quad =-(J' - K') \bigg (\mathrm{e}^{\frac{3}{2} i t (J' + K')}(\mathrm{e}^{\frac{1}{2} i t \mathcal {D}} - \mathrm{e}^{\frac{1}{2} i t (\mathcal {D} + 4 \mathcal {Q})})~\mathcal {D} \nonumber \\&\qquad -\,4 (\mathrm{e}^{i t (\mathcal {D} + \mathcal {Q})} + \mathrm{e}^{i t \mathcal {Q}})~\mathcal {Q}\bigg ), \end{aligned}$$
(26)

where \(\mathcal {Q}=\sqrt{(J'-K')^2 + q^2}\) and \(\mathcal {D} = \sqrt{25 (J'-K')^2 + 4 (J'-K') q + 4 q^2}\). It can be shown that if one puts \(q = b~(J'-K')\) where \(b \in \mathbb {R}\), the above equality cannot be satisfied for any realistic value of t. For this reason, we obtain various results for q and t when various values of \(J'\) and \(K'\) are assumed (satisfying the condition \((J-K)=(J'-K')\)).

Fig. 4
figure 4

Same as in Fig. 3 but for the initial state \(|\varPsi _1 (0) \rangle \)

Full size image

4 Conclusions

We have studied the dynamics of the system composed of ultra-cold bosons with the hyperfine-spin \(S = 1\) confined in an optical superlattice. In particular, starting from the product state we have considered the disturbance of the two-site dynamics by coupling the dimer to an ancilla. This ancilla has also been chosen to be a hyperfine-spin \(S = 1\) particle. We have shown that such a coupling can significantly change the two-site dynamics even in the weak interaction \(J_0'/J_0\) regime. We have shown that the crucial role is played by the relationship \(J-K= J'-K'\), linking the inter-dimer interactions with the disturbance coupling. The fulfillment of this condition results in generating the wave function identical to that describing the homogeneous system in the three-site ring. In consequence, such wave function exhibits translational invariance despite the strong asymmetry of the lattice. Moreover, we have proposed a method of dynamical generation of the states which demonstrate various types of entanglement. We have shown that at specific moments of time during the system’s evolution (when magnetic field is properly chosen) various interesting, from the quantum information theory point of view, states can be produced. In particular, we have proposed a scheme of generating the total hyperfine-spin-singlet state that (as we believe) should be easy to implement in realistic experiment. Preparation of such maximally entangled states, especially the genuine tripartite entangled states and bipartite singlet states, seems to be especially meaningful. Moreover, we believe that proposals presented here can be useful not only in quantum information applications but also can serve as a promising tool that would let us create some exotic many-body states.