Duality quantum computer and the efficient quantum simulations

Abstract

Duality quantum computing is a new mode of a quantum computer to simulate a moving quantum computer passing through a multi-slit. It exploits the particle wave duality property for computing. A quantum computer with n qubits and a qudit simulates a moving quantum computer with n qubits passing through a d-slit. Duality quantum computing can realize an arbitrary sum of unitaries and therefore a general quantum operator, which is called a generalized quantum gate. All linear bounded operators can be realized by the generalized quantum gates, and unitary operators are just the extreme points of the set of generalized quantum gates. Duality quantum computing provides flexibility and a clear physical picture in designing quantum algorithms, and serves as a powerful bridge between quantum and classical algorithms. In this paper, after a brief review of the theory of duality quantum computing, we will concentrate on the applications of duality quantum computing in simulations of Hamiltonian systems. We will show that duality quantum computing can efficiently simulate quantum systems by providing descriptions of the recent efficient quantum simulation algorithm of Childs and Wiebe (Quantum Inf Comput 12(11–12):901–924, 2012) for the fast simulation of quantum systems with a sparse Hamiltonian, and the quantum simulation algorithm by Berry et al. (Phys Rev Lett 114:090502, 2015), which provides exponential improvement in precision for simulating systems with a sparse Hamiltonian.

Appendices

Appendix 1: An example of the Childs–Wiebe algorithm in duality quantum computing

Suppose we want to realize the quantum simulation with $k=1,\ell _q= q$, then

$$\begin{aligned} U(t)=M_{k,k}(t)=\sum _{q=1}^{k+1} C_q S_k(t/\ell _q)^{\ell _q}, \end{aligned}$$

(50)

where $\ell _q$ $(q\in \lbrace 1,k+1=2\rbrace )$ represent distinct natural numbers and $\sum _{q=1}^{k+1} C_q=1$, $(C_1,\ldots ,C_{k+1} \in R)$. When $k=1,\ell _q= q$,

$$\begin{aligned} U(t)=M_{1,1}(t)= \frac{4S_1(t/2)^{2}}{3}-\frac{S_1(t)}{3}+O(t^{5}), \end{aligned}$$

and

$$\begin{aligned} C_1= -\frac{1}{3},\quad C_2= \frac{4}{3}. \end{aligned}$$

For convenient, let $r=1$, put $-1$ into $S_1(t)$. The duality quantum gate in this case is

$$\begin{aligned} L=\dfrac{3}{{5}}\left( \frac{4}{3}U_{2}+\frac{1}{3}U_{1}\right) , \end{aligned}$$

where $U_{1}=-S_1(t)$, $U_{2}=S_1(t/2)^{2}$.

The QWD is simulated by the unitary operation V and the QWC is simulated by unitary operation W respectively,

$$\begin{aligned} V= & {} \sqrt{\dfrac{1}{{5}}}\left( \begin{array}{c@{\quad }ccc} 1 &{} -2 \\ 2 &{} 1 \\ \end{array} \right) , \end{aligned}$$

(51)

$$\begin{aligned} W= & {} \sqrt{\dfrac{1}{{5}}}\left( \begin{array}{c@{\quad }ccc} 1 &{} 2 \\ -2 &{} 1 \\ \end{array} \right) . \end{aligned}$$

(52)

The simulation procedure in the duality quantum computing formalism is illustrated in Fig. 4. Starting from the initial state is $|0\rangle |\varPsi \rangle$. First, the QWD operation V is performed on the auxiliary qubit, and this transforms the auxiliary qubit through the following transformation,

$$\begin{aligned} |0\rangle \longrightarrow \frac{1}{\sqrt{5}}|0\rangle +\frac{2}{\sqrt{5}}|1\rangle , \end{aligned}$$

Fig. 4

Quantum circuit of the Childs–Wiebe algorithm in duality quantum computing when $k=1,\ell _q= q$. $|\varPsi \rangle$ denotes the initial state of duality quantum computer, and auxiliary qubit is in the $|0\rangle$ state. The squares represent unitary operations and the circles represent the state of the controlling qubit. Unitary operations $U_{1}$, $U_{2}$ are activated only when the auxiliary qubit is $|0\rangle$ and $|1\rangle$, respectively

Then we perform the auxiliary qubits $|0\rangle$ controlled operation $U_{1}$ and $U_{2}$ on the computer. We have

$$\begin{aligned} |0\rangle |\varPsi \rangle \rightarrow \frac{1}{\sqrt{5}}|0\rangle U_{1}|\varPsi \rangle +\frac{2}{\sqrt{5}}|1\rangle U_{2} |\varPsi \rangle \end{aligned}$$

(53)

We perform the QWC operations W on the state $\frac{1}{\sqrt{5}}|0\rangle +\frac{2}{\sqrt{5}}|1\rangle$. We have the following

$$\begin{aligned} |0\rangle |\varPsi \rangle \rightarrow \frac{1}{5}|0\rangle U_{1}|\varPsi \rangle + \frac{4}{5}|0\rangle U_{2}|\varPsi \rangle + \frac{2}{5}|1\rangle (U_{2}- U_{1})|\varPsi \rangle \end{aligned}$$

(54)

The total process can be described as:

$$\begin{aligned} WV\otimes U(t)|0\rangle |\varPsi \rangle = \frac{3}{5}\left( \frac{1}{3} U_{1} + \frac{4}{3} U_{2}|0\rangle |\varPsi \rangle \right) + \frac{2}{5}|1\rangle (U_{2}- U_{1})|\varPsi \rangle \end{aligned}$$

(55)

So, the probability of the auxiliary state $|0\rangle$ being detected is $\Vert \frac{3}{5}|0\rangle (\frac{1}{3} U_{1} + \frac{4}{3} U_{2})|\varPsi \rangle \Vert ^{2}$, which is the successful probability of the algorithm. Considering the simple case that Hamiltonian has two terms, namely $m=2$.

$$\begin{aligned} H=\left( \begin{array}{c@{\quad }c} 1 &{} 1 \\ 1 &{} -1 \\ \end{array} \right) ,\quad H_{1}=\left( \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right) ,\quad H_{2}=\left( \begin{array}{c@{\quad }c} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} \right) . \end{aligned}$$

(56)

Then $S_1(t)=\mathrm{e}^{-iH_{1}t}\mathrm{e}^{-2iH_{2}t}\mathrm{e}^{-iH_{1}t}$ and $S_1(t/2)^{2}=\mathrm{e}^{-iH_{1}t/2}\mathrm{e}^{-iH_{2}t}\mathrm{e}^{-iH_{1}t}\mathrm{e}^{-iH_{2}t}\mathrm{e}^{-iH_{1}t/2}$. In this case, setting $t=1$, the probability of implementing U(t) on the target state $|\varPsi \rangle$ successfully is

$$\begin{aligned} \begin{aligned} 1-P_{f} \!&=\! 1- \frac{4}{25} \Vert \mathrm{e}^{-iH_{1}t/2}\mathrm{e}^{-iH_{2}t}\mathrm{e}^{-iH_{1}t}\mathrm{e}^{-iH_{2}t}\mathrm{e}^{-iH_{1}t/2} \!+\!\mathrm{e}^{-iH_{1}t}\mathrm{e}^{-2iH_{2}t}\mathrm{e}^{-iH_{1}t} |\varPsi \rangle \Vert ^{2} \\&\approx 0.5712, \end{aligned} \end{aligned}$$

(57)

where $P_{f}$ is the failure probability. If the algorithm fails, one can simply restart from the initial state and repeat the process again. The probability of success after 5 repetitions is $1-(P_{f})^5\approx 0.98$.

Appendix 2: An example of the BCCKS algorithm in duality quantum computing

Suppose $K=2$, $L= 2$, $H=(\alpha _{1}H_{1}+\alpha _{2}H_{2})$, then

$$\begin{aligned} U=1+ \frac{-it}{r}(\alpha _{1}H_{1}+\alpha _{2}H_{2})+\frac{(-it)^{2}}{2r^{2}}(\alpha _{1}H_{1}+\alpha _{2}H_{2})^{2}. \end{aligned}$$

For convenient, let $r=1$, put $-i$ into H , ignore the normalized constant. We only care about the first column in the matrice for the QWD operations, thus we have

$$\begin{aligned} V^{F}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} X &{}X &{} X\\ 0 &{} X &{} X &{} X\\ \sqrt{(\alpha _{1}+\alpha _{2})t} &{} X &{} X &{} X\\ \frac{(\alpha _{1}+\alpha _{2})t}{\sqrt{2}} &{} X &{} X&{} X\\ \end{array} \right) , \end{aligned}$$

(58)

$$\begin{aligned} V^{S}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \sqrt{\alpha _{1}} &{} -\sqrt{\alpha _{2}}\\ \sqrt{\alpha _{2}}&{} \sqrt{\alpha _{1}} \\ \end{array} \right) , \end{aligned}$$

(59)

where X can be an arbitrary element satisfying the condition that the matrix $V^{F}$ is unitary. After implementing the first unitary operations $V^{F}$ in the $|0\rangle ^{2}$ part of the initial state, we get $|00\rangle +\sqrt{(\alpha _{1}+\alpha _{2})t}|10\rangle +\frac{(\alpha _{1}+\alpha _{2})t}{\sqrt{2}}|11\rangle$. After implementing the second unitary operations $V^{S}$ on two $|0\rangle _{L}$ part of initial state, we get two same states $\sqrt{\alpha _{1}}|0\rangle +\sqrt{\alpha _{2}}|1\rangle$.

Fig. 5

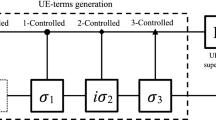
Quantum circuit of the BCCKS algorithm in duality quantum computing when $K = 2;L = 2$. In Part a of Fig. 5, $|\varPsi \rangle$ is the initial state of duality quantum computer and there are 2 numbers of $|0\rangle$ auxiliary controlling qubits and 2 numbers of 2 level $|0\rangle$ auxiliary controlling qudits. Unitary operations $U_{0}$ are activated only when the qubit and qudit holds the respective values indicated in circles. Part b of Fig. 5 is to illustrate that each unitary operation $U_{0}$ is composed of $H_{1}$ and $H_{2}$

We perform the 2 level auxiliary qudit $|0\rangle _{2}$ and 2 auxiliary qubits $|00\rangle$ controlled operations $U_{j}$ on the computer. We change the state into

$$\begin{aligned}&|00\rangle \left( \sqrt{\alpha _{1}}|0\rangle +\sqrt{\alpha _{2}}|1\rangle \right) ^{2}|\varPsi \rangle \nonumber \\&+\,\sqrt{(\alpha _{1}+\alpha _{2})t}|10\rangle \left( \sqrt{\alpha _{1}}|0\rangle +\sqrt{\alpha _{2}}|1\rangle \right) (\sqrt{\alpha _{1}}H_{1}|0\rangle +\sqrt{\alpha _{2}}H_{2}|1\rangle )|\varPsi \rangle \nonumber \\&+\,\frac{(\alpha _{1}+\alpha _{2})t}{\sqrt{2}}|11\rangle (\sqrt{\alpha _{1}}H_{1}|0\rangle +\sqrt{\alpha _{2}}H_{2}|1\rangle )^{2} |\varPsi \rangle . \end{aligned}$$

(60)

Setting $W^{F} =(V^{F} )^{\dagger }$, $W^{S}=( V^{S})^{\dagger }$ and performing the QWC operations $W^{F}$and $W^{S}$ on the state $|{1^k0^{K-k}}\rangle$ and $|\ell \rangle$, respectively. We focus our attention on the terms with the L level auxiliary qudit being in state $|0\rangle _{L}$ and K auxiliary qubits being in state $|0\rangle ^{K}$. We have the following

$$\begin{aligned} |00\rangle |0\rangle |0\rangle |\varPsi \rangle \rightarrow |00\rangle |0\rangle |0\rangle \left\{ 1+ t(\alpha _{1}H_{1}+\alpha _{2}H_{2})+\frac{t^{2}}{2}(\alpha _{1}H_{1}+\alpha _{2}H_{2})^{2}\right\} |\varPsi \rangle . \end{aligned}$$

(61)

Denoting the state orthogonal to $|00\rangle |0\rangle |0\rangle |\varPsi \rangle$ as $|\varPhi \rangle$, the total process can be described as:

$$\begin{aligned}&W^{S}V^{S}\otimes W^{S}V^{S}\otimes W^{F}V^{F}\otimes U|00\rangle |0\rangle |\varPsi \rangle =\sqrt{1-\dfrac{1}{s^{2}}}|\varPhi \rangle \nonumber \\&+\dfrac{1}{s} \left\{ |00\rangle |0\rangle |0\rangle (1+ t(\alpha _{1}H_{1}+\alpha _{2}H_{2})+\frac{t^{2}}{2}(\alpha _{1}H_{1}+\alpha _{2}H_{2})^{2})\right\} |\varPsi \rangle , \end{aligned}$$

(62)

where $s=1+t(\alpha _{1}+\alpha _{2})/r+t^{2}(\alpha _{1}+\alpha _{2}))^{2}/2r^{2}$. So, the probability of detecting the auxiliary state $|00\rangle |0\rangle |0\rangle$ is $P_{s}$, where $P_{s}=\parallel (1+ t(\alpha _{1}H_{1}+\alpha _{2}H_{2})+\frac{t^{2}}{2}(\alpha _{1}H_{1}+\alpha _{2}H_{2})^{2}) |\varPsi \rangle \parallel ^{2}/{s^{2}}$. Namely the probability of implementing U on the target state $|\varPsi \rangle$ successfully is $P_{s}$. If the order of Taylor series K is large enough and $(\alpha _{1}+\alpha _{2})t=\ln 2$, then $\sqrt{ P_{s}} \approx 1/s\approx 1/2, \arcsin \beta =\arcsin (1/s)\approx \pi /6$. The error is bounded in the tolerant range. By using the obvious amplitude amplification procedure once, we have $\sin 3\beta \approx 1$. Now, the probability of detecting the auxiliary state $|00\rangle |0\rangle |0\rangle$ is almost $100 \%$. Namely, we have deterministically implemented U on the target state $|\varPsi \rangle$.