Abstract
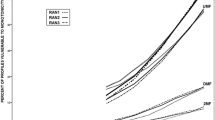
It has long been recognized that Instant Runoff Voting (IRV) suffers from a defect known as nonmonotonicity, wherein increasing support for a candidate among a subset of voters may adversely affect that candidate’s election outcome. The expected frequency of this type of behavior, however, remains an open and important question, and limited access to detailed election data makes it difficult to resolve empirically. In this paper, we develop a spatial model of voting behavior to approach the question theoretically. We conclude that monotonicity failures in three-candidate IRV elections may be much more prevalent than widely presumed (results suggest a lower bound estimate of 15 % for competitive elections). In light of these results, those seeking to implement a fairer multi-candidate election system should be wary of adopting IRV.





Similar content being viewed by others
Notes
Our analysis here closely parallels work by Lepelley et al. (1996) and Miller (2012), but differs in its construction of condition (1). In our analysis of the spatial model (Sect. 4), we ignore cases where two candidates tie for fewest first-place votes, so we include a stronger version of condition (1) than in these previous papers.
For convenience, we define c=c 1+c 2.
The qualitative results presented in this paper are robust to alternate specifications of utility, including city block distance and squared Euclidean distance.
In the polarized case, we ensure that there is at least one candidate in each “camp”, and two in the larger camp.
References
Allard, C. (1996). Estimating the probability of monotonicity failure in a U.K. general election. Voting Matters, 5, 1–7.
De Marchi, S. (1999). Adaptive models and electoral instability. Journal of Theoretical Politics, 11(3), 393–419.
Downs, A. (1957). An economic theory of democracy. New York: Harper.
Fishburn, P., & Brams, S. (1983). Paradoxes of preferential voting. Mathematics Magazine, 56(4), 207–214.
Fraenkel, J., & Grofman, B. (2004). A neo-Downsian model of the alternative vote as a mechanism for mitigating ethnic conflict in plural societies. Public Choice, 121, 487–506.
Horowitz, D. L. (2004). The alternative vote and interethnic moderation: a reply to Fraenkel and Grofman. Public Choice, 121, 507–516.
Kenny, L. W., & Lotfinia, B. (2005). Evidence on the importance of spatial voting models in presidential nominations and elections. Public Choice, 123(3–4), 439–462.
Kollman, K., Miller, J., & Page, S. (1992). Adaptive parties in spatial elections. American Political Science Review, 86, 929–937.
Laatu, J., & Smith, W. (2009). The rank order votes in the 2009 Burlington mayoral election. http://rangevoting.org/JLburl09.txt.
Laver, M. (2005). Policy and the dynamics of political competition. American Political Science Review, 99(2), 263–281.
Lepelley, D., Chantreuil, F., & Berg, S. (1996). The likelihood of monotonicity paradoxes in run-off elections. Mathematical Social Sciences, 31, 133–146.
McKelvey, R. (1986). Covering, dominance, and institution-free properties of social choice. American Journal of Political Science, 30(2), 283–314.
Miller, N. R. (2012). Monotonicity failure in IRV elections with three candidates. In World meeting of the public choice societies, 2012.
Merrill, S. (1988). Making multicandidate elections more democratic. Princeton: Princeton University Press.
Norman, R. Z. (2006). Some properties of STV in close and polarized elections. In 2006 meeting of the society for social choice and welfare.
Norman, R. Z. (2012). Frequency and severity of some STV paradoxes. In World meeting of the public choice societies, 2012.
Smith, J. H. (1973). Aggregation of preferences with variable electorate. Econometrica, 41, 1027–1041.
Acknowledgements
The authors thank Ross A. Hammond and the anonymous reviewers for insightful comments and suggestions. Any errors remain the responsibility of the authors.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ornstein, J.T., Norman, R.Z. Frequency of monotonicity failure under Instant Runoff Voting: estimates based on a spatial model of elections. Public Choice 161, 1–9 (2014). https://doi.org/10.1007/s11127-013-0118-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11127-013-0118-2