Does knowledge spill over across borders and technology regimes?

Abstract

This paper investigates whether technology spills over across national borders and technology regimes. We advocate a modeling strategy where improvements in technical efficiency capture technology spillovers as industries absorb and implement the best-practice technology. Dynamic panel-based techniques are used to determine whether efficiency series move together in the long run (cointegrate) and/or move closer together over time (converge). We control for technological heterogeneity and for cross-sectional dependence in the data. For a panel of manufacturing industries in six EU countries, we find evidence of technology spillovers and convergence among industries’ efficiency levels across countries and mainly across adjacent technology regimes.

1 Introduction

Technology is a major driving force of economic growth (Romer 1990; Rivera-Batiz and Romer 1991; Grossman and Helpman 1991). The non-rival characteristics of technology imply investments in technology do not only benefit the investors but also contribute to the knowledge base that is publicly available to them. These externalities are called technology spillovers (Romer 1990). Through technology spillovers, countries that operate below the production frontier can increase output by learning from the best practice. Countries benefit from technology flows if they have the ‘appropriate’ technology (Abramovitz 1986; Basu and Weil 1998) and sufficient ‘absorptive capacity’ (Abramovitz 1986; Cohen and Levinthal 1989).

A large literature has examined the significance of purely domestic spillovers (see Mohnen 1996, for a survey), or domestic spillovers in conjunction with foreign spillovers (Coe and Helpman 1995).¹ Technology transmission, both domestic and foreign, has been found to play a significant role in promoting productivity and economic growth.

The purpose of this paper is to investigate whether technology flows across industries in the EU manufacturing sector. In particular, we would like to investigate whether industries located in homogenous and presumably integrated countries benefit from technology spillovers from industries in other countries or from technology spillovers from different technology regimes. We focus on industries in the manufacturing sector rather than countries in order to account for aggregation bias due to heterogeneity in existing technologies (Bernard and Jones 1996a, b).

The present paper contributes to the existing literature in three distinct ways. A first contribution of this paper is that we measure technology spillovers in a simple and rather ‘pure’ manner. We propose a flexible modeling approach in exploring technology spillovers by estimating a stochastic production frontier. The latter is the empirical analog of the theoretical production possibility frontier and enables us to measure the maximum frontier output. One important advantage of focusing on maximum (frontier) output, rather than observable output, is that deviations from maximum output reflect sluggish absorption and implementation of the best practice (frontier) technology, whereas improvements in efficiency represent productivity catch-up via technology diffusion. In contrast the vast majority of the productivity literature focuses on total factor productivity (TFP), which, as a residual, measures ‘anything and everything’ of output growth that is not accounted by input growth. The translog index TFP growth measure ignores the concept of technical inefficiency (by unrealistically assuming that all industries are technically efficient) and inaccurately interprets technical change as TFP growth.² While the frontier effect indicates how far the efficient frontier itself has shifted over time due to the use of better technology and equipment, the catching up effect reflects how far the industry has moved towards the efficient frontier due to the better use of technology and equipment.

Industries in the manufacturing sector, however, are characterized by different technologies. Recent theoretical and empirical contributions (Basu and Weil 1998; Acemoglu and Zilibotti 2001; Bos et al. 2010b, a) have stressed the ‘appropriateness’ of technology as countries (industries) choose the best technology available to them, given their input mix. Industries are members of the same technology regime (club) if their input/output combinations can be described by the same production technology (Jones 2005). Not accounting for different technologies and estimating a single stochastic frontier function can result in biased estimates of the ‘true’ underlying technology. Furthermore, omitted technological differences may be erroneously labeled as inefficiency (Orea and Kumbhakar 2004). Allowing for different production frontiers to account for heterogeneity in technologies in the manufacturing sector has been largely ignored by the studies that have performed frontier analyses for studying technology spillovers and catch-up (see, for instance, Semenick Alam and Sickles 2000; Kneller and Stevens 2006). To the best of our knowledge, only a handful of studies allow for heterogenous technologies and growth experiences (Koop 2001; Bos et al. 2010a).

Our second contribution, therefore, lies in the way we account for differences in technologies. We estimate separate production frontiers for each of the four technology regimes (high tech, medium-high tech, medium-low tech and low tech) in the manufacturing sector as defined by the OECD (2005) technology classification.³ As a result, we obtain efficiency levels for industries in each of the technology regimes that reflect the distance to their appropriate technology.

While a large strand in the literature explores technology spillovers across industries (countries), only a few studies pay attention to the time series properties of these spillovers (see Coe et al. 2009, for a survey). A number of studies derive their spillover estimates from (OLS) regressions, which, with non-stationary data, result in super-consistent (Stock 1987) but imprecise coefficient estimates with standard errors ill-suited for statistical inference (Kao and Chiang 2000). Ignoring integration and cointegration properties of the data it is not clear whether one estimates a structural long-run relationship or a spurious one.⁴ In this paper, we rely on cointegration and convergence to determine whether efficiency levels move together in the long-term (cointegrate), or, in fact, move closer together over time (converge). For instance, increased integration and competition in the EU can lead to more efficient use of resources among industries. Thus efficiency levels may track one another over time as industries attempt to follow each other’s efficiency advances in order to remain competitive. Therefore, accepting the cointegration null for a set of industries would indicate a long-run relationship in the technology transfer within the cointegrated set and potential convergence; in contrast, lack of cointegration of an industry’s efficiency score with those of its counterparts may reflect the industry’s inability to absorb the existing technology.

To the best of our knowledge, there have been only two studies that are close to our modeling (frontier) approach and investigate the time series properties of technical efficiency in the context of technology spillovers and convergence. Cornwell and Wächer (1999) examine whether a long-term relationship exists between country-level technical efficiencies in a sample of 26 OECD countries and whether these efficiencies converge. Semenick Alam and Sickles (2000) present a firm-level study on the role of market structure and the developments in efficiency for the US airline industry. Their results support fairly strong evidence of cointegration and convergence among EU countries (Cornwell and Wächer 1999) and existence of a long-run relationship of efficiency levels and, over time, convergence among US carriers (Semenick Alam and Sickles 2000).

Notwithstanding, both aforementioned studies as well as studies that investigate R&D trade-related technology spillovers using cointegration analysis (Frantzen 2000, 2002) rely on cointegration techniques that do not allow for potential cross-sectional dependence. Cross-sectional dependence, which only very recently has gained some attention in the literature, appears to be, however, the case in many macroeconomic applications (e.g. convergence hypothesis tests) where time series are contemporaneously correlated due to (spatial) spillover effects, common unobserved shocks, or a combination of these factors (Pesaran 2004). If there is cross-sectional dependence, the traditional assumption of orthogonality of the individual series’ error terms is violated, and cointegration test statistics are biased. Furthermore, none of the aforementioned related studies proceeds with estimating long-run cointegrating relationships, discussing the nature of potential long-term linkages. Therefore, the third contribution of this paper lies in the use of recently developed dynamic panel-based cointegration techniques to determine whether efficiency series have moved together in the long-run (cointegrate) and to estimate these long-run linkages using appropriate estimators, which take into consideration cross-sectional dependencies.

We apply the proposed methodology to a sample of 21 manufacturing industries for six European countries, over the period 1980–1997. Each industry is allocated to one of the four technology regimes, as classified by the OECD (2005): high, medium-high, medium-low and low technology. Taking annual averages for each technology regime in each country, we explore the properties of a total of 24 (4 × 6) series, with three sets of questions in mind: (1) are there technology spillovers across countries? (2) are there technology spillovers across technology regimes? and lastly (3) is there any evidence of convergence?

Overall, our results reveal that there is fairly strong evidence that industries’ efficiency levels have moved together in the long-run (cointegrate) mainly across technology regimes and across borders. It appears that competitive forces in the EU have led, to a certain extent, to more efficient use of resources among industries as their efficiency levels have tracked one another over time in an attempt to follow each other’s efficiency advances in order to remain competitive. The estimation of the long-run relationships between efficiency levels indicates that technological proximity is of the upmost importance. Finally, industries’ efficiency levels have also moved closer together over time (converge) both in cross-country and cross-regime analysis. However, the extent to which convergence takes place across countries and across technology regimes differs significantly.

The remainder of the paper proceeds as follows. Section 2 considers a model of production that allows for technical inefficiency and presents the econometric methodology and specifications for estimation. Section 2.4 introduces the data. Empirical results are presented in Sect. 3. Section 4 summarizes the findings and concludes.

2 Methodology and data

In this section, we first discuss the concept of technical efficiency and introduce a model of production that enables us to allow for inefficiency. Next, we discuss recent developments in panel-based integration and cointegration analysis to examine whether there is a long-run structural relationship among the efficiency series across countries or across technology regimes. Lastly, we describe the convergence tests we shall use to examine whether there is convergence across across countries or technology regimes.

2.1 Technical efficiency in a stochastic Frontier model of production

An industry is technically efficient if an increase in its output requires an increase in at least one input. A technically inefficient industry can produce the same output with less of at least one input. Alternatively, it can use the same inputs to produce more of at least one output (Koopmans 1951).⁵

Fig. 1

Technical efficiency

We demonstrate the concepts of technical efficiency and production frontiers with a simple one output, one input example in Fig. 1. In the graph, we consider three cases. An industry operating under the frontier of Regime 1 in (a) cannot increase output without increasing its input, whereas an industry operating under the frontier of Regime 1 in (b) can try to absorb the (superior) production skills of (a) and increase its technical efficiency. Similarly, an industry operating under the frontier of Regime 2 in (d) can increase its efficiency by absorbing the production skills of an industry operating under the frontier of Regime 2 in (c). The latter industry, however, can not increase its output without either increasing its input, or through positive technical change, i.e. an outward shift of the regime’s frontier over time.

To measure efficiency, we estimate the following translog stochastic frontier production specification:⁶

$$\begin{aligned} \ln Y_{ijt}&= \beta _{ij}+\beta _{1}\ln K_{ijt}+\beta _{2}\ln L_{ijt}+\tfrac{1}{2}\beta _{3}\ln K_{ijt}^{2} +\tfrac{1}{2}\beta _{4}\ln L_{ijt}^{2}+\beta _{5}\ln K_{ijt}\ln L_{ijt}\nonumber \\&+\quad \gamma _{t}D_{t} + \delta _{kt}\ln K_{ijt}D_{t}+\delta _{lt}\ln L_{ijt}D_{t}+\nu _{ijt}-u_{ijt} \end{aligned}$$

(1)

where $Y_{ijt}$ is the level of output in country i, in industry j, at time $t; u_{ijt}\ge 0$ is normally distribution, truncated at $\mu , |N(\mu , \sigma _u^{2})|$, and independent from the noise term, $\nu _{ijt}; \beta _{ij}$ are country-industry specific fixed effects.

An industry is inefficient ($TE = \exp \{-u_{ijt}\}<1$) if it fails to absorb the best-practice technology. In this respect, our approach is comparable to non-frontier studies (Bernard and Jones 1996a, b; Scarpetta and Tressel 2002; Griffith et al. 2004; Cameron et al. 2005) that measure impediments to this absorptive capacity using total factor productivity (TFP) changes. However, in their framework the latter can be seen as a combination of technical change (frontier shift) and efficiency change (catching up effect).

As Baltagi and Griffin (1988) have shown, Solow’s general index of technical change relies on three restrictive assumptions: “constant returns to scale, neutral technical change, and perfect competition in both output and factor input markets” (p. 23).⁷ We follow Baltagi and Griffin (1988) and include a set of time dummies $D_t$, which—interacted with K and L—allow us to measure a more general Tornqvist index of technical change as proposed by Diewert (1976).

Manufacturing industries can be grouped into four technology regimes: high, medium-high, medium-low and low regime. The division of the industries into technology regimes is based on the OECD (2005) classification.⁸ Accordingly, we estimate four production frontier functions, based on the specification defined in Eq. (1), one for each regime. Industries in each one of the four technology regimes are benchmarked against each group’s production frontier and technical efficiencies are calculated. In our second stage analysis, we rely on cointegration and convergence tests to determine whether these efficiency levels have moved together in the long-term (cointegrate), or, in fact, move closer together over time (converge).

For our first stage frontier estimation, we want to impose as little additional constraints as possible on the distribution and behavior (over time) of efficiency. Therefore, we follow Greene (2005) and estimate a ‘true’ fixed effects model, in which the fixed effects are allowed to be correlated with the other parameters, but they are truly independent of the error term and inefficiency. To see why this is important, consider the case in which an industry is inefficient, but its inefficiency is constant over time. In that case, if we estimate a fixed effect model in which our fixed effects behave like standard dummy variables, this industry’s fixed effect will absorb the inefficiency, and the industry will appear to be efficient. A second problem, in light of our analysis, that is solved by Greene’s model is fact that in previous fixed effects panel formulations, inefficiency was assumed to be time invariant.⁹

Nevertheless, given that we shall use the efficiency scores generated by the true fixed effects model in a second stage cointegration analysis, we have to face a second set of problems. Simar and Wilson (2007) list a total of four issues we need to consider.¹⁰ First, they emphasize that since the sample used for estimating the efficient frontier does not include all possible efficient production possibilities, the estimated efficiency scores are upwardly biased (see for example Barros and Dieke 2008). Since we are interested in the dynamics of efficiency scores, rather than their level, and estimate a stochastic frontier model—as opposed to the deterministic models (Simar and Wilson 2007) refer to—we do not think this issue carries a lot of weight in light of our analysis. The same holds for the second problem Simar and Wilson (2007) address: the fact that a second-stage analysis typically includes additional covariates, that may be correlated with the covariates used in the first stage. The only covariates we shall use in our second stage are efficiency scores generated by other frontier estimations, and in so doing we include appropriate (country- and/or technology-specific) fixed effects in our second stage. Third, Simar and Wilson (2007) emphasize that a second stage estimation should take into account the fact that the efficiency scores generated in the first stage are restricted to a [0,1] interval. Therefore, after estimating our stochastic frontier model outlined in Eq. (1), we shall use the untransformed scores $u_{i,t} \sim |N(\mu , \sigma _u^{2})|$, rather than the transformed $\exp \{-u_{ijt}\}$, which are indeed defined on the interval [0,1]. In doing so, we conveniently benefit from the fact that we bootstrap in this second stage, and can therefore accommodate the non-normality of the untransformed scores with some confidence.

The final problem discussed by Simar and Wilson (2007), is the most important in light of our second stage cointegration analysis: as emphasized in their paper, since the true efficiency scores are not directly observed in the first stage, the usual assumption of independently distributed error terms is (likely to be) violated. To address this problem, we make use of recent developments in panel cointegration tests, allowing for cross-sectional dependence (Bai and Ng 2004; Palm et al. 2008). This is also the main reason why we opt for a two-stage approach, rather than follow Battese and Coelli (1995), and impose a common linear trend on $\nu _{ijt}$. Not only could we then not test for the significance of the time trend in a pannel setting in the same manner we do now, but more importantly we risk biasing our results further by not allowing for cross-sectional dependence. Given that without the latter, it is hard to argue that there can be spillovers at all, we pursue our two stage procedure here.

We next turn to our approach regarding the panel unit root and panel cointegration analysis.

2.2 Panel unit root and cointegration analysis

The main goal of the paper is to identify and explain the long-run dynamics between efficiency levels of different technology regimes of the EU manufacturing industries in our sample. Increased trade and competition in the EU could lead to more efficient use of the resources among industries. In that case, efficiency levels should track one another over time as industries within each regime attempt to follow each other’s efficiency advances in order to remain competitive; otherwise lack of efficiency co-movement could indicate inability to capitalize on technology other industries are employing.

To examine the long-run properties of technology spillovers, captured by the efficiency series, we employ cointegration techniques.¹¹ Cointegration examines the existence of stationary relationships between non-stationary variables and indicates that variables possess a long run common feature. A series possesses a unit root, i.e. it has a stochastic trend or is non-stationary if its statistical properties depend on time, and it is said to be integrated of order d, I(d) if its d-difference does not posses a stochastic trend. If two or more series are themselves non-stationary, but a linear combination of them is stationary, then the series are said to be cointegrated. Cointegrated variables share similar stochastic patterns in the long-run and cannot move too far away from another. In contrast, lack of cointegration suggests that there is no long-term link between each other.

Panel-based cointegration techniques are particularly well-suited for the study of technology spillovers for a number of reasons. First, the focus is on the long-run relationships, which would be obscured if the equations are estimated in first differences instead of in levels of the variables. Second, the increased power of the tests comes from exploiting commonalities across industries (countries), given the limited time span.¹² Third, parameter estimates are super-consistent and therefore robust to omitted variables, simultaneity and endogeneity problems. Thus, one can avoid the difficult task of finding valid instruments for some variables that would be necessary in the case of estimating a short-run relationship (Coe et al. 2009).

The implementation of the cointegration procedure entails first confirmation that the data are indeed non-stationary. Combining time-series information with cross-sectional information, panel unit root tests can be more precise and powerful by reducing the error-in-rejection probability (size distortion), especially when the time-series is not very long. Consider the following AR(1) process for panel data:

$$y_{it}=\rho _{i}y_{it-1}+\varepsilon _{it}$$

(2)

where y represents the dependent variable, x is a vector of independent variables, $\rho$ is a coefficient and $\varepsilon$ is the disturbance term.

Depending on assumptions regarding the homogeneity (heterogeneity) of correlations in the data, several tests have been developed to identify unit roots in panel data The seminal study of Levin et al. (2002) (LLC hereafter) considers a homogenous autoregressive root under the alternative hypothesis.¹³ More specifically, the tests proposed by LLC assume that there is a common unit-root process between cross-sections so that $\rho _{i}=\rho$ for all i. Im et al. (1997, (2003) relax the homogeneity assumption and propose panel unit root tests that permit heterogeneity of the autoregressive root under the alternative so that $\rho _{i}$ may vary freely between cross-sections. They present two group-mean panel unit root tests designed against the heterogenous alternatives. The two tests are executed with a t-test based on ADF regressions (IPS hereafter) and a Lagrange multiplier (LM) test. Nevertheless, these tests, labeled as “first generation” tests, do not take into account the cross-sectional dependence. To overcome this shortcoming, a “second generation” of panel unit root tests have been proposed.¹⁴ Among them, the tests developed by Palm et al. (2008) and Bai and Ng (2004) are particularly designed for finite samples. Palm et al. (2008) propose a bootstrap version of the LLC and IPS tests while Bai and Ng (2004) suggest a modified version of the panel unit root test of Maddala and Wu (1999) but on the idiosyncratic component, i.e. once common component has been removed. We examine the stationarity of our efficiency series based on these two tests.

Having established the presence of a unit root in all series of interest, the next step consists of testing for cointegration among efficiency levels. Like panel unit root tests, panel cointegration tests have been motivated by the search for more powerful tests than those obtained by applying individual time series cointegration tests, which have lower power, especially when the time dimension is rather small.

Most panel cointegration tests are built from the residuals previously obtained by the panel regression model:

$$y_{it}=x'_{it}\beta +\varepsilon _{it}$$

(3)

where $y_{it}$ and $x_{it}$ are I(1). Several tests have been proposed, such as Dickey-Fuller (DF) and Augmented Dickey Fuller (ADF)-type unit root tests for $\varepsilon _{it}$ as a test for the null of cointegration (or no cointegration).

The statistical properties of such tests are derived under the assumption of cross-sectional independence, which greatly simplifies the derivation of limiting distributions of the panel test statistics. Cross-sectional independence is not however a tenable assumption when countries (industries) are hit by the same shocks such as oil price shocks, technological revolutions, exchange rate shocks, monetary shocks and so forth.¹⁵ For our six EU countries it is very difficult to assume that technology developments are entirely independent. Violation of the independence assumption leads to test statistics that are biased favoring the existence of cointegration and to coefficient estimates that are not super consistent.

For this purpose, a number of (‘second generation’) tests have been proposed (Phillips and Sul 2003; Groen and Kleinbergen 2003) to allow for cross-sectional dependence. We test for the null hypothesis of no cointegration following a methodology proposed in the recent work of Fachin (2007). This study introduces block-bootstrapped versions of the well known panel cointegration test of Pedroni (1999). Fachin proposes two bootstrapped tests (FDB1, FDB2) that both rely on the fast distribution bootstrapping procedures suggested by Davidson and MacKinnon (2000).¹⁶ Both procedures incorporate the standard assumptions for efficient maximum likelihood estimators, but generate statistics that have limit properties that are less affected by sample size than standard bootstrapping procedures. FDB1 differs from FDB2 in that the former has, in theory, slightly better limit properties, whereas the latter is somewhat less computationally demanding. As Davidson and MacKinnon (2000, p. 7) point out, “it is almost costless to compute FDB2 if FDB1 is already being computed, it may be useful to do so as a check on the accuracy of the latter.” In the original paper, Fachin (2007) shows the validity of the bootstrapped versions of the cointegration tests via Monte-Carlo simulations, but recently Palm et al. (2008) have demonstrated theoretically that the bootstrap approach behaves adequately in such a framework. The bootstrapped versions of the group-t and median-t statistics for the null hypothesis of no cointegration are robust to cross-sectional dependence and small sample bias.¹⁷

Lastly, one can proceed with estimating the long-run cointegrated relationship. Chen et al. (1999) have proven that the ordinary-least-squares (OLS) estimator is biased in a cointegrated panel framework and thus may lead to spurious regression. Fully-Modified OLS (FMOLS) addresses potential endogeneity of the regressors and serial correlation in order to obtain asymptotically unbiased estimates of the long run parameters. More specifically, FMOLS is a non-parametric approach that controls for possible correlation between the error term and the first differences of the regressors and removes nuisance parameters (Dreger and Reimers 2005; Pedroni 2001).¹⁸ Nevertheless, Bai et al. (2009) (BKN hereafter) prove that in presence of cross-sectional dependence generated by unobserved global stochastic trends traditional FMOLS estimator is biased.¹⁹ They thus propose an iterative procedure to extract the common factor and to estimate the model simultaneously. These common factors, whatever they may be, allow us to have an estimation robust to cross-sectional dependence, which is not the case when implementing DOLS or FMOLS methods.

More formally, whereas FMOLS considers the following, general model:

$$y_{it}=\alpha _{i}+\beta _{i}x_{it}+u_{it}$$

(4)

where $x_{it}=x_{it-1}+\varepsilon _{it}$, and $\omega _{it}=(u_{it},\varepsilon _{it})'$.

BKN model the cross-section dependence by imposing a factor structure on $u_{it}$. Therefore, the general version of their model becomes:

$$y_{it}=\alpha _{i}+\beta _{i}x_{it}+\lambda _{i}F_{it}+e_{it}$$

(5)

where $F_{it}$ is a qx1 vector of latent common factors, $e_{it}$ is a qx1 vector of factor loadings.²⁰

We employ the BKN estimator for dynamic heterogenous panels to estimate long-run equations for cross-border and cross-regime spillovers. As normalization is performed with respect on a certain country, we estimate the following equation:²¹

$$TE_{crt}=\alpha _{r}+\sum ^{5}_{\mathop {i \ne c}\limits ^{i=1}}TE^{'}_{irt}\beta _{i} + \varepsilon _{irt},$$

(6)

where i is the country subscript ($i=1,\ldots ,5$), c is the country on which the equation is normalized, t is the time subscript ($t=,1\ldots ,18$), r is the regime subscript ($r=H, MH, ML, L$), and regime-specific fixed effects $\alpha _{r}$ are included.

Equation (6) is estimated normalizing on each of the six countries, respectively. Similarly, for cross-regime spillovers normalizing on the low technology regime, we estimate the following equation:

$$TE_{igt}=\alpha _{i}+\sum ^{3}_{\mathop {r \ne g}\limits ^{r=1}}TE^{'}_{irt}\beta _{r} + \varepsilon _{irt},$$

(7)

where g is the technology regime on which the equation is normalized, i is the country subscript ($i=1,\ldots ,6$), country-specific fixed effects $\alpha _{i}$ are included and other subscripts are the same as for Eq. (6). Equation (7) is also estimated normalizing on each of the technology regimes, respectively.

2.3 Convergence

The presence of cointegration indicates a long-run relationship between the efficiency series. However, this does not necessarily imply convergence of efficiency levels. Tests of convergence in the economic growth literature (Baumol 1986) determine whether there is a closing of the gap between inefficient and efficient industries over time.

To investigate the convergence hypothesis, we run simple regressions of time-averaged efficiency growth rates on the initial level of efficiency:

$$\Delta TE_{ij}=\beta _0+\beta _1 TE_{ij, 1980} + \varepsilon _{ij}$$

(8)

where $\Delta TE_{ij}$ denotes the average growth rate of the efficiency level of industry j in country i between 1980 and 1997, $TE_{ij,1980}$ is the initial level of efficiency in year 1980 and $\varepsilon _{ij}$ an error term.

We test for convergence across technology regimes, by estimating equation (8) for all industries in a country, controlling for technology regime-specific fixed effects. Convergence across technology regimes in all countries is tested in the same manner, but with country-technology regime-specific fixed effects. We also test for convergence within technology regimes, by estimating equation (8) for all industries in a technology regime. Again, we perform this test both for each country and for all countries jointly, and include country-specific fixed effects in the latter case.

In the tradition of Baumol (1986) and Barro (1991, (1997), a negative and statistically significant coefficient on the initial level of efficiency can be interpreted as indication of convergence of efficiency levels. The higher the initial level of efficiency is, the slower that level should grow. This phenomenon is the result of the public nature of technology that spills over from leaders to followers, as the latter group learns from the former and tries to catch-up.

2.4 Data

Our aim is to include as many industries as possible, since we are primarily interested in comparing industries that—potentially—produce using different technologies. Our analysis covers 21 two-, three- and four-digit industries in manufacturing for six countries (Finland, France, Germany, Italy, Netherlands and Spain) over the period 1980–1997, where the time span is determined by the data availability for the highest level of disaggregation.

The current selection of EU countries is the largest number of countries in the Euro area—the area which is characterized by common economic policies, high competition and volume of trade—for which the data are available for a wide selection of industries and for a large time span. For instance, gross fixed capital formation (for constructing physical capital) data on the industry level are largely missing for a number of industries for Greece, Luxembourg, Portugal and Belgium.²² Overall, choosing to investigate more countries would significantly decrease the number of industries in our sample, as well as result in a higher aggregation of industries.²³ Our fairly homogenous sample reduces the possibility of additional unobserved factors driving our result of economically and statistically significantly different technology regimes and potential technology spillovers.

We start our data collection at the two-digit level, using the International System of Industries Classification Code (ISIC, revision 3) classification. If data on output, capital stock and labor are available at a higher disaggregation level (three- or four-digit), we disaggregate further. Clearly, we avoid double counting by only including the latter at the highest disaggregation level. The manufacturing industries considered in our analysis and their ISIC codes are presented in the “Appendix” Table 6.

Annual raw data are retrieved from various sources. Data on industry output (value added) and investment (for constructing capital stocks) are retrieved from the OECD (2002) Structural Analysis Database (STAN). Data on labor (annual total hours worked) are extracted from the Groningen Growth and Development Centre (GGDC) (2006) 60-Industry Database.²⁴ The same ISIC code is used for all data sources. Definitions of the variables are provided in the “Appendix”.

3 Results

3.1 Frontier results

We estimate equation (1) for each technology regime. Table 1 contains the most important frontier results.²⁵ Both $\sigma$ (the composite standard deviation) and $\lambda$ (the ratio of the standard deviation of efficiency over the standard deviation of the noise term) are highly significant for all technology regimes. For high-tech industries, $\lambda$ is 1.954, and significant at the 1 % level, indicating that the variance in inefficiency is about twice the size of noise in this technology regime. Much the same holds for medium-high, medium-low and low-tech industries, where $\lambda$ is 1.947, 2.251 and 2.891, respectively, and also always significant at the 1 % level.

Table 1 Frontier results

For industries in each technology regime, we also calculated the marginal rate of technical substitution (MRTS), as the negative of the ratio of the marginal product of labor capital. The MRTS measures the rate at which labor can be substituted for capital, keeping output constant. As expected, the MRTS gradually increases as we move from the high technology regime to the low technology regime and thereby increase capital intensity.

Fig. 2

Technical efficiency distribution for all technology regimes

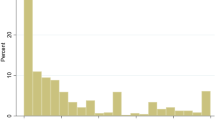
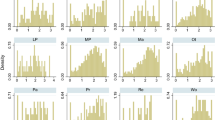
Compared to their own frontier, industries in the low technology regime are on average the most efficient (78.4 %). The least efficient, on average, are industries in the high technology regime (48.4 %). The spread of efficiency, however, is the highest for this regime. Figure 2 shows the efficiency distributions for each technology regime. Compared to their own frontier, industries in the medium-high and low technology regime are on average the most efficient. Also, the spread of efficiency levels is relatively low in these regimes. Medium-low technology industries are, compared to their own frontier, on average less efficient. But the spread of efficiency levels in this regime is much higher than the spread in the medium-high technology regime.

Fig. 3

Technical efficiency distribution in high-tech over time

Apparently, both the mean level and the spread of efficiency are affected by the diversity of industries in a technology regime. The latter, is particular apparent for industries in the high technology regime, which includes for example the aerospace (AER) and the medical industry (MED), and for industries in the medium-low technology regime, which includes for example the shipbuilding industry (SHI) and the other non-metallic mineral products industry (ONM). As a result, the high and medium-low regimes may have the most potential for convergence (an issue to which we return in Sect. 3.3). Some evidence of the latter can already be gathered by simply considering the development of efficiency within each regime over time. As an example, consider Fig. 3, which shows that over time average efficiency increased and its standard deviation decreased for industries in the high-tech regime.

Table 2 contains average efficiency levels as well as average growth rates of efficiency over the sample period for each industry in each technology regime in each country. On the whole, Table 2 reveals few straightforward patterns. The fast growing industries in the medium-high, medium-low and low technology regimes are located in the Netherlands (Motor vehicles (MOT), petroleum products (COK) and food products (FOD), respectively). Overall, the industries in the high technology regime are the fastest growers.

Table 2 Mean technical efficiency and growth of technical efficiency

3.2 Panel unit root and panel cointegration results

In this subsection, we examine the co-movement of technical efficiency levels across countries and across regimes, respectively. We take annual averages of each technology regime in each country and study the properties of the resulting 24 series following a two-step procedure. The first step consists of examining whether each of the series (country- or regime-specific) are non-stationary by testing for unit roots. Evidence of panel unit roots (i.e., technical efficiency levels ‘move’) allows us to proceed to the second step, and test whether the series are cointegrated (i.e., whether the technical efficiency levels in different groups ‘co-move’). As a further investigation, we examine the long-run linkages between the cointegrated series. To avoid biasing our results, we apply tests and estimators that account for cross-sectional dependence across the series.

3.2.1 Are there spillovers across national borders?

The first question we ask is whether there are any spillovers across countries. This is a question that a large strand of literature have concerned about. To answer such a question within our framework, we first need to test for panel unit roots in the efficiency series. Table 7a reports results from the Palm et al. (2008) test statistics and Table 8a from the Bai and Ng (2004) tests (see the “Appendix”). Overall, the panel-unit root tests provide strong support of unit root evidence, as the null hypothesis cannot be rejected at a 5 % nominal size. In the presence of contradictory findings, for instance, for the case of Germany in Table 8a, we retain the results from the Palm et al. (2008) tests, as these tests explicitly consider the finite dimension of our panel whereas the Bai and Ng (2004) tests assume asymptotic distribution. We can therefore conclude that the efficiency series in each country are non-stationary and all of them must be included in the cointegration analysis, which is our next step.

In Table 3a, we report two cointegration tests (FDB1 and FDB2), which are based on fast distribution bootstrap methods proposed by Fachin (2007) and control for cross-sectional dependence. Both test statistics reject the null hypothesis of no cointegration at 10 % and the hypothesis of one cointegrating vector is accepted. Support of cointegration of efficiency scores across borders implies that increased integration and competition in the EU have led to more efficient use of resources among industries in the countries of our sample. Thus efficiency levels have tracked one another over time as industries have attempted to follow each other’s efficiency advances in order to remain competitive. Therefore, there is a long-run relationship in the technology transfer within the cointegrated set of the efficiency levels in the countries under investigation—a finding consistent with past related literature (Cornwell and Wächer 1999)—and potential convergence; in contrast, lack of cointegration could reflect a country’s (industry’s) inability to absorb the existing technology and potentially inability to converge with the rest of the set.

As a further exploration, we would like to investigate whether we can infer anything about the nature of long-run linkages among efficiency levels across countries. These linkages can be positive or negative, depending on the mechanisms at work. For instance, competition can force industries to increase their competitive capacity by reforming management styles and updating production technology, therefore enhancing the adoption of existing advanced technology. But it can also hamper the absorption of technology in case industries draw inputs from limited resource spaces and produce output to satisfy demand that typically is not completely inelastic. In the latter case, an industry may absorb technology at the expense of another industry (Aitken et al. 1997; Aitken and Harrison 1999; Girma 2005). As a result, either market-stealing (on the output side) or skill-stealing (on the input side) results in a negative long-run linkage among efficiency developments. Geographical proximity and intensity of trade also have a dual effect on spillovers (Audretsch and Feldman 2004). Industries in countries that trade more than others and/or share a common border, ceteris paribus, could experience stronger positive or negative long-run linkages in their technology absorption, either via higher technology flows, or via skill-stealing, assuming that labor is sufficiently mobile.

Table 3 Panel cointegration and estimation across countries

To assess the long-term linkages among efficiency levels in these countries, we use the BKN estimator for dynamic heterogeneous panels to estimate the long-run equations (6) for cross-border spillovers. However, we have to be careful in interpreting the results as they depend on normalization. Table 3b reports the estimation results based on all different normalizations (i.e., every row of the table shows results based on the normalization of a certain country).²⁶

As Table 3b shows, we find evidence of negative long-run linkages among most of countries, most notably between neighboring countries such as France and Germany $(-0.371, -0.831)$ and France and Italy $(-1.232, -0.099)$, and Germany and Italy $(-0.997, -0.068)$. These negative linkages are not driven by technology spillovers, but rather by various forces such as market-stealing or skill-stealing that this study cannot precisely identify. For a small number of countries, for example France and the Netherlands (0.045, 0.147) and the Netherlands and Spain (0.381, 0.066), we find positive long-run linkages. The latter, however, are hardly ever significant.

Lastly, for a number of pairs of countries we observe opposite signs for the long-run linkages. For example, whereas the coefficient for Italy in the panel estimation for Spain is 0.449, the coefficient for Spain in the panel estimation for Italy is −0.807. However, since most of the other results with opposite signs are not statistically significant and may depend on the normalization, we refrain from giving further economic meaning to these results.

To highlight the economic significance of these results, consider the following example: ceteris paribus, how much is the average change in output for industries in France that results from the sample period change in technical efficiency in, say, Finland? From Table 3b, we observe that for France, $\beta _{FI}$ is −0.869. Using the period average efficiency scores for France and for Finland, we can calculate the elasticity, the effect of a percentage change in the average efficiency in Finland on the average efficiency in France, which is −0.85. Given that Finnish industries on average increase their efficiency by 41.76 % over the sample period, French industries are expected to decrease their average efficiency by −35.65 % ($-0.85\times 41.76$), purely as a result of the negative spillovers from Finland. From the average value added level in 1980, we can calculate the average reduction in 1980 value added that would result from these negative spillovers, as the percentage drop in efficiency multiplied by the valued added in 1980. The result turns out to be a reduction in value added of 2469.08 million euros, or 23.28 % of the average 1980 output of French industries.

Although we find efficiency co-movements across countries in our sample, a justified concern is that aggregate (country-level) analysis of technology spillovers may mask important variations in efficiency patterns due to different technologies (or technological regimes) across industries (Scarpetta and Tressel 2002). A more appropriate way to investigate whether there are technology spillovers across the EU is to examine whether the efficiency scores of technologically neighboring or very far apart regimes are cointegrated (co-move) or not. Our next section proceeds with such an investigation.

3.2.2 Are there spillovers across technology regimes?

The second question we ask is, therefore, whether technology spills over across technology regimes. First, we test for panel unit roots in the efficiency series. Panel unit root tests for technical efficiency levels for each technology regime in our sample are reported in Tables 7b and 8b in the “Appendix”. As the tests indicate, we find strong support for unit roots for all regimes. As before, in the presence of contradictory findings, for instance, for the case of medium-high technology regime in Table 8, we retain the results from the Palm et al. (2008) tests, as these tests explicitly consider the finite dimension of our panel whereas the Bai and Ng (2004) tests assume asymptotic distribution. Therefore, in each technology regime the efficiency series in the six countries are non-stationary.

Hence, we include all regimes in the panel cointegration tests reported in Table 4a. Both test statistics, FDB1 and FDB2, are slightly above 10 % indicating that test statistics is close to the nominal size. We thus take the decision to consider that the null hypothesis is rejected and thus to conclude in favor of the hypothesis of one cointegrating relationship.

So far, we have established that there is co-movement of the efficiency of industries with different technologies in the EU manufacturing sector. In order to investigate the type of long-run linkages implied between the different technology regimes, we proceed by estimating long-run cointegrating equation (7), using the same set of estimators described previously for our country analysis. Table 4b reports the BKN estimator for dynamic heterogeous panels to estimate the long-run equations for cross-regime spillovers.²⁷

Table 4 Panel cointegration and estimation across regimes

From Table 4b we can infer that technology spills over to neighboring technology regimes. We observe significant positive long-run linkages between industries in the medium-low and low (0.418, 0.142) as well as between medium-high and medium-low regimes (0.415, 0.082). In these types of regimes, technology tends to be rather stable which appears to have facilitated technology spillovers. In contrast, the evidence on the long-run relationship between the last pair of adjacent technology regimes, high and medium-high, is mixed (0.391, -0.212).²⁸

Mixed long-run linkages are also found for other regime combinations. For instance, there is a negative association between less technologically advanced regimes, namely the medium-high, medium-low and low regime and the most advanced regime, the high technology regime. A similar finding is also reported between the low and medium-high regimes. Since the estimator in these cases behaves differently, depending on the normalization, we are reluctant to provide further economic meaning to these results. We can only say that advanced technology industries tend to specialize in specific products/market niches, which reduces the scope for technological spillovers.²⁹ The dominance of one (or few) technologies gives scope for some positive spillovers from more advanced to less advanced technology regimes but not the other way around. Perhaps, in the long-run, there is some skill-stealing from the advanced technology regimes as skillful workforce in the less advanced technology regimes migrate to technology advanced regimes, in case of skill compatibility.

Positive linkages between adjacent technology regimes and weak (or even negative) linkages between technologically-distant regimes suggest that it is indeed easiest to appropriate technology that is closely related to your own (Scarpetta and Tressel 2002; Garcia Pascual and Westermann 2002). In his overview paper on R&D spillovers, Griliches (1992) introduces a simple model where spillovers are decreasing in technological distance. He subsequently describes a number of studies that report the same evidence. Maurseth and Verspagen (2002), in their patent citation analysis for European regions also find that patent citations are industry specific and occur more often when the technological linkages between industries are stronger. Moretti (2004) studies human capital spillovers, and uses input-output flows, technological specialization, and patent citations to measure technological and economic distance. He finds that spillovers are decreasing in all three alternative measures.

Overall, we conclude that the greater the technology distance, the smaller the spillover effects are, and the learning effect takes places from more advanced to less advanced technology regimes. A possible channel for the latter is the forward and backward linkages between industries.³⁰

We can illustrate the economic significance of these results in the same manner as for the cross-border spillovers. For technology regime spillovers, consider the following question: ceteris paribus, how much is the average change in output for industries in the medium-high technology regime that results from the period change in technical efficiency in the high technology regime? From Table 4b, we observe that for medium-high technology industries, $\beta _{H}$ is −0.212. Using the period average efficiency scores, we can calculate the elasticity, which is −0.13. As high technology industries on average have increased their efficiency by 28.83 % over the sample period, medium-high technology industries are expected to increase their average efficiency by $-3.80\,\% (-0.13\times 28.83)$ as a result of the positive spillovers from the high-technology industries. From the average value added level in 1980, we can again calculate the average reduction in 1980 value added that would result from these negative spillovers, which turns out to be 287.45 million euros, or 2.91 % of the average 1980 output of medium-high technology industries.

3.3 Convergence results

We now turn to the analysis of convergence. We start by examining whether there is convergence in the manufacturing sector as a whole within each country and across all countries of our sample. We then go one step further, and test the convergence hypothesis within each technology regime.

3.3.1 Is there convergence across national borders?

We start by estimating equation (8) for the manufacturing sector in each country and across countries. Table 5a reports the convergence coefficient, $\beta _1$, for each country and all countries. The results also provide evidence of convergence within each of the countries. However, the evidence appears to be the strongest for Finland and Germany. The Netherlands and Spain follow at a modest distance, and convergence is the lowest in France and Spain.

It is interesting to relate these findings with the past literature. Our results run counter to the lack of (or very little) evidence of convergence documented in the literature for the manufacturing sector (Hansson and Henrekson 1997; Bernard and Jones 1996a, b). This is mainly due to the fact that the majority of the past studies test for convergence in total factor productivity (TFP) as a proxy of the technology level. TFP is measured as a growth accounting (Solow-) residual under rather limiting assumptions about the existing technology (represented by a Cobb-Douglas production function and Hicks neutral technology change) and the behavior of economic units (optimizing behavior with no room for inefficiency).

Table 5 Convergence across and within technology regimes in the manufacturing sector

To benefit from spillovers, industries have to incur (costly) input changes. In contrast, we are line with Arcelus and Arocena (2000), who also perform a frontier analysis and focus on efficiency to measure technology spillovers. Efficiency changes do not require input changes and therefore they can be considered a more ‘pure’ measure of technology adoption. Indeed, Arcelus and Arocena (2000) find a high degree of catching-up among 14 OECD countries over 1970–1990 in the manufacturing sector.

3.3.2 Is there convergence across technology regimes?

Although convergence in the manufacturing comes out particularly strong in each and every country and across countries in our sample, a justified concern is that aggregate (manufacturing sector) analysis of technology spillovers and productivity can mask important variations in convergence patterns due to different technology across industries (Garcia Pascual and Westermann 2002; Scarpetta and Tressel 2002; Boussemart et al. 2006).

This concern, that heterogeneity in existing technologies might be an issue in efficiency performance and in studying the convergence hypothesis in the manufacturing, has been validated in previous sections of our paper. In Sect. 3.1, we described the mean and growth of efficiency in four technology regimes (groups) across countries in our sample. From Fig. 2, we observed that the average efficiency was relatively low for industries in high and medium-low technology regimes. In addition, the spread of efficiency was relatively high for these technology regimes. Table 2 then showed that almost all industries in all technology regimes and countries exhibited positive growth of efficiency. In sum, our frontier results suggest that there is ample room for (differences in) convergence, in particular among industries located in high and medium-low technology regimes.

Our next step, therefore, involves investigation of convergence across industries with a similar technology. Table 5b contains the results from estimating equation (8), per technology regime and across countries. Negative and significant values for $\beta _1$ indicate that there is convergence in all technology regimes. Indeed, the high technology regime experiences the strongest convergence. In the medium-low technology regime, convergence is also strong, as in the low technology regime, while the medium-high technology regime, on average, experiences the lowest level of convergence.

In the lower technology regimes (low and medium-low), the fact that the existing technology tends to be rather stable appears to have facilitated technology spillovers and convergence. This finding is in line with the literature (Scarpetta and Tressel 2002). In contrast, our finding of strong convergence in the high technology regime appears at first to be surprising, since patent laws, product and market differentiation can reduce the scope for technology spillovers. Our results suggest the presence of some dominant technologies in the high technology regime industries could be responsible for the evidence of convergence. Perhaps, persisting institutional differences, in particular related to product and labor market regulations, affect technology adaptation, particularly for the most technologically advanced and innovative industries.³¹

Overall, our findings yield (1) strong evidence of convergence across countries is documented when technical efficiency is used to study the convergence hypothesis in the manufacturing sector; and (2) even stronger evidence of convergence across technology regimes, when we disaggregate the manufacturing sector into different sub-sectors and control for differences in technology. However, the strength of the convergence varies, depending on the regime.

4 Conclusion

It has been long recognized that international technology transfer is an important source of growth and that the progress of nations may be determined in part by its extent. This paper investigates whether technology spills over across national borders and technology regimes. We advocate a modeling strategy where changes in technical efficiency capture technology spillovers as industries absorb and implement the best-practice (frontier) technology. By estimating a frontier model of production we are able to measure the technical efficiency with which industries employ their production technology.

We contribute to the literature by controlling for technological heterogeneity and for cross-sectional dependence in the data. More specifically, we take into account the appropriateness of the technology that industries use and benchmark each industry against other industries within the same technology regime. Hence, in our analysis, a (positive) technology spillover (i.e., an increase in efficiency) is indeed an improvement in the use of the existing technology, rather than a change in the latter. Also, we control for the fact that countries and technology regimes are not necessarily cross-sectionally independent and use recently developed dynamic panel-based techniques to determine whether efficiency series move together in the long run (cointegrate) and/or move closer together over time (converge).

We use a panel of 21 manufacturing industries in four technology regimes and six EU countries over the period 1980–1997, and—after taking country- and regime-specific annual averages—study the properties of the resulting 24 technical efficiency series. We, first, ask whether technology spills over across borders, and find that technical efficiency series are cointegrated with each other across all countries. A further analysis of the long-run linkages reveals that cross-country technology spillovers are predominantly negative, indicating possible market- and/or skill-stealing. Next, we ask whether technology spills over across regimes, and find that technical efficiency series are cointegrated with each other across all technology regimes. Among technology regimes, long-run linkages are predominantly positive, emphasizing therefore the importance of technological rather than geographical proximity for technology spillovers.

We also find fairly strong evidence of convergence, both across countries and technology regimes. Over time, the technical efficiency series of industries in the manufacturing sector have moved closer together. However, the extent to which this has happened differs. In the northern countries (Finland, Germany), convergence is the strongest. In particular, industries in the high technology regime emerge as the drivers behind the convergence of efficiency.

Appendix

1.1 Variables and sources

Value-Added (Y): gross value-added expressed in 1995 constant prices (euros). Gross value-added was deflated by implicit value-added deflators to yield deflated gross value-added expressed in 1995 constant prices (euros). We follow the OECD (2002) practice for the construction of the implicit value-added deflators. Data on gross value-added are retrieved from the OECD (2002) STAN Structural Analysis Database.

Physical capital (K): gross capital stock expressed in 1995 constant prices (euros). Following common practice in the literature (e.g. Hall and Jones, 1999), we employ the perpetual inventory method to construct a proxy for capital stock, using data on gross fixed capital formation (GFCF). The initial value for the 1980 capital stock is specified as $K_{1980} = GFCF_{1980}/(g + \delta )$, where g is the average geometric growth rate of the gross fixed capital formation (constant prices) series from 1970 to 1980 and $\delta$ is the depreciation rate. Instead of assuming a constant depreciation rate, we use the average service life (ASL) of capital per industry (OECD 1993). Each industry’s capital stock is constructed as capital stock minus depreciated capital stock plus gross fixed capital formation ($K_t = (1 - \delta )\times K_{t - 1} + GFCF_t$). Data on gross fixed capital formation are retrieved from the OECD (2002) STAN Structural Analysis Database.

Labor (L): annual total hours worked in an industry (in thousands). Data are retrieved from the Groningen Growth and Development Centre (GGDC 2006) 60-Industry Database (Table 6).

Table 6 Manufacturing industries

1.2 Panel unit root tests

See Tables 7 and 8.

Table 7 Palm et al. (2008) bootstrap tests

Table 8 Bai and Ng (2004) two common factors test